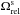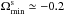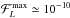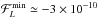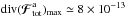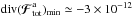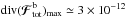| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 18 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201731088 | |
| Published online | 05 January 2018 | |
The secular evolution of discrete quasi-Keplerian systems
II. Application to a multi-mass axisymmetric disc around a supermassive black hole
1 Institute for Advanced Study, Einstein Drive, Princeton, NJ 08540, USA
e-mail: fouvry@ias.edu
2 Institut d’Astrophysique de Paris and UPMC, CNRS (UMR 7095), 98bis boulevard Arago, 75014 Paris, France
3 Korea Institute for Advanced Study (KIAS), 85 Hoegiro, 02455 Seoul Dongdaemun-gu, Republic of Korea
4 Laboratoire de Physique Théorique (IRSAMC), CNRS and UPS, Univ. de Toulouse, 31062 Toulouse, France
Received: 2 May 2017
Accepted: 13 September 2017
A discrete self-gravitating quasi-Keplerian razor-thin axisymmetric stellar disc orbiting a massive black hole sees its orbital structure diffuse on secular timescales as a result of a self-induced resonant relaxation. In the absence of collective effects, such a process is described by the recently derived inhomogeneous multi-mass degenerate Landau equation. Relying on Gauss’ method, we computed the associated drift and diffusion coefficients to characterise the properties of the resonant relaxation of razor-thin discs. For a disc-like configuration in our Galactic centre, we showed how this secular diffusion induces an adiabatic distortion of orbits and estimate the typical timescale of resonant relaxation. When considering a disc composed of multiple masses similarly distributed, we have illustrated how the population of lighter stars will gain eccentricity, driving it closer to the central black hole, provided the distribution function increases with angular momentum. The kinetic equation recovers as well the quenching of the resonant diffusion of a test star in the vicinity of the black hole (the “Schwarzschild barrier”) as a result of the divergence of the relativistic precessions. The dual stochastic Langevin formulation yields consistent results and offers a versatile framework in which to incorporate other stochastic processes.
Key words: galaxies: kinematics and dynamics / galaxies: nuclei / diffusion / gravitation
© ESO, 2017
1. Introduction
The dynamical evolution of stellar clusters in the vicinity of galactic centres’ supermassive black holes (SMBH) has triggered some interest over the last couple of decades (Morris & Serabyn 1996; Gillessen et al. 2009), amplified by the recent direct detection of gravitational waves through the coalescence of intermediate mass black holes (Abbott et al. 2016). Understanding the dynamics of stars in the vicinity of our galaxy’s SMBH is now one of the prime goal of the new generation of interferometers such as Gravity (Jocou et al. 2014). Within the next decade, the community will also build the LISA observatory1 to detect gravitational waves from systems of black holes with masses ranging from a few to 108M⊙ (Amaro-Seoane et al. 2012).
SMBHs absorb stars and debris whose orbits reach its loss-cone (Frank & Rees 1976; Shapiro & Lightman 1976), where they are either taken directly into the black hole or close enough to interact strongly with it (see a review of the loss-cone theory in Merritt 2013b). The continuous loss of stars reshapes the central stellar distribution (Genzel et al. 2000), also affecting the secular evolution of the SMBH’s mass and spin (e.g. Volonteri et al. 2016). This dynamical process triggers different observational signatures depending on the mass of the stars, such as binary capture and hyper-velocity star ejection (Hills 1988), tidal heating and disruption of stars (Syer & Ulmer 1999; Magorrian & Tremaine 1999; Alexander & Morris 2003), and gravitational waves generation by inspiraling compact remnants (Hils & Bender 1995). These signatures provide indirect evidence of the existence of the central black hole and can be used to test the theory of gravity in the strong field regime (Merritt et al. 2009). It is therefore timely to model the wide range of masses involved in nuclear clusters – from brown dwarfs up to intermediate black holes – to understand their long-term dynamics near SMBHs, which should eventually allow us to predict for example the rate of extreme mass ratio inspirals (EMRI; see review in Sigurdsson 2003).
The dynamics of stars in galactic nuclei comprise numerous processes (see reviews in Alexander 2005, 2017; Merritt 2013a). To a first approximation, because of the domination of the central SMBH’s potential, stars follow elliptical orbits that maintain their orientation for many orbital periods. The cluster may then be thought as a collection of massive wires, where the mass of each star is smeared along its quasi-Keplerian orbit. This is Gauss’ method for secular dynamics (Touma et al. 2009). The coherence of stars’ orbits over many dynamical times leads then to an efficient diffusion of the wires’ angular momentum, via a process called (scalar) resonant relaxation (Rauch & Tremaine 1996; Hopman & Alexander 2006a; Merritt 2015). In addition, stars also undergo a diffusion of their orbits’ orientation via vector resonant relaxation (Kocsis & Tremaine 2011, 2015), and a diffusion of their semi-major axes via two-body (non-resonant) encounters (Chandrasekhar 1944; Binney & Tremaine 2008). These last two effects will not be considered in the present work.
Recently, Fouvry et al. (2017b, hereafter Paper I) presented the kinetic equation that describes self-consistently the secular resonant relaxation of a large set of particles of various masses orbiting a SMBH (or a protoplanetary debris disc surrounding a star). This set of so-called Balescu-Lenard and Landau kinetic equations was obtained by simply averaging the BBGKY equations over the fast angle that describes motion along the Keplerian ellipses2. It describes self-consistently the long-term evolution of the distribution of multi mass quasi-Keplerian orbits around the central object. It models the diffusion and drift of their actions, induced through their mutual resonant interaction. Hence, this set is the master equation that describes the secular effects of resonant relaxation (Rauch & Tremaine 1996), and should now be implemented to predict the joint dynamical evolution of the central SMBH and its nuclear cluster.
Following Paper I, the aim of this paper is now to implement this kinetic equation for the Galactic centre’s inner stellar cluster. Specifically, it will quantify the adiabatic distortion of its orbits, the stalled diffusion of test stars near the so-called Schwarzschild barrier (Merritt et al. 2011), the induced mass segregation in eccentricity and the corresponding quantitative kinematic signatures. As such, it will also provide a first complete implementation of the inhomogeneous multi-mass Landau formalism in an astrophysical context.
The paper is organised as follows. Section 2 presents quasi-Keplerian discs and introduces the degenerate inhomogeneous Landau kinetic equation describing self-consistently these discs’ resonant relaxation. Section 3 applies this self-consistent diffusion formalism to the self-induced resonant relaxation of a discrete razor-thin quasi-Keplerian disc. Section 4 investigates the stochastic resonant diffusion of individual test stars, in particular the quenching of the diffusion in the neighbourhood of the central BH, the Schwarzschild barrier. Section 5 wraps up. Appendix A details the method used to compute the interaction potential between two Keplerian wires.
2. Secular evolution of quasi-Keplerian discs
This paper focusses on the long-term dynamics of a razor-thin axisymmetric disc of stars surrounding a central SMBH. Section 2.1 briefly recalls the appropriate angle-action coordinates that may be used to describe the motion of particles in such a system. Section 2.2 presents the disc model that will be considered throughout the paper, while Sect. 2.3 introduces the degenerate Landau equation. This equation describes self-consistently the long-term evolution of razor-thin discrete quasi-Keplerian discs induced by finite-N effects (in the limit where collective effects are not accounted for).
2.1. The disc’s geometry
Let us assume that the system takes the form of a razor-thin axisymmetric disc, so that the dimension of configuration space is d = 2. Following the conventions from Paper I, let us introduce the angle-action coordinates 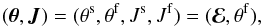 (1)where ℰ = (J,θs) corresponds to the coordinates of a given Keplerian wire, that are all conserved along the Keplerian motion induced by the central BH. Here, the angles and actions are respectively given by
(1)where ℰ = (J,θs) corresponds to the coordinates of a given Keplerian wire, that are all conserved along the Keplerian motion induced by the central BH. Here, the angles and actions are respectively given by 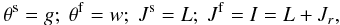 (2)where θs = g, being the slow angle, is conserved along the motion and corresponds to the argument of the periapse, while θf = w stands for the mean anomaly and is the fast angle that describes the phase of the particle along its Keplerian motion. Finally, Eq. (2)also introduced L and Jr as the angular momentum and radial action of a given orbit (Binney & Tremaine 2008). Here, I = L + Jr is the fast action associated with the orbit, which is adiabatically conserved during the resonant relaxation. For prograde orbits, the mapping (θ,J) → x is given by (Sridhar & Touma 1999; Binney & Tremaine 2008)
(2)where θs = g, being the slow angle, is conserved along the motion and corresponds to the argument of the periapse, while θf = w stands for the mean anomaly and is the fast angle that describes the phase of the particle along its Keplerian motion. Finally, Eq. (2)also introduced L and Jr as the angular momentum and radial action of a given orbit (Binney & Tremaine 2008). Here, I = L + Jr is the fast action associated with the orbit, which is adiabatically conserved during the resonant relaxation. For prograde orbits, the mapping (θ,J) → x is given by (Sridhar & Touma 1999; Binney & Tremaine 2008) 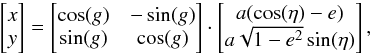 (3)where the semi-major axis a, the eccentricity e, and the eccentric anomaly η are given by
(3)where the semi-major axis a, the eccentricity e, and the eccentric anomaly η are given by 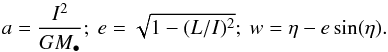 (4)The mapping from Eq. (3)also allows us to obtain the mapping to the polar coordinates (θ,J) → (R,φ) as
(4)The mapping from Eq. (3)also allows us to obtain the mapping to the polar coordinates (θ,J) → (R,φ) as ![\begin{equation} R = a (1 - e \cos (\eta)) \; ; \; \phi = g + \text{Arg} \big[ \cos (\eta) - e \,; \sqrt{1 - e^{2}} \sin (\eta) \big] . \label{mapping_R_phi} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq20.png) (5)
(5)
2.2. The disc model
Let us now specify the disc model that will be considered throughout the paper. This disc is chosen to somewhat mimic some of the features of the “clockwise disc” of the Galactic centre, considered in Kocsis & Tremaine (2011). In order to consider dimensionless quantities, the mass, length and time units are such that 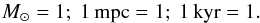 (6)Within these units, the central BH and the surrounding razor-thin disc are characterised by
(6)Within these units, the central BH and the surrounding razor-thin disc are characterised by 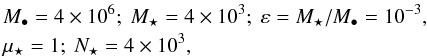 (7)where M• is the mass of the central BH, M⋆ the total mass of the disc composed of N⋆ stars of individual mass μ⋆.
(7)where M• is the mass of the central BH, M⋆ the total mass of the disc composed of N⋆ stars of individual mass μ⋆.
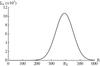 |
Fig. 1 Illustration of the disc’s surface density Σ⋆(R), as given by Eq. (11). Following the units from Eq. (6), the disc extends between 0.2 pc and 0.6 pc. |
Because the BH dominates the dynamics, one has ε = M⋆/M• ≪ 1. For simplicity, let us assume that the star’s DF takes the form of a quasi-isothermal DF (Binney & Tremaine 2008), reading ![\begin{equation} \Fs (L ,I) = \frac{1}{M_{\star}} \frac{\Omega_{\rm Kep} (L) \Sigma_{\star} (L)}{\pi \kappa_{\rm Kep} (L) \sigma_{r}^{2} (L)} \, \exp \bigg[- \frac{\kappa_{\rm Kep} (L)}{\sigma_{r}^{2} (L)} (I - L) \bigg] , \label{DF_disc} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq31.png) (8)which satisfies the normalisation condition
(8)which satisfies the normalisation condition 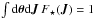 . Equation (8)introduced the azimuthal and radial orbital frequencies ΩKep and κKep (Binney & Tremaine 2008), which in the Keplerian case depend only on I and read
. Equation (8)introduced the azimuthal and radial orbital frequencies ΩKep and κKep (Binney & Tremaine 2008), which in the Keplerian case depend only on I and read 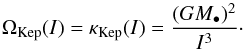 (9)In Eq. (8), the Keplerian orbital frequencies have to be evaluated in the vicinity of circular orbits, that is where I = L. Finally, Eq. (8)also introduced the local velocity dispersion σr(L) and the disc’s surface density Σ⋆(L). For a Keplerian potential, the mapping between the angular momentum L and the guiding radius Rg of the corresponding circular orbit is straightforwardly given by
(9)In Eq. (8), the Keplerian orbital frequencies have to be evaluated in the vicinity of circular orbits, that is where I = L. Finally, Eq. (8)also introduced the local velocity dispersion σr(L) and the disc’s surface density Σ⋆(L). For a Keplerian potential, the mapping between the angular momentum L and the guiding radius Rg of the corresponding circular orbit is straightforwardly given by 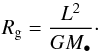 (10)Relying on this mapping, the disc’s surface density Σ⋆, expressed as a function of radius takes the form
(10)Relying on this mapping, the disc’s surface density Σ⋆, expressed as a function of radius takes the form ![\begin{equation} \Sigma_{\star} (R) = \frac{1}{2 \pi} \frac{M_{\star}}{\sqrt{2 \pi \sigma_{\Sigma}^{2}}} \frac{1}{R} \exp \left [ - \frac{(R - R_{\Sigma})^{2}}{2 \sigma_{\Sigma}^{2}} \right] , \label{def_Sigmastar} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq43.png) (11)where RΣ is the mean radius of the disc, and σΣ its radial extent. Such a surface density satisfies very closely the constraint ∫dRRdφΣ⋆ = M⋆. Finally, in units of Eq. (6), we choose
(11)where RΣ is the mean radius of the disc, and σΣ its radial extent. Such a surface density satisfies very closely the constraint ∫dRRdφΣ⋆ = M⋆. Finally, in units of Eq. (6), we choose 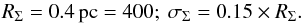 (12)Figure 1 illustrates the disc’s surface density Σ⋆(R). In Eq. (8), the radial velocity dispersion σr is chosen to be
(12)Figure 1 illustrates the disc’s surface density Σ⋆(R). In Eq. (8), the radial velocity dispersion σr is chosen to be 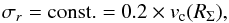 (13)where vc(RΣ) = L(RΣ) /RΣ stands for the circular velocity at the radius RΣ. The larger σr, the hotter the disc, and therefore the more eccentric the orbits. In order not to consider a domain of infinite extent in the (L,I)-plane, in all the subsequent numerical applications, we will restrict ourselves to the trapezoidal region
(13)where vc(RΣ) = L(RΣ) /RΣ stands for the circular velocity at the radius RΣ. The larger σr, the hotter the disc, and therefore the more eccentric the orbits. In order not to consider a domain of infinite extent in the (L,I)-plane, in all the subsequent numerical applications, we will restrict ourselves to the trapezoidal region 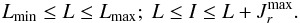 (14)In Eq. (14), it is bounded in angular momentum by
(14)In Eq. (14), it is bounded in angular momentum by ![\begin{equation} L_{\rm min} = L \big[ R_{\Sigma} - 2.5 \times \sigma_{\Sigma} \big];~ L_{\rm max} = L \big[ R_{\Sigma} + 2.5 \times \sigma_{\Sigma} \big] , \label{bound_L} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq53.png) (15)using the mapping L = L [ Rg] from Eq. (10). In addition, in Eq. (14), the value of
(15)using the mapping L = L [ Rg] from Eq. (10). In addition, in Eq. (14), the value of 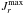 is chosen so that the exponential factor in Eq. (8)is small enough, namely
is chosen so that the exponential factor in Eq. (8)is small enough, namely 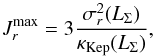 (16)where LΣ = L [RΣ]. Finally, let us pave the domain of Eq. (14)with a grid of constant step distance ΔJ defined as
(16)where LΣ = L [RΣ]. Finally, let us pave the domain of Eq. (14)with a grid of constant step distance ΔJ defined as 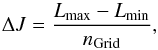 (17)where nGrid is an integer which characterises the density of the considered grid. A fairly sparse grid is used given the computational costs associated with the computation of the wire-wire interaction potential (see Appendix A). Derivatives on the grid are computed by finite differences, so that for example, one has [∂f/∂L] (L,I) = [f(L + ΔJ,I)−f(L−ΔJ,I)] / (2ΔJ). All the subsequent numerical applications were performed with nGrid = 30. Figure 2 illustrates the disc’s DF, F⋆, from Eq. (8)on the considered grid. Finally, as detailed in Appendix A, the gravitational interaction potential is softened so that
(17)where nGrid is an integer which characterises the density of the considered grid. A fairly sparse grid is used given the computational costs associated with the computation of the wire-wire interaction potential (see Appendix A). Derivatives on the grid are computed by finite differences, so that for example, one has [∂f/∂L] (L,I) = [f(L + ΔJ,I)−f(L−ΔJ,I)] / (2ΔJ). All the subsequent numerical applications were performed with nGrid = 30. Figure 2 illustrates the disc’s DF, F⋆, from Eq. (8)on the considered grid. Finally, as detailed in Appendix A, the gravitational interaction potential is softened so that 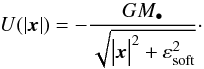 (18)In all the upcoming applications, the softening length is given by εsoft = 10-3 × RΣ.
(18)In all the upcoming applications, the softening length is given by εsoft = 10-3 × RΣ.
 |
Fig. 2 Illustration of the disc’s DF F⋆ from Eq. (8), in action space J = (L,I). It was assumed here that all stars are prograde, so that L> 0. Moreover, the action coordinates satisfy I ≥ L, so that I = L corresponds to circular orbits. The contours are spaced linearly between 95% and 5% of the DF maximum. The grey dashed lines correspond to the domain in action space from Eq. (14), to which the computations are restricted. |
2.3. The degenerate Landau equation
Because it is made of a finite number of stars, the razor-thin disc presented in Sect. 2.2 will undergo a self-induced resonant diffusion on secular timescales. This is the process of resonant relaxation (Rauch & Tremaine 1996). Paper I recently derived the appropriate master equations to describe such a long-term self-consistent and self-induced evolution. These are the inhomogeneous degenerate Balescu-Lenard and Landau equations. For a razor-thin axisymmetric disc, and in the limit where the contributions from the self-gravitating amplification are neglected, resonant relaxation is governed by the inhomogeneous degenerate Landau equation for razor-thin disc (Sridhar & Touma 2017, Paper I), which reads ![\begin{eqnarray} \frac{\partial \Fs}{\partial \tau}& = & \, \frac{\pi}{N_{\star}} \frac{\partial }{\partial L_{1}} \left [ \int \rd \bm{J}_{2} \, \delta_{\rD} (\Omega^{\rs} (\bm{J}_{1}) - \Omega^{\rs} (\bm{J}_{2})) \right . \nonumber \\ && \, \left . \times \big| A_{\rm tot} (\bm{J}_{1} , \bm{J}_{2}) \big|^{2} \bigg( \frac{\partial }{\partial L_{1}} - \frac{\partial }{\partial L_{2}} \bigg) \, \Fs (\bm{J}_{1}) \, \Fs (\bm{J}_{2}) \right] , \label{Landau_Kep_disc} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq72.png) (19)Eq. (19)describes the self-induced resonant evolution of the disc’s DF as a result of its discreteness. Following the notations from Paper I, Eq. (19)introduced the rescaled time τ defined as τ = 2πεt, with ε = M⋆/M•. This equation also involves the disc’s total bare susceptibility coefficients Atot(J1,J2), defined as
(19)Eq. (19)describes the self-induced resonant evolution of the disc’s DF as a result of its discreteness. Following the notations from Paper I, Eq. (19)introduced the rescaled time τ defined as τ = 2πεt, with ε = M⋆/M•. This equation also involves the disc’s total bare susceptibility coefficients Atot(J1,J2), defined as 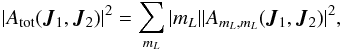 (20)where the bare susceptibility coefficients AmL,mL(J1,J2) are given by the Fourier transform in angle of the wire-wire interaction potential
(20)where the bare susceptibility coefficients AmL,mL(J1,J2) are given by the Fourier transform in angle of the wire-wire interaction potential 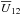 . They read
. They read 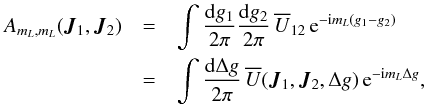 (21)since for wires belonging to the same orbital plane, the wire-wire interaction potential
(21)since for wires belonging to the same orbital plane, the wire-wire interaction potential 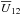 only depends on the phase difference between the two pericentres, Δg = g1−g2. Equation (21)introduces the wire-wire interaction potential,
only depends on the phase difference between the two pericentres, Δg = g1−g2. Equation (21)introduces the wire-wire interaction potential, 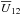 , given by
, given by ![\begin{equation} \oU (\bm{J}_{1} , g_{1} , \bm{J}_{2} , g_{2}) = \int \frac{\rd w_{1}}{2 \pi} \frac{\rd w_{2}}{2 \pi} U \big( | \bm{x}_{1} [ \bR_{1} , w_{1}] - \bm{x}_{2} [\bR_{2} , w_{2}] | \big) . \label{oU_disc} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq82.png) (22)Let us emphasise that the additional symmetry of the interaction potential in Eq. (21)is the very reason why the Landau Eq. (19)for discs can be written without any sum on resonance vectors. The effective calculation of the interaction potential from Eq. (22)remains a difficult numerical computation, which is the bottleneck of all the upcoming numerical applications. Appendix A details how this potential may be computed efficiently in practice, following Gauss’ method (Touma et al. 2009).
(22)Let us emphasise that the additional symmetry of the interaction potential in Eq. (21)is the very reason why the Landau Eq. (19)for discs can be written without any sum on resonance vectors. The effective calculation of the interaction potential from Eq. (22)remains a difficult numerical computation, which is the bottleneck of all the upcoming numerical applications. Appendix A details how this potential may be computed efficiently in practice, following Gauss’ method (Touma et al. 2009).
Equation (19)finally involves a resonance condition on the in-plane precession frequency Ωs of the Keplerian wires. In the present context, the precession frequencies are given by 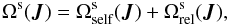 (23)where
(23)where 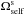 stands for the mass precession due to the disc’s potential, and
stands for the mass precession due to the disc’s potential, and 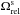 for the relativistic precession induced by the central BH. Section 3.1 details how these frequencies may be computed. In Fig. 3, we illustrate the variation of these precession frequencies for circular orbits (i.e. for I = L) as a function of the wires’ angular momentum L.
for the relativistic precession induced by the central BH. Section 3.1 details how these frequencies may be computed. In Fig. 3, we illustrate the variation of these precession frequencies for circular orbits (i.e. for I = L) as a function of the wires’ angular momentum L.
 |
Fig. 3 Dependence of the precession frequencies |
One can note that in the neighbourhood of the disc (i.e. for 7 × 104 ≲ L ≲ 10 × 104), the wire’s precession is dominated by the self-consistent mass precession frequency 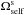 . Such a precession is said to be retrograde because
. Such a precession is said to be retrograde because 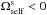 for L> 0. Section 3 investigates the properties of the disc’s self-consistent resonant relaxation in this region of action space. In the vicinity of BH (i.e. L ≲ 3 × 104), the wire’s precession is dominated by the relativistic precession frequency
for L> 0. Section 3 investigates the properties of the disc’s self-consistent resonant relaxation in this region of action space. In the vicinity of BH (i.e. L ≲ 3 × 104), the wire’s precession is dominated by the relativistic precession frequency 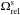 . Such a precession is said to be prograde because
. Such a precession is said to be prograde because 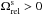 for L> 0. Section 4 investigates the properties of the resonant diffusion of a test wire in such a region of action space, where its precession is dominated by relativistic effects.
for L> 0. Section 4 investigates the properties of the resonant diffusion of a test wire in such a region of action space, where its precession is dominated by relativistic effects.
We refer the reader to Paper I for a detailed discussion of the physical content of the kinetic Eq. (19). Let us however emphasise that in the present approach, one has to enforce the 2D symmetry of the system, by constraining all wires to remain in the plane of the disc. The direction of each wire’s angular momentum vector remains therefore the exact same during the evolution. Wires can only see the norm of their angular momentum L change on secular timescales. This corresponds to the process of scalar resonant relaxation (Rauch & Tremaine 1996). Such an approach neglects the contributions from out-of-plane precessions, and cannot therefore capture the process of vector resonant relaxation (Kocsis & Tremaine 2011, 2015). Similarly, because this approach relies on the orbit-average of particles into wires, it cannot describe the diffusion associated with two-body non-resonant relaxation (Bahcall & Wolf 1976). Let us finally note that the kinetic Eq. (19)is limited to the description of the dynamics of axisymmetric razor-thin discs. Should one be interested in the secular evolution of a non-axisymmetric razor-thin disc (corresponding for example to the expected configuration of the galactic centre of M31 (Tremaine 1995)), the derivation of the kinetic equation presented in Paper I would have to be revisited. Indeed, as a result of the global non-axisymmetries, such a disc would precess as a whole, so that its unperturbed mean state would not per se be in a collisionless equilibrium. This new derivation would first involve identifying new angle-action coordinates for the non-axisymmetric configuration (i.e. by placing oneself within the appropriate rotating frame), before extending the formalism accordingly.
In order to emphasise the respective contributions of the diffusion tensor and the friction force by polarisation (Heyvaerts et al. 2017), one can also rewrite the Landau Eq. (19)by explicitly introducing the disc’s drift and diffusion coefficients. It becomes ![\begin{equation} \frac{\partial \Fs}{\partial \tau} = \frac{\partial }{\partial L_{1}} \left [A (\bm{J}_{1}) \, \Fs (\bm{J}_{1}) + D (\bm{J}_{1}) \, \frac{\partial \Fs}{\partial L_{1}} \right] , \label{Landau_Kep_disc_AD} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq95.png) (24)where the drift and diffusion coefficients A(J1) and D(J1) are respectively given by
(24)where the drift and diffusion coefficients A(J1) and D(J1) are respectively given by 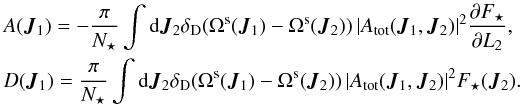 (25)In order to stress the conservation of the number of wires during diffusion, the Landau Eq. (19)can finally be written as the divergence of a flux as
(25)In order to stress the conservation of the number of wires during diffusion, the Landau Eq. (19)can finally be written as the divergence of a flux as ![\begin{equation} \frac{\partial \Fs}{\partial \tau} = \frac{\partial }{\partial L_{1}} \left [\mathcal{F}_{L} (\bm{J}_{1}) \right] = \frac{\partial }{\partial \bm{J}_{1}} \cdot \left [\bm{\mathcal{F}}_{\rm tot} (\bm{J}_{1}) \right] = \text{div} (\bm{\mathcal{F}}_{\rm tot}) , \label{Landau_Kep_disc_Div} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq99.png) (26)where the flux ℱL(J1) in the L-direction and the total flux ℱtot(J1) in the (L,I)-space are respectively defined as
(26)where the flux ℱL(J1) in the L-direction and the total flux ℱtot(J1) in the (L,I)-space are respectively defined as 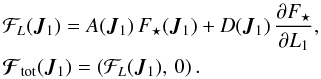 (27)We note that the diffusion flux ℱtot(J) is always zero in the I-direction, which corresponds to the adiabatic conservation of the fast action Jf = I during the resonant relaxation, which implies the conservation of the wires’ semi-major axis. We also note that for an isotropic DF, F⋆(J) = F⋆(I), the drift coefficients, A(J1), from Eq. (25)exactly vanish. Finally, we recall that the equilibrium states of the self-consistent diffusion Eq. (19)are given by the Boltzmann DFs (Chavanis 2012; Sridhar & Touma 2017), reading
(27)We note that the diffusion flux ℱtot(J) is always zero in the I-direction, which corresponds to the adiabatic conservation of the fast action Jf = I during the resonant relaxation, which implies the conservation of the wires’ semi-major axis. We also note that for an isotropic DF, F⋆(J) = F⋆(I), the drift coefficients, A(J1), from Eq. (25)exactly vanish. Finally, we recall that the equilibrium states of the self-consistent diffusion Eq. (19)are given by the Boltzmann DFs (Chavanis 2012; Sridhar & Touma 2017), reading ![\begin{equation} F_{\rm eq} (L , I) = C (I) \, \exp \left [{ -} \beta \, H_{\rm eq} (L , I) + \gamma L \right] , \label{equilibrium_Boltzmann} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq107.png) (28)where β stands for an inverse temperature, γ is the Lagrange multiplier associated with the conservation of the total angular momentum. Here, the energy Heq(L,I) is given by the primitive
(28)where β stands for an inverse temperature, γ is the Lagrange multiplier associated with the conservation of the total angular momentum. Here, the energy Heq(L,I) is given by the primitive 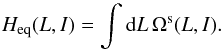 (29)In Eq. (28), the function C(I) is imposed by the initial conditions. Indeed, because of adiabatic invariance
(29)In Eq. (28), the function C(I) is imposed by the initial conditions. Indeed, because of adiabatic invariance 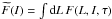 is conserved throughout the diffusion, so that C(I) is determined by
is conserved throughout the diffusion, so that C(I) is determined by 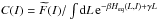 . In the high temperature limit, β → 0, the equilibrium distribution reduces to Feq(L,I) = C(I)exp [ γL] (Rauch & Tremaine 1996). Let us note that this end state differs from the relaxed power law density cusp, F = F(I) = Ip, associated with two-body non-resonant relaxation (Bahcall & Wolf 1976). Such a difference is of course expected as the degenerate Balescu-Lenard and Landau equations capture the long-term evolution induced by resonant interaction between orbit-averaged wires, while Bahcall & Wolf (1976) investigated the relaxation induced by direct (non-resonant) interactions between particles (i.e. without orbit-average). In particular, during the non-resonant relaxation, particles can exchange I, while during the resonant relaxation, I is an adiabatically conserved quantity, so that wires can only exchange L. As can be seen in the end state of Eq. (28), the I-dependence of the equilibrium DF of resonant relaxation is fixed by the initial conditions, so that one cannot expect it to generically relax to the F = F(I) = Ip equilibrium state predicted in Bahcall & Wolf (1976).
. In the high temperature limit, β → 0, the equilibrium distribution reduces to Feq(L,I) = C(I)exp [ γL] (Rauch & Tremaine 1996). Let us note that this end state differs from the relaxed power law density cusp, F = F(I) = Ip, associated with two-body non-resonant relaxation (Bahcall & Wolf 1976). Such a difference is of course expected as the degenerate Balescu-Lenard and Landau equations capture the long-term evolution induced by resonant interaction between orbit-averaged wires, while Bahcall & Wolf (1976) investigated the relaxation induced by direct (non-resonant) interactions between particles (i.e. without orbit-average). In particular, during the non-resonant relaxation, particles can exchange I, while during the resonant relaxation, I is an adiabatically conserved quantity, so that wires can only exchange L. As can be seen in the end state of Eq. (28), the I-dependence of the equilibrium DF of resonant relaxation is fixed by the initial conditions, so that one cannot expect it to generically relax to the F = F(I) = Ip equilibrium state predicted in Bahcall & Wolf (1976).
3. Self-consistent resonant relaxation
Having specified the properties of the considered discrete quasi-Keplerian disc and the master equation describing self-consistently its self-induced resonant relaxation, let us now detail how the Landau flux from Eq. (19)may be computed.
3.1. Computing the Landau flux
Relying on the fact that in razor-thin discs, the wire-wire interaction potential only depends on the pericentre’s phase shift Δg = g1−g2, one may perform a harmonic expansion of the form 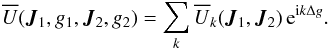 (30)One may then compute this harmonic expansion for each pair (J1,J2) in the grid from Eq. (14). In the subsequent numerical applications, the Fourier coefficients are computed by FFT using NFFT = 27 points. The calculation of the harmonic development of the wire-wire interaction potential in Eq. (30)allows then for the computation of two quantities: the self-consistent mass precession frequencies and the bare susceptibility coefficients appearing in the resonance condition from Eq. (19).
(30)One may then compute this harmonic expansion for each pair (J1,J2) in the grid from Eq. (14). In the subsequent numerical applications, the Fourier coefficients are computed by FFT using NFFT = 27 points. The calculation of the harmonic development of the wire-wire interaction potential in Eq. (30)allows then for the computation of two quantities: the self-consistent mass precession frequencies and the bare susceptibility coefficients appearing in the resonance condition from Eq. (19).
Turning to the total precession frequencies Ωs from Eq. (23), which originate from both the disc mass precession and the relativistic corrections, the self-consistent mass precession frequencies are given by 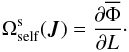 (31)Equation (31)involves the self-consistent potential
(31)Equation (31)involves the self-consistent potential 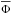 of the disc. It is given by
of the disc. It is given by 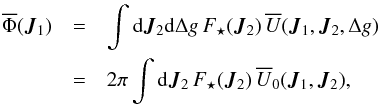 (32)relying on the harmonic development of the interaction potential from Eq. (30). The 1PN Schwarzschild relativistic precession frequencies induced by the central BH were obtained in Appendix A of Paper I. They read
(32)relying on the harmonic development of the interaction potential from Eq. (30). The 1PN Schwarzschild relativistic precession frequencies induced by the central BH were obtained in Appendix A of Paper I. They read 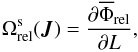 (33)where the relativistic potential
(33)where the relativistic potential 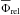 , when correctly normalised, is given by
, when correctly normalised, is given by 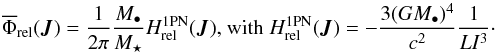 (34)The relativistic precession frequencies can then be explicitly computed and read
(34)The relativistic precession frequencies can then be explicitly computed and read 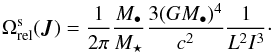 (35)Equations (31)and (35)jointly characterise the precession frequencies that come into play in the resonance condition of the Landau Eq. (19).
(35)Equations (31)and (35)jointly characterise the precession frequencies that come into play in the resonance condition of the Landau Eq. (19).
Finally, the harmonic expansion from Eq. (30)also allows us to evaluate the disc’s total bare susceptibility coefficients from Eq. (20), which become 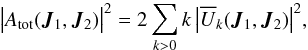 (36)relying on the fact that
(36)relying on the fact that 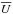 being real, one has
being real, one has 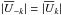 .
.
 |
Fig. 4 Total precession frequencies |
Having determined the system’s precession frequencies as well as the total bare susceptibility coefficients, the computation of the r.h.s. of Eq. (19)involves dealing with the resonance condition encapsulated by the Dirac delta δD(Ωs(J1)−Ωs(J2)), by identifying the critical lines of resonance. To do so, let us first recall the generic definition of the composition of a Dirac delta and a smooth function (Hörmander 2003), which gives 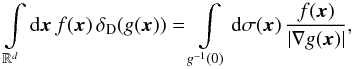 (37)where g-1(0) = { x | g(x) = 0 } is the hypersurface of (generically) dimension (d−1) defined by the constraint g(x) = 0, and dσ(x) is its surface measure. In the present context, the resonance condition is given by the function
(37)where g-1(0) = { x | g(x) = 0 } is the hypersurface of (generically) dimension (d−1) defined by the constraint g(x) = 0, and dσ(x) is its surface measure. In the present context, the resonance condition is given by the function 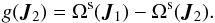 (38)For any given value of J1, and introducing ω = Ωs(J1), one may then define the critical resonant curve γ(ω) as
(38)For any given value of J1, and introducing ω = Ωs(J1), one may then define the critical resonant curve γ(ω) as 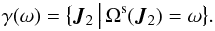 (39)This curve corresponds to the location in action space of all the wires which are in resonance with the precessing wire of action J1. This is illustrated in Fig . 4 for the disc from Sect. 2.2. Once these resonant lines have been identified, the Landau drift and diffusion coefficients from Eq. (25)may straightforwardly be computed, and read
(39)This curve corresponds to the location in action space of all the wires which are in resonance with the precessing wire of action J1. This is illustrated in Fig . 4 for the disc from Sect. 2.2. Once these resonant lines have been identified, the Landau drift and diffusion coefficients from Eq. (25)may straightforwardly be computed, and read 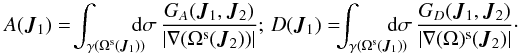 (40)Equation (40)introduced the two functions GA and GD as
(40)Equation (40)introduced the two functions GA and GD as 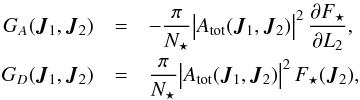 (41)as well as the resonant contribution | ∇(Ωs(J2)) | given by
(41)as well as the resonant contribution | ∇(Ωs(J2)) | given by ![\begin{equation} | \nabla (\Omega^{\rs} (\bm{J}_{2})) | = \sqrt{ \left [\frac{\partial \Omega^{\rs}}{\partial L_{2}} \right]^{2} + \left [\frac{\partial \Omega^{\rs}}{\partial I_{2}} \right]^{2}} \cdot \label{definition_resonant_contribution} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq154.png) (42)
(42)
 |
Fig. 5 Diffusion flux, ℱL, predicted by the degenerate Landau Eq. (26)for the razor-thin quasi-Keplerian disc introduced in Sect. 2.2. Following the convention from Eq. (26), the direction of diffusion of individual wires in action space is given by −ℱL. Red contours, for which ℱL< 0, correspond to regions where wires tend to diffuse towards larger L, that is decrease their eccentricity. Blue contours, for which ℱL> 0, are associated with regions in action space, where individual wires tend to diffuse towards smaller L, that is increase their eccentricity. The contours are spaced linearly between the minimum and the maximum of ℱL. Within the units of Eq. (6), the maximum value for the positive blue contours is given by |
3.2. Self-induced resonant diffusion
Equipped with the bricks presented in the previous section, one may then study how the disc’s DF, F⋆, from Eq. (8)will get to diffuse on secular timescales under the effect of its own discreteness. This involves i) evaluating the pairwise interaction potential  on the grid elements following the Gauss method from Appendix A; ii) determining the precession frequencies (illustrated in Fig. 4), as well as the disc’s total bare susceptibility coefficients | Atot | 2; iii) integrating Eq. (40)along the associated resonant lines, and iv) computing the disc’s self-consistent drift and diffusion coefficients, A(J) and D(J). These steps allow finally for the computation of the total diffusion flux ℱL, introduced in Eq. (26).
on the grid elements following the Gauss method from Appendix A; ii) determining the precession frequencies (illustrated in Fig. 4), as well as the disc’s total bare susceptibility coefficients | Atot | 2; iii) integrating Eq. (40)along the associated resonant lines, and iv) computing the disc’s self-consistent drift and diffusion coefficients, A(J) and D(J). These steps allow finally for the computation of the total diffusion flux ℱL, introduced in Eq. (26).
The contours of this flux are illustrated in Fig. 5. Let us first recall that because the equations of motion were averaged w.r.t. the fast Keplerian orbital motion, that is w.r.t. w the angle associated with the action I, the diffusion is one-dimensional only: individual Keplerian wires conserve their fast action I (i.e. conserve their semi-major axis), and can only diffuse in the L-direction (i.e. change their eccentricity). In Fig. 5, this translates to the fact that wires diffuse along horizontal lines. Following the convention from Eq. (27), one can note that individual wires will diffuse along the direction of −ℱL, so that in Fig. 5, most of the individual wires will diffuse towards lower L, that is towards larger eccentricities. The self-consistent diffusion of the system therefore tends to dynamically heat up the system by making it more eccentric.
Following the calculation of ℱL, it is straightforward to compute the divergence of the diffusion flux, div(ℱtot), whose contours are illustrated in Fig. 6. It is the first application of the degenerate Landau equation in the context of galactic centres, and constitutes a main result of this paper.
 |
Fig. 6 Divergence of the diffusion flux, div(ℱtot), predicted by the degenerate Landau Eq. (26)for the razor-thin quasi-Keplerian disc introduced in Sect. 2.2. Red contours, for which div(ℱtot) < 0, correspond to regions from which the wires will be depleted, whereas blue contours, for which div(ℱtot) > 0, are associated with regions in action space, where the value of the disc’s DF will increase during the resonant relaxation. The contours are spaced linearly between the minimum and the maximum of div(ℱtot). Within the units of Eq. (6), the maximum value for the positive blue contours is given by div(ℱtot)max ≃ 5 × 10-14, while the minimum value for the negative red contours reads div(ℱtot)min ≃ −10-13. |
This allows us to describe the self-induced local changes of the disc’s DF, that is to determine the value of [∂F⋆/∂t] (t = 0+). We note from Fig. 6 that the self-consistent diffusion is associated with an increase in the orbits’ eccentricities. It is similar to the localised “heating” found in Fouvry et al. (2015a,b) when studying the secular self-consistent diffusion of discrete razor-thin self-gravitating stellar discs. There, diffusion induced a heating of the system’s DF, which was very localised in action space, taking the form of a narrow resonant ridge. It was amplified by the disc’s self-gravitation, as accounted for by the Balescu-Lenard framework. Figure 6 limits itself to the computation of the Landau flux, for which collective effects are not considered. Should the disc be strongly self-gravitating, one expects the self-gravitating amplification not only to accelerate the overall diffusion of the system, but also to enhance it in specific locations in action space where collective effects are the strongest, leading to the appearance of narrow ridges of diffusion.
Let us now estimate the typical timescale associated with this self-consistent resonant diffusion. The contours of F⋆ presented in Fig. 2 are separated by an increment equal to 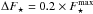 , where
, where 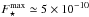 is the maximum of the disc’s DF from Eq. (8). In order to observe the effects of the secular diffusion, the value of the disc’s DF should typically change by an amount of the order of ΔF⋆. From the contours of Fig. 6, one can note that the maximum of the norm of the divergence of the diffusion flux is typically of the order of | div(ℱtot) | max ≃ 10-13. Equation (26)then allows us to write the relation ΔF⋆ ≃ ΔτLd. | div(ℱtot) | max, where ΔτLd. is the typical (rescaled) time during which the Landau Eq. (26)has to be evolved for the disc to undergo a significant diffusion. With the previous numerical values, one gets ΔτLd. ≃ 103. Following the convention from Eq. (19), the associated diffusion time is given by ΔtLd. = ΔτLd./ (2πε), with ε = M⋆/M• = 10-3. Using the units from Eq. (6), one finally gets
is the maximum of the disc’s DF from Eq. (8). In order to observe the effects of the secular diffusion, the value of the disc’s DF should typically change by an amount of the order of ΔF⋆. From the contours of Fig. 6, one can note that the maximum of the norm of the divergence of the diffusion flux is typically of the order of | div(ℱtot) | max ≃ 10-13. Equation (26)then allows us to write the relation ΔF⋆ ≃ ΔτLd. | div(ℱtot) | max, where ΔτLd. is the typical (rescaled) time during which the Landau Eq. (26)has to be evolved for the disc to undergo a significant diffusion. With the previous numerical values, one gets ΔτLd. ≃ 103. Following the convention from Eq. (19), the associated diffusion time is given by ΔtLd. = ΔτLd./ (2πε), with ε = M⋆/M• = 10-3. Using the units from Eq. (6), one finally gets 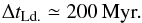 (43)The self-consistent diffusion captured by the Landau Eq. (19)and computed in Fig. 6 allows therefore the disc to resonantly diffuse on timescales much shorter than the age of the universe, and also much shorter than the timescale associated with the self-induced relaxation of galactic stellar discs (Fouvry et al. 2015b). When accounting for collective effects, the total bare susceptibility coefficients from Eq. (36)should then be replaced by their dressed analogues. As was already observed for non-degenerate stellar discs (Fouvry et al. 2015b), provided the disc is sufficiently massive and self-gravitating, one expects that accounting for the wires’ polarisation will lead to an acceleration of the disc’s self-induced diffusion, and therefore to a reduction of the typical timescale of diffusion from Eq. (43).
(43)The self-consistent diffusion captured by the Landau Eq. (19)and computed in Fig. 6 allows therefore the disc to resonantly diffuse on timescales much shorter than the age of the universe, and also much shorter than the timescale associated with the self-induced relaxation of galactic stellar discs (Fouvry et al. 2015b). When accounting for collective effects, the total bare susceptibility coefficients from Eq. (36)should then be replaced by their dressed analogues. As was already observed for non-degenerate stellar discs (Fouvry et al. 2015b), provided the disc is sufficiently massive and self-gravitating, one expects that accounting for the wires’ polarisation will lead to an acceleration of the disc’s self-induced diffusion, and therefore to a reduction of the typical timescale of diffusion from Eq. (43).
Following the estimation of div(ℱtot) in Fig. 6, let us finally investigate how this diffusion impacts the disc’s surface density. Recalling the normalisation convention 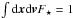 , the disc’s surface density Σ⋆ is given by
, the disc’s surface density Σ⋆ is given by 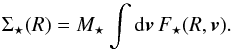 (44)Appendix B briefly details how Eq. (44)may be computed. For sufficiently short diffusion times, the Landau Eq. (26)allows us to approximate the perturbed DF as
(44)Appendix B briefly details how Eq. (44)may be computed. For sufficiently short diffusion times, the Landau Eq. (26)allows us to approximate the perturbed DF as 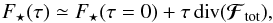 (45)where the value of the divergence of the diffusion flux is taken for τ = 0. One may then use this perturbed DF to estimate the associated perturbed surface density. This is illustrated in Fig. 7, for which the diffusion has been integrated for a time ΔτLd. as given by Eq. (43).
(45)where the value of the divergence of the diffusion flux is taken for τ = 0. One may then use this perturbed DF to estimate the associated perturbed surface density. This is illustrated in Fig. 7, for which the diffusion has been integrated for a time ΔτLd. as given by Eq. (43).
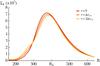 |
Fig. 7 Evolution of the disc’s surface density Σ⋆(R,τ) as a function of time. As already illustrated in Fig. 6 in phase space, one can note that on a timescale of the order of ΔtLd. (see Eq. (43)), the disc undergoes a self-induced resonant relaxation which broadens it. |
In this figure, one can note that as a result of resonant relaxation, the surface density of the disc gets to diffuse towards smaller radii. Let us finally emphasise that in order to describe the evolution of the disc’s surface density on longer timescales, one cannot assume anymore the disc’s drift and diffusion coefficients to be stationary in time. Indeed, as imposed by the self-consistency of the kinetic equation, one has to update the diffusion flux as the disc’s DF gets to evolve.
3.3. Multi-component self-consistent diffusion
The previous section considered the self-consistent diffusion of the disc’s wires, assuming that all the wires in the disc have the same individual mass. In galactic centres, the range of masses of stars and lighter black holes orbiting the central one is likely to be the key to understand the dynamics of the central cluster and possible EMRIs. The effects associated with the presence of a broad mass spectrum have been the subject of various studies (Bahcall & Wolf 1977; Hopman & Alexander 2006b; Freitag et al. 2006; Keshet et al. 2009; O’Leary et al. 2009). In particular, Bahcall & Wolf (1976) showed how the two-body relaxation of a multi-component 3D cluster around a central point mass leads to a mass segregation of the different components. The more massive objects segregate from the lower mass ones by relaxing towards a steeper power-law density profile. Let us note that such a mass segregation is the outcome of the non-resonant relaxation of a 3D spherical isotropic galactic centre. In the present work, we focus on describing the resonant relaxation of a 2D disc, so that the results from Bahcall & Wolf (1977) do not directly translate to this regime.
This section will now show how the Landau Eq. (19)allows us to describe self-consistently the simultaneous evolution of multiple components. Let us therefore assume that the disc from Sect. 2.2 is composed of two distinct components, denoted with the letters “a” and “b”. The component “a” is assumed to be composed of Na stars of individual mass μa, so that the total mass of this population is given by 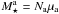 . Similar notations for the component “b” are used. As in Sect. 2.2, the total stellar mass of the system is defined as M⋆, so that one has
. Similar notations for the component “b” are used. As in Sect. 2.2, the total stellar mass of the system is defined as M⋆, so that one has 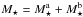 . Let us also assume that up to a normalisation the two populations initially follow the same DF, so that one has
. Let us also assume that up to a normalisation the two populations initially follow the same DF, so that one has 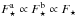 , where F⋆ stands for the total stellar DF introduced in Eq. (8). Keeping track of the normalisations of the multi-component DF (see Paper I), the DFs of the components “a” and “b” initially satisfy
, where F⋆ stands for the total stellar DF introduced in Eq. (8). Keeping track of the normalisations of the multi-component DF (see Paper I), the DFs of the components “a” and “b” initially satisfy 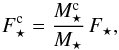 (46)where the index “c” runs over the two populations “a” and “b”. We note that these DFs satisfy the normalisation conventions
(46)where the index “c” runs over the two populations “a” and “b”. We note that these DFs satisfy the normalisation conventions 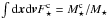 . In this multi-component context, the Landau Eq. (19)for razor-thin quasi-Keplerian discs now describes the evolution of each component, and reads
. In this multi-component context, the Landau Eq. (19)for razor-thin quasi-Keplerian discs now describes the evolution of each component, and reads ![\begin{eqnarray} \frac{\partial \Fsa}{\partial \tau}& = & \, \pi \frac{\partial }{\partial L_{1}} \left [\int \rd \bm{J}_{2} \, \delta_{\rD} (\Omega^{\rs} (\bm{J}_{1}) - \Omega^{\rs} (\bm{J}_{2})) \right . \nonumber \\ & & \left . \times \big| A_{\rm tot} (\bm{J}_{1} , \bm{J}_{2}) \big|^{2} \, \sum_{\rc} \bigg( \eta_{\rc} \frac{\partial }{\partial L_{1}} - \eta_{\ra} \frac{\partial }{\partial L_{2}} \bigg) \, \Fsa (\bm{J}_{1}) \, \Fsc (\bm{J}_{2}) \right] , \label{Landau_Kep_multi} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq198.png) (47)where the rescaled time τ is still defined as τ = 2πεt, with ε = M⋆/M•. Equation (47)also introduced the small parameter ηa = μa/M⋆, which replaces the factor 1 /N⋆ present in Eq. (19). Following Eq. (28), it is straightforward to obtain that the equilibrium of the coupled evolution Eq. (47)is given by the Boltzmann DF reading
(47)where the rescaled time τ is still defined as τ = 2πεt, with ε = M⋆/M•. Equation (47)also introduced the small parameter ηa = μa/M⋆, which replaces the factor 1 /N⋆ present in Eq. (19). Following Eq. (28), it is straightforward to obtain that the equilibrium of the coupled evolution Eq. (47)is given by the Boltzmann DF reading ![\begin{equation} F_{\rm eq}^{\ra} (L , I) = C^{\ra} (I) \, \exp \left [ {-} \beta \, \eta_{\ra} \, H_{\rm eq} (L , I) + \eta_{\ra} \gamma L \right] , \label{equilibrium_Boltzmann_multi} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq202.png) (48)where Ca(I) are functions imposed by the initial conditions, the inverse temperature β and the multiplier γ are the same for all the populations, and the energy Heq(L,I) was introduced in Eq. (29).
(48)where Ca(I) are functions imposed by the initial conditions, the inverse temperature β and the multiplier γ are the same for all the populations, and the energy Heq(L,I) was introduced in Eq. (29).
 |
Fig. 8 Divergence of the diffusion flux, div(ℱtot), predicted by the multi-component Landau Eq. (47)and following the conventions from Fig. 6. Left panel: for the population “a” of light wires of individual mass μa = 1. The maximum value for the positive blue contours is given by |
Following Eq. (24), one can introduce multi-component drift and diffusion coefficients to rewrite Eq. (47)as ![\begin{equation} \frac{\partial \Fsa}{\partial \tau} = \frac{\partial }{\partial L_{1}} \left [\sum_{\rc} \left\{ \eta_{\ra} A^{\rc} (\bm{J}_{1}) \, \Fsa (\bm{J}_{1}) + \eta_{\rc} D^{\rc} (\bm{J}_{1}) \, \frac{\partial \Fsa}{\partial L_{1}} \right \} \right] , \label{Landau_Kep_disc_multi_AD} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq212.png) (49)where the drift and diffusion coefficients Ac(J1) and Dc(J1) depend on the component “c” used as the underlying DF to estimate them. Accounting for normalisations, they read
(49)where the drift and diffusion coefficients Ac(J1) and Dc(J1) depend on the component “c” used as the underlying DF to estimate them. Accounting for normalisations, they read 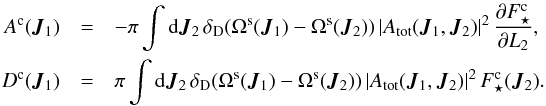 (50)Equation (49) can finally be rewritten as
(50)Equation (49) can finally be rewritten as ![\begin{equation} \frac{\partial \Fsa}{\partial \tau} = \frac{\partial }{\partial L_{1}} \left [ \eta_{\ra} A^{\rm tot} (\bm{J}_{1}) \, \Fsa (\bm{J}_{1}) + D^{\rm tot} (\bm{J}_{1}) \, \frac{\partial \Fsa}{\partial L_{1}} \right] , \label{Landau_Kep_disc_multi_tot_AD} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq216.png) (51)where the total drift and diffusion coefficients are
(51)where the total drift and diffusion coefficients are 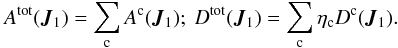 (52)Equation (46)assumes that the two populations “a” and “b” follow a DF proportional to the one introduced in Eq. (8)for the one-component problem. As a consequence, the calculations of the multi-component drift and diffusion coefficients from Eq. (50)are, up to changes in normalisations, the same as the ones performed in Sect. 2.3 for the one-component problem. Following the normalisations from Eq. (46), the multi-component drift and diffusion coefficients from Eq. (50)are given by
(52)Equation (46)assumes that the two populations “a” and “b” follow a DF proportional to the one introduced in Eq. (8)for the one-component problem. As a consequence, the calculations of the multi-component drift and diffusion coefficients from Eq. (50)are, up to changes in normalisations, the same as the ones performed in Sect. 2.3 for the one-component problem. Following the normalisations from Eq. (46), the multi-component drift and diffusion coefficients from Eq. (50)are given by 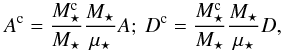 (53)where A and D stand for the drift and diffusion coefficients introduced in Eq. (24)for the one-component problem, and μ⋆ is the individual stellar mass of the one-component problem. Following Eq. (52), the total drift and diffusion coefficients are then given by
(53)where A and D stand for the drift and diffusion coefficients introduced in Eq. (24)for the one-component problem, and μ⋆ is the individual stellar mass of the one-component problem. Following Eq. (52), the total drift and diffusion coefficients are then given by ![\begin{eqnarray} A^{\rm tot} & =& \bigg[ \frac{M_{\star}^{\ra}}{M_{\star}} \frac{M_{\star}}{\mu_{\star}} + \frac{M_{\star}^{\rb}}{M_{\star}} \frac{M_{\star}}{\mu_{\star}} \bigg] = \frac{M_{\star}}{\mu_{\star}} A , \nonumber \\ D^{\rm tot} & =& \bigg[ \frac{\mu_{\ra}}{M_{\star}} \frac{M_{\star}^{\ra}}{M_{\star}} \frac{M_{\star}}{\mu_{\star}} + \frac{\mu_{\rb}}{M_{\star}} \frac{M_{\star}^{\rb}}{M_{\star}} \frac{M_{\star}}{\mu_{\star}} \bigg] D = \frac{M_{\star}^{\ra} \mu_{\ra} + M_{\star}^{\rb} \mu_{\rb}}{M_{\star} \mu_{\star}} D . \label{calculation_Atot_Dtot} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq221.png) (54)These total multi-component drift and diffusion coefficients then allow us to compute the flux appearing in Eq. (51), given the specific normalisation of the multi-component DFs in Eq. (46).
(54)These total multi-component drift and diffusion coefficients then allow us to compute the flux appearing in Eq. (51), given the specific normalisation of the multi-component DFs in Eq. (46).
Let us illustrate this multi-component diffusion by considering the exact same disc profile as in Sect. 2.2. However, here it will be assumed that half of the mass of the disc is due to a population of stars whose individual mass is ten times larger than the individual mass considered in the one-component case. Following the units from Eq. (7), the two populations “a” and “b” are such that 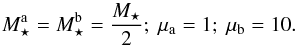 (55)One may then reuse the calculations presented in Sect. 3.2 to compute the divergence of the diffusion flux of each of the two populations “a” and “b”. This is illustrated in Fig. 8. In this figure, one can note that the population “a” of light wires tends to diffuse toward larger eccentricities, while the population “b” of heavy wires diffuses towards smaller eccentricities. This segregation is of particular astrophysical interest in galactic centres in order to investigate how a sub-population of intermediate mass black holes (represented by the heavy wires) may diffuse in these regimes compared to the stellar population. In the present case, the diffusion coefficient from the degenerate Landau equation presented in Fig. 8 predicts that the heavy population circularise as a result of the self-induced resonant relaxation. The mass segregation observed in Fig. 8 has a direct counterpart in configuration space, as illustrated in Fig. 9.
(55)One may then reuse the calculations presented in Sect. 3.2 to compute the divergence of the diffusion flux of each of the two populations “a” and “b”. This is illustrated in Fig. 8. In this figure, one can note that the population “a” of light wires tends to diffuse toward larger eccentricities, while the population “b” of heavy wires diffuses towards smaller eccentricities. This segregation is of particular astrophysical interest in galactic centres in order to investigate how a sub-population of intermediate mass black holes (represented by the heavy wires) may diffuse in these regimes compared to the stellar population. In the present case, the diffusion coefficient from the degenerate Landau equation presented in Fig. 8 predicts that the heavy population circularise as a result of the self-induced resonant relaxation. The mass segregation observed in Fig. 8 has a direct counterpart in configuration space, as illustrated in Fig. 9.
 |
Fig. 9 Illustration in configuration space of the mass segregation of the two different components obtained in Fig. 8. Here, the population of red orbits has a lighter individual mass than the blue population. Left panel: illustration of the initial orbits of the wires, where the blue and red wires have the same semi-major axis and eccentricity. Right panel: illustration of the wires’ orbits after the resonant mass segregation. During the resonant relaxation, the wires conserve their semi-major axis, but, following Fig. 8, the light red wires get larger eccentricities, while the heavy blue wires diffuse towards smaller eccentricities and circularise. Because of this segregation, one can note that red orbits get closer to the central BH, as illustrated by the dashed circles. |
In closing, let us briefly recover the mass segregation observed in Fig. 8 by computing the initial rate of change of the mean angular momentum of each population. Defining 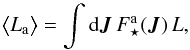 (56)and following Eq. (51), one has
(56)and following Eq. (51), one has 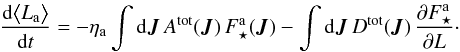 (57)Thanks to Eq. (54), the value of d⟨La⟩ / dt at the initial time is given by
(57)Thanks to Eq. (54), the value of d⟨La⟩ / dt at the initial time is given by 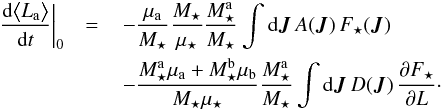 (58)The disc’s total angular momentum being conserved (Sridhar & Touma 2017), one has
(58)The disc’s total angular momentum being conserved (Sridhar & Touma 2017), one has 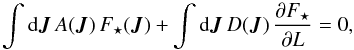 (59)so that Eq. (58)can finally be rewritten as
(59)so that Eq. (58)can finally be rewritten as 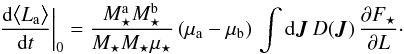 (60)Following Fig. 2, let us assume that ∂F⋆/∂L> 0 (which is true in most of action space). The diffusion coefficient D(J) being always positive, one has
(60)Following Fig. 2, let us assume that ∂F⋆/∂L> 0 (which is true in most of action space). The diffusion coefficient D(J) being always positive, one has 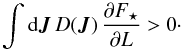 (61)As a consequence, for μa<μb, one has d⟨La⟩ / dt | 0< 0 and d⟨Lb⟩ / dt | 0> 0. Equation (60)therefore predicts that as a result of resonant relaxation, the light wires will see a decrease in their mean angular momentum (i.e. an increase in eccentricity), while the heavy wires will see an increase in their mean angular momentum (i.e. a decrease in eccentricity). This corresponds to the segregation observed in Fig. 8. Let us finally emphasise that except for specific cases (e.g. here ∂F⋆/∂L> 0 , ∀J), it remains difficult to predict a priori the direction of mass segregation for other arbitrary initial conditions, as the calculation of the Landau diffusion fluxes from Eq. (49)is very intricate. Such a 2D resonant mass segregation is associated with a different dynamical regime than the 3D non-resonant mass segregation considered in Bahcall & Wolf (1977).
(61)As a consequence, for μa<μb, one has d⟨La⟩ / dt | 0< 0 and d⟨Lb⟩ / dt | 0> 0. Equation (60)therefore predicts that as a result of resonant relaxation, the light wires will see a decrease in their mean angular momentum (i.e. an increase in eccentricity), while the heavy wires will see an increase in their mean angular momentum (i.e. a decrease in eccentricity). This corresponds to the segregation observed in Fig. 8. Let us finally emphasise that except for specific cases (e.g. here ∂F⋆/∂L> 0 , ∀J), it remains difficult to predict a priori the direction of mass segregation for other arbitrary initial conditions, as the calculation of the Landau diffusion fluxes from Eq. (49)is very intricate. Such a 2D resonant mass segregation is associated with a different dynamical regime than the 3D non-resonant mass segregation considered in Bahcall & Wolf (1977).
4. Reaching the Schwarzschild barrier
The previous section investigated the self-induced diffusion of the disc’s DF as a whole. The long-term self-consistent diffusion of this DF is then described by the degenerate Landau Eq. (19), which is quadratic in the system’s DF. Instead of describing the evolution of the disc’s DF as a whole, it is of interest to follow the stochastic evolution of arbitrary individual stellar wires, perturbed by the 1 /N noise due to the disc. This would allow us for instance to investigate the impact of the stellar disc on the evolution of stars or intermediate mass black holes in the vicinity of the SMBH. Such stochastic dynamics are captured by a Langevin equation, as described below. In this context, the quasi-Keplerian disc will be treated as a bath, so that its mean DF, F⋆, does not evolve on the relevant timescale. Similarly to the wires forming the razor-thin disc, these test wires are assumed to lie within the same plane than the razor-thin disc, and are constrained throughout their diffusion to remain within this plane (i.e. the direction of their angular momentum is conserved). The wires from the razor-thin disc and the test wires are therefore coplanar.
4.1. The stochastic Langevin equation
Let us consider a given test star, and represent its statistics by the probability distribution function (PDF), P. This PDF describes the stochastic dynamical evolution of individual test wires driven by the 1 /N noise of the disc (the bath). The PDF P obeys a Fokker-Planck equation (Heyvaerts et al. 2017, and references therein) reading ![\begin{equation} \frac{\partial P}{\partial \tau} = \frac{\partial }{\partial L} \bigg[ A (\bm{J}) \, P (\bm{J}) + D (\bm{J}) \, \frac{\partial P}{\partial L} \bigg] , \label{FP_disc} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq237.png) (62)where the drift and diffusion coefficients, A(J) and D(J), are induced by the disc, and were introduced in Eq. (24)3. In practice, this equation is obtained by replacing F⋆ by P in the flux of Eq. (24). The corresponding Langevin equation describes the stochastic dynamics of an individual test wire of action Jt = (Lt,It) (Risken 1996). It reads
(62)where the drift and diffusion coefficients, A(J) and D(J), are induced by the disc, and were introduced in Eq. (24)3. In practice, this equation is obtained by replacing F⋆ by P in the flux of Eq. (24). The corresponding Langevin equation describes the stochastic dynamics of an individual test wire of action Jt = (Lt,It) (Risken 1996). It reads 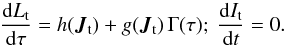 (64)Equation (64)introduces the 1D Langevin coefficients h(Jt) and g(Jt) defined as
(64)Equation (64)introduces the 1D Langevin coefficients h(Jt) and g(Jt) defined as 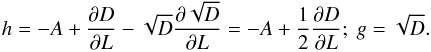 (65)Finally, Eq. (64)also introduces a Gaussian white noise Γ(τ), whose statistics obeys
(65)Finally, Eq. (64)also introduces a Gaussian white noise Γ(τ), whose statistics obeys 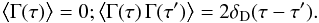 (66)As expected, the stochastic evolution Eq. (64)allows only for diffusion in the Lt-direction, while the fast action It of the test wire remains conserved during the resonant relaxation. This stochastic rewriting of the dynamics of a test wire directly connects to the Monte-Carlo approaches considered in Madigan et al. (2011) and the η-formalism presented in Bar-Or & Alexander (2014, 2016). The equilibrium solutions of the Fokker-Planck Eq. (62)are straightforwardly given by
(66)As expected, the stochastic evolution Eq. (64)allows only for diffusion in the Lt-direction, while the fast action It of the test wire remains conserved during the resonant relaxation. This stochastic rewriting of the dynamics of a test wire directly connects to the Monte-Carlo approaches considered in Madigan et al. (2011) and the η-formalism presented in Bar-Or & Alexander (2014, 2016). The equilibrium solutions of the Fokker-Planck Eq. (62)are straightforwardly given by ![\begin{equation} P_{\rm eq} (L , I ) = C (I) \, \exp \big[ - V_{\rm eq} (L , I) \big] , \label{equilibrium_FP} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq249.png) (67)where C(I) is an arbitrary function, and where the potential Veq(L,I) is imposed by the bath and is given by the primitive
(67)where C(I) is an arbitrary function, and where the potential Veq(L,I) is imposed by the bath and is given by the primitive 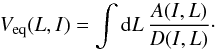 (68)If one considers a test wire evolving in a Boltzmann (thermal) bath as given by Eq. (28), the Fokker-Planck Eq. (62)takes the simpler form
(68)If one considers a test wire evolving in a Boltzmann (thermal) bath as given by Eq. (28), the Fokker-Planck Eq. (62)takes the simpler form ![\begin{equation} \frac{\partial P}{\partial \tau} = \frac{\partial }{\partial L} \bigg[ D (\bm{J}) \, \bigg\{ \frac{\partial P}{\partial L} + (\beta \Omega^{\rs} (\bm{J}) - \gamma) \, P (\bm{J}) \bigg\} \bigg] , \label{FP_Boltzamnn_FP} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq252.png) (69)thanks to the Einstein relation A(J) = (βΩs(J)−γ) D(J) satisfied by the drift and diffusion coefficients. In the high temperature limit, β → 0, the Einstein relation becomes A(J) = −γD(J). Finally, for an isotropic bath, F⋆ = F⋆(I), following Eq. (25), the drift coefficients exactly vanish, that is A(J) = 0. The associated Fokker-Planck equilibrium states from Eq. (67)are then also isotropic and read Peq(L,I) = C(I).
(69)thanks to the Einstein relation A(J) = (βΩs(J)−γ) D(J) satisfied by the drift and diffusion coefficients. In the high temperature limit, β → 0, the Einstein relation becomes A(J) = −γD(J). Finally, for an isotropic bath, F⋆ = F⋆(I), following Eq. (25), the drift coefficients exactly vanish, that is A(J) = 0. The associated Fokker-Planck equilibrium states from Eq. (67)are then also isotropic and read Peq(L,I) = C(I).
4.2. Diffusion of an eccentric particle
In the context of the so-called last parsec problem, relying on the stochastic Langevin Eq. (64), let us investigate how a given test wire diffuses in the vicinity of the central BH under the effect of the noise due to the discrete quasi-Keplerian disc. This section will show in particular how the diffusion of this test wire strongly quenches as it reaches large eccentricities, a phenomenon called the Schwarzschild barrier, first observed in Merritt et al. (2011) in the context of 3D quasi-Keplerian systems. In short, because the relativistic precession frequencies diverge in the neighbourhood of the BH (see for example Fig. 3), wires that diffuse inwards closer to the BH experience a rise in their precession frequency. This prevents them from resonating anymore with the wires from the disc, therefore strongly suppressing further inwards resonant diffusion. This region of action space where the diffusion is suppressed is the so-called Schwarzschild barrier4. Let us finally note that Merritt et al. (2011) included the effects associated with gravitational wave emission, which are not included in the present work. The contributions from this process on the Schwarzschild barrier are expected to be negligible as the capture rate of stars is determined primarily by dynamical interactions that take place far beyond the Schwarzschild radius (see e.g. Fig. 1 in Bar-Or & Alexander 2016).
Following Fig. 10, let us therefore consider a test wire of individual mass μt = μ⋆ and of fast action It(at) = It(102.5), where the fast action It and the associated semi-major axis at are directly related by Eq. (4).
 |
Fig. 10 Diffusion of an individual test wire in the (j,a) = (L/I,I2/ (GM•))-space. Because of the adiabatic conservation of the fast action I, wires diffuse on horizontal lines. The red line corresponds to the last stable orbit (LSO), aLSO(j) = Rg(4 /j)2, with Rg = GM•/c2 (Bar-Or & Alexander 2016). The contours of the disc’s DF, F⋆, introduced in Eq. (8)are represented by the blue lines. The background lines correspond to some of the level lines of the precession frequency |
 |
Fig. 11 Drift and diffusion coefficients for a retrograde test wire diffusing in the inner region of the system along the grey dashed line, It = const., identified in Fig. 10. Left panel: illustration of the drift coefficient Lt → A(Lt,It), as introduced in Eq. (62). Right panel: illustration of the diffusion coefficient Lt → D(Lt,It), as introduced in Eq. (62). As the test wire gets closer to the centre of the system, the drift and diffusion coefficients tend to 0: this is the Schwarzschild barrier, which prevents individual stars to diffuse closer to the central BH as a sole result of resonant relaxation. The quenching of the resonant diffusion is very abrupt in razor-thin discs, as a result of the limitation to 1:1 resonance in the degenerate Landau Eq. (19). This is specific to the razor-thin geometry. |
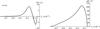 |
Fig. 12 Stochastic Langevin coefficients associated with the drift and diffusion coefficients shown in Fig. 11. Left panel: illustration of the Langevin drift coefficient Lt → h(Lt,It). Following Eq. (64), this coefficient gives the mean direction of motion for a given location in action space. Right panel: illustration of the Langevin diffusion coefficient Lt → g(Lt,It). This coefficient describes the jitter of wires around the mean flow given by h. In particular, it allows wires to stochastically penetrate the barrier. |
Any wire in the system undergoes two simultaneous precessions, given by 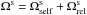 . As emphasised in Kocsis & Tremaine (2011) and in Fig. 3, one can note that the self-consistent mass precession frequencies
. As emphasised in Kocsis & Tremaine (2011) and in Fig. 3, one can note that the self-consistent mass precession frequencies 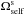 induced by the disc are retrograde precessions in the vicinity of the disc (i.e.
induced by the disc are retrograde precessions in the vicinity of the disc (i.e. 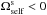 for L> 0), while the relativistic precession frequencies
for L> 0), while the relativistic precession frequencies 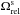 are prograde precessions (i.e.
are prograde precessions (i.e. 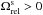 for L> 0). Because the mass precession dominates the precessions in the vicinity of the disc, a wire located within the disc region will undergo a retrograde precession, while a wire located close to the central BH will mainly precess as a result of the relativistic precessions and therefore will undergo a prograde precession. We note that the resonance condition present in the Landau Eq. (19)is sign-dependent, that is requests to exactly match the precession of the resonating wires so that Ωs(J1) = Ωs(J2). As a consequence, for a test wire located close to the central BH to be able to resonate with a disc composed only of prograde orbits (i.e. L> 0), this test wire has to be retrograde (i.e. Lt< 0), as we will now assume. Should the test wire in the central wire be also prograde, no efficient resonant couplings would be permitted by the Landau Eq. (19)and the associated diffusion would tend to 0. Let us note that this requirement on the central test wire direction of rotation arises from the additional constraints associated with the disc’s geometry. For a 3D spherical quasi-Keplerian systems, the Landau Eq. (19)would allow for additional resonances. This will be the subject of a future work.
for L> 0). Because the mass precession dominates the precessions in the vicinity of the disc, a wire located within the disc region will undergo a retrograde precession, while a wire located close to the central BH will mainly precess as a result of the relativistic precessions and therefore will undergo a prograde precession. We note that the resonance condition present in the Landau Eq. (19)is sign-dependent, that is requests to exactly match the precession of the resonating wires so that Ωs(J1) = Ωs(J2). As a consequence, for a test wire located close to the central BH to be able to resonate with a disc composed only of prograde orbits (i.e. L> 0), this test wire has to be retrograde (i.e. Lt< 0), as we will now assume. Should the test wire in the central wire be also prograde, no efficient resonant couplings would be permitted by the Landau Eq. (19)and the associated diffusion would tend to 0. Let us note that this requirement on the central test wire direction of rotation arises from the additional constraints associated with the disc’s geometry. For a 3D spherical quasi-Keplerian systems, the Landau Eq. (19)would allow for additional resonances. This will be the subject of a future work.
As shown in Fig. 10, one may then study the stochastic diffusion of such a retrograde test wire along the grey segment where it may resonate with the outer quasi-Keplerian disc. This is illustrated in Fig. 11 where the drift and diffusion coefficients associated with the diffusion of this test wire are computed following Eq. (62). Recall that because the test star is assumed to be retrograde, one has Lt< 0. In Fig. 11, one can note that for | Lt | ≲ 2.7 × 103, the drift and diffusion coefficients tend to 0. This is the Schwarzschild barrier. Wires of high eccentricity, that is wires which get close to the central BH undergo a large relativistic precession. For eccentricities large enough, this relativistic precession gets so large that it prevents any coupling between the test wire and wires within the disc. The resonant relaxation stops. For a razor-thin disc, the quenching is very abrupt, and for low enough | Lt |, the drift and diffusion coefficients tend to 0. This is a direct consequence of the Landau Eq. (19), which for razor-thin discs, only allows for 1:1 resonances. For 3D systems, the geometric constraint on the allowed resonances weakens. Higher-order resonances, while associated with weaker coupling factors, are allowed by the kinetic equation, so that the quenching of the resonant relaxation in the vicinity of the Schwarzschild barrier is expected to be less abrupt compared to what has been obtained in Fig. 11. In practice, this suppression of the diffusion is tempered by simple two-body relaxation, not accounted for in the present orbit-averaged diffusion. This provides an additional mechanism allowing stars to diffuse closer to the BH, once resonant relaxation becomes inefficient. As demonstrated in Bar-Or & Alexander (2016), the effects of resonant relaxation are limited to regions well away of the loss cone, so that the dynamics of stars’ accretion is only moderately affected by the presence of resonances.
Following the computation of the drift and diffusion coefficients in Fig. 11, one may then rely on Eq. (65)to estimate the Langevin coefficients, h and g, characterising the stochastic diffusion of the test wire. These coefficients are illustrated in Fig. 12. As already noted in Fig. 11, the Langevin coefficients tend to 0 for | Lt | ≲ 2.7 × 103, which corresponds to the Schwarzschild barrier. In the Langevin Eq. (65), the coefficient h corresponds to the drift coefficient and describes the mean deterministic motion followed by the test particle. Here, it is negative right before the barrier, so that retrograde test wires in the vicinity of the barrier diffuse in average towards larger | Lt |, that is towards smaller eccentricities. In Eq. (65), the coefficient g is associated with the stochastic diffusion of the test wire. It describes the jitter of the test wire around the mean flow due to h. On the long-term, it can allow wires to stochastically penetrate the diffusion barrier. Finally, while the drift coefficient −A(Jt) is always positive in Fig. 11, the contributions from the diffusion coefficient in Eq. (65)lead to a Langevin drift coefficient h taking both positive and negative values in Fig. 12.
Figures 11 and 12 recover the diffusion barrier for a retrograde test wire of fast action It. The location of this quenching of the resonant diffusion can be interpreted as being given by the value of the slow action LSchw., such that 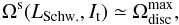 (70)where
(70)where 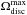 is the typical maximum precession frequency in the disc region, that is the maximum value of Ωs in Fig. 4. For a retrograde test wire such that | Lt | ≲ LSchw., its relativistic Schwarzschild precession makes it precess too fast to allow for a resonant coupling with the disc and the diffusion quenches. Following the criterion from Eq. (70), the location of the barrier for retrograde test stars is then given in action space by the curve γSchw., such that
is the typical maximum precession frequency in the disc region, that is the maximum value of Ωs in Fig. 4. For a retrograde test wire such that | Lt | ≲ LSchw., its relativistic Schwarzschild precession makes it precess too fast to allow for a resonant coupling with the disc and the diffusion quenches. Following the criterion from Eq. (70), the location of the barrier for retrograde test stars is then given in action space by the curve γSchw., such that 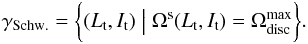 (71)The location of this barrier is illustrated in Fig. 10, where it is given by the left-most level contours of Ωs. Retrograde test wires below this barrier are precessing too fast to resonate anymore with the disc. Different retrograde test wires having different fast actions It will therefore see their stochastic diffusion quench for different values of their slow action Lt.
(71)The location of this barrier is illustrated in Fig. 10, where it is given by the left-most level contours of Ωs. Retrograde test wires below this barrier are precessing too fast to resonate anymore with the disc. Different retrograde test wires having different fast actions It will therefore see their stochastic diffusion quench for different values of their slow action Lt.
Having computed the Langevin coefficients h and g in Fig. 12, it is then straightforward to integrate the Langevin Eq. (64)forward in time. Such realisations are illustrated in Fig. 13,
 |
Fig. 13 Stochastic motion, t → Lt(t), of a retrograde test star of mass μt = μ⋆ for different initial conditions. The trajectory of the star is described by the Langevin Eq. (64), with the Langevin coefficients h and g obtained in Fig. 12. Because these coefficients tend to 0 for low enough angular momentum (| Lt | ≲ 2.7 × 103), retrograde test stars cannot diffuse closer to the BH. This quenching of the resonant diffusion in the inner regions of the system is associated with the Schwarzschild barrier and is illustrated with the grey region. |
which shows again that wires cannot diffuse below the Schwarzschild barrier. These evolution equations share some similarities with the equations of motions of individual stars. However, the significant gain of this framework is that it directly describes the stochastic motion of Keplerian wires, so that the Keplerian motion of stars along their quasi-Keplerian ellipses does not have to be resolved anymore. This allows for much larger timesteps in Eq. (64), which are orders of magnitude larger than those required to solve the individual trajectories of stars. Relativistic effects and the associated post-Newtonian corrections are also effortlessly accounted for.
Not only can one use the Langevin Eq. (64)to describe the evolution of an individual test particle, but also the secular diffusion of a population of wires as a whole. This is illustrated in Fig. 14, which shows how the long-term diffusion of the PDF of a population of retrograde test wires may also be estimated.
 |
Fig. 14 Diffusion of a population of retrograde test wires of individual mass μt = μ⋆ as a function of time. The evolution of each star is driven by the Langevin Eq. (64). The initial PDF of the population is represented by the red histogram, while the coloured histograms describe the statistics of the population after a time ΔT = 200 and 2ΔT. Solving the dynamics of this population via the Langevin Eq. (64)allows for the integration forward in time of the Fokker-Planck Eq. (62), which describes the diffusion of the test wires’ PDF as a whole, without resorting to direct N-body simulations. |
The method followed in Fig. 14 allows indeed for the effective integration forward in time of the Fokker-Planck Eq. (62). To do so, one samples the test particle’s PDF, P, with test wires. The stochastic motion of each test wire is then integrated forward in time via the Langevin Eq. (64)for a time ΔT that can be much larger than the Keplerian dynamical time of the system. After a time ΔT, the population of test wires is then distributed according to the PDF P(t = ΔT), illustrated in Fig. 14. In this figure, even if the time of integration was short, one can already note that some wires tend to accumulate at the Schwarzschild barrier, where the diffusion quenches.
The sampling method used in Fig. 14 may also be used to integrate forward in time the self-consistent Landau Eq. (19). To do so, one has to estimate the disc’s drift and diffusion coefficients A(J) and D(J). The disc’s initial DF, F⋆, is then sampled by a finite number of test stars Nsamp.. Assuming temporarily that the drift and diffusion coefficients are frozen, one may then integrate the motion of these Nsamp. test stars following the Langevin Eq. (64). This allows for the estimation of P(t = ΔT) ≃ F⋆(t = ΔT), provided that ΔT is not too large compared to the timescale of resonant relaxation. Having estimated the disc’s new DF at the time ΔT, one may then recompute the new drift and diffusion coefficients of the disc, A(J,ΔT) and D(J,ΔT). Sampling once again this new DF with Nsamp. test stars, one can proceed further. Provided that the timestep ΔT is chosen accordingly, so that the disc’s self-consistent drift and diffusion coefficients do not change much on the timescale ΔT, the present step-by-step approach allows therefore for the integration forward in time of the self-consistent Landau Eq. (19).
4.3. Resonant dynamical friction on a massive perturber
The previous section described the stochastic diffusion of an individual test star, whose individual mass is identical to that of the stars forming the discrete quasi-Keplerian disc. Inspired by the multi-component calculations presented in Sect. 3.3, one could also consider the individual diffusion of a massive perturber whose mass would not be the same as the wires from the discrete bath. Noting the mass of this test perturber as μt and the individual mass of the wires of the bath as μ⋆, the Fokker-Planck Eq. (62)becomes ![\begin{equation} \frac{\partial P}{\partial \tau} = \frac{\partial }{\partial L} \bigg[\frac{\mu_{\rt}}{\mu_{\star}} \, A (\bm{J}) \, P (\bm{J}) + D (\bm{J}) \, \frac{\partial P}{\partial L} \bigg] , \label{FP_disc_heavy} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq301.png) (72)where P is the PDF of the massive perturber. In Eq. (72), the drift and diffusion coefficients, A(J) and D(J), were already introduced in Eq. (24)and are sourced by the discrete quasi-Keplerian disc. When accounting for a possible different mass for the test particle, the equilibrium solution from Eq. (67)immediately becomes
(72)where P is the PDF of the massive perturber. In Eq. (72), the drift and diffusion coefficients, A(J) and D(J), were already introduced in Eq. (24)and are sourced by the discrete quasi-Keplerian disc. When accounting for a possible different mass for the test particle, the equilibrium solution from Eq. (67)immediately becomes ![\begin{equation} P_{\rm eq} (L , I) = C (I) \, \exp \left [ {-} ( \mu_{\rt}/\mu_{\star} ) V_{\rm eq} (L , I) \right] , \label{equilibrium_FP_multi} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq302.png) (73)where the potential Veq(L,I) was introduced in Eq. (68).
(73)where the potential Veq(L,I) was introduced in Eq. (68).
Following Eq. (65), one can straightforwardly obtain the Langevin coefficients associated with the Fokker-Planck Eq. (72). They read 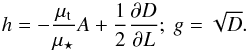 (74)In Eq. (74), one can note that only the Langevin drift coefficient h depends on the mass of the test particle. Figure 15 illustrates this coefficient for a retrograde massive test wire of mass μt = 100μ⋆.
(74)In Eq. (74), one can note that only the Langevin drift coefficient h depends on the mass of the test particle. Figure 15 illustrates this coefficient for a retrograde massive test wire of mass μt = 100μ⋆.
 |
Fig. 15 Stochastic Langevin coefficient Lt → h(Lt,It) associated with the stochastic diffusion of a retrograde massive perturber of mass μt = 100μ⋆ along the grey dashed line, It = const., identified in Fig. 10. The coefficient g associated with the stochastic of this massive perturber is the same as in Fig. 12. Following Eq. (72), one can note that for a massive enough perturber (or for light enough bath wires), one has h(Jt) → −(μt/μ⋆)A(Jt) and g(Jt) → 0. This non-vanishing contribution is the friction force by polarisation, which drives dynamical friction. |
Let us note that the definition from Eq. (25)is such that the disc’s drift and diffusion coefficients, A(J) and D(J), satisfy A,D ∝ μ⋆. The larger the number of wires in the disc, the slower the diffusion. As a consequence, in the limit of a collisionless bath, that is when μ⋆ → 0, only the drift component remains in Eq. (72). This corresponds to the friction force by polarisation, which does not vanish in the collisionless limit (Heyvaerts et al. 2017). Following Eq. (74), one can note that in this collisionless limit only the drift coefficient h(Jt) → −(μt/μ⋆) A(Jt) remains in the Langevin Eq. (64). The evolution of the test wire is fully deterministic and, following Eq. (64), reads 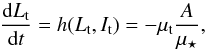 (75)where, following Eq. (25), A/μ⋆ is independent of μ⋆. Equation (75)is the equation describing dynamical friction. Comparing Figs. 12 and 15, one can note that for a test wire of individual mass μt = 100μ⋆, the Langevin coefficients satisfy g ≲ h. As a consequence, the evolution of such a heavy wire can be approximated by the deterministic Eq. (75). From Figs. 12 and 15, one can also note that for a massive enough retrograde test particle, one has h(Lt) > 0 for Lt< 0. As a consequence, the dynamical friction undergone by this retrograde massive perturber induces a drift towards smaller | Lt |, that is towards higher eccentricities: the orbit of this retrograde massive perturber gets more eccentric.
(75)where, following Eq. (25), A/μ⋆ is independent of μ⋆. Equation (75)is the equation describing dynamical friction. Comparing Figs. 12 and 15, one can note that for a test wire of individual mass μt = 100μ⋆, the Langevin coefficients satisfy g ≲ h. As a consequence, the evolution of such a heavy wire can be approximated by the deterministic Eq. (75). From Figs. 12 and 15, one can also note that for a massive enough retrograde test particle, one has h(Lt) > 0 for Lt< 0. As a consequence, the dynamical friction undergone by this retrograde massive perturber induces a drift towards smaller | Lt |, that is towards higher eccentricities: the orbit of this retrograde massive perturber gets more eccentric.
Expanding on Sect. 3.3, let us finally investigate the process of mass segregation using the Langevin formalism. Having already estimated the disc’s drift and diffusion coefficients in Fig. 11, one may now rely on Eq. (74)to compute the Langevin coefficients of populations of retrograde test stars of different individual mass. Figure 16 presents the respective diffusion of two populations of retrograde test stars of individual mass μt = μ⋆ and μt = 10μ⋆, distributed initially according to the same PDF.
 |
Fig. 16 Diffusion of two populations of retrograde test stars of different individual mass. The two populations are initially distributed according to the same PDF, illustrated with the black histogram. The evolution of each test star is described by the Langevin equation associated with the Fokker-Planck Eq. (72). After a time ΔT = 200, the PDF of the light population (of individual mass μt = μ⋆) is given by the red histogram, while the heavy population (of individual mass μt = 10μ⋆) follows the PDF given by the blue histogram. Because of the prefactor (μt/μ⋆) present in Eq. (72), populations of different individual mass do not follow the same stochastic motions, and the system undergoes a mass segregation. Light (red) wires tend to become less eccentric and heavy (blue) wires tend to become more eccentric. |
Figure 16 predicts that populations of retrograde test wires of different mass segregate in the vicinity of the disc. The heavier wires will tend towards orbits of smaller angular momentum, that is towards more eccentric orbits. One can also note that some heavy wires already tend to accumulate at the Schwarzschild barrier, where resonant diffusion stops.
Figure 8 emphasises that heavy prograde stars in the disc would tend to diffuse towards smaller eccentricities, while Fig. 16 shows that heavy retrograde test stars would preferentially segregate towards higher eccentricities. Let us clarify the origin of this dichotomy. Such differences in the behaviours of prograde and retrograde massive test stars originate from the fact that the razor-thin degenerate Landau Eq. (19)only allows for 1:1 resonances, and that the quasi-Keplerian razor-thin disc considered in Eq. (8)is only composed of prograde stars. Let us illustrate this property by computing the sign of the friction force by polarisation undergone by a massive perturber, as given by Eq. (75). Following Fig. 2, let us assume that ∂F⋆/∂L> 0 (this is true in most of action space). The expression of the drift coefficients from Eq. (25)gives us then that A(J) ≤ 0 for all J, that is whatever the sign of L and therefore for both prograde and retrograde stars. As a consequence, the direction of the associated dynamical friction given by Eq. (75)reads 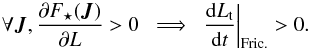 (76)We note that the result from Eq. (76)is independent of the sign of the angular momentum Lt of the considered test star. As a consequence, for a prograde test star (i.e. Lt> 0), the friction force leads to a diffusion towards larger | Lt |, that is towards smaller eccentricities, while for a retrograde test star (i.e. Lt< 0), the friction force leads to a diffusion towards smaller | Lt |, that is towards larger eccentricities. This dichotomy is related to the “secular dynamical anti-friction” put forward in Madigan & Levin (2012). Should one consider a quasi-Keplerian disc made of both prograde and retrograde stars, the condition ∂F⋆/∂L> 0 would not hold anymore, and the direction of dynamical friction cannot be predicted using Eq. (76). Similarly, in 3D quasi-Keplerian systems, the associated Landau equation does not impose anymore the restriction to 1:1 resonances, which also prevents us from relying on Eq. (76).
(76)We note that the result from Eq. (76)is independent of the sign of the angular momentum Lt of the considered test star. As a consequence, for a prograde test star (i.e. Lt> 0), the friction force leads to a diffusion towards larger | Lt |, that is towards smaller eccentricities, while for a retrograde test star (i.e. Lt< 0), the friction force leads to a diffusion towards smaller | Lt |, that is towards larger eccentricities. This dichotomy is related to the “secular dynamical anti-friction” put forward in Madigan & Levin (2012). Should one consider a quasi-Keplerian disc made of both prograde and retrograde stars, the condition ∂F⋆/∂L> 0 would not hold anymore, and the direction of dynamical friction cannot be predicted using Eq. (76). Similarly, in 3D quasi-Keplerian systems, the associated Landau equation does not impose anymore the restriction to 1:1 resonances, which also prevents us from relying on Eq. (76).
5. Conclusion
We investigated the secular dynamics of a razor-thin axisymmetric discrete quasi-Keplerian disc surrounding a SMBH. In the limit where collective effects are not accounted for, such an evolution induced by finite-N effects is described by the degenerate inhomogeneous Landau Eq. (19), recently derived in Sridhar & Touma (2017) and Fouvry et al. (2017b). This is the master equation of resonant relaxation (Rauch & Tremaine 1996). The present paper presented the first effective implementation of this kinetic equation to quasi-Keplerian systems5.
In Sect. 3, we computed the self-consistent diffusion flux of the quasi-Keplerian disc and predicted the associated timescale of resonant relaxation. We also considered the simultaneous relaxation of two components of different individual mass, which leads to a mass segregation of the two components. For the specific disc considered here, we showed that heavier wires would diffuse towards smaller eccentricities and would therefore circularise, while lighter wires would diffuse towards larger eccentricities and therefore approach the central BH. More generally, all discs for which ∂F⋆/∂L> 0 obey such a trend.
In Sect. 4, we illustrated how the same formalism also describes the stochastic diffusion of individual wires, by relying on the associated Langevin Eq. (64). We identified the quenching of the diffusion in the central region of the system, a phenomenon called the Schwarzschild barrier (Merritt et al. 2011). This rewriting of the dynamics in terms of the diffusion of individual wires may be used to integrate forward in time the evolution of the system’s DF as a whole. Hence the present method offers an effective alternative to direct N-body or Monte-Carlo methods, in order to integrate self-consistently in time the evolution of a system’s DF driven by resonant relaxation. Most of the tools presented in this paper could also be implemented in the context of protoplanetary debris discs (Tremaine 1998).
The present work should be extended in various ways. It is currently limited to razor-thin axisymmetric discs for which the kinetic Eq. (19)takes a simpler form. In particular, it only involves 1:1 resonances on the precession frequencies. As shown in Fouvry et al. (2017b), 3D spherical systems are also quasi-stationary states whose resonant relaxation can be described by a very similar inhomogeneous degenerate kinetic equation. However, because of the additional vertical dimension, higher order resonances are allowed. For such systems, following Fig. 11, one should investigate how the resonant diffusion quenches in the central regions and how populations of different masses may segregate in eccentricities. In addition, by accounting for vector resonant relaxation and the induced changes in the orientation of each wire, one could investigate how the plane of the razor-thin disc gets slowly distorted by out-of-plane precessions (see e.g. Chen & Amaro-Seoane 2014). Another venue would be to investigate the long-term evolution of non-axisymmetric razor-thin discs (e.g. Tremaine 1995), which requires to extend accordingly the derivation presented in Paper I. In the present calculations, we accounted only for the 1PN Schwarzschild in-plane relativistic precession. It might be of interest to investigate the possible effects associated with the 1.5PN Lense-Thirring relativistic precession, which can in particular induce a precession of the wire’s orbital plane. The kinetic equations considered rely on the orbit-averaging of the fast Keplerian motions and can only account for resonant diffusion. As such, it cannot capture mean motion resonances. A subsequent improvement would be to add the secondary effects of two-body non-resonant relaxation in the Langevin Eq. (64). In particular, this two-body non-resonant relaxation allows particles to exchange energy, that is to change their fast action I, which cannot occur via resonant relaxation (Amaro-Seoane et al. 2013).
One could also be interested in investigating the long-term effect of stellar binaries on the cluster’s diffusion (see e.g. Perets et al. 2007; O’Leary et al. 2009; Perets 2009; Antonini & Perets 2012; Witzel et al. 2014; Pfuhl et al. 2014; Prodan et al. 2015; Stephan et al. 2016; Hoang et al. 2017; Witzel et al. 2017). Binaries could first be treated as a second population of effective particles of higher individual masses (as in Sect. 3.3), and their respective resonant relaxation would be governed by the present kinetic theory. Yet, these methods cannot account for the binaries’ additional degree of freedom, their associated energy. This plays for example an essential role in the gravothermal catastrophe of globular clusters (Lynden-Bell & Wood 1968). Moreover, the detailed interactions between a stellar binary and a passing-by star could not be accounted for as such, because they correspond effectively to three-body effects out of reach of a kinetic framework based on a truncation at order 1 /N of the evolution equations. A final venue would be to consider a central binary black hole and its orbiting stellar cluster (following e.g. Rothe & Schäfer 2010), where the corresponding extra internal orbital degree of freedom may provide a range of intermediate frequencies, allowing the stars to pass the barrier and/or the binary to tighten, leading for example to EMRIs. Predicting the impact of resonant relaxation with the stellar cluster on the corresponding rates should be of interest when preparing for LISA.
This paper implemented the inhomogeneous Landau equation while neglecting collective effects. In order to account for the self-gravitating amplification of the system one should rely on Fouvry et al. (2017b), which derived the corresponding inhomogeneous degenerate Balescu-Lenard equation. For quasi-Keplerian systems, accounting for collective effects requires the evaluation of the disc’s averaged response matrix, a quantity which characterises the strength of the self-gravitating amplification in the system (see Tremaine 2005; Polyachenko et al. 2007; Jalali & Tremaine 2012 for examples of stability investigations in the quasi-Keplerian context). Because of the BH’s prevalence on the dynamics of individual stars, it is not straightforward to determine the amplitude of the gravitational polarisation in these degenerate systems, seen as a collection of Keplerian wires. This will be the subject of a future work.
This approach relies on a long tradition of kinetic theory, starting from the seminal papers of Landau (1936) and Chandrasekhar (1942, 1943a,b), followed by Balescu (1960) and Lenard (1960), and using the recent developments of Luciani & Pellat (1987), Mynick (1988), Heyvaerts (2010) and Chavanis (2012). See Heyvaerts et al. (2017) for a review.
Equation (62)can also straightforwardly be rewritten under the traditional form (Binney & Tremaine 2008)
![\begin{equation} \frac{\partial P}{\partial \tau} = \frac{\partial }{\partial L} \bigg[ - D^{(1)} (\bm{J}) \, P (\bm{J}) + \frac{\partial }{\partial L} \bigg[ D^{(2)} (\bm{J}) \, P (\bm{J}) \bigg] \bigg] , \nonumber \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq238.png) (63)
where the first- and second-order diffusion coefficients are given by D(1) = −A + ∂D/∂L and D(2) = D. Here, D(1) captures the true friction force, while −A captures the friction force by polarisation (Chavanis 2012; Heyvaerts et al. 2017).
(63)
where the first- and second-order diffusion coefficients are given by D(1) = −A + ∂D/∂L and D(2) = D. Here, D(1) captures the true friction force, while −A captures the friction force by polarisation (Chavanis 2012; Heyvaerts et al. 2017).
Let us note that the mechanism of the Schwarzschild barrier shares some analogies with the phenomenon of kinetic blocking observed in the kinetic theory of point vortices in 2D hydrodynamics (Chavanis & Lemou 2007). In these systems, a suppression of the resonant diffusion occurs for monotonic profiles of angular frequencies.
More generally, it has only been applied to a handful of systems: 2D razor-thin non-degenerate stellar discs (Fouvry et al. 2015a,b), 3D thickened stellar discs (Fouvry et al. 2017a), or to the 1D inhomogeneous HMF model (Benetti & Marcos 2017).
Acknowledgments
We thank Scott Tremaine, Ben Bar-Or, James Binney, John Magorrian and Marta Volonteri for stimulating discussions. We thank the anonymous referee for numerous valuable comments. Support for Program number HST-HF2-51374 was provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. This research is also part of ANR grant Spin(e) (ANR-13-BS05-0005, http://cosmicorigin.org). This work has made use of the Horizon cluster hosted by the Institut d’Astrophysique de Paris (we thank S. Rouberol for running it smoothly for us), as well as of the Hyperion cluster hosted by the Institute for Advanced Study.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Alexander, T. 2005, Phys. Rep., 419, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, T. 2017, ARA&A, 55, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, T., & Morris, M. 2003, ApJ, 590, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012, Class. Quantum Gray., 29, 124016 [Google Scholar]
- Amaro-Seoane, P., Sopuerta, C. F., & Freitag, M. D. 2013, MNRAS, 429, 3155 [NASA ADS] [CrossRef] [Google Scholar]
- Antonini, F., & Perets, H. B. 2012, ApJ, 757, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1977, ApJ, 216, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Balescu, R. 1960, Phys. Fluids, 3, 52 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bar-Or, B., & Alexander, T. 2014, Class. Quant. Grav., 31, 244003 [NASA ADS] [CrossRef] [Google Scholar]
- Bar-Or, B., & Alexander, T. 2016, ApJ, 820, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, F. P. C., & Marcos, B. 2017, Phys. Rev. E, 95, 022111 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, second edition (Princeton University Press) [Google Scholar]
- Chandrasekhar, S. 1942, Principles of Stellar Dynamics (University of Chicago Press) [Google Scholar]
- Chandrasekhar, S. 1943a, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943b, ApJ, 97, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1944, ApJ, 99, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2012, Physica A, 391, 3680 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H., & Lemou, M. 2007, EpJB, 59, 217 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chen, X., & Amaro-Seoane, P. 2014, ApJ, 786, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J. B., Pichon, C., & Chavanis, P. H. 2015a, A&A, 581, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouvry, J. B., Pichon, C., Magorrian, J., & Chavanis, P. H. 2015b, A&A, 584, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouvry, J.-B., Pichon, C., Chavanis, P.-H., & Monk, L. 2017a, MNRAS, 471, 2642 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J.-B., Pichon, C., & Magorrian, J. 2017b, A&A, 598, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., & Rees, M. J. 1976, MNRAS, 176, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Freitag, M., Amaro-Seoane, P., & Kalogera, V. 2006, ApJ, 649, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Pichon, C., Eckart, A., Gerhard, O. E., & Ott, T. 2000, MNRAS, 317, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J. 2010, MNRAS, 407, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., Fouvry, J.-B., Chavanis, P.-H., & Pichon, C. 2017, MNRAS, 469, 4193 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
- Hils, D., & Bender, P. L. 1995, ApJ, 445, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, B.-M., Naoz, S., Kocsis, B., Rasio, F. A., & Dosopoulou, F. 2017, ApJ, submitted [arXiv:1706.09896] [Google Scholar]
- Hopman, C., & Alexander, T. 2006a, ApJ, 645, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Hopman, C., & Alexander, T. 2006b, ApJ, 645, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Hörmander, L. 2003, The analysis of linear partial differential operators. I (Springer-Verlag) [Google Scholar]
- Jalali, M. A., & Tremaine, S. 2012, MNRAS, 421, 2368 [NASA ADS] [CrossRef] [Google Scholar]
- Jocou, L., Perraut, K., Moulin, T., et al. 2014, in Optical and Infrared Interferometry IV, 9146, 91461J [Google Scholar]
- Keshet, U., Hopman, C., & Alexander, T. 2009, ApJ, 698, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Kocsis, B., & Tremaine, S. 2011, MNRAS, 412, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Kocsis, B., & Tremaine, S. 2015, MNRAS, 448, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. 1936, Phys. Z. Sowj. Union, 10, 154 [Google Scholar]
- Lenard, A. 1960, Ann. Phys., 10, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Luciani, J. F., & Pellat, R. 1987, J. Phys., 48, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Wood, R. 1968, MNRAS, 138, 495 [NASA ADS] [Google Scholar]
- Madigan, A.-M., & Levin, Y. 2012, ApJ, 754, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Madigan, A.-M., Hopman, C., & Levin, Y. 2011, ApJ, 738, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., & Tremaine, S. 1999, MNRAS, 309, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 2013a, Dynamics and Evolution of Galactic Nuclei (Princeton University Press) [Google Scholar]
- Merritt, D. 2013b, Class. Quant. Grav., 30, 244005 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 2015, ApJ, 804, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Mikkola, S., Will, C., Alexander, T., & Harfst, S. 2009, in APS Meeting Abstracts [Google Scholar]
- Merritt, D., Alexander, T., Mikkola, S., & Will, C. M. 2011, Phys. Rev. D, 84, 044024 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Mynick, H. E. 1988, J. Plasma Phys., 39, 303 [NASA ADS] [CrossRef] [Google Scholar]
- O’Leary, R. M., Kocsis, B., & Loeb, A. 2009, MNRAS, 395, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B. 2009, ApJ, 698, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., Hopman, C., & Alexander, T. 2007, ApJ, 656, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Pfuhl, O., Alexander, T., Gillessen, S., et al. 2014, ApJ, 782, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Polyachenko, E. V., Polyachenko, V. L., & Shukhman, I. G. 2007, MNRAS, 379, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Prodan, S., Antonini, F., & Perets, H. B. 2015, ApJ, 799, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, K. P., & Tremaine, S. 1996, New Astron., 1, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Risken, H. 1996, The Fokker-Planck Equation (Berlin Heidelberg: Springer) [Google Scholar]
- Rothe, T. J., & Schäfer, G. 2010, J. Math. Phys., 51, 082501 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Lightman, A. P. 1976, Nature, 262, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S. 2003, Class. Quant. Grav., 20, S45 [NASA ADS] [CrossRef] [Google Scholar]
- Sridhar, S., & Touma, J. 1999, MNRAS, 303, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Sridhar, S., & Touma, J. R. 2017, MNRAS, 465, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Stephan, A. P., Naoz, S., Ghez, A. M., et al. 2016, MNRAS, 460, 3494 [NASA ADS] [CrossRef] [Google Scholar]
- Syer, D., & Ulmer, A. 1999, MNRAS, 306, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Touma, J. R., Tremaine, S., & Kazandjian, M. V. 2009, MNRAS, 394, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S. 1995, AJ, 110, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S. 1998, AJ, 116, 2015 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S. 2005, ApJ, 625, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Dubois, Y., Pichon, C., & Devriendt, J. 2016, MNRAS, 460, 2979 [Google Scholar]
- Witzel, G., Ghez, A. M., Morris, M. R., et al. 2014, ApJ, 796, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, G., Sitarski, B. N., Ghez, A. M., et al. 2017, ApJ, 847, 80 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The wire-wire interaction potential
Let us compute the wire-wire interaction potential 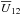 from Eq. (22). The difficulty with such a calculation is that it requires to integrate over the fast orbital angle of each of the two wires involved. This turns out to be numerically very demanding, in particular when the two wires share the same orbital plane. Fortunately, Gauss’ method (Touma et al. 2009) allows us to perform explicitly one of these two integrals. We will not repeat the calculations presented in Touma et al. (2009), but will rather detail how they may be adapted to the present context.
from Eq. (22). The difficulty with such a calculation is that it requires to integrate over the fast orbital angle of each of the two wires involved. This turns out to be numerically very demanding, in particular when the two wires share the same orbital plane. Fortunately, Gauss’ method (Touma et al. 2009) allows us to perform explicitly one of these two integrals. We will not repeat the calculations presented in Touma et al. (2009), but will rather detail how they may be adapted to the present context.
In order to avoid divergences associated with crossing orbits or identical orbits, the pairwise interaction potential is softened according to Eq. (18), for which the method of Touma et al. (2009) can also be applied. Using the notations from Eq. (18), the interaction potential from Eq. (22)requires us to evaluate ![\appendix \setcounter{section}{1} \begin{eqnarray} \oU_{12} (\bR_{1} , \bR_{2}) &=& - \frac{G M_{\bullet}}{(2 \pi)^{2}} \nonumber \\ &&\times \int \rd w_{1} \rd w_{2} \, \frac{1}{\sqrt{ \big| \bm{x}_{1} [\bR_{1} , g_{1}] - \bm{x}_{2} [\bR_{2} , w_{2}] \big|^{2} + \esoft^{2}}} \cdot \nonumber \label{start_ww} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq321.png) In order to emphasise the fact that one of the two angle integrals will be performed analytically, let us rewrite this equation as
In order to emphasise the fact that one of the two angle integrals will be performed analytically, let us rewrite this equation as ![\appendix \setcounter{section}{1} \begin{equation} \oU_{12} (\bR_{1} , \bR_{2}) = \frac{1}{2 \pi} \int \rd w_{1} \, \oUr ( \bm{x} [\bR_{1} , w_{1}] , \bR_{2} ) , \label{cal_I_ww} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq322.png) (A.1)where
(A.1)where 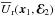 was introduced as
was introduced as ![\appendix \setcounter{section}{1} \begin{equation} \oUr (\bm{x}_{1} , \bR_{2}) = - \frac{G M_{\bullet}}{2 \pi} \int \rd w_{2} \, \frac{1}{\sqrt{\big| \bm{x}_{1} - \bm{x}_{2} [\bR_{2} , w_{2}] \big|^{2} + \esoft^{2}}} \cdot \label{definition_oUr} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq324.png) (A.2)Here, the potential
(A.2)Here, the potential 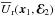 corresponds to the potential induced at position x1 by the wire of coordinates ℰ2. This potential involves an average over the orbital phase w2 of the second particle, which is the integration that will be performed explicitly via Gauss’ method. Given the mapping from Eq. (4), one can rewrite Eq. (A.2)as an integral over the eccentric anomaly η2. It becomes
corresponds to the potential induced at position x1 by the wire of coordinates ℰ2. This potential involves an average over the orbital phase w2 of the second particle, which is the integration that will be performed explicitly via Gauss’ method. Given the mapping from Eq. (4), one can rewrite Eq. (A.2)as an integral over the eccentric anomaly η2. It becomes 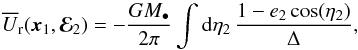 (A.3)where the distance Δ is introduced as
(A.3)where the distance Δ is introduced as ![\appendix \setcounter{section}{1} \begin{equation} \Delta^{2} = \big| \bm{x}_{1} - \bm{x}_{2} [\bR_{2} , \eta_{2}] \big|^{2} + \esoft^{2} . \label{definition_Delta_ww} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq331.png) (A.4)The non-trivial dependence of Δ with η2 is the reason for the difficulty of computing Eq. (A.3). Let us first rewrite the distance Δ in a simpler manner. One can note that the angle-action mapping from Eq. (3)takes the form
(A.4)The non-trivial dependence of Δ with η2 is the reason for the difficulty of computing Eq. (A.3). Let us first rewrite the distance Δ in a simpler manner. One can note that the angle-action mapping from Eq. (3)takes the form ![\appendix \setcounter{section}{1} \begin{equation} \bm{x} [\bR , \eta] = \bm{\mathcal{R}} (g) \cdot \bm{t} (\bm{J} , \eta) , \label{mapping_rot} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq332.png) (A.5)where the rotation matrix ℛ(g) and the vector t(J,η) (independent of g) read
(A.5)where the rotation matrix ℛ(g) and the vector t(J,η) (independent of g) read 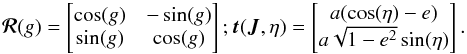 (A.6)If the location x1 considered in Eq. (A.3)is associated with the angle-action coordinates (ℰ1,η1), one can then write
(A.6)If the location x1 considered in Eq. (A.3)is associated with the angle-action coordinates (ℰ1,η1), one can then write  (A.7)From Eq. (A.7), one recovers again that the wire-wire interaction potential only depends on the phase difference Δg = g1−g2, as in Eq. (21). Introducing the notation
(A.7)From Eq. (A.7), one recovers again that the wire-wire interaction potential only depends on the phase difference Δg = g1−g2, as in Eq. (21). Introducing the notation 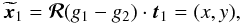 (A.8)one can finally rewrite the distance Δ2 from Eq. (A.4)as
(A.8)one can finally rewrite the distance Δ2 from Eq. (A.4)as 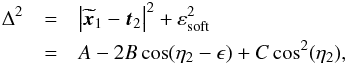 (A.9)given the quantities
(A.9)given the quantities 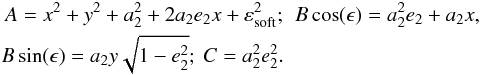 (A.10)We note the presence in Eq. (A.9)of the quadratic term in Ccos2(η2). This term is the reason why one cannot apply Gauss’ method to get an explicit expression for the potential
(A.10)We note the presence in Eq. (A.9)of the quadratic term in Ccos2(η2). This term is the reason why one cannot apply Gauss’ method to get an explicit expression for the potential  from Eq. (A.3). However, if instead of the potential, one considers the force by differentiating w.r.t.
from Eq. (A.3). However, if instead of the potential, one considers the force by differentiating w.r.t.  , since C is independent of
, since C is independent of  , this quadratic term vanishes and Gauss’ method may be applied to obtain an explicit expression for the force. Equation (A.3)gives us
, this quadratic term vanishes and Gauss’ method may be applied to obtain an explicit expression for the force. Equation (A.3)gives us ![\appendix \setcounter{section}{1} \begin{eqnarray} - \frac{\partial \oUr (\widetilde{\bm{x}}_{1} , \bR_{2})}{\partial \widetilde{\bm{x}}_{1}}& = & ~ \frac{G M_{\bullet}}{2 \pi} \, \int \rd \eta_{2} \, \frac{1 - e_{2} \cos (\eta_{2})}{\Delta^{3}} \nonumber \\ && \, \times \big[ \bm{F}_{0} + \bm{F}_{1} \sin(\eta_{2}) + \bm{F}_{2} \cos (\eta_{2}) \big] , \label{force_ww} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq346.png) (A.11)where the vectors F0, F1, and F2 obey
(A.11)where the vectors F0, F1, and F2 obey 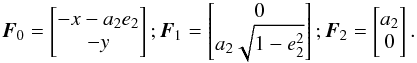 (A.12)Equation (A.11)gives the force created at the position
(A.12)Equation (A.11)gives the force created at the position  by the wire of coordinates ℰ2. Using Gauss’ method, this force may be computed analytically and is given by Eq. (67) of Touma et al. (2009), to which we refer.
by the wire of coordinates ℰ2. Using Gauss’ method, this force may be computed analytically and is given by Eq. (67) of Touma et al. (2009), to which we refer.
Once the force from Eq. (A.11)has been computed, one may finally compute the wire-wire interaction potential from Eq. (A.2). Recalling the definition of  from Eq. (A.8), the interaction potential from Eq. (A.1)may be rewritten as
from Eq. (A.8), the interaction potential from Eq. (A.1)may be rewritten as ![\appendix \setcounter{section}{1} \begin{eqnarray} && \oU_{12} \big[\bR_{1} , \bR_{2} \big] =\, \frac{1}{2 \pi} \!\!\int \!\! \rd \eta_{1} \, (1 - e_{1} \cos (\eta_{1})) \, \oUr \big[ \bm{\mathcal{R}} (g_{1} - g_{2}) \cdot \bm{t}_{1} , \bR_{2} \big] \nonumber \\ &&~ = \frac{1}{2 \pi} \bigg[ (\eta_{1} - e_{1} \sin (\eta_{1})) \, \oUr \big[ \bm{\mathcal{R}} (g_{1} - g_{2}) \cdot \bm{t}_{1} , \bR_{2} \big] \bigg]_{0}^{2 \pi} \nonumber \\ && ~~ - \frac{1}{2 \pi} \!\! \int \!\! \rd \eta_{1} \, (\eta_{1} - e_{1} \sin (\eta_{1})) \, \frac{\partial \oUr \big[ \bm{\mathcal{R}} (g_{1} - g_{2}) \cdot \bm{t}_{1} , \bR_{2} \big]}{\partial \eta_{1}} \nonumber \\ && ~ = \oUr \big[ \bm{\mathcal{R}} (g_{1} - g_{2}) \cdot \bm{t}_{1} (\eta_{1} = 0) , \bR_{2} \big] \label{calculation_oU_ww} \\ && \, + \frac{1}{2 \pi} \!\! \int \!\! \rd \eta_{1} \, (\eta_{1} - e_{1} \sin (\eta_{1})) \, \frac{\partial (\bm{\mathcal{R}} (g_{1} - g_{2}) \cdot \bm{t}_{1})}{\partial \eta_{1}} \!\cdot\! \left [ - \frac{\partial \oUr \big[ \widetilde{\bm{x}}_{1} , \bR_{2} \big]}{\partial \widetilde{\bm{x}}_{1}} \right] , \nonumber \end{eqnarray}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq351.png) (A.13)where the last term is given by the force from Eq. (A.11)via Gauss’ method. In Eq. (A.13), the term involving a derivative w.r.t. η1 is straightforward to compute via the mapping from Eq. (A.6). The two remaining terms in Eq. (A.13)involve both only one integration and are therefore estimated by relying on the trapezoidal rule. For a 2π-periodic function f, we consider K equally spaced points on [0; 2π] given by
(A.13)where the last term is given by the force from Eq. (A.11)via Gauss’ method. In Eq. (A.13), the term involving a derivative w.r.t. η1 is straightforward to compute via the mapping from Eq. (A.6). The two remaining terms in Eq. (A.13)involve both only one integration and are therefore estimated by relying on the trapezoidal rule. For a 2π-periodic function f, we consider K equally spaced points on [0; 2π] given by ![\appendix \setcounter{section}{1} \begin{equation} \big[ \theta_{1} , ... , \theta_{K} \big] = \big[ 0 ; \, 2 \pi/K ; ... ; 2 \pi (K - 1)/K \big] . \label{spacing_grid_trapz} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq357.png) (A.14)Integrations are then approximated as
(A.14)Integrations are then approximated as 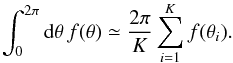 (A.15)In Eq. (A.13), the first term is estimated by sampling K points in η2 to compute Eq. (A.3), while the second term is estimated by sampling K points in η1, using the explicit expression of the force obtained from Gauss’ method in Eq. (A.11). In order to ensure an appropriate numerical convergence, the numerical applications presented in Sects. 3 and 4 used an estimation of the wire-wire interaction potential with K = 104 sampling points.
(A.15)In Eq. (A.13), the first term is estimated by sampling K points in η2 to compute Eq. (A.3), while the second term is estimated by sampling K points in η1, using the explicit expression of the force obtained from Gauss’ method in Eq. (A.11). In order to ensure an appropriate numerical convergence, the numerical applications presented in Sects. 3 and 4 used an estimation of the wire-wire interaction potential with K = 104 sampling points.
Appendix B: Computing the disc’s surface density
In this Appendix, for the sake of completeness, we briefly detail how the integral from Eq. (44)may be computed in order to determine the disc’s surface density associated with a given disc’s DF. To do so, we introduce the radial and tangential velocities v = (vr,vt). The tangential velocity is given by vt = L/R, while the radial one satisfies 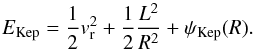 (B.1)Equation (B.1)introduced the Keplerian potential induced by the BH as ψKep(R) = −(GM•) /R, while the Keplerian energy EKep of the wire depends only on the fast action I and reads EKep(I) = −(1 / 2)(GM•/I)2. One can then write
(B.1)Equation (B.1)introduced the Keplerian potential induced by the BH as ψKep(R) = −(GM•) /R, while the Keplerian energy EKep of the wire depends only on the fast action I and reads EKep(I) = −(1 / 2)(GM•/I)2. One can then write 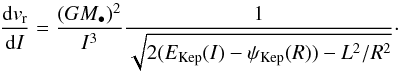 (B.2)\newpage\noindentPaying a careful attention to the fact that the radial velocity can be both positive and negative, Eq. (44)becomes
(B.2)\newpage\noindentPaying a careful attention to the fact that the radial velocity can be both positive and negative, Eq. (44)becomes 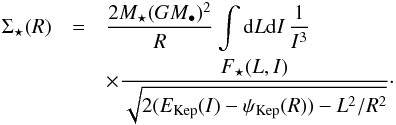 (B.3)In Eq. (B.3), the integration over (L,I) has to be limited to the domain where the argument of the square root is positive, that is one must have
(B.3)In Eq. (B.3), the integration over (L,I) has to be limited to the domain where the argument of the square root is positive, that is one must have 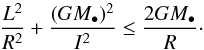 (B.4)This first asks for the action L to be such that L ∈ [Lmin;Lmax], with
(B.4)This first asks for the action L to be such that L ∈ [Lmin;Lmax], with 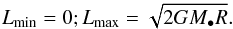 (B.5)Then, for such a value of L, the action I, which also has to satisfy the constraint I ≥ L, is restricted to the domain I ∈ [Imin;Imax], with
(B.5)Then, for such a value of L, the action I, which also has to satisfy the constraint I ≥ L, is restricted to the domain I ∈ [Imin;Imax], with ![\appendix \setcounter{section}{2} \begin{equation} I_{\rm min} = \text{Max} \bigg[ L , \, \frac{R G M_{\bullet}}{\sqrt{2 G M_{\bullet} R - L^{2}}} \bigg] ;~ I_{\rm max} = + \infty . \label{constraint_I_Sigmastar} \end{equation}](/articles/aa/full_html/2018/01/aa31088-17/aa31088-17-eq373.png) (B.6)Equation (B.3)is the equation that was used in Fig. 7 to compute the evolved surface density Σ⋆(τ).
(B.6)Equation (B.3)is the equation that was used in Fig. 7 to compute the evolved surface density Σ⋆(τ).
All Figures
 |
Fig. 1 Illustration of the disc’s surface density Σ⋆(R), as given by Eq. (11). Following the units from Eq. (6), the disc extends between 0.2 pc and 0.6 pc. |
| In the text | |
 |
Fig. 2 Illustration of the disc’s DF F⋆ from Eq. (8), in action space J = (L,I). It was assumed here that all stars are prograde, so that L> 0. Moreover, the action coordinates satisfy I ≥ L, so that I = L corresponds to circular orbits. The contours are spaced linearly between 95% and 5% of the DF maximum. The grey dashed lines correspond to the domain in action space from Eq. (14), to which the computations are restricted. |
| In the text | |
 |
Fig. 3 Dependence of the precession frequencies |
| In the text | |
 |
Fig. 4 Total precession frequencies |
| In the text | |
 |
Fig. 5 Diffusion flux, ℱL, predicted by the degenerate Landau Eq. (26)for the razor-thin quasi-Keplerian disc introduced in Sect. 2.2. Following the convention from Eq. (26), the direction of diffusion of individual wires in action space is given by −ℱL. Red contours, for which ℱL< 0, correspond to regions where wires tend to diffuse towards larger L, that is decrease their eccentricity. Blue contours, for which ℱL> 0, are associated with regions in action space, where individual wires tend to diffuse towards smaller L, that is increase their eccentricity. The contours are spaced linearly between the minimum and the maximum of ℱL. Within the units of Eq. (6), the maximum value for the positive blue contours is given by |
| In the text | |
 |
Fig. 6 Divergence of the diffusion flux, div(ℱtot), predicted by the degenerate Landau Eq. (26)for the razor-thin quasi-Keplerian disc introduced in Sect. 2.2. Red contours, for which div(ℱtot) < 0, correspond to regions from which the wires will be depleted, whereas blue contours, for which div(ℱtot) > 0, are associated with regions in action space, where the value of the disc’s DF will increase during the resonant relaxation. The contours are spaced linearly between the minimum and the maximum of div(ℱtot). Within the units of Eq. (6), the maximum value for the positive blue contours is given by div(ℱtot)max ≃ 5 × 10-14, while the minimum value for the negative red contours reads div(ℱtot)min ≃ −10-13. |
| In the text | |
 |
Fig. 7 Evolution of the disc’s surface density Σ⋆(R,τ) as a function of time. As already illustrated in Fig. 6 in phase space, one can note that on a timescale of the order of ΔtLd. (see Eq. (43)), the disc undergoes a self-induced resonant relaxation which broadens it. |
| In the text | |
 |
Fig. 8 Divergence of the diffusion flux, div(ℱtot), predicted by the multi-component Landau Eq. (47)and following the conventions from Fig. 6. Left panel: for the population “a” of light wires of individual mass μa = 1. The maximum value for the positive blue contours is given by |
| In the text | |
 |
Fig. 9 Illustration in configuration space of the mass segregation of the two different components obtained in Fig. 8. Here, the population of red orbits has a lighter individual mass than the blue population. Left panel: illustration of the initial orbits of the wires, where the blue and red wires have the same semi-major axis and eccentricity. Right panel: illustration of the wires’ orbits after the resonant mass segregation. During the resonant relaxation, the wires conserve their semi-major axis, but, following Fig. 8, the light red wires get larger eccentricities, while the heavy blue wires diffuse towards smaller eccentricities and circularise. Because of this segregation, one can note that red orbits get closer to the central BH, as illustrated by the dashed circles. |
| In the text | |
 |
Fig. 10 Diffusion of an individual test wire in the (j,a) = (L/I,I2/ (GM•))-space. Because of the adiabatic conservation of the fast action I, wires diffuse on horizontal lines. The red line corresponds to the last stable orbit (LSO), aLSO(j) = Rg(4 /j)2, with Rg = GM•/c2 (Bar-Or & Alexander 2016). The contours of the disc’s DF, F⋆, introduced in Eq. (8)are represented by the blue lines. The background lines correspond to some of the level lines of the precession frequency |
| In the text | |
 |
Fig. 11 Drift and diffusion coefficients for a retrograde test wire diffusing in the inner region of the system along the grey dashed line, It = const., identified in Fig. 10. Left panel: illustration of the drift coefficient Lt → A(Lt,It), as introduced in Eq. (62). Right panel: illustration of the diffusion coefficient Lt → D(Lt,It), as introduced in Eq. (62). As the test wire gets closer to the centre of the system, the drift and diffusion coefficients tend to 0: this is the Schwarzschild barrier, which prevents individual stars to diffuse closer to the central BH as a sole result of resonant relaxation. The quenching of the resonant diffusion is very abrupt in razor-thin discs, as a result of the limitation to 1:1 resonance in the degenerate Landau Eq. (19). This is specific to the razor-thin geometry. |
| In the text | |
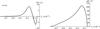 |
Fig. 12 Stochastic Langevin coefficients associated with the drift and diffusion coefficients shown in Fig. 11. Left panel: illustration of the Langevin drift coefficient Lt → h(Lt,It). Following Eq. (64), this coefficient gives the mean direction of motion for a given location in action space. Right panel: illustration of the Langevin diffusion coefficient Lt → g(Lt,It). This coefficient describes the jitter of wires around the mean flow given by h. In particular, it allows wires to stochastically penetrate the barrier. |
| In the text | |
 |
Fig. 13 Stochastic motion, t → Lt(t), of a retrograde test star of mass μt = μ⋆ for different initial conditions. The trajectory of the star is described by the Langevin Eq. (64), with the Langevin coefficients h and g obtained in Fig. 12. Because these coefficients tend to 0 for low enough angular momentum (| Lt | ≲ 2.7 × 103), retrograde test stars cannot diffuse closer to the BH. This quenching of the resonant diffusion in the inner regions of the system is associated with the Schwarzschild barrier and is illustrated with the grey region. |
| In the text | |
 |
Fig. 14 Diffusion of a population of retrograde test wires of individual mass μt = μ⋆ as a function of time. The evolution of each star is driven by the Langevin Eq. (64). The initial PDF of the population is represented by the red histogram, while the coloured histograms describe the statistics of the population after a time ΔT = 200 and 2ΔT. Solving the dynamics of this population via the Langevin Eq. (64)allows for the integration forward in time of the Fokker-Planck Eq. (62), which describes the diffusion of the test wires’ PDF as a whole, without resorting to direct N-body simulations. |
| In the text | |
 |
Fig. 15 Stochastic Langevin coefficient Lt → h(Lt,It) associated with the stochastic diffusion of a retrograde massive perturber of mass μt = 100μ⋆ along the grey dashed line, It = const., identified in Fig. 10. The coefficient g associated with the stochastic of this massive perturber is the same as in Fig. 12. Following Eq. (72), one can note that for a massive enough perturber (or for light enough bath wires), one has h(Jt) → −(μt/μ⋆)A(Jt) and g(Jt) → 0. This non-vanishing contribution is the friction force by polarisation, which drives dynamical friction. |
| In the text | |
 |
Fig. 16 Diffusion of two populations of retrograde test stars of different individual mass. The two populations are initially distributed according to the same PDF, illustrated with the black histogram. The evolution of each test star is described by the Langevin equation associated with the Fokker-Planck Eq. (72). After a time ΔT = 200, the PDF of the light population (of individual mass μt = μ⋆) is given by the red histogram, while the heavy population (of individual mass μt = 10μ⋆) follows the PDF given by the blue histogram. Because of the prefactor (μt/μ⋆) present in Eq. (72), populations of different individual mass do not follow the same stochastic motions, and the system undergoes a mass segregation. Light (red) wires tend to become less eccentric and heavy (blue) wires tend to become more eccentric. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.