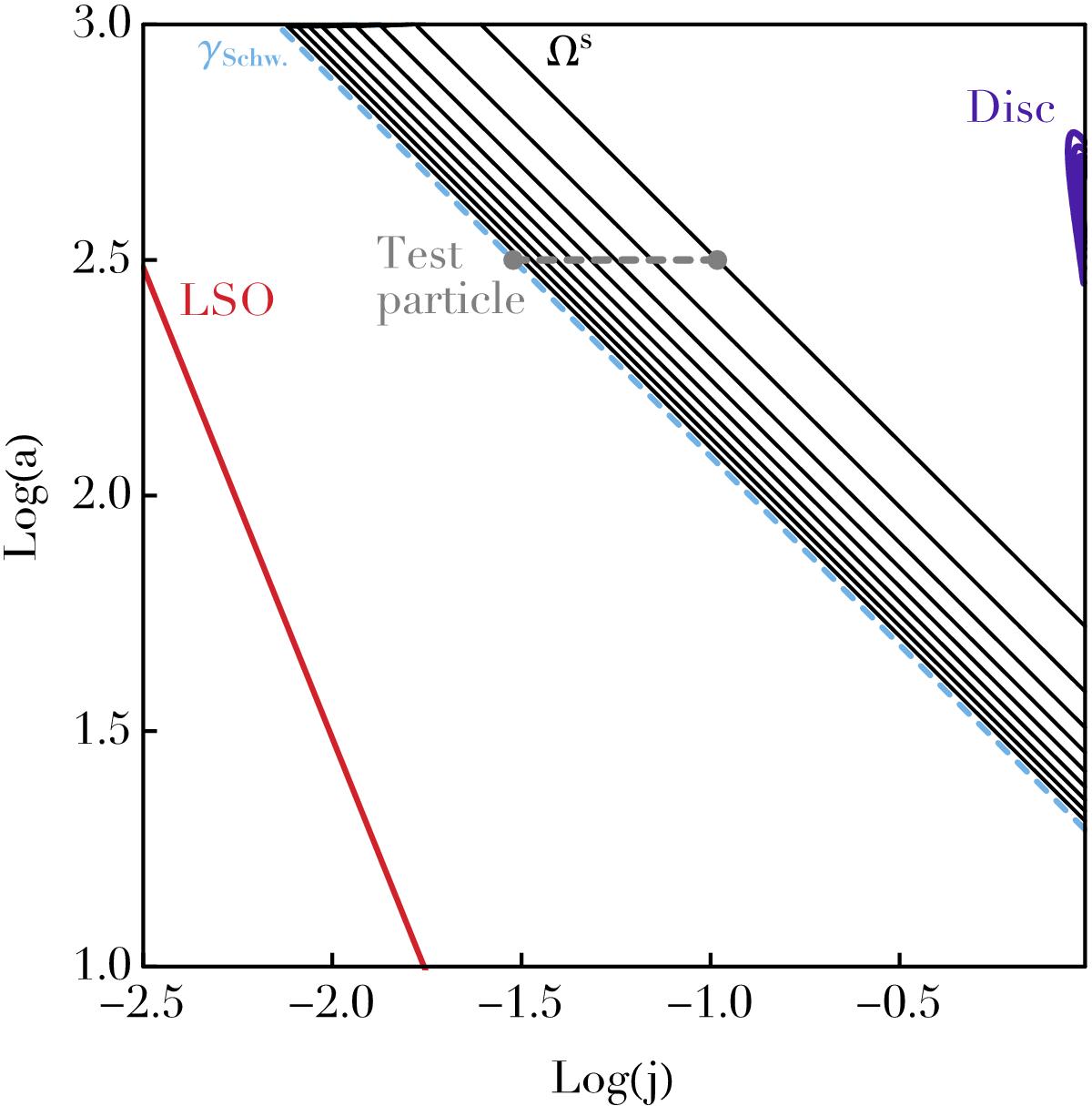
Diffusion of an individual test wire in the (j,a) = (L/I,I²/ (GM_•))-space. Because of the adiabatic conservation of the fast action I, wires diffuse on horizontal lines. The red line corresponds to the last stable orbit (LSO), a_LSO(j) = R_g(4 /j)², with R_g = GM_•/c² (Bar-Or & Alexander 2016). The contours of the disc’s DF, F_⋆, introduced in Eq. (8)are represented by the blue lines. The background lines correspond to some of the level lines of the precession frequency , which are dominated by the relativistic precession for such eccentric orbits. These contours are computed for a retrograde test star, and are therefore associated with negative precession frequencies. They are spaced linearly between the maximum and the minimum precession frequency in the region of the disc, which are dominated by the self-consistent precession . The dashed grey line corresponds to the segment along which the drift and diffusion coefficients for the test wire are computed in Fig. 11. (Recall that the test star is assumed to be retrograde, i.e. L_t< 0, but for clarity, it is represented on the same diagram than the disc.) The cyan line illustrates the location of the Schwarzschild barrier, γ_Schw., for retrograde test stars defined in Eq. (71). Retrograde test wires to the left of this barrier will precess too fast to resonate with this disc, see Figs. 11 and 12. Such wires do not undergo any resonant relaxation, and can only diffuse as a result of additional diffusion mechanisms, such as two-body non-resonant relaxation.