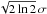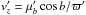| Issue |
A&A
Volume 608, December 2017
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201731518 | |
| Published online | 07 December 2017 | |
The observed velocity distribution of young pulsars
Institute of Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
e-mail: F.Verbunt@astro.ru.nl; A.Igoshev@astro.ru.nl; E.Cator@science.ru.nl
Received: 6 July 2017
Accepted: 29 September 2017
We argue that comparison with observations of theoretical models for the velocity distribution of pulsars must be done directly with the observed quantities, that is parallax and the two components of proper motion. We have developed a formalism to do so, and applied it to pulsars with accurate VLBI measurements. For computational convenience, we model the data with Maxwellians. We find that a distribution with two Maxwellians improves significantly on a single Maxwellian. The “mixed” model takes into account that pulsars move away from their place of birth, a narrow region around the Galactic plane. The best model has 42% of the pulsars in a Maxwellian with average velocity 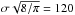 km s-1, and 58% in a Maxwellian with average velocity 540 km s-1. About 5% of the pulsars has a velocity at birth less than 60 km s-1. For the youngest pulsars (τc < 10 Myr), these numbers are 32% with 130 km s-1, 68% with 520 km s-1, and 3%, with appreciable uncertainties. Our analysis shows that the velocity distribution is wider than can be described with a single Maxwellian; it does not prove that two Maxwellians provide a better description than other wide models.
km s-1, and 58% in a Maxwellian with average velocity 540 km s-1. About 5% of the pulsars has a velocity at birth less than 60 km s-1. For the youngest pulsars (τc < 10 Myr), these numbers are 32% with 130 km s-1, 68% with 520 km s-1, and 3%, with appreciable uncertainties. Our analysis shows that the velocity distribution is wider than can be described with a single Maxwellian; it does not prove that two Maxwellians provide a better description than other wide models.
Key words: stars: neutron / pulsars: general / methods: statistical
© ESO, 2017
1. Introduction
The study of the velocities of pulsars is interesting on its own account, as a pointer to the formation process of a neutron star, but also has ramifications beyond this. In particular, some neutron stars are found in binaries and in globular clusters, as accreting X-ray sources or as pulsars. These neutron stars were born with velocities less than the escape velocity from the binary or from the cluster.
Neutron stars that have the same velocities as their progenitors, move with the rotation of the galaxy, with small velocities with respect to the local standard of rest (LSR), unless their progenitor is a member of a close binary or a runaway star. To investigate the velocities that neutron star acquires at birth in addition to the progenitor velocity, one therefore investigates their velocity v with respect to the LSR.
This investigation is complicated for pulsars with large velocities as these are affected by an acceleration in the Galactic potential that varies between their place of birth and their current location, and because their current LSR differs from the LSR at their place of birth. Thus the current v of a pulsar differs from the v at birth. If the age and full space velocities were known, we could solve this complication by integrating the pulsar orbit back in time, but proper motion studies only provide two of the three velocity components, and ages of pulsars are usually uncertain. By limiting the study to young pulsars, one may reduce the effect of these complications. As well described by Brisken et al. (2003a, in particular Sect. 5.1), correlations between spin-axis and velocity, between luminosity and velocity, and/or between velocity and distance to the Galactic plane, among others, introduce selection effects in the observations. Such selection effects can only be corrected for in a full population study. Even so, determining the observed v distribution is a useful step toward a full population study, and various efforts have been published (see Table 5).
Arzoumanian et al. (2002) compare synthesized model populations with the observed periods, period derivatives, dispersion measures, fluxes, and the absolute values of Galactic latitudes and of proper motions. They conclude that the velocity distribution of pulsars is bimodal, with a low-velocity and a high-velocity component.
Brisken et al. (2003a) investigate the velocity component vl in the direction of Galactic longitude. Their study is based on interferometric proper motion measurements (mostly their own). For each pulsar, they compute a probability distribution P(D) for the distance D (based on the parallax or on the dispersion measure DM, allowing for the limited accuracy in converting DM to D) and combine this with the probability function P(μl) for the proper motion μl (allowing for measurement uncertainty) to compute the probability distribution P(vl). The set of P(vl) is fitted with a model in which this distribution is described by two zero-centred Gaussian distributions, representing a slow and a fast component.
Hobbs et al. (2005) construct velocity distributions P(v1D) where v1D is either vl or vb and P(v2D) where 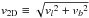 for a larger sample of pulsars, including measurements based on timing. vb is the velocity component in the direction of latitude. Hobbs et al. assume that these observed v1D and v2D distributions are projections of an isotropic velocity distribution P(v), and then reconstruct P(v) by using a clean algorithm to deconvolve P(v1D) and P(v2D). The advantage of this method is that it is non-parametric, that is it does not assume a prescribed form for P(v). The reconstructed form turns out to be well described by a Maxwellian, with σ = 265 km s-1.
for a larger sample of pulsars, including measurements based on timing. vb is the velocity component in the direction of latitude. Hobbs et al. assume that these observed v1D and v2D distributions are projections of an isotropic velocity distribution P(v), and then reconstruct P(v) by using a clean algorithm to deconvolve P(v1D) and P(v2D). The advantage of this method is that it is non-parametric, that is it does not assume a prescribed form for P(v). The reconstructed form turns out to be well described by a Maxwellian, with σ = 265 km s-1.
Faucher-Giguère & Kaspi (2006) extend the method of Brisken et al. (2003a) in two ways. First they consider a variety of models for the distribution of vl, and second they extend the maximum-likelihood model with a Bayesian analysis of probability ratios for the comparison of different models.
Whereas these studies agree that the space (that is 3D) velocities of neutron stars are high, averaging as much as 450 km s-1, they differ on the fraction of low-velocity neutron stars. Hobbs et al. (2005) argue that the low-velocity tail of the pulsar velocity distribution is due to projection effects, and that very few pulsars have space velocities below 60 km s-1. (For a Maxwellian with σ = 265 km s-1 the fraction is 0.003.) In the acceptable models discussed by Faucher-Giguère & Kaspi (2006) the derived fraction of pulsars with space velocities less than 60 km s-1 varies from 0.012 (for a two-component Gaussian) to 0.135 (for the Paczyński distribution).
One reason for us to make a new study of the pulsar velocities is to resolve the differences between the predicted numbers of low-velocity pulsars in these recent studies. Among nine very accurate pulsar velocities v⊥ (=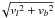 ) listed by Brisken et al. (2002, Table 5), two are smaller than 40 km s-1. The probability of finding two such low-v⊥ pulsars in a sample of nine is 0.004 for an isotropic Maxwellian with σ = 265 km s-1. This suggests that the pulsar velocities may be overestimated by Hobbs et al. (2005).
) listed by Brisken et al. (2002, Table 5), two are smaller than 40 km s-1. The probability of finding two such low-v⊥ pulsars in a sample of nine is 0.004 for an isotropic Maxwellian with σ = 265 km s-1. This suggests that the pulsar velocities may be overestimated by Hobbs et al. (2005).
A second reason for a new study is the development by Verbiest et al. (2012), of a Bayesian method to combine different distance indicators into a single probability distribution P(D) for each pulsar. The main distance indicator is the parallax, where the Lutz-Kelker (1973) effect is taken into account, with the Galactic pulsar distribution as a prior. For the study of pulsar velocities we correct some errors in the equations given by Verbiest et al. (2012) for use of the parallax (see Igoshev et al. 2016 and Bailer-Jones 2015), and add the measurements of the proper motions. The third and final reason for our new study of pulsar velocities is the increased number of accurately measured proper motions and parallaxes (see Table 2).
In Sect. 2 we describe the master list of observed proper motions that we use in our study. We describe the ingredients of the likelihood function for pulsars and their use in determining the parameters of the velocity distribution in Sect. 3, and apply these to various models: a single isotropic Maxwellian in Sect. 4, the sum of two isotropic Maxwellians in Sect. 5, and a mixture of one or two isotropic and semi-isotropic Maxwellians in Sect. 7. (In the semi-isotropic Maxwellian distribution velocities towards the Galactic plane are excluded, as explained in Sect. 6.) We use Maxwellians for computational convenience: an isotropic Maxwellian may be decomposed in three independent Gaussians in any three mutually perpendicular directions, and as a result a large part of the calculations can be done analytically. The use of Maxwellians futhermore enables direct comparisons with previous papers, most of which also use Maxwellians. We leave the rather more complicated study of other models to future work.
Before we proceed, we describe the notation we use: we differentiate between the actual (and generally unknown) properties of the pulsar, and the measured (or nominal) values, by indicating the latter with a prime (′). The actual proper motion is the sum of three components: one due to the peculiar velocity of the pulsar, one due to the difference between the local standards of rest of the pulsar and of the Sun, and one due to the peculiar motion of the Sun (Eqs. (6)–(9)). The measured parallax and proper motion differs from the actual values due to measurement errors (Eqs. (1)–(3)), and may be skewed due non-uniform distributions of positions and velocities (Fig. 2). For convenience, our notation is summarized in Table 1.
Notation used in this paper.
2. Data
To obtain a master list of pulsars with measured proper motions, we start by collating articles with proper motion measurements. The ATNF Catalogue, version 1.541 (Manchester et al. 2005), was very helpful in this.
Brisken et al. (2000) note that VLBI measurements of proper motions need to be corrected for ionospheric refraction. We therefore do not use articles with proper motions from VLBI published before 2000. To select first-born, single pulsars we reject recycled pulsars (that is those with Ṗ < 5 × 10-18 s s-1), pulsars in binaries, and pulsars in globular clusters.
In this first application of our new method we prefer to use relatively accurate measurements. We therefore omit pulsars with distances determined only from dispersion measures, and pulsars with proper motions determined from pulse timing. In both cases, the errors are at least an order of magnitude larger than the errors obtained with VLBI, and often only correspond to (upper or lower) limits. Distances from dispersion measures have uncertainties dominated by systematic effects, with highly non-Gaussian distributions. (For pulsars distances and dispersion measures, see for example Yao et al. 2017; for proper motions from timing, see Hobbs et al. 2004.) We also omit proper motions of pulsars derived from displacements in X-ray or optical images, which are relative to other objects in the field of view. The conversion to absolute proper motions in the International celestial reference system (ICRS) adds significantly to the error.
Sources for proper motions in our master list.
 |
Fig. 1 Illustrations of data from our master list of pulsars Table D.1. Top: celestial distribution in Galactic coordinates. The blue lines show the observed proper motion μ′ and the red lines the correction due to Galactic rotation (for nominal distance D′), in 0.5 Myr. Below left: nominal velocities in the celestial plane. The circle indicates the median value for v⊥ for the projection of a Maxwellian: |
This leaves us with the VLBI measurements of the articles listed in Table 2. Although the measurement of the proper motion components are not independent of each other, the covariance value is only provided by Brisken et al. (2003a) who give no parallax values. We therefore ignore covariances between 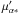 and
and 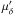 . In the majority of the measurements, the errors are symmetric, and where asymmetric, the difference is small. We simplify our analysis by taking the largest error when errors are asymmetric. (Test calculations in which the smallest error is taken give the same results.)
. In the majority of the measurements, the errors are symmetric, and where asymmetric, the difference is small. We simplify our analysis by taking the largest error when errors are asymmetric. (Test calculations in which the smallest error is taken give the same results.)
The resulting master list of observed proper motions in equatorial coordinates is given in Table D.1. The proper motions in this table are the observed proper motions 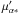 and
and 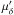 , not corrected for Galactic rotation and peculiar solar velocity. The celestial distribution, measured proper motions and nominal velocities of the pulsars in our master list are illustrated in Fig.1. From the top figure we learn that the correction for Galactic motion in general is small. The lower figures add to our suspicion that a single Maxwellian with σ = 265 km s-1 seriously underestimates the number of pulsars with low velocities.
, not corrected for Galactic rotation and peculiar solar velocity. The celestial distribution, measured proper motions and nominal velocities of the pulsars in our master list are illustrated in Fig.1. From the top figure we learn that the correction for Galactic motion in general is small. The lower figures add to our suspicion that a single Maxwellian with σ = 265 km s-1 seriously underestimates the number of pulsars with low velocities.
3. Ingredients
3.1. Probabilities
To determine the pulsar velocity distribution we use the measured values of the parallax ϖ′ and of the two components of the proper motion 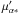 and
and 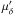 . The conditional probabilities of obtaining these measured values when the actual values are ϖ = 1 /D, μα ∗ and μδ can be written separately as
. The conditional probabilities of obtaining these measured values when the actual values are ϖ = 1 /D, μα ∗ and μδ can be written separately as ![\begin{eqnarray} &&g_D(\varpi'|D)\Delta\varpi' = {1\over\sqrt{2\pi}\sigma_\varpi} \exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right] \Delta\varpi', \label{e:erpar} \\ &&g_\alpha(\mu'_{\alpha*}|\mu_{\alpha*})\Delta\mu'_{\alpha*} = {1\over\sqrt{2\pi}\sigma_\alpha} \exp\left[-\,{(\mu_{\alpha*}-\mu'_{\alpha*})^2\over2{\sigma_\alpha}^2}\right] \Delta\mu'_{\alpha*}, \label{e:ermua} \\ &&g_\delta(\mu'_{\delta}|\mu_{\delta})\Delta\mu'_{\delta} = {1\over\sqrt{2\pi}\sigma_\delta} \exp\left[-\,{(\mu_{\delta}-\mu'_{\delta})^2\over2{\sigma_\delta}^2}\right] \Delta\mu'_{\delta}, \label{e:ermud} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq60.png) where σϖ, σα and σδ are the measurement errors for the parallax and for the two components of the proper motion, respectively. To obtain the joint probability of the measured and actual values, these equations must be complemented with the equations indicating the probability density functions of the actual distance and proper motion.
where σϖ, σα and σδ are the measurement errors for the parallax and for the two components of the proper motion, respectively. To obtain the joint probability of the measured and actual values, these equations must be complemented with the equations indicating the probability density functions of the actual distance and proper motion.
The probability density fD(D) of the distance D of the pulsar to the Earth for a galactocentric pulsar distribution is given by Verbiest et al. (2012). In the notation of Igoshev et al. (2016): ![\begin{equation} f_D(D)\propto D^2R^{1.9}\exp\left[-{|z(D,b)|\over h}-{R(D,l,b)\over H}\right] \equiv D^2\mathcal{F}(D), \label{e:fd} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq65.png) (4)with
(4)with 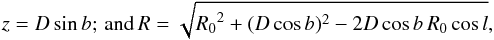 (5)where R and R0 are the galactocentric distance of the pulsar and the Sun, respectively, projected on the Galactic plane. Through ℱ(D) also fD(D) is a function of Galactic coordinates l,b.
(5)where R and R0 are the galactocentric distance of the pulsar and the Sun, respectively, projected on the Galactic plane. Through ℱ(D) also fD(D) is a function of Galactic coordinates l,b.
3.2. Proper motions
The proper motion of a pulsar μα ∗,μδ is the sum of the proper motion of its standard of rest with respect to the Sun μα ∗ ,G,μδ,G and the proper motion caused by its velocity with respect to its local standard of rest μα ∗ ,v,μδ,v: 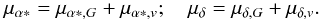 (6)The derivation of μα ∗ ,G and μδ,G is described in Appendices A and B. The velocity of the local standard of rest is assumed to be the Galactic rotation velocity, vR(R0) for the Sun and vR(R) for the pulsar. The peculiar velocity of the Sun is [U, V, W], where the components are respectively in the direction from the Sun towards the Galactic centre, in the direction of the Galactic rotation, and perpendicular to the Galactic plane. In Galactic coordinates
(6)The derivation of μα ∗ ,G and μδ,G is described in Appendices A and B. The velocity of the local standard of rest is assumed to be the Galactic rotation velocity, vR(R0) for the Sun and vR(R) for the pulsar. The peculiar velocity of the Sun is [U, V, W], where the components are respectively in the direction from the Sun towards the Galactic centre, in the direction of the Galactic rotation, and perpendicular to the Galactic plane. In Galactic coordinates ![\begin{equation} D\,\mu_{l*,G}=U\sin l-[V+v_R(R_{0})]\cos l +v_R(R)\cos(\theta+l), \label{e:vsubl} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq82.png) (7)and
(7)and ![\begin{eqnarray} D\,\mu_{b,G} &=& \Big[U\cos l+[V+v_R(R_{0})]\sin l -v_R(R)\sin(\theta+l)\Big]\sin b\phantom{and} \nonumber\\ &&\quad-W\cos b. \label{e:vsub} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq83.png) (8)The angle (θ + l) is computed from:
(8)The angle (θ + l) is computed from: 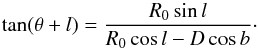 (9)The values for [U, V, W], vR and R0 that we use are listed in Table 3. To compare velocities expressed in km s-1 with proper motions expressed in mas/yr, we use the conversion
(9)The values for [U, V, W], vR and R0 that we use are listed in Table 3. To compare velocities expressed in km s-1 with proper motions expressed in mas/yr, we use the conversion 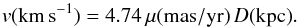 (10)The pair μl ∗ ,G,μb,G, is converted to the pair in equatorial coordinates μα ∗ ,G,μδ,G with the rotation given by Eqs. (B.12) and (B.13). μl ∗ ,G and μb,G depend on the (unknown) distance. This is the reason that Table D.1 gives the observed proper motions, not corrected for Galactic rotation and solar motion. μα ∗ ,v and μδ,v depend on the peculiar velocity v of the pulsar and on the direction of this velocity.
(10)The pair μl ∗ ,G,μb,G, is converted to the pair in equatorial coordinates μα ∗ ,G,μδ,G with the rotation given by Eqs. (B.12) and (B.13). μl ∗ ,G and μb,G depend on the (unknown) distance. This is the reason that Table D.1 gives the observed proper motions, not corrected for Galactic rotation and solar motion. μα ∗ ,v and μδ,v depend on the peculiar velocity v of the pulsar and on the direction of this velocity.
Values of constants defining coordinate transformations and velocity corrections.
3.3. Best solution and fiducial intervals
In the following sections we will discuss a number of models, and for each model compute a likelihood Li(σ) for an individual pulsar labelled i, as a function of the parameter vector σ. We then construct the deviance ℒ with 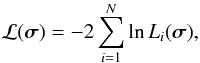 (11)where N is the number of pulsars. σopt is the parameter vector for which Eq. (11) reaches its minimum. We write differences with the optimal solution as
(11)where N is the number of pulsars. σopt is the parameter vector for which Eq. (11) reaches its minimum. We write differences with the optimal solution as 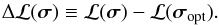 (12)For appropriate choices of Li these differences approximate a χ2 distribution. For a parameter vector consisting of a single parameter, we estimate its 68% range by determining for which values Eq. (12) is equal to 1. To determine the range of values if the vector parameter has three parameters, we proceed as follows. We fix the value of one parameter at an offset from the optimal value, and then determine the combination of the two other parameters that gives the lowest value for Δℒ(σ). We vary the offset until this lowest value is 1. Repeating this for each of the three parameters for positive and negative offsets from the best values gives the ranges listed in Table 4.
(12)For appropriate choices of Li these differences approximate a χ2 distribution. For a parameter vector consisting of a single parameter, we estimate its 68% range by determining for which values Eq. (12) is equal to 1. To determine the range of values if the vector parameter has three parameters, we proceed as follows. We fix the value of one parameter at an offset from the optimal value, and then determine the combination of the two other parameters that gives the lowest value for Δℒ(σ). We vary the offset until this lowest value is 1. Repeating this for each of the three parameters for positive and negative offsets from the best values gives the ranges listed in Table 4.
Results of the model calculations for all 28 pulsars in our master list (A), and for the 19 youngest pulsars (τc < 10 Myr, Y).
The best parameter values and the fiducial ranges determined this way do not depend on the normalization of Li: a constant multiplicative factor x to any Li leads to a constant additive factor −2lnx in Eq. (11) and drops out in Eq. (12). We will also use the deviance to compare different models, using 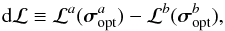 (13)where indices a and b refer to the different models. The distribution of dℒ approximates a χ2 distribution less well than Δℒ, but we will use this difference as a rough indication of relative merit of models.
(13)where indices a and b refer to the different models. The distribution of dℒ approximates a χ2 distribution less well than Δℒ, but we will use this difference as a rough indication of relative merit of models.
4. Maxwellian velocity distribution
The Maxwellian velocity distribution is characterized by a single parameter σ: ![\begin{equation} f(v,\sigma){\rm d}v = \sqrt{2\over\pi} {v^2\over\sigma^3}\exp\left[-{v^2\over2\sigma^2}\right]{\rm d}v; \quad (0<v<\infty). \label{e:maxw} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq126.png) (14)In the isotropic case, the Maxwellian may be decomposed in three independent Gaussians in any three mutually perpendicular directions. We choose the directions of increasing right ascension, increasing declination, and the radial direction. This enables us to write the joint probability of measured values ϖ′,
(14)In the isotropic case, the Maxwellian may be decomposed in three independent Gaussians in any three mutually perpendicular directions. We choose the directions of increasing right ascension, increasing declination, and the radial direction. This enables us to write the joint probability of measured values ϖ′, 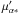 ,
, 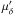 and actual values D, vα = Dμα ∗ ,v and vδ = Dμδ,v as
and actual values D, vα = Dμα ∗ ,v and vδ = Dμδ,v as ![\begin{eqnarray} &&P_\mathrm{maxw}(\varpi',\mu'_{\alpha*},\mu'_\delta,D,v_\alpha,v_\delta,v_r)= G(v_\alpha,\sigma)G(v_\delta,\sigma)G(v_r,\sigma) \nonumber\\ &&\quad\times{f_D(D)\over\int_0^{D_\mathrm{max}}f_D(D){\rm d}D}\, {1\over\sigma_\varpi\sqrt{2\pi}}\exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right] \nonumber \\ &&\quad\times{1\over\sigma_\alpha\sqrt{2\pi}}\exp\left[-\,{(\mu_{\alpha*,G}(D)+v_\alpha/D -\mu'_{\alpha*})^2\over2{\sigma_\alpha}^2}\right] \nonumber \\ &&\quad\times{1\over\sigma_\delta\sqrt{2\pi}}\exp\left[-\,{(\mu_{\delta,G}(D)+v_\delta/D -\mu'_{\delta})^2\over2{\sigma_\delta}^2}\right] , \label{e:definejm} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq129.png) (15)where
(15)where ![\begin{equation} G(v,\sigma) = {1\over\sigma\sqrt{2\pi}}\exp\left[-{v^2\over2\sigma^2}\right]; \quad (-\infty<v<\infty). \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq130.png) (16)To obtain the value of σ which gives the most likely correspondence with the measurements, we must take into account contributions to the likelihood of all distances and velocities. We therefore define the likelihood for the Maxwellian as
(16)To obtain the value of σ which gives the most likely correspondence with the measurements, we must take into account contributions to the likelihood of all distances and velocities. We therefore define the likelihood for the Maxwellian as 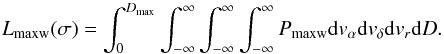 (17)The radial velocities occur only in G(vr,σ), and thus the integral over vr can be computed separately:
(17)The radial velocities occur only in G(vr,σ), and thus the integral over vr can be computed separately: 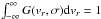 . The integrals over vα and vδ are more involved, but can also be solved analytically. Thus, for vα
. The integrals over vα and vδ are more involved, but can also be solved analytically. Thus, for vα![\begin{eqnarray} &&\int_{-\infty}^\infty \exp\left\{-{1\over2}\left[{{v_\alpha}^2\over\sigma^2} +{\Big(v_\alpha+D(\mu_{\alpha*,G}-\mu'_{\alpha*})\Big)^2\over D^2{\sigma_\alpha}^2} \right] \right\} {\rm d}v_\alpha \nonumber\\ &&\quad= \sqrt{2\pi}\,\left({1\over\sigma^2}+{1\over D^2{\sigma_\alpha}^2}\right)^{-1/2} \exp\left[-{1\over2}{D^2(\mu_{\alpha*,G}-\mu'_{\alpha*})^2\over \sigma^2+D^2{\sigma_\alpha}^2}\right], \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq137.png) (18)and analogously for vδ. Taken together these results lead to
(18)and analogously for vδ. Taken together these results lead to ![\begin{equation} L_\mathrm{maxw}(\sigma)=\mathcal{C}\int_0^{D_\mathrm{max}} f_D(D)\exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right]\mathcal{I}_\alpha\mathcal{I}_\delta {\rm d}D, \label{e:fin_maxw} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq138.png) (19)where
(19)where ![\begin{eqnarray} \mathcal{C} &\equiv& \left[(2\pi)^{3/2}\sigma_\varpi\sigma_\alpha\sigma_\delta \int_0^{D_\mathrm{max}} f_D(D) {\rm d}D\right]^{-1},\nonumber\\ \mathcal{I}_\alpha & \equiv& \left(1+{\sigma^2\over D^2{\sigma_\alpha}^2}\right)^{-1/2} \exp\left[-{1\over2}{(D\,\mu_{\alpha*,G}-D\,\mu'_{\alpha*})^2\over \sigma^2+D^2{\sigma_\alpha}^2}\right], \nonumber \\ \mathcal{I}_\delta& \equiv & \left(1+{\sigma^2\over D^2{\sigma_\delta}^2}\right)^{-1/2} \exp\left[-{1\over2}{(D\,\mu_{\delta,G}-D\,\mu'_{\delta})^2\over \sigma^2+D^2{\sigma_\delta}^2}\right]\cdot\nonumber \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq139.png) The integral over distances in Eq. (19) is computed numerically, out to Dmax = 10 kpc.
The integral over distances in Eq. (19) is computed numerically, out to Dmax = 10 kpc. 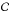 ensures that each distribution in Eq. (15) is normalized to unity; in the computations
ensures that each distribution in Eq. (15) is normalized to unity; in the computations  may be ignored, as it only adds a constant in the deviance (Eq. (11)) and drops out in Eq. (12).
may be ignored, as it only adds a constant in the deviance (Eq. (11)) and drops out in Eq. (12).
 |
Fig. 2 Illustration for two pulsars of the contributions to the integrand of the likelihood Lmaxw(σ) (Eq. (19)) of the separate factors fD(D)gD(ϖ′ | D) (top graphs; Eqs. (1) and (4)), Iα and Iδ (middle graphs). Each curve has been normalized separately to maximum unity. Iα and Iδ are shown for for three values σ of the Maxwellian (Eq. (14)). The lower graphs show the integrand of the likelihood Lmaxw(σ) for three values of σ, as a function of distance, normalized to the highest maximum of the three. The measurements of PSR J0034−0721 (left) favour a low value of σ. Those of PSR B1508+55 (right) require a high value of σ, and the integrands for σ = 50 and 100 km s-1 are indistinguishable from zero in this graph. |
To illustrate the effect of the various factors in the integrand of Eq. (19) we show these separately in Fig. 2, for two pulsars. For a fixed velocity, the proper motion scales inversely with the distance. The large parallax of PSR 0034−0721, combined with its relatively small proper motion, favours a Maxwellian with a small average velocity, but still allows a Maxwellian with a high average velocity as this has a finite tail at low velocities. In contrast, the smaller parallax of PSR B1508+55 combined with its large proper motion, demands a Maxwellian with a large average velocity, because high velocities have vanishingly low probability in a Maxwellian with a low average velocity.
Labelling the likelihoods of Eq. (19) for each of N pulsars with i, we compute the deviance ℒ with Eq. (11). Δℒ(σ) (Eq. (12)) is shown for three pulsar samples in Fig. 3. The sample of all 28 pulsars in our master list (Table D.1) leads to σopt ≃ 244 km s-1, with a range of about 50 km s-1 found from Δℒ = 1; see Table 4. To illustrate the influence of a single pulsar, we also show Δℒ(σ) for the sample of 27 pulsars remaining after removing PSR B1508+55, the pulsar with the worst likelihood for σ = 245 km s-1. This sample has σopt ≃ 210 km s-1. The reason for this shift is evident from Fig. 2: the measurements of PSR B1508+55 require a large value of σ. Removing any one of the 27 other pulsars from the full sample leads to a much smaller shift.
The pulsar velocities of young pulsars, less affected by acceleration in the Galactic gravitational field, are more indicative of the pulsar velocities at birth, and therefore we also investigate the sample of the 19 youngest pulsars with characteristic age τc < 10 Myr. This leads to a higher optimal distribution parameter σopt ≃ 280 km s-1. The smaller number of pulsars also leads to a wider range of σ for which Δℒ(σ) < 1. An upper limit to τc of 5 Myr leads to the same σopt as for 10 Myr, but further widens the uncertainty range. Removing PSR B1508+55 from the sample of young pulsars reduces the optimal distribution sample to σopt ≃ 235 km s-1.
Figures 1 and 2 indicate that a single Maxwellian is not a good description of the velocity distribution of young radio pulsars. We are therefore not unduly worried about the shifts in σopt between the different samples, but move on to investigate more promising models.
5. Sum of two Maxwellians
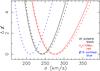 |
Fig. 3 Variation of ℒ with velocity distribution parameter σ for the model with a single isotropic Maxwellian (dotted lines), and for the mixed model in which most pulsars have an assumed semi-isotropic velocity distribution (solid lines). The colour coding indicates the pulsar sample: all 28 pulsars in our master list, the 27 pulsars remaining after removing PSR B1508+55, and the 19 youngest (τ < 10 Myr) pulsars. |
We investigate a velocity distribution which is the sum of two Maxwellians, one to explain the lower observed velocities, and one for the higher velocities. Defining the vector of parameters σ = [σ1,σ2,w] we write ![\begin{equation} f_v (v, \vec\sigma) {\rm d}v = \sqrt {\frac{2}{\pi}} v^2 \left[\frac{w}{\sigma_1^3} \exp \left( -\frac{1}{2} \frac{v^2}{\sigma_1^2} \right) \! + \!\frac{(1-w)}{\sigma_2^3} \exp \left( -\frac{1}{2} \frac{v^2}{\sigma_2^2} \right) \right] {\rm d}v. \label{e:twomaxw} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq161.png) (20)The likelihood for the sum of two Maxwellians is the sum of the likelihoods of the two Maxwellians: in analogy with Eq. (19) we have
(20)The likelihood for the sum of two Maxwellians is the sum of the likelihoods of the two Maxwellians: in analogy with Eq. (19) we have 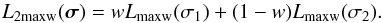 (21)We compute Lmaxw(σ) on a grid of values of σ, in steps of 1 km s-1, and use the subroutine AMOEBA of Press et al. (1986), which implements the downhill simplex method of Nelder and Mead, to obtain the optimal values of w, σ1 and σ2 for which ℒ, computed from Eq. (21) with Eq. (11), has its minimum. The results are listed in Table 4, and illustrated in Fig. 4.
(21)We compute Lmaxw(σ) on a grid of values of σ, in steps of 1 km s-1, and use the subroutine AMOEBA of Press et al. (1986), which implements the downhill simplex method of Nelder and Mead, to obtain the optimal values of w, σ1 and σ2 for which ℒ, computed from Eq. (21) with Eq. (11), has its minimum. The results are listed in Table 4, and illustrated in Fig. 4.
 |
Fig. 4 Contours of ℒ(σ) in three σ1,σ2 planes with fixed w, for the model with two isotropic Maxwellians. Contours of constant Δℒ(σ) (Eq. (12)) are shown for values 1 and 4, in each plane, The best solution is indicated with •. Top: all pulsars. σopt = (77 km s-1, 321 km s-1, 0.42). Below: pulsars with τc < 10 Myr. σopt = (83 km s-1, 335 km s-1, 0.32). |
To decide on the significance of the second Maxwellian, we note that it adds two parameters to the model with one Maxwellian, and compute the deviance difference dℒ with Eq. (13). We first investigate the sample of all 28 pulsars in our master list (sample A). For this sample, dℒ = −14, indicating that the addition of a second Maxwellian is very significant (Δχ2 = −14 corresponds to a 99.8% confidence level for two added parameters). The low-velocity component represents between 29% and 54% of the pulsar population. Figure 4 shows that the values of σ1 and σ2 are mildly correlated with w: a larger (smaller) fraction of the low-velocity component leads to larger (smaller) values of σ1 and σ2. The shift, however, lies well within the error range of σ1 and σ2; the main effect of the correlation between σ1 and σ2 is to mitigate the drop of pulsar numbers with velocities between σ1 and σ2.
The sample of 19 pulsars in our list with characteristic age τc < 10 Myr (sample Y) leads to the same result, but with somewhat lager error margins for the parameters σ. For these young pulsars, the evidence for a second Maxwellian is still significant (Δχ2 = −6 is 95% confidence).
 |
Fig. 5 Nominal distance from the Galactic plane z′ = sinb/ϖ′, range sinb/ (ϖ′ ± σϖ), as a function of longitude. The blue points indicate pulsars nominally moving away from the plane, that is z′ and |
6. Semi-isotropic Maxwellian velocity distribution
The isotropic Maxwellian velocity distribution has a major advantage in enabling us to compute three out of four integrals in Eq. (17) analytically. However, once the pulsar has moved away from the Galactic plane, we have more information, that we will put to use in this section: the pulsar velocity must be directed away from its place of birth, which for sufficiently large | z | implies that vz > 0 when z > 0 and vz < 0 when z < 0. For these pulsars we assume an intrinsic distribution for the velocity which is an isotropic distribrution from which the velocities towards the Galactic plane have been removed: and refer to this distribution as semi-isotropic.
To quantify “sufficiently large” we show the nominal values of distance to the Galactic plane z′ = D′sinb in Fig. 5, together with a band indicating the scale height of O stars, as a proxy for the place of birth of pulsars. Five pulsars in our list of 28 are moving towards the Galactic plane. Two of these, PSR B0329+54 (#4 in our master list) and PSR J0538+2817 (#7) are within the region where pulsars are born, and thus may well be moving towards the plane. PSR J2144−3933 (#26) is the oldest pulsar in our sample, and may well be a returning pulsar. PSR B0818−13 (#11) and PSR B1237+25 (#15) are too young – assuming their characteristic age is indicative of their real age – to have reversed motion, and their motion towards the Galactic plane must be apparent. We may write vz as (see Fig. B.1) 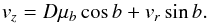 (22)Hence a pulsar is moving away from the plane if
(22)Hence a pulsar is moving away from the plane if 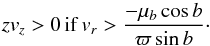 (23)Entering the nominal values ϖ′ and
(23)Entering the nominal values ϖ′ and 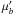 , we obtain vr > 120 km s-1 (#11) and vr > 12 km s-1 (#15), indicating that these pulsars may well be moving as expected: away from the plane.
, we obtain vr > 120 km s-1 (#11) and vr > 12 km s-1 (#15), indicating that these pulsars may well be moving as expected: away from the plane.
In computing for the case of semi-isotropic Maxwellians, we choose axes parallel to the (local) direction of right ascension and declination, and along the line of sight, and write the spatial velocity as 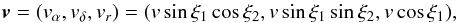 (24)where
(24)where
 To determine which velocities lead to vz away from the Galactic plane, we first convert the velocities to Galactic coordinates using Eqs. (A.9), (A.10):
To determine which velocities lead to vz away from the Galactic plane, we first convert the velocities to Galactic coordinates using Eqs. (A.9), (A.10): 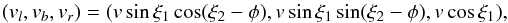 (25)where φ is given by Eq. (A.11). Entering vb and vr from Eq. (25) into (22) we obtain
(25)where φ is given by Eq. (A.11). Entering vb and vr from Eq. (25) into (22) we obtain ![\begin{equation} v_z=v[\sin\xi_1\sin(\xi_2-\phi)\cos b + \cos\xi_1\sin b] . \label{e:vzcorrect} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq195.png) (26)Thus, the sign of vz does not depend on the speed v. The condition vz > 0 if b > 0 and vz < 0 if b < 0 may be written
(26)Thus, the sign of vz does not depend on the speed v. The condition vz > 0 if b > 0 and vz < 0 if b < 0 may be written 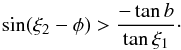 (27)We rewrite the joint probability of Eq. (15) for the semi-isotropic case as
(27)We rewrite the joint probability of Eq. (15) for the semi-isotropic case as ![\begin{eqnarray} &&P_\mathrm{sim}(\varpi',\mu'_{\alpha*},\mu'_\delta,D,v,\xi_1,\xi_2)=0\qquad \mathrm{if}\quad zv_z<0, \nonumber\\ &&P_\mathrm{sim}(\varpi',\mu'_{\alpha*},\mu'_\delta,D,v,\xi_1,\xi_2)=\mathcal{C} \exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right] \phantom{oliebololiebol} \nonumber\\ &&\quad\times\exp\left[-\,{(\mu_{\alpha*,G}(D)+v\sin\xi_1\cos\xi_2/D -\mu'_{\alpha*})^2\over2{\sigma_\alpha}^2}\right] \nonumber \\ &&\quad\times\exp\left[-\,{(\mu_{\delta,G}(D)+v\sin\xi_1\sin\xi_2/D -\mu'_{\delta})^2\over2{\sigma_\delta}^2}\right] \nonumber \\ &&\quad \times f_D(D)\sin\xi_1\,2\sqrt{\frac{2}{\pi}}{v^2\over\sigma^3}\exp\left[-\,{v^2\over2\sigma^2}\right] \quad \mathrm{if}\quad zv_z>0. \label{e:definejmsi} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq199.png) (28)Here
(28)Here 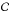 is defined with Eq. (19), and a factor 2 is added to normalize the semi-Maxwellian. The likelihood for the semi-isotropic Maxwellian follows:
is defined with Eq. (19), and a factor 2 is added to normalize the semi-Maxwellian. The likelihood for the semi-isotropic Maxwellian follows: 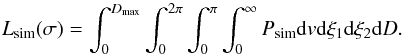 (29)Equation (26) shows that the condition that vz is in the correct direction is determined by the angles ξ1 and ξ2 and does not depend on v, and this allows the integral in Eq. (29) over the velocity to be done analytically. The integrals over the angles and distance are done numerically. Details are given in Appendix C.
(29)Equation (26) shows that the condition that vz is in the correct direction is determined by the angles ξ1 and ξ2 and does not depend on v, and this allows the integral in Eq. (29) over the velocity to be done analytically. The integrals over the angles and distance are done numerically. Details are given in Appendix C.
7. The mixed model
In our mixed model we assume that the pulsars in the grey band in Fig. 5 (#4, 5, 7, 9, 19) and the oldest pulsar (#26) are drawn from an isotropic velocity distribution, whereas all others are drawn from a semi-isotropic distribution, in which the velocities towards the Galactic plane are excluded. The distribution parameter σ for the semi-isotropic distribution is equal to the σ for the isotropic distribution. In analogy with Eq. (11) we define the deviance for the mixed model as 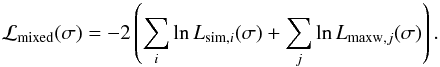 (30)Where the sums over i and over j are for the pulsars whose velocity is drawn from a semi-isotropic distribution and an isotropic distribution, respectively. The best value for σ is the value for which Eq. (30) reaches its minimum, and its range is determined from Δℒ = 1. The results are given in Table 4 and Fig. 3, and are not very different from those for the single isotropic Maxwellian, both for sample A of all pulsars, and for sample Y for the youngest pulsars. For the dℒ value it is seen that the mixed model is a significant improvement on the isotropic model. We return to this below, for the more interesting case of two Maxwellians.
(30)Where the sums over i and over j are for the pulsars whose velocity is drawn from a semi-isotropic distribution and an isotropic distribution, respectively. The best value for σ is the value for which Eq. (30) reaches its minimum, and its range is determined from Δℒ = 1. The results are given in Table 4 and Fig. 3, and are not very different from those for the single isotropic Maxwellian, both for sample A of all pulsars, and for sample Y for the youngest pulsars. For the dℒ value it is seen that the mixed model is a significant improvement on the isotropic model. We return to this below, for the more interesting case of two Maxwellians.
In a more realistic model the semi-isotropic distribution is composed of two semi-Maxwellians, with the same distribution parameters σ as the two isotropic Maxwellians that compose the isotropic distribution. In analogy with Eq. (21) we now have 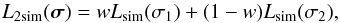 (31)and in analogy with Eq. (30)
(31)and in analogy with Eq. (30) 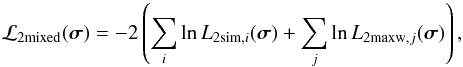 (32)where the sums over i and over j are for the pulsars whose velocity is drawn from a semi-isotropic distribution and an isotropic distribution, respectively. We use the subroutine AMOEBA of Press et al. (1986) to obtain the optimal values of w, σ1 and σ2 for which ℒ2mixed has its minimum, and Δℒ = 1 for the range of these parameters. The results are given in Table 4 and Fig. 6.
(32)where the sums over i and over j are for the pulsars whose velocity is drawn from a semi-isotropic distribution and an isotropic distribution, respectively. We use the subroutine AMOEBA of Press et al. (1986) to obtain the optimal values of w, σ1 and σ2 for which ℒ2mixed has its minimum, and Δℒ = 1 for the range of these parameters. The results are given in Table 4 and Fig. 6.
 |
Fig. 6 As Fig. 4, now for the mixed model. σopt for all pulsars and for the youngest pulsars are listed in Table 4. |
The best values and the ranges for σ1, σ2 and w for the semi-isotropic model are not significantly different from those of the isotropic model. Contour plots in the σ1-σ2 planes also are not significantly different from those for the model with two isotropic Maxwellians shown in Fig. 4.
The factor 2 in (the last line of) Eq. (28) ensures that the semi-Maxwellian is normalized to unity. As remarked above, a constant multiplicative factor for any likelihood drops out in Eq. (12), and thus does not affect the best solution and its range(s) within one model. However, to compare between models one must use the same normalizations of the separate distributions between the different models, and this requires the factor 2 in Eq. (28). The dℒ values listed in Table 4 show that the mixed model is a highly significant improvement above the isotropic Maxwellian model, for the full sample A, and that it is still significant for sample Y of young pulsars.
It is interesting to look at this is some more detail. Suppose for the moment that the contributions to the integral of Eq. (17) are zero for vz velocities towards the plane, then the only difference between L2maxw(σ) and L2mixed(σ) is the multiplicative factor 2 in Eq. (28). In sample A for all pulsars, this affects only the 22 pulsars for which a semi-Maxwellian applies, and leads to an added term in Eq. (32) equal to −2 × 22 × ln2 ≃ −30.5. In sample Y 14 of the young pulsars are affected, leading to an added term −2 × 14 × ln2 ≃ −19.4. The actual differences dℒ in deviance between the mixed models and purely isotropic models are smaller than this, which indicates that vz velocities towards the plane in fact do contribute to the integral of Eq. (17), also for pulsars for which such velocities are not expected. This implies that the isotropic model overestimates the likelihoods for these pulsars. PSR B0818−13 (#11) is a case in point: its apparent 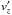 velocity is towards the plane (Fig. 5), and thus vz velocities towards the plane may be expected to contribute noticeably to integral Eq. (17).
velocity is towards the plane (Fig. 5), and thus vz velocities towards the plane may be expected to contribute noticeably to integral Eq. (17).
 |
Fig. 7 Ratio of the likelihoods in the mixed and isotropic models shown for each pulsar . The red colour indicates old pulsars, with τc > 10 Myr. To illustrate the pure effect of the normalization of the velocity distribution, we use the same parameters σ = (76 km s-1, 318 km s-1, 0.32) for both likelihoods. Use of σopt for each model separately gives rise to small shifts. |
In Fig. 7 we show the ratio of the likelihoods for the mixed and isotropic two-Maxwellian model for each pulsar separately. The six pulsars whose velocities are drawn from an isotropic velocity distribution also in the mixed model by definition have a ratio of one of the likelihoods for the mixed and isotropic two-Maxwellian model. The eleven pulsars with ratios closest to the maximum possible, 1.8 <Lmixed/Liso < 2 say, are all young. For these pulsars, almost all velocities contributing to Li in the isotropic model contribute also in the mixed model. For 11 pulsars (sample A) or 3 pulsars (sample Y) the velocity range that contributes to Li is restricted by the condition that vz be away from the Galactic plane, as shown by the difference of their Lmixed/Liso from the normalization factor 2.
8. The distribution of longitudinal velocities
Comparison of the results of our best model with those obtained in some earlier studies.
For comparison with earlier studies we also determine the model parameter σ by only using the measurements of the parallax and the measurements 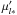 of the proper motion in the direction of Galactic longitude. For this we choose the coordinates in the directions of Galactic longitude and latitude, and radial. We rewrite Eqs. (15) and (17) as
of the proper motion in the direction of Galactic longitude. For this we choose the coordinates in the directions of Galactic longitude and latitude, and radial. We rewrite Eqs. (15) and (17) as ![\begin{eqnarray} &&P_\mathrm{gauss}(\varpi',\mu'_{l*},D,v_l,v_b,v_r)=\mathcal{C}_l f_D(D)G(v_l,\sigma)G(v_b,\sigma)G(v_r,\sigma)\phantom{olieb} \nonumber\\ &&\quad\times\exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right] \nonumber \\ &&\quad\times\exp\left[-\,{(\mu_{l*,G}(D)+v_l/D -\mu'_{l*})^2\over2{\sigma_l}^2}\right] , \label{e:jointl} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq220.png) (33)where
(33)where ![\begin{eqnarray*} \mathcal{C}_l \equiv \left[2\pi\sigma_\varpi\sigma_l\int_0^{D_\mathrm{max}} f_D(D) {\rm d}D\right]^{-1}, \end{eqnarray*}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq221.png) and
and 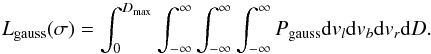 (34)μl ∗ and its error σμ are obtained from μα ∗, μδ and their errors with Eq. (A.9). The integrals over vb and vr are decoupled from the other integrals, and equal to 1. Equation (34) is rewritten:
(34)μl ∗ and its error σμ are obtained from μα ∗, μδ and their errors with Eq. (A.9). The integrals over vb and vr are decoupled from the other integrals, and equal to 1. Equation (34) is rewritten: ![\begin{equation} L_\mathrm{gauss}(\sigma) =\mathcal{C}_l\int_{0}^{D_\mathrm{max}}f_D(D) \exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right] \mathcal{I}_l\,{\rm d}D, \label{e:likgauss} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq225.png) (35)where
(35)where ![\begin{eqnarray*} \mathcal{I}_l \equiv \left(1+{\sigma^2\over D^2{\sigma_l}^2}\right)^{-1/2} \exp\left[-{1\over2}{(D\,\mu_{l*,G}-D\,\mu'_{l*})^2\over \sigma^2+D^2{\sigma_l}^2}\right]\cdot \end{eqnarray*}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq226.png) In this case, there is no difference between the isotropic and mixed model, because vz does not affect vl. We compute the deviance (Eq. (11)) with Eq. (35), to determine the values σopt for which the deviance reaches its minimum, and their range from Δℒ = 1. The results are listed in Table 4 and shown in Fig. 8. Interestingly, PSR B1508+55 is not an outlier in vl: its proper motion is almost completely in the direction of Galactic latitude (see Fig. 1). For sample A (all pulsars), σopt is the same as for the isotropic or semi-isotropic single Maxwellian; for sample Y (youngest pulsars) it is marginally lower. The limitation to only one component of the proper motion leads to a reduced accuracy of σopt, as expected. As a consequence the superposition of two Gaussians (that is components of two Maxwellians in the direction of Galactic longitude) does not improve significantly over the single Maxwellian description (σ = 109 km s-1,277 km s-1,0.27, dℒ = 1).
In this case, there is no difference between the isotropic and mixed model, because vz does not affect vl. We compute the deviance (Eq. (11)) with Eq. (35), to determine the values σopt for which the deviance reaches its minimum, and their range from Δℒ = 1. The results are listed in Table 4 and shown in Fig. 8. Interestingly, PSR B1508+55 is not an outlier in vl: its proper motion is almost completely in the direction of Galactic latitude (see Fig. 1). For sample A (all pulsars), σopt is the same as for the isotropic or semi-isotropic single Maxwellian; for sample Y (youngest pulsars) it is marginally lower. The limitation to only one component of the proper motion leads to a reduced accuracy of σopt, as expected. As a consequence the superposition of two Gaussians (that is components of two Maxwellians in the direction of Galactic longitude) does not improve significantly over the single Maxwellian description (σ = 109 km s-1,277 km s-1,0.27, dℒ = 1).
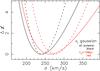 |
Fig. 8 Variation of ℒ with σ when only measurements of the parallax ϖ′ and of the proper motion |
9. Conclusions and discussion
Previous work derived the velocity distribution of pulsars from the observed distances and proper motions, and then compared this distribution with model distributions. This reduces the information present in the observations, complicates error propagation, and has lead to wrong likelihood definitions. The uncertainties in the proper motions determined from timing are two to three orders of magnitude larger than those of the proper motions in our master list, that are determined from VLBI. The larger number of such proper motions (less than one order of magnitude) does not make up for their larger uncertainties, so that inclusion of these proper motions does not significantly improve the analysis. The use of distances determined from dispersion measures further complicates the analysis, because the related distance uncertainties are dominated by systematic effects, and cannot be described with a Gaussian, even in approximation.
Our approach is more reliable because we a) derive predictions for the observed parameters (parallax and proper motion) from the model, and compare these directly with the relevant measurements; b) only use VLBI determinations from after 2000 of both parallax and proper motion, whose uncertainties are well described with Gaussians; and c) include the intrinsic Galactic distribution of pulsars (as expressed in fD(D), Eq. (4)). Our mixed model furthermore takes into account that velocity component vz perpendicular to the Galactic plane of a young pulsar well away from that plane must be in the direction away from the plane.
Applying this to the pulsars in our master list, we find that the description of the velocity distribution of the pulsars with two Maxwellians improves significantly on the description with a single Maxwellian. Our model describing vl with a single Gaussian gives a similar value for σ as the (mixed or isotropic) single Maxwellian, as expected for an isotropic velocity distribution. Comparison with earlier results, compiled in Table 5, shows that our more accurate method leads to more accurately determined model parameters. We show in Fig. 1 that our best solution corresponds well with the observed distribution of v⊥. One would be tempted to conclude that our whole analysis apparatus can be replaced with a straightforward fit of the cumulative v⊥ according to the model to the observed cumulative data for 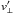 ! The reasons for the succes of the simpler method are the relatively small errors in the parallax, which limit the importance of fD(D), and the smallness of the correction for Galactic rotation with respect to the observed proper motions:
! The reasons for the succes of the simpler method are the relatively small errors in the parallax, which limit the importance of fD(D), and the smallness of the correction for Galactic rotation with respect to the observed proper motions: 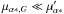 and
and  (Fig. 1). Indeed, ignoring the corrections for Galactic rotation hardly affects the results (Verbunt & Cator 2017). Corrections for Galactic motion matter only for distances much larger than those of the pulsars in our master list.
(Fig. 1). Indeed, ignoring the corrections for Galactic rotation hardly affects the results (Verbunt & Cator 2017). Corrections for Galactic motion matter only for distances much larger than those of the pulsars in our master list.
Whereas our results indicate that the available velocity measurements are adequately described by the sum of two (isotropic or semi-isotropic) Maxwellians, they do not prove that the actual distribution is given by this model, in preference to for example (sums of) isotropic Gaussians, Paczyński functions (see Eqs. (4), (5) of Paczyński 1990), or exponentials – all of which incidentally peak at zero velocity. Indeed, Maxwellians may be somewhat unlikely, as the condition required for the Maxwellian distribution in a mono-atomic gas, that is continuous redistribution of kinetic energy by frequent elastic collisions between atoms, certainly is not met by young pulsars. Our results do indicate that the velocity distribution is wide, with relative contributions of higher and lower velocities which appear incompatible with a single Gaussian, Paczyński function or exponential. The adequateness of two Maxwellians for the description of the currently available data (as suggested by Fig. 1) implies that more velocity data are necessary to discriminate between this model and models that use other functional forms.
With the exception of Brisken et al. (2003a), who do not give error estimates, all previous authors find significantly higher velocities for the high-velocity component than we do. The compilation in Table 5 illustrates that the fraction of pulsars in the high-velocity component (1−w) is inversely related to the characteristic velocity of that component. A small number of erroneously very high velocities leads to a high value of σ2. Because the combination of σ2 > 500 km s-1 with a low value of w, thus high 1−w, would lead to a much higher fraction of pulsars with v⊥ > 370 km s-1, say, than observed, the high value of σ2 forces a high value of w. We suggest that the higher velocities derived by previous authors are affected by the inclusion of unreliable distances determined from dispersion measures. In the case of Arzoumanian et al. (2002) we note that all parallaxes are from before 2000, that is not corrected for differential ionospheric refraction. As Hartman (1997) has shown, underestimating velocity errors leads to overestimating velocities.
The analysis by Hobbs et al. (2005) is based on the nominal velocities 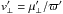 , and does not take into account the large errors in both distances and proper motions of their sample. These errors blur the intrinsic distribution. We suggest that this prevents Hobbs et al. from recognising the presence of low velocities, and from recovering a bimodal velocity distribution in their analysis. The best model with two velocity components by Faucher-Giguère & Kaspi (2006) allows w = 1, that is the second component is not significant. Our analysis in Sect. 8 suggests that this is due to their small sample size (34 pulsars, of which only eight have a measured parallax).
, and does not take into account the large errors in both distances and proper motions of their sample. These errors blur the intrinsic distribution. We suggest that this prevents Hobbs et al. from recognising the presence of low velocities, and from recovering a bimodal velocity distribution in their analysis. The best model with two velocity components by Faucher-Giguère & Kaspi (2006) allows w = 1, that is the second component is not significant. Our analysis in Sect. 8 suggests that this is due to their small sample size (34 pulsars, of which only eight have a measured parallax).
 |
Fig. 9 Top: our best velocity distribution for all pulsars and for the youngest pulsars, together with a single Maxwellian. The vertical dotted lines indicates the median velocities: 313, 370 and 408 km s-1. Below: fraction f( <v) of pulsars with velocity less than v, for the best mixed model for all pulsars (black), and for the lowest and highest value in the range of σ1 (red, blue). Solid lines: all pulsars; dashed lines: pulsars with τc < 10 Myr. In grey we show the fraction for a single Maxwellian (Hobbs et al. 2005). |
Our results imply that the velocity contrast between the low- and high-velocity components is a factor 3 to 6, and that 30 to 50% of the pulsars arise from the low-velocity component. It has been suggested (Podsiadlowksi et al. 2004) that pulsars formed from small iron cores or via electron capture would have a lower kick velocity than those formed from higher-mass core collapse, which may lead to a bimodal velocity distribution of pulsars. The existence of a class of neutron stars with low birth velocity has been derived from the properties of Be X-ray binaries (Pfahl et al. 2002) and the properties of millisecond pulsars binaries (Van den Heuvel 2004).
The fact that some pulsars are born in binaries and others from single stars will also affect the velocity distribution of single pulsars. Whether the observed bimodal velocity distribution reflects these different origins can be investigated in a population synthesis.
One of the goals of our work was to determine the fraction of pulsars with velocities small enough to remain bound to a globular cluster, or in a binary. In Fig. 9 we show the fraction of pulsars with velocity less than v as a function of v. For a typical escape velocity of a globular cluster, 60 km s-1 say, it is seen that this fraction is about 5% in our best model (mixed, for sample A). It varies from about 3% to about 7.5% in the range of σ1. At these low velocities, the fraction of pulsars is dominated completely by the low-velocity component, and therefore varies linearly with w for fixed σ1 and σ2.
Finally, we mention two reasons why the determination of pulsar velocities from a local sample may lead to an underestimate of the average velocity. The first one is Galactic drift: motion in the Galactic gravitational potential leads to reduction of the velocity of a pulsar that moves away from the center of the galaxy, and an increase if it moves towards the center. Thus if pulsars with an origin closer to the Galactic center contribute more to the locally observed sample than pulsars with an origin further out, the locally measured velocity distribution underestimates the distribution at birth (Hansen & Phinney 1997). The second reason is related to the velocity perpendicular to the plane: pulsars with a high | vz | move further from the plane, and thus must have a higher luminosity to be detected. In a flux-limited sample this leads to an over-representation of the low-velocity pulsars. These effects can be studied best in a population synthesis that takes these and other selection effects into account. Since such a synthesis involves also a larger number of parameters, a first step would be the measurement of more pulsar distances and proper motions.
Acknowledgments
We thank Gijs Nelemans for useful discussions.
References
- Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Benson, J. M., Beasley, A. J., et al. 2000, ApJ, 541, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Benson, J. M., Goss, W. M., & Thorsett, S. E. 2002, ApJ, 571, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Fruchter, A. S., Goss, W. M., Herrnstein, R. M., & Thorsett, S. E. 2003a, AJ, 126, 3090 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Thorsett, S. E., Golden, A., & Goss, W. M. 2003b, ApJ, 593, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Cordes, J. M., Lazio, T. J. W., et al. 2001, ApJ, 550, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Cordes, J. M., Vlemmings, W. H. T., et al. 2004, ApJ, 604, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Brisken, W. F., Vlemmings, W. H. T., et al. 2009, ApJ, 698, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Tingay, S. J., Bailes, M., & Reynolds, J. E. 2009, ApJ, 701, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Kaspi, V. M. 2006, ApJ, 643, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Phinney, E. S. 1997, MNRAS, 291, 569 [NASA ADS] [Google Scholar]
- Hartman, J. W. 1997, A&A, 322, 127 [NASA ADS] [Google Scholar]
- Hobbs, G., Lyne, A. G., Kramer, M., Martin, C. E., & Jordan, C. 2004, MNRAS, 353, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Igoshev, A., Verbunt, F., & Cator, E. 2016, A&A, 591, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirsten, F., Vlemmings, W., Campbell, R. M., Kramer, M., & Chatterjee, S. 2015, A&A, 577, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lane, A. P. 1979, PASP, 91, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, T. E., & Kelker, D. H. 1973, PASP, 85, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1990, ApJ, 348, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Pfahl, E., Rappaport, S., Podsiadlowski, P., & Spruit, H. 2002, ApJ, 574, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1986, Numerical recipes: the art of scientific computing (Cambridge University Press) [Google Scholar]
- Smart, W. M. 1938, Stellar dynamics (Cambridge University Press) [Google Scholar]
- van den Heuvel, E. P. J. 2004, in 5th INTEGRAL Workshop on the INTEGRAL Universe, eds. V. Schoenfelder, G. Lichti, & C. Winkler, ESA SP, 552, 185 [Google Scholar]
- Verbiest, J. P. W., Weisberg, J. M., Chael, A. A., Lee, K. J., & Lorimer, D. R. 2012, ApJ, 755, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Cator, E. 2017, J. Astrophys. Astron., 38, 40 [Google Scholar]
- Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Transformations of equatorial to Galactic coordinates
For the convenience of the reader we summarize the equations for coordinate transformations that we use. Lane (1979) gives (two of the three) equations for conversion from Galactic to equatorial for B1950.0. He notes that the equatorial coordinates of the Galactic pole αGP, δGP and the Galactic longitude lΩ of the node where the Galactic plane (b = 0) crosses the equator, define the coordinate transformation and thus also the equatorial coordinates of the centre l = b = 0. We note that this centre does not coincide exactly with the actual centre of the galaxy (for example as defined by Sgr A∗). We give all three equations, rewriting them slightly to show explicitly the role of αGP, δGP, and lΩ. The coordinate transformation is composed of three rotations: one around the Galactic z-axis to bring the Galactic centre to the node (this replaces l with l−lΩ), one around the equatorial z-axis to bring the spring node to the node (this replaces α with 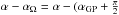 ), and finally around the now common x-axis over an angle
), and finally around the now common x-axis over an angle 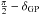 to align the Galactic pole with the equatorial pole. The resulting equations are (see also Lane 1979),
to align the Galactic pole with the equatorial pole. The resulting equations are (see also Lane 1979),  To find the equatorial coordinates αGC, δGC for the centre of the coordinate system, we enter l = b = 0 and combine Eqs. (A.1), (A.2) to find:
To find the equatorial coordinates αGC, δGC for the centre of the coordinate system, we enter l = b = 0 and combine Eqs. (A.1), (A.2) to find: 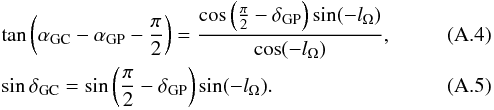 Perryman et al. (1997) give the pole and node longitude for J2000.0 as
Perryman et al. (1997) give the pole and node longitude for J2000.0 as 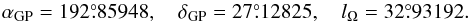 (A.6)and with Eqs. (A.1)–(A.3), these define the coordinate transformation for J2000.0 in the ICRS system. Entering these values in Eqs. (A.4), (A.5) we find
(A.6)and with Eqs. (A.1)–(A.3), these define the coordinate transformation for J2000.0 in the ICRS system. Entering these values in Eqs. (A.4), (A.5) we find  (A.7)For later reference we combine Eqs. (A.1), (A.2) for the Galactic center l = b = 0 into
(A.7)For later reference we combine Eqs. (A.1), (A.2) for the Galactic center l = b = 0 into 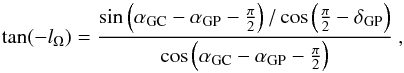 (A.8)and verify that entering the coordinates for pole and centre from Eqs. (A.6), (A.7) in Eq. (A.8) we re-obtain lΩ correctly.
(A.8)and verify that entering the coordinates for pole and centre from Eqs. (A.6), (A.7) in Eq. (A.8) we re-obtain lΩ correctly.
The next step is to determine the transformation of the proper motions. This is done by Smart (1938, Chap. 1.41), who notes that it corresponds to a rotation over an angle φ between the local directions of the lines of constant l and constant α, or equivalently between the lines of constant b and constant δ. With the notation μl ∗ ≡ μlcosb and μα ∗ ≡ μαcosδ we write Smart’s Eqs. (4), (5) as 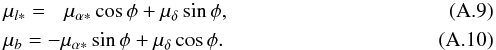 From spherical trigonometry the angle φ is given by
From spherical trigonometry the angle φ is given by 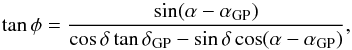 (A.11)(Smart 1938, Eq. (3)). The angle φ may also be found by taking the time derivative of the equation defining the transformation equatorial coordinates to Galactic latitude (cf. Lane 1979)
(A.11)(Smart 1938, Eq. (3)). The angle φ may also be found by taking the time derivative of the equation defining the transformation equatorial coordinates to Galactic latitude (cf. Lane 1979) 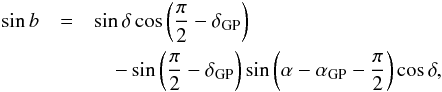 (A.12)and equating the result to Eq. (A.10).
(A.12)and equating the result to Eq. (A.10).
For Galactic to equatorial we may write analogously to Eqs. (A.9) and (A.10): 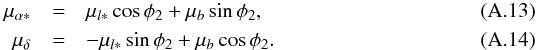 We equate the time derivative of Eq. (A.3) to (A.14) to obtain
We equate the time derivative of Eq. (A.3) to (A.14) to obtain 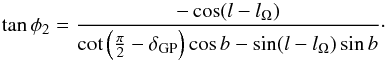 (A.15)Applied to the same source, φ = −φ2, and thus either angle may be computed with Eq. (A.11) or with Eq. (A.15).
(A.15)Applied to the same source, φ = −φ2, and thus either angle may be computed with Eq. (A.11) or with Eq. (A.15).
Appendix B: Proper motions and velocity corrections
 |
Fig. B.1 Definition of angles and distances in the Galactic plane (z = 0), and (inset) of the projected distance Dp to the pulsar. S is the Sun, GC the Galactic centre, P the pulsar and Pp the projection of the pulsar position on the Galactic plane. |
The space velocity of a star in the Galaxy may be decomposed into the average space velocity of its surroundings and its velocity with respect to this average, that is its peculiar velocity. The velocity of the local standard of rest for the Sun is its Galactic rotation velocity, vR(R0), where R0 is the distance to the Galactic centre. The peculiar velocity of the Sun is usually written [U, V, W], where the components are respectively in the direction from the Sun towards the Galactic centre, in the direction of the Galactic rotation, and perpendicular to the Galactic plane. The total velocity of the Sun may thus be written ![\appendix \setcounter{section}{2} \begin{equation} \vec{v}_\odot = [U,V+v_R(R_{0}),W]. \label{e:vsun} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq271.png) (B.1)For a pulsar in the Galactic plane, with b = 0, the velocity of the local standard of rest is also given by the rotation velocity vR(R) around the centre of the galaxy, at the galactocentric distance of the pulsar R (see Fig. B.1). This velocity is in the plane of the galaxy, in the direction perpendicular to the line connection the pulsar to the Galactic center. For a pulsar far from the plane, the meaning of the Local Standard of Rest is less obvious, because the halo stars do not participate in the rotation of the disk. The birthplace of the neutron star is (with the few exceptions mentioned above) in the Galactic plane, therefore we use for its local standard of rest the Galactic rotation vR(R) of its projection on the Galactic plane. The total velocity of a pulsar at distance D and Galactic coordinates l,b, may be written in the same coordinate frame as used for the Sun (see Fig. B.1):
(B.1)For a pulsar in the Galactic plane, with b = 0, the velocity of the local standard of rest is also given by the rotation velocity vR(R) around the centre of the galaxy, at the galactocentric distance of the pulsar R (see Fig. B.1). This velocity is in the plane of the galaxy, in the direction perpendicular to the line connection the pulsar to the Galactic center. For a pulsar far from the plane, the meaning of the Local Standard of Rest is less obvious, because the halo stars do not participate in the rotation of the disk. The birthplace of the neutron star is (with the few exceptions mentioned above) in the Galactic plane, therefore we use for its local standard of rest the Galactic rotation vR(R) of its projection on the Galactic plane. The total velocity of a pulsar at distance D and Galactic coordinates l,b, may be written in the same coordinate frame as used for the Sun (see Fig. B.1): ![\appendix \setcounter{section}{2} \begin{equation} \vec{v}_p = [U_p+v_R(R)\sin\theta,V_p+v_R(R)\cos\theta,W_p], \label{e:vpulsar} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq273.png) (B.2)with [Up,Vp,Wp] the peculiar velocity of the pulsar. To obtain the velocity in the l-direction, we write the unit vector in this direction as:
(B.2)with [Up,Vp,Wp] the peculiar velocity of the pulsar. To obtain the velocity in the l-direction, we write the unit vector in this direction as: ![\appendix \setcounter{section}{2} \begin{equation} \vec{l} = [-\sin l,\cos l,0]. \label{e:ell} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq275.png) (B.3)Thus the observed relative velocity in the longitude direction is
(B.3)Thus the observed relative velocity in the longitude direction is 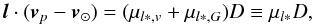 (B.4)where the peculiar velocity in the longitude direction is
(B.4)where the peculiar velocity in the longitude direction is 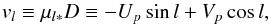 (B.5)and the correction for Galactic rotation and solar peculiar velocity is
(B.5)and the correction for Galactic rotation and solar peculiar velocity is ![\appendix \setcounter{section}{2} \begin{equation} \mu_{l*, G}\,D\equiv U\sin l-[V+v_R(R_{0})]\cos l +v_R(R)\cos(\theta+l). \label{e:deltamul} \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq278.png) (B.6)The angle (θ + l) may be computed from (see Fig. B.1):
(B.6)The angle (θ + l) may be computed from (see Fig. B.1):  (B.7)with Dp the projected distance towards the pulsar. Equation (7) follows from Eqs. (B.4)–(B.7).
(B.7)with Dp the projected distance towards the pulsar. Equation (7) follows from Eqs. (B.4)–(B.7).
The unit vector in the b-direction may be written ![\appendix \setcounter{section}{2} \begin{equation} \vec{b} = [-\sin b \cos l,-\sin b\sin l, \cos b], \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq280.png) (B.8)and the relative velocity in this direction
(B.8)and the relative velocity in this direction 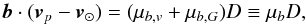 (B.9)with
(B.9)with 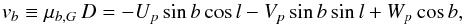 (B.10)and
(B.10)and ![\appendix \setcounter{section}{2} \begin{eqnarray} \mu_{b, G}D&=&U\sin b\cos l+[V+v_R(R_{0})]\sin b\sin l-W\cos b \nonumber \\ && \quad -v_R(R)\sin(\theta+l)\sin b .\label{e:deltamub} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq283.png) (B.11)For a pulsar in direction l,b, we can compute μl ∗ ,G and μb,G, as a function of distance D from Eqs. (B.6), (B.7) and (B.11). Because the rotation of the sum of two vectors is equal to the sum of two rotated vectors, symbolically: ℛ(a + Δa) = ℛ(a) + ℛ(Δa), we may rotate the corrections with Eqs. (A.9), (A.10). Hence:
(B.11)For a pulsar in direction l,b, we can compute μl ∗ ,G and μb,G, as a function of distance D from Eqs. (B.6), (B.7) and (B.11). Because the rotation of the sum of two vectors is equal to the sum of two rotated vectors, symbolically: ℛ(a + Δa) = ℛ(a) + ℛ(Δa), we may rotate the corrections with Eqs. (A.9), (A.10). Hence: 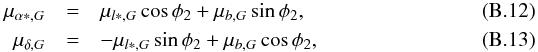 where φ2 is given by Eq. (A.15).
where φ2 is given by Eq. (A.15).
Appendix C: Numerical evalution of the likelihood in for a semi-anisotropic Maxwellian
To integrate Eq. (29), we first separate the terms involving the velocity and define ![\appendix \setcounter{section}{3} \begin{eqnarray} &&I_v = {\rm e}^{-A_3}\int_0^\infty v^2{\rm e}^{-A_1v^2-A_2v}{\rm d}v, \quad\mathrm{where} \nonumber \\[1mm] &&A_1 \equiv{1\over2\sigma^2} + {1\over2}\left({\sin\xi_1\cos\xi_2\over D\sigma_\alpha}\right)^2+ {1\over2}\left({\sin\xi_1\sin\xi_2\over D\sigma_\delta}\right)^2 ,\nonumber \\[1mm] &&A_2\equiv {\sin\xi_1\over D}\left[ {(\mu_{\alpha*,G}-\mu'_{\alpha*})\cos\xi_2\over{\sigma_\alpha}^2}+ {(\mu_{\delta,G}-\mu'_\delta)\sin\xi_2\over{\sigma_\delta}^2}\right] ,\nonumber\\[1mm] &&A_3\equiv {(\mu_{\alpha*,G}-\mu'_{\alpha*})^2\over2{\sigma_\alpha}^2} + {(\mu_{\delta,G}-\mu'_\delta)^2\over2{\sigma_\delta}^2} \cdot \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq289.png) (C.1)The result of this integral is
(C.1)The result of this integral is ![\appendix \setcounter{section}{3} \begin{equation} I_v={A_2{\rm e}^{-A_3}\over4{A_1}^2}\left[\sqrt{\pi}{\rm e}^{E^2}\left({1\over2E}+E\right)\mathrm{erfc}(E)-1\right];\quad E\equiv{A_2\over2\sqrt{A_1}}\cdot \end{equation}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq290.png) (C.2)Entering this in Eq. (29), we obtain:
(C.2)Entering this in Eq. (29), we obtain: ![\appendix \setcounter{section}{3} \begin{eqnarray} L_\mathrm{sim}(\sigma) &=& \int_{0}^{D_\mathrm{max}} \int_0^{2\pi} \int_0^\pi \mathcal{C}f_D(D) \exp\left[-\,{(1/D-\varpi')^2\over2{\sigma_\varpi}^2}\right]\nonumber \\ && \quad\times \sin\xi_1\,2\sqrt{\frac{2}{\pi}}{1\over\sigma^3} I_v(D,\xi_1,\xi_2) {\rm d}\xi_1 {\rm d}\xi_2 {\rm d}D. \label{e:psim} \end{eqnarray}](/articles/aa/full_html/2017/12/aa31518-17/aa31518-17-eq291.png) (C.3)Returning to Eq. (28), we note that for fixed distance D, velocity v and angle ξ1, Psim reaches it maximum when the arguments of the exponents that include the proper motions are zero. The value of ξ2 for which this is the case follows from
(C.3)Returning to Eq. (28), we note that for fixed distance D, velocity v and angle ξ1, Psim reaches it maximum when the arguments of the exponents that include the proper motions are zero. The value of ξ2 for which this is the case follows from 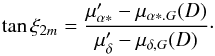 (C.4)Because this angle is the same for every v, the same value of ξ2 also maximizes the integrand of Eq. (C.3). The integration of Eq. (C.3) is done in three steps. First we fix D and ξ1, and determine the range of ξ2 from the condition Eq. (27) (or equivalently by testing with Eq. (26) that vz is in the right direction). We divide this range in three parts, one given by (ξ2m−h) to (ξ2m + h), and the other two dividing the remaining range, and integrate over ξ2 in each part separately with a 64-node Gaussian quadrature.
(C.4)Because this angle is the same for every v, the same value of ξ2 also maximizes the integrand of Eq. (C.3). The integration of Eq. (C.3) is done in three steps. First we fix D and ξ1, and determine the range of ξ2 from the condition Eq. (27) (or equivalently by testing with Eq. (26) that vz is in the right direction). We divide this range in three parts, one given by (ξ2m−h) to (ξ2m + h), and the other two dividing the remaining range, and integrate over ξ2 in each part separately with a 64-node Gaussian quadrature.
Appendix D: Master list
Master list of the pulsars used in our study.
We find that h = 2π/ 70 leads to accurate results. Second, we integrate over ξ1 with one 64-node Gaussian quadrature. Finally, we integrate over D, in steps of 100 pc, for Dmax = 10 kpc.
We compute Lmaxw−si(σ) on a grid of values of σ, in steps of 5 km s-1, interpolate linearly to get a grid with steps of 1 km s-1.
All Tables
Values of constants defining coordinate transformations and velocity corrections.
Results of the model calculations for all 28 pulsars in our master list (A), and for the 19 youngest pulsars (τc < 10 Myr, Y).
Comparison of the results of our best model with those obtained in some earlier studies.
All Figures
 |
Fig. 1 Illustrations of data from our master list of pulsars Table D.1. Top: celestial distribution in Galactic coordinates. The blue lines show the observed proper motion μ′ and the red lines the correction due to Galactic rotation (for nominal distance D′), in 0.5 Myr. Below left: nominal velocities in the celestial plane. The circle indicates the median value for v⊥ for the projection of a Maxwellian: |
| In the text | |
 |
Fig. 2 Illustration for two pulsars of the contributions to the integrand of the likelihood Lmaxw(σ) (Eq. (19)) of the separate factors fD(D)gD(ϖ′ | D) (top graphs; Eqs. (1) and (4)), Iα and Iδ (middle graphs). Each curve has been normalized separately to maximum unity. Iα and Iδ are shown for for three values σ of the Maxwellian (Eq. (14)). The lower graphs show the integrand of the likelihood Lmaxw(σ) for three values of σ, as a function of distance, normalized to the highest maximum of the three. The measurements of PSR J0034−0721 (left) favour a low value of σ. Those of PSR B1508+55 (right) require a high value of σ, and the integrands for σ = 50 and 100 km s-1 are indistinguishable from zero in this graph. |
| In the text | |
 |
Fig. 3 Variation of ℒ with velocity distribution parameter σ for the model with a single isotropic Maxwellian (dotted lines), and for the mixed model in which most pulsars have an assumed semi-isotropic velocity distribution (solid lines). The colour coding indicates the pulsar sample: all 28 pulsars in our master list, the 27 pulsars remaining after removing PSR B1508+55, and the 19 youngest (τ < 10 Myr) pulsars. |
| In the text | |
 |
Fig. 4 Contours of ℒ(σ) in three σ1,σ2 planes with fixed w, for the model with two isotropic Maxwellians. Contours of constant Δℒ(σ) (Eq. (12)) are shown for values 1 and 4, in each plane, The best solution is indicated with •. Top: all pulsars. σopt = (77 km s-1, 321 km s-1, 0.42). Below: pulsars with τc < 10 Myr. σopt = (83 km s-1, 335 km s-1, 0.32). |
| In the text | |
 |
Fig. 5 Nominal distance from the Galactic plane z′ = sinb/ϖ′, range sinb/ (ϖ′ ± σϖ), as a function of longitude. The blue points indicate pulsars nominally moving away from the plane, that is z′ and |
| In the text | |
 |
Fig. 6 As Fig. 4, now for the mixed model. σopt for all pulsars and for the youngest pulsars are listed in Table 4. |
| In the text | |
 |
Fig. 7 Ratio of the likelihoods in the mixed and isotropic models shown for each pulsar . The red colour indicates old pulsars, with τc > 10 Myr. To illustrate the pure effect of the normalization of the velocity distribution, we use the same parameters σ = (76 km s-1, 318 km s-1, 0.32) for both likelihoods. Use of σopt for each model separately gives rise to small shifts. |
| In the text | |
 |
Fig. 8 Variation of ℒ with σ when only measurements of the parallax ϖ′ and of the proper motion |
| In the text | |
 |
Fig. 9 Top: our best velocity distribution for all pulsars and for the youngest pulsars, together with a single Maxwellian. The vertical dotted lines indicates the median velocities: 313, 370 and 408 km s-1. Below: fraction f( <v) of pulsars with velocity less than v, for the best mixed model for all pulsars (black), and for the lowest and highest value in the range of σ1 (red, blue). Solid lines: all pulsars; dashed lines: pulsars with τc < 10 Myr. In grey we show the fraction for a single Maxwellian (Hobbs et al. 2005). |
| In the text | |
 |
Fig. B.1 Definition of angles and distances in the Galactic plane (z = 0), and (inset) of the projected distance Dp to the pulsar. S is the Sun, GC the Galactic centre, P the pulsar and Pp the projection of the pulsar position on the Galactic plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.