| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201730757 | |
| Published online | 22 November 2017 | |
Are over-massive haloes of ultra-diffuse galaxies consistent with extended MOND?
School of Physics and Astronomy, University of St Andrews, St Andrews, KY16 9SS, UK
e-mail: aoh2@st-andrews.ac.uk
Received: 9 March 2017
Accepted: 24 August 2017
Aims. A sample of Coma cluster ultra-diffuse galaxies (UDGs) are modelled in the context of extended modified Newtonian dynamics (EMOND) with the aim to explain the large dark matter-like effect observed in these cluster galaxies.
Methods. We first built a model of the Coma cluster in the context of EMOND using gas and galaxy mass profiles from the literature. Assuming that the dynamical mass of the UDGs satisfies the fundamental manifold of other ellipticals and that the UDG stellar mass-to-light ratio matches their colour, we then verified the EMOND formulation by comparing two predictions of the baryonic mass of UDGs.
Results. We find that EMOND can explain the UDG mass, within the expected modelling errors, if they lie on the fundamental manifold of ellipsoids, but given that measurements show one UDG lying off the fundamental manifold, observations of more UDGs are needed to confirm this assumption.
Key words: gravitation / galaxies: clusters: general / galaxies: general / dark matter
© ESO, 2017
1. Introduction
Gravitational potential wells of galaxy clusters have been powerful laboratories to test the current model of dark matter (ΛCDM) and its alternatives. While acknowledging many shortfalls of the ΛCDM model in galaxies (e.g. Walker & Peñarrubia 2011; Dubinski & Carlberg 1991; Klypin et al. 1999; Moore et al. 1999; Boylan-Kolchin et al. 2012, 2011; Ibata et al. 2013; Pawlowski et al. 2015; Kroupa et al. 2010; Kroupa 2012, 2015; Donato et al. 2009), few models in the cluster arena can compete with the ΛCDM model, especially those alternatives that a priori assume that particle dark matter does not exist, but that what we are seeing is instead a breakdown of Newtonian dynamics.
Observations of rotation curves in galaxies showed that dark matter effects were only required in low-acceleration environments 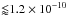 m s-2. This eventually led to the construction of the empirical gravitational paradigm known as modified Newtonian dynamics (MOND; Milgrom 1983a,b,c; Bekenstein & Milgrom 1984). The main function of MOND is to modify gravity in these low-acceleration environments such that the gravitational acceleration falls proportional to 1 /r, in contrast to the Newtonian 1 /r2. Newtonian dynamics are still preserved in the high-acceleration environments. In order to achieve this, an acceleration scale was introduced to define what is meant by high- and low-acceleration environments, a0 ≈ 1.2×10-10 m s-2, such that Newtonian behaviour is recovered when a ≫ a0 and the 1 /r gravity law (Deep-MOND regime) occurs when a ≪ a0, where a is the total gravitational acceleration.
m s-2. This eventually led to the construction of the empirical gravitational paradigm known as modified Newtonian dynamics (MOND; Milgrom 1983a,b,c; Bekenstein & Milgrom 1984). The main function of MOND is to modify gravity in these low-acceleration environments such that the gravitational acceleration falls proportional to 1 /r, in contrast to the Newtonian 1 /r2. Newtonian dynamics are still preserved in the high-acceleration environments. In order to achieve this, an acceleration scale was introduced to define what is meant by high- and low-acceleration environments, a0 ≈ 1.2×10-10 m s-2, such that Newtonian behaviour is recovered when a ≫ a0 and the 1 /r gravity law (Deep-MOND regime) occurs when a ≪ a0, where a is the total gravitational acceleration.
The MOND paradigm has had success on the galaxy scale, see Famaey & McGaugh (2012) for an extensive review. One of the main problems in MOND is its inability to explain galaxy clusters. In the outer regions of galaxy clusters, MOND is able to reduce the mass deficit to within a factor of 2−3 of the predicted mass, and in the inner regions, the mass discrepancy is more severe (e.g. Sanders 1999, 2003; Milgrom 2014). Galaxy clusters tend to have an internal acceleration of the order a0 and thus the MOND effect is weak. However, galaxy clusters show a large mass discrepancy from Newtonian predictions, much more than MOND is able to account for. This means that either 1) there exists a ΛCDM dark matter halo; 2) there is missing matter that we are yet to detect in the form of non-luminous baryonic matter or some form of neutrinos; or 3) MOND is not a complete gravity theory and needs to be generalised. Work on point 2 has achieved mixed results. Angus et al. (2008) have shown that the 2 eV neutrino was insufficient to explain the galaxy cluster problem as their inclusion could not explain mass discrepancy in the centre of the clusters. The neutrino idea was then reinvestigated in Angus (2009), where 11 eV sterile neutrinos were tested. This work enjoyed more success in explaining the galaxy cluster problem in MOND and also had success in explaining the cosmic microwave background (CMB) anisotropies. However, cosmological simulations conducted by Angus & Diaferio (2011) and Angus et al. (2013) showed that using neutrinos as hot dark matter in the MOND paradigm produces too many high-mass galaxy clusters. It should be made clear that the simulations performed in Angus & Diaferio (2011) and Angus et al. (2013) assumed that the cosmic expansion history was described by ΛCDM cosmology. Therefore the effect of introducing a covariant MOND framework is yet unknown and thus MOND + neutrinos cannot be ruled out by the over-production of massive haloes in these simulations.
A recent addition to the galaxy cluster problem in MOND is the discovery of ultra-diffuse galaxies (UDGs; Koda et al. 2015; Roman & Trujillo 2017; Mihos et al. 2015; van Dokkum et al. 2015). These galaxies have very little gas and are composed almost entirely of dark matter. Recent studies of a UDG in the Virgo cluster (Beasley et al. 2016) and the Coma cluster (van Dokkum et al. 2016) have shown that two UDGs, VC1287 and DF44, show a very high dark-to-stellar mass ratio. It should be noted, however, that current models of these objects thus far make many assumptions, including spherical symmetry and virial equilibrium, and therefore the prediction of a large dark matter content needs to be confirmed. The work of Kroupa (1997) has highlighted that objects with non-isotropic velocity dispersions, out of dynamical equilibrium and no sphericity could show a high observed mass-to-light ratio with the true mass-to-light ratio being much lower. It may be the case that the UDGs are similar to the objects discovered in Kroupa (1997) in that the observed dark matter content is smaller.
In this work, we are interested in the nature of UDGs in the context of MOND. In a MONDian paradigm, it is possible to create a large dark matter-like effect if the gravitational acceleration across the system is very low. The MOND paradigm has an interesting feature called the external field effect (EFE; see for example Derakhshani & Haghi 2014; Blanchet & Novak 2011; Haghi et al. 2016; Wu & Kroupa 2013, 2015). The EFE states that even a constant acceleration from an external source can affect the internal dynamics of a system. For example, a stellar cluster located close to the Milky Way disk should behave differently if it is moved farther away from the disk because the gravitational acceleration across the cluster from the Milky Way would be less. In the context of the UDGs, if they were isolated objects, MOND would predict a large dark matter-like effect, but as they are within the strong gravitational field of the galaxy cluster, MOND predicts they should behave closer to Newtonian.
Taking this into consideration, if MOND is to be generalised to try and explain the missing mass in galaxy clusters, it must also explain the nature of these UDGs. One attempt to refine MOND with new physics is that of the extended MOND (EMOND; Zhao & Famaey 2012). This extension of MOND changes the acceleration scale a0 from being constant to being a function of gravitational potential, A0(Φ), such that the effective acceleration scale in galaxy clusters is much larger than a0. This allows deviations from Newtonian dynamics, and hence the inducing of dark matter-like effects, to occur at higher accelerations. The EMOND paradigm introduces a second interpolation function in addition to the function used to transition between Newtonian and deep-MOND regimes, which describes the evolution of the acceleration scale with gravitational potential. This function is chosen such that EMOND tends to regular MOND in galaxies. Further still, it is assumed that the value of a0 in EMOND rises to a constant value, such that when the potential and acceleration are very deep, for instance, in black holes and the central regions of galaxies, regular MOND results hold true.
We explored EMOND in Hodson & Zhao (2017) with a sample of 12 galaxy clusters. Hodson & Zhao (2017) showed that EMOND has some success with the basic formulation, but no attempt was made to explore the boundary conditions of the gravitational potential to try to obtain better fits. In addition, the exact form of the baryonic mass profile is relevant when determining the EMOND prediction, and thus different mass models should be tested in future. As a consequence of this, the paradigm requires more rigorous testing.
Recent work on the UDGs has allowed dynamical mass estimates to be made, that is, the total mass of the UDGs including any dark component, for a sample of galaxies from the Coma and Virgo clusters using scaling relations (Zaritsky 2017). This method takes advantage of the fundamental manifold (FM; Zaritsky et al. 2006b,a, 2008) to calculate velocity dispersions of the UDGs from their effective radius and surface brightness. The FM is an extension of the fundamental plane (Djorgovski & Davis 1987; Dressler et al. 1987). From the velocity dispersions, it is then possible to estimate a dynamical mass for the objects. It is also possible to estimate the stellar mass of the UDGs from their g−i colour. This technique was performed in van Dokkum et al. (2016) for DF44 by using the colour-M⋆/L correlation from Taylor et al. (2011). Therefore it is possible to derive both dynamical and stellar mass estimates for a sample of UDGs. We should stress that this simplified modelling adopts the assumptions of sphericity and virial equilibrium, which, as we have mentioned, may not be valid.
By modelling the Coma cluster in the context of EMOND, we can find the value of A0(Φ) in the cluster as a function of radius. Assuming this value is constant across any UDG, we can estimate the stellar mass of the UDGs from dynamical mass estimates using the EMOND recipe and compare the result to stellar mass predicted from the colour. By doing this, we can determine whether the EMOND recipe can predict both the mass profile of the Coma cluster and the dynamical-to-stellar mass fraction of the UDGs simultaneously.
This paper is organised as follows. Section 2 discusses the MOND and EMOND paradigm. Section 3 discusses the Coma cluster model we adopt. Section 4 discusses the UDG dynamical and stellar mass estimates from the literature. The UDG modelling in the context of MOND and EMOND is discussed in Sect. 5. We show our results in Sect. 6. In Sect. 7 we show how the constraints on the EMOND formalism from the UDG modelling affect the results of Hodson & Zhao (2017). In Sect. 8 we discuss possible differences with observational data. We then conclude in Sect. 9.
2. Extended MOND
We begin our discussion of EMOND by reviewing the standard MOND equations. In gravitational dynamics, the gravitational acceleration and matter density are linked via a Poisson equation. The MOND Poisson equation is (Bekenstein & Milgrom 1984), ![\begin{equation} 4\pi G \rho = \nabla \cdot \left[ \mu\left(\frac{|\nabla \Phi|}{a_{0}} \right) \nabla \Phi \right], \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq18.png) (1)where ρ is the matter density and Φ is the total gravitational potential. The function μ(x) is called the interpolation function, which models the transition between the Newtonian regime and the deep-MOND regime. μ(x) must have limits such that when x ≪ 1, μ(x) = x and when x ≫ 1, μ(x) = 1. The form for the interpolation function that we use in this work is a modified simple interpolation (see Famaey & Binney 2005; Zhao & Famaey 2006 for the simple interpolation function),
(1)where ρ is the matter density and Φ is the total gravitational potential. The function μ(x) is called the interpolation function, which models the transition between the Newtonian regime and the deep-MOND regime. μ(x) must have limits such that when x ≪ 1, μ(x) = x and when x ≫ 1, μ(x) = 1. The form for the interpolation function that we use in this work is a modified simple interpolation (see Famaey & Binney 2005; Zhao & Famaey 2006 for the simple interpolation function), ![\begin{equation} \mu(x)= {\rm max} \left[\frac{x}{1+x}, \frac{\epsilon}{1 + \epsilon} \right], \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq26.png) (2)where ϵ is a small number. The EMOND version of the MOND Poisson equation is Zhao & Famaey (2012). The additional T2 term arises from the non-relativistic EMOND Lagrangian. Merely making the change a0 → A0(Φ) in the Poisson equation will not satisfy the Euler-Lagrange equation.
(2)where ϵ is a small number. The EMOND version of the MOND Poisson equation is Zhao & Famaey (2012). The additional T2 term arises from the non-relativistic EMOND Lagrangian. Merely making the change a0 → A0(Φ) in the Poisson equation will not satisfy the Euler-Lagrange equation. ![\begin{equation} 4 \pi G \rho = \nabla \cdot \left[\mu\left( \frac{|\nabla \Phi|}{A_{0}(\Phi)} \right) \nabla \Phi \right] - T_{2}, \label{EMONDPoiss} \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq30.png) (3)where
(3)where ![\begin{equation} T_{2} = \frac{1}{8\pi G}\left| \frac{{\rm d} (A_{0}(\Phi))^{2}}{{\rm d}\Phi} \right|\left[ y F'(y) - F(y) \right]. \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq31.png) (4)In addition,
(4)In addition, 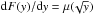 and y = | ∇Φ | 2/A0(Φ)2. It was shown explicitly in Hodson & Zhao (2017) that the T2 term is negligible in clusters, and thus the approximate spherical version of the EMOND Poisson equation reduces to
and y = | ∇Φ | 2/A0(Φ)2. It was shown explicitly in Hodson & Zhao (2017) that the T2 term is negligible in clusters, and thus the approximate spherical version of the EMOND Poisson equation reduces to 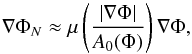 (5)where ∇ΦN is the Newtonian acceleration. The functional form of A0(Φ) we use here is
(5)where ∇ΦN is the Newtonian acceleration. The functional form of A0(Φ) we use here is ![\begin{equation} A_{0}(\Phi) = \frac{a_{0}}{\epsilon} \mu\left[ \left( \frac{\Phi}{\Phi_{0}} \right)^{2q}\right], \label{A0tan} \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq36.png) (6)where A0 max is the maximum value that we allow A0 to take ≈ 100a0, Φ0 is a scale potential analogous to the MOND scale acceleration with units of m2 s-2, and q is a dimensionless parameter that controls the slope of A0(Φ). We define ϵ to be ϵ = a0/A0 max. Equation (6)says that when the potential is high (Φ ≫ Φ0), A0(Φ) = A0 max and when the potential is low, (Φ ≪ Φ0), A0(Φ) = a0. This is analogous to the MOND interpolation function, μ(x). The consequence of this function is that in the central regions of galaxy clusters, A0(Φ) ≈ A0 max and at the edge of galaxy clusters (and in galaxies) A0(Φ) ≈ a0. In this work, we show results for q = 1 and q = 2. The change in choice of q warrants a change of scale potential, Φ0, as well. For q = 2, the scale potential is unchanged from Hodson & Zhao (2017) with magnitude Φ0 ≈ −2 700 0002 m2 s-2. For q = 1, the scale potential is empirically chosen to be Φ0 ≈ −3 800 0002 m2 s-2. Therefore given a boundary potential (which we discuss in latter sections), we can solve Eq. (5)and determine the EMOND-predicted acceleration profile and hence EMOND-predicted dynamical mass.
(6)where A0 max is the maximum value that we allow A0 to take ≈ 100a0, Φ0 is a scale potential analogous to the MOND scale acceleration with units of m2 s-2, and q is a dimensionless parameter that controls the slope of A0(Φ). We define ϵ to be ϵ = a0/A0 max. Equation (6)says that when the potential is high (Φ ≫ Φ0), A0(Φ) = A0 max and when the potential is low, (Φ ≪ Φ0), A0(Φ) = a0. This is analogous to the MOND interpolation function, μ(x). The consequence of this function is that in the central regions of galaxy clusters, A0(Φ) ≈ A0 max and at the edge of galaxy clusters (and in galaxies) A0(Φ) ≈ a0. In this work, we show results for q = 1 and q = 2. The change in choice of q warrants a change of scale potential, Φ0, as well. For q = 2, the scale potential is unchanged from Hodson & Zhao (2017) with magnitude Φ0 ≈ −2 700 0002 m2 s-2. For q = 1, the scale potential is empirically chosen to be Φ0 ≈ −3 800 0002 m2 s-2. Therefore given a boundary potential (which we discuss in latter sections), we can solve Eq. (5)and determine the EMOND-predicted acceleration profile and hence EMOND-predicted dynamical mass.
One challenge of EMOND is how to determine the value of the boundary potential. Currently, as we have no way of doing this, we leave it as an empirically determined free parameter. However, we expect that if EMOND was made covariant (e.g. in a TeVeS-like manner), the boundary potential would be set by the cosmological background solution. Because we lack a consistent cosmology, we are at this stage limited to empirically fitting. Future work on EMOND can determine whether our empirical fit is acceptable.
3. Modelling the Coma cluster
The first step to modelling the Coma cluster UDGs is to build a model of the Coma cluster itself. We adopted the model of Łokas & Mamon (2003), which has an intra-cluster gas component and cluster galaxy component. There is also a dark matter component in standard gravity, which we can compare with the effective phantom halo predicted by EMOND.
The distribution of intra-cluster gas was modelled via a β density profile, for which the expression for enclosed mass is 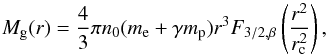 (7)where n0 is the central electron number density of the emitting X-ray gas in the cluster, β is a dimensionless parameter, rc is a scale length of the gas density, γ is a parameter that converts the electron number density into a mass density, and
(7)where n0 is the central electron number density of the emitting X-ray gas in the cluster, β is a dimensionless parameter, rc is a scale length of the gas density, γ is a parameter that converts the electron number density into a mass density, and 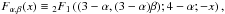 where
where 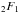 is a hyper-geometric function.
is a hyper-geometric function.
The distribution of galaxies was modelled via ![\begin{equation} M_{\rm Gal}(r) = 4 \pi L_{\star} \Upsilon r_{\rm s}^{3} \left[ \log\left( \frac{r+ r_{\rm s}}{r_{\rm s}} \right)-\frac{r}{r+r_{\rm s}} \right], \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq61.png) (8)where rs is a scale radius, L⋆ is a luminosity normalisation constant, and Υ is a mass-to-light ratio.
(8)where rs is a scale radius, L⋆ is a luminosity normalisation constant, and Υ is a mass-to-light ratio.
Finally, in the work of Łokas & Mamon (2003), the distribution of dark matter was modelled via 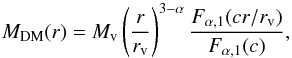 (9)where Mv is the virial mass, rv is the virial radius, c is the concentration, and α is a dimensionless parameter.
(9)where Mv is the virial mass, rv is the virial radius, c is the concentration, and α is a dimensionless parameter.
We show the values taken from Łokas & Mamon (2003) that we used for the gas, galaxy, and dark matter profile in Table 1.
Coma cluster mass model values.
We plot the mass components of the Coma cluster as a function of radius in Fig. 1, mimicking the top panel of Fig. 8 in Łokas & Mamon (2003). We over-plot the EMOND predicted mass profile (blue solid line) determined by first solving Eq. (5)for EMOND gravity, which we call ∇ΦEMOND, and then calculating the effective EMOND mass via 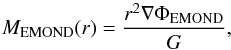 (10)where the Newtonian gravity used to determine ∇ΦEMOND is
(10)where the Newtonian gravity used to determine ∇ΦEMOND is 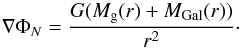 (11)To make the plot, we empirically took a value of the EMOND gravitational potential at the virial radius to be Φ(rv) = −2.5 × 1012 m2 s-2. We can see that the dark matter dominates the gas and galaxy contributions.
(11)To make the plot, we empirically took a value of the EMOND gravitational potential at the virial radius to be Φ(rv) = −2.5 × 1012 m2 s-2. We can see that the dark matter dominates the gas and galaxy contributions.
 |
Fig. 1 Model of the Coma cluster that we adopt from Łokas & Mamon (2003). The green thin line shows the contribution from the intra-cluster gas, and the red thin line is the contribution from the stars. Using these, we can calculate the EMOND-predicted dynamical mass from Eq. (10), which is the solid blue line for the q = 1 model and the solid magenta line for the q = 2 model (see Eq. (6)). We also plot the dark matter profile from Łokas & Mamon (2003; black dashed line) for comparison. We see that our EMOND mass matches the dark matter mass very well. For this, we assumed an EMOND boundary potential at the virial radius Φ(rv) = −2.5 × 1012 m2 s-2. |
The plot also shows that the EMOND-predicted mass seems to match the dark matter profile to exceptional accuracy, although the q = 2 model shows some problem in the outer regions of the cluster. This is a very good result for the EMOND paradigm. In previous EMOND work, Hodson & Zhao (2017) found that EMOND had mixed success in describing the 12 clusters from Vikhlinin et al. (2006). We note that the Coma cluster was not part of this original study. The work in question used a different baryonic mass profile for both the gas and the galaxies. This result suggests that the EMOND modelling of Hodson & Zhao (2017) might be improved by invoking a different functional form for the baryonic mass profile.
Now that we have derived the EMOND mass profile of the Coma cluster, we can make a plot of A0(Φ) vs radius to show how the EMOND acceleration scale varies in the cluster environment. We show this in Fig. 2.
 |
Fig. 2 Profile of the EMOND-calculated A0(Φ) /a0 as a function of cluster radius. The blue dashed line is the q = 2 model, and the red solid line is the q = 1 model. The q = 1 model produces a shallower transition from high to low A0(Φ) and a smaller magnitude of A0(Φ) than the q = 2 model (see Eq. (6)). We only show radii > 100 kpc as this is the important range for the UDGs. |
From Fig. 2, it is clear that the q = 1 model creates a gentler transition of A0(Φ) from the outside of the cluster to the centre than the q = 2 model. It is also clear that the magnitude of A0(Φ) that the q = 1 model predicts is much lower than the q = 2 model. This is due in part to the gentler transition, but mainly to the choice of Φ0, which stops A0(Φ) reaching A0 max. We describe the effect of this in the following sections.
4. UDG properties
A note on conventions. Throughout the following sections we refer to several mass quantities that we need to define clearly. The “dynamical” mass of the UDGs is the inferred mass from dynamics, thus is the total mass of the system. In a ΛCDM context, this would be the mass of the stars plus the mass of the dark matter halo. In MOND/EMOND, this would be the baryons + phantom dark matter. The baryonic mass is the total visible mass contained within the UDGs, which we assume to be entirely composed of stars and which is determined from the colour-stellar mass relations outlined in Sect. 4.2. Finally, the MOND/EMOND mass is the predicted baryonic mass determined from the MOND/EMOND Poisson equation. The MOND/EMOND mass should be equivalent to the baryonic mass if no dark matter is required.
When we modelled the UDGs in MOND/EMOND, we took the dynamical mass of the UDG at the effective radius and determined the MOND/EMOND mass at that radius using the MOND/EMOND recipe. We then compared this to the baryonic mass of these galaxies. Therefore, we need to determine both the dynamical and the baryonic mass for these systems. To do this, we followed the techniques used in Zaritsky (2017) and Zaritsky et al. (2008) for the dynamical mass and van Dokkum et al. (2015) for the baryonic mass. We outline the techniques used in these works below.
4.1. Dynamical mass
The dynamical mass of the UDGs is determined from the velocity dispersion and effective radius, assuming virial equilibrium and spherical symmetry, via the formula Wolf et al. (2010; also see Eq. (1) in van Dokkum et al. 2016) 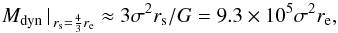 (12)where Mdyn( <rs) is the total enclosed dynamical mass at the spherical half-mass radius
(12)where Mdyn( <rs) is the total enclosed dynamical mass at the spherical half-mass radius 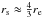 , where the re is the usual effective radius, that is, the projected circularised half-light radius, σ is the velocity dispersion in km s-1 and re is the effective 2D radius in kpc. The effective radius was determined and corrected for ellipticity for 46 UDGs within the Coma cluster, and these radii are given in van Dokkum et al. (2015). Currently, there is only one UDGs (Dragonfly 44 (DF44)) in the Coma cluster that has a measured value for the velocity dispersion. We note that the full sample from van Dokkum et al. (2015) has 47 objects, but 1 object has incomplete data in the table and thus we disregard this entry. To estimate velocity dispersions for all 46 galaxies in the Coma cluster sample, some assumptions have to be made.
, where the re is the usual effective radius, that is, the projected circularised half-light radius, σ is the velocity dispersion in km s-1 and re is the effective 2D radius in kpc. The effective radius was determined and corrected for ellipticity for 46 UDGs within the Coma cluster, and these radii are given in van Dokkum et al. (2015). Currently, there is only one UDGs (Dragonfly 44 (DF44)) in the Coma cluster that has a measured value for the velocity dispersion. We note that the full sample from van Dokkum et al. (2015) has 47 objects, but 1 object has incomplete data in the table and thus we disregard this entry. To estimate velocity dispersions for all 46 galaxies in the Coma cluster sample, some assumptions have to be made.
We took a slightly different approach for our study than did Zaritsky (2017). Zaritsky (2017) determined the velocity dispersions for the UDGs in the Coma cluster by making use of the fundamental manifold (FM). This relation links effective radius, mean surface brightness within the effective 2D radius, and the internal kinematics of the system in question via a nearly power-law-like relation, 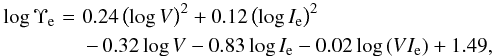 (13)where Υe is the mass-to-light ratio, Ie is the mean surface brightness within re, and V describes the kinematics of the system, mainly the velocity dispersion and rotation, such that
(13)where Υe is the mass-to-light ratio, Ie is the mean surface brightness within re, and V describes the kinematics of the system, mainly the velocity dispersion and rotation, such that 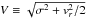 (Zaritsky 2017). This was then solved along with the known relation log re = 2log V−log Ie−log Υe−C, which is derived from Eq. (12), to determine V and Υe. Zaritsky (2017) then assumed that V ≈ σ. This value of the velocity dispersion was then corrected via log σcorr = (log σ−0.061) / 0.833 to account for a “slight systematic deviation from the expectation”. Therefore Zaritsky (2017) were able to obtain estimates for the velocity dispersions and thus dynamical masses for the UDGs.
(Zaritsky 2017). This was then solved along with the known relation log re = 2log V−log Ie−log Υe−C, which is derived from Eq. (12), to determine V and Υe. Zaritsky (2017) then assumed that V ≈ σ. This value of the velocity dispersion was then corrected via log σcorr = (log σ−0.061) / 0.833 to account for a “slight systematic deviation from the expectation”. Therefore Zaritsky (2017) were able to obtain estimates for the velocity dispersions and thus dynamical masses for the UDGs.
When we use the FM relation from a previous study by Zaritsky et al. (2008), there exists a relationship between Ie, re, and σ, without having to solve the system of equations in Zaritsky (2017), 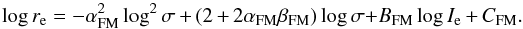 (14)In this equation, αFM, βFM, BFM, and CFM are constants that are empirically determined, taking values (Eq. (8) and Fig. 11 from Zaritsky et al. 2006b)
(14)In this equation, αFM, βFM, BFM, and CFM are constants that are empirically determined, taking values (Eq. (8) and Fig. 11 from Zaritsky et al. 2006b) 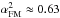 , 2 + 2αFMβFM ≈ 3.7, BFM ≈ −0.705 and CFM ≈ −2.75. We can use Eq. (14)to find the velocity dispersion analytically using the data given in van Dokkum et al. (2015). The only other difference between our method and that of Zaritsky (2017) is that we did not make the correction to the velocity dispersion and assumed, for now, that all the UDGs lie on the FM. The FM line in Fig. 11 of Zaritsky et al. (2006b) seems to align well with the data points, hence we do not make a correction. We discuss the implications of this later.
, 2 + 2αFMβFM ≈ 3.7, BFM ≈ −0.705 and CFM ≈ −2.75. We can use Eq. (14)to find the velocity dispersion analytically using the data given in van Dokkum et al. (2015). The only other difference between our method and that of Zaritsky (2017) is that we did not make the correction to the velocity dispersion and assumed, for now, that all the UDGs lie on the FM. The FM line in Fig. 11 of Zaritsky et al. (2006b) seems to align well with the data points, hence we do not make a correction. We discuss the implications of this later.
The final discussion point is to convert the data table in van Dokkum et al. (2015) into the correct units for the fundamental manifold equation. The fundamental manifold has a 2D effective radius in units of kpc and a mean surface brightness in units of L⊙/ pc2. To determine the correct radius, we need to take the radii in Col. 5 (which is the major-axis radius) of the table in van Dokkum et al. (2015) and multiply it by the square root of the axis ratio, given in Col. 7 of the table. For the surface brightness, we need to use a standard conversion to change the central surface brightness, given in Col. 4 of the table in van Dokkum et al. (2015) in mag/arcsec2, into the mean surface brightness within an effective radius in L⊙/ pc2. This is done by 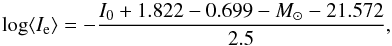 (15)where in this case, M⊙ is the solar magnitude in the given band, ⟨ Ie ⟩ is the mean surface brightness within an effective radius in L⊙/ pc2, and I0 is the central surface brightness in mag/arcsec2. See Appendix A for the derivation of Eq. (15). The given formula for converting the surface brightness can be more general depending on the S
(15)where in this case, M⊙ is the solar magnitude in the given band, ⟨ Ie ⟩ is the mean surface brightness within an effective radius in L⊙/ pc2, and I0 is the central surface brightness in mag/arcsec2. See Appendix A for the derivation of Eq. (15). The given formula for converting the surface brightness can be more general depending on the S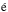 rsic index of the modelling. As van Dokkum et al. (2015) used a S
rsic index of the modelling. As van Dokkum et al. (2015) used a S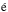 rsic value of 1 for all UDGs, the above formula is valid for all the galaxies in our sample.
rsic value of 1 for all UDGs, the above formula is valid for all the galaxies in our sample.
After we applied these conversions, we used Eq. (14)to determine the estimated velocity dispersion for each UDG and used Eq. (12)to determine the enclosed mass within the 3D radius.
4.2. Estimating the baryonic mass at the effective radius
In the following sections we outline how we inferred the predicted MOND/EMOND mass of the UDGs from the dynamical mass estimate described above. Therefore, to test the validity of the MOND/EMOND formula, we required the approximate enclosed baryonic mass at the effective radius for each UDG in the Coma cluster, which we assumed to be just the inferred stellar mass. In order to do this, we followed the technique used in van Dokkum et al. (2015). This work takes advantage of the relation between colour and mass-to-light ratio, used in Taylor et al. (2011), which describes a link between the (g−i) colour and the stellar mass-to-light ratio in the i band, ![\begin{equation} \log_{10} \left[ M_{\star}{/M_{\odot}}\right] = 1.15 + 0.7(g-i) - 0.4 M_{i}, \label{Mstellar} \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq113.png) (16)where Mi is the absolute magnitude in the i band and M⊙ is the solar mass, not to be confused with the solar magnitude used previously. We note that in Taylor et al. (2011) the stellar populations were modelled using a canonical initial mass function (IMF; Chabrier 2003; Kroupa 2001; Kroupa et al. 2013). From this, we calculated the stellar mass using only colour and magnitude. The g-band magnitude is given for 46 UDGs in the Coma cluster in van Dokkum et al. (2015). For the sample, the average g−i colour is ⟨ g−i ⟩ ≈ 0.8 ± 0.1. This is the value we adopted for each UDG. Therefore the i-band magnitude can be calculated from the quoted g-band magnitude via Mi ≈ Mg−0.8. We therefore have all the necessary quantities to derive a stellar mass for the UDGs. We note that the mass calculated via Eq. (16)is the total stellar mass. The stellar mass within rs, which is what we are interested in, is half of M⋆.
(16)where Mi is the absolute magnitude in the i band and M⊙ is the solar mass, not to be confused with the solar magnitude used previously. We note that in Taylor et al. (2011) the stellar populations were modelled using a canonical initial mass function (IMF; Chabrier 2003; Kroupa 2001; Kroupa et al. 2013). From this, we calculated the stellar mass using only colour and magnitude. The g-band magnitude is given for 46 UDGs in the Coma cluster in van Dokkum et al. (2015). For the sample, the average g−i colour is ⟨ g−i ⟩ ≈ 0.8 ± 0.1. This is the value we adopted for each UDG. Therefore the i-band magnitude can be calculated from the quoted g-band magnitude via Mi ≈ Mg−0.8. We therefore have all the necessary quantities to derive a stellar mass for the UDGs. We note that the mass calculated via Eq. (16)is the total stellar mass. The stellar mass within rs, which is what we are interested in, is half of M⋆.
4.3. Distance from the centre of the cluster
As we only have the 2D projected map of the Coma cluster and the UDGs, it is not possible to derive their exact radii from the centre of the cluster. We can calculate the minimum radius at which the UDGs should be from the right ascension and declination of the UDGs, however, as given in van Dokkum et al. (2015). If we assume that all the UDGs lie at the same distance as the Coma cluster itself, we can find their minimum distance from 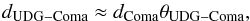 (17)where dComa is the distance to the Coma cluster and θUDG−Coma is the angular separation in radians between the UDG and the Coma cluster centre.
(17)where dComa is the distance to the Coma cluster and θUDG−Coma is the angular separation in radians between the UDG and the Coma cluster centre.
 |
Fig. 3 Minimum projected distance between the centre of the Coma cluster and the UDGs in kpc. The average distance is approximately 1300 kpc. Note that this is the projected distance and the true 3D distance will be higher than this. |
Figure 3 shows that the average distance is approximately 1300 kpc, quite far from the cluster centre, with minimum and maximum values of 296 kpc and 2811 kpc, respectively. However, as stated, the actual 3D radii will be on average higher than this.
5. MOND and EMOND modelling
In this section we describe how the UDGs were modelled in the regular MOND and EMOND paradigms. To do this, we took the dynamical mass, derived from the predicted velocity dispersions (Sect. 4.1), and substituted the value into the MOND (and EMOND) formula. From this, we determined the MOND/EMOND mass, which is required to satisfy the MOND/EMOND equations. Assuming that the galaxy is dominated by stellar mass, we then compared this MOND/ EMOND mass to the baryonic mass derived in Sect. 4. If the MOND/EMOND paradigm is correct, these two methods should be consistent. All this modelling was conducted under the assumption that the UDGs are spherical and in dynamical equilibrium. We note that the average b/a ratio for the sample is 0.74.
5.1. MOND
To begin the MOND modelling, we started by assuming that the UDGs are isolated systems. If they are isolated, we can use the simple spherical MOND relation to model them, 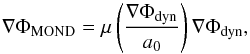 (18)where ∇ΦMOND is the MOND-predicted baryonic mass and ∇Φdyn = GMdyn(r) /r2 is the dynamical acceleration. As discussed, we can then find the MOND mass from the calculated dynamical mass of the UDGs.
(18)where ∇ΦMOND is the MOND-predicted baryonic mass and ∇Φdyn = GMdyn(r) /r2 is the dynamical acceleration. As discussed, we can then find the MOND mass from the calculated dynamical mass of the UDGs.
However, this is not the correct picture as UDGs are not isolated, they are within the external field of the cluster. The MOND formula has to be modified to take into consideration the external field of the cluster (e.g. Bekenstein & Milgrom 1984; Famaey et al. 2007; Wu et al. 2008; Haghi et al. 2016), 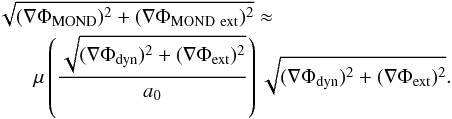 (19)The results are found to be nearly the same when we assume that a and gext are orthogonal. Assuming that the external field is entirely dominated by the Coma cluster, we determined the magnitude of the external field from our model of the Coma cluster in Sect. 3. The external field used for each UDG was determined from the distance it lies away from the centre of the cluster, which we calculated in Sect. 4.3.
(19)The results are found to be nearly the same when we assume that a and gext are orthogonal. Assuming that the external field is entirely dominated by the Coma cluster, we determined the magnitude of the external field from our model of the Coma cluster in Sect. 3. The external field used for each UDG was determined from the distance it lies away from the centre of the cluster, which we calculated in Sect. 4.3.
We expect that the external field increases the overall acceleration across the UDGs, pushing the internal dynamics closer to Newtonian as the MOND interpolation function argument is increased. This highlights the tension between the MOND paradigm and the UDG observations. Although we repeat that this modelling assumes equilibrium and sphericity. Relaxing this may yield less tension in the MOND framework.
5.2. EMOND
As we have seen in our Coma cluster EMOND model, the effective value of a0 is increased within the cluster. This could raise the dark matter-like effects within the UDGs even with the external field of the cluster dominating the dynamics. This is due to the so-called external potential effect. As the UDGs are in the deep potential well of the Coma cluster, under the prediction of the EMOND paradigm, the internal dynamics of the UDGs are affected. The modified version of Eq. (19)for EMOND is 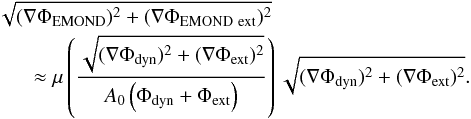 (20)Making the assumption that A0(Φ) is approximately constant across the UDGs as they are so small, we can rewrite Eq. (20) as
(20)Making the assumption that A0(Φ) is approximately constant across the UDGs as they are so small, we can rewrite Eq. (20) as 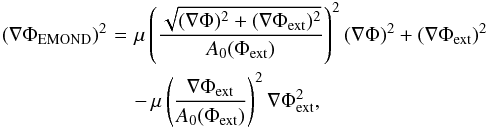 (21)where we have eliminated ∇ΦEMOND ext from Eq. (20)via ∇ΦEMOND ext=
(21)where we have eliminated ∇ΦEMOND ext from Eq. (20)via ∇ΦEMOND ext=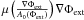 . Although the gravitational potential of the Coma clusters dominates the UDGs in our model, the gravitational accelerations of the UDGs are still relevant and thus we do not neglect them.
. Although the gravitational potential of the Coma clusters dominates the UDGs in our model, the gravitational accelerations of the UDGs are still relevant and thus we do not neglect them.
To highlight the meaning of the different mass symbols, if the MOND paradigm is correct, ∇ΦMOND should be equivalent to the acceleration from the baryons, ∇Φb ≡ GL∗/r2 (M/L∗). In galaxy clusters, if no dark matter is present, ∇ΦMOND> ∇Φb. The hope is that the EMOND formalism can fix this such that ∇ΦEMOND ≈ ∇Φb (within modelling and data errors). In galaxies, as MOND should be a limit of EMOND, we should have the relation ∇ΦEMOND = ∇ΦMOND ≈ ∇Φb.
Equations (18), (19), and (21)can then be used to calculate the predicted MOND/EMOND mass of the UDGs given the dynamical mass of the UDGs and the external field and potential, which is derived from the fundamental manifold (see Sect. 4.1) and the Coma model, respectively.
6. Results
For our results, we did not perform a rigorous error analysis as there are many sources of errors from all the measurements and modelling of the UDGs as well as scatter from the FM and the model of the Coma cluster. We aim to determine whether EMOND is a possible explanation for the UDG over-massive dark haloes.
In the following plots we show the ratio of the predicted by the MOND/EMOND mass and the baryonic mass calculated from the colour. Ideally, this ratio should be 1. If the ratio is lower than 1, either the MOND/EMOND paradigm predicts that there should be less mass than is permitted by the stellar mass estimates, or the stellar mass estimate is too high. If the ratio is higher than 1, the MOND formulation predicts that there should be more mass present than is permitted by the stellar mass estimates, or the stellar mass estimates are too low. This conclusion rests heavily on the assumption that the dynamical mass estimates for the UDGs are correct, which they may not be.
We begin by showing the result for a MOND model with no effects from the Coma cluster (Fig. 4). We see that for a regular MOND model, the overall trend seems to be that the ratio is lower than 1 by a factor of approximately 2. Therefore, perhaps within the errors, MOND with no external field might be sufficient in explaining the UDG masses.
 |
Fig. 4 Ratio of the MOND mass to the estimated stellar mass from colour as a function of the distance to the cluster centre. No effect from the Coma cluster is considered. |
We next show in Fig. 5 how the external field affects the result. As expected, the cluster boosts the acceleration across the UDGs, increasing the argument in the MOND interpolation function, and thus driving the systems closer to Newtonian physics. We therefore see that including the external field makes the MOND model a poorer fit, the ratio is higher than 1, therefore requiring much more stellar mass than is available according to the colour estimate.
 |
Fig. 5 Same as Fig. 4, except that we include the external field from the Coma cluster. The MOND mass is much higher than the colour-predicted stellar mass. |
We then show how the EMOND effect of increasing a0 across the UDGs changes the result (Fig. 6). We find that the EMOND prediction improves the MOND fit substantially within the expected errors. We also note that the q = 2 model (top panel) seems to produce a trend such that the farther out the UDG, the higher the predicted EMOND mass from the EMOND formalism compared to the stellar mass. This is less of an issue with the q = 1 model, demonstrating that the UDGs provide a stringent constraint in the allowed functional form of A0(Φ). This might be an indication that rigorous numerical testing and a larger sample of UDGs might find that further refining the EMOND parameters and interpolation function might produce an even better fit. This is beyond the scope of this paper. Another point of note is the fact that the outer UDG values are similar in the MOND and EMOND case. The reason is that the EMOND formalism asymptotically tends to MOND in the outer part of the cluster, as desired.
 |
Fig. 6 Same as Fig. 5, except with the EMOND correction to the MOND acceleration scale. The top panel shows the q = 2 model and the bottom panel the q = 1 model (see Eq. (6)). The EMOND paradigm predicts a reasonable EMOND mass for the UDG sample in both models. The q = 2 model shows that the required mass-to-light ratio increases with distance, which is an undesirable feature. The q = 1 model shows that a constant mass-to-light ratio with distance is a good fit to the data, which seems more plausible. |
The above results seem to show that when we take the dynamical mass of the UDGs, the stellar mass of the UDGs, the EMOND function, and the model of the Coma cluster at face value, EMOND is able to explain the Coma cluster mass profile and the UDGs within it. The q = 1 model produces a better fit to the data than the q = 2 model in terms of how the distance of the UDGs from the centre of the Coma cluster is affected by EMOND.
There will undoubtedly be sources of errors within these calculations from spherical symmetry assumptions, scatter around the FM, the error in the Coma cluster mass model, etc. that will alter the result. The main source of error is most likely the uncertainty in the stellar mass-to-light ratio and the use of the M/L−(g−i) relation.
For an idea of the error in the stellar mass-to-light ratio, we recreate Figure 13 from Taylor et al. (2011) in Fig. 7 with the stellar mass-to-light ratio used in this work (red band) and the (Bell et al. 2003) function (blue band). These two estimates of the M/L ratio disagree to some extent. It is possible to reverse-engineer the question by assuming that the EMOND formalism is correct and determining the required value of the stellar mass-to-light ratio of each object. For this, we assumed that each UDG lies on the ⟨ g−i ⟩ = 0.8 line. We also assumed that both functions have an approximate error of 0.1 dex (coloured band region for each function), which is reasonable according to the literature (Taylor et al. 2011). We then determined the required value of the stellar mass to match the EMOND mass and determined where on the mass-to-light plot each UDG lies. We show this in Fig. 7. We recall at this point that the 0.8 value is an average with an error of ± 0.1, therefore there is an extra source of uncertainty.
 |
Fig. 7 Stellar mass-to-light functions from Taylor et al. (2011; red) and Bell et al. (2003; blue) as a function of g−i colour. We show approximate error bars of 0.1 dex for each case. The top panel shows the results for the q = 2 model, and the bottom panel shows the q = 1 model (see Eq. (6)). The blue dots show where the UDGs must lie assuming that the EMOND formulation is correct. This shows that it may be possible for most of the UDGs to be explained by EMOND within the range of stellar mass-to-light ratio allowed. The q = 1 model again shows better results. |
Figure 7 shows that there seems to be a very large scope for error in the mass-to-light ratio of the stars in the UDG, within which most UDGs in our sample lie. We can therefore conclude that adjusting the stellar mass-to-light ratio can explain the UDGs mass, within the error bars, assuming that the EMOND modelling of the UDGs is valid.
7. Adjusting the EMOND formulation
The above results show that the q = 1 model explains the UDGs better than the q = 2 model used in Hodson & Zhao (2017). For completeness, we therefore need to repeat the analysis of Hodson & Zhao (2017) to confirm that the q = 1 model is consistent with the cluster sample of Vikhlinin et al. (2006). To do this, we briefly review the Hodson & Zhao (2017) work and recreate their Figs. 17–22 with the updated function for A0(Φ).
One method of testing modified gravity theories is by comparing the estimated “total” mass, calculated from dΦ / drr2/G, where Φ is the total gravitational potential derived from the Poisson equation, and the mass calculated by assuming the intra-cluster gas is in hydrostatic equilibrium, which we call the dynamical mass. The expression for dynamical mass, assuming Newtonian physics, is determined by solving the equation of hydrostatic equilibrium, ![\begin{equation} M_{\rm dyn}(r) = -\frac{kT(r)r}{G wm_{\rm p}}\left[ \frac{{\rm d}\! \ln \rho_{\rm g}(r)}{{\rm d}\! \ln r} + \frac{{\rm d}\! \ln T(r)}{{\rm d}\! \ln r} \right], \label{DynamicalMass} \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq143.png) (22)where ρg(r) is the density of the gas, T(r) is the temperature of the gas, k is the Boltzmann constant, mp is the proton mass, and w is the mean molecular weight. Therefore, for a given gas density and temperature, the dynamical mass can be calculated. In theory, the dynamical mass should be comparable to dΦ / drr2/G. In regular MOND, dΦ / drr2/G is much lower than the dynamical mass in galaxy clusters. The original motivation for formulating EMOND was to rectify this discrepancy. This was the goal of Hodson & Zhao (2017).
(22)where ρg(r) is the density of the gas, T(r) is the temperature of the gas, k is the Boltzmann constant, mp is the proton mass, and w is the mean molecular weight. Therefore, for a given gas density and temperature, the dynamical mass can be calculated. In theory, the dynamical mass should be comparable to dΦ / drr2/G. In regular MOND, dΦ / drr2/G is much lower than the dynamical mass in galaxy clusters. The original motivation for formulating EMOND was to rectify this discrepancy. This was the goal of Hodson & Zhao (2017).
As EMOND is sensitive to the magnitude of the gravitational potential, to solve the EMOND Poisson equation, a boundary potential had to be defined (Hodson & Zhao 2017). To estimate this quantity, Hodson & Zhao (2017) used the analytical best-fit Navarro-Frenk-White (NFW) profiles for each cluster and assumed that Φ(rout) ≈ ΦNFW(rout), where rout was defined as some boundary outside the cluster. They then showed the range of solutions from Φ(rout) = (0.5−1.5) × ΦNFW(rout) to obtain an idea of how changing the boundary potential affected the result. To be consistent, we here set the boundary potential at the virial radius for each cluster to take the same value as was used for the Coma cluster. We also show the boundary potential for Φ(rv) = (0.9−1.1) × Φ(rv) in contrast to the previous work. Although we have treated the boundary potential as a free parameter, we hope that in the future, when the EMOND theory has a covariant form, matching the non-linear regime onto the cosmological solution will fix this value for each cluster. Therefore the boundary potential will be determined from the theory and not left as a free parameter. This is beyond current EMOND capabilities, and thus we have set all boundary potentials to be the same for each cluster. In defense of this approximations, we expect that clusters of similar masses should lie in similar potential wells.
For the baryonic mass model for these galaxies, the gas was modelled as in Vikhlinin et al. (2006), Hodson & Zhao (2017). We did change the contribution of the galaxies, however, to have a similar mass profile as the Coma cluster. We note that each cluster will in practice have a different mass contribution from the galaxies. We did not attempt to find the best-fit galaxy model for each cluster. This is best left until the theory of EMOND is clearer, specifically with regard to understanding the boundary potential.
Repeating the above steps for the new A0(Φ) function, we show the updated mass plots for the cluster sample (Figs. 8, B.1−B.5).
 |
Fig. 8 Recreated Figs. 17–22 from Hodson & Zhao (2017) with the modified A0(Φ) function found under the UDG constraints. The red dashed line shows the best-fit ΛCDM model from Vikhlinin et al. (2006), the black line the dynamical mass derived from Eq. (22), and the blue shaded region shows the EMOND-predicted mass. Here we show clusters A133 and A262. |
In these plots, the blue curve denotes the predicted mass by EMOND, with the shaded region showing how the value is affected by different choices of the boundary potential, the red dashed curve is the NFW prediction from Vikhlinin et al. (2006), and the black line is the dynamical mass, predicted from hydrostatic equilibrium. The EMOND blue curve should match the black curve within errors related to modelling assumptions. We can see from Figs. 8, B.1–B.5 that the new form of A0(Φ) gives a better result than Hodson & Zhao (2017), although when the EMOND theory is more evolved, this can be statistically quantified. It is also possible to see in cases such as RXJ1159 and MKW4 that even though the EMOND predicted dynamical mass is far from the dynamical mass from hydrostatic equilibrium, the EMOND curve is consistent with the best-fit NFW curve (red dashed line). Therefore we can conclude that changing the form of the interpolation function is still consistent with the previous EMOND work.
8. Discrepancy with observations
Although our above analysis has shown consistency between the Coma cluster and UDGs masses under the EMOND paradigm, we have made some rather large assumptions, the main assumption being that the FM can be used to determine the velocity dispersion of the UDGs. If we take the estimate for DF44, which is the only UDG in the sample that has been observed (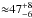 km s-1), the FM under-predicts the velocity dispersion by a factor of ≈2.7 (the FM-predicted velocity dispersion for DF44 is ≈17.4 km s-1). If we then take the published observed data from van Dokkum et al. (2016), EMOND would predict a baryonic mass of ≈ 7.7 × 108M⊙ and thus the ratio between this EMOND (q = 1 model) mass and the baryonic mass is ≈7.5, which is quite a substantial difference. This result is improved if the EMOND boundary potential chosen for the Coma cluster is increased. Choosing the boundary to be 3.5 × 1012 m2 s-2, the ratio is reduced to ≈6. When we chose this potential and took the lowest bound for the velocity dispersion (41 km s-1), the ratio further decreased to ≈4.5. This could be further improved by choosing a higher stellar mass-to-light ratio than is used in van Dokkum et al. (2016). However, it must be checked which values for the boundary potential are allowed by the data for Coma. This would require further work, which is beyond the scope of this paper.
km s-1), the FM under-predicts the velocity dispersion by a factor of ≈2.7 (the FM-predicted velocity dispersion for DF44 is ≈17.4 km s-1). If we then take the published observed data from van Dokkum et al. (2016), EMOND would predict a baryonic mass of ≈ 7.7 × 108M⊙ and thus the ratio between this EMOND (q = 1 model) mass and the baryonic mass is ≈7.5, which is quite a substantial difference. This result is improved if the EMOND boundary potential chosen for the Coma cluster is increased. Choosing the boundary to be 3.5 × 1012 m2 s-2, the ratio is reduced to ≈6. When we chose this potential and took the lowest bound for the velocity dispersion (41 km s-1), the ratio further decreased to ≈4.5. This could be further improved by choosing a higher stellar mass-to-light ratio than is used in van Dokkum et al. (2016). However, it must be checked which values for the boundary potential are allowed by the data for Coma. This would require further work, which is beyond the scope of this paper.
The reason that our UDG dynamical masses differ from the work of Zaritsky (2017) is that these authors corrected the velocity dispersion that is due to the discrepancy between the observed velocity dispersion and the FM estimated value (see Fig. 1 of Zaritsky 2017). In our analysis, we used a different form of the FM. The source of the discrepancy needs to be investigated in further work.
More detailed observations of more UDGs in the Coma cluster are required to determine whether the over-massive dark halo of DF44 is a statistical outlier in the sample or if the interpretation of the FM used in our work disagrees with the current observations. A deeper understanding of UDG properties may arise from studying tidal effects from the cluster and/or comparing formation scenarios with that of remnant systems, such as those described by Kroupa (1997).
9. Conclusion
We modelled the Coma cluster in the EMOND paradigm and compared the predicted enclosed mass profile to that of a pure Newtonian model. We found that the EMOND result bears an extraordinary resemblance to the DM profile used in Łokas & Mamon (2003). This is quite a successful result for the EMOND paradigm. The success of this result warrants further study of EMOND, taking into careful consideration the functional form of the baryonic mass profile and the boundary potential used to solve the Poisson equation.
We then moved on to make a model of UDGs in EMOND. We used this to determine the MOND/EMOND mass required to satisfy the MOND/EMOND formula. We then compared this to the baryonic mass, in the form of stars, that is predicted by the UDG galaxy colour.
Our model seemed to give consistent values of the EMOND mass and the stellar mass derived from colour within the expected error bars of the stellar mass-to-light ratio. Further to this, the UDG sample gave a constraint on the exact function of A0(Φ). Using a slightly different function than the function used by Hodson & Zhao (2017) yielded better results. This function was also checked against the earlier work of Hodson & Zhao (2017), yielding not only consistent, but better results. We can therefore conclude that the q = 1 model is preferred by the EMOND paradigm.
However, the results of this work disagree with observations of UDG DF44. A reanalysis of this calculation must be conducted when more UDG velocity dispersions are observed.
The UDGs serve as a very good test for MOND-like gravity theories and should be studied in more detail. The next step is to conduct the same analysis for the Virgo cluster and its UDG population.
UDGs are still a relatively new discovery, with limited observations and a small sample size. More measurements of the velocity dispersions for the UDGs would produce more accurate dynamical mass estimates. It is hard to discuss possible formation scenarios in the context of EMOND as it is still a relatively new theory on which limited research has been conducted. We have shown that a possible solution to the mass discrepancy in galaxy clusters in a MOND-like paradigm, EMOND, may also hold the answer to the nature of these UDGs. When two problems have one solution, it warrants further investigation, and we hope that EMOND will be investigated further as a result of this.
Acknowledgments
We would like to thank Anne-Marie Weijmans and Benoit Famaey for general comments on the draft. We would also like to thank Dennis Zaritsky for discussions on the fundamental manifold. We must also thank the anonymous referee whose comments were both welcomed and valued. A.O.H. is supported by Science and Technologies Funding Council (STFC) studentship (Grant code: 1-APAA-STFC12).
References
- Angus, G. W. 2009, MNRAS, 394, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., & Diaferio, A. 2011, MNRAS, 417, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Famaey, B., & Buote, D. A. 2008, MNRAS, 387, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Diaferio, A., Famaey, B., & van der Heyden, K. J. 2013, MNRAS, 436, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Beasley, M. A., Romanowsky, A. J., Pota, V., et al. 2016, ApJ, 819, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchet, L., & Novak, J. 2011, MNRAS, 412, 2530 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2012, MNRAS, 422, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Derakhshani, K., & Haghi, H. 2014, ApJ, 785, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, F., Gentile, G., Salucci, P., et al. 2009, MNRAS, 397, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496 [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Rel., 15, 10 [Google Scholar]
- Famaey, B., Bruneton, J.-P., & Zhao, H. 2007, MNRAS, 377, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Haghi, H., Bazkiaei, A. E., Zonoozi, A. H., & Roupa, P. 2016, MNRAS, 458, 4172 [NASA ADS] [CrossRef] [Google Scholar]
- Hodson, A., & Zhao, H. 2017, A&A, 598, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, Nature, 493, 62 [CrossRef] [Google Scholar]
- Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
- Koda, J., Yagi, M., Yamanoi, H., & Komiyama, Y. 2015, ApJ, 807, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 1997, New Astron., 2, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2012, PASA, 29, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2015, Can. J. Phys., 93, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Famaey, B., de Boer, K. S., et al. 2010, A&A, 523, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science+Business Media), 115 [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2003, MNRAS, 343, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Durrell, P. R., Ferrarese, L., et al. 2015, ApJ, 809, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983a, ApJ, 270, 371 [Google Scholar]
- Milgrom, M. 1983b, ApJ, 270, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983c, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2014, Scholarpedia, 9, 31410 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Pawlowski, M. S., Famaey, B., Merritt, D., & Kroupa, P. 2015, ApJ, 815, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Roman, J., & Trujillo, I. 2017, MNRAS, 468, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 1999, ApJ, 512, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2011, MNRAS, 418, 1587 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Abraham, R., Merritt, A., et al. 2015, ApJ, 798, L45 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P., Abraham, R., Brodie, J., et al. 2016, ApJ, 828, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., & Peñarrubia, J. 2011, ApJ, 742, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
- Wu, X., & Kroupa, P. 2013, MNRAS, 435, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., & Kroupa, P. 2015, MNRAS, 446, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D. 2017, MNRAS, 464, L110 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Gonzalez, A. H., & Zabludoff, A. I. 2006a, ApJ, 642, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Gonzalez, A. H., & Zabludoff, A. I. 2006b, ApJ, 638, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Zabludoff, A. I., & Gonzalez, A. H. 2008, in Formation and Evolution of Galaxy Disks, eds. J. G. Funes, & E. M. Corsini, ASP Conf. Ser., 396, 381 [Google Scholar]
- Zhao, H., & Famaey, B. 2012, Phys. Rev. D, 86, 067301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, H. S., & Famaey, B. 2006, ApJ, 638, L9 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Surface brightness conversion
van Dokkum et al. (2015) provided the central surface brightness. The FM required the mean surface brightness at the effective radius. Converting the surface brightness from the value at the centre of the UDG into the mean surface brightness at the effective radius is a simple and standard calculation that we review here for completeness. For a full more detailed look at the calculation, we refer to Graham & Driver (2005), where most of the equations below come from. Light profiles are commonly modelled with a S rsic profile. In terms of the surface brightness, I, the S
rsic profile. In terms of the surface brightness, I, the S rsic profile is
rsic profile is ![\appendix \setcounter{section}{1} \begin{equation} I(r) = I_{\rm e} + \frac{2.5 b_{n}}{\ln 10} \left[ \left(\frac{r}{r_{\rm e}}\right)^{1/n} - 1 \right], \label{surfacebrightness} \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq159.png) (A.1)where n parametrises the S
(A.1)where n parametrises the S rsic index that describes the shape of the profile, and bn is a constant that is defined for each n. As van Dokkum et al. (2015) quoted the central surface brightness and the FM requires the mean surface brightness at the effective radius, the first step is to solve Eq. (A.1)for Ie. All the UDGs in the sample were modelled with a S
rsic index that describes the shape of the profile, and bn is a constant that is defined for each n. As van Dokkum et al. (2015) quoted the central surface brightness and the FM requires the mean surface brightness at the effective radius, the first step is to solve Eq. (A.1)for Ie. All the UDGs in the sample were modelled with a S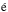 rsic index n = 1. The corresponding b1 value is ≈ 1.678. Therefore
rsic index n = 1. The corresponding b1 value is ≈ 1.678. Therefore 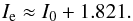 (A.2)Next we transformed this value into the average value at the effective radius. The average intensity is defined to be
(A.2)Next we transformed this value into the average value at the effective radius. The average intensity is defined to be 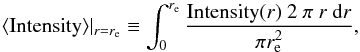 (A.3)
(A.3)
where the intensity can be transformed into surface brightness via I = 2.5log 10(intensity). Solving Eq. (A.3)and moving from intensity to surface brightness, we obtain![\appendix \setcounter{section}{1} \begin{equation} \langle I_{\rm e} \rangle = I_{\rm e} - 2.5 \log_{10} \left[\frac{n \exp(b_{n})}{b_{n}^{2n}}\Gamma(2n)\right]. \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq168.png) (A.4)Inserting the numbers, we arrive at
(A.4)Inserting the numbers, we arrive at 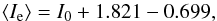 (A.5)where we have expressed the value in terms of the central value of surface brightness. Currently, the mean surface brightness is in units of mag/arcsec2, which we need to convert into L⊙/pc2. This is done via
(A.5)where we have expressed the value in terms of the central value of surface brightness. Currently, the mean surface brightness is in units of mag/arcsec2, which we need to convert into L⊙/pc2. This is done via ![\appendix \setcounter{section}{1} \begin{equation} I(L_{\odot}/{\rm pc^{2}}) = \exp \left[-\frac{(I({\rm mag_{\odot}/arcsec^{2}}) - M_{\odot} - 21.572 )}{2.5}\right], \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq171.png) (A.6)where M⊙ is the solar magnitude in the given band. Therefore,
(A.6)where M⊙ is the solar magnitude in the given band. Therefore, ![\appendix \setcounter{section}{1} \begin{equation} \langle I_{\rm e}\rangle(L_{\odot}/{\rm pc^{2}}) = \exp \left[-\frac{I_{0} + 1.821 -0.699~M_{\odot} - 21.572 }{2.5}\right], \end{equation}](/articles/aa/full_html/2017/11/aa30757-17/aa30757-17-eq172.png) (A.7)where I0 is in mag/arcsec2. This is the derivation of Eq. (15).
(A.7)where I0 is in mag/arcsec2. This is the derivation of Eq. (15).
Appendix B: Additional figures
All Tables
All Figures
 |
Fig. 1 Model of the Coma cluster that we adopt from Łokas & Mamon (2003). The green thin line shows the contribution from the intra-cluster gas, and the red thin line is the contribution from the stars. Using these, we can calculate the EMOND-predicted dynamical mass from Eq. (10), which is the solid blue line for the q = 1 model and the solid magenta line for the q = 2 model (see Eq. (6)). We also plot the dark matter profile from Łokas & Mamon (2003; black dashed line) for comparison. We see that our EMOND mass matches the dark matter mass very well. For this, we assumed an EMOND boundary potential at the virial radius Φ(rv) = −2.5 × 1012 m2 s-2. |
| In the text | |
 |
Fig. 2 Profile of the EMOND-calculated A0(Φ) /a0 as a function of cluster radius. The blue dashed line is the q = 2 model, and the red solid line is the q = 1 model. The q = 1 model produces a shallower transition from high to low A0(Φ) and a smaller magnitude of A0(Φ) than the q = 2 model (see Eq. (6)). We only show radii > 100 kpc as this is the important range for the UDGs. |
| In the text | |
 |
Fig. 3 Minimum projected distance between the centre of the Coma cluster and the UDGs in kpc. The average distance is approximately 1300 kpc. Note that this is the projected distance and the true 3D distance will be higher than this. |
| In the text | |
 |
Fig. 4 Ratio of the MOND mass to the estimated stellar mass from colour as a function of the distance to the cluster centre. No effect from the Coma cluster is considered. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, except that we include the external field from the Coma cluster. The MOND mass is much higher than the colour-predicted stellar mass. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, except with the EMOND correction to the MOND acceleration scale. The top panel shows the q = 2 model and the bottom panel the q = 1 model (see Eq. (6)). The EMOND paradigm predicts a reasonable EMOND mass for the UDG sample in both models. The q = 2 model shows that the required mass-to-light ratio increases with distance, which is an undesirable feature. The q = 1 model shows that a constant mass-to-light ratio with distance is a good fit to the data, which seems more plausible. |
| In the text | |
 |
Fig. 7 Stellar mass-to-light functions from Taylor et al. (2011; red) and Bell et al. (2003; blue) as a function of g−i colour. We show approximate error bars of 0.1 dex for each case. The top panel shows the results for the q = 2 model, and the bottom panel shows the q = 1 model (see Eq. (6)). The blue dots show where the UDGs must lie assuming that the EMOND formulation is correct. This shows that it may be possible for most of the UDGs to be explained by EMOND within the range of stellar mass-to-light ratio allowed. The q = 1 model again shows better results. |
| In the text | |
 |
Fig. 8 Recreated Figs. 17–22 from Hodson & Zhao (2017) with the modified A0(Φ) function found under the UDG constraints. The red dashed line shows the best-fit ΛCDM model from Vikhlinin et al. (2006), the black line the dynamical mass derived from Eq. (22), and the blue shaded region shows the EMOND-predicted mass. Here we show clusters A133 and A262. |
| In the text | |
 |
Fig. B.1 Same as Fig. 8 for clusters A478 and A1413. |
| In the text | |
 |
Fig. B.2 Same as Fig. 8 for clusters A1795 and A1991. |
| In the text | |
 |
Fig. B.3 Same as Fig. 8 for clusters A2029 and RXJ1159. |
| In the text | |
 |
Fig. B.4 Same as Fig. 8 for clusters MKW4 and A383. |
| In the text | |
 |
Fig. B.5 Same as Fig. 8 for clusters A907 and A2390. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


