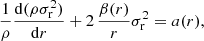EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 627 (July 2019) A&A, 627 (2019) L1 Full HTML
Open Access
Issue
A&A
Volume 627, July 2019
Article Number L1
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/201935840
Published online 27 June 2019

© M. Bílek et al. 2019

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Ultra-diffuse galaxies (UDGs) are very extended (reff >  1.5 kpc) low surface brightness (μV >  25 mag arcsec−2) objects. They have been identified in different galactic environments for decades (e.g., Sandage & Binggeli 1984; Impey et al. 1988). These galaxies have recently experienced a revival (Crnojević et al. 2014; van Dokkum et al. 2015a; Koda et al. 2015; van der Burg et al. 2016; Martínez-Delgado et al. 2016; Merritt et al. 2016; Román & Trujillo 2017a; Venhola et al. 2017; Wittmann et al. 2017; Müller et al. 2018; Mancera Piña et al. 2019). In galaxy clusters, UDGs do not contain gas, while in sparser environments they can be gas dominated (van Dokkum et al. 2015a; Shi et al. 2017; Leisman et al. 2017; Papastergis et al. 2017; Sardone et al. 2019), following the well-known density–morphology relation (Dressler 1980). Several formation scenarios have been proposed in the ΛCDM context; they might be tidal dwarf galaxies, galaxies formed by collapse of gas in galaxy outflows, dwarf galaxies that experienced strong tidal stripping or repeated episodes of intense star formation, among others (e.g. van Dokkum et al. 2015a; Yozin & Bekki 2015; Amorisco & Loeb 2016; Di Cintio et al. 2017; Chan et al. 2018; Toloba et al. 2018). Observations suggest that at least some UDGs form in the field and are then accreted to galaxy clusters where they experience environmental quenching (Román & Trujillo 2017b; Ferré-Mateu et al. 2018; Alabi et al. 2018).

The dynamics of these systems provides exciting insights to the discussion. For instance, van Dokkum et al. (2018a) announced the discovery of a UDG free of dark matter in the field of NGC 1052. Soon, in the same field around NGC 1052 a second galaxy lacking dark matter was found (van Dokkum et al. 2019a). These two galaxies, NGC 1052-DF2 and NGC 1052-DF4, have sparked a vast discussion in the literature (e.g., van Dokkum et al. 2018b; Trujillo et al. 2019; Martin et al. 2018; Kroupa et al. 2018; Famaey et al. 2018; Emsellem et al. 2019; Fensch et al. 2019; Müller et al. 2019a,b; Nusser 2019; Laporte et al. 2019).

As low surface brightness objects, UDGs are expected to show complex dynamical behavior in the context of MOdified Newtonian Dynamics (MOND, Milgrom 1983; here we only consider MOND modified gravity theories and not modified inertia theories). As a historical note, MOND was proposed to solve the missing mass problem in high surface brightness spiral galaxies (e.g., Rubin et al. 1978; Bosma 1981; Rubin et al. 1982) and has since excelled in reproducing the dynamics of a much wider range of galaxies (e.g., McGaugh & de Blok 1998; McGaugh & Milgrom 2013; Lelli et al. 2017, see also the extensive of review in Famaey & McGaugh 2012). At the time MOND was proposed, the existence of UDGs was unknown. In MOND, a dynamical system appears Newtonian when the gravitational acceleration is greater than about the threshold of a0 = 1.2 × 10−13 km s−2 (Milgrom 1983; Begeman et al. 1991). Below this threshold, a departure from Newtonian dynamics occurs such that the system appears to host dark matter. The dark matter behavior is at its full strength only if the galaxy is isolated. In the case when the object resides in a strong gravitational field of the environment, the deviations from Newtonian dynamics can effectively be suppressed (e.g., Milgrom 1983; Bekenstein & Milgrom 1984), which is due to the non-linearity of any MOND theory (Milgrom 2014)1. In other words, the object will appear dark matter-free, even though its internal acceleration is below a0, thanks to the so-called external field effect (EFE). To explain the dynamics of two UDGs of the NGC 1052 group in MOND, NGC 1052-DF2 and NGC 1052-DF4 (if they are not in the foreground of their putative host group, see Trujillo et al. 2019), it is crucial to take the EFE into account, mostly removing the tension for NGC 1052-DF2 (Kroupa et al. 2018; Famaey et al. 2018), and lessening it for NGC 1052-DF4 (Müller et al. 2019a). Interestingly, the UDG Dragonfly 44 in the Coma cluster behaves very differently from the UDGs of the NGC 1052 group. It exhibits a pronounced deviation from Newtonian dynamics. Early measurements of its stellar velocity dispersion yielded ∼47 km s−1 (van Dokkum et al. 2016), well above the nominal isolated MOND prediction. However, all these previous studies relied on the global velocity dispersion estimated at the half-light radius of the galaxy, but did not take into account the overall shape and profile of the velocity dispersion, due to the difficulty in measuring it.

The first velocity dispersion profile of a UDG, namely Dragonfly 44, was recently presented by van Dokkum et al. (2019b). The data was taken with the Keck Cosmic Web Imager (KCWI) on Mauna Kea during 25.3 h of observations. The velocity dispersion profile was studied in the context of Newtonian gravity with several types of dark matter profiles in van Dokkum et al. (2019b). Here we use these data to discuss Dragonfly 44 in MOND.

2. Velocity dispersion profile expected in MOND in isolation

We first study the velocity dispersion profile of Dragonfly 44 as expected by MOND, assuming that the galaxy is far away from the Coma cluster center and any other galaxies, so that the EFE is negligible. We calculated it using the spherically symmetric Jeans equation (e.g., Binney & Tremaine 2008)

1 ρ d ( ρ σ r 2 ) d r + 2 β ( r ) r σ r 2 = a ( r ) , $$ \begin{aligned} \frac{1}{\rho }\frac{\mathrm{d} (\rho \sigma _{\rm r}^2)}{\mathrm{d} r} + 2\,\frac{\beta (r)}{r}\sigma _{\rm r}^2 = a(r), \end{aligned} $$(1)

where ρ is the density of tracers, σr the radial velocity dispersion, β the anisotropy parameter, and a the radial gravitational acceleration. In our case, ρ is the star density of the galaxy that we approximated by a Sérsic sphere whose parameters were obtained by fitting the photometric profile (van Dokkum et al. 2015a, 2016, 2019b), i.e., the I-band luminosity of LI = 3.0 ± 0.6 × 108 L⊙, the effective radius of Re = 4.7 kpc, and the Sérsic index of n = 0.94. We used the analytic approximation for the density of a Sérsic sphere by Lima Neto et al. (1999) with the update by Márquez et al. (2000). The stellar mass-to-light ratio expected from the stellar population synthesis model of Dragonfly 44 is between 1 and 1.5 (van Dokkum et al. 2019b). This density determines the MOND gravitational field a(r) (Milgrom 1983). The Newtonian gravitational field was recalculated to the MOND field assuming the so-called simple interpolation function (see, e.g., Famaey & McGaugh 2012). The parameter β was considered to be zero, corresponding to an isotropic profile. We then obtained the line-of-sight velocity dispersion using the formulas given in the appendix of Mamon & ᴌokas (2005).

We did not perform any fitting. Instead, we assumed a fixed mass-to-light ratio of 1.3 and the best estimate of the galaxy luminosity as 3.0 × 108 L⊙, which lead to our fiducial stellar mass of M*, 0 = 3.9 × 108 M⊙. The resulting line-of-sight velocity dispersion profile is shown in Fig. 1. The agreement with observations in the center of the UDG is remarkably good given that the MOND model had no free parameters.

thumbnail Fig. 1.

Comparison of the measured velocity dispersion profile of the ultra-diffuse galaxy Dragonfly 44 to the MOND no-fitting model and the Newtonian model. A fixed mass-to-light ratio of 1.3 and the best estimate of the galaxy luminosity as 3.0 × 108 L⊙ were assumed, together with isotropy. We illustrate the effect of relaxing some of these assumptions in Fig. 2.

In the dark matter framework, it is important to realize that this central velocity dispersion could have been very different from the MOND prediction, and there would actually be no obvious reason for this agreement to be so good given the unclear origin of UDGs. Indeed, for comparison, the dotted line is an isotropic model employing Newtonian gravity without dark matter, which clearly underestimates the velocity dispersion by more than 3σ.

On the other hand, while the deviation of the MOND models from observation increases with radius, the data points are still within the 2σ uncertainty limit so that the no-fitting model is consistent with the data. We discuss the implications of our results and possible reasons (beyond the possible measurement error) for the deviation in the outer part of the profile in the following section.

3. Discussion

3.1. Dragonfly 44 far from the cluster core

The isotropic MOND model calculated with the assumption of isolation was generally successful in Dragonfly 44 and the Newtonian model was not, which suggests that the UDG has to be far from the Coma cluster core in the framework of MOND. If Dragonfly 44 were sufficiently close to the center of the Coma cluster for a long time, the UDG would be subject to the EFE exerted by the cluster so that the gravity and velocity dispersion would be lower than in isolation, and in the most extreme case they would have Newtonian values (see, e.g., Fig. 1 in Müller et al. 2019a for the predicted impact of the EFE on different UDGs near massive galaxies as a function of their 3D separation). To give an approximate scale of how far away Dragonfly 44 must be from the Coma cluster center in order for the EFE to be negligible, we calculate the separation at which the acceleration caused by the cluster equals the acceleration in the UDG at 1 Re in the isolated case. A dedicated MOND estimate of the mass of the cluster in MOND is 4.6 × 1014 M⊙ (Sanders 2003). This also includes the contribution of the dark matter that MOND predicts for galaxy clusters. We conclude that the distance between Dragonfly 44 and the Coma cluster has to be well beyond 5 Mpc. For comparison, the projected separation is 1.7 Mpc (angular separation of 1° at the distance of 100 Mpc). The wide field map of the UDGs around the Coma cluster by Zaritsky et al. (2019) indeed reveals that UDGs occur at least to the distance of 15 Mpc from the cluster center. The UDGs lie in cosmic filaments of galaxies that seem to flow toward the cluster. Another indication that Dragonfly 44 is quite far from the Coma cluster itself is, as noted by van Dokkum et al. (2019b), that the UDGs close to Dragonfly 44 have similar radial velocities; the differences are much smaller than the average velocity dispersion in the Coma cluster itself. If we require Dragonfly 44 to head toward the cluster, the difference in radial velocities of the cluster and the galaxy (van Dokkum et al. 2015b) implies that the galaxy is in the background of the cluster.

3.2. Effect of anisotropy

The deviation of the predicted versus the observed velocity dispersion profile of Dragonfly 44 is less than 2σ at all radii, and thus it could simply be a systematic error in this difficult observation. The deviation indeed increases as the surface brightness of the object decreases, and the data seem to imply that the dispersion profile is almost flat and then suddenly starts rising, which is very unlikely in the ΛCDM framework as well. Nevertheless, for completeness, we now discuss in the rest of the paper the possibility that the deviation is, at least partly, real.

It is first necessary to discuss the effect of the well-known downside of the Jeans modeling approach, namely that the anisotropy parameter is not known. The effect of changing this parameter is illustrated in Fig. 2. When an anisotropy parameter of 0.5 is assumed, which corresponds to a radial anisotropy value hinted by the observations (van Dokkum et al. 2019b), the expected velocity dispersion profile is decreasing. The choice of an externally radial anisotropy βER = r/(r + 1.4Re), which is isotropic in the center and becomes radial at larger radii, matches the central data points better than both the isotropic and radial anisotropies, but still deviates at larger radii. A similar profile is expected to arise if the galaxy was in the external field dominated regime in the past (Wu et al. 2008). Nevertheless, it is observationally difficult to determine the anisotropy even for much brighter galaxies, and as van Dokkum et al. (2019b) note, the signs of radial anisotropy have other possible interpretations.

thumbnail Fig. 2.

Various models of the MOND velocity dispersion profile of Dragonfly 44 discussed in Sect. 3.2. Top panel: radially anisotropic models. The isotropic model, as in Fig. 1, is shown as a solid line, the externally radial anisotropy model as a dashed line, and the pure radial anisotropy model as a dot-dashed line. Bottom panel: tangentially anisotropic models. Three models for the tangential anisotropy with different stellar masses, as discussed in Sect. 3.2, are shown as solid, dashed, and dash-dotted lines.

The modeled velocity profile for tangential anisotropy with β = −0.5 has a shape similar to the observed profile, but it has systematically lower values than observed. Assuming a higher M/L ratio and galaxy luminosity, each at their 2σ upper limit, leads to the stellar mass of 1.9M*, 0, which reaches the lower 1σ uncertainty limits of most of the data points. Nevertheless, stellar M/L ratios are generally subject to high uncertainties because the evolution of AGB stars and the initial mass function are not known precisely (e.g., Zibetti et al. 2009; Martinsson et al. 2013) such that the uncertainty in M/L given by van Dokkum et al. (2019b) may be underestimated. A higher M/L together with a greater distance caused by Dragonfly 44 lying in the background of the cluster makes a stellar mass of 3 M⊙ plausible. This value together with β = −0.5 provides an excellent model to the data (see the dash-dotted line in Fig. 2).

3.3. Is Dragonfly 44 being disrupted?

Now we consider the possibility that Dragonfly 44 is actually closer to the cluster core. In this case, such a UDG cannot be stable or would need additional dark matter. Hence Milgrom (2015) suggested that UDGs in the Coma cluster could fall on radial orbits into the Coma cluster for the first time, where they would then be disrupted by the combination of the EFE and tidal forces. Again, this possibility is consistent with the observation that UDGs are flow to the Coma cluster in filaments and that several UDGs close to Dragonfly 44 share a similar radial velocity, and with several other observational pieces of evidence that some UDGs form outside clusters (see the references in the Introduction). The tidal radius (Zhao 2005) of Dragonfly 44 is equal to 2Re if the 3D separation from the cluster is 2.6 Mpc. This is larger than the projected on-sky separation so that the possibility that Dragonfly 44 is being affected by tidal forces should be considered seriously.

If the velocity dispersion of the UDG was set in a region where the EFE is negligible, we do not expect that the velocity dispersion would decrease when the UDG entered the EFE dominated regime. That the gravitational well becomes shallower instead means that the object becomes unbound from its own gravity and dissolves. The outer parts of the object would obtain extra acceleration by tidal forces. This could then explain the observed rising velocity dispersion profile of Dragonfly 44. This scenario has a few other appealing features: it would explain why Dragonfly 44 is very elongated for a non-rotating object and why van Dokkum et al. (2019b) noted hints that the stars of the galaxy are on radial orbits. A simulation of a satellite being disturbed by a field of a more massive host is depicted in Fig. 5 of Brada & Milgrom (2000) where we can see that the object is indeed expanding and has an elongated shape.

One could suspect that the downside of this explanation is that we would have to observe the 10 Gyr old UDG (van Dokkum et al. 2019b) in a rather special period of its lifetime. With the expansion velocity estimated as the deviation of the data from the equilibrium isotropic model of around 10 km s−1, the stars pass the effective radius in 460 Myr. If this expansion took a much longer time the object would dissolve. Moreover, the tidal stripping cannot be very effective because the galaxy possesses many globular clusters (∼100). On the other hand, in this scenario we do not observe the galaxy at a random instance of its life; we see it when it has already entered the cluster, so that signs of disruption are more expected based on how close the galaxy is to the cluster. All these considerations clearly need to be supported by future numerical simulations.

3.4. Dragonfly 44 with a halo of baryonic dark matter?

Many UDGs in the Coma cluster field lie within the projected radius where the tidal forces are expected to be substantial, which might suggest that they need additional dark halos to survive in MOND (Milgrom 2015; the density of UDGs as a function of cluster-centric distance was studied in, e.g., van der Burg et al. 2016).

Many independent pieces of evidence suggest that MOND requires dark matter in galaxy clusters that could be made of baryons (see, e.g., the review in Milgrom 2008). One possibility, suggested by Milgrom (2015), is that cluster UDGs could host many of these dark baryons. The observed rising velocity dispersion profile could then be interpreted as a consequence of the presence of such a dark halo around the UDGs. However, a typical dark halo rotation curve would not reproduce the outer spike in velocity dispersions hinted at by the data. We note, however, that the baryonic dark halos of UDGs have likely different density profiles from what we are used for the non-baryonic dark halos in Newtonian gravity (Navarro et al. 1997). Moreover, the fact that the velocity dispersion in the center of Dragonfly 44 matches the MOND prediction for isolation gives us an important information: if Dragonfly 44 is at a great distance from the cluster core, and if the EFE is weak, then its halo must be extended so that it has no strong gravitational influence near the center of the galaxy. On the other hand, if the EFE acting on the UDG is substantial, then the increase in gravity due to the halo in the central parts must coincidentally compensate for the decrease in the MOND boost.

The presence of a dark baryonic halo might be hinted at by the fact that Dragonfly 44 has around ten times more globular clusters than dwarf galaxies of the same luminosity (Amorisco et al. 2018). If we interpret the empirical relation between the galaxy luminosity and number of globular clusters as a relation between the total baryonic mass of the galaxy and the number of globular clusters, then it follows from Fig. 6 in Amorisco et al. (2018) that the baryonic mass of Dragonfly 44 is around 1010 M⊙, i.e., the amount of dark baryons in this galaxy is a few tens of M*, 0.

We should note that Dragonfly 44 can be without a dark matter halo while the UDGs near the cluster center have halos. Many formation scenarios for UDGs were suggested in the ΛCDM context, and therefore the same should be allowed in the MOND context. At least one way to form a UDG without a substantial number of dark baryons is known: some UDGs seem to be tidal dwarf galaxies (Bennet et al. 2018), which are not supposed to contain a much larger proportion of dark baryons than their parent galaxies, i.e., the spiral galaxies, which do not seem to contain many dark baryons (McGaugh et al. 2000; Tiret & Combes 2009).

3.5. How to find the answer?

One of the main uncertainties in interpreting the data for Dragonfly 44 is that we do not know whether the EFE exerted by the cluster is negligible or whether the galaxy is in dynamical equilibrium.

In the case of hypothetical baryonic dark matter halos suggested by Milgrom (2015), the easiest way to detect them would be to focus future observations on UDGs that are in projection far enough from the cluster to be considered isolated. Then a higher-than-predicted velocity dispersion would be a sign of a dark halo. For the Coma cluster and a typical UDG, it means a projected separation of at least 4.5° (assuming the median UDG mass and radius given by van Dokkum et al. 2015a of 6 × 107 M⊙ and re = 2.8 kpc, respectively). Figure 2 suggests that the outer parts of UDGs are particularly suitable for this task since the velocity dispersion profile of Dragonfly 44 is quite insensitive to the precise value of the anisotropy parameter; the reasons for this are probably related to the results of Wolf et al. (2010).

Concerning UDGs in the central parts of the clusters, in order to distinguish the cases of disrupting UDGs or UDGs with dark halos, we would have to compare them to their analogs in simulations on their supposed orbits. From this perspective, it would be very advantageous to observe in the future the UDGs close to cluster centers, but at distances where the internal dynamics of the UDGs are not expected to be influenced by the tidal forces of the main competitors of MOND, the theories supposing Newtonian gravity, and non-baryonic dark matter.

An interesting result would be if all UDGs in clusters came out to have velocity dispersions corresponding to the isolated case similarly to Dragonfly 44. The chance that all of the central UDGs are just lying there in projection and in reality are in the outskirts is quite low (van der Burg et al. 2016). Similarly, the fraction of UDGs having a dark halo whose dynamical effect would precisely compensate the decrease in MOND gravity due to the EFE should also be low. Then two possibilities arise: either MOND is excluded as a modification of gravity (but this would leave the open question of why the observations agree with the isolated MOND prediction) or, as was suggested by Milgrom (2015), the UDGs are on their first radial infall and are in the process of disruption.

We note, however, that some theories actually expect that the internal dynamics of UDGs are not influenced by the cluster. For instance, MOND could be modified such that it does not require dark matter in galaxy clusters, as proposed in Zhao & Famaey (2012). This could help the galaxies survive, but Hodson & Zhao (2017) showed that the high velocity dispersion, now measured at the last data point of Dragonfly 44, could not be explained in this way, which would bring us back to the hypothesis of disruption. Another exotic possibility is that the empirical MOND effect in galaxies is due to the coupling of baryons to the phonons of a dark matter superfluid core, which would encompass their baryonic profile. As extensively discussed in Sect. IX.B of Berezhiani et al. (2018), galaxy clusters have small superfluid cores of about 100 kpc and no EFE would then act on the UDGs residing outside of this core, while they would still obey the isolated MOND prediction in the central parts, but have an additional effect from dark matter itself in the outskirts. Finally, the EFE can be weak in some modified inertia versions of MOND (Milgrom 2011), but this would leave the question open of why UDGs in groups, such as NGC 1052, seem to be affected by the EFE, unless they are in fact foreground objects.

4. Conclusion

Recently, the first velocity dispersion profile of an ultra-diffuse galaxy, namely Dragonfly 44, has been measured and analyzed in the framework of Newtonian dynamics and dark matter (van Dokkum et al. 2019b). Here we computed Jeans models for this galaxy in the framework of MOND. Assuming the galaxy to reside in isolation we found that an isotropic model reproduces the observed velocity dispersion near the center without any ad hoc tuning of free parameters. For the outer parts, the modeled velocity dispersion deviates from the measured data points, but it is still within the 2σ uncertainty limit of the measurement. While the modeled velocity dispersion profile is almost flat, the observed profile is steeply rising in the outer parts.

We proposed several interpretations of our results:

  • 1.

    The galaxy is far from the cluster (thus in isolation), and the outer deviation is simply a measurement error;

  • 2.

    The galaxy is far from the cluster, and the outer deviation is mostly an effect of tangential anisotropy for a very high stellar mass of the galaxy, which yields a discrepancy of less than 1σ;

  • 3.

    The galaxy is closer to the cluster core, and is in the process of disruption: the inner parts are not yet observably affected by the EFE, and the deviation in the outskirts is caused by tidal deformation;

  • 4.

    The deviation is a manifestation of a baryonic dark halo around the UDG, which raises the question of why it then obeys the central velocity dispersion predicted by MOND in isolation.

We also discussed more exotic possibilities such as modifications of inertia without the EFE or superfluid dark matter, in which case the galaxy does not need to be far away from the cluster core to obey the isolated MOND prediction, but still requires an explanation for the mismatch of the outer data points. In order to test these scenarios, it is necessary to measure the velocity dispersion of more of these objects and to perform simulations of the evolution of UDGs moving through galaxy clusters.

1

However, the external field effect can be weak, or even almost negligible, in some modified inertia versions of MOND (Milgrom 2011).

Acknowledgments

O.M. is grateful to the Swiss National Science Foundation for financial support.

References

  1. Alabi, A., Ferré-Mateu, A., Romanowsky, A. J., et al. 2018, MNRAS, 479, 3308 [NASA ADS] [CrossRef] [Google Scholar]
  2. Amorisco, N. C., & Loeb, A. 2016, MNRAS, 459, L51 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amorisco, N. C., Monachesi, A., Agnello, A., & White, S. D. M. 2018, MNRAS, 475, 4235 [NASA ADS] [CrossRef] [Google Scholar]
  4. Begeman, K. G., Broeils, A. H., & Sanders, R. H. 1991, MNRAS, 249, 523 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bekenstein, J., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bennet, P., Sand, D. J., Zaritsky, D., et al. 2018, ApJ, 866, L11 [NASA ADS] [CrossRef] [Google Scholar]
  7. Berezhiani, L., Famaey, B., & Khoury, J. 2018, JCAP, 2018, 021 [CrossRef] [Google Scholar]
  8. Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton: Princeton University Press) [Google Scholar]
  9. Bosma, A. 1981, AJ, 86, 1791 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brada, R., & Milgrom, M. 2000, ApJ, 541, 556 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chan, T. K., Kereš, D., Wetzel, A., et al. 2018, MNRAS, 478, 906 [NASA ADS] [CrossRef] [Google Scholar]
  12. Crnojević, D., Sand, D. J., Caldwell, N., et al. 2014, ApJ, 795, L35 [NASA ADS] [CrossRef] [Google Scholar]
  13. Di Cintio, A., Brook, C. B., Dutton, A. A., et al. 2017, MNRAS, 466, L1 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
  15. Emsellem, E., van der Burg, R. F. J., Fensch, J., et al. 2019, A&A, 625, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Relativ., 15, 10 [NASA ADS] [CrossRef] [Google Scholar]
  17. Famaey, B., McGaugh, S., & Milgrom, M. 2018, MNRAS, 480, 473 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fensch, J., van der Burg, R. F. J., Jerabkova, T., et al. 2019, A&A, 625, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Ferré-Mateu, A., Alabi, A., Forbes, D. A., et al. 2018, MNRAS, 479, 4891 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hodson, A. O., & Zhao, H. 2017, A&A, 607, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Impey, C., Bothun, G., & Malin, D. 1988, ApJ, 330, 634 [NASA ADS] [CrossRef] [Google Scholar]
  22. Koda, J., Yagi, M., Yamanoi, H., & Komiyama, Y. 2015, ApJ, 807, L2 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kroupa, P., Haghi, H., Javanmardi, B., et al. 2018, Nature, 561, E4 [CrossRef] [Google Scholar]
  24. Laporte, C. F. P., Agnello, A., & Navarro, J. F. 2019, MNRAS, 484, 245 [NASA ADS] [CrossRef] [Google Scholar]
  25. Leisman, L., Haynes, M. P., Janowiecki, S., et al. 2017, ApJ, 842, 133 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
  27. Lima Neto, G. B., Gerbal, D., & Márquez, I. 1999, MNRAS, 309, 481 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mamon, G. A., & Łokas, E. L. 2005, MNRAS, 363, 705 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mancera Piña, P. E., Aguerri, J. A. L., Peletier, R. F., et al. 2019, MNRAS, 485, 1036 [NASA ADS] [CrossRef] [Google Scholar]
  30. Márquez, I., Lima Neto, G. B., Capelato, H., Durret, F., & Gerbal, D. 2000, A&A, 353, 873 [NASA ADS] [Google Scholar]
  31. Martin, N. F., Collins, M. L. M., Longeard, N., & Tollerud, E. 2018, ApJ, 859, L5 [NASA ADS] [CrossRef] [Google Scholar]
  32. Martínez-Delgado, D., Läsker, R., Sharina, M., et al. 2016, AJ, 151, 96 [NASA ADS] [CrossRef] [Google Scholar]
  33. Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. McGaugh, S., & Milgrom, M. 2013, ApJ, 775, 139 [NASA ADS] [CrossRef] [Google Scholar]
  35. McGaugh, S. S., & de Blok, W. J. G. 1998, ApJ, 499, 66 [NASA ADS] [CrossRef] [Google Scholar]
  36. McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Merritt, A., van Dokkum, P., Danieli, S., et al. 2016, ApJ, 833, 168 [NASA ADS] [CrossRef] [Google Scholar]
  38. Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
  39. Milgrom, M. 2008, New Astron. Rev., 51, 906 [NASA ADS] [CrossRef] [Google Scholar]
  40. Milgrom, M. 2011, Acta Phys. Polonica B, 42, 2175 [Google Scholar]
  41. Milgrom, M. 2014, MNRAS, 437, 2531 [NASA ADS] [CrossRef] [Google Scholar]
  42. Milgrom, M. 2015, MNRAS, 454, 3810 [NASA ADS] [CrossRef] [Google Scholar]
  43. Müller, O., Jerjen, H., & Binggeli, B. 2018, A&A, 615, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Müller, O., Famaey, B., & Zhao, H. 2019a, A&A, 623, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Müller, O., Rich, R. M., Román, J., et al. 2019b, A&A, 624, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  47. Nusser, A. 2019, MNRAS, 484, 510 [NASA ADS] [CrossRef] [Google Scholar]
  48. Papastergis, E., Adams, E. A. K., & Romanowsky, A. J. 2017, A&A, 601, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Román, J., & Trujillo, I. 2017a, MNRAS, 468, 703 [NASA ADS] [CrossRef] [Google Scholar]
  50. Román, J., & Trujillo, I. 2017b, MNRAS, 468, 4039 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rubin, V. C., Ford, Jr., W. K., & Thonnard, N. 1978, ApJ, 225, L107 [NASA ADS] [CrossRef] [Google Scholar]
  52. Rubin, V. C., Ford, Jr., W. K., Thonnard, N., & Burstein, D. 1982, ApJ, 261, 439 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sandage, A., & Binggeli, B. 1984, AJ, 89, 919 [NASA ADS] [CrossRef] [Google Scholar]
  54. Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
  55. Sardone, A., Pisano, D. J., Burke-Spolaor, S., Mascoop, J. L., & Pol, N. 2019, ApJ, 871, L31 [NASA ADS] [CrossRef] [Google Scholar]
  56. Shi, D. D., Zheng, X. Z., Zhao, H. B., et al. 2017, ApJ, 846, 26 [NASA ADS] [CrossRef] [Google Scholar]
  57. Tiret, O., & Combes, F. 2009, A&A, 496, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Toloba, E., Lim, S., Peng, E., et al. 2018, ApJ, 856, L31 [NASA ADS] [CrossRef] [Google Scholar]
  59. Trujillo, I., Beasley, M. A., Borlaff, A., et al. 2019, MNRAS, 486, 1192 [NASA ADS] [CrossRef] [Google Scholar]
  60. van der Burg, R. F. J., Muzzin, A., & Hoekstra, H. 2016, A&A, 590, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. van Dokkum, P. G., Abraham, R., Merritt, A., et al. 2015a, ApJ, 798, L45 [NASA ADS] [CrossRef] [Google Scholar]
  62. van Dokkum, P. G., Romanowsky, A. J., Abraham, R., et al. 2015b, ApJ, 804, L26 [NASA ADS] [CrossRef] [Google Scholar]
  63. van Dokkum, P., Abraham, R., Brodie, J., et al. 2016, ApJ, 828, L6 [NASA ADS] [CrossRef] [Google Scholar]
  64. van Dokkum, P., Danieli, S., Cohen, Y., et al. 2018a, Nature, 555, 629 [NASA ADS] [CrossRef] [Google Scholar]
  65. van Dokkum, P., Danieli, S., Cohen, Y., Romanowsky, A. J., & Conroy, C. 2018b, ApJ, 864, L18 [NASA ADS] [CrossRef] [Google Scholar]
  66. van Dokkum, P., Danieli, S., Abraham, R., Conroy, C., & Romanowsky, A. J. 2019a, ApJ, 874, L5 [NASA ADS] [CrossRef] [Google Scholar]
  67. van Dokkum, P., Wasserman, A., Danieli, S., et al. 2019b, ApJ, submitted [arXiv:1904.04838] [Google Scholar]
  68. Venhola, A., Peletier, R., Laurikainen, E., et al. 2017, A&A, 608, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Wittmann, C., Lisker, T., Ambachew Tilahun, L., et al. 2017, MNRAS, 470, 1512 [NASA ADS] [CrossRef] [Google Scholar]
  70. Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
  71. Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
  72. Yozin, C., & Bekki, K. 2015, MNRAS, 452, 937 [NASA ADS] [CrossRef] [Google Scholar]
  73. Zaritsky, D., Donnerstein, R., Dey, A., et al. 2019, ApJS, 240, 1 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zhao, H. S. 2005, A&A, 444, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Zhao, H., & Famaey, B. 2012, Phys. Rev. D, 86, 067301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Comparison of the measured velocity dispersion profile of the ultra-diffuse galaxy Dragonfly 44 to the MOND no-fitting model and the Newtonian model. A fixed mass-to-light ratio of 1.3 and the best estimate of the galaxy luminosity as 3.0 × 108 L⊙ were assumed, together with isotropy. We illustrate the effect of relaxing some of these assumptions in Fig. 2.
In the text
thumbnail Fig. 2.

Various models of the MOND velocity dispersion profile of Dragonfly 44 discussed in Sect. 3.2. Top panel: radially anisotropic models. The isotropic model, as in Fig. 1, is shown as a solid line, the externally radial anisotropy model as a dashed line, and the pure radial anisotropy model as a dot-dashed line. Bottom panel: tangentially anisotropic models. Three models for the tangential anisotropy with different stellar masses, as discussed in Sect. 3.2, are shown as solid, dashed, and dash-dotted lines.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.