| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 27 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201730942 | |
| Published online | 14 September 2017 | |
Explosion of red-supergiant stars: Influence of the atmospheric structure on shock breakout and early-time supernova radiation
1 Unidad Mixta Internacional Franco-Chilena de Astronomía (CNRS UMI 3386), Departamento de Astronomía, Universidad de Chile, Camino El Observatorio 1515, Las Condes, Santiago Chile
e-mail: Luc.Dessart@oca.eu
2 Department of Physics and Astronomy & Pittsburgh Particle Physics, Astrophysics, and Cosmology Center (PITT PACC), University of Pittsburgh, 3941 O’Hara Street, Pittsburgh, PA 15260, USA
3 Maison de la Simulation, CEA, CNRS, Université Paris-Sud, UVSQ, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
Received: 6 April 2017
Accepted: 6 June 2017
Early-time observations of Type II supernovae (SNe) 2013cu and 2013fs have revealed an interaction of ejecta with material near the star surface. Unlike Type IIn SN 2010jl, which interacts with a dense wind for ~1 yr, the interaction ebbs after 2–3 d, suggesting a dense and compact circumstellar envelope. Here, we use multi-group radiation hydrodynamics and non-local-thermodynamic-equilibrium radiative transfer to explore the properties of red-supergiant (RSG) star explosions embedded in a variety of dense envelopes. We consider the cases of an extended static atmosphere or a steady-state wind, adopting a range of mass loss rates. The shock breakout signal, luminosity and color evolution up to 10 d, and ejecta dynamics are strongly influenced by the properties of this nearby environment. This compromises the use of early-time observations to constrain R⋆. For dense circumstellar envelopes, the time-integrated luminosity over the first 10−15 d can be boosted by a factor of a few. The presence of narrow lines for 2–3 d in 2013fs and 2013cu require a cocoon of material of ~0.01 M⊙ out to 5−10 R⋆. Spectral lines evolve from electron scattering to Doppler broadened with a growing blueshift of their emission peaks. Recent studies propose a super-wind phase with a mass loss rate from 0.001 up to 1 M⊙ yr-1 in the last months or years of the life of a RSG, although there is no observational constraint that this external material is a steady-state outflow. Alternatively, observations may be explained by the explosion of a RSG star inside its complex atmosphere. Indeed, spatially resolved observations reveal that RSG stars have extended atmospheres, with the presence of downflows and upflows out to several R⋆, even in a standard RSG such as Betelgeuse. Mass loading in the region intermediate between star and wind can accommodate the 0.01 M⊙ needed to explain the observations of 2013fs. Signatures of interaction in early-time spectra of RSG star explosions may therefore be the norm, not the exception, and a puzzling super-wind phase prior to core collapse may be superfluous.
Key words: radiation: dynamics / radiative transfer / supernovae: general
© ESO, 2017
1. Introduction
Radiation-hydrodynamic simulations of Type II supernovae (SNe) in the 1970s indicated that their progenitors were red-supergiant (RSG) stars (Grassberg et al. 1971; Falk & Arnett 1977). More recently, the analysis of pre-explosion images has confirmed this (see, e.g., Van Dyk et al. 2003a,b; Smartt 2009). The RSG progenitor properties are however uncertain because of the limitation in our understanding of the physics of RSG envelopes (e.g., in connection to convection; see, e.g., Meakin & Arnett 2007; Arnett et al. 2010), RSG atmospheres and environments (e.g., in connection to mass loss, dust/molecule formation, etc.; Josselin & Plez 2007), or their final core properties at collapse (Couch et al. 2015; Müller et al. 2016).
Single massive stars lose mass through a radiation-driven wind (Castor et al. 1975; de Jager et al. 1988). It is therefore unsurprising that a fraction of SNe exhibit signatures of ejecta interaction with circumstellar material (CSM). The unambiguous signature of interaction with an optically thick CSM moving at very slow speeds with respect to the SN ejecta is the observation of optical emission lines with a narrow core and broad electron-scattering wings. The frequency of such interactions is uncertain but is probably on the order of 5−10% of Type II SNe (e.g., Smith et al. 2011). Such events are classified as Type IIn SNe (Schlegel 1990). SNe IIn come, however, with a huge diversity of properties in light curves and spectra. Some show signatures of interaction1 for a few days (e.g., SN 2013cu; Gal-Yam et al. 2014), a few weeks (SN 1998S; Fassia et al. 2000; Leonard et al. 2000), or a few months (SN 2010jl; Zhang et al. 2012; Fransson et al. 2014), together with a wide range of luminosities. Numerical simulations of interacting SNe connect this diversity to variations in CSM location and structure (Moriya et al. 2011; Dessart et al. 2015). To avoid confusion, here CSM refers to circumstellar material detached from the star and typically located at large distances of 10–100 R⋆. For events in which the signatures of interaction are seen on the discovery spectrum but disappear after a few hours or a few days, such as in SN 2013cu, we refer to the atmosphere and/or wind; this material corresponds to the direct environment of the star, contiguous to the star surface (often referred to as the circumstellar envelope), rather than a standard CSM.
SN 2013fs is a recent example that illustrates the complexity and diversity of such interactions. This SN shows signatures of interaction for only ~2 d after explosion, while it resembles a very standard Type II-P SN at  10 d (plateau light curve in visual bands; standard P-Cygni profiles for H i lines; Yaron et al. 2017). Signs of interaction have been observed at early times in other Type II SNe (Khazov et al. 2016), although most of these do not show the 100-day long plateau light curve of SNe II-P. SN 1998S is a prototypical, well observed event showing narrow line profiles for 10−20 d after discovery and becoming a more standard Type II event with broad lines (Leonard et al. 2000; Fassia et al. 2001). Simulations suggest the early line broadening mechanism is dominated by electron scattering (Chugai 2001; Shivvers et al. 2015; Dessart et al. 2016). By 20 d, the atmosphere or wind is optically thin and the spectrum forms in a fast expanding region with a steeply declining density profile (i.e., at the interface between progenitor and atmosphere/wind), leading to a featureless (and blue) continuum. At later times during the photospheric phase, the spectrum exhibits a standard Type II (non-interacting) SN spectrum with signs of line blanketing, P-Cygni profiles, and excess emission associated with the optically thin, cold, dense shell. These three phases are well traced with radiation-hydrodynamic and non-local-thermodynamic-equilibrium (non-LTE) radiative-transfer modeling. In particular, the simultaneous presence of Doppler-broadened lines forming in the ejecta and narrow lines broadened by electron scattering in the atmosphere/wind is reproduced if the non-monotonicity of the velocity field is explicitly accounted for (Dessart et al. 2016).
10 d (plateau light curve in visual bands; standard P-Cygni profiles for H i lines; Yaron et al. 2017). Signs of interaction have been observed at early times in other Type II SNe (Khazov et al. 2016), although most of these do not show the 100-day long plateau light curve of SNe II-P. SN 1998S is a prototypical, well observed event showing narrow line profiles for 10−20 d after discovery and becoming a more standard Type II event with broad lines (Leonard et al. 2000; Fassia et al. 2001). Simulations suggest the early line broadening mechanism is dominated by electron scattering (Chugai 2001; Shivvers et al. 2015; Dessart et al. 2016). By 20 d, the atmosphere or wind is optically thin and the spectrum forms in a fast expanding region with a steeply declining density profile (i.e., at the interface between progenitor and atmosphere/wind), leading to a featureless (and blue) continuum. At later times during the photospheric phase, the spectrum exhibits a standard Type II (non-interacting) SN spectrum with signs of line blanketing, P-Cygni profiles, and excess emission associated with the optically thin, cold, dense shell. These three phases are well traced with radiation-hydrodynamic and non-local-thermodynamic-equilibrium (non-LTE) radiative-transfer modeling. In particular, the simultaneous presence of Doppler-broadened lines forming in the ejecta and narrow lines broadened by electron scattering in the atmosphere/wind is reproduced if the non-monotonicity of the velocity field is explicitly accounted for (Dessart et al. 2016).
The presence of an atmosphere/wind may also be inferred from the short-lived shock breakout signal. In a shock-driven explosion, the radiation-dominated shock will start to leak photons when the photon diffusion time at the shock tdiff = 3τΔR/c becomes comparable to the shock crossing time tshock = ΔR/vshock through the outer layers of thickness ΔR of the progenitor star2. This shock breakout signal therefore starts at the optical depth τ ~ c/ 3vshock3. For the ~1051 erg Type II SN explosions presented here, the shock speed is about 5000 km s-1 such that the breakout signal starts from an optical depth of about 20. The actual duration of the shock breakout scales with ΔR, which is the length scale between the photosphere and τ = 20. Depending on the RSG atmosphere/wind structure, this length scale may perhaps cover from 0.01 to 0.5 R⋆. For a small scale height, the breakout signal is intrinsically short ( 1000 s). However, the timescale is stretched to at least R⋆/c, hence about 30 min, for a distant observer. KSN 2011d is the first Type II SN to exhibit this shock breakout signal (Garnavich et al. 2016), which indicates the absence of a dense wind or an extended atmosphere around its progenitor RSG. For a large scale height (as in the case of a dense wind), the duration can be hours, hence typically well in excess of R⋆/c. The observations of a one-day long UV burst in PS1-13arp by Gezari et al. (2015) suggests that the shock may have broken out into some dense and extended material. Observations as part of SHOOT by Tanaka et al. (2016) reveal a very short optical rise time that supports such a phenomenon. By lengthening the duration of the shock breakout signal, the presence of a dense atmosphere/wind may facilitate its detection. Although very challenging, high-cadence surveys with a high limiting magnitude can capture the fleeting moment of shock breakout. The HITS survey (Förster et al. 2016) or SHOOT (Tanaka et al. 2016) have not yet been successful, but the KEPLER mission has made one unambiguous detection (Garnavich et al. 2016) – high cadence surveys that fail to capture shock breakout reveal critical information on the early-phase evolution of the SN radiation.
1000 s). However, the timescale is stretched to at least R⋆/c, hence about 30 min, for a distant observer. KSN 2011d is the first Type II SN to exhibit this shock breakout signal (Garnavich et al. 2016), which indicates the absence of a dense wind or an extended atmosphere around its progenitor RSG. For a large scale height (as in the case of a dense wind), the duration can be hours, hence typically well in excess of R⋆/c. The observations of a one-day long UV burst in PS1-13arp by Gezari et al. (2015) suggests that the shock may have broken out into some dense and extended material. Observations as part of SHOOT by Tanaka et al. (2016) reveal a very short optical rise time that supports such a phenomenon. By lengthening the duration of the shock breakout signal, the presence of a dense atmosphere/wind may facilitate its detection. Although very challenging, high-cadence surveys with a high limiting magnitude can capture the fleeting moment of shock breakout. The HITS survey (Förster et al. 2016) or SHOOT (Tanaka et al. 2016) have not yet been successful, but the KEPLER mission has made one unambiguous detection (Garnavich et al. 2016) – high cadence surveys that fail to capture shock breakout reveal critical information on the early-phase evolution of the SN radiation.
Signatures of interaction with the atmosphere/wind may be short lived and therefore generally missed by a delayed spectroscopic follow-up. Numerous events may therefore be classified as Type II-P (or II-L) while an earlier spectroscopic observation would have suggested a classification as Type IIn. One should however wonder whether a SN should be classified as a IIn because it shows narrow lines for a day or two or as a II-P because it shows a 100-d long plateau with all the spectral characteristics of a standard SN II-P at all times past two days. Should the event be classified as a Type IIn if the narrow lines were seen for only one hour? This is not irrelevant. Once a SN has been classified as a Type IIn, it contributes to the number of events considered as interacting SNe, mixed in the sample with objects, such as SN 2010jl, which show signs of interaction at all times. Hence, this has strong implications for the interpretation of SN rates and for the inferences of progenitor properties.
Based on the presence of early-time spectral signatures of interaction, Khazov et al. (2016) and Yaron et al. (2017) have proposed that numerous SNe II-P may undergo a super-wind phase before core collapse. Recently, Morozova et al. (2017) have argued for such super-wind phases and have proposed that the resulting ejecta/wind interaction may explain the difference between Type II-L and Type II-P light curve morphologies. Very early observations were obtained with the Type IIb SN 2013cu, for which Gal-Yam et al. (2014) have proposed that the spectrum at 15.5 h forms in the dense (Ṁ  0.03 M⊙ yr-1) and fast (terminal velocity of 2500 km s-1) wind of a Wolf-Rayet progenitor star. This interpretation rests partly on the idea that line broadening is caused by the Doppler effect. Instead, line broadening is likely caused by electron scattering. In this case, Groh (2014) have proposed a slow (
0.03 M⊙ yr-1) and fast (terminal velocity of 2500 km s-1) wind of a Wolf-Rayet progenitor star. This interpretation rests partly on the idea that line broadening is caused by the Doppler effect. Instead, line broadening is likely caused by electron scattering. In this case, Groh (2014) have proposed a slow ( 100 km s-1) and dense (3 × 10-3 M⊙ yr-1) wind. This has been later refined by Gräfener & Vink (2016) who accounted for time delays. They have proposed a significant increase on the wind mass (to be at least 0.3 M⊙) and that the shock may be embedded within the optically thick wind (whose outer edge is the photosphere) for two weeks. However, the narrow line profiles seen in SN 2013cu are strong at 15.5 h after discovery, but weak at 3 d and absent at 6 d so the bulk of the dense (optically thick) material is probably swept up already after a few days. A total wind mass of 0.3 M⊙ is close to what is found for SN 1998S and narrow line profiles are seen for much longer (
100 km s-1) and dense (3 × 10-3 M⊙ yr-1) wind. This has been later refined by Gräfener & Vink (2016) who accounted for time delays. They have proposed a significant increase on the wind mass (to be at least 0.3 M⊙) and that the shock may be embedded within the optically thick wind (whose outer edge is the photosphere) for two weeks. However, the narrow line profiles seen in SN 2013cu are strong at 15.5 h after discovery, but weak at 3 d and absent at 6 d so the bulk of the dense (optically thick) material is probably swept up already after a few days. A total wind mass of 0.3 M⊙ is close to what is found for SN 1998S and narrow line profiles are seen for much longer (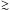 10 d). In any case, despite slight differences in interpretation and modeling techniques, these studies argue for a super-wind phase immediately prior to the core collapse of the progenitor of SN 2013cu. These observations question whether there is something fundamentally missing in the 1-D quasi-steady-state treatment of stellar evolution and stellar winds. The eruptions observed in some very massive stars such as η Car and the inference of ejecta interaction with a massive CSM in super-luminous SNe IIn point to evidence in that direction.
10 d). In any case, despite slight differences in interpretation and modeling techniques, these studies argue for a super-wind phase immediately prior to the core collapse of the progenitor of SN 2013cu. These observations question whether there is something fundamentally missing in the 1-D quasi-steady-state treatment of stellar evolution and stellar winds. The eruptions observed in some very massive stars such as η Car and the inference of ejecta interaction with a massive CSM in super-luminous SNe IIn point to evidence in that direction.
Here, we use 1-D radiation-hydrodynamics and 1-D non-LTE radiative transfer modeling to characterize the bolometric, photometric, and spectroscopic signatures of RSG explosions embedded in an atmosphere/wind of modest extent (within ~10 R⋆) and mass (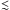 10-1 M⊙). Previous studies that have focused on ejecta/wind interactions used either gray/multi-group radiation hydrodynamics without spectral calculations (Moriya et al. 2011; Morozova et al. 2017) or spectral calculations without dynamics (Yaron et al. 2017).
10-1 M⊙). Previous studies that have focused on ejecta/wind interactions used either gray/multi-group radiation hydrodynamics without spectral calculations (Moriya et al. 2011; Morozova et al. 2017) or spectral calculations without dynamics (Yaron et al. 2017).
The structure of the paper is as follows. In the next section, we discuss the properties of the environment of RSG stars. We then present our numerical approach in Sect. 3. In Sect. 4, we discuss the results from the multi-group radiation-hydrodynamics simulations with heracles, focusing on the properties of the bolometric light curves and the dynamic structure of the interaction between the SN ejecta and the progenitor atmosphere/wind (velocity, density, temperature, and optical depth). These simulations are post-processed with cmfgen using a non-LTE steady-state approach that works for an arbitrary velocity field. The resulting multi-band light curves and spectra are discussed in Sect. 5. We compare our results to observations in Sect. 6. We present our conclusions in Sect. 7.
2. Environment of red-supergiant stars
The complexity of RSG atmospheres prevents a physically consistent description of the density profile above the RSG surface radius (i.e., the location corresponding to R⋆ in a stellar evolution model, as produced for example in mesa; Paxton et al. 2011). Atmospheres of RSGs are very complex, with density inhomogeneities, upflows, and downflows seen out to several stellar radii (Kervella et al. 2009, 2011; Ohnaka et al. 2011; Kervella et al. 2016). These observations suggest that there is no well-defined atmosphere and that the wind is not launched cleanly from R⋆, but is instead slowly accelerated over an extended region.
A RSG model computed by a stellar evolution code (here mesa, but the point applies to all such codes) extends out to a minimum density of 10-9 g cm-3, while the base density of a 10-5 M⊙ yr-1 RSG wind is around 10-14 g cm-3. There is therefore a density drop of 5 orders of magnitude between the R⋆ from mesa and the actual wind. It is in this intermediate region, whose properties are poorly known both observationally and theoretically, that the SN spectrum forms during the first few days after explosion (between roughly 0.5 and 2 × 1014 cm). In the present study, we assume that the distribution of this surrounding material is spherically symmetric around the star.
In the next section, we present two types of density structures for the near environment of the RSG star: an atmosphere with an extended scale height, combined or not combined with a dense wind. Early-time observations of Type II SNe do not allow us to constrain the pre-SN velocity structure of this material, hence we cannot firmly establish the steady-state nature of a wind. One cannot determine whether the atmospheric material is in hydrostatic equilibrium either. This results in part from the limitations of observations, which may not have a high enough spectral resolution. But it also stems physically from the acceleration caused by the intense radiation initially released at shock breakout and persisting for hours to days. Hence, these early-time SN observations only constrain the extent and density/mass of this material. Spatially resolved observations of RSG clearly show that the environment of RSG is neither static nor steady state (Kervella et al. 2009, 2011; Ohnaka et al. 2011; Kervella et al. 2016).
3. Initial conditions and methodology
3.1. Initial conditions
The initial ejecta structure, corresponding to the RSG star explosion, is taken from Dessart et al. (2013). We chose models m15mlt3 (here renamed r1; R⋆ = 501 R⊙) and m15mlt1 (here renamed r2; R⋆ = 1107 R⊙) in order to cover explosions from compact and extended RSG stars. In practice, the initial ejecta structure (radius, velocity, density, and temperature) is taken from the radiation hydrodynamic simulation (carried out with v1d; see Dessart et al. 2013, for details) at 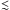 104 s before shock breakout. In other words, the shock is within
104 s before shock breakout. In other words, the shock is within 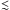 100 R⊙ of the progenitor surface.
100 R⊙ of the progenitor surface.
When embedding the RSG star initial interior structure (the shocked and unshocked envelope layers) in an atmosphere/wind, we adopted a variety of density structures, varying the wind mass loss rate Ṁ, the atmospheric scale height Hρ, or both. In a first set of simulations, we add an atmosphere with a density scale height of 0.01 R⋆, which corresponds to the surface value in the mesa model, until the density reaches down to the wind density corresponding to wind mass loss rates between 10-6 and 10-2 M⊙ yr-1. In our nomenclature, model suffixes w1, w2, w3, w4, w5, and w6 correspond to wind mass loss rates of 10-6, 10-5, 10-4, 10-3, 5× 10-3, and 10-2 M⊙ yr-1. To limit the extent of the dense wind, we smoothly switched to a low mass loss rate of 10-6 M⊙ yr-1 beyond 5 × 1014 cm, except for model r1w5r in which the transition to a low wind density is at 2 × 1014 cm. For model r2, we only studied the case of a low wind mass loss rate (model r2w1) because we believe SNe II-P do not stem from such extended RSG progenitors (Dessart et al. 2013) and also because the presence of a dense wind is the main ingredient controlling the resulting SN radiation; hence such simulations based on model r1 are sufficient.
In two additional models, we studied the impact of increasing the atmospheric density scale height. We used Hρ = 0.3 R⋆ down to 10-12 g cm-3, followed by a power-law density profile with exponent 12 (model r1w1h) or Hρ = 0.1 R⋆ followed by a wind mass loss rate of 5 × 10-3 M⊙ yr-1 (model r1w5h). In both models, the wind density is forced to be at least that for a wind mass loss rate of 10-6 M⊙ yr-1. Such variations in atmospheric scale height may appear large. However, they correspond to variations in density that are not greater than those imposed in models r1w1−r1w6. Secondly, they represent different ways of going from a density of 10-9 g cm-3 at R⋆ to a typical RSG wind density at a few R⋆. We observe RSG atmospheres to be extended, much more than given by the atmospheric scale height in mesa models at R⋆.
Summary of properties of the heracles simulations and their initial conditions.
 |
Fig. 1 Initial density structure used in heracles for models r1w1, r1w2, r1w3, r1w4, r1w1h, r1w5h, r1w5r, r1w6, and r2w1. Model m15mlt3 (r1) is used for the ejecta of model r1w[1–6][h,r] and model m15mlt1 (r2) for the r2w1, taken at a few hours before shock breakout (Dessart et al. 2013). The atmosphere/wind density is built using a variety of wind mass loss rates and atmospheric scale heights. All models transition to a wind mass loss rate of 10-6 M⊙ yr-1 beyond 2−5 × 1014 cm (≡ 5−10 R⋆). (See Sect. 3 and Table 1 for details.) |
In all cases, the atmosphere/wind is given an initial temperature of 2000 K and the terminal velocity v∞ of the wind is 50 km s-1. We assume that the atmosphere is in hydrostatic equilibrium (zero velocity) and that the wind accelerates promptly to v∞ within a fraction of R⋆. The exact choice of velocity profile is irrelevant for various reasons. At shock breakout, the wind base is strongly accelerated to velocities larger than v∞. The shock and ejecta velocity are also 100 times larger. In this context, it is the density profile that matters for the dynamics.
Figure 1 shows the density profile versus radius for the whole set of heracles simulations. The profile for other quantities is shown for model r1w6 in Fig. 2.
Table 1 summarizes the initial model properties. We define the external mass Mext as the added mass beyond R⋆ (as given in the stellar evolution model). This external material is not necessarily the wind itself, which is probably blown from a larger radius, but can be seen as some sort of cocoon of material stagnating at the base of the wind. In reality, the boundary between the star (interior to R⋆), this cocoon of mass, and the external wind is ill defined. Hence, the quoted external mass should be interpreted with caution. One conclusion from this work is that this material may not stem from a super-wind phase but instead corresponds to the cocoon of material that is seen around all spatially resolved RSG atmospheres.
 |
Fig. 2 Initial structure used in heracles for model r1w6. The time is a few hours before shock breakout; the prior evolution of the shock through the stellar interior was computed with v1d (Dessart et al. 2013). |
Table 1 also gives the optical depth of the atmosphere/wind assuming full ionization of H and He. The external material is cold and optically thin in the RSG progenitor and the optical depth of the external material is 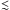 1, although this greatly depends on whether dust or molecules are present; but this material becomes fully ionized (at least for H and He) as soon as the shock breaks out. Hence, the optical depth of the ionized atmosphere/wind matters for the evolution during and after shock breakout. Even in the case of a weak wind mass loss rate of 10-6 M⊙ yr-1, the optical depth of the atmosphere above R⋆ is >100. This implies that shock breakout takes place outside of the region covered by the mesa model. In fact, the SN photosphere stays in this external region for about a week after shock breakout.
1, although this greatly depends on whether dust or molecules are present; but this material becomes fully ionized (at least for H and He) as soon as the shock breaks out. Hence, the optical depth of the ionized atmosphere/wind matters for the evolution during and after shock breakout. Even in the case of a weak wind mass loss rate of 10-6 M⊙ yr-1, the optical depth of the atmosphere above R⋆ is >100. This implies that shock breakout takes place outside of the region covered by the mesa model. In fact, the SN photosphere stays in this external region for about a week after shock breakout.
While we give a velocity profile to the material in the environment of the RSG star, which we call a wind or an atmosphere, the early-time SN radiation is primarily influenced by the extent and density/mass of this material; the influence of the initial velocity is negligible hence unconstrained. So, for all simulations, the results would be unchanged if the velocity of the CSE was set to zero.
3.2. Multi-group radiation-hydrodynamic simulations with HERACLES
The interaction configurations described above are used as initial conditions for the 1-D multi-group radiation-hydrodynamics simulations with the code heracles (González et al. 2007; Vaytet et al. 2011). The approach is identical to that used and described in Dessart et al. (2015, 2016). We used eight groups covering the UV to near-IR: one group for the entire Lyman continuum (including the X-ray range), two groups for the Balmer continuum, two for the Paschen continuum, and three groups for the Brackett continuum and beyond4. A multi-group approach is superior to a gray approach because it better describes the opacity of the material to the radiation when they have widely different temperatures (e.g., high energy radiation crossing a cold gas; see Dessart et al. 2015 for discussion). Because the thermal energy of the gas is a negligible fraction of the total radiation energy in SNe, we adopted a simple equation of state that treats the gas as ideal with γ = 5/3. We carried out tests using a mean-atomic-weight μ = 0.67 (corresponding to full ionization) and 1.35 (neutral) and these yields the same results at early times5.
We concentrate on the early-time properties so we limit the simulations to times prior to ~15 d. For the shock speeds relevant to the present simulations, this requires placing the outer boundary at Rmax = 1.5 × 1015 cm. We cover the ejecta down to a radius of a few 100 R⊙, which is deep enough to cover the reverse shock progressing into the He core.
Eulerian coordinates are not ideal for SN studies in 1-D, although these coordinates are much better than Lagrangian coordinates when we extend such simulations to multiple dimensions (as in Vlasis et al. 2016); this is the case because the structure expands by orders of magnitude through the evolution. Resolving the ejecta at all times requires high resolution. We used 1-D spherical polar coordinates with a total of 10 000 radial points. To better resolve the ejecta at smaller radii (earlier times), we used a grid with a constant spacing from the minimum radius at ~1013 cm up to Rt = 5 × 1014 cm, and then switched to a grid with a constant spacing in the log up to Rmax. The grid is designed to have no sharp jump in spacing at Rt.
Because we focused on early times, we adopted a fixed composition corresponding to the outer ejecta of models m15mlt3 and m15mlt1 (XH = 0.65, XHe = 0.33, and solar metallicity). This composition is only relevant for the computation of the opacities.
The bolometric light curves extracted from the heracles simulations were computed using the total radiative flux at the outer boundary. The bolometric luminosity should not be affected by the LTE assumption for the gas properties. However, multi-band light curves are sensitive to non-LTE effects, the wavelength dependent albedo, line blanketing, and are therefore computed with the 1-D non-LTE code cmfgen. Post-processing an LTE calculation with a non-LTE code is not optimal, but it is a good start. For example, for the same hydrodynamical snapshot, assuming LTE in cmfgen produces redder/cooler spectra than the corresponding non-LTE calculation.
 |
Fig. 3 Ejecta properties computed by heracles for model r1w1 (weak wind mass loss rate of 10-6 M⊙ yr-1) at 0.17, 1, and 2 d after the start of the heracles simulation. The black dot in each of the middle panels corresponds to the electron-scattering photosphere. In the optical-depth panel, the colored numbers correspond to each energy group, ordered from low frequency (group 1 covers the far-IR) to high frequency (group 8 covers the Lyman continuum). The thick black line corresponds to the electron-scattering optical depth. Through this early evolution, we can see the ejecta accelerate, the wind acceleration by the SN radiation, the propagation of the radiation burst that coincided with shock breakout (at ~0.1 d), the heating and rapid ionization of the wind, and the establishment of radiative equilibrium in the optically thin regions at 2 d. |
3.3. Non-LTE radiation-transfer simulations with CMFGEN
At selected epochs in the heracles simulations, the radius-velocity-density-temperature structure is remapped into cmfgen (Hillier & Dessart 2012; Dessart et al. 2015) for the calculation of the emergent flux, from which the multi-band light curves and the spectral evolution are obtained. The code treats the non-monotonic velocity field produced by heracles. Hence, emission, absorption, and scattering from the fast ejecta regions and the slower atmosphere/wind regions are taken into account. We also allowed for the non-coherent frequency redistribution by thermal electrons. We fixed the temperature during the cmfgen calculation because it results in a large part from the dynamics (shock deposited energy).
For a given snapshot, we only extracted the region of the heracles simulation between the electron-scattering optical depths of 10-5 and 50; the inner boundary is optically thick at all wavelengths. The grid in cmfgen uses 100 points with the prescriptions that any two consecutive points should at most have a jump of 5% in radius, 10% in temperature, 10% in electron density, 10% in density, and 10% in the log of the optical depth. If two consecutive points in the heracles simulation violate any of these criteria, additional points are inserted in the cmfgen grid. A finer grid is also used at the inner and outer boundaries.
For our cmfgen calculations, we included H, He, C, N, O, and Fe with the mass fractions 0.63972, 0.349, 0.00142, 0.0031, 0.00541, and 0.00135, respectively. No radioactive decay was accounted for here (all species/isotopes treated are stable) since the early-time evolution of SNe II is unaffected by decay heating. The minor abundance offset from the heracles simulation is irrelevant. Our study focuses primarily on dynamical issues and line profile morphology; slight variations in abundance that may occur through different levels of mixing, overshoot, etc. are not a concern at this stage. The study of their influence on early-time spectroscopic properties is deferred. For example, the early-time observations of SNe 2013cu and 2013fs suggest that their respective progenitors may have different CNO surface abundances (although this may stem partly from different ionization conditions): SN 2013cu shows one strong line of nitrogen (Gal-Yam et al. 2014), while SN 2013fs shows primarily lines of oxygen (Yaron et al. 2017).
Depending on the post-shock breakout phase, we adjust the model atoms to treat only the ions that contribute to the spectrum formation. At most, we include H i, He i– ii, C ii–v, N ii–vi, O ii–vi, and Fe ii–viii.
 |
Fig. 4 Ejecta properties computed by heracles for model r1w6 (strong wind mass loss rate of 10-2 M⊙ yr-1) at 0.5, 2, and 8 d after the start of the heracles simulation. Compared to model r1w1, the ejecta is more decelerated by the dense wind (the maximum ejecta velocity levels off at ~7000 km s-1 compared to 11 000 km s-1), more radiation energy gets trapped within the optically thick wind leading to a delayed but longer lived shock breakout signal and a much more massive cold-dense-shell forms (containing the swept up wind material). All these properties produce unambiguous radiative signatures. |
 |
Fig. 5 Ejecta properties computed by heracles for model r1w1h (model with a weak wind but an extended atmospheric scale height) at 1, 2, and 8 d after the start of the heracles simulation. Compared to model r1w6, the shock is not as strongly decelerated by the atmosphere (which has a steep density profile) and the photosphere remains close to the fast-moving ejecta, inhibiting the formation of a long-lived shock breakout signal. |
4. Results from radiation-hydrodynamic simulations with HERACLES
4.1. Dynamical evolution for representative models of the sample
The dynamical evolution obtained in all heracles simulations is qualitatively similar, but variations in wind mass loss rate and atmospheric scale height introduce important quantitative differences. We describe in some detail below the cases of a weak wind (model r1w1; Fig. 3), a strong wind (model r1w6; Fig. 4), and an extended atmospheric scale height (model r1w1h; Fig. 5). In this section, times are given with respect to the start of the heracles simulation (about 104 s before shock breakout), unless stated otherwise.
Figure 3 shows snapshots at 0.17, 1, and 2 d after the start of the heracles simulation (the shock crosses R⋆ at ~0.1 d). As the shock approaches R⋆, a radiative precursor forms that ionizes the atmosphere and the base of wind. This shifts the photosphere outward, beyond the R⋆ of the mesa model, at a density of about 10-12 g cm-3. This implies that shock breakout actually occurs in regions of the star not covered by the mesa model. This arises because the mesa model has a cold optically thin atmosphere. The radiative precursor heats, ionizes, and accelerates the material that it crosses on a light travel time. The strong radiative flux and energy accelerate both the ejecta and the wind. The ejecta reaches its asymptotic kinetic energy of 1.34 × 1051 erg at 10–15 d. The acceleration timescale depends on ejecta depth. The fastest material reaches 11 500 km s-1 at 0.5 d only (bottom row panels of Fig. A.1), while most of the H-rich ejecta regions are within a few per cent of their asymptotic velocity at 5 d. The deep ejecta layers take much longer because of the reverse shock and slower expansion; the initial radius of the corresponding shells remains a sizable fraction of the current shell radius for longer. Because of the interaction with the low-density wind, the outer ejecta velocity, where it is maximum, is reduced by only ~2% between 0.5 d and 15 d later.
The dynamical evolution is much different if the wind mass loss rate is large. Figure 4 shows snapshots at 0.5, 2, and 8 d after the start of the heracles simulation. As the shock overtakes R⋆, the atmosphere and the wind get progressively ionized. The opacity in the Lyman continuum is initially large (cold wind), so the heating occurs partially by absorption of lower energy photons because they have a greater mean free path. The photosphere progresses outward in the dense wind until ~1d and settles at ~4 × 1014 cm (four times further out at 1 d than in model r1w1). It takes nearly a week for the shock to reach this radius. During that time, energy from the shock is deposited in the wind (which is now optically-thick) and escapes on a diffusion timescale. As previously, the wind is accelerated by the radiation that crosses it, while the ejecta is both accelerated by radiation-pressure gradients and decelerated by the wind. The maximum ejecta velocity is in this case only 7200 km s-1 at 15 d, hence 30% less than in model r1w1 at the same time. The asymptotic kinetic energy is 1.32 × 1051 erg, hence 2 × 1049 erg lower than in the weak-wind model r1w1. This excess energy boosts the SN luminosity over the first week of evolution in the same proportion (see below). The drop in kinetic energy therefore arises because the wind is of sufficiently low density that the shock energy can be sapped by radiative losses.
Varying the wind mass loss rate between 10-6 and 10-2 M⊙ yr-1 or varying the extent of the high wind density region (model r1w5r) produce similar properties that are intermediate between those of models r1w1 and r1w6 (Fig. A.1).
Figure 5 shows snapshots at 1, 2, and 8 d after the start of the heracles simulation for model r1w1h. Increasing the atmospheric scale height enhances the mass exterior to R⋆ but yields properties that are quantitatively different from enhancing the wind density. Indeed, a greater scale height extends the star but the bulk of the atmosphere mass resides in high density layers close to R⋆, so the diffusion time through the atmosphere remains small. Consequently, there is no extended shock breakout signal like in the high mass loss rate model r1w6 and the photosphere after shock breakout remains closer to the fast-moving ejecta layers (rather than within the slowly moving wind such as in model r1w6). The additional mass in the atmosphere leads to maximum velocities that are 1000 km s-1 smaller than in model r1w1. The interaction of the ejecta with the atmosphere/wind (whose mass outside of R⋆ is ~0.16 M⊙) leads to the extraction of 2 × 1049 erg compared to 7 × 1048 erg in model r1w1 (Table 1). As for model r1w6, this energy is primarily radiated, but with a very different power profile, as we discuss in the next section.
 |
Fig. 6 Bolometric light curves computed with heracles for our full set of models. Times are given since the first signal detection at the outer boundary. The time resolution in the heracles simulation is always less than a minute and it is less than a second around the phase of shock breakout. The insets show the same quantity but zooming on the earliest times, concomitant with shock breakout. Progenitors with a larger radius or with a denser atmosphere/wind (here confined to within 5−10 R⋆) have a longer shock breakout signal and an enhanced luminosity at early times powered by the interaction with the atmosphere/wind. |
4.2. Bolometric, far-ultraviolet, ultraviolet, and optical light curves
Figure 6 shows the bolometric light curves for the models computed with heracles (see previous section, Fig. 1, and Table 1 for a summary of initial properties and results). The bolometric luminosity is evaluated at the outer boundary from the sum of the fluxes in each group. Because of the time delay for the radiation to reach the outer boundary at Rmax = 1.5 × 1015 cm, we shift all light curves in time so that the time origin corresponds to the first rise (at Rmax) to a luminosity of 5 × 108 L⊙. Because of optical depth effects, this time differs between models.
4.2.1. Sensivity to the wind mass loss rate
Models with increasing wind mass loss rates and the same atmospheric scale height (r1w[1−6] and r1w5r) have a longer rise time (from 0.03 to 1.72 d), a longer shock breakout signal duration (from about an hour in model r1w1 up to a week in model r1w6, although in the latter the high-brightness phase after breakout includes both the precursor radiation and the leakage of shock-deposited energy in the wind), and a smaller bolometric maximum (from a maximum of 7.4 × 1044 erg s-1 in model r1w1 down to 5.2 × 1043 erg s-1 in model r1w6). Light-travel time effects, which spread the shock breakout signal over R⋆/c, only matter for the weak-wind models. For dense winds, the intrinsic duration of the shock breakout signal exceeds R⋆/c. This lengthening of the shock breakout signal is related to the increasing photon diffusion time through the optically thick atmosphere/wind region. We find that the time-integrated bolometric luminosity over the first 15 days of evolution increases from 7.26 × 1048 erg in the weak wind model r1w1 to 2.02 × 1049 erg in the strong wind model r1w6. The time integrated bolometric luminosity is in all cases equal within a few percent to the change in the total energy (the sum of the kinetic, radiative, and thermal contributions) on the grid. Variations in 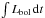 thus reflect energy extraction from the ejecta as it interacts with the wind. Hence, if a dense wind is present, there is both a spread of the shock breakout signal by diffusion through the wind and a boost to the radiative flux from the interaction.
thus reflect energy extraction from the ejecta as it interacts with the wind. Hence, if a dense wind is present, there is both a spread of the shock breakout signal by diffusion through the wind and a boost to the radiative flux from the interaction.
 |
Fig. 7 Far-UV, UV, and optical light curve computed with heracles for models r1w1, r1w1h, r1w5r, and r1w6. In practice, we show the evolution of the luminosity in the energy group number 8 (far-UV), the luminosity from energy groups 6 and 7 between the Lyman and the Balmer edges (UV), and the luminosity from energy groups 4 and 5 between the Balmer and the Paschen edges (optical). Up to one day after the far-UV burst, the bulk of the energy is emitted blueward of the Lyman edge but progressively shifts to the UV until it falls mostly in the optical after about 10 d. Models with a higher mass loss rate (right column) have a broader and redder shock breakout signal. |
The presence of a dense wind leaves unambiguous signatures on the bolometric light curve. In model r1w6 there is a sudden drop in bolometric luminosity at one week, which coincides with the epoch when the interaction with the dense parts of the wind ceases. When the interaction with the dense wind is over in r1w3/r1w4/r1w5r/r1w6 at 5−10 d, the light curve agrees very closely with the weak-wind cases r1w1-r1w2. A short-lived super-wind phase with a mass loss rate greater than a few 10-4 M⊙ yr-1 prior to core collapse should therefore leave an imprint on the bolometric light curve at early times (see also Moriya et al. 2011). If RSG stars have a super-wind phase before core collapse, one should expect a diversity of early-time light curve properties in a large sample of SNe II-P with such breaks occurring at different epochs and with different magnitudes.
4.2.2. Sensivity to the progenitor radius
In model r2w1, the progenitor star at death is more than twice as large. The rise time to bolometric maximum and the shock breakout signal are three times longer than in model r1w1, while the bolometric maximum is about the same (Table 1). The differences are caused by the increased light travel time across the progenitor star.
4.2.3. Sensivity to atmospheric scale height
Models with an extended atmospheric scale height (r1w1h and r1w5h) show a very different behavior from the weak-wind model r1w1. While both the rise time to maximum and the duration of the maximum phase are short, the bolometric luminosity is significantly higher for 10−15 d. The higher density in the atmosphere (but close to R⋆) leads to a strong interaction. Energy is deposited in this outer region of moderate optical depth (i.e., ~5000; see Table 1) and released in the form of radiation for 15 d. The time-integrated bolometric luminosity is 2.06−2.15 × 1049 erg and is comparable to that of model r1w6, but here the distribution of material in the atmosphere is much more confined. In this case, there is no break in the light curve. Compared to model r1w1h, the model r1w5h has a smaller density scale height but a greater density at large distances, producing a longer precursor and a smaller luminosity boost to later times.
4.2.4. Wavelength dependence of the shock breakout signal and observability
The complex morphology of bolometric light curves shown in Fig. 6 appears differently in selected spectral bands. Figure 7 shows the far-UV, UV, and optical light curves from the heracles simulations of models r1w1, r1w5r, r1w1h, and r1w6. If the atmosphere/wind has a negligible mass/extent, a clear burst of radiation is seen simultaneously in the Lyman, Balmer, and Paschen continua (top row of Fig. 7). However, in the presence of a dense/extended atmosphere/wind, optical photons emerge earlier and more progressively than in the Balmer/Lyman continuum. While a clear burst may occur in the far-UV, the optical signal shows a much slower rise with a smaller discontinuity; low-cadence observations may still capture a burst, but this is due to a lack of resolution. The multi-group approach in heracles captures this effect, which arises because the opacity for Lyman-continuum photons is orders of magnitude larger than for optical photons.
 |
Fig. 8 UVW2, B, and R band light curves obtained with cmfgen for models r1w1, r1w1h, r1w4, r1w5h, r1w5r, r1w6, and r2w1. The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). The variations in atmosphere/wind density have considerable impact on the early-time light curves, generally reducing the rise times and potentially introducing breaks in the light curves (e.g., model r1w6). |
For a blackbody at a temperature T the peak of the spectral energy distribution occurs at ~2900 /T4 Å, where T4 = T/ 104 K. Because of the high temperatures in the spectrum formation region (roughly between optical depths 0.1 and 10; see Fig. A.1), the bulk of the flux falls in the Lyman continuum for a few days, then in the Balmer continuum up to about 10 d, and in the optical at later times (this evolution is model dependent). The diversity of atmosphere/wind properties causes a large scatter in this evolution in our set of models. For example, in the strong wind case (model r1w6), the radiation energy from shock breakout Esbo does not immediately escape but instead gets trapped within a large volume ΔV bounded by (roughly) R⋆ and the photospheric radius at about 5×1014 cm. The larger this volume ΔV, the lower the representative radiation temperature Trad because 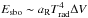 (aR is the radiation constant). In model r1w6, the far-UV flux is much weaker and the UV flux is boosted relative to model r1w1.
(aR is the radiation constant). In model r1w6, the far-UV flux is much weaker and the UV flux is boosted relative to model r1w1.
It is clear from Fig. 7 that the detection of shock breakout is very difficult in the optical, although not impossible (Garnavich et al. 2016). The challenge is both the brightness of the burst in the corresponding spectral range, but also the way the brightness changes with time. Garnavich et al. (2016) have reported the very weak and short-lived bump (<1 h) in the optical light curve of KSN 2011d. We do not actually obtain this bump in our heracles simulations, perhaps because of numerical diffusion and accuracy; the optical flux is one part in 105 of the far-UV/UV flux. Hunting for shock breakout in the UV or the far-UV, where the jump in flux is orders of magnitude greater, is obviously more suitable (Cenko et al. 2017).
 |
Fig. 9 Multi-band UV and optical light curves for the weak-wind model r1w1 (left), the strong wind model r1w5r (center), and the model with an extended scale height r1w1h (right). The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). Models r1w5r and r1w1h both show much shorter rise times in most/all bands than the weak-wind model r1w1. |
 |
Fig. 10 Same as Fig. 9, but now showing multi-epoch optical spectra. We show the rectified flux Fλ/Fc, where Fc is the continuum flux (each ordinate tick mark is separated by 1). The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). All three models show narrow line profiles at the earliest times, but only the models with a dense atmosphere/wind retain this property, for a duration that depends on the density and extent of this external material and the SN shock speed. When spectral lines are primarily electron-scattering broadened, the peak emission is centered on the line rest wavelength. When spectral lines are primarily Doppler broadened, the peak emission is blueshifted, which can compromise a robust identification or lead to an erroneous measure of the redshift if the blueshift is ignored, as in Gezari et al. (2009). |
 |
Fig. 11 Comparison of the multi-epoch spectra of SN 2013fs at early times with the spectra for models r1w5h (top) and r1w5r (bottom). All spectra have been scaled and shifted; the ith spectrum is normalized to its maximum value within the wavelength range displayed, and then shifted by a constant equal to i × 0.25. There is one ordinate tick mark every 0.5. The observations were corrected for redshift but not for reddening. These two models roughly encompass the properties of SN 2013fs with small offsets in the persistence of some lines (e.g., Ovi 3811–3834 Å). See Sect. 5.2 for discussion. |
5. Results from non-LTE steady-state radiative transfer simulations with CMFGEN
For a selection of heracles simulations, we compute cmfgen models that solve for the non-LTE properties of the gas as well as the radiation field; models r1w2 and r1w3 are omitted because they are intermediate cases of adjacent models r1w1 and r1w4. We assume steady state in cmfgen but time dependence is accounted for in heracles. The flux computed in cmfgen at a given time corresponds to a later time in the heracles simulation, by at most 0.5 d. This inconsistency does not affect the relative spectral evolution computed by cmfgen. The bolometric luminosity computed by cmfgen (see Fig. B.1 in the appendix) agrees to within 10−20% with that computed by heracles (modulo the 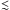 0.5 d shift mentioned above). For each snapshot treated, we also find that the cmfgen results for the electron density and optical depth are within a few per cent of those computed by heracles.
0.5 d shift mentioned above). For each snapshot treated, we also find that the cmfgen results for the electron density and optical depth are within a few per cent of those computed by heracles.
5.1. Multi-band light curves
Figure 8 shows the light curves in UVW2 (Swift filter), B, and R (absolute magnitudes) for our cmfgen simulations. A qualitatively similar evolution is obtained for other UV and optical bands. We find that the brightness increases initially to reach a peak within a maximum of 6 d in UVW2 , from 4−8 d in U, 5−10 d in B, 6 to >15 d in V, and 5 to >15 d in R.
In the weak-wind models r1w1 and r2w1, there is a discontinuity at the earliest times in all three filters. This discontinuity corresponds to the shock breakout signal. The optical brightness jump in model r2w1 is greater than in the corresponding heracles model because in this study cmfgen assumes steady state and therefore ignores light-travel time effects, while heracles is time dependent and accounts for time delays (spreading the breakout signal over R⋆/c). In other models, the extended, dense atmosphere wind spreads that signal (computed by heracles or by cmfgen) and no sharp discontinuity is seen.
In the case of a weak wind, the photometric evolution reflects the combined effects of expansion, which increases the size of the emitting surface, and cooling, which shifts the peak of the spectral energy distribution to longer wavelengths. For a given model, the peak brightness occurs earlier in bluer bands. In a given band, the peak brightness occurs earlier for a more compact progenitor star (compare models r1w1 and r2w1). Models with increasing wind mass loss rates exhibit a brightness boost in all bands from the stronger interaction, but with an obvious break in models r1w4, r1w5r, and r1w6 when that interaction ceases or when the atmosphere/wind has been completely swept up so that it no longer introduces an optical-depth effect.
Apart from model r2w1, all models have the same explosion energy and ejecta mass, so the presence of a dense atmosphere/wind alone can introduce significant UV-optical light curve variations at early times, up to 1−2 mag for this set of models, and displace the times of maximum by more than a week. Once interaction is weak in all models (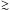 10 d), the magnitude scatter in a given optical band is
10 d), the magnitude scatter in a given optical band is 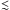 0.2 mag, but remains very large in the UV; if we exclude the strong wind model r1w6 and the model from a bigger star r2w1, the scatter is only 0.6 mag at 15 d.
0.2 mag, but remains very large in the UV; if we exclude the strong wind model r1w6 and the model from a bigger star r2w1, the scatter is only 0.6 mag at 15 d.
Models with strong wind mass loss exhibit a break in all UV/optical bands (as we obtain in the heracles light curves; Fig. 6). This is not a generic property of SNe II light curves, but this jump could be turned into a more progressive decline using a slowly declining mass loss rate (i.e., from >10-4 M⊙ yr-1down to 10-6 M⊙ yr-1; see Fig. 1). In contrast, no break is seen in the models with an extended atmospheric scale height and the rise time to maximum in optical bands is brought to earlier times in better agreement with observations (González-Gaitán et al. 2015).
5.2. Models of the spectral evolution
In this section, we discuss the spectral evolution up to 15 d after shock breakout for three representative models of atmosphere/wind configurations: 1) weak wind (model r1w1; top panel of Fig. 10); 2) strong wind (model r1w5r; middle panel of Fig. 10); 3) extended atmospheric scale height (model r1w1h; bottom panel of Fig. 10). The corresponding multi-band light curves are shown for completeness in Fig. 9. In the appendix, we show the complete set of spectral calculations for all models (Figs. C.1–C.7).
In all cases, the evolution of the spectrum over that timespan reflects the change in ejecta properties in the spectrum formation region. The gas temperature drops from ~105 down to ~104 K; this affects the ionization and hence the sources of opacity/emissivity, which in turn impact the colors and the lines produced. The ejecta and some of the wind material accelerate, while some ejecta deceleration takes place if the wind is very dense; this modulates the Doppler broadening of line profiles. The frequency redistribution by electron scattering ebbs as the atmosphere/wind optical depth drops. In nearly all cases, at least once the spectra show the lines associated with H i 4340 Å, 4862 Å, 6562 Å, He i 5875 Å, 6678 Å, He ii 4686 Å, 4860 Å, 5411 Å, 6562 Å, C iv 5801–5812 Å, 7110 Å, N iv 4057 Å, 7122 Å, Nv 4610 Å, Ov 5597 Å, and Ovi 3811–3834 Å. The spectral evolution is extremely rapid in our models (as observed, e.g., in SN 2013fs; Yaron et al. 2017), so that some lines/ions may only be present for a few hours. What differs between models is the duration over which these lines are seen and their morphologies. The critical element is whether line broadening is dominated by non-coherent scattering with thermal electrons, which produces symmetric lines centered at the rest wavelength, or by large bulk motions, which produce asymmetric lines with a blueshifted peak emission (see Sect. 6.2 and Fig. 15 of Dessart et al. 2009).
For the weak wind case (top panel of Fig. 10), the first spectrum, at the time of shock breakout, shows narrow lines with electron-scattering wings (He ii 4686 Å). At 1.6 h, the spectrum then shows Doppler-broadened lines of Ovi, Nv, and He ii, all with a marked blueshift in peak emission. At 5.6 h, Ovi has disappeared and we see lines of Nv, He ii, and Ov. At 13.6 h, Ov has disappeared and we see lines of N iv, Nv, He ii, and C iv. As the temperature continues to drop, the ionization decreases, the spectrum is less and less blue, and we eventually see the typical Type II-P SN spectrum with lines of H i and He i. Because of optical depth and occultation effects, all lines have a blueshifted peak emission (Dessart & Hillier 2005b; Anderson et al. 2014), except at the first epoch. A blueshifted line emission peak is unambiguous evidence that the line is not primarily broadened by non-coherent electron scattering, which instead tends to cause a symmetric (narrow) profile.
In contrast, for a stronger wind case (model r1w5r; middle panel of Fig. 10; the strong wind case model r1w6 is shown in Fig. C.6), the spectrum exhibits narrow and symmetric emission profiles typical of Type IIn SNe for up to 1 d. At 4.0 h, we see the same lines as in the weak wind case but the lines, which show no absorption component, are now centered on the rest wavelength. Lines form in the slow moving (or weakly accelerating wind) and are affected by frequency redistribution by thermal electrons. At 12.0 h, the ionization has dropped (Ovi has disappeared and Ov is present) but the narrow emission features are still present. After 1 d, there is only weak evidence for the reprocessing of photons by the atmosphere/wind. Its optical depth is too small to produce strong electron-scattering wings, although we do see a very narrow emission in He ii for up to 2 d. The spectrum starts to show P-Cygni profiles with a broad blueshifted absorption and a very weak emission. At this time, the spectrum forms in the dense shell of swept-up atmosphere/wind material. The lack of an emission component in line profiles is caused by the steeply declining density profile within that dense shell. Such properties and evolution are reminiscent of SN 1998S (Dessart et al. 2016).
 |
Fig. 12 Comparison between the optical flux (relative to the flux at 13 d) from our heracles simulations, accounting for the flux between the Balmer and Paschen edges, and the observations of KSN 2011a (left), KSN 2011d (middle; Garnavich et al. 2016) and SN 2006bp (right; Quimby et al. 2007). The time origin is conveniently adjusted to correspond to the rise of the optical flux. A better match to the light curves is obtained for models with a dense/confined atmosphere/wind. None of our models match the fast rise of KSN 2011a. |
For the model r1w1h with an extended atmospheric scale height (bottom panel of Fig. 10), despite the large amount of atmospheric material (more than ten times as much as in model r1w5r), the signatures of interaction (i.e., narrow symmetric lines) are present only in the first spectrum, which coincides with the time of shock breakout. Only He ii 4686 Å shows this morphology. The spectral evolution proceeds as in model r1w1, although emission profiles are much stronger because the density does not fall as steeply as in model r1w1. The biggest difference between model r1w1h and model r1w1 is not spectroscopic but bolometric and photometric, with model r1w1h showing a much more extended phase of high luminosity and an earlier time of maximum in all UV/optical bands (Figs. 6–8).
All models are shown in the appendix with properties that vary somewhat from the above. For example, in the strong wind cases r1w4 and r1w6, the ionization seen in the spectra at all epochs is much lower than in other models with a more confined and tenuous atmosphere/wind. One signature of this is the absence of Ov and Ovi lines in model r1w6. In model r1w4, Ovi is also absent but Ov is present. In model r1w5r, the progenitor environment is dense but less extended. Consequently, the atmosphere/wind temperature reaches much higher temperatures and the spectral lines identified are similar to those in the weak wind model r1w1. In other words, the extent, mass, and density of the atmosphere and wind has a strong influence on the ionization in the spectrum formation region, which complements what can be inferred from the line profile morphology.
While we do not have a model that fits all multi-epoch spectra of SN 2013fs, our set of models shows a good correspondence at selected epochs for a sample of features. For example, model r1w5h follows closely the ionization seen in SN 2013fs (top panel of Fig. 11), while model r1w5r shows a line profile morphology that evolves closely to that seen in SN 2013fs (bottom panel of Fig. 11). Building a full progenitor/explosion/interaction model for any observed SN is obviously a challenge. The model presented in Yaron et al. (2017) fits the observation better, but it does so at one epoch only, has no hydrodynamical consistency, and imposes radiative equilibrium. So, our approach lacks the flexibility needed to achieve a good fit; this would require hundreds of simulations. But our approach has physical consistency so that a grid of models, as presented here, can cover the broad parameter space in which a given SN resides and identify the basic trends.
6. Comparison to other observations
Figure 12 shows a comparison of optical light curves from our heracles simulations, accounting for the flux between the Balmer and Paschen edges, with the observations of KSN 2011a and KSN 2011d (Garnavich et al. 2016), and SN 2006bp (Quimby et al. 2007). Our explosion models from a big star (r2w1) and/or weak winds rise too slowly in the optical. Models accounting for an extended dense wind produce a flux excess in the optical light curve that is not observed. The best match to the KSN 2011d and SN 2006bp is for models with an extended scale height or with a dense wind confined to the surface of the star (model r1w5r)6. None of our models, even with interaction, match the fast rise of KSN 2011a.
Our results are somewhat in tension with Garnavich et al. (2016), who find a good match for KSN 2011d for a RSG with a weak wind or no wind and a radius of 490 R⊙. For KSN 2011a, they argue for wind interaction and/or a compact RSG progenitor with a radius of 280 R⊙. Their inferences are based on the semi-analytical modeling of Rabinak & Waxman (2011), who assume that the progenitor density profile is 1 /r1.5. This density profile corresponds to the deep convective envelope, not the outer layers in which the SN spectrum forms for a week, so this may be the origin of the difference in our results. It still remains very surprising that a RSG could radiate in the optical at 1 d as much as ~50% of the flux that it radiates at 10–15 d. This is the case for SN 1987A, but KSN 2011a does not have a Type II-pec light curve morphology. Optical spectra for this SN would probably have helped understanding this very fast optical rise.
The KSN 2011d observation of Garnavich et al. (2016) also reveals an initial short and weak optical burst of <1 h. As discussed earlier, our heracles simulation do not show such a sharp feature in the optical light curve, probably because of an accuracy issue (numerical diffusion). The cmfgen simulations for model r2w1 show a sharp and small optical burst but this is most likely because of the neglect of time delays. However, in the case of KSN 2011d, the observation of this bump suggests that the RSG progenitor was not surrounded by an extended and dense wind.
In addition, the earliest time spectra of SN 2006bp do not exhibit narrow line profiles with extended symmetric wings. Instead, SN 2006bp shows P-Cygni profiles with a blueshifted emission peak (e.g., He ii 4686 Å, C iv 5808 Å, and Hα) together with a narrow component at the corresponding rest wavelength (Quimby et al. 2007). The strong blueshifted emission is clear evidence that if present at the corresponding epoch, the atmosphere/wind material is already optically thin; otherwise line emission would peak at the rest wavelength and electron-scattering wings would be seen.
In model r1w1, the spectra at 4.9 and 11.9 d show a small dip in the Hα emission component caused by He i 6678 Å, but absent in Type II SN spectra observed at corresponding epochs. This is an another discrepancy, which adds to the discrepant optical light curve rise of model r1w1 with observations of SNe 2006bp and KSN2011d, which do not show signatures of interaction. This may suggest that even standard Type II SNe require a RSG progenitor structure with a dense inner-wind/atmosphere. The feature is nonetheless somewhat ambiguous because of its weakness – our model spectra have a great S/N ratio, while standard observations of much lower S/N and spectral resolution may struggle to reveal such a weak feature.
7. Conclusions
We have used 1-D Eulerian multi-group radiation hydrodynamics and 1-D non-LTE radiative transfer modeling to characterize the bolometric, photometric, and spectroscopic signatures of RSG explosions embedded in an atmosphere/wind of modest extent (within ~10 R⋆) and mass (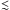 10-1 M⊙). Our work is conceptually analogous to the studies of Moriya et al. (2011) and Morozova et al. (2017) but includes the computation of multi-epoch spectra as a post-treatment of multi-group radiation hydrodynamics. Our initial ejecta/atmosphere/wind structures also extend to low density (and large radii), which ensures the proper computation of the shock breakout and the associated burst of radiation. For the spectral calculations, we work from physical models of the explosion/interaction and make allowance for the non-monotonicity of the velocity field, neither of which were treated in Yaron et al. (2017). The numerical approach is similar to a recent study of SN 1998S (Dessart et al. 2016). Our simulations are 1D and therefore do not predict the disruption of the cold dense shell that forms from the swept-up atmosphere/wind material. We also adopt a spherically symmetric density distribution for this external material initially, although there is ample evidence that RSG environments are structured and complex.
10-1 M⊙). Our work is conceptually analogous to the studies of Moriya et al. (2011) and Morozova et al. (2017) but includes the computation of multi-epoch spectra as a post-treatment of multi-group radiation hydrodynamics. Our initial ejecta/atmosphere/wind structures also extend to low density (and large radii), which ensures the proper computation of the shock breakout and the associated burst of radiation. For the spectral calculations, we work from physical models of the explosion/interaction and make allowance for the non-monotonicity of the velocity field, neither of which were treated in Yaron et al. (2017). The numerical approach is similar to a recent study of SN 1998S (Dessart et al. 2016). Our simulations are 1D and therefore do not predict the disruption of the cold dense shell that forms from the swept-up atmosphere/wind material. We also adopt a spherically symmetric density distribution for this external material initially, although there is ample evidence that RSG environments are structured and complex.
In the case of a weak progenitor wind (model r1w1), the model spectra show a blue nearly featureless spectrum for about a week with lines of He ii, C iv, Nv, Ov, and Ovi that may be present for no more than a few hours. As time passes, the temperature and ionization decrease and eventually H i and He i lines appear, producing a spectrum that is analogous to those of standard SNe II-P. In the absence of interaction, all lines form in the fast expanding ejecta and exhibit a strong peak blueshift at all times. Photometrically, this model shows a rise time in the B band of about 10 d.
In the case of a strong progenitor wind (up to a maximum of 10-2 M⊙ yr-1 in model r1w6), the spectral and photometric evolution during the first 15 d are very different. As long as the spectrum forms in the slow (unshocked) and optically thick wind, the lines exhibit a narrow emission peak with symmetric wings in place of a blueshifted Doppler-broadened emission peak. The dense wind material is eventually swept up into a dense shell. When the spectrum forms in that shell, the profiles start exhibiting a blueshifted and broad absorption with weak or no emission. Eventually, the photosphere recedes through this shell and the spectrum then resembles a more typical SN II spectrum with P-Cygni profile associated with H i and He i lines. Photometrically, the shock breakout in the progenitor environment is fainter and longer, except if the wind material is massive enough to allow the extraction of ejecta kinetic energy. In our simulations, we find that the time-integrated luminosity over the first 10−15 d can be boosted by a factor of a few.
The greater the luminosity boost from the ejecta/wind interaction, the greater the ejecta deceleration. In our strong-wind model r1w6, the maximum velocity is only ~7000 km s-1 at 10 d, compared to ~11 000 km s-1 in our weak-wind model r1w1. This implies narrower (Doppler-broadened) line profiles for the SN. In model r1w6, no line shows absorption/emission at 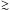 7000km s-1. The greater the wind mass loss rate, the greater the reduction. Because this deceleration does not affect the inner ejecta, the ejecta interaction with a dense wind should produce SNe that have narrower lines at early-time and normal line widths at later times. Faran et al. (2014) report that faster-declining Type II SNe indeed have narrower line profiles early on, but also broader line profiles at late times, which suggests ejecta/wind interaction alone may not explain fast-declining Type II. This needs to be considered when assessing the suitability of ejecta/wind interaction to explain SNe II-L (Morozova et al. 2017).
7000km s-1. The greater the wind mass loss rate, the greater the reduction. Because this deceleration does not affect the inner ejecta, the ejecta interaction with a dense wind should produce SNe that have narrower lines at early-time and normal line widths at later times. Faran et al. (2014) report that faster-declining Type II SNe indeed have narrower line profiles early on, but also broader line profiles at late times, which suggests ejecta/wind interaction alone may not explain fast-declining Type II. This needs to be considered when assessing the suitability of ejecta/wind interaction to explain SNe II-L (Morozova et al. 2017).
Early interaction with a dense wind reduces the rise time in optical bands and may help reduce the discrepancies with the observations (González-Gaitán et al. 2015). The early-time light curve depends, however, on the properties of the atmosphere/wind (i.e., the atmospheric scale height and the wind density/extent). We find that when the interaction with a dense wind (with Ṁ< 10-2 M⊙ yr-1) ebbs, the multi-band light curves show a break that is not obviously seen in Type II SN observations. A second issue with a strong wind is that they should come with a variety of strength in nature, and therefore the observations should reveal a wide range of early-time light curve properties, with breaks occurring at different epochs, which is a function of the extent of the high density wind.
We also investigated configurations in which the RSG atmosphere has a larger scale height. The corresponding change in density profile brings important differences. The bolometric and multi-band light curves no longer show a break, the rise times are very short, the bolometric luminosity may be boosted for 15 d, all of which seem to be in agreement with the observations (González-Gaitán et al. 2015). This stems from the strong interaction with the dense material at the base of the atmosphere. Its optical depth is large but not as large as the underlying ejecta so that the extra shock deposited energy can be released progressively over 15 d. The spectral signatures of atmosphere/wind interaction are short lived. The extra energy in this configuration produces blue colors for longer.
 |
Fig. 13 Left: evolution of the local radiative luminosity (top) and velocity (bottom) for the SN 2013fs model of Morozova et al. (2017, MPV). Right: same as left, but now for model r1w6 characterized by a dense wind (but about 50 times less dense). The filled circle is the location of the photosphere at each epoch. In all panels, the same set of epochs is shown (from 0.17 until 3.83 d after the start of the simulation). In model r1w6, the luminosity maximum occurs well below the photosphere and the slow material in between is at the origin of the narrow line profile cores with extended wings. In the configuration of MPV, this buffer of slow material is absent, there is no radiative precursor, and the event shows broad lines with blueshifted emission peaks immediately after shock breakout. The model of MPV, despite the interaction, therefore does not look like a SN IIn and does not match the earliest spectra of SN 2013fs. |
We find that all our simulations, irrespective of wind density, exhibit narrow line profiles at the earliest times. These narrow spectral signatures last as long the shock is embedded within some optically thick, slow-moving material. If the wind is tenuous, this region is the atmosphere of the RSG. If the wind is dense, this region is the wind itself. Ignoring material acceleration, these narrow line profiles last for the duration of the shock breakout (i.e., until the shock overtakes the photosphere).
Our results reproduce some of the characteristic properties observed in SN 2013fs (Yaron et al. 2017). For about a week, SN 2013fs shows a blue and nearly featureless spectrum. Up until <2 d, the SN exhibits lines from He ii, Nv, Ov, and Ovi with a narrow and symmetric profile. Subsequently, the SN exhibits a blue nearly featureless spectrum with narrow and weak emission line peaks that lack broad wings. This property implies a low electron scattering optical depth at 5 d; the dense external material is overtaken by ~2 d. Our model r1w5r is reminiscent of these properties with a pre-SN mass loss rate of 5 × 10-3 M⊙ yr-1 extending out to about 2 × 1014 cm. These values are consistent with those inferred by Yaron et al. (2017), although observations strongly suggest that the dense wind does not extend to a radius of 1015 cm; it should be no more than about 2 × 1014 cm, hence only a few stellar radii. Our interpretation of the origin of this external material is, however, completely different.
The term flash ionization used to explain the early-time properties (Khazov et al. 2016) is somewhat misleading. The shock breakout radiation is indeed characterized by very high temperatures and a huge ionizing flux, which promptly ionizes all the H and He in the RSG environment. However, in RSG explosions the photospheric temperature and ionizing flux remain large for at least a week. The recombination timescale at the photospheric densities relevant here are on the order of minutes. Hence, the large ionization inferred from spectra stems from the sustained UV flux and large temperatures in the spectrum formation region and not exclusively from a flash associated with shock breakout.
The mechanism at the origin of this external material, which is dense and contiguous to the stellar surface, is unclear. Drawing an analogy from the very massive star eruptions at the origin of superluminous SNe of Type IIn (see, e.g., Smith et al. 2007), one may wonder whether RSG may undergo a super-wind phase in the final stages of their evolution. Various mechanisms involving fluid instabilities, nuclear burning, or pulsations have been proposed (Heger et al. 1997; Shiode & Quataert 2014; Smith & Arnett 2014; Yoon & Cantiello 2010; Woosley & Heger 2015).
Morozova et al. (2017) proposed a model with a strong pre-SN wind mass loss rate of 0.15–1.5 M⊙ yr-1 out to a radius of 1900 R⊙ to explain the observations of SN 2013fs. Such a mass loss rate implies densities on the order of 10-10 g cm-3. When the SN shock enters this wind, there is in fact no precursor because the photon mean free path is too small. In that case, the shock breaks out when it reaches 1900 R⊙ (i.e., their adopted wind merely extends the star) and there is no lengthening of the shock-breakout signal. Because of this, this model cannot produce the IIn signatures seen for 2 d in SN 2013fs. The IIn signatures can only form if there is radiation leakage from the shock into the slow-moving atmosphere/wind above, and this cannot occur if its density is too high7. We have performed an heracles simulation using the initial conditions for SN 2013fs proposed by Morozova et al. and we illustrate the results together with those of model r1w6 in Fig. 13. In the MPV simulation, the photosphere (filled dot) always resides in the fast-moving ejecta after shock breakout – there is no reprocessing by a slow-moving dense wind. Hence, the model of MPV is unable to reproduce the early-time spectra of SN 2013fs. In contrast, in model r1w6, the photosphere is well above the embedded shock for a few days after breakout (from within the star) so that photons emitted at the shock are reprocessed by the slow-moving optically thick wind.
While we were finalizing this work, Moriya et al. (2017) published a study of the effect of the RSG wind velocity profile on the SN light curve. Accounting for the slow wind acceleration from the stellar surface yields a much larger wind density for a given mass loss rate. It is then possible to reproduce the early-time observations of SN 2013fs with a much smaller mass loss rate of about 10-3 M⊙ yr-1, which still remains well above the typical values inferred for observed RSG stars. However, this result, and that of Morozova et al. (2017), rest upon the assumption of a steady-state flow, for which there is no observational evidence.
In reality, the observations of SN 2013fs only provide a constraint on the mass and extent of the external material (~0.01 M⊙ spread over ~2 × 1014 cm) . There is no observational constraint on the velocity profile and in particular, whether this material is static or if it is part of an outflow. These are speculations. There may, however, be a simpler explanation for the observations of SN 2013fs, which has to do with the standard properties of RSG atmospheres, and may therefore apply with different magnitudes in all Type II SNe. Stellar evolution models of RSG stars set the photosphere at a density of about 10-9 g cm-3. This photospheric density is very high for such a large radius because of the low surface temperature, making the contribution of electron scattering to the opacity very small. In contrast, the base of a typical RSG wind is at a density of 10-14 g cm-3 (e.g., Betelgeuse has an inferred wind mass loss rate of about 3 × 10-6 M⊙ yr-1; Harper et al. 2001). This represents a drop in density by 5 orders of magnitude. At the surface of the mesa model, the density scale height is about 0.01 R⋆. Extrapolated down to 10-14 g cm-3, the base of the wind would be ~60 R⊙ above R⋆, hence at about 1.1 R⋆. Observations of RSG atmospheres suggest that the wind is actually launched from further out. The direct environment of Betelgeuse has been spatially resolved with adaptive optics or interferometry. Kervella et al. (2011) report on the detection of emission in the near-infrared (NIR) out to large distances (up to 10 R⋆), with the presence of inhomogeneities (surface brightness variations) or clumps. Ohnaka et al. (2011) discussed the dynamics of this inhomogeneous atmosphere and reported on the presence of upflows and downflows at the 10 km s-1 level out to several R⋆. Similar conclusions are reached by Josselin & Plez (2007). These observations suggest that the wind is driven from larger radii and implies that there is an extended intermediate region where material moves up and down on a timescale of a year and is fed somehow from R⋆, perhaps by pulsations or convective motions. The observations of SN 2013fs may suggest that this buffer region of a few R⋆ may actually contain 0.01–0.1 M⊙ of material. This material is optically thin to electron scattering in the RSG star, but becomes optically thick when the shock breaks out. Such a small mass is then sufficiently optically thick to give rise to the narrow symmetric line profiles observed in SN 2013fs at  2 d.
2 d.
Hence, rather than a super wind, the environment inferred from the observations of some Type II SNe at early times may simply correspond to the cocoon of material that is observed around RSG stars such as Betelgeuse. The shock is simply breaking out into the RSG atmosphere.
Here, we limit the “unambiguous” signature of interaction to the presence of electron-scattering broadened, symmetric, line profiles with a narrow core. In nature, interaction may occur over a much longer time and may be ubiquitous amongst Type II SNe owing to the large mass loss rates of their progenitor massive stars. In contrast, electron-scattering broadened, symmetric, line profiles with a narrow core are observed only rarely, and for a relatively short time, in core-collapse SNe.
Using more groups would make the simulation more costly and would not alter the fundamental results discussed here. At present, most simulations in the community are limited to gray transport. Our eight groups are positioned to capture the relevant photoionization edges; the absorptive opacity varies very smoothly between these edges.
The major drawback is not the neglect of the very small ionization/excitation energy. Rather, the main limitation in radiation-hydrodynamics simulations is the treatment of the gas in LTE at τ~< 20 since the temperature and ionization are influenced by both time dependence and non-LTE effects (Utrobin & Chugai 2005; Dessart & Hillier 2008), while the color temperature is influenced by electron scattering and line blanketing (Eastman et al. 1996; Dessart & Hillier 2005a).
These heracles optical light curves reflect closely the R-band light curve properties obtained with cmfgen (see Fig. 8).
Acknowledgments
L.D. thanks ESO-Vitacura for their hospitality. This work used computing resources of the mesocenter SIGAMM, hosted by the Observatoire de la Côte d’Azur, Nice, France.
References
- Anderson, J. P., Dessart, L., Gutierrez, C. P., et al. 2014, MNRAS, 441, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, D., Meakin, C., & Young, P. A. 2010, ApJ, 710, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Bellm, E. C., Gal-Yam, A., et al. 2017, in AAS Meeting Abstracts, 229, 328.04 [Google Scholar]
- Chugai, N. N. 2001, MNRAS, 326, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, S. M., Chatzopoulos, E., Arnett, W. D., & Timmes, F. X. 2015, ApJ, 808, L21 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2005a, A&A, 439, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2005b, A&A, 437, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2008, MNRAS, 383, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Gezari, S., Basa, S., & Matheson, T. 2009, MNRAS, 394, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Waldman, R., & Livne, E. 2013, MNRAS, 433, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Audit, E., & Hillier, D. J. 2015, MNRAS, 449, 4304 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Audit, E., Livne, E., & Waldman, R. 2016, MNRAS, 458, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, R. G., Schmidt, B. P., & Kirshner, R. 1996, ApJ, 466, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, S. W., & Arnett, W. D. 1977, ApJS, 33, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Faran, T., Poznanski, D., Filippenko, A. V., et al. 2014, MNRAS, 445, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Fassia, A., Meikle, W. P. S., Vacca, W. D., et al. 2000, MNRAS, 318, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Fassia, A., Meikle, W. P. S., Chugai, N., et al. 2001, MNRAS, 325, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Förster, F., Maureira, J. C., San Martín, J., et al. 2016, ApJ, 832, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., Ergon, M., Challis, P. J., et al. 2014, ApJ, 797, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., Arcavi, I., Ofek, E. O., et al. 2014, Nature, 509, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Garnavich, P. M., Tucker, B. E., Rest, A., et al. 2016, ApJ, 820, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Halpern, J. P., Grupe, D., et al. 2009, ApJ, 690, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Jones, D. O., Sanders, N. E., et al. 2015, ApJ, 804, 28 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Audit, E., & Huynh, P. 2007, A&A, 464, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Gaitán, S., Tominaga, N., Molina, J., et al. 2015, MNRAS, 451, 2212 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., & Vink, J. S. 2016, MNRAS, 455, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Grassberg, E. K., Imshennik, V. S., & Nadyozhin, D. K. 1971, Astrophys. Space Sci., 10, 28 [Google Scholar]
- Groh, J. H. 2014, A&A, 572, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harper, G. M., Brown, A., & Lim, J. 2001, ApJ, 551, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Jeannin, L., Langer, N., & Baraffe, I. 1997, A&A, 327, 224 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Dessart, L. 2012, MNRAS, 424, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Josselin, E., & Plez, B. 2007, A&A, 469, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Verhoelst, T., Ridgway, S. T., et al. 2009, A&A, 504, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Perrin, G., Chiavassa, A., et al. 2011, A&A, 531, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Lagadec, E., Montargès, M., et al. 2016, A&A, 585, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khazov, D., Yaron, O., Gal-Yam, A., et al. 2016, ApJ, 818, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Barth, A. J., & Matheson, T. 2000, ApJ, 536, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T., Tominaga, N., Blinnikov, S. I., Baklanov, P. V., & Sorokina, E. I. 2011, MNRAS, 415, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Yoon, S.-C., Gräfener, G., & Blinnikov, S. I. 2017, MNRAS, 469, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Morozova, V., Piro, A. L., & Valenti, S. 2017, ApJ, 838, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, B., Viallet, M., Heger, A., & Janka, H.-T. 2016, ApJ, 833, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Ohnaka, K., Weigelt, G., Millour, F., et al. 2011, A&A, 529, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Quimby, R. M., Wheeler, J. C., Höflich, P., et al. 2007, ApJ, 666, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinak, I., & Waxman, E. 2011, ApJ, 728, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, E. M. 1990, MNRAS, 244, 269 [NASA ADS] [Google Scholar]
- Shiode, J. H., & Quataert, E. 2014, ApJ, 780, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Shivvers, I., Groh, J. H., Mauerhan, J. C., et al. 2015, ApJ, 806, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., & Arnett, W. D. 2014, ApJ, 785, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Foley, R. J., et al. 2007, ApJ, 666, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Filippenko, A. V., & Chornock, R. 2011, MNRAS, 412, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Tominaga, N., Morokuma, T., et al. 2016, ApJ, 819, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2005, A&A, 441, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Dyk, S. D., Li, W., & Filippenko, A. V. 2003a, PASP, 115, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Li, W., & Filippenko, A. V. 2003b, PASP, 115, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Vaytet, N. M. H., Audit, E., Dubroca, B., & Delahaye, F. 2011, JQSRT, 112, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Vlasis, A., Dessart, L., & Audit, E. 2016, MNRAS, 458, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2015, ApJ, 810, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., Perley, D. A., Gal-Yam, A., et al. 2017, Nature Physics, 13, 510 [CrossRef] [Google Scholar]
- Yoon, S.-C., & Cantiello, M. 2010, ApJ, 717, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, T., Wang, X., Wu, C., et al. 2012, AJ, 144, 131 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Dynamical evolution from the HERACLES simulations
 |
Fig. A.1 Evolution of some ejecta properties computed by heracles for our set of models. In the top row, we show the velocity (left) and the radius (right) at an optical depth of 2/3 (solid line) and 10 (dashed line). In the middle row, we show the gas temperature at an optical depth of 2/3 (left) and 10 (right). In the bottom row, the show the evolution of the maximum velocity on the grid (left) and of the total energy on the grid (kinetic: solid line; radiation: dashed line). |
Appendix B: Bolometric light curves from CMFGEN
 |
Fig. B.1 Bolometric light curves obtained with cmfgen for models r1w1, r1w4, r1w1h, r1w5h, r1w5r, r1w6, and r2w1. The time origin corresponds to shock breakout. The cmfgen models are computed by adopting the radius, velocity, density, and gas temperature from the heracles simulations at each epoch. The luminosity offset between the heracles and cmfgen simulations is about 10–20%, and the resulting light curves are very similar (compare with Fig. 6). There is a conceptual difference between the two codes since heracles takes explicit account of time dependence, while cmfgen computes the spectrum in steady state but adopting the time-dependent structure from heracles. heracles treats the gas in LTE while cmfgen uses a non-LTE approach. |
Appendix C: Montage of CMFGEN spectra for all epochs and for all models
 |
Fig. C.1 Montage of spectra for model r1w1 shown at all epochs computed. The time origin corresponds to shock breakout. The spectra are rectified and shifted by one ordinate unit. |
All Tables
All Figures
 |
Fig. 1 Initial density structure used in heracles for models r1w1, r1w2, r1w3, r1w4, r1w1h, r1w5h, r1w5r, r1w6, and r2w1. Model m15mlt3 (r1) is used for the ejecta of model r1w[1–6][h,r] and model m15mlt1 (r2) for the r2w1, taken at a few hours before shock breakout (Dessart et al. 2013). The atmosphere/wind density is built using a variety of wind mass loss rates and atmospheric scale heights. All models transition to a wind mass loss rate of 10-6 M⊙ yr-1 beyond 2−5 × 1014 cm (≡ 5−10 R⋆). (See Sect. 3 and Table 1 for details.) |
| In the text | |
 |
Fig. 2 Initial structure used in heracles for model r1w6. The time is a few hours before shock breakout; the prior evolution of the shock through the stellar interior was computed with v1d (Dessart et al. 2013). |
| In the text | |
 |
Fig. 3 Ejecta properties computed by heracles for model r1w1 (weak wind mass loss rate of 10-6 M⊙ yr-1) at 0.17, 1, and 2 d after the start of the heracles simulation. The black dot in each of the middle panels corresponds to the electron-scattering photosphere. In the optical-depth panel, the colored numbers correspond to each energy group, ordered from low frequency (group 1 covers the far-IR) to high frequency (group 8 covers the Lyman continuum). The thick black line corresponds to the electron-scattering optical depth. Through this early evolution, we can see the ejecta accelerate, the wind acceleration by the SN radiation, the propagation of the radiation burst that coincided with shock breakout (at ~0.1 d), the heating and rapid ionization of the wind, and the establishment of radiative equilibrium in the optically thin regions at 2 d. |
| In the text | |
 |
Fig. 4 Ejecta properties computed by heracles for model r1w6 (strong wind mass loss rate of 10-2 M⊙ yr-1) at 0.5, 2, and 8 d after the start of the heracles simulation. Compared to model r1w1, the ejecta is more decelerated by the dense wind (the maximum ejecta velocity levels off at ~7000 km s-1 compared to 11 000 km s-1), more radiation energy gets trapped within the optically thick wind leading to a delayed but longer lived shock breakout signal and a much more massive cold-dense-shell forms (containing the swept up wind material). All these properties produce unambiguous radiative signatures. |
| In the text | |
 |
Fig. 5 Ejecta properties computed by heracles for model r1w1h (model with a weak wind but an extended atmospheric scale height) at 1, 2, and 8 d after the start of the heracles simulation. Compared to model r1w6, the shock is not as strongly decelerated by the atmosphere (which has a steep density profile) and the photosphere remains close to the fast-moving ejecta, inhibiting the formation of a long-lived shock breakout signal. |
| In the text | |
 |
Fig. 6 Bolometric light curves computed with heracles for our full set of models. Times are given since the first signal detection at the outer boundary. The time resolution in the heracles simulation is always less than a minute and it is less than a second around the phase of shock breakout. The insets show the same quantity but zooming on the earliest times, concomitant with shock breakout. Progenitors with a larger radius or with a denser atmosphere/wind (here confined to within 5−10 R⋆) have a longer shock breakout signal and an enhanced luminosity at early times powered by the interaction with the atmosphere/wind. |
| In the text | |
 |
Fig. 7 Far-UV, UV, and optical light curve computed with heracles for models r1w1, r1w1h, r1w5r, and r1w6. In practice, we show the evolution of the luminosity in the energy group number 8 (far-UV), the luminosity from energy groups 6 and 7 between the Lyman and the Balmer edges (UV), and the luminosity from energy groups 4 and 5 between the Balmer and the Paschen edges (optical). Up to one day after the far-UV burst, the bulk of the energy is emitted blueward of the Lyman edge but progressively shifts to the UV until it falls mostly in the optical after about 10 d. Models with a higher mass loss rate (right column) have a broader and redder shock breakout signal. |
| In the text | |
 |
Fig. 8 UVW2, B, and R band light curves obtained with cmfgen for models r1w1, r1w1h, r1w4, r1w5h, r1w5r, r1w6, and r2w1. The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). The variations in atmosphere/wind density have considerable impact on the early-time light curves, generally reducing the rise times and potentially introducing breaks in the light curves (e.g., model r1w6). |
| In the text | |
 |
Fig. 9 Multi-band UV and optical light curves for the weak-wind model r1w1 (left), the strong wind model r1w5r (center), and the model with an extended scale height r1w1h (right). The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). Models r1w5r and r1w1h both show much shorter rise times in most/all bands than the weak-wind model r1w1. |
| In the text | |
 |
Fig. 10 Same as Fig. 9, but now showing multi-epoch optical spectra. We show the rectified flux Fλ/Fc, where Fc is the continuum flux (each ordinate tick mark is separated by 1). The time origin corresponds to shock breakout (taken to be when the luminosity at the photosphere rises to 1042 erg s-1). All three models show narrow line profiles at the earliest times, but only the models with a dense atmosphere/wind retain this property, for a duration that depends on the density and extent of this external material and the SN shock speed. When spectral lines are primarily electron-scattering broadened, the peak emission is centered on the line rest wavelength. When spectral lines are primarily Doppler broadened, the peak emission is blueshifted, which can compromise a robust identification or lead to an erroneous measure of the redshift if the blueshift is ignored, as in Gezari et al. (2009). |
| In the text | |
 |
Fig. 11 Comparison of the multi-epoch spectra of SN 2013fs at early times with the spectra for models r1w5h (top) and r1w5r (bottom). All spectra have been scaled and shifted; the ith spectrum is normalized to its maximum value within the wavelength range displayed, and then shifted by a constant equal to i × 0.25. There is one ordinate tick mark every 0.5. The observations were corrected for redshift but not for reddening. These two models roughly encompass the properties of SN 2013fs with small offsets in the persistence of some lines (e.g., Ovi 3811–3834 Å). See Sect. 5.2 for discussion. |
| In the text | |
 |
Fig. 12 Comparison between the optical flux (relative to the flux at 13 d) from our heracles simulations, accounting for the flux between the Balmer and Paschen edges, and the observations of KSN 2011a (left), KSN 2011d (middle; Garnavich et al. 2016) and SN 2006bp (right; Quimby et al. 2007). The time origin is conveniently adjusted to correspond to the rise of the optical flux. A better match to the light curves is obtained for models with a dense/confined atmosphere/wind. None of our models match the fast rise of KSN 2011a. |
| In the text | |
 |
Fig. 13 Left: evolution of the local radiative luminosity (top) and velocity (bottom) for the SN 2013fs model of Morozova et al. (2017, MPV). Right: same as left, but now for model r1w6 characterized by a dense wind (but about 50 times less dense). The filled circle is the location of the photosphere at each epoch. In all panels, the same set of epochs is shown (from 0.17 until 3.83 d after the start of the simulation). In model r1w6, the luminosity maximum occurs well below the photosphere and the slow material in between is at the origin of the narrow line profile cores with extended wings. In the configuration of MPV, this buffer of slow material is absent, there is no radiative precursor, and the event shows broad lines with blueshifted emission peaks immediately after shock breakout. The model of MPV, despite the interaction, therefore does not look like a SN IIn and does not match the earliest spectra of SN 2013fs. |
| In the text | |
 |
Fig. A.1 Evolution of some ejecta properties computed by heracles for our set of models. In the top row, we show the velocity (left) and the radius (right) at an optical depth of 2/3 (solid line) and 10 (dashed line). In the middle row, we show the gas temperature at an optical depth of 2/3 (left) and 10 (right). In the bottom row, the show the evolution of the maximum velocity on the grid (left) and of the total energy on the grid (kinetic: solid line; radiation: dashed line). |
| In the text | |
 |
Fig. B.1 Bolometric light curves obtained with cmfgen for models r1w1, r1w4, r1w1h, r1w5h, r1w5r, r1w6, and r2w1. The time origin corresponds to shock breakout. The cmfgen models are computed by adopting the radius, velocity, density, and gas temperature from the heracles simulations at each epoch. The luminosity offset between the heracles and cmfgen simulations is about 10–20%, and the resulting light curves are very similar (compare with Fig. 6). There is a conceptual difference between the two codes since heracles takes explicit account of time dependence, while cmfgen computes the spectrum in steady state but adopting the time-dependent structure from heracles. heracles treats the gas in LTE while cmfgen uses a non-LTE approach. |
| In the text | |
 |
Fig. C.1 Montage of spectra for model r1w1 shown at all epochs computed. The time origin corresponds to shock breakout. The spectra are rectified and shifted by one ordinate unit. |
| In the text | |
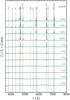 |
Fig. C.2 Same as Fig. C.1 but now for model r1w4. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.1 but now for model r1w1h. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.1 but now for model r1w5h. |
| In the text | |
 |
Fig. C.5 Same as Fig. C.1 but now for model r1w5r. |
| In the text | |
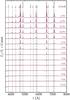 |
Fig. C.6 Same as Fig. C.1 but now for model r1w6. |
| In the text | |
 |
Fig. C.7 Same as Fig. C.1 but now for model r2w1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


