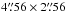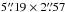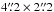| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201730703 | |
| Published online | 04 September 2017 | |
The extended molecular envelope of the asymptotic giant branch star π1 Gruis as seen by ALMA
I. Large-scale kinematic structure and CO excitation properties
1 Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
e-mail: lam.doan@physics.uu.se
2 Department of Earth and Space Sciences, Chalmers University of Technology, 43992 Onsala, Sweden
3 Department of Astrophysics, University of Vienna, Türkenschanzstr. 17, 1180 Vienna, Austria
4 South African Astronomical Observatory, PO Box 9, 7935 Observatory, South Africa
5 Astronomy Department, University of Cape Town, University of Cape Town, 7701 Rondebosch, South Africa
6 National Institute for Theoretical Physics, Private Bag X1, 7602 Matieland, South Africa
7 Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, Campus Plaine CP 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
8 European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
Received: 27 February 2017
Accepted: 19 May 2017
Context. The S-type asymptotic giant branch (AGB) star π1 Gru has a known companion at a separation of 2.̋7 (≈400 AU). Previous observations of the circumstellar envelope (CSE) show strong deviations from spherical symmetry. The envelope structure, including an equatorial torus and a fast bipolar outflow, is rarely seen in the AGB phase and is particularly unexpected in such a wide binary system. Therefore a second, closer companion has been suggested, but the evidence is not conclusive.
Aims. The aim is to make a 3D model of the CSE and to constrain the density and temperature distribution using new spatially resolved observations of the CO rotational lines.
Methods. We have observed the J = 3–2 line emission from 12CO and 13CO using the compact arrays of the Atacama Large Millimeter/submillimeter Array (ALMA). The new ALMA data, together with previously published 12CO J = 2–1 data from the Submillimeter Array (SMA), and the 12CO J = 5–4 and J = 9–8 lines observed with Herschel/Heterodyne Instrument for the Far-Infrared (HIFI), is modeled with the 3D non-LTE radiative transfer code SHAPEMOL.
Results. The data analysis clearly confirms the torus-bipolar structure. The 3D model of the CSE that satisfactorily reproduces the data consists of three kinematic components: a radially expanding torus with velocity slowly increasing from 8 to 13 km s-1 along the equator plane; a radially expanding component at the center with a constant velocity of 14 km s-1; and a fast, bipolar outflow with velocity proportionally increasing from 14 km s-1 at the base up to 100 km s-1 at the tip, following a linear radial dependence. The results are used to estimate an average mass-loss rate during the creation of the torus of 7.7 × 10-7 M⊙ yr-1. The total mass and linear momentum of the fast outflow are estimated at 7.3 × 10-4 M⊙ and 9.6 × 1037 g cm s-1, respectively. The momentum of the outflow is in excess (by a factor of about 20) of what could be generated by radiation pressure alone, in agreement with recent findings for more evolved sources. The best-fit model also suggests a 12CO/13CO abundance ratio of 50. Possible shaping scenarios for the gas envelope are discussed.
Key words: stars: AGB and post-AGB / stars: mass-loss / stars: individual:π1Gru / stars: general / radio lines: stars / binaries: general
© ESO, 2017
1. Introduction
Asymptotic giant branch (AGB) stars are believed to evolve from low- to intermediate-mass (0.8–8 M⊙) main sequence stars. The evolution of AGB stars is governed by the massive wind from the stellar surface (typical expansion velocity, vexp ~ 10 km s-1, and mass-loss rate, Ṁ∽ 5 × 10-7 M⊙ yr-1; e.g., Ramstedt et al. 2009), which creates an expanding circumstellar envelope (CSE) of molecular gas and dust already on the AGB. The physical processes behind the AGB-star wind are comparatively well understood and current radiation-hydrodynamical models reproduce observed properties well (Eriksson et al. 2014; Bladh et al. 2015). However, several important aspects still need to be investigated further, such as the wind evolution over time and the formation of complex large-scale structures, to establish the formation scenario for planetary nebulae (PNe).
Planetary nebulae are large, tenuous emission nebulae glowing at visible wavelengths through recombination and forbidden lines from ionized (atomic) gas. Expansion velocities of PNe are on average about a factor of two larger (~20 km s-1; Gesicki & Zijlstra 2000; Huggins et al. 2005) than typical AGB wind velocities, but more extreme velocities in excess of ~100 km s-1 are also found in post-AGB stars and PNe (e.g., Vlemmings et al. 2006; Clyne et al. 2015). Bujarrabal et al. (2001) studied the CO emission from 30 protoplanetary nebulae (P-PNe) and found that almost all of the sample sources have both a slowly expanding envelope (probably the remnant AGB wind) and fast (often bipolar) outflows. The momenta of the envelopes are consistent with a wind driven by radiation pressure on dust grains (as on the AGB), but an alternative mechanism is necessary to accelerate fast outflows. Imaging surveys of PNe (see, e.g., Sahai 2014, and references therein) show that less than 5% of PNe are round, as would be expected if they were the direct result of an isotropic wind, while a majority of the AGB envelopes seem to be spherically symmetric (Castro-Carrizo et al. 2010) on large scales. This further supports the idea that strong dynamical evolution takes place before AGB stars become PNe. While different shaping agents (binary interaction, large planets, and global magnetic fields) have been suggested (see Balick & Frank 2002), much work remains before the theoretical models can be confirmed observationally.
In this context, molecular line observations of transitional objects are extremely valuable since they trace the remnant material of the AGB wind and give kinematic information (e.g., Sánchez Contreras & Sahai 2012). The unsurpassed potential of the Atacama Large Millimeter/submillimeter Array (ALMA) to study these transitional objects has already been demonstrated with Early Science capabilities (Bujarrabal et al. 2013; Olofsson et al. 2015). To add to previous studies, we observed four binary stars on the AGB (R Aqr, Mira, W Aql, and π1 Gru) with ALMA to investigate the dependence of the circumstellar shaping and morphology on the AGB on the binary separation and wind properties. The observations of Mira (o Cet) already revealed how the massive AGB wind has been sculpted by the fast, thinner wind from the companion (Ramstedt et al. 2014), and in this paper, we present the initial results on the largest separation source of our sample, π1 Gru.
π1 Gru is an evolved, S-type AGB star (Van Eck et al. 1998a) at a distance of about 150 pc (Perryman et al. 1997) and log(L/L⊙) = 3.86 (Van Eck et al. 1998b). A fast bipolar molecular outflow was discovered by Sahai (1992) in 12CO J = 1–0 and 2–1 emission. Sahai (1992) also observed the 13CO J = 1–0 line emission and found a 12C/13C abundance ratio in the range 25–50. π1 Gru has a known G0V companion (Feast 1953; Ake & Johnson 1992) at 2.̋7 separation, but Sahai (1992) already mentioned that a closer unknown companion would be required to explain the observed morphology. The 12CO J = 2 − 1 emission was mapped by Knapp et al. (1999) and later by Chiu et al. (2006) using the SMA (with a synthesized beam of 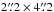 ). Chiu et al. (2006) built on the model by Knapp et al. (1999) and suggested that the star is surrounded by a thick, low-velocity (11 km s-1) expanding torus with a faster bipolar outflow that is oriented perpendicular to the torus; this torus is referred to as a flared disk, but we use torus throughout this paper, since the structure shows no sign of rotating. Herschel/PACS observations show a large arc, possibly a spiral arm, reaching out at ~40′′ to the east of the star (Mayer et al. 2014) and possibly shaped by the known 2.̋7 companion. Mayer et al. (2014) have also analyzed VLTI/MIDI and AMBER data, together with Hipparcos and Tycho observations to search for a closer companion. Although the second companion is not directly detected in the VLTI observations, they have found support for a closer companion (at 10–30 AU separation) from the combined analysis of the available data.
). Chiu et al. (2006) built on the model by Knapp et al. (1999) and suggested that the star is surrounded by a thick, low-velocity (11 km s-1) expanding torus with a faster bipolar outflow that is oriented perpendicular to the torus; this torus is referred to as a flared disk, but we use torus throughout this paper, since the structure shows no sign of rotating. Herschel/PACS observations show a large arc, possibly a spiral arm, reaching out at ~40′′ to the east of the star (Mayer et al. 2014) and possibly shaped by the known 2.̋7 companion. Mayer et al. (2014) have also analyzed VLTI/MIDI and AMBER data, together with Hipparcos and Tycho observations to search for a closer companion. Although the second companion is not directly detected in the VLTI observations, they have found support for a closer companion (at 10–30 AU separation) from the combined analysis of the available data.
We observed π1 Gru in 12CO and 13CO J = 3–2 with ALMA. In this paper we construct a 3D kinematic and radiative transfer model based on the ALMA Atacama Compact Array (ACA) and Total Power (TP) observations, together with the previously published 12CO J = 2–1 SMA observations from Chiu et al. (2006) via the publicly available radiative transfer code SHAPEMOL (Santander-García et al. 2015). We present the new ALMA observations and the previously published observations (SMA and Herschel/HIFI) in Sect. 2 and the ALMA and SMA observational results in Sect. 3. The radiative transfer modeling is described in Sect. 4 and the model results are given in Sect. 5. We give the Discussion and Summary in Sects. 6 and 7.
2. Observations
2.1. New CO radio line observations with ALMA
The 12CO and 13CO J = 3–2 emission was observed with the ALMA-ACA in 2013. The observations consist of a four-point mosaic. They were performed using four spectral windows with a width of 2 GHz each, centered on 331, 333, 343, and 345 GHz. The u − v coverage of an interferometer is always incomplete. Insufficient u − v coverage can cause artificial features when imaging. Observations with the ALMA-TP array was performed in cycle 2 (in 2015) to recover the most extended emission from the source and produce high fidelity images. This array included three 12m antennas, and the observations were performed in single-dish, on-the-fly mapping mode.
Summary of the interferometric observations and final image cubes.
We used the Common Astronomy Software Application (CASA) for calibration and imaging (McMullin et al. 2007). Firstly, the interferometric data was calibrated and preliminary imaged to combine with the TP images later on. Quasars J0006-0623 and J2235-4835 were used as bandpass and complex gain calibrators, respectively. Uranus was used for flux calibration. Because of the low signal-to-noise ratio of the 13CO J = 3–2 emission relative to 12CO J = 3–2, the 13CO J = 3–2 visibility data was imaged using natural weighting to improve the sensitivity. The spectral resolution was about 0.5 km s-1, but has been binned to 2 km s-1 for 12CO J = 3–2 and 3 km s-1 for 13CO J = 3–2 to improve the signal-to-noise ratio in the images cubes. The resulting line profiles with a recovered flux in the ALMA-ACA observation are discussed in Sect. 3.2.
Secondly, the TP observation calibration were carried out with quasars J2230-4416 for focusing, J2230-4416 for pointing, and both of these and π1 Gru for atmospheric calibration. The brightness of the TP observation was first given in main-beam brightness temperature scale (Tmb) and then converted to Jy beam-1. The conversion factors of the data from K to Jy beam-1 are 43.2 at 345 GHz and 45.0 at 330 GHz. The beam size of the TP observation is 19″ at 345 GHz and the rms noise level of the images is 0.6 Jy beam-1 for 12CO J = 3–2 and 0.58 Jy beam-1 for 13CO J = 3–2. The overall uncertainty of the TP calibration is about 5%.
The data was finally combined using CASA packages. Owing to the difference in spatial pixel sizes and spectral ranges between the TP map and the ALMA-ACA map, the TP map was first regridded to the coordinate system of the ALMA-ACA map. Then the ALMA-ACA data was re-imaged using the CLEAN package in an iterative procedure with a decreasing threshold parameter. In this procedure the ALMA-TP map was used as a model for initial cleaning. Finally, the ALMA-TP and ALMA-ACA images were combined via the FEATHER package. A summary of the observations and the final image cubes is given in Table 1.
 |
Fig. 1 Total flux of the 12CO J = 3–2 (left) and 13CO J = 3–2 (middle) emission from the ALMA-ACA data (red) and the combined (ACA+TP) data (black). The spectra were generated by convolving the images with the APEX beam (FWHM = 18″). The 12CO J = 3–2 spectrum (Ramstedt et al. 2006) from APEX (FWHM = 18″) is plotted for comparison. Owing to the artificial feature (explained in Sect. 3.2) in the blueshifted wing of the 13CO J = 3–2 line, the line profile of the combined data was only plotted from –35 km s-1. The 12CO J = 2–1 spectrum (right) from the SMA observation (Chiu et al. 2006) was generated by convolving the image with the SMA primary beam of 55″. |
2.2. Previously published CO radio line observations
SMA Observations: the 12CO J = 2–1 observation was performed in 2004 using the SMA with a 2 GHz bandwidth correlator and a 812.5 kHz channel separation over 256 channels. The source was observed with 28 baselines and the longest baseline was about 83 kλ. The calibrators were observed along with the target. The data has previously been published by Chiu et al. (2006).
In this study, the upper sideband data has been recalibrated and reimaged using CASA. The bandpass calibration was carried out using Uranus. The nearby quasar 2258-279 was set as the complex gain calibrator and absolute flux calibrator (instead of Uranus as in Chiu et al. 2006). We applied the Briggs weighting method for imaging and an active mode for cleaning the dirty maps in which the emitting region was carefully selected to avoid the strong noise speaks. This resulted in some differences in the line profile compared to that found in Chiu et al. (2006, see Sect. 3.2). The observations and the final image cube are summarized in Table 1.
Herschel/HIFI observations: the 12CO J = 5–4, 9–8, and 14–13 observations were part of the Herschel SUCCESS program (Teyssier et al. 2011; Danilovich et al. 2015) and observed with the onboard instrument HIFI (de Graauw et al. 2010). The signal-to-noise ratio of the 12CO J =14–13 line was about 2 to 3 and because of this high uncertainty we decided to omit this line from our analysis. The telescope beam sizes of 12CO J = 5–4 and 9–8 observations are 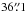 and
and 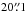 , respectively. The technical setup, data reduction, and line profiles were published in Danilovich et al. (2015). The line profiles were plotted in main beam temperature scale with a noise rms of 15 mK at a channel resolution of 3 km s-1. In this paper, we adopted the line profiles without any recalibration.
, respectively. The technical setup, data reduction, and line profiles were published in Danilovich et al. (2015). The line profiles were plotted in main beam temperature scale with a noise rms of 15 mK at a channel resolution of 3 km s-1. In this paper, we adopted the line profiles without any recalibration.
3. Observational results and discussion
3.1. The continuum flux
A single continuum source was detected from the line-free channels of the ALMA-ACA and SMA observations. Neither the known companion, nor a closer companion, such as that proposed by Mayer et al. (2014), would be resolved. The continuum flux densities are 32.7 ± 6 mJy at 230 GHz and 82.2 ± 4.7 mJy at 343 GHz. Assuming optically thick blackbody emission from a stellar photosphere with a temperature of 3000 K (Vanture & Wallerstein 2002; Abia & Wallerstein 1998) and a stellar radius of 2.2 × 1013 cm (Chiu et al. 2006), the flux densities would be 35 mJy and 78 mJy, respectively. The measured continuum flux is consistent with the thermal emission of the stellar photosphere. Since the stellar temperature, radius, and flux measurement are highly uncertain, it is not enough to determine whether there is a contribution from dust continuum emission.
3.2. Line profiles
Figure 1 (left and middle) shows the line profiles of the combined (ACA+TP) 12CO J = 3–2 and 13CO J = 3–2 data generated by integrating over a circular region with the width of the APEX beam (18″) centered on the stellar position. The 12CO J = 3–2 line profile from APEX (Ramstedt et al. 2006) is also plotted to evaluate the recovered flux in the combined ALMA data. A comparison shows that the ALMA-ACA observations recovered a fraction of less than 50% of the flux observed in the TP observation. The combined ALMA maps contain ∽90% of the flux observed by APEX in 2005, which is within the calibration uncertainties. The lower sideband containing the 13CO line was affected by the mirrored 12CO line from the upper sideband. This resulted in an artificial feature in the blueshifted wing of the 13CO J = 3–2 line profile. The line is therefore only plotted from –35 km s-1 in Fig. 1 (middle). The 12CO J = 2–1 emission observed with the SMA (Chiu et al. 2006), shown in Fig. 1 (right), is convolved with the SMA primary beam (FWHM of 55″).
 |
Fig. 2 Contour maps of the 12CO J = 3–2 emission from the combined ALMA data. Contour levels are at 3, 5, 9, 15, 20, 25, and 30σ (σ = 1.2 Jy beam-1 for the middle rows, derived from the plotted channels), and at 3, 5, 7, and 9σ (σ = 0.08 Jy beam-1 for the first and last rows, derived from the plotted channels). The synthesized beam size of |
 |
Fig. 3 Same as Fig. 2, for the 13CO J = 3–2 emission from the combined ALMA data. Contour levels are at 3, 5, 7, 9 15, and 20σ (σ = 0.055 Jy beam-1, derived from the full data set). The synthesized beam size of |
 |
Fig. 4 Same as Fig. 2, for the recalibrated and reimaged 12CO J = 2–1 emission from the SMA (Chiu et al. 2006). Contour levels are at 3, 5, 7, 9, 13, 15, and 20σ (σ = 0.3 Jy beam-1, derived from the full data set). The synthesized beam is shown in the lower left corner of the 0 km s-1 channel and is |
All emission lines (except the 13CO J = 3–2) show a double-horned profile with steep sides at intermediate velocity and extended wings. The double-horned core of the spectral line shows a slowly expanding component, while the high-velocity wings, reaching out to ±60 km s-1 relative to the systemic velocity, are indicative of an outflow that is much faster than a typical AGB wind. There is no sign of an asymmetry in the 12CO J = 3–2 data observed with the mosaic field ∽40″. Chiu et al. (2006) suggested that an over-resolved inhomogeneous structure caused the stronger peak at the blueshifted velocities in the 12CO J = 2–1 line profile from their analysis of the data. In contrast, the peak is seen on the redshifted side of both the line profile observed by Knapp et al. (1999) and the line profile from our recalibration of the data. This discrepancy may be due to the different calibration and data reduction strategy, as already mentioned in Sect. 2.2.
3.3. Images
12COJ = 3–2: the channel maps of the 12CO J = 3–2 emission from the combined data, shown in Fig. 2, were constructed by integrating over 2 km s-1 close to the systemic velocity (from –30 km s-1 to 8 km s-1) and over 4 km s-1 for the high velocities (from –62 km s-1 to –46 km s-1 and from 20 km s-1 to 36 km s-1) to increase the signal to noise of the high-velocity channels in which the emission is weaker.
The emission at the systemic velocity, VS = − 12 km s-1, shows what looks like an elongated torus along the east-west (EW) direction. The emission has a maximum close to the stellar position. When moving away from the systemic velocity, the size of the emitting region decreases. Also, the emission gradually moves from the south to the north from blue- to redshifted velocities. This spatial shift of the emission distribution at low relative velocities can be interpreted that the radially expanding torus is inclined relative to the line of sight.
The high-velocity channel maps are shown in the first and last rows of Fig. 2. In agreement with the 12CO J = 2–1 emission (Chiu et al. 2006), the north-south (NS) orientation of the higher velocity emission is opposite to that at lower velocities. Furthermore, the 12CO J = 3–2 emission seen in the channels from –58 to –46 km s-1 and 20 to 32 km s-1 shows an extended region with two separated parts. We propose that this bimodal distribution can be possibly interpreted as emission coming from the lobe walls of a bipolar outflow, while the –62 km s-1 and 36 km s-1 channels may show the lobe tips or lobe edges at the highest line-of-sight velocity of the bipolar outflow.
In Fig. 2, as well as in the position-velocity (PV) diagram in Fig. 5, the emission is divided into two components around –46 km s-1 and +20 km s-1. At blueshifted velocities, the southern component is just slightly north of the stellar position while the second, northern component is found approximately 5′′ to the north. Assuming that the velocity of the high-velocity outflow increases radially and the system is inclined relative to the line of sight, the gas moving along the edges of lobes have different line-of-sight velocities at the same distance from the equator. For example, the gas moving along the edge of the northern lobe facing the observer, has a higher line-of-sight velocity than the gas moving along the edge away from the observer at the same distance from the equator. This can explain the bimodal distribution seen at, for example –50 km s-1. At this velocity channel, the southern emission component would come from the closer lobe edge and the northern emission component would come from the more distant lobe edge, where the same line-of-sight velocity is reached further away from the equator of the system. The exact distribution of the emission as a function of velocity is an intricate function of the gas distribution, i.e., inclination and curvature of the high-velocity outflow and the clumpiness of the gas, and kinematics.
13COJ = 3–2: the J = 3–2 emission from the less abundant 13CO isotopologue was imaged by integrating over 3 km s-1 (Fig. 3). The emission is very weak compared to the 12CO emission and the gas is mostly concentrated and excited in the inner parts of the envelope. At the systemic velocity, the emission has two peaks on either side of the stellar position along the EW direction. Even if the data was convolved with an identical beam as the 12CO J = 3–2, the image would still have this distribution. Any emission is below the noise level at velocities beyond –25 km s-1 and 2 km s-1.
12COJ = 2–1: the channel maps from the rereduced 12CO J = 2–1 line emission are given in Fig. 4. As previously described (Chiu et al. 2006), the emission at the systemic velocity, VS = − 12 km s-1, shows a torus structure that is flared and elongated along the EW direction, similar to the 12CO J = 3–2 distribution. The slightly larger spatial size at each channel velocity compared to the J = 3–2 emission is caused by the lower minimum kinetic temperature required for the J = 2–1 excitation. Moreover, the emission has a two-peak (on either side of the stellar position) distribution that differs from the new 12CO J = 3–2 data. The gap between the two peaks has been attributed to a central cavity (Chiu et al. 2006), but that is not required to explain the new 12CO J = 3–2 data. The orientation of the synthesized beams (see Figs. 4 and 2) can contribute to the different distribution of the 12CO J = 2–1 and 12CO J = 3–2, but not fully explain the difference. This is discussed further in the following sections.
 |
Fig. 5 Position-velocity diagram for the 12CO J = 3–2 emission along a cut at a PA of 0° made by integrating over a 2 km s-1 velocity interval: low velocity and high signal-to-noise ratio at the middle panel with contour levels at 3, 5, 9, 15, 20, 30σ (σ = 1.2 Jy beam-1); high velocity and low signal-to-noise ratio at the left and right panels with contour levels at 3, 5, 9, 15, 20σ (σ = 0.06 Jy beam-1). The vertical and horizontal dashed lines show the systemic velocity (−12 km s-1) and the stellar position, respectively. |
3.4. Position-velocity diagrams
The PV diagrams of the 12CO J = 3–2 emission shown in Fig. 5 were made along a NS cut (one pixel wide at a PA of 0°) through the stellar position. A different correlation between the velocity vector field and the position vector is seen for the equatorial torus and the fast bipolar outflow, separately.
The NS PV 12CO J = 3–2 diagram is similar to that of 12CO J = 2–1 (see Chiu et al. 2006), but less extended in spatial offset than the 12CO J = 2–1 emission (as already seen in the channel maps). The emission at low relative velocity (plotted in the central plot of Fig. 5) is consistent with an expanding, inclined equatorial torus, extended to the north at redshifted velocity, and to the south at blueshifted velocity.
The emission at higher velocities originates from the fast outflow component (plotted in the far left and right plot of Fig. 5) and shows the opposite pattern: a redshifted velocity to the south and blueshifted velocity to the north. In this part of the figure, the position is directly proportional to the velocity, i.e., emission with higher velocity comes from a position further away from the center. The offset emission regions seen at blue- and redshifted velocities (with a Dec-offset beyond about ±5″) correspond to the bimodal distributions also seen in the channel maps in Fig. 2. We do not detect significant emission beyond –70 km s-1 in the blueshifted part and +40 km s-1 in the redshifted part. This corresponds to a maximum projected gas velocity of about 60 km s-1 in the CSE.
4. Circumstellar model
4.1. Geometry and velocity field
As mentioned above, Chiu et al. (2006) built on the flared-disk model to reproduce the low-velocity component seen in the 12CO J = 2–1 SMA maps, but they never attempted to model the fast component. In this study, we reconstructed the gas envelope using both a low-velocity torus and a fast bipolar outflow to study the full 3D morphology and kinematics of the system. The combined ALMA data are used as observational constraints, together with the previously published SMA data. The structure of the modeled gas envelope is schematically illustrated in Fig. 6. The modeled envelope was constructed as a system with the following three components:
-
(1)
A radially expanding torus in the shape of a flared disk with anopening angle of2ϕ0, an inner radius of d/ 2, and an outer radius of R1. The radius R1 is just the maximum radius used in the model computation. It does not necessarily represent a density-cutoff radius, i.e., the physical outer boundary of the torus; nebular layers beyond R1 do not contribute significantly to the observed emission for the density and temperature laws adopted in our model. The outer radius was constrained by the observed angular size at the central channel. The radial gas velocity inside the torus depends on the distance from the center and latitude above or below the equator,
![\begin{equation} \label{eq:eqq1} \centering v_{1}=\left[ v_{\rm{1a}}+v_{\rm{1b}} \frac{r}{R_{1}}\right]f_{\varphi}, \end{equation}](/articles/aa/full_html/2017/09/aa30703-17/aa30703-17-eq60.png) (1)where the constants v1a and v1b were chosen to produce line profiles with the same width as the line cores of the observational data and r is the radial distance from the center (
(1)where the constants v1a and v1b were chosen to produce line profiles with the same width as the line cores of the observational data and r is the radial distance from the center (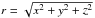 ). The fϕ factor increases linearly with latitude. It has the value of f0° = 1 at the equator and the values of f± ϕ0 at the top and bottom edges were determined by fitting the data.
). The fϕ factor increases linearly with latitude. It has the value of f0° = 1 at the equator and the values of f± ϕ0 at the top and bottom edges were determined by fitting the data. -
(2)
A central, radially expanding component originating at the center and placed inside the torus. The velocity is constant, v2. Its shape is cylindrical with diameter d and height h.
-
(3)
A faster bipolar outflow perpendicular to the torus extends from the central component. The lobes have a radially expanding velocity field linearly increasing with the distance from the equator,
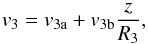 (2)where v3a and v3b were chosen so that the velocity increases from the central component velocity to the highest velocity inferred from the data and z is the vertical distance from the equator. The radius R3 is just the maximum radius used in the model computation. It is not the physical outer boundary of the outflow. The R3 value was poorly constrained by the observations because of the low signal-to-noise ratio at very high velocities and the dependence on the inclination of the system.
(2)where v3a and v3b were chosen so that the velocity increases from the central component velocity to the highest velocity inferred from the data and z is the vertical distance from the equator. The radius R3 is just the maximum radius used in the model computation. It is not the physical outer boundary of the outflow. The R3 value was poorly constrained by the observations because of the low signal-to-noise ratio at very high velocities and the dependence on the inclination of the system.
4.2. Density and temperature distribution
Some simplifying assumptions are necessary to limit the number of free parameters of the 3D model. The density distribution was chosen assuming the following hypothetical, but realistic, scenario for the shaping of the current CSE: the torus (1) is presumably formed in the earlier AGB phase. At some point, the bipolar outflow was triggered and the faster moving material has plowed through the polar regions giving rise to the central component (2), in which the current dynamics are the result of the interaction between the fast outflow and the slower AGB wind. Further out, the bipolar outflow (3) is the faster moving material that has escaped the AGB envelope. The gas density distribution of a spherically expanding AGB envelope created by a constant mass-loss rate, Ṁ, and expansion velocity, ve, decreases outward according to 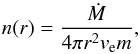 (3)where m is the particle mass. Since the gas velocity inside the torus depends on the radius according to Eq. (1), the H2 number density of the torus was set to be proportional to r-3,
(3)where m is the particle mass. Since the gas velocity inside the torus depends on the radius according to Eq. (1), the H2 number density of the torus was set to be proportional to r-3, ![\begin{equation} \label{eq:eqq4} \centering n_{1}(r,\varphi)=n_{\rm{1a}}\left[ \frac{r}{10^{15} \rm{~cm}}\right]^{-3} \frac{1}{f_{\varphi}}, \end{equation}](/articles/aa/full_html/2017/09/aa30703-17/aa30703-17-eq82.png) (4)where n1a is a scaling factor, r is the radial distance from the center, and the fϕ factor is due to the linear dependence of the torus velocity on the latitude (Eq. (1)). The constant velocity of the central component (2) motivates an r-2 dependence of the H2 number density,
(4)where n1a is a scaling factor, r is the radial distance from the center, and the fϕ factor is due to the linear dependence of the torus velocity on the latitude (Eq. (1)). The constant velocity of the central component (2) motivates an r-2 dependence of the H2 number density, ![\begin{equation} \label{eq:eqq5} \centering n_{2}(r)=n_{\rm{2a}}\left[ \frac{r}{10^{15}~ \rm{cm}}\right]^{-2}\cdot \end{equation}](/articles/aa/full_html/2017/09/aa30703-17/aa30703-17-eq86.png) (5)The scaling factors, n1a and n2a, were initially set using Eq. (3) with the mass-loss rate chosen as an average of previous results (1 × 10-6 M⊙ yr-1) and a constant expansion velocity (11 km s-1), but then varied to fit the data.
(5)The scaling factors, n1a and n2a, were initially set using Eq. (3) with the mass-loss rate chosen as an average of previous results (1 × 10-6 M⊙ yr-1) and a constant expansion velocity (11 km s-1), but then varied to fit the data.
For bipolar planetary nebulae, a velocity distribution that follows the Hubble law expansion is often found (Sánchez Contreras & Sahai 2004). Assuming that the velocity increases radially in the outflow component (3), the density was initially set as an inverse cubic function of the radius, ![\begin{equation} \label{eq:eqq6} \centering n_{3}(r)=n_{\rm{3a}}\left[ \frac{r}{10^{15}~ \rm{cm}}\right]^{-3+\alpha}\rm{,} \end{equation}](/articles/aa/full_html/2017/09/aa30703-17/aa30703-17-eq90.png) (6)and then both the scaling factor na3 and the exponent α were varied until the data could be reproduced at high velocities (see Sect. 5.2). The 12CO abundance (relative to H2) was assumed to be constant for all three components and a value of 6.5 × 10-4 (Knapp et al. 1999) was adopted. The 13CO abundance was changed to fit the 13CO J = 3–2 data once all the other parameters had been obtained from fitting the 12CO lines.
(6)and then both the scaling factor na3 and the exponent α were varied until the data could be reproduced at high velocities (see Sect. 5.2). The 12CO abundance (relative to H2) was assumed to be constant for all three components and a value of 6.5 × 10-4 (Knapp et al. 1999) was adopted. The 13CO abundance was changed to fit the 13CO J = 3–2 data once all the other parameters had been obtained from fitting the 12CO lines.
A description of the gas kinetic temperature as a function of radius in a spherical envelope was presented by Goldreich & Scoville (1976). Chiu et al. (2006) and Knapp et al. (1999) successfully applied this temperature distribution when they modeled the torus. A similar dependence on radius, ![\begin{equation} \label{eq:eqq7} \centering T=T_{0} \left[ \frac{r}{10^{15}~ \rm{cm}}\right] ^{-0.7+\beta} \rm{K}, \end{equation}](/articles/aa/full_html/2017/09/aa30703-17/aa30703-17-eq95.png) (7)was adopted for the whole envelope. The scaling factor, T0, was varied from 100 K to 500 K, while the exponent was slightly varied around –0.7 through the free parameter β.
(7)was adopted for the whole envelope. The scaling factor, T0, was varied from 100 K to 500 K, while the exponent was slightly varied around –0.7 through the free parameter β.
4.3. Radiative transfer modeling and imaging
In the radiative transfer model, the parameters introduced in Eqs. (1)–(2) and (4)–(7), together with the inclination angle of the torus relative to the line of sight, and the PA of the equator were varied until all the available spatially resolved data could be reproduced. The radiative transfer calculation was performed via SHAPE+SHAPEMOL (Steffen et al. 2011; Santander-García et al. 2015), which is a 3D modeling tool for complex gaseous structures. To solve the radiative transfer equations for 12CO and 13CO, the code uses tabulated absorption and emission coefficients that are appropriate for different geometries and kinematic, and calculates the non-LTE level populations via the large velocity gradient (LVG) approximation. We believe the LVG approximation is valid for π1 Gru because the expansion velocity is larger than the local line width (the thermal contribution is less than 1 km s-1) and owing to the large velocity gradient across the CSE. The output simultaneously depends on the gas density, kinetic temperature, velocity distribution, CO isotopologue abundance, and logarithmic velocity gradient ((dV/dr)(r/V)). A microturbulent velocity of 2 km s-1 (Chiu et al. 2006) was adopted. The calculation is conducted for the 17 lowest rotational transitions of the ground-vibrational state of both 12CO and 13CO, including collisions with H2 (see Santander-García et al. 2015, for details). The envelope was constructed of 1283 grid cells and rendered through a velocity interval of ±100 km s-1 around the systemic velocity. The velocity band is divided into 150 channels.
The comparison between the model and observations requires that the effects of the interferometer, for example, the missing u − v coverage, noise of the atmosphere, and electric systems, are included before imaging. Using the SIMOBSERVE task in CASA, we simulated the visibilities of the observation using the resulting brightness distribution from the radiative transfer calculation. The SMA and ALMA-ACA simulated data has the on-source duration and the antenna configurations of the original observations. The data was then imaged in the same way as the real observational data. The ALMA-TP simulation was performed inside SHAPE+SHAPEMOL by convolving the 3D model with the ALMA primary beam. The ALMA-ACA simulated images were finally combined with the ALMA-TP simulated images using the same procedure as for the real data.
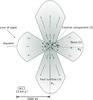 |
Fig. 6 Sketch illustrating the three components used to model the CSE of π1 Gru. |
 |
Fig. 7 Line profiles from the observations (black) and the model (red). The black dashed line in the upper right panel shows the observed profile multiplied by a factor of 2 to correct for the missing flux according to Chiu et al. (2006). |
 |
Fig. 8 Contour maps of the 12CO J = 3–2 emission from the model simulating the combined (ACA+TP) ALMA observation. The contour levels are the same as those of the observational result plotted in Fig. 2. |
 |
Fig. 9 Contour maps of the 12CO J = 2–1 emission from the model simulating the SMA observation. The contour levels are the same as those of the observational result plotted in Fig. 4. |
5. Modeling and interpretation
5.1. Finding the best-fit model
All free parameters were first adjusted to fit the 12CO J = 3–2 line emission. With the many adjustable parameters of the 3D model, the goodness of fit has to be evaluated by taking several different aspects into account. The velocity distribution and inclination angle of the torus were set to reproduce the observed line shapes and spatial distribution seen in the channel maps. The sizes of the different components were constrained by fitting the spatial extent seen in the channel maps (by eye) assuming a distance of 150 pc (Perryman et al. 1997). The density and temperature distribution were primarily chosen to fit of the strength of the emission in the 12CO J = 3–2 line. Those best values were applied to successfully reproduce the 12CO J = 2 − 1. Then the high-J transition lines 12CO J = 5–4 and J = 9–8 could be fitted by refining the temperature function since the line ratios are sensitive to the kinetic temperature. The 13CO J = 3–2 data was matched by only adjusting the 13CO/H2 fractional abundance. Some additional test models with different velocity fields, morphologies, and temperature distributions (see Appendix A) were considered to find the best-fit model. A chi-square measure was used to evaluate the goodness of the fit from the line profiles, 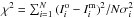 , where
, where 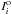 and
and 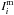 are the beam corrected flux of the observations and the model at channel i, respectively, N is the number of channels, and σ is the measurement uncertainty of the observed flux, assumed to be 20% on average.
are the beam corrected flux of the observations and the model at channel i, respectively, N is the number of channels, and σ is the measurement uncertainty of the observed flux, assumed to be 20% on average.
Input parameters for the best-fit model.
5.2. Best-fit model and comparison to previous results
The parameters of the best-fit model are given in Table 2. The outer radius (R1 = 3 × 1016 cm), and opening angle (ϕ0 = 25°) of the torus agree with the model by Chiu et al. (2006). The introduced central component is smaller (angular width ≈1.7′′) than the synthesized beam of the ALMA-ACA observation and does not affect the fit significantly. At a given radial distance, the gas velocity at the top and bottom edges of the torus is 2.5 times (fϕ0 = 2.5) higher than the gas velocity along the equator. An inverse cubic density law (i.e., α = 0) for the fast bipolar outflow resulted in images very similar to those observed, meaning that the best fit is achieved when the density distribution of the torus and the outflow have the same dependence on radius. Only the scaling factors of the density functions (Eqs. (4) and (6)) differ slightly. The best-fit model has a PA of 5° and the inclination of the torus relative to the line of sight is 40°, which agrees with what was found in previous studies (Chiu et al. 2006; Knapp et al. 1999). If the inclination is decreased (or increased) by more than 10° relative to the best-fit value, the model line profiles have a parabolic shape (or a U-shaped profile with a deep center) in contrast to observed data. If the PA is changed by more than 10°, the relative intensity of the line peaks is not reproduced.
The model shows that the temperature distribution suggested by Knapp et al. (1999) for the torus cannot be applied to reproduce the high-J transition lines as well. The temperature in our model is lower (T0 = 190 K instead of 300 K) and decreases outward more rapidly (β = − 0.15) than that found by Knapp et al. (1999). The model gives a value of 50 for the 12CO/13CO abundance ratio, which is in agreement with upper limit for π1 Gru derived by Sahai (1992), but is twice the median value of 25 found for S-type AGB stars (Ramstedt & Olofsson 2014).
The model line profiles are plotted (Fig. 7) together with the observed line profiles and overall they match the data very well. The SMA 12CO J = 2–1 observation only recovered less than 50% of the total flux as mentioned by Chiu et al. (2006). Therefore, in the very right panel of Fig. 7, the line intensity has been scaled by a factor of 2 to be able to compare the line shapes. This is only an approximation because the missing flux mainly comes from the extended parts of the envelope with higher velocity, whereas the flux of line core comes from the inner parts and would be better recovered. The peak intensity of the predicted 12CO J = 9–8 line is about 20% less than that from the observation. Our model cannot reproduce the different peak strengths seen in the 12CO J = 9–8 and the 13CO J = 3–2 line. This can be an indication that the LVG approximation does not perfectly apply to the torus where the velocity gradient is less steep than in the outflow.
The spatial distribution of the 12CO J = 3–2 and J = 2–1 is shown in the model channel maps in Figs. 8 and 9. At the systemic velocity, the model has successfully reproduced the two-peaked distribution seen in the 12CO J = 2–1 data without a cavity at the center and the central peak distribution seen in the 12CO J = 3–2 data. This means that the model without the central cavity can reproduce the data features. In general, the model images at each channel are very similar to the observations for low to intermediate velocities. The weak bimodal emission distribution at very high-velocity channels (Fig. 2) was not reproduced by our model. As suggested above, the emission could come from the gas at the edges of the two bipolar lobes, but it would depend on the detailed structure and temperature distribution of the outflow, and an exact fit was not attempted.
Figure 10 shows the line-of-sight optical depth (along the system equator at the systemic velocity) as a function of distance from the center for all three modeled lines. Since the emission is optically thin, the peak position of the optical depth indicates where the gas is maximally excited, and agrees with the positions of the emission peaks of the channel map at the systemic velocity (Fig. 4). The maximum optical depth of the 12CO J = 3–2 line occurs inside 5′′ and the corresponding two emission peaks are unresolved by the beam.
 |
Fig. 10 Line-of-sight optical depth, calculated from the model, along the equator at the line rest frequencies. The 13CO J = 3–2 optical depth was scaled by a factor of 30. |
5.3. Outflow linear momentum
The terminal gas velocity along the torus equator is about 13 km s-1. If this value is representative of the expansion velocity of the CSE before the formation of the outflow, this corresponds to an average mass-loss rate of about 7.7 × 10-7 M⊙ yr-1. This agrees with the value estimated by Chiu et al. (2006), and is almost half of that estimated in Knapp et al. (1999) when fitting the single-dish 12CO J = 2–1 emission. From the sizes of the structures and the expansion velocity distributions, the kinematic timescale of the torus and outflow is about 730 yr and 160 yr, respectively.
The bipolar outflow of the best-fit model suggested has a density distribution that is comparable to the torus at the same radial distance. The estimated total mass of the bipolar outflow is Moutflow = 7.3 × 10-4M⊙ when applying an average particle mass of 3 × 10-24 g and integrating the density distribution across the structure. The highest deprojected gas velocity is about 100 km s-1 corresponding to a Doppler shift velocity of about 60 km s-1 in the lines. This results in a linear momentum of the outflow, which is the total outflow mass multiplied by the outflow velocity integrated over the velocity distribution, of Poutflow = 9.6 × 1037 g cm s-1. If radiation pressure alone is responsible for lifting the outflow, this process would take about 3300 yr (calculated from Poutflow/(L/c)). This means that the radiation pressure alone would not be sufficient to drive the fast outflow with a kinematic timescale of 160 yr, which is in agreement with the findings for more evolved sources (e.g., Bujarrabal et al. 2001; Olofsson et al. 2015).
6. Discussion
6.1. Excitation properties
All line profiles in this work show a slowly expanding component at the line core and a high-velocity component at the wings. The less extended wings of the 12CO J = 5–4 and J = 9–8 line profiles indicate that the CO molecules are mostly excited to the high-J states in the central regions where the temperature and density are high enough. The minimum kinetic temperature (~250 K) of the 12CO J = 9–8 transition, needed for significant collisional excitation, is only reached in regions close to central star. The transition is mainly radiatively excited.
The differences in spatial distribution of the emission from the CO lines are also due to the different excitation requirements. The higher excitation temperature of the J = 3–2 transition than the J = 2–1 makes the emission more compact at every channel and particularly at the systemic velocity. Our model can reproduce the different apparent spatial distributions of the two 12CO lines, and the 13CO line, reasonably well without including a central cavity (as suggested by Chiu et al. 2006, from only having access to the 12CO J = 2–1 line). If the cavity actually exists, it must be smaller than the synthesized beam in the case of the 12CO J = 3–2 emission. The apparent shape is dependent on the observational setup, line excitation, and actual distribution of the gas, and shows that it is very important to perform detailed radiative transfer modeling before drawing conclusions about the physical distribution of the gas in these types of objects.
6.2. Envelope shaping mechanisms
The formation of the torus+outflow structure seen in π1 Gru, poses a challenge to the understanding of stellar evolution theory, as do the typical bipolar structures in PNe. The gravitational perturbation of the known companion of π1 Gru is not strong enough to concentrate material onto the orbital plane and form the torus (e.g., Mayer et al. 2014). Even if the orbit is extremely eccentric and the envelope could be compressed at the periastron passage, the timescale for the creation of the torus is too short for it to still be significantly affected. If the orbit is assumed circular, the period would be 6200 yr to be compared to the kinematic timescale of the torus on the order of 730 yr. Stellar wind models for AGB stars (assuming a dust-driven wind) typically show wind velocities less than 30 km s-1 (e.g., Eriksson et al. 2014; Bladh et al. 2015). For π1 Gru, the fast (≤100 km s-1) bipolar outflow has a linear momentum that is higher than the maximum value available from the radiation pressure of the star, which suggests that a different mechanism is required to drive the outflow.
The torus could be created if the star itself is rotating already on the AGB. Dorfi & Hoefner (1996) have shown that the effect of a slow rotation (the order of 2 km s-1), combined with the strong temperature and density dependence of the dust formation process in AGB stars, can lead to an enhanced equatorial mass loss and produce an elliptical envelope. By applying the wind compressed disk model to AGB stars, Ignace et al. (1996) showed that the coriolis effect, effective if the star is rotating fast enough, can produce a disk-like structure. A close companion or a binary merger can spin-up AGB stars to the rotation rate required for the wind-compressed disk to be formed. However, there is no evidence for rotation observed in π1 Gru, but a velocity below 2 km s-1 cannot be excluded. The gravitational effect of a close companion star, or a giant planet, can play an important role in the formation of a torus (Iben & Livio 1993).
Whether single stars can form bipolar morphologies was initially investigated in interacting wind models (see, e.g., Balick & Frank 2002, and references therein). In these models, a fast isotropic wind is launched inside a slowly expanding torus (without investigating the formation of the torus itself) with a density contrast between the pole and the equator. A hot bubble is created in the post-shock gas and the bubble expands at constant pressure. The expansion velocity of the bubble depends on the density distribution of the torus and varies inversely from the pole to the equator (e.g., Icke 1988). The very high gas velocity at the poles eventually launches the bipolar outflow. Wind-interaction models including detail hydrodynamics and microphysics (e.g., Frank & Mellema 1994) have confirmed the dependence of the shaping on the density distribution of the previously ejected gas envelope. A density contrast (between the torus equator and the pole) from 2 to 5 results in a fast bipolar outflow. A higher value results in a highly collimated outflow. Within the modeled torus, the best-fit model of π1 Gru has a density contrast of 2.5 between the equator and the edge at an angle of 25°. If a linear dependence with angle is assumed, the contrast between the equator and the pole is 6.4, which is a reasonable agreement between the results from the interacting wind models and the observed morphology.
The kinematic timescales for the torus and fast outflow in our model are similar to the typical values found for PPNe and PNe (Bujarrabal et al. 2001), showing the same circumstellar structures. The momentum excess (compared to what is available from radiation pressure alone) implies the need for an additional wind driver. Wind formation and the collimation of bipolar outflows have also been studied using magneto-hydrodynamics (MHD) models where the wind is driven by magnetic pressure (García-Segura et al. 1999, 2005). These models are successful in creating bipolar structures and highly collimated jets when the magnetic field is strong enough and the rotational velocity is sufficient. However, recent investigations combining the results of MHD and stellar evolution models, have shown that the rotational velocities retained at the end of the AGB are not sufficient to form bipolar PNe (García-Segura et al. 2016). Matt et al. (2000) used MHD models to show that a modest magnetic field (of order a few G at the surface, similar to what has been measured on some AGB stars; Lèbre et al. 2014) is sufficient to form a dense equatorial disk around an AGB star with a slow, massive wind. In combination with the interacting wind models described above, this gives another possible explanation for the observed morphology. Again, the origin of the magnetic field or the launching of the fast wind are not explained, but would require an extra source of angular momentum, e.g., a binary companion.
The suggested second companion remains to drive the formation of the observed morphology. If close enough, it could also accrete the wind through an accretion disk and possibly drive the fast outflow. The low velocity of the torus sets favorable conditions for wind Roche-lobe overflow (wRLOF; Mohamed & Podsiadlowski 2012), where a slowly expanding wind first fills the Roche lobe of the primary star (the AGB star) and then flows through the inner Lagrangian point onto the accretion disk of the companion. Models including the wRLOF scenario can produce substantial accretion rates also in larger separation binaries (e.g., Mira, R Scl, Ramstedt et al. 2014; Maercker et al. 2012), where traditional Bondi-Hoyle accretion models fail to reproduce the observations. The exact requirements to drive an outflow with the momentum observed in π1 Gru will be the subject of a future publication.
The CSE of π1 Gru is not the only case where a torus plus bipolar structure has been observed around an AGB star. The CO line observations of V Hya also shows a similar structure (Sahai et al. 2003). Using the CO J = 2–1 and 3–2 line observation, Hirano et al. (2004) have distinguished three components in the CSE of V Hya based on its kinematic properties, which are similar to the results in this study. These authors also suggested a similar explanation for generating an intermediate-velocity component as the central component in our model. Another similar example is the post-AGB star, CRL 618, with a very fast, collimated outflow rising from a low-velocity, dense core (Sánchez Contreras et al. 2004). Owing to the complex geometry showing features commonly found in stars of the next evolutionary phase, π1 Gru is an extremely interesting case to study in order to find the missing link between the spherical outflows of AGB stars and the bipolar outflows observed at later stages.
7. Summary
We have presented the analysis of new ALMA-ACA data of the 12CO J = 3–2 and 13CO J = 3–2 line emission, together with previously observed 12CO J = 2–1 data from the S-type AGB star π1 Gru. The high-sensitivity ALMA observations recovered the extended emission, and for the first time, resolved the high-velocity component. The analysed data, including low-J transitions (from ALMA and SMA observations) high-J transition (from Herschel/HIFI observations) provided sufficient constraints for a 3D radiative transfer model. The best-fit model reconstructing the gas envelope has satisfactorily reproduced the line profiles, channel maps, and suggested a reasonable value for the abundance of 12CO/13CO. The gas envelope is modeled as a system of three separate components: a radially expanding torus with the velocity linearly increasing with latitude and radial distance, a central, radially expanding component that may have resulted from the dynamical interaction between the fast outflow and the torus, and a fast bipolar flow perpendicular to the equator with a radially expanding velocity field. The outflow momentum excess found in our model rules out a scenario in which radiation pressure alone can lift the high-velocity outflow. The density contrast between the equator and polar regions suggested from various formation mechanisms can successfully reproduce the data. This supports that the gravitational effect of a close companion is involved the torus formation, while the wind interaction mechanism and/or a bipolar magnetic field could be included when considering the outflow formation.
Acknowledgments
The authors would like to thank the staff at the Nordic ALMA ARC node for their indispensable help and support. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2012.1.00524.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. We are grateful to T. Danilovich for helping us with the Herschel/HIFI data. S. Mohamed is grateful to the South African National Research Foundation (NRF) for a researchgrant. W. H. T. Vlemmings acknowledges support from ERC consolidator grant 614264. C. Paladini is supported by the Belgian Fund for Scientific Research F.R.S.- FNRS.
References
- Abia, C., & Wallerstein, G. 1998, MNRAS, 293, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ake, T. B., & Johnson, H. R. 1992, in AAS Meeting Abstracts #180, BAAS, 24, 788 [NASA ADS] [Google Scholar]
- Balick, B., & Frank, A. 2002, ARA&A, 40, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Bladh, S., Höfner, S., Aringer, B., & Eriksson, K. 2015, A&A, 575, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Sánchez Contreras, C. 2001, A&A, 377, 868 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., et al. 2013, A&A, 557, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Carrizo, A., Quintana-Lacaci, G., Neri, R., et al. 2010, A&A, 523, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiu, P.-J., Hoang, C.-T., Dinh-V-Trung, et al. 2006, ApJ, 645, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Clyne, N., Akras, S., Steffen, W., et al. 2015, A&A, 582, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Teyssier, D., Justtanont, K., et al. 2015, A&A, 581, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorfi, E. A., & Hoefner, S. 1996, A&A, 313, 605 [NASA ADS] [Google Scholar]
- Eriksson, K., Nowotny, W., Höfner, S., Aringer, B., & Wachter, A. 2014, A&A, 566, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feast, M. W. 1953, MNRAS, 113, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., & Mellema, G. 1994, ApJ, 430, 800 [NASA ADS] [CrossRef] [Google Scholar]
- García-Segura, G., Langer, N., Różyczka, M., & Franco, J. 1999, ApJ, 517, 767 [NASA ADS] [CrossRef] [Google Scholar]
- García-Segura, G., López, J. A., & Franco, J. 2005, ApJ, 618, 919 [NASA ADS] [CrossRef] [Google Scholar]
- García-Segura, G., Villaver, E., Manchado, A., Langer, N., & Yoon, S.-C. 2016, ApJ, 823, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Gesicki, K., & Zijlstra, A. A. 2000, A&A, 358, 1058 [NASA ADS] [Google Scholar]
- Goldreich, P., & Scoville, N. 1976, ApJ, 205, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, N., Shinnaga, H., Dinh-V-Trung, et al. 2004, ApJ, 616, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Huggins, P. J., Bachiller, R., Planesas, P., Forveille, T., & Cox, P. 2005, ApJS, 160, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
- Icke, V. 1988, A&A, 202, 177 [NASA ADS] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1996, ApJ, 459, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R., Young, K., & Crosas, M. 1999, A&A, 346, 175 [NASA ADS] [Google Scholar]
- Lèbre, A., Aurière, M., Fabas, N., et al. 2014, A&A, 561, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maercker, M., Mohamed, S., Vlemmings, W. H. T., et al. 2012, Nature, 490, 232 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Matt, S., Balick, B., Winglee, R., & Goodson, A. 2000, ApJ, 545, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, A., Jorissen, A., Paladini, C., et al. 2014, A&A, 570, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2012, Balt. Astron., 21, 88 [Google Scholar]
- Olofsson, H., Vlemmings, W. H. T., Maercker, M., et al. 2015, A&A, 576, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323 [Google Scholar]
- Ramstedt, S., & Olofsson, H. 2014, A&A, 566, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Schöier, F. L., Olofsson, H., & Lundgren, A. A. 2006, A&A, 454, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Schöier, F. L., & Olofsson, H. 2009, A&A, 499, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Mohamed, S., Vlemmings, W. H. T., et al. 2014, A&A, 570, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahai, R. 1992, A&A, 253, L33 [NASA ADS] [Google Scholar]
- Sahai, R. 2014, in Asymmetrical Planetary Nebulae VI Conference, 87 [Google Scholar]
- Sahai, R., Morris, M., Knapp, G. R., Young, K., & Barnbaum, C. 2003, Nature, 426, 261 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sánchez Contreras, C., & Sahai, R. 2004, ApJ, 602, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Contreras, C., & Sahai, R. 2012, ApJS, 203, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Contreras, C., Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Sargent, A. 2004, ApJ, 617, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Santander-García, M., Bujarrabal, V., Koning, N., & Steffen, W. 2015, A&A, 573, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steffen, W., Koning, N., Wenger, S., Morisset, C., & Magnor, M. 2011, IEEE Transactions on Visualization and Computer Graphics, 17, 454 [Google Scholar]
- Teyssier, D., Alcolea, J., Bujarrabal, V., et al. 2011, in The Molecular Universe, eds. J. Cernicharo, & R. Bachiller, IAU Symp., 280 [Google Scholar]
- Van Eck, S., Jorissen, A., Udry, S., Mayor, M., & Pernier, B. 1998a, A&A, 329, 971 [NASA ADS] [Google Scholar]
- Van Eck, S., Jorissen, A., Udry, S., Mayor, M., & Pernier, B. 1998b, A&A, 329, 971 [NASA ADS] [Google Scholar]
- Vanture, A. D., & Wallerstein, G. 2002, ApJ, 564, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Vlemmings, W. H. T., Diamond, P. J., & Imai, H. 2006, Nature, 440, 58 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Appendix A: Finding the best-fit model
Some alternative models that were tested to find the best-fit model are presented here. The models with different velocity fields, morphologies, and temperature distributions were constrained by both the channel maps and line profiles.
A model using a constant expansion velocity for the whole torus could not reproduce the line profile nor the channel maps. Indeed the line profile of the 12CO J = 3–2 line from such a model has an intensity at the systemic velocity that is much smaller than that of the peaks (at about ±6 km s-1), while the center and peak intensities are comparable in the observed line profile. The model channel maps are rather sensitive to the assumed velocity field. If v1 is reduced by 10%, the 12CO J = 2–1 emission in the velocity channel beyond ±12 km s-1 is reduced below the noise level. The best-fit velocity distribution is also dependent on the chosen inclination angle of the torus, which was constrained by the flattened shape of the torus seen at the systemic velocity in the channel maps (Fig. 2). Finally, the PA of the torus was set to reproduce the relative intensity of the two peaks compared to each other in the observed line profiles (see Sect. 5.2).
A collimated velocity field, which is typically found in P-PNe and PNe in which the outflow gas velocity is perpendicular to the equatorial plane, was first attempted to model the fast bipolar component. This gave line profiles similar to the observed profiles, however, it also resulted in a very large intensity ratio between the central velocity channel and the nearby channels, which is not seen in the observed images.
An alternative model, without the central component (2), was also tested. In that model, the torus reaches regions close to the central star and is shaped like a flared disk. The fast bipolar outflow rises on top of the torus. This model successfully reproduced the spatial distribution of the 12CO J = 2–1 and the 12CO J = 3–2 emission, in particular the two-peaked distribution of the 12CO J = 2–1 emission, as well as the single central peak of the 12CO J = 3–2 emission at the systemic velocity (without a central cavity). However, in order to reproduce the data, the innermost outflow velocity had to be lower than the velocity of the torus at the same position, which would be unphysical.
The temperature distribution, as suggested by Knapp et al. (1999), results in a good agreement with the observations in the low-J transition lines, the 12CO J = 2–1 and J = 3–2, and 13CO J = 3–2 line. However, it overestimates the intensity of the 12CO J = 5–4 and J = 9–8 lines that are excited in the central regions. The two lines are sensitive to temperature and can be simultaneously fitted when the temperature decreases outward more rapidly than that found in Knapp et al. (1999, see Sect. 4.2).
All Tables
All Figures
 |
Fig. 1 Total flux of the 12CO J = 3–2 (left) and 13CO J = 3–2 (middle) emission from the ALMA-ACA data (red) and the combined (ACA+TP) data (black). The spectra were generated by convolving the images with the APEX beam (FWHM = 18″). The 12CO J = 3–2 spectrum (Ramstedt et al. 2006) from APEX (FWHM = 18″) is plotted for comparison. Owing to the artificial feature (explained in Sect. 3.2) in the blueshifted wing of the 13CO J = 3–2 line, the line profile of the combined data was only plotted from –35 km s-1. The 12CO J = 2–1 spectrum (right) from the SMA observation (Chiu et al. 2006) was generated by convolving the image with the SMA primary beam of 55″. |
| In the text | |
 |
Fig. 2 Contour maps of the 12CO J = 3–2 emission from the combined ALMA data. Contour levels are at 3, 5, 9, 15, 20, 25, and 30σ (σ = 1.2 Jy beam-1 for the middle rows, derived from the plotted channels), and at 3, 5, 7, and 9σ (σ = 0.08 Jy beam-1 for the first and last rows, derived from the plotted channels). The synthesized beam size of |
| In the text | |
 |
Fig. 3 Same as Fig. 2, for the 13CO J = 3–2 emission from the combined ALMA data. Contour levels are at 3, 5, 7, 9 15, and 20σ (σ = 0.055 Jy beam-1, derived from the full data set). The synthesized beam size of |
| In the text | |
 |
Fig. 4 Same as Fig. 2, for the recalibrated and reimaged 12CO J = 2–1 emission from the SMA (Chiu et al. 2006). Contour levels are at 3, 5, 7, 9, 13, 15, and 20σ (σ = 0.3 Jy beam-1, derived from the full data set). The synthesized beam is shown in the lower left corner of the 0 km s-1 channel and is |
| In the text | |
 |
Fig. 5 Position-velocity diagram for the 12CO J = 3–2 emission along a cut at a PA of 0° made by integrating over a 2 km s-1 velocity interval: low velocity and high signal-to-noise ratio at the middle panel with contour levels at 3, 5, 9, 15, 20, 30σ (σ = 1.2 Jy beam-1); high velocity and low signal-to-noise ratio at the left and right panels with contour levels at 3, 5, 9, 15, 20σ (σ = 0.06 Jy beam-1). The vertical and horizontal dashed lines show the systemic velocity (−12 km s-1) and the stellar position, respectively. |
| In the text | |
 |
Fig. 6 Sketch illustrating the three components used to model the CSE of π1 Gru. |
| In the text | |
 |
Fig. 7 Line profiles from the observations (black) and the model (red). The black dashed line in the upper right panel shows the observed profile multiplied by a factor of 2 to correct for the missing flux according to Chiu et al. (2006). |
| In the text | |
 |
Fig. 8 Contour maps of the 12CO J = 3–2 emission from the model simulating the combined (ACA+TP) ALMA observation. The contour levels are the same as those of the observational result plotted in Fig. 2. |
| In the text | |
 |
Fig. 9 Contour maps of the 12CO J = 2–1 emission from the model simulating the SMA observation. The contour levels are the same as those of the observational result plotted in Fig. 4. |
| In the text | |
 |
Fig. 10 Line-of-sight optical depth, calculated from the model, along the equator at the line rest frequencies. The 13CO J = 3–2 optical depth was scaled by a factor of 30. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.