EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 605 (September 2017) A&A, 605 (2017) A57 Full HTML
Free Access
Issue
A&A
Volume 605, September 2017
Article Number A57
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201730527
Published online 08 September 2017

© ESO, 2017

1. Introduction

The origin of life, as we know it, requires the simultaneous presence of at least two “ingredients”: liquid water and carbon atoms. In the past years, a lot of work has been devoted to the search for water reservoirs in all the evolutionary steps that lead to the formation of Sun-like stars, from pre-stellar cores (Caselli et al. 2012), to accreting protostars (Ceccarelli et al. 1999; Jørgensen et al. 2010), to protoplanetary disks (Hogerheijde et al. 2012; Podio et al. 2013; Cleeves et al. 2014). However, relatively little is known about the presence and growth of carbon chains, which might be an important reservoir of carbon atoms usable to build large biotic molecules (e.g. Loison et al. 2014; Balucani et al. 2000; Balucani 2009). In this respect, cyanopolyynes, that is, carbon chain molecules with an atom of hydrogen at one end and a cyano group at the other (generic formula: HC2n+1N), are among the best species to study in order to understand the formation of carbon chains. Indeed, they are ubiquitous in the interstellar medium and are detected in the Milky Way, as well as in external galaxies (e.g. Broten et al. 1978; Bell et al. 1992; Mauersberger et al. 1990). Even more interesting in an astrobiological context, cyanoplyynes were detected in protoplanetary disks (Chapillon et al. 2012; Öberg et al. 2015), on Titan’s atmosphere (e.g. Vuitton et al. 2007) and comets (e.g. Mumma & Charnley 2011), the continuous rain of which may have enriched the primitive Earth of carbon usable for synthesising biological molecules. All this makes cyanopolyynes excellent potential reservoirs of molecular carbon for the formation of longer chains of (pre-)biological importance.

The largest cyanopolyyne detected so far in the interstellar medium is HC9N (Broten et al. 1978). However, only relatively small cyanopolyynes, up to HC7N, have been detected in Solar-type protostars and in a relatively small sample: L1521E (Hirota et al. 2004), L1527 (Sakai et al. 2008), L1512 and L1251A (Cordiner et al. 2011), Cha-MMS1 (Cordiner et al. 2012), and IRAS 16293-2422 (Jaber Al-Edhari et al. 2017). Hence, what makes cyanopolyynes thrive in Solar-type protostellar environments is still an open question. In this paper, we report observations of HC5N and HC3N towards the source OMC-2 FIR4  obtained with the interferometer NOEMA within the Large Program SOLIS (Seeds Of Life In Space: Ceccarelli et al., in prep.).

OMC-2 FIR4 is part of the Orion Molecular Cloud 2, north of the famous KL object, at a distance of ~420 pc (Menten et al. 2007; Hirota et al. 2007). It lies on a bridge of material, probably a filament where new protostars are forming (Chini et al. 1997). FIR4 is in between two other young protostars: FIR3 (also known as SOF 2N or HOPS 370: Adams et al. 2012), about 30′′ north-west, and FIR5 (SOF 4 or HOPS 369: Adams et al. 2012), about 20′′ south-east (Mezger et al. 1990). OMC-2 FIR4 is itself a young proto-cluster that harbours several embedded low- and intermediate-mass protostars (Shimajiri et al. 2008; López-Sepulcre et al. 2013a). High-velocity symmetric wings in high-J CO and water lines detected by Herschel suggest the presence of a yet unveiled compact outflow from one of the embedded sources of the FIR4 cluster. The total mass of FIR4 is around 30 M⊙ (Mezger et al. 1990; Crimier et al. 2009) and its luminosity is less than 1000 L⊙ (Crimier et al. 2009; Furlan et al. 2014), respectively. Adams et al. (2012) found a mid-IR source, SOF 3 or HOPS 108, whose bolometric luminosity is estimated to be 38 L⊙ by Furlan et al. (2014), associated with the extended FIR4 millimeter emission, but not coincident with its emission peak, whose bolometric luminosity is estimated to be 38 L⊙ by Furlan et al. (2014). No specific observations focused on FIR3 and FIR5, the status of which, therefore, remains poorly understood. Finally, Herschel observations have revealed the presence of an inner source of energetic (≥10 MeV) particles which ionise the surrounding envelope up to a distance of 3500–5000 AU (Ceccarelli et al. 2014). Intriguingly, the derived irradiation dose is of the same order of magnitude as that experienced by the young Sun and whose trace is recorded in meteoritic material, by the so-called Short-Lived Radionuclides (SLRs: e.g. Gounelle et al. 2013). This and the mounting evidence that the Sun was born in a crowded cluster of stars (even including massive stars) rather than in an isolated clump (Adams 2010) make OMC-2 FIR4 the closest analogue of what must have been the environment of our Sun at the very beginning of its formation. In this context, the study of the cyanopolyynes towards OMC-2 FIR4 provides constraints on their growth in a similar natal environment.

2. Observations and results

Observations with the IRAM NOEMA Interferometer of HC3N (9–8) and HC5N (31−30), at rest frequencies 81.881468 GHz (Thorwirth et al. 2000) and 82.539039 GHz (Bizzocchi et al. 2004), respectively, towards OMC-2 FIR4 have been carried out over 5 days between the 5th and the 19th of August, 2015. We used the array in D configuration, with baselines from 15 to 95 m, providing an angular resolution of ~9.5 × 6.1′′ at the frequency of both lines. The phase centre was RA(J2000) = 05h35m26.′′97, Dec(J2000) = –05°09′56.′′8, and the local standard of rest velocity was set to 11.4 km s-1. The primary beam is ~61′′. The system temperature was in between 100 and 200 K in all tracks, and the amount of precipitable water vapour was generally around 10 mm. The calibration of the bandpass was performed on 3C 454.3, while 0524+034 was used for calibration of the gains in phase and amplitude. The absolute flux scale was set by observing MWC349 (~1.0 Jy at 82.1 GHz) when observable (three out of five days), and LKHA101 (~0.21 Jy at 82.1 GHz) during the other days.

Table 1

Line spectroscopic parameters, and integrated flux density of the HC3N (9–8) and HC5N (31–30) lines extracted from the regions indicated in Fig. 1.

The HC3N line was observed in the Widex band correlator, providing a resolution in velocity of ~7.15 km s-1, while the HC5N line was observed also in the Narrow band correlator with a resolution in velocity of ~0.57 km s-1. The following analysis of the HC5N line is conducted using mainly the higher-resolution spectrum. We show in the following that the the difference in the spectral resolutions has a negligible effect on our analysis, which is focused on comparing the integrated intensities of the two lines. The continuum was imaged by averaging the line-free channels of the Widex and Narrow correlator units. Calibration and imaging were performed using the CLIC and MAPPING softwares of the GILDAS1 package using standard procedures. The continuum image was self-calibrated, and the solutions were applied to the lines. Other lines detected in the Widex broad band correlator will be presented in accompanying papers.

The line strength and energy of the upper level of the two transitions are given in Table 1, and are taken from the Cologne Database for Molecular Spectroscopy (CDMS; Müller et al. 2001, 2005).

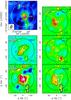thumbnail Fig. 1

Panel a: 82 GHz continuum emission obtained with IRAM NOEMA towards OMC-2 FIR4. The first contour level is at 1.8 × 10-3 Jy beam-1, corresponding to the 3σ rms level of the map, and the others are 2, 3, 5, 8, and 10 times the 3σ rms level. The white solid circle shows the NOEMA field of view, while the dashed one is the IRAM-30 m HPBW (~30′′). The triangles indicate the position of FIR3, FIR4 and FIR5, while the open star corresponds to the mid-IR protostar detected at 8, 24, and 70 μm by Furlan et al. (2014). Panel b: integrated intensity map of HC5N (31–30) obtained from the Widex correlator integrated in the velocity channels with signal. The contour levels are 3, 5, and 7 times the 1σ rms of the map, equal to ~ 8.9 × 10-4 Jy beam-1. The solid circle (in this panel and in all panels from b) to f) represents the NOEMA field of view (equal to the white circle in panel a. Panel c: integrated intensity map of HC3N (9–8). Both the first level and step correspond to the 3σ rms value of the integrated map (1σ ~ 6.3 × 10-3 Jy beam-1). Panels d–f: map of HC5N (31–30) obtained averaging the emission in the three different velocity ranges indicated in the top right corner extracted from the Narrow correlator unit. In all panels, both the first contour level and step correspond to the 3σ rms value of the total integrated map, showed in panel f (1σ ~ 3.6 × 10-3 Jy beam-1). Finally, in panels c and f, the red and white contours correspond to the emitting region of HC3N towards FIR4 with high and low HC5N emission, respectively. From these contours, we have extracted the spectra discussed in Sect. 4. The blue contour indicates FIR5 as detected in the total integrated map of HC5N (panel f).

From the presented dataset, we have detected both the HC3N (9–8) and HC5N (31–30) transitions towards OMC-2 FIR4 with excellent signal-to-noise ratio (larger than 10 for both lines). Figure 1 shows the morphology of the continuum emission at ~82 GHz (panel a), and that of the velocity-averaged emission of both lines in panels b–f. In Fig. 1, panels b and f show the emission map of HC5N (9–8) obtained by integrating the line over the channels with signal (in the Widex and Narrow spectra, respectively). Both plots indicate that the HC5N emission arises mainly from two condensations associated with FIR4 and FIR5.

In panel c, we show the integrated emission of HC3N (9–8), which also arises mainly from FIR4 and FIR5, but significant emission is detected also towards FIR3. Overall, the continuum emission is more consistent with that of HC3N (compare panels a and c) than with that of HC5N (compare panels a and b or f), although in both lines the emission is clearly shifted (and more extended) to the east of the continuum peak.

Concerning the comparison between the two carbon-chain species, the HC3N emission is well centred towards FIR4, while the HC5N emission is clearly displaced east of the map centre (compare panel c with panel b or f). Towards FIR5, both lines show faint and compact emission. Interestingly, the HC5N emission seems clearly associated with the mid-IR embedded protostar detected at 8, 24, and 70 μm by Furlan et al. (2014), indicated by the open star in Fig. 1. This suggests an enhanced formation of HC5N close to this protostar. Moreover, there is possibly a link between the different distribution of the two cyanopolyynes and the free-free emission detected with the JVLA (Lopez-Sepulcre, priv. comm.) east of FIR4. We return to this point with more detail in Sect. 4. However, a comparison with the JVLA data goes beyond the scope of this work and will be discussed in a forthcoming paper.

In both lines, we resolve out a significant fraction of the extended flux. Figure A.1 shows the comparison between the NOEMA and IRAM-30 m spectra extracted from the IRAM-30 m beam: we find that in FIR4 we recover only 20% of the total flux in HC5N, and ~15% in HC3N. Therefore, even though our maps are certainly resolving out a lot of extended emission, the fraction of this emission is comparable (within the calibration errors), and it is related to the same angular scale (because the observations of the two lines are simultaneous). Therefore, the comparison between the two maps should be only marginally affected by the differential filtering. Details on how we have estimated the missing flux are given in Appendix A.1.

As stated before, our analysis on HC5N is mainly based on the higher-spectral-resolution data extracted from the Narrow correlator. However, we have evaluated whether the different spectral resolution had an effect in the comparison of the two lines: for this purpose, we have also extracted the spectrum of the HC5N line from the Widex correlator. As an example, in Fig. A.1, we show the comparison between the Narrow and Widex spectra of HC5N extracted from the region FIR4-HC5N (red contour in Fig. 1). We found that the difference in the integrated intensity between the Widex and Narrow spectrum is only ~7%; smaller than the calibration uncertainty. Thus, because our analysis is based on the total integrated intensity of the two lines, our conclusions are not affected by the different spectral resolutions. Moreover, by comparing the maps of the total integrated emission of HC5N obtained from the Widex (panel b) and the Narrow (panel f) correlators, it is apparent that the two correlators do not produce maps with major overall differences in the morphology of the HC5N emission.

Due to the low spectral resolution of the HC3N observations (~7.15 km s-1), it is impossible to derive any kinematical information from this line. On the other hand, HC5N (31–30) was observed with a spectral resolution of ~0.5 km s-1, which allows us to spectrally resolve the line. We find that the bulk of the emission towards FIR4 is at a velocity of ~10.9 km s-1 (panel d), while that towards FIR5 is at ~11.5 km s-1 (panel e), indicating a small but significant difference in the velocities of the two condensations (the systemic one being ~11.4 km s-1, e.g. Lopez-Sepulcre et al. 2013a). However, as shown in panels b and f of Fig. 1, smoothing the HC5N line to the same spectral resolution of the HC3N does not significantly change the morphology of the line emission. The same effect is thus expected for the HC3N, which allows us to conclude that the fact that HC3N is more extended to the west than HC5N is not due to its lower spectral resolution (and thus higher sensitivity). One can reasonably expect the same effect on the HC3N line, because the HC5N line shape of the spectra extracted from Widex is similar to that of HC3N. As an example, in Fig. A.1 we show this comparison for the spectra of the two lines extracted in the region FIR4-HC5N.

Because the velocity-averaged emission of HC3N and HC5N show morphological differences, we have extracted the spectra of both molecules from three sub-regions, indicated in panels b and f of Fig. 1 by a red, a blue, and a white contour. The red and blue contours represent the regions of FIR4 and FIR5, respectively, in which the velocity-averaged emission of both HC3N and HC5N are above 3σ rms. The white contour instead indicates the regions of FIR4 where the velocity-averaged emission of HC3N is above 3σ rms, while that of HC5N is under this value. The integrated flux densities of the lines extracted from these three regions, as well as those extracted from the total FIR4 region, are reported in Table 1.

In summary, the analysis reported above shows that:

  • (i)

    HC3N emission is mostly associated with FIR4with a weak peak associated with FIR3 and FIR5;

  • (ii)

    HC5N emission is also associated mainly with FIR4, but a strong peak is also associated with FIR5;

  • (iii)

    HC3N and HC5N emission do not spatially coincide in FIR4: specifically, while HC3N emission overlaps relatively well with the continuum emission, HC5N emits only in the eastern-half of it.

3. Modelling

3.1. HC3N/HC5N abundance ratio

As mentioned in the Introduction, the main goal of this work is to understand the cyanopolyyne formation/growth. We therefore analysed the HC3N/HC5N intensity ratio in the three regions reported in Table 1, FIR4-HC5N (red contour in Fig. 1), FIR4-lowHC5N (white contour), and FIR5 (blue contour) to estimate the HC3N/HC5N abundance ratio in each of them. To this end, we computed the HC3N/HC5N line intensity ratio assuming Local thermodynamic Equilibrium (LTE) and optically thin lines, as a function of the gas temperature and assuming various HC3N/HC5N abundance ratios. We note that the estimated gas temperature in the FIR4 extended envelope is 35–45 K (Ceccarelli et al. 2014), whereas no estimates of the gas temperature exist towards FIR5.

The results of the optically thin LTE modelling and their comparison with the observed line intensity ratios are reported in Fig. 2 and Table 1. They imply that: (a) in FIR4-HC5N,  the HC3N/HC5N abundance ratio is between 4 and 12; (b) in FIR4-lowHC5N,  the HC3N/HC5N abundance ratio is between 10 and 30; and (c) in FIR5, the HC3N/HC5N abundance ratio is less than 6, regardless of the the gas temperature (within 10 and 60 K).

We note that single-dish observations towards OMC-2 FIR4 show that the two lines are optically thin or only moderately optically thick (Jaber Al-Edhari et al., in prep.). In Appendix A.2, we show the IRAM-30 m spectra of the HC3N (9–8) line and its three 13C isotopologues, from which we have deduced the opacity of the main isotopologue line. Concerning the possible non-LTE excitation, since non-LTE effects would be much more severe for the HC5N line than the HC3N line (the HC5N line has the higher upper level energy, and therefore it is more difficult to populate it according to LTE), the HC3N/HC5N abundance ratio found by the LTE analysis could be an overestimate.

thumbnail Fig. 2

Theoretical HC3N (9–8)/HC5N (31–30) line intensity ratio assuming LTE and optically thin conditions as a function of the gas temperature for different values of the HC3N/HC5N abundance ratio as marked (black curves). The range of values observed within a 2σ error bar towards the three regions listed in Table 1 are showed as dashed areas: FIR4-HC5N (blue), FIR4-lowHC5N (green) and FIR5 (red). We note that the temperature of FIR4 was estimated to be ~40 K (Ceccarelli et al. 2014) while no estimates for FIR5 exist.

Another possible explanation for the observed difference in the HC3N/HC5N line intensity ratio is a slight temperature gradient across FIR4. Assuming that the average temperature of FIR4 is about 40 K (Ceccarelli et al. 2014), if one allows the gradient to be about 10 K, with the eastern region FIR4-HC5N being the warmer (Fig. 2), this leads to two possibilities: A) in FIR4-HC5N the temperature is at most as high as ~50 K: the HC3N/HC5N would be in the 4−14 range in FIR4-HC5N, while it remains 10−30 in FIR4-lowHC5N. In this case, the ratio might be constant, 10−14, across the whole region; or B), in FIR4-lowHC5N the temperature is as low as 30 K: the HC3N/HC5N remains in the 4−12 range in FIR4-HC5N, while it would be 8−30 in FIR4-lowHC5N. In this case the ratio may be constant, around 8−12, across the region. Therefore, while a temperature gradient could explain the observed line ratio gradient, it would imply a HC3N/HC5N abundance ratio lower than 14. Please note that, since the amount of missing flux is comparable in the two lines (see Sect. 2), our column density ratios are expected to be affected by this by less than 30%.

Finally, we estimated the abundance of HC3N in the three regions illustrated in Fig. 1 (FIR4-HC5N, FIR4-lowHC5N, and FIR5) from the line integrated intensity and continuum emission. The total column density of HC3N was calculated assuming LTE for the line population, optically thin conditions, and gas temperatures between 10 and 50 K. The H2 column densities, N(H2), were derived from the dust mass computed from the 3 mm continuum emission (panel a in Fig. 1) from the equation: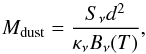(1)where: Sν is the total integrated flux density; d is the source distance; κν is the dust mass opacity coefficient, extrapolated at 3 mm from the value of 1 cm2 g-1 at 250 GHz (Ossenkopf & Henning 1994), assuming a dust opacity index β = 2, that is, a spectral index 2 + β = 4; and Bν(T) is the Planck function at dust temperature T. The equation is valid for optically thin emission. Then, we computed the H2 mass by multiplying Mdust for a mass gas-to-dust ratio of 100, from which we computed the average H2 volume density assuming a spherical source, and finally computed N(H2) by multiplying the volume density for the average diameter of the sources. We used dust temperatures in the range 10–50 K, as for the gas. We obtained the following N(H2) values: ~1−5 × 1023 cm-2 in FIR4-HC5N; ~2–9 × 1023 cm-2 in FIR4-lowHC5N; and ~1.5–7 × 1023 cm-2 in FIR5. The resulting HC3N abundance with respect to H atoms is in the range 0.5–5 × 10-11.

3.2. Chemistry

Large cyanopolyynes are commonly associated with the early chemical evolution of molecular clouds, when carbon atoms are not yet completely locked up into CO (e.g. Loison et al. 2014, and references therein) and, hence, no protostar is yet present. An important chemical process relevant for the cyanopolyynes in protostars is the differential freeze-out of light versus heavy molecules, with the former sticking onto the dust grains faster/earlier than the latter, which would introduce a so-called “freeze-out peak” of cyanopolyyne abundance in the gas (e.g. Brown & Charnley 1990). Furthermore, the sublimation of methane from ices, when the dust temperature exceeds about 30 K, introduces carbon atoms into the gas-phase for reactions leading to cyanopolyynes (Sakai et al. 2008; Hassel et al. 2008). Grain surface chemistry may also play an important role in the evolution of the abundances of cyanopolyynes (see Graninger et al. 2014).

Based on the analysis made in Sect. 3, the cyanopolyynes growth appears different in the three regions of Table 1, with the HC3N/HC5N abundance ratio being smaller (≤6) in FIR5, larger (10–30) in FIR4-lowHC5N and in between 4 and 12 in FIR4-HC5N. In order to understand the origin of this difference, we run a time-dependent astrochemical model with different parameters. We used a modified version of Nahoon with an upgraded version of the chemical network KIDA2. The modifications of Nahoon are to improve its usage flexibility, while the modifications of KIDA take into account the upgrade of the carbon chains chemistry by Loison et al. (2014), new reactions by Balucani et al. (2015) and Barone et al. (2015), and new values for the reactions CN + C4H2→ HC5N + H, C2H + HC3N → HC5N + H, and C3N + C2H2→ HC5N + H, following laboratory experiments and computations by Cheikh (2012), Fournier (2014) and Fournier et al. (in prep.) Details on these reactions are reported in Appendix A.3.

thumbnail Fig. 3

Contour plots of the HC3N/HC5N abundance ratio as a function of the O/H and C/H gaseous elemental abundance. The grey zone marks the region where the C/O elemental ratio is ≥1, which is unrealistic (see text). The solid lines mark the loci where the HC3N abundance is equal to the measured one, namely between 0.5 and 5 × 10-11. The models were obtained for a gas temperature of 40 K and a H2 density of 1.2 × 106 cm-3, valid for the envelope of FIR4 (Ceccarelli et al. 2014). Left panel: solution for FIR4-HC5N and FIR5, where the the measured HC3N/HC5N abundance ratio is 4–12 and ≤6, respectively. The cosmic-ray ionisation rate is 4 × 10-14 s-1 and the time is 3 × 104 yr. Right panel: a possible solution for FIR4-lowHC5N, where the measured HC3N/HC5N abundance ratio is 10–30. The cosmic-ray ionisation rate is 1 × 10-17 s-1 and the time is 1 × 105 yr.

The code was run assuming that H2 is initially molecular, while the other elements are either ionised or atomic. We note that all abundances are given with respect to H nuclei. Gaseous oxygen AO and carbon AC elemental abundances are varied from 0.5 to 2 × 10-4 and 0.3 to 1.5 × 10-4, respectively, to simulate the freezing-out of these two elements into the grain mantles. We assumed that the nitrogen abundance AN scales by the same factor as carbon, since CO and N2, the major carbon and nitrogen reservoirs in molecular gas, have the same binding energies (e.g. Bisschop et al. 2006; Noble et al. 2015). We therefore computed AN according to the formula 6.2 × 10-5 × AC/ 1.7 × 10-4. The other elements are depleted by a factor 100 with respect to the Solar photosphere values following Jenkins et al. (2009), as in several similar modelling works (e.g. Wakelam et al. 2010; Kong et al. 2015). We assumed the gas temperature and density are equal to those measured in the envelope of FIR4, namely T ~ 40 K and nH2 ~ 1.2 × 106 cm-3 (Ceccarelli et al. 2014). For FIR5 we used the same values. For the temperature, this assumption is justified by the study of Friesen et al. (2017) who have found, from ammonia measurements, that the temperature changes by a few degrees in the whole region encompassing FIR3, FIR4, and FIR5. Finally, we ran three grids of models with the cosmic-ray ionisation rate ζ equal to 1 × 10-17, 3 × 10-16, and 4 × 10-14 s-1, respectively. The first represents the “canonical” value for galactic molecular clouds (e.g. Padovani et al. 2009), the second one is the value measured in the diffuse cloud in the vicinity of FIR4 (Lopez-Sepulcre et al. 2013b), and the last one is the value measured in the envelope of FIR4 (Ceccarelli et al. 2014).

In order to find the solution(s) that best fit the observations, we plotted the contours of the HC3N/HC5N abundance ratio and overlapped them with the HC3N abundance contours. For the latter, we considered the range 0.5–5.0 × 10-11 (see Sect. 3.1). We produced plots at 1 × 104, 3 × 104, 1 × 105, 3 × 105, and 1 × 106 yr. Sample results discussing the case of ζ = 4 × 10-14 s-1 and ζ = 1 × 10-17 s-1 are shown in Fig. 3. All plots produced for the different ionisation rates at five different times from 1 × 104 yr to 1 × 106 yr are shown in Appendix A.4. We note that the gaseous C/O abundance ratio is very likely to be lower than 1 because, when the oxygen starts to be trapped in water ices, CO is already formed and, therefore, has already segregated as much oxygen as carbon. Therefore, we marked the C/O ≥ 1 region in the figure as unlikely.

FIR4-HC 5 N:

we first discuss the case of FIR4-HC5N, where the measured HC3N/HC5N abundance ratio is 4–12. We found no solutions that simultaneously reproduce the measured HC3N abundance and HC3N/HC5N abundance ratio, if ζ = 1 × 10-17 or 3 × 10-16 s-1. On the contrary, we found solutions when ζ = 4 × 10-14 s-1 is considered. Specifically, the best solution, shown in the left panel of Fig. 3, is found at 3 × 104 yr and provides stringent constraints on the gaseous elemental abundances of carbon and oxygen as well: the C/O abundance ratio must be very close to unity, O/H has to be lower than 1.4 × 10-4 and C/H lower than 1.3 × 10-4. Slightly different (~20%) solutions are also found for an age within 1 × 104 and 3 × 105 yr.

FIR4-lowHC 5 N:

in FIR4-lowHC5N the measured HC3N/HC5N abundance ratio is 10–30. In this case, a solution is found for ζ = 4 × 10-14 s-1 similar to the FIR4-HC5N, but with slightly larger C/O ratios, as shown in the left panel of Fig. 3. However, solutions are also found with lower ζ. The right panel of Fig. 3 shows the case obtained with ζ = 1 × 10-17 s-1 and time = 1 × 105 yr. An HC3N/HC5N abundance ratio between about 15 and 30 can be reproduced with a carbon abundance between 9 and 6 × 10-5. We note that no solutions exist for <1 × 105 and 3 × 105 yr.

FIR5:

in FIR5 the measured HC3N/HC5N abundance ratio is lower than 6. Assuming a gas temperature and density similar to those in FIR4, the left panel of Fig. 3 applies to this source too. No solutions are found for ζ< 4 × 10-17 s-1. The constraint on the C/O gaseous elemental abundance ratio is even more stringent than in FIR4-HC5N, and has to be very close to unity.

4. Discussion and conclusions

The high-spatial-resolution SOLIS observations show that cyanopolyynes are present in the three sources encompassed by the NOEMA primary beam: FIR3, FIR4, and FIR5. In FIR3, only HC3N is detected, whereas both HC3N and HC5N are detected in FIR4 and FIR5. FIR4 is composed of two regions: an eastern half, FIR4-HC5N, in which the HC5N is strong, and a western half, FIR4-lowHC5N, with faint HC5N emission. The measured HC3N/HC5N abundance ratio is ≤6, 4–12, and 10–30 in FIR5, FIR4-HC5N, and FIR4-lowHC5N, respectively.

Our analysis indicates that the FIR4-HC5N and FIR5 sources are young, with an age between 104 and 3 × 105 yr, and demonstrates the presence of a high cosmic-ray ionisation rate, ζ ~ 4 × 10-14 s-1, permeating these sources. In addition, the C/O gaseous elemental abundance ratio is very close to unity, the O abundance is ≤1.4 × 10-4 and the carbon abundance is ≤1.3 × 10-4. Conversely, the lower value of the HC3N/HC5N abundance ratio in FIR4-lowHC5N can either be due to a lower cosmic rays ionisation rate or to a larger C/O gaseous abundance ratio.

The C/O gaseous elemental abundance ratio being close to unity, and the relatively low carbon and oxygen abundances, are consistent with the idea that FIR4 and FIR5 have passed through a cold phase where icey mantles have locked up a large fraction of oxygen (probably in the form of H2O) and carbon (e.g. iced CO, CO2, CH4; e.g. Boogert et al. 2015; Ruffle et al. 1997). If the hypothesis that the difference between FIR4-HC5N and FIR4-lowHC5N is caused by a lower C/O ratio in FIR4-lowHC5N is correct, it would imply that the freezing has been less efficient in FIR4-lowHC5N. This could be due to warmer dust, but the source of the heating is not obvious, or to a lower density, so that the timescale for freezing is larger. Lacking measurements able to provide the gradient in density in FIR4, we cannot reach a firm conclusion on that.

More interesting, the low (≤12) measured HC3N/HC5N abundance ratio in FIR5 and FIR4-HC5N requires an enhanced cosmic-ray ionisation rate, which is what Ceccarelli et al. (2014) claimed for FIR4 based on a totally different dataset (high-J HCO+ and N2H+ lines observed by Herschel). Ceccarelli et al. argued that the enhanced cosmic-ray ionisation rate is due to an embedded source of high-energy (≥10 MeV) particles, similar to what happened to the young Solar System (see Sect. 1). In addition to confirming that claim, these new observations suggest that there may be a gradient in the cosmic-ray ionisation rate across the FIR4 condensation, with the eastern half strongly irradiated and the western region partially shielded and with a lower ζ. Let us now discuss this possibility. The observed gradient would be consistent with the observed region of bright free-free emission partially overlapping with the FIR4-HC5N region and extending outside the eastern border of FIR4 (Reipurth et al. 1999; Lopez-Sepulcre et al. 2013a, and discussion there) and the possibility that the source(s) of energetic particles permeating FIR4-HC5N and FIR5 lie there. In addition, there would not be the need to claim a gradient in the density, the cause of which would be mysterious, and, most importantly, a very narrow range of possible ages, around 1 × 105 yr. We conclude that, although not fully proven, the hypothesis of one or more sources of high-energy particles to the east of FIR4 and FIR5 remains the most appealing and consistent to explain the observations so far.

An alternative explanation is a temperature gradient (see Sect. 3), with temperature decreasing across FIR4 from east to west, which, as discussed in Sect. 3, would rule out a gradient in the irradiation by cosmic rays. However, for gradients of 10–20 K, a HC3N/HC5N abundance ratio ≤14 can be reproduced only if a high cosmic-ray ionisation rate is present. Therefore, this possibility is still consistent with a high irradiation of FIR4.

In conclusion, even though the HC3N/HC5N line intensity ratio gradient in FIR4 can be caused by a gradient in temperature, the measured HC3N/HC5N abundance ratio points, nevertheless, to a strong irradiation by cosmic-rays/energetic particles of the region. We find that energetic particle irradiation promotes the production of carbon chains. As irradiation was also present during the early phases of our Solar System, it is tempting to speculate that such energetic processes have also promoted the production of important carbon reservoirs in the Solar Nebula. Such reservoirs could then be delivered to the early Earth to foster pre-biotic chemistry evolution. The energetic particle irradiation experienced by the young Solar Nebula and the emergence of life on Earth being connected is a wild but intriguing hypothesis crying out for more dedicated work, possibly in collaboration with biophysicists.

1

The GILDAS software is developed at the IRAM and the Observatoire de Grenoble, and is available at http://www.iram.fr/IRAMFR/GILDAS

2

The original network and code are publicly available at http://kida.obs.u-bordeaux1.fr (Wakelam et al. 2014).

Acknowledgments

We thank the IRAM staff for their help in the data reduction. Many thanks to the anonymous referee for his/her constructive comments. This work was supported by the French program Physique et Chimie du Milieu Interstellaire (PCMI) funded by the Conseil National de la Recherche Scientifique (CNRS) and Centre National d’Études Spatiales (CNES), and by a grant from LabeX Osug@2020 (Investissements d’avenir – ANR10LABX56). Partial salary support for A. Pon was provided by a Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship. P.C., A. Punanova, A.C., and J.E.P. acknowledge support from the European Research Council (project PALs 320620). C.F. acknowledges founding from French space agency CNES.

References

  1. Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adams, J. D., Herter, T. L., Osorio, M., et al. 2012, ApJ, 749, L24 [NASA ADS] [CrossRef] [Google Scholar]
  3. Balucani, N. 2009, Int. J. Mol. Sci., 10, 2304 [CrossRef] [Google Scholar]
  4. Balucani, N., Asvany, O., Huang, L. C. L., Lee, Y. T., & Kaiser, R. I. 2000, ApJ, 545, 892 [NASA ADS] [CrossRef] [Google Scholar]
  5. Balucani, N., Ceccarelli, C., & Taquet, V. 2015, MNRAS, 449, L16 [Google Scholar]
  6. Barone, V., Latouche, C., Skouteris, D., et al. 2015, MNRAS, 453, L31 [Google Scholar]
  7. Bell, M. B., Avery, L. W., MacLeod, J. M., & Matthews, H. E. 1992, ApJ, 400, 551 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bell, M. B., Feldman, P. A., Travers, M. J., et al. 1997, ApJ, 483, L61 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bizzocchi, L., Degli Esposti, C., & Botschwina, P. 2004, J. Mol. Spectr., 225, 145 [NASA ADS] [CrossRef] [Google Scholar]
  11. Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
  12. Broten, N. W., Oka, T., Avery, L. W., MacLeod, J. M., & Kroto, H. W. 1978, ApJ, 223, 105 [NASA ADS] [CrossRef] [Google Scholar]
  13. Brown, P. D., & Charnley, S. B. 1990, MNRAS, 244, 432 [NASA ADS] [Google Scholar]
  14. Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
  15. Ceccarelli, C., Dominik, C., López-Sepulcre, A., et al. 2014, ApJ, 790, L1 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cernicharo, J., & Guélin, M. 1996, A&A, 309, L27 [NASA ADS] [Google Scholar]
  17. Chapillon, E., Dutrey, A., Guilloteau, S., et al. 2012, ApJ, 756, 58 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cheikh, S. E. 2012, Ph.D. Thesis, Université de Rennes [Google Scholar]
  19. Chini, R., Reipurth, B., Ward-Thompson, D., et al. 1997, ApJ, 474, L135 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cleeves, L. I., Bergin, E. A., Alexander, C. M. O.’D., et al. 2014, Science, 345, 1590 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cordiner, M. A., Charnley, S. B., Buckle, J. V., Walsh, C., & Millar, T. J. 2011, ApJ, 730, L18 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cordiner, M. A., Charnley, S. B., Wirström, E. S., & Smith, R. G. 2012, ApJ, 744, 131 [NASA ADS] [CrossRef] [Google Scholar]
  23. Crimier, N., Ceccarelli, C., Lefloch, B., & Faure, A. 2009, A&A, 506, 1229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Dauphas, N., & Chaussidon, M. 2011, AREPS, 39, 351 [Google Scholar]
  25. Fournier, M. 2014, Ph.D. Thesis, Université de Rennes [Google Scholar]
  26. Friesen, R. K., Pineda, J. E., Rosolowsky, E., et al. 2017, ApJ, 843, 63 [NASA ADS] [CrossRef] [Google Scholar]
  27. Furlan, E., Megeath, S. T., Osorio, M., et al. 2014, ApJ, 786, 26 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gounelle, M, Chaussidon, M., & Rollion-Bard, C. 2013, ApJ, 763, L33 [NASA ADS] [CrossRef] [Google Scholar]
  29. Graninger, D. M., Herbst, E., Öberg, K. I., & Vasyunin, A. I. 2014, ApJ, 787, 74 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hassel, G. E., Herbst, E., & Garrod, R. T. 2008, ApJ, 681, 1385 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hirota, T., Maezawa, H., & Yamamoto, S. 2004, ApJ, 617, 399 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hirota, T., Bushimata, T., Choi, Y. K., Honma, M., & Imai, H. 2007, PASJ, 59, 897 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2012, Proc. Symp., From Atoms to Pebbles: Herschel’s view of Star and Planet Formation, Grenoble, France, March 20–23, ed. J.-C. Augereau [Google Scholar]
  34. Jaber, A. A., Ceccarelli, C., Kahane, C., et al. 2017, A&A, 597, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jørgensen, J. K., & van Dishoeck, E. F. 2010, ApJ, 710, L72 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kong, S., Caselli, P., Tan, J. C., et al. 2015, ApJ, 804, 98 [NASA ADS] [CrossRef] [Google Scholar]
  38. Loison, J.-C., Wakelam, V., Hickson, K. M., Bergeat, A., & Mereau, R. 2014, MNRAS, 437, L430 [Google Scholar]
  39. López-Sepulcre, A., Taquet, V., Sánchez-Monge, Á., et al. 2013a, A&A, 556, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. López-Sepulcre, A., Kama, M., Ceccarelli, C., et al. 2013b, A&A, 549, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Mauersberger, R., Henkel, C., & Sage, L. J. 1990, A&A, 236, 63 [NASA ADS] [Google Scholar]
  42. Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Mezger, P. G., Zylka, R., & Wink, J. E. 1990, A&A, 228, 95 [NASA ADS] [Google Scholar]
  44. Milam, S. S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  45. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Müller, H. S. P., Schlüder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
  48. Noble, J. A., Theule, P., Congiu, E., et al. 2015, A&A, 576, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Öberg, K. I., Guzmán, V. V., Furuya, K., et al. 2015, Nature, 520, 198 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  50. Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  51. Podio, L., Kamp, I., Codella, C., et al. 2013, ApJ, 766, L5 [NASA ADS] [CrossRef] [Google Scholar]
  52. Reipurth, B., Rodríguez, L. F., & Chini, R. 1999, AJ, 118, 983 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ruffle, D. P., Hartquist, T. W., Taylor, S. D., & Williams, D. A. 1997, MNRAS, 291, 235 [NASA ADS] [CrossRef] [Google Scholar]
  54. Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shimajiri, Y., Takahashi, S., Takakuwa, S., Saito, M., & Kawabe, R. 2008, ApJ, 683, 255 [NASA ADS] [CrossRef] [Google Scholar]
  56. Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2000, J. Mol. Spectr., 204, 133 [NASA ADS] [CrossRef] [Google Scholar]
  57. Vuitton, V., Yelle, R. V., & McEwan, M. J. 2007, Icarus, 191, 722 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wakelam, V., Herbst, E., Le Bourlot, J., et al. 2010, A&A, 517, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Wakelam, V., Vastel, C., Aikawa, Y., et al. 2014, MNRAS, 445, 2854 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A

Appendix A.1 Derivation of missing flux

To estimate how much flux is resolved out by the interferometer, we compared IRAM-30 m spectra with interferometric spectra extracted from a region corresponding to the beam of the single-dish observations (~30′′). The IRAM-30 m spectra were converted from main beam temperature units (TMB) to flux density units (Fν) by assuming that the telescope beam is Gaussian and the source size is smaller than the beam, via the formula Fν = 2k(ν2/c2) [(π/ 4ln2)(ΘMB)2] TMB, where k is the Boltzmann constant, ΘMB is the half power beam width of the IRAM-30 m Telescope, and ν is the line rest frequency. The resulting spectra are shown in panels a and b of Fig. A.1: with the NOEMA we are recovering ~14−15% of the flux detected with the IRAM-30 m telescope in HC3N, and ~20% in HC3N.

thumbnail Fig. A.1

a) Spectrum of HC3N (9–8) obtained with the IRAM-30 m Telescope (black histogram) in the framework of the ASAI large program, and SOLIS-NOEMA spectrum (red histogram) extracted from a circular region equal to the IRAM-30 m HPBW (~30′′). We note that the flux resulting from the convolved NOEMA observations have been multiplied by a factor 7 to match those of the 30 m Telescope: we thus recover about the 15% of the total flux. b) Same as panel a for HC5N (31–30). In this case, the NOEMA spectrum has been multiplied by a factor 5. From the plot, it is apparent that we recover slightly less than the 20% of the total flux. c) Comparison between the Narrow (black) and Widex (red) spectrum of HC5N (31–30), both integrated on the region FIR4-HC5N (red contour in Fig. 1). The integral under the channel with signal is different by ~7% (see Sect. 2). d) Widex spectra of HC3N (black) and HC5N (red) intergated over the same region as in panel c. The HC5N spectrum has been multiplied by 7 for clarity of the figure.

Appendix A.2 IRAM-30 m spectra of 13C isotopologues of HC3N

In Fig. A.2, we show the IRAM-30 m spectrum of HC3N (9–8), and those of the two isotopologues HCC13CN and HC13CCN in the same transition. The integrated intensities for the three transitions are: 7.1 ± 0.7 K km s-1 in HC3N, 0.16 ± 0.02 K km s-1 in HCC13CN, and 0.11 ± 0.01 K km s-1 in HC13CCN. We note that the (9–8) line of the third isotopologue, H13CCCN, lies outside the observed frequency range. Using the other two detected isotopologues, the 12C/13C line ratio is 44 ± 8 and 64 ± 12, respectively. Therefore, considering an elemental 12C/13C ratio of ~68 for the local interstellar medium (Milam et al. 2005), the line of the main isotopologue is optically thin or at most slightly thick. We note that the difference in the 12C/13C intensity ratio between the two isotopologues is present in all the other detected lines and it is, therefore, real and due to the HC3N chemistry, specifically its formation route. This is the focus of a forthcoming article by Jaber Al-Edhari et al. (in prep.).

thumbnail Fig. A.2

IRAM-30 m spectra of the HC3N, HCC13CN and HC13CCN (9–8) line (Jaber Al-Edhari et al., in prep.). The (9–8) line of the third isotopologue, H13CCCN, lies outside the observed frequency range.

Appendix A.3 New reactions rates for HC5N

We adopted, as a base, the KIDA chemical database for the network of reactions. We modified it following the works by Loison et al. (2014), Balucani et al. (2015) and Barone et al. (2015). In addition, we modified the rate k of two reactions involving the formation of HC5N and included a new reaction, following the experimental results from Cheikh (2012), Fournier (2014) and Fournier et al. (in prep.). The new rates are listed in Table A.1, where we reported the coefficients α, β, and γ defined, as usual, by the formula: (A.1)

Appendix A.4 Chemical model predictions

In this appendix we show the predictions of the chemical model described in Sect. 3.2 for three different values of the cosmic rays ionisation rate: ζ = 1 × 10-17 s-1 (Fig. A.3), ζ = 3 × 10-16 s-1 (Fig. A.4), and ζ = 4 × 10-14 s-1 (Fig. A.5), at five different times: 1 × 104 yr, 3 × 104 yr, 1 × 105 yr, 3 × 105 yr, and 1 × 106 yr.

Table A.1

Modified and new reactions involving the formation of HC5N.

thumbnail Fig. A.3

Predictions of the HC3N/HC5N abundance ratio from the chemical models described in Sect. 3.2 for ζ = 1 × 10-17 at the five different times (from top to bottom): 1 × 104 yr, 3 × 104 yr, 1 × 105 yr, 3 × 105 yr, and 1 × 106 yr. All symbols used (contour plots, grey zone, etc.) are the same as in Fig. 3.

thumbnail Fig. A.4

Same as Fig. A.3 for ζ = 3 × 10-16.

thumbnail Fig. A.5

Same as Fig. A.3 for ζ = 4 × 10-14.

All Tables

Table 1

Line spectroscopic parameters, and integrated flux density of the HC3N (9–8) and HC5N (31–30) lines extracted from the regions indicated in Fig. 1.

In the text
Table A.1

Modified and new reactions involving the formation of HC5N.

In the text

All Figures

thumbnail Fig. 1

Panel a: 82 GHz continuum emission obtained with IRAM NOEMA towards OMC-2 FIR4. The first contour level is at 1.8 × 10-3 Jy beam-1, corresponding to the 3σ rms level of the map, and the others are 2, 3, 5, 8, and 10 times the 3σ rms level. The white solid circle shows the NOEMA field of view, while the dashed one is the IRAM-30 m HPBW (~30′′). The triangles indicate the position of FIR3, FIR4 and FIR5, while the open star corresponds to the mid-IR protostar detected at 8, 24, and 70 μm by Furlan et al. (2014). Panel b: integrated intensity map of HC5N (31–30) obtained from the Widex correlator integrated in the velocity channels with signal. The contour levels are 3, 5, and 7 times the 1σ rms of the map, equal to ~ 8.9 × 10-4 Jy beam-1. The solid circle (in this panel and in all panels from b) to f) represents the NOEMA field of view (equal to the white circle in panel a. Panel c: integrated intensity map of HC3N (9–8). Both the first level and step correspond to the 3σ rms value of the integrated map (1σ ~ 6.3 × 10-3 Jy beam-1). Panels d–f: map of HC5N (31–30) obtained averaging the emission in the three different velocity ranges indicated in the top right corner extracted from the Narrow correlator unit. In all panels, both the first contour level and step correspond to the 3σ rms value of the total integrated map, showed in panel f (1σ ~ 3.6 × 10-3 Jy beam-1). Finally, in panels c and f, the red and white contours correspond to the emitting region of HC3N towards FIR4 with high and low HC5N emission, respectively. From these contours, we have extracted the spectra discussed in Sect. 4. The blue contour indicates FIR5 as detected in the total integrated map of HC5N (panel f).
In the text
thumbnail Fig. 2

Theoretical HC3N (9–8)/HC5N (31–30) line intensity ratio assuming LTE and optically thin conditions as a function of the gas temperature for different values of the HC3N/HC5N abundance ratio as marked (black curves). The range of values observed within a 2σ error bar towards the three regions listed in Table 1 are showed as dashed areas: FIR4-HC5N (blue), FIR4-lowHC5N (green) and FIR5 (red). We note that the temperature of FIR4 was estimated to be ~40 K (Ceccarelli et al. 2014) while no estimates for FIR5 exist.
In the text
thumbnail Fig. 3

Contour plots of the HC3N/HC5N abundance ratio as a function of the O/H and C/H gaseous elemental abundance. The grey zone marks the region where the C/O elemental ratio is ≥1, which is unrealistic (see text). The solid lines mark the loci where the HC3N abundance is equal to the measured one, namely between 0.5 and 5 × 10-11. The models were obtained for a gas temperature of 40 K and a H2 density of 1.2 × 106 cm-3, valid for the envelope of FIR4 (Ceccarelli et al. 2014). Left panel: solution for FIR4-HC5N and FIR5, where the the measured HC3N/HC5N abundance ratio is 4–12 and ≤6, respectively. The cosmic-ray ionisation rate is 4 × 10-14 s-1 and the time is 3 × 104 yr. Right panel: a possible solution for FIR4-lowHC5N, where the measured HC3N/HC5N abundance ratio is 10–30. The cosmic-ray ionisation rate is 1 × 10-17 s-1 and the time is 1 × 105 yr.
In the text
thumbnail Fig. A.1

a) Spectrum of HC3N (9–8) obtained with the IRAM-30 m Telescope (black histogram) in the framework of the ASAI large program, and SOLIS-NOEMA spectrum (red histogram) extracted from a circular region equal to the IRAM-30 m HPBW (~30′′). We note that the flux resulting from the convolved NOEMA observations have been multiplied by a factor 7 to match those of the 30 m Telescope: we thus recover about the 15% of the total flux. b) Same as panel a for HC5N (31–30). In this case, the NOEMA spectrum has been multiplied by a factor 5. From the plot, it is apparent that we recover slightly less than the 20% of the total flux. c) Comparison between the Narrow (black) and Widex (red) spectrum of HC5N (31–30), both integrated on the region FIR4-HC5N (red contour in Fig. 1). The integral under the channel with signal is different by ~7% (see Sect. 2). d) Widex spectra of HC3N (black) and HC5N (red) intergated over the same region as in panel c. The HC5N spectrum has been multiplied by 7 for clarity of the figure.
In the text
thumbnail Fig. A.2

IRAM-30 m spectra of the HC3N, HCC13CN and HC13CCN (9–8) line (Jaber Al-Edhari et al., in prep.). The (9–8) line of the third isotopologue, H13CCCN, lies outside the observed frequency range.
In the text
thumbnail Fig. A.3

Predictions of the HC3N/HC5N abundance ratio from the chemical models described in Sect. 3.2 for ζ = 1 × 10-17 at the five different times (from top to bottom): 1 × 104 yr, 3 × 104 yr, 1 × 105 yr, 3 × 105 yr, and 1 × 106 yr. All symbols used (contour plots, grey zone, etc.) are the same as in Fig. 3.
In the text
thumbnail Fig. A.4

Same as Fig. A.3 for ζ = 3 × 10-16.
In the text
thumbnail Fig. A.5

Same as Fig. A.3 for ζ = 4 × 10-14.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.