| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201730599 | |
| Published online | 06 July 2017 | |
Evidence for photometric activity cycles in 3203 Kepler stars⋆
1 Institut für Astrophysik, Georg-August-Universität Göttingen, 37077 Göttingen, Germany
e-mail: reinhold@mps.mpg.de
2 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
3 Center for Space Science, NYUAD Institute, New York University Abu Dhabi, PO Box 129188, Abu Dhabi, UAE
Received: 10 February 2017
Accepted: 5 May 2017
Context. In recent years it has been claimed that the length of stellar activity cycles is determined by the stellar rotation rate. It has been observed that the cycle period increases with rotation period along two distinct sequences, known as the active and inactive sequences. In this picture the Sun occupies a solitary position between the two sequences. Whether the Sun might undergo a transitional evolutionary stage is currently under debate.
Aims. Our goal is to measure cyclic variations of the stellar light curve amplitude and the rotation period using four years of Kepler data. Periodic changes in the light curve amplitude or the stellar rotation period are associated with an underlying activity cycle.
Methods. Using a recent sample of active stars we compute the rotation period and the variability amplitude for each individual Kepler quarter and search for periodic variations of both time series. To test for periodicity in each stellar time series we consider Lomb-Scargle periodograms and use a selection based on a false alarm probability (FAP).
Results. We detect amplitude periodicities in 3203 stars between 0.5 < Pcyc < 6 yr covering rotation periods between 1 < Prot < 40 days. Given our sample size of 23 601 stars and our selection criteria that the FAP is less than 5%, this number is almost three times higher than that expected from pure noise. We do not detect periodicities in the rotation period beyond those expected from noise. Our measurements reveal that the cycle period shows a weak dependence on rotation rate, slightly increasing for longer rotation periods. We further show that the shape of the variability deviates from a pure sine curve, consistent with observations of the solar cycle. The cycle shape does not show a statistically significant dependence on effective temperature.
Conclusions. We detect activity cycles in more than 13% of our final sample with a FAP of 5% (calculated by randomly shuffling the measured 90-day variability measurements for each star). Our measurements do not support the existence of distinct sequences in the Prot−Pcyc plane, although there is some evidence for the inactive sequence for rotation periods between 5–25 days. Unfortunately, the total observing time is too short to draw sound conclusions on activity cycles with similar lengths to that of the solar cycle.
Key words: Sun: activity / stars: activity / starspots / stars: rotation / techniques: photometric
A table containing all cycle periods and time series is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/603/A52
© ESO, 2017
1. Introduction
The origin of the 11-year solar activity cycle is one of the most important questions in solar and stellar physics. Over the course of one cycle the Sun undergoes phases of strong and weak activity. During the active phase of the solar cycle, dark sunspots appear on the solar surface. These spots have lifetimes lasting from days to a few months (Petrovay & van Driel-Gesztelyi 1997), decaying into smaller magnetic concentrations which are bright (called faculae). Individual faculae have short lives, as the magnetic flux associated with them is buffeted by turbulent convective motions; however, since magnetic flux is conserved, the faculae reform and the lifetime of extended patches of faculae have much longer lifetimes. The magnetic cycle of the Sun is thus accompanied by brightness variations. This variability, which is an evolving combination of dark and bright features on the rotating surface of the Sun, is weak during times of minimum activity and strong during times of maximum activity. Although these activity phenomena act on different timescales, they can all be detected in the total solar irradiance (TSI) data (see, e.g., Domingo et al. 2009).
On stars other than the Sun, cyclic activity has also been observed through (long-term) brightness changes caused by epochs of increased occurrence of active regions on the surface or in the low stellar atmosphere. The magnetic field of the active regions transports energy into the chromosphere, which leads to increased chromospheric emission, most evident in the cores of the Ca ii H&K lines. The strength of this enhancement in the emission is usually described by the Mount Wilson S-index (Vaughan et al. 1978) or the related quantity 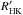 (Linsky et al. 1979). A long-term study of chromospheric activity of main-sequence stars in the solar neighborhood was initiated at the Mount Wilson observatory in the late 1960s. Wilson (1978) presented Ca ii H&K flux measurements with the first evidence of cyclic variations. Vaughan & Preston (1980) found that FGKM stars exhibit different levels of chromospheric activity with a deficiency of stars of intermediate activity. These authors explained the dearth of intermediate active stars in terms of an activity decline with age. In contrast, Noyes et al. (1984a) found a tight correlation between
(Linsky et al. 1979). A long-term study of chromospheric activity of main-sequence stars in the solar neighborhood was initiated at the Mount Wilson observatory in the late 1960s. Wilson (1978) presented Ca ii H&K flux measurements with the first evidence of cyclic variations. Vaughan & Preston (1980) found that FGKM stars exhibit different levels of chromospheric activity with a deficiency of stars of intermediate activity. These authors explained the dearth of intermediate active stars in terms of an activity decline with age. In contrast, Noyes et al. (1984a) found a tight correlation between 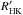 activity and the Rossby number Ro = Prot/τc (defined as rotation period Prot divided by the convective overturn time τc), but could not detect evidence of the – nowadays called – Vaughan-Preston gap. Noyes et al. (1984b) detected cyclic variations of the chromospheric activity levels in 13 main-sequence stars providing the relation
activity and the Rossby number Ro = Prot/τc (defined as rotation period Prot divided by the convective overturn time τc), but could not detect evidence of the – nowadays called – Vaughan-Preston gap. Noyes et al. (1984b) detected cyclic variations of the chromospheric activity levels in 13 main-sequence stars providing the relation 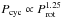 between the cycle period and the rotation period. Baliunas et al. (1995) investigated stars of spectral type G0-K5 and found that these can be roughly separated by their mean S-index: fast rotators are assumed to be young objects with high S-indices, whereas older stars rotate more slowly and show lower values of the S-index, again providing evidence for the Vaughan-Preston gap. Baliunas et al. (1996) tried to understand cyclic activity in terms of stellar dynamo theory, proving a relation between the ratio of the cycle and rotation period and the dynamo number D according Pcyc/Prot ∝ D0.74. Brandenburg et al. (1998) and Saar & Brandenburg (1999) studied the relation between magnetic dynamo cycle period, rotation period, activity level, and stellar age. These authors were the first to claim the existence of the active (A) and inactive (I) sequences, two almost parallel branches separated by a factor of six in Pcyc following the relation Pcyc/Prot ∝ Ro0.5. Additionally, for fast rotators with Prot< 3 d these authors found evidence for a third branch with opposite slope Pcyc/Prot ∝ Ro-0.4. Böhm-Vitense (2007) confirmed that chromospherically active stars follow the A- and I-sequences in the Prot−Pcyc plane. Slow rotators exhibit shorter cycle periods populating the I-sequence, whereas stars rotating faster than the Sun exhibit long cycle periods located on the A-sequence. Some A-sequence stars exhibit secondary cycle periods located on the I-branch. The Sun is located in between the two branches. In contrast, do Nascimento et al. (2015) found that the Sun does not have a solitary position between the two branches, but lies on a newly proposed solar-analog sequence.
between the cycle period and the rotation period. Baliunas et al. (1995) investigated stars of spectral type G0-K5 and found that these can be roughly separated by their mean S-index: fast rotators are assumed to be young objects with high S-indices, whereas older stars rotate more slowly and show lower values of the S-index, again providing evidence for the Vaughan-Preston gap. Baliunas et al. (1996) tried to understand cyclic activity in terms of stellar dynamo theory, proving a relation between the ratio of the cycle and rotation period and the dynamo number D according Pcyc/Prot ∝ D0.74. Brandenburg et al. (1998) and Saar & Brandenburg (1999) studied the relation between magnetic dynamo cycle period, rotation period, activity level, and stellar age. These authors were the first to claim the existence of the active (A) and inactive (I) sequences, two almost parallel branches separated by a factor of six in Pcyc following the relation Pcyc/Prot ∝ Ro0.5. Additionally, for fast rotators with Prot< 3 d these authors found evidence for a third branch with opposite slope Pcyc/Prot ∝ Ro-0.4. Böhm-Vitense (2007) confirmed that chromospherically active stars follow the A- and I-sequences in the Prot−Pcyc plane. Slow rotators exhibit shorter cycle periods populating the I-sequence, whereas stars rotating faster than the Sun exhibit long cycle periods located on the A-sequence. Some A-sequence stars exhibit secondary cycle periods located on the I-branch. The Sun is located in between the two branches. In contrast, do Nascimento et al. (2015) found that the Sun does not have a solitary position between the two branches, but lies on a newly proposed solar-analog sequence.
All the cycle period measurements above are based on cyclic Ca ii H&K emission, but long-term brightness variations also indicate cyclic activity (see, e.g., Baliunas & Vaughan 1985, which nicely links solar activity to photometric and chromospheric activity on stars other than the Sun). Oláh et al. (2000) and Oláh & Strassmeier (2002) investigated activity cycles from long-term V-band photometry. Messina & Guinan (2002) found evidence of cyclic activity in six solar-analog stars also using long-term V-band observations. In a subsequent paper, Messina & Guinan (2003) found that the mean rotation period also changes over the course of the activity cycle. Lockwood et al. (2007) provided parallel measurements of photometric and chromospheric variability, but unfortunately did not determine any cycle periods. Oláh et al. (2009) found a positive correlation between rotational and cycle periods for 20 active stars using time-frequency analysis. A similar approach was applied to Kepler light curves of very fast rotators (Prot ≤ 1 d) by Vida et al. (2014). These authors found hints of cyclic activity on timescales of 300–900 days analyzing cyclic changes of the mean rotation period. Using CoRoT data Ferreira Lopes et al. (2015) detected cyclic variability in 16 FGK type stars. These authors found evidence of a possible third sequence, parallel to the previously identified active and inactive sequences, but shifted by a factor of 1/4 towards shorter cycle periods. Lehtinen et al. (2016) found evidence of activity cycles in 18 solar-type stars using decades-long photometric observations. The cycle periods follow the sequences defined by Saar & Brandenburg (1999), bridging chromospherically and photometrically derived activity cycles. In recent years, activity cycles have also been detected from asteroseismology through periodic shifts in the mode frequencies (García et al. 2010; Salabert et al. 2016).
The primary Kepler mission provides continuous, high-precision photometry of thousands of stars over four years of observation. Owing to the presence or absence of active regions on the visible hemisphere (e.g., spots, plage) the stellar flux gradually changes. Such long-term changes are observed in the TSI data, showing significant changes over the course of the 11-year cycle. In addition, the preferred latitude of active region occurrence changes. Owing to differential rotation equatorial spots have a shorter rotation period than higher latitude spots. Our main goal is to detect cyclic changes of the light curve amplitude and the stellar rotation period, which we interpret as an indication of a photometric activity cycle. The largest sample with accurately determined rotation periods is provided by McQuillan et al. (2014, hereafter McQ14). This huge sample of 34 030 active stars forms the basis of our activity cycle survey.
2. Data and method
2.1. Motivation from the Sun
As mentioned in the introduction, the brightness of the Sun (as measured by the TSI) varies due to the passage of dark sunspots and bright plage regions across the solar disk. The top panel of Fig. 1 shows the TSI time series from Shapiro et al. (2016) produced with the SATIRE-S model (Yeo et al. 2014). It is readily seen that at times of activity maxima (1979, 1989, 2000, 2014) the TSI varies rapidly, while there are only small variations during times of activity minima (1976, 1986, 1996 and 2008).
To quantify the time-dependent variability in a manner which we can easily extend to the Kepler data, we begin by rebinning the TSI data from a 1-min cadence to a 1-day cadence. We then break the data into N = 73 segments of 90-day length, and following Basri et al. (2011), we define the variability range Rvar for that 90-day period as the difference between the 5th and 95th percentiles of the TSI measurements in the 90-day segment. This activity measure is similar to the magnetic index Sph defined by Mathur et al. (2014). For each of the N = 73 segments we thus obtain a measurement of the variability Rvar(n),n = 1,...,N. Using the midpoints of each 90-day time segment we create a time series Rvar(t), shown in the lower panel of Fig. 1. Computing the Lomb-Scargle periodogram of the time series Rvar(t) reveals a peak at Pcyc, var = 10.98 ± 0.26 yr, which is compatible with other estimates of the solar cycle length. This shows that this method is capable of detecting the correct cycle period from the variability of a star’s light curve.
 |
Fig. 1 Upper panel: measured total solar irradiance, binned in 1-day intervals, covering more than 40 yr of observations. The approximately 11-year solar cycle can be seen as the Sun’s brightness changes from almost constant during activity minima to highly variable during activity maxima. Lower panel: variability range of the TSI data, Rvar, as a function of time. We define Rvar as the difference between the 5th and 95th percentiles of the 1-day binned intensity in each 90-day period in time. The red curve shows a sine fit to the Rvar time series with a period Pcyc, var = 10.98 ± 0.26 yr. |
2.2. Kepler data
Most Kepler data is released in segments of ~90 days (known as quarters) with exceptions for the quarters Q0 (~10 days), Q1 (~33 days), and Q17 (~32 days). There is an ongoing debate regarding how to remove instrumental effects from the time series. The data studied in this paper rely on the PDC-MAP pipeline using the following versions1: Version 2.1 for Q0-Q4 & Q9-Q11; Version 3.0 for Q5-Q8 & Q12-Q14; and Version 5.0 for Q15-Q17. For each star we create a time sequence t(n),n = 0,...,17, consisting of the midpoints of the time segments covered by the quarters Qn when a star was observed.
The upper panel of Fig. 2 shows the light curve of the Kepler star KIC 2714077. Each light curve is normalized and centered around zero by dividing the flux by its median value and subtracting unity. This normalization is necessary because the Kepler spacecraft rolls between consecutive quarters, so the stars fall on different CCDs accompanied by offsets of the PDC-MAP flux between the quarters. Because the stellar variability we are interested in is that due to the rotation of spots and faculae across the disk, we further fit and subtract a second-order polynomial from the data in each quarter. This will substantially reduce the influence of possible longer term instrumental issues, while only slightly affecting modulation comparable to or faster than the rotation period of the star. We then use the Rvar defined in the same way as for the Sun as a measure of the variability. The red triangles in the upper panel of Fig. 2 indicate the 5th and 95th percentiles of the relative flux in each quarter. The difference between the 5th and 95th percentiles equals Rvar, which is shown as time series Rvar(t) in the middle panel of Fig. 2. The time series Rvar(t) shows strong periodicity with a period of Pcyc, var = 3.51 yr, shown as red sine fit to the data.
In addition to measuring Rvar, for each star we also measure the stellar rotation period in each quarter using the Lomb-Scargle periodogram resulting in a time series Prot(t), which is shown for the same stars in the lower panel of Fig. 2. The quarterly measured rotation periods scatter around the mean rotation period Prot = 13.88 d. In contrast to Rvar the time series Prot(t) does not show strong periodicity. The Lomb-Scargle periodogram finds a peak at a period of less than one year, which is visualized by the red sine fit to the data. As we show in the following, strong periodicity of the variability range and random scatter of the rotation period time series is quite common for many stars in our sample.
Owing to the limited quarter length we set upper limits on the detectable rotation periods: 10 days for Q0, 30 days for Q1 and Q17, and 45 days for the other quarters. All period measurements deviating by more than 30% from the median period of all quarters were discarded. The Rvar measurements of these quarters were also discarded because instrumental artifacts might dominate the photometry. To achieve meaningful variability and rotation period time series we require measurements in at least N = 12 quarters. These conditions shrink the initial McQ14 sample to 23 601 stars. We suspect that there might be more candidates with detectable activity cycle that have been missed, due to our constraints.
 |
Fig. 2 Upper panel: Kepler light curve of the star KIC 2714077. Vertical red lines indicate the quarters Q1-Q17. Red triangles at the bottom and the top show the 5th and 95th percentile of the intensity, respectively. For each quarter we measure the intensity difference between the upper and the lower triangle, which equals Rvar. Middle panel: time series of the variability range Rvar(t) of the same star, defined as the difference between the 5th and 95th percentiles in each quarter. Lower panel: time series of the rotation periods Prot(t) of the same star. The red curve in the middle and lower panels show the best sine fit to the Rvar(t) and Prot(t) time series, respectively. |
 |
Fig. 3 Time series Rvar(t) of the quarterly measured variability ranges of four Kepler stars. The time series in panels a)–c) pass our selection criterion that randomly permuting the time series Rvar of this star yields a higher peak in the Lomb-Scargle periodogram in less than 5% of all tested cases (FAP < 5%), whereas panel d) shows a time series with (FAP > 5%). The red curve shows the best sine fit to the data, and the dashed black line indicates the mean variability of the star. The Rvar(t) time series shown in panels a)–d) exhibit false alarm probabilities FAP = 1.0%, FAP = 0.5%, FAP = 0.3%, and FAP = 17.9%, respectively. |
2.3. Analysis of the time series
For each star we have three time series, t(n), Rvar(n), and Prot(n) of length N, which is the number of quarters where a rotation period could be measured. The Lomb-Scargle periodogram is a straightforward way to look for periodicities in unevenly sampled data. We compute the Lomb-Scargle periodogram of the time series Rvar and Prot (using the time series t) to test for periodicity. We call these periods associated with the highest peaks in the Lomb-Scargle periodograms Pcyc, var and Pcyc, rot, respectively.
Because we are simply taking the highest peak in the Lomb-Scargle periodogram, Pcyc, var and Pcyc, rot will be defined for every star. To define a subset of the stars where the inferred periodicity is more likely to be real, we introduce a false alarm probability (FAP) threshold. We calculate the FAP by considering 1000 random permutations of Rvar and Prot. For each permutation we have three time series t, 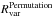 , and
, and 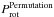 . We then create Lomb-Scargle periodograms for these new sequences and again concentrate on the highest peaks. We define the FAP for Rvar as the number of cases where a higher peak appears in the Lomb-Scargle periodogram of
. We then create Lomb-Scargle periodograms for these new sequences and again concentrate on the highest peaks. We define the FAP for Rvar as the number of cases where a higher peak appears in the Lomb-Scargle periodogram of 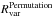 than the peak found for Rvar divided by the number of permutations considered.
than the peak found for Rvar divided by the number of permutations considered.
We define the periodic sample by selecting those stars for which the FAP was less then 5%. The samples are defined independently for Pcyc, var and Pcyc, rot. The time series Rvar(t) of three representative stars from the periodic sample are shown in panels (a)–(c) in Fig. 3. For comparison panel (d) shows a star with FAP > 5%. We discuss the issue of false positives in the results section.
2.4. Method sensitivity
To test the sensitivity of the method to different cycle periods, we created a set of 1000 synthetic time series 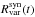 . We randomly selected N data points, 12 ≤ N ≤ 18, from the time series t(n). The time series
. We randomly selected N data points, 12 ≤ N ≤ 18, from the time series t(n). The time series 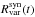 are pure sine functions with input periods Pcyc, in uniformly distributed between 0.5 yr < Pcyc, in < 10 yr. The amplitudes are uniformly distributed random numbers, comparable to the sine fit amplitudes of the periodic sample. We add noise to the time series
are pure sine functions with input periods Pcyc, in uniformly distributed between 0.5 yr < Pcyc, in < 10 yr. The amplitudes are uniformly distributed random numbers, comparable to the sine fit amplitudes of the periodic sample. We add noise to the time series 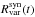 , which we define as the standard deviation of the difference between Rvar(t) and the best sine fit from the periodic sample. The noise distribution is Gaussian. Because the quantity Rvar describes a relative flux difference, the sine amplitude and the noise are linearly correlated. For simplicity, the phase and the offset of the sine curves are set to zero. We analyze the set of synthetic light curves using the Lomb-Scargle periodogram, and compare the returned cycle periods Pcyc, out to the input periods Pcyc, in in Fig. 4. This Monte Carlo test reveals that we can trust cycle periods of up to six years.
, which we define as the standard deviation of the difference between Rvar(t) and the best sine fit from the periodic sample. The noise distribution is Gaussian. Because the quantity Rvar describes a relative flux difference, the sine amplitude and the noise are linearly correlated. For simplicity, the phase and the offset of the sine curves are set to zero. We analyze the set of synthetic light curves using the Lomb-Scargle periodogram, and compare the returned cycle periods Pcyc, out to the input periods Pcyc, in in Fig. 4. This Monte Carlo test reveals that we can trust cycle periods of up to six years.
 |
Fig. 4 Monte Carlo test using a set of 1000 simulated light curves showing the input periods Pcyc, in and the returned periods Pcyc, out. The black lines show different Pcyc, out: Pcyc, in period ratios: the dotted line shows the 1:1 period ratio, and the upper and lower dashed line show the 2:1 and 1:2 period ratio, respectively. The cycle period uncertainties (shown as red error bars) were estimated from ten different sets of 1000 simulated light curves for each input period bin between 0.5–10 yr. The red crosses show the median value of Pcyc, out and the error bars show the median absolute difference between Pcyc, in and Pcyc, out. We omit error bars for Pcyc, in > 7 yr because the uncertainties become huge. |
The uncertainties of the derived cycle periods have been estimated in the same way. For different cycle period bins between 0.5–10 years we created a set of 1000 synthetic light curves for each bin, and applied the above analysis. In Fig. 4 the red crosses show the median value of Pcyc, out and the error bars show the median absolute difference between Pcyc, in and Pcyc, out. We omit error bars for Pcyc, in > 7 yr because the uncertainties become huge. The associated periods and uncertainties up to Pcyc, in< 7 yr are given in Table 1.
3. Results
3.1. Cycle periods
The cycle period distribution of Pcyc, var for all stars satisfying FAP < 5% is shown in black in the left panel of Fig. 5, and the distribution of Pcyc, rot for all stars satisfying FAP < 5% is shown in black in the right panel of Fig. 5. Assuming the time series Rvar(t) and Prot(t) do not contain any periodic signals, 1180 stars would be obtained after applying a limit of FAP < 5% to a total sample of 23 601 stars. For the cycle periods Pcyc, var of the variability amplitude Rvar(t) we detect 3203 cycles. This number is significantly higher than the expected number of false-positive detections.
 |
Fig. 5 Left panel: distribution of cycle periods Pcyc, var derived from all time series Rvar which satisfied our selection criterion FAP < 5%. The black distribution shows all cases where random permutations of time series Rvar yielded a higher peak in the Lomb-Scargle periodogram than the original time series in less than 5% of all cases. The red curve shows the results from a Monte Carlo experiment where the analysis was performed on random permutations of each Rvar time series for the whole sample. Error bars are based on the Monte Carlo simulations and show one standard deviation. Right panel: distribution of Pcyc, rot, the cycle period determined from variations in the determined rotation periods Prot, satisfying the selection criterion of FAP < 5%. Again the black histogram shows the cycle period distribution of the 5% strongest periodicity data, and the red curve shows the period distribution obtained from the Monte Carlo experiments. |
To test whether the different number of detections might be an artifact of the method, we performed a Monte Carlo simulation where we replaced the time series Rvar(t) of each star with a random permutation of that star’s time series. We then applied exactly the same analysis as was applied to the original time series (see Sect. 2.3).
This randomization process is repeated 500 times for the whole sample. Comparing the peak height of the initially randomized time series to the peak heights of the remaining ones yields the false alarm probability FAPMC for each star. We repeated this process 500 times, and found that on average 1122 stars satisfied our selection criterion. This is consistent with the expectation from the condition FAPMC< 5% applied to 23 601 stars.
The averaged cycle period distribution from the Monte Carlo experiment is shown in red in Fig. 5, with error bars showing the standard deviation of different realizations. It is obvious that the distributions of Pcyc, var of the original and the randomized data are very different. The distribution of the real data has a maximum of around three years, whereas the randomized sample mostly contains short cycles between one and two years.
In the right panel the distribution of Pcyc, rot reveals a completely different picture. The distributions of the real data and the randomized sample are largely consistent, and the total number of detections is almost identical. This shows that we cannot distinguish whether a cyclic change of the rotation period might indicate an activity cycle or if this change occurs just by chance. We conclude that we cannot use the quantity Pcyc, rot to search for activity cycles. Thus, we concentrate on Pcyc, var in the following.
Figure 6 shows the dependence of Pcyc, var on the stellar rotation period Prot for all 3203 stars of the periodic sample. The number of stars in each bin on the abscissa is given in black above the color bins.
 |
Fig. 6 Distribution of periodic stars with FAP < 5% in the Prot−Pcyc, var plane; the gray area indicates the limits of our detection reliability. The different black symbols represent cycle period measurements from other authors: circles: Ferreira Lopes et al. (2015), upside down triangle: Egeland et al. (2015), normal triangle: Salabert et al. (2016), square: Moutou et al. (2016), star: Flores et al. (2016), and diamond: Boro Saikia et al. (2016). The solid black lines show the active (A), inactive (I), and short-cycle (S) sequences as defined by Ferreira Lopes et al. (2015). The numbers above the color bins denote the total number of stars in each column. |
 |
Fig. 7 Distribution of the cycle periods in the Prot−Pcyc, var plane expected from noise (determined using Monte Carlo experiments). |
We turn now to the issue of the cycle period’s dependence on rotation period. Our observations only allow activity periods of less than six years to be detected. From Fig. 6 it is obvious that most cycle periods have a length between 2–4 years (compare Fig. 5), slightly clumping at rotation periods between 10–20 days. Up to rotation periods of 25 days the cycle period slightly increases with rotation period. For stars rotating even more slowly the cycle period behavior is hard to determine from the data. Using unit weights for all data points a linear fit yields Pcyc, var = 0.04 Prot + 2.40 yr, i.e., a weak dependence of the cycle on rotation period. This result is confirmed by the small Pearson correlation coefficient r = 0.20 between the two quantities.
Some previous authors have reported a correlation between the rotation period of a star and the period of its activity cycle, with periods preferentially lying on active and inactive branches (shown in Fig. 6), and with some stars having detectable periodicities of their activity cycles lying on both branches. Clearly our detection scheme cannot find multiple activity periodicities, and we find that most of our detections are concentrated along the inactive branch; however, the distributions are broad.
For comparison photometric cycle measurements of 16 CoRoT stars (Ferreira Lopes et al. 2015) are shown as black circles in Fig. 6. The upside down triangle, normal triangle, square, star, and diamond show measurements from Egeland et al. (2015), Salabert et al. (2016), Moutou et al. (2016), Flores et al. (2016), and Boro Saikia et al. (2016), respectively. Egeland et al. (2015) have also detected a longer activity cycle of ~12 yr for the same star (HD 30495).
To check that the data are not due to a hidden selection bias, we prepared the same figure beginning from the Monte Carlo simulations discussed above. The result is shown in Fig. 7. As expected from pure noise, most cycle period detections lie in the range of 1–2 yr because the periodogram interprets the noise as short cycles. Furthermore, the sample shows a flat distribution, i.e., no dependence on rotation. The associated Pearson correlation coefficient equals r = 0.01, on average, showing that Pcyc, var and Prot are uncorrelated.
 |
Fig. 8 Phase-folded Rvar(t) curves of all 3203 stars with strong periodicity. Error bars show the standard error of the Rvar(t) distribution in each phase bin. |
 |
Fig. 9 Phase-folded Rvar(t) curves of all periodic stars split up into different temperature bins as indicated on the top of each panel. |
3.2. Cycle shapes
So far we have focused on the cycle periods, but have not considered the shape of the variability. Figure 8 shows a phase-folded curve of the variability range Rvar averaged over all stars of the periodic sample. All Rvar time series are phase-folded with the measured cycle period and shifted so that they all lie in phase. The mean variability level is subtracted, and the curves are normalized by their amplitudes. The average over all curves is shown in black and the red curve shows a sine fit. The error bars show the standard error in each phase bin. It is clear that the shape of the variability shows some deviation from a pure sine curve. At maximum activity the observed variability curve is more spiky than a sine curve. At minimum activity the variability is rather flat. Applying the same analysis to the Rvar time series of the TSI data (compare Fig. 1) we also find a flat shape at minimum activity, but a large scatter at maximum activity. To quantify the deviation of the data from the sine curve we compute the reduced chi-square and the associated p-value to be 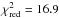 and p = 0.002, indicating a high statistical significance for the deviation from a sinusoidal shape.
and p = 0.002, indicating a high statistical significance for the deviation from a sinusoidal shape.
Figure 9 shows the same curve as Fig. 8 for different temperature bins. In each bin the stars have roughly the same cycle period distribution. The coolest stars are nicely represented by a sine curve. Neither the spiky top nor the flat bottom are visible. The shape of the curve gradually changes towards hotter stars. The top becomes more spiky and the bottom flattens out. To quantify the temperature dependence we calculate the difference between each of the six possible pairs of the average curves (a)–(d) in Fig. 9. We do not find a statistically significant difference between the pairs that would indicate a temperature dependence of the cycle period. The slightly different cycle shape in panel (a) might be explained by the smaller number of stars in this temperature bin.
4. Summary
We detected periodicity of the variability amplitude Rvar in 3203 stars of the McQ14 sample, which we interpreted as an indication of an underlying activity cycle. To account for random detections, the original sample was compared to a randomized sample. It was found that the number of activity cycle detections was three times higher than expected from pure noise. We did not detect cyclic changes in the rotation period beyond those expected from noise. The Prot−Pcyc plane revealed that the cycle period Pcyc, var shows weak dependence on the rotation period, slightly increasing with rotation period. In contrast to previous studies (Noyes et al. 1984b; Baliunas et al. 1996; Saar & Brandenburg 1999; Böhm-Vitense 2007; Ferreira Lopes et al. 2015; Lehtinen et al. 2016) we did not find evidence of a tight functional dependence between the cycle and the rotation period. Our measurements show a large scatter around the inactive branch. Previous studies (Saar & Brandenburg 1999; Böhm-Vitense 2007) have shown stars with multiple periodicities on the A- and I-branches. These studies were based on chromospheric activity indices, which will have different sensitivities to spots and plages than the photospheric variability detected using Kepler data. Hence it is possible that our finding of a strong I-branch and little evidence of the A- and S-branches might indicate that the I-branch has a stronger signature in the photosphere than the A- or S-branches. In good agreement with the solar cycle the average shape of all activity cycles was found to deviate from a pure sine curve. We could not detect a statistically significant temperature dependence of the activity cycle shape.
Acknowledgments
The research leading to these results received funding from the EU FP7 collaborative project “Exploitation of space data for innovative helio- and asteroseismology” (SpaceInn) under grant agreement No. 312844. L.G. acknowledges support from the NYU Abu Dhabi Institute under grant G1502. This work was supported in part by the German space agency (Deutsches Zentrum für Luft- und Raumfahrt) under PLATO grant 50OO1501. Part of the research leading to the presented results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 338251 (StellarAges).
References
- Baliunas, S. L., & Vaughan, A. H. 1985, ARA&A, 23, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Nesme-Ribes, E., Sokoloff, D., & Soon, W. H. 1996, ApJ, 460, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., Walkowicz, L. M., Batalha, N., et al. 2011, AJ, 141, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Boro Saikia, S., Jeffers, S. V., Morin, J., et al. 2016, A&A, 594, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Saar, S. H., & Turpin, C. R. 1998, ApJ, 498, L51 [NASA ADS] [CrossRef] [Google Scholar]
- do Nascimento, Jr., J.-D., Saar, S. H., & Anthony, F. 2015, in 18th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. G. T. van Belle, & H. C. Harris, Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, 18, 59 [Google Scholar]
- Domingo, V., Ermolli, I., Fox, P., et al. 2009, Space Sci. Rev., 145, 337 [Google Scholar]
- Egeland, R., Metcalfe, T. S., Hall, J. C., & Henry, G. W. 2015, ApJ, 812, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira Lopes, C. E., Leão, I. C., de Freitas, D. B., et al. 2015, A&A, 583, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flores, M., González, J. F., Jaque Arancibia, M., Buccino, A., & Saffe, C. 2016, A&A, 589, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2016, A&A, 588, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., McClintock, W., Robertson, R. M., & Worden, S. P. 1979, ApJS, 41, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Ballot, J., et al. 2014, A&A, 562, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Messina, S., & Guinan, E. F. 2002, A&A, 393, 225 [Google Scholar]
- Messina, S., & Guinan, E. F. 2003, A&A, 409, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Donati, J.-F., Lin, D., Laine, R. O., & Hatzes, A. 2016, MNRAS, 459, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984a, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984b, ApJ, 287, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., & Strassmeier, K. G. 2002, Astron. Nachr., 323, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., & Strassmeier, K. G. 2000, A&A, 356, 643 [NASA ADS] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovay, K., & van Driel-Gesztelyi, L. 1997, Sol. Phys., 176, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Salabert, D., Régulo, C., García, R. A., et al. 2016, A&A, 589, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Solanki, S. K., Krivova, N. A., Yeo, K. L., & Schmutz, W. K. 2016, A&A, 589, A46 [Google Scholar]
- Vaughan, A. H., & Preston, G. W. 1980, PASP, 92, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Vida, K., Oláh, K., & Szabó, R. 2014, MNRAS, 441, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Yeo, K. L., Krivova, N. A., Solanki, S. K., & Glassmeier, K. H. 2014, A&A, 570, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: measured total solar irradiance, binned in 1-day intervals, covering more than 40 yr of observations. The approximately 11-year solar cycle can be seen as the Sun’s brightness changes from almost constant during activity minima to highly variable during activity maxima. Lower panel: variability range of the TSI data, Rvar, as a function of time. We define Rvar as the difference between the 5th and 95th percentiles of the 1-day binned intensity in each 90-day period in time. The red curve shows a sine fit to the Rvar time series with a period Pcyc, var = 10.98 ± 0.26 yr. |
| In the text | |
 |
Fig. 2 Upper panel: Kepler light curve of the star KIC 2714077. Vertical red lines indicate the quarters Q1-Q17. Red triangles at the bottom and the top show the 5th and 95th percentile of the intensity, respectively. For each quarter we measure the intensity difference between the upper and the lower triangle, which equals Rvar. Middle panel: time series of the variability range Rvar(t) of the same star, defined as the difference between the 5th and 95th percentiles in each quarter. Lower panel: time series of the rotation periods Prot(t) of the same star. The red curve in the middle and lower panels show the best sine fit to the Rvar(t) and Prot(t) time series, respectively. |
| In the text | |
 |
Fig. 3 Time series Rvar(t) of the quarterly measured variability ranges of four Kepler stars. The time series in panels a)–c) pass our selection criterion that randomly permuting the time series Rvar of this star yields a higher peak in the Lomb-Scargle periodogram in less than 5% of all tested cases (FAP < 5%), whereas panel d) shows a time series with (FAP > 5%). The red curve shows the best sine fit to the data, and the dashed black line indicates the mean variability of the star. The Rvar(t) time series shown in panels a)–d) exhibit false alarm probabilities FAP = 1.0%, FAP = 0.5%, FAP = 0.3%, and FAP = 17.9%, respectively. |
| In the text | |
 |
Fig. 4 Monte Carlo test using a set of 1000 simulated light curves showing the input periods Pcyc, in and the returned periods Pcyc, out. The black lines show different Pcyc, out: Pcyc, in period ratios: the dotted line shows the 1:1 period ratio, and the upper and lower dashed line show the 2:1 and 1:2 period ratio, respectively. The cycle period uncertainties (shown as red error bars) were estimated from ten different sets of 1000 simulated light curves for each input period bin between 0.5–10 yr. The red crosses show the median value of Pcyc, out and the error bars show the median absolute difference between Pcyc, in and Pcyc, out. We omit error bars for Pcyc, in > 7 yr because the uncertainties become huge. |
| In the text | |
 |
Fig. 5 Left panel: distribution of cycle periods Pcyc, var derived from all time series Rvar which satisfied our selection criterion FAP < 5%. The black distribution shows all cases where random permutations of time series Rvar yielded a higher peak in the Lomb-Scargle periodogram than the original time series in less than 5% of all cases. The red curve shows the results from a Monte Carlo experiment where the analysis was performed on random permutations of each Rvar time series for the whole sample. Error bars are based on the Monte Carlo simulations and show one standard deviation. Right panel: distribution of Pcyc, rot, the cycle period determined from variations in the determined rotation periods Prot, satisfying the selection criterion of FAP < 5%. Again the black histogram shows the cycle period distribution of the 5% strongest periodicity data, and the red curve shows the period distribution obtained from the Monte Carlo experiments. |
| In the text | |
 |
Fig. 6 Distribution of periodic stars with FAP < 5% in the Prot−Pcyc, var plane; the gray area indicates the limits of our detection reliability. The different black symbols represent cycle period measurements from other authors: circles: Ferreira Lopes et al. (2015), upside down triangle: Egeland et al. (2015), normal triangle: Salabert et al. (2016), square: Moutou et al. (2016), star: Flores et al. (2016), and diamond: Boro Saikia et al. (2016). The solid black lines show the active (A), inactive (I), and short-cycle (S) sequences as defined by Ferreira Lopes et al. (2015). The numbers above the color bins denote the total number of stars in each column. |
| In the text | |
 |
Fig. 7 Distribution of the cycle periods in the Prot−Pcyc, var plane expected from noise (determined using Monte Carlo experiments). |
| In the text | |
 |
Fig. 8 Phase-folded Rvar(t) curves of all 3203 stars with strong periodicity. Error bars show the standard error of the Rvar(t) distribution in each phase bin. |
| In the text | |
 |
Fig. 9 Phase-folded Rvar(t) curves of all periodic stars split up into different temperature bins as indicated on the top of each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


