| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730502 | |
| Published online | 11 July 2017 | |
Spatially resolved evolution of the local H2O production rates of comet 67P/Churyumov-Gerasimenko from the MIRO instrument on Rosetta⋆
1 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: marshall@mps.mpg.de
2 Jet Propulsion Laboratory, Califonria Institute of Technology, 4800 Oak Grove Dr., Pasadena, CA 91109, USA
3 LESIA-Observatoire de Paris, CNRS, UPMC, Université Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
4 LERMA, Observatoire de Paris, PSL Research University, CNRS, UMR 8112, UPMC, 75014 Paris, France
5 National Central University, Jhongli, 32001 Taoyuan City, Taiwan
Received: 26 January 2017
Accepted: 3 April 2017
Aims. Using spectroscopic and continuum data measured by the MIRO instrument on board Rosetta of comet 67P/Churyumov-Gerasimenko, it is possible to derive and track the change in the water production rate, to learn how the outgassing evolves with heliocentric distance. The MIRO data are well suited to investigate the evolution of 67P, in unprecedented spatial and temporal detail.
Methods. To obtain estimates of the local effective Haser production rates we developed an efficient and reliable retrieval approach with precalculated lookup tables. We employed line area ratios (H216O/H218O) from pure nadir observations as the key variable, along with the Doppler shift velocity, and continuum temperature. This method was applied to the MIRO data from August 2014 until April 2016. Perihelion occurred on August 13, 2015 when the comet was 1.24 AU from the Sun.
Results. During the perihelion approach, the water production rates increased by an order of magnitude, and from the observations, the derived maximum for a single observation on August 29, 2015 is (1.42 ± 0.51) ×1028. Modeling the data indicates that there is an offset in the peak outgassing, occurring 34 ± 10 days after perihelion. During the pre-perihelion phase, the production rate changes with heliocentric distance as rh−3.8±0.2; during post-perihelion, the dependence is rh−4.3±0.2. The comet is calculated to have lost 0.12 ± 0.06 % of its mass during the perihelion passage, considering only water ice sublimation. Additionally, this method provides well sampled data to determine the spatial distribution of outgassing versus heliocentric distance. The time evolution is definitely not uniform across the surface. Pre- and post-perihelion, the surface temperature on the southern hemisphere changes rapidly, as does the sublimation rate with an exponent of ~−6. There is a strong latitudinal dependence on the rh exponent with significant variation between northern and southern hemispheres, and so the average over the comet surface may only be of limited importance. We present more detailed regional variation in the outgassing, demonstrating that the highest derived production rates originate from the Wosret, Neith and Bes regions during perihelion.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / submillimeter: general / techniques: spectroscopic
The dataset used to make Fig. 4 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/603/A87
© ESO, 2017
1. Introduction
The water production rate of comet 67P/Churyumov-Gerasimenko has been measured by a variety of instruments on board Rosetta. In June 2014, MIRO (Microwave Instrument for the Rosetta Orbiter; see Sect. 2 for more details) measured the water production rate at a heliocentric distance of 3.9 AU to be 1025 molec/s, increasing to 4 × 1025 molec/s by late August (Gulkis et al. 2015). Only Bockelee-Morvan et al. (2010) and de Val-Borro et al. (2014) have determined water outgassing rates from comets at larger heliocentric distances. Also in August 2014, Lee et al. (2015) demonstrated that the outgassing across the surface can vary by a factor of 30 from 0.1×1025 molec/s/sr to 3.0 × 1025 molec/s/sr. In the next month, MIRO estimated the production of the water isotopologue H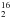 O as (4.9 ± 2.5) × 1025 molec/s on September 7 at 3.41 AU from the Sun (Biver et al. 2015). The ROSINA-COPS (Rosetta Orbiter Spectrometer for Ion and Neutral Analysis − COmetary Pressure Sensor) instrument found production rates in the range of 8.7 × 1025–1.1 × 1026 molec/s between August and November 2014, which then increased by a factor of 2 between November and January 2015 (Bieler et al. 2015). Fougere et al. (2016) present results from ROSINA-DFMS (Double Focusing Mass Spectrometer), which show the outgassing increasing from <1026 molec/s at 3.5 AU (August 2014) to >1027 molec/s at 1.5 AU from the Sun (May 2015). A mean production rate of 8 × 1025 molec/s agrees with results from VIRTIS-H (Visible InfraRed Thermal Imaging Spectrometer) between November 2014 and January 2015 (Bockelée-Morvan et al. 2015), and data in April 2015 from VIRTIS-M suggest that the rate increases to about 1027 molec/s (Migliorini et al. 2016). The ROSINA spectrometer is an in situ instrument unlike MIRO and VIRTIS, which are remote sounding instruments.
O as (4.9 ± 2.5) × 1025 molec/s on September 7 at 3.41 AU from the Sun (Biver et al. 2015). The ROSINA-COPS (Rosetta Orbiter Spectrometer for Ion and Neutral Analysis − COmetary Pressure Sensor) instrument found production rates in the range of 8.7 × 1025–1.1 × 1026 molec/s between August and November 2014, which then increased by a factor of 2 between November and January 2015 (Bieler et al. 2015). Fougere et al. (2016) present results from ROSINA-DFMS (Double Focusing Mass Spectrometer), which show the outgassing increasing from <1026 molec/s at 3.5 AU (August 2014) to >1027 molec/s at 1.5 AU from the Sun (May 2015). A mean production rate of 8 × 1025 molec/s agrees with results from VIRTIS-H (Visible InfraRed Thermal Imaging Spectrometer) between November 2014 and January 2015 (Bockelée-Morvan et al. 2015), and data in April 2015 from VIRTIS-M suggest that the rate increases to about 1027 molec/s (Migliorini et al. 2016). The ROSINA spectrometer is an in situ instrument unlike MIRO and VIRTIS, which are remote sounding instruments.
Together, these data demonstrate the increasing activity of the comet towards perihelion. In this work, we present the long-term evolution of the water production rate of comet 67P from MIRO observations as it approaches and recedes from the Sun, between August 2014 and April 2016, with the aim to spatially resolve the water outgassing. Through this, we can analyse the behaviour of the comet with respect to heliocentric distance and the change in activity across the surface. We use a lookup table method for the inversion of line areas into column densities and production rates and hence derive local effective Haser production rates of water (defined in Sect. 3.2) from the line area ratios of H216O and H218O. This approach is simple, producing results that are consistent with other measurements from Rosetta instruments along with ground-based observations. Our methodology enables large quantities of data to be inverted quickly and reliably, allowing the production rates from the 21-month MIRO dataset to be calculated in minutes and enabling us to study the outgassing evolution with good spatial resolution. With the spatially resolved data, we can study the processes driving the gas activity and investigate how the shape and illumination modulate this behaviour. The lookup table method is fully described in Sect. 3 along with a thermal sublimation model to help interpret the results, which are given in Sect. 4. The work is then summarised in Sect. 5. The next section gives a brief description of MIRO, the observations and the shape model.
2. MIRO observations
The Microwave Instrument for the Rosetta Orbiter (MIRO) is a small millimetre/sub-millimetre spectrometer with a 30 cm offset parabolic reflector telescope and two heterodyne receivers. The millimetre receiver operates at a centre-band frequency of 188 GHz (1.6 mm wavelength) while the sub-millimetre receiver is tuned at 562 GHz (0.5 mm). Each frequency band contains a single broadband channel for the measurement of near surface temperatures. The continuum data have been previously analysed by Schloerb et al. (2015) and for polar night conditions by Choukroun et al. (2015). For our work, we are interested in the data from the Chirp Transform Spectrometer (CTS; Hartogh & Hartmann 1990), which is connected to the sub-millimetre receiver.
The CTS has 4096 channels with a spectral resolution of 44 kHz, corresponding to a resolution of ν/ Δν = 107 for the sub-mm channel. It can observe three isotopologues of water (H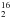 O, H
O, H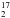 O, and H
O, and H O), three methanol lines, carbon monoxide and ammonia at frequencies of 547 GHz to 580 GHz. A high spectral resolution is necessary for observing the narrow, Doppler broadened spectral lines of the low temperature, low pressure coma. MIRO collects spectral data every 30 s in a frequency switched mode. For the full technical details of the instrument, see Gulkis et al. (2007). We focus on the MIRO data collected from 3.62 AU in August 2014 to 1.24 AU at perihelion on August 13, 2015, and on the outbound leg to 2.02 AU in April 2016. In this time interval, the nucleus of the coma was fully resolved during the nadir observations.
O), three methanol lines, carbon monoxide and ammonia at frequencies of 547 GHz to 580 GHz. A high spectral resolution is necessary for observing the narrow, Doppler broadened spectral lines of the low temperature, low pressure coma. MIRO collects spectral data every 30 s in a frequency switched mode. For the full technical details of the instrument, see Gulkis et al. (2007). We focus on the MIRO data collected from 3.62 AU in August 2014 to 1.24 AU at perihelion on August 13, 2015, and on the outbound leg to 2.02 AU in April 2016. In this time interval, the nucleus of the coma was fully resolved during the nadir observations.
We use a digital shape model of the comet (SHAP5 v1.2, Preusker et al. 2015) with 200 000 triangular facets and the SPICE software provided by the Jet Propulsion Laboratory (JPL; Acton 1996) to calculate the intersection geometry. With the shape model, the SPICE software and the beam pointing provided by the project, we can track the movement of the spacecraft and the comet to determine the facet-averaged position of the MIRO beam, solar illumination, solar zenith angle and viewing angle.
 |
Fig. 1 Time evolution of the line area of H |
3. Method
We employed an efficient method using lookup tables to determine the water production rate of comet 67P. The basic idea of lookup table inversion is straight forward. We precalculated a table of water production rate, Q, versus line area via a forward radiative transfer model (Sect. 3.2). Once the tables are calculated, the radiative transfer calculations are no longer required, and the measured line area ratios entered into a lookup table obtain the corresponding water production rate. In the application to the MIRO data, we used additional information to provide more unique mapping (using more than one table), such as the observed Doppler shift and continuum temperature. It is necessary to use more than one lookup table to test the sensitivity of the production rate measurements to each variable (Doppler shift and continuum temperature). We considered only nadir absorption spectra in this work and treated the line area ratio, H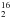 O/H
O/H O, as the fundamental variable. Below, the details of the methodology and measurement selection are provided.
O, as the fundamental variable. Below, the details of the methodology and measurement selection are provided.
Our approach is different from work by Biver et al. (2016), who have tracked the change in the global water production of 67P with heliocentric distance, as well as other molecules. In this work, we looked exclusively at nadir observations of the comet to derive local production rates and we neglected any geometrical effects. We then used the local production rates to track the evolution of the outgassing in each region as function of heliocentric distance.
3.1. Water absorption lines
In this analysis we focus only on the nadir absorption lines for the two water isotopes, H216O and H218O owing to their different opacities, and because they are routinely detected in the time period of interest (August 2014 to April 2016). Examples of these absorption lines can be seen in Gulkis et al. (2015), Biver et al. (2015), and Lee et al. (2015) (Fig. 3), where the latter makes a distinction between the appearance of nadir, off-nadir, and limb viewing spectra. Processing the spectra involves several steps. First, we excluded spectra with low signal to noise (the line area must be greater than 2 K km s-1 for both isotopes), and then we excluded any emission lines, including limb and partial limb spectra. The 2 K km s-1 value for the noise limit was determined by calculating the average line area for continuum emission spectra without a line feature and with only random noise. The observations were averaged into 30-minute time intervals to reduce random noise; for example, in April 2016, the noise level decreased from 1 K km s-1 to 0.14 K km s-1 as we increased the time interval for averaging the spectra from 30 s to 30 min. Subsequently, we smoothed the spectra with an 8 point box car filter. This smoothing has a minimal effect on the determination of the spectral line areas (<0.1%), but allows for a better determination of the Doppler shift by the automatic lookup method. The Doppler shift was simply calculated from the velocity shift of the minimum value of an absorption line.
We found the line area by integrating in the region where the line forms, between –2 and 1.1 km s-1, which is wide enough to ensure that broadened lines are not cut off even for the wide H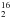 O lines in the case of high gas production. The estimates for the line area error come from the random noise in the line wings (greater than 1.2 km s-1) and calculated with the equation,
O lines in the case of high gas production. The estimates for the line area error come from the random noise in the line wings (greater than 1.2 km s-1) and calculated with the equation, 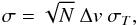 (1)where N is the number of data points between –2 and 1.1 km s-1, Δv is the average velocity interval between each point in the spectrum, and σT is the standard deviation of the antenna temperature points in the wings (>1.2 km s-1).
(1)where N is the number of data points between –2 and 1.1 km s-1, Δv is the average velocity interval between each point in the spectrum, and σT is the standard deviation of the antenna temperature points in the wings (>1.2 km s-1).
In Fig. 1, the time evolution of the nadir line areas for the two isotopes are presented. For both isotopologues, the activity increases towards perihelion owing to the increase in outgassing, and decreases after perihelion, but with a delay (discussed later). The line area uncertainties due to random noise are small, typically 0.2 K km s-1 for both isotopologues with measurements in the range of 13–385 K km s-1 for H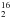 O and from 2–135 K km s-1 for H
O and from 2–135 K km s-1 for H O (see Fig. 1).
O (see Fig. 1).
The line area ratio is a sensitive tracer of opacity and column density in the coma (Fig. 1). Providing that the optical depth is less than unity, the line area is linearly related to the column density. However, as the column density increases further, line area growth loses this linearity and the dependence becomes 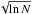 , where N is the number density (Goldsmith & Langer 1999). The line is said to be saturated, as the amplitude does not change with increasing column density. The H
, where N is the number density (Goldsmith & Langer 1999). The line is said to be saturated, as the amplitude does not change with increasing column density. The H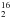 O and H
O and H O lines observed by MIRO follow this pattern. Because these two lines have different opacities, the H
O lines observed by MIRO follow this pattern. Because these two lines have different opacities, the H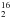 O line is always saturated with an opacity >10 (Gulkis et al. 2015) whereas the H
O line is always saturated with an opacity >10 (Gulkis et al. 2015) whereas the H O line starts out with a small amplitude and is optically thin (opacity <0.1) but then grows with the column density. By combining them in a ratio we produce a more favourable line growth curve with greater sensitivity as we approach the saturated part of the growth curve.
O line starts out with a small amplitude and is optically thin (opacity <0.1) but then grows with the column density. By combining them in a ratio we produce a more favourable line growth curve with greater sensitivity as we approach the saturated part of the growth curve.
In Fig. 1, the ratio indicates that in August 2014 the H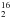 O is optically thick as the highest values are around 60–70, much lower than the isotopic ratio of 498.7 (terrestrial value). The ratios further decrease towards the perihelion as even the H
O is optically thick as the highest values are around 60–70, much lower than the isotopic ratio of 498.7 (terrestrial value). The ratios further decrease towards the perihelion as even the H O line becomes optically thick, and the ratio reaches values as low as 2.5. About 90 days after perihelion the ratio grows again significantly as the water production goes down.
O line becomes optically thick, and the ratio reaches values as low as 2.5. About 90 days after perihelion the ratio grows again significantly as the water production goes down.
3.2. Generating the lookup tables
We performed the lookup table calculations with a non-LTE forward model. For radiative transfer in comets, two different computational methods are typically used: a locally approximated escape probability approach (Bockelée-Morvan 1987; Litvak & Kuiper 1982) and a direct ray transfer Monte Carlo approach (Hogerheijde & van der Tak 2000). Both methods have been found to produce similar results numerically (Zakharov et al. 2007) and in comparison to observations (Hartogh et al. 2010; de Val-Borro et al. 2010). Building a lookup table involves hundreds of calculations, which with the Monte Carlo approach, would take weeks to compute. We instead used the escape probaility approach following Lee et al. (2015) (see references therein for detailed description and accuracy), which required substantially less computational time.
The atmospheric inputs are defined radially over 500 km from the nucleus surface with grid points (integer index i) calculated at 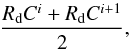 (2)where Rd is the radius of the comet, taken as 2 km, multiplied by a scaling constant, C = 1.02, to define 278 logarithmic grid points over 500 km. The temperature profile follows an adiabatic expansion. The inputs are the surface temperature parameter, Ts, and the terminal temperature, which is estimated from the line cores of the H
(2)where Rd is the radius of the comet, taken as 2 km, multiplied by a scaling constant, C = 1.02, to define 278 logarithmic grid points over 500 km. The temperature profile follows an adiabatic expansion. The inputs are the surface temperature parameter, Ts, and the terminal temperature, which is estimated from the line cores of the H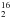 O lines observed by MIRO and fixed at 30 K. The velocity profile is modelled by a hyperbolic tangent function and increases from zero to the terminal expansion velocity, vexp, as described in Lee et al. (2015). The radial molecular number density profile is dictated by the Haser model (Haser 1957) which depends on the production rate, Q, expansion velocity profile and β parameter, which is also taken from Lee et al. (2015). The β parameter is the photodissociation rate with a value of 1.4 × 10-5 s-1 at a distance of 1 AU, but it is not critical for deriving Q. In addition, we assume the H
O lines observed by MIRO and fixed at 30 K. The velocity profile is modelled by a hyperbolic tangent function and increases from zero to the terminal expansion velocity, vexp, as described in Lee et al. (2015). The radial molecular number density profile is dictated by the Haser model (Haser 1957) which depends on the production rate, Q, expansion velocity profile and β parameter, which is also taken from Lee et al. (2015). The β parameter is the photodissociation rate with a value of 1.4 × 10-5 s-1 at a distance of 1 AU, but it is not critical for deriving Q. In addition, we assume the H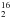 O/H
O/H O ratio and the ortho-para ratio to be 500 and 3, respectively, in our forward calculations, as in previous works. In total, three atmospheric parameters are varied to generate two lookup tables for the water production rate: the surface temperature, Ts (K); the terminal expansion velocity, vexp (km s-1); and Q (molec s-1).
O ratio and the ortho-para ratio to be 500 and 3, respectively, in our forward calculations, as in previous works. In total, three atmospheric parameters are varied to generate two lookup tables for the water production rate: the surface temperature, Ts (K); the terminal expansion velocity, vexp (km s-1); and Q (molec s-1).
In the first table, the production rate varies from 1023 to 1030 molecules s-1 over seven different velocities (0.4–1 km s-1) and produces the curves given in Fig. 2. To avoid interpolation within the tables, a ninth order polynomial is fitted through each curve with an accuracy of >0.02%, which then provides an analytic expression for each function. The errors on the ratios are treated as upper and lower bounds which are also calculated with the same polynomial equation to give the errors on the production rates. Only the production rate and velocity parameters are varied; the surface temperature parameter, Ts, is kept at 200 K in the temperature profile.
 |
Fig. 2 Log-log plot of the H |
In order to correct the measurements for temperature sensitivity, we created a second lookup table. It is made in a similar way but now Ts is allowed to vary from 50–300 K, while the velocity parameter is held at a constant value of 0.7 km s-1. Variations in Ts would change the line contrast. The production rate ranges from 1024 to 1029 molec s-1. Here, for each value of the production rate, the temperature is increased and the ratio between the two absorption lines is calculated again. Figure 3 shows these functions with line area ratio versus continuum temperature. Each contour line represents a different production rate with the lowest rate (1024 molec s-1) at the top of the figure and the highest rate (1029 molec s-1) at the bottom. We took the measured MIRO data, overplotted them onto these curves, and performed a linear interpolation between the lines to find the water production rate. This was also performed for the line area ratio errors as before to produce upper and lower bounds on the production rate estimates. For each production rate, as the continuum temperature increases, the ratio between the two absorption lines also increases.
The weaker H O line is formed mainly near the nucleus. The temperature decreases from the surface, so there is a smaller contrast between the H
O line is formed mainly near the nucleus. The temperature decreases from the surface, so there is a smaller contrast between the H O line core and the continuum temperature. On the other hand, the opaque H
O line core and the continuum temperature. On the other hand, the opaque H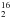 O line forms further from the nucleus, at altitudes where the temperature profile is approaching the terminal temperature (estimated to be 30 K, as discussed earlier in this section), and therefore has a larger contrast. Increasing the continuum temperature therefore increases the ratio of line areas between the strong and weak lines.
O line forms further from the nucleus, at altitudes where the temperature profile is approaching the terminal temperature (estimated to be 30 K, as discussed earlier in this section), and therefore has a larger contrast. Increasing the continuum temperature therefore increases the ratio of line areas between the strong and weak lines.
 |
Fig. 3 Log-linear plot of the H |
A second lookup table is needed to test the sensitivity of the production rates to temperature, which was assumed to be constant in the first lookup table. The effect of this second table is a small correction which typically increases the production rates derived from the first lookup table by about 20–25%. The relative uncertainty on the production rates with these lookup tables are in the range of 30–50%. This uncertainty grows though with increasing Q when Q> 1028. This particular method is not suitable for deriving water production rates where Q> 1029 as the line area versus production rates loses sensitivity above this threshold because both the H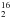 O and H
O and H O lines become saturated. As illustrated in Figs. 2 and 3, the close spacing of the contour lines limits the accuracy on determining Q from the lookup tables, but as we want to examine the relative behaviour of the production rate from the comet, this method still provides fast and reliable information.
O lines become saturated. As illustrated in Figs. 2 and 3, the close spacing of the contour lines limits the accuracy on determining Q from the lookup tables, but as we want to examine the relative behaviour of the production rate from the comet, this method still provides fast and reliable information.
The Haser model gives the global production rate for a spherical comet but our calculated results are local production rates determined for the viewing position of the beam on the comets surface. Each measurement is then a local effective Haser production rate, meaning that the localised beam viewing spot appears to be outgassing as if it was a spherical comet with a single global production rate. This local effective Haser production rate is proportional to the derived MIRO column density.
3.3. Thermal sublimation model
For later interpretation of results, we now describe a basic thermal model for predicting the water outgassing rate, which relies on the comet A model in Keller et al. (2015). We used the SHAP2 shape model (Sierks et al. 2015), which has fewer facets than SHAP5. We performed the described calculations for each facet of the digital shape model, except that we neglected self-heating mechanisms and shadowing. Keller et al. (2015) compare their A, B, and C models with and without self-illumination and show that self-illumination mainly plays a role when the comet is far away from the Sun (>3.5 AU). In the time period examined here, the difference in water production rate is negligible if self-illumination is ignored. The sublimation rate can be expressed as 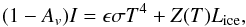 (3)where Av is the bolometric Bond albedo, taken as 0.01, I is the solar flux received by a facet, ϵ = 0.9 is the emissivity, σ is the Stefan-Boltzmann constant, T is the facet temperature, Z is the facet sublimation rate, and Lice = 2.6 × 106 J/kg is the latent heat of sublimation for water ice, which we take to be constant. The sublimation rate, water vapour pressure, and thermal velocity are given by (Eq. (5) from Panale & Salvail 1984)
(3)where Av is the bolometric Bond albedo, taken as 0.01, I is the solar flux received by a facet, ϵ = 0.9 is the emissivity, σ is the Stefan-Boltzmann constant, T is the facet temperature, Z is the facet sublimation rate, and Lice = 2.6 × 106 J/kg is the latent heat of sublimation for water ice, which we take to be constant. The sublimation rate, water vapour pressure, and thermal velocity are given by (Eq. (5) from Panale & Salvail 1984) ![\begin{eqnarray} Z(T) &=& 2P(T) / (\pi v_{\rm th})\\ P(T) &=& 3.56 \times 10^{12} \exp(-6141.667/T)~~[\rm kg ~m^{-1} ~s^{-2}]\\ v_{\rm th}(T) &=& \sqrt{8RT/\pi \mu}. \end{eqnarray}](/articles/aa/full_html/2017/07/aa30502-17/aa30502-17-eq57.png) The surface temperature in this model plateaus at around 200 K, which is the same result found for Model A in Fig. 4 of Keller et al. (2015). It is worth noting the non-linear temperature sensitivity of the water vapour pressure and hence the sublimation rate. Increasing the temperature from 140 K to 200 K also increases the vapour pressure from 10-7Pa to 10-1Pa so that even small variations within this range of temperatures has profound effects on the sublimation rate.
The surface temperature in this model plateaus at around 200 K, which is the same result found for Model A in Fig. 4 of Keller et al. (2015). It is worth noting the non-linear temperature sensitivity of the water vapour pressure and hence the sublimation rate. Increasing the temperature from 140 K to 200 K also increases the vapour pressure from 10-7Pa to 10-1Pa so that even small variations within this range of temperatures has profound effects on the sublimation rate.
The production rate is proportional to the sublimation rate: 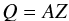 (7)where A is the area of the active surface; we assume all facets to be active. By investigating how and why the sublimation rate changes in this thermal model, we can infer how the production rate changes as well.
(7)where A is the area of the active surface; we assume all facets to be active. By investigating how and why the sublimation rate changes in this thermal model, we can infer how the production rate changes as well.
The shape model gives the average daily illumination of every facet and Eq. (3)allows for the calculation of the temperature and sublimation rate for each facet. With this information, the average temperature and sublimation rate of the facets across the surface can hence be determined for a given day with these averages weighted by the area of each facet. Using the same latitude bins described in Sect. 4.2, we also calculate the average sublimation rate for six subset regions. It is possible to go one step further, and divide the grid into 20 longitude bins and hence calculate the sublimation rate of 120 sections across the surface. The model is used from 250 days before perihelion to 250 days afterwards to track the behaviour of the sublimation rate. The sublimation rate at each point in time is plotted to determine the rh exponents before and after perihelion. The dataset from the thermal model is trimmed so that we only calculate the exponents over the period of time for where there are observations.
4. Results
4.1. Water production rate
Figure 4 shows the derived local effective Haser production rates of water from 250 days before and after perihelion. For comparison, we overplotted other measurements made by instruments on board Rosetta (red) and ground-based observations (blue). In addition, modelled production rates from Keller et al. (2015) are shown for completeness. There is a general qualitative agreement between all the data included; the MIRO estimates derived here from the lookup tables are consistent with early results (–400 to –100 days from perihelion) from VIRTIS-H (Bockelée-Morvan et al. 2015), VIRTIS-M (Migliorini et al. 2016; Fink et al. 2016), ROSINA-DFMS (Fougere et al. 2016), and ROSINA-COPS (Bieler et al. 2015) along with previous MIRO estimates (Gulkis et al. 2015). Around 120 days before and after perihelion, the derived MIRO estimates and ground-based observations (Bertaux et al. 2014; Crovisier et al. 2002; Feldman et al. 2004; Hanner et al. 1985; Ootsubo et al. 2012; Schleicher 2006) are in rather good agreement, although these were made for previous perihelion passages of comet 67P. In addition, a power law line shown in Fougere et al. (2016) and a model result for a comet with a perpendicular spin axis and an active area of 2% from Cowan & A’Hearn (1979) cross through the derived MIRO production rates. Hansen et al. (2016) (not shown in Fig. 4) have derived the long-term variation in the global water production rate of comet 67P from ROSINA data, but our local production rates are generally lower than their findings, as are the VIRTIS measurements (Bockelée-Morvan et al. 2015). We find that the largest local production rate for a single observation is (1.42 ± 0.51) × 1028 molecules s-1 on August 29, 2015, and this is a factor of 3 lower than the maximum outgassing given by Hansen et al. (2016). The difference may be because we derive local Haser production rates whereas their work calculates global production rates. Additionally, the two instruments use different acquisition techniques: ROSINA is an in situ instrument whereas MIRO measures line-of-sight spectra. Hansen et al. (2016) discuss how their result is a factor of two larger than results from VIRTIS, which is also a line-of-sight instrument.
Fourteen-day moving average applied to the local effective Haser production rates of water calculated from the MIRO data.
The scatter seen in the local water production rates are indicative of the variation in latitude from the subsolar point of each observation. In Fig. 4, the peaks in the local effective Haser production rates can be seen to occur when MIRO views latitudes close to the subsolar latitude and conversely, the dips correspond to times when latitudes away from the subsolar latitude are observed.
A 14-day moving average smoothing is applied to the MIRO data to give a qualitative description of the mean behaviour over the observational period, shown in orange and in Table 1. The moving average assumes that day- and night side observations are equally weighted. The water outgassing increases from (3.16 ± 1.00) × 1026 molecules s-1 in the first averaging bin (i.e. 231 days before perihelion, ~2.4 AU from the Sun) to (5.05 ± 2.46) × 1027 molecules s-1 a week before perihelion. Then 245 days after perihelion (the last averaging bin), the water production rate drops to (1.93 ± 0.46) × 1026 molecules s-1. The bias in the latitudinal sampling means that the moving average is close to, but does not represent, the global production rate: the average may over- or underestimate the true global value depending upon the distribution of the observed latitudes. Nevertheless, the qualitative agreement between the moving average and global production rates from other instruments and ground-based observations is good, and these global measurements also fall within the point cloud of the local effective Haser production rates derived in this work.
The black lines for models A and D represent a comet with an even, homogeneous covering of ice across the surface, whereas models E and F represent a comet with a spotted, heterogeneous distribution of ice (Keller et al. 2015). Model A reproduces the production rates reasonably well at perihelion but the model values are higher in comparison to other models during the approach to perihelion as also noted in Keller et al. (2015), who found that results were enhanced by a factor of 16. The case is the same for Model D, which additionally considers thermal inertia. In these two models, all facets are deemed to be active. For models E and F, which have different values of thermal inertia, some facets are switched off and the abundance of ice is increased elsewhere. The production rate around perihelion for these models does not change in comparison to models A and D, but the outgassing is reduced pre and post-perihelion. This is more consistent with the derived MIRO results. Hence, qualitatively, the average two week production rate (orange line) appears to be more consistent with the heterogenous surface outgassing as described in models E and F in Keller et al. (2015). The authors of this paper also found that these two models were more consistent with pre- and post-perihelion ground-based observations (Schleicher 2006; Hanner et al. 1985; Ootsubo et al. 2012) than the other models.
 |
Fig. 4 Top panel: calculated local effective Haser production rates of water from 250 days before and after perihelion from the MIRO dataset (grey). Results from other Rosetta instruments of global production rates (red) and ground-based observations from previous perihelion passages (blue) are shown for comparison as well as results from modelling (black lines). A two-week moving average of the MIRO data is also included (orange line). Bottom panel: the latitude for each MIRO observation (grey points) and the position of the subsolar latitude over time (black line). |
The data also clearly demonstrate that the maximum production is shifted away from perihelion. To investigate this, linear fits are made through the pre- and post-perihelion data that converge on a solution where the two lines intercept. In order to do this, it is necessary to restrict the dataset, as the H O line is small at distances greater than about 2.5 AU (before February 2015). As a consequence, the H
O line is small at distances greater than about 2.5 AU (before February 2015). As a consequence, the H O line area can be below the desired signal-to-noise level and without the lowest line areas, we sometimes miss the highest ratios and therefore the lowest water production rate measurements. This can be seen in Fig. 4 in the apparent plateauing of the MIRO results 180 days before perihelion (orange line). For the offset calculation, we hence restrict the dataset to look at results within 1 AU of perihelion (March 2015–February 2016), where this effect is not prevalent. The intercept from linear fitting in log Q-log rh space gives the solution as 34 ± 10 days after perihelion. Previous work by Bondarenko & Medvedev (2011) and Ferrín (2010) found from cometary light curves that the offset occurred approximately 33 days after perihelion. Schleicher (2006) also found an offset in the peak outgassing from perihelion by 1 month using OH gas production rates. Furthermore, observations of 67P around its three previous perihelion visits (1996, 2002 and 2009) suggest that the activity peaks 16 ± 5 days after perihelion and then again 40 days after perihelion (Bertaux et al. 2014). The offset found here is consistent with Bondarenko & Medvedev (2011), Ferrín (2010) and the second peak from Bertaux et al. (2014), but we are unable to resolve the first peak in this latter work. There is a data gap in mid-September 2015 when the spacecraft goes above 500 km, which limits the determination of the offset. Above 500 km, the MIRO beam is larger than the comet and includes contributions from the background and the nucleus, so MIRO does not collect pure nadir absorption spectra in this period.
O line area can be below the desired signal-to-noise level and without the lowest line areas, we sometimes miss the highest ratios and therefore the lowest water production rate measurements. This can be seen in Fig. 4 in the apparent plateauing of the MIRO results 180 days before perihelion (orange line). For the offset calculation, we hence restrict the dataset to look at results within 1 AU of perihelion (March 2015–February 2016), where this effect is not prevalent. The intercept from linear fitting in log Q-log rh space gives the solution as 34 ± 10 days after perihelion. Previous work by Bondarenko & Medvedev (2011) and Ferrín (2010) found from cometary light curves that the offset occurred approximately 33 days after perihelion. Schleicher (2006) also found an offset in the peak outgassing from perihelion by 1 month using OH gas production rates. Furthermore, observations of 67P around its three previous perihelion visits (1996, 2002 and 2009) suggest that the activity peaks 16 ± 5 days after perihelion and then again 40 days after perihelion (Bertaux et al. 2014). The offset found here is consistent with Bondarenko & Medvedev (2011), Ferrín (2010) and the second peak from Bertaux et al. (2014), but we are unable to resolve the first peak in this latter work. There is a data gap in mid-September 2015 when the spacecraft goes above 500 km, which limits the determination of the offset. Above 500 km, the MIRO beam is larger than the comet and includes contributions from the background and the nucleus, so MIRO does not collect pure nadir absorption spectra in this period.
4.2. Behaviour with heliocentric distance
Linear fitting in log Q-log rh space around perihelion of the local effective Haser production rates, allows for the estimation of the change in water outgassing with heliocentric distance by evaluating the rh exponents, which we define as α. We find that these have values of −3.8 ± 0.2 and −4.3 ± 0.2, within 1 AU pre- and post-perihelion, respectively, taking into account the offset described in the last section. This means that the local effective Haser production rate, Q, across the entire surface is roughly symmetrical and proportional to the heliocentric distance, rh, as approximately 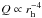 . The thermal modelling described in Sect. 3.3 calculates α for pre- and post-perihelion as −3.5 ± 0.01 and −3.9 ± 0.03 for the entire surface.
. The thermal modelling described in Sect. 3.3 calculates α for pre- and post-perihelion as −3.5 ± 0.01 and −3.9 ± 0.03 for the entire surface.
We further investigated the behaviour by calculating α at different latitudes. We split the dataset into six latitude bins: 90° to 25°; 25° to 0°; 0° to –20°; –20° to –30°; –30° to –45°; and –45° to –90°. These bins were chosen so that each bin has the same number of data points (200). As Fig. 5 shows, α has a latitudinal dependence: the slopes steepen from north to south for pre- and post- perihelion, from rh exponents of about –2 to –6 (right panel). The error bars reflect the standard error of the linear fitting. In addition, the data indicate that there is a line intersection where the post-perihelion slopes are steeper than the pre-perihelion slopes for latitudes greater than 0°, but at more southern latitudes, the slopes are steeper during pre-perihelion than post-perihelion.
To explain this behaviour, we turn to the results of the thermal sublimation model (Keller et al. 2015) which are shown in the left panel of Fig. 5. This panel shows the α values for the sublimation rate before and after perihelion in the six latitude bins. There is also a steepening of the slopes from north to south similar to the trend seen in calculated production rates. The standard deviation reflects the variation in longitude for each latitude bin.
The steepening of the slopes from north to south in the MIRO data and the model can be explained by the rotation axis of the comet which has been found to be tilted by about 50° to the orbital axis and so the subsolar latitude moves from approximately 40°N in August 2014 to –50°S in September 2015, just after perihelion (Keller et al. 2015). The northern latitudes are well illuminated when the comet is further away from the Sun (3.5 AU) but not illuminated during perihelion when the received solar flux increases. As a result, the surface temperature of the northern hemisphere does not change that much in the period for which there are observations and, therefore, neither does the sublimation rate, which is very sensitive to changes in temperature, as already discussed. Conversely, the southern latitudes are not illuminated when the comet is more than 1.8 AU from the Sun, but very well illuminated at perihelion. The change in the surface temperature of the southern hemisphere is quick and as a result, so is the sublimation rate. The resulting exponents for the southern hemisphere are therefore less than in the northern hemisphere.
The line intersection described above is also present in the model, as the post-perihelion slopes are steeper than the pre-perihelion slopes at northern latitudes but the situation is reversed at southern latitudes. In the southern hemisphere, during the pre-perihelion phase, the surface temperature increases very suddenly before perihelion but the decrease in temperature afterwards is slower, so the slope for the sublimation rate is steeper before perihelion than afterwards. For the northern hemisphere, during the approach to perihelion, the sublimation rate changes very little and only increases slightly, whereas the decrease is more pronounced after the approach to perihelion.
The data and model results show that α varies with latitude and that a single α value representing the whole comet surface may not be of fundamental significance. The production rate is a strong non-linear function of temperature, which in turn, depends upon the shape, morphology, and obliquity of the comet, along with the rate of change of illumination; therefore a single α value on its own may not reveal much about comet activity. It appears that the same distribution of ices over a sphere would produce completely different results for α. The latitudinal dependence is more important and it can help to reveal areas of the comet that are particularly active or inactive. This can only be investigated by in situ measurements as collected by MIRO.
There are some differences between the α values from the measured production rates and the calculated sublimation rates. However, all of the measurements from the MIRO data are within 1 standard deviation from the model results except for the post-perihelion points north of –20 latitude and the pre-perihelion point north of 25°, which are within 2 standard deviations and have overlapping error bars. For most of points, the standard deviation is between 0.7 and 1.5 but the more southern latitudes have a much larger variation in longitude pre-perihelion. We have already stated that the more southern latitudes experience a sudden increase in temperature but owing to the local morphology of the surface it can be even more extreme at some longitudes than at others. There is then, a broad range of possible α values across the longitudinal plane. Despite the simplicity of the thermal sublimation model that we used here, it captures and reproduces much of the behaviour seen in the MIRO data to a good degree of accuracy. One of our modelling assumptions is that the active area is constant across the comet, which is probably not true (Keller et al. 2015). In addition, the highest (>70°) and lowest latitudes (<–80°) are not really sampled by MIRO and could be excluded from the model; also there may be a longitudinal sampling bias in the data, although this is accounted for in the error bars of the model.
 |
Fig. 5 Left: modelled pre- and post-perihelion slopes (α) of water sublimation rate as a function of latitude averaged over several bins (see text for detailed description). Right: pre- and post-perihelion slopes of water production rate from the data derived from MIRO measurements. The error bars on the modelled data reflect longitudinal variability, which is very large in southern hemisphere owing to rapid temperature variations. The MIRO data error bars also reflect the data variability at 1σ level. |
It should be noted that there is a slight difference between how the sublimation rate and the MIRO production rates are calculated. The sublimation rate is calculated from the thermal model, which takes into account a whole latitude band, spanning the day- and night sides, and all longitudes. On the other hand, the production rates only come from a spot on the nucleus where the MIRO beam is observing, which could be day or night, and only at a certain longitude. However, with an appropriate level of sampling (approximately 200 MIRO measurements per latitude bin) enough of the surface is observed to average out the effects of longitudinal variance. A more sophisticated approach where only the facets of the shape model observed by the beam are used to calculate the sublimation rate would be more representative of the actual measurements, but the simple thermal model has captured the essence of the results and can explain some of the features.
4.3. Regional variations
The large dataset obtained through the fast inversion can be also spatially partitioned to study regional activity variations using the latitude and longitude co-ordinates of the beam position. There are 26 identified regions on 67P defined by El-Maarry et al. (2016) and we can identify the regional source of the produced water from the shape model using the average beam position for each measurement.
 |
Fig. 6 Change in water production rate 250 days before and after perihelion sorted by regions, as defined by El-Maarry et al. (2016). The first panel shows the results from the six southernmost regions, Anhur, Geb, Bes, Sobek, Neith, and Wosret. The largest production rates are found here, specifically from the Bes, Wosret, and Neith regions. The second panel contains the results from four regions located around –30° latitude: Atum, Anubis, Khonsu, and Imhotep. These show reasonable outgassing rates (as high as ~ 9 × 1027 molec s-1) and Imhotep in particular is well sampled in this time frame. Six regions that straddle the equator are in the third panel: Ap, Anuket, Maftet, Bastet, Khepry, and Aker. These is an apparent drop here in the production rate around perihelion as we start to look at more northern regions. Seth, Ash, Aten, Babi, and Hapi − the five northernmost regions – are in the fourth panel. Even though these regions do not receive much solar flux due to the rotation axis of the comet, Seth and Ash are still quite active. The remaining five regions, Hathor, Hatmehit, Ma’at, Nut, and Serqet are all located on the head lobe and shown in the fifth panel. The average daily solar flux for each region is shown underneath for comparison. |
First, however, if we assume that molecules move radially away from the comet, then we must restrict our dataset to measurements with a low viewing angle (i.e. the angle between surface normal and beam direction) to ensure that we are only observing the production from the region that we are interested in. Using a large viewing angle means that the MIRO beam cuts through layers of the coma where the water production originates from other areas. We hence choose measurements with a viewing angle of less than 30° to reduce the uncertainty in the regional location of the MIRO beam. This is calculated from the SHAP5 shape model and it is the average viewing angle of all the facets within the beam. We assume that all the contributions to the local effective Haser production rate in the line of sight originate from the MIRO footprint beam. This assumption is only an approximation as it is possible that a particular line-of-sight column density is influenced by other regions owing to the complex nucleus shape and larger phase angles. These potential contributions should be carefully quantified, but it is out of the scope of this work.
The results are given in Fig. 6, showing regional variations in the water outgassing across the surface of the comet. The average daily solar flux for each region is given in the lower panel for comparison. It is calculated from the solar flux constant and the average cosine solar zenith angle for each facet within the region.
For all regions, the water production rate increases as 67P approaches perihelion and decreases afterwards. The change in production rate is not uniform though. The southernmost regions (Anhur, Geb, Bes, Sobek, Neith and Wosret) experience a dramatic change in outgassing and are the origins of the largest measured production rates around perihelion. As already mentioned, the subsolar latitude moves south and goes below –50° latitude just after perihelion. These southernmost regions are therefore the most illuminated and receive the largest amount of flux at perihelion (between 400 and 600 W/m2). This may result in a stronger depletion of water and potentially other volatiles in these regions.
There are four regions (Atum, Anubis, Khonsu, and Imhotep) at about –30° latitude that are also reasonably well illuminated around perihelion (with fluxes between 200 and 400 W/m2) and have reasonable local effective Haser production rates (as high as ~9 × 1027 molec s-1), although these are slightly lower than most southern regions. As we look further north, to the equator, the water production rates from Ap, Anuket, Maftet, Bastet, Khepry, and Aker are considerably smaller. Due to the obliquity, the northern regions spend most of their time facing away from the Sun at perihelion (whilst the southern hemisphere is well illuminated) so the received flux is lower. This explains why the H2O outgassing is lower as we look towards northern latitudes. Indeed, for the regions around the north pole (Seth, Ash, Aten, Babi, and Hapi) as well as on the head lobe (Hathor, Hatmehit, Ma’at, Nut, and Serqet), the production rates are found to be about 50% lower than in the south at perihelion.
Generally, the regions with high received solar fluxes (>200 W/m2) have consistently high water production rates (see two leftmost panels in Fig. 6) and that insolation explains most of the activity. In the other regions, the flux is lower (<200 W/m2) and the production rates are suppressed. It is notable that, for all regions, the largest production rates are shifted towards perihelion even though in some areas, the received flux is low: for example, in Seth and Ash, the flux drops below 100 W/m2 but several of the production rate measurements are as high as those seen in the well-illuminated southern regions. Possibly in regions like these, solar insolation is not the only driver of activity but it is hard to draw too many concrete conclusions. It is also possible that these large production rates seen in Seth and Ash include contributions in the line of sight of the MIRO beam from other outgassing areas. A more in-depth study of these and other measurements is needed to properly identify any particularly active or inactive areas from the MIRO dataset.
5. Conclusions
The line area lookup tables method is a fast and computationally inexpensive way to calculate the production rate of water from comet 67P/Churyumov-Gerasimenko. Our results are consistent with measurements from other Rosetta instruments as well as ground-based observations and produces the time dependence accurately. The uncertainty on each water production rate measurement is between 30%–50%. Systematic errors dominate the uncertainty, as can be seen in Fig. 2, for example, where the ratio curves converge to unity and are flat for large water production rates, so errors in the ratio can give large error bounds on these estimates. In fact, when Q> 1029, this method does not provide accurate results as the uncertainty can be a factor of 2–3. The errors in the line area measurements from random noise are small, as detailed in Sect. 3.1. The retrieved data variability in a given time period is of the order of σ = 2, which reflects true data variability due to illumination and nucleus inhomogeneities, but also includes modelling errors from simplifications. These however, do not contribute more than 50%. The rapid inversion approach enables us to obtain nearly complete data coverage on the nucleus over time, and study in detail the spatial distribution of outgassing activity and the evolution with heliocentric distance. In combination with the shape model, the dataset can be partitioned by location on the nucleus surface with latitude and longitude co-ordinates. With this, we can determine active regions of the comet and investigate why the activity changes.
The following conclusions can be drawn from the results:
-
During the approach to perihelion, the derived results for the localeffective Haser production rates of water are consistent withprevious global production rates measured by MIRO, ROSINAand VIRTIS.
-
The MIRO 14-day mean average changes by an order of magnitude during the 500-day window around perihelion: 231 days beforehand, the outgassing rate is (3.24 ± 1.79) × 1026 molec s-1, a week before perihelion it is (5.05 ± 2.46) × 1027 molec s-1, and then 245 days after perihelion it decreases to (1.72 ± 0.54) × 1026 molec s-1.
-
By integrating this average outgassing curve, the comet is found to have lost (2.4 ± 1.1) × 109 kg of water in this time period, which for a dust-to-gas ratio γ = 4 (Rotundi et al. 2015) is (1.2 ± 0.6) × 1010 kg of material or 0.12 ± 0.06% of the comets mass, assuming a total mass of 1.0 × 1013 kg (Sierks et al. 2015). For comparison, Hansen et al. (2016) give the mass loss of water as 6.4 × 109 kg from 3.6 AU inbound to 3.0 AU outbound and a mass loss of 4–8 × 1010 kg in this period. Both of these results are a little higher than what we report here. Additionally, Bertaux (2015) derived a water mass loss of (2.7 ± 0.4) × 109 kg per orbit from SWAN/SOHO measurements and Keller et al. (2015) calculated the comet would lose 6.5 × 1010 kg of water during an orbit within their Model A. This latter result is significantly higher than what is derived here for the MIRO results but this is to be expected: Model A in their work assumes a homogeneously active surface, which leads to production rates that are as much as 16 times higher than observations during the early perihelion passage and therefore leads to a higher estimate for the water production over one orbit.
-
The maximum local effective Haser production rate of a single observation occurs on August 29, 2015 with a value of (1.42 ± 0.51) × 1028 molec s-1 or (426 ± 153) kg s-1. The outgassing appears to peak 34 ± 10 days after perihelion. These results are also consistent with ground-based observations of 67P from previous apparitions.
-
Linear fitting in log Q-log rh space finds that the change in the water production rate across the surface of the comet follows power laws of
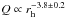 pre-perihelion and
pre-perihelion and 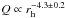 post-perihelion. A thermal sublimation model derives similar values for the exponents with values of −3.5 ± 0.01 and −3.9 ± 0.03, respectively. The MIRO results also indicate that there is a latitudinal dependence on the production rate for which northern and southern regions have rh exponents (α), as seen in Fig. 5. This can be explained by the orientation and orbit of the comet. The sublimation rate model driven by the solar illumination indicates that the northern hemisphere does not experience dramatic illumination changes during perihelion approach and it is in shadow 20 days before perihelion. On the other hand, the southern hemisphere suddenly becomes illuminated at perihelion, causing a dramatic increase in the sublimation rate. The subsolar latitude moves south quickly in the first half of 2015 but the return north is slower after perihelion.
post-perihelion. A thermal sublimation model derives similar values for the exponents with values of −3.5 ± 0.01 and −3.9 ± 0.03, respectively. The MIRO results also indicate that there is a latitudinal dependence on the production rate for which northern and southern regions have rh exponents (α), as seen in Fig. 5. This can be explained by the orientation and orbit of the comet. The sublimation rate model driven by the solar illumination indicates that the northern hemisphere does not experience dramatic illumination changes during perihelion approach and it is in shadow 20 days before perihelion. On the other hand, the southern hemisphere suddenly becomes illuminated at perihelion, causing a dramatic increase in the sublimation rate. The subsolar latitude moves south quickly in the first half of 2015 but the return north is slower after perihelion. -
The retrieved local effective Haser production rates can also be used to identify the most active regions on the comet, particularly those that experience an increase in illumination around perihelion. The southernmost regions, including Wosret, Neith, and Bes, are the most active regions in this period. Despite the fact that the received solar flux in the northernmost regions and on the head lobe drops significantly (see rightmost panels in Fig. 6), the local effective Haser water production rates can still be relatively high; for example, in the Seth region just after perihelion, the production rate was measured to be ~ 9 × 1027 molec s-1 even though the average daily flux was ~50 W/m2. Further work is needed to quantify the effects of geometry and phase angle on the water column determination from these particular regions.
As noted by Maquet (2015) and Guzzo & Lega (2015), comet 67P has had a chaotic orbital history. It was only brought onto an orbit with a perihelion distance of 1.3 AU after a close encounter with Jupiter in 1959. The comet has now experienced nine perihelion passages at this distance. Before the 1959 encounter with Jupiter, the estimated closest approach to the Sun was 2.7 AU. Even though this comet might have spent most of its time relatively far from the Sun, it is likely that the major observed geomorphological forms, the apparent layering, and the variations in lateral volatile ice are all a result of evolutionary processing (Guilbert-Lepoutre et al. 2016). In addition, the loss of volatiles is currently modulated by the actual nucleus shape and spin axis orientation (Keller et al. 2015). Modern models of the long-term evolution of cometary bodies demonstrate that even a non-uniform surface albedo distribution produces varying thermal gradients, which leads to inhomogeneous ice distribution and composition (Guilbert-Lepoutre & Jewitt 2011). Rosenberg & Prialnik (2010) also show strong evidence that an initial heterogeneous distribution of internal porous ice patches strongly affects the production rates and mass loss. In this connection, it is conceivable that the chaotic path of 67P may have induced the radial and lateral distribution of the cometary refractory and volatile content in the comet, which could explain the observed activity pattern of different volatiles. Huebner et al. (2006) provide a comprehensive overview of the effects of multi-stage injection into the inner solar system on the internal structure of the nucleus. Hence, establishing a possible relationship between the present state and the original state of the comet is an important but difficult and unresolved task, which includes the estimates of the fraction of volatiles that the comet 67P has lost so far. Appropriate modelling efforts are needed to yield insights into these questions.
Acknowledgments
The authors acknowledge support from their institutions and funding agencies. The research was carried out at the Max-Planck-Institut für Sonnensystemforschung with financial support from the Max Planck Geselleschaft within the IMPRS programme.
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J.-L. 2015, A&A, 583, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertaux, J.-L., Combi, M., Quémerais, E., & Schmidt, W. 2014, Planet. Space Sci., 91, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biver, N., Hofstadter, M., Gulkis, S., et al. 2015, A&A, 583, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biver, N., Hofstadter, M., von Allmen, P., et al. 2016, in AAS/Division for Planetary Sciences Meeting Abstracts, 48 [Google Scholar]
- Bockelée-Morvan, D. 1987, A&A, 181, 169 [NASA ADS] [Google Scholar]
- Bockelee-Morvan, D., Biver, N., Crovisier, J., et al. 2010, in BAAS, 42, 946 [Google Scholar]
- Bockelée-Morvan, D., Debout, V., Erard, S., et al. 2015, A&A, 583, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondarenko, Y. S., & Medvedev, Y. D. 2011, Sol. Sys. Res., 45, 330 [Google Scholar]
- Choukroun, M., Keihm, S., Schloerb, F., et al. 2015, A&A, 583, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, J. J., & A’Hearn, M. F. 1979, The Moon and the Planets, 21, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J., Colom, P., Gérard, E., Bockelée-Morvan, D., & Bourgois, G. 2002, A&A, 393, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Hartogh, P., Crovisier, J., et al. 2010, A&A, 521, L50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Bockelée-Morvan, D., Jehin, E., et al. 2014, A&A, 564, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Maarry, M., Thomas, N., Gracia-Berná, A., et al. 2016, A&A, 593, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, P. D., A’Hearn, M. F., & Festou, M. C. 2004, in The New Rosetta Targets (Springer), 47 [Google Scholar]
- Ferrín, I. 2010, Planet. Space Sci., 58, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, U., Doose, L., Rinaldi, G., et al. 2016, Icarus, 277, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Fougere, N., Altwegg, K., Berthelier, J.-J., et al. 2016, A&A, 588, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert-Lepoutre, A., & Jewitt, D. 2011, ApJ, 743, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert-Lepoutre, A., Rosenberg, E. D., Prialnik, D., & Besse, S. 2016, MNRAS, 462, S146 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Frerking, M., Crovisier, J., et al. 2007, Space Sci. Rev., 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Guzzo, M., & Lega, E. 2015, A&A, 579, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanner, M., Tedesco, E., Tokunaga, A., et al. 1985, Icarus, 64, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Hartogh, P., & Hartmann, G. 1990, Measurement Science, 1, 592 [Google Scholar]
- Hartogh, P., Crovisier, J., de Val-Borro, M., et al. 2010, A&A, 518, L150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haser, L. 1957, Bull. Soc. Roy. Sci. Liège, 43, 740 [Google Scholar]
- Hogerheijde, M. R., & van der Tak, F. F. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
- Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, Heat and gas diffusion in comet nuclei (International Space Science Institute) [Google Scholar]
- Keller, H. U., Mottola, S., Davidsson, B., et al. 2015, A&A, 583, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, S., von Allmen, P., Allen, M., et al. 2015, A&A, 583, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Litvak, M., & Kuiper, E. R. 1982, ApJ, 253, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Maquet, L. 2015, A&A, 579, A78 [Google Scholar]
- Migliorini, A., Piccioni, G., Capaccioni, F., et al. 2016, A&A, 589, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ootsubo, T., Kawakita, H., Hamada, S., et al. 2012, ApJ, 752, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Panale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenberg, E. D., & Prialnik, D. 2010, Icarus, 209, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, 3905 [Google Scholar]
- Schleicher, D. G. 2006, Icarus, 181, 442 [CrossRef] [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharov, V., Bockelée-Morvan, D., Biver, N., Crovisier, J., & Lecacheux, A. 2007, A&A, 473, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Fourteen-day moving average applied to the local effective Haser production rates of water calculated from the MIRO data.
All Figures
 |
Fig. 1 Time evolution of the line area of H |
| In the text | |
 |
Fig. 2 Log-log plot of the H |
| In the text | |
 |
Fig. 3 Log-linear plot of the H |
| In the text | |
 |
Fig. 4 Top panel: calculated local effective Haser production rates of water from 250 days before and after perihelion from the MIRO dataset (grey). Results from other Rosetta instruments of global production rates (red) and ground-based observations from previous perihelion passages (blue) are shown for comparison as well as results from modelling (black lines). A two-week moving average of the MIRO data is also included (orange line). Bottom panel: the latitude for each MIRO observation (grey points) and the position of the subsolar latitude over time (black line). |
| In the text | |
 |
Fig. 5 Left: modelled pre- and post-perihelion slopes (α) of water sublimation rate as a function of latitude averaged over several bins (see text for detailed description). Right: pre- and post-perihelion slopes of water production rate from the data derived from MIRO measurements. The error bars on the modelled data reflect longitudinal variability, which is very large in southern hemisphere owing to rapid temperature variations. The MIRO data error bars also reflect the data variability at 1σ level. |
| In the text | |
 |
Fig. 6 Change in water production rate 250 days before and after perihelion sorted by regions, as defined by El-Maarry et al. (2016). The first panel shows the results from the six southernmost regions, Anhur, Geb, Bes, Sobek, Neith, and Wosret. The largest production rates are found here, specifically from the Bes, Wosret, and Neith regions. The second panel contains the results from four regions located around –30° latitude: Atum, Anubis, Khonsu, and Imhotep. These show reasonable outgassing rates (as high as ~ 9 × 1027 molec s-1) and Imhotep in particular is well sampled in this time frame. Six regions that straddle the equator are in the third panel: Ap, Anuket, Maftet, Bastet, Khepry, and Aker. These is an apparent drop here in the production rate around perihelion as we start to look at more northern regions. Seth, Ash, Aten, Babi, and Hapi − the five northernmost regions – are in the fourth panel. Even though these regions do not receive much solar flux due to the rotation axis of the comet, Seth and Ash are still quite active. The remaining five regions, Hathor, Hatmehit, Ma’at, Nut, and Serqet are all located on the head lobe and shown in the fifth panel. The average daily solar flux for each region is shown underneath for comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


