| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201630143 | |
| Published online | 30 June 2017 | |
Simultaneous detection and analysis of optical and ultraviolet broad emission lines in quasars at z ~ 2.2⋆,⋆⋆
1 Dipartimento di Fisica e AstronomiaUniversità di Firenze, via G. Sansone 1, 50019 Sesto Fiorentino, Firenze, Italy
e-mail: susanna@arcetri.astro.it
2 INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
3 APC, Astroparticules et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
4 Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, PR China
5 Department of Astronomy, School of Physics, Peking University, Beijing 100871, PR China
6 Max-Planck Institüt für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching bei München, Germany
Received: 25 November 2016
Accepted: 23 February 2017
We studied the spectra of six z ~ 2.2 quasars obtained with the X-shooter spectrograph at the Very Large Telescope. The redshift of these sources and the X-shooter’s spectral coverage allow us to cover the rest of the spectral range ~1200−7000 Å for the simultaneous detection of optical and ultraviolet lines emitted by the broad-line region. Simultaneous measurements, avoiding issues related to quasars variability, help us understand the connection between the different broad-line region line profiles generally used as virial estimators of black hole masses in quasars. The goal of this work is to compare the different emission lines for each object to check on the reliability of Hα, Mg ii and C iv with respect to Hβ. Hα and Mg ii linewidths correlate well with Hβ, while C iv shows a poorer correlation, due to the presence of strong blueshifts and asymmetries in the profile. We compared our sample with the only other two whose spectra were taken with the same instrument and for all examined lines our results are in agreement with the ones obtained with X-shooter at z ~ 1.5−1.7. We finally evaluate C iii] as a possible substitute of C iv in the same spectral range and find that its behaviour is more coherent with those of the other lines: we believe that, when a high quality spectrum such as the ones we present is available and a proper modelization with the Fe ii and Fe iii emissions is performed, it is more appropriate to use this line than that of C iv if not corrected for the contamination by non-virialized components.
Key words: galaxies: active / galaxies: nuclei / galaxies: Seyfert / quasars: emission lines / quasars: general
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile, under programme 086.B-0320(A).
The reduced spectra (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/603/A1
© ESO, 2017
1. Introduction
Black holes (BH) are believed to be the origin of quasars’ extreme phenomenology and, more generally, of active galactic nuclei (AGN; Rees 1984). The growth of BHs occurs by accretion of the gas available in its proximity (Shakura & Sunyaev 1973).
Sample and observations properties.
The gravitational force and angular momentum of the super massive BH forces the gas to rotate around it and the gas emission reveals the properties of the motion. Broad (width > 2000 km s-1) emission lines detected in the spectra of quasars are a consequence of this process. These lines are believed to form in the near proximity of the BH (d ≪ 1 pc) in the so-called broad-line region (BLR). Given the spatial dimensions involved and the distances of these luminous sources, the study of the BLR emissions is one of the few ways available to have an insight into the nuclear region, otherwise inaccessible to observations. This is why the technique known as reverberation mapping (or echo mapping) (Blandford & McKee 1982; Peterson 1993) has received so much attention. Since its development, which originally aimed to improve knowledge of the geometrical properties of the BLR (Bahcall et al. 1972), it has then provided the opportunity of measuring the mass of the central body (Peterson et al. 2004; Bentz & Katz 2015). As long as the gas in the central regions is forced to rotate under the gravitational influence exerted by the BH, the width of the emission lines coming from these regions is a measurement of the BH mass, according to the equation 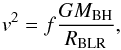 (1)where f, the virial factor, accounts for the geometry of the BLR (Collin et al. 2006; Netzer & Marziani 2010), still mostly unknown. The term RBLR is the dimension of the BLR as deduced by reverberation mapping, v is the velocity of the emitting gas, and G is the gravitational constant. In addition, the presence of a relation between the size of the BLR and the continuum luminosity (Kaspi et al. 2000; Bentz et al. 2013) enables us to give a measurement of the central mass with a single spectroscopic observation in all the sources for which we can see the emissions coming from the BLR (type 1 AGN), avoiding the limits imposed by spatially resolved kynematic measurements and by the long observational times required by reverberation mapping. The measurement of BH masses through the analysis of spectroscopic features then opens up the possibility of a statistical study of these peculiar sources.
(1)where f, the virial factor, accounts for the geometry of the BLR (Collin et al. 2006; Netzer & Marziani 2010), still mostly unknown. The term RBLR is the dimension of the BLR as deduced by reverberation mapping, v is the velocity of the emitting gas, and G is the gravitational constant. In addition, the presence of a relation between the size of the BLR and the continuum luminosity (Kaspi et al. 2000; Bentz et al. 2013) enables us to give a measurement of the central mass with a single spectroscopic observation in all the sources for which we can see the emissions coming from the BLR (type 1 AGN), avoiding the limits imposed by spatially resolved kynematic measurements and by the long observational times required by reverberation mapping. The measurement of BH masses through the analysis of spectroscopic features then opens up the possibility of a statistical study of these peculiar sources.
The BLR emission line most used for virial mass determination is by far Hβλ4861, mostly because this line is known to be emitted by gas in virialized conditions and also because of its prominence in the optical spectral window. For very distant sources the optical range is no more available and we have to find a replacement for Hβ. The most promising candidates for this role are C ivλ1549 and Mg iiλ2800 (McLure & Jarvis 2002), both in the UV rest spectral range of the sources; in using these lines we assume that they are emitted by approximatively the same region as Hβ, by gas in virialized conditions, and therefore that they have widths comparable with that of this line. However, it is well known that the BLR is stratified in terms of ionization potential (Dietrich et al. 1993; Peterson & Wandel 1999). The C iv line has a much higher ionization potential than Hβ and even more so than Mg ii. Moreover, C iv emission has very different behaviours depending on the source and exhibits very often a blueshift and a general asymmetry. This fact does not fit well in an ordered Keplerian motion scenario and it is believed to be associated with outflows or winds in the gas (Murray et al. 1995; Richards 2012). It is then clear why the use of Balmer lines is more advisable in general and why Mg ii can be considered a more reasonable replacement. When the redshift of the source allows the use of C iv alone, we are, however, compelled to find a different solution. The most important point, therefore, consists of identifying which part of the line can be associated with the gas of the BLR in Keplerian motion and which part we should instead consider in a non-virial state (Denney 2012). Furthermore, the emission variability of AGN is more important for shorter wavelengths and a comparison of C iv with the optical lines is not truly reliable if these lines are not simultaneously detected. The simultaneous detection eludes the problems connected with the very fast variability of these lines, a typical signature of AGN spectroscopic emissions, and helps us in the search for possible connections between the properties of the lines to obtain rules that could be used when the optical virial estimator (Hβ) is not available.
2. Sample selection, observations and data reduction
X-shooter (Vernet et al. 2011) is a three-arm, single object echelle spectrograph which started operations in October 2009. The instrument covers simultaneously the wavelength range from 300 to 2400 nm in the three arms: UVB (Δλ = 300−550 nm), VIS (Δλ = 550−1020 nm) and NIR (Δλ = 1020−2400 nm), respectively. For our observations we used slit widths of 1.3, 1.2 and 1.2 arcsec respectively for the three arms resulting in resolving powers R = λ/ Δλ = 4000, 6700 and 4300.
The sample was selected with the goal of extending the work presented in (Ho et al. 2012, Paper I hereafter) at higher redshift. In that paper a sample of relatively bright (r ~ 18−19) quasars from the SDSS DR7 release (Abazajian et al. 2009) with redshift around ~1.5 was analyzed. The redshift choice ensures a simultaneous coverage from C iv to Hα with X-shooter. For this effort we selected, again from the SDSS DR7 release, QSOs with redshift around ~2.3 ensuring again that X-shooter would detect C iv to Hα shifted at higher wavelengths with respect to the previous sample. In order to obtain higher S/N spectra, especially in the near infra-red (NIR) where the spectra are noisier, we selected slightly brighter (r ~ 17.5−18.5) QSOs observable in a single night at the Very Large Telescope. The resulting sample contained eight QSOs. After selection we also checked from the SDSS spectra that the selected objects have broad emission lines suitable to BH mass estimation and that they have no obvious broad absorption features. The average broad lines full width at half-maximum (FWHM) of the sources in the sample is consistent with the average at these redshifts. However the average bolometric luminosity is ⟨ log Lbol ⟩ = 47.25, higher than the average bolometric luminosity of QSOs at this redshift, log Lbol = 46.8 ± 0.3 (Shen et al. 2011), but compatible within 1.5σ. This ensures that our sample is not strongly biased.
Observations were performed in the framework of the French Guaranteed Time and took place on March the 10th 2011. In Table 1 we report the properties and the characteristics of the observations for all our sources.
The night was not photometric and the observing conditions were changing. Therefore during the night we monitored the spectra that were reduced online and we increased or decreased the observing time of the targets depending on their quality. The data collection that night was also hampered by strong winds whose speed was near (and sometimes over) the 12 m/s limit1 which prevents pointing towards northern targets such as ours. These strong winds caused a loss of about two and a half hours of observing time on our programme forcing us to drop two targets. The six observed targets are listed in Table 1 with exposure times, average airmass and seeing.
Each observation consisted of four different exposures of 450 s to 750 s each for a total of 1800 to 3000 s. The exposures were taken using the nodding along the slit technique with an offset of 5 arcsec between exposures in a standard ABBA sequence. The slit was put at parallactic angle. Every observation was preceded by an observation of a telluric A0V standard at similar airmass.
We processed the spectra using version 1.3.0 of the X-shooter data reduction pipeline (Goldoni et al. 2006; Modigliani et al. 2010). The pipeline performed the following actions. The raw frames were first subtracted and cosmic ray hits were detected and corrected using the method developed by van Dokkum (2001). The frames were then divided by a master flat field obtained by using day-time flat field exposures with halogen lamps. The orders were extracted and rectified in wavelength space using a wavelength solution previously obtained from calibration frames. The resulting rectified orders were then shifted and added to superpose them thus obtaining the final 2D spectrum. The orders were then merged and in the overlapping regions the merging was weighted by the errors which were being propagated during the process. From the resulting 2D merged spectrum a one dimensional spectrum was extracted at the source’s position. The one dimensional spectrum with the corresponding error file and bad pixel map was the final product of the reduction.
To perform flux calibration we used different procedures for the UVB data and for the VIS-NIR data. In the UVB band we extracted a spectrum from a staring observation of the flux standard LTT3218 (Hamuy et al. 1992, 1994) taken in the beginning of the night. We then reduced the data using the same steps as above but in this case we subtracted the sky emission lines using the Kelson (2003) method. This spectrum was divided by the flux table of the same star delivered with the pipeline to produce the response function. The response was then applied to the spectrum of the sources. For the VIS and NIR arm, we used the A0V stars as flux and telluric standards. We extracted the A0V spectra with the same procedure used for the flux standard. We then used these spectra to apply telluric corrections and flux calibrations simultaneously using the Spextool software (Vacca et al. 2003). We then verified if the final spectra of the three arms were compatible in the common wavelength regions and performed a correction using the UVB spectra as reference where needed. The spectral shapes are compatible with the ones of the SDSS spectra, while the fluxes are on average ~50% weaker. Relying on the accurate SDSS flux calibration, we finally scaled our spectra in order to match them with SDSS spectra in common wavelength regions reasonably free from emission lines.
3. Spectral fitting
As a preliminary step we de-redshifted the spectra according to their SDSS redshifts as reported in Shen et al. (2011) and corrected them for galactic extinction using the E(B−V) values from Schlafly & Finkbeiner (2011) as listed in the NASA/IPAC Extragalactic Database2 and the reddening law of Fitzpatrick (1999) with RV = 3.1.
We then fitted the spectra with a procedure that uses the IDL MPFIT package (Markwardt 2009), written with the purpose of a simultaneous fitting of continuum, Fe ii and other emission lines. Broad lines are fitted with a broken power law, convolved with a Gaussian function to avoid the presence of a cusp at the peak (Nagao et al. 2006); the expression for the broken power law is ![\begin{equation} f(\lambda)\propto \begin{cases} \left(\frac{\lambda}{\lambda_{0}}\right)^{\beta} & \mbox{if}\; \lambda<\lambda_{0} \\[3mm] \left(\frac{\lambda}{\lambda_{0}}\right)^{\alpha} & \mbox{if} \; \lambda>\lambda_{0}, \end{cases} \label{eq:broaddoublepowerlawcomponent} \end{equation}](/articles/aa/full_html/2017/07/aa30143-16/aa30143-16-eq82.png) (2)where λ0 is the central wavelength and α and β are the slopes for red and blue tail respectively. The choice of such a function allows us to reproduce with only five parameters (flux, λ0, α, β and the σ of the Gaussian function with which the double power law is convolved) the profiles which are commonly fitted with at least two Gaussian functions, involving six parameters. This is particularly useful when dealing with emission line complexes, in which the use of a single component for every line helps in limiting the degeneracy in the fits. Moreover, when we do not fit lines separately, but several lines together, the use of a single fitting function allows us to set the same profile for all the lines with similar excitation conditions (high or low ionisation). The results obtained by fitting with the function in Eq. (2)are consistent with those obtained by fitting with multiple Gaussians, as long as the total spectrum is well reproduced by the fit. Narrow lines are fitted instead with a simple Gaussian, because their emissions are generally very well reproduced by this function. Where a blue asymmetry is present, as in the case of [O iii] λ5007 Å, a second Gaussian takes into account this feature.
(2)where λ0 is the central wavelength and α and β are the slopes for red and blue tail respectively. The choice of such a function allows us to reproduce with only five parameters (flux, λ0, α, β and the σ of the Gaussian function with which the double power law is convolved) the profiles which are commonly fitted with at least two Gaussian functions, involving six parameters. This is particularly useful when dealing with emission line complexes, in which the use of a single component for every line helps in limiting the degeneracy in the fits. Moreover, when we do not fit lines separately, but several lines together, the use of a single fitting function allows us to set the same profile for all the lines with similar excitation conditions (high or low ionisation). The results obtained by fitting with the function in Eq. (2)are consistent with those obtained by fitting with multiple Gaussians, as long as the total spectrum is well reproduced by the fit. Narrow lines are fitted instead with a simple Gaussian, because their emissions are generally very well reproduced by this function. Where a blue asymmetry is present, as in the case of [O iii] λ5007 Å, a second Gaussian takes into account this feature.
First we obtained the slope of the continuum for fits of the entire UV region (wavelength range ~ 1400−3500 Å, containing C iv, C iii] and Mg ii) and for the optical window (wavelength range ~ 4000−7300 Å, containing Hβ and Hα). We then used these slopes in the fits for the four narrower windows – for C iv-C iii], Mg ii, Hβ and Hα emissions. When necessary we applied a mask to the spectral regions contaminated by sky emissions (this was particularly required in the case of Hβ spectral window).
For the UV spectral window we took into account several emission lines, following the prescriptions proposed in Nagao et al. (2006): emissions are separated in two groups, high and low ionization lines (HIL: O ivλ1402.06, N iv] λ1486.496, C ivλ1549.06, He iiλ1640.42; LIL: Si ivλ1396.76, O iii] λ1663.48, Al iiiλ1857.40, Si iiiλ1892.03, C iii] λ1908.73, Al iiλ2669.95, O iiiλ2672.04), whose velocity profiles are known to have systematically different behaviours, so that some parameters pertaining to one group, such as the central velocity and the two power law indexes for blue and red tails, can be tied for each line. We determined these fitting parameters using C iv for the HIL group and C iii] for the LIL group. The Mg ii doublet was instead fitted independently of the other lines. This line should in theory be included in the LIL and therefore be tied to C iii] parameters, but since Mg ii is one of our investigation target it did not make sense to tie it to another line (considering also that the C iii] complex, with three emission lines present, can be degenerate). The optical window includes the Balmer lines, Hβ and Hα, and a few other lines not always present in the spectra (Hδλ4103, Hγλ4342, He iλ4472, [O iii] λ4959,5007, [N ii] λ6585,6550 and He iλ7067). Hβ and Hα were fitted independently.
The fitting procedure also includes Fe ii emissions; they are reproduced convolving emission templates with a Gaussian that accounts for the velocity of the emitting gas. We used two types of template: the first one is the I Zw 1 Fe ii template by Véron-Cetty et al. (2004), valid only for the visible band, and the second one is a series of model templates obtained with the photoionization code Cloudy (Ferland et al. 2013).
The Cloudy templates were computed with the following setup:
-
we used the 371 levelsFe ii model (Verneret al. 1999) instead of thesimplified model (Willset al. 1985);
-
we considered a continuum emission similar to that examined in Mathews & Ferland (1987), resembling the spectrum of a typical radio-quite AGN;
-
we assumed a plane-parallel geometry with maximum cloud column density of 1023 cm-2;
-
we used ten combinations of ionizing photon flux and column density to consider the possible physical conditions of the BLR;
-
for all models we also considered the possibility of a 100 km s-1 microturbulence velocity.
The above assumptions result in 20 different templates, which are shown in Table 2. For the C iv-C iii] spectral window, Fe iii emissions were also taken into account. Specifically we used the Vestergaard & Wilkes (2001) empirical template for Fe ii and Fe iii as deduced from the I Zwicky 1 spectrum.
During the fitting procedure the templates are combined with a positive weight (free parameter of the fit) and convolved with a Gaussian function accounting for the velocity of the emitting gas (whose central value and σ are free parameters of the fit as well).
Different combinations of the ionizing photons flux emitted by the primary source (Φ(H)) and electronic density in the BLR clouds (Ne), used as input for Cloudy Fe ii simulated templates for different physical condition of the BLR.
None of the examined lines exhibits an evident narrow component. We decided to then fit all of the permitted lines with a single double power law function. Also the [NII] doublet in the Hα window is not recognisable at all and we did not consider it among the emission lines in the fitting procedure. For Hα in J093147 alone, the shape of the line profile reveals the presence of [NII] and, as a consequence of this we considered the doublet in the fitting process. A special case is represented instead by J123120, for which we originally considered only broad lines but the fit improved considerably taking into account an emission from the NLR too (see Sect. 4 and Fig. A.4). In Fig. 1 an example for the UV and optical windows for one of the sources is presented, along with the individual windows for C iv, C iii] and Mg ii, Hβ and Hα lines (fits for the rest of the sources are shown in Appendix A). In the large UV window some wide regions were masked during the fitting process for the following reasons: the presence of strong emission blending, a non representativeness of the Fe ii templates, a lack of knowlegde about what kind of emission is able to reproduce such features (this is for example the case of the red-shelf of C iv), or the presence of noise.
The regions usually excluded from the fit are the red shelf of C iv, the bump of emission between O iii] λ1663.48 Å and the C iii] complex, when present, and the wide spectral region between 2000 and ~ 2450 Å (see Nagao et al. 2006). This choice affects neither the continuum slope determination nor the line analysis, since the proper examination of the lines is performed on the individual spectral line windows.
For all the sources the FWHM and the σ were estimated on the best fit profile for each line. They are connected to the shape of the line; while the FWHM is more representative of the core, the σ depends more on the tails of the line (Shen 2013). Choosing one or the other leads to different results in BH virial mass estimations, especially if we are dealing with poor quality data (Denney et al. 2016).
To give an estimate of the errors of these quantities we used a Monte Carlo approach, extracting 1000 independent values for every parameter pertaining to the line. On these synthetic profiles we evaluated 1000 values for FWHM and σ; from the distributions of the 1000 value of the FWHM and the σ we were able to infer the relative error to be associated with a given measurement. As a consistency check, we also performed the fit of 100 mock realizations of the original spectra, obtained with a random extraction, within its 1σ uncertainty, of the flux in each channel. We measured the properties of the profile for all the 100 best fit and determined the standard deviation of the distribution. This, then, is the error associated with the property for the best fit of the true spectrum. This check was repeated for the lines in every spectral window. The errors on the measured quantities obtained in this way are consistent with those determined with the Monte Carlo approach. The errors on the UV and optical slopes and on the luminosities at 1350, 1450, 3000 and 5000 Å are instead computed performing, for every source, fits of various regions of the spectra and then evaluating the differences between these results and those obtained in the original fit (Pita et al. 2014). All the measured quantities are listed in Table 3.
We noticed that the central wavelength of the [O iii] λ5007 Å line, from which the redshift was estimated (Shen et al. 2011), in almost every case was not close to the nominal wavelength. We then corrected the redshift using only the principal component of [O iii] (excluding the blueshifted component from the whole profile, which is instead considered in the estimate of Shen et al. 2011). A more accurate estimate of the redshift of the sources can improve the analysis of the shifts of the lines with respect to their nominal wavelengths. The corrected redshifts are listed in Table 1 and have been used in the following analysis.
 |
Fig. 1 Fits for all the examined spectral windows (C iv-C iii]-Mg ii and Hβ-Hα large windows, C iv-C iii], Mg ii, Hβ and Hα small windows) for J093147. The black line is the original spectrum. The blue solid lines are the best fit models for the emissions (continuum, Fe ii and emission lines) and the red solid line is the total best fit. The lower panels show residuals between best fit model and original spectrum. The coloured regions are those we chose to mask (refer to main text for details). |
Measured quantities for the examined spectral windows.
4. Results
4.1. Line comparison
For a visual comparison in Fig. 2 we show the best fit profiles for every line in all spectra. The profiles are normalized to their peak values and presented on a velocity scale. As a general trend, Hα, Hβ and Mg ii behave similarly, according to what expected if the three lines are all emitted from regions in a virialized condition (McLure & Jarvis 2002; Greene & Ho 2005; Marziani et al. 2013). They all show symmetric profiles and small shifts in the central wavelengths, generally below 300 km s-1 (Table 3). Surprisingly, the most asymmetric line among these (usually in the red wing) is Hβ. We suspect this is the result of a possible degeneration within the Hβ-[O iii] complex, especially when He i and Fe ii, whose emission are difficult to disentangle by the fitting procedure, are present. The most asymmetric line of all is C iv. This line frequently shows a significant shift in the central wavelength, about − 730 km s-1 on average, and all cases show the presence of a prominent blueshift. We notice that, in contrast with what found in Paper I, C iii] does not seem to behave so differently from the other lines. All sources do not present a large shift (~ 90 km s-1 on average). Furthermore, in all sources C iii] does not show a prominent blueshift as, instead, does C iv.
 |
Fig. 2 Comparison of all the examined line profiles. The profiles are normalized to their peak values and referred to their laboratory wavelength on a velocity scale. |
4.2. Line widths comparison
Figure 3 (second, third and fourth columns) shows a comparison of FWHM for every pair of lines commonly examined for virial estimates, Hβ, Mg ii, Hα and C iv. The measurements used in the final analysis are indicated on the figure.
 |
Fig. 3 FWHM correlations between line pairs. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations for the C iii] line. The black dashed line represents the 1:1 relation, while the light green one represents the best fit to our data, considering a linear relation between the logarithm of the FWHM for every pair of lines. The solid yellow line is the best fit when not considering J121911 in the sample. Intercept and scatter for all the relations are given in Table 6. In the case of relations involving C iii], we do not plot the different measurements for linewidths of J123120 (i.e. broad lines only vs. broad and narrow lines considered in the fit). As in the case of the other lines, however, we take into account the FWHM measurements pertaining to the broad component when the narrow component is present. 2nd, 3rd and 4th columns: correlations for all the lines commonly considered in virial estimates. The red and magenta points are the measurements used in the final analysis. The black point represents the measurement taking into account only broad components for J123120, while the magenta point is the measurement including also narrow components in the fit and used in the final analysis. The grey point is the alternative measurement including the narrow component that we did not choose to use (refer to main text for details). The black dashed line represents the 1:1 relation, while the light green one represents the bestfit to our data (red and magenta points), considering a linear relation between the logarithms of the FWHM for every pair of lines. Intercept and scatter for all the relations are reported in Table 4. |
For J123120 we decided to perform two fits, one using only the broad components (black points) and one including also the narrow ones. The latter fit was done in two ways: the first one leaving the width of the narrow component as a free parameter and the other one fixing it to the one of C iii] in the UV range and to the one of [O iii] and Hβ in the optical range. The points we adopted for the following analysis correspond to the case in which we tie the narrow component in the UV spectrum and to the case in which we left it free in the optical range. While in the UV we could use the obvious technique of linking together the widths of the narrow components, we could not do the same in the optical because the narrow Hα component is much broader than the [O iii] one and they cannot be reasonably linked together. The presence of a narrow component in J123120 is particularly evident for the Mg ii line, although it improved the fits also fot the other lines.
Even for our small sample a correlation between FWHM of Hβ, Hα and Mg ii is present. Instead, C iv has a less strong correlation with the other lines: this is not surprising given the blueshift of the line in almost every source of the sample. We report the results of the linear fit assuming a relation between the linewidths of the form log (FWHM1) = m·log (FWHM2) + c, with m = 1, in Table 4. Concerning the parametrization of the line width, although the σ is in principle a more reliable estimator, especially when data quality is poor (Collin et al. 2006; Denney et al. 2016), most of the recent works use instead the FWHM (Ho et al. 2012; Trakhtenbrot & Netzer 2012; Ho & Kim 2015, among the others), justifying it with a smaller scatter between different lines (Mejia-Restrepo et al. 2016).
Linewidth correlations between line pairs.
In our measurements we do not observe such a larger scatter in the relationships involving the line dispersion σ with respect to the FWHM (see Fig. 4 and Table 4). The only exceptions are the relationships involving Mg ii, for which essentially the J123120 point is an outlier. Of course the smallness of our sample plays an important role in this respect, stressing the presence of outliers that would probably not be such in a larger sample. The analysis presented by Mejia-Restrepo et al. (2016) highlights the difference between measurements performed under a global (considering a continuum fitted on the whole SED of accretion disk, BLR and NLR emissions) and a local approach (the more common case, in which the fit on the line is performed only on a smaller spectral window including the line). The line measurements they report are those obtained under the local approach and for which they recognize the presence of a large scatter for the line dispersion, ascribable to the subtraction of a non proper fitted continuum. We notice, however, that their local approach take into account rather narrow spectral windows, while our measurements are performed on wider wavelength ranges and, moreover, take into account a preliminar continuum evaluation, performed on even wider windows. Given the data quality and the spectral range that our fits cover, we are confident that our line dispersions could be considered for a virial estimate. Nonetheless, since we are especially interested in the comparison with some of the works mentioned before and our data quality allows the use of the FWHM, we will focus our analysis on this quantity.
 |
Fig. 4 Line dispersion correlations between line pairs. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations for the C iii] line. The black dashed line represents the 1:1 relation, while the light green one represents the best fit to our data, considering a linear relation between the line dispersions. The function we fit is log(σ1)= m·log(σ2)+ c, with m = 1. The solid yellow line is the best fit when not considering J121911 in the sample. Intercept and scatter for all the relations are given in Table 6. 2nd, 3rd and 4th columns: correlations for all the lines commonly considered in virial estimation. The black dashed line represents the 1:1 relation, while the light green one represents the bestfit for our data (red points), considering a linear relation between the line dispersions for every pair of lines. The function we fit is log (σ1) = m·log (σ2) + c, where the slope m = 1. Intercept and scatter for all the relations are reported in Table 4. |
4.3. MBH and Eddington ratios
Although we took into account several previous works (Vestergaard & Peterson 2006; Bentz et al. 2013; Wang et al. 2009; Vestergaard & Osmer 2009; Ho & Kim 2015; Jun et al. 2015), we focus our analysis on the comparison of our data with the only two other sample with the same characteristics, that is whose spectra were taken with the X-shooter spectrograph and therefore cover a spectral range including all the broad lines of interest, Paper I and Mejia-Restrepo et al. (2016). We notice that, while both these samples cover the same redshift range z ~ 1.5, ours goes to higher redshift (z ~ 2.2) and therefore can be interesting to make a comparison in terms of mass and Eddington ratio. Since the quasars in our sample are selected to be slightly brighter than those selected in Paper I, we expect them to be characterized by higher values for at least one of these two quantities.
In Fig. 5 (second, third and fourth columns) we report the measurements of MBH obtained with the new prescriptions of Mejia-Restrepo et al. (2016) for our sample (see Table 5) and for the Paper I sample, for which only the measurements pertaining to three lines out of four are present (in this work results for Hβ are not included, given the poor signal to noise in this spectral range, and all the comparison are made with Hα). In the same figure we also show the Mejia-Restrepo et al. (2016) sample. As for the Hα-based masses, we use their Hα prescription with the luminosity at 5100 Å, the same we used for the other samples. For all the lines we used the third column of Mejia-Restrepo et al. (2016) Table 7 – “local approach MBH calibrations, but corrected for the small systematics with respect to the global approach MBH calibrations”. The C iv-based MBH for the Ho et al. (2012) sources are computed using L1350 instead of L1450, because this is the closest continuum luminosity available for this sample. Our sample (red data points) fits very well in all cases and, on average, is located in the upper part of the global distribution.
We then compute the Eddington ratios for our sources and for Mejia-Restrepo et al. (2016) and Paper I samples, with the same prescription used in Paper I (bolometric luminosity from McLure & Dunlop 2004, and Eddington luminosity LEdd = 1.26 × 1038 (MBH/M⊙) erg s-1) to verify if our sample is composed by higher accreting black holes. We evaluate the Eddington ratio for our objects both with Hβ and with Hα as virial estimators, while for Mejia-Restrepo et al. (2016) we recompute the Hα,L5100 based values. In this way we can compare these values with those found in Paper I, for which only Hα measurements are available.
We find that our Eddington ratios (Table 5, Fig. 6) are much higher on average than those of both Paper I and Mejia-Restrepo et al. (2016). The higher luminosity of our sample is therefore due both to the presence of more massive BHs and to the fact that they are accreting, on average, at higher rates.
Mass estimations with Mejia-Restrepo et al. (2016) prescriptions for our sample.
Correlations of C iii] based virial masses with the other lines.
4.4. Can C iii] be used as a virial estimator?
Unlike what found in Paper I, when looking at the C iii] profile we do not recognize a different behaviour of the line with respect to the others (see Fig. 2). We then decide to examine the relationships between the FWHM of C iii] with those of the other lines. Although C iii] is not commonly used, some works analyse this line (Greene et al. 2010; Shen & Liu 2012). Greene et al. (2010) find only a slight correlation of C iii] with Mg ii FWHM, while Shen & Liu (2012) state that C iii] linewidths correlates with C iv and therefore these lines could be emitted by the same region, then being characterized by the same issues (i.e. non virialization of the emitting region). We find that this correlation (log (FWHMC iv)−log (FWHMC iii ])) has a larger scatter with respect to those of Hβ and Hα and comparable with that of Mg ii (see Table 4 and Fig. 3, first column). However, the sample of Shen & Liu (2012) has much higher luminosity than ours and is composed of lower redshift sources. Moreover, they fit the line profiles on much narrower wavelenght ranges than ours. Additionally, for the line profile model they use two Gaussians tied to give a symmetric broad component for C iii]. All these differences could then contribute to the discrepancy with their results.
In Fig. 3 (first column) we notice the presence of only one outlier, J121911, for which the C iii] complex appears to have a more “boxy” shape with respect to those the other sources, resulting in an more asymmetric C iii] profile with an extended red wing (see the figures in Appendix A for the results on the complete sample and Fig. 2 for a comparison of the line profiles). We have checked that including or excluding this point does not affect the fit and thus, we decide to leave it in the sample. The reason for this is that this point has larger errors, since the IDL routine we use to fit the linear relation (MPFITEXY, Williams et al. 2010; based on the MPFIT package, Markwardt 2009) considers the errors in both x and y variables. J121911 does not stand out evidently in the case of the line dispersion (Fig. 4, first column), but for the same reason we do not consider it as a reliable measurement. Results of fits assuming a linear correlation between the quantities are listed in Table 4.
The C iii] line is not usually mentioned among the possible virial estimators. This is mostly due to (1) its smaller intensity and (2) to the blend with other emission lines in the same complex. The use of only one component to fit the broad lines, instead of two or more Gaussians, is more robust against the degeneracy in the profile fitting, also thanks to the good quality of our data. The C iv line should not be used in virial estimates because, although it is more intense, it is contaminated by non-virial components. On the contrary, the preliminary line comparison (Fig. 2) shows that C iii] behaves very similarly to the lines that are mostly virialized (Hβ, Hα and Mg ii). Therefore, we attempt to find a virial relationship for C iii] comparing measurements for this line with virial masses based on the other lines.
 |
Fig. 5 Correlations between virial masses. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations between C iii]-based virial masses and masses derived from the other lines. The black dashed line represents the 1:1 relation. Intercept and scatter for all the relations are given in Table 6. 2nd, 3rd and 4th columns: MBH measurements for Mejia-Restrepo et al. (2016, (black points), Ho et al. (2012, green points) and this work (red points) samples obtained with the prescriptions by Mejia-Restrepo et al. (2016, see the main text for details on the used prescriptions and the luminosities). Black dashed lines represent the 1:1 relation. MBH estimates for our sources are given in Table 5. |
Given the smallness of our sample, in addition to a fixed dependence of the MBH on the velocity of the emitting gas according to the virial assumption, we also fix the dependence on the luminosity as MBH ∝ L0.5. This choice is perfectly consistent with the hypothesis of photoionization in the BLR and with what found in previous works (Bentz et al. 2013). The BH mass is then given by the equation 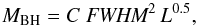 (3)where the only free parameter is the scaling factor C. We chose to use the luminosity at 1450 Å, as the closest to the C iii] line that we can measure in a continuum window reasonably free by other emissions. In Table 6 we report our results (scaling factor C and scatter Δ) for the comparison of the C iii] based MBH with those from all the other lines except C iv (Fig. 5, first column). Since C iv, if not corrected, does not share the property of virialization of the emitting region, we do not consider this line for this comparison. Table 6 also shows the MBH estimates for all the sources derived from the C iii] line. The scatter in these relations is comparable (only in the case of MBH(C iii])-MBH(Hβ) is larger) with those of the mass relations involving C iv (0.14, 0.15 and 0.16 dex with the only six objects in our sample and 0.23, 0.21 and 0.20 dex for the whole sample, for Hβ, Hα and Mg ii, respectively). However, the strong similarity of the C iii] profile with the lines emitted by virialized gas (Hβ and Mg ii) suggests that, at least for this sample, we can use this line as a virial estimator. The use of the double power law function as a model to fit broad components helps in removing the degeneracy in the Al iii, Si iii] and C iii] complex and, therefore, in retrieving the C iii] profile more accurately. Despite the scatter in the C iii] virial relationships is as large as that of C iv, this line does not seem to be affected by contamination by not-reverberating components. Of course this sample is composed only of six sources, one of which (J121911) represents an outlier for what concerns the C iii] behaviour, therefore a significantly enlarged sample is needed to ensure the goodness of this line as a virial estimator. Moreover, due to the strong blending of the 1900 Å complex, spectra of very high quality and S/N are required in order to disentangle the different emission components. This fact can therefore limit the use of this line but, in principle, C iii] seems a better choice with respect to C iv as it is.
(3)where the only free parameter is the scaling factor C. We chose to use the luminosity at 1450 Å, as the closest to the C iii] line that we can measure in a continuum window reasonably free by other emissions. In Table 6 we report our results (scaling factor C and scatter Δ) for the comparison of the C iii] based MBH with those from all the other lines except C iv (Fig. 5, first column). Since C iv, if not corrected, does not share the property of virialization of the emitting region, we do not consider this line for this comparison. Table 6 also shows the MBH estimates for all the sources derived from the C iii] line. The scatter in these relations is comparable (only in the case of MBH(C iii])-MBH(Hβ) is larger) with those of the mass relations involving C iv (0.14, 0.15 and 0.16 dex with the only six objects in our sample and 0.23, 0.21 and 0.20 dex for the whole sample, for Hβ, Hα and Mg ii, respectively). However, the strong similarity of the C iii] profile with the lines emitted by virialized gas (Hβ and Mg ii) suggests that, at least for this sample, we can use this line as a virial estimator. The use of the double power law function as a model to fit broad components helps in removing the degeneracy in the Al iii, Si iii] and C iii] complex and, therefore, in retrieving the C iii] profile more accurately. Despite the scatter in the C iii] virial relationships is as large as that of C iv, this line does not seem to be affected by contamination by not-reverberating components. Of course this sample is composed only of six sources, one of which (J121911) represents an outlier for what concerns the C iii] behaviour, therefore a significantly enlarged sample is needed to ensure the goodness of this line as a virial estimator. Moreover, due to the strong blending of the 1900 Å complex, spectra of very high quality and S/N are required in order to disentangle the different emission components. This fact can therefore limit the use of this line but, in principle, C iii] seems a better choice with respect to C iv as it is.
 |
Fig. 6 MBH vs. Eddington Ratios for Mejia-Restrepo et al. (2016, black points), Ho et al. (2012, green points) and this work (red points) sources. For the Eddington Ratios, we follow McLure & Dunlop (2004) for the bolometric luminosity and use LEdd = 1.26 × 1038 (MBH/M⊙) erg s-1 for the Eddington luminosity. We use the Hα-based MBH, because this is the only Balmer line available for all the samples. The values for our objects are listed in Table 5. |
Since we are comparing our C iii] based masses with those obtained using the Mejia-Restrepo et al. (2016) prescription and since they do not provide virial relationships for σ, we limit our analysis to the FWHM.
5. Summary
We examined a sample of six quasars at redshift z ~ 2.2, whose spectra were taken with the X-shooter spectrograph. This instrument covers a very large spectral range, allowing the simultaneous comparison of the most used virial estimators. We compare our results with those of the only two other samples observed with X-shooter (Paper I and Mejia-Restrepo et al. 2016). The analysis gives the following results:
-
1.
The comparison of the line profiles shows that Hβ, Hα and Mg ii behave in a similar way, as expected for virialized gas.
-
2.
C iv is by far the line that deviates most from this condition because of its strong blueshifts and asymmetry.
-
3.
We find C iii] to behave consistently with the other lines, in contrast to C iv.
-
4.
Comparisons of the linewidths obtained for every line give a similar scatter for the FWHM and the line dispersion σ. However, we chose to focus our analysis on FWHM, to be consistent with the works we are comparing our sample to.
-
5.
We compute virial masses for our sample and for the sources in Paper I, using the prescriptions by Mejia-Restrepo et al. (2016). All the sources follow the relations. A comparison with Paper I and Mejia-Restrepo et al. (2016) shows that our higher redshift sample has larger MBH and higher accreting rates.
-
6.
Notwithstanding the smallness of our sample, we suggest a new virial mass prescription based on the FWHM of C iii], which can be considered as a valid substitute of C iv for sources in which only this spectral window is present, if a high quality spectrum is available and a proper modelization of the Fe ii and Fe iii emissions is included in the analysis. Unlike C iv in fact, this line seems to share the behaviour of the lines emitted by virialized gas.
Acknowledgments
The authors would like to thank the anonymous referee for helpful comments and suggestions that considerably improved the work. They also thank Alvaro Alvarez for support during the observations and Marianne Vestergaard for kindly providing the I Zw 1 iron templates from Vestergaard & Wilkes (2001). L.C.H. acknowledges support from the Chinese Academy of Science (grant No. XDB09030102), National Natural Science Foundation of China (grant No. 11473002), and Ministry of Science and Technology of China (grant No. 2016YFA0400702). G.P. acknowledges the Bundesministerium für Wirtschaft und Technologie/Deutsches Zentrum für Luft- und Raumfahrt (BMWI/DLR, FKZ 50 OR 1408 and FKZ FKZ 50 OR 1604) and the Max Planck Society.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Kozlovsky, B.-Z., & Salpeter, E. E. 1972, ApJ, 171, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., & Katz, S. 2015, PASP, 127, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denney, K. D. 2012, ApJ, 759, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D., Horne, K., Shen, Y., et al. 2016, ApJS, 224, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Kollatschny, W., Peterson, B. M., et al. 1993, ApJ, 408, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, in Ground based and Airborne Instrumentation for Astronomy, Proc. SPIE, 6269, 62692K [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Peng, C. Y., & Ludwig, R. R. 2010, ApJ, 709, 937 [Google Scholar]
- Hamuy, M., Walker, A. R., Suntzeff, N. B., et al. 1992, PASP, 104, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Suntzeff, N. B., Heathcote, S. R., et al. 1994, PASP, 106, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., & Kim, M. 2015, ApJ, 809, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Goldoni, P., Dong, X.-B., Greene, J. E., & Ponti, G. 2012, ApJ, 754, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Jun, H. D., Im, M., Lee, H. M., et al. 2015, ApJ, 806, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marziani, P., Sulentic, J. W., Plauchu-Frayn, I., & del Olmo, A. 2013, A&A, 555, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2004, MNRAS, 352, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Jarvis, M. J. 2002, MNRAS, 337, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mejia-Restrepo, J. E., Trakhtenbrot, B., Lira, P., Netzer, H., & Capellupo, D. M. 2016, MNRAS, 460, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in Proc. SPIE, 7737, 773728 [Google Scholar]
- Murray, N., Chiang, J., Grossman, S. A., & Voit, G. M. 1995, ApJ, 451, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Marconi, A., & Maiolino, R. 2006, A&A, 447, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H., & Marziani, P. 2010, ApJ, 724, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., & Wandel, A. 1999, ApJ, 521, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pita, S., Goldoni, P., Boisson, C., et al. 2014, A&A, 565, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T. 2012, in AGN Winds in Charleston, eds. G. Chartas, F. Hamann, & K. M. Leighly, ASP Conf. Ser., 460, 67 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shen, Y. 2013, Bull. Astron. Soc. India, 41, 61 [NASA ADS] [Google Scholar]
- Shen, Y., & Liu, X. 2012, ApJ, 753, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Trakhtenbrot, B., & Netzer, H. 2012, MNRAS, 427, 3081 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, E. M., Verner, D. A., Korista, K. T., et al. 1999, ApJS, 120, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Véron-Cetty, M.-P., Joly, M., & Véron, P. 2004, A&A, 417, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestergaard, M., & Osmer, P. S. 2009, ApJ, 699, 800 [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-G., Dong, X.-B., Wang, T.-G., et al. 2009, ApJ, 707, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, M. J., Bureau, M., & Cappellari, M. 2010, MNRAS, 409, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., Netzer, H., & Wills, D. 1985, ApJ, 288, 94 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Complete sample fits
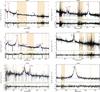 |
Fig. A.1 Fits for all the examined spectral windows (C iv-C iii]-Mg ii and Hβ-Hα large windows, C iv-C iii], Mg ii, Hβ and Hα small windows) for J103325. The black line is the original spectrum. The blue solid lines are the best fit models for the emissions (continuum, Fe ii and emission lines) and the red solid line is the total best fit. The lower panels show the residuals between the best fit model and the original spectrum. The coloured regions are those we chose to mask (refer to main text for details). |
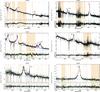 |
Fig. A.2 Same as Fig. A.1 but for J105239. |
 |
Fig. A.3 Same as Fig. A.1 but for J121911. |
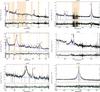 |
Fig. A.4 Same as Fig. A.1 but for J123120. For this source we consider also the presence of narrow components. |
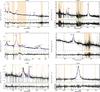 |
Fig. A.5 Same as Fig. A.1 but for J124220. |
All Tables
Different combinations of the ionizing photons flux emitted by the primary source (Φ(H)) and electronic density in the BLR clouds (Ne), used as input for Cloudy Fe ii simulated templates for different physical condition of the BLR.
All Figures
 |
Fig. 1 Fits for all the examined spectral windows (C iv-C iii]-Mg ii and Hβ-Hα large windows, C iv-C iii], Mg ii, Hβ and Hα small windows) for J093147. The black line is the original spectrum. The blue solid lines are the best fit models for the emissions (continuum, Fe ii and emission lines) and the red solid line is the total best fit. The lower panels show residuals between best fit model and original spectrum. The coloured regions are those we chose to mask (refer to main text for details). |
| In the text | |
 |
Fig. 2 Comparison of all the examined line profiles. The profiles are normalized to their peak values and referred to their laboratory wavelength on a velocity scale. |
| In the text | |
 |
Fig. 3 FWHM correlations between line pairs. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations for the C iii] line. The black dashed line represents the 1:1 relation, while the light green one represents the best fit to our data, considering a linear relation between the logarithm of the FWHM for every pair of lines. The solid yellow line is the best fit when not considering J121911 in the sample. Intercept and scatter for all the relations are given in Table 6. In the case of relations involving C iii], we do not plot the different measurements for linewidths of J123120 (i.e. broad lines only vs. broad and narrow lines considered in the fit). As in the case of the other lines, however, we take into account the FWHM measurements pertaining to the broad component when the narrow component is present. 2nd, 3rd and 4th columns: correlations for all the lines commonly considered in virial estimates. The red and magenta points are the measurements used in the final analysis. The black point represents the measurement taking into account only broad components for J123120, while the magenta point is the measurement including also narrow components in the fit and used in the final analysis. The grey point is the alternative measurement including the narrow component that we did not choose to use (refer to main text for details). The black dashed line represents the 1:1 relation, while the light green one represents the bestfit to our data (red and magenta points), considering a linear relation between the logarithms of the FWHM for every pair of lines. Intercept and scatter for all the relations are reported in Table 4. |
| In the text | |
 |
Fig. 4 Line dispersion correlations between line pairs. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations for the C iii] line. The black dashed line represents the 1:1 relation, while the light green one represents the best fit to our data, considering a linear relation between the line dispersions. The function we fit is log(σ1)= m·log(σ2)+ c, with m = 1. The solid yellow line is the best fit when not considering J121911 in the sample. Intercept and scatter for all the relations are given in Table 6. 2nd, 3rd and 4th columns: correlations for all the lines commonly considered in virial estimation. The black dashed line represents the 1:1 relation, while the light green one represents the bestfit for our data (red points), considering a linear relation between the line dispersions for every pair of lines. The function we fit is log (σ1) = m·log (σ2) + c, where the slope m = 1. Intercept and scatter for all the relations are reported in Table 4. |
| In the text | |
 |
Fig. 5 Correlations between virial masses. The lines labelled in the upper left of every panel refer to Y and X axis respectively. 1st column: correlations between C iii]-based virial masses and masses derived from the other lines. The black dashed line represents the 1:1 relation. Intercept and scatter for all the relations are given in Table 6. 2nd, 3rd and 4th columns: MBH measurements for Mejia-Restrepo et al. (2016, (black points), Ho et al. (2012, green points) and this work (red points) samples obtained with the prescriptions by Mejia-Restrepo et al. (2016, see the main text for details on the used prescriptions and the luminosities). Black dashed lines represent the 1:1 relation. MBH estimates for our sources are given in Table 5. |
| In the text | |
 |
Fig. 6 MBH vs. Eddington Ratios for Mejia-Restrepo et al. (2016, black points), Ho et al. (2012, green points) and this work (red points) sources. For the Eddington Ratios, we follow McLure & Dunlop (2004) for the bolometric luminosity and use LEdd = 1.26 × 1038 (MBH/M⊙) erg s-1 for the Eddington luminosity. We use the Hα-based MBH, because this is the only Balmer line available for all the samples. The values for our objects are listed in Table 5. |
| In the text | |
 |
Fig. A.1 Fits for all the examined spectral windows (C iv-C iii]-Mg ii and Hβ-Hα large windows, C iv-C iii], Mg ii, Hβ and Hα small windows) for J103325. The black line is the original spectrum. The blue solid lines are the best fit models for the emissions (continuum, Fe ii and emission lines) and the red solid line is the total best fit. The lower panels show the residuals between the best fit model and the original spectrum. The coloured regions are those we chose to mask (refer to main text for details). |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but for J105239. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for J121911. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 but for J123120. For this source we consider also the presence of narrow components. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1 but for J124220. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


