| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201630258 | |
| Published online | 21 April 2017 | |
Observations of the Lyman series forest towards the redshift 7.1 quasar ULAS J1120+0641
1 Astrophysics Group, Blackett Laboratory, Imperial College London, London SW7 2AZ, UK
e-mail: rhys.barnett09@imperial.ac.uk
2 Department of Physics & Astronomy, University of California, Riverside, 900 University Avenue, Riverside, CA 92521, USA
3 Department of Mathematics, Imperial College London, London SW7 2AZ, UK
4 Department of Astronomy, Stockholm University, Albanova, 10691 Stockholm, Sweden
5 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
6 Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
7 Gemini Observatory, Northern Operations Center, N. A’ohoku Place, Hilo, HI 96720, USA
8 Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received: 15 December 2016
Accepted: 9 February 2017
We present a 30 h integration Very Large Telescope X-shooter spectrum of the Lyman series forest towards the z = 7.084 quasar ULAS J1120+0641. The only detected transmission at S/N > 5 is confined to seven narrow spikes in the Lyα forest, over the redshift range 5.858 <z < 6.122, just longward of the wavelength of the onset of the Lyβ forest. There is also a possible detection of one further unresolved spike in the Lyβ forest at z = 6.854, with S/N = 4.5. We also present revised Hubble Space Telescope F814W photometry of the source. The summed flux from the transmission spikes is in agreement with the F814W photometry, so all the transmission in the Lyman series forest may have been detected. There is a Gunn-Peterson (GP) trough in the Lyα forest from z = 6.122 all the way to the quasar near zone at z = 7.04. The trough, of comoving length 240 h-1 Mpc, is over twice as long as the next longest known GP trough. We combine the spectroscopic and photometric results to constrain the evolution of the Lyα effective optical depth (τGPeff) with redshift, extending a similar analysis by Simpson et al. We find τGPeff ∝ (1 + z)ξ where ξ = 11.2+ 0.4-0.6, for z > 5.5. The data nevertheless provide only a weak limit on the volume-weighted intergalactic medium (IGM) hydrogen neutral fraction at z ~ 6.5, xH i > 10-4, similar to limits at redshift z ~ 6 from less distant quasars. The new observations cannot extend measurements of the neutral fraction of the IGM to higher values because absorption in the Lyα forest is already saturated near z ~ 6. For higher neutral fractions, other methods such as measuring the red damping wing of the IGM will be required.
Key words: cosmology: observations / quasars: individual: ULAS J1120+0641 / quasars: absorption lines / dark ages, reionization, first stars
© ESO, 2017
1. Introduction
It is now over 50 years since Gunn & Peterson (1965, GP) noted the lack of Lyman-α (Lyα) absorption in the spectra of (at the time) high redshift quasars. The cross-sections of the Lyman series transitions are so high that even a small neutral hydrogen fraction (xH i ~ 10-4) should result in an intergalactic medium (IGM) that is effectively opaque to photons at wavelengths shorter than that of Lyα emission, 1215.67 Å. However, using observations of the z = 2.01 quasar 3C 9 (Schmidt 1965), Gunn & Peterson (1965) were able to demonstrate an extremely low density of neutral hydrogen (xH i< 10-5) in the IGM near z = 2.
 |
Fig. 1 VLT X-shooter spectrum of ULAS J1120+0641 (black), covering restframe wavelengths between 850 and 1400 Å. The spectrum has been binned to a pixel size of 150 km s-1 using inverse variance weighting. The observed wavelengths of Lyα, Lyβ and the Lyman limit are marked. The only transmission detected in the spectrum is confined to spikes over the wavelength range marked by α, in the pure Lyα forest, corresponding to the redshift range 5.858 < z < 6.122 (Sect. 3.2). The corresponding wavelength range for Lyβ absorption is marked β and lies blueward of the restframe Lyman limit. Plotted as the blue dotted line is the (scaled) total system throughput curve for the ACS F814W filter. |
More recently, the Lyα forest has been used to constrain the end of reionization by attempting to measure the extent of Lyα absorption at redshifts of around six. The lack of GP troughs in the spectra of SDSS quasars with z < 6 (e.g. Fan et al. 2000, 2001; Djorgovski et al. 2001; Songaila & Cowie 2002) indicated that the IGM was highly ionized, since a low volume weighted neutral fraction (~10-4) would be sufficient to result in complete absorption of Lyα photons. The first GP trough was reported by Becker et al. (2001) towards the z = 6.28 quasar SDSS J1010+0524 (see also White et al. 2003). They concluded that the neutral fraction must increase sharply at z ~ 6.
A seminal study of Lyman series absorption was that of Fan et al. (2006a, see also Fan et al. 2006b, who presented the largest individual sample of high redshift quasars to date. From the spectra of 19 z ~ 6 sources, they noted a sharp increase in the effective optical depth to Lyα photons ( ). Their conclusion was that there is an acceleration of the evolution of the IGM ionization state at z ≳ 5.7. Importantly, Fan et al. (2006a) reported a large line-of-sight dependence, indicating patchiness in the IGM neutral fraction that could be related to cosmic reionization. Fan et al. (2006a) also measured a dramatic increase in the average length of dark gaps (in this case defined as contiguous regions with optical depth τ > 3.5) for z > 6, suggesting that Lyα troughs could be a powerful probe of the IGM at higher redshifts.
). Their conclusion was that there is an acceleration of the evolution of the IGM ionization state at z ≳ 5.7. Importantly, Fan et al. (2006a) reported a large line-of-sight dependence, indicating patchiness in the IGM neutral fraction that could be related to cosmic reionization. Fan et al. (2006a) also measured a dramatic increase in the average length of dark gaps (in this case defined as contiguous regions with optical depth τ > 3.5) for z > 6, suggesting that Lyα troughs could be a powerful probe of the IGM at higher redshifts.
The detection of a ~ 110 h-1 Mpc GP trough covering the redshift range 5.523 ≤ z ≤ 5.879 in the Lyα forest towards the z = 5.98 quasar ULAS J0148+0600 by Becker et al. (2015) recently strengthened the case for patchiness. Comparing the observations to hydrodynamical simulations, they argue that significant fluctuations in the hydrogen neutral fraction as late as z ≃ 5.6–5.8 are required to explain the data.
Measurements of dark pixels in the Lyα and Lyβ forests have also been used to place the first model independent constraints on reionization. Rather than attempting to measure optical depths based on a continuum model, Mesinger (2010) proposed a novel approach, where the fraction of pixels that have zero measured flux in both Lyα and Lyβ is used to directly measure an upper limit to the volume-weighted mean neutral hydrogen fraction. Applying the idea to observed spectra, McGreer et al. (2011, 2014) conclude that reionization must be (almost) complete by z ~ 6.
The most recent optical depth measurements from Planck, integrated to the last scattering surface (z ~ 1100), yield τ = 0.055 ± 0.009, suggesting a model-dependent redshift of reionization between ~7.8 and ~8.8 (Planck Collaboration XLVI; Planck Collaboration XLVII 2016).
These various results both from spectroscopic analyses and Planck motivate extending observations of Lyα absorption to higher redshifts. ULAS J1120+0641 (Mortlock et al. 2011) remains the only known quasar with z> 7 (z = 7.084; Venemans et al. 2012). In this paper we analyse the Lyα forest towards ULAS J1120+0641 by combining Hubble Space Telescope (HST) imaging from the Advanced Camera for Surveys (ACS), first presented by Simpson et al. (2014), with new spectroscopy from the Very Large Telescope (VLT)/X-shooter instrument (Vernet et al. 2011). The spectrum of ULAS J1120+0641 is shown in Fig. 1. In Sect. 2 we present the data, paying close attention to the effects of charge transfer efficiency (CTE) losses in the case of HST. We remeasure the ACS F814W (i-band) image of the quasar. In Sect. 3 we analyse the X-shooter spectrum. We discuss the limitations of spectroscopy for determining optical depth measurements towards the source, and search for significant transmission in the spectrum. In Sect. 4 we combine our photometric and spectroscopic measurements in order to constrain the evolution of effective optical depth towards the quasar, and use simulations to set limits on xH i. We summarise in Sect. 5.
All magnitudes are on the AB system (Oke & Gunn 1983). We have adopted a concordance cosmology with h = 0.7, ΩM = 0.3, and ΩΛ = 0.7.
2. Observations and data reduction
2.1. VLT X-shooter spectroscopy
The source was observed with the X-shooter spectrograph over several nights spanning 2011 March to 2014 April, providing a total of 30 h integration on source1. The Visual-red (VIS) arm of X-shooter, with MIT/LL CCD detectors, spans the wavelength range 5500–10 000 Å, and the Near-IR arm (NIR), with a Hawaii 2RG array detector, spans the wavelength range 10 000–25 000 Å, or 1.0–2.5 μm. The quasar’s Lyα emission line lies at 9827 Å, close to the boundary between the two arms. In the current paper we analyse the Lyman series absorption in the spectrum, i.e., the wavelength range from the quasar Lyman limit at 7371 Å up to the Lyα emission line. This wavelength range lies entirely within the VIS arm.
The data reduction, including flux calibration, is described more fully in Bosman et al. (2017), who provide the spectrum redward of Lyα, and present the results of a search for metal lines in that region. Briefly, sky subtraction was performed using a custom idl implementation of the optimum sky subtraction routines outlined in Kelson (2003). This approach involves transforming the (x,y) CCD coordinates into a wavelength and slit position for each pixel in the two-dimensional frame. Slit positions for each order were defined using a standard star trace. In orders where the quasar has little flux, such as in the Lyα forest, the offset from the standard trace and the spatial profile of the object were extrapolated from orders where flux is present, assuming that there is minimal atmospheric dispersion between orders2. This assumption is reasonable given that the Lyα forest for ULAS J1120+0641 falls at fairly red wavelengths, and because the object was generally observed at moderate airmass (less than 1.5). Optimal techniques (Horne 1986) were used to extract a one-dimensional spectrum simultaneously from all exposures for a given spectrograph arm after a relative flux calibration was applied to each order in the two-dimensional frames.
Great care was taken to minimise bias in the sky-subtraction stage of the data reduction, since we are interested in measuring the degree of absorption in the Lyman series forest relative to the continuum. Systematics, where the sky level to subtract is consistently over- or under-estimated, are more important for ULAS J1120+0641 than for several of the other high-redshift quasars used for measuring transmission in the Lyα forest because the source is fainter. For example, three quasars in which long GP troughs have been detected, ULAS J0148+0600, z = 5.98 (Becker et al. 2015), and SDSS J1030+0524, z = 6.31 and SDSS J1148+5251, z = 6.42 (White et al. 2003), are respectively factors 3.9, 2.1, and 2.9 brighter than ULAS J1120+0641. Subtle systematics can be present depending on the algorithm used. For example, a weighted least squares fit to the sky where the variance is a Poisson estimate based on the measured counts will systematically underestimate the sky and so leave a positive residual (see White et al. 2003, for a related discussion). To avoid such a bias, we instead used a least-squares linear fit. Likewise, combining multiple exposures using inverse variance weighting can produce a small positive bias when the variance is calculated using a Poisson estimate based on amplitude of the sky fit (plus a contribution from read noise). The bias occurs because exposures in which the sky is underestimated (and hence the object flux overestimated) at a particular wavelength will be assigned a lower variance, and hence a larger weight. To mitigate this bias, we estimated the variance as a function of wavelength using the measured scatter in the two-dimensional counts about the sky fit. A Poisson contribution from the object, based on the extracted counts, is also added along the object trace.
The observations were made with a 0.̋9 slit width, providing a nominal resolving power of R = 8800, or a resolution of 34 km s-1. Inspection of the telluric absorption lines, however, indicates that the true mean resolving power was somewhat better, R ~ 10 000, or a resolution of 30 km s-1, as a consequence of good average seeing during the observations. The bin size used for the final spectrum is 10 km s-1. The spectrum was flux calibrated using observations of a spectrophotometric standard. Due to slit losses the zero point (i.e. overall scaling) will be uncertain. Accordingly the spectrum was then scaled by matching to the GNIRS spectrum presented in Mortlock et al. (2011) over the region of overlap, redward of the Lyα forest, 9800–10 000 Å. The GNIRS spectrum itself was calibrated to UKIRT photometry, from 2011. The quasar was observed in 2013 March with HST (Sect. 2.2) in the F814W, F105W, and F125W filters (Simpson et al. 2014), and found to have faded by 0.16 mag. compared to the UKIRT YJ photometry. Because we use the F814W photometry in our analysis of the Lyα forest, we have applied this additional flux correction to the spectrum, meaning that the normalization differs from that used by Bosman et al. (2017).
The new X-shooter spectrum is presented in Fig. 1, binned to a pixel size of 150 km s-1. As detailed below, the only detectable transmission over the entire Lyman series is confined to the small range in wavelengths marked by α in Fig. 1, corresponding to the redshift range 5.858–6.122, in the pure Lyα forest, and just redward of the onset of the Lyβ forest, at λobs = 8291.92 Å, z = 5.821. The remainder of the Lyα forest from z = 6.122 up to the edge of the quasar near zone at z = 7.04 is completely absorbed, as is the entire region of the Lyβ,γ and higher series, down to the Lyman limit. The bin width of 150 km s-1 in Fig. 1 was chosen to emphasise the GP absorption in the plot.
We checked the computed error spectrum by analysing the distribution of signal-to-noise ratio (S/N) in pixels in the long GP trough. We first subtracted off any large-scale systematic residual (Sect. 3.1) using a 301 pixel median filter, before calculating the S/Ns. We applied a 3σ clip and fit a Gaussian to the resulting histogram, which should have a dispersion of unity if the errors are correct. We bin the data for this particular analysis, e.g., by factors of 2, 4, etc., to account for the slight smoothing at the pixel-to-pixel level introduced by rebinning at the wavelength calibration stage. Scaling the noise array by a factor of 1.05 resulted in a Gaussian fit to the residuals with a dispersion of unity. As noted by Bosman et al. (2017), the sky subtraction is imperfect close to the peak of the brightest OH sky lines. Again fitting a Gaussian to the S/N histogram for pixels close to the peak of strong lines, we were able to treat the imperfect sky subtraction by further increasing the errors by a factor of 1.15 for the five pixels centred on each skyline peak.
The errors are on average substantially smaller than in the spectra of the three quasars listed earlier. For example compared to ULAS J1120+0641, in the GP troughs in the spectra of ULAS J0148+0600, z = 5.98, SDSS J1030+0524, z = 6.31, and SDSS J1148+5251, z = 6.42, measured over the same wavelength regions, the errors are on average larger by factors 1.6, 2.5, and 1.8, respectively (consistent with the difference in integration times).
Measured flux density in GP troughs.
2.2. HST imaging
 |
Fig. 2 CTE correction (mcorrected−muncorrected) applied to objects detected in the F814W frame, shown as blue stars. The red circle indicates ULAS J1120+0641. Yellow crosses represent the median correction in the indicated bins of 0.5 mag (upper) or 200 pixels (lower). Upper: correction as a function of corrected F814W magnitude. Lower: correction as a function of Δy, the number of pixels from the readout register. |
HST observed the field of ULAS J1120+0641 with the ACS and WFC3 instruments in the three filters F814W, F105W, and F125W, during 2013 March (Simpson et al. 2014). As shown in Fig. 1 the wavelength range of the ACS F814W filter rather neatly spans the Lyman series forest of ULAS J1120+0641, and so photometry of ULAS J1120+0641 in this filter provides valuable information on the Lyman series absorption. The F814W image had a total exposure time of 28 448 s spread across five visits made over 2013 March 27–29; it is substantially deeper than the Subaru i′-band image presented in Barnett et al. (2015). Each visit comprised six dithered exposures, with the exception of the final visit where a single exposure was taken. The 25 pipeline-processed frames were then combined using the pyraf routine astrodrizzle.
Simpson et al. (2014) measured i814 = 28.59 ± 0.20 for ULAS J1120+0641 with aperture photometry, using the result to constrain the evolution of the effective optical depth towards the quasar (Sect. 4.1). The source is close to the limit of detectability, and in ACS images the effect of CTE losses can be important for such faint sources. As the counts in a detected source are clocked down to the serial register, some charge gets left behind and appears in a trail after the source (Anderson & Bedin 2010; Chiaberge 2012). The problem is more severe the lower the background and proportionally greatest for the faintest sources, increasing linearly with distance of the source from the serial register, i.e., with the parallel clocking distance. The placement of ULAS J1120+0641 close to the centre of the field of view of the ACS instrument unfortunately means that the object lies at the edge of one of the CCDs. The distance to the serial register is maximised, as is the charge loss. Therefore, it is important to assess the effect of CTE losses on the photometry.
Two solutions to the problem of CTE losses have been devised by the ACS team. The first (Chiaberge 2012) quantifies the losses as a function of sky background, source brightness, and location on the CCD, and provides formulae to correct measured photometry. The second (Anderson & Bedin 2010) attempts to put the trailed charge back into the sources, by applying an ingenious algorithm that uses a model for the CCD traps (defects) that cause the CTE losses. The latter method has proved so successful that it is now applied by default in the ACS data reduction pipeline (although there is an option to turn it off), and the image measured by Simpson et al. (2014) was corrected in this manner.
ULAS J1120+0641 is located close to the ecliptic, resulting in a comparatively bright sky background. In a single frame the average sky level in our F814W frames is ~105e−. This is a considerably higher background than the levels explored by Chiaberge (2012). As the background level rises the CTE corrections become smaller, and the coefficients provided by Chiaberge (2012) allow one to estimate the background level at which the CTE correction becomes zero. Although it becomes necessary to extrapolate their results, the level is ~70e−, implying that any CTE corrections in our frames should actually be very small. We consulted with the ACS instrument team on the issue of the CTE correction, and they recommended that at such high background levels losses should indeed be small, and that we should use frames without the Anderson & Bedin (2010) corrections applied, since for high background the algorithm will simply add noise.
As a check, we used astrodrizzle to produce co-added frames of the dithered F814W exposures both with and without the Anderson & Bedin (2010) correction in order to quantify the CTE corrections made as a function of source brightness, and of location on the CCD. We paid close attention to the choice of input parameters to astrodrizzle to avoid the cores of bright objects being masked as cosmic rays. We used SExtractor (Bertin & Arnouts 1996) to produce a catalogue of objects in the HST frames, detected in the corrected F814W image. We performed aperture photometry at the positions specified by the catalogue in both the corrected and uncorrected F814W images. Ideally the sample would be restricted to point sources, but star/galaxy discrimination is unreliable for sources as faint as ULAS J1120+0641, so we included all catalogued sources. CTE corrections for galaxies will be larger than for point sources, as they cover more pixels, so any measured trends may in fact overestimate the CTE correction for a point source. The centroid of the image of ULAS J1120+0641 is also uncertain as the source is so faint. We therefore used the F105W frame to define the position of the quasar, before measuring photometry in the two F814W frames. However, the F105W proved a poor choice to define the whole catalogue, as it is shallower than the F814W observation and so fewer objects were detected. Finally, we calculated the CTE corrections (Δ m = mcorrected−muncorrected) for all sources. These are presented as a function of corrected magnitude in Fig. 2a, and of the distance in pixels from the serial register, Δy, in Fig. 2b. In each of these plots very weak trends, at the level of few hundredths of a magnitude are visible in the mean correction for all objects at a particular magnitude or clocking distance, but these are much smaller than the standard deviation. Furthermore, as noted above, these trends may overestimate the required correction, as the sample is dominated by galaxies. We conclude that when the background is this high the Anderson & Bedin (2010) algorithm simply introduces additional noise, and the best photometry is provided by the uncorrected frame. The correction for ULAS J1120+0641 itself is large: the quasar lies in the tail of the distributions and is brightened by 0.47 mag. This unusually large correction appears to be due to chance.
 |
Fig. 3 Close-up of the Lyα forest towards ULAS J1120+0641, binned to a pixel size of 20 km s-1 for display purposes. Upper: spectrum (black) and 1σ errors (red). Lower: S/N at each pixel found by running the Gaussian matched filter at the narrowest width over the unbinned spectrum (pixel size 10 km s-1). |
The uncorrected frame has a stripy appearance from (fractionally small) CTE losses in bright sources. Therefore, we flattened the sky background before aperture photometry by subtracting a median-filtered version of the frame. We measured the counts in a 3-pixel radius (rather than the 2.5 pixel aperture preferred by Simpson et al. 2014, to minimise digitisation issues), and applied an aperture correction to 10 pixel radius (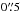 ), derived from bright stars. This was then further corrected to the nominal “infinite” aperture radius of the ACS of
), derived from bright stars. This was then further corrected to the nominal “infinite” aperture radius of the ACS of 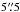 using the quoted encircled energy fraction of 0.914 in the
using the quoted encircled energy fraction of 0.914 in the 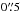 aperture, quoted in the ACS Data Handbook. The final photometry result is i814 = 28.85, with S/N = 2.9. We quote the error as a signal-to-noise ratio as the errors are Gaussian in flux, but at such low significance the equivalent posterior distribution in magnitudes is extremely skewed, and we do not quote it here.
aperture, quoted in the ACS Data Handbook. The final photometry result is i814 = 28.85, with S/N = 2.9. We quote the error as a signal-to-noise ratio as the errors are Gaussian in flux, but at such low significance the equivalent posterior distribution in magnitudes is extremely skewed, and we do not quote it here.
3. Analysis of the spectrum
3.1. Systematic errors in sky subtraction
In exploring the Lyα forest in the new spectrum, smoothing on different scales, we found that despite the care taken in the data reduction to minimise such effects (Sect. 2.1), there are systematic errors present in the form of a small positive residual signal at an average level of fλ ~ 3 × 10-20 erg s-1 cm-2 Å-1. The excess corresponds to only ~0.05% of the counts from the sky within the extraction aperture, or ~0.15 of the average random error per pixel. We used synphot (Laidler et al. 2008) to measure synthetic photometry from the spectrum, obtaining a value i814 = 27.2, which is a factor 4.5 brighter than the HST photometry. The low-level sky residual is difficult to characterise quantitatively, since a 3σ detection alone requires binning over 400 pixels (~120 Å). However, the residual does not correlate directly with the error spectrum, in the sense that on large scales they do not share the same shape. Neither is the residual significantly greater in the wavelength ranges of the bands of OH sky lines, compared to the line-free regions. Therefore it does not seem to be an effect associated with the difficulty of subtracting the sharp OH sky lines, and is apparently a smooth feature.
Systematic errors in sky subtraction have not been reported or quantified in previous measurements of the Lyman-series effective optical depth. We checked whether a residual at the level seen in the spectrum of ULAS J1120+0641 would have been detected in the GP troughs seen in the spectra of the three quasars ULAS J0148+0600 (Becker et al. 2015), SDSS J1030+0524, and SDSS J1148+5251 (White et al. 2003). In these papers, the transmission in the GP troughs is measured in bins of width ~50 Mpc, and transformed to an effective optical depth. Using the same bins we have measured the average flux density in the spectra, using inverse-variance weighting, and the results are provided in the fourth column of Table 1. In three of the bins the measured flux is consistent with zero, while significant flux is recorded in the GP trough 6.10 <z< 6.32 in the spectrum of SDSS J1148+5251. We then measured the average flux density over the same four bins in the spectrum of ULAS J1120+0641, after subtracting the few transmission spikes seen in the spectrum (Sect. 3.2), in order to measure the smooth residual. These results are listed in the final column of Table 1. In the spectrum of ULAS J1120+0641 we measure significant flux at the level of ~3 × 10-20 erg s-1 cm-2 Å-1 in all four bins.
The detection of significant flux in the redshift bin 6.10 <z< 6.32 in the spectrum of SDSS J1148+5251 is interesting, because it is the only other case where significant flux has been measured where no transmission spikes in Lyα have been detected. In the original paper, White et al. (2003) speculated that this was due to flux from a faint intervening galaxy, a suggestion which has subsequently been ruled out by HST imaging (White et al. 2005). Systematic errors in the sky subtraction may provide a simpler explanation. In fact, comparing the values in Cols. 4 and 5 of Table 1, in each bin the measurements agree at the 2.5σ level. This means that systematic errors could be present in the other spectra at a similar level, and the reason they are reported here for the first time is because it is the deepest spectrum yet taken at these redshifts.
3.2. Detection of transmission spikes
To remove the systematic residual we subtracted a median-filtered version of the spectrum using a box of length 301 pixels, i.e., ~90 Å. At these redshifts transmission in the Lyman-series forest will be in isolated spikes, so the application of a median filter of such a long box length should have a negligible effect on any inferred transmission. The region of the spectrum covering the Lyα forest, binned by a factor two for display purposes, i.e., pixels of 20 km s-1, is shown in Fig. 3, together with the error spectrum. Note, however, that we use the unbinned spectrum to search for regions of significant transmission. To search for spikes in the Lyman series forest (7370 Å ≤ λobs ≤ 9770 Å) we employ a Gaussian matched filter (Hewett et al. 1985; Bolton et al. 2004), with a range of widths. The narrowest profile has a standard deviation Σ = 15 km s-1, corresponding to the nominal spectral resolution of 34 km s-1FWHM. A range of profiles successively increasing in width by 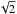 was employed, Σ = 15, 21, 30, ..., 120 km s-1. We fit a Gaussian at every pixel, 8535 in total. To illustrate the process we plot the S/N at each pixel for the narrowest template in the bottom panel of Fig. 3. Then, for each pixel, we recorded the S/N of the most significant detection over all the templates, whether positive or negative, and the corresponding value of Σ.
was employed, Σ = 15, 21, 30, ..., 120 km s-1. We fit a Gaussian at every pixel, 8535 in total. To illustrate the process we plot the S/N at each pixel for the narrowest template in the bottom panel of Fig. 3. Then, for each pixel, we recorded the S/N of the most significant detection over all the templates, whether positive or negative, and the corresponding value of Σ.
The distribution of these S/N values is shown in Fig. 4. This distribution is non-Gaussian, because we recorded the maximum absolute value for each pixel. Since negative spikes, which are not real, extend down to nearly S/N = −4, we cannot be sure positive spikes are real unless the S/N is substantially greater than 4. In fact one might expect a somewhat more extended tail in the positive direction, of spikes that are not real, because of cosmic rays that are not perfectly subtracted. For these reasons we set our detection threshold at S/N = 5. The matched filter finds seven significant flux transmission spikes, at observed wavelengths 8337 Å ≤ λobs ≤ 8659 Å, redshifts 5.858 <z< 6.122. These are summarised in Table 2 and plotted in Fig. 5. These seven spikes are also identifiable in both panels of Fig. 3. To confirm that the detections are real, for each spike we compared the measured flux at the detected wavelength in subsets of the data, and found no significant differences between subsets. We also checked the goodness of the fit of the Gaussian template to the data, finding the χ2 values to be satisfactory. The observed transmission features are very narrow: with the exception of the largest spike at 8337 Å, the template width Σ which yielded the highest S/N was 15 km s-1, i.e., the spikes are unresolved. We integrate the template transmission spectrum to find a total transmitted flux of (1.02 ± 0.03) × 10-17 erg s-1 cm-2, of which approximately half is contained in the largest spike.
 |
Fig. 4 S/N of spikes extracted from the X-shooter spectrum. We have extracted the highest value of |S/N| from all template widths. |
 |
Fig. 5 Significant transmission of flux in the Lyα forest towards ULAS J1120+0641. The unbinned X-shooter spectrum of ULAS J1120+0641 is shown in grey with a pixel size of 10 km s-1. Shown in blue is the 1σ error spectrum, and the derived transmission spectrum is overlaid in red. The seven detections presented in Table 2 are indicated. |
Transmission spikes detected in the Lyα forest with the matched filter.
Using synphot we measure i814 = 29.00 ± 0.03 for these seven spikes. Our value is consistent with the HST photometry (Sect. 2.2; i814 = 28.85, S/N = 2.9), raising the question of whether the seven spikes account for all the transmission in the spectrum. In considering this question we refer to Table 3 which sets out the wavelength ranges in the spectrum and the corresponding redshifts over which absorption in the four transitions Lyα, β, γ, δ are recorded. It is noticeable that the seven spikes all lie close to the blue end of the pure Lyα forest, which is to be expected. Starting at the red end of the Lyα forest, on the edge of the quasar near zone (near 9770 Å), and moving to shorter wavelengths, the Lyα opacity reduces, down to 8291 Å, zα = 5.82, where the high-opacity Lyβ forest at zβ = 7.08 cuts in. Moving to shorter wavelengths from 8291 Å the opacity in Lyβ becomes lower, but will still be very high at 7862 Å, corresponding to zβ = 6.61, at which point the Lyγ forest cuts in at zγ = 7.08. The result is that the most transparent window in the spectrum is just redward of 8291 Å. Therefore if there is any more transmitted flux in the spectrum, which will be in the form of narrow spikes below 5σ significance, most of it is expected to lie in the wavelength range 8291–8700 Å. Looking at the spikes with S/N in the range 3–5 these are approximately uniformly distributed along the spectrum, with no excess detected in the wavelength range 8291–8700 Å. Even if all the 3–5σ spikes in this wavelength range were real, they would only contribute an additional 10% to the transmitted flux. The region of Lyβ absorption corresponding to the transmission spikes, is marked β in Fig. 1. It is beyond the quasar Lyman limit, and is consequently not useful for measuring transmission.
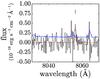 |
Fig. 6 As Fig. 5, but focused on the region of the spectrum in the Lyβ forest in the vicinity of the possible transmission spike at λ = 8056 Å, which is indicated. |
Wavelength and redshift ranges recording Lyα, β, γ, δ absorption.
There is a single unresolved spike in the range of ambiguity 4 <S/N< 5. It is detected at S/N = 4.5, and lies at λ = 8056 Å, corresponding to zα = 5.627 and zβ = 6.854. The spike is plotted in Fig. 6. A region of transmission at z = 6.854 would be very unexpected given the rapid evolution of the hydrogen neutral fraction seen around z ~ 6, so the feature is potentially interesting. We checked that the fluxes measured in subsets of the data are consistent. The putative line lies six pixels from the centre of a strong OH sky line, sufficiently far away that it should not be affected by poor sky subtraction. Unfortunately it is not possible to be sure if the line is real or not.
If the spike is real, it requires that the opacities along the line of sight to the quasar at redshifts zα = 5.627 and zβ = 6.854 are both low. We are able to quantify this statement by following a line of reasoning used by White et al. (2005) in discussing a Lyβ transmission spike in the spectrum of SDSS J1148+5251. In the spectrum of ULAS J1120+0641, the fractional transmission measured over five pixels centred on the Lyβ spike is 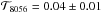 . The effective optical depth at 8056 Å, which is the sum of contributions from both the Lyα and Lyβ forests, is τ8056 = 3.2 ± 0.3 = τα(z = 5.6) + τβ(z = 6.9). The transmission at the corresponding wavelength in the Lyα forest, zα = 6.854, λ = 9548 Å, measured over 5 pixels, is
. The effective optical depth at 8056 Å, which is the sum of contributions from both the Lyα and Lyβ forests, is τ8056 = 3.2 ± 0.3 = τα(z = 5.6) + τβ(z = 6.9). The transmission at the corresponding wavelength in the Lyα forest, zα = 6.854, λ = 9548 Å, measured over 5 pixels, is 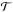 (9548)=−0.01 ± 0.01, meaning an optical depth τα(z = 6.9) > 4.0 at 2σ. Taking the ratio of effective optical depths τα/τβ ~ 2.25 from Fan et al. (2006a), the measurement at λ = 9548 Å, implies 1.8 <τβ(z = 6.9) < 3.2, and 0 <τα(z = 5.6) < 1.4. The range on τα(z = 5.6) is not unreasonable, meaning that our analysis does not weaken the case that the line is real. Combining the two transmission measurements, and assuming τα/τβ ~ 2.25, leads to the constraint 4.0 <τα(z = 6.9) < 7.2 for this spike.
(9548)=−0.01 ± 0.01, meaning an optical depth τα(z = 6.9) > 4.0 at 2σ. Taking the ratio of effective optical depths τα/τβ ~ 2.25 from Fan et al. (2006a), the measurement at λ = 9548 Å, implies 1.8 <τβ(z = 6.9) < 3.2, and 0 <τα(z = 5.6) < 1.4. The range on τα(z = 5.6) is not unreasonable, meaning that our analysis does not weaken the case that the line is real. Combining the two transmission measurements, and assuming τα/τβ ~ 2.25, leads to the constraint 4.0 <τα(z = 6.9) < 7.2 for this spike.
3.3. Measurement of the effective GP optical depth
Measurements of the transmission fraction  and effective optical depth
and effective optical depth  in bins of Δz = 0.15 towards ULAS J1120+0641.
in bins of Δz = 0.15 towards ULAS J1120+0641.
Narrow features are essentially unaffected by the application of the long median filter, and so we use the filtered spectrum to measure the effective optical depth in the Lyman series forest. To normalise the spectrum and hence estimate the transmitted flux ratio 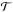 , we divide the X-shooter spectrum by the model intrinsic spectrum described in Mortlock et al. (2011). Here the blue wing of the Lyα emission line comes from a composite spectrum created from sources with similar CIV blueshifts, and the spectrum is extended bluewards as a power law Fλ ∝ λ-0.5.
, we divide the X-shooter spectrum by the model intrinsic spectrum described in Mortlock et al. (2011). Here the blue wing of the Lyα emission line comes from a composite spectrum created from sources with similar CIV blueshifts, and the spectrum is extended bluewards as a power law Fλ ∝ λ-0.5.
In Table 4 we present measurements of 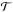 and effective GP optical depth
and effective GP optical depth  over the redshift range 5.07–7.02, covering practically the entire Lyman series forest. We follow the prescription of Fan et al. (2006a), making measurements in fixed-size bins of Δz = 0.15. The redshift bin 6.87–7.02 was excluded as the median filtered spectrum is affected by the quasar Lyα emission line in this region. To estimate
over the redshift range 5.07–7.02, covering practically the entire Lyman series forest. We follow the prescription of Fan et al. (2006a), making measurements in fixed-size bins of Δz = 0.15. The redshift bin 6.87–7.02 was excluded as the median filtered spectrum is affected by the quasar Lyα emission line in this region. To estimate 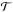 we calculate the transmission fraction in each pixel before taking the inverse-variance weighted average for each bin, i.e.,
we calculate the transmission fraction in each pixel before taking the inverse-variance weighted average for each bin, i.e., 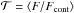 . If we detect transmission below a level of 2σ, we adopt a lower limit for
. If we detect transmission below a level of 2σ, we adopt a lower limit for  based on a value of
based on a value of 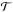 equal to twice the uncertainty3.
equal to twice the uncertainty3.
 |
Fig. 7 Evolution of |
We also consider the effect of the adopted power-law slope at wavelengths below Lyα. We recalculate  values using a bluer continuum, Fλ ∝ λ-1.4 (Lusso et al. 2015). The effect on
values using a bluer continuum, Fλ ∝ λ-1.4 (Lusso et al. 2015). The effect on  is found to be small. In the lowest-redshift bin we find
is found to be small. In the lowest-redshift bin we find  > 6.54, while in the highest redshift bins the difference is negligible. In the bin beginning at z = 5.82 we measure
> 6.54, while in the highest redshift bins the difference is negligible. In the bin beginning at z = 5.82 we measure  = 5.15 ± 0.15, i.e., consistent with the value presented in Table 4.
= 5.15 ± 0.15, i.e., consistent with the value presented in Table 4.
In Fig. 7 we show our measurements of  , as well as the power law evolution of
, as well as the power law evolution of  determined using HST photometry (Sect. 4.1). We do not include the bins for which zα< 5.82 in Fig. 7, since these have contributions from Lyβ and higher order transitions, as well as Lyα. In principle, observations of Lyβ in the redshift range 6.61 <z< 7.08 might provide a more sensitive measurement of the effective optical depth, if corrected for the coincident absorption by Lyα at 5.47 <z< 5.82. Although a statistical correction for foreground Lyα is possible at lower redshifts, the recent results of Becker et al. (2015) show that this is not possible at z ≳ 5.5, as some lines of sight are completely absorbed in Lyα.
determined using HST photometry (Sect. 4.1). We do not include the bins for which zα< 5.82 in Fig. 7, since these have contributions from Lyβ and higher order transitions, as well as Lyα. In principle, observations of Lyβ in the redshift range 6.61 <z< 7.08 might provide a more sensitive measurement of the effective optical depth, if corrected for the coincident absorption by Lyα at 5.47 <z< 5.82. Although a statistical correction for foreground Lyα is possible at lower redshifts, the recent results of Becker et al. (2015) show that this is not possible at z ≳ 5.5, as some lines of sight are completely absorbed in Lyα.
The results for ULAS J1120+0641 lend support to the steadily-growing body of evidence that  climbs rapidly at high redshift, and that therefore we are observing the tail-end of the epoch of reionization. However, it is also clear from Fig. 7 that we are unable to make especially useful measurements of
climbs rapidly at high redshift, and that therefore we are observing the tail-end of the epoch of reionization. However, it is also clear from Fig. 7 that we are unable to make especially useful measurements of  for z ≳ 6.5. Absorption in the spectrum becomes saturated, and so no further information can be gained by measuring up to redshifts of seven since we can only determine lower limits which are similar in value to the measurements of
for z ≳ 6.5. Absorption in the spectrum becomes saturated, and so no further information can be gained by measuring up to redshifts of seven since we can only determine lower limits which are similar in value to the measurements of  from lower redshift sources. As expected, the most useful constraints on
from lower redshift sources. As expected, the most useful constraints on  come from z ~ 6.
come from z ~ 6.
4. Analysis and discussion
4.1. IGM opacity
Fan et al. (2006a) used the spectra of 19 z > 6 quasars to measure  along different lines of sight. They found the best-fit power law to be:
along different lines of sight. They found the best-fit power law to be: ![\begin{equation} \label{eq:tauz} \tau_{\rm GP}^{\rm eff}(z) = \begin{cases} \,0.85 \left(\frac{1 + z}{5} \right)^{4.3} \quad z \leq 5.5\\ \\[-2.5ex] \,2.63 \left(\frac{1 + z}{6.5} \right)^{\xi}\hphantom{^{.3}} \quad z > 5.5,\\ \end{cases} \end{equation}](/articles/aa/full_html/2017/05/aa30258-16/aa30258-16-eq197.png) (1)empirically determining a limit of ξ > 10.9. We now wish to measure a value of ξ following a procedure similar to that used by Simpson et al. (2014), using our revised photometry. We have an additional constraint on ξ, namely the transmission spikes detected in the X-shooter spectrum.
(1)empirically determining a limit of ξ > 10.9. We now wish to measure a value of ξ following a procedure similar to that used by Simpson et al. (2014), using our revised photometry. We have an additional constraint on ξ, namely the transmission spikes detected in the X-shooter spectrum.
 |
Fig. 8 Synthetic F814W photometry measured by determining |
The intrinsic quasar emission below Lyα is modelled using the power law chosen by Mortlock et al. (2011), 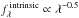 , which is normalised to the observed spectrum at 1280 Å. Absorption in the IGM is modelled using Eq. (1). The wavelength of each pixel is converted to a Lyα redshift, which is used to calculate
, which is normalised to the observed spectrum at 1280 Å. Absorption in the IGM is modelled using Eq. (1). The wavelength of each pixel is converted to a Lyα redshift, which is used to calculate  for a particular value of ξ. Measuring the absorbed spectrum with synphot produces a synthetic i814 magnitude that we can compare directly to the F814W result. We show the fluxes measured for a range of ξ values in Fig. 8. Combining the synthetic photometry with spectroscopy, we determine a posterior distribution for ξ, shown in Fig. 9. We have assumed a uniform prior for ξ> 0, and a Gaussian distribution for the i814 measurement which is equivalent to (1.047 ± 0.356) × 10-8 Jy. The sharp cut-off results from determining a lower limit to the i814 flux from the transmission spectrum derived in Sect. 2.1, measured as 0.914 × 10-8 Jy (AB 29.00, S/N ~ 30). Higher values of ξ are excluded, as the resulting i814 measurements are below this secure lower flux limit. The posterior peaks at ξ = 11.2, for which the synthetic photometry yields the HST result (Fig. 9). The 68% highest posterior density credible interval is shaded, giving
for a particular value of ξ. Measuring the absorbed spectrum with synphot produces a synthetic i814 magnitude that we can compare directly to the F814W result. We show the fluxes measured for a range of ξ values in Fig. 8. Combining the synthetic photometry with spectroscopy, we determine a posterior distribution for ξ, shown in Fig. 9. We have assumed a uniform prior for ξ> 0, and a Gaussian distribution for the i814 measurement which is equivalent to (1.047 ± 0.356) × 10-8 Jy. The sharp cut-off results from determining a lower limit to the i814 flux from the transmission spectrum derived in Sect. 2.1, measured as 0.914 × 10-8 Jy (AB 29.00, S/N ~ 30). Higher values of ξ are excluded, as the resulting i814 measurements are below this secure lower flux limit. The posterior peaks at ξ = 11.2, for which the synthetic photometry yields the HST result (Fig. 9). The 68% highest posterior density credible interval is shaded, giving 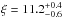 . The resulting evolution of
. The resulting evolution of 
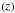 is shown in Fig. 7.
is shown in Fig. 7.
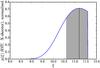 |
Fig. 9 Posterior distribution for ξ, constrained by photometry and spectroscopy. The 68% highest posterior density credible interval is shaded and the peak of the distribution is indicated at ξ = 11.2. The cut-off at ξ = 11.6 arises from determining a lower limit to the i814 flux from the transmission spectrum derived in Sect. 2.1. |
4.2. Flux distribution in the Lyα forest: the longest GP trough to date
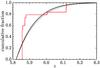 |
Fig. 10 Cumulative distribution of Lyα forest flux contained in the detected transmission spikes (red), compared with the expected distribution of flux transmission based on our model for optical depth with ξ = 11.2 (black; Sect. 4.1). The dashed black lines indicate the uncertainty on our model for |
The detected transmission spikes account for (87 ± 34)% of the quasar flux detected by HST, with the uncertainty dominated by the photometry measurement. Therefore all of the transmission in the spectrum may have been detected. Even if there are any additional lower-significance transmission features they are likely to be found in the same redshift range and to follow a similar distribution. The shape of the cumulative distribution of the transmitted flux therefore provides a noisy estimate of the shape of the cumulative transmission of the Lyα forest, and so it is interesting to compare this to the model.
In Fig. 10 we present the cumulative proportion of flux contained in transmission spikes with redshift i.e. the cumulative transmitted flux as a function of redshift, normalised to the total transmitted flux. The result from spectroscopy is compared to the  model derived in Sect. 4.1, which we use to produce an average transmission spectrum. In both cases the distributions are normalised to the total transmitted flux as we wish to compare the relative shapes.
model derived in Sect. 4.1, which we use to produce an average transmission spectrum. In both cases the distributions are normalised to the total transmitted flux as we wish to compare the relative shapes.
Broadly speaking, the distributions are in good agreement. In particular, our model for  predicts effectively zero transmission for z ≳ 6.2, which is consistent with the transmission spectrum.
predicts effectively zero transmission for z ≳ 6.2, which is consistent with the transmission spectrum.
The distribution of transmission features is consistent with an extremely long GP trough extending to the quasar’s near-zone, covering the redshift range 6.12 ≤ z ≤ 7.04, equivalent to a comoving distance of 240 h-1 Mpc. This is more than twice the length of the next longest trough reported by Becker et al. (2015) towards the z = 5.98 quasar ULAS J0148+0600, although that trough extends to significantly lower redshifts (5.52 ≤ z ≤ 5.88).
4.3. Constraints on the IGM neutral fraction
Previous studies have used the evolution of the IGM Lyα opacity to constrain xH i up to z = 6.3 (Fan et al. 2006a; Becker et al. 2015). The large cross-section of Lyα means that the forest will be almost completely absorbed by z ~ 6 even for xH i ~ 10-4 (e.g. Fan et al. 2006a), and density evolution will naturally make the IGM even more opaque at z > 6. Nevertheless, we wish to determine what we can learn about xH i from the long trough towards ULAS J1120+0641.
In order to constrain xH i we use artificial spectra generated from the Sherwood suite of hydrodynamical simulations, which are described in detail in Bolton et al. (2017). Briefly, they were run using a modified version of the parallel Tree-PM SPH code P-GADGET-3, which is an updated version of the publicly available GADGET-2 (Springel 2005). The models use a ΛCDM cosmology consistent with recent Planck results (Planck Collaboration XVI 2014). Here we use the reference 40–2048 model, which uses a 40 h-1 Mpc box and 2 × 20483 particles, giving a gas particle mass of 9.97 × 104M⊙. Reionization occurs at zr = 15, whereafter the gas temperature and ionization fraction evolve assuming a spatially uniform Haardt & Madau (2012) ionizing ultraviolet background (UVB). Simulation outputs were captured in redshift steps of Δz = 0.1, and one-dimensional Lyα forest skewers were generated from the outputs following standard methods (e.g., Theuns et al. 1998).
Our goal is to set limits on the neutral fraction required to produce the 240 h-1 Mpc trough over 6.12 ≤ z ≤ 7.04 seen towards ULAS J1120+0641, and we generate mock Lyα forest spectra with properties matched to the data using the following approach:
-
1.
For each trial, six individual 40 h-1 Mpc skewers are selected at random from the simulation, with the simulation redshifts chosen to most closely match the observed line-of-sight.
-
2.
The Lyα optical depths (τα) are scaled according to the ratio of our desired xH i to the native xH i in the simulation.
-
3.
Transmitted fluxes are computed as F = e− τα.
-
4.
The spectra are smoothed to the nominal instrumental resolution of FWHM = 34 km s-1 and binned using 10 km s-1 pixels, as in the real data.
-
5.
Random Gaussian noise is added with dispersion given by the ULAS J1120+0641 error spectrum (normalized by a power law fit to the flux redward of the Lyα emission line and extrapolated over the forest).
-
6.
A matched-filter search for transmission peaks is then performed following the procedure described in Sect. 3.2. For efficiency, we use only the narrowest filter width (Σ = 15 km s-1), although our results are not highly sensitive to this choice.
We parametrize the evolution in the neutral fraction as a power law of the form xH i(z) = x0 [(1 + z)/7.1] β, where x0 is the volume-weighted neutral fraction at z = 6.1, i.e., near the start of the trough. For reference, the simulation has a native xH i evolution given by xH i(z) ≃ (1.4 × 10-4) [(1 + z)/7.1] 9.1 over the redshift range of interest. We generate 104 mock spectra for each combination of x0 and β. Our 95% confidence limits on these parameters are those for which no transmission peaks are detected with S/N ≥ 5 in at least 5% of the trials. For β = 0, we find x0 ≥ 1.4 × 10-4. Increasing β to 9 gives x0 ≥ 1.1 × 10-4, which is consistent with using a Haardt & Madau (2012) UVB. The limits on x0 are thus largely insensitive to β, as expected if most of the constraining power comes from the low-redshift end of the trough.
In summary, we find that the Lyα trough towards ULAS J1120+0641, while remarkably long, provides only a weak lower limit to the volume-weighted neutral fraction of the IGM (xH i ≳ 10-4), consistent with a highly ionized IGM. The weakness of this constraint is because the trough lies at very high redshift (z ≥ 6.1), where large Lyα opacities are more easily produced due to high IGM densities. We note that we have only considered an IGM model with a spatially uniform UVB and temperature-density relation, which implicitly assumes that the most transmissive regions of the IGM will be low-density voids. There is evidence that xH i is significantly patchy on large scales at z ≳ 5.5 (Becker et al. 2015). Models that attribute this patchiness to a non-uniform background produced by star-forming galaxies tend to predict that the UVB intensity will be anti-correlated with large-scale density enhancements (Davies & Furlanetto 2016; D’Aloisio et al. 2016). In these models, the highest transmission tends to come from high-density regions, and thus a lower xH i would be required to produce significant Lyα transmission. Alternatively, the xH i patchiness may be due to residual large-scale temperature fluctuations from an extended reionization process (D’Aloisio et al. 2015). In that model, high transmission tends to occur in hot (T ~ 20 000–30 000 K), low-density regions that have only recently been reionized. Since these regions would be hotter than we have assumed and the neutral fraction scales as T-0.7, Lyα transmission might appear even if the globally-averaged xH i is somewhat larger than our constraint.
The constraints on xH i from the Lyα trough towards ULAS J1120+0641 are considerably weaker than those determined from Lyα damping wing absorption, first measured by Mortlock et al. (2011), who found xH i> 0.1 at z = 7.1. The most recent Lyα damping wing constraints on the volume-weighted neutral fraction come from an analysis of the FIRE infrared spectrometer spectrum of ULAS J1120+0641 (Simcoe et al. 2012) by Greig et al. (2016), who find xH i (z = 7.1) = 0.4 ± 0.2. Greig & Mesinger (2016) argue that the measured Lyα damping wing absorption towards ULAS J1120+0641 provides one of the strongest constraints on reionization that are currently available. As we begin to probe ever-higher neutral fractions, measurements of Lyα damping wing absorption will likely provide far more useful constraints than the Lyα forest. A further analysis of the damping wing towards ULAS J1120+0641 using the deeper X-shooter spectrum will be presented in Hewett et al. (in prep.).
5. Summary
We have analysed a deep X-shooter spectrum and HST F814W photometry of ULAS J1120+0641 to probe the Lyα forest to z ≃ 7 along the line of sight to the quasar. Our main results are as follows:
-
1.
We revise F814W photometry ofULAS J1120+0641 to bei814 = 28.85, with S/N = 2.9. For a faint source such as ULAS J1120+0641 which is measured against a high background, the Anderson & Bedin (2010) CTE correction included in the ACS pipeline merely introduces noise to the photometry.
-
2.
Significant transmission in the Lyman series forest is restricted to the redshift range 5.856 <z< 6.121, where seven spikes were detected at S/N> 5.
-
3.
Photometry provides us with more useful constraints on effective optical depth, while spectroscopy can still be used to derive a lower limit on transmitted flux. Using data for ULAS J1120+0641 alone and assuming a fixed normalization at z = 5.5, for redshifts z> 5.5 we find
 ∝ (1 + z)ξ where
∝ (1 + z)ξ where 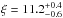 .
. -
4.
We detect an extremely long dark gap extending from the final transmission spike to the quasar’s near-zone, equivalent to a comoving distance of 240h-1 Mpc. The GP trough nevertheless provides only a weak limit on the IGM neutral fraction xH i ≳ 10-4 at 95% confidence. This is a generic limitation of observations of the Lyα forest at such high redshifts.
A more elegant approach would be to deduce a posterior probability density function for  and hence
and hence  . The true value of
. The true value of 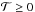 , so by assuming a uniform prior for
, so by assuming a uniform prior for 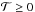 and a Gaussian likelihood, it would be possible to determine posterior confidence intervals for
and a Gaussian likelihood, it would be possible to determine posterior confidence intervals for  . By adopting a 2σ upper limit for
. By adopting a 2σ upper limit for 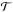 , we have followed the method used to measure existing limits on
, we have followed the method used to measure existing limits on  (e.g. Fan et al. 2006a; Becker et al. 2015). Given that absorption in the Lyα forest is saturated at z ~ 6.5, our choice is ultimately not very important.
(e.g. Fan et al. 2006a; Becker et al. 2015). Given that absorption in the Lyα forest is saturated at z ~ 6.5, our choice is ultimately not very important.
Acknowledgments
We are grateful to the referee, Michael Strauss, who provided constructive comments and improvements. We would like to thank the A.C.S. instrument team for their helpful guidance on the effects of CTE losses. We also thank Jamie Bolton for the use of the Sherwood simulations. This work was supported by Grants ST/K502042/1 and ST/N000838/1 from the Science and Technology Facilities Council. S.J.W. gratefully acknowledges the support of the Leverhulme Trust through the award of a Leverhulme Research Fellowship. G.D.B. is supported by the National Science Foundation under Grant AST 1615814. P.C.H. and R.G.M. acknowledge support from the STFC via a Consolidated Grant to the Institute of Astronomy, Cambridge. B.P.V. acknowledges funding through the ERC grant “Cosmic Dawn”.
References
- Anderson, J., & Bedin, L. R. 2010, PASP, 122, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Barnett, R., Warren, S. J., Banerji, M., et al. 2015, A&A, 575, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, R. H., Fan, X., White, R. L., et al. 2001, AJ, 122, 2850 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, G. D., Bolton, J. S., Madau, P., et al. 2015, MNRAS, 448, 19 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, A. S., Burles, S., Schlegel, D. J., Eisenstein, D. J., & Brinkmann, J. 2004, AJ, 127, 1860 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Puchwein, E., Sijacki, D., et al. 2017, MNRAS, 464, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Bosman, S. E. I., Becker, G. D., Haehnelt, M. G., et al. 2017, MNRAS, in press [Google Scholar]
- Chiaberge, M. 2012, Instrument Science Report ACS 2012-05 [Google Scholar]
- D’Aloisio, A., McQuinn, M., & Trac, H. 2015, ApJ, 813, L38 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aloisio, A., McQuinn, M., Davies, F. B., & Furlanetto, S. R. 2016, MNRAS, submitted [arXiv:1611.02711] [Google Scholar]
- Davies, F. B., & Furlanetto, S. R. 2016, MNRAS, 460, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S. G., Castro, S., Stern, D., & Mahabal, A. A. 2001, ApJ, 560, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., White, R. L., Davis, M., et al. 2000, AJ, 120, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Narayanan, V. K., Lupton, R. H., et al. 2001, AJ, 122, 2833 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006a, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, X., Carilli, C., & Keating, B. 2006b, ARA&A, 44, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Greig, B., & Mesinger, A. 2016, MNRAS, 465, 4838 [Google Scholar]
- Greig, B., Mesinger, A., Haiman, Z., & Simcoe, R. A. 2017, MNRAS, 466, 4239 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 2012, ApJ, 746, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P., Irwin, M., Bunclark, P., et al. 1985, MNRAS, 213, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelson, D. D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Laidler, V., Boffi, F., Barlow, T., et al. 2008, Synphot Data User’s Guide (Baltimore, STScI) [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- McGreer, I. D., Mesinger, A., & Fan, X. 2011, MNRAS, 415, 3237 [NASA ADS] [CrossRef] [Google Scholar]
- McGreer, I. D., Mesinger, A., & D’Odorico, V. 2014, MNRAS, 447, 499 [Google Scholar]
- Mesinger, A. 2010, MNRAS, 407, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XLVII. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, M. 1965, ApJ, 141, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Simcoe, R. A., Sullivan, P. W., Cooksey, K. L., et al. 2012, Nature, 492, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C., Mortlock, D., Warren, S., et al. 2014, MNRAS, 442, 3454 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., & Cowie, L. L. 2002, AJ, 123, 2183 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., Leonard, A., Efstathiou, G., Pearce, F. R., & Thomas, P. A. 1998, MNRAS, 301, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Venemans, B. P., McMahon, R. G., Walter, F., et al. 2012, ApJ, 751, L25 [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. L., Becker, R. H., Fan, X., & Strauss, M. A. 2003, AJ, 122, 34 [Google Scholar]
- White, R. L., Becker, R. H., Fan, X., & Strauss, M. A. 2005, AJ, 129, 2102 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Measurements of the transmission fraction 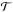 and effective optical depth
and effective optical depth  in bins of Δz = 0.15 towards ULAS J1120+0641.
in bins of Δz = 0.15 towards ULAS J1120+0641.
All Figures
 |
Fig. 1 VLT X-shooter spectrum of ULAS J1120+0641 (black), covering restframe wavelengths between 850 and 1400 Å. The spectrum has been binned to a pixel size of 150 km s-1 using inverse variance weighting. The observed wavelengths of Lyα, Lyβ and the Lyman limit are marked. The only transmission detected in the spectrum is confined to spikes over the wavelength range marked by α, in the pure Lyα forest, corresponding to the redshift range 5.858 < z < 6.122 (Sect. 3.2). The corresponding wavelength range for Lyβ absorption is marked β and lies blueward of the restframe Lyman limit. Plotted as the blue dotted line is the (scaled) total system throughput curve for the ACS F814W filter. |
| In the text | |
 |
Fig. 2 CTE correction (mcorrected−muncorrected) applied to objects detected in the F814W frame, shown as blue stars. The red circle indicates ULAS J1120+0641. Yellow crosses represent the median correction in the indicated bins of 0.5 mag (upper) or 200 pixels (lower). Upper: correction as a function of corrected F814W magnitude. Lower: correction as a function of Δy, the number of pixels from the readout register. |
| In the text | |
 |
Fig. 3 Close-up of the Lyα forest towards ULAS J1120+0641, binned to a pixel size of 20 km s-1 for display purposes. Upper: spectrum (black) and 1σ errors (red). Lower: S/N at each pixel found by running the Gaussian matched filter at the narrowest width over the unbinned spectrum (pixel size 10 km s-1). |
| In the text | |
 |
Fig. 4 S/N of spikes extracted from the X-shooter spectrum. We have extracted the highest value of |S/N| from all template widths. |
| In the text | |
 |
Fig. 5 Significant transmission of flux in the Lyα forest towards ULAS J1120+0641. The unbinned X-shooter spectrum of ULAS J1120+0641 is shown in grey with a pixel size of 10 km s-1. Shown in blue is the 1σ error spectrum, and the derived transmission spectrum is overlaid in red. The seven detections presented in Table 2 are indicated. |
| In the text | |
 |
Fig. 6 As Fig. 5, but focused on the region of the spectrum in the Lyβ forest in the vicinity of the possible transmission spike at λ = 8056 Å, which is indicated. |
| In the text | |
 |
Fig. 7 Evolution of |
| In the text | |
 |
Fig. 8 Synthetic F814W photometry measured by determining |
| In the text | |
 |
Fig. 9 Posterior distribution for ξ, constrained by photometry and spectroscopy. The 68% highest posterior density credible interval is shaded and the peak of the distribution is indicated at ξ = 11.2. The cut-off at ξ = 11.6 arises from determining a lower limit to the i814 flux from the transmission spectrum derived in Sect. 2.1. |
| In the text | |
 |
Fig. 10 Cumulative distribution of Lyα forest flux contained in the detected transmission spikes (red), compared with the expected distribution of flux transmission based on our model for optical depth with ξ = 11.2 (black; Sect. 4.1). The dashed black lines indicate the uncertainty on our model for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


