EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 601 (May 2017) A&A, 601 (2017) A138 Full HTML
Free Access
Issue
A&A
Volume 601, May 2017
Article Number A138
Number of page(s) 7
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201630010
Published online 22 May 2017

© ESO, 2017

1. Introduction

The direct collapse scenario for black hole (BH) formation in the early Universe has received much attention in recent years, in particular for its ability to explain the formation of BHs with masses ≳109M⊙ within the first billion years of cosmic history (e.g. Mortlock et al. 2011; Wu et al. 2015). The key ingredients for the formation of the massive (~105M⊙) seed BHs in this theory are (1) primordial gas collapsing into an atomic cooling dark matter halo and (2) a sufficiently low fraction of H2 molecules in the gas to prevent cooling below the ~104 K cooling limit of atomic hydrogen (for reviews see Volonteri 2012; Haiman 2013; Johnson & Haardt 2016; Latif & Ferrara 2016).

The main ways that are envisioned for keeping the primordial gas devoid of molecules is photodissociation of H2 due to so-called Lyman-Werner (LW) radiation at energies 11.2–13.6 eV and photodetachment of the H− ion, which is an intermediary in the formation of H2 (e.g. Bromm & Larson 2004), by photons with energies >0.76 eV (e.g. Chuzhoy et al. 2007). The relative importance of each of these processes has been found to be strongly dependent on the spectrum of the incident radiation (e.g. Shang et al. 2010; Sugimura et al. 2014; Glover 2015; Agarwal et al. 2015; Latif et al. 2015; Wolcott-Green et al. 2016), presumably produced by a nearby star-forming galaxy (e.g. Dijkstra et al. 2008; Agarwal et al. 2012; Visbal et al. 2014; Regan et al. 2016a).

An additional source of radiation which contributes to the photodetachment of H− and so limits the formation rate of H2 is the trapped Lyman α cooling radiation that is emitted from the collapsing atomic gas in the halo itself (Spaans & Silk 2006; Schleicher et al. 2010). Here we explore the impact that this trapped radiation has on the production of H2 molecules in the gas and, in turn, on its ability to cool below the ~104 K required for direct collapse black hole (DCBH) formation. In the next section, we outline the one-zone chemical and cooling model that we employ for our study and we describe our approach to modeling the photodetachment of H− by Lyman α cooling radiation. In Sect. 3 we present the basic results of our calculations, and in Sect. 4 we explore the impact of Lyman α feedback on the critical LW flux required for DCBH formation. Finally, we give our conclusions and provide a brief discussion of our results in Sect. 5.

2. Feedback from Lyman α cooling radiation

For our study, we begin with the same one-zone model for the collapse of the primordial gas as presented in Johnson & Bromm (2006), which is very similar to other one-zone models that have been routinely applied to DCBH formation (e.g. Omukai et al. 2005, 2008; Schleicher et al. 2010; Agarwal et al. 2016a). The model assumes that the density of the primordial gas increases on the free-fall timescale, and the non-equilibrium chemical and thermal evolution of the collapsing gas is calculated. All of the pertinent primordial chemical species are included, as are all of the pertinent radiative processes.

While the reader is referred to Johnson & Bromm (2006) for more details, here we describe the key ingredients in the model that we draw on for our study of the direct collapse scenario. One important update to this code has been the adoption of the H2 self-shielding prescription presented in Wolcott-Green et al. (2011; see also Hartwig et al. 2015; Wolcott-Green et al. 2016), which replaced the simpler prescription presented in Bromm & Loeb (2003). We have also updated the collisional dissociation rate of H2 to that presented in Martin et al. (1996), which is now the commonly adopted rate (e.g. Shang et al. 2010; Agarwal et al. 2016a). The model includes the main cooling processes that are relevant for the direct collapse scenario, which are atomic hydrogen line cooling and molecular (H2) line cooling (e.g. Cen 1992; Abel et al. 1997). In addition, the model tracks the non-equilibrium chemistry of the primordial gas and the formation of H2 molecules, the main channel for which is the following two reactions:

where e− is a free electron and γ is a photon. Given that H− is the main precursor to H2, the photodetachment of H− is a key reaction to track in order to accurately calculate the formation rate of H2. Thus, we track the photodetachment of H− as well as the photodissociation of H2 in our model, adopting the rates presented in Shang et al. (2010) as functions of the temperature of the radiation field1.

We solve additional equations in order to assess the impact of photodetachment of H− by Lyman α photons. To begin, we make the simple assumption that the luminosity of Lyman α cooling emission in the cloud balances the rate of gravitational potential energy release during the collapse of the cloud (e.g. Dijkstra et al. 2016a,b). This is a sound approximation, as it has been shown in numerous cosmological simulations that the collapse of primordial gas in atomic cooling halos is roughly isothermal and occurs on the free-fall timescale (e.g. Wise et al. 2008; Regan & Haehnelt 2009). Thus, we adopt the following simple expression for the Lyman α luminosity: (3)where tff = (3π/32Gρ)1/2 is the free-fall time, where G is Newton’s constant and ρ is the density of the collapsing gas. Here Mcloud = 106M⊙ is the typical mass of the central gas cloud collapsing in an atomic cooling halo (e.g. Wise et al. 2008; Johnson et al. 2011, 2014; Latif et al. 2013; Choi et al. 2013). Assuming a uniform cloud density, which is appropriate for our simplified one-zone calculations, this implies a cloud radius of rcloud = 30pc(n/ 102cm-3)−1/3 where n is the number density of hydrogen nuclei. As the gas cools, this is the characteristic length scale over which Lyman α photons must diffuse in order to escape the cloud.

The diffusion of Lyα photons out of the cloud enhances the energy density in Lyα photons by an amount that depends on the cloud column density, NH. The total line center optical depth to Lyα is given by 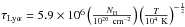, where T is the temperature of the gas and the column density of hydrogen atoms is NH = rcloudn (e.g. Osterbrock & Ferland 2006). Following Adams (1975; see also Smith et al. 2017 for an updated discussion), the pathlength traversed by the photons in escaping the cloud is enhanced by a factor ℳF ~ (avτLyα)1/3, where av = 4.7 × 10-4 (T/104 K)−1/2 is the Voigt parameter. We estimate the total energy density in Lyα radiation, uα, to be 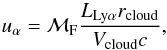(4)where Vcloud denotes the volume of the cloud, and ℳF equals 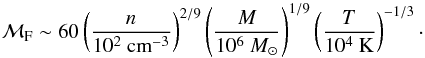(5)Assuming that the Lyman α radiation field is isotropic within the cloud due to the large optical depth to scattering, we can then approximate the photodetachment rate Rdetach of H− ions by Lyman α photons as 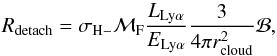(6)where the cross section for this process is σH − = 5.9 × 10-18 cm2 and ELyα = 10.2 eV is the energy of a Lyman α photon (e.g. de Jong 1972; Shapiro & Kang 1987). As the dependence on the optical depth to scattering shows, this rate is elevated due to the many scatterings that Lyman α photons make in passing out of the cloud. Finally, ℬ accounts for the fact that spatial diffusion of Lyα photons does not necessarily uniformly enhance the Lyα intensity throughout the cloud, especially when Lyα emission is concentrated more towards the center of the cloud (see Fig. A.1). In Appendix A we show that ℬ can be as large as ℬ ~ 10 toward the center of the cloud, which is where the DCBH forms. Throughout, we will investigate the impact of varying ℬ within the range ℬ = 1−10.

Combining the above equations, we obtain the following expression for the photodetachment rate as a function of cloud temperature, mass and density: 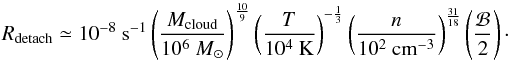(7)This is the equation that we include in our calculations in order to assess the role that Lyman α feedback plays in the formation of DCBHs.

3. Basic results

Here we show our results for two sets of calculations, one in which the effect of H− detachment by Lyman α photons is included and another in which it is neglected. In both cases, we also include the effect of a background LW radiation field, which is assumed to only contribute to the photodissociation of H2 molecules and not to the detachment of H− ions. In the next Section, we explore how the inclusion of the photodetachment rate due to the background radiation impacts the evolution of the collapsing gas. Finally, here we only consider cases with ℬ = 1, corresponding to the simplest case of uniform Lyman α emission from the collapsing cloud. We explore cases with higher ℬ values, corresponding to strongly centralized emission, in the next section.

thumbnail Fig. 1

Evolution of the H2 molecule fraction as a function of the number density of hydrogen nuclei, with (solid lines) and without (dashed lines) accounting for the effect of photodetachment of H− ions by Lyα photons. The colors denote calculations assuming different background radiation fields, as labeled, which are assumed only to dissociate H2 molecules. In all cases shown here ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.

thumbnail Fig. 2

Evolution of the gas temperature as a function of the number density of hydrogen nuclei, with (solid lines) and without (dashed lines) accounting for the effect of photodetachment of H− ions by Lyα photons. The colors denote calculations assuming different background radiation fields which are assumed only to dissociate H2 molecules. With no photodetachment the temperatures remain too low for DCBH formation in all cases, but with this effect included DCBH formation can occur for a background radiation field with J21~ 103. As in Fig. 1, here ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.

Figure 1 shows the evolution of the H2 fraction of the gas, as a function of density, both with and without the above equations for Lyman α photodetachment included. The three sets of curves correspond to different values of the LW background radiation field J21, which is expressed in the standard units of 10-21 erg s-1 cm-2 Hz-1 sr-1. As expected, the H2 fraction is steadily depressed as the level of the background radiation increases. The impact of Lyman α photodetachment is also evident, resulting in the peak H2 abundances dropping by orders of magnitude in the cases with relatively high background radiation levels J21> 100.

The thermal evolution of the gas in these same sets of calculations is shown in Fig. 22. Due to the depressed H2 fraction, molecular cooling is less effective with higher levels of the background radiation field. However, in all cases shown here the gas is still able to cool to ≲103 K when H− detachment is not included in the calculation. With this effect included, the cooling of the gas is suppressed at high density, resulting in much higher temperatures. Importantly, we find that with photodetachment included, the temperature remains high enough for DCBH formation in the case with J21 = 103. Thus, H− detachment by Lyman α photons has the effect of lowering the critical value of the background radiation level required for the formation of DCBHs.

thumbnail Fig. 3

Rate of H− photodetachment by Lyα cooling radiation (Eq. (7)), for the same calculations shown in Figs. 1 and 2. The photodetachment rate is slightly higher for lower levels of the background radiation J21 due to the temperature dependence of the cross section for Lyman α scattering. At low densities the gas evolves adiabatically, leading to the scaling Rdetach∝n3/2, whereas at higher densities the scaling is better approximated assuming the gas is isothermal, leading to the scaling Rdetach∝n31/18. Note that, in all cases, the photodetachment rate rises above the critical rate of ~10-5 s-1 found in calculations assuming a constant background rate and a weak H2-dissociating radiation field by Agarwal et al. (2016a).

To more fully elucidate the impact of photodetachment, the photodetachment rates in our calculations, as a function of the cloud density, are shown in Fig. 3. The density and time dependence of the photodetachment rate makes comparison with previous determinations of the critical rate of photodetachment for DCBH formation difficult (e.g. Sugimura et al. 2014; Agarwal et al. 2016a; Wolcott-Green et al. 2016), as constant photodetachment rates have typically been assumed. However, it is clear that the photodetachment rates we find rise well above the critical value of ~10-5 s-1 found, for instance, by Agarwal et al. (2016a) for the case of a weak H2-dissociating radiation field. Thus, in this sense, our results are consistent with, and can be understood in the context of, previous work. Noting from Fig. 2 that the gas evolves roughly adiabatically up to n~ 102 cm-3 such that T∝n2/3, the scaling Rdetach∝n3/2 provides a good match to our calculations, as shown in Fig. 3. At higher densities an isothermal scaling of Rdetach∝n31/18 provides a better fit, as is also shown in the figure. We next turn to assessing the impact of Lyman α feedback on the value of the critical LW flux required for DCBH formation.

Table 1

Calculated values of the critical LW radiation.

4. The Impact on the critical Lyman-Werner flux

Here we consider how our results change when including the H− photodetachment rate due to the background radiation. To do so, we carry out the same calculations as shown in Fig. 2, but now including also the H− detachment rate due to the background radiation field. We adopt the rates presented in Shang et al. (2010) assuming simple blackbody spectra at Trad = 104 and 105 K, and we evaluate the critical LW flux J21,crit that is required to maintain the gas at ~104 K, leading to the formation of a DCBH.

Our results are presented in Figs. 4 and 5, and are summarized in Table 1. As shown in the left panels of Figs. 4 and 5, for a relatively low background radiation temperature of Trad = 104 K the additional suppression of H2 cooling due to Lyman α feedback is relatively small, as the LW flux required to maintain the gas at ≃104 K at a density of n~ 105 cm-3 is J21,crit≃ 26 neglecting the effect and J21,crit≃ 22−24, depending on the geometry of the Lyman α emission (i.e. for ℬ = 1−10), when accounting for it. However, as shown in the right panels of Figs. 4 and 5, for a larger background radiation temperature of Trad = 105 K accounting for Lyman α feedback results in a much larger drop in the critical flux from J21,crit≃ 1.1 × 103 to ≃200−900, depending on the geometry of the Lyman α emission. Thus, for the spectra expected from hot, young stars in the early Universe, the impact of Lyman α feedback may be especially important. As shown in Fig. 3 and in Eq. (7), it is detachment rates due to Lyman α feedback at high densities, which are higher than the detachment rate due to the background radiation field, that result in a lower critical LW background flux.

It is important to note the reason for the much larger difference in the critical flux in the case of the higher background radiation temperature. This is ultimately due to the much lower rate of H− photodetachment, relative to the H2 photodissociation rate, for the higher temperature background radiation field. Specifically, the photodetachment rate at a given value of J21 is some four orders of magnitude lower for a background temperature of 105 K than it is for one of 104 K (Shang et al. 2010). This implies that the rate of photodetachment by Lyman α photons, which is independent of the spectrum of the background radiation field, is much higher relative to the rate due to the background radiation for the hotter spectrum than it is for the colder one. This leads directly to the much larger drop in the critical value of J21 due to Lyman α feedback that we find for the hotter background spectrum than for the colder one.

The values we find for the critical LW flux (J21,crit) in the cases neglecting Lyman α feedback are broadly consistent with the values found by previous authors (see e.g. Omukai et al. 2008; Sugimura et al. 2014; Latif et al. 2015; Hartwig et al. 2015; Agarwal et al. 2016a,b; Glover 2016), although they are different in detail due to differences in the models adopted in these studies (see also Glover 2015 on rate coefficient uncertainties). As shown in Table 1, however, we can conclude from our calculations that the impact of Lyman α feedback can be strong and, importantly, results in a particularly large drop in the critical LW background flux required for DCBH formation for background radiation temperatures characteristic of young, hot stars in the early Universe (e.g. Tumlinson et al. 2001; Bromm et al. 2001; Oh et al. 2001; Schaerer 2002).

thumbnail Fig. 4

Just as Fig. 2, but now with photodetachment of H− ions by the background radiation field, assumed to be described by a blackbody spectrum with a temperature of Trad = 104 K (left panel) and 105 K (right panel), included. The values of J21 shown in each panel bracket the critical values required to maintain the temperature at ~104 K at a density of 105 cm-3 that are inferred both with and without Lyman α feedback included, as summarized in Table 1. The case shown here assumes ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.

thumbnail Fig. 5

Just as Fig. 4, but now with a Lyman α flux enhancement ℬ = 10, an extreme case expected for strongly centralized Lyman α emission.

Recent analyses have pointed out that it is more accurate to go beyond Jcrit, and quantify the requirements for direct collapse in terms of both the photodetachment rate of H− and the photodissociation rate of H2 (e.g. Sugimura et al. 2014; Agarwal et al. 2016a; Wolcott-Green et al. 2016). These works show that once Rdetach ≳ 10-7 s-1, the photodissociation rate that is required for direct collapse decreases rapidly. Our calculations indicate that the constraint Rdetach ≳ 10-7 s-1 is reached for log [n/ cm-3]≳ 2.5, implying that the thermal evolution of the gas at these high densities becomes strongly impacted by Lyman α feedback.

5. Discussion and conclusions

We have applied a one-zone chemical and thermal evolution model to investigate the role that trapped Lyman α cooling radiation, generated during the collapse of atomic cooling halos, has in suppressing molecular cooling. We find that, while this feedback from Lyman α emission is not strong enough on its own to suppress H2 cooling, it does have the effect of lowering the intensity of the background LW radiation level that is required for the formation of DCBHs. While our modeling is simplified, the effect can be pronounced, potentially dropping the critical LW flux by up to a factor of a few for the background radiation temperatures expected to be produced by young, hot stars in the early Universe.

One implication of our results is that the number density of DCBHs may be higher than previously anticipated based on calculations neglecting H− detachment by cooling radiation. Previous works have shown that the number density of DCBHs increases roughly as 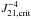(Dijkstra et al. 2008, 2014; Inayoshi & Tanaka 2015; Chon et al. 2016), which suggests that the impact of H− detachment by Lyman α photons results in a large increase of up to a factor of order 102 in the number density of DCBHs in regions of the early Universe illuminated by bright, young stellar populations. This is important, as DCBH formation may have to occur relatively early in the epoch of galaxy formation, when stellar populations are still young, in order to be the seeds for the highest-redshift quasars. The lower values of J21,crit implied by our results also mean that overall higher rates of DCBH formation may be realized, perhaps high enough for DCBHs to account for the BHs residing in the centers of a fraction of normal galaxies today (e.g. Habouzit et al. 2016). We do note, however, that perhaps the most likely sources of the LW radiation that leads to DCBH formation are metal-enriched stellar populations which are likely to emit radiation with characteristic temperatures intermediate between the 104 and 105 K that we have considered here (e.g. Agarwal et al. 2012; Johnson et al. 2013). The precise enhancement of the DCBH formation rate that is due to Lyman α feedback will clearly depend on the spectra of the sources producing the LW radiation, and it is possible that if the spectra are sufficiently soft then the impact of this feedback may be limited.

The extremely bright Lyman α emitter known as CR7 is an intriguing candidate for a high-redshift quasar that may be powered by accretion onto a DCBH (Sobral et al. 2015). Recent modeling efforts have demonstrated that a nearby galaxy may well have produced a high enough level of LW radiation to induce the formation of a DCBH in this galaxy and that the nebular emission could be explained by an accreting BH with a mass consistent with formation as a DCBH (e.g. Pallottini et al. 2015; Agarwal et al. 2016c; Hartwig et al. 2016; Smidt et al. 2016; Smith et al. 2016; Dijkstra et al. 2016a)3. In suggesting that the critical LW flux may be lower than previously thought, our results lend support to DCBH scenario for the origin of CR7. We note that this is also consistent with recent work suggesting that a massive cluster of Population III stars, an alternative explanation for the origin of CR7 (e.g. Sobral et al. 2015; Visbal et al. 2016; see also Johnson 2010), is dubious since it is unknown how a sufficiently high mass of Population III stars could be assembled rapidly enough to explain the observed extremely bright emission (e.g. Hartwig et al. 2016; Yajima & Khochfar 2016; Xu et al. 2016; Visbal et al. 2017).

We note that we have neglected the 2-photon and other hydrogen line emission that is produced at very high densities (≳106 cm-3) where Lyman α photons can be destroyed before escaping the collapsing cloud (e.g. Schleicher et al. 2010; Dijkstra et al. 2016b). While not resonant emission lines, these photons are energetic enough to detach H− and, in fact, the cross section for this process is greater at these photon energies than for Lyman α photons (e.g. de Jong 1972). Thus, neglecting this emission may also lead to a slight overestimate of the critical LW flux.

We note also, though, that we have neglected the absorption of Lyman α photons by H2 molecules, as described in Neufeld (1990; see also Dijkstra et al. 2016b). However, we estimate that this results in a reduction in the Lyman α flux of, at most, a factor of two at the column densities (NH~ 1023 cm-2) and the low H2 fractions (fH2~ 10-7) that occur with an elevated background radiation field. In addition, the LW photons produced in the subsequent radiative decay of the H2 molecules are also able to detach H−. Thus, we do not expect that accounting for this effect would strongly impact our conclusions.

Our results also carry implications for the impact of X-rays on the collapse of gas in atomic cooling halos, which numerous authors have shown is to produce free electrons which catalyze H2 formation, resulting in an increase in the critical flux J21,crit (e.g. Inayoshi & Omukai 2011; Inayoshi & Tanaka 2015; Latif et al. 2015; Glover 2016; Regan et al. 2016b). We note, in particular, that our results for the critical LW flux for DCBH formation are in reasonable agreement with those of Glover (2016) for the case neglecting X-ray feedback. While X-rays may have the effect of raising the critical flux by up to two orders of magnitude in the absence of Lyman α feedback for a hard spectrum (Glover 2016), another impact of X-rays is to enhance the Lyman α emission within the halo (e.g. Dijkstra et al. 2016a). As we have shown, this should result in an enhanced rate of H− photodetachment that will again lower the critical flux.

Finally, we note that atomic cooling halos which grow rapidly, due to mergers or due to growth in high density environments, likely produce Lyman α cooling radiation at a higher rate than assumed in our calculations. This more intense emission leads, in turn, to larger photodetachment rates and lower values for the critical externally-produced LW flux required for DCBH formation. As the earliest supermassive black holes form in relatively rare, overdense regions, this implies that Lyman α feedback may play an especially strong role in paving the way for the formation of the DCBH seeds of the earliest bright quasars (e.g. Mortlock et al. 2011; Wu et al. 2015). Future work incorporating the feedback effect of Lyman α radiation on the chemical evolution of atomic cooling halos in 3D cosmological simulations will further elucidate the role that this process plays in determining the overall rate of DCBH formation.

1

While H is also a precursor to H2 formation in the primordial gas, the rate of H2 formation via this channel is much lower than that through the H− channel for the relatively hot radiation spectra (≥104 K) that are of interest here (see e.g. Sugimura et al. 2016). For this reason, we neglect the radiative destruction of H in our modeling.

2

Note that we recover the canonical cooling behavior of the gas for the case with no background radiation (J21 = 0) and no H− photodetachment (e.g. Bromm & Larson 2004; Greif 2015), as expected since we are employing effectively the same code as in previous studies of such processes (Johnson & Bromm 2006).

3

We note that recent observations of CR7 suggest that the bright Lyman α source may be enriched to some degree with heavy elements (Bowler et al. 2016), suggesting that it is somewhat evolved if it did intially host the formation of a DCBH (see e.g. Aykutalp et al. 2014; Agarwal et al. 2017).

Acknowledgments

Work at LANL was done under the auspices of the National Nuclear Security Administration of the US Department of Energy at Los Alamos National Laboratory under Contract No. DE-AC52-06NA25396. J.L.J. would like to thank Aaron Smith, Bhaskar Agarwal, Zoltan Haiman, Marta Volonteri, Aycin Aykutalp, Nicole Lloyd-Ronning and Simon Glover for helpful discussions. J.L.J. also acknowledges support for this work from the LANL LDRD program.

References

  1. Abel, T., Anninos, P., Zhang, Y., & Norman, M. L. 1997, New Astron., 2, 181 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adams, T. F. 1975, ApJ, 201, 350 [NASA ADS] [CrossRef] [Google Scholar]
  3. Agarwal, B., Khochfar, S., Johnson, J. L., et al. 2012, MNRAS, 425, 2854 [NASA ADS] [CrossRef] [Google Scholar]
  4. Agarwal, B., Smith, B., Glover, S., Natarajan, P., & Khochfar, S. 2016a, MNRAS, 459, 4209 [NASA ADS] [CrossRef] [Google Scholar]
  5. Agarwal, B., Cullen, F., Khochfar, S., et al. 2016b, MNRAS, submitted [arXiv:1609.08605] [Google Scholar]
  6. Agarwal, B., Johnson, J. L., Zackrisson, E., et al. 2016c, MNRAS, 460, 4003 [NASA ADS] [CrossRef] [Google Scholar]
  7. Agarwal, B., Johnson, J. L., Khochfar, S., et al. 2017, MNRAS, submitted [arXiv:1702:00407] [Google Scholar]
  8. Aykutalp, A., Wise, J. H., Meijerink, R., & Spaans, M. 2014, ApJ, 797, 139 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bowler, R. A. A., McLure, R. J., Dunlop, J. S., et al. 2016, MNRAS, accepted [arXiv:1609.00727] [Google Scholar]
  10. Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bromm, V., Kudritzki, R. P., & Loeb, A. 2001, ApJ, 552, 464 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cen, R. 1992, ApJS, 78, 341 [NASA ADS] [CrossRef] [Google Scholar]
  14. Choi, J.-H., Shlosman, I., & Begelman, M. C. 2013, ApJ, 774, 149 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chon, S., Hirano, S., Hosokawa, T., & Yoshida, N. 2016, ApJ, 832, 134 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chuzhoy, L., Kuhlen, M., & Shapiro, P. R. 2007, ApJ, 665, L85 [NASA ADS] [CrossRef] [Google Scholar]
  17. de Jong, T. 1972, A&A, 20, 263 [NASA ADS] [Google Scholar]
  18. Dijkstra, M., Haiman, Z., & Spaans, M. 2006, ApJ, 649, 14 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  20. Dijkstra, M., Ferrara, A., & Mesinger, A. 2014, MNRAS, 442, 2036 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dijkstra, M., Gronke, M., & Sobral, D. 2016a, ApJ, 823, 74 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dijkstra, M., Sethi, S., & Loeb, A. 2016b, ApJ, 820, 10 [NASA ADS] [CrossRef] [Google Scholar]
  23. Glover, S. C. O. 2015, MNRAS, 453, 2901 [NASA ADS] [CrossRef] [Google Scholar]
  24. Glover, S. C. O. 2016, MNRAS, submitted [arXiv:1610.05679] [Google Scholar]
  25. Greif, T. H. 2015, Comput. Astrophys. Cosmology, 2, 3 [NASA ADS] [CrossRef] [Google Scholar]
  26. Habouzit, M., Volonteri, M., Latif, M., Dubois, Y., & Peirani, S. 2016, MNRAS, 463, 529 [NASA ADS] [CrossRef] [Google Scholar]
  27. Haiman, Z. 2013, in The First Galaxies, Astrophys. Space Sci. Lib. (Springer Verlag), 396, 293 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hartwig, T., Glover, S. C. O., Klessen, R. S., Latif, M. A., & Volonteri, M. 2015, MNRAS, 452, 1233 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hartwig, T., Latif, M. A., Magg, M., et al. 2016, MNRAS, 462, 2184 [NASA ADS] [CrossRef] [Google Scholar]
  30. Inayoshi, K., & Omukai, K. 2011, MNRAS, 416, 2748 [NASA ADS] [CrossRef] [Google Scholar]
  31. Inayoshi, K., & Tanaka, T. L. 2015, MNRAS, 450, 4350 [NASA ADS] [CrossRef] [Google Scholar]
  32. Johnson, J. L. 2010, MNRAS, 404, 1425 [NASA ADS] [Google Scholar]
  33. Johnson, J. L., & Bromm, V. 2006, MNRAS, 366, 247 [NASA ADS] [Google Scholar]
  34. Johnson, J. L., & Haardt, F. 2016, PASA, 33, 7 [NASA ADS] [CrossRef] [Google Scholar]
  35. Johnson, J. L., Khochfar, S., Greif, T. H., & Durier, F. 2011, MNRAS, 410, 919 [NASA ADS] [CrossRef] [Google Scholar]
  36. Johnson, J. L., Dalla Vecchia, C., & Khochfar, S. 2013, MNRAS, 428, 1857 [NASA ADS] [CrossRef] [Google Scholar]
  37. Johnson, J. L., Whalen, D. J., Agarwal, B., Paardekooper, J.-P., & Khochfar, S. 2014, MNRAS, 445, 686 [NASA ADS] [CrossRef] [Google Scholar]
  38. Latif, M. A., & Ferrara, A. 2016, PASA, 33, e51 [NASA ADS] [CrossRef] [Google Scholar]
  39. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013, MNRAS, 436, 2989 [NASA ADS] [CrossRef] [Google Scholar]
  40. Latif, M. A., Bovino, S., Grassi, T., Schleicher, D. R. G., & Spaans, M. 2015, MNRAS, 446, 3163 [NASA ADS] [CrossRef] [Google Scholar]
  41. Martin, P. G., Schwarz, D. H., & Mandy, M. E. 1996, ApJ, 461, 265 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  43. Neufeld, D. A. 1990, ApJ, 350, 216 [NASA ADS] [CrossRef] [Google Scholar]
  44. Oh, S. P., Haiman, Z., & Rees, M. J. 2001, ApJ, 553, 73 [NASA ADS] [CrossRef] [Google Scholar]
  45. Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
  46. Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [NASA ADS] [CrossRef] [Google Scholar]
  47. Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito, CA: University Science Books) [Google Scholar]
  48. Pallottini, A., Ferrara, A., Pacucci, F., et al. 2015, MNRAS, 453, 2465 [NASA ADS] [Google Scholar]
  49. Regan, J. A., & Haehnelt, M. G. 2009, MNRAS, 393, 858 [NASA ADS] [CrossRef] [Google Scholar]
  50. Regan, J. A., Johansson, P. H., & Wise, J. H. 2016a, MNRAS, 459, 3377 [NASA ADS] [CrossRef] [Google Scholar]
  51. Regan, J. A., Johansson, P. H., & Wise, J. H. 2016b, MNRAS, 461, 111 [NASA ADS] [CrossRef] [Google Scholar]
  52. Schaerer, D. 2002, A&A, 382, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
  54. Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shapiro, P. R., & Kang, H. 1987, ApJ, 318, 32 [NASA ADS] [CrossRef] [Google Scholar]
  56. Smidt, J., Wiggins, B. K., & Johnson, J. L. 2016, ApJ, 829, L6 [NASA ADS] [CrossRef] [Google Scholar]
  57. Smith, A., Bromm, V., & Loeb, A. 2017, MNRAS, 464, 2963 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sobral, D., Matthee, J., Darvish, B., et al. 2015, ApJ, 808, 139 [NASA ADS] [CrossRef] [Google Scholar]
  59. Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sugimura, K., Omukai, K., & Inoue, A.-K. 2014, MNRAS, 445, 544 [NASA ADS] [CrossRef] [Google Scholar]
  61. Sugimura, K., Coppola, C. M., Omukai, K., Galli, D., & Palla, F. 2016, MNRAS, 456, 270 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tumlinson, J., Giroux, M., & Shull, J. M. 2001, ApJ, 550, L1 [NASA ADS] [CrossRef] [Google Scholar]
  63. Visbal, E., Haiman, Z., & Bryan, G. L. 2014, MNRAS, 445, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  64. Visbal, E., Haiman, Z., & Bryan, G. L. 2016, MNRAS, 460, L59 [NASA ADS] [CrossRef] [Google Scholar]
  65. Visbal, E., Bryan, G. L., & Haiman, Z. 2017, MNRAS, submitted [arXiv:1701.00814] [Google Scholar]
  66. Volonteri, M. 2012, Science, 337, 544 [NASA ADS] [CrossRef] [Google Scholar]
  67. Wise, J. H., Turk, M. J., & Abel, T. 2008, ApJ, 682, 745 [NASA ADS] [CrossRef] [Google Scholar]
  68. Wolcott-Green, J., Haiman, Z., & Bryan, G. L. 2011, MNRAS, 418, 838 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wolcott-Green, J., Haiman, Z., & Bryan, G. L. 2016, MNRAS, submitted [arXiv:1609.02142] [Google Scholar]
  70. Wu, X.-B., Wang, F., Fan, X., et al. 2015, Nature, 518, 512 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  71. Xu, H., Norman, M. L., O’Shea, B. W., & Wise, J. H. 2016, ApJ, 823, 140 [NASA ADS] [CrossRef] [Google Scholar]
  72. Yajima, H., & Khochfar, S. 2016, MNRAS, 467, L51 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Radial dependence of Lyα trapping

In one-zone models, the physical conditions of the collapsing gas cloud are described completely by its temperature and density. When we interpret one-zone models as clouds of uniform density in which Lyα emission is produced uniformly (as we did when deriving Eq. (7), the energy density in Lyα photons is enhanced almost uniformly throughout the cloud (see discussion below and Fig. A.1). The spatial diffusion of Lyα photons out of the cloud introduces only small gradients in the Lyα energy density. However, larger gradients exist if Lyα is not emitted uniformly throughout the cloud, as is generally the case in more realistic scenarios, in which we expect Lyα cooling to increase towards the center of the cloud.

Here we compute the radial dependence of the Lyα energy density in a suite of spherical gas clouds. We vary the HI column density of the cloud and where Lyα is emitted, and compute ℬ by comparing this energy density to our estimate for uα given by Eq. (4). Lyα transfer through static, spherical clouds of uniform density can generally be solved analytically for large line-center optical depths τ0. Dijkstra et al. (2006) derive expressions for the (angle-averaged) Lyα intensity J as a function of radius r and frequency x in a spherical cloud of radius Rcl (see their Eq. (C12)). For a central Lyα point source (at rs = 0) their expression for the total (integrated over frequency) intensity simplifies to 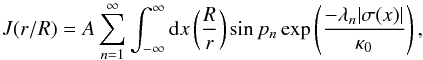(A.1)where A is a normalization constant, and

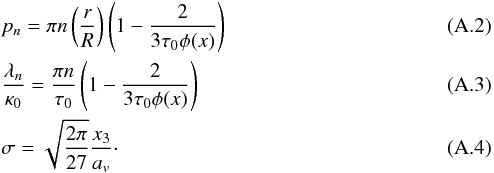We obtain ℬ by dividing the energy density uα(r/R) = 4πJ(r/R) /c to uα given by Eq. (4).

thumbnail Fig. A.1

Lines: radial dependence of the boost factor ℬ for a central Lyα point source surrounding a uniform gas cloud of density n = 102 cm-3 (black), n = 103 cm-3 (red), and n = 104 cm-4 (blue). When normalized to the cloud radius R, ℬ(r/R) does not depend on n. The grey line shows analytic solution from Dijkstra et al. (2006). The black line shows a case in which Lyα is produced uniformly throughout the cloud, and ℬ ~ 1, which shows that the calculations presented in the paper are quite accurate if Lyα is emitted uniformly throughout the cloud.

Figure A.1 shows ℬ as a function of r/R for the analytic model (thick grey line). This line is independent of τ0 provided that avτ0 ≳ 103. We overplot 3 lines with different colors, which we obtained from Monte Carlo simulations of the Lyα radiativetransfer. The blue, red, and black lines represent the cloud when its density is n = 102, 103, and 104 cm-3, respectively. First, we note that (not shown here) the total average trapping time we found for Lyα photons in the Monte Carlo simulation agreed well with our estimate used for Eq. (4). Figure A.1 shows clearly that ℬ > 1 at r< 0.6 Rcl, and that ℬ > 10 at r< 0.2 Rcl. That is, in the case of a central Lyα source, photodetachment of H− by Lyα is signficantly more important for the inner ~104M⊙ of gas than in the exterior regions. Clearly, the case of a central point source represents an extreme case of centrally enhanced Lyα emission, and we consider the values of ℬ that we obtain for these models to represent upper limits.

For completeness, the black line shows ℬ obtained from our Monte Carlo simulations in which Lyα photons are produced uniformly throughout the cloud. For clarity, we have only shown the case n = 102 cm-3, but we have verified that the curve does not change for higher densities. The Lyα energy density is enhanced close to uniformly throughout the cloud, and at a level that is in good agreement with Eq. (4).

All Tables

Table 1

Calculated values of the critical LW radiation.

In the text

All Figures

thumbnail Fig. 1

Evolution of the H2 molecule fraction as a function of the number density of hydrogen nuclei, with (solid lines) and without (dashed lines) accounting for the effect of photodetachment of H− ions by Lyα photons. The colors denote calculations assuming different background radiation fields, as labeled, which are assumed only to dissociate H2 molecules. In all cases shown here ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.
In the text
thumbnail Fig. 2

Evolution of the gas temperature as a function of the number density of hydrogen nuclei, with (solid lines) and without (dashed lines) accounting for the effect of photodetachment of H− ions by Lyα photons. The colors denote calculations assuming different background radiation fields which are assumed only to dissociate H2 molecules. With no photodetachment the temperatures remain too low for DCBH formation in all cases, but with this effect included DCBH formation can occur for a background radiation field with J21~ 103. As in Fig. 1, here ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.
In the text
thumbnail Fig. 3

Rate of H− photodetachment by Lyα cooling radiation (Eq. (7)), for the same calculations shown in Figs. 1 and 2. The photodetachment rate is slightly higher for lower levels of the background radiation J21 due to the temperature dependence of the cross section for Lyman α scattering. At low densities the gas evolves adiabatically, leading to the scaling Rdetach∝n3/2, whereas at higher densities the scaling is better approximated assuming the gas is isothermal, leading to the scaling Rdetach∝n31/18. Note that, in all cases, the photodetachment rate rises above the critical rate of ~10-5 s-1 found in calculations assuming a constant background rate and a weak H2-dissociating radiation field by Agarwal et al. (2016a).
In the text
thumbnail Fig. 4

Just as Fig. 2, but now with photodetachment of H− ions by the background radiation field, assumed to be described by a blackbody spectrum with a temperature of Trad = 104 K (left panel) and 105 K (right panel), included. The values of J21 shown in each panel bracket the critical values required to maintain the temperature at ~104 K at a density of 105 cm-3 that are inferred both with and without Lyman α feedback included, as summarized in Table 1. The case shown here assumes ℬ = 1, corresponding to uniform Lyman α emission within the collapsing cloud.
In the text
thumbnail Fig. 5

Just as Fig. 4, but now with a Lyman α flux enhancement ℬ = 10, an extreme case expected for strongly centralized Lyman α emission.
In the text
thumbnail Fig. A.1

Lines: radial dependence of the boost factor ℬ for a central Lyα point source surrounding a uniform gas cloud of density n = 102 cm-3 (black), n = 103 cm-3 (red), and n = 104 cm-4 (blue). When normalized to the cloud radius R, ℬ(r/R) does not depend on n. The grey line shows analytic solution from Dijkstra et al. (2006). The black line shows a case in which Lyα is produced uniformly throughout the cloud, and ℬ ~ 1, which shows that the calculations presented in the paper are quite accurate if Lyα is emitted uniformly throughout the cloud.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.