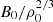EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 684 (April 2024) A&A, 684 (2024) A195 Full HTML
Open Access
Issue
A&A
Volume 684, April 2024
Article Number A195
Number of page(s) 20
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202347783
Published online 24 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

It is known that supermassive black holes (SMBHs) are present in the nuclei of most galaxies, and through high-redshift surveys their existence with masses of about 109 M⊙ was revealed at z ≥ 6 (Mortlock et al. 2011; Bañados et al. 2018; Schleicher 2019). This implies that they existed when the Universe was less than 800 Myr old, and the formation and nature of their seeds are mysteries of the Universe that remain to be solved. Now, with the upcoming observations thanks to the launch of new telescopes such as the James Webb Space Telescope (JWST) the number of these objects will increase as it has been shown that these telescopes could detect seeds of the first quasars at z ≲ 20 (Whalen et al. 2020). Recent observations performed by the JWST have already allowed the detection of massive and bright galaxies at very high redshift (z ∼ 10), which has also now been confirmed spectroscopically (Curtis-Lake et al. 2023; Robertson et al. 2023; Arrabal Haro et al. 2023). In the coming decade, with surveys by Euclid and the Nancy Grace Roman Space Telescope (RST) it will be possible to find even more of these objects at z ≲ 6 − 8, and even at higher redshift thanks to gravitational lensing (Vikaeus et al. 2022). Furthermore, Latif et al. (2024) showed that the first quasars could also be detected by the Square Kilometer Array (SKA) up to z ∼ 16 and by the Next-Generation Very Large Array (ngVLA) at z ∼ 14. This leads to the need to further update the theory behind the formation of these massive objects with respect to these upcoming observations. The models that have been proposed to potentially explain the formation of SMBHs include the merging and accretion of Pop III remnants (Abel et al. 2002; Yoshida et al. 2008; Latif et al. 2013b), the collapse of dense stellar clusters (Omukai et al. 2008; Devecchi & Volonteri 2009; Boekholt et al. 2018; Reinoso et al. 2018) and the direct collapse of protogalactic gas clouds in which the primordial gas in a massive halo collapses directly into a central and massive object ( ∼ 105 M⊙) without fragmentation (Bromm & Loeb 2003; Begelman et al. 2006; Latif et al. 2013a; Shlosman et al. 2015). This last model seems to be the most promising scenario as it provides the most massive black hole seeds, which then can grow via moderate accretion rates to form SMBHs (Latif et al. 2013d). The most likely cradles to assemble these direct collapse black holes (DCBHs) are known as atomic cooling halos, which are metal-free very massive halos with virial temperatures ≥104 K at z ∼ 15 − 10.

The main coolant in the early Universe is molecular hydrogen (H2), which efficiently cools the gas to a few hundred K, possibly triggering fragmentation and therefore impeding the atomic-cooling halos to collapse into a DCBH. It is therefore important to suppress the H2 cooling process. In this respect, the presence of an intense UV flux produced by Pop III or Pop II stars is mandatory in order to inhibit the H2 formation through the direct dissociation of this molecule or by H− photodetachment (Schleicher et al. 2010b), which can be achieved if the halo is close to a star-forming galaxy (Dijkstra et al. 2008).

The required UV background field to maintain the gas in an atomic state (i.e. the critical strength of the radiation flux 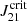, where J21 = 1 corresponds to the specific intensity just below the Lyman limit (13.6 eV) in units of 10−21 erg cm−2 sr−1 s−1 Hz−1) has been obtained performing one-zone and three-dimensional (3D) simulations (Omukai et al. 2008; Shang et al. 2010; Latif et al. 2014a). The critical value depends on the chemical model and the spectral shape of the radiation field. This radiation field is commonly described as an idealised spectrum with blackbody radiation temperatures of Trad = 105 K and Trad = 104 K for Pop III and Pop II, respectively. The 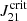parameter has a direct impact on the estimation of the DCBH number density (nDCBH), affecting the feasibility of this scenario, so that it is of importance to estimate the value of 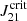with high precision (Dijkstra et al. 2014; Yue et al. 2014; Habouzit et al. 2016). In this context, Sugimura et al. (2014) estimated the value of 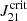using a one-zone model including more realistic spectra, and found a critical value of 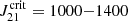. In addition, Latif et al. (2015) performed 3D simulations and used realistic spectra (Trad = 2 × 104 − 105 K); they found a higher value for 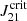of a few times 104, suggesting that the DCBHs might be even rarer than suggested before. Nevertheless, primordial gas with trace amounts of H2 still can form massive objects (Latif et al. 2014b), even if fragmentation is not fully suppressed.

An alternative mechanism to inhibit H2 cooling includes the presence of magnetic fields. Magnetic fields are ubiquitous in astrophysical systems and the evidence of their presence at high redshift is growing (Bernet et al. 2008; Murphy 2009). However, the origin and strength of these primordial fields is still an open question. A possible explanation of their formation includes astrophysical processes, such as the Biermann battery or the Weibel instability (Biermann 1950; Schlickeiser & Shukla 2003). Furthermore, it has been proposed that primordial magnetic fields may have appeared during cosmological inflation or through electroweak or quantum chromodynamical phase transitions (see the review by Grasso & Rubinstein 2001). More recent seeding models include the photoionisation process by photons provided by the first luminous sources (Langer et al. 2005) and charge segregation ahead of ionisation fronts during the Epoch of Reionisation, among others (Garaldi et al. 2021). Regardless of their origin, theory predicts the seed fields to be typically weak (Subramanian 2016). Neronov & Vovk (2010) reported a lower limit of B ≳ 3 × 10−16 G, and the Planck results provide an upper limit of a nG level at a scale of 1 Mpc (Planck Collaboration XIX 2016; Paoletti et al. 2019, 2022). Therefore, it is of relevant importance to understand how these fields are amplified during structure formation.

The presence of turbulence during the collapse and accretion in the primordial gas has been revealed through several high-resolution simulations of mini-halos and massive halos, playing an important role in regulating the angular momentum and the fragmentation of the gas (Abel et al. 2002; Yoshida et al. 2008; Greif et al. 2008; Van Borm et al. 2014). This suggests that in addition to the gravitational compression under the constraint of flux freezing, the amplification of the initial magnetic seed field may be generated by the small-scale dynamo process that transforms the turbulent energy into magnetic energy amplifying the small initial field on very short timescales (Kazantsev 1968; Brandenburg & Subramanian 2005).

Due to the difficulty in achieving the large dynamical range in space and time for an entire system in numerical simulations, previous studies have employed turbulent boxes to study the growth rate of the magnetic field through the small-scale dynamo, showing that the magnetic energy grows exponentially (see e.g. Haugen et al. 2004; Cho & Lazarian 2009; Federrath et al. 2011a). On the other hand, in a gravitational collapse environment, where the structures are highly non-linear and not in equilibrium, the signatures of this regime will always be visible. If the magnetic field amplification is due to the compression, the field strength will be directly related to the gas density; however, even for a saturated dynamo, the magnetic field strength should scale with gas density as well, as all relevant energy components such as thermal energy or turbulent kinetic energy will scale with the density during the collapse. Therefore, in this regime the expected results found in turbulent boxes cannot be applied unless high resolution is achieved, and therefore the effects of gravity and gravitational collapse have to be taken into account. Schmidt et al. (2013) and Latif et al. (2013c) showed that in a self-gravitating turbulent gas the magnetic field amplification is well correlated with density; they also found that the amplification due to the small-scale dynamo and the amplification due to compression are comparable. The latter is directly related to the numerical resolution of the simulation, where if the turbulence is not sufficiently resolved, the small-scale dynamo contribution to the magnetic field amplification might be smaller than the contribution due to compression as the dynamo will not be in an efficient regime. Due to the difficulties in resolving turbulence in numerical simulations, most simulations of gravitational collapse tend to remain within the kinematic regime, unless the initial field strength is sufficiently high to allow saturation to be reached. The test of possible saturation of the dynamo thus have typically involved the systematic variation in the initial magnetic field strength, essentially looking for a slope in the ratio of the physical magnetic field versus the field expected from pure compression; however, even if the dynamo saturation is reached, the amplification by gravitational compression will continue until the system evolves towards a complete saturation (Sur et al. 2012).

The efficiency of the dynamo is directly related to the numerical resolution of the simulation. Simulations with different resolutions effectively have different numerical viscosities and resistivities, and only once the viscosity is sufficiently low can the turbulence in the gas be resolved, and therefore numerically modelled. From small-scale dynamo theory, it is also well-known that the growth rate in the kinematic regime depends on the Reynolds number, defined as Re = VL/ν with V and L being the characteristic turbulent velocity and length scale, respectively, and ν the viscosity of the gas. This indicates that the growth rate increases with the Reynolds number, which depends on the numerical resolution (Brandenburg & Subramanian 2005; Schober et al. 2012b; Bovino et al. 2013). This can only continue until saturation occurs, which may depend on the typical Mach numbers in the gas and on the available turbulent energy (see e.g. Federrath et al. 2011a; Schober et al. 2015).

During gravitational collapse, the Jeans length is the critical scale for driving turbulent motions, so it is of huge importance to resolve it well, especially when the dynamo operates. In the context of Pop III star formation in mini-halos, Sur et al. (2010) performed the first systematic study about the implications of varying the resolution in the behaviour of turbulent gas during collapse and how it interacts with the magnetic field. It was found that the vorticity and the magnetic field strength in the gas increase in simulations of high numerical resolution. They found an additional amplification beyond compression in simulations with a resolution of 64 cells per Jeans length. Federrath et al. (2011b) performed a Fourier analysis of the magnetic energy in these simulations and found that the spectra of these magnetic fields show the typical signatures that are present in the small-scale dynamo for sufficiently high resolution to resolve the turbulence (i.e. more than 30 cells per Jeans length). Moreover, Turk et al. (2012) and Latif et al. (2013c) performed a similar study focusing on the evolution of the magnetic field during the gravitational collapse in cosmological simulations, and found that the amplification beyond compression is reduced due to the more diffusive numerical scheme employed, suggesting that a higher Jeans resolution of ≥64 cells is required. In addition, Turk et al. (2012) reported for mini-halos, when using a resolution of 64 cells per Jeans length, that the magnetic field strength increases by 7 orders of magnitude over the effect of compression, while the density shows an increment of 16 orders of magnitude; on the other hand, Latif et al. (2013c) reported for atomic cooling halos, when employing a resolution of 128 cells per Jeans length, that the amplification due to the small-scale dynamo is 2 orders of magnitude above the compression, and decreases when using a smaller resolution. This illustrates the challenge of capturing and identifying such effects in numerical simulations.

Furthermore, it has been shown that the fragmentation of primordial clouds is influenced by the magnetic field. For atomic cooling halos, the small-scale dynamo can efficiently amplify the magnetic field into a saturated state in the presence of strong accretion shocks, thereby helping to suppress fragmentation via additional magnetic pressure (Schleicher et al. 2010a; Latif et al. 2013c, 2014c). Recently, Grete et al. (2019) included for the first time a subgrid scale (SGS) model for unresolved magnetohydrodynamic (MHD) turbulence to explore its impact on the formation of DCBHs, finding that the fragmentation during the collapse is intermittent with accretion rates sufficiently high to support the direct collapse scenario.

Until recently these studies explored how the magnetic fields were generated and amplified, and how they evolved across different scales, but due to numerical constraints it was difficult to study how the magnetic fields affected the initial mass function (IMF) of these objects. Sharda et al. (2020, 2021) answered this question in the context of the mini-halos, showing firstly that an initial weak magnetic field can grow via small-scale and large-scale mean-field dynamos, and secondly that the fragmentation differs significantly from simulations without magnetic fields, and therefore concluded that magnetic fields have a significant impact on the primordial IMF. This marks the starting point of further investigations in this area, as the impact of magnetic fields in the larger atomic cooling halos is not yet understood.

Hirano et al. (2021) studied the effect of the magnetic field on star formation in atomic-cooling halos focusing on the early accretion phase of the atomic gas cloud. They showed that the magnetised atomic gas clouds fragment to a number of dense cores that merge intermittently into the most massive core, due to the transfer of angular momentum by the magnetic field. Moreover, ignoring the effect of turbulence, they showed that the magnetic field is efficiently amplified by the motion of the dense cores. Similarly, Latif et al. (2023) conducted cosmological simulations and evolved them for longer times, and found that in the MHD case, the initial clump masses are higher, but the fragmentation is reduced because the disks are more stable. In contrast, in the non-MHD case, the initial clump mass is lower, but the higher merger rate observed due to the fragmentation yields masses of the central clump that are similar to the MHD case. They did not include H− cooling in their chemical network, which, as shown in Latif et al. (2016), causes small-scale fragmentation. Therefore, they suggest that future simulations should include this process. Hirano et al. (2023) explored the effect of metals in magnetised atomic cooling halos (though without resolving smaller-scale turbulence, and therefore the small-scale dynamo process). They found that although increasing the metallicity reduces mass accretion, many protostars form in the collapsing central region, which is gravitationally and thermally unstable. This leads to an increase in the magnetic field and promotes subsequent gas accretion and coalescence of the low-mass protostars regardless of the initial magnetic field strength. These findings imply that magnetic fields can reduce some of the requirements for the direct collapse scenario, and further investigation with more realistic cosmological scenarios by also including the effect of molecular cooling is needed.

In this paper we explore the evolution of magnetic fields in halos with ≳107 M⊙ collapsing at redshifts z ≳ 12 under different conditions, particularly for different strengths of the Lyman-Werner background corresponding to the regimes of atomic and molecular hydrogen cooling, including different initial values of the magnetic field strength. We present our methodology in Sect. 2, the results in Sect. 3, and our summary and discussions in Sect. 4.

2. Computational methods

We conducted cosmological MHD zoom-in simulations by using the 3D MPI-parallel, Eulerian, block structured, adaptive mesh refinement (AMR) code ENZO (Bryan et al. 2014; Brummel-Smith et al. 2019). This code is open source, and was designed for self-graviting compressible fluid dynamics, including the effects of radiative transfer, magnetic fields, and multiple subgrid and microphysical processes. The main physical equations solved by the code are the Eulerian equation of cosmological (comoving) ideal MHD including gravity. Additionally, the Poisson equation for the gravitational potential is solved. In order to solve the MHD equations, we employed the Dedner method, which is based on the Godunov MUSCL scheme and cleans the divergence constraint ∇ ⋅ B = 0 with a wave-like hyperbolic cleaner (Dedner et al. 2002). For the reconstruction of the variables we used the piecewise linear method (PLM) (van Leer 1979), and to solve the Riemann problem we used the Harten-Lax-van Leer (HLL) Riemann solver (Toro 1997). It is important to note that the Riemann solver used here is somewhat more diffusive compared to the HLL3R scheme used in similar works with the Flash code (see e.g. Sur et al. 2010, 2012; Federrath et al. 2011b); therefore, the required Jeans resolution to resolve the turbulence can be higher (Turk et al. 2012; Latif et al. 2013c).

2.1. Initial conditions

To perform cosmological zoom-in simulations, we followed the approach of Grete et al. (2019). We generated our cosmological nested grid initial conditions with MUSIC (Hahn & Abel 2011), which uses Lagrangian perturbation theory to obtain initial velocity and displacement fields based on numerical solutions of Poisson’s equation. Additionally, the density perturbations are generated through Gaussian random fields that follow a prescribed power spectrum. For the cosmological parameters we used the following data provided by Planck Collaboration XIII (2016): Ωm  =  0.3089, Ωb  =  0.048598, ΩΛ  =  0.6911, σ8  =  0.8159, h  =  0.677, and n  =  0.9667.

We started with a unigrid dark matter (DM)-only simulation within a computational box with a side length of 1 Mpc h−1 at z = 100 using a top grid resolution of 10243 cells. We evolved the simulations until z = 12 and identified the most massive halo using the Rockstar halo finder (Behroozi et al. 2012) to then trace back the DM particle positions in the Lagrangian volume of the halo within a region of two times its virial radius at the initial redshift. After this procedure we were able to generate new nested initial conditions, and therefore we ran the simulations again, this time including baryons and additional physics using a top grid resolution of 2563 cells. Two additional nested refined levels, each with the same resolution, were employed yielding an effective spatial resolution of 10243 cells, identically to our DM-only simulations. We repeated this process three times varying our initial conditions by using different random seeds in MUSIC, which allowed us to analyse three different halos. From this we were able to reach a maximum DM mass resolution of 99 M⊙ with ∼2 × 107 DM particles on the halos. We further added 22 to 26 levels of refinement that allowed us to reach a density peak of about 3 × 10−13 g cm−3. This is the density at which we stopped all our simulations, and therefore our spatial resolution ranges between 19.3 au and 2.2 au, depending on the halo. In this work a grid is refined if one of the following criteria is triggered: a DM overdensity of a factor of 4; a baryon overdensity of a factor of 4 with a refinement level exponent of −0.3, which makes the refinement super-Lagrangian; and the Jeans length resolution where we employed four different values, 32, 64, 128, and 256 cells. These higher values are used to resolve the turbulent eddies for which small-scale dynamo gets excited and may exponentially amplify magnetic fields, as found in previous studies (Latif et al. 2013c; Grete et al. 2019). We smoothed the DM particles at the refinement level 12 to avoid numerical artefacts; this corresponds to 1.4 pc in comoving units. Furthermore, we started our simulations with three uniform magnetic field seeds, each with a proper strength of 10−14 G, 10−10 G, and 10−8 G. According to Planck Collaboration XIX (2016) the upper limits for the primordial magnetic field in the CMB is a few comoving nG at a scale of 1 Mpc, and the values used in this work for the initial magnetic field are below that limit (10−9 nG, 10−5 nG, and 10−3 nG in comoving units).

2.2. Chemical model

We solved the chemical and thermal evolution of the gas using the open-source chemistry package KROME (Grassi et al. 2014). We used the primordial chemical model presented in Latif et al. (2016), which solves the rate equations of nine different chemical species (e−, H−, H, H+, He, He+, He++, H2, 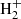) self-consistenly with the MHD simulations. Among the relevant processes that this model includes are chemical heating, chemical cooling, atomic cooling, H2 cooling, H2 self-shielding, H2 photodissociation heating, and H− photodetachment heating. It also includes H− cooling at higher densities. Additionally, for completeness and based on Glover (2015a,b), we included extra chemical reactions, such as collisional ionisation of atomic hydrogen due to H–H collisions and collisions with neutral helium. Chemical species related to deuterium were not considered in the model as they are relevant at lower temperatures and get easily dissociated with lower LW fluxes. We assumed a uniform UV background and varied its strength from J21 = 102 to J21 = 105 using blackbody shaped spectra with temperatures of Trad = 2 × 104 K to explore the amplification of magnetic fields in different environments including the effect of the molecular hydrogen cooling.

3. Results

In the following we present our results concerning magnetic field amplification and saturation in more complex primordial cooling scenarios under the influence of Lyman-Werner radiation. In Sect. 3.1 we present results regarding the amplification and saturation of the magnetic field by using different initial magnetic field seeds and different Jeans resolutions, while in Sect. 3.2 we focus particularly on the effect resulting from the strength of the Lyman-Werner background. We simulated three different halos, but as they presented similar results, here we based the analysis on halo 1 which is the one that includes our highest Jeans resolution simulations. The radial profiles in this section show mass-weighted average quantities (for comparison with other statistical methods see Appendix A); all of them are presented in proper units. In addition, the results and physical and/or magnetic properties for the other halos are provided in Appendix B.

3.1. Amplification and saturation of the magnetic field

We start by presenting the simulations for halo 1 pursued for different Lyman-Werner backgrounds and varying the resolution per Jeans length. The properties of the three simulated halos for B0 = 10−14 G (proper) are listed in Table 1. In addition, as we aim to at least obtain an approximate idea for which magnetic field strength the dynamo saturates and no further dynamo amplification occurs (though compression via collapse may continue), we pursued simulations where we adopted a higher initial magnetic field strength. We study the saturation level of magnetic fields by increasing the initial magnetic field strength due to the difficulty in achieving high Reynolds numbers in numerical simulations. Otherwise we might underestimate their growth rate (Schober et al. 2012a). A list of the properties of these simulations is given in Table 2 for B0 = 10−10 G and in Table 3 for B0 = 10−8 G. These simulations were evolved until they reached a peak density of about 3 × 10−13 g cm−3, which corresponds to a maximum refinement level of 22 − 26 (depending on the initial conditions).

Table 1.

Properties of the simulated halos using an initial magnetic field seed strength of B0 = 10−14 G (proper).

Table 2.

Same as Table 1, but for a higher initial magnetic field seed strength of B0 = 10−10 G (proper).

Table 3.

Same as Table 1, but for a higher initial magnetic field seed strength of B0 = 10−8 G (proper).

Figure 1 shows the density-weighted projection of the density in the central 4000 au of halo 1, using an initial magnetic field seed of B0 = 10−14 G (proper). From visual inspection it is clearly recognizable that the density structure in the central region changes considerably with the Jeans resolution. For 32 cells per Jeans length we cannot see turbulent structures in the central part of the halo and the structures appear rather compact, sometimes elongated and sometimes more round. With a Jeans resolution of 64 cells, the turbulence seems to be better resolved and more complex structures start to become visible. This effect becomes more pronounced in case of 128 cells per Jeans length, where turbulent filamentary structures fill a significant part of the central volume. For 256 cells per Jeans length the turbulence is even better resolved, where the complex structures appear in more detail compared to the previous cases. These trends in principle occur for all of the values of the Lyman-Werner background that we have considered. Even though we start to resolve some turbulence using a resolution of 64 cells per Jeans length, as suggested by previous works (see e.g. Turk et al. 2012; Latif et al. 2013c; Grete et al. 2019), we find that more complex structures start to appear in this particular halo with a Jeans resolution of ≥128 cells, which reflects the challenge of resolving turbulence in numerical simulations.

thumbnail Fig. 1.

Density-weighted projections of the density along the z-axis with a physical width of 4000 au for halo 1 when reaching a peak density of 3 × 10−13 [g cm−3] using an initial magnetic field of B0 = 10−14 [G] (proper). From top to bottom the Jeans resolution was varied using 32, 64, 128, and 256 cells per Jeans length, and from left to right the strength of the radiation background was varied to J21 = 102, 103, 104, and 105. The halo shows more complex structures with increasing Jeans resolution as the turbulence seems to be better resolved. This occurs regardless of the value of J21.

In Fig. 2 we show the projection of the magnetic field in the central region of the halo. In the runs with 64 cells per Jeans length the magnetic field is centrally concentrated or in elongated filaments, while for the higher resolutions per Jeans length we clearly see how the magnetic field structure becomes more volume filling, the magnetic field strength increases, and its structures become more complex due to the interaction with the underlying velocity field. This effect seems to be rather independent of the adopted value of J21.

thumbnail Fig. 2.

Density-weighted projection of magnetic field magnitude along the z-axis with a physical width of 4000 au for halo 1 when reaching a peak density of 3 × 10−13 [g cm−3] using an initial magnetic field of B0 = 10−14 [G] (proper). From top to bottom the Jeans resolution was varied using 32, 64, 128, and 256 cells per Jeans length, and from left to right the strength of the radiation background was varied to J21 = 102, 103, 104, and 105. As the Jeans resolution increases, the structure of the magnetic field starts to become more complex and begins to expand outwards, filling more volume in the halo.

For a more quantitative analysis of the structure of the halos and its physical properties, we present in Fig. 3 the radial profiles of the density, temperature, radial velocity, vorticity squared, and sonic Mach number for halo 1 for a subset of simulations, focusing on J21 = 103 and J21 = 105 and on the different initial magnetic field seeds for comparison. In this plot we fixed the Jeans resolution to 128 cells. The density profile is almost independent of the initial magnetic field seed and the adopted Lyman-Werner background and approximately follows the profile of an isothermal sphere in the outer parts of the halo, while it becomes approximately flat at the centre. At a scale roughly of the order of 10−4 kpc, a small bump is present in the B0 = 10−14 G run for J21 = 103 due to inhomogeneities in the density field. This also happens in our strongest initial magnetic field run for J21 = 103 in which a bump is present at a scale in the range 10−3 − 10−2 kpc.

thumbnail Fig. 3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for halo 1 when reaching a peak density of 3 × 10−13 g cm−3 using a fixed Jeans resolution of 128 cells per Jeans length. The quantity B/ρ2/3 is normalised by with B0 the initial magnetic field strength and ρ0 the cosmic mean baryon density at z = 100. The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The solid lines are for runs with B0 = 10−8 [G] (proper), dashed lines for runs with B0 = 10−10 [G] (proper), and dotted lines for runs with B0 = 10−14 [G] (proper). The infall velocity tends to be higher and the vorticity tends to be larger for the simulations using J21 = 105, while the sonic mach number tends to be smaller compared to the simulations with J21 = 103 following the thermal evolution of the halo. Magnetic field strength, B/ρ2/3 and EB/EK also tend to be higher for the simulations in the atomic cooling regime, which is consistent with the behaviour of the physical properties of the halo.

The radial profile of temperature is the same for all runs, at least on large scales where it is driven by the virialisation shock and chemistry at low densities where molecular hydrogen is fully dissociated in all simulations. From a scale of roughly 10−2 kpc, however, the behaviour starts to diverge, and simulations with J21 = 105 remain at a high temperature of ∼8000 K due to H2 photodissociation until it reaches a scale of about 10−3 kpc, where the gas cools down to 5000 − 6000 K, keeping these temperatures even on smaller scales due to the presence of H− cooling (as was found in Latif et al. 2016). Instead, for J21 = 103 molecular hydrogen efficiently forms and the gas cools, leading to a temperature minimum of ∼500 K on a scale of ∼10−3 kpc with a subsequent moderate increase towards smaller scales, as the de-excitation due to collisions becomes more important at higher densities compared to radiative losses. The difference in the temperature also leads to a moderate difference in the density on scales below 10−2 kpc, where the density is higher for simulations with J21 = 105 compared to J21 = 103. Overall, it should also be noted that the changes in temperature are moderate below that scale, which is also the reason why the density remains close to an isothermal profile.

The radial velocity of the gas reflects the thermal properties; in general, the velocities are negative due to inflow, and they are larger for J21 = 105 compared to J21 = 103. As we follow here the collapse of the first density peak in the halo, this behaviour makes sense as the radial infall should then approximately follow the sound speed, which is more moderate for J21 = 103 where the temperature is lower. Within the central region of the halo the radial velocity then approaches zero as the very central part of the cloud is not collapsing yet.

The vorticity structure shows two very interesting trends in this halo; first, the vorticity tends to be larger in halos with J21 = 105 reflecting the higher velocities. In addition, for both values of J21, we also see that the vorticity is smaller for the simulation with our strongest initial magnetic field seed.

For the sonic Mach number, we note that overall the motion is supersonic and it is the same on large scales, where the thermal evolution is also the same. On smaller scales the Mach number is larger for the runs with J21 = 103 where the temperature is reduced, reflecting the lower sound speed. While we previously noted that the radial velocity is also reduced in the lower-temperature runs, we see here that it is not fully proportional to the difference in the sound speed. In a free-fall collapse, the radial velocity would be the same in all simulations. While the collapse speed can be affected by thermal pressure, runs with lower temperatures typically show higher Mach numbers.

The evolution of the magnetic properties for the same simulations are shown in Fig. 3. For the radial profile of the magnetic field strength itself, we note that in general, independent of the initial magnetic field seed, the magnetic field strength is larger in the simulations with J21 = 105 compared to J21 = 103. This change is consistent with the behaviour of the density, which is also higher in the case of higher J21 and indicates that a higher degree of compression has occurred in these simulations. In addition, we note the larger vorticity in the simulations with higher J21 as well as the smaller Mach number, both of which are expected to favour a more efficient amplification of the magnetic field.

To understand how much of the magnetic field amplification is due to compression versus dynamo amplification, we can make some simple considerations. In the case of spherical symmetry, the density is expected to increase in a contracting sphere as ρ ∝ r−3. On the other hand, if we assume flux freezing, the magnetic field strength should increase as B ∝ r−2, implying that B ∝ ρ2/3 as a result of compression. In Fig. 3, we therefore plot B/ρ2/3 in order to determine if an additional enhancement is present as a result of turbulence. We normalise this value by 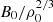, where B0 is the initial magnetic field strength and ρ0 is the cosmic mean baryon density at z = 100. By plotting this quantity we can see that on large scales this ratio is comparable independent of the value of J21 and B0; however, it starts to change towards the centre. For this fixed high Jeans resolution the normalised B/ρ2/3 is higher for simulations with stronger radiation background compared to those with weaker radiation background, a behaviour that is also reflected in the magnetic field strength. In addition, the lowest values of B/ρ2/3 are obtained for the simulations with B0 = 10−8 G. Sur et al. (2012) found that the dynamo saturation in a self-gravitating system can be identified from a change in the slope of B/ρ2/3. For the strongest seed field we find that this ratio decreases towards the centre of the halo, suggesting that the magnetic field is already close to the saturation state.

Finally, in Fig. 3, we also show the ratio of magnetic to kinetic energy for halo 1. This ratio indicates that when magnetic energy reaches a fraction of equipartition, saturation occurs. Additionally, it is strongly dependant on the Mach number and the turbulence injection mechanism giving lower values for supersonic flows with compressible turbulence (Brandenburg & Subramanian 2005; Federrath et al. 2011a; Schober et al. 2015). For this halo, independent of the strength of the initial magnetic field seed, we find the highest ratio for higher values of J21, the same behaviour that is present in the other magnetic quantities. For the simulations with B0 = 10−14 G (proper) it can be seen that even though the energy ratio increases towards the centre, indicating that the magnetic energy is growing at these radii, the value that it reaches is in the range of 10−14 − 10−12 depending on the value of J21, and therefore the motion of the halo is entirely driven by kinetic dynamics. For B0 = 10−10 G (proper) the ratio reaches values of the order of 10−5 − 10−4, and thus the magnetic field still has practically no dynamical impact. On the other hand, for our strongest initial magnetic field seed, this ratio reaches values greater than 10−3, which means that here the magnetic field starts to play a bigger role for the motion of the gas, and therefore it starts to become dynamically relevant. Furthermore, we observe that the energy ratio can reach values of 0.1 at lower radii even though not all the kinetic energy contributes to the dynamo amplification, indicating that the magnetic field is almost saturated.

While the previous analysis focuses on the magnetic field amplification and saturation driven on the smallest scales with a fixed Jeans resolution, we also study the Jeans resolution effect on the amplification and saturation of the magnetic field. For this purpose, in Fig. 4 we show the magnetic properties of the same simulations, but varying the Jeans resolution. We note here that for different Jeans resolutions the degree of turbulence changes and consequently the physical viscosity and resistivity does not remain constant. Moreover Grete et al. (2023) show that even in high-resolution magnetised turbulence simulations, the MHD turbulence does not converge from an energy dynamics point of view. Therefore, we do not expect a convergent behaviour in the growth rate of the dynamo.

thumbnail Fig. 4.

Mass-weighted spherically binned radial profiles of magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for halo 1 when reaching a peak density of 3 × 10−13 g cm−3. The first, second, and third column of this multiple plot shows the magnetic properties of the runs with a proper initial magnetic field strength of B0 = 10−14 [G], B0 = 10−10 [G], and B0 = 10−8 [G], respectively. The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length. Independently of the value of J21, the magnetic field strength, as well as the other magnetic properties, increases with increasing Jeans resolution for the runs with B0 = 10−14 [G]. When increasing the initial magnetic field the simulations with J21 = 103 start to present a dependency loss on the Jeans resolution at lower B0 in comparison with the atomic cooling runs, which suggest that potentially the saturation occurs first in these simulations.

We start by analysing column 1 for B0 = 10−14 G. Similar to what is discussed above, the magnetic field strength radial profile shows that it is higher in the atomic cooling runs (J21 = 105), especially for our highest Jeans resolution simulations. In addition, we also find that the magnetic field strength for a fixed value of J21 is higher with increasing Jeans resolution. We found that the vorticity increases with increasing resolution per Jeans length, an expected behaviour as vorticity is known to increase on smaller scales within a turbulent cascade, providing indirect confirmation that we have started to resolve the turbulence better and showing the potential to amplify the magnetic field through solenoidal motions (see Fig. B.1 for the physical properties of this halo for different Jeans resolutions and B0 = 10−14 G).

By plotting B/ρ2/3 we observe again that this quantity is comparable for runs with the same Jeans resolution independent of the value of J21 for almost all scales; however, this occurs especially for our lower Jeans resolution runs. For the higher resolution runs, particularly in this halo (for comparison, see Fig. B.2 for halo 2 and Fig. B.3 for halo 3), we find that B/ρ2/3 is higher for the simulations with J21 = 105 compared to those with J21 = 103 considering the same Jeans resolution. Another thing that became apparent from plotting this quantity is that for fixed values of J21, the highest values of B/ρ2/3 are obtained for the simulations with the highest resolution per Jeans length where the magnetic field is amplified between 1 and 2 orders of magnitude above the maximum amplification expected from flux freezing.

Finally, we plot the magnetic-to-kinetic energy ratio, and find the highest ratio for the highest resolutions per Jeans length. Nonetheless, the ratio is ≤10−9, and therefore the motion of the halo is entirely driven by kinetic dynamics.

The radial profile of the magnetic properties where we re-simulate halo 1 with B0 = 10−10 G is shown in Col. 2 of Fig. 4 for different resolutions per Jeans length and for J21 = 103 and J21 = 105. In the atomic cooling runs, the behaviour is similar to that found before (i.e. the largest magnetic field strengths and the highest ratio of B/ρ2/3 are found for the highest resolution per Jeans length). On the other hand, for the simulations where molecular hydrogen cooling becomes relevant (J21 = 103), a clear resolution dependence can no longer be seen, which may suggest that perhaps the dynamo is already saturated in those simulations. Considering that the thermal and kinetic energy densities are higher in simulations with atomic hydrogen cooling compared to molecular hydrogen cooling, it would not be unexpected if the magnetic field strength for saturation were larger as well in the atomic cooling regime.

We finally make a comparison with a set of simulations of the same halo but an even larger initial magnetic field strength of B0 = 10−8 G. The radial profiles of the main magnetic quantities of halo 1 are given in Col. 3 from Fig. 4. In the molecular hydrogen regime the situation remains as before, in that there is no clear dependence on resolution for B or B/ρ2/3. In the atomic cooling runs, for our highest Jeans resolution simulation we note that B/ρ2/3 decreases towards the centre. This is due to the decrease in temperature that this halo shows from a radius of about 10−5 kpc towards the interior, where molecular hydrogen starts forming more efficiently and so the cooling becomes more efficient when using 256 cells per Jeans length. Even though this happens when using the highest strength for the radiation background, this effect is not surprising and it is known from previous studies that the transition from atomic to molecular cooling does not correspond to one fixed value of J21, but varies from halo to halo, and also changing the resolution may change the properties within one specific halo and affect this transition to some degree. In addition, this decrease in the temperature leads to an increase in the sonic Mach number disfavouring the efficiency of the magnetic field amplification (see Fig. B.6 for the physical properties of these runs). For the simulations with different Jeans resolution in the atomic hydrogen regime, while in a significant part of the radial profile the 128 cells per Jeans length run has the highest B/ρ2/3 ratio, it is comparable on some scales with the 64 cells per Jeans length simulation where it becomes higher in some radii. In the central region, the B/ρ2/3 ratio for the 128 cells per Jeans length simulation starts to decrease, while it increases in our lowest Jeans resolution simulation reaching the same magnetic field strength. Moreover, we see the change in the slope of B/ρ2/3 and in the slope of the magnetic-to-kinetic energy ratio in almost all the simulations here. In some cases the energy ratio even reaches EB/EK ∼ 0.1, indicating that the magnetic field is almost saturated. It is important to note that although the dynamo-generated magnetic field may reach saturation during gravitational collapse, the magnetic field can still be amplified by gravitational compression (Sur et al. 2012).

3.2. UV background effect

In the previous subsection, we explore the amplification of magnetic fields considering simulations with two fixed values of J21 and varying the resolution and initial magnetic field strength to determine the magnetic field amplification and saturation coming from small scales. In this section we explore instead the dependence on J21 itself, comparing simulations that were pursued with 128 cells per Jeans length and an initial magnetic field strength of B0 = 10−14 G.

We start our analysis with halo 1 in the first column of Fig. 5, comparing the radial profiles of the magnetic properties in simulations with four different values of J21 for a resolution of 128 cells per Jeans length. We find an enhancement of the magnetic field strength in runs with atomic hydrogen cooling on scales from 10−4 kpc to 10−7 kpc. At a radius of about 10−2 kpc, the simulation with J21 = 100 shows a small enhancement of the magnetic field that occurs at the same scale where a density bump is present (for the physical properties of this halo, see Fig. C.1). In the ratio of B/ρ2/3, we see a similar behaviour. On larger scales B/ρ2/3 is higher particularly for the simulation with J21 = 100; however, on smaller scales it seems to be higher for runs in the atomic hydrogen cooling regime. For the ratio of magnetic to kinetic energy we see that the lower ratio is for J21 = 103, which is the simulation that shows the lowest magnetic field amplification, and therefore the lowest magnetic energy. On the other hand, the atomic cooling runs show a lower ratio in comparison with the J21 = 100 run; however, at a scale of about 10−6 kpc the ratio of the simulation with J21 = 104 starts to increase. This happens at the same scale where an enhancement on B/ρ2/3 occurs.

thumbnail Fig. 5.

Mass-weighted spherically binned radial profiles of magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for the three different halos when reaching a peak density of 3 × 10−13 g cm−3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The first, second, and third column of this multiple plot shows the magnetic properties of halo 1, halo 2, and halo 3, respectively. The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105. The effect of the UV background on the amplification of the magnetic field can vary from halo to halo; however, independently of this value, the magnetic field is amplified by ∼7 − 10 orders of magnitude.

A systematic comparison of the magnetic properties for halo 2 is shown in the second column of Fig. 5. In this case we find that the simulation with J21 = 100 reaches a magnetic field strength of about 10−6 G in the centre of the halo, similar to what we found in halo 1. However, particularly in this halo, the other runs with a higher value of J21 reach stronger magnetic field strengths where, unlike halo 1, the magnetic field strength reached in the simulation with J21 = 103 is almost the same as in the simulation with J21 = 104. For the magnetic field amplification B/ρ2/3 we see the lowest B/ρ2/3 for the simulation with J21 = 100, and it keeps this lower value even on smaller scales. On scales above 10−6 kpc the B/ρ2/3 ratio is comparable for runs with J21 = 103 and 105, while the amplification for the simulation with J21 = 104 is smaller; however, at scales below 10−6 kpc this changes and the J21 = 104 starts to increase reaching a magnetic field amplification similar to the simulation with J21 = 103. In addition, we see that this halo presents the highest amplification by the small-scale dynamo without considering the case using J21 = 100. The small-scale dynamo provides an additional magnetic field amplification of more than one order of magnitude above the regular amplification driven by compression. The ratio of magnetic to kinetic energy exhibits a similar behaviour where the lowest ratio is for J21 = 100 and the highest ratios are for the intermediate values of J21 with a maximum value of about 10−9, two orders of magnitude higher than the energy ratios reached on halo 1.

Finally, for comparison, we present in the third column of Fig. 5 the same quantities, but for halo 3. Similarly to what we found for halo 1, we find an enhancement of the magnetic field strength on scales from 10−4 kpc to 10−7 kpc for the runs where the atomic hydrogen cooling dominates. On larger scales the situation is somewhat less clear, and in particular the simulation with J21 = 100 shows a relevant but temporary enhancement of the magnetic field. In addition, we note that the magnetic field strength becomes comparable towards the centre, independently of the value of J21, reaching a value of about 10−5 G. In the ratio of B/ρ2/3, we see a similar behaviour, though somewhat more pronounced for J21 = 100 at a radius of about 10−2 kpc. The ratio of the magnetic to kinetic energy appears slightly lower in the J21 > 100 runs.

From the comparison of these three halos, we see that the effect of J21 on the amplification of the magnetic field varies from halo to halo. In addition, we have to keep in mind that the amplification of the magnetic field B/ρ2/3 can vary statistically by two orders of magnitude for virtually identical halos, as shown in Grete et al. (2019); however, independently of the value of J21 the magnetic field is efficiently amplified by many orders of magnitude (between 7 to 10).

4. Summary and conclusions

We have presented here a suite of numerical simulations modelling three different halos with masses of the order of 107 M⊙ collapsing at redshifts z ≳ 12, for which we varied the initial magnetic field strength, the resolution per Jeans length, and the strength of the Lyman-Werner background parametrised via J21. Our main goal was to study the evolution of the magnetic field and its amplification and saturation via the small-scale dynamo (in addition to gravitational compression) under the different conditions explored here.

As in previous studies, here we found that weak initial magnetic fields can be efficiently amplified via the small-scale dynamo for sufficiently high resolutions per Jeans length. Particularly, we found that the strongest magnetic fields are usually obtained for the simulations with 128 and 256 cells per Jeans length, which were the highest resolution runs we could usually pursue. This result was found for all three halos and independently of the value of J21 that was employed, so it is true in both: in halos where the cooling is dominated by atomic hydrogen and in halos where the molecular hydrogen cooling becomes important during the evolution.

We analysed the behaviour of the magnetic field not only via the magnetic field strength B itself, but we also considered the quantity B/ρ2/3, as under the assumption of flux freezing and for spherically symmetric compression we should have B ∝ ρ2/3 in the absence of further amplification mechanisms (see also Sur et al. 2010; Schleicher et al. 2010a). This quantity was also found to increase with increasing resolution per Jeans length when plotted as a function of radius, and very similar trends were found in the ratio of magnetic to kinetic energy density.

To understand when saturation occurs, we varied the magnetic field strength and found tentative evidence that saturation occurs for somewhat lower initial field strength of 10−10 G in halos where cooling is driven via molecular hydrogen, while halos cooling via atomic hydrogen may require larger initial field strength of ∼10−8 G for saturation. This behaviour is not fully unexpected, as the radial velocities as well as the vorticity are found to be enhanced under conditions of atomic hydrogen cooling, while the respective components are smaller under molecular cooling conditions. Assuming that saturation occurs at a constant ratio of magnetic over turbulent energy, it is thus natural to expect that stronger magnetic fields will be produced in the atomic cooling regime. As our simulations show that the Mach numbers are reduced in the atomic cooling regime, it is even conceivable that the energy ratio at which saturation occurs will also be somewhat higher in the atomic cooling regime (see also Federrath et al. 2011a).

Our study thus confirms that magnetic field amplification via the small-scale dynamo should occur under a large range of conditions, both in the atomic and molecular hydrogen cooling regime. We also found that the saturation levels of the magnetic field are likely different for the two cases. In the future it will be important to study the subsequent evolution, which may include the formation of a disk where an α − Ω dynamo may also operate (see Sharda et al. 2020, 2021). Similarly, Latif et al. (2014c) show that at the transition point towards an adiabatic core, magnetic field amplification can be strongly enhanced due to the presence of shocks, and the resulting magnetic fields may reduce subsequent fragmentation. It will thus be important to further study the effects of the presence of such magnetic fields during the formation of massive objects in these halos.

Acknowledgments

VBD acknowledges financial support from ANID (ANID-PFCHA/DOCTORADO DAAD-BECAS CHILE/62200025) as well as financial support from DAAD (DAAD/Becas Chile funding program ID 57559515). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02). The authors gratefully acknowledge the computing time granted by the Resource Allocation Board and provided on the supercomputer Lise and Emmy at NHR@ZIB and NHR@Göttingen as part of the NHR infrastructure. The calculations for this research were conducted with computing resources under the project hhp00057. DRGS gratefully acknowledges support by the ANID BASAL projects ACE210002 and FB210003, via the Millenium Nucleus NCN19-058 (TITANs) and via Fondecyt Regular (project code 1201280). DRGS also thanks for funding via the Alexander von Humboldt – Foundation, Bonn, Germany. MAL thanks the UAEU for funding via UPAR grants No. 31S390 and 12S111. RB acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101030214. The visualization and analysis of this research was done thanks to the YT project, an open-source, community-developed python package for astrophysical data (Turk et al. 2011).

References

  1. Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [CrossRef] [Google Scholar]
  2. Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023, Nature, 622, 707 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [Google Scholar]
  4. Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
  5. Behroozi, P. S., Wechsler, R. H., & Wu, H.-Y. 2012, ApJ, 762, 109 [Google Scholar]
  6. Bernet, M. L., Miniati, F., Lilly, S. J., Kronberg, P. P., & Dessauges-Zavadsky, M. 2008, Nature, 454, 302 [NASA ADS] [CrossRef] [Google Scholar]
  7. Biermann, L. 1950, Zeitschrift Naturforschung Teil A, 5, 65 [NASA ADS] [Google Scholar]
  8. Boekholt, T. C. N., Schleicher, D. R. G., Fellhauer, M., et al. 2018, MNRAS, 476, 366 [Google Scholar]
  9. Bovino, S., Schleicher, D. R. G., & Schober, J. 2013, New J. Phys., 15, 013055 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [Google Scholar]
  12. Brummel-Smith, C., Bryan, G., Butsky, I., et al. 2019, J. Open Source Software, 4, 1636 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bryan, G. L., Norman, M. L., O’Shea, B. W., et al. 2014, ApJS, 211, 19 [Google Scholar]
  14. Cho, J., & Lazarian, A. 2009, ApJ, 701, 236 [NASA ADS] [CrossRef] [Google Scholar]
  15. Curtis-Lake, E., Carniani, S., Cameron, A., et al. 2023, Nat. Astron., 7, 622 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
  17. Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dijkstra, M., Ferrara, A., & Mesinger, A. 2014, MNRAS, 442, 2036 [CrossRef] [Google Scholar]
  20. Federrath, C., Chabrier, G., Schober, J., et al. 2011a, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
  21. Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011b, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
  22. Garaldi, E., Pakmor, R., & Springel, V. 2021, MNRAS, 502, 5726 [NASA ADS] [CrossRef] [Google Scholar]
  23. Glover, S. C. O. 2015a, MNRAS, 451, 2082 [NASA ADS] [CrossRef] [Google Scholar]
  24. Glover, S. C. O. 2015b, MNRAS, 453, 2901 [Google Scholar]
  25. Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [Google Scholar]
  26. Grasso, D., & Rubinstein, H. R. 2001, Phys. Rep., 348, 163 [NASA ADS] [CrossRef] [Google Scholar]
  27. Greif, T. H., Johnson, J. L., Klessen, R. S., & Bromm, V. 2008, MNRAS, 387, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  28. Grete, P., Latif, M. A., Schleicher, D. R. G., & Schmidt, W. 2019, MNRAS, 487, 4525 [NASA ADS] [CrossRef] [Google Scholar]
  29. Grete, P., O’Shea, B. W., & Beckwith, K. 2023, ApJ, 942, L34 [CrossRef] [Google Scholar]
  30. Habouzit, M., Volonteri, M., Latif, M., Dubois, Y., & Peirani, S. 2016, MNRAS, 463, 529 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hahn, O., & Abel, T. 2011, MNRAS, 415, 2101 [Google Scholar]
  32. Haugen, N. E. L., Brandenburg, A., & Mee, A. J. 2004, MNRAS, 353, 947 [Google Scholar]
  33. Hirano, S., Machida, M. N., & Basu, S. 2021, ApJ, 917, 34 [CrossRef] [Google Scholar]
  34. Hirano, S., Machida, M. N., & Basu, S. 2023, ApJ, 952, 56 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kazantsev, A. P. 1968, Sov. J. Exp. Theor. Phys., 26, 1031 [NASA ADS] [Google Scholar]
  36. Langer, M., Aghanim, N., & Puget, J. L. 2005, A&A, 443, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013a, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  38. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013b, ApJ, 772, L3 [NASA ADS] [CrossRef] [Google Scholar]
  39. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013c, MNRAS, 432, 668 [NASA ADS] [CrossRef] [Google Scholar]
  40. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013d, MNRAS, 436, 2989 [Google Scholar]
  41. Latif, M. A., Bovino, S., Van Borm, C., et al. 2014a, MNRAS, 443, 1979 [NASA ADS] [CrossRef] [Google Scholar]
  42. Latif, M. A., Schleicher, D. R. G., Bovino, S., Grassi, T., & Spaans, M. 2014b, ApJ, 792, 78 [NASA ADS] [CrossRef] [Google Scholar]
  43. Latif, M. A., Schleicher, D. R. G., & Schmidt, W. 2014c, MNRAS, 440, 1551 [CrossRef] [Google Scholar]
  44. Latif, M. A., Bovino, S., Grassi, T., Schleicher, D. R. G., & Spaans, M. 2015, MNRAS, 446, 3163 [CrossRef] [Google Scholar]
  45. Latif, M. A., Schleicher, D. R. G., & Hartwig, T. 2016, MNRAS, 458, 233 [NASA ADS] [CrossRef] [Google Scholar]
  46. Latif, M. A., Schleicher, D. R. G., & Khochfar, S. 2023, ApJ, 945, 137 [NASA ADS] [CrossRef] [Google Scholar]
  47. Latif, M. A., Whalen, D. J., & Mezcua, M. 2024, MNRAS, 527, L37 [Google Scholar]
  48. Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [Google Scholar]
  49. Murphy, E. J. 2009, ApJ, 706, 482 [Google Scholar]
  50. Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [Google Scholar]
  51. Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [Google Scholar]
  52. Paoletti, D., Chluba, J., Finelli, F., & Rubiño-Martín, J. A. 2019, MNRAS, 484, 185 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paoletti, D., Chluba, J., Finelli, F., & Rubiño-Martín, J. A. 2022, MNRAS, 517, 3916 [NASA ADS] [CrossRef] [Google Scholar]
  54. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Planck Collaboration XIX. 2016, A&A, 594, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Reinoso, B., Schleicher, D. R. G., Fellhauer, M., Klessen, R. S., & Boekholt, T. C. N. 2018, A&A, 614, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
  58. Schleicher, D. R. G. 2019, in Formation of the First Black Holes, eds. M. Latif, & D. R. G. Schleicher, 223 [CrossRef] [Google Scholar]
  59. Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010a, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010b, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
  61. Schlickeiser, R., & Shukla, P. K. 2003, ApJ, 599, L57 [NASA ADS] [CrossRef] [Google Scholar]
  62. Schmidt, W., Collins, D. C., & Kritsuk, A. G. 2013, MNRAS, 431, 3196 [NASA ADS] [CrossRef] [Google Scholar]
  63. Schober, J., Schleicher, D., Bovino, S., & Klessen, R. S. 2012a, Phys. Rev. E, 86, 066412 [NASA ADS] [CrossRef] [Google Scholar]
  64. Schober, J., Schleicher, D., Federrath, C., et al. 2012b, ApJ, 754, 99 [NASA ADS] [CrossRef] [Google Scholar]
  65. Schober, J., Schleicher, D. R. G., Federrath, C., Bovino, S., & Klessen, R. S. 2015, Phys. Rev. E, 92, 023010 [CrossRef] [Google Scholar]
  66. Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  67. Sharda, P., Federrath, C., & Krumholz, M. R. 2020, MNRAS, 497, 336 [NASA ADS] [CrossRef] [Google Scholar]
  68. Sharda, P., Federrath, C., Krumholz, M. R., & Schleicher, D. R. G. 2021, MNRAS, 503, 2014 [NASA ADS] [CrossRef] [Google Scholar]
  69. Shlosman, I., Choi, J.-H., Begelman, M. C., & Nagamine, K. 2015, MNRAS, 456, 500 [Google Scholar]
  70. Subramanian, K. 2016, Rep. Prog. Phys., 79, 076901 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sugimura, K., Omukai, K., & Inoue, A. K. 2014, MNRAS, 445, 544 [NASA ADS] [CrossRef] [Google Scholar]
  72. Sur, S., Schleicher, D. R. G., Banerjee, R., Federrath, C., & Klessen, R. S. 2010, ApJ, 721, L134 [NASA ADS] [CrossRef] [Google Scholar]
  73. Sur, S., Federrath, C., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2012, MNRAS, 423, 3148 [NASA ADS] [CrossRef] [Google Scholar]
  74. Toro, E. F. 1997, Riemann Solvers and Numerical Methods for Fluid Dynamics (Berlin Heidelberg: Springer) [Google Scholar]
  75. Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
  76. Turk, M. J., Oishi, J. S., Abel, T., & Bryan, G. L. 2012, ApJ, 745, 154 [NASA ADS] [CrossRef] [Google Scholar]
  77. Van Borm, C., Bovino, S., Latif, M. A., et al. 2014, A&A, 572, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. van Leer, B. 1979, J. Comput. Phys., 32, 101 [Google Scholar]
  79. Vikaeus, A., Whalen, D. J., & Zackrisson, E. 2022, ApJ, 933, L8 [CrossRef] [Google Scholar]
  80. Whalen, D. J., Surace, M., Bernhardt, C., et al. 2020, ApJ, 897, L16 [NASA ADS] [CrossRef] [Google Scholar]
  81. Yoshida, N., Omukai, K., & Hernquist, L. 2008, Science, 321, 669 [NASA ADS] [CrossRef] [Google Scholar]
  82. Yue, B., Ferrara, A., Salvaterra, R., Xu, Y., & Chen, X. 2014, MNRAS, 440, 1263 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Statistical comparison

To explore how our results change with different statistical methods, we plot our results for two different simulations. Figure A.1 shows the mass-weighted average, mean, median, and interquartile range of the physical and magnetic properties of halo 1 for a simulation with J21 = 103 and 105 using a Jeans resolution of 128 cells per Jeans length and an initial magnetic field of B0 = 10−14G. It can be seen that the physical properties of the halo follow a similar behaviour when using the mass-weighted average, mean, and median converging in the centre at the same point. In addition, the quantities are within the interquartile range in almost the entire radius. A difference in the values, especially in the temperature, can be seen at a scale between 10−4 − 10−2 kpc for the simulation in the molecular hydrogen cooling regime, where the mass-weighted average presents a smaller decrease compared to the mean and median values; however, this is not surprising as it occurs in the range where the H2 cooling and the HI cooling phase co-exists. For the magnetic properties we can see that even though the median tends to show smaller values compared to the mean and the mass-weighted average, the behaviour that all these quantities follow is similar. In this work we used the mass-weighted quantities as they are the most relevant for a collapse problem; however, from a volume-weighted average point of view the results might show some differences.

thumbnail Fig. A.1.

Spherically binned radial profiles of density, temperature, radial velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using 128 cells per Jeans length, J21 = 105 (red line) and 103 (light blue line) and B0 = 10−14G (proper). The solid lines show the mass-weighted average of the quantities, the dotted lines show the mean values, the dashed lines show the median values, and the shaded areas correspond to the interquartile range of the simulations.

Appendix B: Jeans resolution effect: Additional halos

For comparison, here we show the results obtained for the two additional halos we simulated. The properties of these halos using different initial conditions are presented in Tables 1, 2, and 3. We also provide here the physical properties of halo 1.

B.1. Halos with B0 = 10−14 G

The radial profiles of the main physical quantities of halo 1 for different Jeans resolutions are presented in Fig. B.1. We note that the density profile is almost independent of the resolution per Jeans length and follows an isothermal profile. The temperature for J21 = 105 remains high, while in the runs with J21 = 103 the gas cools down in the interior of the halo due to the molecular hydrogen. While our results mostly remain qualitatively similar, a difference can be noted in the simulation with J21 = 105 and 256 cells per Jeans length, where the temperature is initially high, but then starts dropping from a radius of about 10−4 kpc towards small scales.

thumbnail Fig. B.1.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.

The radial velocity for the atomic cooling regime is negative due to inflow and larger compared to the runs in the molecular hydrogen cooling regime. We note that the resolution per Jeans length introduces a relevant scatter in the radial velocities, though without following a systematic trend. The tangential velocity shows a very similar behaviour, and again we note that it is typically higher in the simulations with J21 = 105 for essentially the same reasons. However, and particularly for this halo, this is not the case in all the resolutions, especially for our highest one where the tangential velocity for J21 = 103 is higher compared to J21 = 105. Only on large scales is the tangential velocity instead driven by effects from the cosmological environment, and therefore similar in all runs. We note also here the significant scatter introduced by the resolution per Jeans length.

The vorticity is larger in halos dominated by atomic cooling and, independently of the value of J21, it increases with increasing the Jeans resolution. For the sonic Mach number, we finally note that it is larger for the runs in the molecular hydrogen regime where the temperature is reduced.

Figure B.2 shows the radial profile of the main physical and magnetic quantities of halo 2. We note that the overall behaviour is very similar to what we found in halo 1, with the density approximately following an isothermal profile, and the H2 cooling kicking in for cases with J21 = 103. The behaviour of temperatures affects the radial velocity, tangential velocity, vorticity, and sonic Mach number in a similar way to that already noted for halo 1. As for the magnetic properties, the effect of the amplification of the magnetic field is even more pronounced for this halo, and the two runs with a resolution of 128 cells per Jeans length show the larger magnetic field strength in the radial profile and also the highest ratios of B/ρ2/3. The same is true also for the ratio of magnetic to kinetic energy.

thumbnail Fig. B.2.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 2 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.

Quite similarly, we analysed the radial structure and magnetic properties of halo 3, which are shown in Fig. B.3. The results are very similar to what we obtained for halo 1 and 2. In this halo we can see more clearly that the infall velocity is enhanced in the simulations with higher J21, which is also reflected in the tangential velocities and in the vorticity. The sonic mach number is larger in the simulations with lower J21 due to the lower temperature. For the magnetic quantities we again obtain a picture consistent with the results from the other halos; in particular, we found the largest magnetic field strengths in the highest resolution runs. In addition, in this halo we can better appreciate how runs with the same resolution per Jeans length show a similar behaviour of B/ρ2/3, regardless of the value of J21.

thumbnail Fig. B.3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.

B.2. Halos with B0 = 10−10 G

We present in Fig. B.4 the radial profile of the physical quantities for halo 1, which we resimulate using a stronger initial magnetic field. Within the physical properties of the halo, particularly density, temperature, and the velocity components, the behaviour remains very similar to what we discussed before. However, in the simulations with J21 = 105 and 256 cells per Jeans length, we observe a difference compared to the corresponding simulation with a weaker initial magnetic field. While the temperature shows a drop from a radius of about 10−4 kpc towards the centre when using an initial magnetic field of B0 = 10−14 G (as shown in Fig. B.1), here we can see that the temperature remains at high values, as in all simulations with J21 = 105. In addition, we find that the tangential velocity is lower and the sonic Mach number is smaller in the simulation with J21 = 103 and 256 cells per Jeans length compared to the same simulation but using B0 = 10−14 G. Potentially, this could be considered a result of angular momentum transport due to magnetic braking, or potentially part of a change in the non-linear evolution induced by the presence of a stronger magnetic field.

thumbnail Fig. B.4.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−10G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.

The radial profiles for halo 3 using B0 = 10−10 G are shown in Fig. B.5 where the behaviour of the physical properties of this halo is consistent with our findings for halo 1. The magnetic field related properties of this halo again show similar results to those for halo 1. For simulations in the atomic cooling regime we find the strongest magnetic fields and highest B/ρ2/3 ratio in the higher Jeans resolution runs; however, in the molecular hydrogen cooling regime the Jeans resolution dependence disappears, which could imply that these simulations are reaching the saturation state.

thumbnail Fig. B.5.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−10G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.

B.3. Halos with B0 = 10−8 G

We show in Fig. B.6 the main physical properties of the simulations of halo 1, but with an even higher initial magnetic field strength of B0 = 10−8 G. These properties again resemble the behaviour that we previously discussed; however, a difference in temperature can be observed again in the simulation with J21 = 105 and 256 cells per Jeans length. The temperature remains high up to a radius of about 10−5 kpc where the gas cools down to smaller scales. We observe that the gas stays hot for smaller radii compared to the same simulation using B0 = 10−14 G where the temperature drops from a radius of 10−4 kpc (see Fig. B.1). The temperature difference also leads to an increase in the sonic Mach number from a scale of 10−5 kpc, the same scale where the temperature starts to decrease in the simulation with J21 = 105 and 256 cells per Jeans length.

thumbnail Fig. B.6.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−8G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.

Finally, we present in Fig. B.7 the main physical and magnetic properties of halo 3 using an initial magnetic field of B0 = 10−8 G, where again the behaviour is consistent with the results of the previous simulations. From the magnetic properties of the halo we can observe the unclear resolution dependence of the magnetic field strength, and that B/ρ2/3 in the runs dominated by molecular hydrogen cooling remains the same. Also in the atomic hydrogen regime, while the highest resolution simulation still has the strongest magnetic field in a significant part of the radial profile, in the central region it becomes weaker compared to the lowest resolution run, similar to halo 1. This is also reflected in B/ρ2/3 and the energy ratios. Even though we cannot fully exclude that some turbulent magnetic field amplification still happens in the simulation in the atomic cooling regime, the dependency loss of the magnetic field strength and amplification on the Jeans resolution plus the fact that the magnetic-to-kinetic energy density ratio decreases towards the centre reaching values of about 0.1 indicates that the simulations in the atomic cooling regime may be close to the stage of saturation.

thumbnail Fig. B.7.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic to kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−8G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.

Appendix C: UV background effect: physical properties

Here we show the physical properties of the simulations presented in section 3.2. We compare the radial profiles of our three different halos by varying the values of J21 with a fixed Jeans resolution.

The physical properties of halo 1 are shown in Fig. C.1. The radial profile of the density distribution still approximately corresponds to an isothermal profile, with a bump due to inhomogeneities on a scale of about ∼10−4 kpc in the simulation with J21 = 105 and J21 = 104. In general, on scales between 10−3 kpc and 10−6 kpc, the density tends to be higher for larger values of J21. This can be understood as a result of the increase in temperature due to the dissociation of H2, which leads to an increase in the Jeans mass and effectively means that a larger amount of mass has collapsed once a certain peak density is reached. In the temperature profile we find that H2 cooling becomes possible for J21 ≤ 103, while for larger values cooling is regulated via atomic hydrogen. The profiles of radial velocity, tangential velocity, vorticity, and sonic Mach number follow the previously discussed behaviour for runs with atomic hydrogen and molecular hydrogen cooling.

thumbnail Fig. C.1.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.

Overall, halo 2 and halo 3 present similar trends on its physical properties, as shown in Fig. C.2 and Fig. C.3, respectively. The density profile approximately follows the isothermal profile. The temperature remains high in the simulations with J21 ≥ 104 in the regime of atomic hydrogen cooling, while molecular cooling becomes active in simulations with J21 ≤ 103 leading to lower temperatures in the interior. The infall velocity and tangential velocity are higher in the simulations in the atomic cooling regime opposite to the sonic mach number, which is lower when the atomic cooling dominates the cooling. For the sonic mach number, a difference is observed for the simulation using J21 = 105 in halo 2, where instead of maintaining a low value at small radii such as halos 1 and 3, it starts to increase towards the centre (see Fig. C.2). For the vorticity the difference is minor, but it appears somewhat enhanced on intermediate scales (10−3 kpc − 10−6 kpc) in the presence of atomic hydrogen cooling in both halos.

thumbnail Fig. C.2.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 2 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.

thumbnail Fig. C.3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.

All Tables

Table 1.

Properties of the simulated halos using an initial magnetic field seed strength of B0 = 10−14 G (proper).

In the text
Table 2.

Same as Table 1, but for a higher initial magnetic field seed strength of B0 = 10−10 G (proper).

In the text
Table 3.

Same as Table 1, but for a higher initial magnetic field seed strength of B0 = 10−8 G (proper).

In the text

All Figures

thumbnail Fig. 1.

Density-weighted projections of the density along the z-axis with a physical width of 4000 au for halo 1 when reaching a peak density of 3 × 10−13 [g cm−3] using an initial magnetic field of B0 = 10−14 [G] (proper). From top to bottom the Jeans resolution was varied using 32, 64, 128, and 256 cells per Jeans length, and from left to right the strength of the radiation background was varied to J21 = 102, 103, 104, and 105. The halo shows more complex structures with increasing Jeans resolution as the turbulence seems to be better resolved. This occurs regardless of the value of J21.
In the text
thumbnail Fig. 2.

Density-weighted projection of magnetic field magnitude along the z-axis with a physical width of 4000 au for halo 1 when reaching a peak density of 3 × 10−13 [g cm−3] using an initial magnetic field of B0 = 10−14 [G] (proper). From top to bottom the Jeans resolution was varied using 32, 64, 128, and 256 cells per Jeans length, and from left to right the strength of the radiation background was varied to J21 = 102, 103, 104, and 105. As the Jeans resolution increases, the structure of the magnetic field starts to become more complex and begins to expand outwards, filling more volume in the halo.
In the text
thumbnail Fig. 3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for halo 1 when reaching a peak density of 3 × 10−13 g cm−3 using a fixed Jeans resolution of 128 cells per Jeans length. The quantity B/ρ2/3 is normalised by with B0 the initial magnetic field strength and ρ0 the cosmic mean baryon density at z = 100. The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The solid lines are for runs with B0 = 10−8 [G] (proper), dashed lines for runs with B0 = 10−10 [G] (proper), and dotted lines for runs with B0 = 10−14 [G] (proper). The infall velocity tends to be higher and the vorticity tends to be larger for the simulations using J21 = 105, while the sonic mach number tends to be smaller compared to the simulations with J21 = 103 following the thermal evolution of the halo. Magnetic field strength, B/ρ2/3 and EB/EK also tend to be higher for the simulations in the atomic cooling regime, which is consistent with the behaviour of the physical properties of the halo.
In the text
thumbnail Fig. 4.

Mass-weighted spherically binned radial profiles of magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for halo 1 when reaching a peak density of 3 × 10−13 g cm−3. The first, second, and third column of this multiple plot shows the magnetic properties of the runs with a proper initial magnetic field strength of B0 = 10−14 [G], B0 = 10−10 [G], and B0 = 10−8 [G], respectively. The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length. Independently of the value of J21, the magnetic field strength, as well as the other magnetic properties, increases with increasing Jeans resolution for the runs with B0 = 10−14 [G]. When increasing the initial magnetic field the simulations with J21 = 103 start to present a dependency loss on the Jeans resolution at lower B0 in comparison with the atomic cooling runs, which suggest that potentially the saturation occurs first in these simulations.
In the text
thumbnail Fig. 5.

Mass-weighted spherically binned radial profiles of magnetic field strength, magnetic field amplification B/ρ2/3, and the magnetic-to-kinetic energy density ratio EB/EK for the three different halos when reaching a peak density of 3 × 10−13 g cm−3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The first, second, and third column of this multiple plot shows the magnetic properties of halo 1, halo 2, and halo 3, respectively. The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105. The effect of the UV background on the amplification of the magnetic field can vary from halo to halo; however, independently of this value, the magnetic field is amplified by ∼7 − 10 orders of magnitude.
In the text
thumbnail Fig. A.1.

Spherically binned radial profiles of density, temperature, radial velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using 128 cells per Jeans length, J21 = 105 (red line) and 103 (light blue line) and B0 = 10−14G (proper). The solid lines show the mass-weighted average of the quantities, the dotted lines show the mean values, the dashed lines show the median values, and the shaded areas correspond to the interquartile range of the simulations.
In the text
thumbnail Fig. B.1.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.
In the text
thumbnail Fig. B.2.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 2 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.
In the text
thumbnail Fig. B.3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−14G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.
In the text
thumbnail Fig. B.4.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−10G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.
In the text
thumbnail Fig. B.5.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic-to-kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−10G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.
In the text
thumbnail Fig. B.6.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−8G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, solid for 128 cells, and dotted for 256 cells per Jeans length.
In the text
thumbnail Fig. B.7.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, sonic Mach number, magnetic field strength, magnetic field amplification B/ρ2/3, and magnetic to kinetic energy density ratio for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using B0 = 10−8G (proper). The light blue lines represent the simulations with J21 = 103 where the cooling is driven via molecular hydrogen, and the red lines are for simulations with J21 = 105 where the cooling is driven by atomic hydrogen. The different line styles represent different Jeans resolutions: dash-dotted for 32 cells, dashed for 64 cells, and solid for 128 cells per Jeans length.
In the text
thumbnail Fig. C.1.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 1 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.
In the text
thumbnail Fig. C.2.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 2 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.
In the text
thumbnail Fig. C.3.

Mass-weighted spherically binned radial profiles of density, temperature, radial velocity, tangential velocity, vorticity squared, and sonic Mach number for halo 3 when reaching a peak density of 3 × 10−13g/cm3 using a fixed Jeans resolution of 128 cells and B0 = 10−14 [G] (proper). The dash-dotted blue line is for J21 = 102, the dashed light blue line is for J21 = 103, the dotted orange line is for J21 = 104, and the solid red line is for J21 = 105.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.