| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201629750 | |
| Published online | 23 May 2017 | |
Carbon stars in the X-shooter Spectral Library
II. Comparison with models⋆
1 Observatoire Astronomique de Strasbourg, Université de Strasbourg, CNRS, UMR 7550, 11 rue de l’Université, 67000 Strasbourg, France
e-mail: anais.gonneau@astro.unistra.fr
2 Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV, Groningen, The Netherlands
3 University of Vienna, Department of Astrophysics, Türkenschanzstraße 17, 1180 Wien, Austria
4 Dipartimento di Fisica e Astronomia Galileo Galilei, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
5 CRAL-Observatoire de Lyon, Université de Lyon, Lyon I, CNRS, UMR5574, France
6 New York University Abu Dhabi, Abu Dhabi, PO Box 129188, Abu Dhabi, United Arab Emirates
Received: 19 September 2016
Accepted: 20 January 2017
In a previous paper, we assembled a collection of medium-resolution spectra of 35 carbon stars, covering optical and near-infrared wavelengths from 400 to 2400 nm. The sample includes stars from the Milky Way and the Magellanic Clouds, with a variety of (J−Ks) colors and pulsation properties. In the present paper, we compare these observations to a new set of high-resolution synthetic spectra, based on hydrostatic model atmospheres. We find that the broad-band colors and the molecular-band strengths measured by spectrophotometric indices match those of the models when (J−Ks) is bluer than about 1.6, while the redder stars require either additional reddening or dust emission or both. Using a grid of models to fit the full observed spectra, we estimate the most likely atmospheric parameters Teff, log (g), [Fe/H] and C/O. These parameters derived independently in the optical and near-infrared are generally consistent when (J−Ks) < 1.6. The temperatures found based on either wavelength range are typically within ±100 K of each other, and log (g) and [Fe/H] are consistent with the values expected for this sample. The reddest stars ((J−Ks) > 1.6) are divided into two families, characterized by the presence or absence of an absorption feature at 1.53 μm, generally associated with HCN and C2H2. Stars from the first family begin to be more affected by circumstellar extinction. The parameters found using optical or near-infrared wavelengths are still compatible with each other, but the error bars become larger. In stars showing the 1.53 μm feature, which are all large-amplitude variables, the effects of pulsation are strong and the spectra are poorly matched with hydrostatic models. For these, atmospheric parameters could not be derived reliably, and dynamical models are needed for proper interpretation.
Key words: stars: carbon / stars: atmospheres / infrared: stars
© ESO, 2017
1. Introduction
Modeling the spectra of luminous red stars, such as red supergiants or luminous asymptotic giant branch stars, remains an immense challenge. These stars have hugely extended atmospheres that host molecules and sometimes dust. Their heavy element abundance ratios are non-solar as the result of dredge-up episodes in their previous evolutionary history (e.g. Iben & Renzini 1983). This is particularly true for carbon stars (C stars), whose atmospheres have carbon-to-oxygen abundance ratios higher than 1. Many – if not all – luminous red stars are photometric variables as a result of pulsation of the stellar interior (e.g. Wood 2015), which triggers shock waves that propagate through the atmospheres. In addition, interferometric observations have demonstrated significant departures from spherical symmetry in some of these objects, which have been interpreted as the signatures of large-scale convective cells. In the case of red supergiants, these inhomogeneities have been identified as a plausible cause of differences between the stellar effective temperatures estimated from optical molecular bands on one hand, and from the spectral energy distribution on the other hand (e.g. Davies et al. 2013). Qualitatively similar inhomogeneities have been discovered in asymptotic giant branch stars (van Belle et al. 2013).
Luminous red giants can be observed at very large distances, and they contribute significantly to the light of galaxies especially at red and near-infrared (NIR) wavelengths (e.g. Melbourne et al. 2012). Their relative numbers are predicted to be sensitive functions of the age and initial metallicity of the host systems. Underestimating the contribution of the thermally pulsing asymptotic giant branch (TP-AGB) stars to galaxy spectral energy distributions (SEDs) can bias determinations of their properties, such as stellar masses (Ilbert et al. 2010). Their importance in studies of the stellar populations of local and extragalactic galaxies justifies the continuous efforts devoted to empirically characterizating and to modeling them (e.g. Lyubenova et al. 2010, 2012; Zibetti et al. 2013).
In a previous article (Gonneau et al. 2016, hereafter Paper I), we described spectroscopic observations of carbon stars obtained with the ESO/VLT/X-shooter instrument as part of the XSL project (X-shooter Spectral Library, P.I. S. C. Trager). This collection is the first to provide simultaneous optical and NIR observations at a resolving power of R = λ/δλ ~ 8000. Hence it offers a unique possibility to test synthetic spectra of C stars. For stars that can be reproduced in a satisfactory way, estimates of the fundamental stellar parameters may be derived. These estimates are essential if the empirical spectra are to be used as templates in future studies of the stellar populations of galaxies.
A recent series of four articles has provided the largest current collection of model atmospheres and low-resolution theoretical spectra for C stars (Aringer et al. 2009; Nowotny et al. 2011, 2013; Eriksson et al. 2014; they are respectively referred to as Papers T1 to T4 hereafter). While in T1, the authors investigated synthetic spectra and photometry based on a grid of hydrostatic model atmospheres, T2 to T4 are based on dynamical model atmospheres. These papers demonstrate that only the SEDs of relatively blue asymptotic giant branch C stars (J−K ≤ 1.5) can be reproduced by hydrostatic models. The SEDs of redder objects result from the combination of photospheric emission and reprocessing of this radiation by the dusty circumstellar material, which is produced naturally as a result of pulsation. Dynamic model atmospheres taking into account the effects of pulsation-enhanced dust-driven winds are needed to reproduce the observable properties of such evolved objects (e.g. their location in a number of color–magnitude and color–color diagrams, their wind velocities and mass-loss rates, cf T2 and following).
In this article, we focus on the hydrostatic models presented in T1. Paladini et al. (2011) used early synthetic spectra based on these models to analyze low-resolution spectra (400 <R< 1800) of C stars with no circumstellar dust in the near-infrared (0.9 <λ< 4.2 μm), together with interferometric observations. These models allowed the authors to select a preferred treatment of the C2 opacity. They concluded that the C2H2 feature at 3.1 μm was the spectral signature most sensitive to changes in effective temperature. A large grid of new high-resolution theoretical spectra based on the hydrostatic models of T1 has been computed for the present article. High-resolution theoretical spectra for the dynamical models of T2, T3, T4 are not yet available.
The following questions guide our comparisons with the X-shooter observations. Can the full spectra (from the optical to the near-infrared) be matched reasonably well, at least for stars with little or no evidence of circumstellar dust? To what extent are parameters estimated from optical wavelengths compatible with those obtained from NIR wavelengths? In this article, the analysis was performed at an intermediate spectral resolution: R ~ 2000. At the full resolution of XSL, line profiles become difficult to model, in part because of instrumental effects and in part because the velocity field in the atmospheres of long-period variables (LPVs) has noticeable consequences (Nowotny et al. 2010). This interesting aspect of the study of C-star spectra is postponed to future articles.
The paper is organized as follows. Section 2 describes the observed carbon-rich spectra, and Sect. 3 presents the theoretical grid of models. Section 4 shows the first part of the study: a comparison between models that helps evaluate to what precision stellar parameters can be recovered from ideal C-star spectra. In Sect. 5 we use the results from Sect. 4 and compare our observations with the grid of models. In Sect. 6 we summarize the results and conclude.
2. Observations
For our sample of 35 carbon stars, we obtained medium-resolution spectra by using the European Southern Observatory (ESO/VLT) spectrograph X-shooter (Vernet et al. 2011). This instrument allows simultaneous acquisition of spectra from 0.3 to 2.5 μm, using two dichroics to split the beam into three arms: ultraviolet-blue (UVB), visible (VIS), and near-infrared (NIR).
The C-star spectra were acquired as part of the X-shooter Spectral Library (hereafter XSL, Chen et al. 2014a), through an ESO Large Programme (Chen et al. 2014b). This empirical library contains about 700 stars, observed at a moderate resolving power (7700 ≤ R ≤ 11 000 depending on the arm) and covering a wide range of stellar atmospheric parameters.
Our sample of carbon stars includes stars from the Milky Way (MW) and the Large and Small Magellanic Clouds (LMC, SMC). Details about the star selection and the data reduction can be found in Paper I.
Our sample presents quite a diversity in global SED and absorption-line characteristics. It exhibits a bimodal behavior of carbon stars with relatively red near-infrared colors. Some of our carbon stars with (J−Ks) > 1.6 display an absorption band at 1.53 μm, for which HCN and C2H2 are usually considered responsible (Gautschy-Loidl et al. 2004). In our sample, the appearance of the 1.53 μm feature is also associated with a smoother aspect of the near-infrared spectrum and an energy distribution with two components, one peaking at red optical wavelengths, the other at longer wavelengths (cf. Fig. 18 of Paper I). Paper I noted that all stars displaying the 1.53 μm feature in the sample are large-amplitude variables, but that large-amplitude variability does not systematically imply the presence of that feature in the spectrum.
In Paper I, our sample of spectra was divided into four groups, numbered 1 to 4, based on the (J−Ks) color of the corresponding target. In the following, the discussion again uses four groups, but this time with a different focus because we concentrate on the spectral features in the redder objects. We reclassify our groups 1 to 4 in Paper I into groups A to D as follows.
The first group (A) contains the bluest C stars from our sample, with (J−Ks) < 1.2. It remains the same as Group 1. The second group (B) contains the classical C stars with 1.2 < (J−Ks) < 1.6, as did Group 2. The last two groups contain all the carbon stars with (J−Ks) > 1.6. We separate these stars based on the presence or absence of the 1.53 μm absorption feature. The stars from the former Groups 3 and 4 without this absorption feature are placed in Group C. All other red stars with the absorption feature are placed in Group D.
Table 1 lists the observed carbon stars used in this paper. All spectra are plotted in the appendix of Paper I. Star V CrA, a star of type R Coronae Borealis (R CrB), are not be discussed in this work because it was undergoing an obscuration event at the time of observation1. Its spectrum is dominated by circumstellar emission to the point of not showing any photospheric features. T Cae, a former star from Group C, was removed from our sample as its spectrum appears to be partially saturated in the near-infrared wavelength range.
Main properties of the sample of observed carbon stars.
3. Models
We use a grid of synthetic spectra computed specifically for this study and based on the C-rich COMARCS model atmospheres of T1, in an updated version as presented in Aringer et al. (2016). These represent hydrostatic dust-free carbon-rich giants under the assumption of spherical symmetry.
3.1. Original spectral library
The original series of models (T1) covers a wide range of effective temperatures, surface gravities, carbon-to-oxygen ratios, and a few different masses. In addition, subgrids with various metallicities were computed to reproduce stars in the Milky Way and the Magellanic Clouds.
In T1 and subsequent papers, the hydrostatic COMARCS atmospheres were then used to compute a grid of synthetic spectra covering the range between 0.444 and 25.0 μm with a resolution of R = 10 000. Owing to the statistical nature of the opacity sampling in these calculations, only the average over a large number of wavelength points (usually 20 to 100) gives a realistic representation of observed stellar spectra, which reduces the useful resolution from 10 000 to a few hundred.
3.2. New grid of synthetic spectra
For the resolution of the X-shooter spectra (≃8000), the original resolution of the synthetic spectra was insufficient. A new grid of theoretical spectra was computed using the existing atmospheric models, this time with a resolving power of 200 000. We then smoothed the spectra to match the resolution of the observations.
The atmosphere models used for this grid assume a stellar mass of 1.0 M⊙ and surface gravities of −0.4, 0 or 2 (values of log (g), with g in cm s-2). The effective temperatures range from 2500 to 4000 K, with a step of 100 K. The main model grid has [Fe/H] = 0, and a subset of models with [Fe/H] = −0.5 was also computed. The spectral synthesis assumes a microturbulent velocity of 2.5 km s-1, which is consistent with the opacities used to construct the models. Solar-scaled abundances are adopted except for carbon, which is enhanced at a given [Fe/H] to sample a range of carbon-to-oxygen ratios: C/O = 1.01, 1.05, 1.10, 1.40 and 2.0.
Figure 1 shows a schematic representation of all the synthetic spectra available, as a function of the parameters listed above. It is important to keep in mind that although this grid is a good starting point, it does not vary all the relevant parameters. The turbulent velocity parameters and the nitrogen abundance, for instance, are expected also to affect the relative strengths of molecular bands, but are set to fixed values here.
 |
Fig. 1 Schematic overview showing the parameters of our grid of synthetic spectra. Each square corresponds to a given temperature. |
3.3. Illustrative examples of synthetic spectra
Figure 2 shows an example of a synthetic spectrum at high resolution (R = 200 000) as a black spectrum and its smoothed version (R ≃ 8000) as a red spectrum. By downgrading the spectral resolution, it is worth noting that we lose direct access to the continuum.
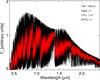 |
Fig. 2 Example of a synthetic spectrum at high resolution (R = 200 000, black spectrum) and smoothed to XSL resolution (R ≃ 8000, red spectrum). |
Figure 3 shows three hydrostatic models that share the same properties, except for the effective temperature. The temperature decreases from the top to the bottom. The peak of the SED shifts from the blue to the red – as the stars become cooler. The strongest bandheads and the ragged aspect of the spectra are mostly due to numerous lines from CN and C2, which tend to increase in intensity with decreasing temperature. The signatures with a weaker dependence on Teff over the plotted range, such as those of CO around 1.65 and 2.3 μm, are progressively masked by the forest of other features when Teff decreases.
 |
Fig. 3 Examples of synthetic spectra of C-rich giants with different temperatures (log (g) = 0, C/O = 1.10 and [Fe/H] = 0). The spectra are smoothed to R = 2000 and normalized around 1.35 μm for display purposes. |
The effects of the fundamental parameters on the spectra are not obvious to the eye in plots of the whole spectrum. They are more efficiently summarized by index measurements, as shown below.
3.4. Molecular indices based on model spectra
In Paper I (see Table 2), we defined spectroscopic indices for carbon stars, to quantify the strengths of selected spectral features. We also calculated the values of these indices for all the spectra in the model grid.
The index DIP153 was based on the ratio between the flux measured near the center of the 1.53 μm feature and the flux measured on its short wavelength side. A plot of this index versus (J−Ks) separates the stars that display this molecular band well (Paper I), but at a given molecular band strength the value of the index depends strongly on color. This dependence can be quantified by fitting the indices of (observed) stars with no 1.53 μm feature as a function of color. We define a new (almost) color-independent index by subtracting this trend from the original index. ![\begin{equation} {\rm DIP}153b={\rm DIP}153-0.132[1.06-(J-K_{\rm s})]. \label{eq_new_dip} \end{equation}](/articles/aa/full_html/2017/05/aa29750-16/aa29750-16-eq34.png) (1)Figure 4 shows the values of four representative near-infrared indices as a function of the effective temperature of the models. In addition to DIP153b, we plot CN, which measures the strength of the CN molecule at 1.11 μm, C2, which measures the bandhead of the C2 molecule at 1.77 μm, and CO12, which measures the first overtone ro-vibrational band of CO at 2.3 μm. The symbol sizes represent model C/O ratios in the upper panels and model surface gravities in the lower panels.
(1)Figure 4 shows the values of four representative near-infrared indices as a function of the effective temperature of the models. In addition to DIP153b, we plot CN, which measures the strength of the CN molecule at 1.11 μm, C2, which measures the bandhead of the C2 molecule at 1.77 μm, and CO12, which measures the first overtone ro-vibrational band of CO at 2.3 μm. The symbol sizes represent model C/O ratios in the upper panels and model surface gravities in the lower panels.
 |
Fig. 4 Spectro-photometric indices vs. Teff for a representative set of models. The color code of the symbols correspond to different values of C/O in the upper panels and of log (g) in the lower panels. Figure 9 shows more indices. |
As a general trend, molecular bandhead strengths increase with decreasing temperatures. This is the case for CN, C2 and CO. At the lowest temperatures, contamination of the index passbands by lines from other molecules (or other bands of the same molecule) weakens the index values.
At a given Teff, the bands of CN and C2 increase with C/O, while CO decreases. Concerning the surface gravity, the strengths of the bands increase with decreasing log (g). For Teff< 3000 K, the high-gravity models (log (g) = 2) differ strongly from models with lower gravities.
The cooler models (Teff< 3000 K) display the 1.53 μm absorption band, as seen in the left panels of Fig. 4 (DIP153b as a function of temperature). The feature shows weak dependence on the C/O ratio or gravity.
 |
Fig. 5 rmsK index vs. Teff and DIP153b for a representative set of models. The symbols are for C/O in the left panel and for log (g) in the two right panels. |
Paper I defined rmsH and rmsK to measure the apparent strength of the forest of lines in the H and K windows. They are computed as the ratio of the local standard deviation around the mean flux in small regions in the H and K windows, in units of that local mean. Figure 5 shows the evolution of rmsK as a function of Teff and DIP153b. At low temperatures, rmsK is sensitive to gravity. Therefore, the theoretical spectra appear smoother at log (g) = 2 than at low gravities, gravities which are more typical of luminous giants. In the hydrostatic models, the presence of the absorption feature at 1.53 μm feature combined with a “smooth” appearance of the NIR spectrum (i.e., a low value of rmsK) is found at log (g) = 2. rmsH behaves in the same way as rmsK.
4. Comparison of pseudo-observations and models
Before comparing our observations to the grid of models, it is important to evaluate the amount of information present in the models themselves. If the models were perfect representations of reality, with what uncertainties could we estimate the values of the fundamental parameters? To answer this question, we selected a subset of models that we analyzed with the full model grid as if they were observations. We refer to the subset of six models as pseudo-observations. Table 2 summarizes the parameters of the pseudo-observations.
Before analysis, the pseudo-observations were smoothed to a resolving power comparable to X-shooter spectra, that is, R ~ 8000, and they were resampled. Artificial Gaussian noise was added, to reach a signal-to-noise ratio of 75 per pixel. Because these models are hydrostatic and thus dust-free, we reddened them artificially with AV = 1, using the extinction law of Cardelli et al. (1989). The shape of the extinction law matters little in this exercise, considering the way we later analyze the pseudo-observations (Eq. (2)). The added extinction mainly serves to test color-based details of our analysis code and is not essential to results on parameter estimation.
Properties of the subset of models selected as pseudo-observations.
4.1. Method
To compare our pseudo-observations with the models, we performed a χ2 minimization in a four-dimensional space with the following parameters: the effective temperature (Teff), the surface gravity (log (g)), the ratio of carbon over oxygen (C/O), and the metallicity ([Fe/H]).
The useful range of our X-shooter observations extends from 0.4 to 2.4 μm. We chose to perform two comparisons for each observation: one over the visible wavelength range (0.4–1.0 μm), which we refer to as VIS, and one over near-infrared wavelength ranges (1.0–2.4 μm), which we refer to as NIR. The aim is to determine which wavelength range more strongly constrains the various stellar parameters. When applied to observations, these separate studies will allow us to explore whether the parameters derived from optical and near-infrared wavelengths using hydrostatic models are consistent.
To identify the model that best fits a pseudo-observation (and later an X-shooter observation), we used the following step-by-step procedure in each of the VIS and NIR wavelength ranges.
First, in order to avoid unphysical dereddening of the models, we excluded any models intrinsically redder than the analyzed spectrum, based on (R−I) for the VIS range or (J−Ks) for the NIR. At this step, a tolerance of 10% on these colors is included to allow for spectrophotometric errors in the observations.
We then used the ULySS package2 (Koleva et al. 2009) to determine the velocity and the velocity dispersion differences between the pseudo-observations and each model. Each model is convolved with the corresponding Gaussian kernel in velocity space and resampled to match the analyzed spectrum.
Finally, we computed the reduced χ2, expressed as ![\begin{equation} \chi^2_{\rm red} = \frac{1}{N} \sum_{i=1}^{M} W(i) \times \frac{ [F_{\rm obs}(i) - P(i) \times F_{\rm mod}(i) ]^2}{\sigma^2_{F_{\rm obs}}(i)}\cdot \label{eq_chi2} \end{equation}](/articles/aa/full_html/2017/05/aa29750-16/aa29750-16-eq46.png) (2)Here, Fobs and Fmod are the fluxes of the analyzed and theoretical spectra, σ is the noise associated with the observation, and W is the weight assigned to each pixel. We set the weights to 0 in the regions of strong telluric absorption and 1 elsewhere. We masked the following regions: 0.634–0.639 μm, 0.994–1.02 μm, 1.11–1.15 μm, 1.34–1.475 μm, 1.8–1.98 μm, and 2.26–2.28 μm. M is the total number of pixels and N is defined as the sum of the weights. P is the multiplicative spline polynomial that minimizes χ2. It absorbs reddening effects as well as any residual flux calibration errors. The adopted implementation has eight spline nodes in the VIS and seven in the NIR. It is important to note that this polynomial can only mimic multiplicative effects of circumstellar dust such as absorption, and not additive effects such as any thermal emission by dust.
(2)Here, Fobs and Fmod are the fluxes of the analyzed and theoretical spectra, σ is the noise associated with the observation, and W is the weight assigned to each pixel. We set the weights to 0 in the regions of strong telluric absorption and 1 elsewhere. We masked the following regions: 0.634–0.639 μm, 0.994–1.02 μm, 1.11–1.15 μm, 1.34–1.475 μm, 1.8–1.98 μm, and 2.26–2.28 μm. M is the total number of pixels and N is defined as the sum of the weights. P is the multiplicative spline polynomial that minimizes χ2. It absorbs reddening effects as well as any residual flux calibration errors. The adopted implementation has eight spline nodes in the VIS and seven in the NIR. It is important to note that this polynomial can only mimic multiplicative effects of circumstellar dust such as absorption, and not additive effects such as any thermal emission by dust.
4.2. χ2 maps and results
 |
Fig. 6 Example of χ2 maps for one of our pseudo-observations (Teff = 3300 K, log (g) = 0, C/O = 1.05, [Fe/H] = 0) for the VIS wavelength range. The best values (i.e., the values that minimize the χ2 calculation) are represented in white. |
For each pseudo-observation, we computed a χ2 map showing the distribution of the best models in the parameter space of the models. Figures 6 and 7 provide examples of such maps: we fit the VIS and NIR wavelength ranges of a pseudo-observation in these figures, respectively. The best models, which correspond to the lowest values of χ2, are plotted in white.
The χ2 maps demonstrate that the classical degeneracy between metallicity and effective temperature exists for carbon stars: fitting with models at underestimated metallicities leads to underestimated temperatures. In the near-infrared, another degeneracy is found to link the effective temperature and the C/O ratio (Fig. 7). However, this second degeneracy is not seen in the optical range (Fig. 6). The maps for other pseudo-observations confirm these trends. The grid of models available to date is too small to identify any other noteworthy systematics.
In the controlled context of pseudo-observations, the parameters of the analyzed spectrum can all be recovered better than the grid sampling. However, although the number of degrees of freedom are similar while fitting the NIR and VIS ranges, the χ2 valleys are much shallower for the NIR than they are for the VIS range. This indicates that the optical spectra of carbon stars more tightly constrain the stellar parameters than their near-infrared counterpart.
We can illustrate this by examining the distribution of models for which the χ2 distance to a given pseudo-observation is smaller than a threshold. For instance, the condition χ2< 3 is typically fulfilled for only one model in the VIS range, while about five to ten models satisfy this criterion in the NIR.
5. Comparisons of observations and models
In the following, we compare the observed targets with the modeling results in different ways. Section 5.1 presents some color indices in standard broadband filters. Section 5.2 focuses on spectro-photometric indices. Section 5.3 details how we fit our observed spectra and discusses the stellar parameter estimations.
5.1. Broadband colors
A comparison of the colors of the XSL targets and those of the models gives information on the stellar energy distribution as well as on the effects of dust. When the effects of dust are limited, color indices involving an optical and a near-infrared passband are good first-order indicators of the effective temperature, with a low sensitivity to other fundamental parameters (T1). This property is rapidly lost when circumstellar material becomes important.
For this comparison, we computed synthetic photometry for the model grid and the X-shooter spectra, using the Bessell (1990) filters R and I and the 2MASS near-infrared filters J, H and Ks (Cohen et al. 2003). Figures 8 and B.1 of the appendix display the resulting near-infrared color indices. Mira-type stars are identified by green filled symbols3. The spread between Miras and non-Miras is similar to the spread found by Whitelock et al. (2006). On the red side of the two-color diagrams, Mira-type stars tend to spread to much redder colors because of their higher mass-loss rates and the resulting circumstellar shells. On the blue side, it is more difficult to separate the two groups. The extinction vector in Fig. 8 guides the eye to the locus of reddened models and suffices to suggest that some observed spectra re not represented properly with hydrostatic models and a simple extinction law.
 |
Fig. 8 Colors (no correction for interstellar reddening) for our sample of carbon stars (filled symbols), using the 2MASS filters. The green symbols indicate the Mira-type stars, while the gray symbols are for the stars outside of the color range of the models. The synthetic colors (open diamonds) of our grid of hydrostatic models are overplotted for comparison. The orange line shows the effect of reddening using a simple extinction law (Cardelli et al. 1989). The bars plotted show the ± 1σ root-mean-square deviation of our photometry with respect to the literature (large-amplitude variables excluded). This is an upper limit of the uncertainties in the flux calibration and any possible residual variability. |
Group A gathers the bluest stars of our sample, represented as filled triangles in Fig. 8. Two of the stars, HD 202851 and HE 1428-1950, represented as gray triangles, lie outside the color range of the models. Estimates of the temperatures of these two stars are available in the literature. Bergeat et al. (2002) found Teff = 4780 K for HD 202851, and Placco et al. (2011) found Teff = 4562 K for HE 1428-1950. These temperatures are higher than expected for classical carbon stars on the asymptotic giant branch, and in Paper I we suggested that these objects may be extrinsic carbon stars. As the highest temperature of our model grid is Teff = 4000 K, these objects are expected to be out of the grid. They are not considered in the comparison with the models hereafter.
Stars from Group B should be well reproduced by the grid of models as the colors of both sets overlap well. Stars from Group C start to be more affected by circumstellar dust than stars from the previous groups and we are closer to the limits of what can be done with hydrostatic models. By reddening the models, we should be able to reproduce most or all of these observations.
Group D gathers all the stars with the absorption band at 1.53 μm. Although a small number of hydrostatic models contain this feature, the current grid combined with simple extinction does not reach values of (H−Ks) red enough to explain all the observations.
5.2. Molecular indices versus color
Spectrophotometric indices provide a good overview of the models with respect to the XSL data, at a somewhat higher resolution than broadband colors. For brevity, we only discuss the loci as a function of (J−Ks), as already done in Paper I.
Figure 9 displays the values of the molecular indices for both the observed targets and the model atmospheres (cf. Sect. 3.4). The filled symbols stand for our observations, while the open diamonds represent the models.
The error bars shown in Fig. 9 account for the noise per resolution element and uncertainties in the shape of the spectrograph’s response curve in the scale of molecular features. The latter component is usually dominant because the signal-to-noise ratio of the spectra is on the order of 100. Uncertainties in the response curve on the relevant scales are due mostly to imperfect modeling of the telluric absorption that affects the spectro-photometric standard star observations.
Both the data and the model indices present a large dispersion within color bins. In general, the model loci agree well with the locus of the observations of our sample with (J−Ks) < 1.6. This is true in particular for the CN bands.
The CO bands in the H window tend to be too strong in the models compared to the data. These features are sensitive to surface gravity at a given effective temperature. The relative strengths of the first- and second-overtone CO bands (measured by CO12 and COH) are also sensitive to the microturbulent velocity (Origlia et al. 1997; Lançon & Hauschildt 2010). Furthermore, the CO bands are very sensitive to dynamical effects causing emission components in the lines (Nowotny et al. 2010). This may cause weaker bands in some of the observed variable stars. It is unclear as yet what the predominant cause of the systematic difference could be.
Some of the models display the 1.53 μm feature (panels d and g). However, low-gravity models among them do not display damped line forests in the H and K window, as seen in the corresponding observations (panels h and i). In Paper I, the damping of the high-frequency structure in spectra with the 1.53 μm feature was interpreted as veiling by circumstellar dust. The index plots for the dust-free static models are consistent with this picture.
 |
Fig. 9 Spectro-photometric indices derived for our sample of carbon stars (brown symbols) and the grid of models (color symbols) as a function of (J−Ks). The triangles are for stars from Group A, the circles for Group B, the stars for Group, C and the squares for Group D. The filled symbols represent the averaged values of our indices in the groups, and the bars measure the dispersion within the bin. The open diamonds represent the models of solar (in blue) and subsolar metalliticity (red). The models were smoothed to R ≃ 8000 for the purpose of this figure. Typical uncertainties on individual measurements are shown in purple. The orange vector represents the extinction vector (computed for AV = 5). In panel g), the green line was used to define the new index DIP153b (see Eq. (1)). |
5.3. Full spectral fitting
5.3.1. Method
For a direct comparison between the observed and the model spectra, we use a method similar to the method we described in Sect. 4.1. The differences are as follows.
The noise spectra of our observations are those that come out of the X-shooter reduction pipeline. We propagate the errors through the reduction process, including the correction of the telluric features and the flux calibration.
For this study, we degraded the resolution of the XSL spectra to R ~ 2000. Before smoothing, the velocity resolution of the XSL data is ~30 km s-1 (R ~ 10 000). In Mira-type variables, velocity discontinuities with amplitudes larger than 10 km s-1 are expected as shocks propagate through the atmospheres (Nowotny et al. 2005, 2010). They produce significant wavelength shifts that may differ for various molecular bands. Since hydrostatic models cannot cover such effects, we postpone the study of these high-resolution effects to a future article.
For each observed star, the best-fitting model minimizes the χ2 calculation. Models for which  are considered similarly acceptable, and the distribution of their parameters provides our estimate of the uncertainties on the star’s physical properties. It is worth noting that the best model does not always fit the data well. Unfortunately, because the absolute levels of the error spectra produced by the X-shooter pipeline are sometimes unreliable, and because the correlations between noise in neighboring pixels are not completely characterized, the numerical value of the minimum χ2 cannot be reliably used as a direct measure of the quality of the fitting process. The examination of the fitting residuals is safer for this assessment.
are considered similarly acceptable, and the distribution of their parameters provides our estimate of the uncertainties on the star’s physical properties. It is worth noting that the best model does not always fit the data well. Unfortunately, because the absolute levels of the error spectra produced by the X-shooter pipeline are sometimes unreliable, and because the correlations between noise in neighboring pixels are not completely characterized, the numerical value of the minimum χ2 cannot be reliably used as a direct measure of the quality of the fitting process. The examination of the fitting residuals is safer for this assessment.
5.3.2. Results of model fitting
Appendix A shows the models that best fit our X-shooter spectra, ordered by increasing (J−Ks). As mentioned above, the visible wavelength range runs in principle from 0.4 μm to 1.0 μm. However, the reddest carbon stars could not be measured below 0.5 or 0.6 μm. The corresponding part of their spectra was rejected from the fitted models and figures.
The bottom panels of the figures show the residuals and an unsharp-mask filtered version of the model spectrum (the difference between the synthetic spectrum and a heavily smoothed version thereof). In many cases, the residuals are very small compared to the high- and medium-resolution features seen in the filtered spectrum, showing that the models successfully capture the shapes and relative strengths of the dominant molecular bands (mostly of CN). This is the first time the ability of C-star models to fit observations is demonstrated over such an extended wavelength range.
Tables A.1 to A.4 list the results of the fitting procedure. The letter V indicates the values found over the VIS wavelength range, the letter N stands for near-infrared. For each parameter (Teff, log (g), C/O, [Fe/H]), the first column gives the value of the best model (minimum χ2), the second column the weighted average value, and the third and fourth columns the extreme values compatible with our 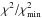 -threshold. The weighted average is given by
-threshold. The weighted average is given by ![\begin{equation} {\rm param\_weighted} = \frac{\sum_{i} {\rm param}(i) \times \exp[-(\chi^2_i/\chi^2_{\rm min})/2]}{\sum_{i} \exp[-(\chi^2_i/\chi^2_{\rm min})/2]}, \label{eq_wei} \end{equation}](/articles/aa/full_html/2017/05/aa29750-16/aa29750-16-eq70.png) (3)where i samples all the available models.
(3)where i samples all the available models.
With only a few exceptions, the favored surface gravity for all our observations is log(g) = 0 (rather than 2), and the favored metallicity is [Fe/H] = −0.5 (rather than 0). These values are satisfactory for TP-AGB stars and for a sample consisting mostly of LMC, SMC, and Milky Way halo stars.
Figure 10 compares the weighted average values of the effective temperatures estimated by fitting the VIS and NIR wavelength ranges. The black dashed line indicates the one-to-one relation. Different symbols indicate the values for the spectra of groups A, B, and C (Group D is omitted for reasons explained). Considering the typical error bars of ±200 K, the NIR and VIS temperatures are consistent with each other. Nevertheless, the temperatures found tend to be warmer in the VIS than in the NIR. The median of the weighted temperatures is 3376.10 ± 160 K for the NIR and 3470.89 ± 100 K for the VIS for the three groups. We now consider each group in turn.
 |
Fig. 10 Comparison of the weighted averaged values found for the effective temperature for both wavelength ranges (VIS and NIR) for Groups A, B, and C. The black dashed line indicates the one-to-one relation, while the red and blue dashed lines correspond to ± 100 K and ± 200 K, respectively. The typical (median) error bars for each group are indicated in the top left corner. |
Group A
The parameters listed in Table A.1 agree quite well between the VIS and the NIR wavelength ranges. Figures A.1 to A.3 show the best-fitting models. Effective temperatures in Group A are above 3600 K.
Two of the three stars in Group A display hydrogen lines in emission. They are large-amplitude variables (Paper I), and these lines are interpreted as signatures of shocks that propagate through the atmosphere. For one of these stars, the fitted model is not quite as good as for the others. However, it is remarkable how well hydrostatic models reproduce the medium-resolution spectral features of these warm pulsators in general.
The CO bands in the H window are too strong in the models compared to the observations. This is particularly visible in Fig. A.3 by comparing the residuals (in green) with the bottom panel curve, which corresponds to the unsharp-mask filtered version of the model (in blue).
Group B
Stars from Group B are expected to be reproduced well by the grid of models, according to Fig. 8. Indeed, the models fit the data well, and the curves of χ2 versus model Teff are well behaved with narrow minima. The best values are summarized in Table A.2. In all but one case (Fig. A.6), the range of Teff derived from the VIS spectrum is narrower than the range accepted based on the NIR data, in agreement with expectations from Sect. 4. The temperatures within Group B range between 3200 and 3800 K. In general, a slightly higher temperature in the VIS than in the NIR is compensated by a higher C/O ratio. In most cases, the optical and near-infrared temperatures are within the uncertainties of each other.
From Figs. A.4 to A.10, some small discrepancies appear progressively. Some are instrumental, like the lack of data around 0.63 μm (due to a bad column). A real systematic difference in the shape and depth of the C2 band at 1.77 μm becomes apparent for (J−Ks) ≥ 1.4. This is discussed further for Group C below.
Group C
 |
Fig. 11 Close-up of the C2 features at 1.77 μm for [ABC89] Cir 18 (cf. Fig. A.23 for full fitting). The black curve corresponds to the stellar spectrum and the red curve to the best model times the best-fitting polynomial. The gray band masks a region with strong telluric absorption. |
Table A.3 summarizes the properties of the best models for the stars of Group C. Stars from Group C are stars with (J−Ks) ≥ 1.6 and are therefore in a color regime that hydrostatic models cannot reproduce without any effects of dust (Aringer et al. 2009). The multiplicative polynomial in our procedure accounts for extinction, and we focus on the spectral features. Figures A.11 to A.23 show the results from fitting.
The range of temperatures found in Group C is similar to that in Group B, despite the redder colors in Group C. Again, the NIR and VIS temperatures are compatible (within the error bars) in most cases, but the error bars tend to become larger than in Group B, and there are a few formally incompatible cases, with significantly higher VIS than NIR temperatures (e.g., Fig. A.15, A.17 and A.18).
The fitted models favor a C/O ratio of 2. The effect of C/O on color, at a given Teff (above 3000 K), is very small and hence C/O does not explain the redder colors of Group C. The difference in color between Groups B and C is mainly driven by circumstellar extinction.
The models struggle to reproduce the depth and shape of the C2 features at 1.77 μm, as shown in Fig. 11. The observations show a feature at 1.75 μm (H2O + 12CO, see Fig. 3 from Lyubenova et al. 2012) that correlates with the depth of the 1.77 μm bandhead. This is also seen in C-star spectra of Lançon & Wood (2000) or IRTF (Rayner et al. 2009), but is not present in the models.
Group D
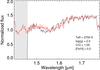 |
Fig. 12 Close-up of the HCN + C2H2 feature at 1.53 μm for SHV 0502469-692418 (cf. Fig. A.25 for full fitting). The black curve corresponds to the stellar spectrum and the red curve to the best model times the best-fitting polynomial. The gray band masks a region with strong telluric absorption. |
Table A.4 summarizes the results for the stars from Group D, that is, the stars that display the 1.53 μm absorption feature. These stars are affected by pulsation. They are all large-amplitude variables (cf. Paper I), and the use of hydrostatic models is a clear limitation. Figures A.24 to A.31 show the best-fitting models. While the χ2 distributions as a function of effective temperature remain relatively well behaved for most of the VIS spectra, the distributions for the NIR are very flat. The NIR best models provide no or only weak constraints on the parameters.
The NIR X-shooter spectra in Group D have a relatively smooth appearance, compared to Groups C and B, as was highlighted in Paper I. As a consequence, the best-fitting models tend to have either relatively high temperatures (>3500 K) and log (g) = 0, or lower temperatures and log (g) = 2 (last panel of Fig. 5).
However, these parameters cannot be relied upon. A hot temperature is difficult to reconcile with the presence of the 1.53 μm feature, and indeed the best-fitting model with high temperature fails to reproduce this feature (e.g., Fig. A.29). The best models with log (g) = 2 combine the presence of this absorption feature with a smooth appeareance (see plot rmsK index vs. DIP153b, from Fig. 5, Sect. 3.4). A gravity that high is difficult to reconcile with the expected location of large-amplitude C-rich variables on the asymptotic giant branch, however. Our favoured interpretation is that these stars have normal AGB gravities and are not as warm as the NIR models at log (g) = 0 may indicate.
Instead, their spectra are profoundly modified by dust that produces both extinction and emission (Nowotny et al. 2011). This combination is known as veiling. The (additive) emission component attenuates the equivalent widths of molecular absorption features produced in the photosphere, and both extinction and emission affect the energy distribution. Parameter estimations based on fits to the absorption features that are produced near the photosphere then become unreliable. The parameters given in Table A.4 based on the NIR spectra should therefore only be used with great caution.
In principle, the parameters derived in the VIS should be more reliable than those based on the NIR, as dust emission is weaker at shorter wavelengths. However, the useful part of the VIS spectrum of highly reddened objects almost exclusively contains signatures of CN, and we should keep in mind that unexplored parameters such as the N abundance could affect them.
Finally, we emphasize two systematic spectral issues. The C2 feature at 1.77 μm is never matched correctly. More interestingly the 1.53 μm feature present in the coolest hydrostatic models does not have the shape of its observed counterpart, as shown in Fig. 12. This suggests that the line lists for the main carriers (C2 on one hand, HCN and C2H2 on the other) may need revision.
6. Conclusions
We have compared optical and near-infrared spectra of carbon stars with hydrostatic models at a spectral resolving power of ~2000. The models provide impressive matches to most of the features in the optical and NIR range, but it remains difficult to fit all features simultaneously with a single model when only extinction is allowed to alter the energy distribution.
In defining a goodness-of-fit criterion, choices can be made that focus either on the high-frequency structure within the bands or on the medium-resolution energy distribution and the shape of the main molecular bands. In this paper, we have emphasized the latter. XSL spectra contain a wealth of high-frequency information that will be exploited more completely in the future. The main difficulty encountered at the native resolution of the XSL data, R ~ 10 000 in the VIS and 8000 in the NIR, is the effect of pulsation. Shocks that travel through the atmospheres of LPVs create velocity discontinuities with amplitudes above 10 km s-1, which will affect the location and shape of lines at the resolution of XSL. Moreover, line lists for carbon-bearing molecules such as C2 or HCN are incomplete and known to contain approximate wavelengths for some of the transitions (e.g. Loidl et al. 2001; Aringer et al. 2009). Smoothing to R ~ 2000 allows us to avoid these difficulties. Nevertheless, the residuals show that it remains difficult to fit all the spectral features even at low resolution, and even when a multiplicative polynomial mimicking extinction and flux calibration corrections is allowed to modify the energy distribution.
For stars from Groups A to C, the effective temperature ranges derived separately from the VIS and NIR wavelength range overlap in general. It is therefore possible to provide a viable Teff estimate for the carbon stars in these groups. When temperature differences are obtained between the two wavelength ranges, the VIS-based temperature is warmer than the NIR-based temperature. It becomes progressively more difficult to obtain reasonable matches of the data for redder observed spectra, in particular for stars from Group D. This is due to a combination of a more complex forest of molecular lines (that is only matched in detail in small parts of the spectra) and to the effects of circumstellar material on the energy distribution (that a simple extinction law cannot reproduce). Veiling by dust is important in the NIR spectra of Group D. At a lower level, this veiling might contribute to explain the differences in temperature seen between the VIS and NIR in a few of the other stars.
For the spectra of Groups A to C, fitting models constrain log (g) and [Fe/H]. The favored surface gravity is log (g) = 0, and the favored metallicity [Fe/H] = −0.5. These values are satisfactory for TP-AGB stars and for a sample consisting mostly of LMC, SMC and Milky Way halo stars. However, the uncertainties are quite large as are result of the small number of values available for these parameters in the model grid and because of the degeneracy between Teff and C/O, and between Teff and [Fe/H].
For now, the fitted models show that the features at R ~ 2000 do not perfectly represent the data. This justifies the use of empirical spectra as templates for C stars in the Universe. At this stage, however, it is not possible to precisely assign an evolutionary stage to individual stars in the collection based on their spectra alone. When using the C-star observations as templates for stellar population models, it will probably be necessary to continue to use averages, as done for instance by Lançon & Mouhcine (2002) for O-rich and C-rich LPVs.
The next step will be to use dynamical models, that is to say models that take into account the pulsating stellar interior as well as the development of dust-driven winds (e.g. Eriksson et al. 2014). It has been suggested that a simple dust-envelope model could be used as an intermediate step before entering the complexity of dynamical models (e.g. Aringer et al. 2009; Paladini et al. 2011). With dust radiative transfer codes, we can expect to reproduce the attenuation of the absorption features and also the overall shift of the SED toward redder wavelengths (Nowotny et al. 2011). The situation is not that straightforward however. First, large-amplitude pulsation and dust production are closely related (Sloan et al. 2016). Second, the appearance of the 13.7 μm C2H2 band in deeply embedded carbon stars points to the fact that acetylene in gas form is producing molecular absorption bands well into, and possibly beyond, the dust-forming region (Matsuura et al. 2006). This complicates the situation for the 1.53 μm feature, most likely carried by HCN + C2H2. Therefore, it seems more promising to directly use the low-resolution version of the pulsating C-star models directly. In particular, a study of their molecular stratification would be useful: the XSL C stars indicate that some CO should be located above dust emission layers (Paper I), and this hypothesis requires verification. If high-resolution versions of the pulsating model spectra can be computed, we could also more quantitatively explore the effects of pulsation on the XSL spectra at R ≃ 8000.
Acknowledgments
We thank the referee, Greg Sloan, for his insightful report that helped to improve the quality of this paper. A.L. and P.P. thank PNCG (Programme National Cosmologie et Galaxies) for support in 2016. B.A. was supported by the ERC Consolidator Grant funding scheme (project STARKEY, G.A. No. 615604, P.I. P. Marigo).
References
- Aringer, B., Girardi, L., Nowotny, W., et al. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Bressan, A. 2016, MNRAS, 457, 3611 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, J., Knapik, A., & Rutily, B. 2002, A&A, 390, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 1990, PASP, 105, 419 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y. P., Trager, S. C., Peletier, R. F., et al. 2014a, A&A, 565, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y.-P., Trager, S. C., Peletier, R. F., et al. 2014b, The Messenger, 158, 30 [NASA ADS] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Kudritzki, R.-P., Plez, B., et al. 2013, ApJ, 767, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, K., Nowotny, W., Höfner, S., et al. 2014, A&A, 566, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., et al. 2004, A&AS, 422, 289 [Google Scholar]
- Gonneau, A., Lançon, A., Trager, S. C., et al. 2016, A&A, 589, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lançon, A., & Hauschildt, P. H. 2010, ASP Conf. Ser., 425, 61 [NASA ADS] [Google Scholar]
- Lançon, A., & Mouhcine, M. 2002, A&A, 393, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lançon, A., & Wood, P. R. 2000, A&AS, 146, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubenova, M., Kuntschner, H., Rejkuba, M., et al. 2010, A&A, 510, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubenova, M., Kuntschner, H., Rejkuba, M., et al. 2012, A&A, 543, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuura, M., Wood, P. R., Sloan, G. C., et al. 2006, MNRAS, 371, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Melbourne, J., Williams, B. F., Dalcanton, J. J., et al. 2012, ApJ, 748, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Nowotny, W., Aringer, B., Höfner, S., et al. 2005, A&A, 437, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Höfner, S., & Aringer, B. 2010, A&A, 514, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Aringer, B., Höfner, S., et al. 2011, A&A, 52, A129 [Google Scholar]
- Nowotny, W., Aringer, B., Höfner, S., et al. 2013, A&A, 552, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Origlia, L., Ferraro, F. R., & Fusi Pecci, F. O. 1997, A&A, 321, 859 [Google Scholar]
- Paladini, C., van Belle, G. T., Aringer, B., et al. 2011, A&A, 533, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Placco, V. M., Kennedy, C. R., Beers, T. C., et al. 2011, AJ, 142, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Kraemer, K. E., McDonald, I., et al. 2016, ApJ, 826, 44 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G., Paladini, C., Aringer, B., et al. 2013, ApJ, 775, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitelock, P. A., Feast, M. W., Marang, F., et al. 2006, MNRAS, 369, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, P. R. 2015, MNRAS, 448, 3829 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Gallazzi, A., & Charlot, S. 2013, MNRAS, 428, 1479 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Models that fit our observations best
Tables A.1 to A.4 show the range of parameters for the models that fit the observed spectra best. Figures A.1 to A.31 show the best-fitting models for each observation. For each figure, the upper panel shows the observation (black curve), the best model times the polynomial (red curve), and the weights used for the χ2
Range of parameters for the best-fitting models for the stars from Group A.
Range of parameters for the best-fitting models for the stars from Group B.
minimization (orange). The middle panel shows the residuals (in green), while the bottom panel shows an unsharp-mask filtered version of the best-model spectrum (the difference between the synthetic spectrum and a heavily smoothed version thereof, in blue). In addition, a small inset shows the output 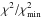 values as a function of the temperatures of the input models.
values as a function of the temperatures of the input models.
Range of parameters for the best-fitting models for the stars from Group C.
Range of parameters for the best-fitting models for the stars from Group D (warning see below).
 |
Fig. A.1 Best-fitting models for Cl* NGC 121 T V8 (Group A). For each observation, the upper panel shows the stellar spectrum as a black curve and the best model times the best-fitting polynomial as a red curve. The weights applied for the χ2 minimization are displayed in orange. The middle panel shows the residuals (in green), while the bottom panel shows an unsharp-mask filtered version of the best-model spectrum (in blue). In addition, a small inset shows the output |
 |
Fig. A.22 Best-fitting models for [ABC89] Cir 18 (Group C, J−Ks = 2.45). Same legend as for Fig. A.1. |
 |
Fig. A.23 Best-fitting models for [ABC89] Cir 18 (Group C, J−Ks = 2.52). Same legend as for Fig. A.1. |
Appendix B: Color–color plots
Figure B.1 shows the color–color plot for our observations and the grid of models.
 |
Fig. B.1 Some color–color plots containing our sample of observed carbon stars (black symbols) and the models (colored diamonds). The triangles are for stars from Group A, the circles for Group B, the stars for Group C, and the squares for Group D. The open diamonds represent the models at solar (in blue) and subsolar metalliticity (red). The bars show the ± 1σ root-mean-square deviation of our photometry with respect to the literature (large-amplitude variables excluded). This is an upper limit of the uncertainties in the flux calibration and any possible residual variability. |
All Tables
Range of parameters for the best-fitting models for the stars from Group D (warning see below).
All Figures
 |
Fig. 1 Schematic overview showing the parameters of our grid of synthetic spectra. Each square corresponds to a given temperature. |
| In the text | |
 |
Fig. 2 Example of a synthetic spectrum at high resolution (R = 200 000, black spectrum) and smoothed to XSL resolution (R ≃ 8000, red spectrum). |
| In the text | |
 |
Fig. 3 Examples of synthetic spectra of C-rich giants with different temperatures (log (g) = 0, C/O = 1.10 and [Fe/H] = 0). The spectra are smoothed to R = 2000 and normalized around 1.35 μm for display purposes. |
| In the text | |
 |
Fig. 4 Spectro-photometric indices vs. Teff for a representative set of models. The color code of the symbols correspond to different values of C/O in the upper panels and of log (g) in the lower panels. Figure 9 shows more indices. |
| In the text | |
 |
Fig. 5 rmsK index vs. Teff and DIP153b for a representative set of models. The symbols are for C/O in the left panel and for log (g) in the two right panels. |
| In the text | |
 |
Fig. 6 Example of χ2 maps for one of our pseudo-observations (Teff = 3300 K, log (g) = 0, C/O = 1.05, [Fe/H] = 0) for the VIS wavelength range. The best values (i.e., the values that minimize the χ2 calculation) are represented in white. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 but for the NIR wavelength range. |
| In the text | |
 |
Fig. 8 Colors (no correction for interstellar reddening) for our sample of carbon stars (filled symbols), using the 2MASS filters. The green symbols indicate the Mira-type stars, while the gray symbols are for the stars outside of the color range of the models. The synthetic colors (open diamonds) of our grid of hydrostatic models are overplotted for comparison. The orange line shows the effect of reddening using a simple extinction law (Cardelli et al. 1989). The bars plotted show the ± 1σ root-mean-square deviation of our photometry with respect to the literature (large-amplitude variables excluded). This is an upper limit of the uncertainties in the flux calibration and any possible residual variability. |
| In the text | |
 |
Fig. 9 Spectro-photometric indices derived for our sample of carbon stars (brown symbols) and the grid of models (color symbols) as a function of (J−Ks). The triangles are for stars from Group A, the circles for Group B, the stars for Group, C and the squares for Group D. The filled symbols represent the averaged values of our indices in the groups, and the bars measure the dispersion within the bin. The open diamonds represent the models of solar (in blue) and subsolar metalliticity (red). The models were smoothed to R ≃ 8000 for the purpose of this figure. Typical uncertainties on individual measurements are shown in purple. The orange vector represents the extinction vector (computed for AV = 5). In panel g), the green line was used to define the new index DIP153b (see Eq. (1)). |
| In the text | |
 |
Fig. 10 Comparison of the weighted averaged values found for the effective temperature for both wavelength ranges (VIS and NIR) for Groups A, B, and C. The black dashed line indicates the one-to-one relation, while the red and blue dashed lines correspond to ± 100 K and ± 200 K, respectively. The typical (median) error bars for each group are indicated in the top left corner. |
| In the text | |
 |
Fig. 11 Close-up of the C2 features at 1.77 μm for [ABC89] Cir 18 (cf. Fig. A.23 for full fitting). The black curve corresponds to the stellar spectrum and the red curve to the best model times the best-fitting polynomial. The gray band masks a region with strong telluric absorption. |
| In the text | |
 |
Fig. 12 Close-up of the HCN + C2H2 feature at 1.53 μm for SHV 0502469-692418 (cf. Fig. A.25 for full fitting). The black curve corresponds to the stellar spectrum and the red curve to the best model times the best-fitting polynomial. The gray band masks a region with strong telluric absorption. |
| In the text | |
 |
Fig. A.1 Best-fitting models for Cl* NGC 121 T V8 (Group A). For each observation, the upper panel shows the stellar spectrum as a black curve and the best model times the best-fitting polynomial as a red curve. The weights applied for the χ2 minimization are displayed in orange. The middle panel shows the residuals (in green), while the bottom panel shows an unsharp-mask filtered version of the best-model spectrum (in blue). In addition, a small inset shows the output |
| In the text | |
 |
Fig. A.2 Best-fitting models for SHV 0517337-725738 (Group A). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.3 Best-fitting models for SHV 0518161-683543 (Group A). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.4 Best-fitting models for 2MASS J00571648-7310527 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.5 Best-fitting models for 2MASS J01003150-7307237 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.6 Best-fitting models for 2MASS J00563906-7304529 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.7 Best-fitting models for 2MASS J00530765-7307477 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.8 Best-fitting models for 2MASS J00493262-7317523 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.9 Best-fitting models for 2MASS J00490032-7322238 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.10 Best-fitting models for 2MASS J00571214-7307045 (Group B). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.11 Best-fitting models for 2MASS J00570070-7307505 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.12 Best-fitting models for [W65] c2 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.13 Best-fitting models for 2MASS J00564478-7314347 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.14 Best-fitting models for 2MASS J00542265-7301057 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.15 Best-fitting models for Cl* NGC 419 LE 27 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.16 Best-fitting models for IRAS 09484-6242 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.17 Best-fitting models for Cl* NGC 419 LE 35 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.18 Best-fitting models for 2MASS J00553091-7310186 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.19 Best-fitting models for SHV 0520427-693637 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.20 Best-fitting models for SHV 0504353-712622 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.21 Best-fitting models for [ABC89] Pup 42 (Group C). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.22 Best-fitting models for [ABC89] Cir 18 (Group C, J−Ks = 2.45). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.23 Best-fitting models for [ABC89] Cir 18 (Group C, J−Ks = 2.52). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.24 Best-fitting models for SHV 0500412-684054 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.25 Best-fitting models for SHV 0502469-692418 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.26 Best-fitting models for SHV 0520505-705019 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.27 Best-fitting models for SHV 0518222-750327 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.28 Best-fitting models for SHV 0527072-701238 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.29 Best-fitting models for SHV 0525478-690944 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.30 Best-fitting models for SHV 0536139-701604 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. A.31 Best-fitting models for SHV 0528537-695119 (Group D). Same legend as for Fig. A.1. |
| In the text | |
 |
Fig. B.1 Some color–color plots containing our sample of observed carbon stars (black symbols) and the models (colored diamonds). The triangles are for stars from Group A, the circles for Group B, the stars for Group C, and the squares for Group D. The open diamonds represent the models at solar (in blue) and subsolar metalliticity (red). The bars show the ± 1σ root-mean-square deviation of our photometry with respect to the literature (large-amplitude variables excluded). This is an upper limit of the uncertainties in the flux calibration and any possible residual variability. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


