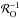| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201630056 | |
| Published online | 04 April 2017 | |
Global simulations of protoplanetary disks with net magnetic flux
I. Non-ideal MHD case
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
e-mail: william.bethune@univ-grenoble-alpes.fr
Received: 14 November 2016
Accepted: 24 January 2017
Context. The planet-forming region of protoplanetary disks is cold, dense, and therefore weakly ionized. For this reason, magnetohydrodynamic (MHD) turbulence is thought to be mostly absent, and another mechanism has to be found to explain gas accretion. It has been proposed that magnetized winds, launched from the ionized disk surface, could drive accretion in the presence of a large-scale magnetic field.
Aims. The efficiency and the impact of these surface winds on the disk structure is still highly uncertain. We present the first global simulations of a weakly ionized disk that exhibits large-scale magnetized winds. We also study the impact of self-organization, which was previously demonstrated only in non-stratified models.
Methods. We perform numerical simulations of stratified disks with the PLUTO code. We compute the ionization fraction dynamically, and account for all three non-ideal MHD effects: ohmic and ambipolar diffusions, and the Hall drift. Simplified heating and cooling due to non-thermal radiation is also taken into account in the disk atmosphere.
Results. We find that disks can be accreting or not, depending on the configuration of the large-scale magnetic field. Magnetothermal winds, driven both by magnetic acceleration and heating of the atmosphere, are obtained in the accreting case. In some cases, these winds are asymmetric, ejecting predominantly on one side of the disk. The wind mass loss rate depends primarily on the average ratio of magnetic to thermal pressure in the disk midplane. The non-accreting case is characterized by a meridional circulation, with accretion layers at the disk surface and decretion in the midplane. Finally, we observe self-organization, resulting in axisymmetric rings of density and associated pressure “bumps”. The underlying mechanism and its impact on observable structures are discussed.
Key words: accretion, accretion disks / magnetohydrodynamics (MHD) / protoplanetary disks / stars: formation / turbulence
© ESO, 2017
1. Introduction
Protoplanetary disks are commonly observed around young stellar objects, linking the young star to its protostellar envelope. Optical and near-infrared images show disks with strong extinctions near the midplane (Padgett et al. 1999). They also reveal bipolar outflows, normal to the disk plane, with inner jets collimated on large scales (Burrows et al. 1996). The structure of these disks can be probed by infrared and radio wavelengths. These images have unveiled a number of features, such as spiral arms (Muto et al. 2012; Benisty et al. 2015), asymmetric dust concentrations (van der Marel et al. 2013; Fukagawa et al. 2013), or axisymmetric rings (Brogan et al. 2015; Nomura et al. 2016).
The diversity of processes occurring in protoplanetary disks is ultimately constrained by the disk lifetime (Haisch et al. 2001; Cieza et al. 2007). On the one hand, any viable planetary formation scenario must be able to build planetesimals out of submicron-sized dust grains in a few million years. On the other hand, the rapid disk dispersal calls for efficient transport mechanisms. Part of the gas is accreted onto the central star, as deduced from their excess continuum emission and redshifted absorption lines (Edwards et al. 1994; Hartigan et al. 1995). The rest of it must be evacuated in the form of an outflow. What drives accretion and ejection remains a central research topic.
Hydrodynamic models fail to account for the observed jets’ collimation and ejection efficiency (Cabrit 2007). Including magnetic fields opens a number of promising perspectives. Magnetized Keplerian disks are prone to the magnetorotational instability (MRI, Balbus & Hawley 1991), which could drive accretion by turbulent angular momentum transport (Hawley et al. 1995). Large-scale magnetic fields could also extract angular momentum by the launching of a magnetohydrodynamic (MHD) wind (Blandford & Payne 1982; Ferreira & Pelletier 1995). In this ideal MHD picture, accretion and ejection are co-dependent aspects of one global process (Pudritz 1985). Thermodynamical effects, and in particular heating, are also important in order to characterize outflow properties. Heating at the disk surface has been shown to increase the outflow mass (Casse & Ferreira 2000), a result recently recovered by Bai et al. (2016), albeit with a prescribed magnetic topology and without solving the disk dynamics.
This ideal MHD picture is compromised when realizing that, due to their optical thickness and low temperatures, protoplanetary disks should be weakly ionized beyond 0.1–1au (Gammie 1996). The concept of a magnetic dead zone emerged, wherein the gas would be weakly coupled to the magnetic field. In principle, such a plasma should be described using a multi-fluid approach (e.g., O’Sullivan & Downes 2006). However, the recombination time in protoplanetary disks is in general much shorter than the orbital time (Bai 2011; Rodgers-Lee et al. 2016, but see Ilgner & Nelson 2008), making the single-fluid approximation perfectly valid and actually preferable to reduce computational costs. In the single-fluid approximation, the reduced ionization fraction is taken into account by incorporating three non-ideal MHD effects: ohmic diffusion, ambipolar diffusion, and the Hall drift (Nakano & Umebayashi 1986; Wardle & Ng 1999). Both diffusive effects can damp magnetic structures, and potentially quench the MRI (Jin 1996; Kunz & Balbus 2004), as supported by numerous non-linear simulations (e.g., Hawley & Stone 1998; Fleming et al. 2000; Bai & Stone 2011).
The Hall drift leads to qualitatively new behavior, due to its dispersive nature. In particular, it induces new branches of instability, and a polarity dependence on the large-scale magnetic field (Wardle 1999; Balbus & Terquem 2001; Sano & Stone 2002; O’Keeffe & Downes 2014). Local simulations, using the shearing-sheet approximation (Goldreich & Lynden-Bell 1965), found the emergence of organized structures from Hall-MHD turbulence. In non-stratified simulations, produces zonal flows (Kunz & Lesur 2013) and magnetized vortices (Béthune et al. 2016). These structures were not observed in the vertically stratified simulations of Lesur et al. (2014) and Bai (2015). Instead, the magnetic field was laminar and filled the disk midplane. As these authors point out, the results were influenced by their vertical boundary conditions.
The only way to ascertain whether these features are caused by boundary effects is to perform global models. Most of the properties of global, stratified and magnetized disks has been studied in the framework of ideal MHD (Fromang & Nelson 2006; Flock et al. 2011), albeit without any global poloidal field, preventing magnetized outflows. The inclusion of an global poloidal field in numerical simulations is notoriously difficult. Inner boundary conditions easily produce numerical artifacts, and high Alfvén speeds in the atmosphere can lead to dramatically small numerical time steps. For these reasons, relativistic simulations of disks around black holes (e.g., Beckwith et al. 2008) are technically easier to achieve. In the context of protoplanetary disks, initial attempts were either severely limited in computational time (Steinacker & Henning 2001) or did not resolve the small-scale dynamics of the disk (Murphy et al. 2010). The more recent models of Suzuki & Inutsuka (2014) improved the situation, but they could not access the outflow acceleration and collimation regimes due to their limited vertical extent. Global simulations including both ohmic and ambipolar diffusion were carried out by Gressel et al. (2015), using realistic estimates for the ionization state of the disk. However, the vertical extent of these simulations was again somewhat limited, casting doubts on the asymptotic properties of the wind. Moreover, they left open the question of Hall-driven self-organization, as this effect was not included in their simulations.
This paper presents a series of global simulations of protoplanetary disks, including all three non-ideal MHD effects in a domain suitable to study disk winds and integrated over many orbital periods. Our primary objective is the characterization of accretion and ejection in a weakly magnetized disk, freed from the limitations of local simulations, and resolving the internal dynamics of the disk. A second goal is to ascertain the role of the Hall drift in producing large-scale, organized structures. The physical framework, including our assumptions, conventions and definitions, are given in Sect. 2. The specific method of resolution is described in Sect. 3, and our results are presented in Sect. 4. A discussion of our results is made in Sect. 5 before summarizing of our main findings in Sect. 6.
2. Framework
2.1. Physical model
We wish to model the dynamics of a protoplanetary disk orbiting a young stellar object. We do not include the star in our model, but rather look at the outer regions of the disk, down to one astronomical unit (au). We will consider the portion of a disk contained in a spherical shell, with an inner radius r0, and covering the largest possible polar extent. We enumerate the main features of our disk model:
-
1.
the disk is geometrically thin;
-
2.
the disk is made of weakly ionized gas;
-
3.
the disk is threaded by a weak magnetic field;
-
4.
the disk is embedded in a warm corona.
We use the non-ideal MHD framework, and thus describe neutral and charged particles as one fluid with internal currents (cf. Sect. 2.3). The disk chemistry is evolved in a very simplified way, always assuming chemical equilibrium (cf. Sect. 2.4). This is made possible by the short time scale of chemical processes in comparison with the local orbital period (Bai 2011). The surrounding radiation field is not solved for; instead, we prescribe the temperature distribution via a cooling/heating function (see Appendix C). We use two coordinate systems:
-
a cylindrical system (r,ϕ,z), with the vertical coordinate z along the cylindrical axis of the disk;
-
a spherical system (R,θ,ϕ), with the polar angle θ ∈ [ 0,π ] increasing from the northern to the southern hemisphere.
The disk will be denoted by the letter 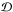 , while the symbols
, while the symbols 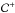 and
and 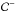 will stand for the northern and southern coronal regions respectively.
will stand for the northern and southern coronal regions respectively.
2.1.1. Disk
Let cs be the midplane sound speed and Ω the local orbital frequency. Under the influence of gravity and thermal pressure alone, a disk in hydrostatic equilibrium must be vertically stratified, its density varying on a characteristic vertical scale h ≡ cs/ Ω. Protoplanetary disks are geometrically thin in the sense that the ratio h/r is typically within 0.03 to 0.2, increasing with cylindrical radius r (Bitsch et al. 2013). We set a constant ratio h/r = 5% at all radii by imposing a constant ratio of sound over Keplerian velocity cs/vK = 5% within the disk.
We only consider disks with a radial profile of surface density Σ(r) ∝ 1 /r. This is flatter than the r− 3/2 often found in the literature since Hayashi (1981), but seems to better fit recent observations (D’Alessio et al. 2001; Williams & Cieza 2011).
The ionization fraction controls the coupling of the magnetic field with the gas. We are not interested in the detailed chemical composition of the medium: the computation of non-ideal MHD effects already comes with computational overhead, and the self-consistent resolution of a full chemical network is prohibitively demanding in CPU hours1. We reduce the disk chemistry to a local ionization fraction, computed dynamically with the evolution of the density distribution, and following the prescriptions of previous dedicated studies (cf. Sect. 2.4).
Large-scale magnetic fields are observed in the vicinity of protoplanetary disks, hosted by the parent molecular cloud and presumably concentrated near the young stellar object (Rao et al. 2014; Segura-Cox et al. 2015; Yang et al. 2016). Their global topology is still not well constrained, but their intensity is always weak in the sense that the midplane ratio of thermal over magnetic pressure β ≡ 2P/B2 ≳ 1 (Donati et al. 2005). Assuming that the global magnetic field has a non-zero vertical component, we will consider disks with initial average (midplane) β ≫ 1, constant with radius. Given our radial density profile, a constant β means that the average (midplane) Alfvén velocity 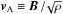 is a constant fraction of the local Keplerian velocity.
is a constant fraction of the local Keplerian velocity.
2.1.2. Corona
To study the global dynamics of protoplanetary disks via direct numerical simulations, previous studies used locally isothermal disk models, where the temperature decreases as a function of the cylindrical radius (Fromang & Nelson 2006; Suzuki & Inutsuka 2014; Gressel et al. 2015). These solutions have their density decreasing exponentially fast with height, ρ/ρ0 ~ exp(−z2/ 2h2). The Alfvén velocity increases exponentially with height; this is particularly appreciable in our case for we want a midplane β ≲ 106 and over ten scale heights of vertical extent. Resolving the dynamics of these Alfvén waves over Keplerian time scales is numerically impractical, so we cannot rely on such cold disk equilibria alone2.
Convertion from code to physical units.
It is known that protoplanetary disks are surrounded by a warm environment of optically thin and well ionized gas (Aresu et al. 2011; Bitsch et al. 2013; Woitke et al. 2016). Assuming hydrostatic equilibrium, the predicted coronal temperatures can go as high as ten thousand degrees at 1 au, above a disk at about 300 K. The corresponding ratios of corona to midplane sound speed range typically from 3 to 6.
To mimic this structure, we make the gas warmer above a certain height H(r). We take a constant corona to midplane temperature ratio at all radii for the sake of self-similarity (Contopoulos & Lovelace 1994; Casse & Ferreira 2000). This ratio is set to 6 in most simulations in order to avoid excessively low densities, so that the maximal Alfvén velocity remains comparable to the maximal Keplerian velocity (see Appendix C).
We set the transition height H based on the expected chemistry at the disk surface. Our ionization model, essentially the same as in Lesur et al. (2014), predicts a high ionization degree for z ≳ 3.6h (cf. their Fig. 1). More complete radiative transfer models also find a disk-corona transition at z ≈ 3h for r ∈ [1,10] au (Aresu et al. 2011). For these reasons, we heat the gas smoothly from H ≡ 3.7h to 4.7h (cf. Fig. 2 and Appendix A). The ratio H/h is held constant for simplicity. A self-consistent treatment of the thermodynamics and radiative transfer in the corona is beyond the scope of the present paper.
2.2. Units and conventions
Unless otherwise stated, all quantities will be evaluated in our code unit system. We use the inner radius r0 and the Keplerian velocity v0 at the inner radius as our distance and velocity units. We use both the orbital frequency Ω0 ≡ v0/r0 and period T0 ≡ 2π/ Ω0 to measure time. Densities are measured in comparison to the initial density ρ0 in the midplane and at the inner radius. The intensity of the magnetic field is measured by the corresponding Alfvén velocity 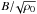 .
.
The estimation of the ionization fraction introduces dimensional constants in the problem. We give in Table 1 the conversion from code to physical units in the fiducial case of a disk around a 1 M⊙ star, with a surface density of Σ(r) = 500 (r/ 1 au)-1 g cm-2, and for the two considered simulation inner radii r0 = 1 au and r0 = 10 au.
We use the pressure scale height h(r) = 0.05r to normalize curvilinear abscissa in most figures; if the cylindrical radius r varies along the profile (for example along a streamline), then h(r) varies as well.
2.3. Dynamical equations
We consider the equations of inviscid, non-ideal MHD. We denote by ρ the bulk mass density, P the gas pressure, v the bulk velocity, B = | B | eb the magnetic field, J ≡ ∇ × B the electric current, Φ the gravitational potential. The three non-ideal MHD effects, namely ohmic diffusion, ambipolar diffusion and the Hall effet, can be characterized by their effective diffusivities ηO, ηA and ηH respectively (Wardle 2007). It will be useful to rewrite the last two as  where the Hall length ℓH and the ion-neutral coupling time τin primarily depend on the ionization fraction and the nature of the charge carriers, but not on the magnetic field amplitude. In a singly charged ion-electron plasma, these coefficients read:
where the Hall length ℓH and the ion-neutral coupling time τin primarily depend on the ionization fraction and the nature of the charge carriers, but not on the magnetic field amplitude. In a singly charged ion-electron plasma, these coefficients read: 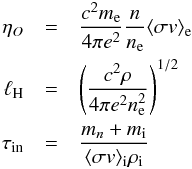 where ⟨ σv ⟩ e,i are respectively the electron-neutral and ion-neutral collision rates, ρi is the ion mass density, n is the neutral number density, ne is the electron neutral density, mn,i,e are the neutral, ion and electron masses and e is the elementary charge.
where ⟨ σv ⟩ e,i are respectively the electron-neutral and ion-neutral collision rates, ρi is the ion mass density, n is the neutral number density, ne is the electron neutral density, mn,i,e are the neutral, ion and electron masses and e is the elementary charge.
The evolution of mass density, momentum and magnetic field are governed by the following equations: ![\begin{eqnarray} &&\partial_t\, \rho = - \vec{\nabla \cdot} \left[ \rho \vec{v} \right], \label{eqn:dyn-rho}\\ &&\partial_t \!\left[ \rho \vec{v} \right] = - \vec{\nabla \cdot} \left[ \rho \vec{v \otimes v} \right] - \bnab P + \vec{J \times B} - \rho\nabla\Phi, \label{eqn:dyn-v}\\ &&\partial_t \vec{B} = \vec{\nabla \times} \left[ \vec{v \times B} - \eta_{\mathrm{O}} \vec{J} - \eta_{\mathrm{H}} \vec{J \times e_b} + \eta_{\mathrm{A}} \vec{J \times e_b \times e_b} \right]. \label{eqn:dyn-b} \end{eqnarray}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq96.png) The pressure distribution is locally isothermal, i.e., the isothermal sound speed
The pressure distribution is locally isothermal, i.e., the isothermal sound speed 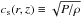 is prescribed beforehand. The detailed treatment of the gas energetics is given in Appendix C.
is prescribed beforehand. The detailed treatment of the gas energetics is given in Appendix C.
2.4. Ionization fraction
The intensity of the non-ideal MHD effects involves the local ionization fraction. We compute it via the same model as Lesur et al. (2014). This model includes stellar X-rays and far ultraviolet (FUV) photons, cosmic rays and radio-active decay. The ionization rates and penetration depths are taken from previous studies (Umebayashi & Nakano 1981, 2009; Bai & Goodman 2009; Perez-Becker & Chiang 2011). The ionization rates from cosmic rays and radioactive decay are respectively ζCR = 10-17 s-1 and ζRAD = 10-19 s-1. The X-ray ionization rate is given by Eq. (21) of Bai & Goodman (2009), with a luminosity LX = 1030 erg s-1. The total ionization rate is balanced by dissociative recombination, without dust grains nor metals (Fromang et al. 2002).
By soaking up electrons, dust grains can become one of the main charge carriers of the gas. Numerical simulations have not shown a drastic qualitative change when including “large” (micron-sized) grains (Lesur et al. 2014; Gressel et al. 2015). However, submicron-sized grains can increase the diffusivities by several orders of magnitude when they are sufficiently abundant (Salmeron & Wardle 2008; Xu & Bai 2016). The impact of small grains on the dynamics is therefore controlled by the dust size distribution, which is largely unconstrained. For this reason, our reaction network does not include grains.
Unlike in the local simulations of Lesur et al. (2014), we compute the ionization fraction every 1/8 inner orbit, consistently with the global evolution of the density distribution. Because we do not track the propagation of ionizing radiation, we simply use the gas column density integrated along the density gradient. The integration is thus performed in the polar direction instead of the vertical one. Both yield similar ionization profiles, because the regions of interest are located near the midplane.
Regarding the X and FUV radiations, they should originate from the central star before being scattered and absorbed in the disk’s upper layers. However, with h/r constant and ρ ~ R-2, the integration of density along spherical radius strongly depends on the lower integration bound. In addition, shadowing effects of the disk by the inner regions, which are excluded from the computational domain, could have an important dynamical impact (Bans & Königl 2012). We however ignore this additional degree of complexity in our model. We therefore use the polar column density to compute the X and FUV ionizing rates, affecting only the surface layers of the disk and mimicking a global flaring (Woitke et al. 2016; Aresu et al. 2011).
It is important to note that our ionization model is unable to model thermal ionization in the hot corona. For this reason, we assume the gas is fully ionized in the hot corona region by setting the diffusion coefficients to zero (see Sect. 3.3).
2.5. Main diagnostics and definitions
The averaging of a quantity X over the azimuthal angle is: 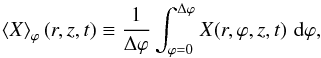 (6)where Δϕ is the total azimuthal extent of the considered disk. Multiple indices denote consecutive averagings. Radial profiles are produced by integration in the disk region only:
(6)where Δϕ is the total azimuthal extent of the considered disk. Multiple indices denote consecutive averagings. Radial profiles are produced by integration in the disk region only: 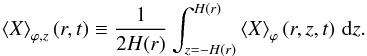 (7)The brackets and indices will be omitted when obvious from the context. Let ⟨X⟩ρ ≡ ⟨ρX⟩ϕ,z/ ⟨ρ⟩ϕ,z be the density weighted average of X. We define the fluctuating Reynolds stress tensor by
(7)The brackets and indices will be omitted when obvious from the context. Let ⟨X⟩ρ ≡ ⟨ρX⟩ϕ,z/ ⟨ρ⟩ϕ,z be the density weighted average of X. We define the fluctuating Reynolds stress tensor by 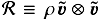 , where
, where 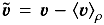 . The Maxwell stress tensor is defined as ℳ ≡ −B ⊗ B, and we define the sum
. The Maxwell stress tensor is defined as ℳ ≡ −B ⊗ B, and we define the sum 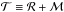 . We normalize these quantities by the local, vertically averaged pressure; although the flow might not be turbulent, we use the same notation as Shakura & Sunyaev (1973):
. We normalize these quantities by the local, vertically averaged pressure; although the flow might not be turbulent, we use the same notation as Shakura & Sunyaev (1973): 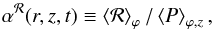 (8)and similarly for αℳ and
(8)and similarly for αℳ and 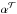 separately. The average radial mass flux can be deduced from the conservation of angular momentum (Balbus & Papaloizou 1999):
separately. The average radial mass flux can be deduced from the conservation of angular momentum (Balbus & Papaloizou 1999): ![\begin{eqnarray} \begin{split} \Sigma \brac{v_r}_{\rho} &\simeq -\frac{1}{\partial_r \left[ r \brac{v_{\varphi}}_{\varphi,z}\right]} \left( \frac{1}{r} \partial_r \left[2 r^2 H(r) \brac{\mathcal{T}_{r\varphi}}_{\varphi,z}\right] - r \left[ \brac{\mathcal{T}_{z\varphi}}_{\varphi}\right]_{-H}^{+H} \right) \\ &\equiv \tau_r + \tau_{z}, \label{eqn:accretor} \end{split} \end{eqnarray}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq115.png) (9)where Σ(r) ≡ 2H(r)⟨ρ⟩ϕ,z is the mass surface density, τr is the mass accretion rate due to to the radial transport of angular momentum, and τz the mass accretion rate due to angular momentum extracted by a wind through the surfaces z = ± H(r). We compute the wind mass loss rates through spherical shells at the outer simulation radius Rout in both hemispheres separately:
(9)where Σ(r) ≡ 2H(r)⟨ρ⟩ϕ,z is the mass surface density, τr is the mass accretion rate due to to the radial transport of angular momentum, and τz the mass accretion rate due to angular momentum extracted by a wind through the surfaces z = ± H(r). We compute the wind mass loss rates through spherical shells at the outer simulation radius Rout in both hemispheres separately: 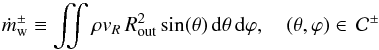 (10)and the total mass lost in the wind per unit time is
(10)and the total mass lost in the wind per unit time is 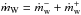 . We quantify the net toroidal magnetic flux through the disk with
. We quantify the net toroidal magnetic flux through the disk with 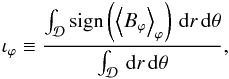 (11)so that ιϕ = ± 1 when a poloidal section of the disk is threaded by positive/negative toroidal field only, and zero when both polarities occupy the same area over this plane. We define
(11)so that ιϕ = ± 1 when a poloidal section of the disk is threaded by positive/negative toroidal field only, and zero when both polarities occupy the same area over this plane. We define 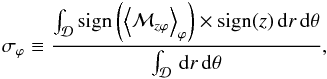 (12)such that σϕ> 0 when the angular momentum flux is directed from the disk to the corona in both hemispheres. The symmetry coefficients ιϕ and σϕ are analogous to the zeroth and first Fourier coefficients of Bϕ(z), respectively related to the net flux
(12)such that σϕ> 0 when the angular momentum flux is directed from the disk to the corona in both hemispheres. The symmetry coefficients ιϕ and σϕ are analogous to the zeroth and first Fourier coefficients of Bϕ(z), respectively related to the net flux 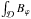 , and to the phase of the large-scale fluctuations of Bϕ(z).
, and to the phase of the large-scale fluctuations of Bϕ(z).
 |
Fig. 1 Northern half of the computational grid; from the midplane to the pole: deep disk region (dark blue), disk surface region (cyan), disk-corona transition layer (yellow) and corona (red). |
3. Method
3.1. Numerical scheme
We use the finite-volume code PLUTO (Mignone et al. 2007) to integrate Eqs. (3)to (5)in time. The simulations are either three-dimensional or axisymmetric two-dimensional. The conservative variables are evolved via an explicit second order Runge-Kutta scheme. Parabolic terms are also included explicitly; this and the dispersive Hall whistler waves introduce strong constraints on the admissible timesteps satisfying the Courant–Friedrichs–Lewy (CFL) criterion. The CFL constraint due to the Keplerian velocity field is weak in comparison, so we do not activate the FARGO orbital advection scheme (Mignone et al. 2012). Inter-cell fluxes are computed with a modified HLL Riemann solver, including the Hall drift in a conservative manner (Lesur et al. 2014). We use a piecewise linear space reconstruction to estimate the Godunov fluxes at cell interfaces, with the Van Leer slope limiter. The solenoidal condition ∇·B = 0 for the magnetic field is maintained to machine precision by the constrained transport method (Evans & Hawley 1988).
3.2. Computational domain and grid
The computational domain is defined in spherical geometry by (R,θ) ∈ [1,10] × [π/ 2−θ0,π/ 2 + θ0], with the extremal polar angle θ0 ≡ 20 (h/r) ≈ π/ 3. We found no significant benefit from increasing this polar range toward the poles but additional numerical difficulties. The hydrostatic equilibrium has an excessively low density in this region, and is numerically unstable. The equilibrium velocity field is also very slow; with very little inertia, spurious radial in-/out-flows develop, with high velocities and associated shear ∂θvR, disturbing the rest of the corona.
 |
Fig. 2 Vertical profiles in runs R1–P4 (from 1 au to 10 au, with weak Bz> 0) at r = 5r0 = 5 au: initial (solid blue) and final (dashed green at 300T0) ionization fractions |
The polar interval is split into several ranges, as illustrated in Fig. 1. The deepest 4h are meshed with 64 uniform grid cells (dark blue region). The remaining range, from two to twenty scale heights (cyan + yellow + red), is meshed with 64 “stretched” cells, increasingly larger as we go to the polar boundary. This separation allows us to properly resolve the small-scale dynamics of the disk while not over-resolving the large volume of the corona.
The radial interval is meshed with a logarithmic grid of 512 cells, i.e., the increment δr is proportional to the local radius r. This grid gets coarser as we go from the inner to the outer radial boundary, keeping a constant aspect ratio of grid cells at a given polar angle, and thus a constant numerical resolution per scale height. With this radial range, the initial mass in the disk region is always 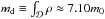 in code units.
in code units.
Three-dimensional runs have an azimuthal extension ϕ ∈ [0,π/ 2] to reduce computational cost compared to a full 2π disk. They are meshed with 128 uniformly distributed azimuthal cells.
3.3. Initial, boundary and internal conditions
We present here only the qualitative features of our numerical setup, and refer the reader to Appendices A to D for the details.
We initialize a cold disk plus warm corona hydrodynamic equilibrium. This thermodynamical configuration is held fixed during the simulation. A proper treatment of the thermodynamics would imply coupling the dynamics to radiative heating due to non-thermal radiation (typically X-rays and extreme UV) which is beyond the scope of this paper. We however motivate our temperature structure from full-blown radiative transfer calculations (e.g. Aresu et al. 2011). The temperature transition is smoothed at the disk surface (yellow transition layer in Fig. 1). The vertical profiles of temperature and ionization fraction at r = 5 au in a typical run are shown in Fig. 2. The overall ionization fraction does not evolve considerably over the duration of a simulation, but it is generally reduced at the disk surface due to the screening by the outflow. The transition from xe< 10-9 to xe> 10-5 is steep, but as desired, it is properly matched by our prescribed temperature increase. The initial magnetic field is vertical everywhere; its intensity decreases with cylindrical radius, so that the midplane β is constant with radius. The sign of the initial magnetic field is given with respect to the rotation axis; it can be either positive (Ω·B> 0) or negative (Ω·B< 0). We take Ω along + ez.
We impose a minimal outflow velocity through the polar and outer radial boundaries. Because the global wind tends to flow radially outward, outflow conditions at the inner radial boundary are inappropriate; we thus allow matter to flow into the computational domain from this side. Buffer zones are added in the vicinity of the radial boundaries to avoid spurious wave reflections and reduce the influence of the boundaries on the flow.
We limit the Alfvén velocity to the Keplerian velocity at the inner disk radius, vA ≤ v0 by artificially increasing the density in the concerned cells. This cap occasionally affects a few percent of the corona region. We relax the temperature toward its initial distribution over a characteristic time of 1/10Ω, so that the flow is locally isothermal to a good approximation.
 |
Fig. 3 Vertical profiles of dimensionless numbers characterizing non-ideal effects in the initial conditions at r = 5 au (left panel) and r = 50 au (right panel): inverse of the ambipolar Elsasser number |
We draw in Fig. 3 the initial profiles of dimensionless numbers characterizing non-ideal effects. The ambipolar Elsasser number ΛA and ohmic Reynolds number ℛO are defined by 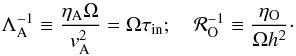 (13)These numbers do not depend on the magnetic field. Their radial distribution are comparable to those derived by Simon et al. (2015; see their Fig. 1). Two procedures are applied to non-ideal coefficients deduced from the ionization fraction, as described in Appendix D:
(13)These numbers do not depend on the magnetic field. Their radial distribution are comparable to those derived by Simon et al. (2015; see their Fig. 1). Two procedures are applied to non-ideal coefficients deduced from the ionization fraction, as described in Appendix D:
-
1.
We reduce diffusivity coefficients in the corona, progressivelyfrom z ≳ 3h to z ≲ 8h to account for the fact that the gas should become fully ionized in the corona.
-
2.
We restrict the intensity of ohmic diffusion, the Hall effect and ambipolar diffusion to avoid extremely small time steps. This restriction effectively affects the Hall effect below 2.3r0, and ambipolar diffusion only in runs with the highest magnetization β = 5 × 102.
4. Results
We list in Table 2 the parameters of the runs presented in this paper. Runs are labeled according to their inner radius (R1 at r0 = 1 au, R10 at r0 = 10 au) and initial magnetic field (P for Ω·B> 0, M in the opposite case, followed by the magnitude of the midplane beta). Three dimensional runs are listed at the bottom, the rest being two-dimensional axisymmetric simulations. All axisymmetric runs are integrated over 1000T0, corresponding to approximately 32 orbits at the outer radius. Run 3D-R1-P4 is evolved for 300T0, and the two other 3D runs for 200T0 only. It should be pointed out that each simulation shows a long-term (secular) evolution, where the large-scale configuration evolves over hundreds of local orbits.
The main scalar diagnostics are gathered in Table 3, averaged over representative time intervals. We describe the properties of our reference simulation in Sect. 4.1. This run is not generic in every aspect, so we characterize a variety of other processes in the following sections. In Sect. 4.2, we examine the magnetic polarity dependence introduced by the Hall drift. The properties of the wind in a warm corona are described in Sect. 4.3. In Sect. 4.4, we presents disks in which the vertical flux of angular momentum causes a large-scale meridional circulation, with no net mass accretion. Section 4.5 describes a vertical symmetry breaking, leading to a one-sided magnetic ejection. Section 4.6 is dedicated to a self-organization process leading to the formation of zonal flows. Finally, our set of simulations is considered as a whole for discussion in Sect. 5.
Global parameters for the runs presented in this paper.
Results for the runs presented in this paper.
4.1. Fiducial case
4.1.1. Overview of the disk dynamics
We show in Fig. 4 the instantaneous state of run R10-M3-C2 after 200 inner orbits of integration time (6 outer orbits). The toroidal magnetic field Bϕ changes sign at the midplane, and decreases smoothly with height in the corona. It also changes sign with radius near r ≈ 2.5r0. This change of sign occurs near the inner radial boundary, where the magnetic field follows an inward-pointing wind. This inward orientation of the wind is likely influenced by our outflow polar boundary conditions.
To this magnetic field is associated a flux of angular momentum ℳ·eϕ = −BϕB (purple arrows in the disk of Fig. 4). In the outer half of the disk, this flux is oriented from the midplane toward the corona. The velocity field is organized, with magnitudes reaching four times the local sound speed. In the inner half of the disk, the flux of angular momentum is directed from the disk surface toward its midplane. In this half, the corona is turbulent, with no signature of organized ejection.
 |
Fig. 4 Snapshot of run R10-M3-C2 (fiducial) at t = 200T0, showing the toroidal magnetic field in color background (blue to red), the poloidal velocity field in units of local sound speed (green arrows in the corona), and the orientation of the angular momentum flux caused by magnetic stress (purple arrows in the disk); ⟨Bz⟩ < 0 in this case. |
The length scale of magnetic field variations is comparable to the disk extent, both in the vertical and radial direction. Its characteristic dynamical time is counted in hundreds of local orbits, while the fluid may be streaming at near sonic velocities. The evolution of the magnetic field in the disk may therefore be considered as secular with respect to accretion and ejection. Given a time window, we can decompose the magnetic field in a time and azimuthally averaged component ⟨B⟩ϕ,t plus a fluctuating component 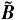 . Under this decomposition, the average magnetic stress is split into two terms:
. Under this decomposition, the average magnetic stress is split into two terms: 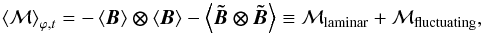 (14)representing a laminar plus a fluctuating contribution to ℳ. We compute the ratio of laminar to total magnetic stress over 30T0 (≈one outer orbit), average it over the poloidal surface of the disk, and find that it exceeds ℳlaminar/ ⟨ℳ⟩ > 90% for every run. Therefore, the magnetic stress in the disk is not due to a turbulent component, but is rather a quasi-steady (laminar) stress. The variability near the inner radius is likely caused by the outflow polar boundary conditions.
(14)representing a laminar plus a fluctuating contribution to ℳ. We compute the ratio of laminar to total magnetic stress over 30T0 (≈one outer orbit), average it over the poloidal surface of the disk, and find that it exceeds ℳlaminar/ ⟨ℳ⟩ > 90% for every run. Therefore, the magnetic stress in the disk is not due to a turbulent component, but is rather a quasi-steady (laminar) stress. The variability near the inner radius is likely caused by the outflow polar boundary conditions.
4.1.2. Disk vertical structure
We show in Fig. 5 a series of vertical profiles in the outer region of the fiducial run R10-M3-C2. In the top panel, we see that the deviations from Keplerian velocity become significant above z ≳ 2h. The radial velocity is the dominant component, with vR/vK ≈ 10%, corresponding to vR/cs ≈ 1 at z = 5h. The polar velocity vθ is second in magnitude, reaching vθ/vK ≈ 5%. The azimuthal velocity decreases by 5% in the corona, compared to the disk midplane value at the same radius. This last trend could be due to the outflow itself, or to the thermal pressure support against gravity in the corona.
The second panel shows that the horizontal magnetic field has an odd symmetry about the midplane. The initial vertical component is negative in this case, and it is the weakest component during the evolution of the simulation. The toroidal component is anti-correlated to the radial one, with a magnitude twenty to a hundred times higher in the disk. The location where Bϕ = Br = 0 corresponds to a thin current sheet.
The third panel shows the horizontal and vertical magnetic stresses. The horizontal magnetic stress ℳrϕ is positive everywhere. It is maximal at the disk surface, where 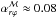 is ten times higher than in the midplane. The vertical stress ℳzϕ changes sign at the midplane, transporting angular momentum downward in the southern hemisphere and upward in the northern one. The large-scale magnetic field thus extracts angular momentum from the disk, and transports it toward the corona.
is ten times higher than in the midplane. The vertical stress ℳzϕ changes sign at the midplane, transporting angular momentum downward in the southern hemisphere and upward in the northern one. The large-scale magnetic field thus extracts angular momentum from the disk, and transports it toward the corona.
In the fourth panel of Fig. 5, the radial mass flux displays a negative peak at the current sheet (i.e., the midplane is accreting), and becomes positive at the base of the wind z ≳ 2h. The accretion stream is very narrow, and accurately fits the profile of radial electric current. We show instead the relative ion-electron radial velocity, vi−ve ≡ J/ne, which drives the Hall drift. Because this disk sees a net vertical magnetic field Bz< 0, the Lorentz force Fϕ ≃ −JrBz< 0 is extremal at the current sheet, thereby slowing matter and causing it to fall inward.
 |
Fig. 5 Vertical profiles in run R10-M3-C2 (fiducial), averaged in time from 200T0 to 600T0, and in spherical radius from 5r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of the vertical field Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses ℳrϕ and ℳzϕ, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and ion minus electron radial velocity, normalized by the local Keplerian velocity and the vertically averaged density. Fifth panel: ambipolar diffusivity ηA (solid blue), ohmic diffusivity ηO (dashed blue, increased by a factor 104 for visibility), and Hall length ℓH (green dots). |
The profile of radial electric current 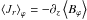 can be linked to the ambipolar diffusivity ηA, drawn in the bottom panel of Fig. 5. The magnetic energy dissipation rate due to ambipolar diffusion is
can be linked to the ambipolar diffusivity ηA, drawn in the bottom panel of Fig. 5. The magnetic energy dissipation rate due to ambipolar diffusion is 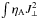 , where J⊥ is the electric current perpendicular to the local magnetic field. To minimize energy dissipation, this current must flow along the circuit with the smallest resistivity. Low density and strong field regions are poorly conducting due to ambipolar diffusion (cf. Eq. (2)). This enforces the current layer to be localized near the midplane and near the current sheet, where ηA takes its smallest value. Ohmic resistivity is unimportant in this region, making ambipolar diffusion the dominant dissipation process. The presence of dust grains should not alter this ordering in the outer regions of protoplanetary disks (see Fig. 1 of Simon et al. 2015). With the present values of ℓH and B0, the region below z ≲ 2h is stable with respect to the Hall-Shear instability (HSI, Balbus & Terquem 2001; Kunz 2008).
, where J⊥ is the electric current perpendicular to the local magnetic field. To minimize energy dissipation, this current must flow along the circuit with the smallest resistivity. Low density and strong field regions are poorly conducting due to ambipolar diffusion (cf. Eq. (2)). This enforces the current layer to be localized near the midplane and near the current sheet, where ηA takes its smallest value. Ohmic resistivity is unimportant in this region, making ambipolar diffusion the dominant dissipation process. The presence of dust grains should not alter this ordering in the outer regions of protoplanetary disks (see Fig. 1 of Simon et al. 2015). With the present values of ℓH and B0, the region below z ≲ 2h is stable with respect to the Hall-Shear instability (HSI, Balbus & Terquem 2001; Kunz 2008).
4.1.3. Mass and momentum fluxes
We draw in Fig. 6 the radial profiles of stress in our fiducial run R10-M3-C2. The horizontal Maxwell stress ℳrϕ is positive at all radii, transporting angular momentum radially outward, with 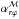 increasing from 10-2 to 10-1 from 10 au to 100 au. The vertical component ℳzϕ is positive beyond 2.5r0, transporting angular momentum from the disk to the corona. The fact that ℳϕz < 0 in the inner region is possibly related to our polar outflow boundary conditions. The Reynolds stress
increasing from 10-2 to 10-1 from 10 au to 100 au. The vertical component ℳzϕ is positive beyond 2.5r0, transporting angular momentum from the disk to the corona. The fact that ℳϕz < 0 in the inner region is possibly related to our polar outflow boundary conditions. The Reynolds stress 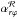 is negative for r ≳ 4.6r0. This is because above z> 1h, the velocity fluctuations
is negative for r ≳ 4.6r0. This is because above z> 1h, the velocity fluctuations 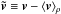 display
display  and
and  . Because | ℳrϕ | > 10 | ℛrϕ |, we will focus on the Maxwell stress for transport-related processes.
. Because | ℳrϕ | > 10 | ℛrϕ |, we will focus on the Maxwell stress for transport-related processes.
 |
Fig. 6 Radial profiles of normalized stress in R10-M3-C2 (fiducial), averaged in time between 200T0 and 600T0. The radial components of Maxwell (red dots) and Reynolds (dashed blue) are averaged over the disk height, whereas the vertical Maxwell stress (solid green) is measured at the disk surface z = ± H. |
The absence of correlation 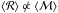 , so as the fact that ⟨ℛ⟩ϕ,z< 0, are discrepant with a state of MRI turbulence (Pessah et al. 2006). It was mentioned in Sect. 4.1.1 that the flow cannot be considered as turbulent, and that there is no clear spatial scale separation between the magnetic structures and the entire disk. For these reasons, the α viscosity prescription should not be applied in this context (Balbus & Papaloizou 1999). However, conservation of angular momentum still applies and we can use Eq. (9) to compute the accretion rate separately caused by radial and vertical angular momentum fluxes; this decomposition is represented in Fig. 7. We find that the vertical transport of angular momentum τz is the main driver of accretion. Conversely, the radial contribution τr oscillates about zero and causes no accretion on average. We recall that it does not contradict the presence of a significant radial stress (cf. Fig. 6) since accretion is controlled by the stress divergence. Finally, we find the average mass flux in this box is Σ⟨vr⟩ρ ≈ −4 × 10-6 in code units, corresponding to an average accretion rate ṁr ≡ | 2πrΣ⟨vr⟩ρ | ≈ 1.1 × 10-7M⊙ yr-1 at 50 au around a solar-mass star.
, so as the fact that ⟨ℛ⟩ϕ,z< 0, are discrepant with a state of MRI turbulence (Pessah et al. 2006). It was mentioned in Sect. 4.1.1 that the flow cannot be considered as turbulent, and that there is no clear spatial scale separation between the magnetic structures and the entire disk. For these reasons, the α viscosity prescription should not be applied in this context (Balbus & Papaloizou 1999). However, conservation of angular momentum still applies and we can use Eq. (9) to compute the accretion rate separately caused by radial and vertical angular momentum fluxes; this decomposition is represented in Fig. 7. We find that the vertical transport of angular momentum τz is the main driver of accretion. Conversely, the radial contribution τr oscillates about zero and causes no accretion on average. We recall that it does not contradict the presence of a significant radial stress (cf. Fig. 6) since accretion is controlled by the stress divergence. Finally, we find the average mass flux in this box is Σ⟨vr⟩ρ ≈ −4 × 10-6 in code units, corresponding to an average accretion rate ṁr ≡ | 2πrΣ⟨vr⟩ρ | ≈ 1.1 × 10-7M⊙ yr-1 at 50 au around a solar-mass star.
We find that τr ≈ 0 in all our simulations, meaning that the radial flux of angular momentum is divergence-free. This is a fortuitous consequence of our initial Σ(r), β(r), etc. We will therefore focus on the vertical transport of angular momentum.
 |
Fig. 7 Accretion in the disk region of run R10-M3-C2 (fiducial), between r ∈ [3,8]r0; the actual mass flux (solid black) is decomposed into radial (dashed blue) and vertical (red dots) torques as explicited in Eq. (9); the sum is drawn (dashed cyan) to validate this decomposition. |
4.1.4. Cold, magnetized wind
We have shown that a wind is launched by the outer half of the disk, where the Maxwell stress transports angular momentum from the disk to the corona. We qualify these winds as “cold” since the ratio of sound speeds between the disk and the corona is set to k = 2 (which corresponds to a factor 4 in temperature).
To characterize these winds, we first look at the dynamics of a fluid element. We average every quantity in azimuth and time, and compute the characteristic velocities along a streamline in the poloidal plane. We recall the definition of the slow (minus sign) and fast (plus sign) magnetosonic waves velocity: 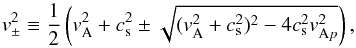 (15)where the index p stands for the poloidal component of a vector. These velocities are relevant only in the ideal MHD regime.
(15)where the index p stands for the poloidal component of a vector. These velocities are relevant only in the ideal MHD regime.
As apparent in Fig. 8, the fluid poloidal velocity monotonically increases, and crosses all characteristic MHD velocities. Surprisingly, the fast-magnetosonic point is located right before the domain boundary. The same is true in several, but not all runs (see for example Fig. 13). This fact was already observed in stratified, shearing-box simulations (Fromang et al. 2013). It indicates that our boundary conditions are still, somehow, constraining the flow structure down to the disk in this run.
 |
Fig. 8 Velocities projected on a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, and normalized by the Keplerian velocity at the launching radius vK0; flow velocity v (solid black), sound speed cs (dashed orange), Alfvén velocity vA (dashed green), slow magnetosonic speed v− (dashed blue) and fast magnetosonic speed v+ (red dots). |
The mass transported by the wind is computed via Eq. (10). We estimate its average value ṁW ≈ 2.6 × 10-4 in code units, corresponding to approximately 2.3 × 10-7M⊙ yr-1 for this run.
We compute separately the acceleration ap ≡ vp∂pvp, and the acceleration caused by the forces F along the streamline. These include the thermal pressure gradient, the Lorentz force, and the inertial force due to gravitational and centrifugal accelerations: 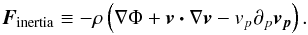 (16)We present the resulting accelerations F/ρ in Fig. 9, normalized by the Keplerian value
(16)We present the resulting accelerations F/ρ in Fig. 9, normalized by the Keplerian value 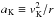 at the streamline base. The sum of the forces decently reproduces the true acceleration in spite of the variability of the flow. The thermal pressure gradient helps accelerating the flow, but it is significantly weak than the Lorentz force. The latter barely compensates the inertial term, resulting in an overall small wind acceleration ap/aK0 ≲ 2%.
at the streamline base. The sum of the forces decently reproduces the true acceleration in spite of the variability of the flow. The thermal pressure gradient helps accelerating the flow, but it is significantly weak than the Lorentz force. The latter barely compensates the inertial term, resulting in an overall small wind acceleration ap/aK0 ≲ 2%.
 |
Fig. 9 Acceleration along a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, normalized by the Keplerian acceleration aK0 at the streamline base. The sum of the different forces (dashed cyan) is shown to validate this decomposition. |
We split the specific angular momentum of a fluid element into its matter and magnetic contributions: 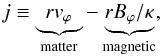 (17)where κ ≡ ρvp/Bp is the ratio of mass over magnetic flux along the streamline. Both j and κ should be invariant along streamlines for stationary, axisymmetric, ideal MHD flows (Chandrasekhar 1956; Pelletier & Pudritz 1992). We show in Fig. 10 that the total specific angular momentum j is approximately constant above z ≳ 5h. The magnetic torque transfers angular momentum back to the outflowing plasma, leading to an increase of the kinetic content up to the domain boundary. This demonstrates that the wind is magnetocentrifugally accelerated. Below 5h, the variations of j indicate that the average flow does not behave as an ideally conducting plasma. This is caused by ambipolar diffusion above the disk surface. It should be noted that the outflow is already super-Alfvénic when entering the ideal MHD regime z ≳ 5h (cf. Fig. 8). As a consequence, only the sonic and fast-magnetosonic critical points can impose regularity conditions on the outflow (Ferreira & Pelletier 1995).
(17)where κ ≡ ρvp/Bp is the ratio of mass over magnetic flux along the streamline. Both j and κ should be invariant along streamlines for stationary, axisymmetric, ideal MHD flows (Chandrasekhar 1956; Pelletier & Pudritz 1992). We show in Fig. 10 that the total specific angular momentum j is approximately constant above z ≳ 5h. The magnetic torque transfers angular momentum back to the outflowing plasma, leading to an increase of the kinetic content up to the domain boundary. This demonstrates that the wind is magnetocentrifugally accelerated. Below 5h, the variations of j indicate that the average flow does not behave as an ideally conducting plasma. This is caused by ambipolar diffusion above the disk surface. It should be noted that the outflow is already super-Alfvénic when entering the ideal MHD regime z ≳ 5h (cf. Fig. 8). As a consequence, only the sonic and fast-magnetosonic critical points can impose regularity conditions on the outflow (Ferreira & Pelletier 1995).
The magnetic contribution to j is only 0.4j0, corresponding to a magnetic lever arm λ ≈ 1.4, much smaller than expected from strongly magnetized jets (see Fig. 4 of Ferreira 1997). For a magnetic lever arm smaller than 3/2, the Bernoulli invariant of a cold flow should be negative (Casse & Ferreira 2000); this is indeed the case in this simulation. It follows that the outflow cannot escape the gravitational field on its own energy content when it reaches the domain boundary. The outflow can have ℬ < 0, and still be both stationary and super fast-magnetosonic. Effectively, ℬ < 0 corresponds to an outflow which is gravitationally bound when z → ∞, but it is not necessarily bound for the gravitational potential restricted to the computation box.
 |
Fig. 10 Angular momentum along a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, normalized to its value at the streamline base; the total angular momentum (solid black) is decomposed into matter (dashed blue) and magnetic (red dots) components as explicited in Eq. (17). |
4.2. Hall and magnetic field polarity
It is known that the Hall drift discriminates between the two polarities of the vertical magnetic field (Balbus & Terquem 2001). When Ω·B> 0, the Hall drift acts to enhance angular momentum transport; in the opposite case Ω·B< 0, the Hall drift tends to stabilize the flow, and greatly reduce angular momentum transport (Lesur et al. 2014).
We draw in Fig. 11 the vertical profiles of horizontal stress ℳrϕ for the two orientations of the initial magnetic field. When Bz> 0 (run 3D-R1-P4), there are three regions of important magnetic stress: the midplane and the two disk-corona interfaces. The midplane stress reaches 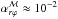 and decreases exponentially fast with height. Near z ≈ 2.7h, the surface stress becomes dominant, and increases up to z ≈ H, where it reaches
and decreases exponentially fast with height. Near z ≈ 2.7h, the surface stress becomes dominant, and increases up to z ≈ H, where it reaches 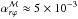 . This profile is similar to what was found in local shearing-box simulations (see Fig. 13 of Lesur et al. 2014). In the opposite case Bz< 0 (run 3D-R1-M4), the surface stress is essentially the same, but the midplane stress is now
. This profile is similar to what was found in local shearing-box simulations (see Fig. 13 of Lesur et al. 2014). In the opposite case Bz< 0 (run 3D-R1-M4), the surface stress is essentially the same, but the midplane stress is now 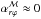 .
.
The vertical distribution of ℓH is overlaid in Fig. 11. It reaches ℓH/h ~ 1 deep in the disk, and decreases rapidly with height. In run 3D-R1-M4, below z ≲ 2h, the combination of a strong Hall length and a negative vertical magnetic field stabilizes the disk with respect to the HSI. At z ≳ 3h, the Hall drift becomes negligible regarding the linear stability of the flow, and we retrieve a polarity-independent system.
 |
Fig. 11 Vertical profiles of horizontal magnetic stress, normalized by the vertically averaged pressure in the disk ℳrϕ/ ⟨P⟩z in runs 3D-R1-P4 (solid blue, Ω·B> 0) and 3D-R1-M4 (dashed red, Ω·B< 0), averaged in time over 50T0 and radially from 3r0 to 6r0; the green dots show the average ratio ℓH/h in this same region. |
The volume-averaged values of 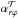 differ only by a factor two between run R1-P3 (R10-P3), and the equivalent run with a reversed field R1-M3 (resp. R10-M3, cf. Table 3). This estimated
differ only by a factor two between run R1-P3 (R10-P3), and the equivalent run with a reversed field R1-M3 (resp. R10-M3, cf. Table 3). This estimated 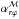 includes the disk up to z ≤ H, so part of it is due to the polarity-independent surface stress. Also, the midplane is not magnetically dead when Bz< 0 and the initial magnetization β ≤ 5 × 103 (see third panel of Fig. 5). As the intensity of the net magnetic flux increases, so does the magnetic stress at the disk surface, and the ambipolar diffusivity. The magnetic field can then diffuse, from the surface to the midplane, over a few tens of local orbits (cf. Sect. 5.1). The surface over midplane stress contrast is smaller at larger radii, where the Hall drift is weaker (see fifth panel of Fig. 5).
includes the disk up to z ≤ H, so part of it is due to the polarity-independent surface stress. Also, the midplane is not magnetically dead when Bz< 0 and the initial magnetization β ≤ 5 × 103 (see third panel of Fig. 5). As the intensity of the net magnetic flux increases, so does the magnetic stress at the disk surface, and the ambipolar diffusivity. The magnetic field can then diffuse, from the surface to the midplane, over a few tens of local orbits (cf. Sect. 5.1). The surface over midplane stress contrast is smaller at larger radii, where the Hall drift is weaker (see fifth panel of Fig. 5).
We conclude that ℳrϕ ≈ 0 in the midplane only when the midplane is Hall-shear stable, and the intensity of the background field is sufficiently weak. For stronger magnetic fields, the surface-driven torque can reach the midplane (see for example Wardle & Koenigl 1993; Salmeron et al. 2011).
4.3. Warm winds
We described the launching and acceleration of a cold, magnetized wind in our reference simulation with k = 2. In this section, we investigate the role of thermal pressure with a warmer corona. We consider a corona over disk temperature ratio of 36, i.e., a ratio of k = 6 in isothermal sound speed.
4.3.1. Overview
We show in Fig. 12 the average flow morphology in run R10-M3, initially threaded by a negative Bz< 0. The density in the disk has homogeneously decreased by 10%, maintaining its radial and vertical stratification profiles. Magnetic field lines are straight in the disk, as one can expect in a diffusion-dominated regime. In the inner regions of the corona, the field lines remain vertical or bend inward. Because the magnetic field is the weakest in these regions, it exerts no constraints on the fluid. The velocity field in the innermost region appears to be affected by our outflow polar boundary conditions.
The initial magnetic field has been substantially reduced for radii as far as 3r0, where positive magnetic flux has entered the domain from the inner radial boundary. Although this phenomenon is artificially caused by our boundary conditions, it calls for a dedicated study of the Hall-driven transport of magnetic flux in protoplanetary disks (Bai & Stone 2016). The outer corona displays a laminar structure. Field lines bend outward, with an inclination greater than 60° at the disk surface, favorable to magnetocentrifugal acceleration. The poloidal velocity and magnetic field lines are aligned in this region, consistently with a quasi-steady and ideal MHD wind. The average wind mass loss rate is ṁW ≈ 2.7 × 10-5 in code units. This corresponds to approximately 1.7 × 10-7M⊙ yr-1 at 100 au, comparable to our fiducial case despite the temperature difference.
 |
Fig. 12 Averaged flow poloidal map for run R10-M3 (from 10 au to 100 au, with Bz< 0) from 400T0 to 700T0; magnetic field lines are regularly sampled along the midplane, and the velocity field is indicated with green arrows over the background density field. |
We select a streamline in the poloidal plane, passing through (r = 7r0,z = 5h). The flow and the characteristic MHD velocities are projected on this streamline in Fig. 13. The increase in sound speed, from z = 3.7h to 4.7h, marks the disk-corona temperature transition. As for the fiducial, cold corona case (cf. Fig. 8), the slow-magnetosonic and Alfvén critical points are crossed at z ≈ 4h. The fast-magnetosonic critical point is now clearly within the computational domain. It is crossed by the outflow way before reaching the outer radial boundary, so the base of the wind should be causally disconnected from the boundary.
 |
Fig. 13 Same as Fig. 8 for a streamline passing through (r = 7r0,z = 5h) in run R10-M3, averaged from 400T0 to 700T0. The fast-magnetosonic point is clearly crossed within the computational domain. |
The magnetic field again contributes to 0.4j0 in the specific angular momentum along this streamline. According to steady-state MHD jet theory, a small magnetic lever arm λ ≈ 1.4 corresponds to an ejection efficiency ξ ≡ ∂log ṁW/∂log r ~ 1 (Ferreira & Pelletier 1993; Ferreira 1997). This is consistent with the high ratio of mass outflow over mass accretion rates observed in our simulation. In this case, there would be too much matter loaded into the wind to obtain a steady and trans-Alfvénic outflow without coronal heating (cf. Eq. (40) of Ferreira 1997).
4.3.2. Energy budget
We examine the energetics of the outflow by means of the Bernoulli invariant. Following Suzuki & Inutsuka (2009), we decompose the ideal MHD Poynting flux as: 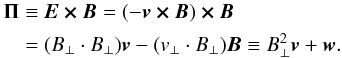 (18)The first term can be thought of as the advection of magnetic energy by the flow; the second term gives the wave-like transport of energy. Given a streamline, we can decompose the integral
(18)The first term can be thought of as the advection of magnetic energy by the flow; the second term gives the wave-like transport of energy. Given a streamline, we can decompose the integral 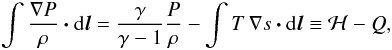 (19)respectively an enthalpy contribution minus a heating term. The first corresponds to the adiabatic work exerted by the fluid, whereas the second measures its variation of specific entropy s. By dotting Eq (4)with v, we can construct a quantity constant along stationary streamlines, the Bernoulli invariant:
(19)respectively an enthalpy contribution minus a heating term. The first corresponds to the adiabatic work exerted by the fluid, whereas the second measures its variation of specific entropy s. By dotting Eq (4)with v, we can construct a quantity constant along stationary streamlines, the Bernoulli invariant: 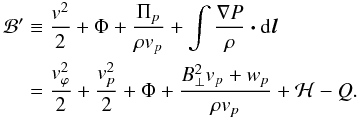 (20)Because Q keeps an integral form, the value of ℬ′ along a streamline depends on the choice of integration bounds. We choose to subtract from ℬ′ the heat input
(20)Because Q keeps an integral form, the value of ℬ′ along a streamline depends on the choice of integration bounds. We choose to subtract from ℬ′ the heat input 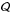 evaluated at the domain boundary: ℬ ≡ ℬ′ + Qend. With this definition, a fluid element having ℬ > 0 is able to escape the gravitational potential on its own energetic content, without additional heating past the domain boundary.
evaluated at the domain boundary: ℬ ≡ ℬ′ + Qend. With this definition, a fluid element having ℬ > 0 is able to escape the gravitational potential on its own energetic content, without additional heating past the domain boundary.
We draw the various contributions to ℬ along the streamline in Fig. 14. The poloidal component  keeps increasing, as already apparent in Fig. 13. The toroidal component
keeps increasing, as already apparent in Fig. 13. The toroidal component  is initially the main energy reservoir against gravity, and slowly decreases. This is because the fluid specific angular momentum rvϕ is approximately constant above z ≳ 5h, so vϕ decreases as 1 /r along the streamline. The wave-like Poynting flux
is initially the main energy reservoir against gravity, and slowly decreases. This is because the fluid specific angular momentum rvϕ is approximately constant above z ≳ 5h, so vϕ decreases as 1 /r along the streamline. The wave-like Poynting flux 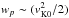 is strong at the disk surface z ≈ 3.2h, and most of it has been consumed at the end of the streamline. However, it is efficiently converted into kinetic energy only in the ideal-MHD region z ≳ 5h. The thermal contributions to the Bernoulli invariant, namely ℋ and
is strong at the disk surface z ≈ 3.2h, and most of it has been consumed at the end of the streamline. However, it is efficiently converted into kinetic energy only in the ideal-MHD region z ≳ 5h. The thermal contributions to the Bernoulli invariant, namely ℋ and 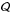 , both increase at the disk-corona transition. Beyond z ≳ 5.5h, the enthalpy ℋ decreases, while the heating
, both increase at the disk-corona transition. Beyond z ≳ 5.5h, the enthalpy ℋ decreases, while the heating 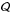 keeps increasing. The decrease in enthalpy corresponds to the adiabatic cooling of the fluid, exerting a mechanical work and thus contributing to the outflow acceleration. The increase in
keeps increasing. The decrease in enthalpy corresponds to the adiabatic cooling of the fluid, exerting a mechanical work and thus contributing to the outflow acceleration. The increase in 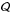 means that the fluid keeps receiving heat, because it is always colder than the prescribed temperature at a given location.
means that the fluid keeps receiving heat, because it is always colder than the prescribed temperature at a given location.
 |
Fig. 14 Contributions to the Bernoulli invariant ℬ (solid black) as explicited in Eq. (20), along a streamline passing through (r = 7r0,z = 5h) in run R10-M3, averaged from 400T0 to 700T0; the gravitational contribution is not shown. |
The final value of 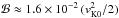 is positive in this case, so the outflow has the potential to escape from the gravitational field. We note that the heating
is positive in this case, so the outflow has the potential to escape from the gravitational field. We note that the heating 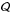 is necessary to make ℬ > 0. The quantity
is necessary to make ℬ > 0. The quantity 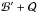 increases along the streamline, and it becomes positive at z ≈ 5.1h. In principle, we could stop heating above this height, and keep a potentially released flow.
increases along the streamline, and it becomes positive at z ≈ 5.1h. In principle, we could stop heating above this height, and keep a potentially released flow.
The analysis of the Bernoulli invariant suggests that magnetic acceleration is important only at the wind basis, whereas most of the remaining acceleration along the streamline is due to coronal heating. This association constitutes the key mechanism at the origin of the magnetothermal winds we observe in these simulations. This is an extension of the situation described by Casse & Ferreira (2000), with the important difference that the flow becomes super-Alfvénic in the non-ideal MHD zone.
4.3.3. Ejection mechanism
We examine the role of coronal heating in the lifting and acceleration of material along a streamline in run R10-M3. The acceleration of a fluid element and its decomposition into pressure, Lorentz and inertial forces are drawn in Fig. 15. The true acceleration ap is about 15% stronger than the sum reconstructed from the averaged forces. This bias may be due to the correlated fluctuations of density with the Lorentz force, or between velocity components in the inertial term. We verified that it is entirely removed in runs showing better stationarity properties.
At the surface of the disk z ≲ H, the streamline is nearly vertical. In this direction, the inertial potential precisely cancels the vertical pressure gradient, as required from the initial, hydrostatic equilibrium. In the transition region z/h ∈ [3.7,4.7], matter from the disk is being pushed down toward the midplane by the hot gas at the base of the corona. The inertial acceleration is negligible in this region, and it is the Lorentz force that provides the kick lifting matter up into the hotter wind region.
Because the streamlines strongly bend outward at z> 4.7h, the radial pressure gradient becomes favorable to the outflow, whereas the Lorentz force is negligible in this region. For z> 6h, the acceleration produced by thermal pressure gradients decreases, whereas magnetic acceleration increases again. This is generic to all magnetically-ejecting runs with a warm corona.
 |
Fig. 15 Same as Fig. 9 in run R10-M3, averaged in time between 400T0 and 700T0, with a streamline passing through (r = 7r0,z = 5h). |
We conclude that in our warm corona simulations, mass is still loaded into the wind by the Lorentz force. The vertical temperature gradient acts against the launching of a wind. The radial temperature gradient bends the magnetic field lines, and causes the outward acceleration of the flow along these lines.
4.4. Non-accreting disks
Some of our simulations do not exhibit accretion streams in the midplane. In this section, we describe the opposite configurations, where the radial mass flux is directed outward in the midplane and inward at the disk surface, resulting in a large-scale meridional circulation (Fromang et al. 2011). We focus on run R1-P4-C4, which adopted this configuration over the entire duration of the simulation. Although R1-P4-C4 differs from our fiducial case R10-M3-C2 by four control parameters, only the orientation of the net magnetic field seems to affect this outcome in our simulations (cf. Sect. 5.1).
4.4.1. Overview
We show in Fig. 16 the morphology of the flow in run R1-P4-C4. We note several differences with our fiducial case (cf. Fig. 4). First, the entire corona exhibits a disorganized velocity structure. There are no signatures of acceleration above the disk, and the flow reaches moderate velocities. Second, the toroidal magnetic field does not expand to the corona, but remains confined within the disk instead. Finally, the large-scale magnetic field transport angular momentum from the disk surface to its midplane.
 |
Fig. 16 Snapshot of run R1-P4-C4 (from 1 au to 10 au, with weak Bz> 0) at t = 1000T0, showing the toroidal magnetic field in color background (blue to red), the poloidal velocity field in units of local sound speed (green arrows in the corona), and the orientation of the angular momentum flux caused by magnetic stress (purple arrows in the disk). The orientation of the angular momentum flux is reversed compared to the fiducial, accreting case. |
As mentioned in Sect. 4.1.1, studying this configuration isolately makes sense because magnetic structures evolve over long time scales. However, the accreting property can vary in space (cf. Sect. 4.4.4), and in time for a given simulation.
4.4.2. Vertical structure
We show in Fig. 17 the vertical structure of the flow in run R1-P4-C4. In the first panel, the radial velocity is negative at the disk surface, where it reaches vR/cs ≈ −0.4. It becomes positive above z ≈ 4.3h, with vR/vK ≈ 5%, two times smaller than the fiducial case. The azimuthal velocity drops at z ≈ H, where the gas is heated. The polar velocity vθ is negligible up to z ≈ 4.3h, beyond which it increases to 2% of vK, again small compared to the fiducial case (cf. Fig. 5). This outflow is launched twice higher than in the fiducial case, near the temperature transition at z ≈ H, suggesting a predominantly thermal wind launching.
The second panel shows that the toroidal magnetic field is dominant in the disk, twenty to eighty times greater than the radial one. Unlike the fiducial accreting case, the toroidal field Bϕ vanishes at z ≈ 4.7h, and does not expand to the corona.
The resulting vertical stress ℳzϕ is negligible in the corona. The disk thus receives no angular momentum from the corona, and a fortiori from our polar boundary conditions. Within the disk, the Maxwell stress ℳzϕ is positive in the southern hemisphere, and negative in the northern one. This induces a flux of angular momentum from the disk surface toward its midplane.
The fourth panel shows that mass is now streaming outward in the midplane, and inward at the surface. This is consistent with the idea that angular momentum is extracted from the surface, and provided to the midplane by magnetic stress. We emphasize that the net radial mass flux is approximately zero through this meridional circulation. The disk does not receive angular momentum from the corona, and mass accretion is solely caused by the radial flux of angular momentum, τr ≈ 0, as shown in Fig. 7.
 |
Fig. 17 Vertical profiles in run R1-P4-C4, averaged in time from 400T0 to 1000T0, and in spherical radius from 5r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of the vertical field Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and electron minus ion radial velocity, normalized by the local Keplerian velocity and the vertically averaged density. |
The property of being accreting or not essentially depends on the sign of ℳzϕ ≡ −BzBϕ. Because the disk is threaded by a net vertical magnetic field, and because the flow is laminar, the orientation of the angular momentum flux is given by the sign of Bϕ in both hemispheres. We will refer to this as the vertical phase of the toroidal field. When Bϕ has a non-accreting phase, the radial velocity is oriented outward in the midplane, and inward at the disk surface. The radial pressure gradient is negative in the corona, so it opposes the launching of a wind directed inward. This imposes a meridional circulation within the disk.
The pressure gradient forces the radial velocity to change sign above z ≳ H. The resulting outflow is thermally driven. It reaches moderate velocities, and it is not organized on large scales. We were not able to reconstruct streamlines leaving the disk surface, because of the time-variability of the flow in the corona. We presume that the outflow mass loading results from turbulence above the accretion layers. Forcing an outflow velocity at the domain boundaries greatly improved the numerical stability of our setup in such configurations.
We measured the phase of Bϕ in every run via σϕ, as defined by Eq. (12). Runs having σϕ> 0 should be accreting, whereas σϕ< 0 corresponds to predominantly non-accreting configurations. Runs with σϕ ≈ 0 are the object of Sect. 4.5. Time-averaged values of σϕ for every runs are given in Table 3.
4.4.3. Magnetic equilibrium
We raise two questions regarding the magnetic equilibrium of the non-accreting configuration. First, if there is no outflow to remove toroidal magnetic flux, another process must be responsible for the saturation of the MRI. Second, because the corona rotates slower than the disk, the net vertical field should always exert a global torque on the disk, favoring the accreting configuration. To address these issues, we split the induction Eq. (5)into several terms, labeled by the associated physical process: ![\begin{eqnarray} \begin{split} \brac{\frac{\partial B_R}{\partial t}}_{\varphi} &= \frac{1}{R} \left( \cot(\theta) + \frac{\partial}{\partial_{\theta}} \right) \cdot \left[ \underbrace{\brac{v_R B_{\theta}}}_\text{stretch} - \underbrace{\brac{v_{\theta} B_{R}}}_\text{outflow} \right.\\ &\left.\quad -\underbrace{\brac{\id{\eta}{O} J_{\varphi}}}_\text{Ohm} -\underbrace{\brac{\id{\eta}{H} \left( J \times e_b \right)_{\varphi}}}_\text{Hall} - \underbrace{\id{\eta}{A} \left(\left( J \times e_b \right) \times e_b \right)_{\varphi}}_\text{ambipolar} \right] \label{eqn:split_br} \end{split} \\ \begin{split} \brac{\frac{\partial B_{\varphi}}{\partial t}}_{\varphi} &= \left( \frac{1}{R} + \frac{\partial}{\partial R} \right) \cdot \left[ \underbrace{ \brac{ v_{\varphi} B_R}}_\text{shear} -\underbrace{\brac{v_R B_{\varphi}}}_\text{advection} \right]\\ &\quad - \frac{1}{R} \frac{\partial}{\partial \theta} \left[ \underbrace{\brac{v_{\theta} B_{\varphi}}}_\text{outflow} - \underbrace{\brac{v_{\varphi} B_{\theta}}}_\text{stretch} \right] - \underbrace{\left( \nabla \times \brac{ \mathcal{E}_{\mathrm{O}, \mathrm{H}, \mathrm{A}}} \right)_{\varphi}}_\text{Ohm, Hall, ambipolar}, \label{eqn:split_bp} \end{split} \end{eqnarray}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq394.png) where the electromotive field ℰO,H,A contains the three non-ideal effects, as developped in Eq (21).
where the electromotive field ℰO,H,A contains the three non-ideal effects, as developped in Eq (21).
We represent in Fig. 18 these contributions to the induction of toroidal magnetic field ∂tBϕ. The ohmic and Hall induction terms are not shown for they are negligible in this case.
The sum of the outflow plus advection terms has a minor effect, located at z ≈ H. Deep in the disk, the shearing of BR is only balanced by ambipolar diffusion. At z ≈ 3.4h, where the toroidal Alfvén velocity is maximal, ambipolar diffusion transports the toroidal field toward the surface, and not toward the midplane. In the surface layers z ≈ H, we find a competition between the stretching of Bz and the shearing of BR. Since the stretching term favors an accreting phase for Bϕ, the non-accreting configuration sustains a counteracting BR at the surface.
 |
Fig. 18 Contributions to the induction of toroidal magnetic field in run R1-P4-C4, as explicited in Eq. (22), averaged in time from 400T0 to 1000T0 and in spherical radius from 5r0 to 8r0, normalized by the local Keplerian frequency and the local initial magnetic field. |
The same decomposition is performed for the radial component BR in Fig. 19. The ohmic contribution is negligible again, so we do not plot it. The Hall term is effective below z ≲ 2h, balanced by ambipolar diffusion. At the surface z ≳ 3h, the outflow term has a moderate amplitude, and we find a competition between ambipolar diffusion and the stretching of Bθ.
The region z< 2h is separated from the disk surface. Near the midplane, it is the HSI that causes the growth of horizontal magnetic field. Near the surface, the feedback loop corresponds to the MRI: the accretion layers stretch Bz into Br, which is sheared into Bϕ; the resulting stress ℳzϕ removes angular momentum from the surface, thereby enhancing the accretion layers. Ambipolar diffusion is responsible for the saturation of the HSI in the midplane, and of the MRI at the disk surface.
4.4.4. Coexistence of accreting and non-accreting regions
All the cases presented so far were relatively symmetric with respect to the disk midplane. In particular, the inward or outward mass streams were located near the midplane. Yet we have disks exhibiting both accreting and non-accreting behaviors at the same time. We show the radial transition between two different portions of the same disk in Fig. 20.
 |
Fig. 20 Same as Fig. 16 for run R1-P4 at t = 1000T0. The disk exhibits both an accreting (inner) and a non-accreting (outer) region. |
As mentionned in Sect. 4.1.2, the mass flux actually follows the Bϕ = 0 layer, where the electric current is extremal. The transition from an accreting to a non-accreting disk region necessarily comes with the current sheet reaching the surface of the disk. In a region where Bϕ has a non-accreting phase, there is no magnetized outflow, and Bϕ ≈ 0 above the disk. In this case, the mass flux follows closed circulation loops along the current sheet, inward at the surface and outward in the midplane. At the intersection with an accreting region, part of this mass flux is reoriented into the wind, and part of it goes to the midplane.
4.5. Vertical symmetry breaking
This section describes a spontaneous breaking of the up/down symmetry identified in our simulations. It is related to the emergence of a favored magnetic polarity over long time scales.
4.5.1. Overview
Within our stratified setup, the horizontal magnetic flux is free to leave the disk in the vertical direction. One polarity can be removed or amplified faster than the other, leaving the disk with only one sign of Bϕ. This was observed in stratified shearing-box simulations (Lesur et al. 2014; Bai 2015), but considered unlikely to be directly connected to a global flow geometry. Focusing on the horizontal magnetic field, we will refer to these as even configurations with respect to the disk midplane in opposition to states showing an odd symmetry.
Such a configuration is illustrated in Fig. 21 for run R1-M3. The entire disk sees Bϕ< 0; the Keplerian and Hall shears ensure that Br> 0 is also even about the midplane. In the inner half of the northern corona, the magnetic field lines do not guide the velocity field. Because the corona obeys ideal MHD, this implies that this part of the flow is turbulent, resulting in an effective “turbulent diffusion” for the time-averaged flow. On the contrary, the outflow in the southern corona is very laminar and stationary. A magnetic collimation effect is observed in this hemisphere.
 |
Fig. 21 Averaged flow poloidal map for run R1-M3 (from 1 au to 10 au, with moderate Bz< 0) from 800T0 to 1000T0; magnetic field lines are sampled along the midplane, and the velocity field is indicated with green arrows over the background toroidal field. The polar asymmetry and the absence of Bϕ sign reversal within the disk are obvious. |
4.5.2. Vertical structure
The vertical structure of run R1-M3 is represented in Fig. 22. A strong outflow is launched in the southern hemisphere, with vθ/vK ≈ 20% at z ≈ −8h. The toroidal velocity is higher than the local Keplerian value, down to z ≈ −6h. The outflow receives angular momentum via the Maxwell stress ℳzϕ, and transports mass at a rate 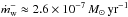 . Picking a streamline passing through (r = 6r0,z = −5h), its total angular momentum is 1.5 times larger than the Keplerian value at the wind base, it crosses the fast-magnetosonic velocity before reaching the domain boundary, and its Bernoulli invariant
. Picking a streamline passing through (r = 6r0,z = −5h), its total angular momentum is 1.5 times larger than the Keplerian value at the wind base, it crosses the fast-magnetosonic velocity before reaching the domain boundary, and its Bernoulli invariant 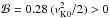 .
.
On the other side, the northern hemisphere displays the properties of a non-accreting disk (cf. Fig. 17). The radial velocity is oriented inward at the disk surface, and the outflow has a moderate velocity. The toroidal field Bϕ = 0 at z ≈ 4h, beyond which the vertical flux of angular momentum is essentially zero.
Because Bz and Bϕ keep the same sign within the disk, the vertical flux of angular momentum ℳzϕ is unidirectional. We find ℳzϕ ≈ 0 for z ≳ + 4h, and ℳzϕ< 0 below. The gradient ∂zℳzϕ thus takes angular momentum from the disk northern surface, and transports it toward the southern hemisphere. This causes both the radial flows at the disk surface, and the magnetic wind launching in the southern hemisphere. Since ℳzϕ ≈ 0 in the northern corona, the disk is not pumping angular momentum from the northern domain boundaries.
 |
Fig. 22 Vertical profiles in run R1-M3, averaged in time from 800T0 to 1000T0, and in spherical radius from 6r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and ion minus electron radial velocity, normalized by the local Keplerian velocity and average density. |
The fourth panel of Fig. 22 shows an accretion layer at the northern surface, and a decreting layer at the southern one. On average, the net mass flux is slowly accreting, with τz = (−4 ± 5) × 10-7. We have separated the southern and northern wind mass loss rates 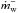 and
and 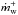 (cf. Eq. (10)). Table 3 confirms that
(cf. Eq. (10)). Table 3 confirms that  when ιϕ × sign(Bz) > 0, i.e., the magnetically ejecting side transports more mass.
when ιϕ × sign(Bz) > 0, i.e., the magnetically ejecting side transports more mass.
4.5.3. Secular evolution of vertical symmetries
We examine the onset of an even configuration in run R1-P2, which did not immediately choose a favored polarity. We draw in Fig. 23 the symmetry coefficients ιϕ and σϕ over time, respectively defined by Eqs. (11)and (12). ιϕ defines the average polarity of Bϕ in the disk, whereas σϕ characterizes Bϕ symmetry across the midplane, the ejecting configurations with accretion in the disk midplane corresponding to σϕ > 0.
During the first 100 T0, ιϕ ≈ 0 indicates that both polarities of Bϕ are equally present in the disk. The average phase of Bϕ evolves from an accreting configuration σϕ > 0 to a non-accreting one σϕ < 0 in this interval. From 100T0 to 200T0, the increase in ιϕ means that the positive Bϕ > 0 polarity is filling the disk. The fact that σϕ goes to zero confirms that the disk is adopting an even Bϕ symmetry.
 |
Fig. 23 Evolution of the symmetry coefficients ιϕ and σϕ in run R1-P2; data have been averaged over bins of 10T0. |
We consider a space-time window in which the transition from an odd to an even Bϕ symmetry is taking place (between t = 120 T0 and t = 130 T0), and look at vertical transport of the horizontal magnetic field. We decompose the induction of radial field BR in Fig. 24. In the upper panel, we see that the electric current layer is displaced of z ≈ −1.5h from the midplane, coinciding with the current sheet where Br = 0. This current layer keeps drifting downward in time, and eventually leaves the disk (fourth panel of Fig. 22).
 |
Fig. 24 Vertical profiles in run R1-P2, averaged in time between 120T0 and 130T0, and in spherical radius between 5.5r0 and 6r0; upper panel: sonic Mach number for the radial Alfvén velocity (solid blue) and electron minus ion velocity, normalized by the Keplerian velocity (dashed red); lower panel: induction of radial magnetic field. |
In the lower panel of Fig. 24, we show that the transport of negative BR < 0, from the midplane toward the southern surface, is mainly driven by ambipolar diffusion. The outflow and Hall contributions have a negligible impact on this process. Similar symmetry-breaking solutions have been observed in shearing box simulations (Lesur et al. 2014; Bai 2015). The cause of this phenomenon is yet unknown, but it appears to be robust.
4.6. Self-organization: zonal flows
This section describes the emergence of zonal flows in our simulations, characterized by axisymmetric density rings, together with magnetic field accumulations.
4.6.1. Overview
We illustrate in Fig. 25 the morphology of the flow in run R1-P2. We see a series of density bumps in the disk, radially separated by approximately the local disk thickness 2H. The magnetic flux is concentrated in low density regions, and this foliation is maintained in both coronae. Some magnetic flux accumulations can momentarily be as narrow as eight grid cells in the disk. However, with a magnetic Reynolds number ℛA ≈ 3, we believe that this width is primarily attributed to physical diffusivity and not numerical diffusion. This run also displays an even Bϕ symmetry, causing the tilting of magnetic field lines through the disk. As in run R1-M3 (cf. Fig. 21), ejection is thermally driven in the northern corona, and magnetically enhanced in the southern one.
 |
Fig. 25 Averaged flow poloidal map for run R1-P2 (from 1 au to 10 au, with strong Bz > 0), from 500T0 to 700T0; magnetic field lines are sampled along the midplane, and the velocity field is indicated with green arrows over the background density field. Magnetic field lines are accumulated in low density rings. |
Density and magnetic field fluctuations are anti-correlated. Table 3 shows that runs with Bz < 0 or β > 5 × 103 do not exhibit such structures. These are the runs in which the disk midplane is Hall-shear stable, or has linear growth rates smaller than 0.01Ω. Because our 3D simulations were integrated over shorter time intervals, the indicated number of zonal flows cannot directly be compared between equivalent 2D and 3D runs.
4.6.2. Self-organization mechanism
The induction of Bz is governed by the toroidal electromotive force (EMF), the same as in Eq. (21): 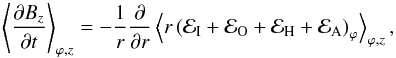 (23)so the average Bz increases in time where ℰϕ decreases with radius. The ideal, Hall and ambipolar EMFs can be expressed as:
(23)so the average Bz increases in time where ℰϕ decreases with radius. The ideal, Hall and ambipolar EMFs can be expressed as: 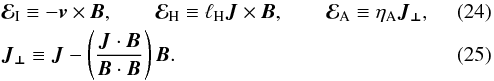 The first panel of Fig. 26 shows the anti-correlated fluctuations of density and magnetic field. In the second panel, we plot the averaged EMFs. The ohmic contribution has been omitted for it is negligible and cannot confine magnetic flux. The ideal term ℰIϕ increases with radius at the location of each magnetic field concentration. The velocity field thus acts as a turbulent diffusion. The ambipolar term precisely balances the ideal one, so it decreases with radius at the location of each band. This was already noted by Bai & Stone (2014; see their Fig. 8). Ambipolar diffusion is therefore responsible for the accumulation of Bz. Apart from being negligible by a factor 50, the Hall term acts against the accumulation of magnetic flux. Hall-driven self-organization requires the magnetic stress and flux to be anti-correlated (Kunz & Lesur 2013). This is possible in non-stratified simulations, when the net magnetic flux becomes strong enough to stabilize the HSI. In stratified simulations, the wind-driven stress − BϕBp is known to correlate with the net magnetic flux for β ≫ 1 (Lesur et al. 2014). Self-organization can thus be inhibited if the wind drives the magnetic stress in Hall-shear stable (i.e., strong field) regions.
The first panel of Fig. 26 shows the anti-correlated fluctuations of density and magnetic field. In the second panel, we plot the averaged EMFs. The ohmic contribution has been omitted for it is negligible and cannot confine magnetic flux. The ideal term ℰIϕ increases with radius at the location of each magnetic field concentration. The velocity field thus acts as a turbulent diffusion. The ambipolar term precisely balances the ideal one, so it decreases with radius at the location of each band. This was already noted by Bai & Stone (2014; see their Fig. 8). Ambipolar diffusion is therefore responsible for the accumulation of Bz. Apart from being negligible by a factor 50, the Hall term acts against the accumulation of magnetic flux. Hall-driven self-organization requires the magnetic stress and flux to be anti-correlated (Kunz & Lesur 2013). This is possible in non-stratified simulations, when the net magnetic flux becomes strong enough to stabilize the HSI. In stratified simulations, the wind-driven stress − BϕBp is known to correlate with the net magnetic flux for β ≫ 1 (Lesur et al. 2014). Self-organization can thus be inhibited if the wind drives the magnetic stress in Hall-shear stable (i.e., strong field) regions.
 |
Fig. 26 Radial profiles in run R1-P2, vertically averaged through the disk from 500T0 to 700T0; first panel: density (solid blue) and vertical magnetic field (dashed red), normalized by their initial profiles; second panel: ideal (solid blue) ambipolar (dashed red) and Hall (black dots, multiplied by 50 for visibility) electromotive forces, given by Eq. (24); third panel: toroidal component of the electric current Jϕ (solid blue), and of its projection J⊥ ϕ normal to the magnetic field; the vertical lines mark the location of magnetic field maxima. |
 |
Fig. 27 Ambipolar-driven self-organization mechanism: the electric current J is mainly radial, and the magnetic field B is mainly toroidal; as a result, the signs of Jϕ and J⊥ ϕ are opposed; this is equivalent to a negative diffusivity for Bz (cf. Eq. (24)). |
The direction of the ambipolar EMF is given by the electric current projected perpendicularly to the local magnetic field. Upon projection, the sign of the toroidal component J⊥ ϕ can become opposed to the sign of Jϕ. This is what happens in our simulations featuring zonal flows, as shown in the bottom panel of Fig. 26. In this case, the toroidal component of ℰA yields a negative effective resistivity (cf. Eq. (24)).
 |
Fig. 28 Radial profiles of normalized stress in R1-P2, averaged in time between 500T0 and 700T0. |
The typical configuration occurring in such simulations is sketched in Fig. 27. The magnetic field is mainly toroidal in the disk, and the dominant component of J is the radial one. The signs of Jϕ and J⊥ ϕ are opposed, and they remain opposed when flipping the orientation of J and/or B. Ambipolar diffusion remains a dissipative process when considering all three spatial directions. With J⊥ ≃ Jr and ∂ϕ ≃ 0, the diffusion occurs primarily on Bϕ in the vertical direction. We verified that the same sign inversion occurred in the ambipolar run ABS presented by Béthune et al. (2016), which also featured magnetic flux concentrations without Hall drift.
We show in Fig. 28 the radial profiles of magnetic stress in the saturated state containing zonal flows. The radial stress ℳrϕ is maximal in regions of magnetic field accumulation. The resulting stress divergence pushes mass away from stress maxima, causing the observed anti-correlation between Bz and ρ.
4.6.3. Hydrodynamic properties and saturation mechanism
Zonal flows refer to quasi-steady deviations from the Keplerian rotation profile of the disk. We characterize these by the fluctuations of angular velocity Ω relative to the Keplerian one ΩK, and by the dimensionless shear q ≡ ∂log Ω /∂log r. The radial profiles of these two diagnostics are drawn in Fig. 29 for run R1-P2, showing five distinct oscillations. Since β ≫ 1, magnetic pressure gradients do not provide a significant support against gravity. Given the density fluctuations, the deviations from a Keplerian profile follow the condition of geostrophic equilibrium: ![\begin{equation} \label{eqn:geostrophic} v'_{\varphi} \equiv v_{\varphi} - \id{v}{K} \simeq \frac{c_{\rm s}^2}{2 \id{\Omega}{K}} \frac{1}{\rho_0} \frac{\partial}{\partial r} \left[ \rho - \rho_0\right]. \end{equation}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq461.png) (26)One important issue regarding zonal flows is their ability to trap dust particles (Weidenschilling 1977). Several objects have now revealed axisymmetric structures in their dust distribution, such as rings and gaps (Brogan et al. 2015; Nomura et al. 2016). One possible scenario involves zonal flows. Dust particles undergo a drag force from the gas as they orbit the star at the local Keplerian velocity, whereas the gas can rotate slower or faster depending on its radial pressure gradient. If the gas rotates faster, it will transfer angular momentum to the dust and make it migrate outward, or inward if it rotates slower. Dust grains are thus accumulated in pressure maxima. We prove in Fig. 29 that the zonal flows produced in our simulations are actually able to cause transitions from sub- to super-Keplerian rotation. These zonal flows would therefore act as dust traps.
(26)One important issue regarding zonal flows is their ability to trap dust particles (Weidenschilling 1977). Several objects have now revealed axisymmetric structures in their dust distribution, such as rings and gaps (Brogan et al. 2015; Nomura et al. 2016). One possible scenario involves zonal flows. Dust particles undergo a drag force from the gas as they orbit the star at the local Keplerian velocity, whereas the gas can rotate slower or faster depending on its radial pressure gradient. If the gas rotates faster, it will transfer angular momentum to the dust and make it migrate outward, or inward if it rotates slower. Dust grains are thus accumulated in pressure maxima. We prove in Fig. 29 that the zonal flows produced in our simulations are actually able to cause transitions from sub- to super-Keplerian rotation. These zonal flows would therefore act as dust traps.
 |
Fig. 29 Radial profiles in run R1-P2, vertically averaged through the disk from 500T0 to 700T0, of the variations of angular velocity Ω relative to Keplerian ΩK (solid blue), and dimensionless radial shear ∂log ρ/∂log r (dashed red). |
The profile of dimensionless shear is superimposed to the rotation profile in Fig. 29, and tells us about the saturation of this process. In the limit q → −2, the distribution of specific angular momentum is flat and the flow is marginally stable with respect to Rayleigh’s criterion. This criterion appears to set the lower bound for the shear, as if any deviation q< −2 would instantly reorganize the flow to prevent hydrodynamic instability. However, we do not observe any evidence of purely hydrodynamic turbulence in these simulations. The disk therefore never crosses the Rayleigh line.
4.6.4. Three-dimensional simulations
We now ascertain that these structures are not restricted to two-dimensional simulations. The formation of axisymmetric rings in run R1-P3 and in its three-dimensional equivalent run 3D-R1-P3 are shown in Fig. 30. We observe the emergence of zonal flows on the same time-scale at about the same location, and with the same radial separation. The structures form very early in the simulation (50T0 at 4r0, i.e., five local orbits), the contrast in 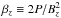 increases in time up to two orders of magnitude. They evolve over hundreds of local orbits, but we still count seven bands in run R1-P3 after 1000T0.
increases in time up to two orders of magnitude. They evolve over hundreds of local orbits, but we still count seven bands in run R1-P3 after 1000T0.
 |
Fig. 30 Space-time diagram of vertically and azimuthally averaged βz in runs R1-P3 (upper panel) and 3D-R1-P3 (lower panel); only the first 300T0 of the two-dimensional run are shown. |
The present self-organization phenomenon is thus not inhibited in three-dimensional simulations. Regarding the non-axisymmetric stability of these structures, they could be Rossby wave unstable for the criterion given by Lovelace et al. (1999). Nevertheless, run 3D-R1-P3 proves that they are stable over 20 local orbits to all modes fitting in a quarter disk. Three-dimensional simulations of a full disk with an increased resolution and/or a less diffusive numerical scheme will be required to confirm their stability over long time scales.
5. Discussion
5.1. Large-scale configuration of the magnetic field
We gather the symmetry coefficients σϕ and ιϕ from Table 3, and plot them in Fig. 31. We distinguish three populations in this area. Runs with Bz< 0 are the only ones on the right half of the figure (σϕ> 0), i.e., overall loosing angular momentum in the wind and therefore accreting. The blue square associated with run R10-M3 is close to the origin, because its outer half is accreting while the inner half is non-accreting. On the left side σϕ< 0, we find runs with a positive and weak magnetic field. The third population is located near (σϕ,ιϕ) ≈ (0, ± 1), i.e., only one sign of Bϕ in the disk, accreting in one hemisphere and non-accreting on the other. These runs mostly have Bz> 0 and a strong magnetization β ≤ 5 × 103.
 |
Fig. 31 Symmetry coefficients σϕ and ιϕ in our set of 2D simulations, averaged over representative time intervals; colors indicate the initial midplane magnetization β, blue corresponding to Bz< 0; runs in [ 1,10 ] au are plotted with circles, runs in [ 10,100 ] au are plotted with squares; different background colors correspond to different disk-corona temperature contrast k; the error bars correspond to standard deviations over time. |
It is tempting to see a correlation between the sign of Bz and the presence of magnetized outflows. However, we believe that this correlation is fortuitous. Indeed, the vertical phase of Bϕ seems to be set at least partially by the noise injected in our initial conditions. This is illustrated in Fig. 32 showing the evolution of Bϕ as a function of time. From 10T0 to 40T0, the MRI amplifies Bϕ at z ≈ 3h, causing σϕ to alternate from positive to negative as the instability saturates and eventually settles with σϕ> 0. In this example, σϕ> 0 is clearly set by the initial phase and saturation mechanism of the most unstable MRI mode, which itself depends on how the MRI was initially seeded.
 |
Fig. 32 Evolution of the toroidal magnetic field Bϕ along a vertical cut at r = 5r0 and over the first 150T0 (color scale) of run R10-M3-C2 (accreting); values have been normalized by the initial, unsigned vertical field at this radius. |
Several hundred inner orbits later, one polarity of the toroidal magnetic field can be vertically removed out of the disk, leading to a one-sided outflow. Among these runs with ιϕ = ± 1, most have Bz> 0 and β< 5 × 104, the exception being run R1-M3. These configurations are stable attractors in the sense that these disks never return to an odd symmetry of Bϕ about the midplane.
5.2. Magnetothermal winds
We have shown that all runs display a vertical outflow, although it is disorganized for non-accreting disks (cf. Sect. 4.4). We observed no difference between two and three-dimensional winds. Our winds exhibit several properties of steady-state, magnetically-driven jets. However, they become super-Alfvénic before reaching the ideal MHD regime, contrarily to all published models of magnetically-driven jets from accretion disks. This could explain why, although they also heated the base of the wind, Casse & Ferreira (2000) never achieved an ejection efficiency as high as the one we obtain. It should be possible to design models going continuously from thermally-driven to magnetically-driven winds. Our simulations provide such a link.
One important control parameter for magnetically-driven winds is the disk magnetization (1 /β). At a comparably low disk magnetization, Murphy et al. (2010) also obtained super-fast-magnetosonic winds, but with a larger magnetic lever arm (see their Figs. 8 and 14, and also Stepanovs & Fendt 2016). However, they used constant α viscosity and resistivity coefficients, with prescribed vertical profiles to mimic turbulent transport in the disk. This suggests that different transport regimes within disk may lead to different wind properties.
 |
Fig. 33 Wind mass loss rate relative to the disk mass ṁW/md as a function of the initial midplane magnetization β; the symbols and color coding are the same as in Fig. 31; the two dashed lines indicate the ṁW ~ β− 1/2 scaling for R1 and R10 runs, bottom and top, respectively. |
We plot the wind mass loss rate ṁW of our two-dimensional runs in Fig. 33 as a function of the midplane magnetization β. Runs R1-M3 (blue circle) and R10-P3 (red square), both of which have ιϕ = ± 1 (cf. Fig. 31), also have higher mass loss rates than the other simulations of the same radial range. Given this degree of freedom, we find no clear dependence of ṁW with the polarity of the initial magnetic field alone. There is no apparent correlation of ṁW with the temperature contrast k either.
The wind mass loss rate typically scales as ṁW ~ β− 1/2 in runs R1 and R10 taken separately. This is consistent with the shearing-box measurements of Bai & Stone (2013), regardless of the fast-magnetosonic point being crossed in the computational domain (see Sect. 4.1.4 of this paper, and Sect. 3.4 of Lesur et al. 2013). In physical units, the wind mass loss rate is 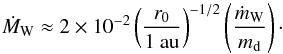 (27)The fact that ṁW/md increases by a factor
(27)The fact that ṁW/md increases by a factor 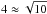 , from R1 runs to R10 runs, means that ṀW is roughly independent of the inner radius. We can sum the contributions over [ 1,100 ] au to get
, from R1 runs to R10 runs, means that ṀW is roughly independent of the inner radius. We can sum the contributions over [ 1,100 ] au to get 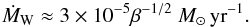 (28)
(28)
6. Summary
We have performed global simulations of protoplanetary disks in the non-ideal MHD framework. Our model includes both radial and vertical density stratification, spanning one decade in radius to separately cover the ranges from 1 au to 10 au and from 10 au to 100 au, with 20 disk scale heights vertically. The ionization fraction is computed dynamically, and all three non-ideal MHD effects are accounted for. The disk is embedded in a warm corona, with several temperature contrasts.
In the disk, the flow is essentially laminar and evolves over hundreds of local orbital periods. Angular momentum is transported by a large-scale magnetic stress, unsuited for an α viscosity prescription. The radial transport of angular momentum causes no net mass accretion in our disk model. The vertical flux of angular momentum can take both orientations through the disk. If angular momentum is transported from the disk midplane to the surface, then a magnetized wind is launched and the disk accretes at rates on the order of 10-7M⊙/ yr. Conversely, angular momentum can be transported from the disk surface to the midplane, resulting in a large-scale meridional circulation. This circulation is characterized by the gas flowing radially inward at the surface, and outward in the midplane. In this case, a turbulent and low density wind is observed, causing no net mass accretion. Accreting and non-accreting regions can coexist in one single disk, the boundary between the two domains evolving on secular timescales. The Hall drift can reduce the angular momentum flux in the midplane, depending on the polarity of the vertical magnetic field threading the disk, but the overall contrast in stress is only within a factor of three.
Because of the presence of a warm corona, the winds we obtain are magnetothermal. They constitute a new class of solutions because the plasma can reach super-Alfvénic speeds before entering the ideal MHD regime. The mass loading of the wind is driven by the Lorentz force, but the subsequent acceleration is predominantly thermal. We have linked the wind mass loss rate to the disk magnetization, and recovered the ṁW ∝ β− 1/2 relation. Several of our simulations also exhibit asymmetric winds where magnetic ejection occurs on one side of the disk only. We have associated this state with the expulsion of the electric current sheet, usually located near the disk midplane. We speculate that this configuration is a stable attractor for the disk, allowing it to evacuate angular momentum at higher rates than the symmetric situation. One-sided molecular outflows (Pety et al. 2006) could be a consequence of such magnetic configurations.
Finally, we have identified a self-organization process leading to the formation of axisymmetric density rings. To these density rings are associated zonal flows, able to trap dust particles. The vertical magnetic flux becomes concentrated in density minima. We have argued that ambipolar diffusion alone is responsible for this process. Bai & Stone (2014) also observed enhanced magnetic flux concentrations in MRI turbulence simulations. They proposed a mechanism driven by ideal MHD electromotive forces. In our case, we have shown that the concentration mechanism relies solely on ambipolar diffusion. We are therefore looking at a different mechanism from the one they proposed. We presume that Gressel et al. (2015) did not observe this phenomenon because of the lower magnetization and ionization fraction in their simulations. We have shown that the Hall drift works against the confinement of magnetic flux in our case. This demonstrates that Hall-driven self-organization (Kunz & Lesur 2013; Béthune et al. 2016) is inefficient in stratified simulations, as already suggested by stratified shearing boxes (Lesur et al. 2014; Bai 2015).
We note that we have not explored systematically the global transport of poloidal magnetic flux in our simulations. The poloidal field being a key ingredient for MHD winds, any long-term prediction for the evolution of these disks implies a parametrization for the evolution of this field (Suzuki et al. 2016). This transport depends strongly on the vertical disk structure (e.g. Guilet & Ogilvie 2012, 2013), and non-ideal effects add more complications to this picture (Bai & Stone 2016). In our simulations, we found that transport of flux was highly sensitive to the presence of self-organized structures, which act as physical boundaries for the radial transport of poloidal field. This is to be expected since self-organization is after all a consequence of poloidal flux transport. For this reason, we believe that any description of poloidal flux transport needs to incorporate the possibility of self-organization, without which flux transport could be largely overestimated.
The main caveats of our study are related to the thermodynamics and chemistry of protoplanetary disks. The validity of our prescription for the temperature distribution should be compared with self-consistent, radiative transfer simulations. By omitting small dust grains, we may also have severely underestimated the magnitude of non-ideal plasma effects. Our main justification is practical in nature since both these treatments come with large computational overhead. These limitations will need to be addressed in future work.
Reduced chemical models can nonetheless be computationally affordable, see for example Turner et al. (2007), Ilgner & Nelson (2008).
Unless limiting the Alfvén velocity by some artificial procedure; see for example the appendix of Miller & Stone (2000).
Acknowledgments
We thank Matthew Kunz and Mario Flock, as well as our anonymous referee for providing thoughtful comments on the manuscript. This work was granted access to the HPC resources of IDRIS under the allocation 2016-042231 made by GENCI. Some of the computations presented in this paper were performed using the Froggy platform of the CIMENT infrastructure (https://ciment.ujf-grenoble.fr), which is supported by the Rhône-Alpes region (GRANT CPER07_13 CIRA), the OSUG@2020 labex (reference ANR10 LABX56), and the Equip@Meso project (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervized by the Agence Nationale pour la Recherche.
References
- Aresu, G., Kamp, I., Meijerink, R., et al. 2011, A&A, 526, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bai, X.-N. 2011, ApJ, 739, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N. 2015, ApJ, 798, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Goodman, J. 2009, ApJ, 701, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2011, ApJ, 736, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2014, ApJ, 796, 31 [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2016, ApJ, submitted [arXiv:1612.03912] [Google Scholar]
- Bai, X.-N., Ye, J., Goodman, J., & Yuan, F. 2016, ApJ, 818, 152 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Papaloizou, J. C. B. 1999, ApJ, 521, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Terquem, C. 2001, ApJ, 552, 235 [Google Scholar]
- Bans, A., & Königl, A. 2012, ApJ, 758, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, ApJ, 678, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Juhász, A., Boccaletti, A., et al. 2015, A&A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthune, W., Lesur, G., & Ferreira, J. 2016, A&A, 589, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Perez, L. M., Hunter, T. R., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, C. J., Stapelfeldt, K. R., Watson, A. M., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S. 2007, Lect. Notes Phys., 723, 21 [Google Scholar]
- Casse, F., & Ferreira, J. 2000, A&A, 361, 1178 [NASA ADS] [Google Scholar]
- Chandrasekhar, S. 1956, ApJ, 124, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., Padgett, D. L., Stapelfeldt, K. R., et al. 2007, ApJ, 667, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, J., & Lovelace, R. V. E. 1994, ApJ, 429, 139 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Paletou, F., Bouvier, J., & Ferreira, J. 2005, Nature, 438, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Edwards, S., Hartigan, P., Ghandour, L., & Andrulis, C. 1994, AJ, 108 [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1993, A&A, 276, 625 [NASA ADS] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1995, A&A, 295, 807 [NASA ADS] [Google Scholar]
- Fleming, T. P., Stone, J. M., & Hawley, J. F. 2000, ApJ, 530, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Dzyurkevich, N., Klahr, H., Turner, N. J., & Henning, T. 2011, ApJ, 735, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., González, M., & Commerçon, B. 2013, A&A, 560, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fricke, K. 1968, ZAp, 68, 317 [Google Scholar]
- Fromang, S., & Nelson, R. P. 2006, A&A, 457, 343 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Fromang, S., Terquem, C., & Balbus, S. A. 2002, MNRAS, 329, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Lyra, W., & Masset, F. 2011, A&A, 534, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Latter, H., Lesur, G., & Ogilvie, G. I. 2013, A&A, 552, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukagawa, M., Tsukagoshi, T., Momose, M., et al. 2013, PASJ, 65 [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Turner, N. J., Nelson, R. P., & McNally, C. P. 2015, ApJ, 801, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Guilet, J., & Ogilvie, G. I. 2012, MNRAS, 424, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Guilet, J., & Ogilvie, G. I. 2013, MNRAS, 430, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Stone, J. M. 1998, ApJ, 501, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ilgner, M., & Nelson, R. P. 2008, A&A, 483, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, L. 1996, ApJ, 457, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W. 2008, MNRAS, 385, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Balbus, S. A. 2004, MNRAS, 348, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Lesur, G. 2013, MNRAS, 434, 2295 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., Ferreira, J., & Ogilvie, G. I. 2013, A&A, 550, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, M.-K., & Youdin, A. N. 2015, ApJ, 811, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Flock, M., Stute, M., Kolb, S. M., & Muscianisi, G. 2012, A&A, 545, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, K. A., & Stone, J. M. 2000, ApJ, 534, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, G. C., Ferreira, J., & Zanni, C. 2010, A&A, 512, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, T., & Umebayashi, T. 1986, MNRAS, 218, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., Gressel, O., & Umurhan, O. M. 2013, MNRAS, 435, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., Tsukagoshi, T., Kawabe, R., et al. 2016, ApJ, 819, L7 [NASA ADS] [CrossRef] [Google Scholar]
- O’Keeffe, W., & Downes, T. P. 2014, MNRAS, 441, 571 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S., & Downes, T. P. 2006, MNRAS, 366, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Padgett, D. L., Brandner, W., Stapelfeldt, K. R., et al. 1999, AJ, 117, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, G., & Pudritz, R. E. 1992, ApJ, 394, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Perez-Becker, D., & Chiang, E. 2011, ApJ, 735, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., Chan, C.-K., & Psaltis, D. 2006, MNRAS, 372, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J., Gueth, F., Guilloteau, S., & Dutrey, A. 2006, A&A, 458, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pudritz, R. E. 1985, ApJ, 293, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, R., Girart, J. M., Lai, S.-P., & Marrone, D. P. 2014, ApJ, 780, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers-Lee, D., Ray, T. P., & Downes, T. P. 2016, MNRAS, 463, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Salmeron, R., & Wardle, M. 2008, MNRAS, 388, 1223 [NASA ADS] [Google Scholar]
- Salmeron, R., Königl, A., & Wardle, M. 2011, MNRAS, 412, 1162 [NASA ADS] [Google Scholar]
- Sano, T., & Stone, J. M. 2002, ApJ, 577, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Segura-Cox, D. M., Looney, L. W., Stephens, I. W., et al. 2015, ApJ, 798, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Simon, J. B., Lesur, G., Kunz, M. W., & Armitage, P. J. 2015, MNRAS, 454, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Steinacker, A., & Henning, T. 2001, ApJ, 554, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanovs, D., & Fendt, C. 2016, ApJ, 825, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Stoll, M. H. R., & Kley, W. 2014, A&A, 572, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S.-I. 2009, ApJ, 691, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S.-I. 2014, ApJ, 784, 121 [Google Scholar]
- Suzuki, T. K., Ogihara, M., Morbidelli, A., Crida, A., & Guillot, T. 2016, A&A, 596, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, N. J., Sano, T., & Dziourkevitch, N. 2007, ApJ, 659, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Umebayashi, T., & Nakano, T. 1981, PASJ, 33, 617 [NASA ADS] [Google Scholar]
- Umebayashi, T., & Nakano, T. 2009, ApJ, 690, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V., & Brandenburg, A. 1998, MNRAS, 294, 399 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wardle, M. 1999, MNRAS, 307, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M. 2007, Ap&SS, 311, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M., & Koenigl, A. 1993, ApJ, 410, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M., & Ng, C. 1999, MNRAS, 303, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, R., & Bai, X.-N. 2016, ApJ, 819, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L., & Stephens, I. 2016, MNRAS, 456, 2794 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Initial conditions
We construct steady, locally isothermal, hydrodynamic disk solutions to the mass and momentum Eqs. (3)and (4). We first prescribe an isothermal sound speed distribution 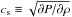 . The use of
. The use of 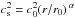 helps building simple analytical solutions. The distance unit r0 = 1 in this section. With the gravitational potential Φ = −1 /R, the momentum equations in spherical coordinates can be written
helps building simple analytical solutions. The distance unit r0 = 1 in this section. With the gravitational potential Φ = −1 /R, the momentum equations in spherical coordinates can be written 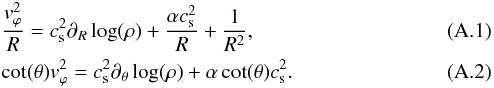 We can isolate vϕ and equate the two lines; defining f ≡ log (ρ), x ≡ log (R) and y ≡ −log (sin(θ)), we obtain
We can isolate vϕ and equate the two lines; defining f ≡ log (ρ), x ≡ log (R) and y ≡ −log (sin(θ)), we obtain 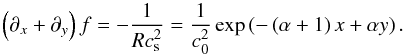 (A.3)This can be solved by the method of characteristics, once a midplane density profile ρ(r,z = 0) = ρ0(r/r0)n has been prescribed:
(A.3)This can be solved by the method of characteristics, once a midplane density profile ρ(r,z = 0) = ρ0(r/r0)n has been prescribed: ![\appendix \setcounter{section}{1} \begin{equation} \rho (R,r) = \rho_0 \left( \frac{r}{r_0} \right)^n \exp\left[ \frac{1}{c^2_{\rm s}(r)} \left( \frac{1}{R} - \frac{1}{r} \right) \right], \label{eqn:rho}\\ \end{equation}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq501.png) (A.4)and it is straightforward to obtain for the velocity field
(A.4)and it is straightforward to obtain for the velocity field 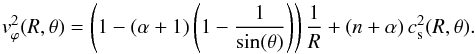 (A.5)To have a constant opening angle of the disk, we set a constant sound to Keplerian speed ratio: cs,disk/vKepler = 5%, i.e., α = −1. In this case, the disk midplane density must decrease with n = −2 in order to produce the desired surface density profile Σ(r) ≡ ∫ρdz ~ r−1.
(A.5)To have a constant opening angle of the disk, we set a constant sound to Keplerian speed ratio: cs,disk/vKepler = 5%, i.e., α = −1. In this case, the disk midplane density must decrease with n = −2 in order to produce the desired surface density profile Σ(r) ≡ ∫ρdz ~ r−1.
We define the disk-corona transition as the location where the disk equilibrium density is one thousandth of the local midplane density: ρ(r,zi) = 10-3ρ(r,z = 0). The transition angle is then given by sin(θi) = 1 + log (10-3) (h/r)2, corresponding to a constant zi ≈ 3.72h ≡ H.
At a given cylindrical radius, the isothermal sound speed is increased up to a factor k higher than the midplane value. This ratio of corona to disk temperature is constant with cylindrical radius, and fixed to k = 6 for most runs. The transition from the disk to the warm corona is smoothed in the interval sin(θ) ∈ [sin(θi)−0.2(h/r),sin(θi)], such that 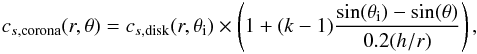 (A.6)in order to avoid strong gradients and, if possible, resolve the physics at the transition. The gas in the corona is thus fully heated at a height zc/h ≈ 4.68.
(A.6)in order to avoid strong gradients and, if possible, resolve the physics at the transition. The gas in the corona is thus fully heated at a height zc/h ≈ 4.68.
The coronal density distribution takes the same form as in Eq. (A.4), except this time the solution is extended from the disk surface and not from the midplane. In order to continuously match the isothermal pressure fields  at the interface, the factor ρ0 in Eq. (A.4)must be replaced by ρ0 → ρ(R,θi)[cs,disk(R,θi) /cs,corona(R,θ)]2.
at the interface, the factor ρ0 in Eq. (A.4)must be replaced by ρ0 → ρ(R,θi)[cs,disk(R,θi) /cs,corona(R,θ)]2.
The velocity field in the corona takes exactly the same form as (A.5). Due to the vertical temperature gradient, there is a vertical shear in azimuthal velocity in the transition layer ∂zvϕ ≠ 0; we verified via hydrodynamic simulations that this layer quickly relaxes to a steady and stable state. We add a white noise to the three components of the initial velocity field, with amplitude 1% of the local sound speed, so as to quickly trigger the MRI.
The initial magnetic field has only Bz ≠ 0. It is initialized via its vector potential B = ∇ × A to ensure the solenoidal condition ∇·B = 0 from the beginning. To set a constant average/midplane β, the magnetic field intensity must decrease as r− 3/2, whence 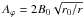 , with B0 the intensity of the magnetic field at the inner radius r0 (see the appendix of Suzuki & Inutsuka 2014). The initial conditions deviates from a true MHD equilibrium, but only at order 1 /β.
, with B0 the intensity of the magnetic field at the inner radius r0 (see the appendix of Suzuki & Inutsuka 2014). The initial conditions deviates from a true MHD equilibrium, but only at order 1 /β.
Appendix B: Boundary conditions
Three dimensional simulations are periodic in the azimuthal direction. The remaining boundary conditions are listed below. These boundary conditions are designed to prevent boundary-driven flows while remaining relatively simple. To isolate the corners at the inner radial boundary, we define the critical radius rc/r0 ≡ (1 + sin(π/ 2−θ0))/2, with θ0 = 20(h/r) the polar extent of the computational domain in one hemisphere.
-
ρ: zero gradient through all boundaries, with a lower bound ρc = 10-6ρ0 at the inner radial boundary;
-
P: isothermal distribution ρcs(r,θ)2 at all boundaries;
-
vR: zero gradient through all boundaries; outward cs(R,θ) as lower bound at the outer radial boundary in the corona;
-
vθ: zero gradient through all boundaries; outward cs(R,θ) as lower bound at both polar boundaries;
-
vϕ: zero gradient through polar and outer radial boundaries; at the inner radial boundary: initial Keplerian velocity in the disk, constant angular velocity vϕ/R in the corona;
-
BR: zero gradient through polar boundaries if r>rc, zero value otherwise;
-
Bθ: zero value at inner radial boundary, zero gradient through outer radial boundary;
-
Bϕ: zero gradient through radial and polar boundaries if r>rc, zero value otherwise.
We complete these boundary conditions with buffer zones, inside the computational domain to limit the influence of the boundaries on the disk. The inner buffer includes both the disk and the corona in {(R,θ) | R< 1.05r0}. The outer buffer includes only the disk in 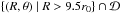 . Let wb be the radial width of the considered buffer. Within the buffer, we explicitly relax a given field X to some prescribed distribution X0:
. Let wb be the radial width of the considered buffer. Within the buffer, we explicitly relax a given field X to some prescribed distribution X0: 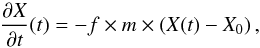 (B.1)with a characteristic frequency scale
(B.1)with a characteristic frequency scale 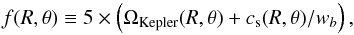 (B.2)and a linear modulation m(R), equal to 1 at the domain boundary and 0 at the other edge of the buffer (in the active domain). Only the three components of the velocity field are modified inside the buffers in continuity with the boundary conditions:
(B.2)and a linear modulation m(R), equal to 1 at the domain boundary and 0 at the other edge of the buffer (in the active domain). Only the three components of the velocity field are modified inside the buffers in continuity with the boundary conditions:
-
vR: relaxed to zero at both boundaries;
-
vθ: relaxed to maintain a constant angular velocity vθ/R, sampled at the edge of the buffer on the active domain side;
-
vϕ: relaxed to the initial velocity in the disk region of both buffers, and to a constant angular velocity vϕ/R in the corona region of the inner buffer, also sampled at the buffer edge.
Appendix C: Internal conditions
In addition to the buffer zones, we control the values of each computational grid cell and at each time step. The first reason is to avoid excessively high Alfvén velocities, imposing small time steps to satisfy the CFL stability criterion. This is one of the main difficulties with global, stratified MHD simulations including a net magnetic flux. A common remedy is to impose a lower bound, i.e., a floor value on the density. However, we checked that arbitrarily low densities are well handled in the absence of magnetic field, and we found that a density floor could produce significant pressure gradients in the outer corona. We therefore increase the density only when the Alfvén velocity becomes too large. With our prescribed temperature distribution, the Alfvén velocity seldom reaches vA ≲ v0, which we set as its upper limit.
The second control performed on the whole computational domain is related to the gas temperature distribution. Since we do not solve for the radiation field, we enforce a locally isothermal equilibrium, i.e., a constant sound speed distribution c0(r,z). For a steady toroidal flow, the vertical shear of azimuthal velocity is given by ![\appendix \setcounter{section}{3} \begin{equation} \label{eqn:baroclin} \frac{\partial}{\partial z} \frac{v^2_{\varphi}}{r} = \left[\frac{\nabla P \vec{\times} \nabla \rho}{\rho^2} \right] \vec{\cdot e}_{\varphi}, \end{equation}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq540.png) (C.1)which depends on the thermodynamics of the flow. Our locally isothermal equilibrium has a non-zero vertical shear, and is therefore subject to the vertical shear instability (Goldreich & Schubert 1967; Fricke 1968; Urpin & Brandenburg 1998). It was shown by Nelson et al. (2013) that this instability could be strongly attenuated by letting the entropy distribution reorganize, and then relaxing the temperature distribution over a fraction of orbital period. For this reason, we evolve the total energy density assuming an ideal gas:
(C.1)which depends on the thermodynamics of the flow. Our locally isothermal equilibrium has a non-zero vertical shear, and is therefore subject to the vertical shear instability (Goldreich & Schubert 1967; Fricke 1968; Urpin & Brandenburg 1998). It was shown by Nelson et al. (2013) that this instability could be strongly attenuated by letting the entropy distribution reorganize, and then relaxing the temperature distribution over a fraction of orbital period. For this reason, we evolve the total energy density assuming an ideal gas: ![\appendix \setcounter{section}{3} \begin{eqnarray} &&E \equiv \frac{P}{\gamma - 1} + \frac{1}{2} \left( \rho v^2 + B^2\right) + \rho \Phi, \\ &&\partial_t E = - \vec{\nabla \cdot} \left[ \left(E + P + B^2/2\right) \vec{v} - \left( \vec{v \cdot B}\right) \vec{B} \right] \label{eqn:dyn-E} \end{eqnarray}](/articles/aa/full_html/2017/04/aa30056-16/aa30056-16-eq541.png)
with γ = 7/5 corresponding to cold diatomic molecules. We then bring the isothermal sound speed 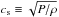 back to its initial distribution, over a fraction of local orbital period:
back to its initial distribution, over a fraction of local orbital period: 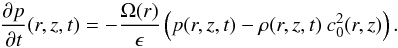 (C.4)Radiative transfer simulations predict short cooling rates in the bulk of the disk (Flock et al. 2013; Stoll & Kley 2014). We verified via hydrodynamic simulations that ϵ = 1/10 would, indeed, force this instability to saturate at an imperceptibly small level. This value is comparable to the threshold derived by Lin & Youdin (2015) with our set of parameters, ϵ0 ~ 1/8.
(C.4)Radiative transfer simulations predict short cooling rates in the bulk of the disk (Flock et al. 2013; Stoll & Kley 2014). We verified via hydrodynamic simulations that ϵ = 1/10 would, indeed, force this instability to saturate at an imperceptibly small level. This value is comparable to the threshold derived by Lin & Youdin (2015) with our set of parameters, ϵ0 ~ 1/8.
Appendix D: Caps on non-ideal MHD effects
We apply two different limiters on non-ideal effects. In the first place, our simplified chemical model cannot properly represent the strong degree of ionization high in the corona. We therefore multiply the diffusivities ηO,H,A in Eq. (5)by a factor exp(−xe/ 10-8). This coefficient ensures a smooth decrease of the ambipolar diffusivity until up to eight scale heights.
Because we use an explicit integration scheme, all three non-ideal effects impose severe constraints on the admissible timesteps satisfying the Courant-Friedrich-Lewy (CFL) stability criterion. We add a second cap to prevent excessively small timesteps. The strongest constraint come from the Hall drift, so we choose to limit the ratio ℓH/h(r) ≤ 4. This limit affects only the inner region r ≲ 2.3r0 for runs at r0 = 1 au, and does not concern runs at r0 = 10 au. The ohmic and ambipolar diffusivities are limited via their associated Reynolds numbers RO,A ≡ Ωh2/ηO,A ≥ 1/4. This limiter only affects ambipolar diffusion in the surface layers z ≳ 3h of the disk. Once we have applied the first cap on the ionization fraction, this second limiter forces the saturation values of ηA only in runs R1-P2 and R10-P2, i.e., where the initial magnetization is the strongest. In these two runs, the Reynolds number is saturated at RA ≈ 1/4 in the surface layers from z ≳ 2.6h to 3h.
All Tables
All Figures
 |
Fig. 1 Northern half of the computational grid; from the midplane to the pole: deep disk region (dark blue), disk surface region (cyan), disk-corona transition layer (yellow) and corona (red). |
| In the text | |
 |
Fig. 2 Vertical profiles in runs R1–P4 (from 1 au to 10 au, with weak Bz> 0) at r = 5r0 = 5 au: initial (solid blue) and final (dashed green at 300T0) ionization fractions |
| In the text | |
 |
Fig. 3 Vertical profiles of dimensionless numbers characterizing non-ideal effects in the initial conditions at r = 5 au (left panel) and r = 50 au (right panel): inverse of the ambipolar Elsasser number |
| In the text | |
 |
Fig. 4 Snapshot of run R10-M3-C2 (fiducial) at t = 200T0, showing the toroidal magnetic field in color background (blue to red), the poloidal velocity field in units of local sound speed (green arrows in the corona), and the orientation of the angular momentum flux caused by magnetic stress (purple arrows in the disk); ⟨Bz⟩ < 0 in this case. |
| In the text | |
 |
Fig. 5 Vertical profiles in run R10-M3-C2 (fiducial), averaged in time from 200T0 to 600T0, and in spherical radius from 5r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of the vertical field Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses ℳrϕ and ℳzϕ, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and ion minus electron radial velocity, normalized by the local Keplerian velocity and the vertically averaged density. Fifth panel: ambipolar diffusivity ηA (solid blue), ohmic diffusivity ηO (dashed blue, increased by a factor 104 for visibility), and Hall length ℓH (green dots). |
| In the text | |
 |
Fig. 6 Radial profiles of normalized stress in R10-M3-C2 (fiducial), averaged in time between 200T0 and 600T0. The radial components of Maxwell (red dots) and Reynolds (dashed blue) are averaged over the disk height, whereas the vertical Maxwell stress (solid green) is measured at the disk surface z = ± H. |
| In the text | |
 |
Fig. 7 Accretion in the disk region of run R10-M3-C2 (fiducial), between r ∈ [3,8]r0; the actual mass flux (solid black) is decomposed into radial (dashed blue) and vertical (red dots) torques as explicited in Eq. (9); the sum is drawn (dashed cyan) to validate this decomposition. |
| In the text | |
 |
Fig. 8 Velocities projected on a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, and normalized by the Keplerian velocity at the launching radius vK0; flow velocity v (solid black), sound speed cs (dashed orange), Alfvén velocity vA (dashed green), slow magnetosonic speed v− (dashed blue) and fast magnetosonic speed v+ (red dots). |
| In the text | |
 |
Fig. 9 Acceleration along a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, normalized by the Keplerian acceleration aK0 at the streamline base. The sum of the different forces (dashed cyan) is shown to validate this decomposition. |
| In the text | |
 |
Fig. 10 Angular momentum along a streamline passing through (r = 6r0,z = 5h) in run R10-M3-C2 (fiducial), averaged from 400T0 to 500T0, normalized to its value at the streamline base; the total angular momentum (solid black) is decomposed into matter (dashed blue) and magnetic (red dots) components as explicited in Eq. (17). |
| In the text | |
 |
Fig. 11 Vertical profiles of horizontal magnetic stress, normalized by the vertically averaged pressure in the disk ℳrϕ/ ⟨P⟩z in runs 3D-R1-P4 (solid blue, Ω·B> 0) and 3D-R1-M4 (dashed red, Ω·B< 0), averaged in time over 50T0 and radially from 3r0 to 6r0; the green dots show the average ratio ℓH/h in this same region. |
| In the text | |
 |
Fig. 12 Averaged flow poloidal map for run R10-M3 (from 10 au to 100 au, with Bz< 0) from 400T0 to 700T0; magnetic field lines are regularly sampled along the midplane, and the velocity field is indicated with green arrows over the background density field. |
| In the text | |
 |
Fig. 13 Same as Fig. 8 for a streamline passing through (r = 7r0,z = 5h) in run R10-M3, averaged from 400T0 to 700T0. The fast-magnetosonic point is clearly crossed within the computational domain. |
| In the text | |
 |
Fig. 14 Contributions to the Bernoulli invariant ℬ (solid black) as explicited in Eq. (20), along a streamline passing through (r = 7r0,z = 5h) in run R10-M3, averaged from 400T0 to 700T0; the gravitational contribution is not shown. |
| In the text | |
 |
Fig. 15 Same as Fig. 9 in run R10-M3, averaged in time between 400T0 and 700T0, with a streamline passing through (r = 7r0,z = 5h). |
| In the text | |
 |
Fig. 16 Snapshot of run R1-P4-C4 (from 1 au to 10 au, with weak Bz> 0) at t = 1000T0, showing the toroidal magnetic field in color background (blue to red), the poloidal velocity field in units of local sound speed (green arrows in the corona), and the orientation of the angular momentum flux caused by magnetic stress (purple arrows in the disk). The orientation of the angular momentum flux is reversed compared to the fiducial, accreting case. |
| In the text | |
 |
Fig. 17 Vertical profiles in run R1-P4-C4, averaged in time from 400T0 to 1000T0, and in spherical radius from 5r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of the vertical field Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and electron minus ion radial velocity, normalized by the local Keplerian velocity and the vertically averaged density. |
| In the text | |
 |
Fig. 18 Contributions to the induction of toroidal magnetic field in run R1-P4-C4, as explicited in Eq. (22), averaged in time from 400T0 to 1000T0 and in spherical radius from 5r0 to 8r0, normalized by the local Keplerian frequency and the local initial magnetic field. |
| In the text | |
 |
Fig. 19 Same as Fig. 18 for the radial magnetic field BR; see Eq. (21). |
| In the text | |
 |
Fig. 20 Same as Fig. 16 for run R1-P4 at t = 1000T0. The disk exhibits both an accreting (inner) and a non-accreting (outer) region. |
| In the text | |
 |
Fig. 21 Averaged flow poloidal map for run R1-M3 (from 1 au to 10 au, with moderate Bz< 0) from 800T0 to 1000T0; magnetic field lines are sampled along the midplane, and the velocity field is indicated with green arrows over the background toroidal field. The polar asymmetry and the absence of Bϕ sign reversal within the disk are obvious. |
| In the text | |
 |
Fig. 22 Vertical profiles in run R1-M3, averaged in time from 800T0 to 1000T0, and in spherical radius from 6r0 to 8r0. First panel: fluid velocity, normalized by the local Keplerian value vK; the disk mean value has been subtracted from the azimuthal component. Second panel: magnetic field, normalized by the vertically averaged value of Bz. Third panel: horizontal (solid blue) and vertical (dashed red) magnetic stresses, normalized by the vertically averaged pressure (cf. Eq. (8)). Fourth panel: radial mass flux (solid blue), and ion minus electron radial velocity, normalized by the local Keplerian velocity and average density. |
| In the text | |
 |
Fig. 23 Evolution of the symmetry coefficients ιϕ and σϕ in run R1-P2; data have been averaged over bins of 10T0. |
| In the text | |
 |
Fig. 24 Vertical profiles in run R1-P2, averaged in time between 120T0 and 130T0, and in spherical radius between 5.5r0 and 6r0; upper panel: sonic Mach number for the radial Alfvén velocity (solid blue) and electron minus ion velocity, normalized by the Keplerian velocity (dashed red); lower panel: induction of radial magnetic field. |
| In the text | |
 |
Fig. 25 Averaged flow poloidal map for run R1-P2 (from 1 au to 10 au, with strong Bz > 0), from 500T0 to 700T0; magnetic field lines are sampled along the midplane, and the velocity field is indicated with green arrows over the background density field. Magnetic field lines are accumulated in low density rings. |
| In the text | |
 |
Fig. 26 Radial profiles in run R1-P2, vertically averaged through the disk from 500T0 to 700T0; first panel: density (solid blue) and vertical magnetic field (dashed red), normalized by their initial profiles; second panel: ideal (solid blue) ambipolar (dashed red) and Hall (black dots, multiplied by 50 for visibility) electromotive forces, given by Eq. (24); third panel: toroidal component of the electric current Jϕ (solid blue), and of its projection J⊥ ϕ normal to the magnetic field; the vertical lines mark the location of magnetic field maxima. |
| In the text | |
 |
Fig. 27 Ambipolar-driven self-organization mechanism: the electric current J is mainly radial, and the magnetic field B is mainly toroidal; as a result, the signs of Jϕ and J⊥ ϕ are opposed; this is equivalent to a negative diffusivity for Bz (cf. Eq. (24)). |
| In the text | |
 |
Fig. 28 Radial profiles of normalized stress in R1-P2, averaged in time between 500T0 and 700T0. |
| In the text | |
 |
Fig. 29 Radial profiles in run R1-P2, vertically averaged through the disk from 500T0 to 700T0, of the variations of angular velocity Ω relative to Keplerian ΩK (solid blue), and dimensionless radial shear ∂log ρ/∂log r (dashed red). |
| In the text | |
 |
Fig. 30 Space-time diagram of vertically and azimuthally averaged βz in runs R1-P3 (upper panel) and 3D-R1-P3 (lower panel); only the first 300T0 of the two-dimensional run are shown. |
| In the text | |
 |
Fig. 31 Symmetry coefficients σϕ and ιϕ in our set of 2D simulations, averaged over representative time intervals; colors indicate the initial midplane magnetization β, blue corresponding to Bz< 0; runs in [ 1,10 ] au are plotted with circles, runs in [ 10,100 ] au are plotted with squares; different background colors correspond to different disk-corona temperature contrast k; the error bars correspond to standard deviations over time. |
| In the text | |
 |
Fig. 32 Evolution of the toroidal magnetic field Bϕ along a vertical cut at r = 5r0 and over the first 150T0 (color scale) of run R10-M3-C2 (accreting); values have been normalized by the initial, unsigned vertical field at this radius. |
| In the text | |
 |
Fig. 33 Wind mass loss rate relative to the disk mass ṁW/md as a function of the initial midplane magnetization β; the symbols and color coding are the same as in Fig. 31; the two dashed lines indicate the ṁW ~ β− 1/2 scaling for R1 and R10 runs, bottom and top, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.