| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201629369 | |
| Published online | 24 March 2017 | |
Evolution of the real-space correlation function from next generation cluster surveys
Recovering the real-space correlation function from photometric redshifts
1 Université Côte d’Azur, OCA, CNRS, Lagrange, UMR 7293, CS 34229, 06304 Nice Cedex 4, France
e-mail: ssridhar@oca.eu
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 Dipartimento di Fisica e Astronomia – Università di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
4 INFN–Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
Received: 22 July 2016
Accepted: 1 December 2016
Context. The next generation of galaxy surveys will provide cluster catalogues probing an unprecedented range of scales, redshifts, and masses with large statistics. Their analysis should therefore enable us to probe the spatial distribution of clusters with high accuracy and derive tighter constraints on the cosmological parameters and the dark energy equation of state. However, for the majority of these surveys, redshifts of individual galaxies will be mostly estimated by multiband photometry which implies non-negligible errors in redshift resulting in potential difficulties in recovering the real-space clustering.
Aims. We investigate to which accuracy it is possible to recover the real-space two-point correlation function of galaxy clusters from cluster catalogues based on photometric redshifts, and test our ability to detect and measure the redshift and mass evolution of the correlation length r0 and of the bias parameter b(M,z) as a function of the uncertainty on the cluster redshift estimate.
Methods. We calculate the correlation function for cluster sub-samples covering various mass and redshift bins selected from a 500 deg2 light-cone limited to H < 24. In order to simulate the distribution of clusters in photometric redshift space, we assign to each cluster a redshift randomly extracted from a Gaussian distribution having a mean equal to the cluster cosmological redshift and a dispersion equal to σz. The dispersion is varied in the range 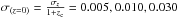 and 0.050, in order to cover the typical values expected in forthcoming surveys. The correlation function in real-space is then computed through estimation and deprojection of wp(rp). Four mass ranges (from Mhalo > 2 × 1013h-1M⊙ to Mhalo > 2 × 1014h-1M⊙) and six redshift slices covering the redshift range [0, 2] are investigated, first using cosmological redshifts and then for the four photometric redshift configurations.
and 0.050, in order to cover the typical values expected in forthcoming surveys. The correlation function in real-space is then computed through estimation and deprojection of wp(rp). Four mass ranges (from Mhalo > 2 × 1013h-1M⊙ to Mhalo > 2 × 1014h-1M⊙) and six redshift slices covering the redshift range [0, 2] are investigated, first using cosmological redshifts and then for the four photometric redshift configurations.
Results. From the analysis of the light-cone in cosmological redshifts we find a clear increase of the correlation amplitude as a function of redshift and mass. The evolution of the derived bias parameter b(M,z) is in fair agreement with theoretical expectations. We calculate the r0−d relation up to our highest mass, highest redshift sample tested (z = 2,Mhalo > 2 × 1014h-1M⊙). From our pilot sample limited to Mhalo > 5 × 1013h-1M⊙(0.4 < z < 0.7), we find that the real-space correlation function can be recovered by deprojection of wp(rp) within an accuracy of 5% for σz = 0.001 × (1 + zc) and within 10% for σz = 0.03 × (1 + zc). For higher dispersions (besides σz > 0.05 × (1 + zc)), the recovery becomes noisy and difficult. The evolution of the correlation in redshift and mass is clearly detected for all σz tested, but requires a large binning in redshift to be detected significantly between individual redshift slices when increasing σz. The best-fit parameters (r0 and γ) as well as the bias obtained from the deprojection method for all σz are within the 1σ uncertainty of the zc sample.
Key words: galaxies: clusters: general / large-scale structure of Universe / techniques: photometric / methods: statistical
© ESO, 2017
1. Introduction
One of the major challenges in modern cosmology is to explain the observed acceleration of the cosmic expansion, determining if it is due to a positive cosmological constant, a time-varying dark energy component or a modified theory of gravity. Major galaxy surveys are currently ongoing or in preparation in order to address this fundamental question through the analysis of various complementary cosmological probes with different systematics, as for instance weak lensing, galaxy clustering (baryon acoustic oscillations, redshift-space distortions) and galaxy clusters. In fact galaxy cluster counts as a function of redshift and mass are sensitive to dark energy through their dependence on the volume element and on the structure growth rate. One intrinsic difficulty in constraining the cosmological models with galaxy cluster counts comes from uncertainties in cluster mass estimates and on the difficulty to calibrate related mass proxies. One can overcome this difficulty adding the information related to the clustering properties of clusters, due to the fact that their power spectrum amplitude depends mainly on the halo mass. When combining the redshift-averaged cluster power spectrum and the evolution of the number counts in a given survey, the constraints on the dark energy equation of state are dramatically improved (Majumdar & Mohr 2004). Recent cosmological forecasting based on galaxy clusters confirms that the figure of merit significantly increases when adding cluster clustering information (Sartoris et al. 2016).
Cluster clustering can be measured through the two-point correlation function, the Fourier transform of the power spectrum, which is one of the most successful statistics for analysing clustering processes (Totsuji & Kihara 1969; Peebles 1980). In cosmology, it is a standard tool to test models of structure formation and evolution. The cluster correlation function is much higher than that of galaxies, as first shown by Bahcall & Soneira (1983) and Klypin & Kopylov (1983). This is a consequence of the fact that more massive haloes correspond to higher and rarer density fluctuations, which have a higher correlation amplitude (Kaiser 1984). Galaxy clusters are associated to the most massive virialised dark matter haloes, and as a consequence their correlation function is strongly amplified. The evolution of the cluster halo mass, bias and clustering has been addressed analytically (Mo & White 1996; Moscardini et al. 2000; Sheth et al. 2001), and also numerically (Governato et al. 1999; Angulo et al. 2005; Estrada et al. 2009). The increase of the correlation length with cluster mass and redshift has been used to constrain the cosmological model and the bias (Colberg et al. 2000; Bahcall et al. 2004; Younger et al. 2005).
The first large local surveys such as the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2011) have led to significant progress in this field. Clustering properties of cluster catalogues derived from SDSS were done by Estrada et al. (2009), Hütsi (2010) and Hong et al. (2012). More recently, Veropalumbo et al. (2014) have shown the first unambiguous detection of the Baryon Acoustic Oscillation (BAO) peak in a spectroscopic sample of ~25 000 clusters selected from the SDSS, and measured the peak location at 104 ± 7h-1 Mpc. Large surveys at higher redshifts which are ongoing such as the Dark Energy Survey (DES), Baryon Oscillation Spectroscopic Survey (BOSS), Kilo-Degree Survey (KIDS) and Panoramic Survey Telescope and Rapid Response System (Pan-STARRS) or in preparation such as the extended Roentgen Survey with an Imaging Telescope Array (eROSITA), Large Synoptic Survey Telescope (LSST) and Euclid open a new window for the analysis of cluster clustering. The wide areas covered will give access to unprecedented statistics (~100 000 clusters expected with DES, eROSITA and Euclid survey) that will allow us to cover the high mass, high redshift tail of the mass distribution, to control cosmic variance, and to map the large scales at which the BAO signature is expected (~ 100 Mpc).
However, among the several difficulties to be overcome in using clusters as cosmological probes is the impact of photometric redshift errors. While some of these surveys have (in general partially) a spectroscopic follow up, many forthcoming large galaxy surveys will have only the photometric information in multiple bands, so that their cluster catalogues will be built on the basis of state-of-the-art photometric redshifts. Using those instead of real redshifts will cause a positional uncertainty along the line of sight inducing a damping of clustering at small scales and a smearing of the acoustic peak (Estrada et al. 2009). It is therefore of major interest to check the impact of this effect on the recovery of the real-space correlation function. Our objective is to optimize the analysis of cluster clustering from forthcoming cluster catalogues that will be issued from the ongoing and future large multiband photometric surveys. Here we focus on the determination of the two-point correlation function, and the aim of our paper is i) to determine the clustering properties of galaxy clusters from state-of-the-art simulations where galaxy properties are derived from semi-analytical modelling (Merson et al. 2013), and ii) to test how much the clustering properties evidenced on ideal mock catalogues can be recovered when degrading the redshift information to reproduce the photometric uncertainty on redshift expected in future cluster experiments.
The paper is organised as follows. In Sect. 2 we describe the simulation with which we work. In Sect. 3 we investigate the two-point correlation function evolution with redshift and mass without any error on the redshift to check consistency with theory. The bias is calculated for different mass cut samples along with the evaluation of clustering strength with mass at different redshift and is compared with the theoretical expectation of Tinker et al. (2010). We also calculate the mean intercluster comoving separation (d) and compare it with r0, and perform an analytic fit to this r0 vs. d relation. Section 4 presents the deprojection method we use to recover the real-space correlation function from mock photometric catalogues generated using a Gaussian approximation technique. The results obtained from the deprojection method along with the redshift evolution of the samples with redshift uncertainty are presented. In Sect. 5, the overall results obtained from our study are summarised and discussed.
2. Simulations
We use a public light-cone catalogue constructed using a semi-analytic model of galaxy formation (Merson et al. 2013) onto the N-body dark matter halo merger trees of the Millennium Simulation, based on a lambda cold dark matter (ΛCDM) cosmological model with the following parameters: ΩM,ΩΛ,Ωb,h = 0.25,0.75,0.045,0.73 (Springel et al. 2005), corresponding to the first year results from the Wilkinson Microwave Anisotropy Probe (Spergel et al. 2007). The Millennium simulation was carried out using a modified version of the GADGET2 code (Springel 2005). Haloes in the simulation were resolved with a minimum of 20 particles, with a resolution of Mhalo = 1.7 × 1010h-1M⊙ (M⊙ represents the mass of the Sun). The groups of dark matter particles in each snapshot were identified through a Friends-Of-Friends algorithm (FOF) following the method introduced by Davis et al. (1985).
However, the algorithm was improved with respect to the original FOF, to avoid those cases where the FOF algorithm merge groups connected for example by a bridge, while they should be considered instead as separated haloes (Merson et al. 2013). The linking length parameter for the initial FOF haloes is b = 0.2. We notice, however, that haloes were identified with a method different from the standard FOF. The FOF algorithm was initially applied to find the haloes, but then their substructures were identified using the so-called SUBFIND algorithm: depending on the evolution of the substructures and their merging, a new final halo catalogue was built. The details of this method are described by Jiang et al. (2014).
A comparison between the masses obtained with this improved D-TREES algorithm, Mhalo, and the classical MFOF, and their relation with M200, was done by Jiang et al. (2014), where it is shown that at redshift z = 0 on average, Mhalo overestimates M200, but by a lower factor with respect to MFOF: they found that only 5% of haloes have Mhalo/M200> 1.5. However, when comparing the halo mass function of the simulation with that expected from the Tinker et al. (2010) approximation, it appears that there is a dependence on redshift, and beyond z ≈ 0.3 the Mhalo/M200 ratio becomes less than one (Mauro Roncarelli, priv. comm.). This has to be taken into account in further analysis using the masses.
Galaxies were introduced in the light-cone using the Lagos 12 GALFORM model (Lagos et al. 2012). The GALFORM model populates dark matter haloes with galaxies using a set of differential equations to determine how the baryonic components are regulated by “subgrid” physics. These physical processes are explained in detail in a series of papers (Bower et al. 2006; Font et al. 2008; Lagos et al. 2012; Merson et al. 2013; Guo et al. 2013; Gonzalez-Perez et al. 2014). The area covered by the light-cone is 500 deg2; the final mock catalogue is magnitude–limited to H = 24 (to mimic the Euclid completeness) with a maximum redshift at z = 3.
For each galaxy the mock catalogue provides different quantities, such as the identifier of the halo in which it resides, the magnitude in various passbands, right ascension and declination, and the redshift, both cosmological and including peculiar velocities. For each halo in the cluster mass range (see below), the redshift was estimated as the mean of the redshifts of its galaxies, while the central right ascension and declination were estimated as those of the brightest cluster galaxy (BCG), and by construction, the BCG is the centre of mass of the halo.
3. Evolution of the real-space two-point correlation function in the simulations
3.1. Estimation of the two-point correlation function
In order to measure the clustering properties of a distribution of objects, one of the most commonly used quantitative measure is the two-point correlation function (Totsuji & Kihara 1969; Davis & Peebles 1983). We can express the probability dP12(r) of finding two objects at the infinitesimal volumes dV1 and dV2 separated by a vector distance r (assuming homogeneity and isotropy on large scales, r = | r |): ![\begin{equation} \label{eqn:prob} {\rm d}P_{12} = n^{2}[1+\xi(r)]{\rm d}V_{1}{\rm d}V_{2} , \end{equation}](/articles/aa/full_html/2017/04/aa29369-16/aa29369-16-eq49.png) (1)where n is the mean number density and the two-point correlation function ξ(r) measures the excess probability of finding the pair relative to a Poisson distribution.
(1)where n is the mean number density and the two-point correlation function ξ(r) measures the excess probability of finding the pair relative to a Poisson distribution.
Among the various estimators of the correlation function discussed in the literature we use the Landy & Szalay (1993) estimator, which has the best performance (comparable to the Hamilton 1993 estimator) and is the most popular, being less sensitive to the size of the random catalogue and better in handling edge corrections (Kerscher et al. 2000): 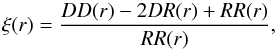 (2)where DD is the number of data-data pairs counted within a spherical shell of radius r and r + dr, DR refers to the number of data-random pairs, and RR refers to the random-random pairs.
(2)where DD is the number of data-data pairs counted within a spherical shell of radius r and r + dr, DR refers to the number of data-random pairs, and RR refers to the random-random pairs.
The peculiar motions of galaxies produce redshift-space distortions that have to be taken into account in order to recover the real-space clustering (Kaiser 1987); this means that Eq. (2) cannot be used directly to estimate the 3D real-space correlation function when distances are derived from redshifts. We will use it only for the analysis of simulations, where the cosmological redshift is available.
The real-space correlation function is expected to follow a power-law as a function of the separation r (Peebles 1980): 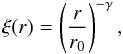 (3)where r0 is the correlation length and γ is the slope.
(3)where r0 is the correlation length and γ is the slope.
The random catalogues we use reproduce the cluster redshift selection function, estimated by smoothing the cluster redshift distribution through a kernel density estimation method. The bandwidth of the kernel is carefully adjusted in order to follow the global shape but not the clustering fluctuations in the redshift distribution. To ensure that, we use a Gaussian kernel two times larger than the bin size, and sample the data in 30 redshift bins. Figure 1 shows the redshift distributions of the simulation and of the random catalogue for the whole sample. The random catalogue is ten times denser than the simulated sample in order to minimize the effect of shot noise.
In the following, we estimate the correlation functions for different sub-samples of the original catalogue with different cuts in redshift and limiting mass. Errors are calculated from the covariance matrices using the jackknife resampling method (Zehavi et al. 2005; Norberg et al. 2011). To perform a jackknife estimate we divide the data into N equal sub-samples and we calculate the two-point correlation function omitting one sub-sample at a time. For k jackknife samples and i bins, the covariance matrix is then given by: 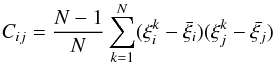 (4)where
(4)where 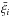 is the average of the values obtained for bin i. We make use of N = 9 sub-samples in our calculation.
is the average of the values obtained for bin i. We make use of N = 9 sub-samples in our calculation.
To measure the two-point correlation function for all our samples, we use CosmoBolognaLib (Marulli et al. 2016), a large set of Open Source C++ libraries for cosmological calculations1.
3.2. Redshift evolution of the cluster correlation function
 |
Fig. 1 Redshift distribution of the entire catalogue with 0.0 < zc < 3.0. The data distribution is shown as the histogram along with the blue line specifying the distribution of the random catalogue we use for calculating the two-point correlation function. |
 |
Fig. 2 Left panel: Correlation functions for clusters with Mhalo > 5 × 1013h-1M⊙ in six different redshift slices. The dashed lines show the corresponding power-law best-fits. The parameter values for the fits can be found in Table 1. Right panel: Correlation functions in the redshift slice 0.4 < zc < 0.7 for four different mass cuts (with units h-1M⊙). The dashed lines show the corresponding power-law best-fits. The parameter values for the fits can be found in Table 1. Error bars are the square root of the diagonal values of the covariance matrix calculated from the jackknife resampling method. |
 |
Fig. 3 Evolution of r0 and γ for clusters observed in different redshift slices and with mass Mhalo > 5 × 1013h-1M⊙. The values of r0 and γ can be found in the second panel of Table 1. |
The redshift evolution of the cluster correlation function has been studied both observationally (Bahcall & Soneira 1983; Huchra et al. 1990; Peacock & West 1992; Croft et al. 1997; Borgani et al. 1999; Veropalumbo et al. 2016, numerically (Bahcall et al. 2004Younger et al. 2005; Marulli et al. 2017) and theoretically (Mo & White 1996; Governato et al. 1999; Moscardini et al. 2000; Sheth et al. 2001). Two main results are prominent from these works:
-
The cluster correlation amplitude increases with redshift for bothlow- and high-mass clusters.
-
The increase of the correlation amplitude with redshift is stronger for more massive clusters compared to low-mass ones.
Future large surveys are expected to probe the high redshift domain with good statistics. This will enable us to study the redshift evolution of clustering on a large range of redshifts and provide independent cosmological tests (Younger et al. 2005). In this section, we investigate the expected redshift evolution of the cluster correlation function in the redshift range [0, 2], assuming a concordant ΛCDM model and using the light-cone catalogue detailed in Sect. 2.
The correlation functions for clusters with a mass cut of Mhalo> 5 × 1013h-1M⊙ are estimated in six redshift slices, from 0.1 < zc < 0.4 to 1.6 < zc < 2.1 (where zc refers to the cosmological redshift), and are shown in Fig. 2a. The figure shows that, as expected, the amplitude of the cluster correlation function increases with redshift.
For each sub-sample, the correlation function is fitted by a power-law (Eq. (3)) leaving both r0 and γ as free parameters. The results of the fits can be visualised in Fig. 3. The redshift range, the values of the best-fit parameters, the number of clusters, and the bias (discussed in Sect. 3.4) for each sub-sample are given in the second panel of Table 1. The fit is performed in the range 5−50 h-1 Mpc and the error bars are obtained using the jackknife estimate method (see Sect. 3.1).
The power-law has a relatively stable slope varying between 1.9 and 2.1. In the two highest redshift slices, however, the slope appears to be slightly higher, but the variation is at the ~ 2σ level for the 1.3 < zc < 1.6 sub-sample and at the ~ 1σ level for the 1.6 < zc < 2.1 sub-sample. On the average, γ ≈ 2.0 is close to the measured value for galaxy clusters as done by Totsuji & Kihara (1969) and Bahcall & West (1992) on observed galaxy clusters.
On the contrary, the increase in the correlation length is systematic and statistically significant. When we fix the slope at γ = 2.0, r0 is shown to increase from 11.97 ± 0.25h-1 Mpc for the lowest redshift slice (0.1 < zc < 0.4), to 20.05 ± 1.13h-1 Mpc for the highest redshift slice (1.6 < zc < 2.1). Our results can be compared to Younger et al. (2005, see their Fig. 5) and are in good agreement with their analysis of the high-resolution simulations of Hopkins et al. (2005).
3.3. The redshift evolution of clustering as a function of mass
In this section we investigate the redshift evolution of clustering as a function of mass. For this purpose, four different mass thresholds are considered: Mhalo > 2 × 1013h-1M⊙, Mhalo> 5 × 1013h-1M⊙, Mhalo > 1 × 1014h-1M⊙ and Mhalo > 2 × 1014h-1M⊙. The analysis is performed in the same redshift slices previously defined. The correlation function is fitted with a power-law as it can be seen from Fig. 2b, both with a free slope and with a fixed slope γ = 2.0. The mass range, the values of the best-fit parameters, the number of clusters, and the bias for each sub-sample are given in the four panels of Table 1. Each panel corresponds to a different selection in mass. In both cases, the correlation length r0 increases with the limiting mass at any redshift and increases with redshift at any limiting mass, as shown in Fig. 4. The higher the mass threshold, the larger is the increase of r0 with redshift. For example, the ratio of the correlation lengths for the [1.3–1.6] and the [0.1–0.4] redshift slices is 1.25 with Mhalo > 2 × 1013h-1M⊙, while it reaches 1.8 with Mhalo > 1 × 1014h-1M⊙. For the largest limiting mass (Mhalo > 2 × 1014h-1M⊙), the number of clusters becomes small at high z and the analysis must be limited to z = 1.
 |
Fig. 4 Evolution of r0 with redshift for different limiting masses (with units h-1M⊙). The filled symbols connected by solid lines correspond to the free slope fits, while the open symbols connected by dashed lines correspond to a fixed slope γ = 2.0. The different limiting masses are colour coded as shown in the figure. The values of r0 and γ for all the samples can be found in Table 1. |
 |
Fig. 5 Bias as a function of redshift for different limiting masses (with units h-1M⊙) where the solid lines just connect the points. The dashed line is the theoretical expectation of the bias as given by Tinker et al. (2010) for the same limiting masses and evolving redshift. The different limiting masses are colour coded as shown in the figure. The bias values for all the samples can be found in Table 1. |
Best-fit values of the parameters of the real-space correlation function ξ(r) for the light-cone at different (1) mass thresholds and (2) redshift ranges.
We can again compare our results with the analysis of Younger et al. (2005). who used a Tree Particle Mesh (TPM) code (Bode & Ostriker 2003) to evolve N = 12603 particles in a box of 1500 h-1 Mpc, reaching a redshift z ≈ 3.0. We find a good agreement (see their Fig. 5) for the common masses and redshift ranges tested; our analysis probes the correlation function of Mhalo> 1 × 1014h-1M⊙ clusters up to z ≈ 1.6, and of Mhalo> 2 × 1014h-1M⊙ clusters up to z ≈ 0.8, thus extending the r0(z) evolution shown by Younger et al. (2005) to higher redshifts for these high mass clusters.
3.4. Bias evolution
Starting from the initial matter density fluctuations, structures grow with time under the effect of gravity. The distribution of haloes, and hence of galaxies and clusters, is biased with respect to the underlying matter distribution, and on large scales it is expected that the bias is linear: 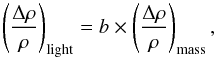 (5a)where b is the bias factor and ρ is the density. The higher the halo mass, the higher the bias. The amplitude of the halo correlation function is amplified by a b2 factor with respect to the matter correlation function:
(5a)where b is the bias factor and ρ is the density. The higher the halo mass, the higher the bias. The amplitude of the halo correlation function is amplified by a b2 factor with respect to the matter correlation function: 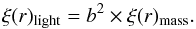 (5b)
The amplitude of the matter correlation function increases with time and decreases with redshift, but the halo bias decreases with time and increases with redshift. As a result, the cluster correlation amplitude increases with redshift, as shown clearly in Fig. 3.
(5b)
The amplitude of the matter correlation function increases with time and decreases with redshift, but the halo bias decreases with time and increases with redshift. As a result, the cluster correlation amplitude increases with redshift, as shown clearly in Fig. 3.
We estimate the cluster bias through Eq. (5b). The power spectrum of the dark matter distribution is calculated with the cosmological parameters of the light-cone we use and we obtain its Fourier transform ξ(r). We use the function xi_DM from the class Cosmology from CosmoBolognaLib. The comparison is not straightforward because, as we have previously noticed, in the simulation halo masses are not M200, but the so-called Dhalos masses Mhalo.
The evolution of bias with redshift for the four sub-samples with different limiting masses is shown in Fig. 5 along with the theoretical predictions of Tinker et al. (2010) for the same limiting masses used. The values of the bias for the different sub-samples are provided in Table 1. We can see that at fixed redshifts more massive clusters have a higher bias; at fixed mass threshold the bias increases with redshift, and evolves faster at higher redshifts. It can also be seen clearly that the bias obtained for the haloes from the simulations are in good agreement with the predictions by Tinker et al. (2010).
At high redshifts (z> 0.8) the bias recovered from the simulations seems to slightly diverge from the theoretical predictions, especially for the Mhalo> 1 × 1014h-1M⊙ sample, but this can be explained by the dependence on redshift for the Mhalo/M200 ratio which becomes smaller than one at these redshifts as previously mentioned. The discrepancy is not significant as our bias measurements are well within 1σ precision from the theoretical expectations.
3.5. The r0 – d relation
The dependence of the bias on the cluster mass is based on theory. A complementary and empirical characterization of the cluster correlation function is the dependence of the correlation length r0 as a function of the mean cluster comoving separation d (Bahcall & Soneira 1983; Croft et al. 1997; Governato et al. 1999; Bahcall et al. 2003), where: ![\begin{equation} d = \sqrt[3]{\tfrac{1}{\rho}} \end{equation}](/articles/aa/full_html/2017/04/aa29369-16/aa29369-16-eq107.png) (6)and ρ is the mean number density of the cluster catalogue on a given mass threshold.
(6)and ρ is the mean number density of the cluster catalogue on a given mass threshold.
According to the theory, more massive clusters have a higher bias, therefore a higher r0; as they are also more rare, they have also a larger mean separation: therefore it is expected that r0 increases with d, that is, r0 = αdβ.
This relation has been investigated both in observational data (Bahcall & West 1992; Estrada et al. 2009) and in numerical simulations (Bahcall et al. 2003; Younger et al. 2005). Younger et al. (2005) gave an analytic approximation in the ΛCDM case in the redshift range z = 0–0.3 for 20 ≤ d ≤ 60h-1 Mpc, with α = 1.7 and β = 0.6.
We determine the r0 dependence with d for the various sub-samples previously defined. The results obtained for a free γ along with the best fit obtained for both free and fixed γ = 2 are shown in Fig. 6. The best-fit parameters for the r0 - d relation in the redshift range 0 ≤ z ≤ 2.1 and for the cluster mean separation range 20 ≤ d ≤ 140 h-1 Mpc are, α = 1.77 ± 0.08 and β = 0.58 ± 0.01. The r0−d relation which appears to be scale-invariant with redshift, is consistent with what was found by Younger et al. (2005) and is also consistent with the theoretical predictions of Estrada et al. (2009, see their Fig. 7).
The scale invariance of the r0−d relation up to a redshift z ≈ 2.0 implies that the increase of the cluster correlation strength with redshift is matched by the increase of the mean cluster separation d. It suggests that the cluster mass hierarchy does not evolve significantly in the tested redshift range: for example, the most massive clusters at an earlier epoch will still be among the most massive at the current epoch.
 |
Fig. 6 Evolution of r0 with d for clusters of different masses in different redshift slices. The points plotted are for the fixed slope γ = 2.0. The green dashed line shows the fit when γ = 2.0 and the red dashed line shows the overall fit obtained for the data points considering a free slope. The analytic approximation in the ΛCDM case obtained by Younger et al. (2005) is shown by the dashed black line. The different redshift slices are colour coded as mentioned in the figure. |
4. Estimating the correlation function with photometric redshifts
Large redshift surveys such as SDSS (Eisenstein et al. 2011), VIMOS VLT Deep Survey (VVDS; Le Fèvre et al. 2005), VIMOS Public Extragalactic Redshift Survey (VIPERS; Garilli et al. 2014; Guzzo et al. 2014) have revolutionised our tridimensional vision of the Universe. However, as spectroscopic follow-up is a very time consuming task, priority has been given either to the sky coverage or to the depth of the survey. An alternative way of recovering the redshift information is to derive it from imaging in multiple bands when available, using the technique of photometry (Ilbert et al. 2006, 2009). While the accuracy of spectroscopic redshifts cannot be reached, this method can be successfully used for several purposes such as, for instance, cluster detection. Several major surveys that will provide imaging in multiple bands and thereby photometric redshifts are in progress or in preparation. For instance, the ongoing DES aims to cover about 5000 deg2 of the sky with a photometric accuracy of σz ≈ 0.08 out to z ≈ 1 (Sánchez et al. 2014). Future surveys such as LSST (Ivezic et al. 2008; LSST Science Collaboration et al. 2009) and Euclid (Laureijs et al. 2011) are expected to make a significant leap forward. For instance, the Euclid Wide Survey, planned to cover 15 000 deg2, is expected to deliver photometric redshifts with uncertainties lower than σz/ (1 + z) < 0.05 (and possibly σz/ (1 + z) < 0.03) (Laureijs et al. 2011) over the redshift range [0, 2]. The performances of photometric redshift measurements have significantly increased over the last decade, making it possible to perform different kinds of clustering analysis which were previously the exclusive domain of spectroscopic surveys. In this section we investigate how well we can recover the cluster correlation function for a sample of clusters with photometric redshifts and test the impact of the photometric redshift errors in redshift and mass bins.
4.1. Generation of the photometric redshift distribution of haloes
From the original light-cone we extracted mock cluster samples with photometric redshifts; these were assigned to each cluster by random extraction from a Gaussian distribution with mean equal to the cluster cosmological redshift and standard deviation equal to the assumed photometric redshift error of the sample.
In this way we built five mock samples with errors σ(z = 0) = σz/ (1 + zc) = 0.001,0.005,0.010,0.030,0.050. These values have been chosen to span the typical uncertainties expected in the context of upcoming large surveys.
The photometric redshift uncertainties in upcoming surveys are expected to be within 0.03 < σz/ (1 + z) < 0.05 for galaxies and within 0.01 < σz/ (1 + z) < 0.03 for clusters (Ascaso et al. 2015). Ideally, the error on the cluster redshift should scale proportionally to Nmem− 1/2 (where Nmem is the number of cluster members), therefore for clusters with ten detected members the error would be reduced by a factor three; but of course contamination from non-member galaxies will affect the redshift estimate.
 |
Fig. 7 Distribution of clusters selected in the top-hat cosmological redshift window compared with the clusters selected in the top-hat photometric redshift window. Filled histograms correspond to distribution of clusters as a function of cosmological redshift when the top-hat selection is done using the cosmological redshift within the range 0.4 < z < 0.7. Solid blue lines correspond to distribution of clusters as a function of cosmological redshift when the top-hat selection is done using the different photometric uncertainties we have used (σz/ (1 + zc) = 0.005, 0.010, 0.030 and 0.050) with the range 0.4 < z < 0.7 and the dashed blue lines correspond to the distribution of clusters as a function of cosmological redshift when the top-hat selection is done using photometric redshifts outside the range 0.4 < z < 0.7. |
4.2. Recovering the real-space correlation function: the method
In the following we will take into account separately the line of sight π and the transverse rp components of the two-point correlation function. Photometric redshifts affect only the line of sight component, introducing an anisotropy in the π−rp plane: the redshift-space correlation function will have a lower amplitude and steeper slope with respect to the real-space correlation function (Arnalte-Mur et al. 2009).
In order to recover the real-space correlation function of the photometric redshift mocks, we apply the deprojection method (Arnalte-Mur et al. 2009; Marulli et al. 2012). The method is based on Davis & Peebles (1983) and Saunders et al. (1992). Pairs are counted at different separations parallel (π) and perpendicular (rp) to the line of sight.
The comoving redshift space separation of the pair is defined as s ≡ x2−x1 and the line of sight vector is 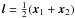 (Fisher et al. 1994). The parallel and perpendicular distances to the pair are given by:
(Fisher et al. 1994). The parallel and perpendicular distances to the pair are given by:  where
where 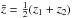 . Counting pairs in both (rp,π) dimensions will then provide the anisotropic correlation function ξ(rp,π) . The projected correlation function can be derived from ξ(rp,π)by:
. Counting pairs in both (rp,π) dimensions will then provide the anisotropic correlation function ξ(rp,π) . The projected correlation function can be derived from ξ(rp,π)by: 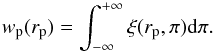 (8)The projected correlation function wp(rp) (Farrow et al. 2015) is related to the real-space correlation function ξ(r) by Eq. (9):
(8)The projected correlation function wp(rp) (Farrow et al. 2015) is related to the real-space correlation function ξ(r) by Eq. (9): 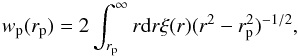 (9)which can be inverted to obtain the real-space correlation function:
(9)which can be inverted to obtain the real-space correlation function: 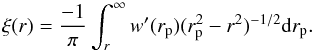 (10)Theoretically, the upper limits of integration are infinite, but in practice we need to choose finite values both in Eqs. (8) and (10) which then become:
(10)Theoretically, the upper limits of integration are infinite, but in practice we need to choose finite values both in Eqs. (8) and (10) which then become: 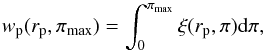 (11)and
(11)and 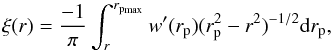 (12)where πmax and rpmax refer respectively to the maximum line of sight separation and the maximum transverse separation.
(12)where πmax and rpmax refer respectively to the maximum line of sight separation and the maximum transverse separation.
Given that above a certain value of π, pairs are uncorrelated and ξ(rp,π)drops to zero, it is possible to find an optimal choice for πmax. This will be explained in detail in Sect. 4.3.2. We estimate the real-space correlation function following the method of Saunders et al. (1992). We use a step function to calculate wp(rp), where wp(rp) = wp(i) in the logarithmic interval centred on rp(i), and we sum up in steps using the equation: 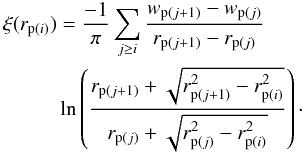 (13)Assuming that the correlation function follows a perfect power-law, wp(rp) is given by the formula:
(13)Assuming that the correlation function follows a perfect power-law, wp(rp) is given by the formula: 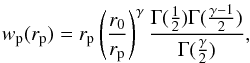 (14)where Γ is the Euler’s gamma function.
(14)where Γ is the Euler’s gamma function.
We compared the values of r0 (with fixed slope) obtained from the fit of the recovered deprojected correlation function ξdep(r) using Eq. (3). We also compared the values from the fit of wp(rp) with the same fixed slope using Eq. (14) and found it to be similar to what we obtain for the recovered deprojected correlation function ξdep(r).
4.3. Application to a cluster mock catalogue
4.3.1. Photo-z catalogue selection
As a first test, we applied the formalism described in the previous section to a mock cluster sample within the fixed redshift slice 0.4 < z < 0.7.
For each cluster, we assigned a photometric redshift zphot following the probability P(zphot | zc) = G(zc,σz) where σz = σ(z = 0) × (1 + zc). As mentioned in Crocce et al. (2011), doing the selection in a top-hat photometric redshift window and in a top-hat cosmological redshift window with the same boundaries is not equivalent. Figure 7 compares the distribution in cosmological redshift of the clusters selected in the top-hat cosmological redshift window 0.4 < zc < 0.7 (given by the filled histogram), the clusters selected by the top-hat photometric redshift window 0.4 < zphot < 0.7 (given by the solid blue line) and the clusters for which the photometric redshifts are outside the slice limits [0.4, 0.7] (given by the dashed blue line) for four of our photometric samples. The distribution in cosmological redshift N(zc) of the objects selected by the top-hat zphot window is broader than that selected by the top-hat zc window, and this effect increases with increasing σz. When performing the selection in zphot window rather than in zc window, a fraction of clusters with zc outside these slice limits but with zphot within the slice limits [0.4, 0.7] are included, resulting then as contaminants. The distribution of clusters with zphot outside the window [0.4, 0.7] is also shown as a dashed blue line. It shows that a fraction of clusters with zphot outside [0.4, 0.7] have zc within the slice limits [0.4, 0.7]. These objects are then lost by the top-hat photometric redshift selection.
The fraction of contaminating and missing clusters depends on the photometric redshift uncertainty and also on the N(z) distribution. We calculate the fraction of common objects between the top-hat zphot and zc selections for the different σz and redshift windows considered. It varies from 99% to 70% for samples with σz/ (1 + zc) = 0.001 (at z ≈ 0.1) to σz/ (1 + zc) = 0.050 (at z ≈ 1.3) respectively. Only the samples with σz/ (1 + zc) = 0.050 and above a redshift of z > 0.7 have less than 80% objects in common, as we know that the photo-z error scales as σz = σ(z = 0) × (1 + zc). In our case there are four samples that fall into this category (fourth panel of Table A.1). For all the other samples we chose, the average fraction of common clusters is more than 80% and so by choosing a direct cut in photo-z space, we expect that the final clustering is not affected by a huge margin. To calculate the effect of N(z) on contaminated and missing clusters, we calculate both the mean and median redshift for the photometric redshift samples we have. It can be seen from Table A.2 that both the mean and the median redshift do not vary much when compared to the mean and median redshift of the cosmological redshift sample. The percentage of contaminants for each redshift slice and given photometric uncertainty along with the Nclusters in zc and zphot window and the number of common clusters is mentioned in Table A.1.
 |
Fig. 8 Recovered correlation function (green line) compared with the real-space correlation function (red line) for five mock photometric samples in the redshift range 0.4 < z < 0.7, with increasing redshift uncertainty. Values of the best-fit parameters obtained are given in Table 2 and the quality of the recovery for each sample is given in Table 3. |
 |
Fig. 9 1σ (shaded brown) and 3σ (shaded green) error ellipses for the parameters r0 and γ. Top panel: Original catalogue with cosmological redshifts. Central and bottom panels: Mock catalogues with increasing photometric redshift errors. The solid star represents the centre of the ellipse for the original catalogue, while the cross denotes the centres of the other ellipses. |
 |
Fig. 10 Evolution of r0 and γ with redshift for clusters with a mass cut Mhalo> 5 × 1013h-1M⊙ for samples with increasing redshift uncertainty (σz/ (1 + zc) = 0.005, 0.010, 0.030 and 0.050). red (0.1 < z < 0.4), green (0.4 < z < 0.7), blue (0.7 < z < 1.0), indigo (1.0 < z < 1.3), gold (1.3 < z < 1.6), magenta (1.6 < z < 2.1). |
4.3.2. Selecting the integration limits
The ξ(rp,π) is calculated on a grid with logarithmically spaced bins both in rp and π. The maximum value of rp depends on the survey dimension in the transverse plane. In the redshift range 0.4 < z < 0.7, the maximum separation across the line of sight direction in our light-cone is ≈500h-1Mpc. For the upper limit of integration in Eq. (12) we fixed a value rp(max) = 400h-1 Mpc, corresponding to 80% of the maximum transversal separation. For higher redshift samples we are aware that the maximum separation across the line of sight increases, but we find that the value of 400 h-1 Mpc includes almost all correlated pairs without adding any noise.
In the case of clusters where we have low statistics as compared to galaxy catalogues, the choice of the bin width must be taken into account, if not the Poisson noise will dominate. A convergence test is performed for choosing the number and the width of bins in rp and πmax.
Since higher photometric errors produce larger redshift space distortions, a different value of πmax has to be fixed for each photometric redshift mock. We determine its value in the following way. We recover the real-space correlation function with the method described in Sect. 4.2, using increasing values of πmax. Initially the amplitude of ξdep(r) is underestimated because many correlated pairs are not taken into account; it increases when increasing πmax up to a maximum value, beyond which it starts to fluctuate and noise starts to dominate. Applying this test to each mock, we select the πmax value corresponding to the maximum recovered amplitude.
Main parameters used for the analysis of the original catalogue and the five mock photometric redshift catalogues.
Best-fit parameters obtained for the real-space correlation function ξ(r) of the original sample and the recovered deprojected correlation function ξdep(r) for the mock photometric redshift samples.
We show an example of the πmax test for the photometric sample with σz = 0.010 × (1 + zc). Figure 11 shows that the amplitude of the correlation function increases with increasing πmax, but only up to a certain value, which we call the maximum recovered amplitude. It can be seen that integrating the function above this value of πmax only results in noise.
 |
Fig. 11 Recovered correlation function with different values of πmax (as colour coded in the figure) for the sample with σz = 0.010 × (1 + zc) in the redshift range 0.4 < z < 0.7. The black line joining the diamonds in both the plots is the real-space correlation function calculated for the cosmological redshift sample (same as the red line in Fig. 8). Poisson error bars are plotted just for convenience. |
It is clear from our tests on simulations (see Fig. 11) that there is an optimal πmax value; integrating beyond that limit increases the noise. In future work on observed cluster samples, using the data themselves, we can examine the value of the observed correlation amplitude as a function of πmax, choosing the πmax value providing the maximum correlation amplitude.
We have checked that by applying this method to the original light-cone with cosmological redshifts we correctly recover its real-space correlation function. The values of πmax used for our reference sample (0.4 < z < 0.7) are given in Table 2.
4.3.3. The quality of the recovery
In Fig. 8 we compare ξdep(r) of our five mocks with the real-space correlation function ξ(r). It is clear that ξdep(r) reproduces quite well ξ(r), but shows increasing fluctuations with increasing σz. The ratio ξdep(r) /ξ(r) is slightly smaller than one but within 1σ at all scales for all the mocks up to σz/ (1 + zc) = 0.05.
The quality of the recovery is determined using Δξ, an “average normalised residual” defined by Arnalte-Mur et al. (2009) as: 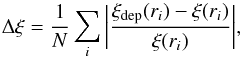 (15)where ri refers to the values in the ith bin considered and ξ(ri) is the real-space correlation function.
(15)where ri refers to the values in the ith bin considered and ξ(ri) is the real-space correlation function.
In the case of real data, where zc is not available, one can still calculate the quality of the recovery using the covariance matrix and is defined as: 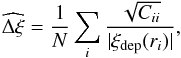 (16)wherein we use the covariance matrix that we have obtained using the jackknife resampling method mentioned in Eq. (4). The values of Δξ and
(16)wherein we use the covariance matrix that we have obtained using the jackknife resampling method mentioned in Eq. (4). The values of Δξ and 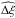 estimated in the range 5–50 h-1 Mpc, are listed in Table 2.
estimated in the range 5–50 h-1 Mpc, are listed in Table 2.
One can see from Table 2 that for the lowest photometric error considered, σz/ (1 + zc) = 0.001, the real-space correlation function is recovered within 5%. For σz/ (1 + zc) = 0.005 and σz/ (1 + zc) = 0.010 it is recovered within 7%, within 9% for σz/ (1 + zc) = 0.030, and finally within 15% for σz/ (1 + zc) = 0.05.
The best-fit parameters of the deprojected correlation functions are shown in Table 3. The fitting is performed with both a free and fixed slope γ = 2.0. The correlation length obtained for our five mock photometric samples is consistent within ~ 1σ with the real-space correlation length r0 = 13.20 ± 0.23h-1 Mpc and r0 = 13.16 ± 0.17h-1 Mpc obtained for the zc sample for ξ(r) (free slope) and ξ(r) (fixed slope) respectively. The best-fit r0 obtained for this particular sample (0.4 < zc < 0.7) seems to have a value that is always lower, regardless of the photometric uncertainty, when compared to the r0 obtained for the true zc sample. This is just a coincidence and is not always the case, as can be seen for other samples with different redshift limits. When the slope is set free, direct comparison of r0 between the samples cannot be made and so in Fig. 9 we plot the three sigma error ellipses around the best-fit values of r0 and γ for all the mocks. As expected, the errors on both r0 and γ increase with the photometric error, but are always within ~ 1σ with respect to the real space values.
We also applied the deprojection method for higher photometric redshift errors to test how far the method could be applied. It was found that from σz/ (1 + zc) = 0.1, the error on the recovery is very large and the recovered correlation function becomes biased.
4.3.4. Recovering the redshift evolution of the correlation function from sub-samples selected using photometric redshifts
We checked how accurately we can follow the redshift evolution of the cluster real-space correlation function when using photometric redshifts and the deprojection method to retrieve the real-space correlation function. We have previously shown this for the light-cone with cosmological redshifts in Fig. 3.
For this purpose, we analysed four mocks with redshift uncertainties of σz/ (1 + zc) = 0.005,0.010,0.030, and 0.050 respectively, in five redshift slices, from 0.1 < z < 0.4 to 1.6 < z < 2.1 with the same mass cut Mhalo> 5 × 1013h-1M⊙ as done in Sect. 3.2. The results are shown in Fig. 10 and the values of the best-fit parameters for all the four photometric samples are given in Table A.2 along with the number of clusters (Nclusters) and the mean and median redshift for each sample.
Figure 10 shows the evolution of the best-fit parameters r0 and γ for the different redshift slices. The four panels correspond to the different photometric redshift errors tested. It can be compared to Fig. 3 which shows the values of r0 and γ estimated for the same redshift slices but using cosmological redshifts. The fits are performed in the range within which ξ(r) can be described using a power-law. As in Fig. 3, r0 and γ are shown to increase with redshift but the errors on their estimates become larger as the photometric redshift error increases. As a result, the error bars on the r0 estimates for consecutive redshift slices tested tend to superimpose when considering large values of σz. The increase of r0 with redshift remains detectable, but a larger binning in redshift is needed to detect this effect significantly when working with large σz. We note that the parameters estimated from the deprojected correlation function are within 1σ from the ones estimated directly in real-space, and that remains true even for high redshifts and for high values of the photometric errors. The large error bars for the last two redshift slices (1.3 < z < 1.6 and 1.6 < z < 2.1) are both due to the small number of clusters at high redshift (see the histogram shown in Fig. 1) and the scaling of the photometric error σz = σ(z = 0) × (1 + zc). However, we can see that the low number of clusters makes the correlation function hard to measure even using cosmological redshifts. From our tests we can conclude that the correlation function can be recovered from photometric redshift surveys using the deprojection method up to a redshift of z ≈ 2.0 within 10% percent with a photometric redshift error of σz/ (1 + zc) = 0.030. In this sense, the recovery performed with this method can be considered as successful. Even in the last redshift slice chosen (1.6 < z < 2.1), the correlation function can be recovered within 1σ for all the four photometric redshift uncertainties tested. It can be numerically visualised in the last panel of Table A.2. This point is of particular importance as the 1.5 < z < 2.0 redshift range has been shown to be very discriminant for constraining cosmological parameters with clusters (Sartoris et al. 2016).
We also estimated the bias as defined in Sect. 3.4 for σz/ (1 + zc) = 0.005,0.010,0.030, and 0.050. Our values are given in Tables A.3 and A.4 along with the number of clusters (Nclusters) in each sample. The results can be seen in Fig. 12. The bias values obtained for the photo-z samples are consistent with the values obtained for the reference sample and are within 1σ error bars. For the first two mass cut samples (Mhalo > 2 × 1013h-1M⊙ and 5 × 1013h-1M⊙), the calculated bias from the photometric samples are within 1σ even up to a median redshift of z ≈ 1.8. Up to a mass cut of Mhalo > 1 × 1014h-1M⊙ one can see that the redshift evolution of the bias can be traced very well (even up to redshifts of z ≈ 1.5).
However we notice that for the highest mass cut sample (Mhalo > 2 × 1014h-1M⊙) chosen, only the bias values obtained for the photometric sample with σz/ (1 + zc) = 0.005 seem to be similar to that obtained by the reference sample. The remaining three photometric samples depict a much higher bias (even though they fall within 1σ) when compared to the reference sample. One reason for this behaviour and also for the large error bars for this mass cut sample is due to the smaller abundance of clusters at this mass threshold cut as it can be seen from Tables A.3 and A.4. We also believe that it could be due to the percentage of contaminants that are present in this mass cut sample for three different photometric uncertainties. We have calculated the contaminants for this mass cut sample and they seem to be higher at certain redshifts when compared to the contaminants at the same redshifts found for the low mass cut samples.
However, up to a mass cut of Mhalo> 5 × 1013h-1M⊙, the evolution in redshift and mass of the bias is clearly distinguished, that too up to the highest redshift tested (z ≈ 2.1).
 |
Fig. 12 Evolution of bias with redshift and mass (with units h-1M⊙) for the zc sample (solid lines) compared with the photometric samples (dashed lines) with redshift uncertainties of σz/ (1 + zc) = 0.005,0.010,0.030 and σz/ (1 + zc) = 0.050. |
5. Discussion and conclusions
In future, most of the cluster detections in large galaxy surveys will be based on photometric catalogues. Therefore the main aim of this work was to apply a method for recovering the spatial two-point correlation function ξ(r) of clusters using only photometric redshifts and assess its performance.
In order to estimate the real-space correlation function ξ(r), we applied a method originally developed to correct for peculiar velocity distortions, first estimating the projected correlation function wp(rp), then applying Eq. (12) to deproject it.
For our analysis we used the 500 deg2 light-cone of Merson et al. (2013). Mock photometric redshifts were generated from the cosmological redshifts assuming a Gaussian error σz = σ(z = 0) × (1 + zc) (as described in Sect. 4.1). This represents a first approximation, sufficient for the scope of the present work; a more realistic approach will have to include real photo-z distributions and catastrophic failures.
Here are our main results.
-
1.
We directly estimate the cluster correlation function in real-space (i.e. using cosmological redshifts) for sub-samples of the light-cone in different redshift intervals and with different mass thresholds (see Sects. 3.2 and 3.3). As expected, we find an increasing clustering strength with both redshift and mass threshold. At a fixed mass threshold, the correlation amplitude increases with redshift, while at a fixed redshift the correlation amplitude increases with mass threshold. The increase of the correlation amplitude with redshift is larger for more massive haloes: for example, for Mhalo > 2 × 1013h-1M⊙, r0 = 9.89 ± 0.20 at z = 0.25 and r0 = 12.41 ± 0.42 at z = 1.45; for Mhalo > 1 × 1014h-1M⊙, r0 = 14.60 ± 0.35 at z = 0.25 and r0 = 26.09 ± 4.10 at z = 1.45.
-
2.
We fit the relation between the clustering length r0 and the mean intercluster distance d in the redshift interval 0.1 ≤ z ≤ 2.1 up to z ≈ 2.0, finding r0 = 1.77 ± 0.08(d)0.58 ± 0.01h-1 Mpc, which is consistent with the relation r0 = 1.70(d)0.60h-1 Mpc obtained by Younger et al. (2005) for the local redshift range 0 ≤ z ≤ 0.3.
-
3.
We estimate the bias parameter directly in real-space (using cosmological redshifts), with different mass thresholds. Analogously to the correlation amplitude, the bias increases with redshift, and the increase is larger for more massive clusters. Our results are consistent with Estrada et al. (2009) and with the theoretical prediction of Tinker et al. (2010).
-
4.
We finally apply the deprojection method to recover the real-space correlation function ξ(r) of different sub-samples using photometric redshifts. We recover ξ(r) within ~7% on scales 5 < r < 50h-1 Mpc with a photometric error of σz/ (1 + zc) = 0.010 and within ~9% for samples with σz/ (1 + zc) = 0.030; the best–fit parameters of the recovered real–space correlation function, as well as the bias, are within 1σ of the corresponding values for the direct estimate in real-space, up to z ~ 2.
Our results are promising in view of future surveys such as Euclid and LSST that will provide state-of-the-art photometric redshifts over an unprecedented range of redshift scales. This work represents the first step towards a more complete analysis taking into account the different observational problems to be faced when determining cluster clustering from real data. We are planning to extend this study to the use of more realistic photo-z errors. We are also planning to apply the deprojection method to cluster catalogues produced by cluster detection algorithms. This implies taking into account the selection function of the cluster catalogue, and investigating the impact of purity and completeness on clustering. Another important issue to be faced is that mass in general is not available for cluster catalogues derived from data so that a proxy of mass such as richness has to be used. The fact that the scatter of the relation between mass and richness introduces another uncertainty has to be taken into account when using clusters for constraining the cosmological parameters (see e.g. Berlind et al. 2003; Kravtsov et al. 2004; Zheng et al. 2005; Rozo et al. 2009; Rykoff et al. 2012). Another important constraint for cosmological parameters is given by the BAO feature in the two-point correlation function (Veropalumbo et al. 2014, 2016). As we have pointed out in Sect. 2, the size of the light-cone we used (500 deg2) is not large enough to detect the BAO feature. It will be interesting to extend this analysis to forthcoming all-sky simulations to test if the BAO feature can be detected using photometric redshifts, and if so with what accuracy, in next generation surveys.
More information about CosmoBolognaLib can be found at http://apps.difa.unibo.it/files/people/federico.marulli3/CosmoBolognaLib/Doc/html/index.html
Acknowledgments
We thank Dr. Alex Merson (previously at University College London) and Carlton Baugh (Durham University) for fruitful discussions on the simulation used in this work. We thank Dr. Pablo Arnalte-Mur (Universitat de València) for a detailed discussion on the deprojection method used and Gianluca Castignani for giving us insights into the subjects of error analysis and other statistical methods used in this research. We would also like to thank the anonymous referee for helpful comments. The authors acknowledge the Euclid Consortium, the European Space Agency and the support of the agencies and institutes that have supported the development of Euclid. A detailed complete list is available on the Euclid web site (http://www.euclid-ec.org). We thank in particular the Agenzia Spaziale Italiana, the Centre National d’Études Spatiales, the Deutches Zentrum’ fur Luft- and Raumfahrt, the Danish Space Research Institute, the Fundação para a Cienca e a Tecnologia, the Ministerio de Economia y Competitividad, the National Aeronautics and Space Administration, the Netherlandse Onderzoekschool Voor Astronomie, the Norvegian Space Center, the Romanian Space Agency, the United Kingdom Space Agency and the University of Helsinki. Srivatsan Sridhar is supported by the Erasmus Mundus Joint Doctorate Program by Grant Number 2013-1471 from the agency EACEA of the European Commission. Christophe Benoist, Sophie Maurogordato and Srivatsan Sridhar acknowledge financial support from CNES/INSU131425 grant. This research made use of TOPCAT and STIL: Starlink Table/VOTable Processing Software developed by Taylor (2005) and also the Code for Anisotropies in the Microwave Background (CAMB; Lewis et al. 2000; Howlett et al. 2012). The Millennium Simulation databases (Lemson & Virgo Consortium 2006) used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. Srivatsan Sridhar would also like to thank Sridhar Krishnan, Revathy Sridhar and Madhumitha Srivatsan for their support and encouragement during this work.
References
- Angulo, R. E., Baugh, C. M., Frenk, C. S., et al. 2005, MNRAS, 362, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Arnalte-Mur, P., Fernández-Soto, A., Martínez, V. J., et al. 2009, MNRAS, 394, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Ascaso, B., Mei, S., & Benítez, N. 2015, MNRAS, 453, 2515 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & West, M. J. 1992, ApJ, 392, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Soneira, R. M. 1983, ApJ, 270, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., Dong, F., Hao, L., et al. 2003, ApJ, 599, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., Hao, L., Bode, P., & Dong, F. 2004, ApJ, 603, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Weinberg, D. H., Benson, A. J., et al. 2003, ApJ, 593, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, P., & Ostriker, J. P. 2003, ApJS, 145, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Borgani, S., Plionis, M., & Kolokotronis, V. 1999, MNRAS, 305, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Colberg, J. M., White, S. D. M., Yoshida, N., et al. 2000, MNRAS, 319, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Crocce, M., Cabré, A., & Gaztañaga, E. 2011, MNRAS, 414, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., Dalton, G. B., Efstathiou, G., Sutherland, W. J., & Maddox, S. J. 1997, MNRAS, 291, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Estrada, J., Sefusatti, E., & Frieman, J. A. 2009, ApJ, 692, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Farrow, D. J., Cole, S., Norberg, P., et al. 2015, MNRAS, 454, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, K. B., Davis, M., Strauss, M. A., Yahil, A., & Huchra, J. P. 1994, MNRAS, 267, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Bower, R. G., McCarthy, I. G., et al. 2008, MNRAS, 389, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez-Perez, V., Lacey, C. G., Baugh, C. M., et al. 2014, MNRAS, 439, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Babul, A., Quinn, T., et al. 1999, MNRAS, 307, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Angulo, R. E., et al. 2013, MNRAS, 428, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, T., Han, J. L., Wen, Z. L., Sun, L., & Zhan, H. 2012, ApJ, 749, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bahcall, N. A., & Bode, P. 2005, ApJ, 618, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Howlett, C., Lewis, A., Hall, A., & Challinor, A. 2012, JCAP, 1204, 027 [Google Scholar]
- Huchra, J. P., Henry, J. P., Postman, M., & Geller, J. M. 1990, ApJ, 365, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Hütsi, G. 2010, MNRAS, 401, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., Tyson, J. A., Abel, B., et al. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
- Jiang, L., Helly, J. C., Cole, S., & Frenk, C. S. 2014, MNRAS, 440, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, 13 [Google Scholar]
- Klypin, A. A., & Kopylov, A. I. 1983, Sov. Astron. Lett., 9, 41 [NASA ADS] [Google Scholar]
- Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Bayet, E., Baugh, C. M., et al. 2012, MNRAS, 426, 2142 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemson, G., & Virgo Consortium, t. 2006, ArXiv e-prints [arXiv:astro-ph/0608019] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- LSST Science Collaboration, Abell, P. A., Allison, J., et al. 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Majumdar, S., & Mohr, J. J. 2004, ApJ, 613, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Veropalumbo, A., & Moresco, M. 2016, Astron. Comput., 14, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Veropalumbo, A., Moscardini, L., Cimatti, A., & Dolag, K. 2017, A&A, 599, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merson, A. I., Baugh, C. M., Helly, J. C., et al. 2013, MNRAS, 429, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Moscardini, L., Matarrese, S., Lucchin, F., & Rosati, P. 2000, MNRAS, 316, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Norberg, P., Gaztañaga, E., Baugh, C. M., & Croton, D. J. 2011, MNRAS, 418, 2435 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., & West, M. J. 1992, MNRAS, 259, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton, N.J.: Princeton University Press), 435 [Google Scholar]
- Rozo, E., Rykoff, E. S., Koester, B. P., et al. 2009, ApJ, 703, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Koester, B. P., Rozo, E., et al. 2012, ApJ, 746, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, C., Carrasco Kind, M., Lin, H., et al. 2014, MNRAS, 445, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoris, B., Biviano, A., Fedeli, C., et al. 2016, MNRAS, 459, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., & Lawrence, A. 1992, MNRAS, 258, 134 [NASA ADS] [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Totsuji, H., & Kihara, T. 1969, PASJ, 21, 221 [NASA ADS] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2014, MNRAS, 442, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2016, MNRAS, 458, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Bahcall, N. A., & Bode, P. 2005, ApJ, 622, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2005, ApJ, 630, 1 [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Values of best-fit parameters from the two-point correlation fit and bias values for photometric redshift catalogues
Table A.2 shows the values of the best-fit parameters (as shown in Fig. 10) for the two-point correlation function of the four sub-samples with redshift errors σz/ (1 + zc) = 0.005,0.010,0.030, and 0.050, and the corresponding values obtained for the parent catalogue with cosmological redshift (zc).
Number of clusters in a given redshift range for zc and zphot with mass cut Mhalo > 5 × 1013h-1M⊙.
For the same four sub-samples and the parent sample with cosmological redshift (zc), Tables A.3 and A.4 show the bias values (see also Fig. 12).
Parameters obtained from the fit for the real-space correlation function ξ(r) on the ideal zero-error simulation for the different redshift cut catalogues and the same obtained from the photometric redshift catalogues with σz/ (1 + zc) = 0.005,0.010,0.030, and 0.050.
Bias values obtained for the first two photometric redshift catalogues (σz/ (1 + zc) = 0.005 and 0.010) with the four mass threshold cuts in the five redshift bins used.
Bias values obtained for the last two photometric redshift catalogues (σz/ (1 + zc) = 0.030 and 0.050) with the four mass threshold cuts in the five redshift bins used.
All Tables
Best-fit values of the parameters of the real-space correlation function ξ(r) for the light-cone at different (1) mass thresholds and (2) redshift ranges.
Main parameters used for the analysis of the original catalogue and the five mock photometric redshift catalogues.
Best-fit parameters obtained for the real-space correlation function ξ(r) of the original sample and the recovered deprojected correlation function ξdep(r) for the mock photometric redshift samples.
Number of clusters in a given redshift range for zc and zphot with mass cut Mhalo > 5 × 1013h-1M⊙.
Parameters obtained from the fit for the real-space correlation function ξ(r) on the ideal zero-error simulation for the different redshift cut catalogues and the same obtained from the photometric redshift catalogues with σz/ (1 + zc) = 0.005,0.010,0.030, and 0.050.
Bias values obtained for the first two photometric redshift catalogues (σz/ (1 + zc) = 0.005 and 0.010) with the four mass threshold cuts in the five redshift bins used.
Bias values obtained for the last two photometric redshift catalogues (σz/ (1 + zc) = 0.030 and 0.050) with the four mass threshold cuts in the five redshift bins used.
All Figures
 |
Fig. 1 Redshift distribution of the entire catalogue with 0.0 < zc < 3.0. The data distribution is shown as the histogram along with the blue line specifying the distribution of the random catalogue we use for calculating the two-point correlation function. |
| In the text | |
 |
Fig. 2 Left panel: Correlation functions for clusters with Mhalo > 5 × 1013h-1M⊙ in six different redshift slices. The dashed lines show the corresponding power-law best-fits. The parameter values for the fits can be found in Table 1. Right panel: Correlation functions in the redshift slice 0.4 < zc < 0.7 for four different mass cuts (with units h-1M⊙). The dashed lines show the corresponding power-law best-fits. The parameter values for the fits can be found in Table 1. Error bars are the square root of the diagonal values of the covariance matrix calculated from the jackknife resampling method. |
| In the text | |
 |
Fig. 3 Evolution of r0 and γ for clusters observed in different redshift slices and with mass Mhalo > 5 × 1013h-1M⊙. The values of r0 and γ can be found in the second panel of Table 1. |
| In the text | |
 |
Fig. 4 Evolution of r0 with redshift for different limiting masses (with units h-1M⊙). The filled symbols connected by solid lines correspond to the free slope fits, while the open symbols connected by dashed lines correspond to a fixed slope γ = 2.0. The different limiting masses are colour coded as shown in the figure. The values of r0 and γ for all the samples can be found in Table 1. |
| In the text | |
 |
Fig. 5 Bias as a function of redshift for different limiting masses (with units h-1M⊙) where the solid lines just connect the points. The dashed line is the theoretical expectation of the bias as given by Tinker et al. (2010) for the same limiting masses and evolving redshift. The different limiting masses are colour coded as shown in the figure. The bias values for all the samples can be found in Table 1. |
| In the text | |
 |
Fig. 6 Evolution of r0 with d for clusters of different masses in different redshift slices. The points plotted are for the fixed slope γ = 2.0. The green dashed line shows the fit when γ = 2.0 and the red dashed line shows the overall fit obtained for the data points considering a free slope. The analytic approximation in the ΛCDM case obtained by Younger et al. (2005) is shown by the dashed black line. The different redshift slices are colour coded as mentioned in the figure. |
| In the text | |
 |
Fig. 7 Distribution of clusters selected in the top-hat cosmological redshift window compared with the clusters selected in the top-hat photometric redshift window. Filled histograms correspond to distribution of clusters as a function of cosmological redshift when the top-hat selection is done using the cosmological redshift within the range 0.4 < z < 0.7. Solid blue lines correspond to distribution of clusters as a function of cosmological redshift when the top-hat selection is done using the different photometric uncertainties we have used (σz/ (1 + zc) = 0.005, 0.010, 0.030 and 0.050) with the range 0.4 < z < 0.7 and the dashed blue lines correspond to the distribution of clusters as a function of cosmological redshift when the top-hat selection is done using photometric redshifts outside the range 0.4 < z < 0.7. |
| In the text | |
 |
Fig. 8 Recovered correlation function (green line) compared with the real-space correlation function (red line) for five mock photometric samples in the redshift range 0.4 < z < 0.7, with increasing redshift uncertainty. Values of the best-fit parameters obtained are given in Table 2 and the quality of the recovery for each sample is given in Table 3. |
| In the text | |
 |
Fig. 9 1σ (shaded brown) and 3σ (shaded green) error ellipses for the parameters r0 and γ. Top panel: Original catalogue with cosmological redshifts. Central and bottom panels: Mock catalogues with increasing photometric redshift errors. The solid star represents the centre of the ellipse for the original catalogue, while the cross denotes the centres of the other ellipses. |
| In the text | |
 |
Fig. 10 Evolution of r0 and γ with redshift for clusters with a mass cut Mhalo> 5 × 1013h-1M⊙ for samples with increasing redshift uncertainty (σz/ (1 + zc) = 0.005, 0.010, 0.030 and 0.050). red (0.1 < z < 0.4), green (0.4 < z < 0.7), blue (0.7 < z < 1.0), indigo (1.0 < z < 1.3), gold (1.3 < z < 1.6), magenta (1.6 < z < 2.1). |
| In the text | |
 |
Fig. 11 Recovered correlation function with different values of πmax (as colour coded in the figure) for the sample with σz = 0.010 × (1 + zc) in the redshift range 0.4 < z < 0.7. The black line joining the diamonds in both the plots is the real-space correlation function calculated for the cosmological redshift sample (same as the red line in Fig. 8). Poisson error bars are plotted just for convenience. |
| In the text | |
 |
Fig. 12 Evolution of bias with redshift and mass (with units h-1M⊙) for the zc sample (solid lines) compared with the photometric samples (dashed lines) with redshift uncertainties of σz/ (1 + zc) = 0.005,0.010,0.030 and σz/ (1 + zc) = 0.050. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


