| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526454 | |
| Published online | 05 April 2017 | |
SOFIA/GREAT [C ii] observations in nearby clouds near the lines of sight towards B0355+508 and B0212+735 ⋆
1 I. Physikalisches Institut Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
e-mail: glueck@ph1.uni-koeln.de
2 SOFIA-USRA, NASA Ames Research Center, Mail Stop 232-12, Moffett Field, CA 94035-0001, USA
3 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 3 May 2015
Accepted: 23 May 2016
We present SOFIA/GREAT [C ii] 2P3/2 →2P1/2 (1.9005369 THz) observations of nearby clouds near the lines of sight towards the quasars B0355+508 and B0212+735. These clouds have previously been identified as warm non-LTE diffuse clouds with a temperature of T ≳ 30 K and sub-thermally excited CO lines. They are highly structured in CO with small-scale bright spots (I(CO J = 1–0)~ 5–20 K km s-1), both spectrally and spatially. This small-scale structure has been interpreted as small-scale variations in the chemistry, not as density and column-density structure. We did not detect [C ii] 158 μm emission within the rms noise of ~0.1–0.3 K. Our non-detection in [C ii] contradicts the above scenario. In diffuse clouds, the efficiency of photo-electric heating is highest. Under the assumption that [C ii] is the dominant coolant in diffuse clouds, we can calculate the predicted [C ii] emission arising from these clouds. Based on the derived hydrogen column densities for the diffuse clouds, a line width in [C ii] of similar order to that of CO, and when at least the minimum amount of heating in the clouds is due to cosmic-ray heating, [C ii] line intensities ≳1.5 to 5 K km s-1 are expected, which is a factor ~3 to 15 above the upper limits of the observations. The upper limits of the [C ii] and the observed CO line intensities are, however, consistent with the intensities predicted for photon-dominated region (PDR) surfaces on regular cold (T ~ 15 K) low-density cloud fragments. Lower temperatures lead to less excited [C ii]. The assumption of lower densities, which would equally lower the [C ii] excitation, contradicts the observed cloud sizes and column densities. The CO(2–1)/CO(1–0) line ratios observed in these clouds are consistent with cloud temperatures of T ~ 15 K. The KOSMA-τ PDR-model of a cold moderate-density clump or an ensemble of such clumps with a canonical mass-size relation and mass spectrum, consistent with the total column densities derived for low density, shows that cold PDRs can reproduce the observed CO intensities, the observed CO(1–0) and CO(2–1) ratio, and the observed upper limits for [C ii].
Key words: ISM: clouds / photon-dominated region (PDR) / ISM: structure
The reduced spectra (FITS files) are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/600/A94
© ESO, 2017
1. Introduction
1.1. Conditions in diffuse clouds
Interstellar clouds are in general classified as diffuse, dense, or translucent (e.g. Snow & McCall 2006). Diffuse clouds have a typical column density of N(H)< 2 × 1021 cm-2 (Av< 1 mag), dense (and dark) clouds have a typical column density of N(H)~ 1022 cm-2 (Av> 4 mag), and the column densities of translucent clouds falls somewhere in between.
Diffuse and translucent clouds have been identified mainly by means of their absorption spectra against bright mm-wave or optical background sources (Sonnentrucker et al. 2007; Burgh et al. 2007; Sheffer et al. 2007, 2008) and by optical extinction mapping (Savage et al. 1977).
Liszt & Lucas (1998) succeeded in detecting CO(J = 1–0) and CO(J = 2–1) emission, identified to be associated with presumably diffuse clouds because of their matching velocity characteristics with mm-wave absorption spectra, in a representative sample of mm-wave absorption lines-of-sight against background quasar sources. Liszt & Pety (2012) were able to map the CO (1–0) emission with a few arcmin extent around these positions. The typical total hydrogen column density N(H) = N(H i) + 2N(H2) in these clouds was derived to be a few times 1021 cm-2 with a typical H2 fraction of ≲1/3 (Liszt et al. 2010; Liszt & Pety 2012).
The observations show that the clouds in the sample of Liszt & Pety (2012), presumably located near the edge of the Local Bubble at distances of about 150 pc from the Sun (Liszt & Pety 2012), are surprisingly highly structured with small-scale bright spots in CO, localised both spatially (≲1 × 10-2 pc) and spectrally (Δv ~ 1–2 km s-1).
Position of the [C ii] observations.
Small-scale CO variations were interpreted as variations in the chemistry and not the density, or column-density variations in the clouds (Pety et al. 2011). The observed high line intensities of CO (J = 1–0), typically I(CO)~ 5–20 K km s-1, together with the observed almost uniform CO (J = 2–1)/(J = 1–0) integrated intensity ratio of around 0.725 (Liszt & Lucas 1998; Pety et al. 2008), were explained as sub-thermal excitation in a diffuse cloud (Goldreich & Kwan 1974; Pety et al. 2008) with kinetic temperatures above 30 K, typically T ≈ 40–80 K (Pety et al. 2008). We note here that the CO (J = 2–1) vs. (J = 1–0) line ratios observed in the clouds towards B0355+508 by Pety et al. (2008), however, are also consistent with the ratio expected in cold (T ≈ 14K) dense gas (Pety et al. 2008). The CO spectra shown in Liszt & Lucas (1998) imply a similar CO (J = 2–1)/(J = 1–0) ratio for the clouds towards B0212+735 and B0355+508. The clouds furthermore show a mean 12CO/13CO brightness temperature ratio of T(12CO)/T(13CO)~ 10 to 15 (e.g. Pety et al. 2011). The ratio was explained by chemical fractionation of 12/13CO and 12/13C+ in diffuse clouds (Pety et al. 2008, 2011; Liszt et al. 2010). In the diffuse-cloud scenario the typical CO column densities are a few times 1016 cm2. The derived hydrogen column densities N(H) in diffuse clouds of a few times 1021 cm2 (cf. Sect. 4) imply that only about ~4–7% of the carbon in diffuse clouds is in the form of CO (Sofia et al. 2004; Pety et al. 2011). The majority of carbon (~90%) therefore must exist in another form, presumably ionised carbon [C ii] (Sofia et al. 2004; Liszt & Lucas 2000). Thus, the [C ii] 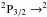 P1/2 fine-structure transition at 1.9005369 THz is the main cooling line in the diffuse intrastellar medium (ISM) (Dalgarno & McCray 1972; Tielens & Hollenbach 1985a). For the translucent regime the neutral carbon hyperfine transitions (
P1/2 fine-structure transition at 1.9005369 THz is the main cooling line in the diffuse intrastellar medium (ISM) (Dalgarno & McCray 1972; Tielens & Hollenbach 1985a). For the translucent regime the neutral carbon hyperfine transitions (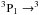 P0 and
P0 and 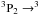 P1) are expected to contribute up to ~30% of the [C ii] cooling amount of the cloud cooling (Juvela et al. 2003).
P1) are expected to contribute up to ~30% of the [C ii] cooling amount of the cloud cooling (Juvela et al. 2003).
These predictions provided the motivation to search for the [C ii] emission from these clouds using SOFIA/GREAT1.
2. Observations and data processing
In November 2013 and February 2014 we performed [C ii] observations of the interstellar clouds near the lines of sight towards B0355+508 and B0212+735 (cf. Table 1 and Fig. 1) using the dual-channel single-pixel German REceiver for Astronomy at Terahertz frequencies (GREAT; Graf et al. 2006; Heyminck et al. 2012) on-board the airborne Stratospheric Observatory for Infrared Astronomy (SOFIA; Stutzki 2006; Becklin et al. 2007; Gehrz et al. 2009; Young et al. 2012). A Fourier transform spectrometer (FFTS) with 8192 channels and a bandwidth of 1.5 GHz was used, providing a native resolution of ~0.03 km s-1. The observations were performed in single-point total power mode.
 |
Fig. 1 Integrated CO (J = 1–0) emission around B0355+508 (Liszt & Pety 2012) and B0212+735 (Pety & Liszt, in prep.). Small crosses mark the positions observed in [C ii]. The large cross in the middle marks the lines of sight towards B0355+508 and B0212+735. The length of the white bar corresponds to 0.05 pc in B0355+508 and 0.1 pc in B0212+735 for an assumed source distances of 150 pc (Liszt & Pety 2012). |
Out of a sample of five sources, selected for their expected high [C ii] brightness from the CO maps by Liszt & Pety (2012), B0355+508 and B0212+735 were selected because they matched the flight plan of SOFIA.
In each individual source we observed two positions. One position was centred on the brightest CO emission (CO-peak). The second position was pointed towards a region with faint but clearly detectable CO emission (CO-void). These positions are marked in Fig. 1, and their coordinates are given in Table 1. This observation strategy was designed to collect information about the C+ abundance and [C ii] cooling in these clouds.
The off-source positions for B0355+508 and B0212+735 (coordinates see Table 1) were selected at regions with minimal 100 μm emission (IRAS, Neugebauer et al. 1984) and a minimal Av (from EB−V FIRAS/COBE measurements, Schlegel et al. 1998). Owing to their expected low column and volume densities, these positions are hence likely to be free of detectable [C ii]-emission. Additional CO(1–0) data of the B0212+735 off-position (Pety, priv. comm.) show these positions to be free of CO emission.
2.1. GREAT data processing
The calibration of the data was performed with the standard pipeline for GREAT data (Guan et al. 2012). All spectra were converted into a main-beam brightness temperature scale using 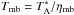 , with a main beam efficiency ηmb = 0.67 (Heyminck et al. 2012).
, with a main beam efficiency ηmb = 0.67 (Heyminck et al. 2012).
The [C ii] data were processed with the software package CLASS, version: jan14a2.
A fifth-order baseline was subtracted from all spectra. In spectra that showed sinusoidal standing wave patterns, sinusoidal baselines with standing wave periods between 8 and 27 km s-1 were fitted to the spectra. If the fit improved the rms by more than 20% compared to a linear baseline fit, the fitted sinusoidal pattern was subtracted from the spectrum.
The data for B0212+735 and B0355+508 were smoothed to 0.4 km s-1 and 0.8 km s-1, respectively, which is a factor ~3 below the CO line widths, for a better comparison.
2.2. Observational results
-
B0355+508
Sixteen minutes of integration time were spent on the CO-peak, and we achieved an rms of0.09 K in a velocity bin of0.8 km s-1, corresponding to one-third of the line width of the brightest CO line. Two minutes of integration time were spent on the CO-void, from which we achieved an rms of 0.17 K. In neither position did we detect [C ii] emission. The 3σ upper limit for [C ii] lines with widths corresponding to those of the CO lines thus are ≲0.37 K km s-1 for the CO-peak and ≲0.71 K km s-1 for the CO-void.
-
B0212+735
About ten minutes integration time were spent on each position in B0212+735. We reached an rms of ≈0.21 K in the CO-peak and ≈0.22 K in the CO-void in a velocity bin of 0.4 km s-1, corresponding to one-third of the line width of the CO line of ~1.5 km s-1. No line could be detected within the rms. The 3σ upper limit for the [C ii] line thus is ≲0.45 K km s-1 at both positions.
The listed 3σ limits are upper limits to the integrated [C ii]-line intensities, derived from the rms of the velocity bins given. Additional smoothing of the data shows no signs of [C ii] lines broader than the CO lines.
2.3. Complementary observations
In the following sections we discuss three positions for each cloud, the CO-peak (marked P), CO-void (V), and the line of sight (Q) towards the quasar. CO(1–0) emission spectra are available for all positions. HCO+ and H i absorption spectra are only available for the LOS towards the quasars.
Upper limits for the intensity compared to CO lines intensities of separated CO velocity components at the observed positions of the CO-peak and CO-void in B0355+508 and B0212+735.
The CO(2–1) and CO(1–0) emission spectra along the LOS towards the quasars have been observed by Liszt & Lucas (1998) and Liszt & Pety (2012). The CO(1–0) emission spectra towards the CO-peak and -void positions were extracted from maps with a few arcmin extent around the quasars observed by Liszt & Pety (2012) and Pety & Liszt (in prep.). As errors for the CO data we assumed standard calibration uncertainties of 15%.
HCO+ absorption along the line of sight towards the quasars B0355+508 and B0212+735 have been observed with the Plateau de Bure Interferometer by Lucas & Liszt (1996) and Liszt & Lucas (2000). Complementary H i 21 cm absorption spectra towards the quasars are available from Dickey et al. (1983).
 |
Fig. 2 [C ii] (black) and CO (red; Liszt & Pety 2012) spectra at the positions CO-peak and CO-void in B0355+508 (left) and B0212+735 (right). The spectra of B0355+508 are smoothed to a velocity resolution of Δv = 0.8 km s-1; B0212+735 spectra are smoothed to Δv = 0.4 km s-1. The blue dashed line shows the HCO+ absorption spectra along the lines of sight towards the quasars B0355+508 and 0212+735 (Liszt & Lucas 1996, 2000). The red letters mark CO velocity components in the CO-peak and the CO-void, blue letters mark HCO+ absorption components along the line of sight towards the quasar. Identical capital letters mark related velocity components in the three positions. For better clarity we do not show the identified HCO+ absorption component FQ at vLSR = 2.5 km s-1 in B0212+735 (cf. Table 3) reported by Lucas & Liszt (1996). |
3. CO, HCO+, and H i in B0355+508 and B0212+735
In the following we describe the individual velocity components seen in emission and absorption along the line of sight towards the quasars (Sects. 3.1 and 3.2). The association of these absorption components with corresponding CO emission components at the CO-peak and CO-void is discussed in Sects. 3.3 and 3.4.
3.1. Line of sight towards B0355+508
B0355+508 is located at a Galactic latitude of b = −1.6°. This low Galactic latitude implies that several diffuse clouds are observed simultaneously along the line of sight.
The H i absorption features in the spectra are very broad. The line width is ~55 km s-1 and the absorption is located between vLSR ≈ −40 km s-1 and +10 km s-1. Except for the molecular absorption features at vLSR = −10 km s-1 and vLSR = −8 km s-1 (velocity components CandD in Table 3), the H i absorption spectra show no direct correspondence to the molecular lines (cf. Liszt & Pety 2012). This implies that a large amount of H i is in the foreground and background of the source.
The molecular absorption line profiles of CO(1–0) and HCO+ show a complex structure along the line of sight towards B0355+508 (cf. Liszt & Pety 2012). Five individual HCO+ components can be distinguished between vLSR ≃ −17 km s-1 and vLSR ≃ −5 km s-1. Two CO emission components at vLSR ≈ −17.2 km s-1 and − 10.3 km s-1 can be observed. They are associated with the two HCO+ absorption velocity components AQ and CQ (Table 3).
3.2. Line of sight towards B0212+735
B0212+735 is located at Galactic latitude b ~ 12°. Two prominent H i absorption features can be observed in B0212+735 (cf. Liszt & Pety 2012). The largest amount (~80%) of H i absorption arises from a broad deep feature at a centre velocity of vLSR ~ −12 km s-1 (cf. Liszt & Pety 2012). Roughly 20% of the total H i absorption arises from a fainter H i absorption component, located at ~+4 km s-1. Interestingly, all molecular absorption lines and the CO emission line are located in the velocity range of the fainter H i absorption component. No molecular absorption line lies within the strong H i absorption feature. Lucas & Liszt (1996) identified two close-by narrow HCO+ absorption lines at vLSR = 2.5 and 3.5 km s-1 by using a Gaussian decomposition of the line profile (components FQ and GQ in Table 3), whereby the majority of the absorption arises from the component GQ. Because of similar velocities, the CO emission component at this position (Liszt & Lucas 1998) can be associated with the HCO+ absorption component GQ at 3.5 km s-1.
3.3. CO-peak and CO-void of B0355+508
At the CO-peak of B0355+508 two bright spectral components can be observed in CO (components AP, and CP; cf. Fig. 2 and Table 2). These components are associated with the components AQ and CQ along the line of sight towards B0355+508 (Table 3). A possible third faint CO component (BP) may be associated with the HCO+ absorption component BQ (cf. Fig. 2 and Table 2).
Similar to the CO-peak, three spectral CO-components can be resolved at the CO-void, AV, BV and CV , which are associated with the CO and HCO+ components along the line of sight towards the quasar analogous to their counterparts at the CO-peak. (cf. Tables 2 and 3 and Fig. 2).
3.4. CO-peak and CO-void of B0212+735
The CO-peak position shows one prominent CO component (GP), at vLSR = 3.5 km s-1 with a width of Δv ≈ 1.4 km s-1. It is located within the HCO+ absorption features. The same component appears in the CO-void GV), although at a slightly lower velocity of vLSR = 2.3 km s-1.
In conclusion, all CO emission spectra at the observed positions are associated with HCO+ absorptions along the lines of sight towards the quasars, while not all HCO+ absorptions are associated with CO emission velocity components. Liszt & Pety (2012) took this discrepancy as an indication that the 12CO(1–0) spatial distribution maps chemical fluctuations and not the cloud density.
HCO+ absorption and CO emission along the line of sight towards B0355+508 and B0212+735.
4. Hydrogen densities
In the following we discuss the amount of molecular, neutral, and total hydrogen in the observed clouds. The calculations of the molecular hydrogen column densities N(H2) from the HCO+ absorption and CO emission are based on two different approaches.
-
In the interpretation of Liszt & Lucas (2000)the molecular hydrogen densities derived from the HCO+absorptions are representative of the densities of the wholecloud. The CO intensity fluctuations in the specific CO-maps were interpreted as local variations in the cloudchemistry, induced by local changes of the ambient phys-ical circumstances, for instance temporary dissipationof turbulent energy, not as variations of the cloud density(Liszt & Lucas 2000; Liszt &Pety 2012). As a consequence, regions with a lowCO abundance should have a higher C+ abundance than regionswith a high CO abundance (Liszt & Lucas 2000, cf.Sect. 5).
-
Alternatively, deriving the molecular hydrogen column N(H2) from the CO line-integrated emission is based on the assumption that the CO-maps trace the intrinsic density structure of the source. In this case the position with a high CO emission would have a high column density as well. In consequence, also the [C ii] emission would be higher in these positions, as I([C ii]) is proportinal to the N(H) (cf. Sects. 5 and 6).
In the following we estimate the integrated [C ii] intensities that are expected in these two scenarios and discuss alternatives to explain the non-detection of [C ii] reported here. We first review the different ways that were previously used to estimate the amount of molecular hydrogen in these clouds from HCO+ absorption and CO emission (Sect. 4.1). Section 4.2 discusses the estimated molecular and total hydrogen column densities in the positions. Section 5 tests and discusses these two approaches by estimating the expected integrated [C ii] intensities. Finally, Sect. 6 proposes an alternative scenario to explain the observations.
Molecular, neutral, and total hydrogen column densities and volume densities in the positions CO-peak, CO-void, and the LOS towards the quasars.
4.1. Calculating molecular hydrogen density
A detailed derivation and description of the N(H2) estimation based on HCO+ absorptions can be found in Liszt & Lucas (1996) and Liszt et al. (2010). The latter derive an H2 fraction of typically f(H2) = 2N(H2)/(2 N(H2) + N(C+))= 0.35. The molecular hydrogen column density N(H2) in diffuse clouds can then be determined through ![\begin{eqnarray} \label{eq:H2fromHCO+} N\mathrm{(H_2)}_\mathrm{\element[+]{HCO}} \approx \frac{N(\mathrm{HCO^{+}})}{8 \times 10^{-10}\left( 2+ \frac{1-f\mathrm{(H_2)}}{f\mathrm{(H_2)}} \right)} = \frac{N(\mathrm{HCO^{+}})}{3.1 \times 10^{-9}} \cdot \end{eqnarray}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq133.png) (1)The last equation refers to an assumed H2 fraction of f(H2) = 0.35. The HCO+ column density can be calculated from the optical depth; N(HCO+) = 1.12 × 1012 cm-2∫τ(HCO+)dν (cf. Table 3; Liszt et al. 2010; Liszt & Pety 2012).
(1)The last equation refers to an assumed H2 fraction of f(H2) = 0.35. The HCO+ column density can be calculated from the optical depth; N(HCO+) = 1.12 × 1012 cm-2∫τ(HCO+)dν (cf. Table 3; Liszt et al. 2010; Liszt & Pety 2012).
Alternatively, the molecular hydrogen column density in diffuse clouds can be estimated from the integrated CO(1–0) line intensity by use of a CO-H2 conversion factor XCO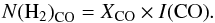 (2)Liszt et al. (2010) derived a XCO = 2.04 × 1020 cm-2 for diffuse clouds. We note that this value is coincidentally equal to the mean CO-H2 conversion factor measured in the Milky Way (Bolatto et al. 2013), as is discussed in Pety et al. (2011).
(2)Liszt et al. (2010) derived a XCO = 2.04 × 1020 cm-2 for diffuse clouds. We note that this value is coincidentally equal to the mean CO-H2 conversion factor measured in the Milky Way (Bolatto et al. 2013), as is discussed in Pety et al. (2011).
4.2. Neutral, molecular, and total hydrogen densities in B0355+508 and B0212+735
Table 4 summarises the molecular hydrogen column densities for the individual velocity components derived with Eqs. (1) and (2). For almost all CO velocity components in all discussed positions the derived N(H2)CO exceeds the N(H2)HCO+ of their counterparts along the line of sight to the quasar derived from the HCO+ absorptions. If the densities in the observed clouds are roughly constant, the CO velocity components would overestimate the expected amount of molecular hydrogen by up to a factor of ~10 (e.g. velocity component C in B0355+508). On the other hand, CO would significantly underestimate the amount of molecular hydrogen for HCO+ velocity components that have no or only faint corresponding counterparts in CO. In this case we would expect, especially for the velocity components BP, BV, EP, EV , and GV, a relatively bright [C ii] emission because they show relatively faint CO emissions combined with strong HCO+ absorptions.
If the CO emission traces the intrinsic density structure of the source, then the [C ii] emission should have a distribution similar to the CO emission.
The total amount of H i in the cold interstellar gas along the lines of sight towards the quasars is listed in Table 4 (Dickey et al. 1983). The total amount of hydrogen for the individual velocity components identified is hard to determine as there are no H i absorption measurements available at the CO-peak and CO-void. In addition, the H i absorptions lines towards the line of sight to the quasars are relatively broad (Δv(H i) ≫ Δv(HCO+)), so that the fractional amount of neutral hydrogen associated with the individual HCO+ absorption features cannot be easily determined. As the N(H2)HCO+ calculations are based on an H2 fraction of 35%, resulting in N(H i)≈ 3.7N(H2), we therefore assume in the following a total hydrogen column densities ofN(H)HCO + = 2 × N(H![\hbox{$_\mathrm{2})_\mathrm{\element[+]{HCO}}+N$}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq145.png) (H i)= 5.7 × N(H
(H i)= 5.7 × N(H![\hbox{$_\mathrm{2})_\mathrm{\element[+]{HCO}}$}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq147.png) based on the HCO+ absorptions. As a lower limit for the total hydrogen based on the CO emission, we assume that all hydrogen is in molecular form; N(H)CO = 2 × N(H2)CO. The total hydrogen column densities derived in this way for the individual velocity components are listed in Table 4. We note that these total hydrogen column densities for the majority of the velocity components are ≳2 × 1021 cm-2; corresponding to an Av ≳ 1 mag. These Av classify the majority of the clouds at the upper limit of the diffuse regime or even in the translucent regime.
based on the HCO+ absorptions. As a lower limit for the total hydrogen based on the CO emission, we assume that all hydrogen is in molecular form; N(H)CO = 2 × N(H2)CO. The total hydrogen column densities derived in this way for the individual velocity components are listed in Table 4. We note that these total hydrogen column densities for the majority of the velocity components are ≳2 × 1021 cm-2; corresponding to an Av ≳ 1 mag. These Av classify the majority of the clouds at the upper limit of the diffuse regime or even in the translucent regime.
With the assumption that the cloud diameter dC is equal to the depth of the cloud, it is possible to estimate the volume hydrogen density n(H) in the individual clouds with n(H)= N(H)/dC. Based on the typical size of the structural features in the CO(1–0)-maps (Fig. 1), we estimated a cloud diameter of 0.15 pc (200′′) for B0355+508 and 0.3 pc (400′′) for B0212+735 based on assumed cloud distances of 150 pc (Liszt & Pety 2012). The cloud diameter (in parsec) is given by dC[pc] ≈ 4.85 × 10-6ρ[′′] d[pc], where ρ[′′] is the diameter of the cloud in arcsec and d[pc] the cloud distance in parsec. The n(H) derived in this way for the individual velocity components are listed in Table 4. The densities derived from N(H)HCO + span between ~4000 to 7000 cm-3 and between ~2400 to 17 000 cm-3 derived from N(H)CO. These densities are unusually high for diffuse clouds. Diffuse clouds are typically associated with a n(H)~ 100 cm-3 (cf. Tielens 2010), roughly 20–100 times lower than the derived values. These densities are commonly found in translucent and dense molecular clouds, respectively.
5. Expected diffuse cloud [C ii] intensities
We now discuss the heating (Sect. 5.1) and cooling (Sect. 5.2) in diffuse clouds. With the assumption that the cooling of diffuse clouds is dominated by [C ii] , we calculated the expected lower limit of the integrated [C ii] intensity, I([C ii]), emitting from the observed positions (Sect. 5.2).
5.1. Heating in diffuse clouds
In diffuse clouds with a visual extinction of about unity and an ambient interstellar radiation field of G0 = 1 (Habing 1968), photo-electric heating is expected to be the main heating source. For low-density clouds with a density ≲3 × 103 cm-3 and a temperature T ≲ 100 K, the efficiency of photo-electric heating is highest (Tielens 2010), and the heating amounts to aboutΓ ≃ 5 × 10-26G0 erg (H-Atom)-1 s-1(Bakes & Tielens 1994; Tielens 2010), about 17 times stronger than the penetrating cosmic-ray heating of ~3 × 10-27 erg (H-Atom)-1 s-1 (Tielens 2010). Additional heating may be due to turbulent dissipation, resulting in local hot spots, a mechanism favoured to explain the unexpectedly high abundance of some species in diffuse clouds, in particular CH+ (Falgarone et al. 2010a,b; Godard et al. 2010). In addition, the formation of H2 may contribute some heating to the clouds (Liszt & Lucas 1996). Hence photoelectric heating alone provides a lower limit to the heating. Further heating of the diffuse clouds may be induced by magnetohydrodynamic shocks and C-shocks (Pineau des Forets et al. 1986; Draine & Katz 1986; Gusdorf et al. 2008). Chemical reactions induced by these shocks would significantly increase the C+ column densities in diffuse gas and could explain the detected HCO+ (Draine & Katz 1986).
5.2. Cooling of diffuse clouds; expected I([C II]) in diffuse clouds
The [C ii] 158 μm fine structure line is expected to be the dominant coolant in diffuse clouds (Hollenbach & Tielens 1999). Owing to its relatively low critical density (~3 × 103 cm-3) (Goldsmith et al. 2012), [C ii] is easily excited in diffuse clouds. Oxygen is neutral in diffuse gas, but the [OI] 63 μm ground-state fine structure line has a much too high critical density to be significantly excited (Tielens & Hollenbach 1985b; Wolfire et al. 1990); nitrogen will be neutral and hence cannot radiate. Where the carbon is in molecular form (CO), carbon monoxide rotational line cooling should dominate. This line of reasoning allows us to estimate an expected [C ii] brightness of the CO-clouds near the lines of sight towards B0355+508 and B0212+735, assuming they are indeed diffuse clouds.
The contribution of [C i] cooling does not exceed ~30% of the [C ii] cooling (Juvela et al. 2003). Therefore it is not considered in the following.
In thermal equilibrium the cloud heating is in balance with the cooling. The expected integrated [C ii] line intensity can be estimated by equating the photoelectric heating at a given G0 with the [C ii] cooling function,![\begin{eqnarray} \label{eq:Heatingrate=ICII} I\mathrm{([\ion{C}{ii}])\;\left[ \mathrm{\frac{K}{km\;s}} \right]} &= &\frac{1}{4 \pi} \frac{ c^{3} }{2 k_\mathrm{B} \nu^\mathrm{3}} 10^{-5} \varGamma \; G_\mathrm{0} N\mathrm{(H)} \nonumber \\ &= &1.1 \times 10^{4} \; \varGamma \; G_\mathrm{0} N\mathrm{(H).} \end{eqnarray}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq164.png) (3)For an assumed photo-electric heating rate of Γ≃5 × 10-26 erg (H-Atom)-1 s-1 and an ambient interstellar field of G0 = 1, Eq. (3) gives an expected integrated [C ii] line intensity I( [ C ii ]) of
(3)For an assumed photo-electric heating rate of Γ≃5 × 10-26 erg (H-Atom)-1 s-1 and an ambient interstellar field of G0 = 1, Eq. (3) gives an expected integrated [C ii] line intensity I( [ C ii ]) of ![\begin{equation} \label{eq:ICIIexpected} I\mathrm{([\ion{C}{ii}])\;\left[ \mathrm{\frac{K}{km\;s}} \right]} = 5.7\times 10^{-22} N\mathrm{(H)} \mathrm{\left[ \mathrm{\frac{K}{km\;s}} \right]} \cdot \end{equation}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq170.png) (4)The expected I([C ii]) for the total hydrogen column densities (cf. Table 4) of the individual velocity components derived with Eq. (4) are listed in Table 5.
(4)The expected I([C ii]) for the total hydrogen column densities (cf. Table 4) of the individual velocity components derived with Eq. (4) are listed in Table 5.
-
In the scenario where the spatial variations in the CO-mapsare indeed induced by chemical and not by density varia-tions, the expected I([C ii]) is based on thetotal hydrogen column density derived from the HCO+absorption, N(H)HCO+. The resulting intensities range fromI([C ii])= 1.3 K km s-1to 3.5 K km s-1,a factor ~3 to 7 above the upper limits for a 3σ [C ii]detection in the observed positions.
We note that these intensities are based on an assumed H2fraction of 35%. Neglecting the additional hydrogen col-umn in H i would still lead to an expectedI([C ii])≈ 0.5 K km s-1in B0355+508 and 1.2 K km s-1in B0212+735. Even in this case, [C ii] lines >3σshould have been observed for almost all velocity components.
-
In the scenario where the CO emission traces the density and not chemical variations, the derived lower limits of the [C ii] emission are a factor ~3 to 15 above the upper limits for a 3σ [C ii] detection for the majority of the velocity components. The expected I([C ii]) spans from ~0.3 (BP) to 4.7 K km s-1 (CP), where the majority of the components have an expected I([C ii]) of 1–2 K km s-1. We note that these densities are lower limits; adding the additional (but unknown) HI-column density in these positions would increase the total.
The fraction of neutral carbon is undetermined in these clouds. It cannot be excluded that a fraction of the cloud cooling occurs by the C0 hyperfine transitions, thus leading to fainter [C ii] emission lines. Using the upper limit for C0-cooling of ~30% estimated by Juvela et al. (2003), the emission should still have been detected.
 |
Fig. 3 Expected I([C ii]) for n(H)= 4500 cm-3 (left) and n(H)= 2300 cm-3 (right) at different total hydrogen column densities N(H) and temperatures calculated from Eq. (5). The filled grey areas show the expected I([C ii]) for a T = 30 K. The blue areas show the expected I([C ii]) for a cold cloud with a kinetic gas temperature of 14 K, as indicated by the CO(2–1)/CO(1–0) ratio. The dashed lines (---) represent the I([C ii]) for a beam filling factor of Φb = 0.5. The upper and lower edge of the grey and blue filled areas shows the I([C ii]) for a beam filling factor of Φb = 1 and Φb = 0.1, respectively. The red areas mark the upper limits of the [C ii] observations. |
In summary, the balance between heating and cooling calculated for the diffuse cloud case predicts that the integrated [C ii] intensity would be roughly a factor ~3 up to a factor 15 above the 3σ detection limit for the cloud components identified in CO. This indicates that the underlying assumption of the clouds being diffuse and warm is not adequate: there is no way to hide the [C ii] column that complements the detected CO, unless the [C ii] is less excited. This can be the case either with lower densities, resulting in a conflict with the sizes and column densities of the clouds, or with lower temperature, as discussed below.
6. [C ii] and CO emission from cold dense clouds
In the following we show that observed low-J CO line intensities and the upper limits on the integrated [C ii] intensities are consistent with the scenario of photon-dominated region (PDR) layers on cold and dense cloud fragments.
We note that the scenario of dense clouds is supported by the derived high molecular hydrogen volume and column densities of the individual velocity components (cf. Table 4). As described in Sect. 4.2, the derived N(H) correspond to optical extinction of Av ≈ 1–4 mag. These Av classify them as translucent and as dense molecular clouds, respectively, which is also consistent with the derived n(H) density of a few times 103 cm-3. In translucent clouds the photoelectric heating is less efficient, thus the clouds would be colder and [C ii] would be less excited. In such clouds (n ~ few 103 cm-3; T< 20 K) bright CO lines in the absence of [C ii] are expected and observed (e.g. Pineda et al. 2013), as only molecules with a low excitation energy, such as the low-J CO lines, are excited.
We first show that a cold cloud, with a temperature consistent with the low-J CO intensity ratio in the thermalized limit, which hypothetically has all its carbon in the form of C+, by itself has a sufficiently low [C ii] intensity consistent with the upper limits of the observations. We then show by applying PDR-modelling that the predicted [C ii] intensity stays below the upper limit for the observed intensity even if a PDR layer is included in such a dense cold cloud fragment.
6.1. Temperature dependency of I([C II])
Observations by Liszt & Lucas (1998) and Pety et al. (2008) found an almost uniform CO(2–1)/CO(1–0) ratio of ≃0.725 in the observed clouds. This would indicate a gas temperature of 14 K for a cloud in local thermal equilibrium (LTE). Pety et al. (2008) rejected such an LTE solution in favour of a non-LTE explanation with sub-thermally excited CO lines (Goldreich & Kwan 1974; Pety et al. 2008) with cloud temperatures above 30 K, typically T ≈ 40 to 80 K (Pety et al. 2008).
As we have shown in the previous section, the [C ii] intensity expected from such a warm low-density cloud would be well above the observed upper limit. We now show that for the observed column densities, a cold dense cloud would have [C ii] intensities well below the observed upper limit, even if the full column density has all carbon in the form of C+.
By adapting formula A3 in Crawford et al. (1985), the [C ii] emission for a low-density cloud is given by ![\begin{eqnarray} \label{eq:ICII_Crawford} I([\ion{C}{ii}]) &=& 1.3 \times 10^{-3} {\rm e}^{-91/T} X_{\element[+]{C}} \;n\mathrm{(H)} \; N\mathrm{(H)}_\mathrm{21} \varPhi_\mathrm{b} \; \mathrm{ \left[ \frac{ergs}{ s \; cm^{2} \; sr} \right]} \nonumber \\ &\approx& 185 \;{\rm e}^{-91/T} X_{\element[+]{C}} \; n\mathrm{(H)} \; N\mathrm{(H)}_\mathrm{21} \varPhi_\mathrm{b} \; \mathrm{\left[K \; \frac{km}{s} \right]}, \end{eqnarray}](/articles/aa/full_html/2017/04/aa26454-15/aa26454-15-eq189.png) (5)where N(H)21 is the total hydrogen column density in units of 1021 cm-2 and n(H) the volume hydrogen density in cm-3. The following calculations use a C+ abundance of XC + = 1.4 × 10-4 (cf. Langer et al. 2014). As the spatial extent of the clouds exceeds the beam of SOFIA and to take the clumpy structure of clouds into account, we assumed a beam filling factor of Φb = 0.5 for a conservative estimate.
(5)where N(H)21 is the total hydrogen column density in units of 1021 cm-2 and n(H) the volume hydrogen density in cm-3. The following calculations use a C+ abundance of XC + = 1.4 × 10-4 (cf. Langer et al. 2014). As the spatial extent of the clouds exceeds the beam of SOFIA and to take the clumpy structure of clouds into account, we assumed a beam filling factor of Φb = 0.5 for a conservative estimate.
Figure 3 illustrates the expected I([C ii]) for gas temperatures of T = 14 K and 30 K and typical column and volume densities as found in the observed clouds. As an example, for a T = 14 K and typical densities of n(H)= 4500 cm-3 and N(H)= 2 × 1021 cm-2, Eq. (5) gives an I([C ii])≈ 0.17 K km s-1. That is well below the 3σ detection limit for the [C ii] observations.
On the other hand, in the scenario of warm clouds with temperatures of T ≳ 30 K this simple analysis confirms that the [C ii] line should have been detectable for all velocity components, except for the lowest total hydrogen column densities. Even for a low beam filling factor of Φb = 0.1, [C ii] line detections would have been expected for the two volume densities we discussed here (cf. Fig. 3).
Low temperatures imply shielding of the clouds from the ambient radiation field. This can be realised by cloud cores embedded within large HI-clouds, which absorb the majority of the incoming radiation. The observed wide H i absorption lines embedding the narrow HCO+ and CO velocity components (Sect. 3) can be interpreted this way. Effectively, such a shielding layer is a photon-dominated surface layer with carbon being atomic and ionised. Hence we investigate in the following whether the observed intensities are consistent with such a PDR scenario.
6.2. PDR modelling of the observations
The PDR modelling can reproduce the observed CO intensities and the observed upper limits for [C ii], as we show below.
We modelled the observations with the stationary KOSMA-τ PDR-model (Röllig et al. 2006, 2013; Röllig & Ossenkopf 2013; Andree-Labsch et al. 2017). The numerical KOSMA-τ code simultaneously solves the energy balance, chemical equilibrium, and radiative transfer of spherical clumps. The chemical fraction of carbon in PDRs is also included (Röllig & Ossenkopf 2013). The clumps are characterised by their total hydrogen mass, the surface hydrogen volume density, the strengths of the incident FUV field, and the metallicity. We only consider solar metallicities in the following. Pre-shielding of the penetrating FUV radiation by a H i envelope is not considered. The code is applicable for a single clump as well as for an ensemble of clumps. We handle both in the following. The radial volume density of the clump(s) is determined by a power-law function of the clump radius and the individual surface hydrogen volume density (e.g.Stoerzer et al. 1996; Cubick et al. 2008). We note that the KOSMA-τ code is a stationary PDR-model. The initial conditions of the cloud formation are not considered.
We modelled single clumps and ensembles of clumps with total masses in the range of M = 1–10 M⊙, embedded in the standard Drain field of χ = 1. The calculations for the single clump refer to a beam filling factor of Φb = 0.5.
Figure 4 shows that the upper intensity limits for [C ii], the observed absolute CO intensities, and the observed CO(2–1)/CO(1–0) ratio of ≃0.73 ± 0.16 can be reproduced by PDR modelling. The model gives integrated line intensities in the order of I(CO(1–0) ≃ 10 K km s-1 and I([C ii])≲ 0.3 km s-1 for cloud volume hydrogen densities of n(H)≈ 103.5 to 104 cm-3 for all the studied cases. The simulations also yield a 12CO/13CO ratio of ~11 for a n(H)~ 103 cm-3 and ~5 for a n(H)~ 104 cm-3. The ratio therefore roughly agrees with the observations. The 12CO/13CO ratio is affected by the density of the clumps. 12CO is less self-absorbed in clumps with a lower density so that the 12CO/13CO ratio is increased compared to denser clumps. A higher 12CO/13CO ratio can therefore be explained by a halo of smaller clouds around an ensemble of clumps with higher densities. Hence the clouds do not have to be diffuse to produce the observed 12CO/13CO ratio.
We note that the assumed cloud masses in the PDR model are consistent with the anticipated cloud diameters of the clouds. A cloud mass of 10 M⊙ and a density of n(H)= 5000 cm-3 corresponds to a diameter of dC ≈ 0.4 pc; 1 M⊙ is equal to dC ≈ 0.2 pc.
 |
Fig. 4 PDR modelling (KOMSA-τ model; Röllig et al. 2006) of clumps with masses of M = 1 and 10 M⊙ for surface volume hydrogen densities of n(H)= 103 to 105 cm-3. The images on the left (A) and C)) illustrate the modelling for an ensemble of clumps. The images on the right (B) and D)) show the modelling for a single clump. For the single clump we anticipated a beam filling factor of Φb = 0.5. The images at the top (A) and B)) show the modelled [Cii] and 12CO(1–0) integrated line intensities. The black and grey lines show the modelled integrated line intensities of CO(1–0) and [C ii]. The style of the line marks the anticipated clump mass. The grey areas show the rough lower and/or upper limits of the CO(1–0) and [C ii] observations. The images at the bottom (C) and D)) illustrate the modelled CO(2–1)/CO(1–0) ratio for clumps with M = 1 and 10 M⊙. The range of the observed CO(2–1)/CO(1–0) ratio (≃0.73 ± 0.16) is marked by the grey area. |
The modelled chemical profiles meet the expectations of a standard PDR. The carbon towards the PDR-surface is dominated by C+, while the inner region of the PDR is dominated by CO. The transition zone between C+/C0/CO is located at an AV ~ 0.5 mag. C+ is associated with kinetic gas temperatures of T ~ 30 K to 20 K, while CO is associated with T ~ 15 K gas. The hydrogen is predominantly in molecular form throughout the simulated clumps. HCO+ has a similar distribution as CO in all simulated cases. The fraction of HCO+ increases beyond the C+/C0/CO transition zone. HCO+ is formed at slightly higher AV than CO (~0.7 mag compared to ~0.5 mag). The 12/13CO/HCO+ ratio is thus highest near the C+/C0/CO transition zone (12CO/HCO+ ≈ 1 × 107) and decreases towards the centre of the clumps (12CO/HCO+ ≈ 0.5 × 107). The simulations show no significant variations of the ratio in clumps with n(H)= 103 cm-3 and n(H)= 104 cm-3. The detailed chemical profile and the temperature profile are shown as an example in Fig. 5.
However, a 12CO/13CO ratio higher than ~5 requires clumps with masses significantly lower than 1 M⊙ because both CO lines tend to become optically thick, pushing the line ratio towards unity. Clumpy PDR ensembles do not suffer from this and are able to reproduce ratios 12CO/13CO > 10 for higher masses as well.
The observations can therefore be explained as emission from PDRs. An ensemble of cold dense clumps, with n(H)~ 3000 to 10 000 cm-3 penetrated by a Draine field of χ = 1, reproduces the observed CO intensities, the upper limits for [Cii], the 12CO/13CO line ratio, and clump sizes. We note that the hydrogen volume densities are also fully consistent with those calculated in Sect. 4.2.
 |
Fig. 5 Chemical profile of a clump with a surface volume hydrogen densities of n(H)= 103 cm-3 and a mass of 10 M⊙ penetrated by a standard Drain field of χ = 1. The relative densities of H0, H2, C+, C0, 12/13CO, and HCO+ as function of AV are shown by the black/grey lines (left axis). The temperature profile within the clump is shown by the red line (right axis). |
7. Summary and conclusion
We observed the [C ii] 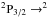 P1/2 transition in two nearby molecular clouds near the lines of sight towards the quasars B0355+508 and B0212+735. No [C ii] line was detected within the rms of ~0.1–0.3 K in either of the positions.
P1/2 transition in two nearby molecular clouds near the lines of sight towards the quasars B0355+508 and B0212+735. No [C ii] line was detected within the rms of ~0.1–0.3 K in either of the positions.
The observed upper [C ii] intensity limits of I([C ii])≲ 0.5 K km s-1 contradict with the scenario proposed by Pety et al. (2008) and Liszt & Pety (2012) of warm non-LTE diffuse clouds (T ≳ 30 K) with sub-thermally excited CO bright lines. In diffuse clouds the photo-electric heating rate is highest and the cooling is dominated by [C ii]. We estimated the upper [C ii] intensity limits in the observed cloud by balancing the heating with the cooling. If the observed clouds were indeed diffuse, the expected integrated [C ii] intensities should be a factor ~3 up to 15 above the 3σ detection limit for the cloud components identified in CO emissions.
The [C ii] non-detection implies that C+ is less excited than expected for diffuse clouds. As lower densities contradict the cloud sizes and column densities, the gas must therefore be colder. Cloud temperatures of ~15 K are supported by the observed CO(2–1)/CO(1–0) ratios. In addition, the total hydrogen column density in the clouds corresponds to an Av ~ 1 to 4 mag, and their volume density is typically n(H)~ 5000 cm-3, which is hard to reconcile with clouds being diffuse. These densities classify the clouds as being in the translucent regime, or even as moderately dense molecular clouds.
The observed low-J CO absolute line intensities and their ratio, the non-detection of [C ii] 158 μm within the observed upper limits, and the observed 12CO/13CO ratio are consistent with a PDR scenario (using the KOSMA-τ PDR model) where the PDR clump densities agree with our derived column and volume densities. The observations, the derived column and volume densities, and the size of the cloud are thus consistent with an ensemble of cold dense clumps.
In summary, the observations, calculations, and simulations indicate that the clouds along the line of sight towards B0355+508 and B0212+735 consist of an ensemble of cold dense clumps, with volume densities of n(H)~ 103.5 cm-3 to 104 cm-3 and core temperatures of T ~ 15 K. The observations are not compatible with the scenario of warm diffuse clouds.
The study is based on a small sample of positions and relatively short integration times. Further mapping would significantly increase the statistical representativeness of this study. It would be worthwhile to investigate whether the emission from other clouds that have been identified as being diffuse are also consistent with a cold and dense clump scenario when the [Cii] intensity is observed and taken into account
Available at http://www.iram.fr/IRAMFR/GILDAS
Acknowledgments
Our special thanks go to Jérôme Pety and Harvey Liszt for their dedicated support and their helpful and critical comments. We would like to express our sincere thanks to the referee for providing constructive comments and the help in improving the quality of this paper. We thank the SOFIA operations and the GREAT instrument teams, whose support has been essential for the GREAT accomplishments, and the DSI telescope engineering team. This publication is based in part on observations made with the NASA/DLR Stratospheric Observatory for Infrared Astronomy (SOFIA). SOFIA is jointly operated by the Universities Space Research Association, Inc. (USRA), under NASA contract NAS2-97001, and the Deutsches SOFIA Institut (DSI) under DLR contract 50 OK 0901 to the University of Stuttgart. The Financial support from the Deutsche Forschungsgemeinschaft (DFG) through the Sonderforschungsbereich (SFB) 956 is gratefully acknowledged.
References
- Andree-Labsch, S., Ossenkopf, V., & Röllig, M. 2017, A&A, 598, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Becklin, E. E., Tielens, A. G. G. M., Gehrz, R. D., & Callis, H. H. S. 2007, in Infrared Spaceborne Remote Sensing and Instrumentation XV, Proc. SPIE, 6678, 66780 [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Burgh, E. B., France, K., & McCandliss, S. R. 2007, ApJ, 658, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, M. K., Genzel, R., Townes, C. H., & Watson, D. M. 1985, ApJ, 291, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Cubick, M., Stutzki, J., Ossenkopf, V., Kramer, C., & Röllig, M. 2008, A&A, 488, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., Kulkarni, S. R., van Gorkom, J. H., & Heiles, C. E. 1983, ApJS, 53, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Katz, N. 1986, ApJ, 306, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Godard, B., Cernicharo, J., et al. 2010a, A&A, 521, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Ossenkopf, V., Gerin, M., et al. 2010b, A&A, 518, L118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrz, R. D., Becklin, E. E., de Pater, I., et al. 2009, Adv. Space Res., 44, 413 [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., Hily-Blant, P., & de Luca, M. 2010, A&A, 520, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Langer, W. D., Pineda, J. L., & Velusamy, T. 2012, ApJS, 203, 13 [Google Scholar]
- Graf, U. U., Heyminck, S., Güsten, R., et al. 2006, Proc. SPIE Conf. Ser., 6275, 62750 [CrossRef] [Google Scholar]
- Guan, X., Stutzki, J., Graf, U. U., et al. 2012, A&A, 542, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau Des Forêts, G. 2008, A&A, 482, 809 [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Heyminck, S., Graf, U. U., Güsten, R., et al. 2012, A&A, 542, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Juvela, M., Padoan, P., & Jimenez, R. 2003, ApJ, 591, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Velusamy, T., Pineda, J. L., Willacy, K., & Goldsmith, P. F. 2014, A&A, 561, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., & Lucas, R. 1996, A&A, 314, 917 [NASA ADS] [Google Scholar]
- Liszt, H. S., & Lucas, R. 1998, A&A, 339, 561 [NASA ADS] [Google Scholar]
- Liszt, H., & Lucas, R. 2000, A&A, 355, 333 [NASA ADS] [Google Scholar]
- Liszt, H. S., & Pety, J. 2012, A&A, 541, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., Pety, J., & Lucas, R. 2010, A&A, 518, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Pety, J., Lucas, R., & Liszt, H. S. 2008, A&A, 489, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Liszt, H. S., & Lucas, R. 2011, in EAS Pub. Ser. 52, eds. M. Röllig, R. Simon, V. Ossenkopf, & J. Stutzki, 151 [Google Scholar]
- Pineau des Forets, G., Roueff, E., & Flower, D. R. 1986, MNRAS, 223, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. L., Langer, W. D., Velusamy, T., & Goldsmith, P. F. 2013, A&A, 554, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., & Ossenkopf, V. 2013, A&A, 550, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Szczerba, R., Ossenkopf, V., & Glück, C. 2013, A&A, 549, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., Lambert, D. L., & Gredel, R. 2007, ApJ, 667, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Lauroesch, J. T., Meyer, D. M., & Cartledge, S. I. B. 2004, ApJ, 605, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Welty, D. E., Thorburn, J. A., & York, D. G. 2007, ApJS, 168, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Stoerzer, H., Stutzki, J., & Sternberg, A. 1996, A&A, 310, 592 [Google Scholar]
- Stutzki, J. 2006, in Rev. Mod. Astron. 19, ed. S. Roeser, 293 [Google Scholar]
- Tielens, A. G. G. M. 2010, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985a, ApJ, 291, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985b, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Tielens, A. G. G. M., & Hollenbach, D. 1990, ApJ, 358, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Young, E. T., Becklin, E. E., Marcum, P. M., et al. 2012, ApJ, 749, L17 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Upper limits for the intensity compared to CO lines intensities of separated CO velocity components at the observed positions of the CO-peak and CO-void in B0355+508 and B0212+735.
HCO+ absorption and CO emission along the line of sight towards B0355+508 and B0212+735.
Molecular, neutral, and total hydrogen column densities and volume densities in the positions CO-peak, CO-void, and the LOS towards the quasars.
All Figures
 |
Fig. 1 Integrated CO (J = 1–0) emission around B0355+508 (Liszt & Pety 2012) and B0212+735 (Pety & Liszt, in prep.). Small crosses mark the positions observed in [C ii]. The large cross in the middle marks the lines of sight towards B0355+508 and B0212+735. The length of the white bar corresponds to 0.05 pc in B0355+508 and 0.1 pc in B0212+735 for an assumed source distances of 150 pc (Liszt & Pety 2012). |
| In the text | |
 |
Fig. 2 [C ii] (black) and CO (red; Liszt & Pety 2012) spectra at the positions CO-peak and CO-void in B0355+508 (left) and B0212+735 (right). The spectra of B0355+508 are smoothed to a velocity resolution of Δv = 0.8 km s-1; B0212+735 spectra are smoothed to Δv = 0.4 km s-1. The blue dashed line shows the HCO+ absorption spectra along the lines of sight towards the quasars B0355+508 and 0212+735 (Liszt & Lucas 1996, 2000). The red letters mark CO velocity components in the CO-peak and the CO-void, blue letters mark HCO+ absorption components along the line of sight towards the quasar. Identical capital letters mark related velocity components in the three positions. For better clarity we do not show the identified HCO+ absorption component FQ at vLSR = 2.5 km s-1 in B0212+735 (cf. Table 3) reported by Lucas & Liszt (1996). |
| In the text | |
 |
Fig. 3 Expected I([C ii]) for n(H)= 4500 cm-3 (left) and n(H)= 2300 cm-3 (right) at different total hydrogen column densities N(H) and temperatures calculated from Eq. (5). The filled grey areas show the expected I([C ii]) for a T = 30 K. The blue areas show the expected I([C ii]) for a cold cloud with a kinetic gas temperature of 14 K, as indicated by the CO(2–1)/CO(1–0) ratio. The dashed lines (---) represent the I([C ii]) for a beam filling factor of Φb = 0.5. The upper and lower edge of the grey and blue filled areas shows the I([C ii]) for a beam filling factor of Φb = 1 and Φb = 0.1, respectively. The red areas mark the upper limits of the [C ii] observations. |
| In the text | |
 |
Fig. 4 PDR modelling (KOMSA-τ model; Röllig et al. 2006) of clumps with masses of M = 1 and 10 M⊙ for surface volume hydrogen densities of n(H)= 103 to 105 cm-3. The images on the left (A) and C)) illustrate the modelling for an ensemble of clumps. The images on the right (B) and D)) show the modelling for a single clump. For the single clump we anticipated a beam filling factor of Φb = 0.5. The images at the top (A) and B)) show the modelled [Cii] and 12CO(1–0) integrated line intensities. The black and grey lines show the modelled integrated line intensities of CO(1–0) and [C ii]. The style of the line marks the anticipated clump mass. The grey areas show the rough lower and/or upper limits of the CO(1–0) and [C ii] observations. The images at the bottom (C) and D)) illustrate the modelled CO(2–1)/CO(1–0) ratio for clumps with M = 1 and 10 M⊙. The range of the observed CO(2–1)/CO(1–0) ratio (≃0.73 ± 0.16) is marked by the grey area. |
| In the text | |
 |
Fig. 5 Chemical profile of a clump with a surface volume hydrogen densities of n(H)= 103 cm-3 and a mass of 10 M⊙ penetrated by a standard Drain field of χ = 1. The relative densities of H0, H2, C+, C0, 12/13CO, and HCO+ as function of AV are shown by the black/grey lines (left axis). The temperature profile within the clump is shown by the red line (right axis). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


