EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 599 (March 2017) A&A, 599 (2017) A18 Full HTML
Free Access
Issue
A&A
Volume 599, March 2017
Article Number A18
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201629459
Published online 21 February 2017

© ESO, 2017

1. Introduction

The inclusion of hydrodynamic transport processes that are due to rotation in a stellar evolution code can lead to significant changes in the global and internal properties of stellar models (e.g., Maeder 2009). The changes induced by rotation are found to be sensitive to the prescriptions used for the modeling of these dynamical processes, and in particular to the modeling of the transport of chemical elements and angular momentum by meridional circulation and shear instabilities (e.g., Meynet et al. 2013). We are still far from having a clear understanding of the various transport processes at work in stellar interiors. Direct observations of internal properties of stars, and in particular of internal rotation rates, are thus extremely valuable to progress in the modeling of these processes. Measurements of rotational splittings of solar-like oscillations for stars with different masses and at different evolutionary stages are especially promising.

The rotation profile of the Sun is a first important constraint for stellar models that take the internal transport of angular momentum into account. From measurements of rotational splittings of solar pressure modes, an approximately flat rotation profile is deduced in the solar radiative zone (see, e.g., Brown et al. 1989; Elsworth et al. 1995; Kosovichev et al. 1997; Couvidat et al. 2003; García et al. 2007). Rotating models of the Sun that include the transport of angular momentum by hydrodynamic processes that are due to rotation predict a rapidly rotating core at the solar age (e.g., Pinsonneault et al. 1989; Chaboyer et al. 1995; Charbonnel & Talon 2005; Eggenberger et al. 2005; Turck-Chièze et al. 2010). This discrepancy with helioseismic data indicates that current prescriptions for meridional currents and shear instability are not able to produce a sufficent coupling in the solar case. An efficient mechanism for angular momentum transport is thus required in the radiative zone of the Sun.

The wealth of information provided by the solar five-minute oscillations has inspired the detection of solar-like oscillations that have been characterized for a large number of stars. While it is difficult to obtain information about the internal rotation of main-sequence solar-type stars from asteroseismic measurements of pressure modes, which mainly propagate in the external stellar layers (see, e.g., Lund et al. 2014; Benomar et al. 2015; Nielsen et al. 2015), constraints on the core rotation rates can be obtained for red giants. Mixed oscillation modes, which behave similarly to pressure modes in the external stellar layers and similarly to gravity modes in the stellar center, can indeed be observed for these evolved stars. With the launch of the Kepler spacecraft (Borucki et al. 2010), information about the internal rotation are now available for red giants (Beck et al. 2012; Deheuvels et al. 2012, 2014, 2015; Mosser et al. 2012; Di Mauro et al. 2016).

Rotational frequency splittings of mixed modes have first been measured for the red giant KIC 8366239 (Beck et al. 2012). Based on these data, Beck et al. (2012) deduced that solid-body rotation can be ruled out and that the core of this star is rotating at least ten times faster than its surface. Stellar models including rotational effects predict fast-rotating cores during the red giant phase as a result of the rapid central contraction occurring after the main sequence (e.g., Palacios et al. 2006; Eggenberger et al. 2010b). However, rotating models of KIC 8366239 predict too steep rotation profiles compared to asteroseismic constraints. Similarly to the solar case, we conclude that an efficient mechanism for the internal transport of angular momentum is at work during the post-main-sequence phase in addition to hydrodynamic processes (hydrodynamic processes refer here only to mechanisms related to rotation, namely the transport of angular momentum by meridional circulation and shear instabilities) (Eggenberger et al. 2012; Marques et al. 2013; Cantiello et al. 2014).

This conclusion was obtained for the red giant KIC 8366239, which is massive enough (mass of about 1.5 M⊙) to exhibit a convective core during the main sequence. Deheuvels et al. (2012) deduced the core rotation rate of the low-mass red giant KIC 7341231 (mass of about 0.84 M⊙) and an upper limit for its surface rotation rate. Comparison with models of KIC 7341231 computed with shellular rotation shows that an efficient mechanism for angular momentum transport is also required in addition to hydrodynamic processes for this low-mass red giant, which has a radiative core during the main sequence (Ceillier et al. 2012, 2013).

While asteroseismic observations point toward the need for an efficient transport of angular momentum in stellar radiative zones of evolved stars, the physical nature of such a process remains an open question. As for the Sun, magnetic fields could play an important role for the internal transport of angular momentum. The impact of the Tayler-Spruit dynamo (Spruit 1999, 2002) on the internal rotation of red giants has been investigated by Cantiello et al. (2014). This study indicates that this mechanism does not provide a sufficient coupling to correctly reproduce the low values of core rotation rates deduced for red giants. A preliminary study of the effects of internal gravity waves on the transport of angular momentum in the interior of red giants also suggests that these waves are not able to extract angular momentum from the stellar core (Fuller et al. 2014). The transport of angular momentum by mixed oscillation modes has also been investigated (Belkacem et al. 2015). Belkacem et al. (2015) showed that this transport seems to play a negligible role during the subgiant and the early red-giant phase, but it could be important for more evolved red giants.

To reveal the physical nature of this unknown transport mechanism, we have to characterize its efficiency. This has been done for the 1.5 M⊙ red giant KIC 8366239 by introducing an additional viscosity νadd that corresponds to the unknown process in the equation describing the internal transport of angular momentum. In the case of KIC 8366239, we find that the mean value for the efficiency of this transport mechanism is strongly constrained by asteroseismic measurements to the value of νadd = 3 × 104 cm2 s-1 (Eggenberger et al. 2012). It is also important to study how the efficiency of this process changes with the global stellar parameters. Comparison with measurements of core rotation rates for a large number of red giants reported by Mosser et al. (2012) indicates that the value of νadd must increase when evolution proceeds on the red giant branch (Cantiello et al. 2014; Eggenberger 2015; Spada et al. 2016). Spada et al. (2016) have shown that a value of νadd that increases during the evolution with the radial rotational shear leads to a good agreement with the core rotation rates of Mosser et al. (2012). This interesting result has been obtained for a fixed mass of 1.25 M⊙, a fixed value for the initial rotation of the star, and by assuming solid-body rotation before the post-main-sequence phase. It is thus interesting to study the impact of the stellar mass on the efficiency of the internal transport of angular momentum for red giants at a similar evolutionary stage. It is also important to investigate how the constraints obtained on νadd from asteroseismic measurements of red giants are sensitive to the numerous uncertainties related to the modeling of rotational effects before the post-main-sequence phase.

In the present paper, we first investigate how the additional viscosity can be determined for the low-mass red giant KIC 7341231 from the value of the core rotation rate and the upper limit on its surface rotation rate deduced by Deheuvels et al. (2012). In particular, we study the impact of the uncertainties related to the modeling of the magnetic braking of the stellar surface and the internal transport of angular momentum during the main sequence on the determination of the efficiency required for this process during the post-main sequence. We then discuss how the mean viscosity associated with the additional transport mechanism changes with the stellar mass and the evolutionary stage.

2. Additional viscosity needed for KIC 7341231

2.1. Physics of the models

Rotating stellar models are computed with the Geneva stellar evolution code (Eggenberger et al. 2008). This code includes a comprehensive treatment of shellular rotation (Zahn 1992; Maeder & Zahn 1998). The details of the inclusion of rotational effects in the Geneva code are not repeated here, but can be found in Sect. 2 of Eggenberger et al. (2010a).

Continuing the work done for the red giant KIC 8366239, we introduce a constant viscosity νadd corresponding to the unknown angular momentum transport process. This viscosity is included in addition to the diffusive transport of angular momentum by the shear instability and the advective transport by meridional currents. Of course, we do not pretend that the physical nature of the unkown additional transport process is such that it should effectively result in a constant viscosity in stellar radiative zones. Introducing this additional viscosity is a valuable mean, however, to first investigate whether asteroseismic data of red giants are able to provide us with quantitative constraints on the efficiency of this undetermined mechanism. Then we can try to deduce its mean efficiency as a function of global stellar parameters such as the mass and the evolutionary stage. The additional process is only taken into account for the transport of angular momentum, but not for the transport of chemical elements. This is motivated by the solar case, where the approximately uniform rotation in the solar radiative zone indicates a very efficient transport of angular momentum, while the surface abundances of light elements require a low efficiency of rotational mixing. The following equation is then solved to follow the transport of angular momentum in radiative zones: 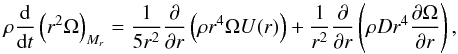(1)with r and ρ the characteristic radius and the mean density on an isobar, respectively. Ω(r) is the mean angular velocity, and U(r) denotes the velocity of the meridional circulation in the radial direction. The total diffusion coefficient D takes into account the transport of angular momentum by both the shear instability and the additional viscosity associated with the undetermined transport process: D = Dshear + νadd. A constant value of the angular velocity as a function of the radius is assumed in convective zones, in accordance with the solar case.

The modeling of KIC 7341231 including the additional viscosity is performed in the continuity of the study by Ceillier et al. (2013), which focussed only on models computed with rotational effects. The metallicity is then fixed to [Fe/H] =−1 with an initial helium mass fraction Yini = 0.260. The solar chemical mixture of Grevesse & Noels (1993) is used together with a solar-calibrated value for the mixing-length parameter. As in Ceillier et al. (2013), models that simultaneously reproduce the observed values of the large frequency separation and the asymptotic period spacing are considered as representative models of KIC 7341231. In this way, Ceillier et al. (2013) determined a mass of 0.84 M⊙ for KIC 7341231, in good agreement with the detailed modeling of KIC 7341231 done by Deheuvels et al. (2012) using non-rotating models. This also illustrates that the impact of rotational mixing on global parameters is negligible for models of red giants computed with low initial rotation velocities on the zero-age main sequence (ZAMS). Figure 1 shows the location in the HR diagram of a representative model of KIC 7341231 (red square), which corresponds to a 0.84 M⊙ star with a low initial velocity on the ZAMS of 2 km s-1. The location of the model corresponding to the more massive target KIC 8366239 is also shown (blue dot in Fig. 1).

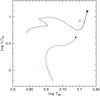thumbnail Fig. 1

Evolutionary tracks in the HR diagram for representative rotating models of KIC 7341231 (red lines) and KIC 8366239 (blue line). The square and dot indicate the location of models of KIC 7341231 and KIC 8366239, respectively. The open triangle corresponds to a more evolved model of KIC 7341231, which shares the same value of log g as the more massive star KIC 8366239.

2.2. Models with an additional viscosity of 3 × 104 cm2 s-1

As mentioned in the introduction, a first constraint on the efficiency of the missing angular momentum transport process has been obtained from rotational splittings of mixed oscillation modes for the red giant KIC 8366239 (Eggenberger et al. 2012). A viscosity of 3 × 104 cm2 s-1 has been found for this target. Interestingly, this value is similar to the viscosities obtained from models aiming at reproducing the internal rotation of the Sun (e.g., Rüdiger & Kitchatinov 1996; Spada et al. 2010) and to viscosities deduced from observations of the spin-down of stars in open clusters (e.g., Denissenkov et al. 2010). Does this mean that the same efficiency of internal angular momentum transport is required during the main-sequence and the red-giant phase? Recalling that KIC 8366239 is a 1.5 M⊙ early red giant, does this mean that the same efficiency is required for stars with different masses, and in particular for stars with a convective (such as KIC 8366239) or a radiative core during the main sequence?

As a first step to study how the efficiency of the required additional transport process changes with stellar properties, we try to characterize the additional viscosity needed for the low-mass red giant KIC 7341231. This is done by using the values of the core rotation rate Ωc = 710 ± 51 nHz and of the upper limit on the surface rotation rate Ωs< 150 ± 19 nHz determined by Deheuvels et al. (2012) from rotational splittings of mixed modes. Following the results obtained for KIC 8366239, we first compute a small grid of rotating models for KIC 7341231 with an additional viscosity fixed to νadd = 3 × 104 cm2 s-1. These first models are computed for different initial rotation velocities on the ZAMS and without braking of the stellar surface by magnetized winds. The latter assumption is of course not realistic in view of observations of surface rotation rates for main-sequence solar-type stars, but is especially interesting to determine whether the post-main-sequence transport of angular momentum can be constrained from asteroseismic measurements of red giants independently of the past history of the star. This is particularly important in view of the uncertainties about the exact modeling and efficiency of wind braking, especially for stars that are different from the Sun (see for instance van Saders et al. 2016). This point is addressed in Sect. 3 by comparing the results obtained with these first models without wind braking (which represent an extreme case of an inefficient surface braking) with results obtained from models computed with wind braking. We note that the neglect of wind braking leads to low values of initial velocities on the ZAMS to correctly reproduce the rotation rates deduced from asteroseismic measurements of KIC 7341231.

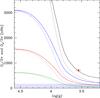thumbnail Fig. 2

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for rotating models of the red giant KIC 7341231 computed with an additional viscosity νadd = 3 × 104 cm2 s-1. Black, blue, red, and green lines indicate models computed with an initial velocity on the ZAMS of 20, 10, 5, and 1 km s-1, respectively. The red dot indicates the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate (Deheuvels et al. 2012).

The evolution of the core and surface rotation rates for rotating models of the red giant KIC 7341231 computed with an additional viscosity of 3 × 104 cm2 s-1 is shown in Fig. 2. Continuous and dotted lines correspond to core and surface rotation rates, respectively. The evolution is shown from the ZAMS to the early red-giant phase as a function of gravity. The shaded blue region corresponds to the upper limit of 169 nHz on the surface rotation rate of KIC 7341231. The red dot indicates the core rotation rate of 710 ± 51 nHz and the asteroseismic value of gravity log g = 3.55 ± 0.03 determined for KIC 7341231 (see Deheuvels et al. 2012, for more details). Colors correspond to the initial velocities of the models on the ZAMS: black, blue, red, and green lines indicate ZAMS velocities of 20, 10, 5, and 1 km s-1, respectively. Figure 2 shows that none of these models is able to simultaneously reproduce the asteroseismic constraints on the core and surface rotation rates available for KIC 7341231. Models with low initial rotation velocities are compatible with the upper limit on the surface rotation rate, but predict core rotation rates that are too low. Similarly, a model with a higher initial velocity on the ZAMS of 20 km s-1 correctly reproduces the core rotation rate of KIC 7341231, but predicts a surface rotation rate that is too high. We thus conclude that the viscosity νadd = 3 × 104 cm2 s-1 leads to a transport of angular momentum in the radiative interior that is too efficient, which is not compatible with the lower limit on the degree of radial differential rotation deduced from asteroseismic data of KIC 7341231. The mean viscosity corresponding to the undetermined transport process is thus found to be lower for KIC 7341231 than for KIC 8366239.

2.3. Determination of the additional viscosity

We have shown that the mean value of additional viscosity required in the case of the more massive red giant KIC 8366239 leads to a coupling that is too efficient to correctly reproduce the asteroseismic constraints available for KIC 7341231. We now investigate which constraints can be brought to bear on the efficiency of the additional transport mechanism for this star.

While the determination of the additional viscosity is performed here for the specific case of KIC 7341231, we note that such a study is more general. It illustrates the constraints that can be obtained about the internal transport of angular momentum in the case of red giants, for which a value of the core rotation rate, but only an upper limit on the surface rotation, is deduced from asteroseismic measurements. We recall here that obtaining only an upper limit on the surface rotation rate from asteroseismic data is common for stars on the red giant branch because it is difficult to evaluate the contribution from the central layers to the envelope kernel (see Sect. 5 of Deheuvels et al. 2012).

Rotating models that correctly reproduce the global properties of KIC 7341231 are computed for various values of the additional viscosity νadd and different initial velocities on the ZAMS. For a given value of the additional viscosity, an initial velocity on the ZAMS is then determined to predict a core rotation rate that is compatible with the one deduced from asteroseismic measurements. Figure 3 shows the change in the ratio between the core and the surface rotation rates as a function of gravity for these models. As expected, the contrast between the rotation in the core and at the stellar surface decreases when the value of the additional viscosity increases, since the internal transport of angular momentum becomes more and more efficient. The ratio of the core to the surface rotation rate is found to be almost insensitive to the adopted initial velocity on the ZAMS. This can be seen by comparing the continuous and dotted red lines in Fig. 3, which correspond to models computed with the same additional viscosity of 2 × 104 cm2 s-1 and an initial velocity of the ZAMS of 15 and 10 km s-1, respectively. This illustrates that the additional viscosity dominates the transport of angular momentum. Of course, both models can be distinguished by using the additional constraint on the core rotation rate: in Fig. 3, all continuous lines indicate models that correctly reproduce the observed core rotation rate (see Fig. 4), while the model shown by the dotted line predicts a rotation rate for KIC 7341231 that is too low as a result of its lower initial velocity.

thumbnail Fig. 3

Ratio of core to surface rotation rate as a function of gravity for rotating models of KIC 7341231. Black, red, blue, and green lines correspond to models computed with an additional viscosity of 3 × 104, 2 × 104, 1 × 104, and 3 × 103 cm2 s-1, and initial velocities on the ZAMS of 20, 15, 8, and 2 km s-1, respectively. The red dotted line corresponds to a model with an additional viscosity of 2 × 104 cm2 s-1 and an initial velocity on the ZAMS of 10 km s-1. Red dashed vertical lines indicate the values of the gravity, while the blue region indicates the lower limit of core-to-surface rotation rate determined for KIC 7341231 (Deheuvels et al. 2012).

As shown in Fig. 3, obtaining an upper limit on the surface rotation rate from asteroseismic data in addition to the core rotation rate enables a precise determination of the maximum mean efficiency allowed for the additional transport mechanism in KIC 7341231. Combining the lower value of the core rotation rate (659 nHz) with the upper limit on the surface rotation rate of 169 nHz leads to a minimal contrast between the angular velocity in the core and at the surface of about 3.9 for KIC 7341231 (blue shaded region in Fig. 3). Rotating models computed with values of the additional viscosity that are too high can then be discarded using this limit. Figure 3 shows that only models with νadd lower than 1 × 104 cm2 s-1 are able to reproduce this observational constraint. This is also illustrated in Fig. 4, which shows the evolution of the core and surface rotation rates as a function of gravity for the models indicated by continuous lines in Fig. 3. Models with high values of the additional viscosity (for instance the black and red lines corresponding to νadd = 3 × 104 and 2 × 104 cm2 s-1, respectively) are then characterized by surface rotation rates that are too high compared to asteroseismic constraints.

While having an upper limit on the surface rotation rate is valuable for determining the maximum efficiency of the additional process for the internal transport of angular momentum, this does not provide any constraint on the minimum efficiency needed for this mechanism. According to Figs. 3 and 4, all models with νadd lower than 1 × 104 cm2 s-1 are compatible with the asteroseismic constraints on the core and surface rotation rates. It seems then difficult to obtain a lower limit on the additional viscosity required for KIC 7341231 based solely on these constraints. To reach the value of the core rotation rate obtained for KIC 7341231, Fig. 4 shows, however, that the initial velocity on the ZAMS has to be significantly decreased when the additional viscosity decreases. In addition to the asteroseismic constraints on the core and surface rotation rates, we can then add a constraint on the minimum value of the initial rotation velocity on the ZAMS that seems reasonable according to observations of rotation periods in young open clusters. In the present study, we then assume that the initial rotation velocity of KIC 7341231 on the ZAMS was not lower than 1 km s-1. For the 0.84 M⊙ star KIC 7341231, this initial rotation velocity on the ZAMS of 1 km s-1 translates into a surface angular velocity of about 0.7 Ω⊙ (rotation period of 36 days) on the ZAMS. According to observations of rotation periods in young open clusters, this corresponds to a conservative lower limit. Using for instance the sample of stars in young open clusters studied by Gallet & Bouvier (2015), we note that no stars are observed on the ZAMS with surface angular velocities lower than 1 Ω⊙ in the mass range 0.7–0.9 M⊙, while a mean value for the 25th rotational percentile of about 4.5 Ω⊙ is observed on the ZAMS for this mass range.

thumbnail Fig. 4

Same as Fig. 2, but for models of KIC 7341231 computed with different values of the additional viscosity. Black, red, blue, and green lines correspond to an additional viscosity of 3 × 104, 2 × 104, 1 × 104, and 3 × 103 cm2 s-1, and initial velocities on the ZAMS of 20, 15, 8, and 2 km s-1, respectively.

thumbnail Fig. 5

Same as Fig. 2, but for models of KIC 7341231 computed with low initial rotation rates. The dashed line indicates the core rotation rate for a model computed with shellular rotation only (i.e., νadd = 0) and an initial velocity on the ZAMS of 1 km s-1. The black and blue lines indicate models computed with an initial velocity on the ZAMS of 1 km s-1 and with an additional viscosity of 1 × 103 and 2 × 103 cm2 s-1, respectively. The red line corresponds to a model with an initial velocity on the ZAMS of 2 km s-1 and an additional viscosity of 3 × 103 cm2 s-1. The green line indicates a model with an initial velocity on the ZAMS of 3 km s-1 and an additional viscosity of 4 × 103 cm2 s-1.

The variation of the core and surface rotation rates as a function of the surface gravity is shown in Fig. 5 for models of KIC 7341231 that are slow rotators on the ZAMS. The dashed magenta line illustrates the evolution of the core rotation rate for a model that does not take into account an additional process for the internal transport of angular momentum. Despite a very low initial velocity on the ZAMS of 1 km s-1, such a model predicts a very rapidly rotating core during the red giant phase, in contradiction with the core rotation rate deduced from asteroseismic data (see also Ceillier et al. 2013). As explained above, models with an initial velocity on the ZAMS of 1 km s-1 are then used to estimate the lower limit required for the efficiency of this process. The continuous black and blue lines in Fig. 5 correspond to such models computed with an additional viscosity of 1 × 103 and 2 × 103 cm2 s-1, respectively. The model with νadd = 1 × 103 cm2 s-1 (black line) predicts a slightly higher rotation rate in the core compared to the asteroseismic value, while the model with νadd = 2 × 103 cm2 s-1 (blue line) leads to a core rotation rate that is too low. Figure 5 also shows that the required additional viscosity rapidly increases when the initial rotation on the ZAMS increases. The red and green lines indicate that an additional viscosity of 3 × 103 cm2 s-1 and a value slightly lower than 4 × 103 cm2 s-1 is needed for an initial velocity of 2 and 3 km s-1, respectively. We thus conclude that a value of νadd = 1 × 103 cm2 s-1 can be safely used as an estimate for the lower limit on the efficiency of the unknown additional mechanism for angular momentum transport. Combining this with the upper limit on the transport efficiency deduced solely from asteroseismic measurements, we conclude that the mean viscosity that characterizes this undetermined transport process can be constrained to νadd = 1 × 103–1 × 104 cm2 s-1 in the case of the red giant KIC 7341231.

3. Impact of the braking of the stellar surface by magnetized winds

The above results about the efficiency of the additional process for internal angular momentum transport have been obtained by computing rotating models of KIC 7341231 that neglect a possible braking of the stellar surface by magnetized winds. Stellar models of the low-mass red giant KIC 7341231 exhibit a convective envelope during the whole main-sequence evolution, which could generate magnetic fields through a dynamo process and hence a braking of the surface by magnetized winds. By increasing the radial differential rotation, we might expect that this braking changes the values for the additional viscosity required for this target. To investigate this point, rotating models of KIC 7341231 are computed by including a braking of the stellar surface by magnetized winds. For this purpose, we adopt the braking law of Krishnamurthi et al. (1997), which expresses the related torque on the stellar surface by the following relation: 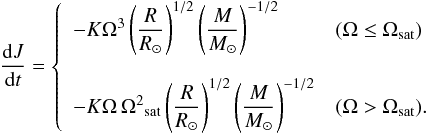(2)Ωsatis introduced to account for the saturation of the magnetic field generation; this critical value is fixed to 8 Ω⊙ in the present computations. The braking constant K is calibrated so that rotating solar models reproduce the solar surface rotational velocity after 4.57 Gyr (K⊙ = 2.7 × 1047 cm2 g s).

thumbnail Fig. 6

Ratio of the core-to-surface rotation rate as a function of gravity for models that include magnetic braking of the stellar surface (with a solar-calibrated value for the braking constant). Black, blue, and red continuous lines correspond to an initial velocity on the ZAMS of 50 km s-1 and an additional viscosity of 3 × 104, 1 × 104, and 4 × 103 cm2 s-1, respectively. The green line corresponds to a similar model with an initial velocity on the ZAMS of 10 km s-1 and νadd = 4 × 103 cm2 s-1. The dotted blue line corresponds to a model without surface magnetic braking, with νadd = 1 × 104 cm2 s-1 and an initial velocity on the ZAMS of 8 km s-1. Red dashed vertical lines indicate the values of the gravity of KIC 7341231, while the blue region indicates the lower limit of the core-to-surface rotation rate determined for KIC 7341231.

Figure 6 shows the evolution of the ratio between the angular velocity in the core and at the surface for rotating models of KIC 7341231 that take into account the braking by magnetized winds as expressed by Eq. (2). As discussed in the preceding section, such a plot is interesting to first estimate an upper limit on the efficiency of the additional transport process. Including magnetic braking does not change the conclusion about the fact that the additional viscosity of 3 × 104 cm2 s-1 determined for the more massive red giant KIC 8366239 (black line in Fig. 6) is too high to correctly reproduce the lower limit on the degree of radial differential rotation obtained for KIC 7341231. We note, however, that the inclusion of surface magnetic braking leads to a slight increase in the ratio of the core-to-surface rotation rates for models computed with the same value of the additional viscosity. This can be seen by comparing models with νadd = 1 × 104 cm2 s-1 (blue lines in Fig. 6), which are computed with (continuous line) and without surface braking (dotted line). At first sight, this suggests that the braking of the stellar surface by magnetized winds could result in an increase of the upper limit on the efficiency of the additional transport mechanism. By decreasing the angular velocity of the convective envelope, magnetized winds increase the radial differential rotation. This increase must then be compensated for by a more efficient transport of angular momentum to reach the same ratio of core-to-surface rotation rates. Figure 6 also illustrates that the rotational properties of models including surface magnetic braking rapidly converge when the initial rotation on the ZAMS increases. This can be seen by comparing models with the same value of νadd = 4 × 103 cm2 s-1, but different initial velocities on the ZAMS (red and green lines in Fig. 6).

thumbnail Fig. 7

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for models with an initial velocity on the ZAMS of 50 km s-1, which account for surface magnetic braking. Black, blue, red, and green lines indicate models with a solar-calibrated braking and an additional viscosity of 3 × 104, 1 × 104, 4 × 103, and 3 × 103 cm2 s-1, respectively. The red dot indicates the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate.

While Fig. 6 suggests that the upper limit on the additional viscosity needed for KIC 7341231 might be slightly higher when surface braking is accounted for, we compare in Fig. 7 the predictions of these models with the value deduced for the core rotation rate. We first note that in addition to predicting a degree of radial differential rotation that is too low, a viscosity of 3 × 104 cm2 s-1 also leads to a core rotation rate that is too low (black line in Fig. 7). Interestingly, this is also the case for the model with νadd = 1 × 104 cm2 s-1 (blue line in Fig. 7); even the model with νadd = 4 × 103 cm2 s-1 (red line in Fig. 7) exhibits a slightly lower core rotation rate than observed. Instead of increasing the value of the upper limit on the efficiency of the additional transport process, the inclusion of surface magnetic braking thus leads to a lower value for this limit (lower than 4 × 103 cm2 s-1 for a solar-calibrated braking constant). This is due to the simultaneous efficient internal transport of angular momentum through the additional viscosity and loss of angular momentum at the stellar surface by magnetized winds. Both effects result in a significant decrease of the angular momentum in the central stellar layers and then in a low core rotation rate at the base of the red giant branch, which is incompatible with the value deduced from asteroseismic data for KIC 7341231. This conclusion is in good agreement with the results of Tayar & Pinsonneault (2013) obtained by using the simple assumption of solid-body rotation of the whole star.

thumbnail Fig. 8

Same as Fig. 7, but for models with an initial velocity on the ZAMS of 2 km s-1. The black, blue, and green lines indicate models computed with a solar-calibrated braking of the stellar surface during the main sequence and an additional viscosity of 1 × 103, 2 × 103, and 3 × 103 cm2 s-1, respectively.

Taking into account a braking of the stellar surface by magnetized winds has only a limited impact on the minimum value of the additional viscosity needed to reproduce the core and surface rotation rates of KIC 7341231. This is shown in Fig. 8 for models computed with the same low initial rotation velocity of 2 km s-1 on the ZAMS. Models computed with a surface braking (using a solar-calibrated value for the braking constant) indicate that a viscosity of about 2 × 103 cm2 s-1 is obtained (blue line in Fig. 8), while models without braking lead to a slightly higher value of 3 × 103 cm2 s-1 (red line in Fig. 8). The slight decrease in the additional viscosity that is needed to reproduce the core rotation rate of KIC 7341231 for models that include surface magnetic braking is also a direct consequence of the loss of angular momentum by magnetized winds.

4. Impact of the internal transport of angular momentum during the main sequence

In Sect. 2.3 we showed that the mean efficiency of the missing transport mechanism for angular momentum can be constrained to the range νadd = 1 × 103–1 × 104 cm2 s-1 using the asteroseismic values of the core rotation rate and the upper limit on the surface rotation rate obtained for KIC 7341231. This range of viscosity is obtained by neglecting the braking of the stellar surface by magnetized winds. The effects of such an assumption have been studied in Sect. 3. Interestingly, the range in νadd is significantly reduced when a braking of the stellar surface is taken into account, with νadd = 1 × 103–4 × 103 cm2 s-1 for a solar-calibrated values of the braking constant.

It is important to underline here that all these results have been obtained by assuming that the unknown transport process is at work from the beginning of the evolution of the star and in particular during the main sequence. Such an assumption seems reasonable in view of the need for an additional efficient angular momentum transport in the solar case (see discussion in Sect. 1). In this sense, the above values for the additional viscosity correspond to a mean efficiency during the whole evolution of the star. However, the main aim of introducing an additional viscosity corresponding to the unknown transport mechanism in the equation describing the angular momentum transport is to determine how asteroseismic observations of red giants can constrain such a process. In particular, it is crucial to investigate whether such asteroseismic measurements can precisely constrain the efficiency of the transport of angular momentum after the main sequence, or whether the efficiency deduced from asteroseismic data of red giants is dominated by the earlier evolution on the main sequence.

thumbnail Fig. 9

Core (continuous lines) and surface (dotted lines) rotation rates for models computed with and without an additional viscosity during the main sequence. These models do not include a braking of the surface by magnetized winds. The black and green lines indicate models with an additional viscosity of 1 × 104 cm2 s-1 during the whole evolution and an initial velocity on the ZAMS of 8 and 10 km s-1, respectively. The blue and red lines correspond to models without an additional viscosity during the main sequence, with an initial velocity on the ZAMS of 8 km s-1, and an additional viscosity during the post-main sequence of 1 × 104 and 1.1 × 104 cm2 s-1, respectively.

For this purpose, new models of KIC 7341231 are computed without an additional viscosity during the evolution on the main sequence; the additional viscosity is then only introduced during the post-main-sequence evolution of the star. These models are first computed without braking of the stellar surface by magnetized winds. The evolution of the core and surface rotation rates of such models are shown in Fig. 9 for an initial rotation velocity on the ZAMS of 8 km s-1 (blue and red lines in Fig. 9). The low efficiency of the transport of angular momentum by meridional currents and the shear instability in radiative zones leads to a large increase in the core rotation rate during the main sequence for models computed without an additional viscosity. This results in a huge increase of the radial differential rotation at the end of the main sequence (compare for instance the black and blue continuous lines in Fig. 9). At the beginning of the post-main-sequence evolution, the additional viscosity is taken into account, which explains the rapid decrease in the core rotation rate for models without an additional viscosity on the main sequence (at a log g of about 4.1 in Fig. 9), and the slight increase in their surface rotation rate. Despite the high value of the core rotation rate reached at the end of the main sequence by these models, we find that the value of the additional viscosity needed during the post-main sequence is very similar to the value deduced by assuming the unknown transport mechanism to be at work during the whole evolution of the star. This is clearly seen in the zoom shown in Fig. 9. The black and blue lines correspond to exactly the same models (same initial velocity of 8 km s-1 and same νadd = 1 × 104 cm2 s-1) computed with and without the additional viscosity during the main sequence, respectively. The fact that the additional viscosity is not accounted for during the main sequence leads only to a very small increase in the core rotation rate predicted for KIC 7341231, while it almost fails to affect the surface rotation rate. To correctly reproduce the precise asteroseismic determination of the core rotation rate of KIC 7341231, a maximum value of the additional viscosity of 1.1 × 104 cm2 s-1 (red line in Fig. 9) is found for models without an additional viscosity on the main sequence (instead of 1 × 104 cm2 s-1 when the additional viscosity is included during the whole evolution of the star). We thus see that the efficiency of the internal transport of angular momentum during the main sequence has a negligible impact on the value of the additional viscosity needed to account for the asteroseismic determination of the rotational properties of KIC 7341231.

thumbnail Fig. 10

Same as Fig. 9 for models computed without additional viscosity during the main sequence. The black line corresponds to a model with an initial velocity on the ZAMS of 8 km s-1, an additional viscosity during the post-main sequence of 1.1 × 104 cm2 s-1, and without braking of the surface by magnetized winds. Blue, red, and green lines indicate models that include a solar-calibrated braking of the stellar surface and an additional viscosity during the post-main sequence of 1.1 × 104, 1.2 × 104, and 1.3 × 104 cm2 s-1, respectively. They are computed for an initial velocity of 20 km s-1 on the ZAMS.

Finally, rotating models of KIC 7341231 without an additional viscosity during the main sequence, but with a solar-calibrated braking of the surface by magnetized winds are computed. The low efficiency of the transport of angular momentum by meridional circulation and shear instability together with the braking of the stellar surface leads to a high degree of radial differential rotation on the main sequence for these models (see Fig. 10). This of course contradicts the approximately flat rotation profile of the Sun, but it corresponds to an extreme case, which is especially interesting for testing the sensitivity of the mean efficiency for the internal transport of angular momentum deduced from asteroseismic measurements of red giants on the past rotational history of the star. The core and surface rotation rates of these models are shown in Fig. 10 for different values of the additional viscosity, which is taken into account only during the post-main-sequence evolution. While the contrast between the rotation velocity in the core and at the surface is much higher at the end of the main sequence for models computed with a surface braking than for models computed without braking, we find that the value obtained for the additional viscosity is very similar in both cases. Only a slight increase of νadd to 1.2 instead of 1.1 × 104 cm2 s-1 is needed to reach the same values for the core and surface rotation rate of KIC 7341231 when a surface braking is taken into account (black and red lines in Fig. 10). As shown with the continuous green line in Fig. 10, a maximum value of νadd = 1.3 × 104 cm2 s-1 is found to correctly reproduce the core rotation rate of KIC 7341231. Using models computed with different assumptions for the modeling of rotational effects, we thus see that a similar value of about 1 × 104 cm2 s-1 is found for the upper limit on the efficiency of the unknown mechanism for the transport of angular momentum. This shows that the asteroseismic constraints on the rotation rates of red giants are able to provide us with strong constraints on the efficiency of this internal transport of angular momentum during the post-main-sequence phase, without being sensitive to the assumptions made for such a transport during the main sequence.

This conclusion is also valid for the uncertainties related to the treatment of rotational effects during the pre-main sequence. This is illustrated in Fig. 11, where a model of KIC 7341231 computed with shellular rotation during the pre-main sequence is compared with a model computed by assuming solid-body rotation on the ZAMS. The model that includes the pre-main-sequence phase has an initial angular velocity of 2 Ω⊙ and a disk lifetime of 3 Myr. The surface angular velocity is kept fixed to the initial value of 2 Ω⊙ during the disk-locking phase. These initial values are chosen so that the model correctly reproduces the asteroseismic constraints on the core and surface rotation rates obtained for the red giant KIC 7341231 (see the inset in Fig. 11). Such a solution is of course not unique, since an increase (decrease) in the initial angular velocity can be compensated for by an increase (decrease) in the disk lifetime to obtain the same value of total angular momentum on the ZAMS. Both models are computed with shellular rotation only before the post-main-sequence phase and with an additional viscosity νadd = 1.2 × 104 cm2 s-1 during the post-main sequence. Figure 11 shows that a high degree of differential rotation is already present at the ZAMS for the model that includes shellular rotation during the pre-main sequence. As a result, significant differences between the rotational properties of these models are seen during the first part of the main sequence. The core and surface rotation rates are then found to converge to similar values at the end of the main sequence. This is because both models have a similar value of total angular momentum at the ZAMS (see Haemmerlé et al. 2013). More importantly, the rotational properties of both models are nearly identical at the evolutionary stage of KIC 7341231. This shows that determining the efficiency of the additional transport mechanism is also almost insensitive to the modeling of the internal angular momentum transport during the pre-main sequence.

thumbnail Fig. 11

Core (continuous lines) and surface (dotted lines) rotation rates as a function of age for a rotating model of KIC 7341231 starting on the ZAMS (blue lines) and a model that includes the pre-main-sequence evolution (red lines). The blue lines correspond to a model with solid-body rotation on the ZAMS and an initial rotation velocity of 20 km s-1. The red lines correspond to a model with an initial angular velocity of 2 Ω⊙ and a disk lifetime of 3 Myr. Both models are computed with hydrodynamic processes only before the post-main sequence, and with νadd = 1.2 × 104 cm2 s-1 during the post-main sequence. A zoom on the variation of the core and surface rotation rates as a function of log g is shown in the inset for these models. The red dot corresponds to the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate.

5. Dependance of the additional viscosity on the stellar mass and the evolutionary stage

The efficiency of the additional viscosity deduced for KIC 7341231 is at least three times lower than the one obtained for KIC 8366239. Being located at the base of the red-giant branch, both stars are in a similar evolutionary stage (see Fig. 1). From core rotation rates deduced for a large sample of red giants by Mosser et al. (2012), it has been established that for a given star, the efficiency of the unknown mechanism for angular momentum transport must increase during its evolution on the red giant branch. This has been shown for 1.5 M⊙ models (e.g., Cantiello et al. 2014; Eggenberger 2015) and for a 1.25 M⊙ star (Spada et al. 2016) at solar metallicity. This effect of the evolutionary stage on the efficiency of the additional angular momentum transport process is also found for the low-mass star KIC 7341231. This is illustrated in Fig. 12, which shows the evolution of the core and surface rotation rates as a function of gravity for models of KIC 7341231. With a constant value of νadd, the values of the core rotation rates deduced for stars at the base of the red giant branch can be correctly reproduced, but an increase in the core rotation rate is then predicted when evolution proceeds, in contradiction with the observations of Mosser et al. (2012). This shows that the efficiency of the transport mechanism increases when the star ascends the red giant branch.

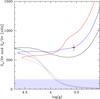thumbnail Fig. 12

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for rotating models with different masses. Black, blue, and red lines indicate a mass of 0.75, 0.84, and 0.95 M⊙, respectively. All models are computed with an initial velocity on the ZAMS of 2 km s-1 and an additional viscosity of 3 × 103 cm2 s-1 (νadd is included during the whole evolution of the model). The red dot corresponds to the core rotation rate of KIC 7341231 (Deheuvels et al. 2012).

While KIC 8366239 and KIC 7341231 are in a similar evolutionary stage, the value of the log g of the latter is slightly higher than the value of KIC 8366239. Since νadd seems to increase when log g decreases, we first investigate whether the difference found between the efficiency of the additional process obtained for both stars cannot be simply explained by this evolutionary effect. We thus follow the evolution of models of KIC 7341231 computed for different values of νadd until they reach the value of log g obtained for KIC 8366239. The location of these models in the HR diagram is indicated by an open triangle in Fig. 1, while the variation in the ratio of core-to-surface rotation rates as a function of log g is shown in Fig. 13. The values of log g corresponding to KIC 7341231 and KIC 8366239 are indicated by the vertical dashed and dotted lines, respectively. As discussed above, the asteroseismic constraint on the minimum degree of radial differential rotation leads to a maximum value of νadd of about 1 × 104 cm2 s-1 for KIC 7341231 (blue line in Fig. 13). The maximum value of the additional viscosity for a more evolved model of KIC 7341231 that has exactly the same value of log g than KIC 8366239 (vertical dotted line) is found to be lower than 2 × 104 cm2 s-1 (green line in Fig. 13). We thus see that the different values of νadd derived from asteroseismic measurements of KIC 8366239 (νadd = 3 × 104 cm2 s-1) and KIC 7341231 are not simply due to a difference in the evolutionary stage of these red giants.

thumbnail Fig. 13

Ratio of the core-to-surface rotation rate as a function of gravity for models of KIC 7341231. Black, green, and blue lines correspond to an additional viscosity of 3 × 104, 2 × 104 and 1 × 104 cm2 s-1, respectively. The red dashed and dotted vertical lines correspond to the gravity of KIC 7341231 and KIC 8366239, respectively. The blue region indicates the ratio of the core-to-surface rotation rate that is compatible with the asteroseismic measurements of KIC 7341231.

The main differences in the global properties of these stars are the mass (1.5 and 0.84 M⊙ for KIC 8366239 and KIC 7341231, respectively) and the metallicity (solar for KIC 8366239 and [Fe/H] =−1 for KIC 7341231). To investigate the impact of the stellar mass on the efficiency needed for the additional angular momentum transport process, rotating models of KIC 7341231 are computed with exactly the same initial parameters except for the mass. Figure 12 shows the evolution of the core and surface rotation rates as a function of gravity for models of 0.75, 0.84, and 0.95 M⊙ with νadd = 3 × 103 cm2 s-1 and an initial velocity on the ZAMS of 2 km s-1. An increase in the mass leads to an increase in the core rotation rate (continuous lines in Fig. 12) during the post-main-sequence phase, while surface rotation rates are very similar (dotted lines in Fig. 12). For models with the same log g as KIC 7341231, an increase in the mass thus results in a more rapidly rotating core together with an increase in the radial differential rotation. A higher efficiency of the internal transport of angular momentum is then required to obtain the same core rotation rate and degree of differential rotation at a given evolutionary stage for more massive models. This shows that in addition to the dependency on the evolutionary stage, the efficiency of the undetermined transport mechanism is also sensitive to the stellar mass. At a given evolutionary stage, the efficiency needed for this transport process is then found to increase with the stellar mass.

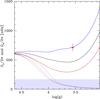thumbnail Fig. 14

Same as Fig. 12 for models with the same mass as 0.84 M⊙, but different metallicities. Blue, black, and red lines correspond to a metallicity [Fe/H] = −1, [Fe/H] = −0.5, and [Fe/H] = 0, respectively.

Another difference between KIC 8366239 and KIC 7341231 is the metallicity, which is solar for KIC 8366239 and equal to [Fe/H] =−1 for KIC 7341231 (Deheuvels et al. 2012). We might then wonder whether the different additional viscosities deduced for these stars could also be due to the difference in metallicity. To investigate this point, additional models of KIC 7341231 are computed with metallicities [Fe/H] = −0.5 and [Fe/H] = 0, but with the same mass of 0.84 M⊙, and the same νadd = 3 × 103 cm2 s-1 and initial velocity on the ZAMS of 2 km s-1. The evolution of the core and surface rotation rates of these models is shown in Fig. 14. An increase in the metallicity leads to a decrease in the core rotation rate at a given value of log g, while surface rotation rates are almost unaffected during the red-giant phase. An increase in the metallicity thus results in a lower degree of radial differential rotation; a lower value for the additional viscosity is then needed to obtain a similar value of the core rotation rate and a similar degree of radial differential rotation during the red giant phase when the metallicity increases. This trend goes in the opposite direction compared to the higher value of νadd obtained for KIC 8366239 with a solar metallicity. This shows that the difference in metallicity is not responsible for the different values of the additional viscosity obtained for KIC 8366239 and KIC 7341231. This difference is dominated by the sensitivity of νadd on the stellar mass. We therefore conclude that asteroseismic measurements of KIC 8366239 and KIC 7341231 indicate that the efficiency of the undetermined mechanism for the internal transport of angular momentum increases with the stellar mass.

6. Conclusion

We have first characterized the mean efficiency of an undetermined mechanism for the transport of angular momentum in radiative zones that is needed to correctly reproduce the asteroseismic constraints on the core and surface rotation rates of the red giant KIC 7341231 obtained by Deheuvels et al. (2012). The mean viscosity νadd corresponding to this additional transport process is then found to be in the range 1 × 103–1.3 × 104 cm2 s-1. This relatively large interval of viscosities corresponds to a conservative value for the constraints on νadd because it includes all the uncertainties on the braking of the stellar surface by magnetized winds, on the efficiency of the internal transport of angular momentun during the pre-main sequence and the main sequence, and on the unknown initial velocity of KIC 7341231. We thus find that the asteroseismic constraints on the internal rotation of KIC 7341231 can provide us with valuable constraints on the efficiency of the internal transport of angular momentum during the post-main sequence independently of the past rotational history of the star. This result is not restricted to the specific case of KIC 7341231 and is valid for any red giant for which a precise core rotation rate and an upper limit on the surface rotation rate can be deduced from asteroseismic measurements of rotational splittings of mixed modes. When we assume that the additional transport mechanism is already at work during the main sequence together with a solar-calibrated braking of the surface by magnetized winds, the value of νadd is then restricted to the interval 1–4 × 103 cm2 s-1.

The efficiency of the transport mechanism obtained for KIC 7341231 is found to be lower than the viscosity of 3 × 104 cm2 s-1 deduced for KIC 8366239. While the efficiency of this additional transport process is known to increase with the evolution of the star during the post-main sequence (e.g., Cantiello et al. 2014; Eggenberger 2015; Spada et al. 2016), we find that this efficiency also appears to increase with stellar mass. This trend, obtained from a direct comparison between the two red giants KIC 7341231 and KIC 8366239 for which detailed asteroseismic observations are available is also suggested by the measurements of core rotation rates for a large sample of red giants by Mosser et al. (2012). We showed that the degree of radial differential rotation and the core rotation rate increase with the stellar mass for models at the same evolutionary stage computed with the same efficiency for the additional transport of angular momentum. As stars with different masses but similar values of core rotation rates can be found at a given evolutionary stage in the sample of Mosser et al. (2012), this also means that the efficiency of the undetermined angular momentum transport mechanism needs to increase with the stellar mass.

Interestingly, the increase in the efficiency of the internal transport of angular momentum with the stellar mass obtained for red giants is similar to the trend deduced from observations of surface rotation rates for young low-mass stars in open clusters (see Gallet & Bouvier 2015). Does this mean that the same physical process for the transport of angular momentum in stellar radiative zones is missing during the whole evolution of the star? It is of course difficult to answer such a question without having a clear idea of the physical nature of this mechanism. We showed, however, that the dependence of the efficiency of this transport process on stellar parameters can be characterized and quantified thanks to asteroseismic measurements of red giant stars. This offers a valuable opportunity of revealing its physical nature and of progressing thereby in our global understanding of transport processes in stellar radiative zones.

Acknowledgments

This work has been supported by the Swiss National Science Foundation grant 200020-160119. N.L. acknowledges financial support from the CNES postdoctoral fellowship 2016. R.A.G., T.C., and S.M. acknowledge funding by the European Community Seventh Framework Program (FP7/2007-2013) under the grant agreement 312844 (SPACEINN) and the CNES PLATO grant at CEA-Saclay. S.M. acknowledges funding by the European Research Council through ERC grant SPIRE 647383. R.H. acknowledges support from the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement No. 306901 and from the World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan.

References

  1. Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
  2. Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015, A&A, 579, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., & García, R. A. 2015, MNRAS, 452, 2654 [NASA ADS] [CrossRef] [Google Scholar]
  4. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  5. Brown, T. M., Christensen-Dalsgaard, J., Dziembowski, W. A., et al. 1989, ApJ, 343, 526 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2012, Astron. Nachr., 333, 971 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 865 [NASA ADS] [CrossRef] [Google Scholar]
  10. Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Couvidat, S., García, R. A., Turck-Chièze, S., et al. 2003, ApJ, 597, L77 [NASA ADS] [CrossRef] [Google Scholar]
  12. Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
  13. Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  16. Di Mauro, M. P., Ventura, R., Cardini, D., et al. 2016, ApJ, 817, 65 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eggenberger, P. 2015, in New Windows on Massive Stars, eds. G. Meynet, C. Georgy, J. Groh, & P. Stee, IAU Symp., 307, 165 [Google Scholar]
  18. Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
  20. Eggenberger, P., Meynet, G., Maeder, A., et al. 2010a, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Eggenberger, P., Miglio, A., Montalban, J., et al. 2010b, A&A, 509, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Elsworth, Y., Howe, R., Isaak, G. R., et al. 1995, Nature, 376, 669 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Grevesse, N., & Noels, A. 1993, in Origin and evolution of the elements: proceedings of a symposium in honour of H. Reeves, held in Paris, June 22–25, 1992, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse (Cambridge, UK: Cambridge University Press), 14 [Google Scholar]
  28. Haemmerlé, L., Eggenberger, P., Meynet, G., Maeder, A., & Charbonnel, C. 2013, A&A, 557, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kosovichev, A. G., Schou, J., Scherrer, P. H., et al. 1997, Sol. Phys., 170, 43 [NASA ADS] [CrossRef] [Google Scholar]
  30. Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lund, M. N., Miesch, M. S., & Christensen-Dalsgaard, J. 2014, ApJ, 790, 121 [NASA ADS] [CrossRef] [Google Scholar]
  32. Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin Heidelberg: Springer) [Google Scholar]
  33. Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
  34. Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Meynet, G., Ekstrom, S., Maeder, A., et al. 2013, Lect. Notes Phys., eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer Verlag), 865, 3 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Nielsen, M. B., Schunker, H., Gizon, L., & Ball, W. H. 2015, A&A, 582, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
  40. Rüdiger, G., & Kitchatinov, L. L. 1996, ApJ, 466, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  41. Spada, F., Lanzafame, A. C., & Lanza, A. F. 2010, MNRAS, 404, 641 [NASA ADS] [CrossRef] [Google Scholar]
  42. Spada, F., Gellert, M., Arlt, R., & Deheuvels, S. 2016, A&A, 589, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
  44. Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Tayar, J., & Pinsonneault, M. H. 2013, ApJ, 775, L1 [NASA ADS] [CrossRef] [Google Scholar]
  46. Turck-Chièze, S., Palacios, A., Marques, J. P., & Nghiem, P. A. P. 2010, ApJ, 715, 1539 [NASA ADS] [CrossRef] [Google Scholar]
  47. van Saders, J. L., Ceillier, T., Metcalfe, T. S., et al. 2016, Nature, 529, 181 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

All Figures

thumbnail Fig. 1

Evolutionary tracks in the HR diagram for representative rotating models of KIC 7341231 (red lines) and KIC 8366239 (blue line). The square and dot indicate the location of models of KIC 7341231 and KIC 8366239, respectively. The open triangle corresponds to a more evolved model of KIC 7341231, which shares the same value of log g as the more massive star KIC 8366239.
In the text
thumbnail Fig. 2

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for rotating models of the red giant KIC 7341231 computed with an additional viscosity νadd = 3 × 104 cm2 s-1. Black, blue, red, and green lines indicate models computed with an initial velocity on the ZAMS of 20, 10, 5, and 1 km s-1, respectively. The red dot indicates the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate (Deheuvels et al. 2012).
In the text
thumbnail Fig. 3

Ratio of core to surface rotation rate as a function of gravity for rotating models of KIC 7341231. Black, red, blue, and green lines correspond to models computed with an additional viscosity of 3 × 104, 2 × 104, 1 × 104, and 3 × 103 cm2 s-1, and initial velocities on the ZAMS of 20, 15, 8, and 2 km s-1, respectively. The red dotted line corresponds to a model with an additional viscosity of 2 × 104 cm2 s-1 and an initial velocity on the ZAMS of 10 km s-1. Red dashed vertical lines indicate the values of the gravity, while the blue region indicates the lower limit of core-to-surface rotation rate determined for KIC 7341231 (Deheuvels et al. 2012).
In the text
thumbnail Fig. 4

Same as Fig. 2, but for models of KIC 7341231 computed with different values of the additional viscosity. Black, red, blue, and green lines correspond to an additional viscosity of 3 × 104, 2 × 104, 1 × 104, and 3 × 103 cm2 s-1, and initial velocities on the ZAMS of 20, 15, 8, and 2 km s-1, respectively.
In the text
thumbnail Fig. 5

Same as Fig. 2, but for models of KIC 7341231 computed with low initial rotation rates. The dashed line indicates the core rotation rate for a model computed with shellular rotation only (i.e., νadd = 0) and an initial velocity on the ZAMS of 1 km s-1. The black and blue lines indicate models computed with an initial velocity on the ZAMS of 1 km s-1 and with an additional viscosity of 1 × 103 and 2 × 103 cm2 s-1, respectively. The red line corresponds to a model with an initial velocity on the ZAMS of 2 km s-1 and an additional viscosity of 3 × 103 cm2 s-1. The green line indicates a model with an initial velocity on the ZAMS of 3 km s-1 and an additional viscosity of 4 × 103 cm2 s-1.
In the text
thumbnail Fig. 6

Ratio of the core-to-surface rotation rate as a function of gravity for models that include magnetic braking of the stellar surface (with a solar-calibrated value for the braking constant). Black, blue, and red continuous lines correspond to an initial velocity on the ZAMS of 50 km s-1 and an additional viscosity of 3 × 104, 1 × 104, and 4 × 103 cm2 s-1, respectively. The green line corresponds to a similar model with an initial velocity on the ZAMS of 10 km s-1 and νadd = 4 × 103 cm2 s-1. The dotted blue line corresponds to a model without surface magnetic braking, with νadd = 1 × 104 cm2 s-1 and an initial velocity on the ZAMS of 8 km s-1. Red dashed vertical lines indicate the values of the gravity of KIC 7341231, while the blue region indicates the lower limit of the core-to-surface rotation rate determined for KIC 7341231.
In the text
thumbnail Fig. 7

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for models with an initial velocity on the ZAMS of 50 km s-1, which account for surface magnetic braking. Black, blue, red, and green lines indicate models with a solar-calibrated braking and an additional viscosity of 3 × 104, 1 × 104, 4 × 103, and 3 × 103 cm2 s-1, respectively. The red dot indicates the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate.
In the text
thumbnail Fig. 8

Same as Fig. 7, but for models with an initial velocity on the ZAMS of 2 km s-1. The black, blue, and green lines indicate models computed with a solar-calibrated braking of the stellar surface during the main sequence and an additional viscosity of 1 × 103, 2 × 103, and 3 × 103 cm2 s-1, respectively.
In the text
thumbnail Fig. 9

Core (continuous lines) and surface (dotted lines) rotation rates for models computed with and without an additional viscosity during the main sequence. These models do not include a braking of the surface by magnetized winds. The black and green lines indicate models with an additional viscosity of 1 × 104 cm2 s-1 during the whole evolution and an initial velocity on the ZAMS of 8 and 10 km s-1, respectively. The blue and red lines correspond to models without an additional viscosity during the main sequence, with an initial velocity on the ZAMS of 8 km s-1, and an additional viscosity during the post-main sequence of 1 × 104 and 1.1 × 104 cm2 s-1, respectively.
In the text
thumbnail Fig. 10

Same as Fig. 9 for models computed without additional viscosity during the main sequence. The black line corresponds to a model with an initial velocity on the ZAMS of 8 km s-1, an additional viscosity during the post-main sequence of 1.1 × 104 cm2 s-1, and without braking of the surface by magnetized winds. Blue, red, and green lines indicate models that include a solar-calibrated braking of the stellar surface and an additional viscosity during the post-main sequence of 1.1 × 104, 1.2 × 104, and 1.3 × 104 cm2 s-1, respectively. They are computed for an initial velocity of 20 km s-1 on the ZAMS.
In the text
thumbnail Fig. 11

Core (continuous lines) and surface (dotted lines) rotation rates as a function of age for a rotating model of KIC 7341231 starting on the ZAMS (blue lines) and a model that includes the pre-main-sequence evolution (red lines). The blue lines correspond to a model with solid-body rotation on the ZAMS and an initial rotation velocity of 20 km s-1. The red lines correspond to a model with an initial angular velocity of 2 Ω⊙ and a disk lifetime of 3 Myr. Both models are computed with hydrodynamic processes only before the post-main sequence, and with νadd = 1.2 × 104 cm2 s-1 during the post-main sequence. A zoom on the variation of the core and surface rotation rates as a function of log g is shown in the inset for these models. The red dot corresponds to the values of the core rotation rate and gravity determined for KIC 7341231, while the blue region indicates the upper limit for its surface rotation rate.
In the text
thumbnail Fig. 12

Core (continuous lines) and surface (dotted lines) rotation rates as a function of gravity for rotating models with different masses. Black, blue, and red lines indicate a mass of 0.75, 0.84, and 0.95 M⊙, respectively. All models are computed with an initial velocity on the ZAMS of 2 km s-1 and an additional viscosity of 3 × 103 cm2 s-1 (νadd is included during the whole evolution of the model). The red dot corresponds to the core rotation rate of KIC 7341231 (Deheuvels et al. 2012).
In the text
thumbnail Fig. 13

Ratio of the core-to-surface rotation rate as a function of gravity for models of KIC 7341231. Black, green, and blue lines correspond to an additional viscosity of 3 × 104, 2 × 104 and 1 × 104 cm2 s-1, respectively. The red dashed and dotted vertical lines correspond to the gravity of KIC 7341231 and KIC 8366239, respectively. The blue region indicates the ratio of the core-to-surface rotation rate that is compatible with the asteroseismic measurements of KIC 7341231.
In the text
thumbnail Fig. 14

Same as Fig. 12 for models with the same mass as 0.84 M⊙, but different metallicities. Blue, black, and red lines correspond to a metallicity [Fe/H] = −1, [Fe/H] = −0.5, and [Fe/H] = 0, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.