| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 26 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628805 | |
| Published online | 01 March 2017 | |
Extrasolar planets and brown dwarfs around AF-type stars⋆,⋆⋆
IX. The HARPS southern sample
Univ. Grenoble Alpes, IPAG; CNRS, IPAG, 38000 Grenoble, France
e-mail: simon.borgniet@univ-grenoble-alpes.fr
Received: 27 April 2016
Accepted: 26 August 2016
Context. Massive, main-sequence (MS) AF-type stars have so far remained unexplored in past radial velocities (RV) surveys due to their small number of spectral lines and high rotational velocities that prevent the classic RV computation method.
Aims. Our aim is to search for giant planets (GPs) around AF MS stars, to get primary statistical information on their occurrence rate and to compare the results with evolved stars and lower-mass MS stars.
Methods. We used the HARPS spectrograph located on the 3.6 m telescope at ESO La Silla Observatory to observe 108 AF MS stars with B−V in the range −0.04 to 0.58 and masses in the range 1.1 to 3.6 M⊙. We used our SAFIR software developed to compute the RV and other spectroscopic observables of these early-type stars. We characterized the detected companions as well as the intrinsic stellar variability. We computed the detection limits and used them as well as the detected companions to derive the first estimates of the close-in brown dwarf (BD) and GP frequencies around AF stars.
Results. We report the detection of a mpsini = 4.51MJup planetary companion with an ~826-day period to the F6V dwarf HD 111998. We also present new data on the two-planet system around the F6IV-V dwarf HD 60532. We also report the detections of 14 binaries with long-term RV trends and/or high-amplitude RV variations combined to a flat RV-bisector span diagram. We constrain the minimal masses and semi-major axes of these companions and check that these constraints are compatible with the stellar companions previously detected by direct imaging or astrometry for six of these targets. We get detection limits deep into the planetary domain with 70% of our targets showing detection limits between 0.1 and 10 MJup at all orbital periods in the 1- to 103-day range. We derive BD (13 ≤mpsini ≤ 80 MJup) occurrence rates in the 1- to 103-day period range of 2-2+5% and 2.6-2.6+6.7% for stars with M⋆ in the ranges 1.1 to 1.5 and 1.5 to 3 M⊙, respectively. As for Jupiter-mass companions (1 ≤ mpsini≤ 13 MJup), we get occurrence rates in the 1- to 103-day period range of 4-0.9+5.9% and 6.3-6.3+15.9% respectively for the same M⋆ ranges. When considering the same Jupiter-mass companions but periods in the 1- to 100-day range only, we get occurrence rates of 2-2+5.2% and 3.9-3.9+9.9%. Given the present error bars, these results do not show a significant difference from companion frequencies derived in the same domains for solar-like MS stars.
Key words: techniques: radial velocities / stars: early-type / planetary systems / stars: variables: general
Based on observations collected at the European southern Observatory, Chile, ESO 072.C-0636, 073.C-0733, 075.C-0689, 076.C-0279, 077.C-0295, 078.C-0209, 080.C-0664, 080.C-0712., 081.C-0774, 082.C-0412, 083.C-0794, 084.C-1039, 184.C-0815, 192.C-0224.
RV and other observable data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/599/A57
© ESO, 2017
1. Introduction
Since the discovery of a giant planet (GP) around a solar-type main-sequence (MS) star, 51 Peg (Mayor & Queloz 1995), made with the ELODIE spectrograph, more than 3000 exoplanets have been found (since the recent Kepler candidate statistical validation from Morton et al. 2016). Most of these exoplanets have been detected by the radial velocities (RV) and transit techniques. While the first detected planets were close-in GPs with a few Jupiter masses and brown dwarfs (BDs), the RV method now allows the detection of Neptune-mass and mini-Neptune planets. The close-in GPs are believed to have formed through the core-accretion (CA) scenario (Pollack et al. 1996; Kennedy & Kenyon 2008), in which quickly-formed massive (10–15 MEarth) rocky cores accrete massive gaseous envelopes. As they represent the bulk of the planetary system mass, GPs play a key role in the shaping and final architecture of the planetary systems. They have already revealed a great diversity in terms of eccentricities, inclinations, orbital motions and especially of separations (Mordasini et al. 2010). The so-called hot planets (hot Jupiters and hot Neptunes) found at very short separations (a fraction of au) have highlighted the importance of dynamical processes such as inward migration (within a disk, or due to interactions with a third body) in the formation and dynamical evolution of planetary systems.
A decisive challenge is now to investigate possible correlations between these close-in (<5–10 au) GPs and the stellar properties of their hosts, so as to better understand the impact of the stars themselves on planetary formation. For instance,the so-called planet-metallicity relation (i.e., a positive correlation between the GP occurrence rate and the stellar metallicity) is now well-established (see e.g. Fischer & Valenti 2005; Reffert et al. 2015), showing that GPs preferentially form in metal-rich proto-planetary disks.
Another important question is the impact of the central star mass on the planetary formation and evolution processes. The impact of the stellar mass M⋆ on the CA formation process and on the GP final properties is still to be fully investigated and understood. The current expectation from CA theory is that the GP frequency increases with an increasing M⋆. Kennedy & Kenyon (2008) predict a linear increase of the GP frequency for stellar masses between 0.4 and 3 M⊙, with a 6% frequency for M⋆= 1 M⊙. These predictions have been more or less validated for solar-like FGK (from F7-8V to mid-K spectral type) dwarf stars (see e.g. Cumming et al. 2008, with a 9 to 10 ± 1.5% frequency of 0.3 to 10 MJup GPs at separations up to 4 to 5 au). Concerning lower-mass M dwarfs, Bonfils et al. (2013) derived a smaller GP frequency of ~1%, corresponding to the expectation from CA theory (Laughlin et al. 2004; Kennedy & Kenyon 2008). However, the increase of the GP frequency in the upper part (from ~1 to 1.3 to ≥3 M⊙) of the M⋆ range explored by Kennedy & Kenyon (2008) is still to be validated for massive, AF-type MS stars. These stars have indeed not been monitored in past RV large surveys due to the specific problems they raise for precise RV computation. Massive (1.2 ≲ M⋆ ≲ 3.5 M⊙) AF (from B9V-A0V to F6V-F7V) dwarfs show far fewer spectral absorption lines and rotate faster than FGK dwarfs. These characteristics prevent measurement of the stars’ RV when using the classical RV computation technique based on the cross-correlation of the stellar spectrum with a binary mask.
Instead, several RV surveys have focused on evolved, GK-type subgiant and giant stars off the MS, based on the assumptions that these stars are both massive (1 ≤ M⋆ ≤ 5 M⊙) and descendants of AF-type MS dwarfs (Johnson et al. 2010a; Bowler et al. 2010). These evolved stars also show more numerous absorption lines and slower rotation rates than AF dwarfs, allowing for classical RV computation (Johnson 2008):
-
Based on an ~160-target sample of GK subgiants with estimated masses in the 1.2- to 2.2-M⊙ range, Johnson (2008), Johnson et al. (2010a) derived a GP (≥0.8 MJup) frequency of 11 ± 2% for separations up to 2.5 au;
-
as for red giants with estimated masses in the 1- to 5-M⊙ range, Reffert et al. (2015) reported an increase of the GP frequency with M⋆ up to 2.5 M⊙ (with a maximum GP rate of ~15% in the range 1.8 to 2.2 M⊙), and a decrease of the GP frequency for higher stellar masses (from 2.5 up to 5 M⊙), based on a 373 GK giant sample observed for 12 yr.
Such results should then confirm the GP frequency correlation to stellar mass predicted by CA theory (Kennedy & Kenyon 2008), provided that the M⋆ estimations are safe. Furthermore, a remarkable GP paucity at short separations (≤1 au) compared to solar-like dwarfs was reported for subgiant and giant stars (Bowler et al. 2010; Johnson et al. 2010b; Reffert et al. 2015). This trend was supposed to originate in different GP evolution mechanisms around FGK and more massive AF dwarfs, respectively (Bowler et al. 2010).
However, a controversy has arisen in the past few years over whether these evolved subgiants and giants are as massive as previously supposed and over whether they are really the descendants of massive MS dwarfs. Lloyd (2011), based on stellar evolutionary models, and Schlaufman & Winn (2013), based on a galactic motion analysis, argued that evolved GK stars did not differ significantly in terms of stellar masses from FGK solar-like dwarfs. These authors argued furthermore that solar-like dwarfs are actually the predecessors of GK subgiants and giants. They finally concluded that the Hot Jupiter paucity around evolved stars was caused by tidal destructionafter the star leaves the MS, instead of early evolutionary processes (Lloyd 2011; Schlaufman & Winn 2013; Villaver et al. 2014). This has led to an ongoing debate on stellar evolution models with Johnson et al. (2013) arguing that the differences picked up by Lloyd (2011) between the classically adopted stellar mass distribution of evolved GP hosts and their mass distribution expected from their position in an H-R diagram have a negligible impact on their stellar mass estimates. Johnson et al. (2013) maintain that these evolved stars are actually more massive than FGK dwarfs (Lloyd 2011, 2013; Johnson et al. 2013, 2014; Johnson & Wright 2013). Besides, transit surveys have revealed a dozen or so Hot Jupiters around AF MS stars: see for example OGLE2-TR-L9 (F3V, Snellen et al. 2009), HD 15082 (A5V, Collier Cameron et al. 2010), or Corot-11 (F6V, Gandolfi et al. 2010). In this context, AF MS stars can become targets of choice to investigate the impact of stellar mass on both the GP frequency and GP period distribution.
Ten years ago we developed SAFIR, Software for the Analysis of the Fourier Interspectrum Radial-velocities (Galland et al. 2005b), dedicated to the RV computation of AF MS stars. For each target, instead of correlating the stellar spectrum with a classical binary mask to measure the RV, SAFIR correlates the spectrum with a reference spectrum built from the median of all the spectra acquired on this target and properly shifted to a common wavelength scale. This procedure has rapidly proved its ability to detect BDs as well as GPs around AF MS stars (see, for example, Galland et al. 2005a,b, 2006). Since 2005, we have initiated and carried out two feasibility surveys dedicated to the search for close-in (up to a few au from the host star) GPs and BDs around AF MS stars: one in the northern hemisphere with the SOPHIE fiber-fed spectrograph (Bouchy & Sophie Team 2006) on the 193 cm telescope at the Observatoire de Haute-Provence (OHP, France), and the other one in the southern hemisphere with the High-Accuracy Radial Velocity Planet Searcher (HARPS; Pepe et al. 2002) on the 3.6 m ESO telescope at La Silla Observatory (Chile). We focus here on the HARPS southern stars. Lagrange et al. (2009) reported on the results of the three first years of this HARPS survey (2005–2008). These authors showed that most of the 185 targets were intrinsically RV variable, and characterized the RV variability. They also made a first assessment of the survey’s sensitivity to substellar companions, achieving detection limits at short periods (≤100 days) deep into the planetary domain for most of the targets, despite early spectral type and/or high RV jitter. Finally, the discovery of a two-GP system in a mean-motion resonance around the F6IV-V dwarf HD 60532 was reported in Desort et al. (2008).
 |
Fig. 1 Our A-F sample properties. Left: HR diagram of our sample, in absolute V-magnitude vs. B−V. The Sun is displayed (red star) for comparison. Middle: vsini vs. B−V distribution. Right: mass histogram. |
Following this feasibility survey, we continued a HARPS survey from 2008 to 2011 with a restricted sample of 108 of the already observed targets, and extended further the observations in 2013–2014 for the most interesting targets. We followed a similar procedure for our SOPHIE observations from 2006 to 2013, and introduced two new GPs (one candidate GP and another confirmed one) detected in the course of this SOPHIE survey in Desort et al. (2009) and Borgniet et al. (2014), respectively. The present paper is dedicated to the description and analysis of the HARPS survey, and a forthcoming publication will present the SOPHIE survey. We detail our sample properties, our observations, our observables and the criteria we use to characterize RV variability in Sect. 2. We introduce the newly reported and/or further characterized GPs in Sect. 3, as well as the detected stellar binaries in Sect. 4. We characterize the RV intrinsic variability of our targets in Sect. 5. Finally, we introduce in Sect. 6 the detection limits we achieved on our targets, and we derive a first estimation of the close-in GP and BD occurrence rates for AF MS stars, before concluding in Sect. 7.
2. Description of the survey
2.1. Sample
Our HARPS sample is made up of 108 MS stars with spectral types (ST) in the B9V to F9V range. The B9V-A0V cut-off roughly corresponds to the earlier ST for which our detection limits are expected to fall into the planetary domain, given our targets vsini and the results of our feasibility survey (Lagrange et al. 2009). The F6V-F9V cut-off more or less corresponds to the earliest ST for which the classical masking technique can be used to compute the RV.
Our sample is limited to nearby stars, with a distance to the Sun less than 67 pc for B9V-A9V dwarfs and less than 33 pc for F0V-F9V dwarfs. The difference in distance between A and F-type stars is meant to keep roughly the same number of stars of each ST range in our sample.
We also note that we first removed any previously known spectroscopic binary from the feasibility survey sample, as well as close visual binaries with a separation under 5 arcsec. Finally, we removed known variable stars of δ Scuti or γ Doradus type, as such pulsators induce high-amplitude RV variations over periods ranging from a few hours to a few days that undermine any search for companions (unless for targets of particular interest such as HR 8799). We also removed known Ap-Am stars that show spectral anomalies and that are often associated with binary systems. This removes a significant number of late A- to early F-type stars at the crossing of the instability strip on the Hertzsprung-Russell (HR) diagram (Fig. 1).
We ended up with 108 stars with B−V in the range −0.04 to 0.58. All of them rotate faster than the Sun (Fig. 1). The mass distribution extends from 1 to 3.6 M⊙ but mostly covers the 1.1 to 2.7 M⊙ range (Fig. 1). The list of our targets, together with their main relevant properties, is provided in Appendix A.
 |
Fig. 2 Observation summary. Left: histogram of the spectrum number per target. Middle: histogram of the separate observation epoch number per target. Right: histogram of the time baselines. |
2.2. Observations
We observed our 108 targets with HARPS mainly between August 2008 and August 2011, in continuation of the survey described by Lagrange et al. (2009), that already covered 2.5 yr (August 2005 to January 2008). As most of our targets were already part of this previous survey, this allowed us to double their observation time baseline. We finally acquired a few additional spectra during 2014 on our most interesting targets. We acquired the HARPS spectra in the 3800 to 6900 Å wavelength range, in high-resolution mode (R ≃ 115 000). We adapted the exposure times (between 60s and 900s, depending on the stars’ magnitudes and on the observing atmospheric conditions) in order to reach a high average signal-to-noise ratio (S/N) of 260 at 550 nm. We made most of the exposures in the fiber spectroscopy mode, for which the HARPS A fiber is centered on the target while the B fiber is not illuminated. This mode is convenient for targets much brighter than the background, such as our AF targets. As for the few spectra acquired in 2014, we acquired them in the simultaneous thorium mode. In that specific case, the first HARPS fiber is centered on the target, while the second is fed by a thorium lamp. The thorium spectrum acquired simultaneously to the stellar one allows us to follow and correct for the drift of the instrument induced by local temperature and pressure variations.
The observing strategy is the same as described by Lagrange et al. (2009). For each pointed star, we recorded at least two consecutive spectra (each pointing is hereafter referred to as an epoch). For each target, we also tried to record data on several consecutive nights to estimate the short-term jitter and detect potential high-frequency variations induced by pulsations. Our typical observation time baseline is ~1900 days (~5.2 yr) per target (Fig. 2). The number of spectra acquired per target depends on its interest and on the potential hint of a companion. For stars with no companion detection, the median number of acquired spectra Nm is in the 20- to 50-spectrum range, roughly corresponding to 15 to 25 different epochs (Fig. 2). The RV computation is described in Sect. 2.3. We made a first selection of the spectra based on two criteria:
-
1.
the S/N at λ = 550 nm must be greater than 80 to eliminate spectra acquired with poor observing conditions, and lower than 380 to avoid saturation;
-
2.
the atmospheric absorption must be kept to a minimum. We defined an absorption parameter, described in Borgniet et al. (2014), that allows us to estimate the absorption by the atmosphere during the observations and thus the quality of the observations.
2.3. Observables
2.3.1. Radial velocities (RV)
We computed the RV with our dedicated SAFIR software. SAFIR and the method used to compute RV for early-type, fast-rotating stars are described in Chelli (2000) and Galland et al. (2005b). We briefly review its principle here. We use the 2D “ed2s” spectra firstly reduced by the HARPS Data Reduction System (DRS) pipeline as the input data to our software. For each star from our sample, we build a first estimate of our reference spectrum by computing the median of the acquired spectra. At this step, we also compute the χ2 of each spectrum compared to the reference spectrum so as to assess its quality. When the χ2 is found to be over 10, the spectrum is not kept in the estimation of the reference. Such cases rarely occur and can originate from bad observing conditions (although this is already taken into account during the selection of the spectra based on the absorption, see above), from technical problems or from line deformations induced by a double-lined spectroscopic binary (SB2). We then compute the correlation (in the Fourier domain) between the reference spectrum and each spectrum to determine a first estimate of the RV. We rebuild a final reference spectrum by computing the median of all the spectra once shifted from the first RV measurement. The final RV value is obtained by correlating, again, each spectrum with the final reference spectrum.
2.3.2. Bisector velocity span (BIS) and full width at half maximum (FWHM) of the spectra cross-correlation function (CCF)
When possible, we computed, for each target, the cross-correlation function (CCF) of the spectrum and the corresponding bisector and bisector velocity span (BIS; see e.g. Queloz et al. 2001; Galland et al. 2005a, 2006). The CCF computation with SAFIR is possible for stars with ST later than A0 and with vsini typically ≤150 km s-1, that is, for stars that have a sufficient number of spectral lines and that are not too rotationally-broadened. The SAFIR CCFs are obtained by cross-correlating each spectrum with an automatically built binary mask based on the deepest and non-blended lines of the reference spectrum. The uncertainty associated to the BIS depends on the vsini and on the number of spectral lines available for the CCF computation (Lagrange et al. 2009).
The BIS and the full width at half maximum (FWHM) of the CCF are very good diagnoses of stellar activity due to magnetically active structures (dark spots and bright faculae) or high-frequency pulsations. Yet, for a low vsini (of the order or smaller than the instrumental spectral resolution), the flux variation induced by a magnetically active structure and the corresponding global CCF distortion will not have a significant effect on the BIS compared to the RV (see, e.g., Desort et al. 2007). Indeed, if the vsini is smaller than the instrumental resolution, the spectral lines are not resolved and the BIS variations are negligible compared to the RV ones. On the contrary, the activity-induced effect on the FWHM should always be noticeable (of the same order of or larger than the RV variations, see Dumusque et al. 2014). For a higher vsini (≥5–6 km s-1), the activity-induced BIS variations will always be noticeable and will be larger than the FWHM variations (Desort et al. 2007; Dumusque et al. 2014). Here, as most of our targets have a high vsini, the BIS will be our main proxy for stellar activity (see below).
2.3.3. Chromospheric emission
SAFIR also allows for the measurement of chromospheric emission in the calcium (Ca) H and K lines, expressed either in the S-index, which gives the ratio of the flux measured in the core of the Ca H and K lines by the flux measured in two continuum bands on either side (blue and red) of the Ca lines, or the log 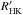 , which gives the log of the S-index from which the photometric emission in the Ca lines has been subtracted (therefore keeping only the chromospheric emission). The log
, which gives the log of the S-index from which the photometric emission in the Ca lines has been subtracted (therefore keeping only the chromospheric emission). The log 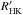 increases with the active region surface coverage or filling factor (in the case of the Sun, for which the bright faculae are much larger than the dark spots, the log
increases with the active region surface coverage or filling factor (in the case of the Sun, for which the bright faculae are much larger than the dark spots, the log 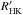 increases linearly with the bright facula coverage and quadratically with the dark spot coverage, according to Shapiro et al. 2014). It is therefore commonly used as a stellar magnetic activity proxy for solar-like stars (see, e.g., Dumusque et al. 2012; Meunier & Lagrange 2013; Santos et al. 2014). When available, we use here the log
increases linearly with the bright facula coverage and quadratically with the dark spot coverage, according to Shapiro et al. 2014). It is therefore commonly used as a stellar magnetic activity proxy for solar-like stars (see, e.g., Dumusque et al. 2012; Meunier & Lagrange 2013; Santos et al. 2014). When available, we use here the log 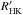 of our targets as an activity proxy complementary to the BIS.
of our targets as an activity proxy complementary to the BIS.
2.4. Classification of the RV variable targets
As in Lagrange et al. (2009), we consider a target as a RV variable if its total RV amplitude is larger than six times the mean RV uncertainty and if its RV standard deviation (equivalent to the RV rms) is larger than twice the RV mean uncertainty. A fully detailed description of how the combined use of RV, CCF and BIS allows us to distinguish between RV variations induced by companions and those induced by intrinsic stellar activity is provided in Lagrange et al. (2009) for AF MS stars. Here we review only the main points of this classification.
In the case of RV variations induced by stellar magnetic activity (i.e., dark spots and bright faculae), the RV and BIS are anti-correlated if the vsini is larger than the instrumental spectral resolution. In a (RV, BIS) diagram, the BIS values are arranged either in a linearly decreasing function of the RV, or in an inclined figure of eight, depending on the vsini, the stellar inclination, and the active structure configuration at the stellar surface (see, e.g., Desort et al. 2007; Boisse et al. 2011; Lagrange et al. 2013). More complex patterns can be found in the case of multiple large structures.
In the case of stellar pulsations, the BIS shows large variations over a much larger range than the RV. The BIS and RV variations are no longer correlated. In the (RV, BIS) diagram, the BIS values show a vertical spread.
In the case of BD or GP companionship as the source of RV variations, the CCF is not distorted as in the case of active magnetic structures and is only shifted in RV. In the case of SB2s, the CCF is strongly distorted due to the two spectra overlapping, inducing strong RV as well as BIS and FWHM variations. However, we removed any known SB2s from our sample, and the SB2s we detected in Lagrange et al. (2009) were also removed. Hence, the present sample should not contain any SB2s with periods up to several hundreds days. Only SB2s with periods of a few to a few tens years should still be present in our sample. Given our typical time baselines, such “long-period” SB2s should be unresolved spectroscopically; that is, the RV shift between the two components remains smaller than the global FWHM over the observation time baseline. In this case, the CCF distortions might be difficult to detect and only FWHM variations correlated to the RV variations should be seen. Moreover, the BIS would not show significant variations (hence an apparently flat (RV, BIS) diagram), and the RV-FWHM correlation would be the only criterion to distinguish this case from a single-lined spectroscopic binary (SB1; Santerne et al. 2015). A SB1 does not induce CCF distortions nor FWHM or BIS variations, whereas the RVs are strongly variable. The corresponding (RV, BIS) diagram is therefore “flat”. We use the same diagnosis for companions of lower mass (BD and GP), though in this case the RV variations are of lower amplitude.
Finally, if the star is both a member of a binary system and active, the (RV, BIS) diagram will be composite, with both a horizontal spread induced by the companion and an inclined or vertical spread induced by active structures or pulsations, respectively. The origin of the dominant spread depends on the activity strength and on the companion properties.
In Appendix A we display the main results in terms of observations, observables and RV analyses for all our targets.
 |
Fig. 3 HD 60532 spectroscopic data. Top row: HD 60532 RV time series (left), Lomb-Scargle periodogram of the RV (middle) and temporal window of the observations (right). The Keplerian fit is superimposed (red solid line) to the RV. On the periodogram, the false-alarm probability (FAP) at 1% (solid line) is indicated in red; the planet periods are indicated in blue. Second and third rows: BIS and FWHM time series, corresponding Lomb-Scargle periodograms and correlations with the RV data. Fourth row: RV residuals from planet c, corresponding Lomb-Scargle periodogram and correlation with BIS. The planet b Keplerian fit is superimposed on to the residuals, and planet b period is superimposed in blue on the periodogram. Fifth row: RV residuals from the two-planet Keplerian fit, corresponding Lomb-Scargle periodogram, and correlation with BIS. |
3. Giant planet detections
The present data set reveals three GP companions to two of our targets. Two GPs were already known to orbit HD 60532 (Desort et al. 2008). We add new RV data to this system. Then, we report the detection of a new GP orbiting the F6V dwarf HD 111998. The stellar characteristics of these two targets are detailed in Table 1.
3.1. The two-GP system around HD 60532
3.1.1. System characteristics
This system was discovered and described in Desort et al. (2008). HD 60532 is a F6IV-V star hosting a system of two GPs with minimal masses of 1.03 ± 0.05 and 2.46 ± 0.09MJup and with semi-major axes (SMA) of 0.759 ± 0.01 and 1.58 ± 0.02 au, respectively. The HD 60532 system shows a 3:1 mean motion resonance (MMR) stable at the Gyr timescale (Desort et al. 2008; Laskar & Correia 2009). We continued to follow HD 60532 during our survey, adding 28 spectra to the 147 already acquired at the beginning of 2008, and expanding consequently the observation time baseline from 2 to 5.5 yr (1949 days). We performed a new fit of the RV data set (i.e., 175 spectra) with a Keplerian two-planet model to test the impact of the new data on the orbital parameters of the system. For that purpose, we used the yorbit software (Ségransan et al. 2011). This software uses a Levenberg-Marquardt algorithm to fit the RV data with Keplerian models, after selecting the values with a genetic algorithm. We found a solution very close to the best model given in Desort et al. (2008), with non-significant differences. This strongly strengthens the detection of the two planets. We give the orbital parameters of the system obtained with the new Keplerian fit in Table 2. The RV data along with the two-planet Keplerian fit are displayed in Fig. 3.
The RV Lomb-Scargle periodogram is strongly dominated by the signal of planet c and its aliasing. We computed the Lomb-Scargle periodogram using the fast-algorithm method of Press & Rybicki (1989), that gives the power spectrum of the RV data (according to the definition of Scargle 1982) versus the period range. We finally display in Fig. 3 the RV residuals from planet c only, and from the two-planet Keplerian fit. We note that the planet b signal dominates the periodogram of the RV residuals from planet c, and that the remaining short-period signals in the final RV residual periodogram are most likely induced by low-intensity stellar activity, given the shape of the (RV residuals, BIS) diagram (Fig. 3).
Stellar properties of our targets with detected GP.
Best orbital solutions.
3.1.2. Remarks on the line profiles
We display all the HD 60532 relevant spectroscopic data (RV, BIS, FWHM) in Fig. 3. As stated in Desort et al. (2008), the (RV, BIS) diagram is flat (with an RV amplitude of 120 m s-1 and a BIS amplitude of 35 m s-1), with no correlation. However, the BIS Lomb-Scargle periodogram shows a strong peak at 309 days. Such a periodicity is hardly noticeable when looking at the BIS time series (Fig. 3). Noting that a similar peak at ~320 days is also present in the observation temporal window, we conclude that the ~300-day BIS peak most probably originates from temporal sampling effects. As for the FWHM periodogram, the main peaks located at ~30 and 140 days are also present in the temporal window, also suggesting sampling effets. The FWHM and, less significantly, the BIS show a long-term trend of low amplitude over the observation time baseline that may be indicative of long-term stellar activity.
3.1.3. Additional remarks
The third version of the Geneva-Copenhagen Survey (GCS III, Holmberg et al. 2009) gives an age of 2.8 Gyr for HD 60532, based on the Padova stellar evolution model (Holmberg et al. 2007). A new analysis of the GCS led to a similar age estimation of 2.4 Gyr (Casagrande et al. 2011), however the GCS often finds ages much older than they actually are in the case of young stars. Nevertheless, HD 60532 is not known to be a member of a young association. Its (U, V, W) space velocities (−37, −49, −3 km s-1) are not compatible with the ones of the known young moving groups listed in Torres et al. (2008) or Nakajima & Morino (2012). Furthermore, its luminosity class (IV-V) and relatively high radius estimation (R⋆ = 2.57 R⊙, Allende Prieto & Lambert 1999) do not indicate a young star.
Orbital analysis and simulations of the 3:1 MMR in the HD 60532 planetary system favour a small inclination of the system (i ~20°, Laskar & Correia 2009; Sándor & Kley 2010). The true masses of HD 60532 planets would then be increased by a factor of approximately three compared to their minimal masses, that is ~3.2 and 7.5 MJup for planets b and c, respectively.
McDonald et al. (2012) reported a weak IR excess around HD 60532 of ~30% in flux on average between 3.5 and 25 μm through SED-fitting. Such a weak excess may be induced by circumstellar dust, however McDonald et al. (2012) does not propose a size for the excess emission. No circumstellar dust has been resolved so far around HD 60532.
3.2. A new GP around HD 111998
3.2.1. RV data
We obtained 127 high S/N HARPS spectra (the average S/N is 275) on 38 Vir (HD 111998, HIP 62875, F6V), covering a 2989-day (8.2 yr) time baseline. The RV data show a clear periodic signal with a peak-to-peak amplitude of 222 m s-1, and a dispersion of 66.4 m s-1. These values are well above the 4.7 m s-1 average uncertainty on the RV (accounting for photon noise and instrumental stability). The RV data and their Lomb-Scargle periodogram are given in Fig. 4. The RV periodogram shows several peaks above the 1% FAP, with the highest by far at a period of ~820 days (which we will attribute to a planet, see below). Another peak at 422 days appears to be an alias of the ~820-day period. Finally, we attribute the 32-day peak to temporal sampling effects, noting that a similar peak is present in the temporal window (Fig. 4).
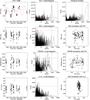 |
Fig. 4 Spectroscopic data for HD 111998. Top row: HD 111998 RV time series (left), RV Lomb-Scargle periodograms (middle) and temporal window of the observations (right). The Keplerian fit is superimposed (red solid line) to the RV, as well as the linear trend (dashed blue line). On the RV periodogram, the FAP at 1% (solid line) is indicated in red; the planet period is indicated in blue. Second and third rows: BIS and FWHM time series, corresponding Lomb-Scargle periodograms and correlations with the RV data. Fourth row: Residuals of the fit as a function of time, periodogram of the residuals and BIS correlation with the residuals. |
3.2.2. Line profile data
We show in Fig. 4 the BIS and FWHM as a function of time, as well as their Lomb-Scargle periodograms, and the (RV, BIS) and (RV, FWHM) diagrams. Although the BIS shows high-amplitude variability (with a dispersion of 67 m s-1 and a peak-to-peak amplitude of 337.5 m s-1), it does not show any significant temporal periodicity in the 100- to 2000-day range. The BIS periodogram shows power at high frequencies (at periodicities in the one- to seven-day range). Moreover, there is no correlation between the RV and the BIS (Pearson’s correlation coefficient of 0.03) despite the large vsini (28 km s-1). The (RV, BIS) diagram clearly shows first a main horizontal (“flat”), long-term spread (pointing towards the presence of a companion), and then a secondary, short-term, slope that corresponds to low-intensity activity. This is better seen when looking at snapshots of the RV and BIS data (Fig. 5). The FWHM of the CCF show variability both in the one- to seven-day range and in the 100- to 400-day range. However, the FWHM periodogram does not exhibit any significant power in the 400 to 2000-day range, and there is no significant correlation between the RV and FWHM data (Pearson coefficient of 0.2). Finally, HD 111998 does not show any significant emission in the calcium H and K lines. We find a mean log 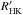 of -4.69, in agreement with previous measurements for HD 111998 (⟨log
of -4.69, in agreement with previous measurements for HD 111998 (⟨log 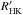 ⟩ = –4.77, –4.44 according to Pace 2013; and Murgas et al. 2013, respectively).
⟩ = –4.77, –4.44 according to Pace 2013; and Murgas et al. 2013, respectively).
3.2.3. Origin of the RV variations
We investigate here the possible origins of the ~820-day periodic RV variation. Stellar pulsations are highly improbable as a periodicity of more than 800 days is far larger than those of any type of known pulsations for MS stars. They would also induce a much larger variability in the BIS at much longer periods than those observed. We also exclude activity-induced variability as dark spots or bright faculae would induce signals with periods of a few days. Indeed, given the star vsini (28 km s-1) and the radius estimations from Allende Prieto & Lambert (1999) and Pasinetti Fracassini et al. (2001) (1.45 and 1.0 R⊙, respectively), the stellar rotational period would be under three days if the star was seen edge-on, and would be even shorter if the star was seen inclined. This is clearly not compatible with the observed ~820-day period. Finally, we also rule out longer-term effects of stellar magnetic activity (i.e., stellar cycles): with this vsini level, such effects on the RV would induce correlated high-amplitude variations on the BIS and FWHM at similar periods, which is not the case. We therefore attribute the ~820-day RV periodic variation to the presence of a companion.
3.2.4. Keplerian fit
We fitted HD 111998 RV data with a one-planet Keplerian model and a linear trend (with a 5.2 ± 1.3 m s-1 yr-1 slope) simultaneously, using the yorbit software. Adding this slight linear trend to the Keplerian model allows to significantly reduce the rms of the residuals (by 1.1 m s-1, see below). The best solution is a companion on an almost circular orbit (e = 0.03 ± 0.04), with a period of 825.9 ± 6.2 days and a semi-amplitude of K = 87.6 ± 3.4 m s-1. Taking the stellar mass and its error bar into account (M⋆= 1.18 ± 0.12M⊙), this corresponds to a GP with mpsini= 4.51 ± 0.50MJup. To test the potential impact of the RV variability observed at high frequencies (for periods of one day or less), we also fitted the RV data averaged over one, two and five days with a one-planet Keplerian model. In all cases, we obtain the same orbital parameters as with the original RV data with differences lower than the uncertainties, showing the reliability of our model. We display the best-fit (Keplerian+linear) model superimposed on the HARPS RV in Fig. 4. The orbital parameters of the HD 111998 planetary system are listed in Table 2 along with their 1σ uncertainties.
The slight long-term RV trend that we fitted simultaneously to the Keplerian model is not seen in the FWHM data, though a similar trend may be present in the BIS data but with an opposite slope. This would imply a stellar origin. The effect of a distant binary companion to HD 111998 might be another explanation to this RV trend. 38 Vir is associated to a ROSAT X-ray source (Haakonsen & Rutledge 2009), which would be consistent with an M-type distant companion. However, this remains quite speculative at this stage, as the slope of the linear trend is very small and we do not have additional information about this potential wide binary companion.
 |
Fig. 5 Top: focus on HD 111998 RV data over 800 days (left) at three distinct epochs (black, red and blue dots); and corresponding (RV, BIS) diagram (right). Bottom: the same for HD 111998 RV residuals. |
3.2.5. Interpretation of the residuals
We display the residuals of our best Keplerian fit as well as their Lomb-Scargle periodogram in Fig. 4. The residuals show a greater dispersion (σO−C = 17.4 m s-1) than the mean RV uncertainty (4.7 m s-1). They do not show any significant power at periodicities above 20 days. The power is mainly located at high frequencies, with two groups of peaks around 2.5 and 5 days. As these peaks correspond to low-amplitude peaks that are present in the BIS or FWHM periodograms, we conclude that they are most likely induced by stellar activity. The 2.5-day peak may correspond to the stellar rotational period if the star is seen nearly edge-on (see above). We note that the correlation coefficient between the RV residuals and the BIS is higher (0.2) than the RV-BIS correlation (<0.1), even if not significant in terms of a correlation (Fig. 4). When looking at the (RV residuals, BIS) diagram for several data snapshots, the inclined or vertical spread corresponding to low-level activity or low-amplitude pulsations is clear (Fig. 5).
 |
Fig. 6 Main HARPS data for our detected binaries (first part). From left to right: RV vs. time (Julian Day – 2 453 000), BIS vs. RV, FWHM vs. time, stacked CCF. From top to bottom: HD 29992, HD 49095, HD 68456, HD 101198, HD 124850, and HD 125276. |
 |
Fig. 7 Main HARPS data for our detected binaries (second part). From left to right: RV vs. time (Julian Day – 2 453 000), BIS vs. RV, FWHM vs. time, stacked CCF. From top to bottom: HD 141513, HD 153363, HD 196385, HD 196724, HD 216627, and HD 223011. |
 |
Fig. 8 HARPS RV for our binaries of very early ST (i.e., without line profile computation). From left to right: RV time series of HD 199254 and HD 224392. |
 |
Fig. 9 Limits on the orbital parameters (mpsini, sma) of the companions to our targets with long-term RV trends, given the observed RV variations. Black solid line: minimal mass vs. sma. Dotted black line: minimal sma given the observation time baseline (i.e., considering that the companion orbital period is at least equal to the time baseline, and assuming a circular orbit). In the case of HD 153363, the mass and sma corresponding to the Keplerian fit derived with yorbit with all parameters free is shown as a black filled dot, and the masses and sma corresponding to the yorbit fits obtained for longer periods are showed as black crosses. The area filled and/or shaded in cyan corresponds to the (mass, sma) domain based on these constraints. Dashed red line: projected separation of the imaged companion (if any), resulting possible mass from the DI study (red diamond), or DI detection limits (solid red line). HD 29992, HD 49095, HD 101198, HD 153363: DI from E10. HD 199254: DI from De Rosa et al. (2014). Blue solid line: sma of the companion detected through astrometric measurements, and mass estimation (blue diamond). HD 124850: astrometry from Gontcharov & Kiyaeva (2010); HD 141513: from Malkov et al. (2012). |
3.2.6. Additional remarks
In the GCS III catalog, the age of HD 111998 is 1.9 Gyr (Holmberg et al. 2009), however, the GCS re-analysis by Casagrande et al. (2011) assigns a much younger age of 600 Myr. This new age estimation would be in agreement with a Hyades cluster membership, as reported by Eggen (1982). Nevertheless, such a Hyades membership for HD 111998 has not been confirmed since.
HD 111998 is not currently known to show a clear IR excess that would suggest the presence of a debris disk. However, to our knowledge, this target has not been included yet in a specific survey dedicated to the search for IR excesses. Given the detection of such a GP companion and its revised age estimation, HD 111998 should be a target of interest for future searches for debris disks, even though there is no clear correlation between cold debris disks and GP detected by RV. More systems need to be investigated to test a hypothetical correlation between RV GP and debris disks. For example, the HD 113337 system hosts both a debris disk (Chen et al. 2014) and at least one RV GP (Borgniet et al. 2014).
4. RV long-term trends and stellar binaries
We describe hereafter 14 spectroscopic binaries or massive companions that were identified in our survey using, firstly, the (RV, BIS) criterion (Sect. 2.4). When possible, we fitted the RV data, either:
-
with a Keplerian model when the observation time baseline ishigher than or covers a significant part of the orbital period, usingthe yorbit software. We then removed the binary signal to searchfor other companions or to characterize stellar activity, and toreach better detection limits;
-
with a first or second-order polynomial fit, when we detected a clear linear or quadratic trend in the RV over the observation time baseline. We also studied the residuals to further explore the system.
The gains on the RV amplitude and rms obtained after correcting for the binary signal/trend are reported in Appendix A. We also looked at the other line profile observables (CCF and FWHM) to further characterize the binary type (SB1, SB2 with large CCF distortions or unresolved SB2) if possible. In addition, we tried to constrain, when possible, the orbital properties of the detected companion, that is, we derived the possible minimal mass versus SMA given the RV trend amplitude and the time baseline. In the case of a RV linear trend 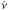 (equivalent to an acceleration), the companion minimal mass MBsini is given by
(equivalent to an acceleration), the companion minimal mass MBsini is given by 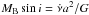 (Winn et al. 2009; Kane et al. 2015), where a is the SMA, and assuming a circular orbit. In the case of a quadratic trend, we considered the RV trend amplitude as a lower boundary on the RV amplitude that would be induced by the companion (assuming a circular orbit), and then deduced the corresponding minimal mass versus sma relation. We used these constraints to verify the compatibility of the detected RV companion with a stellar companion previously detected by direct imaging or astrometric studies. We display the main HARPS data (RV and FWHM time series, (RV, BIS) diagram and CCF) of our detected binaries in Figs. 6–8, and the constraints on the companion orbital properties in Fig. 9.
(Winn et al. 2009; Kane et al. 2015), where a is the SMA, and assuming a circular orbit. In the case of a quadratic trend, we considered the RV trend amplitude as a lower boundary on the RV amplitude that would be induced by the companion (assuming a circular orbit), and then deduced the corresponding minimal mass versus sma relation. We used these constraints to verify the compatibility of the detected RV companion with a stellar companion previously detected by direct imaging or astrometric studies. We display the main HARPS data (RV and FWHM time series, (RV, BIS) diagram and CCF) of our detected binaries in Figs. 6–8, and the constraints on the companion orbital properties in Fig. 9.
4.1. HD 29992
β Cae (HIP 21861, F3IV-V) shows a long-term quadratic RV trend with an 1150 m s-1 amplitude over the 1762-day (~4.8 yr) time baseline of our observations (Fig. 6). This trend is best fitted with a 2nd order polynomial curve and is associated with a composite (RV, BIS) diagram, indicative of both the presence of a companion and of high-frequency pulsations. When corrected from the long-term trend, the (RV residuals, BIS) diagram shows only a remaining vertical spread indicative of pulsations. Taking into account the time baseline, RV trend amplitude and primary mass, and assuming a circular orbit, HD 29992B has a minimal mass of ~40 MJup, and orbits at least 3 au further away than its host star (Fig. 9). It is therefore either a BD or, more probably, a low-mass star. We classify HD 29992 as a spectroscopic binary of probable SB1 type, as the target does not show any significant asymmetry in its CCF, nor any significant trend in its FWHM that would be induced by the secondary spectrum (Fig. 6).
HD 29992 has not been explicitly identified as a binary before. It was classified as a single star in the multiplicity catalog of Eggleton & Tokovinin (2008). Ehrenreich et al. (2010) did not detect any companion to this object, with detection limits excluding companions more massive than 0.07 M⊙ beyond 55 au (Fig. 9). β Cae has been associated with a ROSAT source by Haakonsen & Rutledge (2009), suggesting a late-type stellar companion.
4.2. HD 49095
The binarity of this F6.5V target is clear from the long-term quadratic trend in the RV (with a 49 m s-1 amplitude over the 1951-day observation time baseline) and the corresponding flat (RV, BIS) diagram (Fig. 6). HD 49095 FWHM also shows a loose long-term trend with a large short-term dispersion (Fig. 6), and there is a correlation between the RV and the FWHM data (with a Pearson coefficient of 0.6). We consider that the FWHM long-term variation may be induced by the spectrum of the secondary component of the binary and that HD 49095 is a possible unresolved SB2 with an orbital period much longer than our observation time baseline. There is no noticeable asymmetry in the CCF (Fig. 6).
HD 49095 was flagged as RV variable in Lagrange et al. (2009). It was classified as an astrometric binary by Makarov & Kaplan (2005) and flagged as a proper motion binary in the HIPPARCOS catalog (Frankowski et al. 2007), although no information is given on the orbital properties of the binary. (Ehrenreich et al. 2010, E10) detected a co-moving companion which is itself a close (2.3 au) stellar binary with a total mass of 0.11 M⊙, orbiting at a projected separation of ~31.9 au (~1.3′′) of the primary. Given such parameters and taking M⋆ = 1.2 M⊙ for the primary (Allende Prieto & Lambert 1999), the orbital period of the imaged companion is of at least ~160 yr (considering in this case that the projected separation from E10 is equivalent to the actual physical separation of the binary components). Although the RV trend we detected could still be induced by a planetary-mass companion (Fig. 9), it is compatible with the stellar companion imaged by E10. Since the ~1.3′′ projected separation derived by E10 is slightly larger than, but still close to, the HARPS fiber diameter on the sky (1′′, Pepe et al. 2002), the RV-FWHM correlation characteristic of an unresolved SB2 makes it more probable for this imaged companion to be at the origin of the RV trend we detect.
4.3. HD 68456
This F6V target shows high-amplitude periodic RV variations associated with a flat (RV, BIS) diagram (the amplitudes of the RV and of the BIS are of 4739 m s-1 and 224 m s-1, respectively) and strong CCF variations (but no distortions), illustrative of a SB1 binary with a relatively short period compared to our time baseline (Fig. 6). We used the yorbit software to compute the orbital parameters of the companion to HD 68456. When letting all the orbital parameters free, we found the best solution to correspond to a stellar companion with a minimal mass of 193 ± 12MJup (or 0.18 ± 0.01M⊙) orbiting at 2.15 au (~0.1′′, corresponding to P = 898 ± 0.5 days) around the primary star on a nearly circular orbit (e = 0.12). Once corrected from the Keplerian fit, the RV residuals show a very strong anti-correlation with the BIS (Pearson’s coefficient =−0.96), indicative of stellar activity.
HD 68456 was first reported as a SB1 by Murdoch & Hearnshaw 1993, who also estimated its orbital parameters. These authors found an orbital period of P = 899 ± 0.4 days, an eccentricity of e = 0.12 and a minimal mass for the secondary of mpsini= 0.2M⊙, in close agreement with our yorbit best fit. Another fit of the binary orbital parameters was made by Goldin & Makarov (2007), this time on the base of astrometric HIPPARCOS data. These authors fitted the binary orbit with an optimization algorithm and derived a period of 925 ± 12 days, an eccentricity of 0.08 and an apparent orbit size of 27.3 ± 0.8 mas (0.58 ± 0.02 au). These parameters are also close to our estimation. Remarkably, Goldin & Makarov (2007) also provided an estimation of the system inclination, with i = 30 ± 5°. By combining our RV minimal mass estimate to this astrometric inclination, we can derive an estimation of the actual companion mass: 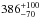 MJup (
MJup (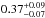 M⊙), for such an inclined system.
M⊙), for such an inclined system.
HD 68456 was also observed in direct imaging with NaCo by Ehrenreich et al. (2010) as part of a search for close companions, but no companion was found. The detection limits derived by E10 exclude companions above 0.07 M⊙ around HD 68456 beyond 40 au, if accounting for an age of 2.5 Gyr as taken from the GCS III. However, a more recent atmosphere model analysis of the primary (Fuhrmann et al. 2011) argues that HD 68456 is probably a much older (~10 Gyr) blue straggler dwarf, and that the secondary is probably a low-mass white dwarf.
4.4. HD 101198
We flagged ι Crt (HIP 56802, F6.5V) as a binary based on its RV variations, which are widely dominated by a positive quadratic trend (with a 269 m s-1 amplitude over a 1988-day observation time baseline), and its associated flat (RV, BIS) diagram (Fig. 6). The FWHM shows a decreasing trend with some dispersion (Fig. 6), and there is a clear (RV, FWHM) anti-correlation (Pearson coefficient of –0.7), meaning that the primary spectrum is slightly blended with that of the companion. As for HD 49095, we therefore conclude that HD 101198 is a probable unresolved SB2 binary with an orbital period much longer than our observation time baseline. The asymmetry in the target CCF is almost negligible (Fig. 6).
HD 101198 was flagged as RV variable in Lagrange et al. (2009). It is classified as an astrometric binary in the HIPPARCOS catalog (Makarov & Kaplan 2005; Frankowski et al. 2007). Ehrenreich et al. (2010) imaged a companion at a projected separation of 25 au (~0.9′′) with an estimated mass of 0.57 M⊙. Assuming that the 25 au projected separation derived by E10 corresponds to the actual sma and a circular orbit, the minimal orbital period of the imaged companion would be ~91 yr. The drift observed in our RV data is compatible with the properties of the companion imaged by E10 (Fig. 9), and the ~0.9′′ projected separation is compatible with a SB2 (see above).
4.5. HD 124850
ι Vir shows a clear quadratic trend in the RV (with a 93 m s-1 amplitude over the 3024-day baseline) that is best fitted by a 2nd order polynomial curve, associated to a composite BIS (RV-BIS correlation coefficient of –0.66, Fig. 6). Once corrected from the RV binary fit, the residuals show an even stronger anti-correlation with the BIS variations (Pearson’s coefficient of –0.83). We conclude that HD 124850 is a spectroscopic binary and is active.
HD 124850 was classified as RV variable in Lagrange et al. (2009). A candidate stellar companion was reported by Raghavan et al. (2010), but no orbital data was available. It has also been associated with a ROSAT source by Haakonsen & Rutledge (2009), which would suggest a late-type stellar companion. Gontcharov & Kiyaeva (2010) derived orbital parameters from a combination of HIPPARCOS data and ground-based astrometric catalogs. The authors estimated an orbital period of 55 yr, an apparent photometric SMA of 200 ± 50 mas (or 4.28 ± 1.07 au given the target parallax) and a relative SMA of 830 ± 20 mas (17.76 ± 0.43 au). They also derived an eccentricity of e = 0.1 ± 0.1, a mass of 0.6 ± 0.2M⊙ for the secondary (given a 1.53 M⊙ mass for the primary) and a system inclination of 60 ± 9°. With such orbital and physical parameters, HD 124850B would induce a RV semi-amplitude of K = 2.4 km s-1. For such a RV curve, the possible RV quadratic trends on our observation time baseline are compatible with the observed RV drift (Fig. 9), and we conclude that the companion we detected with RV is most likely the companion characterized by Gontcharov & Kiyaeva (2010).
4.6. HD 125276
This target shows a strong linear trend in the RV (with a ~65 m s-1 amplitude over the 2989-day observation time baseline) and a flat (RV, BIS) diagram characteristic of a companion (Fig. 6). It is a representative example of the interest of correcting such long-term trends: the RV rms of the residuals is about ten times smaller than the rms of the original RV data, and its amplitude is nearly eight times smaller. HD 125276 FWHM shows an increasing trend with time and is correlated to the RV (Pearson’s coefficient of 0.65, Fig. 6), meaning that the system could be an unresolved SB2. The observed RV trend could still be induced by a planetary-mass or stellar companion with an orbital period longer than our time baseline (Fig. 9).
Based on the comparison of HIPPARCOS and Tycho-2 proper motions, Raghavan et al. (2010) reported a candidate M-type stellar companion to HD 125276 with a projected separation of 144 au, however this possible companion has not been retrieved since. To our knowledge, there is no other occurrence in the literature of a binary companion to HD 125276.
4.7. HD 141513
This A0V target shows a linear trend in its RV with a 1358 m s-1 amplitude over the 1781-day time baseline, along with a flat (RV, BIS) diagram, suggesting a spectroscopic binary status (Fig. 7). μ Ser has been reported as an astrometric binary by Makarov & Kaplan (2005). Its binary status was also reported and characterized by Malkov et al. (2012), who derived a 33.75-yr orbital period, a 255 mas (12.2 au) SMA and a highly eccentric orbit (e = 0.75) for the companion. Another set of orbital parameters was derived by Gontcharov & Kiyaeva (2010) for μ Ser, based on astrometric data. The authors reported an apparent photometric SMA of 110 ± 10 mas (5.3 ± 0.5 au) and a relative SMA of 350 ± 10 mas (16.7 ± 0.5 au), along with an eccentricity of e = 0.4 ± 0.3, a 36 ± 2-yr orbital period and a mass of 2.4 ± 0.4M⊙ for each of the binary components. Our RV observations are compatible with both the parameters derived by Malkov et al. (2012) (Fig. 9) and by Gontcharov & Kiyaeva (2010).
4.8. HD 153363
We acquired 85 spectra on 26 Oph (HIP 83196, F3V), covering a 1995-day baseline (5.5 yr). The RV show large-amplitude (901 m s-1 on our time baseline) variations that are clearly induced by a companion on an eccentric orbit (Fig. 7). The associated (RV, BIS) diagram is composite, indicative of both a companion and of stellar activity (Pearson’s coefficient of –0.32). The FWHM shows both short-term and long-term variations, but there is no correlation with the RV (Pearson’s coefficient <0.1, see Fig. 7).
We used the yorbit software to try to fit a Keplerian model to the RV. Given that our time baseline does not cover a complete orbital period of the companion, there is a large uncertainty on the orbital parameters we derived. We consider that the best fit derived with yorbit gives lower values on the orbital parameters of the companion (especially on the orbital period), rather than a realistic estimation of the parameters. The yorbit best solution corresponds to a mpsini= 44MJup companion with a 3067.5 ± 1926.5-day period (corresponding to a ~4.6 au SMA) and an eccentricity of e = 0.31 ± 0.15. The residuals of the Keplerian fit are clearly correlated to the BIS (Pearson’s correlation coefficient of –0.51), showing that their remaining dispersion is induced by stellar activity.
We already flagged this object as a RV variable in Lagrange et al. (2009). HD 153363 was classified as an astrometric binary by Makarov & Kaplan (2005) and a proper motion binary by Frankowski et al. (2007). Finally, Ehrenreich et al. (2010) imaged a co-moving companion to HD 153363 with a projected separation of 11.3 au (0.35′′) and an estimated mass of 0.7 M⊙. No astrometric information is available in the literature, hence we will discuss here the possibility that our detected RV companion is the object imaged by E10 (HD 153363B). Given the projected separation reported by E10 and taking into account the given mass of 0.7 M⊙, we derived a lower value on HD 153363B orbital period of ~9645 days. We then used yorbit to constrain the RV companion best orbital parameters for larger, increasing orbital periods in the 4800 to 56 000-day range (Fig. 9). For such a period range, the RV companion minimal mass increases from ~62 to ~133 MJup, and its eccentricity also increases from 0.42 to 0.85.
Finally, these results show that the RV variations we detected are compatible with the properties of HD 153363B as determined by E10 (Fig. 9). However, they also show that if the imaged companion corresponds indeed to our RV companion, it should then have a high eccentricity (of at least ~0.6, when assuming that HD 153363B projected separation is equivalent to its physical separation from the primary).
4.9. HD 196385
This target shows a linear trend in the RV with an 94 m s-1 amplitude over the time baseline. The (RV, BIS) diagram is composite (Pearson’s coefficient of –0.26, Fig. 7). Once corrected from the companion-induced trend, the RV residuals have an amplitude two times smaller and a rms two and a half times smaller than before the correction. They also show a significant anti-correlation with the BIS (Pearson’s coefficient of –0.45), corresponding to stellar activity. The Lomb-Scargle periodogram of the RV residuals shows some peaks at about 1.5 and 3 days that are also present in the BIS periodogram. They are therefore most probably induced by the conjunction of stellar activity and stellar rotation. HD 196385 has not been reported as a binary before. Given the RV trend amplitude induced, the companion to HD 196385 could be of either planetary, BD or stellar nature (Fig. 9).
4.10. HD 196724
We only acquired six spectra on 29 Vul over a 1396-day time baseline. However, they allow us to detect high-amplitude (~4 km s-1) RV variations over the observation time baseline along with BIS and FWHM high-amplitude variations, showing that HD 196724 is a spectroscopic binary of probable SB2 type. The CCF are also clearly variable (Fig. 7), however the very small spectrum number prevent us from deriving any constraints on the properties of HD 196724AB. 29 Vul is flagged as a proper-motion binary by Frankowski et al. (2007) and Makarov & Kaplan (2005).
4.11. HD 199254
With too few spectral lines to compute the line profiles, we rely only on the RV data to classify this A5V target as a spectroscopic binary. The 45 RV measurements show an ~2000 m s-1-amplitude quadratic trend on the 2143-day observation time baseline (Fig. 8), suggesting stellar nature (Fig. 9). De Rosa et al. (2014) reported the detection of a stellar companion to HD 199254 through direct imaging, at a projected separation of 13.3 au and with an estimated mass of 0.81 M⊙. Such a companion is compatible to the RV trend we detected.
4.12. HD 216627
We acquired only 13 spectra on δ Aqr (HD 216627, HIP 113136), covering a 389-day time baseline. High-amplitude (9.5 km s-1) RV variations, a flat (RV, BIS) diagram, a clear asymmetry in the CCF (with a broader RV span on their red wing than on their blue wing), and corresponding FWHM variations (correlated to the RV with a Pearson’s coefficient of 0.79) point unambiguously towards a SB2 status for this A3V target (Fig. 7).
δ Aqr was already reported as a binary in Lagrange et al. (2009). A possible member of the Ursa Majoris (UMA) moving group (according to King et al. 2003), it was first reported as an astrometric binary by Goldin & Makarov (2007) on the basis of HIPPARCOS data. These authors derived a primary set of orbital parameters, with a 483 ± 20-day period, a 0.12 ± 0.2 eccentricity and an inclination of 41 ± 16° from edge-on. Ehrenreich et al. (2010) reported no detection in deep imaging, excluding companions more massive than 0.07 M⊙ beyond 100 au. Yet, very interestingly, the companion to HD 216627 was directly detected through IR interferometry made at the Very Large Telescope Interferometer (VLTI; Absil et al. 2011). The authors used the PIONIER four-telescope interferometer to obtain precise closure phase measurements that allowed them to unambiguously detect the companion. These authors derived a contrast of 4.2 in the H-band, leading them to estimate the companion spectral type to be around G5V. However, due to the poor coverage of the (u,v) plan, they were not able to constrain the separation between the two components of the binary, giving only three preferred positions at 37.4, 41 and 46.5 mas from the primary (i.e. projected separations of 1.9, 2 and 2.3 au respectively).
The temporal sampling of our own RV measurements is not sufficient to constrain the orbital parameters of δ Aqr B with a Keplerian fit. Periods can be fitted down to less than ten days (corresponding to minimum masses of a few tens of Jupiter masses), but periods in the range 300–700 days can equally be fitted. The latter period range is compatible with the period derived by Goldin & Makarov (2007) and the interferometric separations derived by Absil et al. (2011).
4.13. HD 223011
HD 223011 (HIP 117219, A7III-IV) shows high-amplitude RV variations (6.3 km s-1 peak-to-peak) and a flat (RV, BIS) diagram that clearly show the presence of a binary companion on an eccentric orbit. The CCF data show strong shifts in radial velocity, characteristic of a SB1, but no noticeable asymmetry that would point towards a SB2 status (Fig. 7). We acquired 46 spectra over 1936 days on HD 223011. Yet, the temporal sampling of our observations is not complete enough to fully constrain the binary orbital parameters: even if our time baseline may cover several orbital periods, most of our data points seem to be located in a restricted phase range, not fully covering the RV variations induced by the companion. When looking at the RV Lomb-Scargle periodogram, multiple peaks are still present above the 1% FAP, with the most pre-eminent at periodicities of ~114, 140, 37 and 92 days. We used the yorbit software to fit the RV with a single Keplerian model. Without putting any prior constraints on the orbital parameters, the best solution corresponds to a companion with a minimal mass of 69 MJup on an eccentric orbit (e = 0.62) with a 37.7-day period (sma = 0.27 au). As in the case of HD 153363, we consider that this fit gives a lower value on the binary orbital parameters but not a definitive determination. The residuals of the fit show a 111.2 m s-1 dispersion without any remaining significant periodicity in their periodogram.
We tried to fit HD 223011 RV data with single Keplerian models corresponding to longer ranges of orbital periods (up to 3000 days) by setting different prior constraints on the period with yorbit. However, all solutions exhibit very high eccentricities (above 0.8) and a significantly larger dispersion of the residuals (always above 200 m s-1). Given that there is no significant asymmetry in the CCF (characteristic of a SB2), the close companion to HD 223011 has probably a contrast of at least two to three magnitudes in the V band with respect to the primary, as a brighter companion would significantly impact the HARPS spectra and distort the CCF. We thus conclude that HD 223011 has a close low-mass stellar companion, with a minimum period of 37.7 days on an eccentric orbit. HD 223011 was already classified as RV variable in Lagrange et al. (2009), and Ehrenreich et al. (2010) did not detect any companion with deep imaging. The detection limits derived by E10 exclude companions more massive than 0.07 M⊙ beyond 130 au.
4.14. HD 224392
Given its high vsini (190 km s-1), we do not have BIS data for η Tuc (HIP 118121, A1V). The RV show high-amplitude variations (~8 km s-1) much larger than the RV dispersion (rms = 1.96 km s-1) induced by the fast rotation (Fig. 8). We conclude that HD 224392 is a probable spectroscopic binary. A stellar companion to η Tuc (member of the ~30 Myr Tucana Horologium young association, see Zuckerman et al. 2011) was directly detected thanks to closure phase and squared visibility measurements made with the PIONIER IR interferometer on the VLTI (Marion et al. 2014). These authors stressed nonetheless that the detection remained somewhat suspicious as the detected companion position was not the same depending on the data type (closure phase or square visibility measurements). New PIONIER observations seem to confirm however the existence of the stellar companion HD 224392B; these new data as well as the properties of this companion will be presented in more detail in a forthcoming paper.
5. Stellar intrinsic variability
Stellar magnetic activity (spots and faculae) and high-frequency pulsations are the two main sources of intrinsic RV variability for our targets (detailed examples can be found in Lagrange et al. 2009). We display in Fig. 10 the RV rms and the mean RV uncertainty versus our target physical properties (B−V, vsini, stellar mass), after subtracting companion-induced RV variations. As expected, the RV rms and the RV mean uncertainty are strongly correlated with the ST and the vsini of our targets; stars of earlier ST (with fewer absorption lines that are more broadened by the rotation rate) have higher RV uncertainties. With earlier-type, more rapidly rotating stars also being the most massive ones, the RV dispersion and mean uncertainty increase with an increasing M⋆. If taken as a whole, the RV rms is larger by an order of magnitude than the typical RV rms for FGK dwarf surveys (e.g. Howard et al. 2011). The “two-peak” shape of the RV and BIS rms distributions (Fig. 11) is probably explained by the relative lack of late A/early F dwarfs in our sample (Sect. 2).
 |
Fig. 10 Stellar intrinsic RV variability vs. stellar properties. For each of our targets, we display the RV rms (first row) and the averaged RV uncertainty (second row) vs. B−V, vsini and M⋆ (from left to right). |
 |
Fig. 11 Stellar intrinsic variability in our observables. First row: RV rms histogram; BIS rms histogram; mean log |
Correction from activity-induced RV jitter.
We display in Fig. 11 the BIS rms versus RV rms distribution. This distribution clearly shows two regimes: i) for RV and BIS rms below ~30 m s-1, the BIS rms increases linearly with the RV rms (Fig. 11); ii) for higher rms, the BIS rms increases much more quickly than the RV rms. These two regimes correspond to the two main sources of RV jitter in our sample, stellar magnetic activity and high-frequency pulsations, respectively. We also display in Fig. 11 the mean log  and log
and log 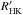 rms versus RV rms distributions. Here, the mean log
rms versus RV rms distributions. Here, the mean log 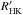 increases steadily with the RV rms, which is in agreement with it being a proxy for the stellar magnetic activity level. On the contrary, the log
increases steadily with the RV rms, which is in agreement with it being a proxy for the stellar magnetic activity level. On the contrary, the log 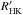 dispersion decreases as the RV rms increases.
dispersion decreases as the RV rms increases.
For some of our later-type, active stars, we can at least partially correct the RV data from the activity-induced jitter by using the correlation between BIS or log 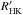 and RV activity-induced variations. We decided to correct the RV from activity for only those targets with a clear enough (RV, BIS) or (RV, log
and RV activity-induced variations. We decided to correct the RV from activity for only those targets with a clear enough (RV, BIS) or (RV, log 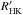 ) correlation. We used the Pearson correlation coefficient to define a quality criterion for the correlation and decided that a minimal absolute Pearson coefficient of 0.7 would be required to consider the (RV, BIS) or (RV, log
) correlation. We used the Pearson correlation coefficient to define a quality criterion for the correlation and decided that a minimal absolute Pearson coefficient of 0.7 would be required to consider the (RV, BIS) or (RV, log 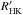 ) correlation significant. We found that eleven of our targets met this criterion in the case of the (RV, BIS) correlation. Two of them have already been corrected from a binary trend. Only one target is corrected in the case of the (RV, log
) correlation significant. We found that eleven of our targets met this criterion in the case of the (RV, BIS) correlation. Two of them have already been corrected from a binary trend. Only one target is corrected in the case of the (RV, log 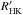 ) correlation (note that for this target, HD 25457, we correct both the activity jitter on the short-term with the RV-BIS correlation and on the long-term with the RV-log
) correlation (note that for this target, HD 25457, we correct both the activity jitter on the short-term with the RV-BIS correlation and on the long-term with the RV-log 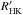 correlation). For these targets, we applied a linear fit to the (RV, BIS) or (RV, log
correlation). For these targets, we applied a linear fit to the (RV, BIS) or (RV, log 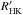 ) data and then removed it from the RV. We display the list of these targets, along with the gains in RV amplitude, rms and on the detection limits in Table 3.
) data and then removed it from the RV. We display the list of these targets, along with the gains in RV amplitude, rms and on the detection limits in Table 3.
6. Detection limits
6.1. Detection limit determination
We estimated the detection limits for each target of our survey, that is, the upper limit on the mpsini of an hypothetical companion that would be detected given the observed RV, at different orbital periods. We computed the detection limits on a grid of 200 log-spaced orbital periods in the 1- to 1000-day range, roughly corresponding to SMA in the 0.02- to 2.5-au range. We used the Local Power Analysis (LPA) method developed by Meunier et al. (2012). These detection limits are computed assuming circular orbits. The LPA method compares the maximum power Pwpl of the RV signal induced by a fake planet of a given mass and a given period (with the same temporal sampling as the actual data) to X times the maximum power Pwdat of the actual RV signal within a localized period range of the periodogram (0.75P-1.25P for a given period P). Contrary to Meunier et al. (2012), who took X = 1, we used here a slightly more restricting X = 1.3 ratio, empirically chosen to correspond to the “naked-eye” detection of a real planet signal in an observed periodogram. The fake planet mpsini is considered to be above the detection limit if, for 100 phase realizations (i.e., a 99% confidence level), Pwpl is always above X times Pwdat. For each orbital period of the grid, the fake planet decreasing mpsini is tested iteratively during several loops, with a narrower mass step at each loop. The upper limit on the considered mpsini range is 100 MJup, and the finest mass step (equivalent to the step of the mpsini grid) is 0.005 MJup. The LPA method gives lower detection limits than bootstrap methods for various stellar types and RV jitter levels (Meunier et al. 2012; Lagrange et al. 2013). When the target was found to have a companion or to be active, we computed the detection limits before and after removing the linear/quadratic RV trends, Keplerian fits or stellar activity correlations.
Note: assuming only circular orbits to compute the detection limits is the common approach in the literature of large RV surveys (see e.g. Cumming et al. 2008; Lagrange et al. 2009; Howard et al. 2011) for two main reasons. It allows considerable reduction of the computation time; and the eccentricity impact on planet detectability is relatively small for eccentricities of up to ~0.5 (see Cumming et al. 2008, and references therein). However, for high eccentricities, the planet detectability can be highly affected as it will increasingly depend on the phase coverage of the planet orbit. Thus, considering one of our targets among others, including eccentric orbits in our upper limit computation would make our mass detection limits for this target higher at specific periods. When considering the whole survey, our mass detection limits would be slightly higher.
 |
Fig. 12 Achieved detection limits for our sample versus main stellar parameters. For all panels, each black dot represents the detection limit for one target. All targets are displayed except for stars with detected GP companions. Left: mean detection limit in the range 1–10 days; middle: mean detection limit in the range 10–100 days; right: mean detection limit in the range 100–1000 days. Top: detection limits vs. B−V; middle top: vs. vsini; middle bottom: vs. M⋆; bottom: in histograms. |
6.2. Results
6.2.1. Detection limits versus physical properties
We display in Fig. 12 the detection limits achieved with the LPA method versus our sample main parameters (B−V, vsini and M⋆). Our LPA detection limits are clearly correlated to these parameters, with higher detection limits for increasing vsini and for earlier ST. This is in agreement with our results in terms of stellar variability (Sect. 5). In terms of vsini, we can roughly distinguish two populations. For vsini lower than 100 km s-1, the detection limits are mostly in the planetary domain (≲10–20 MJup), decreasing well below 1 MJup down to ~0.1 MJup at all periods in the best cases. In contrast, for vsini greater than 100 km s-1, the detection limits are mostly larger than 1 MJup; still a large number of them remain below 10 MJup at all periods, while the remainder are in the BD domain.
In terms of ST, we can also make a rough distinction between our earlier- (B−V ≲ 0.3) and later-type targets. For the later-type stars, the achieved detection limits are in the planetary mass domain, even for periods up to 1000 days. In contrast, for the earlier-type targets, the detection limits are spread over the GP and BD mass domains; yet they can still decrease to a fraction of a MJup for periods of a few- to a few tens of days, and decrease to a few MJup for periods up to 1000 days.
In terms of stellar masses, we can roughly make the same distinction between our targets with M⋆ ≤ 1.5 M⊙, for which the detection limits remain in the planetary domain for periods up to 1000 days, and our targets with higher masses, for which the detection limits spread from less than 1 MJup at short periods, at best, to 100 MJup, at worst. Finally, we note that if we were to extrapolate these detection limits to the solar parameter values, we would find masses in the range of 10–30 MEarth, that is, in the same range as the detection limits we deduced for the Sun based on simulated RV time series of solar magnetic activity (Meunier & Lagrange 2013).
When compared to the typical detection limits obtained by Cumming et al. (2008) or Howard et al. (2011), for example, for later-type (FGK) stars in similar period ranges, we find our detection limits to be generally higher by one order of magnitude in minimal mass. We note that:
-
for very short periods (≲50 days), 90% of our targets have detection limits in the planetary domain, meaning that hot Jupiters can be detected by RV for very early ST and for very high rotation rates (up to 100 km s-1);
-
the same percentage of our targets (90%) have detection limits lower than ~80 MJup for periods of up to 1000 days;
-
70% of our targets have detection limits lower than 10–20 MJup for periods up to 1000 days, meaning that close-in GP (i.e., located at separations similar to most of the GP found by RV around solar-like stars) are detectable around most of the AF MS dwarfs;
-
30% of our targets have detection limits lower than 1 MJup for periods of up to 1000 days, meaning that Saturn-like and even Neptune-like planets can be detected around the most favourable of our targets, such as mid- to late-F dwarfs with low to intermediate vsini (up to 20 to 30 km s-1).
Contrary to what was commonly expected, these results confirm that GPs are widely detectable around MS dwarfs of early spectral type, and prove the usefulness of extending RV surveys from FGK-type stars to AF-type dwarfs.
6.2.2. Sample search completeness
To better characterize our results in terms of detection limits, we derived the search completeness function C(P, mpsini) of our sample in a similar way to Howard et al. (2011), who derived occurrence rates of low-mass planets with short orbital periods around FGK solar-like stars. For given P and mpsini, we have 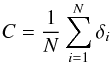 (1)where, for each target i of our sample without a detected planet, δi = 1 if mpsini is higher than the target detection limit at the period P, δi = 0 if mpsini is lower than the target detection limit at P, and N is the number of such targets in our sample. The search completeness C therefore gives the fraction of stars of our sample for which we can rule out a (P, mpsini) planet. Here, we compute C (P, mpsini) over all our targets for which we recorded at least Nm = 15 spectra, excluding two targets for which we had too few spectra (HD 196724 and HD 216627). The completeness must be computed only on stars with no detected planets. Therefore we had N = 104 targets taken into account in Eq. (1) (excluding two stars with detected GP; HD 60532 and HD 111998). We took the detection limits into account in the computation of C(P, mpsini) once we corrected the RV from binary trends or stellar activity correlations, if any. We display C(P, mpsini) in Fig. 13.
(1)where, for each target i of our sample without a detected planet, δi = 1 if mpsini is higher than the target detection limit at the period P, δi = 0 if mpsini is lower than the target detection limit at P, and N is the number of such targets in our sample. The search completeness C therefore gives the fraction of stars of our sample for which we can rule out a (P, mpsini) planet. Here, we compute C (P, mpsini) over all our targets for which we recorded at least Nm = 15 spectra, excluding two targets for which we had too few spectra (HD 196724 and HD 216627). The completeness must be computed only on stars with no detected planets. Therefore we had N = 104 targets taken into account in Eq. (1) (excluding two stars with detected GP; HD 60532 and HD 111998). We took the detection limits into account in the computation of C(P, mpsini) once we corrected the RV from binary trends or stellar activity correlations, if any. We display C(P, mpsini) in Fig. 13.
 |
Fig. 13 GP search completeness of our survey. Black dots: detected GP (mpsini vs. P). Solid lines: survey search completeness (i.e., fraction of stars with good enough detection limits to rule out planets of a given mpsini at a given orbital period P). From bottom to top: 1%, 10% to 90% (10% step) and 99% search completenesses. |
6.3. GP occurrence rates
Taking into account the GP detections and detection limits of our sample, we derived a first estimation of the close-in GP occurrence rate around AF, MS stars. The method we followed to deduce GP occurrence rates, detailed in Sect. 6.3.1, is largely inspired from Howard et al. (2011). These authors counted the number of systems ndet with detected planets in five given domains of P, mpsini. Then, they derived an estimation of the number of planets potentially missed nmiss in each of the (P, mpsini) domains, based on the number of actual detections and on the survey completeness in these domains. They finally computed the planet occurrence rates taking into account both ndet and nmiss and using binomial statistics.
6.3.1. Method
We detail here step by step the method we used to derive our GP detection rates.
[Mass; period] ranges –
We consider three mpsini domains: i) a 13- to 80-MJup range, corresponding to BD companions; ii) a 1- to 13-MJup range, corresponding to Jupiter-like or super-Jupiter GP; and iii) a 0.3- to 1-MJup range, corresponding to Saturn-like or sub-Jupiter GP. We consider this partition as the most meaningful since it fits our results well and since dividing our achieved mpsini range into more domains would not lead to more significant results, due to small-number statistics. We then consider five different orbital period ranges: i) the full 1- to 1000-day range over which we computed our LPA detection limits, to derive occurrence rates for all close-in GP; ii) a 1- to 10-day and a 1- to 100-day ranges to roughly cover the “Hot Jupiter” space and allow a comparison with, e.g., Cumming et al. (2008) and Howard et al. (2011); iii) the complementary 10- to 100-day and 100- to 1000-day ranges.
Search completeness function –
Considering a (P, mpsini) domain D with mpsini in the range mp1sini-mp2sini and P in the range P1–P2, we compute the search completeness function C(P, mpsini) over D as
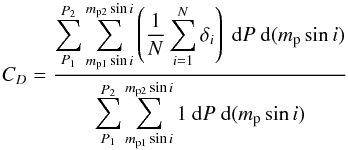 (2)with N = 104 targets. We compute CD on the same period grid we used to compute the LPA detection limits, and on a mass grid fine enough (20000 mass bins from 0 to 100 MJup) to match the mass accuracy reached in the final LPA loop.
(2)with N = 104 targets. We compute CD on the same period grid we used to compute the LPA detection limits, and on a mass grid fine enough (20000 mass bins from 0 to 100 MJup) to match the mass accuracy reached in the final LPA loop.
 |
Fig. 14 Probability density function of the GP occurrence rate for planetary mpsini in the range 1–13 MJup and for periods in the range of 1−1000 days, after correcting for the missed GP. Red: most probable value. Blue: 1σ confidence interval. Hatched blue: 2σ confidence interval. |
“Missed planets” estimation –
To derive significant occurrence rates, we have to correct our results (in terms of actual detections) from our search incompleteness, that is, by statistically estimating the number of GP nmiss that we potentially missed in our survey. We compute nmiss in the same way as in Howard et al. (2011). For each (P, mpsini) domain with a search completeness CD and with ndet systems having one or several detected GP, we have (provided that ndet ≥ 1) 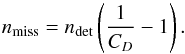 (3)Compared to Howard et al. (2011), our sample is much smaller both in terms of targets and of detections. We have therefore several (P, mpsini) domains with no actual detection and with a search completeness well below 100%. In such a case (ndet = 0 and CD< 100%), we use a number
(3)Compared to Howard et al. (2011), our sample is much smaller both in terms of targets and of detections. We have therefore several (P, mpsini) domains with no actual detection and with a search completeness well below 100%. In such a case (ndet = 0 and CD< 100%), we use a number 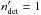 instead of ndet = 0, and compute
instead of ndet = 0, and compute 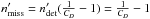 . We then use these
. We then use these 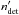 and
and 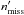 in the same way as ndet and nmiss to compute the companion occurrence rate. Such an approach may appear conservative but we consider it to be the most secure given our target sample size.
in the same way as ndet and nmiss to compute the companion occurrence rate. Such an approach may appear conservative but we consider it to be the most secure given our target sample size.
Occurrence rate computation –
For each of our (P, mpsini) domains, we finally derive the GP occurrence rate and its 1σ and 2σ uncertainties in the same way as Howard et al. (2011), i.e. by using binomial statistics:
-
when ndet ≥ 1, we compute the binomial distribution of ndet systems with at least one GP among the N⋆ = 106 targets with 15 or more spectra from our sample. The probability f of drawing ndet systems with at least one detected GP among the N⋆ targets of our sample is
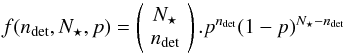 (4)where p is the probability of having at least one GP around one star. We then multiply this probability distribution by (ndet+nmiss)/ndet to account for the missed GP, and thus obtain the probability density function (PDF) of the GP occurrence rate. The GP occurrence rate corresponds to the probability f for which the PDF takes its maximum value (Fig. 14). To derive the 1σ and 2σ confidence intervals, we integrate the PDF and compute the 1σ and 2σ standard deviations. As an example, we display in Fig. 14 the 1- to 13-MJup GP occurrence rate PDF for the full period range of our AF survey, after correcting for the missed GP;
(4)where p is the probability of having at least one GP around one star. We then multiply this probability distribution by (ndet+nmiss)/ndet to account for the missed GP, and thus obtain the probability density function (PDF) of the GP occurrence rate. The GP occurrence rate corresponds to the probability f for which the PDF takes its maximum value (Fig. 14). To derive the 1σ and 2σ confidence intervals, we integrate the PDF and compute the 1σ and 2σ standard deviations. As an example, we display in Fig. 14 the 1- to 13-MJup GP occurrence rate PDF for the full period range of our AF survey, after correcting for the missed GP; -
when ndet = 0, we compute the binomial distribution of
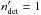 system with GP among the N⋆ targets and multiply the probability distribution by
system with GP among the N⋆ targets and multiply the probability distribution by 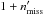 . Then, we derive the companion occurrence rate in the same way as above, that is, by taking the probability for which the PDF is maximal. In this case, we consider the lower limit of the confidence intervals to be zero, and we compute the upper limit of the confidence intervals in the same way as in the ndet ≥ 1 case.
. Then, we derive the companion occurrence rate in the same way as above, that is, by taking the probability for which the PDF is maximal. In this case, we consider the lower limit of the confidence intervals to be zero, and we compute the upper limit of the confidence intervals in the same way as in the ndet ≥ 1 case.
6.3.2. Results and discussion
Given that our sensitivity to GP is significantly different between our less massive (later-type) and more massive (earlier-type) targets, we decided to split our sample into two sub-samples (each having roughly the same number of targets) to better investigate the impact of the stellar mass on the GP occurrence rate and properties. The first sub-sample comprises our 51 targets with M⋆> 1.5 M⊙; the second sub-sample contains the other 57 targets (with M⋆≤ 1.5 M⊙). We note that the two GP systems we detected belong to the M⋆≤ 1.5 M⊙ sub-sample. We hereafter discuss the results obtained from the different (P, mpsini) selected domains. We sum up our main results in terms of constraints on companion occurrence rates in Table 4 and in Fig. 15. Note that in the case where ndet = 0, we report the companion occurrence rate with a “≤” item in Table 4 to emphasize the difference with the ndet ≥ 1 case.
GP occurrence rate around AF dwarf stars.
 |
Fig. 15 Top panel: companion occurrence rate in the 13 to 80-MJupmpsini range for three successive (non-cumulative) P ranges (from left to right: 1- to 10-day, 10- to 100-day and 100- to 1000-day ranges). Blue/cyan: M⋆≤ 1.5 M⊙ sub-sample. Red/orange: M⋆≥ 1.5 M⊙ sub-sample. Full color: occurrence rate computed in the case ndet ≥ 1. Shaded lines: occurrence rate computed in the case ndet = 0. The 1σ confidence intervals are displayed for these two M⋆ sub-samples as blue and red solid lines, respectively. Middle and bottom panels: occurrence rates for the 1- to 13-MJup and 0.3- to 1-MJup ranges, respectively. |
Companion frequency versus mpsini and versus M⋆ –
We first look at BD companions (13 ≤mpsini≤ 80 MJup). We do not detect any BD companion in the 1 to 103-day range, neither in our low-M⋆ nor in our high-M⋆ sub-sample. Moreover, for such mpsini, our survey completeness is almost complete for the investigated periods (C ≥ 85% at any considered P and M⋆ ranges, Table 4). This translates into a close-in BD occurrence rate of 2 to 2.6% (for the low and high-M⋆ sub-samples, respectively), with a 1σ uncertainty up to 6 and 10%, respectively. These companion frequencies are not yet very well constrained due to the relatively small number of targets per M⋆ sub-sample. Still, they are in agreement with the “brown dwarf desert” (i.e., the paucity of BD-mass companions compared to both GP and low-mass stellar companions at SMA below 3–5 au) reported around solar-like FGK dwarfs by transit and RV surveys (with a <1% frequency, see, for example, Grether & Lineweaver 2006).
We then look at Jupiter-like and “super-Jupiter” companions (1 ≤mpsini≤ 13 MJup). In this mpsini domain, we find a GP occurrence rate of 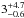 % in the 1- to 103-day range (roughly corresponding to SMA in the 0.02- to ~2.5-au range) when accounting for our whole AF sample. Nonetheless, we must look at our two M⋆ sub-samples separately, as they are significantly different both in terms of detections and achieved sensitivity (see above).
% in the 1- to 103-day range (roughly corresponding to SMA in the 0.02- to ~2.5-au range) when accounting for our whole AF sample. Nonetheless, we must look at our two M⋆ sub-samples separately, as they are significantly different both in terms of detections and achieved sensitivity (see above).
When looking at our low-M⋆ sub-sample only, we are almost sensitive to all possible GP (completeness above 90%); the GP occurrence rate is 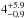 % (at a 1σ confidence level). This value is compatible with the ~4 ± 1% GP rate found by Cumming et al. (2008) in roughly the same (P, mpsini) domain for solar-like FGK stars. Given the error bars, this result is also compatible with the GP frequency derived in more or less the same (P; mpsini) domain and M⋆ range by Johnson et al. (2010a) (~7%) or Reffert et al. (2015) (~4–10%) for sub-giant and giant stars, respectively. Finally, it is lower than, but still compatible with the GP frequency predicted by CA for this M⋆ range (moreover, the CA predictions are made considering all possible separations, see Kennedy & Kenyon 2008).
% (at a 1σ confidence level). This value is compatible with the ~4 ± 1% GP rate found by Cumming et al. (2008) in roughly the same (P, mpsini) domain for solar-like FGK stars. Given the error bars, this result is also compatible with the GP frequency derived in more or less the same (P; mpsini) domain and M⋆ range by Johnson et al. (2010a) (~7%) or Reffert et al. (2015) (~4–10%) for sub-giant and giant stars, respectively. Finally, it is lower than, but still compatible with the GP frequency predicted by CA for this M⋆ range (moreover, the CA predictions are made considering all possible separations, see Kennedy & Kenyon 2008).
By contrast, when looking at our high-M⋆ sub-sample (1.5 ≤M⋆≲ 3 M⊙), we do not detect any GP in the 1- to 13-MJup range and at periods ≤1000 days. In this case, we still reach a completeness of ~ 40% if considering all periods (and of ~60% if considering only Hot Jupiters with periods below a hundred days, Table 4). Our results translate into a GP occurrence rate of ~6% at all periods (and of ~4% for P ≤ 100 days) for stars with M⋆ between 1.5 and ~3 M⊙. However, given our sample size, the uncertainties on these occurrence rates reach high values (~22 and ~14%, respectively). Therefore, our results do not yet allow us to adequately constrain close-in Jovian planet occurrence rates (Fig. 15) to test the proportionality relation between the stellar mass and the GP occurrence rate predicted by CA theory (Kennedy & Kenyon 2008) and seemingly observed for evolved stars.
We finally look at close-in Saturn-like GP (0.3 ≤mpsini≤ 1 MJup). Our high-M⋆ sub-sample is almost insensitive to such GPs (completeness of ~ 0%). We then focus on our low-M⋆ sub-sample. In this case, although our sensitivity is not as good as for more massive GPs, it still reaches almost 50% at all periods (and it is above 60% for smaller periods, see Table 4). However, we do not detect any GP in this (P, mpsini) domain. We derive a GP frequency of 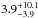 % for periods below 103 days. Therefore, we are not able to detect any significant difference with respect to the close-in Jovian GP frequency for the same M⋆ sub-sample.
% for periods below 103 days. Therefore, we are not able to detect any significant difference with respect to the close-in Jovian GP frequency for the same M⋆ sub-sample.
GP frequency versus orbital period –
All three of our detected GPs orbit with periods above 200 days and no Hot Jupiters were detected in our sample. Yet, our sensitivity is the best when considering only the shortest orbital periods (≤10 days): for mpsini in the 1 to 13-MJup range, we reach C = 96% and C = 75% for our low and high-M⋆ sub-samples, respectively. This translates into Hot Jupiter frequencies of 2 and 3% respectively, with uncertainties up to 7 and ~10% (Fig. 15). These results are compatible with the 0.5 to ~1.5% Hot Jupiter occurrence rates around solar-like FGK stars as derived by transit and RV surveys (see, e.g., Santerne et al. 2016). Due to the limited size of our sub-samples, we cannot yet test if there is a significant difference for the Hot Jupiter frequency between AF massive stars and FGK solar-like stars on the MS, as supposed by Kennedy & Kenyon (2008). As we mentioned in Sect. 1, transiting Hot Jupiters have indeed been found around early-type MS stars. We provide here, to the best of our knowledge, the first constraint on their frequency.
7. Conclusion and perspectives
We have conducted the first systematic RV survey for BDs and GPs with periods in the 1- to 103-day range orbiting early-type (AF) MS stars. We have confirmed that the challenges raised for GP detectability with RV by the early ST of these stars (smaller number of spectral lines and enhanced rotation rate) can be overcome, providing an adapted RV computation and a careful observational strategy.
Among our 108 targets, we detected and characterized one new GP system, and brought additional constraints on a second two-GP system. We additionally detected 14 confirmed or probable companions characterized by RV high-amplitude variations or long-term trends, and brought constraints on their minimal masses and SMA. Based on these constraints, on other spectroscopic observables, and on previous astrometric and/or DI detections, we concluded that most of these companions are of stellar or BD nature; though two of them could still be of planetary nature. We characterized the RV intrinsic variability of our targets, and computed the detection limits for our whole sample in the 1- to 103-day period range. We demonstrated that close-in (SMA ≲ 2.5 au) BD-mass or Jovian-mass companions are detectable around massive MS dwarfs, and that Saturn-mass companions are detectable around early dwarfs with masses up to 1.5 M⊙. We deduced the first estimation of the close-in BD and GP frequencies in the 1- to 103-day range around AF-type stars, finding it compatible both with the “brown dwarf desert” and GP frequency reported in roughly the same (P, mpsini) domains for solar-like stars. Nevertheless, we have not yet been able to bring adequately precise constraints to test the predictions previously made concerning the dependency of the GP occurrence rate on the stellar mass, and concerning the origin of the suggested Hot Jupiter desert around evolved sub-giant and giant stars away from the MS.
The next step of this study will be to associate the results (both in terms of detections and statistics) from the SOPHIE northern survey to the present HARPS results. The detection of a GP on an ~324-day orbit with a ~2.8 MJup minimal mass around the relatively young F5-6V MS dwarf HD 113337 with the SOPHIE spectrograph was already reported in Borgniet et al. (2014). The SOPHIE performances are slightly decreased compared to HARPS (with a spectral resolution of R = 75 000 and a typical RV accuracy of 5 m s-1 against R = 115 000 and 1 m s-1 for HARPS, respectively), but they should not significantly affect a combined statistical study. Such a complete study will allow us to more than double our target sample and thus derive more significant statistical results. It should then allow us to estimate, for the first time, a model of the mass-period distribution of GP and BD around AF MS stars.
As emphasized earlier in this paper, there is a need to test, more systematically, the existence of a correlation between RV-detected GP and cold debris disks indicated by IR excesses. HD 113337, which hosts at least one GP and one debris disk (Chen et al. 2014) is a remarkable example of such a GP+debris disk system. Some of the GP systems that we reported or discussed in this publication (HD 60532, HD 111998) have not, to the best of our knowledge, been fully investigated from this point of view. A systematic search for IR excesses in such GP systems would be useful to test the link between the presence of cold debris disks and GPs, and to better understand their evolution. Younger systems with directly imaged GP at wider separations usually also host debris disks.
Acknowledgments
These results have made use of the SIMBAD database, operated at the CDS, Strasbourg, France. We acknowledge support from the French CNRS and the support of the Agence Nationale de la Recherche (ANR grants BLANC ANR-10-0504.01 and GIPSE ANR-14-CE33-0018). We would like to thank our co-Is on our Harps proposals: D. Ehrenreich, A. Lecavelier and G. Lo Curto. We would also like to thank our anonymous referee for his judicious comments.
References
- Absil, O., Le Bouquin, J.-B., Berger, J.-P., et al. 2011, A&A, 535, A68 [Google Scholar]
- Allen de Prieto, C., & Lambert, D. L. 1999, A&A, 352, 555 [NASA ADS] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgniet, S., Boisse, I., Lagrange, A.-M., et al. 2014, A&A, 561, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., & Sophie Team. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, eds. L. Arnold, F. Bouchy, & C. Moutou, 319 [Google Scholar]
- Bowler, B. P., Johnson, J. A., Marcy, G. W., et al. 2010, ApJ, 709, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chelli, A. 2000, A&A, 358, L59 [NASA ADS] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, ApJS, 211, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- De Rosa, R. J., Patience, J., Wilson, P. A., et al. 2014, MNRAS, 437, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2008, A&A, 491, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2009, A&A, 506, 1469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, O. J. 1982, ApJS, 50, 221 [CrossRef] [Google Scholar]
- Eggleton, P. P., & Tokovinin, A. A. 2008, MNRAS, 389, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Lagrange, A.-M., Montagnier, G., et al. 2010, A&A, 523, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA Special Edition, ed. 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Chini, R., Hoffmeister, V. H., & Stahl, O. 2011, MNRAS, 416, 391 [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005a, A&A, 444, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005b, A&A, 443, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2006, A&A, 452, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Hébrard, G., Alonso, R., et al. 2010, A&A, 524, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldin, A., & Makarov, V. V. 2007, ApJS, 173, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcharov, G. A., & Kiyaeva, O. V. 2010, New Astron., 15, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Haakonsen, C. B., & Rutledge, R. E. 2009, ApJS, 184, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A., Marcy, G., Johnson, J. A., et al. 2011, in American Astronomical Society Meeting Abstracts #217, BAAS, 43, 415.06 [Google Scholar]
- Johnson, J. A. 2008, in Extreme Solar Systems, eds. D. Fischer, F. A. Rasio, S. E. Thorsett, & A. Wolszczan, ASP Conf. Ser., 398, 59 [Google Scholar]
- Johnson, J. A., & Wright, J. T. 2013, ArXiv e-prints [arXiv:1307.3441] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010a, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Bowler, B. P., Howard, A. W., et al. 2010b, ApJ, 721, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Morton, T. D., & Wright, J. T. 2013, ApJ, 763, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Huber, D., Boyajian, T., et al. 2014, ApJ, 794, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, S. R., Barclay, T., Hartmann, M., et al. 2015, ApJ, 815, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. R., Villarreal, A. R., Soderblom, D. R., Gulliver, A. F., & Adelman, S. J. 2003, AJ, 125, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Desort, M., Galland, F., Udry, S., & Mayor, M. 2009, A&A, 495, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A.-M., Meunier, N., Chauvin, G., et al. 2013, A&A, 559, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, J., & Correia, A. C. M. 2009, A&A, 496, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd, J. P. 2011, ApJ, 739, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd, J. P. 2013, ApJ, 774, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [NASA ADS] [CrossRef] [Google Scholar]
- Malaroda, S. 1975, AJ, 80, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, O. Y., Tamazian, V. S., Docobo, J. A., & Chulkov, D. A. 2012, A&A, 546, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marion, L., Absil, O., Ertel, S., et al. 2014, A&A, 570, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, I., Zijlstra, A. A., & Boyer, M. L. 2012, MNRAS, 427, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., & Lagrange, A.-M. 2013, A&A, 551, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., & De Bondt, K. 2012, A&A, 545, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Klahr, H., Alibert, Y., Benz, W., & Dittkrist, K.-M. 2010, ArXiv e-prints [arXiv:1012.5281] [Google Scholar]
- Morton, T. D., Bryson, S. T., Coughlin, J. L., et al. 2016, ApJ, 822, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Murdoch, K., & Hearnshaw, J. B. 1993, The Observatory, 113, 126 [NASA ADS] [Google Scholar]
- Murgas, F., Jenkins, J. S., Rojo, P., Jones, H. R. A., & Pinfield, D. J. 2013, A&A, 552, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakajima, T., & Morino, J.-I. 2012, AJ, 143, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, G. 2013, A&A, 551, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasinetti Fracassini, L. E., Pastori, L., Covino, S., & Pozzi, A. 2001, A&A, 367, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Rupprecht, G., et al. 2002, The Messenger, 110, 9 [NASA ADS] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Rybicki, G. B. 1989, ApJ, 338, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reffert, S., Bergmann, C., Quirrenbach, A., Trifonov, T., & Künstler, A. 2015, A&A, 574, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sándor, Z., & Kley, W. 2010, A&A, 517, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2015, MNRAS, 451, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Moutou, C., Tsantaki, M., et al. 2016, A&A, 587, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schlaufman, K. C., & Winn, J. N. 2013, ApJ, 772, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ségransan, D., Mayor, M., Udry, S., et al. 2011, A&A, 535, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Solanki, S. K., Krivova, N. A., et al. 2014, A&A, 569, A38 [Google Scholar]
- Snellen, I. A. G., Koppenhoefer, J., van der Burg, R. F. J., et al. 2009, A&A, 497, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, C. A. O., Quast, G. R., Melo, C. H. F., & Sterzik, M. F. 2008, in Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, 757 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villaver, E., Livio, M., Mustill, A. J., & Siess, L. 2014, ApJ, 794, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Albrecht, S., et al. 2009, ApJ, 703, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Rhee, J. H., Song, I., & Bessell, M. S. 2011, ApJ, 732, 61 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Sample
Stellar characteristics and detailed results for the 108 targets of our HARPS RV survey.
All Tables
Stellar characteristics and detailed results for the 108 targets of our HARPS RV survey.
All Figures
 |
Fig. 1 Our A-F sample properties. Left: HR diagram of our sample, in absolute V-magnitude vs. B−V. The Sun is displayed (red star) for comparison. Middle: vsini vs. B−V distribution. Right: mass histogram. |
| In the text | |
 |
Fig. 2 Observation summary. Left: histogram of the spectrum number per target. Middle: histogram of the separate observation epoch number per target. Right: histogram of the time baselines. |
| In the text | |
 |
Fig. 3 HD 60532 spectroscopic data. Top row: HD 60532 RV time series (left), Lomb-Scargle periodogram of the RV (middle) and temporal window of the observations (right). The Keplerian fit is superimposed (red solid line) to the RV. On the periodogram, the false-alarm probability (FAP) at 1% (solid line) is indicated in red; the planet periods are indicated in blue. Second and third rows: BIS and FWHM time series, corresponding Lomb-Scargle periodograms and correlations with the RV data. Fourth row: RV residuals from planet c, corresponding Lomb-Scargle periodogram and correlation with BIS. The planet b Keplerian fit is superimposed on to the residuals, and planet b period is superimposed in blue on the periodogram. Fifth row: RV residuals from the two-planet Keplerian fit, corresponding Lomb-Scargle periodogram, and correlation with BIS. |
| In the text | |
 |
Fig. 4 Spectroscopic data for HD 111998. Top row: HD 111998 RV time series (left), RV Lomb-Scargle periodograms (middle) and temporal window of the observations (right). The Keplerian fit is superimposed (red solid line) to the RV, as well as the linear trend (dashed blue line). On the RV periodogram, the FAP at 1% (solid line) is indicated in red; the planet period is indicated in blue. Second and third rows: BIS and FWHM time series, corresponding Lomb-Scargle periodograms and correlations with the RV data. Fourth row: Residuals of the fit as a function of time, periodogram of the residuals and BIS correlation with the residuals. |
| In the text | |
 |
Fig. 5 Top: focus on HD 111998 RV data over 800 days (left) at three distinct epochs (black, red and blue dots); and corresponding (RV, BIS) diagram (right). Bottom: the same for HD 111998 RV residuals. |
| In the text | |
 |
Fig. 6 Main HARPS data for our detected binaries (first part). From left to right: RV vs. time (Julian Day – 2 453 000), BIS vs. RV, FWHM vs. time, stacked CCF. From top to bottom: HD 29992, HD 49095, HD 68456, HD 101198, HD 124850, and HD 125276. |
| In the text | |
 |
Fig. 7 Main HARPS data for our detected binaries (second part). From left to right: RV vs. time (Julian Day – 2 453 000), BIS vs. RV, FWHM vs. time, stacked CCF. From top to bottom: HD 141513, HD 153363, HD 196385, HD 196724, HD 216627, and HD 223011. |
| In the text | |
 |
Fig. 8 HARPS RV for our binaries of very early ST (i.e., without line profile computation). From left to right: RV time series of HD 199254 and HD 224392. |
| In the text | |
 |
Fig. 9 Limits on the orbital parameters (mpsini, sma) of the companions to our targets with long-term RV trends, given the observed RV variations. Black solid line: minimal mass vs. sma. Dotted black line: minimal sma given the observation time baseline (i.e., considering that the companion orbital period is at least equal to the time baseline, and assuming a circular orbit). In the case of HD 153363, the mass and sma corresponding to the Keplerian fit derived with yorbit with all parameters free is shown as a black filled dot, and the masses and sma corresponding to the yorbit fits obtained for longer periods are showed as black crosses. The area filled and/or shaded in cyan corresponds to the (mass, sma) domain based on these constraints. Dashed red line: projected separation of the imaged companion (if any), resulting possible mass from the DI study (red diamond), or DI detection limits (solid red line). HD 29992, HD 49095, HD 101198, HD 153363: DI from E10. HD 199254: DI from De Rosa et al. (2014). Blue solid line: sma of the companion detected through astrometric measurements, and mass estimation (blue diamond). HD 124850: astrometry from Gontcharov & Kiyaeva (2010); HD 141513: from Malkov et al. (2012). |
| In the text | |
 |
Fig. 10 Stellar intrinsic RV variability vs. stellar properties. For each of our targets, we display the RV rms (first row) and the averaged RV uncertainty (second row) vs. B−V, vsini and M⋆ (from left to right). |
| In the text | |
 |
Fig. 11 Stellar intrinsic variability in our observables. First row: RV rms histogram; BIS rms histogram; mean log |
| In the text | |
 |
Fig. 12 Achieved detection limits for our sample versus main stellar parameters. For all panels, each black dot represents the detection limit for one target. All targets are displayed except for stars with detected GP companions. Left: mean detection limit in the range 1–10 days; middle: mean detection limit in the range 10–100 days; right: mean detection limit in the range 100–1000 days. Top: detection limits vs. B−V; middle top: vs. vsini; middle bottom: vs. M⋆; bottom: in histograms. |
| In the text | |
 |
Fig. 13 GP search completeness of our survey. Black dots: detected GP (mpsini vs. P). Solid lines: survey search completeness (i.e., fraction of stars with good enough detection limits to rule out planets of a given mpsini at a given orbital period P). From bottom to top: 1%, 10% to 90% (10% step) and 99% search completenesses. |
| In the text | |
 |
Fig. 14 Probability density function of the GP occurrence rate for planetary mpsini in the range 1–13 MJup and for periods in the range of 1−1000 days, after correcting for the missed GP. Red: most probable value. Blue: 1σ confidence interval. Hatched blue: 2σ confidence interval. |
| In the text | |
 |
Fig. 15 Top panel: companion occurrence rate in the 13 to 80-MJupmpsini range for three successive (non-cumulative) P ranges (from left to right: 1- to 10-day, 10- to 100-day and 100- to 1000-day ranges). Blue/cyan: M⋆≤ 1.5 M⊙ sub-sample. Red/orange: M⋆≥ 1.5 M⊙ sub-sample. Full color: occurrence rate computed in the case ndet ≥ 1. Shaded lines: occurrence rate computed in the case ndet = 0. The 1σ confidence intervals are displayed for these two M⋆ sub-samples as blue and red solid lines, respectively. Middle and bottom panels: occurrence rates for the 1- to 13-MJup and 0.3- to 1-MJup ranges, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


