| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201630107 | |
| Published online | 02 February 2017 | |
Magnetic shuffling of coronal downdrafts⋆
1 Dipartimento di Fisica & Chimica, Università di Palermo, Piazza del Parlamento 1, 90134 Palermo Italy
e-mail: apetralia@astropa.unipa.it
2 INAF−Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
Received: 21 November 2016
Accepted: 19 January 2017
Context. Channelled fragmented downflows are ubiquitous in magnetized atmospheres, and have recently been addressed based on an observation after a solar eruption.
Aims. We study the possible back-effect of the magnetic field on the propagation of confined flows.
Methods. We compared two 3D magnetohydrodynamic simulations of dense supersonic plasma blobs that fall down along a coronal magnetic flux tube. In one, the blobs move strictly along the field lines; in the other, the initial velocity of the blobs is not perfectly aligned with the magnetic field and the field is weaker.
Results. The aligned blobs remain compact while flowing along the tube, with the generated shocks. The misaligned blobs are disrupted and merge through the chaotic shuffling of the field lines. They are structured into thinner filaments. Alfvén wave fronts are generated together with shocks ahead of the dense moving front.
Conclusions. Downflowing plasma fragments can be chaotically and efficiently mixed if their motion is misaligned with field lines, with broad implications for disk accretion in protostars, coronal eruptions, and rain, for example.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: activity / accretion, accretion disks
Movies associated to Figs. 2 and 3 are available at http://www.aanda.org
© ESO, 2017
1. Introduction
The corona is the outer part of the solar atmosphere. It is highly structured by the magnetic field, but it is also highly dynamic: the flows are generated by various mechanisms. For instance, compressions and rarefactions at the footpoints can trigger up- or downflows inside the magnetic channels (e.g., spicules, siphon flows). Depending on the speed, the upflowing plasma can be ejected outside the solar atmosphere (Chen 2011; Webb & Howard 2012) and/or it falls back onto the surface (e.g., Innes et al. 2012,and references therein). Downfalling fragments after an eruption were used as a template for the accretion in young stars in both the high-β and low-β regimes (Reale et al. 2013, 2014; Petralia et al. 2016). The accreting cold material from the circumstellar disk flows along magnetic channels and impacts the stellar surface (Uchida & Shibata 1984; Bertout et al. 1988). The structure and dynamics of the falling material is presumably influenced by both the strength and complexity of the magnetic fields and by the flow inhomogeneity (Matsakos et al. 2013; Orlando et al. 2013; Colombo et al. 2016). Downfalls can be also generated by thermal instability (Parker 1953; Field 1965) in the so-called coronal rain. In this case, a strong heating at loop footpoints can lead to a high plasma density in loops. The high radiative losses exceed the heating and cause a catastrophic plasma cooling and condensation (Antolin & Rouppe van der Voort 2012; Kleint et al. 2014; Fang et al. 2015).
When the plasma falls in a region where the magnetic field is strong, it can be channelled along flux tubes. After a spectacular solar eruption on June 7, 2011, large fragments were spread all over the solar surface (van Driel-Gesztelyi 2014; Innes et al. 2012; Reale et al. 2013, 2014), and Petralia et al. (2016) studied some fragments that fell close to active regions and interacted strongly with the magnetic field. Magnetohydrodynamic (MHD) modelling showed that the shocks ahead of the downfalling fragments brighten the final segment of the magnetic channel. The model also showed that the plasma blobs are warped and further fragmented as soon as their interaction with the field becomes significant. It is clear that the plasma is conditioned by the field and the field by the plasma.
In the present work we investigate this interaction and how it can or cannot determine a significant disruption of the blobs. To this purpose, we compare two similar MHD simulations, one with, the other without this effect.
2. MHD modelling
As in Petralia et al. (2016), we study the propagation of plasma blobs inside a magnetized corona through detailed MHD modelling. Our model solves the same MHD equations as described in Petralia et al. (2016), including thermal conduction and radiative losses. The calculations are performed using the same MHD module available in PLUTO (Mignone et al. 2007, 2012), a modular, Godunov-type code for astrophysical plasmas. We use radiative losses from the CHIANTI code (Version 7; Landi et al. 2012), assuming a density of 109 cm-3 and ionization equilibrium according to Dere (2009). We assume no losses and heating in the chromosphere and inside the initial cold blobs (i.e., for T ≤ 104 K).
Our two simulations describe the evolution of four blobs moving across a magnetized coronal atmosphere. We compare a case in which the blobs are not fully channelled by the magnetic field to another in which they are. We consider a typical coronal field configuration with closed arch-like lines anchored in the photosphere (Reale 2014). This configuration has no special symmetry, and a full 3D description is necessary. However, we can consider a symmetric magnetic field with respect to a plane perpendicular to the surface. Regardless of the initial direction of the blobs, the field geometry and strength will prevent them from moving much across the field lines; therefore, the domain is not needed to be large in that direction, assumed to be the Y direction. We approach the configuration of a loop-populated active region, still keeping it manageable and simple, with a combination of magnetic dipoles, such that the magnetic field is symmetric with respect to the side boundaries and is closed down in the chromosphere. The computational box is three-dimensional and Cartesian X, Y, Z, and 4 × 109 cm, 1.2 × 109 cm, 6 × 109 cm long, respectively. The Z direction is perpendicular to the solar surface. The mesh is uniformly spaced along the three directions with 512 × 128 × 512 cells, and a cell size of ~80 × 90 × 120 km, a good compromise between resolution in all directions (the domain is larger along Z) and computational times. The blobs are resolved well enough (their diameter is 30−40 cells) and the initial atmosphere has been checked to be steady with this resolution. The ambient atmosphere is a stratified corona linked to a much denser chromosphere through a steep transition region. The corona is a hydrostatic atmosphere (Rosner et al. 1978) that extends vertically for 1010 cm. The chromosphere is hydrostatic and isothermal at 104 K and its density is ~1016 cm-3 at the bottom. The atmosphere is plane-parallel along Z. The coronal pressure ranges between 0.29 dyn cm-2 at the top of the transition region and 0.12 dyn cm-2 at Z = 10.5 × 109 cm. The density and temperature are ~2.2 × 108 cm-3 and ~2 × 106 K at Z = 10.5 × 109 cm (Reale 2014). The falling blobs and the atmosphere are very similar to one of the models in Petralia et al. (2016; “dense model”), which are constrained from the observation and therefore realistic. Initially, the four blobs are at a height in the range 3.5 <Z< 4.5 × 109 cm, and at a distance in a range 2.5 <X< 4 × 109 cm from the left boundary side, close to the upper right corner.
Figure 1 shows our initial conditions. For simplicity, we consider spherical blobs, with a radius between 1.4−2 × 108 cm, typical of those in the eruption on 7 June 2011, temperature T = 104 K and density 1010 cm-3, also typical of prominences (e.g. Labrosse et al. 2010; Parenti 2014). We assume that the blobs are optically thick. We expect that the timescales of the radiative transfer from the blobs (not included in the model) is much longer than that of the outside optically thinner plasma (included in the model), which in turn is much longer (e.g. Cargill et al. 1995; Reale 2014) than the very short timescale of the dynamics (only several minutes). Their initial speed is v = 300 km s-1. In one simulation, their motion is aligned cell-by-cell with the magnetic field. The field intensity is ~170 G at the top of the transition region and ~15 G at the initial height of the blobs. In the other simulation, the magnetic field is weaker here, that is, ~35 G and ~3 G, respectively, and the speed of the blobs is set uniform and not totally aligned with the field, but it lies in the XZ plane: two have a horizontal initial direction, the other two have an inclination of 45° downwards.
Boundary conditions are reflective at the left end of the X axis, the magnetic field is forced to be perpendicular to the boundary at the right end. For the other quantities, we set a zero gradient. Fixed conditions were set at the lower end of the Z axis and a zero gradient at the upper end, except for the magnetic field that is fixed. The same conditions were set at the far end of the Y axis. The computational domain was symmetric to a plane in Y = 0, therefore we simulated half a domain and set reflective conditions at the lower end of the Y axis.
 |
Fig. 1 Initial conditions of the two case simulations. Volume rendering of the density (109 cm-3, logarithmic scale). Some magnetic field lines (G, coloured by field intensity) and blobs with initial velocity (red arrows) not aligned (left) and aligned (right) with the field lines are shown. |
 |
Fig. 2 Simulation of blobs not fully channelled by the magnetic field: volume rendering of the density at times t = 20, 60, and 100 s as in Fig. 1. The temporal evolution (movie) is available online. |
 |
Fig. 3 Same as Fig. 2, but for the simulation of blobs that are fully channelled by the field and for the temporal evolution (movie). |
We now describe the evolution of the flowing blobs, starting from those with an initial speed that is not aligned with the magnetic field, shown in Fig. 2 and the associated movie. This case is similar to those illustrated in Petralia et al. (2016), where the blobs crossed a closed magnetic field while falling. The propagation along the field lines is presented for comparison and shows a striking qualitative difference from the other one; this is the main motivation for this work. The initial speed of the blobs (v = 300 km s-1) is not far from a typical free-fall speed from large heights and larger than the local coronal sound speed (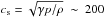 km s-1), which means that shocks are generated immediately. These are slow-mode shocks that do not perturb the magnetic field and propagate along the magnetic field lines ahead of the blobs. In spite of the initial temperature jump at the transition region from the blob to the corona, the large difference in the heat capacity causes the conducted energy to be gradually radiated away, while the blobs dynamics dominate the entire evolution, as shown in previous work (Petralia et al. 2016). However, the blobs themselves do not move parallel to the magnetic field, perturbing and warping it strongly in a few seconds. The ram pressure carried by the blobs is pram = ρv2 ~ 20 dyn cm-2, much higher than the field pressure B2/ 8π ~ 0.3 dyn cm-2; the magnetic tension gives the field enough stiffness to channel the blobs. The net effect is that the moving blobs produce a tailspin that travels along the field lines. Measuring the distance and time taken to arrive at the chromosphere, the speed of this perturbation is ~700 km s-1, meaning that it is an Alfvén wave that moves at an average speed (
km s-1), which means that shocks are generated immediately. These are slow-mode shocks that do not perturb the magnetic field and propagate along the magnetic field lines ahead of the blobs. In spite of the initial temperature jump at the transition region from the blob to the corona, the large difference in the heat capacity causes the conducted energy to be gradually radiated away, while the blobs dynamics dominate the entire evolution, as shown in previous work (Petralia et al. 2016). However, the blobs themselves do not move parallel to the magnetic field, perturbing and warping it strongly in a few seconds. The ram pressure carried by the blobs is pram = ρv2 ~ 20 dyn cm-2, much higher than the field pressure B2/ 8π ~ 0.3 dyn cm-2; the magnetic tension gives the field enough stiffness to channel the blobs. The net effect is that the moving blobs produce a tailspin that travels along the field lines. Measuring the distance and time taken to arrive at the chromosphere, the speed of this perturbation is ~700 km s-1, meaning that it is an Alfvén wave that moves at an average speed (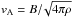 ) in a medium with density 7 × 108 cm-3 and magnetic field ~10 G, reasonable average conditions for the medium where the perturbation is propagating. No MHD instabilities develop, the magnetic field is strong enough to suppress them (see Appendix A). While dragging the field lines, the misaligned and non-uniform motion of the blobs mixes them, and, as metal chords, they soon have a feedback on the blobs, mixing them in turn. As a result, the blobs rapidly lose their initial shape and even their single identity. They first form two separate conglomerates in the initial 30 s, and the conglomerates travel along the tube. They are progressively squashed and elongated into a waterfall-like shape, and in ~2 min they practically coalesce into a single blurred and filamented cloud, as shown in Fig. 2 and in the associated movie. In the meantime, they still flow along the magnetic tube toward the chromosphere. The return shock from the chromosphere contributes to further disrupt and mix the downflowing cloud. At the end of the shuffling, the identity of the blob is completely lost, what remains is a highly inhomogeneous flow structured into filaments that move chaotically along the field lines until they hit the surface in ~200 s.
) in a medium with density 7 × 108 cm-3 and magnetic field ~10 G, reasonable average conditions for the medium where the perturbation is propagating. No MHD instabilities develop, the magnetic field is strong enough to suppress them (see Appendix A). While dragging the field lines, the misaligned and non-uniform motion of the blobs mixes them, and, as metal chords, they soon have a feedback on the blobs, mixing them in turn. As a result, the blobs rapidly lose their initial shape and even their single identity. They first form two separate conglomerates in the initial 30 s, and the conglomerates travel along the tube. They are progressively squashed and elongated into a waterfall-like shape, and in ~2 min they practically coalesce into a single blurred and filamented cloud, as shown in Fig. 2 and in the associated movie. In the meantime, they still flow along the magnetic tube toward the chromosphere. The return shock from the chromosphere contributes to further disrupt and mix the downflowing cloud. At the end of the shuffling, the identity of the blob is completely lost, what remains is a highly inhomogeneous flow structured into filaments that move chaotically along the field lines until they hit the surface in ~200 s.
We have checked that we obtain a similar evolution both for blobs with diverging velocities and for a single blob with an initial speed not aligned to the magnetic field lines, that is, the blobs are shuffled by the field and are disrupted.
Figure 3 and the associated movie show the propagation of blobs with a motion that initially is strictly aligned with the magnetic field lines. The velocity and the atmosphere conditions are equal to the previous case, so that the generation and propagation of the slow mode shocks are the same: once they are generated, they propagate along the magnetic field lines. In this case, the magnetic field intensity is five times greater than in the previous case, thus the magnetic field efficiently channels the blobs, and it is not perturbed significantly. The blobs simply flow along the magnetic field lines as the slow mode shocks do. No magnetic perturbation mixes the blobs, they remain compact during the motion. Their shape only varies because the magnetic channel changes its cross section and direction along the propagation. The blobs do not merge and therefore do not lose their identity during the propagation, as is clearly shown in Fig. 3. Figure 4 emphasises the difference between the evolution of the misaligned and aligned motions. It shows cross sections of the density (Figs. 2 and 3) in vertical YZ planes. The images are taken at slightly different times, that is, t = 100 s and 90 s, when the blobs are approximately in the same Z range (the velocity component along the field lines is slightly different in the two cases). The figure very clearly shows that the evolution is different: a single but structured cloud versus three distant and separate blobs.
3. Discussion and conclusions
 |
Fig. 4 Density (109 cm-3, logarithmic scale) in a plane YZ across the blobs for misaligned (left) at t = 100 s and X = 1.4 × 109 cm, and for aligned blob motion (righ) at t = 90 s and X = 1.5 × 109 cm. |
We studied the different propagations of fast plasma fragments flowing parallel to a coronal magnetic field from others flowing with a tilted direction through detailed 3D MHD modeling. Here we use the same model as in Petralia et al. (2016) to describe the propagation of dense and cold blobs of plasma moving in a magnetized solar atmosphere (including both the chromosphere and the corona). The model includes the effect of the gravity, optically thin radiative losses, thermal conduction along the field lines, and magnetic induction. The magneto-hydrodynamic equations were solved numerically (PLUTO code) in 3D Cartesian geometry. We compared two similar simulations of blobs flowing inside a magnetic field anchored in the solar surface. In one, their motion is fully channelled by the magnetic field, in the other it is only partially channelled because of the initial direction of the motion and because of the strength of the field. We changed the initial conditions of the blobs as little as possible from one case to the other. The compromise was to use the same initial velocity, which the blobs may acquire when they flow inside very large arches, such as in huge prominences. The evolution that we find is strikingly different. In the fully aligned case, the blobs and the slow-mode shocks flow along the field lines and do not perturb the intense magnetic field. The blobs remain compact and move inside independent magnetic channels. In the misaligned case, the shuffling of the field lines driven by the blobs creates a feedback on the blobs themselves and mixes them. At the same time, the conglomeration is structured into thinner filaments. In this case, it is impossible to establish the native channel or the initial shape of the blobs, they lose their identity completely. Misaligned propagation is also an efficient way to excite fast Alfvén wave fronts, which travel ahead of the cloud, in addition to shocks.
In summary, this work highlights the possible back-effect of the confining magnetic field on the propagation of fragmented flows inside it. When they are perfectly channelled, plasma fragments keep their identity as single blobs with no mixing, and the magnetic field is left unchanged as well. When there is some misalignment, the magnetic field can react with a shuffling of the field lines that mixes and merges the fragments, thus changing the plasma configuration completely. This represents a very effective mechanism of plasma mixing in the presence of a magnetic field, different from standard shear-like instabilities. The field lines can be effectively shuffled by irregular plasma motion and its feedback to the plasma is naturally chaotic. We may wonder which is the most common situation: aligned or misaligned fragment motion. We expect that if the plasma is confined since the beginning and the magnetic field does not change much along the track, the motion should be mostly aligned to the field and even more if blob velocity is lower, as in the coronal rain, in which similar blobs fall by gravity and reach loop footpoints with a velocity of about 60 km s-1 (Fang et al. 2013, 2015; Moschou et al. 2015). All our evolution occurs on timescales about two orders of magnitudes shorter than in these other studies, so that our results might only apply to the very final stages of their modelling. On the other hand, downfalling from large distances through a significantly changing magnetic field might result in misaligned fragment motion. A situation like this may occur in the accretion onto young protostars from circumstellar disks, both at the flow origin (disk) and close to the flow impact, where the magnetic field of the star might become very complex. This process might therefore lead to further mixing of downflows and increase their fine substructure. For this exploratory work, the initial conditions of our simulations differ in both the speed alignment and in the strength of the ambient magnetic field. Our aim here is to show that the moving blobs can have two different destinies, but we did not explore the conditions necessary to switch between the two in detail. This exploration is postponed to more extended work. Although this work mainly addresses downfall motions, it might be more general, and may in particular also involve the case of upflows. This is to be addressed in future work.
Online material
Movie of Fig. 2 Access here
Movie of Fig. 3 Access here
Acknowledgments
A.P., F.R., and S.O. acknowledge support from the Italian Ministero dell’Università e Ricerca. PLUTO is developed at the Turin Astronomical Observatory in collaboration with the Department of Physics of the Turin University. We acknowledge the HPC facilities SCAN, of the INAF−Osservatorio Astronomico di Palermo, the CINECA Award HP10B59JKR for the availability of high-performance computing resources and support.
References
- Antolin, P., & Rouppe van der Voort, L. 2012, ApJ, 745, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Mariska, J. T., & Antiochos, S. K. 1995, ApJ, 439, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F. 2011, Liv. Rev. Sol. Phys., 8, 1 [Google Scholar]
- Colombo, S., Orlando, S., Peres, G., Argiroffi, C., & Reale, F. 2016, A&A, 594, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 2009, A&A, 497, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fang, X., Xia, C., & Keppens, R. 2013, ApJ, 771, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Xia, C., Keppens, R., & Van Doorsselaere, T. 2015, ApJ, 807, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Innes, D. E., Cameron, R. H., Fletcher, L., Inhester, B., & Solanki, S. K. 2012, A&A, 540, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleint, L., Antolin, P., Tian, H., et al. 2014, ApJ, 789, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Matsakos, T., Chièze, J.-P., Stehlé, C., et al. 2013, A&A, 557, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Moschou, S. P., Keppens, R., Xia, C., & Fang, X. 2015, Adv. Space Res., 56, 2738 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, S., Bonito, R., Argiroffi, C., et al. 2013, A&A, 559, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Parker, E. N. 1953, ApJ, 117, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Petralia, A., Reale, F., Orlando, S., & Testa, P. 2016, ApJ, 832, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. 2014, in Magnetohydrodynamics of the Sun (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
- Reale, F., Orlando, S., Testa, P., et al. 2013, Science, 341, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., Orlando, S., Testa, P., Landi, E., & Schrijver, C. J. 2014, ApJ, 797, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y., & Shibata, K. 1984, PASJ, 36, 105 [NASA ADS] [Google Scholar]
- van Driel-Gesztelyi, L., Baker, D., Török, T., et al. 2014, ApJ, 788, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, D. F., & Howard, T. A. 2012, Liv. Rev. Sol. Phys., 9, 3 [Google Scholar]
Appendix A: MHD shear instabilities
Appendix A.1: Kelvin-Helmoltz instability
When a heavier fluid (blobs) in motion is sustained against a lighter fluid (the corona) by the magnetic field, Kelvin-Helmoltz instabilities can arise. They are suppressed when the magnetic field is strong enough to satisfy the condition (Priest 2014, and references therein) 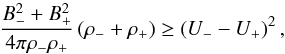 (A.1)where subscripts − and + denote the variables inside and outside the blobs, respectively, B is the magnetic field, ρ is the mass density, and U is the velocity.
(A.1)where subscripts − and + denote the variables inside and outside the blobs, respectively, B is the magnetic field, ρ is the mass density, and U is the velocity.
Considering that the blob density (nb ≈ 1010 cm-3) is much higher than the coronal ambient density (nc ≈ 3 × 108 cm-3), the magnetic field intensity is ~3 G, for the misaligned blobs, and does not change much at the interface of blob and corona, the ambient medium is static, Eq. (A.1) can be simplified to 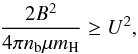 (A.2)\newpagewhere μmH is the mean atomic mass. We obtain 3 × 1015 > 1015 and an even larger difference for the aligned blobs where the magnetic field is 25 times more intense. In our simulations Kelvin-Helmoltz instabilities are therefore efficiently suppressed by the magnetic field.
(A.2)\newpagewhere μmH is the mean atomic mass. We obtain 3 × 1015 > 1015 and an even larger difference for the aligned blobs where the magnetic field is 25 times more intense. In our simulations Kelvin-Helmoltz instabilities are therefore efficiently suppressed by the magnetic field.
Appendix A.2: Rayleigh-Taylor instability
The high ratio between the density of the blobs and the ambient corona could make the separation of the blob-to-corona layer subject to the Rayleigh-Taylor instability. The wave vectorof such perturbations is smaller than a critical threshold given by (Priest 2014, and references therein) 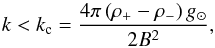 (A.3)with subscripts as in Eq. (A.1). This critical value leads to a lower limit for the characteristic length of the perturbation, which we estimated to be Lc = 2π/kc > 1011 cm. This is much larger than the size of the blobs.
(A.3)with subscripts as in Eq. (A.1). This critical value leads to a lower limit for the characteristic length of the perturbation, which we estimated to be Lc = 2π/kc > 1011 cm. This is much larger than the size of the blobs.
All Figures
 |
Fig. 1 Initial conditions of the two case simulations. Volume rendering of the density (109 cm-3, logarithmic scale). Some magnetic field lines (G, coloured by field intensity) and blobs with initial velocity (red arrows) not aligned (left) and aligned (right) with the field lines are shown. |
| In the text | |
 |
Fig. 2 Simulation of blobs not fully channelled by the magnetic field: volume rendering of the density at times t = 20, 60, and 100 s as in Fig. 1. The temporal evolution (movie) is available online. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for the simulation of blobs that are fully channelled by the field and for the temporal evolution (movie). |
| In the text | |
 |
Fig. 4 Density (109 cm-3, logarithmic scale) in a plane YZ across the blobs for misaligned (left) at t = 100 s and X = 1.4 × 109 cm, and for aligned blob motion (righ) at t = 90 s and X = 1.5 × 109 cm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


