| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628554 | |
| Published online | 19 December 2016 | |
Hydrodynamic modelling of accretion impacts in classical T Tauri stars: radiative heating of the pre-shock plasma
1 Dipartimento di Fisica & Chimica Università di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
e-mail: gcosta@sissa.it
2 Astrophysics sector, SISSA – International School for Advanced Studies, via Bonomea 265, 34136 Trieste, Italy
3 INAF–Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
Received: 18 March 2016
Accepted: 25 August 2016
Context. It is generally accepted that, in classical T Tauri stars, the plasma from the circumstellar disc accretes onto the stellar surface with free-fall velocity and the impact generates a shock. The impact region is expected to contribute to emission in different spectral bands; many studies have confirmed that the X-rays arise from the post-shock plasma but, otherwise, there are no studies in the literature investigating the origin of the observed UV emission which is apparently correlated to accretion.
Aims. We investigated the effect of radiative heating of the infalling material by the post-shock plasma at the base of the accretion stream, with the aim to identify in which region a significant part of the UV emission originates.
Methods. We developed a one-dimensional hydrodynamic model describing the impact of an accretion stream onto the stellar surface; the model takes into account the gravity, the radiative cooling of an optically thin plasma, the thermal conduction, and the heating due to absorption of X-ray radiation. The latter term represents the heating of the infalling plasma due to the absorption of X-rays emitted from the post-shock region.
Results. We found that the radiative heating of the pre-shock plasma plays a non-negligible role in the accretion phenomenon. In particular, the dense and cold plasma of the pre-shock accretion column is gradually heated up to a few 105K due to irradiation of X-rays arising from the shocked plasma at the impact region. This heating mechanism does not affect significantly the dynamics of the post-shock plasma. On the other hand, a region of radiatively heated gas (that we consider a precursor) forms in the unshocked accretion column and contributes significantly to UV emission. Our model naturally reproduces the luminosity of UV emission lines correlated to accretion and shows that most of the UV emission originates from the precursor.
Key words: stars: pre-main sequence / accretion, accretion disks / hydrodynamics / shock waves / X-rays: stars
© ESO, 2016
1. Introduction
Classical T Tauri stars (CTTS) are young (age ≲ 10 Myr), low-mass (M∗ ≃ 1 M⊙) stars surrounded by circumstellar disks and subject to accretion and/or outflow phenomena. These young stars radiate at all wavelength bands and, in particular, are strong UV and X-ray emitters. This evidence, and complementary theoretical studies, supports the widely accepted magnetospheric accretion scenario (e.g. see review by Bouvier et al. 2007). The stellar magnetic field drives the infalling plasma from the truncation radius of the disk (RT ~ 3−10R∗) onto the stellar surface, often at high latitude (Koenigl 1991). The gravitational field accelerates the plasma up to supersonic velocities (~ 300−600km s-1) and then the impact onto the stellar surface generates a strong shock that heats the plasma up to a temperature of a few MK (Calvet & Gullbring 1998).
In the last decade, high spectral resolution X-ray observations have revealed that the X-ray emission from these objects originates from two components: the dense (ne> 1011cm-3) and cold (T ~ 2−5MK) plasma heated by the accretion shock that dominates the soft X-ray emission (E ≤ 1keV) (Kastner et al. 2002; Schmitt et al. 2005; Günther et al. 2007), and the hotter and less dense (ne ≤ 1010cm-3) coronal plasma, with a typical temperature of 10−20MK, that dominates the harder X-ray emission (E > 1keV) (Brickhouse et al. 2010; Argiroffi et al. 2011). Observations of CTTSs in the UV band have shown emission lines of plasma with temperature T ~ 105K clearly related with accretion phenomena, because of the observed Doppler shift (Ardila et al. 2002; Günther & Schmitt 2008; Ardila et al. 2013) and because of much higher luminosity than those observed in young stars without accretion (Johns-Krull et al. 2000). Some authors have suggested that the UV emission may originate from a region in the accretion flow which is immediately before the accretion shock at the base of the column (Herczeg et al. 2002; Ardila et al. 2013).
Several theoretical studies have provided important support to the magnetospheric accretion scenario and crucial knowledge about the accretion shock phenomena. One dimensional (1D) hydrodynamic (HD) models (e.g. Sacco et al. 2008, 2010) studied the dynamics and the structure of the impact region of a continuous accretion inflow onto the stellar surface. These models take into account many important physical effects: the thermal conduction, the radiative cooling from optically thin plasma, the gravity stratification, and a detailed description of the stellar chromosphere. In the case of MP Mus, a well studied CTTS, these models were able to reproduce the main features of its high resolution X-ray spectrum collected with Reflection Grating Spectrometers (RGS) on board the XMM-Newton satellite (Argiroffi et al. 2007), thus showing an excellent agreement between models and observations (Sacco et al. 2008). These models assume that the magnetic field dominates the dynamics and the energetics of the downflowing plasma (i.e. β ≪ 1, where β = gas pressure/magnetic pressure). Sacco et al. (2010) have suggested that the UV emission may arise from the surrounding chromospheric plasma, because of the absorption of X-rays originating in the post-shock region rooted in the chromosphere, or maybe in the accretion stream itself. Studies by Sacco et al. (2010), Reale et al. (2013), and Bonito et al. (2014) have shown that the absorption of X-rays by optically thick material distributed around the post-shock plasma can be significant and may play a relevant role in determining the emission emerging from the impact region.
Further studies were performed with 2D magnetohydrodynamic (MHD) models of the accretion stream impact (Orlando et al. 2010, 2013; Matsakos et al. 2013). These 2D simulations showed that the structure and dynamics of the post-shock plasma strongly depend on the strength and configuration of the ambient magnetic field. If β< 1 then the accretion stream is divided into elementary fibrils, each with a dynamic and evolution independent from those of the others, that can be described by 1D simulations (Sacco et al. 2008, 2010). These 2D models showed that, if β is close to or higher than one, the accretion stream may strongly perturb the nearby stellar atmosphere and, in the case that β ≫ 1, the shock may generate some plasma leaks into the surrounding corona. Studies by Brickhouse et al. (2010) support the idea that the accretion shock may perturb also the stellar corona.
Thanks to the high quality observations and the highly refined HD and MHD models, our knowledge of accretion phenomena in CTTSs has significantly grown in this decade. However, there are several aspects that still remain unclear. There are no theoretical models from which predictions of both UV and X-ray emission are derived at the same time and compared with observations. Many studies have shown that the X-ray emission arises from the shock-heated plasma. However, there is no certainty on where the UV emission comes from. Theoretical models proved that absorption of X-rays in the accretion-shock region is significant (Bonito et al. 2014) but the consequences of local heating due to this absorption are still unexplored. Investigating these aspects could probably help in understanding one of the most debated issues: the evidence that the mass-accretion rates inferred from X-ray observations are systematically lower (even by one or more orders of magnitude) than those derived from near infrared (NIR)/optical/UV observations (Curran et al. 2011).
In this paper, we investigate the radiative heating of the infalling material by the post-shock plasma at the base of the accretion stream. The main aims are to investigate: (1) how the radiative heating affects the dynamics and energetics of the accretion shock; (2) if, and to what extent, the UV and X-ray emission arising from the shocked plasma may heat the cold pre-shock material of the accretion column; (3) the source region(s) of the observed UV emission; (4) if the radiative heating of the pre-shock material may reproduce simultaneously the observed UV and X-ray emission. To answer these questions, we assumed β ≪ 1 and performed 1D HD simulations of accretion impacts (as done in Sacco et al. 2008) but including the effects of radiative heating on the dynamics and energetics of the system. In Sect. 2 we describe our model and numerical setup; in Sect. 3 we describe our results and in Sect. 4 we draw our conclusions.
2. The model
2.1. The hydrodynamic model
Following Sacco et al. (2010), we developed a 1D HD model describing the impact of an accretion stream onto the surface of a CTTS. We assumed that accretion occurs along a magnetic flux tube linking the circumstellar disk to the star, and that the plasma moves and transports energy exclusively along the magnetic field lines (β ≪ 1). Thus our model describes the impact of one fibril of the accretion stream onto the stellar surface.
The impact is modelled by solving the time-dependent HD equations of conservation of mass, momentum, and energy. The model takes into account the gravity, the thermal conduction, the radiative losses from an optically thin plasma, and the heating of the accretion stream plasma due to the absorption of the radiation which arises from the post-shock zone: 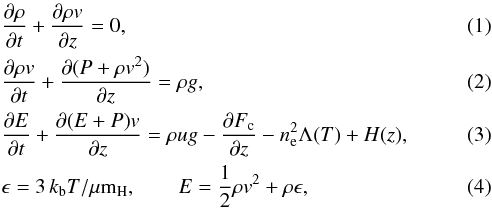 where ρ = μnHmH is the mass density, μ = 1.277 (1.284) is the mean atomic mass, assuming metal abundances of 0.5 (0.8) of the solar value, mH is the mass of the hydrogen atom, nH is the hydrogen number density, t is the time, z is the coordinate along the magnetic field, v is the plasma velocity along z, P is the thermal pressure, g(z) is the gravity of a star with a mass M∗ = 1.2 M⊙ and a radius R∗ = 1.3 R⊙ (the values of the CTTS MP Mus), E is the total energy per unit volume, Fc is the conductive flux, ne is the electron number density, Λ(T) is the radiative losses function per unit emission measure from an optically thin plasma (see Fig. 1), H(z) is the heating function (see Sect. 2.2), ϵ is the internal energy per unit mass, kb is the Boltzmann constant, and T is the plasma temperature. We used the ideal gas law, P = (γ−1)ρϵ, where γ = 5/3 is the ratio between the specific heats.
where ρ = μnHmH is the mass density, μ = 1.277 (1.284) is the mean atomic mass, assuming metal abundances of 0.5 (0.8) of the solar value, mH is the mass of the hydrogen atom, nH is the hydrogen number density, t is the time, z is the coordinate along the magnetic field, v is the plasma velocity along z, P is the thermal pressure, g(z) is the gravity of a star with a mass M∗ = 1.2 M⊙ and a radius R∗ = 1.3 R⊙ (the values of the CTTS MP Mus), E is the total energy per unit volume, Fc is the conductive flux, ne is the electron number density, Λ(T) is the radiative losses function per unit emission measure from an optically thin plasma (see Fig. 1), H(z) is the heating function (see Sect. 2.2), ϵ is the internal energy per unit mass, kb is the Boltzmann constant, and T is the plasma temperature. We used the ideal gas law, P = (γ−1)ρϵ, where γ = 5/3 is the ratio between the specific heats.
The thermal conduction includes the classical and the saturated regime, and a transition between the two given by 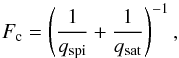 (5)where
(5)where 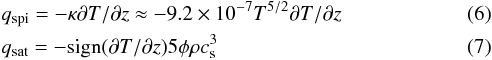 are, respectively, the classical conductive flux (Spitzer 1962) and the saturated flux (Cowie & McKee 1977), where κ is the thermal conduction coefficient, φ ≤ 1 (Borkowski et al. 1989; Fadeyev et al. 2002, and references therein), and cs is the isothermal sound speed.
are, respectively, the classical conductive flux (Spitzer 1962) and the saturated flux (Cowie & McKee 1977), where κ is the thermal conduction coefficient, φ ≤ 1 (Borkowski et al. 1989; Fadeyev et al. 2002, and references therein), and cs is the isothermal sound speed.
The radiative losses per unit emission measure are derived with the PINTofALE spectral code (Package for Interactive Analysis of Line Emission, Kashyap & Drake 2000) adopting the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2013). The radiative losses depend on the metal abundance, ζ, in the range of temperature between 104 < T < 107 K, because the radiative emission is dominated by lines of heavy ions (see Fig. 1). Here we assumed heavy element abundances of 0.5 and 0.8 the solar values, in agreement with X-ray observations of CTTSs by Telleschi et al. (2007).
We noted that, in our simulations, the plasma in the hot slab at the base of the accretion column can be considered to be optically thin, because of its density, temperature, and dimension. The chromosphere is known to be optically thick and we accounted for this by setting the radiative losses equal to zero there. We assumed that the pre-shock material of the accretion stream is cold (T = 103 K) when it starts its falling. Given its density and temperature, the infalling material of the accretion stream cannot be considered to be, in general, optically thin. As a consequence, the radiative losses adopted in our model are not appropriate to describe the material in the unshocked stream. To account for this, we explored two limiting cases by adopting two complementary approaches: (1) we assumed that the stream material is completely opaque to its radiation by setting the radiative losses equal to zero in the unshocked stream; (2) we assumed that the stream material is optically thin and any effect of self-absorption of radiation is negligible. In such a way, the radiative cooling of the plasma in the pre-shock stream is neglected in the first case and overestimated in the second. We discuss the limits of these assumptions in Sect. 2.4.
The model is implemented with PLUTO (Mignone et al. 2007), a modular Godunov-type code for astrophysical plasmas, designed to use massively parallel computers using the Message-Passing Interface (MPI) for interprocessor communications. The HD equations are solved using the linearized Roe Riemann solver based on the characteristic decomposition of the Roe matrix (Roe 1981). PLUTO includes a module to calculate the optically thin radiative losses at the temperature of interest, using a table-lookup and the interpolation method. The thermal conduction is computed with explicit time-stepping schemes for parabolic problems.
 |
Fig. 1 Radiative losses for an optically thin plasma from the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2013), assuming the metal abundance of 0.5 (black line) and 0.8 (red line) of the solar value. |
The star and the accretion flow parameters of the simulations have been chosen to reproduce accretion streams as inferred from X-ray observations of the CTTS MP Mus (Argiroffi et al. 2007), and are expected to produce detectable X-ray emission as described by Sacco et al. (2010). The computational domain extends from 0.98R∗ to 1.7R∗ (where R∗ = 1.3 R⊙); the transition region is at z = 1R∗. It is worth noting that the domain adopted here is much larger than the height of the post-shock slab expected to develop at the base of the accretion column. This choice allowed us to make the effects of the upper boundary (at z = 1.7R∗) negligible for the evolution of the slab. On the other hand, the adopted domain is smaller than the length expected for a stream linking the star to its disk. In fact our study focusses on the impact region close to the stellar surface and our 1D model cannot describe properly the complex geometry expected for the whole stream. We divided the domain into two regions. The first, with the highest resolution (about 1.2 × 106 cm), consists of an uniform grid with 9000 points, which extends from 0.98R∗ to 1.1R∗. The slab is expected to evolve in this region. The second region consists of a non-uniform stretched grid with 11 000 points, which extends from 1.1R∗ to 1.7R∗. In this latter case, the grid spacing grows slowly from ~ 1.2 × 106 cm to ~ 1.3 × 107cm at the end of the domain. We performed a grid convergence study to check how the numerical solution depends on the spatial resolution; in particular, we performed the simulation of our reference case on successively finer grids until the solution does not change by more than a few percent. We found that the adopted grid represents the best compromise between accuracy and computational cost.
The initial condition describes the accretion stream just before the impact onto the stellar chromosphere. Initially the chromosphere extends from the lower boundary (z = 0.98R∗) up to z = 1R∗ and the stream fills the rest of the mesh from z = 1R∗ up to the upper boundary (z = 1.7R∗); the model does not describe the stellar corona between the chromosphere and the stream. The lower boundary (z = 0.98R∗) is set assuming an isothermal chromosphere with Tch = 104K, in hydrostatic equilibrium with a minimum density nch = 7 × 1010cm-3 at z = 1R∗ (namely the top of the chromosphere). We adopted an isothermal chromosphere for simplicity: models with a more accurate chromosphere did not show significant differences in the results (Sacco et al. 2008, 2010). From here the “post” subscript indicates the post-shock quantities, while the “acc” subscript indicates the accretion stream quantities. The upper boundary (z = 1.7R∗) is set assuming a continuous inflow of plasma with fixed values of temperature, Tacc = 103K, and velocity, vacc = −500km s-1. We explored two possible values of stream density, either nacc = 1011cm-3 or nacc = 5 × 1011cm-3, and two possible values of metal abundance, either ζ = 0.5 or ζ = 0.8. Table 1 summarizes the parameters characterizing the models explored: the accretion stream density, nacc, the abundance with respect to the solar one, ζ, temperature, Tpost, density, npost, characteristic quasi-periodic time, Po, maximum post-shock region length, Lpost, precursor region length, Lprec, and maximum precursor temperature, Tprec (the precursor will be defined in Sect. 3.2); in the table note, the accretion velocity, vacc, and the post-shock plasma velocity, vpost. The parameters explored are those required to match the soft X-ray emission of many CTTSs (e.g. MP Mus, Argiroffi et al. 2007; Sacco et al. 2010). In addition these models allowed us to compare our results with those discussed in the literature (Sacco et al. 2008; Orlando et al. 2010). Our simulations follow the evolution of the system for ~ 3.6ks.
Parameters characterizing the models.
2.2. Radiative heating of pre-shock plasma
 |
Fig. 2 Top panel: photonionization cross section as a function of the wavelength from the PINTofALE library (Kashyap & Drake 2000), assuming a heavy element abundance of 0.5 (black line) and 0.8 (red line). Bottom panel: mean free path as a function of the energy, for the two densities used in our models (solid line for nacc = 1011 cm-3, and dashed lines for nacc = 5 × 1011 cm-3). The dotted horizontal line (Ls) indicates the characteristic length of the accretion stream equal to its section radius. |
The main aim of this work is to study the effect of irradiation of the infalling material by the emission arising from the post-shock plasma in the impact region. To this end, we developed a numerical code (hereafter RT code) to derive the fraction of irradiating energy absorbed by cold and dense plasma. Our analysis focuses in the range of energy between the ionization edge of hydrogen (13.6eV) and the soft X-ray emission (up to E ~ 1.3keV), which is characteristic for this type of phenomenon. We assumed that the only source of radiative heating is the hot post-shock plasma with T> 1 MK. We investigated the possible heating only of the pre-shock material, due to this X-ray radiation. Absorption of the cold pre-shock material is regulated by the plasma density along the photons path and by the photoionization cross section (σE) that is shown in Fig. 2 (Panel a). Panel a shows that the probability for a high-energy photon to be absorbed is smaller than that for a low-energy photon. Panel b shows that the mean free path (computed with fixed values of densities and metal abundance related to the different models) of a high-energy photon is greater than the characteristic length of the accretion stream (Ls ~ 1010cm), whereas the mean free path of a photon with low energy can be smaller than Ls even by orders of magnitude. As a result, in general the accretion stream can be considered to be optically thick to UV and soft X-ray radiation.
The RT code is written in C programming language and is coupled to the PLUTO code. In particular the results of the HD simulations from PLUTO are used as input for the RT code to calculate the energy absorption (and the related heating function H(z); see Eq. (3)) along the accretion stream. The absorption is solved in 1D. The RT code consists of the following steps:
-
1.
Reading the HD variables. As a first step the code reads theinput, namely the profiles of temperature (T), density (ρ), and velocity (v) produced by PLUTO, and the cross section (σ) (Fig. 2) derived from the function ISMTAU of the PINTofALE library (Kashyap & Drake 2000).
-
2.
Spectral synthesis. The code identifies the slab of shocked hot plasma by selecting the plasma with T> 1 MK. Then it synthesizes the emitted spectrum (in the energy range between ~ 0.01−1.3 keV) from each grid point of this region (assumed to be optically thin), using the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2013), and integrates all the contributions to obtain the total emerging spectrum:
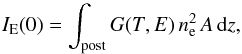 (8)where post is the length of the post-shock zone, ne is the electron number density, G(T,E) is the spectrum of an isothermal optically thin plasma (i.e. the emissivity of the plasma vs. its temperature, T, and the photon energy, E, per unit of emission measure), and A is the section area of the stream. Here we assumed that one half of the total luminosity emitted by the hot slab, IE(0), goes toward the star surface and is unobservable, and the other half propagates outwards along the 1D downflowing plasma (plane parallel approximation, see Sect. 2.4).
(8)where post is the length of the post-shock zone, ne is the electron number density, G(T,E) is the spectrum of an isothermal optically thin plasma (i.e. the emissivity of the plasma vs. its temperature, T, and the photon energy, E, per unit of emission measure), and A is the section area of the stream. Here we assumed that one half of the total luminosity emitted by the hot slab, IE(0), goes toward the star surface and is unobservable, and the other half propagates outwards along the 1D downflowing plasma (plane parallel approximation, see Sect. 2.4). -
3.
Absorption. The code calculates the optical thickness (τE) and computes the transmitted spectrum (IE(z)) for every grid point along the accreting pre-shock material with:
 where σE is the cross section as a function of the energy (Fig. 2), ne(z) is the number density as a function of the coordinate z, l is the distance from the shocked plasma region, dz is the length element, and IE(0) is the spectrum vs. energy from the post-shock zone.
where σE is the cross section as a function of the energy (Fig. 2), ne(z) is the number density as a function of the coordinate z, l is the distance from the shocked plasma region, dz is the length element, and IE(0) is the spectrum vs. energy from the post-shock zone. -
4.
Absorbed energy and volumetric heating. Finally the code calculates the absorbed energy along the stream and, assuming that all this energy produces local heating, it calculates the volumetric heating Ht(z) as
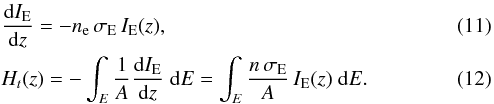 The Ht(z) term is in units of ergs-1cm-3.
The Ht(z) term is in units of ergs-1cm-3.
As mentioned before, in our study we assumed β ≪ 1, and our simulations describe the evolution of a single fibril. Thus the whole accretion stream can be considered as formed by many of these elementary fibrils. Each of them is independent from the others and, in principle, may have a different evolution phase, even though they have the same type of evolution (Orlando et al. 2010).
In order to calculate the average volumetric heating rate, H(z), of a fibril in the central part of the stream, we considered the emission from the surrounding fibrils (each with its own phase). Then we calculated the absorption and the volumetric heating rate along the fibril. This (central) fibril is expected to receive the combined irradiation due to all the fibrils around; since each of them is in a different phase of evolution, we consider the sum of the emission at all the times (or the time average) of one fibril, equal to the average emission of the whole surrounding fibrils in a time lapse (or space average). In Sect. 2.4 we discuss in detail the limits of this assumption.
2.3. Coupling the radiative heating and hydrodynamic computations
The HD and absorption feedback computations are coupled through the volumetric heating function, H(z) (see Eq. (3)). To obtain a self-consistent solution of the coupled equations, we adopted the following iterative method:
-
1.
First the HD Eqs. (1)−(3) are solved without the heating term H(z) in the energy conservation equation using the PLUTO code (see Sect. 2.1).
-
2.
The resulting profiles of temperature, pressure, density, and velocity, are used as input for the RT code (see Sect. 2.2) to solve the absorption along the accretion stream, and to calculate the time-average H(z) function.
-
3.
A new, otherwise identical, simulation is performed using the same parameters of the previous one, but now including the H(z) function calculated in step 2; in this simulation therefore, the feedback of absorption of UV and soft X-ray emission arising from the shock heated plasma is included in the dynamics and energetics of the stream.
-
4.
Since steps 1, 2, and 3 are not performed in a physically self-consistent model, the second and third steps are iterated until the convergence of the HD solution is obtained; the convergence is checked by analyzing the time average of the emission measure distribution vs. the temperature (see Sect. 3.3) of the plasma, and the volumetric heating function H(z). The iterative method is stopped when the relative difference of these quantities is below 1% between two consecutive iterative steps.
2.4. Limits of the model
Here we discuss the assumptions and hypothesis made in this work.
-
Radiative losses from optically thin plasma. As mentioned in Sect. 2.1, our model treats approximately the cooling of the pre-shock material (which, in general, is neither completely thin nor thick). In the models D1e11-A05-RT, D1e11-A08-RT, D5e11-A05-RT, and D5e11-A08-RT (see Table 1) the radiative cooling of the infalling plasma is neglected, thus maximizing the effect of radiative heating. Conversely, in the models D1e11-A05-RT-PR, D1e11-A08-RT-PR, D5e11-A05-RT-PR, and D5e11-A08-RT-PR the radiative cooling is overestimated by the assumption of optically thin plasma, thus minimizing the effect of heating. To further investigate this issue, we calculated the absorption of a spectrum between 0.01−1.3keV emitted by an isothermal plasma, for different values of temperature. Figure 3 shows the characteristic thickness at which ≈ 90% of the luminosity is absorbed assuming a stream density nstr = 1011cm-3. As we will show in Sect. 3, the dimension of the pre-shock material, that is significantly heated by irradiation of X-rays from the post-shock plasma, is indeed comparable with these values of L90%. This evidence confirms that the pre-shock material cannot be considered to be completely thick or thin. Thus we expect that the temperature and density of the radiatively heated pre-shock material are in between the two cases considered in our study. Nevertheless, our approach allowed us to bracket the effect of radiative heating of the unshocked stream and the corresponding contribution to emission in UV and X-ray bands.

Fig. 3 Characteristic thickness at which about 90% of the radiation intensity is absorbed along the pre-shock plasma, with nacc = 1011cm-3.
-
Plasma heating capacity. The ionization state of the plasma changes its ability to transform the absorbed radiation into heat. In our model we assumed that the plasma converts all the absorbed radiation in heating, but the degree of ionization of the plasma at the disk inner edge, and then that of the infalling plasma, is still an issue largely debated in the literature. We can suppose that the plasma in the disk may be ionized for a small fraction and during the fall this fraction grows. So, due to this fact, the photoionization cross section of the material may change as the ionization changes. On the other hand, we used a fixed cross section of a non-ionized gas with a metal abundance of 0.5 of the solar value. From studies by Furlanetto & Stoever (2010), we estimated that, for a plasma with an ionization fraction of 10% and for energy of the ionization photon greater than E ~ 1 keV, the fraction of energy that is converted into heating is about 70%. For lower energies of the ionization photon, this fraction increases. These considerations assure that, at the first order, our results provide an appropriate description of the system.
-
Geometry of the system. In our models we assumed that the accretion flow extends radially up to about 0.7R∗ (R∗ = 9.048 × 1010 cm). However, the plasma streams follow the magnetic field lines which, at large distances from the star, have a configuration close to that of a dipole. A magnetic arc that connects the star with the disk can have a length of about (3−4)R∗ ~ (3−4) × 1011 cm. On the other hand, as discussed in Sect. 3, the radiative heated precursor can be smaller than the arc extension by more than an order of magnitude (see Table 1). Thus our assumption to neglect the curvature of the accretion stream does not affect significantly the description of the precursor. As discussed in Sect. 2.2, we assumed the plane parallel approximation; this approximation is valid only in the inner part of the stream (namely, far away from the stream border) and for distances from the stellar surface much smaller than the cross-section radius of the stream. By comparing the characteristic thickness of the precursor (see Sect. 3) with the adopted cross-section radius of the stream (rf ~ 3.4 × 1010 cm), we conclude that our assumption does not affect significantly the results.
3. Results
3.1. The reference model
As a first step, we performed a simulation of an accretion stream impact onto a stellar surface, neglecting the radiative heating. An estimate of the expected slab parameters can be made using the strong shock limit (Zel’dovich & Raizer 1967). We report the equations below for the convenience of the reader: 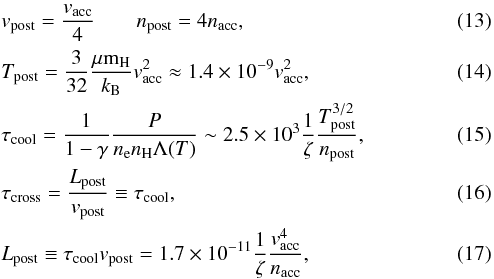 where v is the velocity, n is the number density, T is the temperature, P is the thermal pressure, τcool is the cooling time of the slab, τcross is the crossing time of the slab, and Lpost is the maximum thickness of the slab. Table 2 reports the expected values for the six models explored, calculated according to Eqs. (13)−(17).
where v is the velocity, n is the number density, T is the temperature, P is the thermal pressure, τcool is the cooling time of the slab, τcross is the crossing time of the slab, and Lpost is the maximum thickness of the slab. Table 2 reports the expected values for the six models explored, calculated according to Eqs. (13)−(17).
 |
Fig. 4 Time evolution of plasma density, temperature, pressure, and velocity of the post-shock plasma in the case of the model D1e11-A05. The panels on the left show the expansion phase of the slab, while the panels on the right show the collapse phase. The vertical dashed lines mark the position of the unperturbed transition region. |
Expected parameters of the post-shock zone for the models with different stream density.
After the impact of the accretion stream onto the stellar surface, a hot (few million degrees) and dense (npost ~ 4 × 1011 cm-3) slab of shock heated plasma forms at the base of the stream. The slab is rooted in the chromosphere where the ram pressure of the stream, Pram = ρv2, equals the thermal pressure, PT, of the chromosphere (Sacco et al. 2008). As discussed by several authors (e.g. Sacco et al. 2008), the slab is characterized by quasi-periodic oscillations of the shock-front. Figure 4 shows the evolution of density, temperature, pressure, and velocity during one of these oscillations for the model D1e11-A05 (see Table 1). The left panels show the so-called “expansion phase” during which the slab forms. The continuous downfalling plasma powers the gradual growth of the slab. This process continues until the radiative losses at the base of the slab trigger thermal instabilities there that cause a rapid decrease of temperature and pressure in some parts of the slab which appear as cold structures between portions of hot plasma. This is the so-called “collapse phase” in which the intense radiative cooling robs the slab of pressure support, causing the material above the cooled layers to collapse back before the slab expands again (the relevant evolution is shown on the right panels of Fig. 4). The evolution is then characterized by alternating phases of expansion and collapse of the post-shock region. In the case of model D1e11-A05, the slab has a quasi-periodic evolution with a characteristic time of Po ~ 550 s; it reaches a maximum thickness of Lpost = 3.9 × 109 cm , and a maximum temperature of Tpost = 6.6 × 106 K.
The other models (D1e11-A08, D5e11-A05, D5e11-A08; see Table 1) show an analogous evolution of the post-shock region but, because of the different density and metallicity, the slabs have different characteristics with respect to model D1e11-A05 (see Table 1). As shown in Eqs. (13)− (17), the final velocity and temperature depend only on the initial velocity; the cooling time and the slab thickness depend on the whole set of parameters (namely vacc, nacc, and ζ); so, higher values of density and/or metallicity imply stronger radiative losses and, therefore, smaller cooling times and slab thickness. Furthermore, in the case of higher density, because of its higher ram pressure, Pram, the post-shock zone is rooted deeper in the chromosphere. We found a good agreement between the values derived from the models (see Table 1) and those expected (see Table 2).
3.2. Effects of the radiative heating feedback
Figure 5 shows the radiative heating function H(z) derived with the RT code for the model D1e11-A05; the function shows a peak which corresponds to the maximum extension of the slab. The contact discontinuity between the chromosphere and the slab is at z = 9 × 1010 cm. After the peak, the H(z) function shows a typical exponential trend due to the absorption (see Eq. (10)).
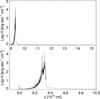 |
Fig. 5 Volumetric heating rate of model D1e11-A05 as a function of the position, z. Top panel: the function in the whole domain; bottom panel: a zoom of the function in the shock region. |
 |
Fig. 6 As in Fig. 4 for model D1e11-A05-RT including the heating function, H(z), due to the X-ray absorption of the accretion stream and neglecting the radiative cooling in the unshocked stream. |
 |
Fig. 7 As in Fig. 4 for model D1e11-A05-RT-PR including both the radiative heating and the radiative losses from optically thin plasma in the unshocked stream. |
As explained in Sect. 2.3, we used the volumetric heating rate, H(z), derived above to perform new HD simulations but now including the heating of the unshocked stream due to absorption of UV and X-ray emission arising from the post-shock plasma. For each model (D1e11-A05, D1e11-A08, D5e11-A05 and D5e11-A08), we explored the two extreme limiting cases discussed in Sect. 2.1: in the first, we neglected any radiative cooling of the material of the unshocked stream; in the second we assumed radiative losses from optically thin plasma in the unshocked stream. Figure 6, in analogy with Fig. 4, shows the evolution of density, temperature, pressure, and velocity for a stream with an initial density of n = 1011 cm-3, and for the case in which the radiative cooling in the unshocked stream is neglected (run D1e11-A05-RT). We found that the evolution of the post-shock zone is roughly the same as that found in run D1e11-A05 which neglects any radiative heating effect (compare Figs. 4 and 6). This was expected because, in the unshocked stream, the ram pressure is much larger than the thermal pressure, Pram ≫ PT, so that the heating of the unshocked material has a negligible effect on the dynamics of the post-shock region. In Fig. 7 we show the evolution of density, temperature, pressure, and velocity if we assume that the unshocked material of the stream is optically thin (run D1e11-A05-RT-PR). Also in this case we found that the evolution of the hot slab is roughly the same as in runs D1e11-A05 and D1e11-A05-RT.
In runs D1e11-A05-RT and D1e11-A05-RT-PR the slab reaches about the same maximum temperature as D1e11-05. It has a maximum thickness of Lpost ~ 4 × 109 cm and the characteristic repetition time is Po ~ 550−600 s. The three models differ mainly in the development of a hot region immediately before the accretion shock, a so-called precursor. In run D1e11-A05-RT (namely that which neglects any radiative losses in the pre-shock stream) the downfalling plasma is gradually heated as it approaches the stellar surface: its temperature increases from Tacc ≈ 103 K (at the upper boundary) up to Tprec ~ 1.4 × 106 K immediately before the accretion shock. The precursor is characterized by a bump in temperature at 9.1 × 1010<z< 9.3 × 1010 cm due to the peak in the volumetric heating at z ≈ 9.25 × 1010 cm (see Fig. 5). The portion of precursor with T> 105 K extends up to Lprec ~ 2.5 × 1010 cm above the stellar surface.
In run D1e11-A05-RT-PR (namely that which assumes optically thin plasma in the unshocked stream), the heating of the downfalling plasma is balanced by the radiative losses for temperatures above 104 K. As a result, the precursor is represented by a temperature bump between z ≈ 9.1 × 1010 cm and z ≈ 9.3 × 1010 cm, corresponding to the position of the peak in the volumetric heating (see Fig. 5). The precursor has a maximum temperature Tprec ~ 0.9 × 105 K lower than that in run D1e11-A05-RT, and extends with T> 104K up to Lprec ~ 3.5 × 109 cm above the stellar surface. In this latter case, the thickness of the precursor depends on the ratio between the heating due to the irradiation and the radiative losses in the unshocked plasma: the stronger the heating the larger the precursor. Given its temperature and density, in both cases examined the precursor is expected to be a strong source of UV emission.
We found similar results in the case of models1 with an accretion stream with metal abundance ζ = 0.8 and/or initial density n = 5 × 1011 cm-3: the radiative heating causes the development of a precursor in the region immediately before the accretion shock. Figure 8 shows the temperature profiles in the whole domain, at the same time, for the twelve models considered. When the radiative heating is taken into account in the computations, each temperature profile shows a precursor which reaches the maximum temperature near the post-shock region. The temperature profiles decrease with the distance from the stellar surface, following the trend of the volumetric heating rate function (see Fig. 5). Figure 8 shows that either denser streams or streams with higher metal abundance have a thinner precursor. Table 1 reports the precursor parameters of the simulations, where Lprec is the characteristic size of the precursor and Tprec is the maximum plasma temperature in the precursor zone.
 |
Fig. 8 Temperature profiles for models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The vertical dashed lines mark the position of the stellar transition region, the horizontal dashed line indicates a temperature of 105 K. |
3.3. Distribution of emission measure versus temperature
 |
Fig. 9 Emission measure distributions versus temperature for models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The figure shows the EM(T) derived for models either with (red and green lines) or without (blue) radiative heating and models either including (blue and green) or neglecting (red) the radiative losses from optically thin plasma in the unshocked stream. |
The distribution of emission measure versus temperature, 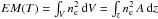 , is a useful tool that gives us information about the components of plasma emitting at various temperatures. We consider here the EM(T) distribution of an accretion stream composed of several elementary fibrils in random phases of evolution. Thus the resulting EM(T) is obtained as the sum of all the contributions from the fibrils and assuming a total accretion rate of LogṀ = −9.2 (with Ṁ in M⊙/ yr). We do not expect, therefore, significant variability of the EM(T) distribution due to the alternating phases of expansion and collapse of the post-shock region. The accretion-rate value considered is consistent with those inferred from optical observations of three CTTSs, namely MP Mus, TW Hya, and V4046 Sgr (data from Curran et al. 2011). The modelled EM(T) can be also directly compared with the EM(T) distributions derived from observations (see e.g. Argiroffi et al. 2009). For each model, the cross-section area A is derived from the adopted accretion rate and from the stream density. In particular, in the case of streams with initial density n = 1011 cm-3, we adopted an area AD1e11 = 3.7 × 1021cm2 (corresponding to a filling factor of 3.6%), whereas in the case of streams with n = 5 × 1011 cm-3, we adopted AD5e11 = 7.4 × 1020cm2 (filling factor of 0.7%).
, is a useful tool that gives us information about the components of plasma emitting at various temperatures. We consider here the EM(T) distribution of an accretion stream composed of several elementary fibrils in random phases of evolution. Thus the resulting EM(T) is obtained as the sum of all the contributions from the fibrils and assuming a total accretion rate of LogṀ = −9.2 (with Ṁ in M⊙/ yr). We do not expect, therefore, significant variability of the EM(T) distribution due to the alternating phases of expansion and collapse of the post-shock region. The accretion-rate value considered is consistent with those inferred from optical observations of three CTTSs, namely MP Mus, TW Hya, and V4046 Sgr (data from Curran et al. 2011). The modelled EM(T) can be also directly compared with the EM(T) distributions derived from observations (see e.g. Argiroffi et al. 2009). For each model, the cross-section area A is derived from the adopted accretion rate and from the stream density. In particular, in the case of streams with initial density n = 1011 cm-3, we adopted an area AD1e11 = 3.7 × 1021cm2 (corresponding to a filling factor of 3.6%), whereas in the case of streams with n = 5 × 1011 cm-3, we adopted AD5e11 = 7.4 × 1020cm2 (filling factor of 0.7%).
Figure 9 shows that, for temperatures above one million degree, all the distributions have roughly the same trend, in particular they show a strong peak of EM at a temperature of a few million degrees. This peak corresponds to the shock heated plasma and is analogous to that studied by Sacco et al. (2010). For temperatures below one million degrees, the models show different EM(T) distributions. In particular, models including the radiative heating of the unshocked stream show values of EM at temperatures around T = 105K higher than those in models without radiative heating. These higher values of EM are due to the precursor. On the other hand, Fig. 9 also shows that models neglecting the radiative losses in the unshocked stream predict a much higher and larger peak of EM at about T = 105K. As discussed in Sect. 2.1, models either with or without the radiative losses in the unshocked stream represent the two extreme limiting cases. We expect that more accurate distributions of EM(T) calculated from models including self-consistently the radiative transfer, are in between the two cases considered here. Since the emission measure depends on the density, the EM(T) distributions of models with high values of density (panel c and d of Fig. 9) show values of EM for T< 1 MK larger than models with lower density (see panel a and b).
3.4. X-ray and UV luminosity of selected lines
 |
Fig. 10 Luminosity of selected lines for three T-Tauri stars (in black), and luminosity synthesized from models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The figure shows the luminosity from models either with (red and green lines) or without (blue) radiative heating and models either including (blue and green) or neglecting (red) the radiative losses from optically thin plasma in the unshocked stream. We note that some of the symbols superimpose each other. |
We compared our results with UV and X-ray observations (Argiroffi et al. 2007; Brickhouse et al. 2010; Argiroffi et al. 2012; Ardila et al. 2013) by synthesizing the luminosity of selected lines (that are known to be strongly correlated to accretion phenomena) from the emission measure distributions derived in Sect. 3.3. The lines considered are listed in Tables 3−5. In the X-ray band, we selected strong emission lines usually ascribed to the post-shock region. In the UV band, we selected lines that are known to have a correlation with accretion phenomena (Ardila et al. 2013).
Observed luminosity of the selected lines in UV and X-ray bands of CTTSs.
Luminosity of the selected lines in UV and X-ray bands derived from models with density nacc = 1011 cm-3 (D1e11-A05 and D1e11-A08).
Luminosity of the selected lines in UV and X-ray bands derived from models with density nacc = 5 × 1011 cm-3 (D5e11-A05, D5e11-A08).
In the following discussion we assumed that the line of sight is perpendicular to the accretion stream. Under such an assumption, the X-ray emission originating from the slab might be partially absorbed by the stellar chromosphere (because the slab is partially rooted in the chromosphere), but not by the stream itself. On the other hand, the UV line emission is not expected to suffer any significant absorption due to the position of the precursor; it is over the stellar chromosphere so the arising UV emission does not suffer any absorption.
Figure 10 shows the luminosity of the selected lines in UV and X-ray bands for the different models. The synthetic luminosities in the figure have error bars equal to or below 10% of the corresponding values. As for the EM(T) distribution, we do not expect any significant variability in the luminosity because the stream is assumed to consist of many elementary fibrils, each in a different random phase of evolution. This is also in agreement with observations (see Drake et al. 2009). Our models without radiative heating in the unshocked stream (blues symbols in the figure) represent the models studied by Sacco et al. (e.g. 2008, 2010). Both the observed and synthesized luminosities are unabsorbed, that is, we did not include any absorption due to the interstellar medium. The X-ray emission arising from impact regions is expected to undergo significant absorption by the optically thick chromosphere in which the accretion column is partially rooted (e.g. Sacco et al. 2010; Curran et al. 2011; Reale et al. 2013; Bonito et al. 2014). Our models do not take into account this local absorption and, in fact, all of them (blue, red, and green symbols in the figure) slightly overestimate the luminosity of X-ray lines.
On the other hand, we note that models without radiative heating (blue symbols) strongly underestimate (even by several orders of magnitude) the luminosity of UV lines, thus failing to reproduce the luminosity of UV emission lines. Models including the radiative heating (green and red symbols in Fig. 10) predict larger luminosity of UV lines that are closer to those observed. In particular the observations are in between the two extreme limiting cases considered, namely models either overestimating (green symbols) or neglecting (red) the radiative cooling in the unshocked stream. Analogous results were found for all the models explored and characterized by different stream density and/or metallicity. We want to stress the fact that the models RT and RT-PR predict a X-ray vs. UV lines luminosity ratio closer to that observed with respect to models without radiative heating, independently from the normalization used. In the light of these results, we suggest that the excess of UV emission observed in CTTSs and related to accretion impacts, originates from material of the unshocked stream being heated radiatively by the post-shock plasma at the base of the stream itself.
4. Summary and conclusions
We modelled the impact of an accretion stream onto the surface of a CTTS and developed a method to investigate the effect of radiative heating of the unshocked stream material by the post-shock plasma at the base of the accretion stream. Our model calculates self-consistently the heating feedback due to the absorption by the accretion stream of the UV/soft-X-ray emission generated by the shocked plasma of the impact region. Our main results are:
-
The accretion stream is optically thick to the UV/soft X-rayemission originating from the post-shock zone, and theabsorption heats the downfalling plasma up to a few 105K before the impact. We defined this pre-heated region precursor.
-
The precursor does not affect the characteristics of the shock heated plasma; the X-ray spectra synthesized from models which either include or neglect the radiative heating of the unshocked stream material are almost the same.
-
We found that the precursor in the inflowing material is an important UV emitter; models including the effect of radiative heating predict the luminosity of UV lines to be larger than that of models without radiative heating; we explored two extreme limiting cases in which the unshocked stream material is assumed to be either optically thick (with no radiative cooling) or optically thin; we found that the range of luminosities of UV lines derived from the models covers the luminosities inferred from observations of three selected CTTSs (namely MP Mus, TW Hya, and V4046 Sgr); we note that models which neglect the radiative heating underestimate the UV emission by several orders of magnitude.
Our study provides insight into the effects of the absorption of X-ray radiation due to the downfalling stream, into their consequences on the dynamics and energetics of the plasma at the base of the accretion column, and into the upper and lower limits of the range of such effects. In particular, our results underline the importance of including the radiative transfer in models describing the accretion phenomenon. This is a necessary step to determine accurately the structure of the impact region and the radiation emerging from the base of the accretion column which is emitted in different bands. The development of a radiation hydrodynamic model (thus including self-consistently the radiative transfer in the calculation) would be the next natural step to address the issue of the optical thickness of the pre-shock material. Some work has been done in this direction (e.g. Chièze et al. 2012; Ibgui et al. 2013; de Sá et al. 2014) but a full detailed study of radiative transfer effects in accretion impacts onto the surface of CTTSs is still missing. In the near future we plan to address this issue by including self-consistently the radiative transfer effects in our model.
Acknowledgments
PLUTO is developed at the Turin Astronomical Observatory in collaboration with the Department of Physics of Turin University. We acknowledge the HPC facility (SCAN) of the INAF – Osservatorio Astronomico di Palermo, for having provided high performance computing resources and support. R.B. acknowledges financial support from INAF under PRIN2013 Programme “Disks, jets, and the dawn of planets”.
References
- Ardila, D. R., Basri, G., Walter, F. M., Valenti, J. A., & Johns-Krull, C. M. 2002, ApJ, 566, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Ardila, D. R., Herczeg, G. J., Gregory, S. G., et al. 2013, ApJS, 207, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Maggio, A., & Peres, G. 2007, A&A, 465, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Maggio, A., Peres, G., et al. 2009, A&A, 507, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Flaccomio, E., Bouvier, J., et al. 2011, A&A, 530, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Argiroffi, C., Maggio, A., Montmerle, T., et al. 2012, ApJ, 752, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Bonito, R., Orlando, S., Argiroffi, C., et al. 2014, ApJ, 795, L34 [Google Scholar]
- Borkowski, K. J., Shull, J. M., & McKee, C. F. 1989, ApJ, 336, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007, Protostars and Planets V, 479 [Google Scholar]
- Brickhouse, N. S., Cranmer, S. R., Dupree, A. K., Luna, G. J. M., & Wolk, S. 2010, ApJ, 710, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Chièze, J.-P., de Sá, L., & Stehlé, C. 2012, in EAS Publ. Ser. 58, eds. C. Stehlé, C. Joblin, & L. d’Hendecourt, 143 [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, R. L., Argiroffi, C., Sacco, G. G., et al. 2011, A&A, 526, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Sá, L., Chièze, J.-P., Stehlé, C., et al. 2014, in Eur. Phys. J. Web Conf., 64, 04002 [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drake, J. J., Ratzlaff, P. W., Laming, J. M., & Raymond, J. 2009, ApJ, 703, 1224 [NASA ADS] [CrossRef] [Google Scholar]
- Fadeyev, Y. A., Le Coroller, H., & Gillet, D. 2002, A&A, 392, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furlanetto, S. R., & Stoever, S. J. 2010, MNRAS, 404, 1869 [NASA ADS] [Google Scholar]
- Günther, H. M., & Schmitt, J. H. M. M. 2008, A&A, 481, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Günther, H. M., Schmitt, J. H. M. M., Robrade, J., & Liefke, C. 2007, A&A, 466, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herczeg, G. J., Linsky, J. L., Valenti, J. A., Johns-Krull, C. M., & Wood, B. E. 2002, ApJ, 572, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., & Linsky, J. L. 2000, ApJ, 539, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap, V., & Drake, J. J. 2000, Bull. Astron. Soc. India, 28, 475 [NASA ADS] [EDP Sciences] [Google Scholar]
- Kastner, J. H., Huenemoerder, D. P., Schulz, N. S., Canizares, C. R., & Weintraub, D. A. 2002, ApJ, 567, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Koenigl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Young, P. R., Dere, K. P., Del Zanna, G., & Mason, H. E. 2013, ApJ, 763, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Matsakos, T., Chièze, J.-P., Stehlé, C., et al. 2013, A&A, 557, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Orlando, S., Sacco, G. G., Argiroffi, C., et al. 2010, A&A, 510, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlando, S., Bonito, R., Argiroffi, C., et al. 2013, A&A, 559, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reale, F., Orlando, S., Testa, P., et al. 2013, Science, 341, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Roe, P. L. 1981, J. Comput. Phys., 43, 357 [Google Scholar]
- Sacco, G. G., Argiroffi, C., Orlando, S., et al. 2008, A&A, 491, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Orlando, S., Argiroffi, C., et al. 2010, A&A, 522, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmitt, J. H. M. M., Robrade, J., Ness, J.-U., Favata, F., & Stelzer, B. 2005, A&A, 432, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases (Interscience Publishers) [Google Scholar]
- Telleschi, A., Güdel, M., Briggs, K. R., Audard, M., & Scelsi, L. 2007, A&A, 468, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zel’dovich, Y. B., & Raizer, Y. P. 1967, Physics of shock waves and high-temperature hydrodynamic phenomena (New York: Academic Press) [Google Scholar]
All Tables
Expected parameters of the post-shock zone for the models with different stream density.
Luminosity of the selected lines in UV and X-ray bands derived from models with density nacc = 1011 cm-3 (D1e11-A05 and D1e11-A08).
Luminosity of the selected lines in UV and X-ray bands derived from models with density nacc = 5 × 1011 cm-3 (D5e11-A05, D5e11-A08).
All Figures
 |
Fig. 1 Radiative losses for an optically thin plasma from the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2013), assuming the metal abundance of 0.5 (black line) and 0.8 (red line) of the solar value. |
| In the text | |
 |
Fig. 2 Top panel: photonionization cross section as a function of the wavelength from the PINTofALE library (Kashyap & Drake 2000), assuming a heavy element abundance of 0.5 (black line) and 0.8 (red line). Bottom panel: mean free path as a function of the energy, for the two densities used in our models (solid line for nacc = 1011 cm-3, and dashed lines for nacc = 5 × 1011 cm-3). The dotted horizontal line (Ls) indicates the characteristic length of the accretion stream equal to its section radius. |
| In the text | |
 |
Fig. 3 Characteristic thickness at which about 90% of the radiation intensity is absorbed along the pre-shock plasma, with nacc = 1011cm-3. |
| In the text | |
 |
Fig. 4 Time evolution of plasma density, temperature, pressure, and velocity of the post-shock plasma in the case of the model D1e11-A05. The panels on the left show the expansion phase of the slab, while the panels on the right show the collapse phase. The vertical dashed lines mark the position of the unperturbed transition region. |
| In the text | |
 |
Fig. 5 Volumetric heating rate of model D1e11-A05 as a function of the position, z. Top panel: the function in the whole domain; bottom panel: a zoom of the function in the shock region. |
| In the text | |
 |
Fig. 6 As in Fig. 4 for model D1e11-A05-RT including the heating function, H(z), due to the X-ray absorption of the accretion stream and neglecting the radiative cooling in the unshocked stream. |
| In the text | |
 |
Fig. 7 As in Fig. 4 for model D1e11-A05-RT-PR including both the radiative heating and the radiative losses from optically thin plasma in the unshocked stream. |
| In the text | |
 |
Fig. 8 Temperature profiles for models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The vertical dashed lines mark the position of the stellar transition region, the horizontal dashed line indicates a temperature of 105 K. |
| In the text | |
 |
Fig. 9 Emission measure distributions versus temperature for models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The figure shows the EM(T) derived for models either with (red and green lines) or without (blue) radiative heating and models either including (blue and green) or neglecting (red) the radiative losses from optically thin plasma in the unshocked stream. |
| In the text | |
 |
Fig. 10 Luminosity of selected lines for three T-Tauri stars (in black), and luminosity synthesized from models with stream density nacc = 1011 cm-3 (upper panels) and nacc = 5 × 1011 cm-3 (lower panels). The figure shows the luminosity from models either with (red and green lines) or without (blue) radiative heating and models either including (blue and green) or neglecting (red) the radiative losses from optically thin plasma in the unshocked stream. We note that some of the symbols superimpose each other. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


