| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629420 | |
| Published online | 30 November 2016 | |
Common-envelope ejection in massive binary stars
Implications for the progenitors of GW150914 and GW151226
1 Argelander-Institut für Astronomie,
Universität Bonn, Auf dem Hügel
71, 53121
Bonn,
Germany
e-mail: mkruckow@astro.uni-bonn.de
2 Max-Planck-Institut für
Radioastronomie, Auf dem Hügel
69, 53121
Bonn,
Germany
3 Astronomical Institute of the Czech
Academy of Sciences, 251
65
Ondřejov, Czech
Republic
4 Department of Astronomy, Oxford
University, Oxford
OX1 3RH,
UK
Received:
28
July
2016
Accepted:
10
October
2016
Context. The recently detected gravitational wave signals (GW150914 and GW151226) of the merger event of a pair of relatively massive stellar-mass black holes (BHs) calls for an investigation of the formation of such progenitor systems in general.
Aims. We analyse the common-envelope (CE) stage of the traditional formation channel in binaries where the first-formed compact object undergoes an in-spiral inside the envelope of its evolved companion star and ejects the envelope in this process.
Methods. We calculated envelope binding energies of donor stars with initial masses between 4 and 115M⊙ for metallicities of Z = ZMilky Way ≃ Z⊙/ 2 and Z = Z⊙/ 50, and derived minimum masses of in-spiralling objects needed to eject these envelopes.
Results. In addition to producing double white dwarf and double neutron star binaries, CE evolution may also produce massive BH-BH systems with individual BH component masses of up to ~50 − 60M⊙, in particular for donor stars evolved to giants beyond the Hertzsprung gap. However, the physics of envelope ejection of massive stars remains uncertain. We discuss the applicability of the energy-budget formalism, the location of the bifurcation point, the recombination energy, and the accretion energy during in-spiral as possible energy sources, and also comment on the effect of inflated helium cores.
Conclusions. Massive stars in a wide range of metallicities and with initial masses of up to at least 115M⊙ may shed their envelopes and survive CE evolution, depending on their initial orbital parameters, similarly to the situation for intermediate- and low-mass stars with degenerate cores. In addition to being dependent on stellar radius, the envelope binding energies and λ-values also depend on the applied convective core-overshooting parameter, whereas these structure parameters are basically independent of metallicity for stars with initial masses below 60M⊙. Metal-rich stars ≳60M⊙ become luminous blue variables and do not evolve to reach the red giant stage. We conclude that based on stellar structure calculations, and in the view of the usual simple energy budget analysis, events like GW150914 and GW151226 might be produced by the CE channel. Calculations of post-CE orbital separations, however, and thus the estimated LIGO detection rates, remain highly uncertain.
Key words: stars: evolution / binaries: close / X-rays: binaries / stars: black holes / gravitational waves
© ESO, 2016
1. Introduction
The majority of all massive stars are found in close binaries that will eventually interact through mass transfer during their stellar lifetimes (Sana et al. 2012). This sometimes leads to the formation of compact stellar X-ray sources (e.g. Tauris & van den Heuvel 2006) and, in some cases, to the eventual production of a pair of compact objects merging within a Hubble time. The evolution of massive single stars (e.g. Heger et al. 2003) has been investigated for many years and is still far from being well understood. The evolution of massive (interacting) binary stars is even more complex and can be significantly different (Podsiadlowski et al. 1992; Langer 2012).
Common-envelope (CE) evolution is thought to play a key role in the formation of many close-orbit binaries containing two compact objects, that is, white dwarfs (WDs), neutron stars (NSs), or black holes (BHs). Given their current small orbital separation (often much smaller that the radii of their progenitor stars), a binary interaction process must have been at work to reduce the orbital energy and angular momentum significantly. CE evolution is a good candidate for such a process since it is accompanied by a drag-force, arising from the motion of the in-spiralling object through the envelope of its companion star, which leads to dissipation of orbital angular momentum and deposition of orbital energy in the envelope. Hence, the global outcome of a CE phase is a reduced binary separation and ejected envelope, unless the system coalesces. The final post-CE separation, however, is difficult to predict as a result of our poor understanding of the complex physical processes involved in envelope ejection. The huge ranges in both length scales and timescales make hydrodynamical simulations troublesome. For general reviews on CE evolution, see for instance Iben & Livio (1993), Taam & Sandquist (2000), Podsiadlowski (2001), Ivanova et al. (2013).
There is strong evidence of past orbital shrinkage (i.e. similar to the expected outcome of a CE phase) in a number of observed close binary pulsars and WD pairs with orbital periods of a few hours or less. Examples include PSR 1913+16 (Hulse & Taylor 1975), PSR J0737−3039 (Burgay et al. 2003), CSS 41177 (Bours et al. 2014), and J0651+2844 (Brown et al. 2011). These systems are tight enough that gravitational-wave radiation will bring the two compact objects (e.g. NS-NS or WD-WD binary) into contact within a Gyr, which in some cases leads to a merger event.
Similarly, the recent, and first, gravitational wave detection GW150914 (Abbott et al. 2016b) of the merger event of two relatively massive stellar-mass BHs (36 + 29M⊙) raises interesting questions about its origin. This system has also been suggested to form through CE evolution (Belczynski et al. 2016). However, for massive stars there are other formations channels in which a binary system may evolve to become a tight pair of BHs. Three main formation channels to produce such a BH-BH pair are
- i)
the CE formation channel (i.e. traditional channel);
- ii)
the chemically homogeneous evolution (CHE) channel with or without a massive overcontact binary (MOB); and
- iii)
the dynamical channel in dense stellar environments.
- i)
The CE formation channel for BHs is similar to that which is believed to produce tight double NS systems (e.g. Tauris & van den Heuvel 2006, and references therein). In this scenario, the systems always enter a CE phase following the high-mass X-ray binary (HMXB) stage, during which the O-type star becomes a red supergiant and captures its BH companion. There are many uncertainties, however, involved in calculations of the in-spiral and the subsequent CE ejection. The evolution is often tidally unstable, and the angular momentum transfer, dissipation of orbital energy, and structural changes of the donor star take place on very short timescales (<103yr, Podsiadlowski 2001). A complete study of the problem requires detailed multi-dimensional hydrodynamical calculations, although early studies in this direction have difficulties ejecting the envelope and securing deep in-spiral (Taam & Sandquist 2000; Passy et al. 2012; Ricker & Taam 2012; Nandez et al. 2014; Ohlmann et al. 2016). The calculations along this route are therefore highly uncertain owing to our current poor knowledge of CE physics (Ivanova et al. 2013). As a consequence, the predicted detection rate of BH-BH mergers from the CE channel is uncertain by several orders of magnitude (Abadie et al. 2010), also partly as a result of the unknown amount of (asymmetric) mass loss that is associated with a possible supernova explosion (i.e. imparted momentum kick) when a BH is formed. Examples of population syntheses investigations of BH-BH binaries following the traditional channel with a CE scenario include Belczynski et al. (2002, 2008, 2016), Voss & Tauris (2003), Dominik et al. (2012), Mennekens & Vanbeveren (2014), Eldridge & Stanway (2016).
- ii)
The two other formation channels of BH-BH binaries avoid the CE phase altogether. In the CHE scenario for binaries (de Mink et al. 2009; Mandel & de Mink 2016; de Mink & Mandel 2016), the stars avoid the usual strong post-main sequence expansion as a result of effective mixing enforced through the rapidly rotating stars through tidal interactions. Hence, this works only for massive stars at low metallicity where strong angular-momentum loss due to stellar winds can be avoided. Marchant et al. (2016) presented the first detailed CHE models leading to the formation of BH-BH systems and demonstrated that MOB systems are particularly suited for this channel, enabling formation of very massive stellar-mass BH-BH mergers, that is in agreement with the detection of GW150914. Lower-mass BH-BH mergers like GW151226 (14 + 8M⊙), however, cannot be formed from this scenario.
- iii)
Finally, the dynamical formation channel (e.g. Sigurdsson & Hernquist 1993; Portegies Zwart & McMillan 2000; Banerjee et al. 2010; Rodriguez et al. 2016) produces BH-BH mergers through encounter interactions in dense stellar clusters and thereby circumvents the need for mass transfer and CE evolution. In analogy to the other production channels mentioned above, the rate of BH-BH mergers from the dynamical formation channel is also difficult to constrain. Recent studies predict that this channel probably accounts for less than about 10% of all BH-BH mergers (e.g. Rodriguez et al. 2016).
- i)
In this paper, we investigate the prospects of envelope ejection from massive stars during the CE stage with an in-spiralling compact object, following the CE formation channel. In Sect. 2 we introduce the CE ejection criterion based on energy budget considerations. In Sect. 3 we present our calculated envelope binding energies and so-called λ-values of donor stars with initial zero-age main-sequence (ZAMS) masses between 4 and 115M⊙ for different metallicities (Milky Way-like: ZMW ≈ Z⊙/ 2, and IZw18-like: Z = Z⊙/ 50), and derive minimum masses of in-spiralling compact objects (or non-degenerate stars) needed to eject these envelopes based on simple energy considerations. In addition, we analyse the stellar structure of pre-CE donor stars, with the aim of better understanding the location of the core boundary. A general discussion of our results is given in Sect. 4, where we also revisit the question of locating the bifurcation point of envelope ejection, debate the possibility of additional energy input from liberated recombination energy or accretion during in-spiral, and comment on the effect of inflated helium cores. Finally, we briefly discuss our results in relation to the LIGO merger events GW150914 and GW151226 in Sect. 5, before summarising our conclusions in Sect. 6.
2. Criterion for common-envelope ejection
The central problem in question is whether a massive binary will survive a CE evolution or result in an early merger event without ever forming a BH-BH system. Whether the donor star envelope is ejected successfully depends on the binding energy of the envelope, the available energy resources to expel it, and the ejection mechanism. Following the (α,λ)-formalism introduced by Webbink (1984) and de Kool (1990), we can write the criterion for successful envelope ejection as Ebind ≤ α ΔEorb, where α is the efficiency of converting released orbital energy into kinetic energy that provides the outward ejection of the envelope. The total binding energy (gravitational plus internal thermodynamic contributions) of the donor star envelope at onset of the CE is given by 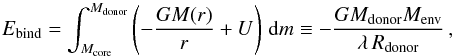 (1)where G is the gravitational constant, M(r) is the mass within the radius coordinate r of the donor star with total radius, Rdonor, total mass, Mdonor, core mass, Mcore, envelope mass, Menv ≡ Mdonor − Mcore, and U is the specific internal energy (Han et al. 1994). Given that Ebind is evaluated at the moment the evolved donor star fills its Roche-lobe and initiates dynamically unstable mass transfer, leading to formation of the CE, we do not include the gravitational potential from the in-spiralling companion when calculating Ebind (see e.g. Podsiadlowski et al. 1992; Iben & Livio 1993, for alternative descriptions).
(1)where G is the gravitational constant, M(r) is the mass within the radius coordinate r of the donor star with total radius, Rdonor, total mass, Mdonor, core mass, Mcore, envelope mass, Menv ≡ Mdonor − Mcore, and U is the specific internal energy (Han et al. 1994). Given that Ebind is evaluated at the moment the evolved donor star fills its Roche-lobe and initiates dynamically unstable mass transfer, leading to formation of the CE, we do not include the gravitational potential from the in-spiralling companion when calculating Ebind (see e.g. Podsiadlowski et al. 1992; Iben & Livio 1993, for alternative descriptions).
From integrations of detailed stellar models, the values of λ in Eq. (1) can be calculated (Dewi & Tauris 2000, 2001; Podsiadlowski et al. 2003) and tabulated (e.g. for use in population synthesis codes). Differences in λ-values may arise, for example, from the use of different stellar models, the degree of available recombination energy (Ivanova et al. 2015), enthalpy considerations (Ivanova & Chaichenets 2011; Wang et al. 2016), and, in particular, from using different definitions of the core-envelope boundary (Tauris & Dewi 2001). The last problem is discussed in Sect. 4.1.
Since the in-spiral of the companion star often decreases the orbital separation by a factor of ~100 or more, we can approximate the change in orbital energy as 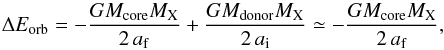 (2)where ai and af denote the initial (pre-CE) and final (post-CE) orbital separation, respectively, and MX is the mass of the in-spiralling object (e.g. MBH for a BH).
(2)where ai and af denote the initial (pre-CE) and final (post-CE) orbital separation, respectively, and MX is the mass of the in-spiralling object (e.g. MBH for a BH).
It is crucial for our purposes to investigate whether the ability of CE ejection depends on the masses of the two stars; that is to say, whether it is possible that the CE ejection will work for producing [8+8 M⊙] BH-BH systems, for instance, but not [30+30 M⊙] BH-BH systems. Hydrodynamical simulations and some observational evidence (see Sect. 3.2) indicate that the envelope ejection efficiency α does depend on the mass of the in-spiralling object, at least in the formation of WD-WD binaries. Furthermore, massive stars producing BHs have more tightly bound envelopes, and therefore higher values of Ebind, than somewhat less massive stars with the same radius. The reason for this are the combined effects of a more shallow decline in mass density with radial coordinate and more envelope mass located outside the core boundary compared to less massive stars. On the other hand, the more massive stars are also able to release more orbital energy from in-spiral to a given final orbital separation. Therefore, we can consider the ratio Ebind/ ΔEorb, which can be rewritten as 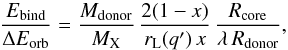 (3)where x ≡ Mcore/Mdonor, q′ ≡ Mcore/MX and rL(q′) ≡ Rcore/af is the dimensionless Roche-lobe radius (Eggleton 1983) of the stripped core with mass Mcore and radius Rcore (see Sect. 4.6 for discussions). For the values of ΔEorb, it is assumed that the in-spiral stops just when the remaining core would fill its Roche lobe.
(3)where x ≡ Mcore/Mdonor, q′ ≡ Mcore/MX and rL(q′) ≡ Rcore/af is the dimensionless Roche-lobe radius (Eggleton 1983) of the stripped core with mass Mcore and radius Rcore (see Sect. 4.6 for discussions). For the values of ΔEorb, it is assumed that the in-spiral stops just when the remaining core would fill its Roche lobe.
As a boundary of the remaining core, we take in this study the mass coordinate where the hydrogen abundance XH = 0.10 (see Sects. 3.3 and 4.1 for extensive discussions).
In the above energy formalism, we have assumed a minimum energy requirement, that is, we have neglected any kinetic energy of the ejected matter and simply assumed that the velocity of the gas is zero at infinity. In reality, the material may be ejected from the binary with a higher velocity. For example, it has been argued (Nandez et al. 2014) that the kinetic energy of the ejecta material at infinity might be comparable to the initial binding energy of the envelope of the donor star. In addition, orbital energy transferred to the ejected material might not have been thermalised (Ivanova et al. 2013). The applied energy formalism used to predict the post-CE separation does not take these effects into account, unless a value of α lower than unity is chosen (see also Sect. 4.3).
As mentioned above, for successful envelope ejection, it is required that (Ebind/ ΔEorb) ≤ α (Livio & Soker 1988). We now investigate Ebind and λ for various stellar models and calculate for which values of MX envelope ejection is possible if the sole energy source to eject the envelope is released orbital energy from the in-spiralling object (which can be a compact object, a star, or a planet).
3. Results
 |
Fig. 1 Binding energy of the envelope, | Ebind | (lower panel), and its associated λ-value (upper panel), as a function of total stellar radius for two sets of models with Z = Z⊙/ 50 (full lines, crosses) and Z = ZMW (dashed lines, squares). Independent of mass and metallicity, and before reaching the giant stages (R ≲ 1000R⊙), the λ-values almost follow a power law with an exponent between −2/3 and −1 (upper and lower grey lines, respectively). The exceptions are stars with initial masses ≳60M⊙ at Z = ZMW (dashed blue line), which either become LBV stars, see Sect. 4.7, or have their envelopes stripped by enhanced wind-mass loss. The absolute binding energies of the 8M⊙ stars drop below the plotted range, down to approximately 2.7 × 1047erg and 7.3 × 1046erg for Z = Z⊙/ 50 and Z = ZMW, respectively. |
In Fig. 1 we have plotted our calculated values of λ and | Ebind | according to Eq. (1) as a function of stellar radii, Rdonor, using the stellar models of Szécsi et al. (2015) for a metallicity of Z = Z⊙/ 50 (resembling the metallicity of the irregular dwarf galaxy: I Zwicky 18) and Brott et al. (2011) for Z = 0.00876 ≈ Z⊙/ 2 (which we assume to represent the average metallicity of the Milky Way, ZMW). The 8M⊙ models are calculated using the same code and input physics as the models of Szécsi et al. (2015) and Brott et al. (2011), respectively.
It is seen that, in general, the envelope becomes less bound with increasing values of Rdonor. Until the giant stages, the values of | Ebind | are moderately declining due to a combination of structural changes (i.e. growing core mass) and wind-mass loss, which affects the mass-density profile and decreases the mass of the envelope. The evolution at these early stages is more or less independent of metallicity, except for stars with ZAMS masses ≳60M⊙, which become luminous blue variable (LBV) stars at high metallicities, cf. Sect. 4.7, or have their envelopes stripped by enhanced wind mass loss (Vink et al. 2001), and therefore do not evolve to become red supergiants (cf. the dashed blue track of the 80M⊙ star with Z = ZMW, which does not expand above 60R⊙).
The resulting change of λ with stellar radius (upper panel) is seen to be significantly stronger than changes caused by different stellar masses or metallicities. During the early stages of the expansion phase (up to R ≃ 1000R⊙), the dependence on radius almost follows a power law with an exponent between −2/3 and −1.
The stellar tracks in Fig. 1 terminate at different evolutionary stages. Depending on stellar mass, the stars will reach the Eddington limit (Sect. 4.7) at different epochs of evolution. When a star reaches the Eddington limit, it initiates cycles of large-amplitude radial pulsations. This explains the horizontal clustering of points at the end of the stellar tracks in the (R, | Ebind |)–diagram. This also explains why some tracks have increasing λ-values near the end (e.g. 15M⊙ stars at Z = ZMW, evolved beyond core carbon burning), whereas others have decreasing values of λ (e.g. 25M⊙ stars at Z = ZMW, only evolved to the end of core helium burning), or more or less constant values of λ (e.g. 40M⊙ stars at Z = ZMW, even less evolved to hydrogen shell burning). A careful inspection of the 15M⊙ track at Z = ZMW shows decreasing and increasing λ-values before reaching the pulsating stage as a giant. This star experiences a final giant stage with significant radial expansion (up to R = 1585R⊙), which results in the strong decline in | Ebind |, causing the increase in λ.
Our calculated λ-values for massive stars (with initial masses of up to 115M⊙) are in broad agreement with those of Dewi & Tauris (2001) and Loveridge et al. (2011). The latter authors demonstrated that the calculated λ-values are largely independent of metallicity and applied wind mass-loss prescription. Our calculations more or less confirm this result, except for massive metal-rich stars (LBVs) or in case models are calculated with a very low mass-loss rate (much lower than for Z = Z⊙/ 50), in which case the λ-values become higher for evolved stars (Podsiadlowski et al. 2003).
 |
Fig. 2 Minimum mass of the in-spiralling object, MX,min which is needed to expel the envelope during a CE evolution with α = 1, for a given donor star radius as indicated by the coloured lines, as a function of ZAMS mass of the donor star, MZAMS for Z = Z⊙/ 50 (upper panel) and Z = ZMW (lower panel). Rmax is the maximum radial extent during the stellar evolution. The grey band between 1.17 and 1.56M⊙ indicates masses of NSs observed in double NS systems (Martinez et al. 2015). |
3.1. CE ejectability and companion star masses
To investigate the ejectability of the CE, we plot in Fig. 2 the minimum mass of the in-spiralling object, MX,min which is needed to successfully expel the envelope during a CE evolution of stars with a given mass and metallicity at different evolutionary stages. The core radii of the stripped donor stars were calculated for naked helium star models (Sect. 4.6) using the stellar evolution code BEC (Yoon et al. 2010), which was also used to calculate our applied models of Szécsi et al. (2015) and Brott et al. (2011).
As expected from the decreasing values of | Ebind | with increasing stellar radius (Fig. 1), it is seen in Fig. 2 that evolved (expanded) donor stars more easily have their envelopes ejected by a relatively less massive in-spiralling companion than less evolved donor stars. In particular for the low-metallicity models (Z = Z⊙/ 50, upper panel), we note the significant difference in envelope ejectability between massive stars evolved to radii R ≲ 1000R⊙ (blue, green, and orange lines) and giants (R> 1000R⊙; red line). For example, for the 88M⊙ model with Z = Z⊙/ 50 we find that it requires an in-spiralling object with a mass of at least 30−50M⊙ to eject the envelope in the former case, but only an object of ~6M⊙ in case the envelope is ejected when the donor star is an evolved giant near its maximum radius of ~3500R⊙.
The scatter of points along the coloured lines in Fig. 2 can be understood from the non-monotonic behaviour of | Ebind | as a function of stellar radius. For a given stellar mass, we see from Fig. 1 that | Ebind | is not monotonically decreasing as a function of increasing value of R. The reason for this are changes in the core structure during the stellar evolution.
We conclude that envelope ejection is facilitated for giant stars compared to less evolved stars, and as long as the in-spiralling BH masses are high enough (above the coloured lines in Fig. 2), they probably succeed in ejecting the envelopes of their host stars. Hence, for a given donor star mass and mass of in-spiralling object, we can define a certain interval of stellar radii of each pre-CE donor star where CE ejection is possible (see Sect. 4.4), which translates into a range of pre-CE orbital periods combining Kepler’s third law with an expression for the dimensionless Roche-lobe radius of the donor star (e.g. Eggleton 1983). For example, our 115M⊙ model star (Z = Z⊙/ 50) might have its envelope ejected successfully when the mass of the in-spiralling BH is above 30−40M⊙ and the star has evolved to R ≳ 100R⊙ (cf. Fig. 2, upper panel). The maximum radius reached by this star as a giant is 3922R⊙, at which point M ≃ 93M⊙. Hence, the orbital period interval for successful ejection of the envelope in this particular binary is between 875 and 7750 days for a 30M⊙ BH.
We stress the important caveat that the above calculations in Fig. 2 all assume a certain core boundary criterion (XH = 0.10). We investigate in Sect. 3.3 more carefully at which bifurcation point we might expect CE ejection. Furthermore, we assume formation of a CE for all binary systems in Fig. 2. It is quite likely that several of these systems, especially with less evolved donor stars or mass ratios close to unity, may undergo stable Roche-lobe overflow (RLO, Pavlovskii et al. 2016). We also recall that in Fig. 2 we solely investigate the possibility of CE ejection regardless of the formation of any given binary. Some of the implied binary configurations in Fig. 2 are unlikely to be produced in nature in an isolated binary system. For example, it would be unexpected to have a 6M⊙ BH orbiting an 88M⊙ star (and, in particular, a 100 or a 115M⊙ star). The reason is that in order for the primary star (the initially most massive of the two ZAMS stars) to evolve first and eventually produce a BH, it must have had a ZAMS mass of more than ~60M⊙ (otherwise the initially least massive of the two stars, the secondary, would not be able to accrete sufficient material to reach 88M⊙). However, the core mass of a 60M⊙ star is ~30M⊙ and thus most likely too massive to leave a BH with a mass of only 6M⊙.
Finally, we note that the cores of the most massive (≥100M⊙) low-metallicity stars exceed 60M⊙ and probably terminate their lives in pair-instability SNe, which lead to the total disruption of the star without leaving behind any BH (Heger & Woosley 2002; Chatzopoulos & Wheeler 2012).
All calculations in Fig. 2 were performed assuming an envelope ejection efficiency parameter of α = 1. The plotted curves therefore represent the most optimistic case for ejectability. Applying more realistic efficiencies of α< 1 would require higher values of MX,min and shift all plotted curves upward. On the other hand, we assumed that the release of orbital binding energy is the sole energy source available to eject the envelope. It is possible that other energy sources are at work as well (see Sect. 4.2), in which case the curves in Fig. 2 would be shifted downward to lower values of MX,min, reflecting that envelope ejection would be facilitated.
3.2. CE ejection: NS-NS and WD-WD binaries
Another interesting result seen in Fig. 2 is that HMXB systems with in-spiralling NSs are also able to eject the envelopes of donor stars with initial masses of up to about 22−25M⊙ (depending on metallicity). These systems eventually evolve to become double NS systems following a post-CE episode of so-called Case BB Roche-lobe overflow (Dewi et al. 2002; Ivanova et al. 2003; Tauris et al. 2015). The grey band between 1.17 and 1.56M⊙ in Fig. 2 indicates the interval of measured NS masses in double NS systems (Martinez et al. 2015). Similarly, we note that evolved donors with masses lower than 8−10M⊙ can have their envelopes ejected by even sub-solar mass objects, thereby allowing formation of tight double WD systems through CE evolution, as confirmed by observations (e.g. Zorotovic et al. 2010).
Interestingly enough, Ivanova et al. (2015) found that less massive in-spiralling stars plunge in faster than more massive in-spiralling stars, which results in a relatively higher heating rate, and low-mass intruders are therefore more effective in ejecting the envelopes since a smaller fraction of the released orbital energy is dissipated in the outer parts of the envelope. This suggests that low-mass stars are more efficient in removing the envelope (i.e. these binaries should have higher α-values than binaries with more massive companion stars, see also Podsiadlowski 2001). This hypothesis is supported by observations that indicate that the ejection efficiency increases for less massive companion stars (de Marco et al. 2011; Davis et al. 2012).
 |
Fig. 3 Energy budget of the in-spiral process for the 88M⊙ donor star model with Z = Z⊙/ 50 at two different evolutionary epochs: at the beginning of the Hertzsprung gap, R = 194R⊙ (upper panel), and when the star reaches its maximum extent as a giant star, R = 3530R⊙ (lower panel). The two solid lines mark the integrated binding energy of the material between the given mass coordinate and the surface. The green line (Ebind) includes the total energy (internal and gravitational binding energy, cf. Eq. (1)), while the red line (Egrav) only considers the gravitational binding energy. The six dashed curves represent the released orbital energy, ΔEorb of an in-spiralling object with a given mass between 1.3 and 80M⊙ (cf. mass values in the legend). For the values of ΔEorb, it is assumed that the in-spiral stops just when the remaining star would fill its Roche lobe. The vertical dotted line indicates the core boundary according to the XH = 0.10 criterion (cf. Sect. 2), and the arrow marks the location of the maximum-compression point (cf. Sect. 4.1). The hatched regions shown at the top indicate convective layers. The black and grey dots mark the crossings when Ebind = ΔEorb, see Sect. 3.3 for details. |
3.3. Bifurcation point of envelope ejection
One of the main problems in our understanding of CE ejection is the difficulty of localising the physical point of envelope ejection, that is, the bifurcation point, which separates the ejected envelope from the remaining core (Tauris & Dewi 2001). The three main categories proposed for determining the bifurcation point are nuclear energy generation, chemical composition, and thermodynamic quantities. A first-order constraint on the location of the core boundary (i.e. bifurcation point) can be taken as follows: it has to be somewhere between the hydrogen-depleted core (XH = 0) and the mass coordinate of the bottom of the convection zone in the pre-CE star. From studies of direct collisions between a NS and a red giant, it was found (Lombardi et al. 2006) that some amount of hydrogen remains bound to the stellar core, following envelope ejection. This result therefore indicates XH> 0. The problem with the upper limit is that the bottom of the outer convection zone often moves in mass coordinate during the CE ejection.
Our chosen core boundary criterion (XH = 0.10) is easy to apply in practice to stars at most evolutionary stages. Changing the mass coordinate of the core-mass boundary by 1% results in only minor different values of Ebind and λ (of the order 10%) for stars in the Hertzsprung gap, whereas the effect of changing Mcore by 1% is much larger (up to a factor 2) for stars on the giant branch that possess a steep density gradient near the core boundary.
In Fig. 3 we plot the integrated binding energy (solid lines) and the released orbital energy (dashed lines, calculated as the difference between Eorb at the starting point and the end point of the in-spiral) as a function of mass coordinate of our 88M⊙ stellar model (Z = Z⊙/ 50) at two different evolutionary epochs of the star. The in-spiralling object corresponds here to either a NS (with a mass of 1.3M⊙) or a BH with a mass between 5 and 80M⊙. The upper panel is based on the structure of the star for R = 194.5R⊙ (M = 86.94M⊙, Mcore = 51.82M⊙) during hydrogen shell burning (Hertzsprung gap star), while the lower panel is for R = 3530R⊙ (M = 76.65M⊙, Mcore = 52.35M⊙) at its maximum expansion point as a giant.
In each panel in Fig. 3, the black points indicate when (during in-spiral) the released orbital energy will become lower than the binding energy of the layers outside the location of these points. Hence, if the in-spiralling object moves further inward than these crossing points, there is no possibility of ejecting the envelope, and the system merges. The location of these black crossing points should be compared to our defined location of the core boundary, shown as a vertical dotted line (XH = 0.10). If the black crossing points are located outside (to the right of) our assumed core boundary, the system is expected to merge. In the upper panel (Hertzsprung gap star), this is the case for MX = 1.3−20M⊙, whereas MX = 40M⊙ and 80M⊙ succeed in envelope ejection. In the lower panel (star at the tip of the giant branch), all in-spiralling objects with masses MX ≳ 5M⊙ are in principle able to eject the envelope of the star1.
In the lower panel of Fig. 3, the additional grey points mark the crossing where the released orbital energy exceeds the binding energy for the first time. Hence, an in-spiralling object has to spiral in at least to this depth to eject the material farther out. As long as there are no other energy sources, the in-spiral leading to successful envelope ejection is expected to stop somewhere between the grey and the black points. Depending on the amount of the internal energy that can actually be used to eject the envelope (see e.g. Han et al. 1994; Ivanova et al. 2015, for discussions), the crossing points should be be located somewhere between the solid green and red lines. The less the available internal energy, the deeper the in-spiral, and the more difficult it is for the binary system to eject the envelope (and survive instead of merging).
It should be noted that the region between the two crossings of ΔEorb and Ebind shown in Fig. 3 has previously been discussed in terms of “the energy expense” (Ivanova 2011), that is, the normalised excess energy available to the envelope after removal of all matter above a given mass coordinate.
3.4. Response of donor star to mass loss
The immediate adiabatic response of the remaining envelope layers depends on whether they are convective or radiative (Hjellming & Webbink 1987). On a longer timescale, the reaction of stripped cores to loss of their envelope depends on the amount of residual material remaining in the envelope. The expansion or contraction of the remaining shell occurs on the thermal timescale of the remaining layer. The residual hydrogen content following envelope ejection has been studied in the formation of WDs (Deinzer & von Sengbusch 1970), and in particular in LMXB systems (Tauris & Savonije 1999; Podsiadlowski et al. 2002; Istrate et al. 2016). However, for more massive stars the situation is less well explored.
In Fig. 4 we plot the lower panel of Fig. 3 in radius coordinates. The convective envelope of this massive giant star spans a wide range in radius, although its mass is lower than the core mass. The core boundary is located near a radius coordinate of r ≃ 1R⊙. At first sight, the in-spiral might be expected to stop at the grey point, considering that at this location enough energy is released to unbind to material of the envelope farther out. However, when this point is well within hydrogen-rich material (which is clearly the case here), the system will not undergo final detachment at this location. As discussed above, the hydrogen-rich layers of the star will re-expand (and during this thermal adjustment the star may develop strong thermal pulses, cf. Ivanova et al. 2013). Hence, the mass transfer will continue and rebuild the CE. At this point, however, the drag force might be too weak to cause significant further in-spiral before the core of the donor star collapses (see e.g. Appendix A in Tauris et al. 2015, for an estimate of the timescale of the in-spiral). It is also possible that a self-regulated in-spiral is followed by additional RLO from either the core of the donor star (depending on the amount of residual hydrogen) or the in-spiralling companion star, and this leads to further plunge-in. This plunge could in turn be followed by an additional self-regulated phase, and so on, such that a repetitive pattern may occur (Ivanova et al. 2013). This pattern may repeat until the in-spiralling object reaches non-convective layers, at which point re-expansion of radiative material will process on a longer timescale. In the case of our giant star model in Fig. 4, the pre-CE convective boundary is located at a radius coordinate of about 8R⊙.
The removal of the innermost hydrogen-rich layers may possibly proceed through dynamical stable mass transfer (this still has to be confirmed by numerical calculations), until the mass of the diluted giant envelope reaches below a critical threshold value and the remaining envelope collapses and the binary finally becomes detached. If mass is removed to below the bifurcation point, then the remaining core contracts on its thermal timescale.
To summarise the above, we conclude that the termination point of the in-spiral is difficult to estimate accurately. We expect that at first, the plunge-in of the in-spiral will stop somewhere in the interval where the green curves bent vertically downward (i.e. where Ebind ≳ 0) in Fig. 3 (lower panel) and Fig. 4. The further evolution and the final post-CE orbital separation is not trivial to calculate and depends on the details of the physics of the CE ejection process, the response of the remaining core to mass loss, and the amount of liberated accretion energy.
 |
Fig. 4 Lower panel of Fig. 3 in radius coordinates. The additional blue solid line indicates where 50% of the internal energy is included in the calculated binding energy of the envelope. |
We also conclude that the in-spiral will only come to an end and lead to successful CE ejection when both of the following conditions are fulfilled:
-
The remaining amount of hydrogen is below the threshold for re-expansion of an envelope (i.e. the bifurcation point is located in a radiative layer with XH> 0).
-
The released orbital energy is sufficient to remove the envelope (i.e. the final location where in-spiral ends is between the black and grey points in Figs. 3 and 4).
It is therefore evident from our analysis that LIGO merger rates estimated from population synthesis of the CE formation channel (e.g. Belczynski et al. 2002; Voss & Tauris 2003; Belczynski et al. 2008; Dominik et al. 2012; Mennekens & Vanbeveren 2014; Belczynski et al. 2016; Eldridge & Stanway 2016) must be highly uncertain and all quoted rates should be taken with a huge grain of salt (let alone other uncertain effects in addition to CE evolution).
4. Discussions
4.1. Bifurcation point revisited
A method suggested by Ivanova (2011) is to locate the core boundary, after thermal readjustment, at the (pre-CE) mass coordinate in the hydrogen shell corresponding to the local maximum of the sonic velocity (i.e. at the maximum-compression point, Mcp where P/ρ has a local maximum). It was argued that if a post-CE star has a final mass smaller than Mcp, then the star will shrink. However, if it has any mass beyond this location, the star will continue to expand on the local thermal timescale. This may give rise to a new episode of mass transfer, or possibly a pulse.
For our calculations of the core boundary in this study, we chose to use the XH = 0.10 criterion (Dewi & Tauris 2000), which is often used in the literature. Interestingly enough, we find that this point coincides closely to the maximum-compression point in the hydrogen shell burning layer in most of our models. For all stellar models we investigated that are evolved beyond core hydrogen burning (independent of mass and metallicity), the locations of the core boundary using the XH = 0.10 criterion and the maximum-compression point Mcp are often consistent to within 1%, and always within 4% (except for our few high-metallicity models with masses <10M⊙, where the discrepancy can be up to 8% in mass coordinate).
This general agreement is evident from comparing our λ-values, calculated with the XH = 0.10 criterion, with those recently calculated by Wang et al. (2016) for population I stars of up to 60M⊙, using the Mcp criterion.
4.2. Other energy sources
According to Ivanova et al. (2013), the question of additional energy sources, other than the release of orbital energy, depends partly on the extent to which the envelope is ejected directly by spiral shocks, developing from the orbital motion and tidal arms trailing the two stars (Ricker & Taam 2012), or indirectly by heating and a pressure gradient. If the donor star core expands as a consequence of mass loss, it could do mechanical work on the envelope and change the boundary conditions for the integral in Eq. (1). Enforcing corotation of the envelope through tidal heating may produce an energy sink.
Ivanova et al. (2015) demonstrated that heat input leading to kinetic energy deposition within the envelope is not just a simple function of radius and mass. It depends on the structure of the pre-CE donor star (e.g. mass density profile and the degree of corotation), the initial mass ratio between the two stars, and on how angular momentum is transported through the CE. In other words, the authors concluded that the envelope ejection process depends on i) the amount; ii) the location; and iii) how rapidly the released energy is transferred to the envelope, and they predict two types of outcomes: “runaway” and “self-regulated” envelope ejection.
4.2.1. Recombination energy
The inclusion of recombination energy of hydrogen and helium (e.g. Han et al. 1994) has been argued to be a promising candidate for producing successful envelope ejection (e.g. Ivanova et al. 2015, and references therein). Recent 3D hydrodynamical modelling (Nandez et al. 2015) taking the released recombination energy reservoir into account, let to the first successful CE ejection and production of a post-CE double WD system.
Figure 5 shows the significance of recombination energy in units of the total internal energy U in the envelopes of our stellar models. Within the core of the star, the internal energy is fully dominated by radiation and gas pressure. The recombination energy contributes strongest to the total internal energy in the outer regions of the envelope with a mass density inversion.
Whereas the recombination energy can be an important contribution (up to ~55% of U) for low- and intermediate-mass stars, it does not play a role for massive stars when we apply the XH = 0.10 criterion for the core boundary (red and blue arrows). For BH progenitors, the contribution is typically lower than 1%, which may potentially lead to problems using current hydrodynamical simulation codes because they apparently only succeed to eject the envelope of low-mass stars when taking the released recombination energy into account (Nandez et al. 2015). As Fig. 5 points out, the metallicity content has no significant effect on this general behaviour.
Changing the bifurcation point criterion, however, such that the remaining core is assumed to include 1M⊙ of hydrogen, causes the relative contribution of recombination energy to be more important (green arrows) and thus play a role in facilitating CE ejection. An additional effect that favours successful ejection of CEs in wide systems is that the released recombination energy is highest for the most extended (coldest) stars.
 |
Fig. 5 Recombination energy in the envelope as a function of ZAMS mass. The plot shows the maximum contribution of recombination energy (from H, He and H2) to the total internal energy (U) obtained during the evolution of the stars. These maximum values are always reached when the stars are near their largest radial expansion as giants. The red arrows are for Z = ZMW and the blue ones for Z = Z⊙/ 50. The green arrows are also calculated for our Z = Z⊙/ 50 models, but assume a larger remaining core that includes 1M⊙ of hydrogen. |
4.2.2. Enthalpy
Ivanova & Chaichenets (2011) argued that including the enthalpy in the energy budget typically results in λ-values that are higher by a factor of 2 to 3 (see also Wang et al. 2016). Whether enthalpy should be included in the CE energy budget at all is controversial and may depend on the timescale of the CE ejection. Rather than being a new energy source, the main contribution of the P/ρ term is that it redistributes energy: it adds more kinetic energy to the gas ejected from the outer envelope regions at the expense of the energy of the inner regions of the envelope (Ivanova et al. 2013). This may cause the formation of a circumbinary disk if the inner envelope material is barely ejected at the escape velocity. Such a circumbinary disk can act as an additional sink of orbital angular momentum losses (e.g. Soberman et al. 1997; Spruit & Taam 2001). As a result of the dispute and uncertainty of potentially including the P/ρ term in Eq. (1), we disregard this term in our modelling.
4.2.3. Liberated accretion energy
Release of accretion energy is an additional energy source. This contribution may even dominate that of orbital energy release in the beginning of the in-spiral, for the reason that in the outer envelope layers the in-spiral timescale is relatively long and the binding energy per unit mass is low. In recent studies of hydrodynamical simulations, MacLeod & Ramirez-Ruiz (2015a,b) found that a compact object such as a NS embedded in a CE only accretes a very modest amount of material during its in-spiral as a result of a density gradient across its accretion radius, which strongly limits accretion by imposing a net angular momentum to the flow around the NS. This conclusion supports earlier work by Ricker & Taam (2012), who also found that the true accretion rate of the accreting star is much lower than predicted by the Bondi-Hoyle prescription. Nevertheless, even modest accretion rates constrained by the Eddington limit can contribute significant heat to the CE energy budget.
Voss & Tauris (2003) introduced in their simulations the inclusion of released accretion energy from the in-spiralling compact object (thus facilitating envelope ejection), and hence demonstrated that the expected aLIGO detection rate of BH-BH mergers should strongly dominate that of NS-NS systems. The energy input from accretion onto a BH during a CE phase is given by 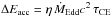 , where the Eddington accretion limit (van den Heuvel 1994) can be estimated as
, where the Eddington accretion limit (van den Heuvel 1994) can be estimated as 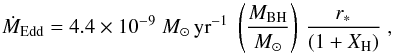 (4)yielding
(4)yielding 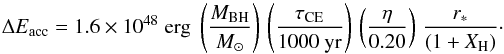 (5)Here, τCE< 103yr is the duration of the CE phase (dictated by the thermal timescale of the envelope, Ivanova et al. 2013), XH is the mass fraction of hydrogen in the donor-star envelope, η is the accretion radiation efficiency, and r∗ = RISCO/ (GMBH/c2) is the location of the innermost stable circular orbit (ISCO). Both η = 0.06−0.42 and r∗ = 1−6 depend on the (here assumed to be prograde) spin of the accreting BH.
(5)Here, τCE< 103yr is the duration of the CE phase (dictated by the thermal timescale of the envelope, Ivanova et al. 2013), XH is the mass fraction of hydrogen in the donor-star envelope, η is the accretion radiation efficiency, and r∗ = RISCO/ (GMBH/c2) is the location of the innermost stable circular orbit (ISCO). Both η = 0.06−0.42 and r∗ = 1−6 depend on the (here assumed to be prograde) spin of the accreting BH.
As an example, a 35M⊙ BH with an Eddington-limited accretion rate (~10-7M⊙ yr-1) would therefore be able to accrete about 10-4M⊙ while embedded in a CE and release a total energy output of ~5 × 1049erg, which can potentially be used to eject the envelope. As can be seen from Fig. 4, a heat input of this amount could significantly facilitate envelope ejection even in massive stars. However, as we discuss in Sect. 4.2.4 below, this possibility depends on the physics of energy transport in the envelope to be ejected.
In addition to heating, we note that accretion can also help in envelope ejection by the possible formation of a jet by the in-spiralling object (Soker 2004, 2016). Especially BHs and NSs are expected to potentially launch very energetic jets. In a scenario recently suggested by Soker (2015), so-called grazing envelope evolution might be made possible if a compact companion star manages to accrete matter at a high rate and launch a jet that removes the outskirts of the giant envelope, hence preventing the formation of a CE. However, further investigation of this model is needed.
4.2.4. Convective energy transport
In order to eject a CE, the liberated energy, either from the in-spiral of the compact companion, from accretion onto this compact companion, or from the recombination of ionised envelope material needs to be converted into mechanical energy. If all these processes take place inside a fully convective envelope, the question arises whether a part of the liberated energy, which is at first present in the form of heat, would be quickly transported to the top of the envelope, where it would be radiated away.
The efficiency of this energy loss will depend on the ratio of the timescale of energy liberation to the convective timescale. If it is small, then convective energy loss will be negligible. If the ratio is near one or higher, convective energy loss may be important. As the convective timescale is of the order of the dynamical timescale of the star, it appears possible that convective energy loss is relevant for all three forms of energy liberation mentioned above. It will require models of time-dependent convection to quantify this effect.
4.3. Ejection efficiency parameter
So far, we have not addressed the value of the ejection efficiency parameter, which we have simply assumed to be α = 1. There are several reasons, however, why a realistic value of the ejection efficiency parameter would be α< 1. An example is radiative losses from the CE (e.g. as discussed above in Sect. 4.2.4) or internal and kinetic energy of the ejecta material.
Energy loss from the envelope photosphere is relevant for relatively slow, thermal timescale CE events (in which case there might also be significant energy input from the naked, hot stellar core). Moreover, recent work by Nandez et al. (2015) demonstrated a case where between 25% to 50% of the released orbital energy is taken away as kinetic energy of the ejected material, implying α< 0.75 from this effect alone.
Assuming lower and more realistic values of α (e.g. 0.3−0.7) would cause all the solid lines in Fig. 2 to move up, and all dashed lines in Figs. 3 and 4 to move down. For example, in Figs. 3 and 4, the line of the 5M⊙ in-spiralling object for α = 1 is comparable to that of a 10M⊙ in-spiralling object with α ≈ 0.5.
4.4. Post-CE orbital separations in population synthesis
 |
Fig. 6 Mapping of pre-CE to post-CE orbital separations as done in population synthesis (see Sect. 4.4) when applying the (α,λ)-formalism. The donor is assumed to be our 88M⊙ (Z = Z⊙/ 50) star. The in-spiralling objects (BHs) have masses of between 5 and 80M⊙. Below the dashed GW lines, the post-CE systems will merge within a Hubble time. Below the dotted CE lines, the in-spiral continues to the core of the donor star and leads to coalescence (i.e. the relaxed He-core fills its Roche-lobe, cf. Sect. 4.6, and the binary will not survive). In the upper panel, the different colours mark the mass of the in-spiralling object (using α = 1); in the lower panel, they represent different values of α (for a fixed value of MX = 35M⊙). The dark green (upper) line in the lower panel was calculated for α = 1 and an additional accretion energy of 5 × 1049erg, see Sect. 4.2.3. The hatched regions indicate systems that are expected to successfully produce LIGO sources. The solid dots mark the models shown in Figs. 3 and 4. |
For a discussion of predicted LIGO detection rates of merging BH-BH, NS-NS, or BH-NS binaries, it is of interest to evaluate the amount of fine-tuning needed for a given binary system to survive CE evolution, and to probe how the mapping of pre-CE orbital separations to post-CE orbital separations are performed in a typical population synthesis code. In such codes, it is usually assumed that all material is removed above a core boundary at XH = 0.10. In the discussion below we therefore apply this bifurcation point criterion.
In Fig. 6 we plot post-CE orbital separations, af as a function of pre-CE orbital separations, ai for the 88M⊙ (Z = Z⊙/ 50) donor star investigated in this paper. In the upper panel, we show the results for in-spiralling companions (BHs) of masses: 5, 10, 35 and 80M⊙, in all cases assuming an envelope ejection efficiency parameter of α = 1. In the lower panel, we assume MX = 35M⊙ (i.e. resembling the progenitor system of GW150914) for different values of α (0.25, 0.50, 0.75 and 1), and including one additional case (for α = 1) where we assumed injection of released accretion energy of ΔEacc = 5 × 1049erg.
In each panel we show GW and CE lines, corresponding to post-CE orbital separations below which the system will merge within a Hubble time (13.8 Gyr) and thus become detectable as a gravitational wave source, or coalesce during the CE in-spiral and thus not survive as a binary system, respectively. For each system, the intervals of ai, for which the binary successfully survives and eventually produces a LIGO merger event within a Hubble time, are marked with a hatched pattern. For example, the upper panel shows that only the two in-spiralling objects with masses MX = 80M⊙ and MX = 35M⊙ can successfully eject the CE of our donor star (which has an initial mass of 88M⊙ and Z = Z⊙/ 50) before it reaches its giant stage. The in-spiralling object with MX = 10M⊙ is only able to eject the envelope of the donor star when the latter has evolved to its very last expansion phase as a giant. The in-spiralling 5M⊙ cannot eject the envelope at all (see also Fig. 2). For MX> 27M⊙, there are two windows of ai intervals that allow CE ejection.
Whereas for a massive in-spiralling object of 80M⊙ we find solutions for the entire interval 60 ≤ ai< 10 000R⊙, an in-spiralling object with MX = 35M⊙ only has solutions for 130 <ai< 400R⊙ and 1300 <ai< 8000R⊙. Given their lower values of af, the MX = 35M⊙ systems produce shorter delay-time binaries (i.e. they merge on a shorter timescale following the CE ejection than the MX = 80M⊙ systems).
In the lower panel of Fig. 6, an envelope ejection efficiency close to 100% (α = 1) is needed for the system with MX = 35M⊙ to survive. An injection of ΔEacc = 5 × 1049erg will result in somewhat less in-spiral and therefore wider post-CE binaries with longer delay-times.
The points on each curve in Fig. 6 were calculated using a specific subroutine of the binary population synthesis code of Kruckow et al. (in prep.), which estimates the post-CE orbital separations. This code makes use of interpolations of stellar tracks using a finite grid resolution of stellar radii that is combined with the dimensionless Roche-lobe radius (Eggleton 1983) to determine ai for each value of MX. The values of af are then determined from tabulated values of λ associated with the stellar grids, following Eq. (1) and combined with | Ebind | = α· | ΔEorb | + ΔEacc.
4.5. Post-CE merger before core collapse?
 |
Fig. 7 Final fate of a post-CE binary system composed of a naked helium core and a BH as a function of orbital separation after envelope ejection. The chosen donor star model is that of the 88M⊙ star (Z = Z⊙/ 50) at its maximum extent as a giant, cf. Figs. 3 (lower panel) and 4. The mass of the exposed helium core is M = 52.35M⊙ and the BH is assumed to have a mass of 30M⊙. The blue line (GWR) represents the merger time due to gravitational-wave radiation, the orange line (SN) represents the remaining lifetime of the core until it collapses, and the red dotted line (Wind) represents the timescale (a/ȧwind) of orbital widening due to stellar wind mass loss. The yellow shaded region marks the core region (XH< 0.10). See Sect. 4.5. |
For massive binaries undergoing CE evolution with deep in-spiral of the BH, we investigated if it is possible that the timescale of gravitational-wave radiation (GWR) of the post-CE binary is shorter than the remaining lifetime of the exposed core. The result is illustrated in Fig. 7. We studied the fate of our 88M⊙ star (Z = Z⊙/ 50) under the assumption of onset of a CE when this star is near its maximum extent as a giant (R = 3530R⊙ at an age of 2.83 Myr, cf. Fig. 3 lower panel, and Fig. 4). Furthermore, we assumed a mass of the in-spiralling BH of 30M⊙.
In Fig. 7 region I marks the extreme case where GWR would be strong enough to merge the binary before a BH-BH binary is produced, that is, before the collapse of the exposed core. However, the vertical dotted line marks the orbital separation of the BH where the core would fill its Roche lobe and continue mass transfer. Hence, regions I and II would most likely lead to an early merger in any case. In region III, the orbit will decrease in size before core collapse as a result of GWR, while in region IV the orbit widens before core collapse as a result of the stellar wind.
For this system, we estimate the remaining lifetime of the post-CE exposed core (M = 52.35M⊙) to be about 30 kyr (given that the progenitor star was evolved close to the onset of carbon burning). For the merger time of the binary we find from integration (assuming time-independent point masses M1 and M2 in a circular orbit with separation, a, following Peters 1964) 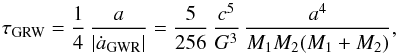 (6)where c is the speed of light. The steep dependence on a means that systems will spend most of their in-spiral time at a large separation. They only evolve to half their initial separation in about 94% of the full merger time calculated from Eq. (6). Therefore, taking into account the finite size of the exposed core only changes the true merger time slightly.
(6)where c is the speed of light. The steep dependence on a means that systems will spend most of their in-spiral time at a large separation. They only evolve to half their initial separation in about 94% of the full merger time calculated from Eq. (6). Therefore, taking into account the finite size of the exposed core only changes the true merger time slightly.
It is seen in Fig. 7 that if a post-CE survival criterion is that the exposed core is not allowed to fill its Roche lobe (i.e. ruling out all post-CE orbital separations to the left of the vertical dotted line), then at least for this particular system, it is not possible for the post-CE system to merge as a result of GWR before the naked core terminates its life and undergoes core collapse to form a BH. Hence, all systems to the right of the dotted line would produce BH-BH binaries and eventually become LIGO sources.
We can determine the critical separation at which the orbital decay due to GWR (ȧGWR) is exactly opposed by the orbital widening due to (fast, Jeans mode) stellar wind mass loss (ȧwind) with a rate of Ṁwind as 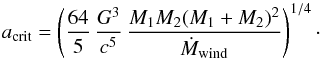 (7)For the system in Fig. 7, we find acrit = 3.65R⊙ (cf. red circle) for Ṁwind = 10-4M⊙ yr-1.
(7)For the system in Fig. 7, we find acrit = 3.65R⊙ (cf. red circle) for Ṁwind = 10-4M⊙ yr-1.
4.6. Extended envelopes of helium stars
Massive, luminous stars, both hydrogen-rich and helium (Wolf-Rayet) stars, reach the Eddington limit in their interiors and develop inflated and extremely diluted envelopes (Ishii et al. 1999; Petrovic et al. 2006; Sanyal et al. 2015). Applying these extended radii for naked helium star models would prevent in-spiral to small separations if a criterion for survival of the CE ejection would be that the exposed helium core is not allowed to fill its Roche lobe. Hence, our estimated values of Rcore (and thus MX,min) would be much higher if such a conservative criterion was at work, which would make CE ejection even more difficult.
In our estimates of Rcore for naked helium stars, we followed Sanyal et al. (2015) and defined the core radius as the distance from the centre of the star to where the ratio β of gas pressure to total pressure drops below 0.15 for the first time. This definition agrees fairly well with the location of the point where the density gradient is steepest (∂2log ρ/∂m2 = 0).
To check the validity of this relaxed criterion for Rcore, we performed calculations of Roche-lobe overflow for a BH placed inside the extended envelope of a helium star, using the stellar evolution code BEC (Yoon et al. 2010, and references therein). As expected, the BH simply peels off the outer envelope of the star, which might have been lost in a strong wind in any case.
To summarise, applying the relaxed criterion on Rcore does not result in yet another episode of dynamically unstable mass transfer, and by applying these smaller core radii, we therefore probe the conditions under which the CE is most easily ejected.
4.7. Luminous blue variables
In our galaxy as well as in the Large Magellanic Cloud, stars more massive than ~60M⊙ are not found to be cooler than about 20 000 K (Humphreys & Davidson 1994; Castro et al. 2014). That single stars in the considered luminosity range are thought to develop into hydrogen-poor Wolf-Rayet stars (Langer et al. 1994; Meynet & Maeder 2005) implies that they do loose their envelope even without the help from a binary companion. The so-called luminous blue variables (LBVs) are located close the this observational border (Smith et al. 2004), and the LBV variability and outbursts are thought to be connected to the stellar Eddington limit (Ulmer & Fitzpatrick 1998; Sanyal et al. 2015).
The envelopes of stellar models near the Eddington limit may have very low binding energies (Gräfener et al. 2012; Sanyal et al. 2015). In the limit of near zero binding energies, a companion star could indeed kick off these envelopes without the requirement of a significant in-spiral. A similar situation is reached in the final phases of the AGB evolution of low- and intermediate mass stars. For stars in this mass range, there is observational evidence that in some cases, the common envelope ejection occurs with an insignificant orbital decay (Nelemans et al. 2000).
Consequently, stars near their Eddington limit, when they capture a companion into their envelope, may be prone to loose their envelope easily, but they will not produce sufficiently tight binaries to serve as progenitors for double compact mergers. The mapping of the Eddington limit throughout the parameter space of mass and metallicity is far from complete. Ulmer & Fitzpatrick (1998) pointed out that the Eddington limit is reached at higher masses for lower metallicity. This is confirmed by Sanyal et al. (in prep.), who find a limiting mass of ~100M⊙ at the metallicity of the Small Magellanic Cloud.
4.8. Convective core overshooting
The models presented in this work apply a convective core-overshooting parameter of δOV = 0.335 pressure scale heights (Hp), meaning that the radius of the convective core is equal to the radius given by the Ledoux criterion at the formal core boundary plus an extension equal to 0.335 Hp. Neglecting, or strongly reducing, the amount of convective core overshooting leads to a significantly different interior structure, not only because of its reduced core mass, but also owing to the star burning the main part of its helium core already in the Hertzsprung gap, before ascending the giant branch. For example, for our 20M⊙ model with Z = ZMW at the base of the giant branch, the central helium mass abundance, Yc = 0.24 for δOV = 0.0 compared to the case of Yc = 0.99 for δOV = 0.335. The calculated envelope binding energies and λ-values are therefore also affected by the choice of δOV. For example, for the 20M⊙ star mentioned above, we find that when it is evolved to a radius of R = 1200R⊙, then | Ebind | can be almost a factor 10 smaller (and λ a factor of 10 larger) using δOV = 0.0 compared to δOV = 0.335. The corresponding core masses are about 5.9M⊙ and 7.2M⊙, respectively. However, for the former case (δOV = 0.0) the central mass density is significant higher, leading to less tightly bound envelopes. For a 40M⊙ star we find that the impact of changing δOV is smaller.
5. Implications for LIGO detected BH-BH binaries
5.1. GW150914
The two merging BHs in GW150914 were located at a redshift of about z ≃ 0.09 (~400Mpc) and reported to have masses of 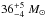 and
and 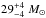 (Abbott et al. 2016b). These masses, as well as preliminary aLIGO detection rate estimates, agree well with the predictions of Marchant et al. (2016) and de Mink & Mandel (2016). Unfortunately, the spins of the individual BHs were not well constrained from this event. The question is whether the CE formation channel can also reproduce an event like GW150914.
(Abbott et al. 2016b). These masses, as well as preliminary aLIGO detection rate estimates, agree well with the predictions of Marchant et al. (2016) and de Mink & Mandel (2016). Unfortunately, the spins of the individual BHs were not well constrained from this event. The question is whether the CE formation channel can also reproduce an event like GW150914.
Based on the analysis presented in this paper, we conclude that the CE formation channel might work (in a low-metallicity environment) to produce relatively massive BH-BH systems like GW150914 (which require MZAMS ≳ 50M⊙). A caveat is that there are still many uncertain aspects of CE ejection and that 3D hydrodynamical modelling in this direction is only at its infant stage, so far with no simulations of envelope ejections from a compact object embedded in the envelope of a massive star.
5.2. GW151226
GW151226 was reported to consist of a pair of BHs of masses 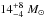 and
and 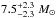 and is also located at a redshift of z ≃ 0.09 (Abbott et al. 2016a). It is notable that its total mass is about three times lower than the spectacular first event GW150914. Thus the formation of GW151226 cannot be explained by the CHE/MOB scenario (which in addition to BH masses ≳25M⊙ also predicts a mass ratio very close to unity). From the simple energy budget analysis presented here, the CE formation channel could work for GW151226 in both a low- and high-metallicity environment (see Fig. 2), assuming that the 14M⊙ BH formed first. In the (somewhat unlikely) case that the 7.5M⊙ BH formed first, however, an origin in a high-metallicity environment seems difficult. According to Fig. 2, we can see that such a BH can only remove the CE of a Z = ZMW star when the star has an initial mass lower than about 40M⊙ (and only when it is evolved to near its very maximum radial extent on the giant branch), which means that the mass of the collapsing core would be lower than about 18M⊙, according to our models. Hence, even modest mass loss of ≳4M⊙ in the BH formation process would rule out this possibility, depending on the exact masses of the two BHs.
and is also located at a redshift of z ≃ 0.09 (Abbott et al. 2016a). It is notable that its total mass is about three times lower than the spectacular first event GW150914. Thus the formation of GW151226 cannot be explained by the CHE/MOB scenario (which in addition to BH masses ≳25M⊙ also predicts a mass ratio very close to unity). From the simple energy budget analysis presented here, the CE formation channel could work for GW151226 in both a low- and high-metallicity environment (see Fig. 2), assuming that the 14M⊙ BH formed first. In the (somewhat unlikely) case that the 7.5M⊙ BH formed first, however, an origin in a high-metallicity environment seems difficult. According to Fig. 2, we can see that such a BH can only remove the CE of a Z = ZMW star when the star has an initial mass lower than about 40M⊙ (and only when it is evolved to near its very maximum radial extent on the giant branch), which means that the mass of the collapsing core would be lower than about 18M⊙, according to our models. Hence, even modest mass loss of ≳4M⊙ in the BH formation process would rule out this possibility, depending on the exact masses of the two BHs.
5.3. Comparison to other work
In a recent paper by Belczynski et al. (2016), a CE formation channel was put forward for GW150914. While the various aspects of CE evolution discussed here in this paper are generic, comparing our results directly with those of Belczynski et al. (2016) is difficult since few details of their applied stellar models are given. From their model (see their Fig. 1), we can deduce that the suggested 82.2M⊙ donor star (Z ≃ Z⊙/ 30) has a radius of about 1700R⊙ at the onset of the CE phase with a 35.1M⊙ BH accretor. From our computed stellar structure models of an 80.0M⊙ star, we find λ ~ 0.01 (in agreement with Dewi & Tauris 2001), which yields | Eenv | ≃ 5 × 1050erg. However, after the in-spiral of the BH, the orbital separation in the Belczynski et al. model is quoted to be af = 43.8R⊙, which corresponds to a released orbital energy of | Eorb | ≃ 5.4 × 1049erg, that is, about 10 times too small to eject the envelope. However, such an apparent discrepancy could be an artefact of simply applying different convective core-overshooting parameters, and given the relatively low stellar core masses in their illustrated scenario, we suspect that Belczynski et al. (2016) applied stellar models with small convective core overshooting. Alternatively, it is possible that they included released accretion energy as a main energy source in their budget, although this aspect is not discussed in their paper.
5.4. BH-BH formation: stability of the first RLO
Following the CE scenario for producing BH-BH binaries, we can also make predictions for the dynamical stability of the first mass-transfer phase (RLO). To lower the binding energy of the envelope during the CE phase and thus enhance the chance for surviving the in-spiral of the BH, the pre-CE binary system must be wide to secure an evolved donor star (Figs. 1 and 2). To fulfil the requirement of a wide pre-CE system, this means that the first mass-transfer phase from the primary star (the progenitor of the first-formed BH) to the (less evolved) secondary star must be dynamically stable or, in case of unstable RLO (see also Sect. 4.7), the orbital separation is only slightly reduced. Otherwise, if this first mass-transfer phase would form an effective CE, it would either reduce the orbital size drastically or result in an early coalescence, thus preventing the subsequent formation of a BH-BH system. However, the stability of mass transfer in massive binaries with non-degenerate stars is largely unexplored in the literature. In particular, we question to which extent binary systems would be dynamically stable at this stage since the timescale of the mass transfer is often much shorter than the thermal timescale of the accreting star. As a possible result, the accreting star may expand, initiate mass loss through the second Lagrangian point and result in a CE. It cannot be ruled out therefore that a significant fraction of the systems would merge already in this early phase. However, further investigations are needed in this direction before any conclusion can be drawn.
6. Conclusions
We have analysed the CE ejection process in post-HMXB systems. From our investigation of stellar structures and energy budget considerations, we find that CE evolution, in addition to producing double WD and double NS binaries, may in principle also produce massive BH-BH systems with individual BH component masses of up to 60M⊙ (beyond which point a pair-instability SN is expected to lead to complete disruption of the progenitor star and not leaving behind any compact remnant, cf. Heger & Woosley 2002; Chatzopoulos & Wheeler 2012). The potential for successful CE ejection is particularly good for donor stars evolved to giants beyond the Hertzsprung gap.
We find that the change in the λ-parameter with stellar radius is significantly more important than changes caused by different stellar masses or metallicities (although some mass dependence is noted on the giant branch). The associated binding energies of the stellar envelopes increase with stellar mass (independent of evolutionary status), but are generally independent of metallicity (except for massive high-metallicity stars that evolve to become LBV stars). The convective core-overshooting parameter applied in stellar models, δOV, however, can strongly affect the calculated values of λ and Ebind (up to a factor of 10).
Based on our detailed analysis of the evolution of the interior structure of massive stars, it is evident that the difficulty in determining the precise bifurcation point (core boundary) remains the key uncertain aspect of the outcome of CE evolution (Tauris & Dewi 2001). Whereas the hydrogen abundance (XH = 0.10, Dewi & Tauris 2000) and the maximum-compression point criteria (Ivanova 2011) roughly yield similar locations for the core boundary, it remains uncertain if the in-spiral continues significantly below the bottom of the convection zone in the envelope. Until future 3D hydrodynamical simulations will succeed in ejecting the CE of massive stars, the estimated LIGO detection rates from population synthesis of merging BH-BH and NS-NS binaries (Abadie et al. 2010) will remain highly uncertain, not to mention all other aspects of binary evolution and interactions not investigated in this work.
We explored the importance of additional energy sources to help ejecting the CE. We confirm that recombination energy makes an important contribution to the total internal energy in low- and intermediate-mass stars. However, for massive (>30M⊙) stars the contribution may be less than 1%, depending on the core boundary. Hence, liberated recombination energy may not play any significant role in forming BH-BH binaries through CE evolution.
The release of accretion energy, on the other hand, from an in-spiralling compact object (BH or NS), can be significant for the energy budget and may help to facilitate the CE ejection process. However, models of time-dependent energy transport in the convective envelope are needed to quantify this effect.
Although a deep in-spiral of a BH is possible in massive binaries that may eject their envelope, the exposed core will most likely terminate its evolution, and collapse before GWR would cause such post-CE binaries to coalesce. Hence, once a post-CE system is formed composed of a helium (Wolf-Rayet) star and a BH, the outcome is expected to be a BH-BH binary.
While it is difficult to estimate the outcome of CE evolution with high confidence, the arguments presented in this paper taken together suggest that it seems realistic to expect that production of BH-BH binaries are possible through the CE formation channel, leading to events such as GW150914 and GW151226.
In Fig. 2 the limiting mass for the same model is slightly higher (about 6M⊙) because of differences in estimating the core radius. In Fig. 2 we applied naked (post-CE) helium star models (i.e. with zero pressure at their surfaces), whereas Fig. 3 probes the interior structure before envelope removal (i.e. with a non-zero surface pressure at a given point from the surrounding outer layers). Hence, in the latter case the in-spiralling object can penetrate deeper for a given core mass coordinate, thereby releasing more orbital energy and thus slightly facilitating envelope ejection. See also Sect. 4.6 on extended envelopes of helium stars.
Acknowledgments
M.U.K. acknowledges financial support by the DFG Grant: TA 964/1-1 awarded to T.M.T. D.Sz. was supported by GAČR grant 14-02385S.
References
- Abadie, J., Abbott, B. P., Abbott, R., et al. 2010, Class. Quant.Grav., 27, 173001 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Banerjee, S., Baumgardt, H., & Kroupa, P. 2010, MNRAS, 402, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Bours, M. C. P., Marsh, T. R., Parsons, S. G., et al. 2014, MNRAS, 438, 3399 [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, W. R., Kilic, M., Hermes, J. J., et al. 2011, ApJ, 737, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Burgay, M., D’Amico, N., Possenti, A., et al. 2003, Nature, 426, 531 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatzopoulos, E., & Wheeler, J. C. 2012, ApJ, 748, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, P. J., Kolb, U., & Knigge, C. 2012, MNRAS, 419, 287 [NASA ADS] [CrossRef] [Google Scholar]
- de Kool, M. 1990, ApJ, 358, 189 [NASA ADS] [CrossRef] [Google Scholar]
- de Marco, O., Passy, J., Moe, M., et al. 2011, MNRAS, 28 [Google Scholar]
- de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deinzer, W., & von Sengbusch, K. 1970, ApJ, 160, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2001, in Evolution of Binary and Multiple Star Systems, eds. P. Podsiadlowski, S. Rappaport, A. R. King, F. D’Antona, & L. Burderi , ASP Conf. Ser., 229, 255 [Google Scholar]
- Dewi, J. D. M., Pols, O. R., Savonije, G. J., & van den Heuvel, E. P. J. 2002, MNRAS, 331, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Hulse, R. A., & Taylor, J. H. 1975, ApJ, 195, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
- Ishii, M., Ueno, M., & Kato, M. 1999, PASJ, 51, 417 [NASA ADS] [Google Scholar]
- Istrate, A., Marchant, P., Tauris, T. M., et al. 2016, A&A, 595, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanova, N. 2011, ApJ, 730, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., & Chaichenets, S. 2011, ApJ, 731, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Belczynski, K., Kalogera, V., Rasio, F. A., & Taam, R. E. 2003, ApJ, 592, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Ivanova, N., Justham, S., & Podsiadlowski, P. 2015, MNRAS, 447, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Hamann, W.-R., Lennon, M., et al. 1994, A&A, 290, 819 [NASA ADS] [Google Scholar]
- Livio, M., & Soker, N. 1988, ApJ, 329, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, Jr., J. C., Proulx, Z. F., Dooley, K. L., et al. 2006, ApJ, 640, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Loveridge, A. J., van der Sluys, M. V., & Kalogera, V. 2011, ApJ, 743, 49 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., & Ramirez-Ruiz, E. 2015a, ApJ, 803, 41 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., & Ramirez-Ruiz, E. 2015b, ApJ, 798, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, I., & de Mink, S. E. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T., & Moriya, T. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, J. G., Stovall, K., Freire, P. C. C., et al. 2015, ApJ, 812, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Mennekens, N., & Vanbeveren, D. 2014, A&A, 564, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
- Nandez, J. L. A., Ivanova, N., & Lombardi, Jr., J. C. 2014, ApJ, 786, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Nandez, J. L. A., Ivanova, N., & Lombardi, J. C. 2015, MNRAS, 450, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Verbunt, F., Yungelson, L. R., & Portegies Zwart, S. F. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
- Ohlmann, S. T., Röpke, F. K., Pakmor, R., & Springel, V. 2016, ApJ, 816, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2016, MNRAS, submitted [arXiv:1606.04921] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, P. 2001, in Evolution of Binary and Multiple Star Systems, eds. P. Podsiadlowski, S. Rappaport, A. R. King, F. D’Antona, & L. Burderi, ASP Conf. Ser., 229, 239 [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2000, ApJ, 528, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Chatterjee, S., & Rasio, F. A. 2016, Phys. Rev. D, 93, 084029 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sigurdsson, S., & Hernquist, L. 1993, Nature, 364, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Vink, J. S., & de Koter, A. 2004, ApJ, 615, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Soker, N. 2004, New Astron., 9, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2015, ApJ, 800, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2016, New Astron. Rev., 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 2001, ApJ, 548, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E., & Sandquist, E. L. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & Dewi, J. D. M. 2001, A&A, 369, 170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauris, T. M., & Savonije, G. J. 1999, A&A, 350, 928 [NASA ADS] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2006, Formation and evolution of compact stellar X-ray sources (Cambridge University Press), 623 [Google Scholar]
- Tauris, T. M., Langer, N., & Podsiadlowski, P. 2015, MNRAS, 451, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmer, A., & Fitzpatrick, E. L. 1998, ApJ, 504, 200 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1994, in Saas-Fee Advanced Course 22: Interacting Binaries, eds. S. N. Shore, M. Livio, E. P. J. van den Heuvel, H. Nussbaumer, & A. Orr, 263 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., & Tauris, T. M. 2003, MNRAS, 342, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., Jia, K., & Li, X.-D. 2016, RA&A, 16, 009 [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Binding energy of the envelope, | Ebind | (lower panel), and its associated λ-value (upper panel), as a function of total stellar radius for two sets of models with Z = Z⊙/ 50 (full lines, crosses) and Z = ZMW (dashed lines, squares). Independent of mass and metallicity, and before reaching the giant stages (R ≲ 1000R⊙), the λ-values almost follow a power law with an exponent between −2/3 and −1 (upper and lower grey lines, respectively). The exceptions are stars with initial masses ≳60M⊙ at Z = ZMW (dashed blue line), which either become LBV stars, see Sect. 4.7, or have their envelopes stripped by enhanced wind-mass loss. The absolute binding energies of the 8M⊙ stars drop below the plotted range, down to approximately 2.7 × 1047erg and 7.3 × 1046erg for Z = Z⊙/ 50 and Z = ZMW, respectively. |
| In the text | |
 |
Fig. 2 Minimum mass of the in-spiralling object, MX,min which is needed to expel the envelope during a CE evolution with α = 1, for a given donor star radius as indicated by the coloured lines, as a function of ZAMS mass of the donor star, MZAMS for Z = Z⊙/ 50 (upper panel) and Z = ZMW (lower panel). Rmax is the maximum radial extent during the stellar evolution. The grey band between 1.17 and 1.56M⊙ indicates masses of NSs observed in double NS systems (Martinez et al. 2015). |
| In the text | |
 |
Fig. 3 Energy budget of the in-spiral process for the 88M⊙ donor star model with Z = Z⊙/ 50 at two different evolutionary epochs: at the beginning of the Hertzsprung gap, R = 194R⊙ (upper panel), and when the star reaches its maximum extent as a giant star, R = 3530R⊙ (lower panel). The two solid lines mark the integrated binding energy of the material between the given mass coordinate and the surface. The green line (Ebind) includes the total energy (internal and gravitational binding energy, cf. Eq. (1)), while the red line (Egrav) only considers the gravitational binding energy. The six dashed curves represent the released orbital energy, ΔEorb of an in-spiralling object with a given mass between 1.3 and 80M⊙ (cf. mass values in the legend). For the values of ΔEorb, it is assumed that the in-spiral stops just when the remaining star would fill its Roche lobe. The vertical dotted line indicates the core boundary according to the XH = 0.10 criterion (cf. Sect. 2), and the arrow marks the location of the maximum-compression point (cf. Sect. 4.1). The hatched regions shown at the top indicate convective layers. The black and grey dots mark the crossings when Ebind = ΔEorb, see Sect. 3.3 for details. |
| In the text | |
 |
Fig. 4 Lower panel of Fig. 3 in radius coordinates. The additional blue solid line indicates where 50% of the internal energy is included in the calculated binding energy of the envelope. |
| In the text | |
 |
Fig. 5 Recombination energy in the envelope as a function of ZAMS mass. The plot shows the maximum contribution of recombination energy (from H, He and H2) to the total internal energy (U) obtained during the evolution of the stars. These maximum values are always reached when the stars are near their largest radial expansion as giants. The red arrows are for Z = ZMW and the blue ones for Z = Z⊙/ 50. The green arrows are also calculated for our Z = Z⊙/ 50 models, but assume a larger remaining core that includes 1M⊙ of hydrogen. |
| In the text | |
 |
Fig. 6 Mapping of pre-CE to post-CE orbital separations as done in population synthesis (see Sect. 4.4) when applying the (α,λ)-formalism. The donor is assumed to be our 88M⊙ (Z = Z⊙/ 50) star. The in-spiralling objects (BHs) have masses of between 5 and 80M⊙. Below the dashed GW lines, the post-CE systems will merge within a Hubble time. Below the dotted CE lines, the in-spiral continues to the core of the donor star and leads to coalescence (i.e. the relaxed He-core fills its Roche-lobe, cf. Sect. 4.6, and the binary will not survive). In the upper panel, the different colours mark the mass of the in-spiralling object (using α = 1); in the lower panel, they represent different values of α (for a fixed value of MX = 35M⊙). The dark green (upper) line in the lower panel was calculated for α = 1 and an additional accretion energy of 5 × 1049erg, see Sect. 4.2.3. The hatched regions indicate systems that are expected to successfully produce LIGO sources. The solid dots mark the models shown in Figs. 3 and 4. |
| In the text | |
 |
Fig. 7 Final fate of a post-CE binary system composed of a naked helium core and a BH as a function of orbital separation after envelope ejection. The chosen donor star model is that of the 88M⊙ star (Z = Z⊙/ 50) at its maximum extent as a giant, cf. Figs. 3 (lower panel) and 4. The mass of the exposed helium core is M = 52.35M⊙ and the BH is assumed to have a mass of 30M⊙. The blue line (GWR) represents the merger time due to gravitational-wave radiation, the orange line (SN) represents the remaining lifetime of the core until it collapses, and the red dotted line (Wind) represents the timescale (a/ȧwind) of orbital widening due to stellar wind mass loss. The yellow shaded region marks the core region (XH< 0.10). See Sect. 4.5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


