| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629658 | |
| Published online | 21 November 2016 | |
Constraints on the dark energy dipole from large-scale structures
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza de San Juan, 1, planta 2, 44001 Teruel, Spain
e-mail: ghurier@cefca.es
Received: 6 September 2016
Accepted: 28 October 2016
The high-significance measurement of large-scale structure signals enables testing the isotropy of the Universe. The measurement of cosmological parameters through the large-scale distribution of matter is now a mature domain. This approach is mainly limited by our knowledge of astrophysical processes that are used to observe the large-scale structure. However, when we assume that these astrophysical processes are the same across the Universe, then it is possible to tightly constrain the isotropy of cosmological parameters across the sky. Particularly the X-SZ cross-correlation has been shown to be a probe of the large scale structures that has a high signal-to-noise ratio and low bias. For this analysis, we used a localized measurement of the X-SZ cross-correlation as a test of the cosmological parameter isotropy. Using the scatter of the X-SZ cross-correlation across the sky, we derive cosmological constraints σ8(Ωm/ 0.28)0.34 = 0.78 ± 0.02 and tight isotropy constraints on the dark energy dipole ΔΩΛ < 0.07 at 95% confidence level.
Key words: cosmic background radiation / cosmological parameters / dark energy / large-scale structure of Universe / galaxies: clusters: intracluster medium
© ESO, 2016
1. Introduction
The cosmological principle is a pillar of current cosmological models (e.g., Λ cold dark matter, hereafter ΛCDM). It assumes that the Universe is homogeneous and isotropic at large enough scales (Dodelson 2003).
The cosmic microwave background (CMB) is consistent with statistical isotropy (Planck Collaboration XIII 2016; Planck Collaboration XVI 2016), but there are a few indications of anomalies with respect to ΛCDM prediction (see, e.g. Schwarz et al. 2016).
Some observations might imply that the Universe deviates from statistical isotropy (see Perivolaropoulos 2014, for a review). Even if the Universe seems to be isotropic at the time of the recombination, it is possible to induce late-time anisotropy for example through anisotropies in the dark energy distribution. Thus, testing the isotropy of the local Universe is a powerful probe of potential dark energy anisotropies.
Previous analyses have tested the isotropy of the Universe using the type I supernovae (SNIa) to measure the large-scale variation of the distance modulus across the sky (see, e.g., Antoniou & Perivolaropoulos 2010; Bengaly et al. 2015a; Lin et al. 2016), galaxy cluster catalogs (Bengaly et al. 2015b; de Martino et al. 2016), the local velocity flow (Kocevski & Ebeling 2006), or the X-ray background dipole (Plionis & Georgantopoulos 1999). Previous works derived ΔΩm/ Ωm < 0.43 ± 0.06 (Antoniou & Perivolaropoulos 2010). Supernovae are a powerful probe of isotropy because they enable the measurement of the Universe expansion rate toward a large number of line sight.
The isotropy of the Universe can also be tested using the large-scale structure matter field. The number of galaxy clusters in a given volume strongly depends on the cosmological parameters. There are two approaches to derive cosmological parameters from the large-scale structure distribution: (i) we can use the number count of galaxy clusters and directly compare it with the mass function (see e.g., Tinker et al. 2008) calibrated on numerical simulations; (ii) we can use correlation functions. Both approaches present advantages and drawbacks: (i) the number count is highly sensitive to the selection function and the purity of the considered sample of objects, but directly allows us to explore the mass function in the mass-redshift plane; (ii) correlation functions can be directly applied to signal maps, but they imply that we need to consider a redshift-projected signal and contamination in the maps produced by other astrophysical objects or instrumental systematic effects.
Measurement of cosmological parameters through the large-scale structure distribution is now limited by our knowledge of astrophysical processes and not by statistical uncertainties. Especially the thermal Sunyaev-Zel’dovich (tSZ) effect and the X-ray emission cross-correlation has been detected at very high signal-to-noise ratio (S/N; Hurier et al. 2015) and is less affected than autocorrelation angular power spectra obtained with other astrophysical processes and instrumental systematics. The tSZ effect produces a small spectral distortion in the blackbody spectrum of the CMB (Sunyaev & Zeldovich 1969, 1972). Its intensity is related to the integral of the pressure along the line of sight. Its spectral signature can be used to isolate this effect from other emission on the microwave and submillimeter sky.
The ionized gas in the intracluster medium also produces an X-ray emission through bremsstrahlung. This radiation is proportional to the square of the electron density.
Considering that full-sky catalogs of galaxy clusters derived from tSZ (e.g., Planck Collaboration XXVII 2016) and X-ray (e.g., Piffaretti et al. 2011) have complex selection functions that strongly vary across the sky, we chose to use tSZ and X-ray full-sky maps. The choice of using cross-correlation instead of autocorrelation is motivated because we aim to ensure a better control over systematic effects.
The paper is organized as follows: Sect. 2 briefly presents the data, then Sect. 3 describes the approach we used to perform a localized estimation of the X-SZ cross-correlation, and finally Sect. 4 presents the derived constraints on cosmological parameters and isotropy.
2. Data
We made use of a MILCA tSZ fullsky map (Hurier et al. 2013) at a resolution of 7 arcmin FWHM. This map has been obtained using Planck data (Planck Collaboration I 2016) from 100 to 857 GHz. In addition to the tSZ Compton parameter, the main residuals in these maps are radio point sources and high-redshift cosmic infrared background (CIB, Planck Collaboration XXIII 2016).
We also used the ROSAT all-sky survey (RASS) public data1, which cover 99.8% of the sky, including 97% that have an exposure time longer than 100 s (Voges et al. 1999). Then, we constructed a full-sky map of the photon count rate in the energy range 0.5−2.0 keV from each ROSAT photon event file and exposure map. Lower energy photons were not considered to reduce the impact of neutral hydrogen absorption that may induce some systematic anisotropy at large scales if not considered properly. Finally, we projected each event and the associated exposure over the sky using the HEALPix (Górski et al. 2005) pixelization scheme at a resolution of Nside = 2048.
We constructed a mask to avoid contamination by Galactic or point source emissions in Planck data. Considering that the Planck 857 GHz channel is a good tracer of the thermal dust emission, we chose to mask all regions that present an emission above 3 KCMB2 at this frequency (see Planck Collaboration IX 2014, for unit convention and conversion). We masked all sources from the Planck compact source catalog (Planck Collaboration XXVIII 2014) detected in at least one frequency with a S/N above 5. Therefore, we masked all regions with an exposure below 100 s in the RASS survey. After applying these cuts, we kept about 60% of the sky for the analysis.
3. Methodology
 |
Fig. 1 Correlation matrix of X-SZ cross spectra computed on ≃ 0.1% of the sky. |
The X-SZ cross power spectrum has been detected with a very high S/N (see Hurier et al. 2015, for more details). Such a high-S/N probe of large-scale structures allows us to perform a localized analysis to test the isotropy of the matter field and cosmological parameter.
We used HEALPix pixelization to split the sky into 768 (Nside = 8) independent sky regions that cover a sky area of roughly 7.3 × 7.3 deg (corresponding to fsky ≃ 0.13%). Then, we rejected all regions for which the average of the mask was below 40%, leaving Nreg = 416 regions with a sufficient sky coverage.
We measured the X-SZ cross power spectra in each region and corrected the power spectra for mode-mixing effects induced by partial sky coverage (Tristram et al. 2005). We computed and propagate uncertainties as presented in Hurier et al. (2015), and we modeled the X-SZ cross power spectrum through a halo-model approach as presented in Hurier et al. (2014).
From the measured cross power spectra, 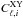 , in a sky region i, we can estimate the
, in a sky region i, we can estimate the 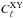 covariance matrix as
covariance matrix as ![\begin{eqnarray} {\cal C}_{\ell,\ell'} = \frac{1}{N_{\rm reg}-1}\left[\sum^{N_{\rm reg}}_i C_{\ell,i}^{\rm XY} C_{\ell',i}^{\rm XY} - \frac{1}{N_{\rm reg}} \left(\sum^{N_{\rm reg}}_i C_{\ell,i}^{\rm XY} \right) \left(\sum^{N_{\rm reg}}_i C_{\ell',i}^{\rm XY} \right) \right]. \end{eqnarray}](/articles/aa/full_html/2016/11/aa29658-16/aa29658-16-eq17.png) (1)Figure 1 presents
(1)Figure 1 presents 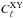 correlation matrix. We observe two separate regions in this correlation matrix. At low ℓ (ℓ < 1000), we observe a very high level of correlation between modes, and this level of correlation is a manifestation of the non-Gaussian X-SZ-X-SZ tri-spectrum (four-point correlation function). The amplitude of this correlation strongly depends on the number of objects that significantly contribute to the power. Consequently, as small sky fractions reduce this number of objects, it enhances the importance of these correlations. At high ℓ (ℓ> 1000), the covariance matrix is dominated by statistical uncertainty produced by the noise level in the MILCA and RASS full-sky map.
correlation matrix. We observe two separate regions in this correlation matrix. At low ℓ (ℓ < 1000), we observe a very high level of correlation between modes, and this level of correlation is a manifestation of the non-Gaussian X-SZ-X-SZ tri-spectrum (four-point correlation function). The amplitude of this correlation strongly depends on the number of objects that significantly contribute to the power. Consequently, as small sky fractions reduce this number of objects, it enhances the importance of these correlations. At high ℓ (ℓ> 1000), the covariance matrix is dominated by statistical uncertainty produced by the noise level in the MILCA and RASS full-sky map.
 |
Fig. 2 X-SZ cross correlation power spectrum, measured on 60% of the sky (solid red line) and measured in small sky regions, fsky < 0.13% (solid gray lines). For readability, uncertainties are not displayed in the figure (see Hurier et al. 2015, for the uncertainty level on the total X-SZ cross power spectrum). |
In Fig. 2 we present the X-SZ cross correlation power spectra measured in independent small sky regions, as demonstrated by the study of the correlation matrix (see Fig. 1). We observe a large scatter at low ℓ (<1000) that is induced by the small-number statistics of bright galaxy clusters.
4. Results
4.1. Cosmological constraints from the cosmic variance
For low-ℓ (ℓ < 1000) modes, testing the isotropy of the matter field implies verifying that the observed scatter for the X-SZ cross spectrum follows a consistent statistics with what is expected from an isotropic Universe. As this scatter depends on cosmological parameters, testing isotropy implies fitting cosmological parameters.
We performed 1000 Monte Carlo simulations of the X-SZ cross power spectra for each set of cosmological parameters. We used Poissonian realizations of the mass function (Tinker et al. 2008) and log-normal realizations of the tSZ and X-ray fluxes consistent with the scaling laws. We observed that the X-SZ-X-SZ tri-spectrum amplitude varies as 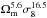 .
.
We note that using different order statistics does not allow us to break the degeneracies between cosmological parameters and astrophysical processes. When using different order statistics, we changed the weighting applied on the mass function. For the power spectrum, the mass function is weighted by YSZLX, where YSZ and LX are the integrated Compton parameter and the X-ray luminosity, respectively. For the X-SZ-X-SZ tri-spectrum, the mass function is weighted by 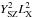 . Thus, we are sensitive to different regions of the mass function in the mass-redshift plane that have different cosmological parameter dependencies. Consequently, the degeneracies between cosmological and astrophysical parameters are near invariant for power-spectra, bi-spectra, and tri-spectra analyses.
. Thus, we are sensitive to different regions of the mass function in the mass-redshift plane that have different cosmological parameter dependencies. Consequently, the degeneracies between cosmological and astrophysical parameters are near invariant for power-spectra, bi-spectra, and tri-spectra analyses.
However, as power-spectra, bi-spectra, and tri-spectra analyses probe different regions of the mass function, they allow us to test the consistency of the best-fitting model for different regions of the mass-redshift plane. In the present case, the X-SZ-X-SZ tri-spectra (measured through the scatter of the X-SZ power-spectra across the sky) leads to σ8(Ωm/ 0.28)0.34 = 0.78 ± 0.02. Similarly to previous tSZ and X-ray analyses, the uncertainties are dominated by the uncertainties over the relation between the mass of the galaxy clusters, tSZ, and X-ray fluxes. These constraints are dominated by objects at low redshift (z < 0.5) and with high mass (M500 ≃ 1015M⊙). This constraint is consistent with previous findings that focused on low-z high-mass galaxy clusters (Planck Collaboration XX 2014).
4.2. Constraints on the dark energy dipole
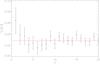 |
Fig. 3 X-SZ cross-correlation amplitude, AXSZ, power spectrum. The black sample presents the measured power spectrum from MILCA and RASS full-sky maps, the red line shows the prediction when isotropy is satisfied. |
For high ℓ (ℓ > 1000), we tested the isotropy of the cosmological parameters derived from the 416 individual regions on the sky. The X-SZ power-spectrum amplitude, AXSZ, strongly depends on cosmological parameters, 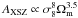 , but the shape of the power spectrum is only marginally affected by cosmology. Thus, we used the best-fitting cosmology found in Hurier et al. (2015) to predict the X-SZ cross power spectrum. For 1000 < ℓ < 2000, we computed AXSZ in each region of the sky through a linear fit of the measured X-SZ cross power spectra (presented in Fig. 2) with the Hurier et al. (2015) X-SZ power spectrum prediction. Consequently, we derived a full-sky map of AXSZ in Healpix Nside = 8 pixellization. From this map, we computed the AXSZ angular power spectrum and corrected it for partial sky coverage effects.
, but the shape of the power spectrum is only marginally affected by cosmology. Thus, we used the best-fitting cosmology found in Hurier et al. (2015) to predict the X-SZ cross power spectrum. For 1000 < ℓ < 2000, we computed AXSZ in each region of the sky through a linear fit of the measured X-SZ cross power spectra (presented in Fig. 2) with the Hurier et al. (2015) X-SZ power spectrum prediction. Consequently, we derived a full-sky map of AXSZ in Healpix Nside = 8 pixellization. From this map, we computed the AXSZ angular power spectrum and corrected it for partial sky coverage effects.
In Fig. 3 we present the power spectrum of AXSZ up to ℓ = 20. When isotropy is satisfied, all the fluctuations we should observe in the AXSZ map should be due to noise and cosmic variance, and should be uncorrelated between independent regions of the sky. Consequently, in the isotropic situation we expect to observe white noise. The dipole of AXSZ is consistent with isotropy at 1.5σ. We observe that all modes up to ℓ = 20 are consistent with isotropy for the large-scale structure matter distribution.
The AXSZ power spectrum can be interpreted as a measurement of the isotropy of the Universe. Considering that the CMB shows that the matter distribution is isotropic at z ≃ 1100, the most natural solution for interpreting an eventual isotropic behavior of the large-scale structure at low-z is through an anisotropic growth factor induced by large-scale dark energy anisotropies. Consequently, we translate our constraints on the AXSZ dipole into constraints on the dark energy large-scale anisotropies.
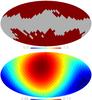 |
Fig. 4 Top panel: footprint of the sky regions used (in red) and rejected (in gray) from the analysis. Bottom panel: best-fitting dark energy dipole in Galactic coordinates. |
In Fig. 4 we present the distribution on the sky of the 416 regions used in the analysis (top panel) and the best-fitting ΩΛ dipole (bottom panel). To facilitate visualization, we display the full-sky best-fitting dipole. The maximum of this dipole is found in the direction (l,b) = (22.5°,24.6°) with a significance of 1.5σ. Considering that the best-fitting dipole maximum is oriented near the Galactic center, we cannot exclude some residual foreground bias in the tSZ MILCA map. This dipole is also oriented toward regions masked by our cuts on the Galactic thermal dust emission, thus its orientation has to be considered carefully for potential residual bias and its very low level of significance. Interpreted as an upper limit, we have ΔΩΛ< 0.07 at 95% confidence level, with ΔΩΛ being the dipole amplitude.
5. Discussion and conclusion
We have demonstrated that the measurement of a large-scale structure power-spectrum can be achieved on a small sky fraction (fsky< 0.13%) that is limited by cosmic variance up to ℓ = 1000.
We showed that the cosmic-variance-dominated part of the SZ-X power spectrum covariance matrix can be used to set cosmological constraints with the same accuracy level than the SZ-X or SZ power spectra. However, owing to the similar degeneracies between cosmological parameters and astrophysical processes for the X-SZ power spectrum and the X-SZ-X-SZ tri-spectrum, such cosmological constraints do not allow us to break degeneracies between cosmology and astrophysical processes. The derived constraints confirm previous results derived from galaxy number counts (e.g., Planck Collaboration XX 2014) and power spectra (e.g., Planck Collaboration XXII 2016; Hurier et al. 2015).
We also present a tight constraint on the dark energy dipole in the local Universe (z< 1), implying that ΩΛ does not vary across the sky by more than 10% at 95% confidence level. These constraints are competitive compared to those derived from the
study of the distance modulus variation through SNIa (Antoniou & Perivolaropoulos 2010; Lin et al. 2016).
References
- Antoniou, I., & Perivolaropoulos, L. 2010, J. Cosmol. Astropart. Phys., 12, 012 [Google Scholar]
- Bengaly, Jr., C. A. P., Bernui, A., & Alcaniz, J. S. 2015a, ApJ, 808, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bengaly, Jr., C. A. P., Bernui, A., Alcaniz, J. S., & Ferreira, I. S. 2015b, ArXiv e-prints [arXiv:1511.09414] [Google Scholar]
- de Martino, I., Martins, C. J. A. P., Ebeling, H., & Kocevski, D. 2016, Phys. Rev. D, 94, 083008 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S. 2003, Modern cosmology (Amsterdam: Academic Press) [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Aghanim, N., & Douspis, M. 2014, A&A, 568, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Douspis, M., Aghanim, N., et al. 2015, A&A, 576, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kocevski, D. D., & Ebeling, H. 2006, ApJ, 645, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H.-N., Wang, S., Chang, Z., & Li, X. 2016, MNRAS, 456, 1881 [NASA ADS] [CrossRef] [Google Scholar]
- Perivolaropoulos, L. 2014, Galaxies, 2, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVIII. 2014, A&A, 571, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2016, A&A, 594, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2016, A&A, 594, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plionis, M., & Georgantopoulos, I. 1999, MNRAS, 306, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, D. J., Copi, C. J., Huterer, D., & Starkman, G. D. 2016, Classical and Quantum Gravity, 33, 184001 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1969, Nature, 223, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astroph. Space Phys., 4, 173 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J. F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Correlation matrix of X-SZ cross spectra computed on ≃ 0.1% of the sky. |
| In the text | |
 |
Fig. 2 X-SZ cross correlation power spectrum, measured on 60% of the sky (solid red line) and measured in small sky regions, fsky < 0.13% (solid gray lines). For readability, uncertainties are not displayed in the figure (see Hurier et al. 2015, for the uncertainty level on the total X-SZ cross power spectrum). |
| In the text | |
 |
Fig. 3 X-SZ cross-correlation amplitude, AXSZ, power spectrum. The black sample presents the measured power spectrum from MILCA and RASS full-sky maps, the red line shows the prediction when isotropy is satisfied. |
| In the text | |
 |
Fig. 4 Top panel: footprint of the sky regions used (in red) and rejected (in gray) from the analysis. Bottom panel: best-fitting dark energy dipole in Galactic coordinates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


