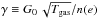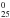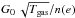| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 27 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628819 | |
| Published online | 25 October 2016 | |
Hydrogenation and dehydrogenation of interstellar PAHs: Spectral characteristics and H2 formation
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: heandrew@strw.leidenuniv.nl
Received: 29 April 2016
Accepted: 24 June 2016
Context. We have modelled the abundance distribution and IR emission of the first 3 members of the coronene family in the north-west photodissociation region of the well-studied reflection nebulae NGC 7023.
Aims. Our aim was 3-fold: i) analyze the distribution of abundances; (ii) examine the spectral footprints from the hydrogenation state of polycyclic aromatic hydrocarbons (PAHs); and (iii) assess the role of PAHs in the formation of H2 in photodissociation regions.
Methods. To model the physical conditions inside the cloud, we used the Meudon PDR Code, and we gave this as input to our kinetic model. We used specific molecular properties for each PAH, based on the latest data available at the present time. We considered the loss of an H atom or an H2 molecule as multiphoton processes, and we worked under the premise that PAHs with extra H atoms can form H2 through an Eley-Rideal abstraction mechanism.
Results. In terms of abundances, we can distinguish clear differences with PAH size. The smallest PAH, coronene (C24H12), is found to be easily destroyed down to the complete loss of all of its H atoms. The largest species circumcircumcoronene (C96H24), is found in its normal hydrogenated state. The intermediate size molecule, circumcoronene (C54H18), shows an intermediate behaviour with respect to the other two, where partial dehydrogenation is observed inside the cloud. Regarding spectral variations, we find that the emission spectra in NGC 7023 are dominated by the variation in the ionization of the dominant hydrogenation state of each species at each point inside the cloud. It is difficult to “catch” the effect of dehydrogenation in the emitted PAH spectra since, for any conditions, only PAHs within a narrow size range will be susceptible to dehydrogenation, being quickly stripped off of all H atoms (and may isomerize to cages or fullerenes). The 3 μm region is the most sensitive one towards the hydrogenation level of PAHs.
Conclusions. Based on our results, we conclude that PAHs with extra H atoms are not the carriers of the 3.4 μm band observed in NGC 7023, since these species are only found in very benign environments. Finally, concerning the role of PAHs in the formation of H2 in photodissociation regions, we find that H2 abstraction from PAHs with extra H atoms is an inefficient process compared to grains. Instead, we propose that photodissociation of PAHs of small-to-intermediate sizes could contribute to H2 formation in PDR surfaces, but they cannot account by themselves for the inferred high H2 formation rates in these regions.
Key words: astrochemistry / photon-dominated region (PDR) / ISM: molecules / infrared: ISM
© ESO, 2016
1. Introduction
Polycyclic aromatic hydrocarbons (PAHs) are a set of molecules consisting of hexagonal aromatic carbon rings, with hydrogen atoms attached at the periphery. Upon absorption of high energy photons they get electronically excited, rapidly redistribute the absorbed energy among all available vibrational states, and relax, either by fragmenting or emitting IR photons through a fluorescence process (Léger & Puget 1984; Allamandola et al. 1989). Their presence in space is now widely accepted as being the carriers of the strong emission bands at 3.3, 6.2, 7.7, 11.3 and 12.7 μm, observed in the mid-IR spectra of UV-rich environments such as photodissociation regions (PDRs). PDRs are then considered to be the best laboratories to study PAH emission since they are the UV illuminated surfaces of molecular clouds, where the PAH emission is found to be the strongest.
Observational studies on PDRs using the ISO and Spitzer space telescopes have examined the emission of PAHs in the mid-IR range (Bregman et al. 1989; Berné et al. 2007; Joblin et al. 2010; Boersma et al. 2012, among others). The combination of these studies with theoretical calculations on the IR emission of different PAH species, has allowed a characterization of the emission of PAHs as a whole (Rapacioli et al. 2005; Berné et al. 2007; Rosenberg et al. 2011; Boersma et al. 2013, 2014, 2015; Andrews et al. 2015). Hundreds of theoretical (and experimental) spectra of PAHs have been compiled in the NASA Ames PAH IR Spectroscopic Database (PAHdb1; Bauschlicher et al. 2010; Boersma et al. 2014) and the Cagliari PAH Database2 (Malloci et al. 2007). The use of such databases has provided great insight on how different classes of PAHs can leave particular footprints in the emission at mid-IR wavelengths. In this regard, spectral variations due to changes in the ionization state of PAH molecules have been well characterized (e.g., Rosenberg et al. 2011; Boersma et al. 2014). Indeed, PAH band ratios such as the 6.2/11.3, 7.7/11.3 and 11.0/11.3 are now used as tracers of the ionization state of the emitting population of PAHs (Galliano et al. 2008; Fleming et al. 2010; Boersma et al. 2014). Likewise, astronomical models have long pointed out the potential importance of hydrogenation for the IR emission spectra (Schutte et al. 1993). Specifically, the 3.4 μm band has been interpreted as due to PAHs with extra H atoms – the so-called, superhydrogenated PAHs (Schutte et al. 1993) – in the emitting zones (Sandford et al. 2013; Bernstein et al. 1996) but other explanations for this band have also been put forward, e.g., methylated PAHs and overtones of the 3.3 μm CH stretching mode (Barker et al. 1987; Geballe et al. 1989; Joblin et al. 1996). Observationally, the ratio of the 3.4 to the 3.3 μm band is known to vary with distance to the illuminating star (Joblin et al. 1996; Pilleri et al. 2015) and this may provide a test for these assignments.
Over the years, even more sophisticated models have been developed to calculate the IR emission spectra, and to aid in the interpretation of the observed spectral variations. Bakes et al. (2001) developed a model to describe the PAH emission under the physical conditions in the Orion bar, using the latest available data (at that time) on symmetric condensed PAHs up to 54 carbon atoms. That work was the first attempt to study the emission of specific PAH molecules, focusing on the spectral variations produced by changes in the charge distribution of the species. However in PDR environments, PAHs are expected to undergo not only changes in their charge states, but also experience further processing due to the interaction with high energy photons. Allain et al. (1996) developed a kinetic model that considered photodissociation of PAHs. They used generic estimates for the rates of direct H-loss, H2-loss and acetylene-loss, and found that small PAHs (<50 carbon atoms) would be destroyed in highly UV illuminated environments. Based on the available experimental data at that time, Le Page et al. (2001, 2003) modelled the ionization and hydrogenation of generic PAHs (up to 200 carbon atoms) in diffuse clouds in terms of abundances only. Montillaud et al. (2013) built a kinetic model for 4 PAHs up to the size of circumcircumcoronene (96 carbon atoms), and modelled the spatial abundance evolution of these species in the north-west NW PDR of NGC 7023. They only considered neutral and cationic species, and hydrogenation states ranging from the pure carbon clusters up to the parent molecule plus 1 extra hydrogen atom. Their novelty was to admit multiphoton events to describe the photodissociation rates. They showed that multiphoton events can cause the fragmentation of large species, that otherwise would never fragment due to large energies required for such processing.
PAH processing can also leave its impression on the environment. In particular, it has been suggested that the H2 formation rate may be affected by the presence of PAHs, as observations of PDRs have revealed H2 formation rates of up to 10-16 cm3/s (Habart et al. 2004), that well exceeds the accepted value for diffuse clouds (3 × 10-17 cm3/s; Jura 1975; Gry et al. 2002). For the diffuse medium, H2 is generally thought to form through surface reactions on dust grains (Hollenbach & Salpeter 1971). Detailed studies have shown that different routes for H2 formation on dust grains are effective in different temperature ranges (e.g., Cuppen & Herbst 2005; Le Bourlot et al. 2012; Bron et al. 2014). While Langmuir Hinshelwood reactions – where two physisorbed mobile H atoms interact and desorb as H2 – have been found to be efficient on grains at temperatures below 20 K (e.g., Pirronello et al. 1997, 1999; Katz et al. 1999), surface reactions involving chemisorbed H atoms in an Eley-Rideal fashion – where a free H atom interacts with a chemisorbed H atom, and desorb as H2 – have been found to be efficient at higher temperatures (e.g., Duley 1996; Habart et al. 2004; Le Bourlot et al. 2012). Surface reactions on PAHs have been proposed as an effective alternative at intermediate temperatures. This is also supported by observational correlations between H2 and PAH emission in PDRs (Habart et al. 2003, 2004). Experimental and theoretical studies on neutral PAHs with extra H atoms suggest PAHs could effectively form H2 through Eley-Rideal abstractions (Bauschlicher 1998; Rauls & Hornekær 2008; Thrower et al. 2011; Mennella et al. 2012). At the same time, PAHs could also contribute to the H2 budget through photodissociation, where H2-loss competes with H-loss, the main fragmentation channel after photon excitation (e.g., Jochims et al. 1994; Ling et al. 1995). Boschman et al. (2015) built a kinetic model based on the coronene molecule (24 carbon atoms), to study the role of PAHs in the formation of H2 in PDRs. They found that a small PAH like coronene would not form H2 through surface reactions, but mainly through direct loss (i.e., photodissociation). It is of interest then to compare these processes in order to assess the role of PAHs in the formation of H2 in PDRs, and describe how these contributions depend on PAH size.
In this work, we model the abundance distribution of PAHs under the physical conditions expected in a prototypical PDR as the NW PDR of NGC 7023. Our aim is to study the variations in the hydrogenation and ionization state of each species, not only in terms of abundances, but also in terms of their emitted spectra. Extending on previous studies, we are able to make use of the greater availability of theoretical and experimental data on specific PAH species. We focus on the study of PAHs of different sizes that are expected to be relevant in the ISM. Thus, here we intend to extend the work of Bakes et al. (2001) by modelling the PAH emission, taking into account also the hydrogenation degree of each species. We expect then to be able to discern the spectral footprint of the hydrogenation of PAHs. In particular, we would like to assess whether it is feasible for superhydrogenated species to be present in PDRs, and be the carriers for the 3.4 μm band whose origin is still unknown (Bernstein et al. 1996; Sandford et al. 2013). Together with this, we will explore the effectiveness of H2 formation on PAHs. For this, we justify our assumptions on the works of Thrower and coworkers, that have proposed H2 abstraction from superhydrogenated PAHs as a feasible pathway for H2 formation (Rauls & Hornekær 2008; Thrower et al. 2011). Here, we will explore this process for PAHs bigger than coronene, and we will establish how photoprocessing of PAHs can contribute to the formation of H2 in highly UV irradiated environments such as PDRs.
The present work is organized as follows: Sects. 2 and 3 present a general description of all the processes admitted in the model, and how the equations are implemented. The results are presented in Sect. 4 in terms of the variations in the ionization state and hydrogenation state of the PAHs (Sect. 4.1), the H2 formation rate from PAHs (Sect. 4.2), and the spectral variations observed in their emission (Sect. 4.3). The discussion of our results and its implications on the PAH population in the NW PDR of NGC 7023 are presented in Sect. 5.
2. Physical−chemical processes
We consider 3 molecules of increasing size within the coronene family: coronene C24H12, circumcoronene C54H18, and circumcircumcoronene C96H24. We chose these molecules since this so-called coronene family is one of the best studied (experimentally and theoretically) set of PAHs. Circumcoronene and circumcircumcoronene consist of a coronene core surrounded by one and two rings of hexagons respectively (see Fig. 1). Because of their similarity in molecular structure, their physical and spectroscopic properties show a global trend (Ricca et al. 2012). The sizes of these three species span the range of astrophysical relevant PAHs (Allamandola et al. 1989; Croiset et al. 2016). Also, given their compact structure, the coronene family is expected to be among the most stable PAHs in the ISM (Ricca et al. 2012).
PAHs in our model absorb photon energies up to Emax = 13.6 eV, as expected in PDRs. All possible ionization states (given this threshold energy) are admitted in our model. In terms of hydrogenation state, we refer to the parent molecule as the molecule with a number of hydrogen atoms NH equal to  , where
, where  corresponds to 12 for coronene, 18 for circumcoronene, and 24 for circumcircumcoronene. Parent molecules will also be referred to as the molecule in the normal hydrogenated state. All molecules with
corresponds to 12 for coronene, 18 for circumcoronene, and 24 for circumcircumcoronene. Parent molecules will also be referred to as the molecule in the normal hydrogenated state. All molecules with 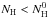 are referred to as dehydrogenated derivatives; while molecules with extra hydrogen atoms
are referred to as dehydrogenated derivatives; while molecules with extra hydrogen atoms 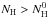 are denominated as molecules in superhydrogenated states (Schutte et al. 1993). Throughout this work we consider that the hydrogenation state of each molecule can go from being completely dehydrogenated (NH = 0) to having up to 4 additional H atoms (
are denominated as molecules in superhydrogenated states (Schutte et al. 1993). Throughout this work we consider that the hydrogenation state of each molecule can go from being completely dehydrogenated (NH = 0) to having up to 4 additional H atoms (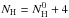 ). A discussion on this choice will be given later in the paper (see Sect. 5). In the following, we will describe all the parameters and assumptions regarding the processes considered in our model.
). A discussion on this choice will be given later in the paper (see Sect. 5). In the following, we will describe all the parameters and assumptions regarding the processes considered in our model.
 |
Fig. 1 PAHs studied in this work. From left to right: coronene (C24H12), circumcoronene (C54H18) and circumcircumcoronene (C96H24). The carbon cores are depicted in grey, while H atoms are depicted in white. |
2.1. Environment
We analyze the PAH abundance and emission spectra in the environment of the northwest NW PDR of the well-studied reflection nebula NGC 7023 (RA (J 2000.0): 21 01 32.3; Dec (J 2000.0): +68 10 25.4). Figure 2 shows the region studied in this work. The NW PDR of NGC 7023 is located ~45′′ from the exciting binary system HD 200775 (Alecian et al. 2008), and it is the brightest one in the mid-IR extending to about 60′′ (Werner et al. 2004). It is often considered as a prototype of a PDR due to its edge-on structure, which shows a clear stratification of the emitting region (Pilleri et al. 2012). The star has created a low-density cavity that is surrounded by a dense molecular cloud apparent in 12CO, 13CO, CO+ and other species (Fuente et al. 1998, 2003). The cavity edge is lined by a layer of H I (Fuente et al. 1998). The molecular cloud surface is traced by fluorescent H2 emission and by bright Extended Red Emission (Lemaire et al. 1996; Witt et al. 2006). Spitzer/IRS observations have revealed the presence of C60 in this nebula (Sellgren et al. 2010; Berné & Tielens 2012; Berné et al. 2015). While the PAH abundance decreases rapidly into the cavity, the fullerene abundance actually increases (Berné & Tielens 2012). The average size of the PAHs at the PDR front is smaller than the sizes of PAHs deeper in the PDR, as well as the PAHs in the cavity (Croiset et al. 2016). All of these effects have been attributed to photoprocessing of PAHs, driving dehydrogenation, graphene formation and isomerization to cages and fullerenes (Berné & Tielens 2012; Berné et al. 2015).
 |
Fig. 2 Composite image of the NW PDR of NGC 7023. The three-color image combines the PACS 70 μm (red), PAH emission at 6.2 μm (green, image courtesy of O. Berné), and MIPS 24 μm (blue) images. The white cross indicates the position of the star HD 200775, while the black crosses indicate the reference extension of the NW PDR (at 45′′ and 60′′ away from the star). |
Input parameters for the modelling of the NW PDR of NGC 7023 using the Meudon PDR Code.
2.2. PDR model
In order to model the physical conditions within the PDR region we use the Meudon PDR Code (version 1.4.4; Le Petit et al. 2006; Le Bourlot et al. 2012). This code has been widely used to describe the NW PDR region (see Joblin et al. 2010; Montillaud et al. 2013; Bernard-Salas et al. 2015, among others). It calculates the steady state structure, solving the radiation transfer equation and the thermal and chemical balance as a function of depth in each plane-parallel slab of the cloud.
 |
Fig. 3 Physical conditions in the NW PDR of NGC 7023. The top panels show the variation of the densities and gas temperature inside the cloud. The H I to H2 transition occurs at an AV ~ 0.9, while the C II–C I transition occurs deeper in the cloud at an AV ~ 4. The bottom panels show the physical parameters relevant for PAH hydrogenation and ionization evolution. The hydrogenation of PAHs is expected to be controlled by the ratio between the UV field intensity G0 and the density of atomic hydrogen, which in our case only varies by about 2 orders of magnitude throughout the cloud. The ionization state of the PAH population on the other hand depends on the so-called ionization parameter, |
Table 1 lists the input parameters we adopted from the literature. We consider an isobaric model following Montillaud et al. (2013). As suggested by the Meudon PDR Code guide, we consider a cloud of finite size (AVmax = 5) being illuminated by the stellar radiation on one side, and a radiation field of standard intensity on the other side. Analysis of the observed far-IR continuum intensity yields an incident UV field of G0 = 2600 Habing field units in the region of interest (Chokshi et al. 1988; Pilleri et al. 2012). We consider the flux of a binary star with both components modelled with a Kurucz stellar spectrum of 15 000 K each (Kurucz 1993; Pilleri et al. 2012). Young Owl et al. (2002) estimated a gas density of 4 × 103 cm-3 from the observed line intensities of [O I] 63 μm and [C II] 158 μm, which is in good agreement with H I observations from Fuente et al. (1998). More recent observations of the cooling lines with Herschel have led to slightly higher density estimates of the region (104 cm-3; Bernard-Salas et al. 2015). SPIRE observations of the CO rotational lines, plus an analysis of the dust continuum emission show the inhomogeneous structure of the NW PDR of NGC 7023, leading to density estimates as high as 105 cm-3 in the filaments and at large distances from the PDR front (Köhler et al. 2014). Here, we adopt a value of 2 × 104 cm-3 as the initial density (Pilleri et al. 2012).
 |
Fig. 4 Ionization potentials and electron affinities assumed in our model. Energies for coronene, circumcoronene and circumcircumcoronene derivatives are shown in black, blue and red, respectively. Given that PAHs in our model can absorb photon energies up to 13.6 eV, the highest charge state for coronene derivatives is the doubly charged one (Z = 2). Circumcoronene derivatives can be doubly ionized, and only those having more than 12 H atoms can be triply ionized (Z = 3). Circumcircumcoronene derivatives on the other hand can be triply ionized, and those having more than 22 H atoms can be found in the +4 charge state. Given the uncertainty in the electron affinities for highly negative charge states (Z< −1), we do not take into account that the more dehydrogenated molecules could also exist in these highly negative states (e.g., Z = −2 for circumcoronene derivatives). |
Figure 3 shows the calculated physical conditions. At the surface of the cloud, hydrogen is mainly in atomic form, and the temperature of the gas is a few hundred K. The conversion from H I to H2 occurs at an extinction of AV = 0.9. The density of the gas increases towards high AV reaching ~105 cm-3, while the gas temperature decreases, reaching values comparable to the dust temperature (Tgas ~ 60 K). Going into the PDR, the abundance of electrons decreases slightly due to neutralization reactions with atomic species, but from AV = 0.4 onwards, the electron abundance follows closely that of ionized carbon. Carbon is mostly in ionized form. The conversion from C II to C I occurs at an AV ~ 4. The CO abundance increases with depth reaching a maximum at AV ~ 4.5, from where it starts dissociating due to photons penetrating from the other side of the cloud.
The physics of PAHs in PDRs is controlled by two parameters: the ionization parameter, 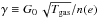 , which controls the ionization balance of PAHs (Bakes & Tielens 1994), and the hydrogenation parameter, G0/n(H), which sets their level of dehydrogenation (Tielens 2005). The variation of these parameters in the NW PDR of NGC 7023 is shown in Fig. 3. The ionization parameter decreases by several orders of magnitude into the PDR due to the attenuation of the UV radiation field, coupled with the relatively constant electron density for this isobaric model. In contrast, the variations in the hydrogenation parameter are more modest, but also show a more complex behaviour as the UV field and the hydrogen abundance decrease inwards but not in lockstep. Starting at the surface of the cloud, as AV increases, G0/n(H) decreases due to the rapid attenuation of the radiation field compared to the density, which stays relatively constant until the H I to H2 transition occurs. Once this point is reached, the decrease in the atomic hydrogen density translates into an increase of G0/n(H) to a maximum value of 1.43 at an AV ~ 2.4. After this point, G0/n(H) rapidly decreases as the UV field attenuates while the hydrogen density hardly changes.
, which controls the ionization balance of PAHs (Bakes & Tielens 1994), and the hydrogenation parameter, G0/n(H), which sets their level of dehydrogenation (Tielens 2005). The variation of these parameters in the NW PDR of NGC 7023 is shown in Fig. 3. The ionization parameter decreases by several orders of magnitude into the PDR due to the attenuation of the UV radiation field, coupled with the relatively constant electron density for this isobaric model. In contrast, the variations in the hydrogenation parameter are more modest, but also show a more complex behaviour as the UV field and the hydrogen abundance decrease inwards but not in lockstep. Starting at the surface of the cloud, as AV increases, G0/n(H) decreases due to the rapid attenuation of the radiation field compared to the density, which stays relatively constant until the H I to H2 transition occurs. Once this point is reached, the decrease in the atomic hydrogen density translates into an increase of G0/n(H) to a maximum value of 1.43 at an AV ~ 2.4. After this point, G0/n(H) rapidly decreases as the UV field attenuates while the hydrogen density hardly changes.
2.3. Molecular characteristics
When absorbing a UV photon, PAHs in our model can either ionize or dissociate through the loss of an H atom or an H2 molecule, as long as the absorbed energy is large enough to open these channels and win over IR relaxation. It is important to mention that we do not consider C nor C2H2-losses, as the kinetics of these processes are rather uncertain. Experiments have shown that, even for small PAHs, H-loss dominates over C-loss (Jochims et al. 1994). For PAHs larger than some 30 C atoms, UV photolysis proceeds by stripping off all H atoms before C-loss sets in (Zhen et al. 2014a,b; Castellanos et al., in prep.). This separates photo fragmentation into two processes where in the first step, the H-coverage of PAHs is set by a balance of UV driven H-loss and hydrogenation reactions, controlled by the hydrogenation parameter, G0/n(H). Only when all H atoms are lost, will C-loss commence and this will occur close to the star. In our analysis, we have ignored this second step. The separation of photolysis into two distinct steps simplifies the model analysis considerably, as only a limited number of species needs to be followed.
Since the internal energies required for fragmentation of large PAHs to be competitive with IR relaxation are very high (e.g., 15 eV for C54H18), we consider photodissociation as a multiphoton process where PAHs can absorb more than one photon before fully cooling down. Details on how we describe the photodissociation rates are given in Sect. 2.4.3.
Superhydrogenated species are allowed to form H2 through Eley-Rideal abstraction. We also consider attachment/recombination with electrons and H-addition reactions. H2-addition is not considered as experimental data indicates that such reactions are not important in PDRs.
In the following we will describe the molecular characteristics we consider in order to calculate the kinetic rates for all the processes taken into account in our work. The mathematical formulation of each rate will be given in Sect. 2.4.
2.3.1. Ionization potentials and electron affinities
We use specific ionization potentials (IP) and electron affinities (EA) for each of the molecules considered. Given the photon energies available (<13.6 eV), we have to consider multiple cationic states. For coronene and circumcoronene we only have to consider the anionic state (Z = −1) but for circumcircumcoronene we have to consider dianions as well (Z = −2). For the normally hydrogenated species, we have taken estimates from experiments when available (Tobita et al. 1994). If no experimental values were available, we then adopted results from quantum theory (Malloci et al. 2007, 2008), or estimates based upon conducting disk behaviour (Bakes & Tielens 1994). See more details in Appendix A.
For dehydrogenated PAHs, we have followed Malloci et al. (2008) who calculated the IPs for the even dehydrogenated states of coronene, i.e., C24H2 n where n = 0−6. Based on their estimated change of IP with hydrogenation level of the PAH, ΔIP, we assume that for each PAH in charge state Z, and with NH number of H atoms, the following relation applies: 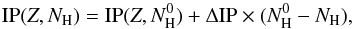 (1)where IP(Z,
(1)where IP(Z, 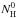 ) is the IP of the parent molecule in charge state Z, and ΔIP is constant (~ 0.1 eV; see Fig. 4). We adopt this for all hydrogenation states allowed (see more in Appendix A).
) is the IP of the parent molecule in charge state Z, and ΔIP is constant (~ 0.1 eV; see Fig. 4). We adopt this for all hydrogenation states allowed (see more in Appendix A).
Regarding EAs, the first EA of C24H12 is 0.47 eV, as derived from both theory and experiments (Duncan et al. 1999; Malloci et al. 2007). An et al. (2008) reports an EA of 1.89 eV for C24, which agrees with the ~0.1 eV variation per dehydrogenation derived from the IPs. Therefore, we also consider the relation given by Eq. (1) for the EAs (see Fig. 4).
2.3.2. Ionization yield and UV absorption cross sections
We adopt the ionization yield, Yion, derived from experiments on small PAHs from Jochims et al. (1996; see also Jochims et al. 1997). These experiments show that the ionization yield scales linearly with energy, until it reaches unity for energies above ~(IP + 9.2) eV. This describes well the ionization yield measured for coronene (Verstraete et al. 1990), supporting the fact that the variation of the ionization yield with energy appears to be rather independent of the size of the PAH.
We have adopted the UV absorption cross sections, σUV, from the Cagliari PAH database for C24H12 and C54H18 (Malloci et al. 2007). For C96H24 no information is available in the literature, and so we adopt the UV cross sections of C54H18 scaled by the number of carbon atoms of circumcircumcoronene.
For the even dehydrogenated states of coronene, we use the DFT results from Malloci et al. (2008). For the other species we use the UV absorption cross section of the molecule with the closest number of H atoms within the same ionization state. We expect this to be a good approximation, based on the analysis of Malloci et al. (2008). Even though the overall shape varies somewhat with dehydrogenation, when calculating the average photon energy absorbed in a given stellar radiation field, the absorbed average energy varies by less than 1 eV for the different hydrogenation states, being slightly higher for dehydrogenated states. Thus, we expect that this assumption will have little impact on our calculations.
2.3.3. IR cross sections and density of states
IR cross sections, 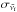 , and frequencies,
, and frequencies, 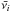 were collected either from the NASA Ames PAH Database (PAHdb; Bauschlicher et al. 2010; Boersma et al. 2014), or from our own ab initio DFT calculations, using B3LYP/4-31G (Becke 1993; Stephens et al. 1994) on Gaussian 09 (Frisch et al. 2009). In the case of dehydrogenated PAHs, several isomers with various multiplicities were calculated. To facilitate our analysis, here we always report the vibrational spectrum of the most stable isomer. Following Langhoff (1996) the vibrational frequencies were scaled by 0.958, except for the modes involving CC triple bonds. Bauschlicher & Ricca (2013) showed that B3LYP/4-31G failed to reproduce the stretching modes of the triple CC bond in C6H4. In order to compensate for this, a specific scaling factor of 0.9097 was used. This was obtained by direct comparison of the calculated frequency for the triple CC bond stretching mode of C6H4, with the experimental result published in Radziszewski et al. (1992).
were collected either from the NASA Ames PAH Database (PAHdb; Bauschlicher et al. 2010; Boersma et al. 2014), or from our own ab initio DFT calculations, using B3LYP/4-31G (Becke 1993; Stephens et al. 1994) on Gaussian 09 (Frisch et al. 2009). In the case of dehydrogenated PAHs, several isomers with various multiplicities were calculated. To facilitate our analysis, here we always report the vibrational spectrum of the most stable isomer. Following Langhoff (1996) the vibrational frequencies were scaled by 0.958, except for the modes involving CC triple bonds. Bauschlicher & Ricca (2013) showed that B3LYP/4-31G failed to reproduce the stretching modes of the triple CC bond in C6H4. In order to compensate for this, a specific scaling factor of 0.9097 was used. This was obtained by direct comparison of the calculated frequency for the triple CC bond stretching mode of C6H4, with the experimental result published in Radziszewski et al. (1992).
Tables summarizing the set of molecules for which IR spectra are available can be found in Appendix A. For the molecules for which we have the intrinsic spectra, density of vibrational states are calculated explicitly using the Beyer-Swinehart counting algorithm (Beyer & Swinehart 1973; Stein & Rabinovitch 1973). Whenever this data is not available, we consider the spectra of the molecule with the closest number of H atoms within the same ionization state.
2.4. Processes
In this section we specify the processes for each molecule, and we describe how we calculate each rate using the parameters described in Sect. 2.3.
2.4.1. Photoionization
The photoionization rate, kion, for a molecule in a given ionization state, Z, and with NH H atoms is given by: 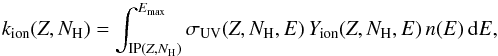 (2)where σUV(Z, NH) is the UV absorption cross section of the molecule, Yion(Z, NH) is the ionization yield, and n(E) corresponds to the flux of photons.
(2)where σUV(Z, NH) is the UV absorption cross section of the molecule, Yion(Z, NH) is the ionization yield, and n(E) corresponds to the flux of photons.
2.4.2. Electron attachment/recombination with electrons
We have adopted electron attachment and recombination rates based on the collisional rates described in Bakes & Tielens (1994), which are in good agreement with experiments for small PAHs (see Appendix A for details).
For the coronene anion formation our estimate gives a value of ~3×10-10 cm3/s, which is slightly smaller than the rate coefficient determined by Denifl et al. (2005). With respect to the measured rates for small cationic PAHs, the experimental values are smaller than our formalism would predict, but they seem to be approaching our adopted conducting disk values with increasing size (Tielens 2008).
Note that electron recombination is an excitation process and can lead to fragmentation if the dissociative channel is energetically accessible (Tobita et al. 1992; Denifl et al. 2005). Therefore, we explored direct H-loss and H2-loss as possible pathways for relaxation after recombination with an electron. However, we found that these channels are, in general, not relevant for the molecules considered. Only for coronene derivatives we find that dissociative recombination can be important for superhydrogenated cations. However, as we will see in Sect. 4, these are not relevant derivatives of coronene.
2.4.3. Photodissociation channels
Dissociation parameters considered in our work.
As mentioned before, we consider dissociation and IR emission as possible relaxation channels after the absorption of non-ionizing photons. We calculate the IR emission rate explicitly using either the IR cross sections of the respective molecule if available, or the IR cross sections from the molecule with the closest number of H atoms, within the same ionization state. Table 2 shows the adopted parameters for each photodissociation process. The explanation of each choice is given below.
H-loss.
For coronene and its dehydrogenated states (NH≤ 12), we will use the activation energies and entropies derived for pyrene cation from the time-dependent mass spectrometry experiments of Ling et al. (1995); that is, activation energies of 4.6 and 4.1 eV, and entropies of 44.8 and 55.6 J/K/mol, for PAHs with an even and odd number of H atoms, respectively (see Table 2).
These values compare well with our theoretically determined dissociation energies for the coronene cation (Z = 1) and its dehydrogenated states (4.9 and 3.9 eV respectively), as well as with Reitsma et al. (2014) for the first 6 H-losses (4.7 and 4.1 eV respectively). Theoretical analysis also shows that the CH interaction is a rather local process, and thus, its energetics remain relatively constant with increasing degree of dehydrogenation of the molecule: considering even and odd dehydrogenated states separately, only small variations of ~0.02 eV are obtained (Candian et al., in prep.). Calculations also predict little difference (<0.4 eV) in the energies between neutral and positively ionized coronene (Paris et al. 2014); and also between their respective neutral and positively ionized dehydrogenated states (Candian et al., in prep.). Concerning anionic species, the energy for the first H-loss from coronene anion is about 4.1 eV according to DFT calculations (Candian et al., in prep.), much less than the 4.9 eV obtained for the other ionization states of coronene. However, calculations on anions require a different level of theory which may add a systematic difference with respect to the values obtained for the other ionization states. Keeping this in mind, we will assume the same energies and entropies for all ionization states.
For C54H18 and C96H24, and their respective dehydrogenated states (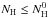 ), we must take into account their edge structure in order to define how these molecules fragment (see Fig. 1). While coronene has a carbon core with 12 H atoms attached in pairs to 6 different rings (i.e., 6 duo rings), C54H18 has 12 H atoms attached in pairs to 6 separate rings (6 duo rings), and 6 H atoms attached to the other 6 peripheral rings (6 solo rings). Circumcircumcoronene has similarly 6 duo rings and 12 solo rings. Given these structures, we will consider that these molecules first lose all the duo H-atoms in the same fashion as the H-losses in coronene. Once the duo H-atoms are gone, then they start losing the solo H-atoms. This assumption is based on theoretical calculations that predict higher binding energies for solo H-atoms than duo H-atoms (Castellanos et al., in prep.).
), we must take into account their edge structure in order to define how these molecules fragment (see Fig. 1). While coronene has a carbon core with 12 H atoms attached in pairs to 6 different rings (i.e., 6 duo rings), C54H18 has 12 H atoms attached in pairs to 6 separate rings (6 duo rings), and 6 H atoms attached to the other 6 peripheral rings (6 solo rings). Circumcircumcoronene has similarly 6 duo rings and 12 solo rings. Given these structures, we will consider that these molecules first lose all the duo H-atoms in the same fashion as the H-losses in coronene. Once the duo H-atoms are gone, then they start losing the solo H-atoms. This assumption is based on theoretical calculations that predict higher binding energies for solo H-atoms than duo H-atoms (Castellanos et al., in prep.).
For the loss of the extra hydrogen atoms (i.e., 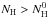 ) we adopt the theoretically derived values from Bauschlicher & Ricca (2014) for the binding energies of the extra H-atom for the C96H25 anion, neutral and cation molecule. We will assume extra H atoms always stick to duo positions, even for C54H18 and C96H24 derivatives that also have solo rings available for attachment. The binding energies of an extra H-atom in a duo position are of 1.4 eV for the anion, 1.4 eV for the neutral and 1.55 eV for the cation. The respective energies for the attachment to a solo position are of 2.2, 1.8 and 2.3 eV. These small differences do not have an impact on the derived rates. Given the lack of data, we will use an activation entropy of 55.6 J/K/mol, as assumed for PAHs with an odd number of H atoms (Ling et al. 1995).
) we adopt the theoretically derived values from Bauschlicher & Ricca (2014) for the binding energies of the extra H-atom for the C96H25 anion, neutral and cation molecule. We will assume extra H atoms always stick to duo positions, even for C54H18 and C96H24 derivatives that also have solo rings available for attachment. The binding energies of an extra H-atom in a duo position are of 1.4 eV for the anion, 1.4 eV for the neutral and 1.55 eV for the cation. The respective energies for the attachment to a solo position are of 2.2, 1.8 and 2.3 eV. These small differences do not have an impact on the derived rates. Given the lack of data, we will use an activation entropy of 55.6 J/K/mol, as assumed for PAHs with an odd number of H atoms (Ling et al. 1995).
 |
Fig. 5 Comparison of IR emission and photodissociation rates as a function of internal energy of the PAH. The rates determined for coronene derivatives are shown in black, while the rates for circumcoronene and circumcircumcoronene are shown in blue and red respectively, following the color scheme of Fig. 4. The grey vertical lines show the activation energies assumed listed in Table 2. The left panel shows the rates for the first dehydrogenated state of each parent molecule in their neutral state (C24H |
H2-loss.
The loss of H2 through photolysis will be considered for normally-to-dehydrogenated molecules, while H2-loss from superhydrogenated molecules will be considered as an abstraction process through an Eley-Rideal mechanism. Test runs show that for superhydrogenated molecules, H2 abstraction by H is more important than H2-loss through photoexcitation. According to DFT calculations (Castellanos et al., in prep.), the activation energies for the H2-loss from a duo and a solo position are of 3.89 and 2.2 eV, respectively. Assuming a change in entropy of −53.1 J/K/mol (Ling et al. 1995), we get that superhydrogenated molecules will preferably lose their extra H atom after UV photon absorption, rather than an H2 molecule, and that superhydrogenated isomers with free C atoms are not relevant species. Thus, we do not consider direct H2-loss from superhydrogenated molecules.
Regarding normally-to-dehydrogenated molecules, due to the lack of experimental data on large PAHs, we will use the activation energy and entropy obtained for pyrene cation from the experiments of Ling et al. (1995); that is, an activation energy of 3.52 eV, and an activation entropy of −53.1 J/K/mol. This energy is small compared to the theoretical calculations for the first H2-losses from coronene cation, which give energies of ~5.0 eV (Reitsma et al. 2014; Paris et al. 2014). However DFT calculations are known to overestimate energies, and so we chose to use the experimental values.
A theoretical study on coronene and its positively ionized states shows that H2-loss from 2 H atoms within the same ring has a lower dissociation energy than the H2-loss from 2 H atoms from different rings (Paris et al. 2014). Thus, we will assume that the H2-loss comes from 2 H atoms in a duo ring. In the case of coronene derivatives, this indicates that direct H2-loss will be considered only for the molecules with an even number of H-atoms. Dehydrogenated coronene derivatives with an odd number of H-atoms will only lose the (more loosely bound) H atom left in the ring.
In the case of C54H18 and C96H24 derivatives (which have solo and duo rings), the H2 molecule will also be assumed to form from 2 H atoms from the same ring (a duo ring). In other words, direct H2-loss will only be considered for molecules having an even number of H atoms until only solo H atoms remain in the molecule. These solo H atoms will be lost 1 by 1 using the activation energies and entropies discussed before (see Table 2).
Dissociation rates.
In order to obtain the multiphoton dissociation rates, we first calculate each rate constant according to the Rice-Rampsberger-Kassel-Marcus (RRKM) theory in the Arrhenius form, using the parameters described above (Tielens 2005).
IR emission rates, kIR(Z,NH,E), were calculated using the so-called thermal approximation (e.g., Schutte et al. 1993; Bakes et al. 2001). In this approximation, the emission from a given vibrational mode corresponds to the average emission of an oscillator connected to a thermal bath at temperature T. The inverse timescale of IR emission is then given by: 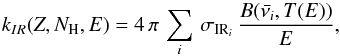 (3)where
(3)where 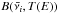 is the Planck function, and σIRi is the IR cross section of mode i at frequency
is the Planck function, and σIRi is the IR cross section of mode i at frequency 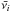 . The T(E) relation is derived from the heat capacity Cv(T) calculated for each molecule (Bakes et al. 2001). Figure 5 compares the calculated IR emission and dissociation rates. H2-loss dominates over H-loss only at low internal energies, where IR emission dominates over both dissociation processes. At an internal energy of 9 eV, H-loss becomes faster than IR emission for neutral coronene. This transition occurs at 17 eV and ~28 eV for C54H
. The T(E) relation is derived from the heat capacity Cv(T) calculated for each molecule (Bakes et al. 2001). Figure 5 compares the calculated IR emission and dissociation rates. H2-loss dominates over H-loss only at low internal energies, where IR emission dominates over both dissociation processes. At an internal energy of 9 eV, H-loss becomes faster than IR emission for neutral coronene. This transition occurs at 17 eV and ~28 eV for C54H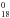 and C96H
and C96H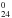 respectively, way above the Lyman limit. The same behaviour is observed for the other ionization states, where the crossing point between the H-loss rate and IR relaxation occurs at slightly higher energies (up to 2 eV) due to the faster IR emission rates of ions compared to those of neutrals. For dehydrogenated states with an odd number of H-atoms, for which we have assumed a smaller activation energy, the crossing point occurs at energies 3–5 eV smaller than for the molecules with an even number of H-atoms, but this is still above the Lyman limit for the larger molecules. For superhydrogenated states, on the other hand, the transition occurs at much lower energies, all below 13.6 eV. Comparing our estimates with Montillaud et al. (2013) for the parent molecules, we get that the H-loss rates as a function of internal energy of the PAH are fairly similar: the curves of Fig. 5 are slightly steeper, leading to smaller rates than theirs at lower energies (near the crossing points), but similar at higher energies. Clearly for superhydrogenated molecules, our rates are significantly larger than theirs given that we assume low energies compared to their 3.2 eV dissociation energy for H-loss from
respectively, way above the Lyman limit. The same behaviour is observed for the other ionization states, where the crossing point between the H-loss rate and IR relaxation occurs at slightly higher energies (up to 2 eV) due to the faster IR emission rates of ions compared to those of neutrals. For dehydrogenated states with an odd number of H-atoms, for which we have assumed a smaller activation energy, the crossing point occurs at energies 3–5 eV smaller than for the molecules with an even number of H-atoms, but this is still above the Lyman limit for the larger molecules. For superhydrogenated states, on the other hand, the transition occurs at much lower energies, all below 13.6 eV. Comparing our estimates with Montillaud et al. (2013) for the parent molecules, we get that the H-loss rates as a function of internal energy of the PAH are fairly similar: the curves of Fig. 5 are slightly steeper, leading to smaller rates than theirs at lower energies (near the crossing points), but similar at higher energies. Clearly for superhydrogenated molecules, our rates are significantly larger than theirs given that we assume low energies compared to their 3.2 eV dissociation energy for H-loss from 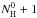 molecule (their maximum hydrogenation state). Montillaud et al. (2013) also compares their rates to the values used in Berné & Tielens (2012) and Le Page et al. (2001). Somewhat different rates are obtained due to the different adopted binding energies (3.3 eV for the H-loss in Berné & Tielens 2012; and 4.8 eV in Le Page et al. 2001) and pre-exponential factors (3 × 1016 s-1 in both studies). For coronene, the H-loss rates of Montillaud et al. (2013) are higher than the ones in Le Page et al. (2001). Compared to Berné & Tielens (2012), the crossing points occur at slightly different energies, but due to the steeper change of the rates of Montillaud et al. (2013), their rates are higher at energies above 11 eV.
molecule (their maximum hydrogenation state). Montillaud et al. (2013) also compares their rates to the values used in Berné & Tielens (2012) and Le Page et al. (2001). Somewhat different rates are obtained due to the different adopted binding energies (3.3 eV for the H-loss in Berné & Tielens 2012; and 4.8 eV in Le Page et al. 2001) and pre-exponential factors (3 × 1016 s-1 in both studies). For coronene, the H-loss rates of Montillaud et al. (2013) are higher than the ones in Le Page et al. (2001). Compared to Berné & Tielens (2012), the crossing points occur at slightly different energies, but due to the steeper change of the rates of Montillaud et al. (2013), their rates are higher at energies above 11 eV.
 |
Fig. 6 Variation of the photodissociation rates with respect to the intensity of the UV field, G0. The rates are shown for the same molecules as in Fig. 5, following the same color scheme. For the smallest molecule (black curves) the rates scale linearly with G0 at the range of interest for NGC 7023 (G0≤ 2600) indicating single photon events occurrence for coronene derivatives. For the larger molecules, multiphoton events are important. Even though H-loss is the dominant dissociation channel, at low G0 values, H2-loss can become a competitive process for the larger circumcoronene and circumcircumcoronene species. |
Assuming that the cooling of a PAH can be described as a Poisson process, we can estimate the temperature probability function of the PAH in a given radiation field following Bakes et al. (2001; see also Purcell 1976; Aannestad & Kenyon 1979). The temperature probability function for a PAH exposed to photons of energy E, G(T,E), is then given by: 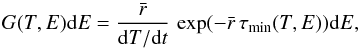 (4)with
(4)with 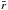 the photon absorption rate, dT/ dt the cooling rate, and τmin the minimum amount of time the PAH requires to cool from a maximum temperature Tmax(E) to T, after absorbing a photon of energy E. Since the PAH is absorbing photons in a stellar radiation field n(E), expression (4) must be averaged over the distribution of photon energies:
the photon absorption rate, dT/ dt the cooling rate, and τmin the minimum amount of time the PAH requires to cool from a maximum temperature Tmax(E) to T, after absorbing a photon of energy E. Since the PAH is absorbing photons in a stellar radiation field n(E), expression (4) must be averaged over the distribution of photon energies: 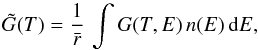 (5)so that
(5)so that 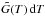 corresponds to the probability of finding the PAH at a temperature between T and T + dT given a single photon event. When considering multiphoton events, we must calculate the temperature probability function for n photon events, Gn(T), in an iterative fashion:
corresponds to the probability of finding the PAH at a temperature between T and T + dT given a single photon event. When considering multiphoton events, we must calculate the temperature probability function for n photon events, Gn(T), in an iterative fashion: 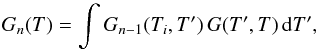 (6)where we are essentially calculating the probability for a PAH to be at temperature T given that n−1 photon events take the PAH to a temperature T′ starting from an initial temperature Ti, and an additional photon event takes the PAH from T′ to a temperature T.
(6)where we are essentially calculating the probability for a PAH to be at temperature T given that n−1 photon events take the PAH to a temperature T′ starting from an initial temperature Ti, and an additional photon event takes the PAH from T′ to a temperature T.
We start by calculating G1(T) considering an initial temperature Ti. In order to make sure the probability distribution is well defined (i.e., integral over T gives unity), we choose a proper initial temperature Ti and a temperature grid for each molecule, based on where the peak of the distribution is expected to be, i.e., the temperature Tpeak at which 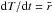 . This procedure also helps in decreasing the time it takes for the calculations to run. At each step we check that Ti> 0 K and that the integral
. This procedure also helps in decreasing the time it takes for the calculations to run. At each step we check that Ti> 0 K and that the integral 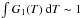 to within a few percent. Once G1(T) is obtained following Bakes et al. (2001), we estimate the H-loss, H2-loss and IR emission rates for each PAH (Z, NH) in a given hydrogenation and ionization state as:
to within a few percent. Once G1(T) is obtained following Bakes et al. (2001), we estimate the H-loss, H2-loss and IR emission rates for each PAH (Z, NH) in a given hydrogenation and ionization state as: 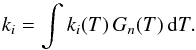 (7)Once convergence is reached between successive iterations, we calculate the probability for each reaction i as:
(7)Once convergence is reached between successive iterations, we calculate the probability for each reaction i as: 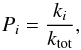 (8)where: ktot = kH,Loss + kH2,Loss + kIR. We perform this calculation for each PAH (Z, NH) for different intensities of the radiation field, i.e., varying G0 between 1 and 106. Figure 6 shows kH,Loss(G0) and kH2,Loss(G0) as a function of G0 for the molecules presented in Fig. 5. Fits to some of these curves can be found in the Appendix B. The variation of both rates scales linearly with G0 for coronene up to very high G0 values, meaning this PAH dissociates through single photon events in our range of interest. Larger molecules need more photons to dissociate (Montillaud et al. 2013): H-loss for C54H
(8)where: ktot = kH,Loss + kH2,Loss + kIR. We perform this calculation for each PAH (Z, NH) for different intensities of the radiation field, i.e., varying G0 between 1 and 106. Figure 6 shows kH,Loss(G0) and kH2,Loss(G0) as a function of G0 for the molecules presented in Fig. 5. Fits to some of these curves can be found in the Appendix B. The variation of both rates scales linearly with G0 for coronene up to very high G0 values, meaning this PAH dissociates through single photon events in our range of interest. Larger molecules need more photons to dissociate (Montillaud et al. 2013): H-loss for C54H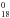 is already a 2 photons event at G0< 10, while at the edge of the NGC 7023 NW PDR, it is expected to be a 3 photons event. C96H
is already a 2 photons event at G0< 10, while at the edge of the NGC 7023 NW PDR, it is expected to be a 3 photons event. C96H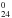 on the other hand, needs ≥3 photons depending on the G0 considered (at G0> 105 it becomes a 4 photons event). As H2-loss occurs at low internal energies of the PAH, it scales linearly with UV field intensity in highly shielded environments, becoming a competitive process with respect to the direct H-loss for the larger molecules (NC> 54).
on the other hand, needs ≥3 photons depending on the G0 considered (at G0> 105 it becomes a 4 photons event). As H2-loss occurs at low internal energies of the PAH, it scales linearly with UV field intensity in highly shielded environments, becoming a competitive process with respect to the direct H-loss for the larger molecules (NC> 54).
The final rate of dissociation for each process is given by the rate of photon absorptions times the probability for each channel to occur given by expression (8).
Electronic relaxation.
As an aside, we note that for small neutral species, electronic fluorescence and phosphorescence can play a role as a de-excitation process. However, for coronene, mean fluorescence and phosphorescence yields are of only 0.2 and 0.1, respectively (Dawson & Kropp 1969). Because of smaller energy gaps, fluorescence and phosphorescence for large species is unimportant (Pino et al. 2011). For ions, internal conversion will be even more important as the energy gaps involved are smaller (cf. Pino et al. 2011). Delayed fluorescence – also sometimes called Poincaré fluorescence, where the excited species revisits the S1 (or T1) state (Léger et al. 1988) – is measured to be unimportant for coronene as it only accounts for a small fraction of the total radiationless de-activation of triplet coronene (Kropp & Dawson 1967). While delayed fluorescence cannot compete with IR relaxation for low levels of excitation, at high internal energies it does become more important. As fragmentation, particularly for the large species, requires high levels of internal energy, delayed fluorescence may play more of a role. Following Berné et al. (2015), and adopting a binding energy of 4.6 eV and an energy gap of 2.1 eV (Fusaro 2012), we have examined the possible effect of electronic relaxation on the H-loss rate of large PAHs. As an example, for circumcoronene, at an internal energy of 25 eV the H-loss rate is calculated to be 5 × 104 s-1, which should be compared to the electronic relaxation rate of ~0.5 s-1 and the IR relaxation rate of ~1 s-1. Likewise for circumcircumcoronene at an internal energy of 37 eV, the H-loss rate is 103 s-1, the electronic relaxation rate is ~1 s-1 and the IR rate is ~1 s-1. Hence we have chosen to ignore electronic fluorescence.
2.4.4. Reactivity with hydrogen
For cationic species we will consider the works of Le Page et al. (1997) and Betts et al. (2006). These studies have experimentally determined rate coefficients for the first and second hydrogenation of small cationic PAHs (NC ≤ 24). The rates for all PAHs agreed within the uncertainties with the rate derived for coronene, 1.4 ± 0.7 × 10-10 cm3/s.
More recent experiments on the hydrogenation of coronene cation reveal that only coronene cations with an odd number of H-atoms are detected through mass spectrometry (Boschman et al. 2012; Reitsma et al. 2014). Transition states calculations predict a small (0.01 eV) barrier for the first hydrogenation to a duo ring, and a barrier of 0.03 eV for the second one within the same ring (Cazaux et al. 2016). Further H-additions have different barriers depending on both, the radical nature of the reactants and the deformation in the carbon structure of the PAH. Low barriers are typically of the order of 0.01 eV, while large barriers are typically of the order of 0.03 eV. As a reference, a 0.01 eV barrier leads to a rate similar as the one derived by Le Page and coworkers assuming the geometrical cross section of coronene (35.7 Å2). Given the lack of data on the hydrogenation of dehydrogenated states, we will adopt the rate of 1.4 × 10-10 cm3/s for all hydrogenation steps of all positively ionized species, irrespective of the barriers.
For neutral species we will consider the work of Rauls & Hornekær (2008) on the hydrogenation of neutral coronene. This work predicts a barrier of 0.06 eV for the first hydrogenation; no barrier for the second; a 0.03 or 0.04 eV barrier for the third extra H atom depending on whether the H atom is attached to an inner or outer edge of the molecule; and no barriers for additional hydrogenations up to 8 extra H atoms. Considering the geometrical cross section of coronene, a 0.06 eV barrier leads to rates of the order of 10-10 cm3/s at the temperature range of relevance (few hundred K). Given the lack of data on the larger molecules we decide to use the geometrical cross sections of each molecule together with the barriers given in Rauls & Hornekær (2008) for all neutral species in normally-to-superhydrogenated states. For the dehydrogenated molecules we do not consider any barrier, and we adopt a 7% efficiency as found for cations by Demarais et al. (2014).
Regarding anionic species, Demarais et al. (2012) performed experiments on the reactivity of deprotonated small PAH anions with H atoms, and found that hydrogenation occurs through associative detachment (i.e., formation of the neutral parent molecule and the release of an electron). For the largest PAH they studied, C14H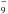 , they found a reaction rate of (7.8 ± 0.2) × 10-10 cm3/s and report that, although energetically feasible, the pure association reaction (C14H
, they found a reaction rate of (7.8 ± 0.2) × 10-10 cm3/s and report that, although energetically feasible, the pure association reaction (C14H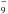 + H → C14H
+ H → C14H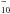 ) is not observed. Thus, we will consider the associative detachment pathway as the H-addition process for all negatively ionized species considered in our work (Z< 0). In their study, the reaction rate decreases slightly with increasing size of the PAH. However given their small sample (benzene, naphthalene and anthracene), and the lack of data on larger PAHs, we will adopt the rate determined for anthracene for all our anionic molecules.
) is not observed. Thus, we will consider the associative detachment pathway as the H-addition process for all negatively ionized species considered in our work (Z< 0). In their study, the reaction rate decreases slightly with increasing size of the PAH. However given their small sample (benzene, naphthalene and anthracene), and the lack of data on larger PAHs, we will adopt the rate determined for anthracene for all our anionic molecules.
It is important to mention that no H2-addition reactions will be considered for any of the molecules since the few experiments that have been carried out on small cationic PAHs have detected little, if not any, reactivity with H2, at least not above a detection threshold of 5 × 10-13 cm3/s (Le Page et al. 1997; Demarais et al. 2012).
 |
Fig. 7 Left panel: relative contribution of dehydrogenated states of circumcoronene as a function of depth into the cloud, AV. The contributions consider all ionization states at which the molecules are present. The curves are shown for the first 4 dehydrogenated states of the parent molecule (NH = 17−4). Other partially dehydrogenated states contribute in smaller fractions. Right panel: distribution of circumcoronene derivatives at different AV values where partially dehydrogenated species are observed. |
2.4.5. H2 abstraction
H2 abstraction from superhydrogenated neutral coronene has been observed in desorption experiments on coronene bombarded with deuterium atoms (Thrower et al. 2011). This has also been analyzed from a theoretical perspective in the work of Rauls & Hornekær (2008). They predict that the H2 abstraction (occurring at the outer edge) from C24H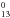 is a barrier-less process, while the abstraction from C24H
is a barrier-less process, while the abstraction from C24H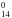 has a small barrier of 0.01 eV. Further abstractions occur in barrier-less processes. Bauschlicher & Bakes (2001) also predict no barriers for H2 abstraction from C24H
has a small barrier of 0.01 eV. Further abstractions occur in barrier-less processes. Bauschlicher & Bakes (2001) also predict no barriers for H2 abstraction from C24H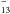 and C54H
and C54H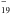 . Experiments on deuteration of coronene films taken at 300 K suggest abstraction cross sections of 0.06 Å2 (Mennella et al. 2012). Considering this cross section for all abstractions, σer, then the Eley-Rideal rate is given by:
. Experiments on deuteration of coronene films taken at 300 K suggest abstraction cross sections of 0.06 Å2 (Mennella et al. 2012). Considering this cross section for all abstractions, σer, then the Eley-Rideal rate is given by: 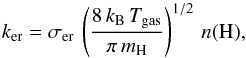 (9)which translates to a rate:
(9)which translates to a rate: 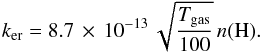 (10)
(10)
3. Model
Once the physical conditions and all processes are defined for each PAH, we proceed to establish the kinetic equation for the abundance of each PAH considered in the model (see Appendix C). We solve the system of equations assuming steady state i.e., d [PAH(Z,NH)] / dt = 0. Once the distribution of PAH abundances were obtained for each species, we calculate the emission spectra following Bakes et al. (2001), i.e., using the temperature probability function described in the previous section. In order to analyze the emission band ratios, we consider an intrinsic shift of the bands of 15 cm-1, and Gaussian line profiles with a FWHM of 15 cm-1 for all spectra (see Boersma et al. 2013). The results regarding the spectral variations will be presented in Sect. 4.3.
4. Results
Here we present the results of our work in terms of the distribution of abundances (Sect. 4.1), the H2 formation rates (Sect. 4.2), and the spectral variations expected from the derived distribution of PAH species (Sect. 4.3).
 |
Fig. 8 Charge distribution of the PAHs considered in our study. The contribution from each ionization state is shown as a function of the ionization parameter γ≡ |
4.1. Abundances
In agreement with Montillaud et al. (2013) and Boschman et al. (2015), the hydrogenation of PAHs varies strongly with PAH size and depth into the PDR (see Appendix D). While coronene is mostly dehydrogenated throughout most of the cloud – only at an AV~ 4.2 do the first hydrogenated states appear –, circumcircumcoronene does not show any dehydrogenation under the same physical conditions. The medium-sized PAH, circumcoronene, shows an intermediate behaviour compared to the other 2 species, with small traces (≲20%) of singly- and di-dehydrogenated states at the surface. The dehydrogenated fraction first decreases with depth in the PDR and then increases again slightly around an AV of 1.7 (see Fig. 7).
We also note that both circumcoronene and circumcircumcoronene, show small amounts of superhydrogenated species deep in the cloud (AV> 4) due to the increase in the atomic H density resulting from UV photons penetrating from the backside of the cloud (this also leads to the appearance of the first hydrogenated states of coronene; see Appendix D). In contrast, Montillaud et al. (2013) reported that circumcircumcoronene is superhydrogenated (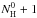 ) throughout the entire cloud. The difference mainly lies in the dissociation parameters we have assumed for the superhydrogenated species (Bauschlicher & Ricca 2014). The low activation energies we have adopted make UV driven H-loss the main dehydrogenation process for superhydrogenated circumcircumcoronene derivatives (e.g., rates of ~10-3 s-1 at AV = 0). Test runs of ±0.4 eV in the activation energies presented in Table 2 for the superhydrogenated species, do not have an impact on this aspect.
) throughout the entire cloud. The difference mainly lies in the dissociation parameters we have assumed for the superhydrogenated species (Bauschlicher & Ricca 2014). The low activation energies we have adopted make UV driven H-loss the main dehydrogenation process for superhydrogenated circumcircumcoronene derivatives (e.g., rates of ~10-3 s-1 at AV = 0). Test runs of ±0.4 eV in the activation energies presented in Table 2 for the superhydrogenated species, do not have an impact on this aspect.
Regarding ionization, we see that the larger the molecule, the higher the contribution from positively ionized species at the surface of the cloud. In the case of coronene derivatives, we find that neutrals contribute ~73% to the total abundance of PAHs at an AV = 0, while cations contribute ~27%. The radiation field intensity is not strong enough to produce dications for this species. For the larger molecules in our sample, the neutral-to-cation ratio inverts with respect to coronene. Positively charged circumcoronene derivatives (Z = 1 and 2) contribute 59%, while neutrals contribute 41%. In the case of circumcircumcoronene, we see higher ionization states than for the smaller species. Here the percentage considering cations and dications adds up to ~74%, while it is 26% for the neutrals. Higher positively ionized species, Z> 2, contribute at negligible levels (<1%). Figure 8 shows the charge distribution variation with respect to the ionization parameter 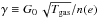 for the 3 species considered in our work. As the UV field intensity decreases, neutrals and anions become the dominant charge states. This appearance of anions occurs at lower AV values as the size of the parent molecule increases: a 10% contribution from anions is expected at a γ = 2.2 × 103, 2 × 103 and 103 for C96H24, C54H18, and C24H12 derivatives. Indeed, anions become the dominant charge states at large depths in the cloud. At AV = 5, anions make up 74%, 84% and 88% of the coronene, circumcoronene and circumcircumcoronene derivatives population. In contrast, the PAH anion abundance is only of 1–2% at the H I to H2 transition (AV ~ 1) depending on the molecule. However, negatively charged species are already important at an AV ~ 2, especially for the larger species.
for the 3 species considered in our work. As the UV field intensity decreases, neutrals and anions become the dominant charge states. This appearance of anions occurs at lower AV values as the size of the parent molecule increases: a 10% contribution from anions is expected at a γ = 2.2 × 103, 2 × 103 and 103 for C96H24, C54H18, and C24H12 derivatives. Indeed, anions become the dominant charge states at large depths in the cloud. At AV = 5, anions make up 74%, 84% and 88% of the coronene, circumcoronene and circumcircumcoronene derivatives population. In contrast, the PAH anion abundance is only of 1–2% at the H I to H2 transition (AV ~ 1) depending on the molecule. However, negatively charged species are already important at an AV ~ 2, especially for the larger species.
While test runs show that the use of different ionization yields does not have an impact on the derived abundances, the adopted dependence of the IPs and EAs on hydrogenation does have an effect on our results, but only for the smallest species in our sample. It is important to recall that previous models on PAH abundances in PDRs have not considered negatively charged species, and/or adopt the IP and EA of the parent molecule for all hydrogenation states within a given charge state (Le Page et al. 2001, 2003; Montillaud et al. 2013; Boschman et al. 2015). Here we find that it is important to use the specific IPs and EAs for each molecule, especially for the smallest species. The large fraction of negatively charged coronene derivatives results from the adopted EAs of the dehydrogenated states of the molecule, where the EA > 1 eV for NH< 8 molecules (see Fig. 4). Indeed if were to adopt the IP and EA of the parent molecule coronene for all de-and-superhydrogenated derivatives, we would obtain that coronene stays neutral in the deepest regions of the cloud (e.g., the electron sticking coefficient is se ~ 10-5 for an EA = 0.47 eV). The larger molecules on the other hand, are not affected by this, since the EA of the parent molecule is large enough to lead to electron attachment.
 |
Fig. 9 Fractional contribution from coronene (top panels), circumcoronene (middle panels) and circumcircumcoronene (bottom panels) derivatives for different G0 and n(H) values. The contributions include all ionization states. The left column shows the contribution from the completely dehydrogenated molecules, C24, C54 and C96; the middle column shows the fraction of the normally hydrogenated molecules; and the right column shows the distribution of the superhydrogenated species. In all cases, we have assumed a fraction of molecular hydrogen of 0.5, and a carbon abundance of 3.5 × 10-4 relative to hydrogen. Black lines represent constant G0/n(H) ratios and are given as a reference. |
We have explored the distribution of hydrogenation states of our three species in a systematic manner over the astrophysical relevant G0-n(H) parameter space (Fig. 9). For these calculations we adopted a gas temperature of 500 K. The results show that coronene is mostly completely dehydrogenated. At a given density, for UV fields exceeding G0 ≳ 0.01 n(H), coronene quickly loses hydrogen and becomes fully dehydrogenated. We emphasize that at that point, carbon loss can become important – limiting the lifetime of the pure carbon cluster – but we have not taken that into account. For G0 values less than ~0.05n(H), we can find superhydrogenated coronene molecules contributing at a 10–15% level. However the greatest contribution in these highly shielded environment comes from partially dehydrogenated species, with very little contribution from the normally hydrogenated molecule C24H12 (<10%).
Unlike coronene, the larger species are far more difficult to dehydrogenate: for circumcoronene, full dehydrogenation requires G0 in excess of ~300n(H) at n(H) = 1 cm-3, and above 5n(H) at n(H) = 103 cm-3. On the other hand, our largest species circumcircumcoronene only dehydrogenates for the highest UV fields and lowest densities (G0> 5 × 104 and n(H) < 3 cm-3). Normally hydrogenated species dominate below these limits until superhydrogenation sets in at G0 ~ 0.005 n(H). For smaller G0 values, these large PAHs are superhydrogenated. We note that these transitions from fully dehydrogenated to normally hydrogenated, and from normally hydrogenated to superhydrogenated are very sharp (cf., Tielens 2005). From this we take that any PAH is very sensitive to small variations in the hydrogenation parameter over a particular range, specific to that molecule, and for circumcoronene that partly overlaps with the G0/n(H) range in the NW PDR of NGC 7023 (e.g., the abundance of partially dehydrogenated derivatives of C54H18 reaches a value of 20% at AV = 1.8 where G0/n(H) = 0.95 and G0 ~ 660; at AV = 2.2, G0/n(H)= 1.35 and G0~ 410, and their contribution decreases to ~10%). Inspection of the distribution of C54H18 in Fig. 9 shows that slightly higher G0/n(H) ratios in this G0-n(H) range would have led to complete dehydrogenation of circumcoronene. Given the non-linearity of the mulitphoton dissociation processes for C54H18, the transition from the normally hydrogenated molecule to the carbon cluster C54 does not occur at a constant G0/n(H) ratio for different G0-n(H) values, and thus we do not see more dehydrogenation at AV = 2.4, where G0/n(H) ~ 1.43 and G0 ~ 325.
4.2. H2 Formation
 |
Fig. 10 Efficiencies of H2 formation from PAHs. The left panel shows the efficiencies of H2 formation through Eley-Rideal abstraction from superhydrogenated species as a function of G0/n(H). Estimates for circumcoronene and circumcircumcoronene superhydrogenated species are shown in blue and red, respectively. The efficiencies have been derived for neutrals and anions, since these are the charge states at which superhydrogenated species can be found according to our model. Two gas temperatures have been assumed as a reference. The right panel shows the efficiencies of H2 formation from photodissociation of PAHs. The efficiencies have been derived for neutral coronene at G0=10, and Z> 0 circumcoronene at G0=103. We have considered different G0 values due to the different dehydrogenation behaviour of the species in the G0-n(H) parameter space (see Fig. 9). As it can be derived from the figure, efficiencies stay below 1% for both mechanisms. |
We have included 3 possible dehydrogenation pathways for the PAHs in our study: direct loss of an H atom or an H2 molecule after photon absorption, and H2 abstraction described as an Eley-Rideal process from superhydrogenated molecules only. Thus, in our model, H2 can be formed from the direct loss of 2 duo H-atoms as an H2 molecule after photon absorption, or from H2 abstraction after superhydrogenation of the normally hydrogenated molecule.
According to our results, direct H-loss is the dominant photodissociation channel for all the molecules in our work. In the case of coronene, complete dehydrogenation is very effective at the surface of the cloud. Direct H2-loss rates at AV= 0 are two orders of magnitude lower than the direct H-loss rates for this molecule. For the larger PAHs the trend is similar. While direct H-loss is also dominant over H2-loss for circumcoronene and circumcircumcoronene, at some point deep into the cloud (AV> 4.5, G0< 10) the two rates become comparable. Inspection of Fig. 6 shows that H2-loss can dominate over H-loss in highly shielded environments where G0< 10. However in such UV-attenuated regions increasing hydrogen densities would tend to superhydrogenate these PAHs, and these, if they were to fragment in any way, would preferentially lose an H atom and not an H2 molecule.
Regarding H2 abstraction by H from superhydrogenated PAHs, we find this mechanism not particularly relevant for the conditions in the NW PDR of NGC 7023. Since the formation of H2 through Eley-Rideal abstraction depends on the gas temperature being sufficient to overcome the addition and abstraction barriers, this mechanism is expected to be important at the surface of the PDR, where also the reservoir of atomic hydrogen is large enough to carry out the addition and abstraction processes. For the smallest molecule in our sample, we obtain that coronene can never reach superhydrogenated states at low AV values, and hence cannot form H2 through this mechanism. Boschman et al. (2015) considered H2 abstraction by H for a wide range of hydrogenation states of coronene (0 ≤ NH ≤ 36), and also found that this is not a dominant process because this PAH is rapidly stripped off of all its hydrogens.
Since large PAHs are expected to be more stable against dehydrogenation, and also more prone towards superhydrogenation than the smaller species, they are expected to be good candidates for the H2 formation through Eley-Rideal H2 abstraction in PDRs. While we do recognize the great stability of large PAHs against dehydrogenation, our results for circumcoronene and circumcircumcoronene show that by the time these molecules are indeed superhydrogenated, it is already at such high extinction values (AV> 4.5), that the gas temperature is too low to lead to high abstraction rates on PAHs.
We have calculated the efficiencies of H2 formation from PAHs through direct H2-loss (i.e., photodissociation of PAHs) and H2 abstraction by H (from superhydrogenated species). The efficiencies, ξH2, for a PAH of a given size (i.e., number of C atoms) and ionization state Z, have been defined as the number of H atoms that collide with the PAH molecules, that are converted to H2: 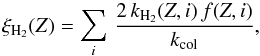 (11)where the sum is over all hydrogenation states, and kcol is a fiducial collision rate of H-atoms with the PAH species, whose expression depends on the PAH charge state under consideration (see Appendix E). In the case of direct H2-loss, kH2 corresponds to the H2 photodissociation rate of species with i number of H atoms in a given charge state; and f(Z,i) corresponds to the fraction of PAHs in charge state Z that release H2 through photodissociation, i.e., normal-to-partially dehydrogenated species with an even number of H atoms greater than the number of solo H atoms. For its part, in the case of H2 abstraction, kH2 corresponds to the H2 abstraction rates, ker, in units of 1/s (Eq. (10)); and f(Z,i) corresponds to the fraction of PAHs in the respective charge state that go through H2 abstraction, i.e., superhydrogenated PAHs with i number of H atoms.
(11)where the sum is over all hydrogenation states, and kcol is a fiducial collision rate of H-atoms with the PAH species, whose expression depends on the PAH charge state under consideration (see Appendix E). In the case of direct H2-loss, kH2 corresponds to the H2 photodissociation rate of species with i number of H atoms in a given charge state; and f(Z,i) corresponds to the fraction of PAHs in charge state Z that release H2 through photodissociation, i.e., normal-to-partially dehydrogenated species with an even number of H atoms greater than the number of solo H atoms. For its part, in the case of H2 abstraction, kH2 corresponds to the H2 abstraction rates, ker, in units of 1/s (Eq. (10)); and f(Z,i) corresponds to the fraction of PAHs in the respective charge state that go through H2 abstraction, i.e., superhydrogenated PAHs with i number of H atoms.
Figure 10 shows the efficiencies for the 3 PAHs in different environments. The left panel shows the efficiencies of H2 abstraction from the anion and neutral circumcoronene and circumcircumcoronene molecules. We have plotted these ionization states, since they are the ionization states of superhydrogenated species, whenever they are abundant. The efficiencies have been calculated for Tgas = 50 K and 500 K for G0/n(H) ratios over which superhydrogenated species are present, going from a ~10% abundance at G0/n(H) = 0.03 to a ~100% abundance at G0/n(H) = 10-4 for both, circumcoronene and circumcircumcoronene species. In this same range, the charge state of the population goes from Z = 0 and Z = −1 states in a 1:3 ratio, to being Z = −1 dominated. The resulting efficiencies increase towards lower G0/n(H) ratios, reaching a plateau once the distribution of species in a given charge state is completely dominated by the PAHs with the largest amount of extra H atoms considered (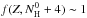 ). Overall, H2 formation efficiencies of anions are greater than those of neutral molecules. However, efficiencies are below 1%. The values derived for anionic species are rather independent of PAH size, but depend on temperature given the fiducial collision rate we adopted. On the other hand, the efficiencies derived for neutral PAHs depend on the geometrical cross section of each PAH. At low G0/n(H) ratios, the efficiencies are independent of the gas temperature. For larger G0/n(H) ratios, the apparent mild temperature dependence is due to <5% differences in the derived fractions of superhydrogenated species within each charge state. In the particular case of NGC 7023, at AV ~ 4.8 the gas temperature is about 50 K and G0/n(H)~ 0.03. Superhydrogenated circumcoronene and circumcircumcoronene species contribute at a 10% level, anions dominate, and the efficiency of H2 abstraction is very low (below 1%).
). Overall, H2 formation efficiencies of anions are greater than those of neutral molecules. However, efficiencies are below 1%. The values derived for anionic species are rather independent of PAH size, but depend on temperature given the fiducial collision rate we adopted. On the other hand, the efficiencies derived for neutral PAHs depend on the geometrical cross section of each PAH. At low G0/n(H) ratios, the efficiencies are independent of the gas temperature. For larger G0/n(H) ratios, the apparent mild temperature dependence is due to <5% differences in the derived fractions of superhydrogenated species within each charge state. In the particular case of NGC 7023, at AV ~ 4.8 the gas temperature is about 50 K and G0/n(H)~ 0.03. Superhydrogenated circumcoronene and circumcircumcoronene species contribute at a 10% level, anions dominate, and the efficiency of H2 abstraction is very low (below 1%).
The efficiencies for the direct H2-loss from photodissociation have been plotted for neutral coronene at G0= 10, and Z> 0 circumcoronene species at G0= 103. These are the relevant charge states for these molecules in the G0/n(H) ratios considered. Neutral coronene derivatives contribute in 70–78% to the total abundance of coronene species at G0/n(H)= 10-4–10-2, range over which the contribution from normal-to-partially dehydrogenated species goes from 26% to 4%. For G0/n(H)> 10-2 coronene is only found as C24. As for circumcoronene species, Z= 1 species dominate the distribution at G0/n(H)= 1–10, and dications start dominating at G0/n(H)> 10. We have plotted the efficiencies in the G0/n(H) range over which the relevant hydrogenation states for H2-loss are present (i.e., normal-to-partially dehydrogenated states with an even number of H atoms above 8). Their contributions go from 51% cations and 14% dications at G0/n(H)= 1, to <1% at G0/n(H)> 25. At higher G0/n(H) ratios circumcoronene is found as C54 (see Fig. 9). At G0/n(H)< 1 circumcoronene can be found mainly in its normal hydrogenated neutral state, down to the regime where superhydrogenated species start becoming abundant (G0/n(H)< 0.01). The efficiencies for H2-loss in these environments are below 10-4. From the Figure we see that efficiencies of direct H2-loss are at a similar level as the efficiencies of H2 abstraction (below 1%). Since the dehydrogenation behaviour is highly PAH size dependent (see left and middle columns of Fig. 9), different PAHs can be equally efficient in different environments. This depends on where in the G0-n(H) space, each PAH can be found in the relevant dehydrogenated states for H2-loss. In the case of NGC 7023, circumcoronene is already found in its normal hydrogenated state, while coronene is completely dehydrogenated. PAHs smaller than NC = 54 but larger than NC = 24 could reach efficiencies of 1% at the surface of the NW PDR of NGC 7023.
4.3. Spectral variations
We calculated the emission spectra of C24H12, C54H18 and C96H24 derivatives at different points inside the NW PDR of NGC 7023 from AV = 0−2, considering the distribution of species presented in Sect. 4.1 (see Appendix F). The emission spectrum at AV = 0−2 is essentially determined by the dominant ionization state of the PAHs at each point inside the cloud. This is due to the lack of strong variations in the hydrogenation states of the species in our work. In the case of coronene, this molecule is completely dehydrogenated, and only changes in ionization state, being mostly neutral with cationic species varying their abundance from 27% at the surface of the cloud, to 2% at an AV = 2. Recall that we do not consider destruction of the carbon skeleton which may be important for highly dehydrogenated species. The main features we see in the emission spectra of coronene derivatives are the appearance of a complex of bands at around 5 μm (4.95 and 5.12 μm), related to stretching modes of the triple bonds in dehydrogenated species; the strong band at 6.71 μm due to stretching modes of the carbon skeleton; and the bands at 10.13, 10.35 and 20.4 μm due to complex deformation modes of the carbon structure. Among these, the bands at 5.12 and 10.35 μm, although weak, increase in intensity with respect to the 4.95, 6.71, 10.13 and 20.4 μm bands towards more highly ionized environments.
As stated before, circumcoronene does present levels of dehydrogenation that vary following the change in the G0/n(H) ratio. We do not have the intrinsic spectra for most of the partially dehydrogenated species (see Appendix A). However, between AV = 0 and 2, partially dehydrogenated species are present only at low AV (AV ~ 0) where ~34% of the emitting species are partially dehydrogenated. These species correspond to the first partially dehydrogenated molecules (e.g., NH= 17–12), and so we expect their emission to be similar as that of the parent molecule. Inspection of the emission spectra from circumcoronene derivatives reflect then mainly the change in the ionization state of C54H18. This is apparent from the decrease with AV in the strength of the 6–9 μm stretching modes relative to the 11–15 μm CH out-of-plane bending modes (Langhoff 1996; Allamandola et al. 1999; Peeters et al. 2002). The signature of positively ionized species is also apparent in the broadening of the 11.25 μm band, which is in fact due to the appearance of the 11.05 μm feature related to CH out-of-plane bending modes in ionized PAHs (Rosenberg et al. 2011; Boersma et al. 2013).
In the case of circumcircumcoronene, as for circumcoronene, the spectrum is also dominated by the changes in the ionization state of the parent molecule. Hence we see the same signatures of ionization as we see for C54H18. At the surface of the cloud, circumcircumcoronene molecules are mostly highly positively ionized (~74%). Close to where the H I to H2 transition occurs, the ratio between neutrals and positively ionized species is close to 1.0. At an AV= 1.6 neutrals still dominate the population with a 73% abundance, while the contribution from anions has increased to 8%, and positively ionized species contribute 19% to the total abundance. At an AV= 2, neutral molecules contribute in 75%, while anions contribute in 15%. We see that this increase in the abundance of anions (and decrease in the abundance of cations) does not have a discernible impact in the emission spectrum.
A comparison between C54H18 and C96H24 derivatives spectra shows that the 3.28/3.3 and 3.28/11.3 peak intensity ratios are larger for the intermediate size molecule than for circumcircumcoronene (3.28/3.30 = 3.58 and 3.28/11.3 = 0.43 for C54H18, against 1.92 and 0.14 respectively for C96H24). Both ratios remain relatively constant, which shows that they are not sensitive to the ionization state of the molecules under these conditions. Instead, they do vary with PAH size (Bauschlicher et al. 2008; Ricca et al. 2012; Croiset et al. 2016).
Up to now, we have focused on the behaviour of the PAH bands with depth into the NW PDR of NGC 7023, where physical conditions vary enough to see spectral changes due to ionization but not due to changes in the hydrogenation state of the PAHs. In order to explore the spectral signatures of large variations in the hydrogenation state of our PAHs we have calculated the emission spectra for different G0/n(H) ratios at G0= 103. These spectra can be found in the Appendix F. Visual inspection of the spectra of coronene species shows that over much of the parameter space, the spectrum of the fully dehydrogenated molecule dominates, and the spectral changes represent the variation in its ionization state (the abundance of Z> 0 species varies from 98% at G0/n(H)= 100 to 4.5% at G0/n(H)= 0.1). For G0/n(H)≤ 0.01 partially dehydrogenated derivatives become more relevant. These are mostly anionic and neutral species for which we do not have the IR spectra. The parent molecule is never important (even at a G0/n(H)= 0.001 C24H12 contributes at a 1% level only), nor the superhydrogenated species (which barely appear at G0/n(H) = 0.001 contributing at a 5% level).
The spectra of the larger species show instead the clear footprints of hydrogenation. As seen in Fig. 9, circumcoronene completely dehydrogenates for G0/n(H)≳ 100 at G0= 103. The dominant species at G0/n(H)= 100 is then C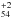 in 83% for which we do not have the IR spectrum, but whose emission is expected to be similar to that of C
in 83% for which we do not have the IR spectrum, but whose emission is expected to be similar to that of C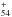 (see Appendix F), except for an even stronger 5 μm band, as typical from carbon cluster cations. Going to lower G0/n(H) values we see circumcoronene mostly in its normally hydrogenated state C54H18, and thus what we observe are essentially the changes in ionization state, being mostly neutral with an increasing abundance of the anionic molecule (from 7% to 18.5%). This is reflected in the increasing 6.4/11.3 ratio and the red-shift of the bands, intrinsic to anionic species. The contribution from superhydrogenated species in this G0/n(H) range goes from ~3 to 35%, which is clear from the inspection of the 3 μm region.
(see Appendix F), except for an even stronger 5 μm band, as typical from carbon cluster cations. Going to lower G0/n(H) values we see circumcoronene mostly in its normally hydrogenated state C54H18, and thus what we observe are essentially the changes in ionization state, being mostly neutral with an increasing abundance of the anionic molecule (from 7% to 18.5%). This is reflected in the increasing 6.4/11.3 ratio and the red-shift of the bands, intrinsic to anionic species. The contribution from superhydrogenated species in this G0/n(H) range goes from ~3 to 35%, which is clear from the inspection of the 3 μm region.
Regarding our largest species, circumcircumcoronene stays normally hydrogenated throughout most of the G0/n(H) space. Therefore down to a G0/n(H)= 0.1 we are basically following the variation in the ionization state of C96H24, from being mostly in Z= 3 state to neutral. Going from G0/n(H)= 0.1 to 0.01 the abundance of superhydrogenated species increases to a 19%, which is only clear in the 3 μm spectral region, although the signal is rather weak. Only at G0/n(H)≤ 0.001 superhydrogenated Z = −1 and Z= 0 species become the dominant species. Their signal would be noticeable only in the 3 μm region, since the spectrum of the parent molecule looks fairly similar to that of the first few superhydrogenated derivatives.
The 3 μm region is particularly sensitive to the superhydrogenation level of PAHs (Bernstein et al. 1996; Sandford et al. 2013). The 3.3 μm aromatic CH stretch shows the two components expected for the coronene family: 3.28 μm band due to duo hydrogens, and 3.3 μm band for the solo hydrogens (Ricca et al. 2012). Even though the differences between the spectrum of the parent molecule and those of superhydrogenated derivatives become far more clear with higher degrees of superhydrogenation, the main differences start to show up in the 3 μm region. With superhydrogenation, new bands appear at longer wavelengths. Zooming in into the 3 μm region of the intrinsic spectra of superhydrogenated species (see comparative spectra in Appendix F), we can distinguish three main bands at 3.3, 3.41 and ~3.5 μm (and weaker bands at 3.57 and 3.67 μm). The 3.5 μm band appears already for a mono superhydrogenated PAH. This band is related to the stretching of each CH2 complex. The band at 3.4 μm instead requires two additional H atoms on the ring. This band is related to the stretching modes of the pair of CH2 groups within the same (duo) ring. Therefore the 3.4 μm band only appears for hydrogenation states 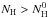 + 1. In fact this pattern is not only seen in the theoretical spectra of these PAHs, but also in that of pyrene, C16H10, and naphthalene, C10H8, derivatives (for which the spectra are provided by the PAHdb). For this last one, there are experimental (argon matrix) spectra of the first superhydrogenated state of the molecule, where they report bands at 3.24 and 3.51 μm, but none at 3.4 μm (Ricks et al. 2009). Instead both the experimental and theoretical spectrum of C10H10 (and further superhydrogenated states) do show a 3.4 μm band (Bernstein et al. 1996). Thus the appearance of the 3.4 μm band appears to be common to PAHs with at least 2 extra H atoms. Once all H-sites on the PAH become superhydrogenated, the 3.3 μm aromatic CH stretch disappears. We also, stress that the G0/n(H) value at which these superhydrogenated signatures appear depends on the size of the PAH (cf., Fig. 9). Specifically, the superhydrogenated species appear at G0/n(H)≲ 0.01 for both circumcoronene and circumcircumcoronene, but their spectral signature would be discernible in the 3 μm region at G0/n(H) ten times lower, where superhydrogenated species contribute in more than 30% to the emission.
+ 1. In fact this pattern is not only seen in the theoretical spectra of these PAHs, but also in that of pyrene, C16H10, and naphthalene, C10H8, derivatives (for which the spectra are provided by the PAHdb). For this last one, there are experimental (argon matrix) spectra of the first superhydrogenated state of the molecule, where they report bands at 3.24 and 3.51 μm, but none at 3.4 μm (Ricks et al. 2009). Instead both the experimental and theoretical spectrum of C10H10 (and further superhydrogenated states) do show a 3.4 μm band (Bernstein et al. 1996). Thus the appearance of the 3.4 μm band appears to be common to PAHs with at least 2 extra H atoms. Once all H-sites on the PAH become superhydrogenated, the 3.3 μm aromatic CH stretch disappears. We also, stress that the G0/n(H) value at which these superhydrogenated signatures appear depends on the size of the PAH (cf., Fig. 9). Specifically, the superhydrogenated species appear at G0/n(H)≲ 0.01 for both circumcoronene and circumcircumcoronene, but their spectral signature would be discernible in the 3 μm region at G0/n(H) ten times lower, where superhydrogenated species contribute in more than 30% to the emission.
5. Discussion
 |
Fig. 11 PAH band ratios in the NW PDR of NGC 7023. The 6.2/11.3 ratio is usually used as a proxy for the ionization level of the PAH population, while the 3.3/11.3 ratio is expected to trace PAH size. Here we have plotted them for circumcoronene in blue, and circumcircumcoronene in red. The spectra for C96H24 derivatives are complete in this AV range. The spectra for C54H18 species are missing only the small contributions from partially dehydrogenated species (read text). Observational studies have derived typical 3.3/11.3 ratios of 0.5 to 0.3 from the surface to the PDR up to distances of about 52 arcsec from the star. As seen in the figure, intermediate size PAHs could potentially reproduce these values. However, the ionization ratio 6.2/11.3 would then be highly underestimated compared to the observations that predict a value of 2 at the surface of the PDR, decreasing in about 14% to a distance of ~55 arcsec from the star. |
We found that small PAHs behave quite differently from intermediate and large species. Small PAHs are easily destroyed in most environments; can rarely be found in their normally hydrogenated state; and only for extremely shielded regions (low G0/n(H) ratios) they can be found in superhydrogenated states. The difference in the abundance distribution between intermediate and large PAHs is related to their dehydrogenation behaviour rather than their superhydrogenation behaviour. The larger the PAH, the more likely it can be found in its normal hydrogenated state. Regarding superhydrogenation of PAHs, intermediate and large PAHs can hardly superhydrogenate in the more diffuse parts of PDRs. These species will lose their extra H atoms very easily, and only in highly shielded environments will reactions with H atoms keep the molecules superhydrogenated. These molecules when dominating the abundance distribution of a given species will be mostly in Z = 0 and Z = −1 charge states. Therefore their spectral signature – if observable – would not only be straightforward from the appearance of more bands in the 3 μm region, but it would also be discernible from a red-shift of the bands (intrinsic to anionic species).
In the particular case of the NW PDR of NGC 7023, we find that small PAHs like coronene will remain completely dehydrogenated throughout most of the cloud. Intermediate and large PAH molecules will remain, mainly, normally hydrogenated but highly positively ionized at the surface of the PDR, where the bulk of the PAH emission is observed. Superhydrogenation is only achieved for the larger species in the more shielded regions of the cloud. Recall we have considered a maximum of 4 additional H atoms as the maximum superhydrogenated state of a PAH. Test runs showed PAHs do not superhydrogenate further in the case of the NW PDR of NGC 7023. Higher superhydrogenation levels can be achieved in more shielded environments; e.g., considering higher hydrogenated states than 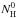 + 4, circumcoronene derivatives with NH> 22 start appearing at G0/n(H) < 0.01 at G0 = 1000, increasing their abundance gradually towards more shielded environments, becoming a 50% of the emitting population at G0/n(H)~ 0.002. Such abundance of highly superhydrogenated molecules would leave a clear footprint in the emission spectra. However, nor the molecular properties nor the energetics involved in the H-addition/H2-abstraction processes have been studied for such superhydrogenated molecules.
+ 4, circumcoronene derivatives with NH> 22 start appearing at G0/n(H) < 0.01 at G0 = 1000, increasing their abundance gradually towards more shielded environments, becoming a 50% of the emitting population at G0/n(H)~ 0.002. Such abundance of highly superhydrogenated molecules would leave a clear footprint in the emission spectra. However, nor the molecular properties nor the energetics involved in the H-addition/H2-abstraction processes have been studied for such superhydrogenated molecules.
From the observations of the NW PDR of NGC 7023 we do see strong emission from the CH modes, and thus, we expect most PAHs to be hydrogenated at some level. Small PAHs like coronene – if present – must contribute at a negligible level to the general population of PAHs in the PDR. Coronene in the NGC 7023 NW PDR environment is the epitome of a fully dehydrogenated species. Its spectrum shows the telltale sign of graphene-like flakes with features in the 5 and 10 μm region. Weak features at 5.25 and 5.75 μm are routinely detected in sources whose spectra are dominated by the IR emission features (Roche et al. 1996; Boersma et al. 2009). These have been ascribed to weak overtones and combination bands involving the CH in-plane and out-of-plane stretching modes (Boersma et al. 2009; Mackie et al. 2015). As our study illustrates, graphene-like flakes show bands around 4.95, 5.12, and 5.35 μm due to stretching modes in triple bonds (Bauschlicher & Ricca 2013). Bands are also observed at 10 and 20 μm due to in-plane stretches of the inner and outer edge C atoms respectively, moving to and outwards the center of the molecule. Hydrogenated PAHs do not show strong bands in the 10 μm region, but can show bands in the 20 μm region (Bauschlicher & Ricca 2013).
Besides the caveat mentioned before that small graphene-like flakes are prone to loss of carbon, we should also mention that isomerization of completely dehydrogenated PAHs towards cages or rings may also be important (Berné & Tielens 2012; Zhen et al. 2014a). This is another aspect of the evolution of PAHs in space that was not included in our modelling efforts, as kinetic data on the processes involved are lacking. Further laboratory studies are required to establish the photolysis routes of such species and to assess the origin of the 5, 10, and 20 μm bands in the interstellar spectra.
It is of interest to compare our model results with observations of PAH band ratios. Combining Spitzer and SOFIA observations, Croiset et al. (2016) derived 3.3/11.3 ratios in NGC 7023. This ratio is expected to serve as a proxy for PAH size. Figure 11 shows the 3.3/11.3 ratios we obtain from our model for circumcoronene and circumcircumcoronene derivatives in the NW PDR of NGC 7023. The 3.3/11.3 ratio varies slightly in our spectra due to the changes in the ionization state of the molecules. Croiset et al. (2016) report values of 0.5 to 0.3 when going from the surface of the PDR to 52 arcsec away from the star. According to our estimates, PAHs of intermediate size can reproduce such values. We do point out though, that the 3.3/11.3 is a good tracer of PAH size as long as a given ionization state dominates the distribution, e.g., at G0/n(H)~ 30 the 3.3/11.3 decreases for C96H24 species because of the dominant abundance of trications that have a lower 3.3/11.3 ratio. Therefore, beside PAH size, the observed variation in the 3.3/11.3 ratio in the NGC 7023 PDR (Croiset et al. 2016) may also be affected by charge variations.
Figure 11 also shows the variation of the 6.2/11.3 ratio in the PDR. We see the 6.2/11.3 ratio decreasing as the dominant ionization state of the PAHs changes from being Z> 0 dominated to neutral dominated (recall that for both species the spectral variations are essentially tracing the variation in the ionization state of the parent molecules). From IRS Spitzer observations, Boersma et al. (2014) derived 6.2/11.3 ratios in the range between 1.7 and 2.0, and 7.7/11.3 ratios between 5 and 7. Fleming et al. (2010) also using IRS data reports an average value for the 7.7/11.3 of 6.06 ± 1.74, with the ratio varying only by 14% from a distance of ~40 to 55 arcsec from the star. Our calculated values are lower than the observed ones. Also, our 6.2/11.3 (and 7.7/11.3) band ratios vary by more than 50% from AV= 0 to AV= 2. Assuming G0= 103, we can obtain ratios close to the observed ones (I6.2/11.3~ 2, and I7.7/11.3~ 6) at G0/n(H) of 1–10, instead of the G0/n(H)~ 0.3 that we get at AV= 0. In other words, if the density at the surface of the cloud were overestimated by a factor of 10, we could reproduce the observed 6.2/11.3 and 7.7/11.3 ratios with intermediate-to-large PAHs.
5.1. Implications on the Origin of the 3.4 μm feature
Observations of Orion and NGC 7023 have both revealed bands at 3.3, 3.4, 3.47, 3.51 and 3.56 μm (Joblin et al. 1996; Pilleri et al. 2015). The origin of these bands has been intensely discussed within the PAH hypothesis. The bands at 3.3 μm have been widely accepted to be due to aromatic CH stretching modes common to the PAH family. The origin of the weaker bands (mainly the 3.4 μm feature) on the other hand, still remains unknown. There are three main candidates for these carriers: (1) the bands may be hot bands of the 3.3 μm CH stretching mode (Barker et al. 1987); (2) the bands may be CH stretching modes of aliphatic side groups attached to the periphery of PAHs, such as methyl groups for example (Duley & Williams 1981; Joblin et al. 1996); and/or (3) the bands may come from superhydrogenated PAHs, where the addition of extra H-atoms disrupts the aromaticity of the molecule creating more bands in the region (Bernstein et al. 1996; Sandford et al. 2013).
In Sect. 4.3 (see also Appendix F) we established that, even though the spectrum of the parent molecule looks similar to those of the first 2 superhydrogenated states, the main differences reside in the 3.4 μm band that appears for hydrogenation states greater than (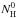 + 1). This band is related to stretching modes of the pair of extra H atoms in the same ring. Indeed, the emission spectra from circumcoronene and circumcircumcoronene superhydrogenated species where the extra H atoms are added to only solo positions do not show a 3.4 μm band. The 3.5 μm feature instead seems to be common to the spectra of all superhydrogenated molecules. This band is related to the stretching of each individual CH2 complex. Note that here we consider superhydrogenated states of up to 4 additional H-atoms. At these superhydrogenation levels, the 3.4 μm band is only observed if the extra H atoms are in duo rings. For higher superhydrogenation states both, the 3.4 and 3.5 μm bands, would also show up for this PAH family, since solo and duo rings would have extra H atoms. However such levels of superhydrogenation are achieved in extremely shielded environments, where the emission from PAHs would come from high density clumps exposed to UV radiation.
+ 1). This band is related to stretching modes of the pair of extra H atoms in the same ring. Indeed, the emission spectra from circumcoronene and circumcircumcoronene superhydrogenated species where the extra H atoms are added to only solo positions do not show a 3.4 μm band. The 3.5 μm feature instead seems to be common to the spectra of all superhydrogenated molecules. This band is related to the stretching of each individual CH2 complex. Note that here we consider superhydrogenated states of up to 4 additional H-atoms. At these superhydrogenation levels, the 3.4 μm band is only observed if the extra H atoms are in duo rings. For higher superhydrogenation states both, the 3.4 and 3.5 μm bands, would also show up for this PAH family, since solo and duo rings would have extra H atoms. However such levels of superhydrogenation are achieved in extremely shielded environments, where the emission from PAHs would come from high density clumps exposed to UV radiation.
From AKARI observations of the NW PDR of NGC 7023, aside the main band observed at 3.3 μm there is a secondary band at 3.4 μm, together with what has been defined as a plateau component at 3.45 μm (Pilleri et al. 2015). The 3.4 μm band appears to become less intense as the plateau widens towards more diffuse environments. Our results indicate that intermediate-to-large PAHs can survive in their normally hydrogenated state in regions where G0/n(H)= 10–100, as it is expected in the more diffuse media of NGC 7023 (Berné & Tielens 2012). It is under these conditions that the 3.3 μm is still evident and the 3.4 μm band starts disappearing immersed in the broadening of the 3.45 μm plateau. However these PAHs would not achieve superhydrogenation. Moreover, from what we have seen, the superhydrogenation pattern of PAHs is very similar for circumcoronene and circumcircumcoronene. Thus, unless the parameters in our model are considerably changed, we would not expect NH> (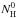 + 1) species at these G0/n(H) ratios.
+ 1) species at these G0/n(H) ratios.
Pilleri et al. (2015) also report 3.4/3.3 band ratios that go from 0.028 to 0.13 from their P1 to P4 positions, where G0 is expected to vary from 7000 to 150 going from the cavity into the NW PDR. If the 3.4 μm band is solely due to superhydrogenated species with extra H atoms in duo rings, such values could be obtained at G0/n(H) ratios 2–3 orders of magnitude lower than what we expect in NGC 7023 (Fig. 12). PAHs smaller than C54H18 could potentially present these ratios at higher G0/n(H) of few times 10-2 at most. Nevertheless as we saw in the case of coronene, these species would probably be completely dehydrogenated, and thus the 3.4 μm band would not be observed. Unless we are underestimating the density in the NW PDR of NGC 7023 by a factor of 100, superhydrogenated species cannot explain the observed 3.4/3.3 ratios.
Unfortunately, other signatures of superhydrogenated species are not as clear as the appearance of bands in the 3 μm region. Such species would also show aliphatic CH deformation modes at 6.85 and 7.25 μm. However these modes are intrinsically very weak and would be completely overpowered by the CC modes in PAH cations. Thus, we find that the main noticeable features of superhydrogenation are the 3 μm bands. Longer wavelength features cannot be clearly distinguished from the ones of the parent molecules.
 |
Fig. 12 Hydrogenation ratio for different G0/n(H) values. The ratios derived from circumcoronene derivatives are shown in blue, while those from circumcircumcoronene derivatives are shown in red. We have assumed a gas temperature of 50 K, and that the fraction of atomic hydrogen is 10% that of molecular hydrogen, in order to model more shielded environments. The 3.4/3.3 ratio traces the superhydrogenation level of the PAHs as the 3.4 μm band is related to the stretching modes of the pair of CH2 complexes within the same ring (which are duo rings for the coronene family). Observed 3.4/3.3 ratios in NGC 7023 range between 0.028 and 0.13, starting from the cavity and going into the NW PDR region, where G0 is expected to vary from 7000–150 (Pilleri et al. 2015). We see that these ratios can be achieved with superhydrogenated species but for G0/n(H) ratios of 0.002–0.006, which is lower than what is expected in the NW PDR of NGC 7023. |
5.2. H2 formation
As mentioned in Sect. 4.2 we have considered two possible ways for PAHs to form H2 molecules in our model: either through H2 abstraction by H, or from direct H2-loss due to photon excitation. It is of some interest then to compare the rates of these processes with those commonly adopted for interstellar dust.
Commonly, H2 is thought to form on dust grains from physisorbed H-atoms recombining through the Langmuir-Hinshelwood mechanism. The standard formulation of the H2 formation rate on dust grains is then given by (Hollenbach & McKee 1979; Burke & Hollenbach 1983):
 (12)where S(T,Td) corresponds to the sticking coefficient of H atoms at temperature T colliding with dust grains at temperature Td; η is the probability that an adsorbed H atom will meet another H atom on the surface of the grain, attach to it and be released in the form of H2; vth is the thermal velocity of the colliding H atoms; n is the total density; nd is the number density of dust grains; and σdnd is the total cross section of dust grains. If we take T = 500 K and Td = 35 K, the sticking coefficient is estimated to be S ≃ 0.2 and the H2 formation efficiency, η, is close to unity (Hollenbach & McKee 1979; Burke & Hollenbach 1983), resulting in Rd(H2) ≃ 6 × 10-18 cm3 s-1. In contrast, experiments on perfect graphite or silicate surfaces measure very low efficiencies (Pirronello et al. 1997, 1999; Katz et al. 1999) – as H atoms quickly evaporate before they can recombine – and the inferred H2 formation rate on such surfaces is negligibly small. The models underpinning the standard dust H2 formation rate assume therefore the presence of so-called enhanced binding sites for physisorbed H, which allow formation at much higher dust temperatures (Hollenbach & Salpeter 1971; Hollenbach & McKee 1979). However, the presence of enhanced binding sites is not well established and their properties are not well known. Hence, this inferred rate should perhaps more properly be considered as an upper limit.
(12)where S(T,Td) corresponds to the sticking coefficient of H atoms at temperature T colliding with dust grains at temperature Td; η is the probability that an adsorbed H atom will meet another H atom on the surface of the grain, attach to it and be released in the form of H2; vth is the thermal velocity of the colliding H atoms; n is the total density; nd is the number density of dust grains; and σdnd is the total cross section of dust grains. If we take T = 500 K and Td = 35 K, the sticking coefficient is estimated to be S ≃ 0.2 and the H2 formation efficiency, η, is close to unity (Hollenbach & McKee 1979; Burke & Hollenbach 1983), resulting in Rd(H2) ≃ 6 × 10-18 cm3 s-1. In contrast, experiments on perfect graphite or silicate surfaces measure very low efficiencies (Pirronello et al. 1997, 1999; Katz et al. 1999) – as H atoms quickly evaporate before they can recombine – and the inferred H2 formation rate on such surfaces is negligibly small. The models underpinning the standard dust H2 formation rate assume therefore the presence of so-called enhanced binding sites for physisorbed H, which allow formation at much higher dust temperatures (Hollenbach & Salpeter 1971; Hollenbach & McKee 1979). However, the presence of enhanced binding sites is not well established and their properties are not well known. Hence, this inferred rate should perhaps more properly be considered as an upper limit.
In our analysis, we can define – analogously – the H2 formation rate through either direct H2-loss (i.e., photodissociation of PAHs) or Eley-Rideal H2 abstractions from PAHs of a given size and charge state Z as: 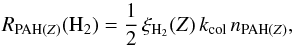 (13)where ξH2(Z) corresponds to our previously defined efficiencies (see Sect. 4.2); kcol corresponds to the fiducial collision rate dependent on the charge state of the molecule (see Appendix E); and nPAH(Z) corresponds to the number density of PAHs of a given size and charge state. From Figure 10 we conclude that the PAHs considered are not able to form H2 efficiently at the surface of the NW PDR of NGC 7023. However, considering a distribution of PAH sizes, there will always be some PAH (e.g., with 30 ≲ NC ≲ 50) that could be found in the relevant hydrogenation states for H2-loss and, hence, could form H2 at efficiencies of ~1% (assuming their molecular properties are similar to those of the coronene family). Assuming that 15% of the carbon is locked in PAHs (with a carbon abundance of 3.5 × 10-4 relative to that of hydrogen), and that all PAHs have ~40 C atoms, then the H2 formation rate due to photodissociation would be a few times 10-19 cm3/s. This is more than an order of magnitude lower than the standard rate generally adopted for dust grains, and certainly much less than the enhanced rate derived by Habart et al. (2004) for PDRs.
(13)where ξH2(Z) corresponds to our previously defined efficiencies (see Sect. 4.2); kcol corresponds to the fiducial collision rate dependent on the charge state of the molecule (see Appendix E); and nPAH(Z) corresponds to the number density of PAHs of a given size and charge state. From Figure 10 we conclude that the PAHs considered are not able to form H2 efficiently at the surface of the NW PDR of NGC 7023. However, considering a distribution of PAH sizes, there will always be some PAH (e.g., with 30 ≲ NC ≲ 50) that could be found in the relevant hydrogenation states for H2-loss and, hence, could form H2 at efficiencies of ~1% (assuming their molecular properties are similar to those of the coronene family). Assuming that 15% of the carbon is locked in PAHs (with a carbon abundance of 3.5 × 10-4 relative to that of hydrogen), and that all PAHs have ~40 C atoms, then the H2 formation rate due to photodissociation would be a few times 10-19 cm3/s. This is more than an order of magnitude lower than the standard rate generally adopted for dust grains, and certainly much less than the enhanced rate derived by Habart et al. (2004) for PDRs.
Bron et al. (2014) recognized the issues facing H2 formation on dust grains in PDRs, and developed a generic model describing H2 formation through the Eley-Rideal mechanism on chemisorbed H-atoms, on a size distribution of dust grains spanning 5–3000 Å. This is implemented in the Meudon PDR Code and was employed by us to calculate the PDR structure, albeit that we excluded the PAH-sized species in the code (cf., Table 1).
First, we recognize that our calculated efficiencies of ~1% are quite comparable to those derived by Bron et al. (2014) (≃5 × 103; see their Fig. 9) for conditions similar as those of NGC 7023 (nH = 104 cm-3, G0 = 1200). This is however completely fortuitous. In their model H2 formation is an Eley-Rideal process on chemisorbed H atoms while in our calculations, under these conditions, the Eley-Rideal mechanism is completely unimportant given the high UV radiation field (ξH2~ few times 10-3). In contrast, in our model, H2 formation is dominated by photolysis. There are some differences in the parameters adopted for the Eley-Rideal mechanism between our model calculations and those of Bron et al. (2014). The main difference is that they use an Eley-Rideal abstraction cross section that is a factor of 100 larger than the value measured for coronene films (Mennella et al. 2012) and adopted by us. Clearly, this cross section is a key factor regulating the ultimate efficiency of the H2 formation of PAHs, and further experimental studies on free-floating PAHs will be very important to settle this issue.
Second, perusing the results of the Meudon PDR Code in more detail, the formation of H2 at low AV in the NW PDR of NGC 7023 is due to Eley-Rideal abstractions from dust grains with sizes larger than ≃20 Å (Bron et al. 2014). The calculated efficiencies for H2 formation on dust grains are of ξH2,dust ≃ 0.4 up to where the H I to H2 transition occurs. This boils down to an H2 formation rate about 5 times the standard value of 3 × 10-17 cm3/s. This is actually larger than what has been observationally inferred for a warm PDR such as NGC 7023 (Habart et al. 2004), which suggests a rate equal to the standard value. Of course, if the abstraction rate for dust grains is a factor 100 lower as experiments on films imply (Mennella et al. 2012), then the Bron et al. (2014) is a gross overestimate. Again, our model predicts that superhydrogenated PAHs are absent at the surface of the NW PDR of NGC 7023 and do not contribute to H2 formation. They only appear deep inside the cloud at AV> 4.5, where the conversion of atomic into molecular hydrogen is essentially complete.
We argue then that at the surfaces of PDRs, PAHs can contribute to the formation of H2 by means of photodissociation only if PAHs of just the “right” size dominate the PAH population in these regions. Their contribution would be then at the 1–10% level of the standard H2 formation rate assumed for dust grains. This assumption depends very much on the kinetic parameters that control the branching ratio of H versus H2 photolysis channels (cf., Figs. 5 and 6), and these have been derived from experiments on the small PAH, pyrene. Further experiments on astrophysically relevant PAHs will be important to make a firm conclusion, but given this caveat, we conclude that PAHs are not the cause of the high inferred H2 formation rates in PDRs.
6. Conclusions
We have developed a kinetic model in order to study the abundance distribution, IR emission, and H2 formation rate for 3 specific PAHs of different sizes in the NW PDR of NGC 7023. The molecules correspond to the first 3 members of the coronene family with PAH sizes between 24 and 96 carbon atoms, which span the astrophysically relevant size range in the ISM. We have chosen to study these species at the molecular specific level, as many of their relevant molecular properties and fragmentation behaviour have been determined.
In order to model the physical conditions inside the cloud we made use of the Meudon PDR Code, and we gave this as input to our kinetic model. We considered the loss of an H atom or an H2 molecule as multiphoton dissociation processes, and we worked under the premise that PAHs with extra H atoms can form H2 through an Eley-Rideal abstraction mechanism. We then derived the abundances under the steady state assumption.
In agreement with earlier studies (Le Page et al. 2001, 2003; Montillaud et al. 2013; Boschman et al. 2012), clear differences emerge in the distribution of species with PAH size. The smallest PAH in our sample, coronene, is found to be a very fragile molecule that is easily destroyed down to its carbon cluster form (assuming no isomerization) for a wide range of G0/n(H) ratios. Only in highly shielded environments (G0/n(H)< 0.01), would a small fraction of this species be found with extra H atoms.
The larger species on the other hand are more stable against dehydrogenation. In fact, the larger the PAH the more likely it is to find it in its normally hydrogenated state (i.e., 1 H atom per C atom at its periphery). Our largest molecule, circumcircumcoronene, is mostly found in its normal hydrogenated state up to very large G0/n(H) ratios (G0/n(H)~ 105), while our intermediate size molecule, circumcoronene, starts losing H atoms at G0/n(H)≳ 1–10 depending on the intensity of the UV field. Regarding the presence of PAHs with extra H atoms, we find that only at G0/n(H)<5 × 10-3 intermediate-to-large PAHs with extra H atoms start dominating the abundance distribution, being in their neutral and anionic charge states.
Comparing our findings with observations of the emission in the NW PDR of NGC 7023, we find that intermediate size PAHs must be dominating the abundance of the emitting population. Small PAHs like coronene – if present – contribute at a negligible level. Together with this, we agree with previous studies on the fact that the spectral variations observed throughout the PDR in the 5–20 μm region are mainly related to variations in the ionization state of the PAHs. The footprint of hydrogenation is only discernible in the 3 μm region through the specific appearance of bands at 3.4 and 3.5 μm. However this region could be affected by other effects such as anharmonicities or the presence of PAHs with methyl groups attached at their periphery. Based on the available AKARI observations of the NW PDR of NGC 7023, we do not expect compact PAHs with extra H atoms to be responsible for the 3.4/3.3 ratio observed in NGC 7023, since superhydrogenated species are only present in more shielded environments where G0/n(H) is 2–3 orders of magnitude lower than what is derived from observations.
Finally, concerning the role of PAHs in the formation of H2 in photodissociation regions, we find that PAHs can form H2 through either Eley-Rideal abstraction of H2 from superhydrogenated PAHs in highly shielded environments, or through photodissociation under PDR-like conditions of “normal” or dehydrogenated PAHs. Our results show that, at the surface of PDRs, Eley-Rideal abstraction is never important. Our calculations are in good quantitative agreement with the model results by Bron et al. (2014) if the difference in abstraction cross section is accounted for. We find that photodissociation of PAHs can be a more important source of H2 in PDR surfaces, but this cannot account for the inferred high rates of H2 formation in PDRs, unless the kinetic parameters governing the branching ratio between H and H2 channels for astrophysically relevant PAHs is very different from those measured for small PAHs in the laboratory.
Acknowledgments
Studies of interstellar PAHs at Leiden Observatory are supported through advanced ERC grant 246976 from the European Research Council, through a grant by the Dutch Science Agency, NWO, as part of the Dutch Astrochemistry Network, and through the Spinoza premie from the Dutch Science Agency, NWO. A.C. acknowledges NWO for a VENI grant (grant No. 639.041.543). DFT calculations were performed with the Cartesius Supercomputer facility (grant SH-362-15).
References
- Aannestad, P. A., & Kenyon, S. J. 1979, ApJ, 230, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Abouelaziz, H., Gomet, J. C., Pasquerault, D., Rowe, B. R., & Mitchell, J. B. A. 1993, J. Chem. Phys., 99, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Alecian, E., Catala, C., Wade, G. A., et al. 2008, MNRAS, 385, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Allain, T., Leach, S., & Sedlmayr, E. 1996, A&A, 305, 602 [NASA ADS] [Google Scholar]
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Allamandola, L. J., Hudgins, D. M., & Sandford, S. A. 1999, ApJ, 511, L115 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- An, W., Shao, N., Bulusu, S., & Zeng, X. C. 2008, J. Chem. Phys., 128, 084301 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, H., Boersma, C., Werner, M. W., et al. 2015, ApJ, 807, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E.L.O., Tielens, A.G.G.M., Bauschlicher, Jr. C.W. 2001, ApJ, 556, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, J. R., Allamandola, L. J., & Tielens, A. G. G. M. 1987, ApJ, 315, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W. 1998, ApJ, 509, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., & Bakes, E. L. O. 2001, Chem. Phys., 274, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., & Ricca, A. 2013, Chem. Phys. Lett., 566, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., & Ricca, A. 2014, Theo. Chem. Acc., 133, 1454 [Google Scholar]
- Bauschlicher, C. W., Peeters, E., & Allamandola, L. J. 2008, ApJ, 678, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., Boersma, C., Ricca, A., et al. 2010, ApJS, 189, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 5648 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard-Salas, J., Habart, E., Köhler, M., et al. 2015, A&A, 574, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berné, O., & Tielens, A. G. G. M. 2012, Proc. of the National Academy of Science of the US, 109, 401 [CrossRef] [Google Scholar]
- Berné, O., Joblin, C., Deville, Y., et al. 2007, A&A, 469, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berné, O., Montillaud, J., Joblin, C. 2015, A&A, 577, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernstein, M. P., Sandford, S. A., & Allamandola, L. J. 1996, ApJ, 472, L127 [CrossRef] [Google Scholar]
- Betts, N. B., Stepanovic, M., Snow, T. P., & Bierbaum, V. M. 2006, ApJ, 651, L129 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Beyer, T., & Swinehart, D. F. 1973, Commun. Assoc. Comput. Machin. 16, 379 [Google Scholar]
- Biennier, L., Alsayed-Ali, M., Foutel-Richard, A., et al. 2006, Discuss. Faraday Soc., 133, 289 [Google Scholar]
- Boersma, C., Mattioda, A. L., Bauschlicher, C. W., et al. 2009, ApJ, 690, 1208 [NASA ADS] [CrossRef] [Google Scholar]
- Boersma, C., Rubin, R. H., & Allamandola, L. J. 2012, ApJ, 753, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Boersma, C., Bregman, J. D., & Allamandola, L. J. 2013, ApJ, 769, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Boersma, C., Bauschlicher, C. W. Jr., Ricca, A., et al. 2014, ApJS, 211, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Boersma, C., Bregman, J., & Allamandola, L. J. 2015, ApJ, 806, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Boschman, L., Reitsma, G., Cazaux, S., et al. 2012, ApJ, 761, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Boschman, L., Cazaux, S., Spaans, M., Hoekstra, R., & Schlathölter, T. 2015, A&A, 579, A72 [Google Scholar]
- Bregman, J. D., Allamandola, L. J., Witteborn, F. C., Tielens, A. G. G. M., & Geballe, T. R. 1989, ApJ, 344, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A&A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., Boschman, L., Rougeau, N., et al. 2016, Nature, DOI: 10.1038/srep19835 [Google Scholar]
- Chokshi, A., Tielens, A. G. G. M., Werner, M. W., & Castelaz, M. W. 1988, ApJ, 334, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Croiset, B. A., Candian, A., Berné, O., & Tielens, A. G. G. M. 2016, A&A, 590, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2005, MNRAS, 361, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, W. R., & Kropp, J. L. 1969, J. Phys. Chem., 73, 693 [CrossRef] [Google Scholar]
- Demarais, N. J., Yang, Z., Martinez, O., et al. 2012, AJ, 746, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Demarais, N. J., Yang, Z., Snow, T. P., & Bierbaum, V. M. 2014, ApJ, 784, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Denifl, S., Ptasińska, S., Sonnweber, B., et al. 2005, J. Ch. Phys., 123, 104308 [Google Scholar]
- Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W. 1996, MNRAS, 279, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W., & Williams, D. A. 1981, MNRAS, 196, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. A., Knight, A. M., Negishi, Y., et al. 1999, Chem. Phys. Lett., 309, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, B., France, K., Lupu, R. E., & McCandliss, S. R. 2010, ApJ, 725, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2009, Gaussian 09, Revision D.01 (Pittsburgh PA: Gaussian, Inc.) [Google Scholar]
- Fuente A., Martín-Pintado J., Rodríguez-Franco A., & Moriarty-Schieven, G. D. 1998, A&A 339, 575 [Google Scholar]
- Fuente, A., Rodríguez-Franco, A., García-Burillo, S., Martín-Pintado, J., & Black, J. H. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fusaro, M. 2012, Struct. Chem., 23, 237 [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Tielens, A. G. G. M., Peeters, E., & Jones, A. P. 2008, ApJ, 679, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T., Tielens, A. G. G. M., Allamandola, L. J., Moorhouse, A., & Brand, P. W. J. L. 1989, ApJ, 341, 278 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gry, C., Boulanger, F., Nehmé, C., et al. 2002, A&A, 391, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., et al. 2003, A&A, 397, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., Walmsley, C. M., & Pineau des Forêts, G. 2004, A&A, 414, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hassouna, M., Le Garrec, J., Rebrion-Rowe, C., Travers, D., & Rowe, B. 2003, Dissociative Recombination of Molecular Ions with Electrons, ed. S. L. Guberman (Kluwer Academic/Plenum Publishers), 451 [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1979, ApJS, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Joblin, C., Tielens, A. G. G. M., Allamandola, L. J., & Geballe, T. R. 1996, ApJ, 458, 610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joblin, C., Pilleri, P., Montillaud, J., et al. 2010, A&A, 521, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jochims, H. W., Rühl, E., Baumgärtel, H., & Leach, S. 1996, A&A, 314, 1003 [NASA ADS] [Google Scholar]
- Jochims, H. W., Rühl, E., Baumgärtel, H., Tobita, S., & Leach, S. 1997, IJMSI, 167/168, 35 [Google Scholar]
- Jura, M. 1975, ApJ, 197, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Kapinus, V. 2004, Ph.D. Thesis, Caltech [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Habart, E., Arab, H., et al. 2014, A&A, 569, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kropp, J. L., & Dawson, W. R. 1967, J. Phys. Chem., 71, 4499 [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog: VI/39 [Google Scholar]
- Langhoff, S. R. 1996, J. Phys. Chem., 100, 2819 [CrossRef] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roue, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Page, V., Keheyan, Y., Bierbaum, V. M., & Snow, T. P. 1997, JACS, 119, 35 [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJSS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, AJ, 584, 316 [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJSS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Léger, A., & Puget, J. L. 1984, A&A, 137, L5 [NASA ADS] [Google Scholar]
- Léger, A., Boissel, P., & d’Hendecourt, L. 1988, Phys. Rev. Lett., 60, 92 [Google Scholar]
- Lemaire, J. L., Field, D., Gerin, M., et al. 1996, A&A, 308, 895 [NASA ADS] [Google Scholar]
- Ling, Y., Gotkis, Y., & Lifshitz, C. 1995, Eur. J. Mass Spectrom., 1, 41 [CrossRef] [Google Scholar]
- Mackie, C. J., Peeters, E., Bauschlicher, C. W., Jr., & Cami, J. 2015, ApJ, 799, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007, Chem. Phys., 332, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Malloci, G., Mulas, G., Cecchi-Pestellini, C., & Joblin, C. 2008, A&A, 489, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, V., Hornekær, L., Thrower, J., & Accolla, M. 2012, ApJ, 745, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Novotný, O., Sivaraman, B., Rebrion-Rowe, C., et al. 2005, J. Chem. Phys., 123, 104303 [NASA ADS] [CrossRef] [Google Scholar]
- Paris, C., Alcamí, M., Martín, F., & Díaz-Tendero, S. 2014, J. Chem. Phys., 140, 204307 [NASA ADS] [CrossRef] [Google Scholar]
- Peeters, E., Hony, S., Van Kerkhoven, C., et al. 2002, A&A, 390, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilleri, P., Montillaud, J., Berné, O., & Joblin, C. 2012, A&A, 542, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilleri, P., Joblin, C., Boulanger, F., & Onaka, T. 2015, A&A, 577, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pino, T., Carpeutier, Y., Féraud, G., et al. 2011, EAS Pub. Ser., 46, 355 [CrossRef] [EDP Sciences] [Google Scholar]
- Pirronello, V., Biham, O., Liu, C., Shen, L., & Vidali, G. 1997, ApJ, 483, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Pirronello, V., Liu, C., Roser, J. E., & Vidali, G. 1999, A&A, 344, 681 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran: The Art of Scientific Computing, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Purcell, E. M. 1976, ApJ, 206, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Radziszewski, J. G., Hess, B. A., & Zahradnik, R. 1992, JAChS, 114, 52 [Google Scholar]
- Rapacioli, M., Joblin, C., & Boissel, P. 2005, A&A, 429, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauls, E., & Hornekær, L. 2008, ApJ, 679, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Rebrion-Rowe, C., Le Garrec, J., Hassouna, M., Travers, D., & Rowe, B. 2003, Int. Jour. Mass Spec., 223, 236 [Google Scholar]
- Reitsma, G., Boschman, L., Deuzeman, M.J., et al. 2014, Phys. Rev. Lett., 113, 053002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ricca, A., Bauschlicher, C. W., Jr., Boersma, C., Tielens, A. G. G. M., & Allamandola, L. J. 2012, ApJ, 754, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Ricks, A. M., Douberly, G. E., & Duncan, M. A. 2009, ApJ, 702, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, P. F., Lucas, P. W., Hoare, M. G., Aitken, D. K., & Smith, C. H. 1996, MNRAS, 280, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, M. J. F., Berné, O., Boersma, C., Allamandola, L. J., & Tielens, A. G. G. M. 2011, A&A, 532, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandford, S. A., Bernstein, M. P., & Materese, C. K. 2013, ApJS, 205, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Schutte, W. A., Tielens, A. G. G. M., & Allamandola, L. J. 1993, ApJ, 415, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Sellgren, K., Werner, M. W., Ingalls, J. G., et al. 2010, ApJ, 722, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, S. E., & Rabinovitch, B. S., 1973, J. Phys. Chem., 58, 2438 [Google Scholar]
- Stephens, P. J., Devlin, F. J., Chabalowski, C. F., & Frisch, M. J. 1994, J. Phys. Chem., 98, 11623 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thrower, J. D., Nilsson, L., Jørgensen, B., et al. 2011, in PAHs and the Universe, eds. C. Joblin, & A. G. G. M. Tielens (Les Ulis: EDP), EAS Pub. Ser. 46, 453 [Google Scholar]
- Tobita, S., Meinke, M., Illenberger, E., et al. 1992, Chem. Phys., 161, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Tobita, S., Leach, S., Jochims, H. W., et al. 1994, Canadian J. Phys., in press [Google Scholar]
- Verstraete, L., Leger, A., d’Hendecourt, L., Defourneau, D., & Dutuit, O. 1990, A&A, 237, 436 [NASA ADS] [Google Scholar]
- Werner, M. W., Uchida, K. I., Sellgren, K., et al. 2004, ApJS, 154, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., Gordon, K. D., Vijh, U. P., et al. 2006, ApJ, 636, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Young Owl, R. C., Meixner, M. M., Fong, D., et al. 2002, ApJ, 578, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Paardekooper, D. M., Linnartz, H., & Tielens, A. G. G. M. 2014a, ApJ, 797, L30 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Molecular characteristics
Appendix A.1: Ionization potentials and electron affinities
Malloci et al. (2008) calculated the IPs for the even dehydrogenated states of coronene, i.e., C24H2 n where n= 0–6. According to their calculations, the IP increases with higher levels of dehydrogenation. This increase is relatively constant, with ΔIP ~ 0.1 eV per dehydrogenation (see Fig. 4). For coronene, the theoretically calculated energies vary from 7.02 eV for C24H12 to 8.25 eV for C24. This last value also agrees with the calculations of An et al. (2008) for C24. The decrease of the IP with hydrogenation has also been reported for anthracene (C14H10) and naphthalene (C10H8) first dehydrogenated and first superhydrogenated states, where ΔIP becomes more constant as the PAH gets larger (Kapinus 2004). Based on this, we decided to adopt this ΔIP with hydrogenation for all molecules and all ionization states.
Ionization potentials and electron affinities of C24H12, C54H18 and C96H24.
Appendix A.2: IR intrinsic spectra
Tables A.2–A.4 list the PAHs for which we have the IR intrinsic spectra. The spectra are either taken from the NASA Ames PAH Database (PAHdb) or from our own calculations (C).
Appendix A.3: Electron attachment/recombination with electrons
Tobita et al. (1992) performed low energy electron impact experiments on small neutral PAHs, and reported rate coefficients for electron attachment of 9 × 10-10 and 2 × 10-10 cm3/s for anthracene (C14H10) and pyrene (C16H10), respectively. Denifl et al. (2005) studied the electron attachment to neutral coronene and corannulene (C20H10), and obtained similar trends as observed in the experiments of Tobita et al. (1992). They estimated the electron recombination cross section to be of 3.8 × 10-16 cm2 for the formation of the coronene anion. Regarding cations, electron recombination rates have been measured for a few small PAH species using flowing afterglow experiments. These studies have determined rate coefficients of 1 × 10-6 for benzene, 3 × 10-7 for naphthalene, 1.1 × 10-6 for azulene, 5.0 × 10-7 for acenaphthene, 2.4 × 10-6 for anthracene, phenanthrene and fluoranthene, and 4.1 × 10-6 cm3/s for pyrene (Abouelaziz et al. 1993; Hassouna et al. 2003; Rebrion-Rowe et al. 2003; Novotný et al. 2005; Biennier et al. 2006). No studies have been done for the PAHs considered here.
PAH Intrinsic spectra available for coronene C24H12 derivatives.
PAH Intrinsic spectra available for circumcoronene C54H18 derivatives.
PAH Intrinsic spectra available for circumcircumcoronene C96H24 derivatives.
Given the lack of experimental studies on large PAHs, we use collisional rates as described in Bakes & Tielens (1994), which take into account the Coulomb interaction between the particles involved: 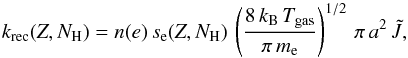 (A.1)where n(e) is the electron density, kB is the Boltzmann constant, Tgas the gas temperature, me the electron mass, se(Z, NH) is the electron sticking coefficient for each molecule, a is the radius of the PAH, and
(A.1)where n(e) is the electron density, kB is the Boltzmann constant, Tgas the gas temperature, me the electron mass, se(Z, NH) is the electron sticking coefficient for each molecule, a is the radius of the PAH, and 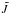 is a function that depends on the electron charge and the charge of the PAH (see full expression in Draine & Sutin 1987). We calculate the radius of each molecule as a = 0.9 × 10-8
is a function that depends on the electron charge and the charge of the PAH (see full expression in Draine & Sutin 1987). We calculate the radius of each molecule as a = 0.9 × 10-8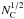 cm, where NC is the number of carbon atoms of the molecule. Since Eq. (A.1) is valid for spherical molecules, we use a 0.82 correction factor as derived by Verstraete et al. (1990) for disk-shaped molecules. For positively ionized molecules we assume a sticking coefficient of unity given the attractive interaction between the particles. Sticking coefficients for neutral species are calculated following Allamandola et al. (1989). Polarizabilities are taken from the Cagliari PAH database for the parent molecules C24H12 and C54H18. To determine the polarizability of C96H24, we performed a fit as a function of size to the polarizabilities of all the PAHs compiled in the database (up to sizes of 54 C atoms) for a given ionization state, and then extrapolated this to NC = 96. We then used the polarizabilities of the parent molecules for all the respective derivatives. The calculated sticking coefficients increase with EA, reaching unity for EA ≳ 1 eV.
cm, where NC is the number of carbon atoms of the molecule. Since Eq. (A.1) is valid for spherical molecules, we use a 0.82 correction factor as derived by Verstraete et al. (1990) for disk-shaped molecules. For positively ionized molecules we assume a sticking coefficient of unity given the attractive interaction between the particles. Sticking coefficients for neutral species are calculated following Allamandola et al. (1989). Polarizabilities are taken from the Cagliari PAH database for the parent molecules C24H12 and C54H18. To determine the polarizability of C96H24, we performed a fit as a function of size to the polarizabilities of all the PAHs compiled in the database (up to sizes of 54 C atoms) for a given ionization state, and then extrapolated this to NC = 96. We then used the polarizabilities of the parent molecules for all the respective derivatives. The calculated sticking coefficients increase with EA, reaching unity for EA ≳ 1 eV.
Appendix B: Photodissociation rates
Tables B.1–B.3 present the fit parameters to the H-loss and H2-loss rates as a function of UV field intensity G0 for the molecules considered in our work. The fits are of the form log 10(ki(G0))=∑ jpj log 10(G0)j from j= 0–4 for each i process (i.e., H-loss and H2-loss). The fits are shown for the molecules for which the IR intrinsic spectra were available.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for coronene derivatives.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for circumcoronene derivatives.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for circumcircumcoronene derivatives.
Appendix C: Model
Since there are (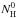 + 5) hydrogenation states for each parent molecule, and NZ ionization states depending on the molecule, for each species we must solve (
+ 5) hydrogenation states for each parent molecule, and NZ ionization states depending on the molecule, for each species we must solve (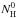 + 5) ×NZ equations of the form:
+ 5) ×NZ equations of the form: ![\appendix \setcounter{section}{3} \begin{eqnarray*} \frac{{\rm d} [\text{PAH}\,(Z, {N}_{\text{H}})]}{{\rm d}t} = \sum(\text{Formation})\, -\, \sum(\text{Destruction}), \end{eqnarray*}](/articles/aa/full_html/2016/11/aa28819-16/aa28819-16-eq303.png) where formation processes (when applicable) include: ionization of PAH (Z−1, NH); electron attachment to PAH (Z + 1, NH); loss of an H atom from PAH (Z, NH + 1); loss of H2 from PAH (Z, NH + 2); H addition to PAH (Z, NH−1) (or PAH (Z−1, NH−1) in the case of associative detachment); and H2 abstraction from PAH (Z, NH + 1). Destruction processes on the other hand (when applicable) are given by: ionization of PAH (Z, NH); electron attachment to PAH (Z, NH); loss of an H atom from PAH (Z, NH); loss of H2 from PAH (Z, NH); H addition to PAH (Z, NH); and H2 abstraction from PAH (Z, NH).
where formation processes (when applicable) include: ionization of PAH (Z−1, NH); electron attachment to PAH (Z + 1, NH); loss of an H atom from PAH (Z, NH + 1); loss of H2 from PAH (Z, NH + 2); H addition to PAH (Z, NH−1) (or PAH (Z−1, NH−1) in the case of associative detachment); and H2 abstraction from PAH (Z, NH + 1). Destruction processes on the other hand (when applicable) are given by: ionization of PAH (Z, NH); electron attachment to PAH (Z, NH); loss of an H atom from PAH (Z, NH); loss of H2 from PAH (Z, NH); H addition to PAH (Z, NH); and H2 abstraction from PAH (Z, NH).
The system of equations can then be written in matrix form as Mx = 0, where M represents the kinetic matrix with all the rate constants calculated for a given set of physical conditions Tgas, n(e), n(H) and G0. For each slab of the PDR this system of equations is solved using the Newton-Raphson Method (Press et al. 1992). This method proved to be fast and reached convergence for every slab considered in our work.
Appendix D: Relative abundance distribution of PAHs in NGC 7023
Figures D.1–D.3 show the fractional contribution from coronene (black), circumcoronene (blue) and circumcircumcoronene (red) derivatives in the NW PDR of NGC 7023, according to the physical conditions modelled by the Meudon PDR Code. Odd and even hydrogenated states have been depicted in slightly different colors for a better visualization.
 |
Fig. D.1 Fractional contribution from coronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Coronene is completely dehydrogenated throughout most of the cloud (NH= 0). No contribution from dicationic species is observed. |
 |
Fig. D.2 Fractional contribution from circumcoronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Unlike coronene, these molecules are found in their normally hydrogenated state (NH= 18) with traces of partial dehydrogenation at the surface of the cloud, and at AV~ 1.8. No contribution from trications is observed. |
 |
Fig. D.3 Fractional contribution from circumcircumcoronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Compared to the smaller species, circumcircumcoronene is mainly found in its normal hydrogenated state (NH= 24). There is no significant contribution from Z> 2 species (trications contribute in only 0.9% at AV= 0). |
Coronene is completely dehydrogenated throughout most of the cloud (NH= 0). Only at an AV> 4 we find traces of the first 4 hydrogenated states. This is driven by a rise in the atomic hydrogen density due to the modelling of the cloud (finite size). In terms of the ionization state of the coronene derivatives, we find that at the surface of the cloud (AV= 0) most molecules are in neutral state, while cations contribute in ~27% to the total PAH abundance.
Unlike coronene, circumcoronene derivatives are found in their normally hydrogenated state (NH= 18) with traces of partial dehydrogenation at the surface of the cloud, and at AV~ 1.8. Regarding ionization, positively ionized species dominate the distribution at the surface of the cloud, contributing in ~59% to the total PAH abundance.
Compared to the smaller molecules, circumcircumcoronene derivatives are mainly found in the normal hydrogenated state (NH= 24). No dehydrogenation is observed. Only minor levels of superhydrogenation appear at high extinction due to the finite cloud size assumption. In terms of ionization, we see a larger contribution from Z> 0 species at the surface of the cloud (~74%) compared to coronene and circumcoronene derivatives. There is no significant contribution from Z= 3 nor Z= 4 species (trications contribute in only 0.9% at AV= 0).
Appendix E: Fiducial collision rates
For neutral species we have considered a fiducial collision rate kcol=σcol × vth × n(H), where σcol corresponds to the geometrical cross section of the parent molecule, and vth corresponds to the thermal velocity of the colliding H atoms. For anions we have considered a fiducial collision rate of kcol= 7.8 × 10-10 × n(H), since we consider the H-addition as an associative detachment reaction (see Sect. 2.4.4). For cations on the other hand, the fiducial collision rate adopted is of kcol= 1.4 × 10-10 × n(H). When calculating the efficiency of H2 formation from direct H2-loss after photon absorption we multiply the fiducial rates by a 0.5 factor given that each photodissociation event removes 2 H atoms from the molecule.
Appendix F: Spectral variations
Appendix F.1: PAH emission spectra in the NW PDR of NGC 7023
For coronene derivatives, the spectra are dominated by that of the completely dehydrogenated molecule. As listed in Table A.2, we do not have the intrinsic spectra of the anionic completely dehydrogenated coronene and thus, its contribution is not considered in the spectra shown in Fig. F.1. However we do not expect this to affect the resulting spectrum since the contribution from C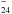 increases smoothly from the surface of the cloud up to only a 7.4% at an AV= 2. In the case of circumcoronene, ~34% of the emitting species are not considered in the spectrum at AV= 0, where traces of the first partially dehydrogenated molecules are observed (e.g., NH= 17–12). The spectra at AV= 0.4 to 1.2 on the other hand, are >85% complete, while at AV= 1.6 and 2.0 the emission is complete to a 80%. Since the contributions from partially dehydrogenated molecules are overall small, and they are not highly dehydrogenated, we expect the spectra to be representative of the actual emission. In the case of our largest species, circumcircumcoronene, all spectra are complete.
increases smoothly from the surface of the cloud up to only a 7.4% at an AV= 2. In the case of circumcoronene, ~34% of the emitting species are not considered in the spectrum at AV= 0, where traces of the first partially dehydrogenated molecules are observed (e.g., NH= 17–12). The spectra at AV= 0.4 to 1.2 on the other hand, are >85% complete, while at AV= 1.6 and 2.0 the emission is complete to a 80%. Since the contributions from partially dehydrogenated molecules are overall small, and they are not highly dehydrogenated, we expect the spectra to be representative of the actual emission. In the case of our largest species, circumcircumcoronene, all spectra are complete.
 |
Fig. F.1 PAH emission spectra at different points inside the NW PDR of NGC 7023. For each species, the spectra have been derived by adding the contributions of all ionization and hydrogenation states, from the abundances presented in Appendix D. The results for C24H12 derivatives are shown in black, while the spectra for C54H18 and C96H24 species are shown in blue and red, respectively. The spectra have been conveniently normalized to the peak intensity of the 6.7 μm band for C24H12 derivatives, and to the 11.2 μm band for the larger species. |
 |
Fig. F.2 Emission spectra for different G0/n(H) ratios at G0= 103. The results for coronene derivatives are shown in black, while the spectra for C54H18 and C96H24 derivatives are shown in blue and red, respectively. The spectra have been conveniently normalized for a better comparison between consecutive G0/n(H) ratios. Given the unavailability of the intrinsic spectra for some of these molecules, the spectra at low G0/n(H) ratios are not complete due to the increasing abundance of highly superhydrogenated anionic species. |
Appendix F.2: PAH emission spectra for different G0/n(H) ratios at G0 = 103
In the case of coronene, the dominant species is the completely dehydrogenated molecule for most G0/n(H) ratios. Only at G0/n(H)≤ 0.01 partially dehydrogenated derivatives in neutral and anionic form become more relevant. The spectrum at G0/n(H)= 0.01 is missing the contribution from 24% of the emitting species mostly due to C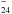 , while the spectrum at G0/n(H)= 0.001 is missing 81.7% due to partially dehydrogenated neutrals and anions. The spectrum of normally hydrogenated coronene is never really important (even at a G0/n(H)= 0.001 C24H12 contributes at a 1% level only). The same applies for superhydrogenated species, which barely appear at G0/n(H)= 0.001 contributing at a 5% level. The spectrum shown in Fig. F.2 is then mainly due to normal-to-superhydrogenated species and not from the partially dehydrogenated molecules, whose contribution would dominate the emission if they were available.
, while the spectrum at G0/n(H)= 0.001 is missing 81.7% due to partially dehydrogenated neutrals and anions. The spectrum of normally hydrogenated coronene is never really important (even at a G0/n(H)= 0.001 C24H12 contributes at a 1% level only). The same applies for superhydrogenated species, which barely appear at G0/n(H)= 0.001 contributing at a 5% level. The spectrum shown in Fig. F.2 is then mainly due to normal-to-superhydrogenated species and not from the partially dehydrogenated molecules, whose contribution would dominate the emission if they were available.
For circumcoronene, the dominant species at G0/n(H)= 100 is C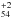 in 83% for which we do not have the IR spectrum. Therefore, the emission shown in Fig. F.2 corresponds mainly to that of C
in 83% for which we do not have the IR spectrum. Therefore, the emission shown in Fig. F.2 corresponds mainly to that of C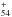 , that contributes only in 12% to the total abundance, with even smaller traces of C54H. Since the spectra of dications is in general similar to that of cations, we expect the actual emission to resemble the one shown in Fig. F.2, except for a stronger 5 μm band, typical from highly positively ionized completely dehydrogenated PAHs. The spectra at G0/n(H)= 10 is missing the emission from 54% of the species due to partially dehydrogenated molecules in positively ionized states. Going to lower G0/n(H) values, the spectra at G0/n(H)= 0.1 and 0.01 are 99 and 79% complete respectively. Both dominated by C54H18. The contribution from superhydrogenated species in this G0/n(H) range goes from ~3 to 35%, which is clear from the inspection of the 3 μm region. The spectra at G0/n(H)= 0.001 is missing 97.5% of the emitting species due to the highly superhydrogenated molecules in anionic and neutral states. Thus the emission presented in the Figure corresponds only to the first superhydrogenated molecules for which we have the spectra.
, that contributes only in 12% to the total abundance, with even smaller traces of C54H. Since the spectra of dications is in general similar to that of cations, we expect the actual emission to resemble the one shown in Fig. F.2, except for a stronger 5 μm band, typical from highly positively ionized completely dehydrogenated PAHs. The spectra at G0/n(H)= 10 is missing the emission from 54% of the species due to partially dehydrogenated molecules in positively ionized states. Going to lower G0/n(H) values, the spectra at G0/n(H)= 0.1 and 0.01 are 99 and 79% complete respectively. Both dominated by C54H18. The contribution from superhydrogenated species in this G0/n(H) range goes from ~3 to 35%, which is clear from the inspection of the 3 μm region. The spectra at G0/n(H)= 0.001 is missing 97.5% of the emitting species due to the highly superhydrogenated molecules in anionic and neutral states. Thus the emission presented in the Figure corresponds only to the first superhydrogenated molecules for which we have the spectra.
 |
Fig. F.3 Intrinsic spectra of different hydrogenation states of the neutral coronene (left), circumcoronene (middle) and circumcircumcoronene (right panel) molecules. Only the 3 μm region is presented. This spectral region is the one where differences in the hydrogenation state of PAHs can be clearly observed. Differences in the hydrogenation state (within a given PAH size and ionization state) are clear from the appearance of more features at 3.4 and 3.5 μm. |
Regarding circumcircumcoronene, the spectra are complete down to a G0/n(H)= 0.1, and show the variation in the ionization state of C96H24, from being mostly in Z= 3 state to neutral. The spectrum at G0/n(H)= 0.01 is missing 19% of the emitting molecules due to highly superhydrogenated Z=−1 and Z= 0 species, which then become the dominant species at G0/n(H)= 0.001. However these will not have a discernible footprint compared to that of the normally hydrogenated molecule which is still the dominating species: C96H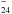 contributes in 8.8% and C96H
contributes in 8.8% and C96H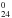 in 68% at G0/n(H)= 0.1, and 26% and 21.6% respectively at G0/n(H)= 0.01. Also, going from G0/n(H)= 0.1 to 0.01 the abundance of superhydrogenated species – for which the spectra is considered in Fig. F.2 – increases by a factor of 10, which is only clear in the 3 μm spectral region, although the signal is rather weak.
in 68% at G0/n(H)= 0.1, and 26% and 21.6% respectively at G0/n(H)= 0.01. Also, going from G0/n(H)= 0.1 to 0.01 the abundance of superhydrogenated species – for which the spectra is considered in Fig. F.2 – increases by a factor of 10, which is only clear in the 3 μm spectral region, although the signal is rather weak.
Appendix F.3: Intrinsic spectra of different hydrogenation states of neutral coronene, circumcoronene and circumcircumcoronene molecules
Figure F.3 shows a comparison of the IR spectra of different hydrogenation states of coronene, circumcoronene and circumcircumcoronene in the 3 μm region. Here we see clearly the aromatic nature of the bands at 3.28–3.30 μm that disappear in the completely dehydrogenated molecules, and in the fully superhydrogenated molecule (e.g., C24H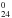 ). We have also checked this for other ionization states. The 3.5 μm band is common to all superhydrogenated states of these species. This band is due to the CH (symmetric and asymmetric) stretching modes in a single CH2 group. In the case of C54H
). We have also checked this for other ionization states. The 3.5 μm band is common to all superhydrogenated states of these species. This band is due to the CH (symmetric and asymmetric) stretching modes in a single CH2 group. In the case of C54H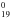 the bandat 3.5 μm is very weak compared to the bands at 3.3 μm (the peak intensity of the 3.28 μm band is of 12 × 105 cm2/mol, whereas the peak intensity of the band at 3.47 μm is of 0.06 × 105 cm2/mol). Thus it cannot be clearly seen with the scale used in this Figure. On the other hand, the band at 3.4 μm appears from the second hydrogenation on, becoming particularly intense for the fully hydrogenated molecule in the case of coronene (C24H24). This band is related to the CH stretches of the CH2 groups in the same (duo) rings. Superhydrogenated PAHs with extra H atoms in solo positions do not present this band.
the bandat 3.5 μm is very weak compared to the bands at 3.3 μm (the peak intensity of the 3.28 μm band is of 12 × 105 cm2/mol, whereas the peak intensity of the band at 3.47 μm is of 0.06 × 105 cm2/mol). Thus it cannot be clearly seen with the scale used in this Figure. On the other hand, the band at 3.4 μm appears from the second hydrogenation on, becoming particularly intense for the fully hydrogenated molecule in the case of coronene (C24H24). This band is related to the CH stretches of the CH2 groups in the same (duo) rings. Superhydrogenated PAHs with extra H atoms in solo positions do not present this band.
All Tables
Input parameters for the modelling of the NW PDR of NGC 7023 using the Meudon PDR Code.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for coronene derivatives.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for circumcoronene derivatives.
Fit parameters to H-loss rate, kH,Loss, and H2-loss rate, kH2,Loss, as a function of UV field intensity G0 for circumcircumcoronene derivatives.
All Figures
 |
Fig. 1 PAHs studied in this work. From left to right: coronene (C24H12), circumcoronene (C54H18) and circumcircumcoronene (C96H24). The carbon cores are depicted in grey, while H atoms are depicted in white. |
| In the text | |
 |
Fig. 2 Composite image of the NW PDR of NGC 7023. The three-color image combines the PACS 70 μm (red), PAH emission at 6.2 μm (green, image courtesy of O. Berné), and MIPS 24 μm (blue) images. The white cross indicates the position of the star HD 200775, while the black crosses indicate the reference extension of the NW PDR (at 45′′ and 60′′ away from the star). |
| In the text | |
 |
Fig. 3 Physical conditions in the NW PDR of NGC 7023. The top panels show the variation of the densities and gas temperature inside the cloud. The H I to H2 transition occurs at an AV ~ 0.9, while the C II–C I transition occurs deeper in the cloud at an AV ~ 4. The bottom panels show the physical parameters relevant for PAH hydrogenation and ionization evolution. The hydrogenation of PAHs is expected to be controlled by the ratio between the UV field intensity G0 and the density of atomic hydrogen, which in our case only varies by about 2 orders of magnitude throughout the cloud. The ionization state of the PAH population on the other hand depends on the so-called ionization parameter, |
| In the text | |
 |
Fig. 4 Ionization potentials and electron affinities assumed in our model. Energies for coronene, circumcoronene and circumcircumcoronene derivatives are shown in black, blue and red, respectively. Given that PAHs in our model can absorb photon energies up to 13.6 eV, the highest charge state for coronene derivatives is the doubly charged one (Z = 2). Circumcoronene derivatives can be doubly ionized, and only those having more than 12 H atoms can be triply ionized (Z = 3). Circumcircumcoronene derivatives on the other hand can be triply ionized, and those having more than 22 H atoms can be found in the +4 charge state. Given the uncertainty in the electron affinities for highly negative charge states (Z< −1), we do not take into account that the more dehydrogenated molecules could also exist in these highly negative states (e.g., Z = −2 for circumcoronene derivatives). |
| In the text | |
 |
Fig. 5 Comparison of IR emission and photodissociation rates as a function of internal energy of the PAH. The rates determined for coronene derivatives are shown in black, while the rates for circumcoronene and circumcircumcoronene are shown in blue and red respectively, following the color scheme of Fig. 4. The grey vertical lines show the activation energies assumed listed in Table 2. The left panel shows the rates for the first dehydrogenated state of each parent molecule in their neutral state (C24H |
| In the text | |
 |
Fig. 6 Variation of the photodissociation rates with respect to the intensity of the UV field, G0. The rates are shown for the same molecules as in Fig. 5, following the same color scheme. For the smallest molecule (black curves) the rates scale linearly with G0 at the range of interest for NGC 7023 (G0≤ 2600) indicating single photon events occurrence for coronene derivatives. For the larger molecules, multiphoton events are important. Even though H-loss is the dominant dissociation channel, at low G0 values, H2-loss can become a competitive process for the larger circumcoronene and circumcircumcoronene species. |
| In the text | |
 |
Fig. 7 Left panel: relative contribution of dehydrogenated states of circumcoronene as a function of depth into the cloud, AV. The contributions consider all ionization states at which the molecules are present. The curves are shown for the first 4 dehydrogenated states of the parent molecule (NH = 17−4). Other partially dehydrogenated states contribute in smaller fractions. Right panel: distribution of circumcoronene derivatives at different AV values where partially dehydrogenated species are observed. |
| In the text | |
 |
Fig. 8 Charge distribution of the PAHs considered in our study. The contribution from each ionization state is shown as a function of the ionization parameter γ≡ |
| In the text | |
 |
Fig. 9 Fractional contribution from coronene (top panels), circumcoronene (middle panels) and circumcircumcoronene (bottom panels) derivatives for different G0 and n(H) values. The contributions include all ionization states. The left column shows the contribution from the completely dehydrogenated molecules, C24, C54 and C96; the middle column shows the fraction of the normally hydrogenated molecules; and the right column shows the distribution of the superhydrogenated species. In all cases, we have assumed a fraction of molecular hydrogen of 0.5, and a carbon abundance of 3.5 × 10-4 relative to hydrogen. Black lines represent constant G0/n(H) ratios and are given as a reference. |
| In the text | |
 |
Fig. 10 Efficiencies of H2 formation from PAHs. The left panel shows the efficiencies of H2 formation through Eley-Rideal abstraction from superhydrogenated species as a function of G0/n(H). Estimates for circumcoronene and circumcircumcoronene superhydrogenated species are shown in blue and red, respectively. The efficiencies have been derived for neutrals and anions, since these are the charge states at which superhydrogenated species can be found according to our model. Two gas temperatures have been assumed as a reference. The right panel shows the efficiencies of H2 formation from photodissociation of PAHs. The efficiencies have been derived for neutral coronene at G0=10, and Z> 0 circumcoronene at G0=103. We have considered different G0 values due to the different dehydrogenation behaviour of the species in the G0-n(H) parameter space (see Fig. 9). As it can be derived from the figure, efficiencies stay below 1% for both mechanisms. |
| In the text | |
 |
Fig. 11 PAH band ratios in the NW PDR of NGC 7023. The 6.2/11.3 ratio is usually used as a proxy for the ionization level of the PAH population, while the 3.3/11.3 ratio is expected to trace PAH size. Here we have plotted them for circumcoronene in blue, and circumcircumcoronene in red. The spectra for C96H24 derivatives are complete in this AV range. The spectra for C54H18 species are missing only the small contributions from partially dehydrogenated species (read text). Observational studies have derived typical 3.3/11.3 ratios of 0.5 to 0.3 from the surface to the PDR up to distances of about 52 arcsec from the star. As seen in the figure, intermediate size PAHs could potentially reproduce these values. However, the ionization ratio 6.2/11.3 would then be highly underestimated compared to the observations that predict a value of 2 at the surface of the PDR, decreasing in about 14% to a distance of ~55 arcsec from the star. |
| In the text | |
 |
Fig. 12 Hydrogenation ratio for different G0/n(H) values. The ratios derived from circumcoronene derivatives are shown in blue, while those from circumcircumcoronene derivatives are shown in red. We have assumed a gas temperature of 50 K, and that the fraction of atomic hydrogen is 10% that of molecular hydrogen, in order to model more shielded environments. The 3.4/3.3 ratio traces the superhydrogenation level of the PAHs as the 3.4 μm band is related to the stretching modes of the pair of CH2 complexes within the same ring (which are duo rings for the coronene family). Observed 3.4/3.3 ratios in NGC 7023 range between 0.028 and 0.13, starting from the cavity and going into the NW PDR region, where G0 is expected to vary from 7000–150 (Pilleri et al. 2015). We see that these ratios can be achieved with superhydrogenated species but for G0/n(H) ratios of 0.002–0.006, which is lower than what is expected in the NW PDR of NGC 7023. |
| In the text | |
 |
Fig. D.1 Fractional contribution from coronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Coronene is completely dehydrogenated throughout most of the cloud (NH= 0). No contribution from dicationic species is observed. |
| In the text | |
 |
Fig. D.2 Fractional contribution from circumcoronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Unlike coronene, these molecules are found in their normally hydrogenated state (NH= 18) with traces of partial dehydrogenation at the surface of the cloud, and at AV~ 1.8. No contribution from trications is observed. |
| In the text | |
 |
Fig. D.3 Fractional contribution from circumcircumcoronene derivatives in the NW PDR of NGC 7023 according to the physical conditions modelled by the Meudon PDR Code. Compared to the smaller species, circumcircumcoronene is mainly found in its normal hydrogenated state (NH= 24). There is no significant contribution from Z> 2 species (trications contribute in only 0.9% at AV= 0). |
| In the text | |
 |
Fig. F.1 PAH emission spectra at different points inside the NW PDR of NGC 7023. For each species, the spectra have been derived by adding the contributions of all ionization and hydrogenation states, from the abundances presented in Appendix D. The results for C24H12 derivatives are shown in black, while the spectra for C54H18 and C96H24 species are shown in blue and red, respectively. The spectra have been conveniently normalized to the peak intensity of the 6.7 μm band for C24H12 derivatives, and to the 11.2 μm band for the larger species. |
| In the text | |
 |
Fig. F.2 Emission spectra for different G0/n(H) ratios at G0= 103. The results for coronene derivatives are shown in black, while the spectra for C54H18 and C96H24 derivatives are shown in blue and red, respectively. The spectra have been conveniently normalized for a better comparison between consecutive G0/n(H) ratios. Given the unavailability of the intrinsic spectra for some of these molecules, the spectra at low G0/n(H) ratios are not complete due to the increasing abundance of highly superhydrogenated anionic species. |
| In the text | |
 |
Fig. F.3 Intrinsic spectra of different hydrogenation states of the neutral coronene (left), circumcoronene (middle) and circumcircumcoronene (right panel) molecules. Only the 3 μm region is presented. This spectral region is the one where differences in the hydrogenation state of PAHs can be clearly observed. Differences in the hydrogenation state (within a given PAH size and ionization state) are clear from the appearance of more features at 3.4 and 3.5 μm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.