| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628993 | |
| Published online | 14 October 2016 | |
Short gamma-ray bursts at the dawn of the gravitational wave era
1 INAF–Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
e-mail: giancarlo.ghirlanda@brera.inaf.it
2 Dipartimento di Fisica G. Occhialini, Università di Milano Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
3 Istituto Nazionale di Fisica Nucleare (INFN) – sede di Milano Bicocca, piazza della Scienza 3, 20123 Milano, Italy
4 Università degli Studi dell’Insubria, via Valleggio 11, 22100 Como, Italy
5 INAF–IASF Milano, via E. Bassini 15, 20133 Milano, Italy
6 Astroparticule et Cosmologie APC, Université Paris Diderot, CNRS/IN2P3, CEA/IRFU, Observatoire de Paris, Sorbonne Paris Cité, 75205 Paris, France
7 Laboratoire Univers et Particules de Montpellier, Université Montpellier 2, 34095 Montpellier, France
8 Universitá degli studi di Urbino “Carlo Bo”, via Saffi 2, 61029 Urbino, Italy
9 INFN, Sezione di Firenze, via G. Sansone 1, 50019 Sesto Fiorentino, Italy
10 Physics Department, University of Trento, via Sommarive 14, 38123 Trento, Italy
11 INFN-TIFPA, Trento Institute for Fundamental Physics and Applications, via Sommarive 14, 38123 Trento, Italy
12 AIM, UMR 7158 CEA/DSM-CNRS-Université Paris Diderot, Irfu/Service d’Astrophysique, Saclay, France
13 GEPI, Observatoire de Paris, CNRS, Univ. Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
14 Università degli Studi di Milano, Physics Department, via Giovanni Celoria 16, 20133 Milano, Italy
Received: 24 May 2016
Accepted: 24 July 2016
We derive the luminosity function φ(L) and redshift distribution Ψ(z) of short gamma-ray bursts (SGRBs) using all the available observer-frame constraints (i.e. peak flux, fluence, peak energy and duration distributions) of the large population of Fermi SGRBs and the rest-frame properties of a complete sample of SGRBs detected by Swift. We show that a steep φ(L) ∝ L− α with α ≥ 2.0 is excluded if the full set of constraints is considered. We implement a Markov chain Monte Carlo method to derive the φ(L) and Ψ(z) functions assuming intrinsic Ep−Liso and Ep−Eiso correlations to hold or, alternatively, that the distributions of intrinsic peak energy, luminosity, and duration are independent. To make our results independent from assumptions on the progenitor (NS−NS binary mergers or other channels) and from uncertainties on the star formation history, we assume a parametric form for the redshift distribution of the population of SGRBs. We find that a relatively flat luminosity function with slope ~0.5 below a characteristic break luminosity ~3 × 1052 erg s-1 and a redshift distribution of SGRBs peaking at z ~ 1.5−2 satisfy all our constraints. These results also hold if no Ep−Liso and Ep−Eiso correlations are assumed and they do not depend on the choice of the minimum luminosity of the SGRB population. We estimate, within ~200 Mpc (i.e. the design aLIGO range for the detection of gravitational waves produced by NS−NS merger events), that there should be 0.007−0.03 SGRBs yr-1 detectable as γ-ray events. Assuming current estimates of NS−NS merger rates and that all NS−NS mergers lead to a SGRB event, we derive a conservative estimate of the average opening angle of SGRBs ⟨ θjet ⟩ ~ 3°−6°. The luminosity function implies a prompt emission average luminosity ⟨L⟩ ~ 1.5 × 1052 erg s-1, higher by nearly two orders of magnitude than previous findings in the literature, which greatly enhances the chance of observing SGRB “orphan” afterglows. Effort should go in the direction of finding and identifying such orphan afterglows as counterparts of GW events.
Key words: gamma-ray burst: general / gravitational waves / methods: numerical
© ESO, 2016
1. Introduction
The population of short gamma-ray bursts (SGRBs) is still poorly understood owing to the relatively few events with measured redshift (see e.g. Berger 2014; D’Avanzo 2015, for recent reviews). Available information is rather sparse, but the low density of the close circumburst medium (Fong & Berger 2013; Fong et al. 2015), the variety of galaxy morphologies (e.g. D’Avanzo 2015), the lack of any associated supernova in the nearby SGRBs, and the possible recent detection of a “kilonova” (Eichler et al. 1989; Li & Paczyński 1998; Yang et al. 2015; Jin et al. 2016, 2015) signature (Berger et al. 2013; Tanvir et al. 2013), all hint to an origin from the merger of two compact objects (e.g. double neutron stars) rather than from a single massive star collapse.
However, the prompt γ-ray emission properties of SGRBs (Ghirlanda et al. 2009, 2015a) and the sustained long-lasting X-ray emission (although not ubiquitous in short GRBs; Sakamoto & Gehrels 2009) and flaring activity suggest that the central engine and radiation mechanisms are similar to long GRBs. Although they are still based on a few breaks in the optical light curves, it seems that SGRBs also have jets: Current measures of θjet are between 3° and 15°, while lower limits seem to suggest a wider distribution (e.g. Berger 2014; Fong et al. 2015). Recently, it has been argued that the customary dividing line at T90 = 2 s between short and long GRBs provides a correct classification for Fermi and CGRO GRBs, but it is somewhat long for Swift bursts (Bromberg et al. 2013).
A renewed interest in the population of SGRBs is following the recent opening of the gravitational wave (GW) “window” by the LIGO-Virgo discovery of GW150914 (Abbott et al. 2016d) and by the most recent announcement of another event, GW151226, detected within the first data acquisition run (Abbott et al. 2016b,d). Although no electromagnetic (EM) counterpart has been identified within the large localization region of this event, there are encouraging prospects that forthcoming GW discoveries will have an EM−GW association, thanks to the aLIGO-Virgo synergy and worldwide efforts for ground- and space-based follow-up observations.
If the progenitors are compact object binary mergers (NS−NS or NS−BH; e.g. Giacomazzo et al. 2013), SGRBs are one of the most promising electromagnetic counterparts of GW events detectable by advanced interferometers. Other EM counterparts are expected in the optical (Metzger & Berger 2012), X-ray (Siegel & Ciolfi 2016a,b; Rezzolla & Kumar 2015) and radio bands (Hotokezaka et al. 2016). The rate of association of GW events with SGRBs is mainly determined by the rate of SGRBs within the relatively small horizon set by the sensitivity of the updated interferometers aLIGO and Advanced Virgo (Abbott et al. 2016e). However, current estimates of local SGRB rates range from 0.1−0.6 Gpc-3 yr-1 (e.g. Guetta & Piran 2005, 2006) to 1−10 Gpc-3 yr-1 (Guetta & Piran 2006; Guetta & Stella 2009; Coward et al. 2012; Siellez et al. 2014; Wanderman & Piran 2015) to even larger values, e.g. 40−240 Gpc-3 yr-1 (Nakar et al. 2006; Guetta & Piran 2006)1.
Such rate estimates mainly depend on the luminosity function φ(L) and redshift distribution Ψ(z) of SGRBs. These functions are usually derived by fitting the peak flux distribution of SGRBs detected by BATSE (Guetta & Piran 2005, 2006; Nakar et al. 2006; Hopman et al. 2006; Salvaterra et al. 2008). Owing to the degeneracy in the parameter space (when both φ(L) and Ψ(z) are parametric functions), the redshift distribution was compared with that of the few SGRBs with measured z. The luminosity function φ(L) is typically modelled as a single or broken power law, and in most cases it is found to be similar to that of long GRBs (i.e. proportional to L-1 and L-2 below and above a characteristic break ~1051−52 erg s-1; Guetta & Piran 2006; Salvaterra et al. 2008; Virgili et al. 2011; D’Avanzo et al. 2014, hereafter D14) or even steeper (L-2 and L-3; Wanderman & Piran 2015, hereafter WP15). Except for the mainstream, Shahmoradi & Nemiroff (2015) modelled all the distributions with lognormal functions.
The redshift distribution Ψ(z) (the number of SGRBs per comoving unit volume and time at redshift z) has always been assumed to follow the cosmic star formation rate with a delay which is due to the time necessary for the progenitor binary system to merge. With this assumption, various authors derived the delay time τ distribution, which could be a single power law P(τ) ∝ τ− δ (e.g. with δ = 1−2; Guetta & Piran2005, 2006; D14; WP15) with a minimum delay time τmin = 10−20 Myr, or a peaked (lognormal) distribution with a considerably large delay (e.g. 2−4 Gyr, Nakar & Gal-Yam2005; WP15). Alternatively, the population could be described by a combination of prompt mergers (small delays) and large delays (Virgili et al. 2011) or to the combination of two progenitor channels, i.e. binaries formed in the field or dynamically within globular clusters (e.g. Salvaterra et al. 2008).
Many past works feature a common approach: parametric forms are assumed for the compact binary merger delay time distribution and for the SGRB luminosity function; free parameters of such functions are then constrained through the small sample of SGRBs with measured redshifts and luminosities and through the distribution of the γ-ray peak fluxes of SGRBs detected by past and/or present GRB detectors. A number of other observer frame properties, though, are available: fluence distribution, duration distribution, observer frame peak energy. The last of these have been considered in Shahmoradi & Nemiroff (2015) which, however, lacks a comparison with rest-frame properties of SGRBs as is done in this article. Another issue was the comparison of the model predictions with small and incomplete samples of SGRBs with measured z. Indeed, only recently has D14 worked with a flux-limited complete sample of SGRBs detected by Swift.
The aim of this paper is to determine the redshift distribution Ψ(z) and the luminosity function φ(L) of the population of SGRBs, using all the available observational constraints of the large population of bursts detected by the Fermi-Gamma Burst Monitor (GBM) instrument. These constraints are (1) the peak flux; (2) the fluence; (3) the observer frame duration; and (4) the observer frame peak energy distributions. We also consider as constraints (5) the redshift distribution; (6) the isotropic energy; and (7) the isotropic luminosity of a complete sample of SGRBs detected by Swift (D14). This is the first work aimed at deriving φ(L) and Ψ(z) of SGRBs, which considers constraints 2−4 and 6−7. Moreover, we do not assume any delay time distribution for SGRBs, but derive directly, for the first time, their redshift distribution by assuming a parametric form.
In Sect. 2 we describe our sample of SGRBs without measured redshifts detected by Fermi/GBM, which provides observer-frame constraints 1−4, and the complete (though smaller) sample of Swift SGRBs of D14, which provides rest-frame constraints 5−7. One of the main results of this paper is that the φ(L) of SGRBs is flatter than has been claimed in the literature: by extending standard analytic tools present in the literature, we show in Sect. 3 that a steep φ(L) is excluded when all the available constraints (1−7) are considered. In Sect. 4 we employ a Monte Carlo code to derive the parameters describing the φ(L) and Ψ(z) of SGRBs. In Sects. 5 and 6 the results on the φ(L) and Ψ(z) of SGRBs are presented and discussed, respectively. In Sect. 7 we compute the local rate of SGRBs, and discus our results in the context of the dawning GW era. We assume standard flat ΛCDM cosmology with H0 = 70 km s-1 Mpc-1 and Ωm = 0.3 throughout the paper.
2. Sample selection
As stated in the preceding section, the luminosity function and redshift distribution of SGRBs have been derived by many authors by taking into account the following two constraints:
the peak flux distribution of large samples of SGRBs detectedby CGRO/BATSE or Fermi/GBM;
the redshift distribution of the SGRBs with measured z.
However, a considerable amount of additional information on the prompt γ-ray emission of SGRBs can be extracted from the BATSE and GBM samples. In particular, we can learn more about these sources by considering the distributions of
the peak energy Ep,o of the observedνFν spectrum;
the fluence F;
the duration T90.
Moreover, for the handful of events with known redshift z, we have also access to the2
isotropic luminosity Liso;
isotropic energy Eiso.
2.1. Observer-frame constraints: Fermi/GBM sample
For the distributions of the observer frame prompt emission properties (constraints 1, 3, 4, 5) we consider the sample of 1767 GRBs detected by Fermi/GBM (from 080714 to 160118) as reported in the online spectral catalogue3. It contains most of the GRBs published in the second spectral catalogue of Fermi/GBM bursts (relative to the first four years) (Gruber et al. 2014), plus events detected by the satellite in the last two years. Of these bursts, 295 in the sample are SGRBs (i.e. with T90 ≤ 2 s). According to Bromberg et al. (2013), for both the Fermi and CGRO GRB populations, this duration threshold should limit the contamination from collapsar-GRBs to less than 10% (see also WP15).
We only select bursts with a peak flux (computed on 64 ms timescale in the 10−1000 keV energy range) larger than 5 ph cm-2 s-1 in order to work with a well-defined sample, less affected by the possible incompleteness close to the minimum detector flux. With this selection, our sample reduces to 211 SGRBs detected by Fermi/GBM in 7.5 yr within its field of view of ~70% of the sky.
We consider the following prompt emission properties of the bursts in the sample to be used as constraints of our population synthesis model:
the distribution of the 64 ms peak flux P64 (integrated in the 10−1000 keV energy range). This is shown by black symbols in the top left panel of Fig. 1;
the distribution of the observed peak energy of the prompt emission spectrum Ep,o (black symbols, bottom left panel in Fig. 1);
the distribution of the fluence F (integrated in the 10−1000 keV energy range) (black symbols, bottom middle panel in Fig. 1);
the distribution of the duration T90 of the prompt emission (black symbols, bottom right panel in Fig. 1);
Short GRB spectra have a typical observer frame peak energy Ep,o distribution (e.g. Ghirlanda et al. 2009; Nava et al. 2011b; Gruber et al. 2014) centred at relatively large values (~0.5−1 MeV), as is also shown by the distribution in the bottom left panel of Fig. 1. For this reason, we adopt here the peak flux P64 and fluence F computed in the wide 10−1000 keV energy range as provided in the spectral catalogue of Fermi bursts rather than the typically adopted 50−300 keV peak flux (e.g. from the BATSE archive), which would sample only a portion of the full spectral curvature.
The distributions of the peak flux, fluence, peak energy, and duration are shown in Fig. 1 with black symbols. Error bars are computed by resampling each measurement (P, F, Ep,o, and T90) within its error with a normal distribution. For each bin, the vertical error bars represent the standard deviation of the bin heights of the resampled distributions.
2.2. Rest-frame constraints: Swift SBAT4 sample
For the redshift distribution and the rest frame properties of SGRBs (constraints 2, 6, and 7) we consider the sample published in D14. It consists of bursts detected by Swift, selected with criteria similar to those adopted for the long GRBs in Salvaterra et al. (2012), with a peak flux (integrated in the 15−150 keV energy range and computed on a 64 ms timescale) P64 ≥ 3.5 photons cm-2 s-1. This corresponds to a flux which is approximately four times larger than the Swift-BAT minimum detectable flux on this timescale; hereafter we call this sample SBAT4 (Short BAT 4). The redshift distribution of the SBAT4 sample is shown in the top right panel of Fig. 1 (solid black line). Within the SBAT4 sample we consider the 11 GRBs with known z and determined Liso and Eiso (the distributions of these quantities are shown in the inset of Fig. 1, top right panel, with black and grey lines respectively). The grey shaded region is spanned by the distribution when the five SGRBs in the sample with unknown z are all assigned the minimum or the maximum redshift of the sample.
 |
Fig. 1 Black dots show the distributions obtained from our Fermi/GBM and Swift SBAT4 samples (Sect. 2). Horizontal error bars are the bin widths, while vertical error bars are 1σ errors on the bin heights accounting for experimental errors on single measurements. The results of our Monte Carlo population synthesis code are shown by solid red lines (assuming Ep−Liso and Ep−Eiso correlations to hold in the population of SGRBs) and by triple dot-dashed orange lines (assuming no correlation). Predictions based on the models of D14 and WP15 are shown by dashed blue and dot-dashed cyan lines, respectively (the latter only in the first three panels; see text). These are obtained by the analytical methods of Sect. 3.1. Top left panel: distribution of the peak flux P of the Fermi/GBM sample. Top right panel: normalized cumulative redshift distribution of the SBAT4 sample. The grey shaded area represents the range spanned by the distribution if the remaining bursts with unknown z are assigned the largest or the lowest z of the sample. The inset shows the cumulative distributions of the isotropic luminosity Liso (solid black line) and energy Eiso (solid grey line) of the same sample. Bottom panels: from left to right, distributions of peak energy Ep,o, fluence, and duration of SGRBs of our Fermi/GBM sample. |
3. The φ(L) and Ψ(z) of SGRBs
Given the incompleteness of the available SGRB samples, particularly with measured z, no direct method (as for the population of long GRBs; see e.g. Pescalli et al. 2016) can be applied to derive the shape of the SGRB luminosity function φ(L) and redshift distribution Ψ(z) from the observations. The typical approach in this case consists in assuming some simple analytical shape for both functions, with free parameters to be determined by comparison of model predictions with observations.
For the luminosity function, a power law 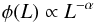 (1)or a broken power law
(1)or a broken power law 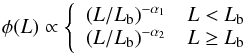 (2)normalized to its integral is usually assumed.
(2)normalized to its integral is usually assumed.
If SGRBs are produced by the merger of compact objects, their redshift distribution should follow a retarded star formation, ![\begin{equation} \Psi(z) = \int_{z}^{\infty} \psi(z')P[t(z)-t(z')]\frac{{\rm d}t}{{\rm d}z'}{\rm d}z'\label{eq:retarded} , \end{equation}](/articles/aa/full_html/2016/10/aa28993-16/aa28993-16-eq50.png) (3)where ψ(z) represents the formation rate of SGRB progenitors in Gpc-3 yr-1, and P(τ) is the delay time distribution, i.e. the probability density function of the delay τ between the formation of the progenitors and their merger (which produces the SGRB). Adopting the point of view that SGRBs are produced by the coalescence of a neutron star binary (or a black hole-neutron star binary), one can assume a delay time distribution and convolve it with a ψ(z) of choice to obtain the corresponding SGRB formation rate Ψ(z). Theoretical considerations and population synthesis (Portegies Zwart & Yungelson 1998; Schneider et al. 2001; Belczynski et al. 2006; O’Shaughnessy et al. 2008; Dominik et al. 2013) suggest that compact binary coalescences should typically follow a delay time distribution P(τ) ∝ τ-1 with τ ≳ 10 Myr. Equation (3) is actually a simplification, in that it implicitly assumes that the fraction of newly formed stars that will end up as members of a NS−NS binary is fixed. The actual fraction very likely depends on metallicity and on the initial mass function, and thus on redshift in a statistical sense.
(3)where ψ(z) represents the formation rate of SGRB progenitors in Gpc-3 yr-1, and P(τ) is the delay time distribution, i.e. the probability density function of the delay τ between the formation of the progenitors and their merger (which produces the SGRB). Adopting the point of view that SGRBs are produced by the coalescence of a neutron star binary (or a black hole-neutron star binary), one can assume a delay time distribution and convolve it with a ψ(z) of choice to obtain the corresponding SGRB formation rate Ψ(z). Theoretical considerations and population synthesis (Portegies Zwart & Yungelson 1998; Schneider et al. 2001; Belczynski et al. 2006; O’Shaughnessy et al. 2008; Dominik et al. 2013) suggest that compact binary coalescences should typically follow a delay time distribution P(τ) ∝ τ-1 with τ ≳ 10 Myr. Equation (3) is actually a simplification, in that it implicitly assumes that the fraction of newly formed stars that will end up as members of a NS−NS binary is fixed. The actual fraction very likely depends on metallicity and on the initial mass function, and thus on redshift in a statistical sense.
Among the most recent studies of the φ(L) and Ψ(z) of SGRBs we consider the work of D14 and WP15 in the following for comparison in more detail. D’Avanzo et al. (2014) assume a power law shape for both the φ(L) and the delay time distribution P(τ), and they adopt the parametric function of Cole et al. (2001) for the cosmic star formation history, with parameter values from Hopkins & Beacom (2006). They assume that SGRBs follow the Ep−Liso correlation Epeak = 337 keV (Liso/ 2 × 1052 erg s-1)0.49 and that their spectrum is a Band function (Band et al. 1993) with low and high energy photon spectral indices −0.6 and −2.3, respectively. They constrain the free parameters by fitting the BATSE peak flux distribution and the redshift distribution of bright Swift short bursts with measured z. They find φ(L) ∝ L-2.17 between 1049 erg s-1 and 1055 erg s-1, and P(τ) ∝ τ-1.5 with a minimum delay of 20 Myr. The dashed blue lines in Fig. 1 are obtained through Eqs. (4) and (5) using the same parameters as D14: their model (limited to Plim ≥ 5 ph cm-2 s-1 in order to be compared with the sample selected in this work) reproduces correctly the peak flux distribution (top left panel of Fig. 1) of Fermi SGRBs and the redshift distribution of the bright SGRBs detected by Swift (top right panel).
The preferred model for φ(L) in WP15 is a broken power law, with a break at 2 × 1052 erg s-1 and pre- and post-break slopes of −1.9 and −3.0, respectively. Their preferred models are either a power law delay time distribution P(τ) ∝ τ-0.81 with a minimum delay of 20 Myr or a lognormal delay time distribution with central value 2.9 Gyr and sigma ≤0.2. Differently from D14, rather than assuming the Ep−Liso correlation they assign to all SGRBs a fixed rest frame Ep,rest = 800 keV. The dot-dashed cyan lines in Fig. 1 are the model of WP15 (for the lognormal P(τ) case).
In the following we show how the results of WP15 and D14, both representative of a relatively steep luminosity function, compare with the other additional constraints (bottom panels of Fig. 1) that we consider in this work.
3.1. From population properties to observables
Given the two functions φ(L) and Ψ(z), the peak flux distribution can be derived as 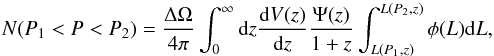 (4)where ΔΩ/4π is the fraction of sky covered by the instrument/detector (which provides the real GRB population with which the model is to be compared) and dV(z)/dz is the differential comoving volume. The flux P corresponding to the luminosity L at redshift z is4
(4)where ΔΩ/4π is the fraction of sky covered by the instrument/detector (which provides the real GRB population with which the model is to be compared) and dV(z)/dz is the differential comoving volume. The flux P corresponding to the luminosity L at redshift z is4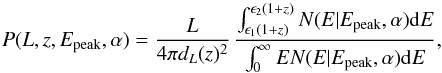 (5)where dL(z) is the luminosity distance at redshift z and N(E | Epeak,α) is the rest frame photon spectrum of the GRB. The photon flux P is computed in the rest frame energy range [(1 + z)ϵ1,(1 + z)ϵ2], which corresponds to the observer frame [ϵ1,ϵ2] band.
(5)where dL(z) is the luminosity distance at redshift z and N(E | Epeak,α) is the rest frame photon spectrum of the GRB. The photon flux P is computed in the rest frame energy range [(1 + z)ϵ1,(1 + z)ϵ2], which corresponds to the observer frame [ϵ1,ϵ2] band.
The SGRB spectrum is often assumed to be a cut-off power law, i.e. N(E | Epeak,α) ∝ E− αexp(−E(2−α) /Epeak), or a Band function (Band et al. 1993). Typical parameter values are α ~ 0.6 (i.e. the central value of the population of SGRBs detected by BATSE and Fermi−Ghirlanda et al. 2009; Nava et al. 2011b; Goldstein & Preece 2010; Gruber et al. 2014) and, for the Band function, β ~ 2.3−2.5. The peak energy is either assumed fixed (e.g. 800 keV in WP15) or derived assuming that SGRBs follow an Ep−Liso correlation in analogy to long bursts (e.g. D14; Virgili et al. 2011). Recent evidence supports the existence of such a correlation among SGRBs (see e.g. D14; Calderone et al. 2015; Tsutsui et al. 2013; Ghirlanda et al. 2009) with similar parameters to those present in the population of long GRBs (Yonetoku et al. 2004).
In order to compare the model peak flux distribution obtained from Eq. (4) with the real population of GRBs, only events with peak flux above a certain threshold Plim are considered. The integral in Eq. (4) is thus performed over the (L,z) range where the corresponding flux is larger than Plim.
In D14 the assumption of the correlation (Ep−Liso) between the isotropic luminosity Liso and the rest frame peak energy Ep also allows us to derive, from Eq. (4), the expected distribution of the observer frame peak energy Ep,o, 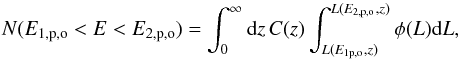 (6)where Ep,o is the peak energy of the observed νF(ν) spectrum, and we let C(z) = [ΔΩ/4π] [Ψ(z)/(1 + z)] [dV(z)/dz]. The limits of the luminosity integral are computed by using the rest frame correlation Ep = YLmy, namely
(6)where Ep,o is the peak energy of the observed νF(ν) spectrum, and we let C(z) = [ΔΩ/4π] [Ψ(z)/(1 + z)] [dV(z)/dz]. The limits of the luminosity integral are computed by using the rest frame correlation Ep = YLmy, namely 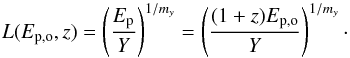 (7)In order to compare the distribution of Ep,o with real data, the integral in Eq. (6), similarly to Eq. (4), is performed over values of L(Ep,o,z) corresponding to fluxes above the limiting flux adopted to extract the real GRB sample (e.g. 5 ph cm-2 s-1 for SGRBs selected from the Fermi sample).
(7)In order to compare the distribution of Ep,o with real data, the integral in Eq. (6), similarly to Eq. (4), is performed over values of L(Ep,o,z) corresponding to fluxes above the limiting flux adopted to extract the real GRB sample (e.g. 5 ph cm-2 s-1 for SGRBs selected from the Fermi sample).
Similarly, by assuming an Ep−Eiso correlation to hold in SGRBs (see D14; Tsutsui et al. 2013; Amati 2006; Calderone et al. 2015), i.e. Ep = AEma, we can derive a relation between luminosity and energy (Liso−Eiso), which reads 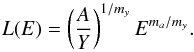 (8)This is then used to compute the fluence distribution, where the fluence is related to the isotropic energy as F = E(1 + z)/4πdL(z)2,
(8)This is then used to compute the fluence distribution, where the fluence is related to the isotropic energy as F = E(1 + z)/4πdL(z)2, 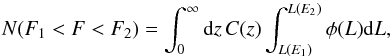 (9)again by limiting the integral to luminosities which correspond to fluxes above the given limiting flux.
(9)again by limiting the integral to luminosities which correspond to fluxes above the given limiting flux.
Finally, considering the spiky light curves of SGRBs, we can assume a triangular shape and thus let 2E/L ~ T in the rest frame of the source. Therefore, it is possible to combine the Ep−Eiso and Ep−Liso correlations to derive the model predictions for the distribution of the duration to be compared with the observed distribution, 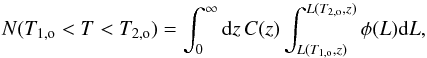 (10)where
(10)where ![\begin{equation} L(T_{\rm o},z) = \left[\left( \frac{Y}{A} \right)^{1/m_a}\frac{2(1+z)}{T_{\rm o}}\right]^{1/(1-m_y/m_a)} \cdot \end{equation}](/articles/aa/full_html/2016/10/aa28993-16/aa28993-16-eq98.png) (11)
(11)
3.2. Excluding a steep luminosity function
The bottom panels of Fig. 1 show the distributions of peak energy Ep,o (left), fluence F (middle), and duration T90 (right) of the sample of short Fermi GRBs described in Sect. 2 (black symbols). Predictions using the same parameters as in D14 are shown by dashed blue lines in Fig. 1: while the P and z distributions are correctly reproduced (top panels of Fig. 1), the model is inconsistent with the distributions of peak energy Ep,o, fluence F, and duration (bottom panels of Fig. 1). For the D14 model we have assumed the Ep−Eiso correlation reported in that paper to derive the fluence and (in combination with the Ep−Liso correlation) the duration distribution. Since WP15 assume a unique value of the peak energy Ep,o, it is not possible to derive the fluence and duration of their model unless independent functions for these parameters are assumed. Therefore, the model of WP15 (dot-dashed cyan line in Fig. 1) is compared only in the peak flux, redshift (top panels), and observed peak energy (bottom left panel of Fig. 1).
In conclusion, a steep φ(L) with either a power law distribution of delay times favouring short delays (as in D14) or a nearly unique long delay time (as in the log-normal model of WP15) correctly reproduce the observer frame peak flux distribution of Fermi GRBs5 and the redshift distribution of Swift bright short bursts. However, they do not reproduce the peak energy, fluence, and duration distributions of the same population of Fermi SGRBs.
Motivated by these results, we implemented a Monte Carlo (MC) code aimed at deriving the φ(L) and Ψ(z) of SGRBs which satisfy all the constraints (1−7) described above. The reason to choose a MC method is that it allows easy implementation of the dispersion of the correlations (e.g. Ep−Liso and Ep−Eiso) and of any distribution assumed (which are less trivial to account for in an analytic approach as that shown above).
4. Monte Carlo simulation of the SGRB population
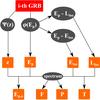 |
Fig. 2 Scheme of the procedure followed in the MC to generate the observables of each synthetic GRB. |
In this section we describe the Monte Carlo (MC) code adopted to generate the model population. This population is then compared with the real SGRB samples described above in order to constrain the model parameters (Sect. 4). Our approach is based on the following choices:
Customarily, Eq. (3) has been used to compute the redshift distribution Ψ(z) of SGRBs from an assumed star formation history ψ(z) and a delay time distribution P(τ). As stated in Sect. 3, this approach implies simplifications that we would like to avoid. To make our analysis as general as possible, we adopt a generic parametric form for the redshift distribution Ψ(z) of SGRBs. A posteriori, if one believes the progenitors to be compact binaries, the delay time distribution can be recovered by direct comparison of our result with the star formation history of choice. We parametrize the Ψ(z) following Cole et al. (2001), namely 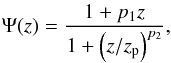 (12)which has a rising and decaying part (for p1> 0, p2> 1) and a characteristic peak roughly6 corresponding to zp;
(12)which has a rising and decaying part (for p1> 0, p2> 1) and a characteristic peak roughly6 corresponding to zp;
In order to have a proper set of simulated GRB parameters, it is convenient to extract Ep from an assumed probability distribution. We consider a broken power law shape for the Ep distribution: 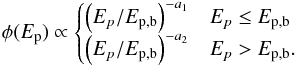 (13)Through the Ep−Liso and Ep−Eiso correlations, also accounting for their scatter, we can then associate with Ep a luminosity Liso and an energy Eiso. The luminosity function of the population is then constructed as a result of this procedure;
(13)Through the Ep−Liso and Ep−Eiso correlations, also accounting for their scatter, we can then associate with Ep a luminosity Liso and an energy Eiso. The luminosity function of the population is then constructed as a result of this procedure;
We assume the correlations Ep−Liso and Ep−Eiso and we write them respectively as 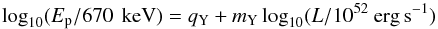 (14)and
(14)and 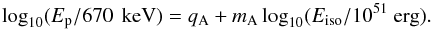 (15)After sampling Ep from its probability distribution (Eq. (13)), we associate with it a luminosity (resp. energy) sampled from a lognormal distribution whose central value is given by Eq. (14) (resp. 15) and σ = 0.2. There are still too few SGRBs with measured redshift to measure the scatter of the corresponding correlations. We assume the same scatter as measured for the correlations holding for the population of long GRBs (Nava et al. 2012);
(15)After sampling Ep from its probability distribution (Eq. (13)), we associate with it a luminosity (resp. energy) sampled from a lognormal distribution whose central value is given by Eq. (14) (resp. 15) and σ = 0.2. There are still too few SGRBs with measured redshift to measure the scatter of the corresponding correlations. We assume the same scatter as measured for the correlations holding for the population of long GRBs (Nava et al. 2012);
For each GRB, a typical Band function prompt emission spectrum is assumed, with low and high photon spectral index −0.6 and −2.5, respectively. We keep these two parameters fixed after checking that our results are unaffected by sampling them from distributions centred around these values7.
For each synthetic GRB, the scheme in Fig. 2 is followed: a redshift z is sampled from Ψ(z) and a rest frame peak energy Ep is sampled from φ(Ep); through the Ep−Liso (Ep−Eiso) correlation a luminosity Liso (energy Eiso) with lognormal scatter is assigned; using redshift and luminosity (energy), the peak flux P (fluence F) in the observer frame energy range 10−1000 keV is derived via the assumed spectral shape. The observer frame duration T is obtained as 2(1 + z)E/L, i.e. the light curve is approximated with a triangle8. Let us refer to this scheme as “case (a)”.
The minimum and maximum values of Ep admitted are Ep,min = 0.1 keV and Ep,max = 105 keV. These limiting values correspond to a minimum luminosity Lmin and a maximum luminosity Lmax which depend on the Ep−Liso correlation. While the maximum luminosity is inessential (in all our solutions the high luminosity slope α2 ≳ 2), the existence of a minimum luminosity might affect the observed distributions. We thus implemented an alternative scheme (“case (b)”) where the minimum luminosity Lmin is a parameter, and values of Ep which correspond to smaller luminosities are rejected.
In order to investigate the dependence of our results on the assumption of the Ep−Liso and Ep−Eiso correlations, we also implemented a third MC scheme (“case (c)”) where independent probability distributions (i.e., independent from the peak energy and between themselves) are assumed for the luminosity and duration. A broken power law 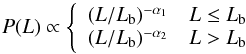 (16)is assumed for the luminosity distribution, and a lognormal shape
(16)is assumed for the luminosity distribution, and a lognormal shape ![\begin{equation} P(T_{\rm{r}}) \propto \exp\left[-\frac{1}{2}\left(\frac{(\log(T_{\rm{r}}) - \log(T_{\rm c})}{\sigma_{T\rm c}}\right)^2\right] \label{eq:tdist} \end{equation}](/articles/aa/full_html/2016/10/aa28993-16/aa28993-16-eq118.png) (17)is assumed for the rest frame duration Tr = T/ (1 + z) probability distribution. Again, the energy of each GRB is computed as E = LTr/ 2, i.e. the light curve is approximated with a triangle.
(17)is assumed for the rest frame duration Tr = T/ (1 + z) probability distribution. Again, the energy of each GRB is computed as E = LTr/ 2, i.e. the light curve is approximated with a triangle.
5. Finding the best fit parameters
In case (a) there are ten free parameters: three (p1,zp,p2) define the redshift distribution (Eq. (12)), three (a1,a2,Ep,b) define the peak energy distribution (Eq. (13)), and four (qY,mY,qA,mA) define the Ep−Liso and Ep−Eiso correlations (Eqs. (14) and (15)). Our constraints are the seven distributions shown in Fig. 1 (including the insets in the top right panel).
 |
Fig. 3 Marginalized densities of our MCMC parameters in case (a) (i.e. with correlations and no minimum luminosity). Black dashed lines indicate the means and black dot-dashed lines indicate the modes of the distributions. |
In order to find the best fit values and confidence intervals of our parameters, we employed a Markov chain Monte Carlo (MCMC) approach based on the Metropolis-Hastings algorithm (Hastings 1970). At each step of the MCMC
we displace each parameter9pi from the last accepted value. The displacement is sampled from a uniform distribution whose maximum width is carefully tuned in order to avoid the random walk remaining stuck in local maxima;
we compute the Kolmogorov-Smirnov (KS) probability PKS,j of each observed distribution to be drawn from the corresponding model distribution;
we define the goodness of fit  of the model as the sum of the logarithms of these KS probabilities10, i.e.
of the model as the sum of the logarithms of these KS probabilities10, i.e. 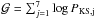 ;
;
we compare 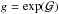 with a random number r sampled from a uniform distribution within 0 and 1: if g>r the set of parameters is “accepted”, otherwise it is “rejected”.
with a random number r sampled from a uniform distribution within 0 and 1: if g>r the set of parameters is “accepted”, otherwise it is “rejected”.
We performed tests of the MCMC with different initial parameters, to verify that a unique global maximum of 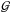 could be found. Once properly set up, 200 000 steps of the MCMC were run. After removing the initial burn in, the autocorrelation length of each parameter in the chain was computed, and the posterior density distribution of each parameter (and the joint distribution of each couple of parameters) was extracted with the getDist python package11. The resulting 1D and 2D marginalized distributions are shown in Fig. 3, where black dashed (black dot-dashed) lines indicate the position of the mean (mode) of the marginalized density of each parameter. The filled contours represent the 68% (darker red) and 95% (lighter red) probability areas of the joint density distributions. The means, modes, and 68% probability intervals of the 1D marginalized distributions are summarized in Table 1a, where the corresponding luminosity function parameters are also reported.
could be found. Once properly set up, 200 000 steps of the MCMC were run. After removing the initial burn in, the autocorrelation length of each parameter in the chain was computed, and the posterior density distribution of each parameter (and the joint distribution of each couple of parameters) was extracted with the getDist python package11. The resulting 1D and 2D marginalized distributions are shown in Fig. 3, where black dashed (black dot-dashed) lines indicate the position of the mean (mode) of the marginalized density of each parameter. The filled contours represent the 68% (darker red) and 95% (lighter red) probability areas of the joint density distributions. The means, modes, and 68% probability intervals of the 1D marginalized distributions are summarized in Table 1a, where the corresponding luminosity function parameters are also reported.
Summary of Monte Carlo Markov Chain results.
For the solution represented by the mean values in Table 1a, the minimum luminosity is Lmin ~ 1047 erg s-1. For comparison, we tested case (b) fixing Lmin = 1050 erg s-1. This is the highest minimum luminosity that can be assumed, since the lowest SGRB measured luminosity in the Swift sample considered is L = 1.2 × 1050 erg s-1 (D14). Table 1b summarizes the results of the analysis after 200 000 MCMC steps. The two cases are consistent within one sigma. The best fit luminosity function in case (b) is slightly shallower at low luminosities (i.e. there is a slight decrease in α1) than in case (a), and it remains much shallower than in D14 and WP15.
Finally, we tested case (c) performing 200 000 MCMC steps. In this case, there are 11 free parameters: three (p1,zp,p2) for Ψ(z) and three (a1,a2,Ep,b) for φ(Ep) as before, plus three (α1,α2,Lb) for the luminosity function (Eq. (16)) and two (Tc,σTc) for the intrinsic duration distribution (Eq. (17)). Consistently with case (a) and case (b) we assumed two broken power laws for φ(Ep) and φ(L). The results are listed in Table 1c. We find that if no correlations are present between the peak energy and the luminosity (energy), the luminosity function and the peak energy distributions become peaked around characteristic values. This result is reminiscent of the findings of Shahmoradi & Nemiroff (2015) who assumed lognormal distributions for these quantities.
6. Discussion of the results
6.1. Luminosity function
In case (a) we find that the luminosity function is shallow (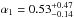 , and flatter than 1.0 within the 68% confidence interval) below a break luminosity ~3 × 1052 erg s-1 and steeper (
, and flatter than 1.0 within the 68% confidence interval) below a break luminosity ~3 × 1052 erg s-1 and steeper (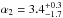 ) above this characteristic luminosity. The minimum luminosity ~5 × 1047 erg s-1 is set by the minimum Ep coupled with the Ep−Liso correlation parameters (see Sect. 4). Similar parameters for the φ(L) are obtained in case (b), where a minimum luminosity was introduced, thus showing that this result is not strongly dependent on the choice of the minimum luminosity of the φ(L).
) above this characteristic luminosity. The minimum luminosity ~5 × 1047 erg s-1 is set by the minimum Ep coupled with the Ep−Liso correlation parameters (see Sect. 4). Similar parameters for the φ(L) are obtained in case (b), where a minimum luminosity was introduced, thus showing that this result is not strongly dependent on the choice of the minimum luminosity of the φ(L).
If we leave out the correlations (case (c)), we find that the distributions of the peak energy and luminosity are peaked. However, the 68% confidence intervals of some parameters, common to cases (a) and (b), are larger in case (c). In particular, the slope α1 of the luminosity function below the break is poorly constrained, although this cannot be steeper than 0.81 (at the 68% confidence level). We believe that the larger uncertainty on the best fit parameters in case (c) is due to the higher freedom allowed by the uncorrelated luminosity function, peak energy distribution, and duration distribution.
6.2. Redshift distribution
Figure 4 shows a comparison of our predicted redshift distributions (case (a): red solid line; case (c): orange triple dot-dashed line; mean values adopted) with the following redshift distributions:
the convolution of the Madau & Dickinson (2014,hereafter star formation history (SFH) with the delay timedistributionP(τ) ∝ τ-1 with τ> 20 Myr, grey dashed line (the normalization is arbitrary);
the redshift distribution of NS−NS mergers as predicted by Dominik et al. (2013) (we refer to the standard binary evolution case in the paper) based on sophisticated binary population synthesis, assuming two different metallicity evolution scenarios: high-end (pink solid line) and low-end (pink dotted line);
the SGRB redshift distribution found by D14, which is obtained convolving the SFH by Hopkins & Beacom (2006) with a delay time distribution P(τ) ∝ τ-1.5 with τ> 20 Myr, blue dashed line;
the SGRB redshift distribution found by WP15, which is obtained convolving an SFH based on Planck results (“extended halo model” in Planck Collaboration XXX 2014) with a lognormal delay time distribution P(τ) ∝ exp[−(lnτ−lnτ0)2/(2σ2)] with τ0 = 2.9 Gyr and σ< 0.2 (we used σ = 0.1), cyan dot-dashed line.
The redshift distribution by D14 peaks between z ~ 2 and z ~ 2.5, i.e. at a higher redshift than the MD14 SFH (which peaks at z ~ 1.9). This is due to the short delay implied by the delay time distribution assumed in D14, and because the Hopkins & Beacom (2006) SFH peaks at higher redshift than the MD14 SFH. On the other hand, the redshift distribution by WP15 peaks at very low redshift (~0.8) and predicts essentially no SGRBs with redshift z ≳ 2 because of the extremely large delay implied by their delay time distribution.
Assuming the MD14 SFH (which is the most recent SFH available) to be representative, our result in case (a) seems to be compatible with the P(τ) ∝ τ-1 delay time distribution (grey dashed line), theoretically favoured for compact binary mergers. In case (c), on the other hand, the redshift distribution we find seems to be indicative of a slightly smaller average delay with respect to case (a). Since the cosmic SFH is still subject to some uncertainty, and since the errors on our parameters (p1,zp,p2) are rather large, no strong conclusion about the details of the delay time distribution can be drawn.
 |
Fig. 4 Comparison between various predicted SGRB redshift distributions. The grey dashed line represents the convolution of the MD14 cosmic SFH with a delay time distribution P(τ) ∝ τ-1 with τ> 20 Myr (the normalization is arbitrary). The pink solid line (pink dotted line) represents the redshift distribution of NS−NS binary mergers predicted by Dominik et al. (2013) in their high end (low end) metallicity evolution scenario (standard binary evolution model). The blue dashed line and cyan dot-dashed line are the SGRB redshift distributions according to D14 and to WP15, respectively. The red solid line is our result in case (a), while the orange triple dot-dashed line is our result in case (c). In both cases we used the mean parameter values as listed in Table 1. |
6.3. Ep – Liso and Ep – Eiso correlations
Our approach allowed us, in cases (a) and (b), to derive the slope and normalization of the intrinsic Ep−Liso and Ep−Eiso correlations of SGRBs. For the Ep−Eiso and Ep−Liso correlations of SGRBs, Tsutsui et al. (2013) finds slope values of 0.63 ± 0.05 and 0.63 ± 0.12, respectively. Although our mean values for mY and mA (Table 1) are slightly steeper, the 68% confidence intervals reported in Table 1 are consistent with those reported by Tsutsui et al. (2013). In order to limit the free parameter space, we assumed a fixed scatter for the correlations and a fixed normalization centre for both (see Eqs. (14) and (15)). This latter choice, for instance, introduces the small residual correlation between the slope and normalization of the Ep−Liso parameters (as shown in Fig. 3).
Inspection of Fig. 3 reveals another correlation in the MCMC chain between the normalizations qY and qA of the Ep−Liso and Ep−Eiso correlations, which is expected because the ratio of the two normalizations is linked to the duration of the burst. Indeed, Eqs. (15) and (14) yield 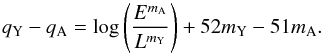 (18)Since mA and mY are close, the argument of the logarithm is ~E/L ∝ T, and since there is a typical duration, this induces an approximately linear correlation between qA and qY, which is what we find.
(18)Since mA and mY are close, the argument of the logarithm is ~E/L ∝ T, and since there is a typical duration, this induces an approximately linear correlation between qA and qY, which is what we find.
 |
Fig. 5 Event rates within redshift z: Solid red line and triple dot-dashed orange line represent the SGRB rates for case (a) and case (c) of this work, respectively. The yellow shaded region represents the 68% confidence level on the rate (red line) of case (a). SGRB rates according to the models of D14 and WP15 are shown by the dashed blue and dot-dashed cyan lines, respectively. The rate of NS−NS mergers is shown by the hatched pink region where the lower (upper) boundary corresponds to the rate derived from population synthesis models (Galactic binaries) in Dominik et al. (2015) and Kim et al. (2015). The vertical grey shaded regions show the present and design ranges of aLIGO for NS−NS mergers. The upper limit (white star) corresponds to the non-detection of NS−NS mergers in the first 48.6 days of the “O1” run of aLIGO. The green vertical bar is the rate of binary BH mergers derived by Abbott et al. (2016b) and shown here at the distance of GW150914 and GW151226. |
7. Local SGRB rate
The local rate of SGRBs is particularly important for the possible connection with gravitational wave events to be detected by the advanced interferometers (Advanced LIGO −Aasi et al. 2015; Abbott et al. 2016a; Advanced Virgo −Acernese et al. 2015).
The first such detection, named GW150914, has been interpreted according to general relativity as the space-time perturbation produced by the merger of two black holes (with masses M1 ~ 29 M⊙ and M2 ~ 36 M⊙) at a distance of ~410 Mpc (z = 0.09). The full analysis of the aLIGO first run cycle revealed a second binary black hole merger event, GW151226 (Abbott et al. 2016b). In this case the involved masses are smaller (M1 ~ 14.2M⊙ and M2 ~ 7.5 M⊙) and the associated distance is only slightly larger (~440 Mpc)12.
GW150914 represents a challenge for the theory of formation and evolution of stellar origin BHs (Abbott et al. 2016c; Belczynski et al. 2016; Spera et al. 2015) being the most massive stellar-mass black hole observed so far. The masses of GW151226 are close to those observed in galactic X-ray binaries (Özel et al. 2010). Both sources are an exquisite direct probe of general relativity in the strong field dynamical sector (Abbott et al. 2016a).
Considering the detections resulting from the analysis of the “O1” aLIGO interferometers, the rate of BH-BH merger is 9−240 Gpc-3 yr-1, assuming different BH mass distributions (Abbott et al. 2016b). For the sake of comparison, in Fig. 5 we show this range of rates (vertical green bar) in yr-1 computed at the distance of GW150914.
However, the best is yet to come in the field of GW. Indeed, while no electromagnetic counterpart has been associated either with GW150914 (Evans et al. 2016a; Troja et al. 2016; Smartt et al. 2016a; Savchenko et al. 2016; Soares-Santos et al. 2016; Annis et al. 2016; Kasliwal et al. 2016; Morokuma et al. 2016; Ackermann et al. 2016, but see Connaughton et al. 2016; Perna et al. 2016; Yamazaki et al. 2016; Zhang 2016; Morsony et al. 2016; Lyutikov 2016) or with GW151226 (Cowperthwaite et al. 2016; Smartt et al. 2016b; Adriani et al. 2016; Evans et al. 2016b; Copperwheat et al. 2016; Racusin et al. 2016), possible future detections of GW produced by compact binary mergers could lead to the first association of an electromagnetic with a gravitational signal (Branchesi et al. 2011; Metzger & Berger 2012). In the case of NS−NS and NS−BH mergers, SGRBs are candidates to search for among other possible counterparts in the optical (Metzger & Berger 2012), X-ray (Siegel & Ciolfi 2016a,b), and radio bands (Hotokezaka et al. 2016).
Short GRB rates in yr-1 (68% errors) within the volume corresponding to different distances.
There is a considerable number of predictions for the rate of SGRBs within the horizon of GW detectors in the literature. The rather wide range of predictions, extending from 0.1 Gpc-3 yr-1 to >200 Gpc-3 yr-1 (e.g. Guetta & Piran 2005, 2006), can be tested and further constrained by forthcoming GW-SGRB associations (Coward et al. 2014; Branchesi et al. 2012). If SGRBs have a jet, one must account for the collimation factor, i.e. multiply the rate by fb = ⟨ (1−cosθjet)-1 ⟩, in order to compare such predictions with the compact binary merger rate. Once the luminosity function and rate of SGRBs is determined, the fraction of SGRBs above a limiting flux Pmin within a given redshift z is 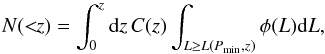 (19)where L(Pmin,z) represents − at each redshift z− the minimum luminosity corresponding to the flux limit Plim (e.g. of a particular GRB detector).
(19)where L(Pmin,z) represents − at each redshift z− the minimum luminosity corresponding to the flux limit Plim (e.g. of a particular GRB detector).
Figure 5 shows the rate of SGRBs within a given redshift z (zoomed up to z< 0.1). The different curves are obtained using the formation rate Ψ(z) and luminosity function φ(L) by D14 and WP15 (shown by the dashed blue and dot-dashed cyan lines, respectively) and the results of our case (a) (solid red line) and case (c) (triple dot-dashed orange line).
These curves represent the population of SGRBs detectable in γ-rays by current flying instruments. At redshifts as low as those shown in Fig. 5, even bursts populating the lowest end of the luminosity function can be observed above the flux limits of available GRB detectors (e.g. the Fermi/GBM). The Ψ(z) that we derive (see Fig. 4) rises, below the peak, in a way similar to those adopted in the literature (e.g. D14 and WP15). The lower rates predicted by our models with respect to those of D14 and WP15 are thus mainly due to our flatter φ(L).
The distance within which aLIGO should have been able to detect NS−NS mergers during “O1” was estimated to be 60–80 Mpc, which corresponds to redshift z ~0.014–0.0185 (dark grey shaded region in Fig. 5) (Martynov et al. 2016). We use this distance to define an upper limit on the NS−NS merger rate (star symbol and arrow in Fig. 5), given the non-detection of any such events in the 48.6 days of “O1” data (Martynov et al. 2016). If SGRBs have a jet, and if the jet is preferentially launched in the same direction as the orbital angular momentum, the inspiral of the progenitor binary could be detected up to a larger distance (up to a factor 2.26 larger, see Chassande-Mottin 2016) because the binary is more likely to be face-on. Let us define the following three typical distances:
we indicate by R (range) the limiting distance for the detection of acompact binary inspiral, averaged over all sky locations and overall binary inclinations with respect to the line of sight;
we indicate by D (distance to face-on) the limiting distance for the detection of a face-on compact binary inspiral, averaged over all sky locations;
we indicate by H (horizon) the maximum limiting distance for the detection of a face-on compact binary inspiral, i.e. the limiting distance at the best sky location.
Table 2 shows R, D, and H for both NS–NS binaries and BH–NS binaries, corresponding to the design sensitivity of Advanced LIGO, together with the expected rates of SGRBs (according to our models (a) and (c)) within the corresponding volumes. The local rate of SGRBs predicted by our model (a) is 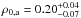 yr-1 Gpc-3 and for model (c)
yr-1 Gpc-3 and for model (c) 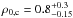 yr-1 Gpc-3. The distance R for NS–NS binary inspiral at design aLIGO sensitivity, which corresponds to 200 Mpc (z ≈ 0.045), is shown by the vertical light grey shaded region in Fig. 5.
yr-1 Gpc-3. The distance R for NS–NS binary inspiral at design aLIGO sensitivity, which corresponds to 200 Mpc (z ≈ 0.045), is shown by the vertical light grey shaded region in Fig. 5.
Figure 5 also shows the predictions of population synthesis models for double NS merger (Dominik et al. 2015) or the estimates based on the Galactic population of NS (Kim et al. 2015) which bracket the pink dashed region in Fig. 5.
By comparing the SGRB models in Fig.5 with these putative progenitor curves, assuming that all NS–NS binary mergers yield a SGRB, we estimate the average jet opening angle of SGRBs as ⟨ θjet ⟩ ~ 3°−6° in case (a) (solid red line in Fig. 5) and 5°−10° in case (c). The local rates by D14 and WP15 instead lead to an average angle ⟨ θjet ⟩ ~ 7°−14°. These estimates represent minimum values of the average jet opening angle, because they assume that all NS–NS binary mergers lead to a SGRB. We note that our range is consistent with the very few SGRBs with an estimated jet opening angle: GRB 051221A (θjet = 7°, Soderberg et al. 2006), GRB 090426 (θjet = 5°, Nicuesa Guelbenzu et al. 2011), GRB 111020A (θjet = 3°−8°, Fong et al. 2012), GRB 130603B (θjet = 4°−8°, Fong et al. 2014), and GRB 140903A (Troja et al. 2016). Similarly to the population of long GRBs (Ghirlanda et al. 2012), the distribution of θjet of SGRBs could be asymmetric with a tail extending towards large angles, i.e. consistently with the lower limits claimed by the absence of jet breaks in some SGRBs (Berger 2014).
8. Conclusions
We derived the luminosity function φ(L), redshift distribution Ψ(z), and local rate of SGRBs. Similarly to previous works present in the literature, we fitted the properties of a synthetic SGRB population, described by the parametric φ(L) and Ψ(z), to a set of observational constraints derived from the population of SGRBs detected by Fermi and Swift. Any acceptable model of the SGRB population must reproduce their prompt emission properties and their redshift distributions. Our approach features a series of improvements with respect to previous works present in the literature:
(observer frame) constraints: We extend the classical set ofobservational constraints (peak flux and – for a few events –redshift distribution) requiring that our model should reproducethe peak flux P, fluence F, peak energy Ep,o, and duration T distributions of 211 SGRBs with P64 ≥ 5 ph s-1 cm-2 as detected by the GBM instrument on board the Fermi satellite. The uniform response of the GBM over a wide energy range (10 keV – few MeV) ensures a good characterization of the prompt emission spectral properties of the GRB population and, therefore, of the derived quantities, i.e. the peak flux and the fluence;
(rest frame) constraints: we also require that our model reproduces the distributions of redshift, luminosity, and energy of a small sample (11 events) of Swift SGRBs with P64 ≥ 3.5 ph s-1 cm-2 (selected by D14). This sample is 70% complete in redshift and therefore it ensures a less pronounced impact of redshift–selection biases in the results;
method: we parametrize Ψ(z) as in Eq. (12) and derive the redshift distribution of SGRBs independently from their progenitor nature and their cosmic star formation history. Instead, the classical approach depends (i) on the assumption of a specific cosmic star formation history ψ(z) and (ii) on the assumption of a delay time distribution P(τ);
method: we derive our results assuming the existence of intrinsic Ep−Liso and Ep−Eiso correlations in SGRBs (case (a)), similarly to what has been observed in the population of long GRBs. However, since evidence of the existence of such correlations in the population of SGRBs is still based on a limited number of bursts, we also explore the case of uncorrelated peak energy, luminosity and energy (case (c)).
Our main results are as follows:
The luminosity function of SGRBs (case (a)),which we model with a broken power law, has a slope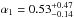 (68% confidence interval) below the break luminosity of
(68% confidence interval) below the break luminosity of 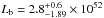 erg s-1 and falls steeply above the break with
erg s-1 and falls steeply above the break with 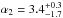 . This solution is almost independent from the specific assumption of the minimum luminosity of the φ(L) (case (b)). Moreover, it implies an average isotropic equivalent luminosity ⟨L⟩ ≈ 1.5 × 1052 erg s-1 (or 3 × 1052 erg s-1 in case (c)), which is much larger than e.g. ⟨L⟩ ≈ 3 × 1050 erg s-1 from D14 or ⟨L⟩ ≈ 4.5 × 1050 erg s-1 from WP15;
. This solution is almost independent from the specific assumption of the minimum luminosity of the φ(L) (case (b)). Moreover, it implies an average isotropic equivalent luminosity ⟨L⟩ ≈ 1.5 × 1052 erg s-1 (or 3 × 1052 erg s-1 in case (c)), which is much larger than e.g. ⟨L⟩ ≈ 3 × 1050 erg s-1 from D14 or ⟨L⟩ ≈ 4.5 × 1050 erg s-1 from WP15;
The redshift distribution of SGRBs Ψ(z) peaks at z ~ 1.5 and falls rapidly above the peak. This result is intermediate between those reported in the literature which assume either a constant large delay or a power law distribution favouring small delays. We find that our Ψ(z) is consistent with the MD14 SFH retarded with a power law delay time distribution ∝τ-1;
As a by-product we find that, if SGRBs feature intrinsic Ep−Liso and Ep−Eiso correlations, they could be slightly steeper than those derived with the current small sample of short bursts with redshift (e.g. Tsutsui et al. 2013), but still consistent within their 68% confidence intervals;
If we assume that there are no correlations between Ep,o and Liso(Eiso) (case (c)), we find similarly that the φ(L) is flat at low luminosities and the formation rate peaks at slightly larger redshift (z ~ 2);
We estimate the rate of SGRBs as a function of z within the explorable volume of advanced LIGO and Virgo for the detection of double NS mergers or NS–BH mergers. Assuming the design aLIGO sensitivity averaged over sky location and over binary orbital plane orientation with respect to the line of sight, NS–NS mergers can be detected up to 200 Mpc (410 Mpc for NS–BH mergers). This is usually referred to as the detection range for these binaries. The rate of SGRBs within the corresponding volume is ~7 × 10-3 yr-1 (0.028 yr-1 for NS–BH merger distance), assuming the existence of Ep−Liso and Ep−Eiso correlations for the population of short bursts (model (a)). Rates larger by a factor of ~4 are obtained if no correlation is assumed (model (c)). If binaries producing observable SGRBs are preferentially face-on (which is the case if the GRB jet is preferentially aligned with the orbital angular momentum), then the actual explorable volume extends to a somewhat larger distance (a factor of ~1.5 larger, see Schutz 2011), increasing the rates of coincident SGRB–GWs of about a factor of 3.4 (Schutz 2011);
We compare our SGRB rates with the rates of NS mergers derived from population synthesis models or from the statistics of Galactic binaries. This enables us to infer an average opening angle of the population of SGRBs of 3°–6° (assuming that all SGRBs are produced by the NS–NS mergers), which is consistent with the few bursts with θjet measured from the break of their afterglow light curve.
Our SGRB rate estimates might seem to compromise the perspective of a joint GW–SGRB observation in the near future. We note, however, that these rates refer to the prompt emission of SGRBs whose jets point towards the Earth. SGRBs not pointing at us can still be seen as orphan afterglows (i.e. afterglows without an associated prompt emission; see e.g. Ghirlanda et al. 2015b; Rhoads 1997 for the population of long GRBs), especially if the afterglow emission is poorly collimated or even isotropic (e.g. Ciolfi & Siegel 2015). The luminosity of the afterglow correlates with the jet kinetic energy, which is thought to be proportional to the prompt luminosity. Point 1 above shows that the average luminosity in the prompt emission, as implied by our result, is nearly two orders of magnitude higher than previous findings. This enhances the chance of observing an orphan afterglow in association with a GW event (e.g. Metzger et al. 2015). Efforts should go in the direction of finding and identifying such orphan afterglows as counterparts of GW events.
For the sake of tidiness, throughout this work we will sometimes drop the “iso” subscript, so that Liso and Eiso will be equivalently be written as L and E. For the same reason, the peak energy Epeak,obs (Epeak,rest) of the νF(ν) spectrum in the observer frame (in the local cosmological rest frame) will be sometimes written as Ep,o (Ep).
Here we consider as a constraint the population of Fermi/GBM GRBs. Nava et al. (2011a) showed that the BATSE SGRB population has similar prompt emission properties of Fermi SGRBs (peak flux, fluence, and duration distribution).
This might seem a rough assumption, since SGRBs sometimes show light curves with multiple peaks. Statistical studies, however, show that the majority of SGRB light curves are composed of a few peaks, with separation much smaller than the average duration (e.g. McBreen et al. 2001), which justifies the use of this assumption in a statistical sense.
getDist is a python package written by Antony Lewis of the University of Sussex. It is a set of tools to analyse MCMC chains and to extract posterior density distributions using Kernel Density Estimation (KDE) techniques. Details can be found at http://cosmologist.info/notes/GetDist.pdf
A third event, LVT151012, was reported in Abbott et al. (2016b) but with a small associated significance implying an ~87% probability of being of astrophysical origin.
Acknowledgments
We acknowledge the financial support of the UnivEarthS Labex program at Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02) and the “Programme PTV de l’Observatoire de Paris” and GEPI for the financial support and kind hospitality during the implementation of part of this work. R.C. is supported by MIUR FIR Grant No. RBFR13QJYF. We acknowledge ASI grant I/004/11/1. We thank the referee for useful comments.
References
- Aasi, J., Abbott, B. P., Abbott, R., et al. (The LIGO Scientific Collaboration) 2015, Class. Quant. Grav., 32, 074001 [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (The LIGO Scientific Collaboration & the Virgo Collaboration). 2016a, Phys. Rev. Lett., 116, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (The LIGO Scientific Collaboration, the Virgo Collaboration) 2016b, ArXiv e-prints [arXiv:1606.04856] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016c, ApJ, 818, L22 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016d, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016e, Liv. Rev. Relativ., 19, 1 [Google Scholar]
- Acernese, F., Agathos, M., Agatsuma, K., et al. 2015, Class. Quant. Grav., 32, 024001 [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2016, ApJ, 823, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2016, ApJ, 829, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Amati, L. 2006, MNRAS, 372, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Annis, J., Soares-Santos, M., Berger, E., et al. 2016, ApJ, 823, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Perna, R., Bulik, T., et al. 2006, ApJ, 648, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2014, ARA&A, 52, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Fong, W., & Chornock, R. 2013, ApJ, 774, L23 [Google Scholar]
- Branchesi, M., Klotz, A., Laas-Bourez, M. et al. (The LIGO Scientific Collaboration & the Virgo Collaboration) 2011, ArXiv e-prints [arXiv:1110.3169] [Google Scholar]
- Branchesi, M., et al. (The LIGO Scientific Collaboration & the Virgo Collaboration) 2012, J. Phys. Conf. Ser., 375, 062004 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2013, ApJ, 764, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghirlanda, G., Ghisellini, G., et al. 2015, MNRAS, 448, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Chassande-Mottin, E. 2016, Horizon to range relation for near face-on binaries, Tech. Rep. VIR-0244A-16 (The Virgo Collaboration) https://tds.ego-gw.it/ql/?c=11552 [Google Scholar]
- Ciolfi, R., & Siegel, D. M. 2015, ApJ, 798, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Norberg, P., Baugh, C. M., et al. 2001, MNRAS, 326, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Connaughton, V., Burns, E., Goldstein, A., et al. 2016, ApJ, 826, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Copperwheat, C. M., Steele, I. A., Piascik, A. S., et al. 2016, MNRAS, 462, 3528 [NASA ADS] [CrossRef] [Google Scholar]
- Coward, D. M., Howell, E. J., Piran, T., et al. 2012, MNRAS, 425, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Coward, D. M., Branchesi, M., Howell, E. J., Lasky, P. D., & Böer, M. 2014, MNRAS, 445, 3575 [NASA ADS] [CrossRef] [Google Scholar]
- Cowperthwaite, P. S., Berger, E., Soares-Santos, M., et al. 2016, ApJ, 826, L29 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P. 2015, J. High Energy Astrophys., 7, 73 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P., Salvaterra, R., Bernardini, M. G., et al. 2014, MNRAS, 442, 2342 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Belczynski, K., Fryer, C., et al. 2013, ApJ, 779, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Berti, E., O’Shaughnessy, R., et al. 2015, ApJ, 806, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Kennea, J. A., Barthelmy, S. D., et al. 2016a, MNRAS, 460, L40 [NASA ADS] [Google Scholar]
- Evans, P. A., Kennea, J. A., Palmer, D. M., et al. 2016b, MNRAS, 462, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., & Berger, E. 2013, ApJ, 776, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Margutti, R., et al. 2012, ApJ, 756, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Metzger, B. D., et al. 2014, ApJ, 780, 118 [Google Scholar]
- Fong, W., Berger, E., Margutti, R., & Zauderer, B. A. 2015, ApJ, 815, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., Celotti, A., & Firmani, C. 2009, A&A, 496, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., et al. 2012, MNRAS, 420, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Bernardini, M. G., Calderone, G., & D’Avanzo, P. 2015a, J. High Energy Astrophys., 7, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Salvaterra, R., Campana, S., et al. 2015b, A&A, 578, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacomazzo, B., Perna, R., Rezzolla, L., Troja, E., & Lazzati, D. 2013, ApJ, 762, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., & Preece, R. 2010, in Proc. Eighth Integral Workshop. The Restless Gamma-ray Universe (INTEGRAL 2010), 94 [Google Scholar]
- Gruber, D., Goldstein, A., Weller von Ahlefeld, V., et al. 2014, ApJS, 211, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Guetta, D., & Piran, T. 2005, A&A, 435, 421 [Google Scholar]
- Guetta, D., & Piran, T. 2006, A&A, 453, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guetta, D., & Stella, L. 2009, A&A, 498, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopman, C., Guetta, D., Waxman, E., & Portegies Zwart, S. 2006, ApJ, 643, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Hotokezaka, K., Nissanke, S., Hallinan, G., et al. 2016, ApJ, submitted [arXiv:1605.09395] [Google Scholar]
- Jin, Z.-P., Li, X., Cano, Z., et al. 2015, ApJ, 811, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z.-P., Hotokezaka, K., Li, X., et al. 2016, Nature Communications, submitted [arXiv:1603.07869] [Google Scholar]
- Kasliwal, M. M., Cenko, S. B., Singer, L. P., et al. 2016, ApJ, 824, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C., Perera, B. B. P., & McLaughlin, M. A. 2015, MNRAS, 448, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [Google Scholar]
- Lyutikov, M. 2016, ArXiv e-prints [arXiv:1602.07352] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Martynov, D. V., Hall, E. D., Abbott, B. P., et al. (The LIGO Scientific Collaboration) 2016, Phys. Rev. D. 93, 112004 [Google Scholar]
- McBreen, S., Quilligan, F., McBreen, B., Hanlon, L., & Watson, D. 2001, A&A, 380, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metzger, B. D., & Berger, E. 2012, ApJ, 746, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Williams, P. K. G., & Berger, E. 2015, ApJ, 806, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Morokuma, T., Tanaka, M., Asakura, Y., et al. 2016, PASJ, 68, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Morsony, B. J., Workman, J. C., & Ryan, D. M. 2016, ApJ, 825, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Gal-Yam, A. 2005, in BAAS, 37, 1418 [Google Scholar]
- Nakar, E., Gal-Yam, A., & Fox, D. B. 2006, ApJ, 650, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011a, MNRAS, 415, 3153 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011b, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nava, L., Salvaterra, R., Ghirlanda, G., et al. 2012, MNRAS, 421, 1256 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Nicuesa Guelbenzu, A., Klose, S., Rossi, A., et al. 2011, A&A, 531, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Shaughnessy, R., Belczynski, K., & Kalogera, V. 2008, ApJ, 675, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., Lazzati, D., & Giacomazzo, B. 2016, ApJ, 821, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Pescalli, A., Ghirlanda, G., Salvaterra, R., et al. 2016, A&A, 587, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., & Yungelson, L. R. 1998, A&A, 332, 173 [NASA ADS] [Google Scholar]
- Racusin, J. L., Burns, E., Goldstein, A., et al. 2016, ApJ, submitted [arXiv:1606.04901] [Google Scholar]
- Rhoads, J. E. 1997, ApJ, 487, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Kumar, P. 2015, ApJ, 802, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., & Gehrels, N. 2009, in AIP Conf. Ser. 1133, eds. C. Meegan, C. Kouveliotou, & N. Gehrels, 112 [Google Scholar]
- Salvaterra, R., Cerutti, A., Chincarini, G., et al. 2008, MNRAS, 388, L6 [NASA ADS] [Google Scholar]
- Salvaterra, R., Campana, S., Vergani, S. D., et al. 2012, ApJ, 749, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Mereghetti, S., et al. 2016, ApJ, 820, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Ferrari, V., Matarrese, S., & Portegies Zwart, S. F. 2001, MNRAS, 324, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Schutz, B. F. 2011, Class. Quant. Grav., 28, 125023 [Google Scholar]
- Shahmoradi, A., & Nemiroff, R. J. 2015, MNRAS, 451, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, D. M., & Ciolfi, R. 2016a, ApJ, 819, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, D. M., & Ciolfi, R. 2016b, ApJ, 819, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Siellez, K., Boër, M., & Gendre, B. 2014, MNRAS, 437, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Chambers, K. C., Smith, K. W., et al. 2016a, MNRAS, 462, 4094 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Chambers, K. C., Smith, K. W., et al. 2016b, ApJ, 827, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Soares-Santos, M., Kessler, R., Berger, E., et al. 2016, ApJ, 823, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Berger, E., Kasliwal, M., et al. 2006, ApJ, 650, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Spera, M., Mapelli, M., & Bressan, A. 2015, MNRAS, 451, 4086 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2013, Nature, 500, 547 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Troja, E., Read, A. M., Tiengo, A., & Salvaterra, R. 2016, ApJ, 822, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Tsutsui, R., Yonetoku, D., Nakamura, T., Takahashi, K., & Morihara, Y. 2013, MNRAS, 431, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Virgili, F. J., Zhang, B., O’Brien, P., & Troja, E. 2011, ApJ, 727, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Wanderman, D., & Piran, T. 2015, MNRAS, 448, 3026 [NASA ADS] [CrossRef] [Google Scholar]
- Yamazaki, R., Asano, K., & Ohira, Y. 2016, Prog. Theor. Exp. Phys., 2016, 051E01 [CrossRef] [Google Scholar]
- Yang, B., Jin, Z.-P., Li, X., et al. 2015, Nat. Commun., 6, 7323 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. 2016, ApJ, 827, L31 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Short GRB rates in yr-1 (68% errors) within the volume corresponding to different distances.
All Figures
 |
Fig. 1 Black dots show the distributions obtained from our Fermi/GBM and Swift SBAT4 samples (Sect. 2). Horizontal error bars are the bin widths, while vertical error bars are 1σ errors on the bin heights accounting for experimental errors on single measurements. The results of our Monte Carlo population synthesis code are shown by solid red lines (assuming Ep−Liso and Ep−Eiso correlations to hold in the population of SGRBs) and by triple dot-dashed orange lines (assuming no correlation). Predictions based on the models of D14 and WP15 are shown by dashed blue and dot-dashed cyan lines, respectively (the latter only in the first three panels; see text). These are obtained by the analytical methods of Sect. 3.1. Top left panel: distribution of the peak flux P of the Fermi/GBM sample. Top right panel: normalized cumulative redshift distribution of the SBAT4 sample. The grey shaded area represents the range spanned by the distribution if the remaining bursts with unknown z are assigned the largest or the lowest z of the sample. The inset shows the cumulative distributions of the isotropic luminosity Liso (solid black line) and energy Eiso (solid grey line) of the same sample. Bottom panels: from left to right, distributions of peak energy Ep,o, fluence, and duration of SGRBs of our Fermi/GBM sample. |
| In the text | |
 |
Fig. 2 Scheme of the procedure followed in the MC to generate the observables of each synthetic GRB. |
| In the text | |
 |
Fig. 3 Marginalized densities of our MCMC parameters in case (a) (i.e. with correlations and no minimum luminosity). Black dashed lines indicate the means and black dot-dashed lines indicate the modes of the distributions. |
| In the text | |
 |
Fig. 4 Comparison between various predicted SGRB redshift distributions. The grey dashed line represents the convolution of the MD14 cosmic SFH with a delay time distribution P(τ) ∝ τ-1 with τ> 20 Myr (the normalization is arbitrary). The pink solid line (pink dotted line) represents the redshift distribution of NS−NS binary mergers predicted by Dominik et al. (2013) in their high end (low end) metallicity evolution scenario (standard binary evolution model). The blue dashed line and cyan dot-dashed line are the SGRB redshift distributions according to D14 and to WP15, respectively. The red solid line is our result in case (a), while the orange triple dot-dashed line is our result in case (c). In both cases we used the mean parameter values as listed in Table 1. |
| In the text | |
 |
Fig. 5 Event rates within redshift z: Solid red line and triple dot-dashed orange line represent the SGRB rates for case (a) and case (c) of this work, respectively. The yellow shaded region represents the 68% confidence level on the rate (red line) of case (a). SGRB rates according to the models of D14 and WP15 are shown by the dashed blue and dot-dashed cyan lines, respectively. The rate of NS−NS mergers is shown by the hatched pink region where the lower (upper) boundary corresponds to the rate derived from population synthesis models (Galactic binaries) in Dominik et al. (2015) and Kim et al. (2015). The vertical grey shaded regions show the present and design ranges of aLIGO for NS−NS mergers. The upper limit (white star) corresponds to the non-detection of NS−NS mergers in the first 48.6 days of the “O1” run of aLIGO. The green vertical bar is the rate of binary BH mergers derived by Abbott et al. (2016b) and shown here at the distance of GW150914 and GW151226. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$z_{\rm{peak}} \approx z_{\rm{p}}\left\lbrace p_2\left[1 + 1/\left(p_1\,z_{\rm{p}}\right)\right]-1\right\rbrace^{-1/p_2}$}](/articles/aa/full_html/2016/10/aa28993-16/aa28993-16-eq333.png)