| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201628888 | |
| Published online | 21 September 2016 | |
High-precision abundances of Sc, Mn, Cu, and Ba in solar twins
Trends of element ratios with stellar age⋆
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: pen@phys.au.dk
Received: 10 May 2016
Accepted: 15 June 2016
Aims. A previous study of correlations between element abundances and ages of solar twin stars in the solar neighborhood is extended to include Sc, Mn, Cu, and Ba to obtain new information on the nucleosynthetic history of these elements.
Methods. HARPS spectra with S/N ≳ 600 are used to derive very precise (σ ~ 0.01 dex) differential abundances of Sc, Mn, Cu, and Ba for 21 solar twins and the Sun. The analysis is based on MARCS model atmospheres with parameters determined from the excitation and ionization balance of Fe lines. Stellar ages with internal errors less than 1 Gyr are obtained by interpolation in the log g – Teff diagram between isochrones based on the Aarhus Stellar Evolution Code.
Results. For stars younger than 6 Gyr, [Sc/Fe], [Mn/Fe], [Cu/Fe], and [Ba/Fe] are tightly correlated with stellar age, which is also the case for the other elements previously studied; linear relations between [X/Fe] and age have 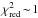 , and for most stars the residuals do not depend on elemental condensation temperature. For ages between 6 and 9 Gyr, the [X/Fe] – age correlations break down and the stars split up into two groups having respectively high and low [X/Fe] for the odd-Z elements Na, Al, Sc, and Cu.
, and for most stars the residuals do not depend on elemental condensation temperature. For ages between 6 and 9 Gyr, the [X/Fe] – age correlations break down and the stars split up into two groups having respectively high and low [X/Fe] for the odd-Z elements Na, Al, Sc, and Cu.
Conclusions. While stars in the solar neighborhood younger than ~ 6 Gyr were formed from interstellar gas with a smooth chemical evolution, older stars seem to have originated from regions enriched by supernovae with different neutron excesses. Correlations between abundance ratios and stellar age suggest that: (i) Sc is made in Type II supernovae along with the α-capture elements; (ii) the Type II to Ia yield ratio is about the same for Mn and Fe; (iii) Cu is mainly made by the weak s-process in massive stars; (iv) the Ba/Y yield ratio for asymptotic giant branch stars increases with decreasing stellar mass; (v) [Y/Mg] and [Y/Al] can be used as chemical clocks when determining ages of solar metallicity stars.
Key words: stars: abundances / stars: fundamental parameters / stars: solar-type / Galaxy: disk / Galaxy: evolution
© ESO, 2016
1. Introduction
Precise determinations of stellar abundances by Meléndez et al. (2009) and Ramírez et al. (2009) have revealed significant variations of abundance ratios among solar twin stars that are correlated with elemental condensation temperature, TC (Lodders 2003). Interestingly, the Sun has a higher ratio of volatile to refractory elements than the majority of solar twins, which could be caused by sequestration of refractory elements in terrestrial planets in the solar system. If so, the slope of [X/Fe] 1 versus TC may be used as a signature of the occurrence of rocky planets around stars. Alternatively, slope differences could be due to dust-gas separation in connection with star formation (Önehag et al. 2014; Gaidos 2015).
High-precision abundance studies based on HARPS spectra also point to variations of the [X/Fe]-TC slope among solar-type stars (González Hernández et al. 2010, 2013; Adibekyan et al. 2014), but the slope does not seem to depend on the occurrence of terrestrial planets. The same conclusion is reached by Schuler et al. (2015) based on detailed abundances of seven Kepler stars hosting small planets. Instead, Adibekyan et al. (2014), Maldonado et al. (2015), and Maldonado & Villaver (2016) find a correlation between the [X/Fe]-TC slope and stellar age. This is confirmed by Nissen (2015, hereafter Paper, who from a study of precise abundances of 21 solar twins in the solar neighborhood finds that the ratio of volatile to refractory elements, for example [C/Fe] and [O/Fe], is correlated with stellar age. The same result is obtained by Spina et al. (2016b) for 13 solar twins belonging to the thin-disk population. In both studies there are, however, indications of significant [X/Fe]-TC slope differences at a given age suggesting that other processes than chemical evolution play a role. This is supported by studies of stellar twins in the binary systems, 16 Cyg (Ramírez et al. 2011; Tucci Maia et al. 2014) and XO-2 (Teske et al. 2015; Biazzo et al. 2015; Ramírez et al. 2015), for which there are differences in [Fe/H] and the [X/Fe]-TC slope between the components.
According to the results obtained in Paper I and by Spina et al. (2016b), the differences of abundance ratios among solar twin stars are mainly due to Galactic chemical evolution. The variation of the [X/Fe]-TC slope is a secondary effect that introduces some scatter in the [X/Fe] – age trends, but it does not prevent us from obtaining new knowledge about nucleosynthesis from the relations between abundance ratios and stellar age. Given that the relative ages of solar twins can be determined with a precision better than 1 Gyr (see Paper I), we may in this way get more direct information on Galactic chemical evolution than by studying the change of abundance ratios as a function of metallicity, which method is hampered by a large scatter in the age-metallicity relation (Edvardsson et al. 1993; Nordström et al. 2004; Haywood et al. 2013).
As shown in Paper I, the abundances of C, O, Mg, Al, and Zn relative to Fe for solar twins belonging to the thin-disk population increase by 0.10 to 0.15 dex as the stellar age increases from ~ 1 to 8 Gyr. This can be explained if C, O, Mg, Al, and Zn are mainly made in high-mass stars exploding as Type II supernovae (SNe) on a relatively short timescale, whereas Type Ia SNe provide an important contribution to Fe on a longer timescale. [Si/Fe], [S/Fe], and [Ti/Fe] change in the same way as a function of age but with an amplitude of about 0.05 dex only. [Ca/Fe] on the other hand is nearly the same for all ages with a scatter of 0.01 dex only, which is a surprise because Ca is normally considered to be an α-capture element mainly produced in Type II SNe like Mg, Si, and S. [Na/Fe] and [Ni/Fe] show considerable scatter among the older stars but are tightly correlated with each other. Furthermore, [Y/Fe] increases steeply with decreasing stellar age, which can be explained by an increasing contribution to the abundance of s-process elements from low-mass asymptotic giant branch (AGB) stars in the course of time (Travaglio et al. 2004).
In the present paper, the study of solar twins in Paper I is extended to include Sc, Mn, Cu, and Ba. The origin and nucleosynthesis of these elements have been much discussed (e.g., Romano et al. 2010; Serminato et al. 2009), which to some extent is due to uncertainties in the metallicity and age trends. In some works, the Sc/Fe ratio is found to be close to solar at all metallicities (Gratton & Sneden 1991; Prochaska & McWilliam 2000), whereas other studies point to enhanced Sc abundances (relative to Fe) in metal-poor thick-disk stars similar to the enhancement of α-elements (Zhao & Magain 1990; Nissen et al. 2000; Reddy et al. 2006; Adibekyan et al. 2012; Battistini & Bensby 2015). Mn and Cu are found to be under-abundant relative to Fe for metal-poor disk and halo stars, if spectral lines are analyzed assuming local thermodynamic equilibrium (LTE) (Sneden et al. 1991; Mishenina et al. 2002, 2015a; Reddy et al. 2006; Feltzing et al. 2007; Nissen & Schuster 2011; Adibekyan et al. 2012; Battistini & Bensby 2015). Corrections for non-LTE effects modify, however, the metallicity trends of [Mn/Fe] and [Cu/Fe] very significantly (Bergemann & Gehren 2008; Yan et al. 2015, 2016). In the case of Ba, some investigations point to enhanced [Ba/Fe] values in young stars (Edvardsson et al. 1993; Bensby et al. 2007). This is, however, not confirmed by Mishenina et al. (2013).
In Sect. 2, the stellar parameters and abundances derived in Paper I are reviewed, and ages based on the Aarhus Stellar Evolution Code (ASTEC) are determined and compared to the stellar ages derived in Paper I from Yonsei-Yale (YY) isochrones. The determination of Sc, Mn, Cu, and Ba abundances is presented in Sect. 3. Trends of abundance ratios as a function of stellar age and elemental condensation temperature are discussed in Sect. 4 together with some considerations about the nucleosynthesis of odd-Z and neutron-capture elements and the use of [Y/Mg] or [Y/Al] as chemical clocks for determining stellar ages. A summary and some conclusions are given in Sect. 5.
2. Stellar parameters and ages
The solar twins were selected from the analysis of HARPS spectra (see Mayor et al. 2003) by Sousa et al. (2008) to have atmospheric parameters that agree with those of the Sun within ± 100 K in effective temperature, Teff, ± 0.15 dex in logarithmic surface gravity, log g, and ± 0.10 dex in metallicity, [Fe/H]. The range in log g is somewhat larger than the range (± 0.10 dex) adopted by Ramírez et al. (2009) in their definition of a solar twin. It is also noted that none of the stars is a “perfect good solar twin” (Cayrel de Strobel 1996) in the sense that it has the same mass, age, and composition as the Sun within the estimated errors. The stars range in age from 0.7 Gyr to about 9 Gyr and show a diversity of chemical compositions including large differences in lithium abundance correlated with stellar age (Carlos et al. 2016).
As an additional selection criteria, only stars having HARPS spectra with a signal-to-noise ratio S/N ≥ 600 were included. This resulted in a list of 21 solar twins, three of which have enhanced [α/Fe] ratios and probably belong to the thick-disk population (Haywood et al. 2013) or a special population of high-α metal-rich (hαmr) stars (Adibekyan et al. 2011). The other 18 stars have typical thin-disk abundances and kinematics. All stars have distances less than 60 pc according to their Hipparcos parallaxes (van Leeuwen 2007).
The extremely high S/N and resolution (R ≃ 115 000) of the HARPS spectra make it possible to determine very precise parameters and abundances of the solar twins relative to the Sun. The analysis in Paper I was made differentially, line-by-line, relative to a HARPS solar flux spectrum with S/N ~ 1200 observed in reflected sunlight from the asteroid Vesta. Teff and log g were determined by requesting that the iron abundances derived have no systematic dependence on excitation and ionization potential of the Fe lines applied. The estimated errors of the parameters are σ(Teff) = ± 6 K and σ(log g) = ± 0.012 dex, and abundances of C, O, Na, Mg, Al, Si, S, Ca, Ti, Cr, Fe, Ni, Zn, and Y were determined with a typical precision of ± 0.01 dex.
By interpolating to the observed values of Teff, log g, [Fe/H], and [α/Fe] in a set of YY isochrones (Yi et al. 2001; Kim et al. 2002), stellar ages were derived in Paper I2. An internal age precision of 0.4 to 0.8 Gyr was estimated, but due to possible systematic errors in the model calculations, the ages of the youngest and oldest stars may be more uncertain. In order to test this, ASTEC stellar models (Christensen-Dalsgaard 2008) have been used to calculate isochrones in the Teff – log g plane for a range of compositions covering those of the solar twins. In contrast to YY models, the ASTEC models include diffusion and settling of heavy elements (Christensen-Dalsgaard et al. 1993). Therefore, the ASTEC ages were obtained by interpolating in the surface heavy element abundance (Zs) for the isochrones to the observed Z-value of the star.
 |
Fig. 1 Comparison of stellar ages derived from YY and ASTEC isochrones. The line shows the linear fit to the data given by Eq. (1). The dotted line shows the 1:1 relation. |
As seen from Fig. 1, the ASTEC ages of the oldest stars are systematically higher than the ages derived from YY isochrones. A linear fit to the data gives ![\begin{eqnarray} Age \, {\rm (ASTEC)} = -0.3 \, (\pm 0.1) + 1.13 \, (\pm 0.02) \,\, Age\,{\rm (YY) \, [Gyr]} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28888-16/aa28888-16-eq22.png) (1)with a standard deviation of 0.28 Gyr corresponding to 0.20 Gyr on each of the two sets of ages. The residuals in the fit are to some degree correlated with stellar metallicity, which may be due to different assumptions about the change of helium abundance as a function of heavy element abundance. For the ASTEC models ΔY/ ΔZ = 1.4 is adopted, whereas the YY models are based on ΔY/ ΔZ = 2.0. In any case, the scatter in the relation between the two sets of ages is smaller than the age errors (0.4 to 0.8 Gyr) arising from the uncertainties in Teff and log g. Hence, the use of a different sets of isochrones has only a small effect when comparing stars of similar age, but it affects the age scale; for the oldest stars, 10% higher ages are derived when applying ASTEC instead of YY isochrones.
(1)with a standard deviation of 0.28 Gyr corresponding to 0.20 Gyr on each of the two sets of ages. The residuals in the fit are to some degree correlated with stellar metallicity, which may be due to different assumptions about the change of helium abundance as a function of heavy element abundance. For the ASTEC models ΔY/ ΔZ = 1.4 is adopted, whereas the YY models are based on ΔY/ ΔZ = 2.0. In any case, the scatter in the relation between the two sets of ages is smaller than the age errors (0.4 to 0.8 Gyr) arising from the uncertainties in Teff and log g. Hence, the use of a different sets of isochrones has only a small effect when comparing stars of similar age, but it affects the age scale; for the oldest stars, 10% higher ages are derived when applying ASTEC instead of YY isochrones.
The YY and ASTEC models are based on similar prescriptions for energy generation, opacity and equations of state, and are calibrated on the Sun adopting a mass ratio of heavy elements to hydrogen of (Z/X)⊙ = 0.0244 at the surface (Grevesse et al. 1996). Both sets of models include helium diffusion, but as mentioned above only the ASTEC models include diffusion of heavy elements, which means that the opacity in the interior of an ASTEC model of an old star is higher than in a YY model with the same surface abundance. This may be the reason for the different age scales.
As a further test of systematic errors in the ages, ASTEC isochrones have been compared to the often used Padova3 (PARSEC) isochrones (Bressan et al. 2012), which are also based on stellar models including diffusion of heavy elements. There is an excellent agreement between the two sets of isochrones at solar heavy element abundance for the Teff – log g ranges of solar twins suggesting that the ASTEC and PARSEC age scales are about the same.
Considering that the inclusion of heavy element diffusion makes the ASTEC models more realistic than the YY models, stellar ages derived from the ASTEC isochrones will be used in the present paper. The relations between abundance ratios and stellar age given in Paper I may be converted to the ASTEC age scale by using Eq. (1).
3. Sc, Mn, Cu, and Ba abundances
Sc, Mn, Cu, and Ba abundances are determined from the spectral lines listed in Table 1. The lines selected have nearby “continuum” regions almost free of lines, and care was taken to use the same continuum windows in all stars. Equivalent widths (EWs) were measured by Gaussian fitting using the IRAF splot task except for the Mn i 5394.69 Å line that has a “boxlike” profile due to hyperfine splitting and was measured by direct integration. This magnetic sensitive line has been found to vary in strength over the solar cycle (Danilovic et al. 2016), but the Mn abundances of the solar twins derived from the Mn i 5394.69 Å line show no excessive variation relative to the Mn abundances derived from the other Mn i lines.
To illustrate the high quality of the spectra, Fig. 2 shows a comparison of the spectrum of HD 96116 with the solar spectrum for the regions of the Cu i 5782.12 Å and Ba ii 5853.70 Å lines. HD 96116 is the youngest star in the sample (age ≃ 0.7 Gyr) and has a somewhat higher temperature (Teff = 5846 K) and surface gravity (log g = 4.50) but almost he same metallicity ([Fe/H] = 0.006) as the Sun. As seen, the Cr i and Fe i lines have nearly the same strengths in the two spectra, whereas the Cu i line is weaker and the Ba ii line is stronger in the spectrum of HD 96116. As we shall see in Sect. 4, this is related to the different trends of [Cu/Fe] and [Ba/Fe] as a function of stellar age.
Line data and equivalent widths measured for the HARPS solar flux spectrum.
 |
Fig. 2 Solar flux HARPS spectrum (red line) in comparison with the HARPS spectrum of HD 96116 (blue line) near the Cu i line at 5782.12 Å (left panel) and the Ba ii line at 5853.70 Å (right panel). The lower panels show the difference (HD 96116 – Sun) between the two spectra. |
The set of MARCS model atmospheres (Gustafsson et al. 2008) described in Paper I and the Uppsala BSYN program were used to calculate equivalent widths as a function of element abundance assuming LTE. Interpolation to the observed EW then provides the stellar abundance. Hyperfine splitting with data from Prochaska et al. (2000) was taken into account as described by Nissen & Schuster (2011). Microturbulence velocities (ξturb) were adopted from Paper I, and collisional broadening was included in the Unsöld (1955) approximation using an enhancement factor of two.
Abundance errors arising from the EW measurements are estimated by comparing abundances derived from the individual lines. Given that a homogeneous set of spectra has been used, we may calculate an average standard deviation of [X/Fe] 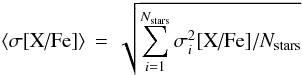 (2)where
(2)where 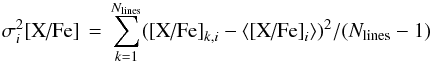 (3)is the variance for a given star. The corresponding average standard error of the mean value of [X/Fe]
(3)is the variance for a given star. The corresponding average standard error of the mean value of [X/Fe] 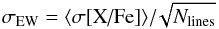 (4)is given in Col. 3 of Table 2. This error is only 0.003 dex in the case of Mn that has seven lines available, but is higher for elements with abundances based on two lines.
(4)is given in Col. 3 of Table 2. This error is only 0.003 dex in the case of Mn that has seven lines available, but is higher for elements with abundances based on two lines.
In addition to the error arising from the EW measurements, the uncertainties in the atmospheric parameters contribute to the total error of the abundances. For some abundance ratios, this error is small, because the derived abundances of two elements may have approximately the same dependence on Teff, log g, [Fe/H], and microturbulence. As a continuation of Table 4 in Paper I, the two sets of errors are given in Table 2 for the abundance ratios discussed in the present paper.
Errors of abundance ratios.
Stellar atmospheric parameters, ages, masses, and abundance ratios.
Because the solar twins have similar atmospheric parameters, differential non-LTE corrections are expected to be small. Still, there could be spurious trends of abundance ratios as a function of Teff, log g, and [Fe/H], if non-LTE effects are not taken into account. Thus, Bergemann & Gehren (2008) found that the non-LTE correction for Mn increases with decreasing metallicity. Using the same model atom, M. Bergemann (priv. comm.) has calculated non-LTE corrections for the solar twins in this paper. The corrections have an amplitude of ± 0.01 dex over the metallicity range from [Fe/H] = −0.10 to +0.10 dex and have been applied although the effect on the [Mn/Fe]-age relation is marginal.
In the case of Cu, Yan et al. (2015, 2016) have derived non-LTE corrections that increase with decreasing metallicity in the same way as for Mn. Based on the corrections for the 5218.2 and 5782.1 Å lines (Yan et al. 2015, Table 2), it is possible to estimate the change of non-LTE corrections relative to those of the Sun as a function of Teff, log g, and [Fe/H]. Applying these relations to the solar twins results in differential non-LTE corrections reaching +0.015 dex for stars having [Fe/H] ~ −0.1 and low gravity. Hence, the corrections are of some importance for the age trends of Cu and have been taken into account. The same method has been applied for Ba adopting non-LTE corrections calculated by Korotin et al. (2015) for the 5853.7 and 6496.9 Å Ba ii lines. This results in rather small differential corrections for the solar twins reaching an extreme of −0.007 dex at the lowest gravities. In the case of Sc, non-LTE effects are very small for Sc ii lines (Zhang et al. 2008, 2014), so differential corrections for solar twins have not been applied.
In Paper I, non-LTE corrections (Lind et al. 2011, 2012) were applied for Na and Fe. For the other elements studied, differential non-LTE effects were either estimated to be negligible or non-LTE calculations were not available. Furthermore, all non-LTE calculations are based on 1D model atmospheres; 3D non-LTE calculations may give somewhat different results. To take this additional uncertainty into account, an error of 0.005 dex as in Paper I has been added in quadrature to the errors arising from the uncertainties in the atmospheric parameters and the EW measurements. This leads to the adopted errors of [X/Fe] given in the last column of Table 2.
4. Results and discussion
The derived values of [Sc/Fe], [Mn/Fe], [Cu/Fe], and [Ba/Fe] are given in Table 3 together with the atmospheric parameters and ages derived from the ASTEC isochrones. Masses determined from the ASTEC evolutionary tracks are also included. They compare very well with the masses determined from YY evolutionary tracks (Yi et al. 2003) given in Paper I; the average deviation (YY – ASTEC) is 0.005 M⊙ with a rms deviation of 0.010 M⊙ suggesting that the masses have a precision of about 0.01 M⊙.
In the following subsections, the new data on Sc, Mn, Cu, and Ba are discussed together with the abundances of C, O, Na, Mg, Al, Si, S, Ca, Ti, Cr, Fe, Ni, Zn, and Y derived in Paper I.
4.1. Age correlations
Figures 3 and 4 show abundances relative to Fe as a function of stellar age. As seen, all ratios are tightly correlated with age for stars younger than 6 Gyr, but the [X/Fe]-age relations of odd-Z elements and Ni tend to break down for the older stars. This is mainly due to a group of five stars marked in red, which have low values of [Na/Fe], [Al/Fe], [Mn/Fe], [Sc/Fe], [Ni/Fe], and [Cu/Fe] relative to the group of three stars marked in green (to be named as low- and high-[Na/Fe] stars, respectively).
Linear fits ([X/Fe] = a + b · Age) for the 10 stars younger than 6 Gyr were determined by a maximum likelihood program that includes errors in both coordinates (Press et al. 1992). The coefficients a and b are given in Table 4 together with the reduced chi-squares, which are satisfactory close to one. For most elements, the [X/Fe]-age slopes are steeper than those given in Paper I, where all stars except the three α-enhanced ones were included in the age fits. These differences in slope arise because [X/Fe] for stars older than 6 Gyr tend to lie below the fits obtained for stars younger than 6 Gyr, not only for the odd-Z elements and Ni but also in the cases of C, Si, S, and Zn.
Linear fits of [X/Fe] as a function of age for stars younger than 6 Gyr, i.e., without including the Sun.
 |
Fig. 3 Abundance ratios as a function of stellar (ASTEC) age. For stars younger than 6 Gyr (black filled circles) the lines show linear fits to the data. The Sun, shown with the ⊙ symbol, was not included in the fits. Red filled circles show five old stars with low [Na/Fe] relative to three stars with similar age shown with green filled circles. Three [α/Fe]-enhanced stars are shown with open blue circles. |
Interestingly, there are also differences in the kinematics of the groups of stars shown in Fig. 3. According to data from the Geneva-Copenhagen survey (Nordström et al. 2004; Holmberg et al. 2009), the ten stars younger than 6 Gyr have about the same mean Galactocentric distance4, Rm, in their orbits. The average value is ⟨ Rm ⟩ = 8.1 kpc (i.e., close to the mean Galactocentric distance of the Sun, Rm, ⊙ ≃ 8.2 kpc) with a rms dispersion of ± 0.4 kpc. Assuming that Rm is a proxy of the Galactocentric distance of the stellar birthplace (Wielen 1977; Grenon 1987; Edvardsson et al. 1993) despite of the possible effect of radial migration (Sellwood & Binney 2002; Schönrich & Binney 2009; Gustafsson et al. 2016), it follows that the solar twins younger than 6 Gyr and the Sun were born within a narrow range in Galactocentric distance. This makes it understandable that these stars originate from interstellar gas with a good mixing of SNe products causing abundance ratios to develop in a smooth and homogeneous way. For solar twins older than 6 Gyr, the dispersion in Rm is larger. The three high-Na stars have ⟨ Rm ⟩ = 7.5 ± 0.7 kpc and the five low-Na stars have ⟨ Rm ⟩ = 7.2 ± 0.8 kpc. Hence, the differences of abundance ratios among stars with ages between 6 and 9 Gyr may be related to spatial inhomogeneities in the chemical evolution of the early Galactic disk.
The differences in [X/Fe] for Na, Al, Sc, Ni, and Cu for stars in the 6 to 9 Gyr age range cannot be explained by spacial variations in the ratio of Type II to Type Ia SNe. Such variations would also affect [X/Fe] for the α-elements, but as seen from Fig. 3, there is no or only a very small difference in [O/Fe], [Mg/Fe], [Si/Fe], [S/Fe], [Ca/Fe], and [Ti/Fe] between the high- and low-[Na/Fe] stars. Instead, the variations in [X/Fe] for odd-Z elements may be connected to a dependence of Type II SNe yields on heavy element abundance (especially C and O) of the progenitors (Kobayashi et al. 2006, Table 3). This dependence arises because the production of the odd-Z elements in core-collapse SNe is affected by the neutron excess, which is controlled by the 22Ne (α,n) 25Mg reaction, where 22Ne comes from double α-capture on 14N made in CNO burning at the expense of C and O. Hence, one could imagine that the low-[Na/Fe] stars were formed in regions having a lower heavy-element abundance than the regions where the high-[Na/Fe] stars were formed. Furthermore, the correlation between variations of [Ni/Fe] and [Na/Fe] may be explained if the yield of the dominating isotope, 58Ni, depends on the neutron excess as suggested by Venn et al. (2004).
There is no significant trend of [X/Fe] as a function of [Fe/H] for Sc, Mn, Cu, and Ba. Excluding the three α-enhanced stars, the average rms scatter at a given [Fe/H] is σ [Sc/Fe] = 0.033, σ [Mn/Fe] = 0.014, σ [Cu/Fe] = 0.042, and σ [Ba/Fe] = 0.071 dex. This lack of correlation between [X/Fe] and [Fe/H] is related to the fact that there is no correlation between metallicity and age for the solar twins, but a very significant dispersion (σ [Fe/H] ~ 0.07 dex) at a given age as seen from the panel with [Fe/H] in Fig. 3.
The [X/Fe]-age slopes given in Table 4 agree remarkably well with the slopes determined by Spina et al. (2016b) for a sample of 13 solar twins with ages less than 6 Gyr. For 14 elements, the b-coefficients agree within 1-sigma and for two elements (O and Ca) within 2-sigma. Only in the case of Mn, there appears to be a significant difference. Spina et al. obtain a steeper slope, b = (18.4 ± 3.2) × 10-3 dex Gyr-1, in comparison with b = (7.2 ± 2.0) × 10-3 dex Gyr-1 in this work.
It is also interesting to compare with the age trends obtained by da Silva et al. (2012) for a sample of 25 solar-type stars having 5500 K <Teff< 6100 K and −0.3 < [Fe/H] < + 0.3 for which they derived [X/Fe] abundance ratios with errors ranging from 0.03 to 0.07 dex. They divided the stars into two groups, younger and older than the Sun, and looked for correlations between [X/Fe] and age for each group. Slope coefficients are not given, but from Fig. 11 in da Silva et al. (2012) it is seen that the trends agree qualitatively with the trends determined in the present paper. [Mg/Fe], [Si/Fe], and [Zn/Fe] increase with age for both age groups, whereas [Ca/Fe] and [Cr/Fe] are nearly constant. [C/Fe], [Na/Fe], and [Ni/Fe] increase with age for the young group. [Y/Fe] and [Ba/Fe] decrease with increasing age, but [Ba/Fe] flattens out for the old stars like in Fig. 4 of this paper. Furthermore, [Mn/Fe] increases with age for the young group but decreases for for the old group as also found in present paper. Altogether, the results of da Silva et al. (2012) suggest that the age trends found for solar twins are shared by solar-type stars with a larger range of metallicities.
Furthermore, Spina et al. (2016a) have recently determined new high-precision abundances and ages for nine solar twins and discussed the trends of abundance ratios with age for a total of 41 solar twins having thin-disk kinematic and ages between 1 and 8 Gyr (on the YY age scale) including the stars in Spina et al. (2016b) and Paper I. Their [X/Fe]-age data agree well with the results shown in Fig. 3 of the present paper, but are fitted by hyperbolic functions, which in the cases of [Na/Fe] and [Ni/Fe] have a maximum at ~5 Gyr. According to this interpretation, [Na/Fe] and [Ni/Fe] increase from 1 to 4 Gyr but decrease from 6 to 8 Gyr. This is an interesting interpretation of the data, but it remains to be seen if a maximum in [Na/Fe] and [Ni/Fe] at ~5 Gyr can be explained by chemical evolution models.
4.2. [X/Fe]-TC trends
It is clear from Fig. 3 and the discussion in Sect. 4.1 that variations in abundance ratios among solar twins younger than 6 Gyr are mainly due to differences in age. Still, it is interesting to investigate if there is a correlation between the residuals in the [X/Fe]-age relations, that is [X/Fe] res = [X/Fe] −(a + b · Age), and elemental condensation temperature (Lodders 2003). As mentioned in Sect. 4.1, the mean Galactocentric orbital distances of these stars are about the same, so a possible dependence of the TC-slope on Rm (Adibekyan et al. 2014, 2016) is not an issue.
Figure 5 shows [X/Fe] res as a function of TC for the Sun and stars younger than 6 Gyr. The lines show linear fits, [X/Fe] res = c + d · TC, obtained by weighting each point by the inverse square of the error of [X/Fe] res calculated by adding σ [X/Fe], b·σ(Age), and the error of the [X/Fe] – age fit at the age of the star in quadrature. Y and Ba are included in the fits, but due to the relatively large error of [X/Fe] res for these two elements, they have only a small effect on the fit.
Linear fits, [X/Fe] res = c + d·TC.
 |
Fig. 5 Abundance ratios corrected for Galactic evolution as a function of elemental condensation temperature for the Sun and ten solar twins with ages less than 6 Gyr. Element designations are shown in the panel for HD 183658. |
The coefficients of the [X/Fe] res–TC fits and their 1-sigma errors are given in Table 5. As seen, only the Sun and HD 96116 show a significant trend of [X/Fe] res as a function of TC. For the other stars, the [X/Fe] res–TC slope deviates less than 2-sigma from zero slope. For the same stars, the (uncorrected) [X/Fe]– TC slope ranges from zero to 7 × 10-5 dex K-1 and depends on stellar age (see Fig. 14 in Paper I). This shows the importance of correcting for Galactic evolution before discussing correlations between [X/Fe] and TC.
Interestingly, the Sun5 has the most significant variation of [X/Fe] res with TC, that is d = (−2.6 ± 0.7) × 10-5 dex K-1. Thus, it seems that the Sun has an exceptional high ratio of volatile to refractory elements when compared to solar twins as first found by Meléndez et al. (2009). They did not correct for Galactic evolution of abundance ratios, but the mean age of their sample of 11 solar twins (4.1 Gyr) is close to the age of the Sun. The variation of [X/Fe] over a TC range of 1800 K was found to be ~ 0.08 dex compared to ~ 0.05 dex in the present paper. An even smaller TC-variation, ~ 0.04 dex, was found by Spina et al. (2016b), when comparing the Sun to 13 solar twins (including corrections for chemical evolution). These different results may arise because the Sun is compared to different samples of solar twins. For the sample in this paper, only one star (HD 96116) out of 10 has a negative [X/Fe] res-TC slope like the Sun, whereas the slopes for the other stars are within ± 1.8 × 10-5 dex K-1. In contrast, Spina et al. (2016b) found evidence of a larger range of TC-slopes, ± 4 × 10-5 dex K-1. Obviously, a larger sample of solar twins is needed to obtain better information on the distribution of the [X/Fe] res-TC slopes to see how exceptional the Sun is.
4.3. Nucleosynthesis and chemical evolution
As discussed in Paper I, the decreasing trend of [X/Fe] with decreasing stellar age for elements made in massive stars is probably due to an increasing contribution of Fe from Type Ia SNe in the course of time. The flat distribution of [Ca/Fe] is a problem, but may be explained if low luminosity SNe synthesizing large amounts of Ca (see Perets et al. 2010) are contributing to the chemical evolution of Ca (Mulchaey et al. 2014). [Cr/Fe] is also nearly constant in time, indicating that the ratio of contributions from Type II and Ia SNe is about the same for Cr and Fe. Furthermore, the steep increase of [Y/Fe] with decreasing age is probably due to the delayed contribution of s-process elements from low-mass AGB stars. In the following, it is discussed how the elements analyzed in this paper (Sc, Mn, Cu, and Ba) fit into these interpretations of the [X/Fe]-age trends.
4.3.1. Scandium
As reviewed by Romano et al. (2010), Sc is made in core-collapse (Type II) SNe during neon burning and explosive oxygen and silicon burning (Woosley & Weaver 1995). Type Ia SNe give a negligible contribution to Sc according to Iwamoto et al. (1999). Calculated yields (e.g., Timmes et al. 1995; Kobayashi et al. 2006) lead to too low Sc/Fe ratios compared to observed values, but this problem may be solved by including neutrino interactions (Fröhlich et al. 2006; Yoshida et al. 2008).
It has been much discussed if Sc follows Fe, that is [Sc/Fe] ~ 0 at all metallicities (Gratton & Sneden 1991; Prochaska & McWilliam 2000) or if Sc behaves like an α-capture element, that is [Sc/Fe] ~ 0.2 in metal-poor halo and thick-disk stars (Zhao & Magain 1990; Nissen et al. 2000; Reddy et al. 2006; Adibekyan et al. 2012; Battistini & Bensby 2015). The solar twin data support the second possibility as seen from Fig. 6. Although there is a rise of [Sc/Mg] with increasing age for stars younger than 6 Gyr and a corresponding decline with age for the older stars, the total variation of [Sc/Mg] is only about 0.05 dex and the various groups of stars agree well with the fitted quadratic relation. In contrast, [Sc/Fe] shows a total variation close to 0.2 dex that cannot be well fitted by a simple function over the whole age range from 1 to 10 Gyr.
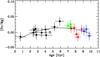 |
Fig. 6 [Sc/Mg] as a function of stellar age with the same symbols as in Fig. 3. The line shows a quadratic least squares fit to the data with all stars and the Sun included. |
4.3.2. Manganese
Mn can be made by explosive silicon burning and nuclear statistical processes in Type II SNe (see Woosley & Weaver 1995) and in Type Ia SNe (Iwamoto et al. 1999). Calculated yields are uncertain, because they depend on assumptions related to the explosion mechanism, mass cut, and number of electrons per nucleon (Thielemann et al. 1996; Mishenina et al. 2015a). According to the calculations of Kobayashi et al. (2006), the Type Ia to Type II yield ratio for Mn is about three times higher than the corresponding ratio for Fe. Since long, this has been considered as an explanation of the increasing trend of [Mn/Fe] with increasing [Fe/H] as found from LTE analysis of Mn i lines in spectra of halo and disk stars (Reddy et al. 2006; Feltzing et al. 2007; Adibekyan et al. 2012; Battistini & Bensby 2015; Mishenina et al. 2015a). In addition, Cescutti et al. (2008) have argued that in order to explain the different [Mn/Fe] – [Fe/H] trends in the Galactic bulge, the solar neighborhood, and the Sagittarius dwarf galaxy, one has to invoke metallicity dependent Type Ia SNe yields.
Interestingly, [Mn/Fe] in the solar twins vary very little with age as seen from Fig. 3. For stars older than 6 Gyr, there is a slight increase in [Mn/Fe] with decreasing age as one would expect if Type Ia SNe are more important contributors to Mn than to Fe. However, at ages less than 6 Gyr, [Mn/Fe] decreases slightly as time goes on. This does not agree with a rize of [Mn/Fe] of about 0.3 dex, when [Fe/H] increases from −1 to solar metallicity, as found when analyzing Mn i lines in LTE. The solar twin results are in better agreement with the near-constancy of [Mn/Fe] as a function of [Fe/H] derived by Bergemann & Gehren (2008) and Battistini & Bensby (2015), when non-LTE effects are taken into account. At [Fe/H] ~ −1, the non-LTE correction for F and G dwarfs amounts to approximately +0.3 dex.
4.3.3. Copper
Two processes have been suggested for the nucleosynthesis of Cu in massive stars: explosive Ne-burning (see Woosley & Weaver 1995) and the weak s-process in which neutrons from the 22Ne (α,n) 25Mg reaction are added to iron-seed nuclei (e.g., Raiteri et al. 1993). Furthermore, Matteucci et al. (1993) argued that a substantial fraction of Cu has to be made in Type Ia SNe in order to explain the increase of [Cu/Fe] with metallicity, but this is not supported by yield calculations (Iwamoto et al. 1999; Kobayashi et al. 2006). More recently, Romano & Matteucci (2007) showed that [Cu/Fe] versus [Fe/H] for stars in the solar neighborhood and in ω Cen (see Cunha et al. 2002; Pancino et al. 2002) can be explained by metallicity dependent Cu yields of massive stars without invoking any contribution from Type Ia SNe.
As seen from Fig. 3, the pattern of [Cu/Fe] versus age looks very much the same as the pattern of [Na/Fe], and the slope coefficients for stars younger than 6 Gyr agree within the errors, that is b = 0.025 ± 0.003 dex Gyr-1 for [Na/Fe] and b = 0.029 ± 0.004 dex Gyr-1 for [Cu/Fe]. This is also seen in Fig. 7, where [Cu/Na] is plotted as a function of stellar age. [Cu/Na] is nearly constant for ages up to 6 Gyr and although the ratio rises somewhat at older ages, high- and low-[Na/Fe] stars (marked in green and red, respectively) as well as the thick-disk stars (marked in blue) follow the same [Cu/Na]-age relation. This points to a close connection between the nucleosynthesis of Na and Cu. Because the differences of [Na/Fe] among the older stars are probably due to differences in the neutron excess arising from the 22Ne (α,n) 25Mg reaction during hydrostatic carbon burning in massive stars, the tight [Cu/Na]-relation suggests that the yield of Cu also depends on the neutron excess, which means that Cu is primarily made by the weak s-process.
 |
Fig. 7 [Cu/Na] as a function of stellar age with the same symbols as in Fig. 3. The line shows a quadratic least squares fit to the data with all stars and the Sun included. |
4.3.4. Barium
In Galactic disk stars, Ba (like Y, Zr, and La) is primarily made by the main s-process during shell He-burning in AGB stars with a minor (10−20%) contribution from the r-process (Arlandini et al. 1999). [Ba/Fe] does not vary significantly as a function of [Fe/H] (e.g., Reddy et al. 2006; Bensby et al. 2014), but Edvardsson et al. (1993), Bensby et al. (2007), and da Silva et al. (2012) found evidence that [Ba/Fe] increases with decreasing age for solar metallicity stars. For open clusters and associations, there is also evidence for an increase of [Ba/Fe] with decreasing age, whereas a corresponding increase of [Y/Fe], [Zr/Fe], and [La/Fe] was not found (D’Orazi et al. 2009; Jacobson & Friel 2013; Mishenina et al. 2015b). This is puzzling, because these s-process elements are expected to behave in the same way as Ba, and the question has been raised if the Ba abundances derived from the rather strong Ba ii lines in spectra of young stars can be trusted (Reddy & Lambert 2015). On the other hand, Maiorca et al. (2011) did find an increase of [Y/Fe], [Zr/Fe]. and [La/Fe] towards younger age of clusters, and suggested that this (and the [Ba/Fe] increase) can be explained if the s-process yields of AGB stars with masses between 1 and 1.5 M⊙ are enhanced by a factor of ~ 4 (see Maiorca et al. 2012) relative to the yields of Busso et al. (2001).
As seen from Fig. 4, both [Y/Fe] and [Ba/Fe] in solar twins show a very clear increasing trend with decreasing stellar age. This indicates that the over-abundance of Ba/Fe derived for young open clusters can be trusted and supports the trend of Y abundances found by Maiorca et al. (2011). There are, however, interesting differences in the [Y/Fe] and [Ba/Fe] trends for the solar twins. While [Y/Fe] continues to decrease with age for the oldest stars, [Ba/Fe] flattens out at a level of about −0.03 dex for stars older than 6 Gyr. Furthermore, the increase of [Ba/Fe] with decreasing age for stars younger than 6 Gyr is steeper than the corresponding increase of [Y/Fe]. Assuming that the increase is due to the delayed contribution of s-process elements from low-mass AGB stars, the different age trends of [Y/Fe] and [Ba/Fe] suggest that the Ba/Y yield ratio increases with decreasing stellar mass. This agrees with recent calculations of AGB yields for solar metallicity models by Karakas & Lugaro (2016). According to their Fig. 15, the ratio of heavy s-process elements (Ba, La, and Ce) to light s-process elements (Sr, Y, and Zr) increases by ~ 0.3 dex when the initial mass of the AGB models decreases from 3 to 1.5 M⊙.
4.4. Chemical clocks
As mentioned in Paper I, there is a tight linear relation between [Y/Mg] and age of the solar twins. Figure 8 shows that the high- and low-[Na/Fe] stars as well as the [α/Fe]-enhanced stars fit the relation very well. A maximum likelihood fit (including all stars and the Sun) with errors in both coordinates taken into account gives ![\begin{eqnarray} \ymg = 0.170 \, (\pm 0.009) - 0.0371 \, (\pm 0.0013) \,\,Age \,{\rm [Gyr]} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28888-16/aa28888-16-eq156.png) (5)with
(5)with 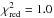 and a rms scatter of 0.024 dex in [Y/Mg] corresponding to a scatter of 0.6 Gyr in age. This relation is valid for the ASTEC ages; using Eq. (1) to convert to the YY age scale, the slope coefficient becomes −0.0419 dex Gyr-1, close to the slope of −0.0404 dex Gyr-1 determined in Paper I, where the three thick-disk stars and the Sun were not included in the fit.
and a rms scatter of 0.024 dex in [Y/Mg] corresponding to a scatter of 0.6 Gyr in age. This relation is valid for the ASTEC ages; using Eq. (1) to convert to the YY age scale, the slope coefficient becomes −0.0419 dex Gyr-1, close to the slope of −0.0404 dex Gyr-1 determined in Paper I, where the three thick-disk stars and the Sun were not included in the fit.
 |
Fig. 8 [Y/Mg] and [Y/Al] versus stellar age with the same symbols as in Fig. 3. The lines show the linear fits given in Eqs. (5) and (6). |
Figure 8 shows that there is also a very good correlation between [Y/Al] and stellar age: ![\begin{eqnarray} \yal = 0.196 \, (\pm 0.009) - 0.0427 \, (\pm 0.0014) \,\, Age \, {\rm [Gyr]}. \end{eqnarray}](/articles/aa/full_html/2016/09/aa28888-16/aa28888-16-eq160.png) (6)Again,
(6)Again, 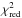 is close to one and the scatter in [Y/Al] is 0.025 dex.
is close to one and the scatter in [Y/Al] is 0.025 dex.
The fact that [Y/Mg] and [Y/Al] both have a tight linear dependence on age means that [Al/Mg] is closely correlated with age, as also seen from Fig. 9. A linear fit to the data provides the relation ![\begin{eqnarray} \almg = -0.027 \, (\pm 0.005) + 0.0057 \, (\pm 0.0008) \,\, Age \, {\rm [Gyr]}. \end{eqnarray}](/articles/aa/full_html/2016/09/aa28888-16/aa28888-16-eq161.png) (7)with a scatter of only 0.011 dex in [Al/Mg]. In particular, the three α-enhanced stars fit the relation very well showing that Al behaves like an α-element with a slightly higher amplitude than Mg.
(7)with a scatter of only 0.011 dex in [Al/Mg]. In particular, the three α-enhanced stars fit the relation very well showing that Al behaves like an α-element with a slightly higher amplitude than Mg.
 |
Fig. 9 [Al/Mg] versus stellar age with the same symbols as in Fig. 3. The line show the linear fit given in Eq. (7). |
The first evidence of a linear correlation between [Y/Mg] and stellar age with a slope similar to the value found in the present paper was presented by da Silva et al. (2012) for a sample of 25 solar-type stars. The dispersion in [Y/Mg] is on the order of ± 0.1 dex, which is probably due to errors in the abundance determinations. Recently, Tucci Maia et al. (2016) has determined high-precision Y and Mg abundances for a sample of 88 solar twins and analogs for which Ramírez et al. (2014) determined stellar parameters and ages. The close correlation between [Y/Mg] and stellar age is confirmed for this larger sample of stars in the solar neighborhood. The slope is about the same as in Eq. (5) but the dispersion in [Y/Mg] (± 0.037 dex) is larger than found in the present paper (± 0.024 dex).
5. Summary and conclusions
Abundances of Sc, Mn, Cu, and Ba have been determined for a sample of 21 solar twin stars with precisions around 0.01 dex relative to the solar abundances. The data are discussed together with high-precision abundances of C, O, Na, Mg, Al, Si, S, Ca, Ti, Cr, Fe, Ni, Zn, and Y derived in Paper I and used to obtain new information about the nucleosynthetic history of elements in the Galactic disk from trends of abundance ratios with stellar age.
Stellar ages with precisions ranging from 0.4 to 0.8 Gyr were derived by comparing the position of stars in the Teff – log g diagram with isochrones based on ASTEC stellar models (Christensen-Dalsgaard 2008). These ages are linearly correlated with the ages derived from YY isochrones (Yi et al. 2001; Kim et al. 2002) in Paper I, but the ASTEC ages are about 10% higher than the YY ages for the oldest stars. This difference of the age scale may be due to the inclusion of metal diffusion in the ASTEC models, which effect is neglected in the YY models.
For stars younger than 6 Gyr and for all elements, [X/Fe] as a function of age can be fitted by linear relations having 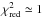 , and for most stars, the residuals do not depend significantly on elemental condensation temperature, TC. The Sun and HD 96116 are exceptions, but in these cases the total amplitude in the TC dependence is only about 0.05 dex. For stars older than 6 Gyr, there is no clear dependence of [X/Fe] on age. Three stars with ages between 9 and 10 Gyr have enhanced [α/Fe] ratios and probably belong to the thick-disk population. Stars with ages between 6 and 9 Gyr tend to split up into two groups with high and low values of [X/Fe] for the odd-Z elements Na, Al, Sc, and Cu. The Type II SNe yield for these elements depends on the neutron excess, and stars older than 6 Gyr may therefore have formed in regions following different chemical evolution paths, whereas stars younger than 6 Gyr (including the Sun) were formed from well-mixed gas. These conclusions are based on a small sample (N = 21) of solar twins, and should be further explored by determining high-precision abundances and ages for larger samples. In particular, it would be interesting to investigate if there are correlations between abundance ratios and kinematics of the stars.
, and for most stars, the residuals do not depend significantly on elemental condensation temperature, TC. The Sun and HD 96116 are exceptions, but in these cases the total amplitude in the TC dependence is only about 0.05 dex. For stars older than 6 Gyr, there is no clear dependence of [X/Fe] on age. Three stars with ages between 9 and 10 Gyr have enhanced [α/Fe] ratios and probably belong to the thick-disk population. Stars with ages between 6 and 9 Gyr tend to split up into two groups with high and low values of [X/Fe] for the odd-Z elements Na, Al, Sc, and Cu. The Type II SNe yield for these elements depends on the neutron excess, and stars older than 6 Gyr may therefore have formed in regions following different chemical evolution paths, whereas stars younger than 6 Gyr (including the Sun) were formed from well-mixed gas. These conclusions are based on a small sample (N = 21) of solar twins, and should be further explored by determining high-precision abundances and ages for larger samples. In particular, it would be interesting to investigate if there are correlations between abundance ratios and kinematics of the stars.
According to the discussion in Sect. 4.3, the trends of abundance ratios for Sc, Mn, Cu, and Ba with stellar age provide new information on nucleosynthesis in the Galactic disk. In summary: (i) The smooth and relatively small variation of [Sc/Mg] with age suggests that Sc is made in Type II SNe along with the α-capture elements; (ii) the near-constancy of [Mn/Fe] with age indicates that the Type Ia to Type II SNe yield ratio for Mn is similar to the corresponding ratio for Fe; (iii) the small scatter in [Cu/Na] at all ages suggests that Cu is primarily made by the weak s-process in massive stars; (iv) the steeper increase of [Ba/Fe] with decreasing stellar age compared to the increase of [Y/Fe] suggests that the Ba/Y yield ratio of AGB stars increases with decreasing stellar mass as recently predicted by Karakas & Lugaro (2016).
Finally, [Y/Mg] and [Y/Al] were found to be sensitive indicators of stellar age, which can be explained by prompt production of Mg and Al in Type II SNe and an increasing contribution of yttrium from low-mass AGB stars as time goes on. For the present sample of 21 solar twins, [Y/Mg] and [Y/Al] depend linearly on age with a slope close to −0.04 dex Gyr-1. This shows that [Y/Mg] or [Y/Al] can be used as chemical clocks to determine relative ages of solar metallicity stars in the solar neigborhood with precisions of about one Gyr. The recent work by Adibekyan et al. (2016) suggests that the [Y/Mg] – age relation is also valid outside the solar neighborhood.
Acknowledgments
Vardan Adibekyan is thanked for a constructive referee report that helped to improve the paper significantly and Bengt Gustafsson for inspiring comments on a first version of the manuscript. Maria Bergemann is acknowledged for calculating non-LTE corrections for the Mn i lines applied to derive Mn abundances and Jørgen Christensen-Dalsgaard for providing ASTEC evolutionary tracks for the mass-range of the solar twins. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant DNRF106). This research made use of the SIMBAD database operated at CDS, Strasbourg, France.
References
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., González Hernández, J. I., Delgado Mena, E., et al. 2014, A&A, 564, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Delgado-Mena, E., Figueira, P., et al. 2016, A&A, 592, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Battistini, C., & Bensby, T. 2015, A&A, 577, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Zenn, A. R., Oey, M. S., & Feltzing, S. 2007, ApJ, 663, L13 [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., & Gehren, T. 2008, A&A, 492, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biazzo, K., Gratton, R., Desidera, S., et al. 2015, A&A, 583, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Carlos, M., Nissen, P. E., & Meléndez, J. 2016, A&A, 587, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel de Strobel, G. 1996, A&ARv, 7, 243 [CrossRef] [Google Scholar]
- Cescutti, G., Matteucci, F., Lanfranchi, G. A., & McWilliam, A. 2008, A&A, 491, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Proffitt, C. R., & Thompson, M. J. 1993, ApJ, 403, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Smith, V. V., Suntzeff, N. B., et al. 2002, AJ, 124, 379 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, R., Porto de Mello, G. F., Milone, A. C., et al. 2012, A&A, 542, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Solanki, S. K., Livingston, W., Krivova, N., & Vince, I. 2016, A&A, 587, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Orazi, V., Magrini, L., Randich, S., et al. 2009, ApJ, 693, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Feltzing, S., Fohlman, M., & Bensby, T. 2007, A&A, 467, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, C., Hauser, P., Liebendörfer, M., et al. 2006, ApJ, 637, 415 [Google Scholar]
- Gaidos, E. 2015, ApJ, 804, 40 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Israelian, G., Santos, N. C., et al. 2010, ApJ, 720, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Delgado-Mena, E., Sousa, S. G., et al. 2013, A&A, 552, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., & Sneden, C. 1991, A&A, 241, 501 [NASA ADS] [Google Scholar]
- Grenon, M. 1987, J. Astrophys. Astron., 8, 123 [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Cosmic Abundances, eds. S. S. Holt & G. Sonneborn, ASP Conf. Ser., 99, 117 [Google Scholar]
- Gustafsson, B., Church, R., Davies, M. B., & Rickman, H. 2016, A&A, in press, DOI: 10.1051/0004-6361/201423916 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jacobson, H. R., & Friel, E. D. 2013, AJ, 145, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., Hansen, C. J., et al. 2015, A&A, 581, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Maiorca, E., Randich, S., Busso, M., Magrini, L., & Palmerini, S. 2011, ApJ, 736, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Maiorca, E., Magrini, L., Busso, M., et al. 2012, ApJ, 747, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., & Villaver, E. 2016, A&A, 588, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., Raiteri, C. M., Busson, M., Gallino, R., & Gratton, R. 1993, A&A, 272, 421 [NASA ADS] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T. V., Kovtyukh, V. V., Soubiran, C., Travaglio, C., & Busso, M. 2002, A&A, 396, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishenina, T. V., Pignatari, M., Korotin, S. A., et al. 2013, A&A, 552, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishenina, T., Gorbaneva, T., Pignatari, M., Thielemann, F.-K., & Korotin, S. A. 2015a, MNRAS, 454, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T., Pignatari, M., Carraro, G., et al. 2015b, MNRAS, 446, 3651 [NASA ADS] [CrossRef] [Google Scholar]
- Mulchaey, J. S., Kasliwal, M. M., & Kollmeier, J. A. 2014, ApJ, 780, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2011, A&A, 530, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Chen, Y. Q., Schuster, W. J., & Zhao, G. 2000, A&A, 353, 722 [NASA ADS] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pancino, E., Pasquini, L., Hill, V., Ferraro, F. R., & Bellazzini, M. 2002, ApJ, 568, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., Gal-Yam, A., Mazzali, P. A., et al. 2010, Nature, 465, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing 2nd edn. (Cambridge: University Press) [Google Scholar]
- Prochaska, J. X., & McWilliam, A. 2000, ApJ, 537, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Naumov, S. O., Carney, B. W., McWilliam, A., & Wolfe, A. M. 2000, AJ, 120, 2513 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Gallino, R., Busso, M., Neuberger, D., & Kaeppeler, F. 1993, ApJ, 419, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., Cornejo, D., Roederer, I. U., & Fish, J. R. 2011, ApJ, 740, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., Bean, J., et al. 2014, A&A, 572, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Khanal, S., Aleo, P., et al. 2015, ApJ, 808, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, A. B. S., & Lambert, D. L. 2015, MNRAS, 454, 1976 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., & Matteucci, F. 2007, MNRAS, 378, L59 [NASA ADS] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., Vaz, Z. A., Katime Santrich, O. J., et al. 2015, ApJ, 815, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Serminato, A., Gallino, R., Travaglio, C., Bisterzo, S., & Straniero, O. 2009, PASA, 26, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Gratton, R. G., & Crocker, D. A. 1991, A&A, 246, 354 [NASA ADS] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Spina, L., Meléndez, J., Karakas, A. I., et al. 2016a, A&A, in press, DOI: 10.1051/0004-6361/201628557 [Google Scholar]
- Spina, L., Meléndez, J., & Ramírez, I. 2016b, A&A, 585, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teske, J. K., Ghezzi, L., Cunha, K., et al. 2015, ApJ, 801, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Thielemann, F.-K., Nomoto, K., & Hashimoto, M.-A. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, ApJ, 790, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci Maia, M., Ramírez, I., Meléndez, J., et al. 2016, A&A, 590, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unsöld, A. 1955, Physik der Sternatmospharen, mit besonderer Berucksichtigung der Sonne (Berlin: Springer) [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H. L., Shi, J. R., & Zhao, G. 2015, ApJ, 802, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H. L., Shi, J. R., Nissen, P. E., & Zhao, G. 2016, A&A, 585, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, T., Umeda, H., & Nomoto, K. 2008, ApJ, 672, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H. W., Gehren, T., & Zhao, G. 2008, A&A, 481, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, H. W., Gehren, T., & Zhao, G. 2014, in Setting the scene for Gaia and LAMOST, eds. S. Feltzing, G. Zhao, N. A. Walton, & P. Whitelock, IAU Symp., 298, 453 [Google Scholar]
- Zhao, G., & Magain, P. 1990, A&A, 238, 242 [NASA ADS] [Google Scholar]
All Tables
Linear fits of [X/Fe] as a function of age for stars younger than 6 Gyr, i.e., without including the Sun.
All Figures
 |
Fig. 1 Comparison of stellar ages derived from YY and ASTEC isochrones. The line shows the linear fit to the data given by Eq. (1). The dotted line shows the 1:1 relation. |
| In the text | |
 |
Fig. 2 Solar flux HARPS spectrum (red line) in comparison with the HARPS spectrum of HD 96116 (blue line) near the Cu i line at 5782.12 Å (left panel) and the Ba ii line at 5853.70 Å (right panel). The lower panels show the difference (HD 96116 – Sun) between the two spectra. |
| In the text | |
 |
Fig. 3 Abundance ratios as a function of stellar (ASTEC) age. For stars younger than 6 Gyr (black filled circles) the lines show linear fits to the data. The Sun, shown with the ⊙ symbol, was not included in the fits. Red filled circles show five old stars with low [Na/Fe] relative to three stars with similar age shown with green filled circles. Three [α/Fe]-enhanced stars are shown with open blue circles. |
| In the text | |
 |
Fig. 4 [Y/Fe] and [Ba/Fe] as a function of stellar age with the same symbols as in Fig. 3. |
| In the text | |
 |
Fig. 5 Abundance ratios corrected for Galactic evolution as a function of elemental condensation temperature for the Sun and ten solar twins with ages less than 6 Gyr. Element designations are shown in the panel for HD 183658. |
| In the text | |
 |
Fig. 6 [Sc/Mg] as a function of stellar age with the same symbols as in Fig. 3. The line shows a quadratic least squares fit to the data with all stars and the Sun included. |
| In the text | |
 |
Fig. 7 [Cu/Na] as a function of stellar age with the same symbols as in Fig. 3. The line shows a quadratic least squares fit to the data with all stars and the Sun included. |
| In the text | |
 |
Fig. 8 [Y/Mg] and [Y/Al] versus stellar age with the same symbols as in Fig. 3. The lines show the linear fits given in Eqs. (5) and (6). |
| In the text | |
 |
Fig. 9 [Al/Mg] versus stellar age with the same symbols as in Fig. 3. The line show the linear fit given in Eq. (7). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


