| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201628883 | |
| Published online | 03 August 2016 | |
Abundance trend with condensation temperature for stars with different Galactic birth places⋆,⋆⋆
1 Instituto de Astrofísica e Ciências
do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762
Porto,
Portugal
e-mail: Vardan.Adibekyan@astro.up.pt
2 Departamento de Física e Astronomia,
Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007
Porto,
Portugal
3 Instituto de Astrofísica de Canarias,
38200 La Laguna,
Tenerife,
Spain
4 Departamento de Astrofísica,
Universidad de La Laguna, 38206 La
Laguna, Tenerife,
Spain
5 Leibniz Institute for Astrophysics
Potsdam (AIP), An der Sternwarte
16, 14482
Potsdam,
Germany
6 Byurakan Astrophysical Observatory, 0213 Byurakan, Aragatsotn
province, Armenia
Received:
9
May
2016
Accepted:
6
June
2016
Context. During the past decade, several studies reported a correlation between chemical abundances of stars and condensation temperature (also known as Tc trend). However, the real astrophysical nature of this correlation is still debated.
Aims. The main goal of this work is to explore the possible dependence of the Tc trend on stellar Galactocentric distances, Rmean.
Methods. We used high-quality spectra of about 40 stars observed with the HARPS and UVES spectrographs to derive precise stellar parameters, chemical abundances, and stellar ages. A differential line-by-line analysis was applied to achieve the highest possible precision in the chemical abundances.
Results. We confirm previous results that [X/Fe] abundance ratios depend on stellar age and that for a given age, some elements also show a dependence on Rmean. When using the whole sample of stars, we observe a weak hint that the Tc trend depends on Rmean. The observed dependence is very complex and disappears when only stars with similar ages are considered.
Conclusions. To conclude on the possible dependence of the Tc trend on the formation place of stars, a larger sample of stars with very similar atmospheric parameters and stellar ages observed at different Galactocentric distances is needed.
Key words: techniques: spectroscopic / stars: abundances / stars: atmospheres / Galaxy: disk / Galaxy: evolution
Based on observations collected with the HARPS spectrograph at the 3.6-m telescope (program ID: 095.D-0717(A)), installed at the La Silla Observatory, ESO (Chile), with the UVES spectrograph at the 8-m Very Large Telescope (program ID: 095.D-0717(B)), installed at the Cerro Paranal Observatory, ESO (Chile). Also based on data obtained from the ESO Science Archive Facility under request numbers: vadibekyan180760, vadibekyan180762, vadibekyan180764, vadibekyan180768, vadibekyan180769, vadibekyan180771, vadibekyan180773, vadibekyan180778, and vadibekyan180779.
Tables with stellar parameters and chemical abundances are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/592/A87
© ESO, 2016
1. Introduction
Stars and planets form from the same material, and as such, some of their properties are expected to be inter-connected. The very first correlation observed in the field of exoplanet research was the dependence of giant-planet occurrence and stellar metallicity (e.g. Gonzalez 1997; Santos et al. 2001, 2004; Fischer & Valenti 2005). This correlation eventually played one of the most important roles on our understanding and constraining of planet formation theories (e.g. Mordasini et al. 2009). Following works showed that the occurrence of different types of planets also may depend on chemical abundances of the hosting stars (e.g. Haywood 2008a; Adibekyan et al. 2012a,b).
The importance of stellar metallicity and chemical properties of stars is not limited to the formation of planets alone. The chemical abundances and some specific abundance ratios of stars with planets provide enormous amounts of information about the planet evolution process (e.g. Bond et al. 2010; Delgado Mena et al. 2010), architecture (e.g. Dawson & Murray-Clay 2013; Beaugé & Nesvorný 2013; Adibekyan et al. 2013), composition of planets (e.g. Thiabaud et al. 2014; Dorn et al. 2015; Santos et al. 2015), and even about the habitability of planets (e.g. Adibekyan et al. 2016b).
During the past decades, astronomers have also been searching for chemical signatures of planet formation on the planet-host stars. Many studies, starting from Gonzalez (1997) and Smith et al. (2001), explored a possible trend between the abundances of chemical elements and the condensation temperature (Tc) of the elements to understand the relative fraction of volatile (low-Tc) and refractory (high-Tc) elements in planet-host and single stars. This trend is called Tc trend, and the slope of the correlation (slope of the linear fit) of [X/Fe] vs. condensation temperature is named Tc slope.
Meléndez et al. (2009) was the first to report that the Sun shows a deficit in refractory elements with respect to other solar twins. They suggested that this is due to these elements being trapped in the terrestrial planets in our solar system. Although the authors discussed the effect of the Galactic evolution (taking into account the possibility that the Sun might have migrated from an inner Galactic orbit, e.g. Wielen et al. 1996), they finally did not consider it a plausible explanation. The same conclusion (presence of planet formation signatures in the atmospheres of stars) was also reached by Ramírez et al. (2009), who analyzed 64 solar twins and analogues. However, the results by González Hernández et al. (2010) and González Hernández et al. (2013) strongly contested the connection between the presence of planets and the abundance peculiarities of the stars. This very exciting and important (possible) connection between chemical peculiarities and formation of planets has also been examined in other works (e.g. Takeda et al. 2001; Ecuvillon et al. 2006; Sozzetti et al. 2006; Schuler et al. 2011b; González Hernández et al. 2013; Maldonado et al. 2015; Nissen 2015; Biazzo et al. 2015; Saffe et al. 2015, 2016), but contradictory conclusions were reached.
The fact that the observed Tc trend may be a relic of the planet formation and evolution process is by far not its only possible explanation. Recently, Adibekyan et al. (2014) used a sample of 148 solar-type stars from González Hernández et al. (2010) and González Hernández et al. (2013) to explore the possible factors responsible for the Tc trend. The authors found that the slope of this trend correlates with the stellar age in a significant way: more evolved (old) stars have a lower refractory-to-volatile ratio. Since we do not expect significant changes of chemical abundances with age for FGK dwarf stars in the main sequence, Adibekyan et al. (2014) concluded that the observed correlation probably reflects the chemical evolution in the Galaxy. Ramírez et al. (2014) also observed a correlation between the Tc slope and stellar age for metal-rich solar analogues, but the sign of the correlation seemed to be opposite to what was obtained in Adibekyan et al. (2014)1. They found that most refractory-element-depleted stars are younger than those with the highest refractory element abundances. In addition to these explanations, it was suggested that the Tc trend strongly correlates with stellar radius and mass (Maldonado et al. 2015; Maldonado & Villaver 2016), it may also depend on stellar environment (Önehag et al. 2014) and internal processes, such as gas-dust segregation in the protostellar disk (Gaidos 2015).
Adibekyan et al. (2014) found tentative evidence that the Tc slopes also correlate with the mean Galactocentric distance of the stars (Rmean), indicating that stars that originated in the inner Galaxy have fewer refractory elements than volatiles. Their sample was composed of stars with different ages and was also lacking stars with low Rmean values (most of the stars were clustered at Rmean≈ 7−8 kpc). It was difficult to firmly conclude about the direct role of Rmean in the observed correlation between Tc slope and Rmean based on this sample alone.
In this context, the study of binary stars is important because the above mentioned mechanisms and processes cannot easily explain trends observed between companions of these systems. Several authors studied the Tc trend in binary stars with and without planetary companions (e.g. Liu et al. 2014; Saffe et al. 2015; Mack et al. 2016) or in binary stars where both components host planets (e.g. Biazzo et al. 2015; Teske et al. 2015, 2016; Ramírez et al. 2015). The results and conclusions of these studies point in different directions and show as a whole that there are no systematic differences in the chemical abundances of stars with and without planets in the binary systems. Moreover, there are discrepancies in the results even for the same individual systems such as 16 Cyg AB (e.g. Laws & Gonzalez 2001; Takeda 2005; Schuler et al. 2011a; Tucci Maia et al. 2014).
Very recently, Saffe et al. (2016) reported a positive Tc trend in the binary system ζ1 Ret – ζ2 Ret, where one of the stars (ζ2 Ret) hosts a debris disk. The deficit of the refractory elements relative to volatiles in ζ2 Ret was explained by the authors as being caused by the depletion of about ~3 M⊕ rocky material. Following their work, Adibekyan et al. (2016a) confirmed the trend observed between the stars based on a very high quality data set. However, they also found that the Tc trends seem to depend on the individual spectrum used (even if always of very high quality). In particular, they observed significant differences in the abundances of the same star derived from different high-quality spectra.
In this work, we explore the possible dependence of the Tc trend on Galactocentric distances for a fixed formation time, that is, for stars with very similar ages. We organized this paper as follows. In Sect. 2 we present the data, in Sects. 3 and 4 we present the methods used to derive the stellar parameters, chemical abundances, and stellar ages. Section 5 explains how we calculate and evaluate the significance of the Tc trends. After presenting the main results in Sect. 6, we conclude in Sect. 7.
Spectroscopic observations and stellar parameters, ages, and Tc slopes of the sample stars.
2. Data and observations
To understand if the abundance trend observed with the condensation temperature is a function of Galactocentric distances for a fixed age of stars, we selected about 40 stars with ages similar to that of the Sun but with different mean Galactocentric distances from the Geneva-Copenhagen Survey sample (GCS, Nordström et al. 2004): with the smallest (Rmean~ 6.5 kpc), largest (Rmean~ 9 kpc), and solar (Rmean~ 8 kpc) Galactocentric Rmean values2. The stars were selected to have Teff = T⊙ ± 500 K, log g> 4.0 dex, [Fe/H] = 0.0 ± 0.2 dex, and an age of 4.6 ± 1 Gyr3. The range of Teff and log g were chosen (not very different from the solar values) to guarantee a high-precision differential chemical analysis. However, we should note that because of the relatively wide range of stellar parameters, the achieved precision in chemical abundances is somewhat lower than the precision obtained for solar twins and solar analogues (e.g. Meléndez et al. 2009; Ramírez et al. 2009; González Hernández et al. 2010; Nissen 2015).
High-resolution and high signal-to-noise (S/N) spectra for these stars were obtained by performing new observations with HARPS (22 stars) and UVES (six stars) ESO spectrographs, and by extracting spectra for 14 stars from the ESO archive4. One star was excluded from our analysis because of very low S/N (HD 216054), HD 213791 was excluded because of its very fast rotation, and HD 184588 was excluded because its spectra are contaminated by the binary component. Our final sample thus contains 39 stars, three of which are known to harbour planets5. The three planet-host stars do not show any significant difference in stellar properties when compared to the rest of the sample stars, thus we did not consider them as a separate group.
For the Sun we used a combined HARPS reflected spectrum from Vesta (extracted from the same public archive, S/N ~ 1300).
3. Stellar parameters and chemical abundances
The stellar parameters (Teff, [Fe/H], log g, and Vtur) and chemical abundances of the stars relative to the Sun were derived by the methods described in Adibekyan et al. (2016a). In brief, first we automatically measured the equivalent widths (EWs) of iron lines (~250 Fe i and ~40 Fe ii lines) using the ARES v2 code6 (Sousa et al. 2008, 2015). Then the spectroscopic parameters were derived by imposing excitation and ionization balance assuming LTE. We used the grid of ATLAS9 plane-parallel model of atmospheres (Kurucz 1993) and the 2014 version of the MOOG7 radiative transfer code (Sneden 1973). The uncertainties of the parameters were derived as in our previous works, and they are well described in Neuforge-Verheecke & Magain (1997). Stellar parameters of the stars are presented in Table 1. For more details on the derivation of stellar parameters we refer to Sousa (2014).
Elemental abundances for the stars were also determined using an LTE analysis and the same tools and codes as for the stellar parameter determination. The line list, atomic data, damping parameter, and the detailed description of the abundance derivation is presented in Adibekyan et al. (2016a). Again, the EWs of the lines were derived with ARES v2 code with careful visual inspection. In a few cases, when the ARES measurements were not satisfactory (this can be caused for instance through cosmics or bad pixels), we measured the EWs using the task splot in IRAF8. The final abundances of the elements (when several spectral lines were available) were calculated as a weighted mean of all the abundances, where we used the distance from the median abundance as a weight (Adibekyan et al. 2015). The average of TiI and TiII was used for Ti abundance. The stellar parameters and abundances of the elements are available at the CDS.
The errors of the [X/H] abundances were calculated as a quadratic sum of the errors that are due to EW measurements and those due to uncertainties in the atmospheric parameters. When three or more lines were available, the EW measurement error was estimated as σ/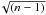 , where σ is the line-to-line abundance-weighted scatter (Adibekyan et al. 2015) and n is the number of the observed lines. The errors arising from uncertainties in the stellar parameters were calculated as a quadratic sum of the abundance sensitivities on the variation of the stellar parameters by their one-σ uncertainties.
, where σ is the line-to-line abundance-weighted scatter (Adibekyan et al. 2015) and n is the number of the observed lines. The errors arising from uncertainties in the stellar parameters were calculated as a quadratic sum of the abundance sensitivities on the variation of the stellar parameters by their one-σ uncertainties.
Slopes of the [X/H] versus metallicity, stellar age, and Rmean.
 |
Fig. 1 Abundance ratio [X/Fe] against [Fe/H] for the sample stars. The chemically peculiar Ba star is shown by the blue triangle. The black line represents the WLS fit of the data (excluding the Ba star). |
 |
Fig. 2 Stellar ages derived in this work using the PARAM web interface against the ages derived by the q2 package. The left panel presents all the stars with derived ages, and the right panel shows the stars that have precise age determinations with errors smaller than 1 Gyr in both methods. |
 |
Fig. 3 Abundance ratio [X/Fe] against age for the stars with the errors in the ages smaller than 1 Gyr. The symbols represent the same as in Fig. 1. The Ba star and the two oldest stars are not considered for the WLS fit. |
Adibekyan et al. (2016a) showed that the σ calculated from two lines is usually smaller than the real expected error. These underestimated errors can play a crucial role in the incorrect determination of the Tc slopes because of their very high weight (if a weighted least-square, WLS, is used to calculate the best fits). For the abundances of elements that have only two observed spectral lines (except for oxygen), more realistic errors were calculated following the procedure described in Adibekyan et al. (2016a). In brief, we first calculated the errors in EWs following Cayrel (1988), then propagated these to derive the abundance uncertainties for each line. The final uncertainties for the average abundance were propagated from the individual errors.
When only one line for a given element was available, as is the case for O (for some stars) and Sr, we determined the error by measuring a second EW with the position of the continuum displaced within the root mean square, rms (due to the noise of the spectra) and by calculating the difference in abundance with respect to the original value.
The two oxygen lines (6158.2 Å and 6300.3 Å) used in this work are very weak and deserve special attention (see e.g. Bertran de Lis et al. 2015). Even when both lines were observed for a spectrum, we calculated individual errors for each line (as described in the previous paragraph) and then propagated the error of the average oxygen abundance.
In Fig. 1 we show [X/Fe] abundance trends relative to the stellar metallicity for the sample of stars. The WLS fit of the data is shown in the plot by a black line. In the linear regression the inverse of the variance (σ2) of the abundances was used as weight. Table 2 presents the slope of the linear dependence and the p-values coming from the F-statistics that test the null hypothesis that the data can be modelled accurately by setting the regression coefficients to zero.
In Fig. 1 a star with strong enhancement in SrI, YII, ZrII, and moderate enhancement in BaII is clearly visible. The chemical anomalies of this star are reminiscent of Ba stars (e.g. Bidelman & Keenan 1951; McClure 1984), although these are usually G-K-giants (e.g. Yang et al. 2016), while our target is warmer and is located in the main sequence. This chemically peculiar star, HD 157060, has an astrometric companion with a mass of about 0.6M⊙ (Tokovinin 2014). Because of the observed anomalies we did not include this star in our statistical analysis, even though it is shown in the plots.
4. Stellar ages
In Sect. 2 we mentioned that the stars employed in this work were initially selected to have ages very similar to that of our Sun. These ages were derived using photometric stellar parameters and BASTI stellar isochrones (Casagrande et al. 2011). We rederived ages of the stars using the new spectroscopic parameters obtained in this work. We used the PARAM web interface9 with PARSEC isochrones (Bressan et al. 2012) for a Bayesian estimation of the stellar ages. In addition to Teff and [Fe/H], this method also requires the stellar magnitude and the parallax as input parameters. The parallaxes of the stars were taken from van Leeuwen (2007) and the V magnitudes from Hauck & Mermilliod (1998). The ages derived in this way vary from about 1 to 11 Gyr (see Table 1), however, while as mentioned above they were selected to have ages very similar to that of our Sun. This once again demonstrates the difficulty of obtaining reliable stellar ages for main-sequence field stars.
Meléndez et al. (2012) claimed that more precise ages can be obtained with the isochrone method when a spectroscopic surface gravity is used as an input parameter instead of the absolute V magnitude (derived from the V magnitude and parallax). However, we note that the derivation of spectroscopic precise log g is not an easy task. We used the q2 Python package10 that uses Yonsei-Yale isochrones (Yi et al. 2001; Kim et al. 2002) and spectroscopic stellar parameters for the derivation of stellar ages. With this method we were able to derive ages for 35 of the 39 stars. For the remaining four stars the code did not provide ages with physical meaning.
In the left panel of Fig. 2 we plot stellar ages derived with the PARAM web interface and the q2 package. The plot shows that although there is no offset between the parameters, the scatter is very large. However, the scatter becomes much smaller when only stars with small errors (smaller than 1 Gyr) in both age estimations are considered (right panel of Fig. 2). It is very interesting to note that stars with errors on age larger than one Gyr mostly lie above the one-to-one line, which means that ages derived by using spectroscopic log g are usually greater. This produces an offset of about one Gyr between the two age estimation methods. Only stars with precise PARAM ages with errors smaller than 1 Gyr are considered in the remainder of this paper when ages are used. The cut in the error of stellar ages can in principle produce a bias because the parallaxes of the stars that are located farther away have larger errors. However, we did not find a strong bias that may change our results significantly for our sample. In particular, we found that the average parallaxes are 20 ± 9 and 25 ± 19 mas for stars with small and large errors on age, respectively. The ages (3.9 ± 2.1 and 4.1 ± 2.5 Gyr) and the Rmean values (7.7 ± 1.1 and 7.2 ± 1.2 kpc) do not deviate dramatically either.
We should note that the comparison shown in Fig. 2 is not a code-to-code comparison, but a comparison of two methods for deriving stellar ages based on parallax and spectroscopic log g. The q2 package also calculates ages with the use of V magnitude and parallaxes. If the same approach were used to derive the stellar ages, then the agreement would be much better, as was demonstrated in Nissen (2015).
 |
Fig. 4 [Y/Mg] versus stellar age for stars with age determination errors smaller than one Gyr. The symbols are the same as in the previous plots. The black solid line is the linear fit of our data without considering the two oldest stars. The blue dashed line and the green dotted lines represent the linear fits from Nissen (2015) and Tucci Maia et al. (2016), respectively. |
 |
Fig. 5 Tc slopes derived by using all the elements against Tc slopes derived by considering only elements that have Tc> 900 K. The black solid line is the linear fit of the data and the blue dashed line represents the one-to-one line. The symbols are the same as in Fig. 1 and the previous plots. |
Recently, Nissen (2015) used a sample of 21 solar-twin stars to study the correlation between [X/Fe] elemental abundances with stellar age. For most of the elements the authors found strong and significant correlations with ages. The correlations of the [X/Fe] ratios with age were later also confirmed by Spina et al. (2016).
In Fig. 3 we plot [X/Fe] abundance ratios against stellar ages. The slopes of the linear WLS fits and the significance of the correlations are presented in Table 2. The two oldest stars are not included in the fit because these older stars might have originated from regions with a different spatial homogeneity of metals that are enriched by supernovae with different neutron excesses (Nissen 2016). The table and corresponding plot show that most of the elements show significant trends with ages, in a good agreement with Nissen (2015). The most significant correlations (at a level of about 3σ) are obtained for C, O, Mg, Si, Ti, and YII. It is interesting to note that for some elements, such as Mg, Si, and Ti (all being α-elements), the scatter around the fit is small.
Nissen (2015) showed that [Y/Mg] can be used to estimate the ages of solar metallicity stars with a precision of about 1 Gyr if a high precision of about 0.04 dex in the [Y/Mg] ratio is achieved. This result was later confirmed by Tucci Maia et al. (2016). In Fig. 4 we show the relation between [Y/Mg] and stellar ages. The figure confirms the strong and tight correlation between this abundances ratio and age. An alternative way of estimating ages of the star would be to apply a multivariate linear regression for the elements that show a strong and significant correlation with age (e.g. Mg, Si, Ti, and Y). In this case a better precision in stellar ages is expected because more elements are used.
5. Tc slope
After we derived the differential abundances and corresponding errors, we searched for abundance trends with Tc. The 50% equilibrium condensation temperatures for a solar system composition gas were taken from Lodders (2003). Although it is common practice to plot [X/Fe] against Tc (and not just [X/H] versus Tc) when searching for a Tc trend, this procedure can produce a bias in the derived slope (Adibekyan et al. 2016a). The main reason for using [X/Fe] instead of [X/H] is to be able to remove the trends related to the Galactic chemical evolution (GCE) from the [X/Fe]−[Fe/H] relations (e.g. González Hernández et al. 2013; Saffe et al. 2016; Liu et al. 2016). Recently, some authors used the [X/Fe]−age relation to correct for the GCE (e.g. Yana Galarza et al. 2016; Spina et al. 2016). However, this correction it is not very simple and straightforward to perform. For example, Spina et al. (2016) introduced a correlation between the Tc slope and metallicity after correcting the Tc slope for the GCE by using the [X/Fe]-age relation. The difficulty of correcting for the GCE is probably that the dependence of the [X/Fe] on age and metallicity is complex and non-linear. Moreover, the stellar ages and metallicities are also related in a quite complex way as a result of migration processes in the Galaxy (e.g. Haywood 2008b; Haywood et al. 2013; Minchev et al. 2013; Bergemann et al. 2014).
We here explore the possible correlation between Tc slope and Rmean, which, if it exists, should be due to the GCE. Therefore we did not correct the Tc slopes for any trends. To avoid any additional biases (see Adibekyan et al. 2016a, for details), we also used the linear dependence of [X/H] on condensation temperature when deriving the Tc trend. In Fig. 5 we plot the Tc slopes derived when considering all the elements against the Tc slopes when only refractory elements with Tc> 900 K were considered. The plot shows that in general the two slope estimates agree, but it also indicates that the slopes derived from refractory elements alone are slightly steeper and the errors are larger. This is probably because the condensation temperature range of the refractory elements is much smaller than the full range of the Tc, while the [X/H] range is almost the same for refractory and volatile elements. For the remainder of the paper we use the Tc slopes derived by considering all the elements. These slopes are also presented in Table 1.
 |
Fig. 6 Tc slopes against stellar parameters. The symbols are the same as in the previous plots. |
Slopes of the WLS calculus between different pairs of parameters.
In Figs. 6 and 7 we plot the dependence of the Tc slope on stellar parameters and on stellar age. The slopes of these dependencies and their significance levels are presented in Table 3. The p-values come from the F-statistics that tests the null hypothesis that the data can be modelled accurately by setting the regression coefficients to zero. None of the trends with stellar parameters appear significant. At maximum, a ~10% false-alarm probability was found for the and Rmean versus Tc slope correlations. When the two oldest stars were excluded, our current data do not show any correlation between the Tc slope and the stellar age as was observed in previous works (e.g. Adibekyan et al. 2014; Nissen 2015). This can be due to relatively lower precision in chemical abundances and smaller size of the sample compared to the previous works.
6. GCE and Rmean
Several studies have suggested that the mean of the apo- and pericentric distances (Rmean) is a good indicator of the stellar birthplace (e.g. Grenon 1987; Edvardsson et al. 1993; Nordström et al. 1999; Rocha-Pinto et al. 2004; Haywood 2008b; Bensby et al. 2014). However, a word of caution should be added here. It has been shown in numerous numerical works, however, that permanent changes in the angular momenta of individual stellar orbits (i.e. in their mean or guiding radii) can result from the effect of transient spiral arms (Sellwood & Binney 2002), the overlap of bar and spiral arms (Minchev & Famaey 2010), and infalling satellites (Quillen et al. 2009). Because the Milky Way is now well established to have a central bar and prominent spiral arms, it is expected that this process, known as radial migration or mixing, has left its footprint on the Galactic disk.
 |
Fig. 7 Tc slopes against stellar age for stars with age determination errors smaller than one Gyr. The two oldest stars and the Ba star are not included in the fit. The symbols are the same as in the previous plots. |
While the Rmean of a star correlates with age (e.g. Rocha-Pinto et al. 2004), the relation should only be considered in a statistical sense (Wielen et al. 1996). Rocha-Pinto et al. (2004) showed that young objects (mostly younger than one Gyr) all have Rmean≈R⊙, while older stars present a higher proportion of objects coming from different Galactocentric radii. In the left panel of Fig. 8 we plot stellar age versus Rmean. Although there is no apparent linear correlation between the two parameters, stars with the smallest and largest mean Galactoentric distances have ages greater than about two Gyr, and the only two stars with the age of about one Gyr have Rmean≈R⊙. This result is well in line with those obtained by Rocha-Pinto et al. (e.g. 2004). In the right panel of Fig. 8 we show only stars with ages from 2.0 to 4.5 Gyr. This is the narrowest age interval where the majority of the stars are clustered. The figure shows that the correlation between Rmean and stellar age in this age regime is also negligible.
The Rmean values for the sample stars were taken from Nordström et al. (2004). Although the authors did not provide the errors for this parameter, we expect an error smaller than 10%, as was estimated in Edvardsson et al. (1993). In Fig. 9 we plot [X/Fe] abundance ratio as a function of Rmean. To minimize the effect of stellar age, only stars with ages from 2.0 to 4.5 Gyr were considered. It is very interesting to see that some elements, such as C, Ca, Ni, and Zr, show statistically significant dependencies on Rmean (see Table 2). Although our sample is small and the stars show a range of ages (we also recall the difficulties of estimating precise ages for field main-sequence stars), these results show that different elements show different dependence on Rmean, that is, different radial gradients. This result qualitatively agrees with the observations of Galactic abundance gradients by Lemasle et al. (2013), where the authors used young Galactic Cepheids for the gradient derivations, and Galactic abundance gradients obtained from open clusters (e.g. Yong et al. 2012; Magrini et al. 2015; Cunha et al. 2016).
 |
Fig. 8 Stellar ages again mean Galactocentric distance for all the stars with errors on age smaller than 1 Gyr (left panel). The same as the left panel, but for stars with ages from 2.0 to 4.5 Gyr. The symbols are the same as in the previous plots and are described in Fig. 1. |
 |
Fig. 9 Abundance ratio [X/Fe] against Rmean for the stars with ages from 2.0 to 4.5 Gyr and with errors on the ages smaller than 1 Gyr. The symbols are the same as in Fig. 1. |
 |
Fig. 10 Tc slope against Rmean for all the stars in the sample (left panel) and for stars with precise ages (error smaller than 1 Gyr) from 2.0 to 4.5 Gyr (right panel). The symbols are the same as in the previous plots. |
6.1. Tc slope and Rmean
It has been shown (see also Sect. 3) that abundances of different elements are correlated with the stellar age in different ways. This dependence, which is due to GCE, produces a correlation between the Tc slope and stellar age. It has been also shown that different elements show different dependencies on the radial distances from the Galactic centre. It is thus logical to expect that this latter dependence, which is also due to Galactic chemical (but not only) evolution, may produce a correlation between the Tc slope and Galactocentric distances of the stars.
Following this logic, Adibekyan et al. (2014) found evidence that the Tc slope depends on the mean Galactocentric distances of the stars, which was used as a first-order proxy for the birthplace of stars. However, because the stars span a wide range of stellar ages, the authors were unable to firmly conclude about the origin of the observed trend.
In Fig. 10 we show the dependence of the Tc slope on Rmean of the stars. In the left panel of the plot, where the full sample is plotted, we can confirm the results of Adibekyan et al. (2014): stars in the solar circle and in the outer disk have positive slopes, while the stars that formed in the inner Galaxy show both negative and positive slopes. The mean value (calculated as a weighted arithmetic mean) of the slope for the stars in the inner disk (at Rmean~ 6.5 kpc) is 0.096 ± 0.438, while in the solar circle (at Rmean~ 8 kpc) and outer disk (at Rmean~ 9 kpc) are 0.331 ± 0.488 and 0.293 ± 0.396, respectively.
In the right panel of Fig. 10 we plot stars in a narrow range of ages (from 2 to 4.5 Gyr) for which the errors on ages are smaller than one Gyr. The plot and corresponding Table 3 show that the trend completely vanishes. It is difficult to conclude whether the weak correlation of the Tc slope with Rmean observed for the full sample is due to a second-order age effect, since the correlation of Rmean with age was negligible. We should also note that the sample plotted in the right panel of Fig. 10 consists of only 18 stars, which is less than the half of the whole sample, thus it suffers (more) from low number statistics.
7. Summary and conclusion
To explore the effect of the star formation place (birthplace) on the chemical abundance trend with the condensation temperature, we selected a sample of main-sequence stars that have similar stellar parameters and expected similar ages as our Sun. The sample consisted of 39 stars, for 25 of which we carried out new observations with HARPS and UVES spectrographs. The spectra of the remaining 14 stars were taken from HARPS and UVES archives (ESO archive). We performed a detailed differential chemical abundance analysis and derived stellar ages for this sample of stars.
When analysing the effect of the GCE on the [X/Fe] elemental ratios, we found that many elements display a strong dependence on stellar metallicity and most of the elements show a statistically significant trend with stellar ages. The latter result ([X/Fe] – age correlation) agrees well with that of Nissen (2015).
To minimize the GCE effect on Tc trend that is due to time or age, we selected a sub-sample of stars that lie in a narrow range of ages from 2 to 4.5 Gyr. The stars were also selected to have errors on ages smaller than one Gyr. For this sub-sample of stars we found that the [X/Fe] abundance ratio of some elements correlates with the mean of the apo- and pericentric distances, Rmean. These Galactic radial abundance gradients qualitatively agree with those obtained from Cepheids (e.g. Lemasle et al. 2013) and from open clusters (e.g. Yong et al. 2012; Magrini et al. 2015).
When considering only stars that are younger than ~7 Gyr, we found no significant dependence of the Tc trend on stellar age, as was observed in previous works (e.g. Adibekyan et al. 2014; Nissen 2015). As in Adibekyan et al. (2014), when using the full sample of stars, we also observed some hint that the Tc slope depends on Rmean, although not in a simple way. However, this dependence completely vanished when a sub-sample of stars with similar ages (the sub-sample mentioned in the previous paragraph) was considered. Here, we should note that this sub-sample consists of only 18 stars.
With this small sample we still cannot firmly conclude whether the Tc trend depends on the formation place of stars. A larger sample size and improvement in the data quality (higher S/N) as well as the use of very similar stars in terms of stellar properties (e.g. metallicity, temperature, age) that are observed at a wide range of Galactocentric distances will help to finally answer this question. In this context, the role of large surveys and missions, such as Gaia (Perryman et al. 2001), Gaia-ESO (Gilmore et al. 2012), and APOGEE (Ahn et al. 2014), is invaluable.
Casagrande et al. (2011) provides revised stellar parameters, ages, Galactic orbital parameters and the space velocity components for the GCS stars.
We used BASTI expectation ages as suggested by Casagrande et al. (2011).
The last version of ARES code (ARES v2) can be downloaded at http://www.astro.up.pt/~sousasag/ares
The source code of MOOG can be downloaded at http://www.as.utexas.edu/~chris/moog.html
The q2 source code is available online at https://github.com/astroChasqui/q2
Acknowledgments
This work was supported by Fundação para a Ciência e Tecnologia (FCT) through national funds (project ref. UID/FIS/04434/2013) and by FEDER through COMPETE2020 (project ref. POCI-01-0145-FEDER-007672). This work was also supported by FCT through the research grants (ref. PTDC/FIS-AST/7073/2014 and ref. PTDC/FIS-AST/1526/2014) through national funds and by FEDER through COMPETE2020 (ref. POCI-01-0145-FEDER-016880 and ref. POCI-01-0145-FEDER-016886). This work results within the collaboration of the COST Action TD1308. P.F., N.C.S., and S.G.S. also acknowledge the support from FCT through Investigador FCT contracts of reference IF/01037/2013, IF/00169/2012, and IF/00028/2014, respectively, and POPH/FSE (EC) by FEDER funding through the program “Programa Operacional de Factores de Competitividade − COMPETE”. PF further acknowledges support from (FCT) in the form of an exploratory project of reference IF/01037/2013CP1191/CT0001. V.A. and E.D.M acknowledge the support of the FCT (Portugal) in the form of the grants SFRH/BPD/70574/2010 and SFRH/BPD/76606/2011, respectively. V.A also acknowledges the support of COST Action TD1308 through STSM grant with reference Number: COST-STSM-TD1308-32051. G.I. acknowledges financial support of the Spanish Ministry project MINECO AYA2011-29060. JIGH acknowledges financial support of the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2013 Ramón y Cajal program MINECO RYC-2013-14875, and the Spanish ministry project MINECO AYA2014-56359-P. This research made use of the SIMBAD database operated at CDS, Strasbourg, France. We thank the referee, Ivan Ramírez, for his interesting comments.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012a, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., et al. 2012b, A&A, 543, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 560, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., González Hernández, J. I., Delgado Mena, E., et al. 2014, A&A, 564, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., Santos, N. C., et al. 2015, A&A, 583, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Delgado-Mena, E., Figueira, P., et al. 2016a, A&A, 591, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Figueira, P., & Santos, N. C. 2016b, Origins of Life and Evolution of Biospheres (Springer) [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., & Nesvorný, D. 2013, ApJ, 763, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biazzo, K., Gratton, R., Desidera, S., et al. 2015, A&A, 583, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bidelman, W. P., & Keenan, P. C. 1951, ApJ, 114, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. C., O’Brien, D. P., & Lauretta, D. S. 2010, ApJ, 715, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
- Cunha, K., Frinchaboy, P. M., Souto, D., et al. 2016, ArXiv e-prints [arXiv:1601.03099] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2010, ApJ, 725, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 577, A83 [EDP Sciences] [Google Scholar]
- Ecuvillon, A., Israelian, G., Santos, N. C., Mayor, M., & Gilli, G. 2006, A&A, 449, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E. 2015, ApJ, 804, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Israelian, G., Santos, N. C., et al. 2010, ApJ, 720, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Delgado-Mena, E., Sousa, S. G., et al. 2013, A&A, 552, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grenon, M. 1987, J. Astrophys. Astron., 8, 123 [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2008a, A&A, 482, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2008b, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, Y.-C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data [Google Scholar]
- Laws, C., & Gonzalez, G. 2001, ApJ, 553, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Lemasle, B., François, P., Genovali, K., et al. 2013, A&A, 558, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, F., Asplund, M., Ramírez, I., Yong, D., & Meléndez, J. 2014, MNRAS, 442, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F., Yong, D., Asplund, M., et al. 2016, MNRAS, 456, 2636 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Mack, III, C. E., Stassun, K. G., Schuler, S. C., Hebb, L., & Pepper, J. A. 2016, ApJ, 818, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Randich, S., Donati, P., et al. 2015, A&A, 580, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., & Villaver, E. 2016, A&A, 588, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, R. D. 1984, PASP, 96, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Bergemann, M., Cohen, J. G., et al. 2012, A&A, 543, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neuforge-Verheecke, C., & Magain, P. 1997, A&A, 328, 261 [NASA ADS] [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E. 2016, A&A, in press, DOI: 10.1051/0004-6361/201628888 [Google Scholar]
- Nordström, B., Andersen, J., Olsen, E. H., et al. 1999, Ap&SS, 265, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., Minchev, I., Bland-Hawthorn, J., & Haywood, M. 2009, MNRAS, 397, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2014, A&A, 561, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Khanal, S., Aleo, P., et al. 2015, ApJ, 808, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha-Pinto, H. J., Flynn, C., Scalo, J., et al. 2004, A&A, 423, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffe, C., Flores, M., & Buccino, A. 2015, A&A, 582, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffe, C., Flores, M., Jaque Arancibia, M., Buccino, A., & Jofre, E. 2016, A&A, 588, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuler, S. C., Cunha, K., Smith, V. V., et al. 2011a, ApJ, 737, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., Flateau, D., Cunha, K., et al. 2011b, ApJ, 732, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Adibekyan, V., Mordasini, C., et al. 2015, A&A, 580, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Cunha, K., & Lazzaro, D. 2001, AJ, 121, 3207 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas at Austin, USA [Google Scholar]
- Sousa, S. G. 2014, Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars, Series: GeoPlanet: Earth and Planetary Sciences, eds. E. Niemczura, B. Smalley & W. Pych (Springer International Publishing) [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Yong, D., Carney, B. W., et al. 2006, AJ, 131, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Spina, L., Meléndez, J., & Ramírez, I. 2016, A&A, 585, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2005, PASJ, 57, 83 [NASA ADS] [Google Scholar]
- Takeda, Y., Sato, B., Kambe, E., et al. 2001, PASJ, 53, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Teske, J. K., Ghezzi, L., Cunha, K., et al. 2015, ApJ, 801, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Teske, J. K., Khanal, S., & Ramírez, I. 2016, ApJ, 819, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. 2014, AJ, 147, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, ApJ, 790, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci Maia, M., Ramírez, I., Meléndez, J., et al. 2016, A&A, 590, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314, 438 [NASA ADS] [Google Scholar]
- Yana Galarza, J., Meléndez, J., Ramírez, I., et al. 2016, A&A, 589, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, G.-C., Liang, Y.-C., Spite, M., et al. 2016, RA&A, 16, 019 [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Carney, B. W., & Friel, E. D. 2012, AJ, 144, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectroscopic observations and stellar parameters, ages, and Tc slopes of the sample stars.
All Figures
 |
Fig. 1 Abundance ratio [X/Fe] against [Fe/H] for the sample stars. The chemically peculiar Ba star is shown by the blue triangle. The black line represents the WLS fit of the data (excluding the Ba star). |
| In the text | |
 |
Fig. 2 Stellar ages derived in this work using the PARAM web interface against the ages derived by the q2 package. The left panel presents all the stars with derived ages, and the right panel shows the stars that have precise age determinations with errors smaller than 1 Gyr in both methods. |
| In the text | |
 |
Fig. 3 Abundance ratio [X/Fe] against age for the stars with the errors in the ages smaller than 1 Gyr. The symbols represent the same as in Fig. 1. The Ba star and the two oldest stars are not considered for the WLS fit. |
| In the text | |
 |
Fig. 4 [Y/Mg] versus stellar age for stars with age determination errors smaller than one Gyr. The symbols are the same as in the previous plots. The black solid line is the linear fit of our data without considering the two oldest stars. The blue dashed line and the green dotted lines represent the linear fits from Nissen (2015) and Tucci Maia et al. (2016), respectively. |
| In the text | |
 |
Fig. 5 Tc slopes derived by using all the elements against Tc slopes derived by considering only elements that have Tc> 900 K. The black solid line is the linear fit of the data and the blue dashed line represents the one-to-one line. The symbols are the same as in Fig. 1 and the previous plots. |
| In the text | |
 |
Fig. 6 Tc slopes against stellar parameters. The symbols are the same as in the previous plots. |
| In the text | |
 |
Fig. 7 Tc slopes against stellar age for stars with age determination errors smaller than one Gyr. The two oldest stars and the Ba star are not included in the fit. The symbols are the same as in the previous plots. |
| In the text | |
 |
Fig. 8 Stellar ages again mean Galactocentric distance for all the stars with errors on age smaller than 1 Gyr (left panel). The same as the left panel, but for stars with ages from 2.0 to 4.5 Gyr. The symbols are the same as in the previous plots and are described in Fig. 1. |
| In the text | |
 |
Fig. 9 Abundance ratio [X/Fe] against Rmean for the stars with ages from 2.0 to 4.5 Gyr and with errors on the ages smaller than 1 Gyr. The symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 10 Tc slope against Rmean for all the stars in the sample (left panel) and for stars with precise ages (error smaller than 1 Gyr) from 2.0 to 4.5 Gyr (right panel). The symbols are the same as in the previous plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


