| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628374 | |
| Published online | 04 July 2016 | |
An extreme planetary system around HD 219828
One long-period super Jupiter to a hot-Neptune host star⋆,⋆⋆
1 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: nuno@astro.up.pt
2 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
3 Observatoire de Genève, Université de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland
4 CIDMA, Departamento de Física, Universidade de Aveiro, Campus de Santiago, 3810-193 Aveiro, Portugal
5 ASD, IMCCE-CNRS UMR 8028, Observatoire de Paris, PSL Research University, 77 Av. Denfert-Rochereau, 75014 Paris, France
6 Aix-Marseille Université, CNRS, Laboratoire d’Astrophysique de Marseille UMR 7326, 13388 Marseille Cedex 13, France
7 European Southern Observatory (ESO), 19001 Casilla, Santiago, Chile
8 Observatoire de Haute-Provence, CNRS/OAMP, 04870 Saint-Michel-l’ Observatoire, France
9 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre & Marie Curie, 98bis boulevard Arago, 75014 Paris, France
10 SUPA, School of Physics and Astronomy, University of St. Andrews, St. Andrews, KY16 9SS, UK
11 European Space Agency (ESA), Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Received: 24 February 2016
Accepted: 10 May 2016
Context. With about 2000 extrasolar planets confirmed, the results show that planetary systems have a whole range of unexpected properties. This wide diversity provides fundamental clues to the processes of planet formation and evolution.
Aims. We present a full investigation of the HD 219828 system, a bright metal-rich star for which a hot Neptune has previously been detected.
Methods. We used a set of HARPS, SOPHIE, and ELODIE radial velocities to search for the existence of orbiting companions to HD 219828. The spectra were used to characterise the star and its chemical abundances, as well as to check for spurious, activity induced signals. A dynamical analysis is also performed to study the stability of the system and to constrain the orbital parameters and planet masses.
Results. We announce the discovery of a long period (P = 13.1 yr) massive (m sini = 15.1 MJup) companion (HD 219828 c) in a very eccentric orbit (e = 0.81). The same data confirms the existence of a hot Neptune, HD 219828 b, with a minimum mass of 21 M⊕ and a period of 3.83 days. The dynamical analysis shows that the system is stable, and that the equilibrium eccentricity of planet b is close to zero.
Conclusions. The HD 219828 system is extreme and unique in several aspects. First, ammong all known exoplanet systems it presents an unusually high mass ratio. We also show that systems like HD 219828, with a hot Neptune and a long-period massive companion are more frequent than similar systems with a hot Jupiter instead. This suggests that the formation of hot Neptunes follows a different path than the formation of their hot jovian counterparts. The high mass, long period, and eccentricity of HD 219828 c also make it a good target for Gaia astrometry as well as a potential target for atmospheric characterisation, using direct imaging or high-resolution spectroscopy. Astrometric observations will allow us to derive its real mass and orbital configuration. If a transit of HD 219828 b is detected, we will be able to fully characterise the system, including the relative orbital inclinations. With a clearly known mass, HD 219828 c may become a benchmark object for the range in between giant planets and brown dwarfs.
Key words: planetary systems / techniques: spectroscopic / techniques: radial velocities / stars: individual: HD 219828
Based on observations collected with the HARPS spectrograph at the 3.6-m ESO telescope (La Silla-Paranal Observatory, Chile), runs ID 072.C-0488, 075.C-0332, 075.C-0332, 076.C-0155, 077.C-0101, 183.C-0972, 091.C-0936, and 192.C-0852, as well as with the ELODIE and SOPHIE spectrographs, at the OHP Observatory, France.
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/592/A13
© ESO, 2016
1. Introduction
At a moment when the number of discovered extrasolar planets is already above 2000 (see e.g. Schneider et al. 2011, http://www.exoplanet.eu), most of the attention in the field is given to detecting planets with increasingly lower mass and to characterising their structure and atmospheres (for some recent reviews see e.g. Mayor et al. 2014; Burrows 2014; Lissauer et al. 2014).
While these efforts have mostly concentrated on short-period planets, which usually have a higher detection probability (through transits and radial velocities) and can be more easily characterised, the detection of long-period giant planets still enjoys considerable interest (see e.g. Feng et al. 2015; Santerne et al. 2016; Moutou et al. 2015).The frequency of systems with long-period giant planets (e.g. Rowan et al. 2016), which are more similar to the solar system gas giants, may provide important clues to the formation of our own system. Giant planets also play a crucial role in shaping the geometry of any planetary system (e.g. Morbidelli et al. 2007). Their detection thus provides important clues to the frequency and architecture of different planetary systems, in particular concerning the existence of other Earth-like worlds, or concerning the formation process and properties of short-period planets (e.g. Nagasawa et al. 2008; Izidoro et al. 2015).
In parallel, the formation of high-mass giant planets, in particular those on the borderline between giant planets and brown dwarfs, is still lively debated. The distinction between the two types of objects has been argued to be related to the deuterium-burning mass limit near 13 MJup (Burrows et al. 2001). The lack of a discontinuity in the mass distribution of companions to solar-type stars at the brown-dwarf regime (Udry & Santos 2007; Sahlmann et al. 2011) suggests, however, that a distinction based on the formation mechanisms may be more representative (Chabrier et al. 2014). The detection and characterisation of high-mass planets in systems where lower mass planets exist (e.g. the derivation of their masses, orbital properties, and relative inclinations) may in this sense provide relevant information.
Melo et al. (2007) presented the discovery of a short-period Neptune-like planet orbiting the bright G0 sub-giant star HD 219828. Evidence for a longer period signal in the data was also presented, although no conclusive orbital solution was proposed. In this paper we present the results of the analysis of new radial-velocity measurements of this star, covering a time span of 16 years. The results allow us to fully confirm the detection of the Neptune-mass companion, but also to constrain the orbital solution and minimum mass for the longer period counterpart. In Sects. 2 and 3 we present our new radial velocity dataset and a comprehensive analysis of the stellar parameters and chemical abundances, respectively. The detected radial-velocity signals are discussed in Sect. 4, and in Sect. 5 we present a dynamical analysis of the system. We then discuss the relevance, uniqueness, and potential of this system in Sect. 6.
2. Observations and data
Melo et al. (2007) presented the discovery of a hot Neptune orbiting HD 219828 based on 22 high-precision radial velocities obtained with the HARPS instrument at the 3.6 m ESO telescope (La Silla-Paranal Observatory, Chile – Mayor et al. 2003). Since then, 69 new HARPS spectra were obtained with the goal of confirming the existence of the short-period Neptune but also to try to constrain the orbit of the longer period companion. A total of 91 HARPS measurements over the same number of nights are now available, spanning from 2005-05-19 to 2013-11-20. We note that two further measurements were obtained in August 2015. However, a major instrument upgrade was made in June 2015 with the introduction of octogonal fibers (see Bouchy et al. 2013, for the SOPHIE example and motivation), and an offset in the radial velocities was introduced that is still not well characterised. As a result, these two new measurements do not allow us to add any relevant information. We thus decided to remove them from the current analysis.
The HARPS measurements were obtained with an exposure time of 900s and a simultaneous calibration using the Fabry-Pérot étalon mode whenever this was available. Otherwise, the traditional ThAr simultaneous calibration mode was used for the older measurements that have been published in Melo et al. (2007). This allowed us to achieve an individual precision of better than 1 m s-1 for most of the measurements (the average noise in our data is 80 cm s-1, including photon noise, calibration noise, and the uncertainty in the measurement of the instrumental drift, with an rms of 20 cm s-1). The exposure time used also allows averaging out the noise produced by stellar oscillation modes (Dumusque et al. 2011), with timescales of the order of a few minutes. This strategy does not allow us to completely overcome the granulation noise, however.
All HARPS spectra were reduced using the latest version of the HARPS pipeline. Precise radial velocities were derived, together with measurements of the bisector inverse slope (BIS), full width at half maximum (FWHM), and contrast of the HARPS cross-correlation function (CCF – Baranne et al. 1996; Pepe et al. 2002). These values are useful to diagnose radial-velocity variations that are intrinsic to the star, for instance caused by stellar activity on its different timescales (e.g. Queloz et al. 2000; Santos et al. 2010; Figueira et al. 2010; Dumusque et al. 2012; Santerne et al. 2015). Values for the chromospheric activity index 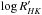 were also derived (see Sect. 3) following a procedure similar to the one adopted in Gomes da Silva et al. (2014; see also Lovis et al. 2011).
were also derived (see Sect. 3) following a procedure similar to the one adopted in Gomes da Silva et al. (2014; see also Lovis et al. 2011).
In addition to the HARPS data, radial-velocity measurements of HD 219828 were also obtained using the ELODIE (Baranne et al. 1996) and SOPHIE (Perruchot et al. 2008) cross-dispersor fiber-fed echelle spectrographs, mounted on the 1.93 m telescope at the Observatoire de Haute-Provence (OHP)1. Albeit with a lower precision when compared with HARPS, the radial velocities derived using these instruments are useful to constrain the period and eccentricity of the long-period companion (see Sect. 4).
A total of four observations were made with ELODIE between 1999 and 2004 as part of the ELODIE planet search program (Perrier et al. 2003). The first of the four observations from the ELODIE database was made without a simultaneous thorium-argon lamp but observed within the same mode immediately before the constant star HD 220773. For this constant star, we determined the radial-velocity offset for observations obtained with and without a simultaneous thorium-argon lamp. We applied the same radial-velocity offset for HD 219828. This allows us to be confident of the measured radial velocity because the instrumental drift between the observations of the two stars is expected to be much lower than the error bar of the measurement (of the order of 15–30 m s-1).
A total of 19 measurements were also acquired with SOPHIE as part of the science verification at the end of 2007 and after the installation of octagonal fibers in 2011 (Bouchy et al. 2013). SOPHIE observations were secured in high-resolution mode and with thorium-argon simultaneous calibration. Exposure times were 900 or 1200 s, and the error bars of individual measurements have a value of 3.4 m s-1 on average. Systematic effects were corrected in the SOPHIE measurements. All the spectra taken before June 2011 are corrected for the seeing effect (Boisse et al. 2010, 2011). Spectra taken after June 2011 are corrected using a set of standard stars that are monitored every night. This correction accounts for any instrumental variations and is described in detail in Courcol et al. (2015).
All the used radial velocities are made available in electronic form in CDS. A sample is provided in Table 1.
Radial velocities (RV) for HD 219828 together with the respective barycentric Julian dates, errors, and instrument used.
3. HD 219828: the star
According to the revised version of the Hipparcos catalogue (van Leeuwen 2007) and SIMBAD, HD 219828 is a G0IV star with a parallax π = 12.83 ± 0.74 mas, an apparent magnitude mv = 8.04, and a colour index B−V = 0.654. These values imply, adopting the bolometric correction from Flower (1996), an absolute magnitude Mv = 3.58 and a luminosity of 3.08 L⊙. Still according to Hipparcos, the star is stable up to 0.013 mag (typical for a constant star of its magnitude).
Using a high-resolution and high signal-to-noise ratio (S/N) HARPS spectrum, Melo et al. (2006) derived precise stellar atmospheric parameters for this star (see also SWEET-Cat – Santos et al. 2013)2. The values are presented in Table 2. The derived effective temperature Teff = 5891 ± 18 K, log g = 4.19 ± 0.05 dex, and [Fe/H] = 0.19 ± 0.02 dex agree well with the spectral type listed in Hipparcos and also with other values from the literature: van Belle & von Braun (2009) derived a temperature of Teff = 5929 ± 90 from SED fitting, and Gonzalez et al. (2010) derived Teff = 5861 ± 38 K and log g = 4.21 dex.
PARSEC evolutionary models (Bressan et al. 2012)3 indicate that HD 219828 has a mass of 1.23 ± 0.06 M⊙ and an age of 4.6 ± 0.7 Gyr. A similar age was found by Casagrande et al. (2011; 5 ± 1.34 Gyr), also compatible with its activity level (Pace 2013, indicating an age above 2 Gyr). A mass of 1.22 M⊙ is also found using the calibration of Torres et al. (2010) based on the spectroscopically derived values of Teff, log g, and [Fe/H], after correcting for the systematics as explained in Mortier et al. (2014) and Santos et al. (2013). We decided to adopt a value of 1.23 M⊙ to which we associated a conservative uncertainty of 0.10 M⊙. A surface gravity value slightly lower than the one found through the spectroscopic analysis (4.09 dex) was derived when we considered the above stellar mass, the bolometric correction, and the Hipparcos distance and magnitude following Eq. (1) of Santos et al. (2004). A similarly lower value (4.08 dex) was also obtained when we corrected the spectroscopic surface gravity using the calibration presented by Mortier et al. (2014). We therefore decided to adopt a lower surface gravity, with a conservative error bar of 0.10 dex.
Our derived lithium (Li) abundance for HD 219828 is log ϵ(Li) = 2.33 ± 0.04, similar to the value found by Gonzalez et al. (2010) (log ϵ(Li) = 2.17 ± 0.06), and typical of early-G dwarfs. Planet-host stars with a temperature close to solar have been suggested to be Li-poor when compared with single field dwarfs of the same age and metallicity (for a recent paper and debate see Figueira et al. 2014, and references therein). However, the Teff of this star lies beyond the temperature range where this effect is observed (5700–5850 K), and hotter stars show higher Li abundances regardless of the presence of planets (e.g. Delgado Mena et al. 2014).
The derived radius of the star, based on the relation of luminosity, temperature, and radius is 1.69 R⊙. This value is slighly above the one derived using the Torres et al. (2010) calibration (1.47 R⊙), the spectral energy distribution (SED) fitting procedure adopted in van Belle & von Braun (2009) (1.58 ± 0.10 R⊙), or the one obtained from the PARSEC interface (da Silva et al. 2006, 1.61 ± 0.12 R⊙).
In brief, HD 219828 is a metal-rich early-G dwarf that is slightly evolved beyond the main sequence. The adopted parameters for the star are listed in Table 2.
HD 219828 has also been found to be a low-activity star: from the HARPS spectra we derive a mean 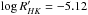 dex, with a small dispersion of only 0.02 dex. These values are even lower than those found in Pace (2013) (
dex, with a small dispersion of only 0.02 dex. These values are even lower than those found in Pace (2013) (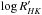 between −4.896 and −4.880), attesting to the low activity level of this star. This low value for the activity level would correspond to a rotational period of 28.7 ± 0.6 days and 31.7 ± 0.8 days, according to the calibrations of Noyes et al. (1984) and Mamajek & Hillenbrand (2008), respectively. A projected rotational velocity v sini = 2.9 km s-1 is derived from the FWHM of the HARPS cross-correlation function (see e.g. Santos et al. 2002)4. With a stellar radius of 1.69 R⊙ and assuming a rotational period of 30 days, HD 219828 should be rotating with Vrot = 2.8 km s-1. These values suggests that the star may be seen almost equator-on.
between −4.896 and −4.880), attesting to the low activity level of this star. This low value for the activity level would correspond to a rotational period of 28.7 ± 0.6 days and 31.7 ± 0.8 days, according to the calibrations of Noyes et al. (1984) and Mamajek & Hillenbrand (2008), respectively. A projected rotational velocity v sini = 2.9 km s-1 is derived from the FWHM of the HARPS cross-correlation function (see e.g. Santos et al. 2002)4. With a stellar radius of 1.69 R⊙ and assuming a rotational period of 30 days, HD 219828 should be rotating with Vrot = 2.8 km s-1. These values suggests that the star may be seen almost equator-on.
The abundances of planet-host stars as well as their origin in the Galaxy have been suggested to have an important influence on the frequency, composition, architecture, and formation history (Adibekyan et al. 2012a; Dawson & Murray-Clay 2013; Adibekyan et al. 2013; Santos et al. 2015). We therefore decided to derive detailed abundances for several α- and iron-peak elements in HD 219828 using a combined HARPS spectrum, built from all the data available at the time of this publication5. The method we adopted is fully explained in Adibekyan et al. (2012b), and we refer to that paper for more details. The stellar atmospheric parameters adopted for the analysis are those listed in Table 2. The final set of abundances, together with the number of element lines used to derive the abundances and respective errors (denoting the error on the mean) are listed in Table 3. Moreover, we also derived abundances of several volatile elements (C, O, S, and Zn) and heavier elements, following the procedures of Ecuvillon et al. (2004) and Bertran de Lis et al. (2015). The values allow us to conclude that HD 219828 is a typical thin-disk star from the solar neighbourhood; its [α/Fe]6 abundance ratios are nearly solar (i.e. ~0.0): no α-element enhancement, typical of thick-disk or halo stars, is observed (see Adibekyan et al. 2012b, and references therein).
4. Radial-velocity fitting
List of free parameters and respective priors used in the MCMC analysis of the radial velocities.
The HARPS, SOPHIE, and ELODIE data were fit simultaneously using the Markov chain Monte Carlo (MCMC) algorithm implemented into the PASTIS software and fully described in Díaz et al. (2014). The priors used are listed in Table 4. The number of Keplerian functions was set to two: one to take the short-period signal into account that has been announced in Melo et al. (2007), and the other to fit the long-term signal that is clear by visual inspection of the data (see also Fig. 1). The offsets between the HARPS, SOPHIE, and ELODIE radial velocities were also fit during the process.
We ran 100 chains of 3 × 105 iterations starting from an initial value randomly drawn from the joint prior. We then removed chains that did not converge to the maximum likelihood. We also removed the burn-in before thinning and merging the remaining chains. This provided 10 000 independent samples of the posterior distribution.
The best-fit parameters of the orbits and their 68.3% confidence interval are listed in Table 5. The best solutions hold for planets b and c, periods of 3.83 and 4791 days, eccentricities of 0.059 ± 0.036 and 0.8115 ± 0.0032, and planet masses of 21 ± 1.4 M⊕ and 15.1 ± 0.85 MJup. The eccentricity value found for HD 219828 b is not significant at a 1.6 sigma level, and we therefore consider that we have no solid ground to assume that it is different from zero. On the other hand, the high value for the eccentricity for HD 219828 c brings this companion to as close as 1.13 AU from its host star at periastron, while at apastron the distance is around 10.8 AU.
We also tested the possibility that an additional long-term drift is present in the data. Adding this additional term to the fitting procedure did not return any significant result. We exclude any linear drift with an amplitude higher than 1 m s-1 yr-1 with 95% confidence.
Table 5 shows that the estimated jitter of the HARPS radial velocities is of the order of 1.64 m s-1, significantly above the average error bar of the individual measurements of 0.8 m s-1. This difference may be caused by the fact that HD 219828 is an early-G star, slightly evolved beyond the main sequence. It is indeed well known that stars of earlier type and more evolved stars present higher granulation noise in radial velocities (see Dumusque et al. 2011, and references therein). It is also known that stellar activity can produce signals that can mimic planetary companions at different timescales (e.g. Saar & Donahue 1997; Queloz et al. 2000; Santos et al. 2010; Dumusque et al. 2012; Kane et al. 2016), even for stars with a low activity level (e.g. Santos et al. 2014). The analysis of the generalized Lomb Scargle (GLS) periodograms of the residuals (O−C) of radial velocities after removing the two Keplerians reveals some power near 30 days (Fig. 2, top left panel). This signal, although not statistically significant, is most likely related to the rotational period of the star, which is estimated to be close to that value (Table 2). To diagnose any activity-induced signal in Fig. 2, we also present the GLS periodogram of the FWHM, BIS, and 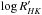 time series. A peak at a period of 30 days is also found in the periodogram of the
time series. A peak at a period of 30 days is also found in the periodogram of the 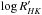 (lower right), again not significant. In all the plots, the dotted and dashed horizontal lines denote the 10% and 1% false-alarm probability levels, respectively. These were derived using a permutation test as done in Mortier et al. (2012). No significant signal appeared in any of the variables. We therefore have no evidence that stellar activity may be contributing to produce the observed signals or any other additional signal in the data, at any timescale. The lack of any long-term significant variability on the BIS and FWHM also excludes the possibility that HD 219828 c is a solar-like stellar companion in a highly inclined orbit (Santerne et al. 2015), since such a companion is expected to leave a trace on these parameters.
(lower right), again not significant. In all the plots, the dotted and dashed horizontal lines denote the 10% and 1% false-alarm probability levels, respectively. These were derived using a permutation test as done in Mortier et al. (2012). No significant signal appeared in any of the variables. We therefore have no evidence that stellar activity may be contributing to produce the observed signals or any other additional signal in the data, at any timescale. The lack of any long-term significant variability on the BIS and FWHM also excludes the possibility that HD 219828 c is a solar-like stellar companion in a highly inclined orbit (Santerne et al. 2015), since such a companion is expected to leave a trace on these parameters.
 |
Fig. 1 Top and middle plots: phase-folded radial-velocity curves and data for planets b and c, respectively. Bottom: combined orbital solution of planets b and c as a function of time. Residuals of the complete fit are presented at the bottom of each diagram. |
We also tested whether this extra noise might indicate another low-amplitude companion to the system. No satisfactory Keplerian fit was found. We therefore find no compelling evidence for additional companions.
In brief, we find clear evidence for the presence of two companions orbiting HD 219828: a Neptune-mass planet in a short-period circular orbit, and a high-mass companion on the borderline between a giant planet and brown dwarf orbiting in a long-period eccentric trajectory. This result fully confirms the detection of Melo et al. (2007), and the fitted parameters are compatible with those listed in the announcement paper within the error bars. We note that using the new dataset alone also leads to an orbital solution for the short-period planet that is compatible with the one presented in Melo et al. We did not detect significant eccentricity for the inner planet either, with an upper limit of 0.15 within a 99% confidence interval.
We also computed the detection limits for additional planets in the system. For this we analysed the residuals of the fit presented above, using a Monte Carlo approach similar to the one used in Mortier et al. (2012). In brief, for each period we injected signals in the best-fit residuals, assuming circular orbits, with varying amplitudes until the false-alarm probability of the detection was higher than 1%. The amplitude of this signal (for each period) sets the mass of the planet that can be detected within the existing data. The results of this analysis are presented in Fig. 3. In the figure, the two vertical lines denote the time span of the HARPS observations and the total time span including the older ELODIE and SOPHIE data. The red line corresponds to the detection limit when we were able to detect a signal corresponding to a circular orbit with a semi-amplitude of 1 m s-1. The results of this analysis suggest that we can exclude additional planets with masses above 10 M⊕ in the period range up to ~100 days. This value decreases to 4 M⊕ when we restrict the period range to shorter than 10 days, and increases to ~20 M⊕ at periods of 1000 days.
Orbital parameters for the two Keplerian solutions and the derived planet minimum mass.
 |
Fig. 2 Periodograms of the radial-velocity residuals to the two-Keplerian fit and of the raw values of FWHM, BIS, and |
5. Dynamical analysis
The orbital solution given in Table 5 shows a planetary system composed of two planets in a very uncommon configuration: a Neptune-mass planet in a compact nearly circular orbit (ab = 0.05 AU, eb = 0.06), together with a brown-dwarf-mass planet in a wide very eccentric orbit (ac = 6.0 AU, ec = 0.81). The stability of the system is not straightforward to gauge since the pericenter of the massive outer planet is nearly at 1 AU. Gravitational perturbations on the inner planet cannot be neglected and may give rise to some instability.
5.1. Stability analysis
 |
Fig. 3 Detection limits for additional planets in the system. |
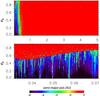 |
Fig. 4 Stability analysis of the nominal fit of the HD 219828 planetary system (Table 5). For fixed initial conditions, the phase space of the system is explored by varying the semi-major axis ab and eccentricity eb of the inner planet. The step size is 10-2 in eccentricity, and 5 × 10-3 (top) or 2 × 10-4 AU (bottom) in semi-major axis. For each initial condition, the system is integrated over 103 yr and a stability criterion is derived with the frequency analysis of the mean longitude (Laskar 1990, 1993). As in Correia et al. (2005, 2009, 2010), the chaotic diffusion is measured by the variation in the frequencies. The red zone corresponds to highly unstable orbits, while the dark blue region can be assumed to be stable on a billion-year timescale. |
To analyse the stability of the nominal solution (Table 5), we performed a global frequency analysis (Laskar 1993) in the vicinity of this solution, in the same way as achieved for other planetary systems (e.g. Correia et al. 2005, 2009, 2010). For each planet, the system is integrated on a regular 2D mesh of initial conditions, with varying semi-major axis and eccentricity, while the other parameters are retained at their nominal values (Table 5). The solution is integrated over 200 yr for each initial condition and a stability indicator is computed to be the variation in the measured mean motion over the two consecutive 100 yr intervals of time (for more details see Correia et al. 2005). For regular motion, there is no significant variation in the mean motion along the trajectory, while it can vary significantly for chaotic trajectories. The result is reported using a colour index in Fig. 4, where red represents the strongly chaotic trajectories and dark blue the extremely stable ones.
In Fig. 4 we show the wide vicinity of the best-fit solution of the inner orbit. We observe that from 0.2 to 5 AU the system is totally unstable as a result of the presence of the outer planet (top). However, when we zoom into the region a< 0.1 AU (bottom), we verify that planet b is stable even for eccentricities up to 0.5. This figure thus show us that the HD 219828 planetary system listed in Table 5 is stable over a timescale of several Gyr.
We can also try to constrain the highest possible masses of the planets if we assume co-planarity of the orbits. By decreasing the inclination of the orbital plane of the system, we increase the mass values of both planets. We repeated a stability analysis of the orbits, like in Fig. 4. With decreasing inclination, the stable dark- blue areas become narrower, to the point that the best-fit solution lies outside the stable zones. At this point, we conclude that the system cannot be stable anymore. It is not straightforward to find a transition inclination between the two regimes, but our analysis suggests that stability of the whole system is still possible for an inclination of 5°, but becomes impossible for lower values. Therefore, we conclude that the highest masses of the planets correspond to a scaling factor of about 10, which would transform the inner planet into a hot Jupiter and the outer one into an M-dwarf star.
5.2. Secular coupling
Fundamental frequencies for the nominal orbital solution in Table 5.
We performed a frequency analysis of the nominal orbital solution listed in Table 5 computed over 105 yr. The orbits of the planets were integrated with the symplectic integrator SABA1064 of Farrés et al. (2013), using a step size of 5 × 10-3 yr and general relativity corrections. The fundamental frequencies of the systems are the mean motions nb and nc, and the two secular frequencies of the pericenters g1 and g2 (Table 6).
To present the solution in a clearer way, it is useful to make a linear change of variables into eccentricity proper modes (see Laskar 1990). In the present case, the linear transformation is numerically obtained with the frequency analysis of the solutions because of the high eccentricity of the outer planet. Using the classical complex notation zp = epeiϖp, for p = b,c, the linear Laplace-Lagrange solution reads  (1)To good approximation, the two proper modes uk (with k = 1,2) are given by uk ≈ ei(gkt + φk), where gk and φk are listed in Table 6. Because the outer planet is much more massive than the inner one, there is almost no effect of the inner planet on the outer orbit: zc ≈ 0.811 u2, and thus ec = | zc | ≈ 0.811 = cte (Eq. (1)).
(1)To good approximation, the two proper modes uk (with k = 1,2) are given by uk ≈ ei(gkt + φk), where gk and φk are listed in Table 6. Because the outer planet is much more massive than the inner one, there is almost no effect of the inner planet on the outer orbit: zc ≈ 0.811 u2, and thus ec = | zc | ≈ 0.811 = cte (Eq. (1)).
Equation (1) usually provides a good approximation for the long-term evolution of the eccentricities. In Fig. 5 we plot the eccentricity evolution of the inner orbit with initial conditions from Table 5. Simultaneously, we plot its evolution given by the above secular, linear approximation (eb = | zb |). We see there is a good agreement with the numerical solution, that is, the eccentricity behaviour is described well by the secular approximation (Eq. (1)). The eccentricity variations result from the perturbation of the outer planet, but they are very limited (0.05786 <eb< 0.05980). These variations are driven mostly by the secular frequency g1, with a period of approximately 14 kyr (Table 6).
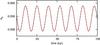 |
Fig. 5 Evolution of the eccentricity of the inner planet with time, starting with the orbital solution from Table 5. The red line gives the complete numerical solution, while the black dashed curve is obtained with the linear approximation (Eq. (1)). |
5.3. Tidal evolution
The inner planet is very close to the star, and it is therefore expected to undergo strong tidal dissipation that slowly damps the eccentricity close to zero (e.g. Hut 1980; Correia 2009). The best-fit determination for the inner planet eccentricity is eb = 0.059 ± 0.036 (Table 5). This value is still compatible with zero, but the question arises whether we measure some residual equilibrium value resulting from the perturbations of the outer massive companion (Mardling 2007; Laskar et al. 2012).
The linear approximation from the previous section (Eq. (1)) provides a direct estimate for the final equilibrium eccentricity. In presence of tides, the proper modes are damped following an exponential decay law | uk | = e− γkt, where γk depends on the tidal dissipation (Laskar et al. 2012). Assuming that dissipation occurs only on the inner body, we obtain γ1 ≫ γ2 and γ2 ≈ 0. Therefore, after some time, the amplitude | u1 | is fully damped, while | u2 | ≈ 1 is almost unchanged. From Eq. (1) we therefore have eb = | zb | = | 0.058828 u1 + 0.000961 u2 | ≈ 0.000961.
To test this scenario, we integrated the system from Table 5 taking tidal dissipation in the inner body and general relativity corrections into account. We adopted the same model as in Sect. 6.3 of Bonfils et al. (2013b) with R = 28 000 km, k2 = 0.5, and Δt = 100 s. In Fig. 6 we show the eccentricity evolution until it reaches its equilibrium value. It stabilises around 0.000964, which agrees with the prediction from the secular model (Eq. (1)). In our model we did not consider the rotational and tidal deformation of the planet, which would decrease the equilibrium eccentricity even more (Laskar et al. 2012). We therefore conclude that the currently observed value eb = 0.059 is most likely overestimated.
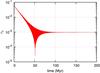 |
Fig. 6 Long-term evolution of the eccentricity of the inner planet with time, starting with the orbital solution from Table 5 and including tidal effects. The eccentricity stabilises around eb = 0.00096, in perfect agreement with the prediction from the secular linear model (Eq. (1)). |
6. Discussion
We presented the discovery of a massive giant planet in a long-period highly eccentric orbit around HD 219828, a G0IV metal-rich star for which a hot Neptune (HD 219828 b) was announced in Melo et al. (2007). With a minimum mass of ~15 MJup, HD 219828 c is intermediate between the giant planet and brown-dwarf classes. The data also allowed us to fully confirm the orbital parameters and mass for the shorter period low-mass companion.
6.1. Statistics and the formation of hot Neptunes
The system discovered around HD 219828 is of interest for several reasons. The first and most evident reason is the fact that the two planets this system consists of are at the high- and low-mass ends of the mass distribution for planet-mass companions to solar-type stars. Studying it therefore may provide important clues to the formation of short-period low-mass planets, as well as about the transition from giant planets to brown dwarfs.
By selecting all the planets discovered using the radial-velocity or transit methods in exoplanet.eu (Schneider et al. 2011), we conclude that the system orbiting HD 219828 presents one of the highest mass ratios detected so far: assuming that the orbits are co-planar, mc/mb ~ 229. The peculiar mass ratio of this system is well illustrated in Fig. 7, where we plot the mass ratio distribution of all multi-planet systems listed in exoplanet.eu. For systems with three or more planets, only the higher mass ratio is used for the histogram (mhigher/mlower). The figure shows that most multi-planet systems have mass ratios below 10, and only very few cases present mass ratios above 200. Except for HD 219828, other systems with a mass ratio above 200 include our solar system (not included in the plot), with a Jupiter-to-Mercury mass ratio of almost 40007, GJ 676 A, an M-dwarf where Anglada-Escudé & Tuomi (2012) announced the presence of 2 + 2 super-Earths+jovian planets (see also Forveille et al. 2011; Bonfils et al. 2013a) with the highest mass ratio of 353, Kepler-94, with a hot Neptune and a moderately long-period (P ~ 820 days) jovian companion (Marcy et al. 2014, a mass ratio of 288, assuming co-planar orbits), and Kepler-454, a system composed of a short-period transiting super-Earth, one jovian gas giant with a period of 524 days, and an additional possible longer period gas giant (Gettel et al. 2016, mass ratio of 207 assuming co-planar orbits). We note, however, that at least one of the low-mass planets in the Gl 676 A system has recently been disputed (e.g. Suárez Mascareño et al. 2015), and for planet c, the higher mass planet in the system, the only evidence presented in Anglada-Escudé & Tuomi (2012) comes from a poorly constrained long-term trend in the data.
 |
Fig. 7 Distribution of mass ratios for all multi-planet systems listed in exoplanet.eu. |
It is currently being discussed how often hot Jupiters are found in systems with additional longer period companions. Recent results using direct imaging and radial-velocity surveys suggest that such companions are frequent around hot-Jupiter hosts: in about 50% of the cases evidence exists for additional companions in the range 1–20 MJup and with an orbital distance of 5–20 AU (e.g. Bryan et al. 2016). This rate is similar to the multiple star rate found in field stars (Raghavan et al. 2010). The presence or absence of companions in longer period orbits may be key to understanding the processes of planet migration: disk induced (e.g. Lin et al. 1996), or dynamically induced (e.g. Nagasawa et al. 2008). To our knowledge, however, a similar study has not been conducted for lower mass short-period planets.
We therefore searched in exoplanet.eu for all systems composed of a hot Neptune or super-Earth and a longer period massive companion (a giant planet) detected using the radial-velocity method. We did not include planets detected by other methods to ensure that no strong bias was introduced (e.g. when the transit method is strongly biased towards short-period planets). We found 40 stars with hot Jupiters, 4 (or 10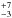 %)8 of them are in multiple systems, all of them with high-mass planet companions (>0.1 MJup). On the other hand, we found 38 stars with hot Neptunes, 28 (or 74
%)8 of them are in multiple systems, all of them with high-mass planet companions (>0.1 MJup). On the other hand, we found 38 stars with hot Neptunes, 28 (or 74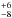 %) of them in multiple systems: 16 (42
%) of them in multiple systems: 16 (42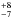 %) have giant-planet companions (>0.1 MJup) and 12 (32
%) have giant-planet companions (>0.1 MJup) and 12 (32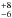 %) have additional low-mass planets (Neptunes or super-Earths). This strongly suggests that the frequency of companions, in particular longer period giant planets, in systems of hot Neptunes is significantly higher than the one found for the hot-Jupiter planets. This result may be a telltale sign that the formation and evolution of hot Neptunes follows a path different to that of their higher mass counterpars, the hot Jupiters.
%) have additional low-mass planets (Neptunes or super-Earths). This strongly suggests that the frequency of companions, in particular longer period giant planets, in systems of hot Neptunes is significantly higher than the one found for the hot-Jupiter planets. This result may be a telltale sign that the formation and evolution of hot Neptunes follows a path different to that of their higher mass counterpars, the hot Jupiters.
6.2. A system full of potential
The interest in the HD 219828 system is also further enhanced because its high mass, the long orbital period, and the very high eccentric orbit of HD 219828 c (it is among the top 10 known exoplanets with higher eccentricity), together with its distance to the Sun (78 pc), make it a prime target for Gaia. The relative semi-major axis of the orbital motion of HD 219828 c is ~5.96 AU, and the semi-major axis of the corresponding barycentric orbit of HD 219828 is ~0.07 AU. This latter value corresponds to about 0.9 mas at the distance of 78 pc. This signal is much stronger than the expected measurement uncertainties and should be detectable with GAIA, even though the nominal 5 yr mission lifetime does not cover one complete orbit. Using the combined astrometric and radial-velocity measurements, we will then be able to derive a precise mass for the companion and also for its orbital parameters, including its orientation with respect to the sky.
Furthermore, given the radius of the star and the orbital period of HD 219828 b, the probability that this planet transits is about 17%. The hot Neptune HD219828 b is very similar to the transiting planet Kepler-8 b (Jenkins et al. 2010), which has a mass of 24.4 ± 3.8M⊕, a period of ~3.21 days, and is transiting a G0IV star. Kepler-8 b has a radius of about 4.0 R⊕. With a mass of 18.8 ± 2.2M⊕ and a period of 4.2 days, the transiting planet HAT-P-26 b (Hartman et al. 2011) is also similar to HD219828 b. However, HAT-P-26 b transits a later-type main-sequence star. It radius has been measured to be 6.3 R⊕. Assuming HD219828 b has a mass of 21.0 M⊕, we can expect its radius to be in the range 4–6 R⊕. Given the stellar radius of 1.69 R⊙ and an inclination of 90°, the transit is expected to have a depth in the range 600–1200 ppm. For the most favourable case, this signal could be detected from the ground (Delrez et al. 2016). It would otherwise be an easy case for space-based photometry with a dedicated observatory such as CHEOPS (Fortier et al. 2014) or TESS (Ricker et al. 2010). Assuming a linear ephemeris for the inner planet, we find that the transit epochs can be computed using the following equation: 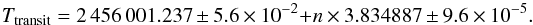 (2)The covariance matrix between the initial transit epoch (T0) and the period (P) is
(2)The covariance matrix between the initial transit epoch (T0) and the period (P) is 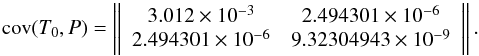 (3)At the time of the launch of CHEOPS, the uncertainty on the transit time is therefore at the level of two hours within a 68.3% probability.
(3)At the time of the launch of CHEOPS, the uncertainty on the transit time is therefore at the level of two hours within a 68.3% probability.
Furthermore, assuming a v sini of 2.9 km s-1 and the above assumptions, the Rossiter-McLaughlin effect is expected to have a semi-amplitude that ranges between 1.4 m s-1 and 2.6 m s-1 and could be detected with an instrument like HARPS. If such a signal is detected, and assuming Gaia will provide an orbital inclination (with respect to the sky) for HD 219828 c, we will be able to derive the relative inclinations of the two companions. Such a unique measurement may allow us to set relevant constraints on the formation models of short-period low-mass planets (see e.g. Moriarty & Ballard 2015).
The long-period planet HD 219828 c has a minimum mass that positions it between a giant planet and a brown dwarf (this value may be known precisely when Gaia data become available) and orbits a bright nearby star. It has the potential of becoming a benchmark object for the study of atmospheres. The 2MASS H magnitude of HD 219828 is 6.6 (Skrutskie et al. 2006). Assuming masses of 15, 50, and 80 times the mass of Jupiter for HD 219828 c, an age of 5 Gyr, and the distance of 78 pc, the COND models of Baraffe et al. (2003) tell us that its apparent H magnitude would be around 26, 20, and 15, respectively. While for the lower mass case the magnitude difference may be too high for a detection using direct imaging techniques, a flux ratio of about 10-4 is expected if the companion is close to the brown dwarf/stellar mass border. An even higher value may be expected at longer wavelengths. Such signals should be easily detectable with recent instruments such as SPHERE or using a detailed spectroscopic analysis (Brogi et al. 2012; Snellen et al. 2014; Martins et al. 2015). We note that the projected distance on the sky between the star and the planet is about 0.14 arcsec at apastron.
The system orbiting the bright HD 219828, with its extreme mass ratio and the high-mass giant planet/brown dwarf companion may thus become a benchmark system for future studies of the formation of planetary systems and of planet atmospheres.
Acknowledgments
We would like to thank G. Chauvin for the interesting discussions. This work was supported by Fundação para a Ciência e a Tecnologia (FCT, Portugal), project ref. PTDC/FIS-AST/1526/2014, through national funds and by FEDER through COMPETE2020 (ref. POCI-01-0145-FEDER-016886), as well as through grant UID/FIS/04434/2013 (POCI-01-0145-FEDER-007672). P.F., N.C.S., and S.G.S. also acknowledge the support from FCT through Investigador FCT contracts of reference IF/01037/2013, IF/00169/2012, and IF/00028/2014, respectively, and POPH/FSE (EC) by FEDER funding through the program “Programa Operacional de Factores de Competitividade – COMPETE”. P.F. and S.G.S. further acknowledge support from FCT in the form of exploratory projects of reference IF/01037/2013CP1191/CT0001 and IF/00028/2014/CP1215/CT0002. A.S. is supported by the European Union under a Marie Curie Intra-European Fellowship for Career Development with reference FP7-PEOPLE-2013-IEF, number 627202. E.D.M and V.Zh.A. acknowledge the support from the FCT in the form of the grants SFRH/BPD/76606/2011 and SFRH/BPD/70574/2010, respectively. A.S. thanks the Laboratoire d’Astrophysique de Marseille for the support in computing resources. J.P.F. acknowledges support from FCT through grant reference SFRH/BD/93848/2013. J.R. acknowledges CONICYT/Becas Chile 72140583. We warmly thank the OHP staff for their support on the 1.93 m telescope. We acknowledge support from the “conseil scientifique” of the Observatory of Paris and CIDMA strategic project UID/MAT/04106/2013. We gratefully acknowledge the Programme National de Planétologie (telescope time attribution and financial support) of CNRS/INSU. This work results within the collaboration of the COST Action TD 1308. This work made use of SIMBAD.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012a, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012b, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 560, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., & Tuomi, M. 2012, A&A, 548, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Eggenberger, A., Santos, N. C., et al. 2010, A&A, 523, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bouchy, F., Chazelas, B., et al. 2011, in Eur. Phys. J. Web Conferences., 16, 02003 [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013a, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Lo Curto, G., Correia, A. C. M., et al. 2013b, A&A, 556, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Díaz, R. F., Hébrard, G., et al. 2013, A&A, 549, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2012, Nature, 486, 502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bryan, M. L., Knutson, H. A., Howard, A. W., et al. 2016, ApJ, 821, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A. S. 2014, Nature, 513, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubbard, W. B., Lunine, J. I., & Liebert, J. 2001, Rev. Mod. Phys., 73, 719 [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, Protostars and Planets VI, 619 [Google Scholar]
- Correia, A. C. M. 2009, ApJ, 704, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2005, A&A, 440, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2009, A&A, 496, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2014, A&A, 562, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Santerne, A., Almenara, J.-M., et al. 2016, MNRAS, 458, 4025 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Almenara, J. M., Santerne, A., et al. 2014, MNRAS, 441, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ecuvillon, A., Israelian, G., Santos, N. C., et al. 2004, A&A, 426, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farrés, A., Laskar, J., Blanes, S., et al. 2013, Celest. Mech. Dyn. Astron., 116, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, Y. K., Wright, J. T., Nelson, B., et al. 2015, ApJ, 800, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Marmier, M., Bonfils, X., et al. 2010, A&A, 513, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figueira, P., Faria, J. P., Delgado-Mena, E., et al. 2014, A&A, 570, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fortier, A., Beck, T., Benz, W., et al. 2014, in SPIE Conf. Ser., 9143, 2 [Google Scholar]
- Forveille, T., Bonfils, X., Lo Curto, G., et al. 2011, A&A, 526, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gettel, S., Charbonneau, D., Dressing, C. D., et al. 2016, ApJ, 816, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Boisse, I., Dumusque, X., & Lovis, C. 2014, A&A, 566, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, G., Carlson, M. K., & Tobin, R. W. 2010, MNRAS, 403, 1368 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kipping, D. M., et al. 2011, ApJ, 728, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., Hersant, F., & Pierens, A. 2015, ApJ, 800, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 724, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, S. R., Thirumalachari, B., Henry, G. W., et al. 2016, ApJ, 820, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D, 67, 257 [Google Scholar]
- Laskar, J., Boué, G., & Correia, A. C. M. 2012, A&A, 538, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Dawson, R. I., & Tremaine, S. 2014, Nature, 513, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Isaacson, H., Howard, A. W., et al. 2014, ApJS, 210, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Mardling, R. A. 2007, MNRAS, 382, 1768 [NASA ADS] [Google Scholar]
- Martins, J. H. C., Santos, N. C., Figueira, P., et al. 2015, A&A, 576, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Lovis, C., & Santos, N. C. 2014, Nature, 513, 328 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Melo, C., Santos, N. C., Pont, F., et al. 2006, A&A, 460, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melo, C., Santos, N. C., Gieren, W., et al. 2007, A&A, 467, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Crida, A., Levison, H. F., & Gomes, R. 2007, AJ, 134, 1790 [NASA ADS] [CrossRef] [Google Scholar]
- Moriarty, J., & Ballard, S. 2015, ArXiv e-prints [arXiv:1512.03445] [Google Scholar]
- Mortier, A., Santos, N. C., Sozzetti, A., et al. 2012, A&A, 543, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Lo Curto, G., Mayor, M., et al. 2015, A&A, 576, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, G. 2013, A&A, 551, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Rupprecht, G., et al. 2002, The Messenger, 110, 9 [NASA ADS] [Google Scholar]
- Perrier, C., Sivan, J.-P., Naef, D., et al. 2003, A&A, 410, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perruchot, S., Kohler, D., Bouchy, F., et al. 2008, in SPIE Conf. Ser., 7014, 0 [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Latham, D. W., Vanderspek, R. K., et al. 2010, in Bull. Am. Astron. Soc., 42, 215 [Google Scholar]
- Rowan, D., Meschiari, S., Laughlin, G., et al. 2016, ApJ, 817, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2015, MNRAS, 451, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Moutou, C., Tsantaki, M., et al. 2016, A&A, 587, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Adibekyan, V., Mordasini, C., et al. 2015, A&A, 580, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Brandl, B. R., de Kok, R. J., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Udry, S., & Santos, N. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., & von Braun, K. 2009, ApJ, 694, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Libr., 350 [Google Scholar]
All Tables
Radial velocities (RV) for HD 219828 together with the respective barycentric Julian dates, errors, and instrument used.
List of free parameters and respective priors used in the MCMC analysis of the radial velocities.
Orbital parameters for the two Keplerian solutions and the derived planet minimum mass.
All Figures
 |
Fig. 1 Top and middle plots: phase-folded radial-velocity curves and data for planets b and c, respectively. Bottom: combined orbital solution of planets b and c as a function of time. Residuals of the complete fit are presented at the bottom of each diagram. |
| In the text | |
 |
Fig. 2 Periodograms of the radial-velocity residuals to the two-Keplerian fit and of the raw values of FWHM, BIS, and |
| In the text | |
 |
Fig. 3 Detection limits for additional planets in the system. |
| In the text | |
 |
Fig. 4 Stability analysis of the nominal fit of the HD 219828 planetary system (Table 5). For fixed initial conditions, the phase space of the system is explored by varying the semi-major axis ab and eccentricity eb of the inner planet. The step size is 10-2 in eccentricity, and 5 × 10-3 (top) or 2 × 10-4 AU (bottom) in semi-major axis. For each initial condition, the system is integrated over 103 yr and a stability criterion is derived with the frequency analysis of the mean longitude (Laskar 1990, 1993). As in Correia et al. (2005, 2009, 2010), the chaotic diffusion is measured by the variation in the frequencies. The red zone corresponds to highly unstable orbits, while the dark blue region can be assumed to be stable on a billion-year timescale. |
| In the text | |
 |
Fig. 5 Evolution of the eccentricity of the inner planet with time, starting with the orbital solution from Table 5. The red line gives the complete numerical solution, while the black dashed curve is obtained with the linear approximation (Eq. (1)). |
| In the text | |
 |
Fig. 6 Long-term evolution of the eccentricity of the inner planet with time, starting with the orbital solution from Table 5 and including tidal effects. The eccentricity stabilises around eb = 0.00096, in perfect agreement with the prediction from the secular linear model (Eq. (1)). |
| In the text | |
 |
Fig. 7 Distribution of mass ratios for all multi-planet systems listed in exoplanet.eu. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


