| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628134 | |
| Published online | 22 August 2016 | |
A reproducible method to determine the meteoroid mass index⋆
1 Department of Physics and
AstronomyUniversity of Western Ontario, London, ON, N6A
3K7, Canada
e-mail: ppokorn2@uwo.ca
2 Centre for Planetary Science and
Exploration, University of Western Ontario, London, ON N6A 3K7
Ontario,
Canada
Received:
14
January
2016
Accepted:
18
April
2016
Context. The determination of meteoroid mass indices is central to flux measurements and evolutionary studies of meteoroid populations. However, different authors use different approaches to fit observed data, making results difficult to reproduce and the resulting uncertainties difficult to justify. The real, physical, uncertainties are usually an order of magnitude higher than the reported values.
Aims. We aim to develop a fully automated method that will measure meteoroid mass indices and associated uncertainty. We validate our method on large radar and optical datasets and compare results to obtain a best estimate of the true meteoroid mass index.
Methods. Using MultiNest, a Bayesian inference tool that calculates the evidence and explores the parameter space, we search for the best fit of cumulative number vs. mass distributions in a four-dimensional space of variables (a,b,X1,X2). We explore biases in meteor echo distributions using optical meteor data as a calibration dataset to establish the systematic offset in measured mass index values.
Results. Our best estimate for the average de-biased mass index for the sporadic meteoroid complex, as measured by radar appropriate to the mass range 10-3 > m > 10-5 g, was s = −2.10 ± 0.08. Optical data in the 10-1 > m > 10-3 g range, with the shower meteors removed, produced s = −2.08 ± 0.08. We find the mass index used by Grün et al. (1985) is substantially larger than we measure in the 10-4 < m < 10-1 g range.
Key words: meteorites, meteors, meteoroids
Our own code with a simple manual and a sample dataset can be found here: ftp://aquarid.physics.uwo.ca/pub/peter/MassIndexCode/
© ESO, 2016
1. Introduction
A fundamental quantity of the dust/meteoroid environment in the solar system is the number distribution of particle sizes with mass. The mass or size frequency distribution (hereafter MFD, SFD respectively) of meteoroids provides insight into the origin, evolution, and eventual destruction of particles in planetary systems. In particular, the collisional lifetime of meteoroids is intimately linked to their present number-mass distribution, and this lifetime is central to dynamical models describing the meteoroid environment (Nesvorný et al. 2011). Moreover, knowledge of the meteoroid mass/size frequency distribution is key to an interpretation of optical and infrared observations of the zodiacal cloud (Nesvorný et al. 2010), the total meteoroid mass influx at the Earth (Plane 2012), optical and radar meteor flux estimates, based on observed rates (Koschack & Rendtel 1990; Kaiser 1960) and empirical models of the interplanetary meteoroid environment (Grün et al. 1985).
Direct measurement of the SFD/MFD is difficult at small meteoroid sizes. Exoatmospheric detection of meteoroids is currently limited to objects of roughly 1 m and larger (Harris & D’Abramo 2015), although meaningful direct estimates of the NEA (Near-Earth asteroid) SFD are not possible below a few tens of meters in size owing to the small number of statistics. The SFD/MFD at smaller meteoroid sizes must be inferred from statistical measurements.
Typically, the MFD/SFD is treated as a free parameter in models and adjusted to fit observations (e.g. Nesvorný et al. 2010). More direct estimates of the MFD may be made through meteor observations in the Earth’s atmosphere, microcrater counting on lunar samples (Morrison & Zinner 1977), or from in situ measurements (Grün et al. 2001).
It is typically assumed that the number of meteoroids, dN, which have mass between M and M + dM, follows a single mass frequency distribution (MFD), 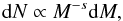 (1)where the exponent s, the differential mass index is typically between 1.5−2.5 (e.g. Jones 1968). Integrating Eq. (1) we have the total number of meteoroids with mass between M1 and M2 as
(1)where the exponent s, the differential mass index is typically between 1.5−2.5 (e.g. Jones 1968). Integrating Eq. (1) we have the total number of meteoroids with mass between M1 and M2 as ![\begin{equation} N(M,\alpha) \propto \int_{M_1}^{M_2}{M^{-s}\mathrm{d}M} = \frac{1}{\alpha} \left[M_2^{-\alpha}-M_1^{-\alpha}\right] , \label{EQ_2} \end{equation}](/articles/aa/full_html/2016/08/aa28134-16/aa28134-16-eq15.png) (2)where α is the cumulative mass index distribution exponent and α = s − 1. Usually, we consider M2 to be orders of magnitude larger than M1; theoretically M2 → ∞, thus Eq. (2) could be rewritten as follows:
(2)where α is the cumulative mass index distribution exponent and α = s − 1. Usually, we consider M2 to be orders of magnitude larger than M1; theoretically M2 → ∞, thus Eq. (2) could be rewritten as follows:  (3)where N is the total cumulative number of meteoroids with mass larger than M. The meteoroid population may also be defined by the differential size frequency distribution, such that the number of particles, dN, with radius between r and r + dr is given by
(3)where N is the total cumulative number of meteoroids with mass larger than M. The meteoroid population may also be defined by the differential size frequency distribution, such that the number of particles, dN, with radius between r and r + dr is given by 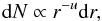 (4)and where u is the differential size index and u = 3s − 2 (McDonnell et al. 2001). For a system in collisional equilibrium, where it is assumed all meteoroids have the same strength, s = 11 / 6 (Dohnanyi 1969), while s = 2 represents a meteoroid distribution where mass is equally distributed per decade of mass. Physically, the smaller the value of s is, the greater the proportion of large meteoroids in a distribution. Typical values for s near the time of maximum of major meteor streams are 1.5–1.9 from both radar (Jones 1968) and visual measurements (McBeath 2014) at mm sizes. The sporadic background, in contrast, is typically found to be richer in smaller meteoroids than showers, with s ranging from 2−2.5 (e.g. Hughes 1978; Thomas et al. 1988; Blaauw et al. 2011) at radar masses (sub-mm sizes to tens of microns).
(4)and where u is the differential size index and u = 3s − 2 (McDonnell et al. 2001). For a system in collisional equilibrium, where it is assumed all meteoroids have the same strength, s = 11 / 6 (Dohnanyi 1969), while s = 2 represents a meteoroid distribution where mass is equally distributed per decade of mass. Physically, the smaller the value of s is, the greater the proportion of large meteoroids in a distribution. Typical values for s near the time of maximum of major meteor streams are 1.5–1.9 from both radar (Jones 1968) and visual measurements (McBeath 2014) at mm sizes. The sporadic background, in contrast, is typically found to be richer in smaller meteoroids than showers, with s ranging from 2−2.5 (e.g. Hughes 1978; Thomas et al. 1988; Blaauw et al. 2011) at radar masses (sub-mm sizes to tens of microns).
Historically, the sporadic mass index was estimated from the distribution of photographic meteor magnitudes. Hawkins & Upton (1958) used Super-Schmidt camera observations to estimate s = 2.34, a value widely adopted in subsequent literature (e.g. Grün et al. 1985). However, using a different set of Super-Schmidt meteors compiled by Dohnanyi (1967), produced an independent estimate of s ~ 2, while Erickson (1968) found s = 2.21, emphasizing the sensitivity of s to both the data used and the analysis methodology. More recently, radar measurements (Baggaley 1999; Galligan & Baggaley 2004) find s ~ 2 as well, albeit for much smaller masses than for Super-Schmidt data (gram sized vs. microgram). That the mass index changes with particle size is unsurprising, but the disparity in measured values for s found in the literature (see Blaauw et al. 2011, for a good summary) makes disentangling true variations with method- or equipment-specific differences challenging.
Here we present an automated, objective technique for the measurement of meteoroid mass indices, with appropriate uncertainty bounds. We apply this approach to both radar data and a suite of previously reduced optical meteor observations with the goal of establishing a best-estimated value for s for the sporadic background at ~mg to μg masses. We extend earlier work by Blaauw et al. (2011) who also used data from the Canadian Meteor Orbit Radar (CMOR) to estimate s by quantifying the role of systematic biases in mass-index measurements from radar data, as first discussed by Jones (1968). We empirically test these biases directly using known height distributions from optical data, applying equivalent attenuation to the height distributions and by comparing results across multiple frequencies, providing both a best global estimate for s and its potential temporal variation.
2. Measuring meteoroid mass indices with radar: theoretical considerations
Meteor radar echoes do not produce direct measurements of an individual meteoroid mass. Rather, some assumptions and model interpretations are required to convert the returned radar signal scattered from electrons produced during the ablation phase of meteoroid entry to some equivalent estimated mass. Here we focus on the measurement of mass indices from the meteor amplitude returns recorded by transverse scattering radars. Radar meteoroid mass distributions may also be estimated by measuring the duration distribution of long-lived (overdense) echoes (Baggaley 2002) as well as the returned power from meteor head echoes (Close et al. 2005).
For a backscatter radar, ignoring the effects of fragmentation, it can be shown (McKinley 1951) that the amplitude received from an underdense meteor trail in a specular scattering is proportional to the electron line density q averaged over the first Fresnel zone along the trail. This is typically a distance of order of a kilometer (or less). Typical meteor trails are an order of magnitude larger than the first Fresnel zone and hence the scattering point may fall randomly along the ionization profile, depending on the scattering geometry. In a statistical sense, it has been previously shown (Jones 1968; McIntosh & Simek 1969; Blaauw et al. 2011; Weryk et al. 2013) that the amplitude distribution can be used as a proxy for the initial meteoroid mass such that the distribution of radar echo amplitudes follows 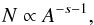 (5)where A is the peak radar amplitude of the echo and N is the cumulative number of echoes with peak amplitude greater than A, assuming there is no change in s across the dynamic range of masses encompassed by the equivalent amplitude range of the radar. Hence, by recording the amplitude distribution from a shower or for the sporadic background, the slope of a plot of log N vs. log A will simply be 1 − s.
(5)where A is the peak radar amplitude of the echo and N is the cumulative number of echoes with peak amplitude greater than A, assuming there is no change in s across the dynamic range of masses encompassed by the equivalent amplitude range of the radar. Hence, by recording the amplitude distribution from a shower or for the sporadic background, the slope of a plot of log N vs. log A will simply be 1 − s.
Complicating this simple picture are biases inherent to meteor radar echo detection. Though several effects tend to reduce both the echo rate and individual echo amplitudes (see Galligan & Baggaley 2004, for an excellent summary) the most important of these is typically produced by the initial trail radius (ITR). This effect, produced when scattered radio waves from the front and back of the meteor trail scatter out of phase and reduce the power reflected back to the radar (Campbell-Brown & Jones 2003), tends to preferentially hide smaller and faster meteoroids from detection as these ablate at higher altitudes (Jones & Campbell-Brown 2005). The net effect is that the measured mass index is lower than the true mass index. Both Jones (1968) and McIntosh & Simek (1969) recognized this bias and attempted to make corrections based on estimates of the initial radius that was then available and assuming single body ablation. They found that in some cases the correction from apparent to true mass index could be as much as + 0.5, a significant difference. We explore this effect on our estimates to quantify the systematic errors using a range of modern estimates for the initial radius.
3. The Canadian Meteor Orbit Radar: equipment and analysis procedures
The majority of the data for this study was gathered between 2011–2015 by the Canadian Meteor Orbit Radar (CMOR). Technical details of CMOR can be found elsewhere (Jones et al. 2005; Brown et al. 2008), but we summarize the main features of the system relevant to this work. CMOR is a tri-frequency broad beam (55 degree width to 3 dB points) vertically directed radar, simultaneously operating at 17.45 MHz, 29.85 MHz, and 38.15 MHz with 6 kW, 12 kW, and 6 kW peak power respectively. All three systems have interferometric capability based on the Jones et al. (1998) crossed-antenna receiver array design. This allows CMOR to constrain the direction to each detected echo, with sub-degree accuracy for each system. All three systems operate at 532 pulses per second with 3 km range sampling. Echo detection is performed by taking the incoherent sum of 14 pulses and searching for excursions in signal amplitude at each range gate that are more than 8σ above the noise background. This typically results in a detection every ~4 s at 29.85 MHz and every ~6 s at 38.15 MHz. Each detection has a start time, peak amplitude, echo interferometric direction, height, range, and noise level recorded. Details of the interferometry algorithms used, the basis for uncertainty estimates and the detection algorithm are described in Weryk & Brown (2012).
The threshold mass of meteoroids detected depends on speed, but the limiting value at 30 km s-1 for single-station detection is slightly larger than 10-8 kg corresponding to particles with diameter above 0.3 mm. We further filter the raw detections by retaining only echoes with heights between 70–120 km. Detections are binned per degree of solar longitude. Figure 1 shows an example of the resulting logarithm of the cumulative number of all echoes log N vs. log A for one solar longitude bin as measured at 29.85 MHz. In this figure we also select only meteor echoes that have interferometric directions within ±5 degrees perpendicular to the Quadrantid shower.
 |
Fig. 1 Logarithm of the cumulative number of echoes log N vs. log A for one solar longitude bin (λ = 283° in 2012) as measured at 29.85 MHz for probable Quadrantid echoes. |
At the lowest amplitudes, the cumulative distribution rolls-off to a near constant value as low amplitude events are missed. In practice, this occurs near an amplitude of ~103 for CMOR. If all echoes were underdense, the log N vs. log A distribution should produce a straight line of slope 1 − s as A ∝ q ∝ m. However, we see in Fig. 1 significant curvature to the log N vs. log A line with pronounced steepening of the slope at higher amplitudes. This is due to the transition between predominantly underdense echoes (where A ∝ q) at lower amplitudes and overdense echoes (where A ∝ q0.25) at higher amplitudes. When the latter regime is reached, the apparent slope changes more closely to 4(1 − s). CMOR’s limiting sensitivity is only slightly more than one decade in mass into the underdense regime, so only the leftmost part of the plot is dominated by underdense echoes. The percentage of echoes that have overdense or transition line densities is further smeared toward the left part of the plot by inclusion of a broad set of ranges in the distribution. As the echo range increases, the overdense/underdense limiting amplitude becomes smaller and the plot curvature rolls leftward.
Blaauw et al. (2011) recognized this effect in an earlier CMOR analysis and found that it could be minimized by selecting only echoes with ranges between 110–130 km from the radar. This range filter together with the broad CMOR gain pattern tends to freeze the amplitude at which the underdense-overdense transition occurs near ~104 amplitude units. Figure 2 shows the same data as Fig. 1, but with the 110–130 km range filter imposed. All subsequent number-amplitude analyses use this range filtering.
The flat underdense portion of the plot becomes clearly visible. However, the exact amplitude limits where a fit should be applied and the resulting value for s have historically been made through subjective means of a least-squares fit (e.g. McIntosh & Simek 1969; Blaauw et al. 2011). As this is a cumulative plot, the individual data points are correlated and thus the uncertainty found from a least-squares fit is actually a significant underestimate of the true uncertainty. The real uncertainty is dominated by the amplitude limits chosen for the fit. In this respect, an objective technique is required to fit the flat underdense portion, as well as provide a more physically meaningful estimate of uncertainty.
 |
Fig. 2 Same echoes as Figure 1, but now with a 110–130 km range filter imposed. |
4. Analysis methodology: MultiNest
For the estimation of uncertainty of our cumulative echo number vs. amplitude fits, we adopted a software package called MultiNest (Feroz & Hobson 2008; Feroz et al. 2009, 2013). MultiNest is a Bayesian inference tool with the ability to calculate the evidence, with an associated error estimate, and provides posterior samples even for complex multiple-mode distributions1.
To use Multinest, we have to define our problem and provide the likelihood function that will allow the code to compare different sets of solutions. Since we assume that the distribution of the cumulative number of echoes above a certain amplitude threshold, N, follows a single power-law our task is reduced to fitting the first-degree polynomial (line) to a collection of data points in log-log space. The first degree polynomial in our case is defined as: log 10N = f(A) = alog 10A + b, with the slope a (equivalent to 1 − s if the fit is entirely in the underdense regime) and the offset b. Fitting the first degree polynomial to a selected dataset is usually a simple task, however, our situation is more complex. Owing to different proxies, observing biases/limitations and echo geometries, we do not know where the lower and upper boundaries of our amplitude fitting range are located. Thus, we define x1 as the lower amplitude bound, and x2 as the upper amplitude bound of our fitting range. Our originally two-dimensional problem becomes four-dimensional, with one dimension being constrained since x1<x2. After several initial tests, we found that logarithmic binning (i.e. uniform binning of echo amplitudes in log-log space) of A provides two significant benefits: (1) the fitting procedure runs faster, where the speedup depends on the number of meteors in the initial data set; and (2) a natural weighting can be applied to every bin, based on the number of echoes in a given bin.
To test the goodness of the fit we introduce a modified version of a weighted chi-squared: ![\begin{equation} \chi^2 = \left( \frac{N_\mathrm{tot}}{N_\mathrm{bin}} \right)^{2} N_\mathrm{obs} \sum_{n=1}^{N_\mathrm{bin}} \frac{ \left[ \log_{10}N(n) - (a \log_{10} A(n) + b) \right]^2 } {\sigma^2(n)} \,, \label{EQ_6} \end{equation}](/articles/aa/full_html/2016/08/aa28134-16/aa28134-16-eq57.png) (6)where Ntot is the total number of bins in the dataset, Nbin is the number of bins within the range (x1,x2), Nobs is the number of observed meteor echoes, n is the index of the particular bin within the range (x1,x2), A(n) is the peak amplitude of the bin, and σ2 is the variance equal to the number of events in a particular bin. We added the first coefficient in Eq. (6) to prioritize fitting over the longest range in (x1,x2) possible, while maintaining considerable goodness of the fit. Without this additional weight, the best solution is usually the shortest interval that is allowed by our fitting settings (e.g. disregarding fits with five or less bins). We tested different powers of the (Ntot/Nbin) term and found the most consistent results were achieved with a square term. For CMOR, our 15-bit ADC (analog-to-digital converter) allows amplitude ranges from 1 to 32 768 (i.e. from 100 to 104.515). This range is divided into 5 000 uniformly spaced bins in logarithmic space.
(6)where Ntot is the total number of bins in the dataset, Nbin is the number of bins within the range (x1,x2), Nobs is the number of observed meteor echoes, n is the index of the particular bin within the range (x1,x2), A(n) is the peak amplitude of the bin, and σ2 is the variance equal to the number of events in a particular bin. We added the first coefficient in Eq. (6) to prioritize fitting over the longest range in (x1,x2) possible, while maintaining considerable goodness of the fit. Without this additional weight, the best solution is usually the shortest interval that is allowed by our fitting settings (e.g. disregarding fits with five or less bins). We tested different powers of the (Ntot/Nbin) term and found the most consistent results were achieved with a square term. For CMOR, our 15-bit ADC (analog-to-digital converter) allows amplitude ranges from 1 to 32 768 (i.e. from 100 to 104.515). This range is divided into 5 000 uniformly spaced bins in logarithmic space.
Multinest effectively searches through our four-dimensional space using a set prior distribution and calculates Bayesian evidence with very high accuracy. Our tests indicate that even when the prior distribution is very vague the code is still able to converge to the correct solution. For the slope a we inspect the range (− 2,0), which translates to the differential mass index range s = (3,1) that covers all reported meteor mass indices (e.g. Elford 1968). The selection of the offset b is arbitrary, depending on the number of observed meteor echoes in the dataset simply reflecting the number of observed meteor echoes in the dataset. For CMOR with echo numbers spanning from 100 up to 5 million. we found the usable range to be b = (1,12). For x1 and x2 (i.e. log A), we use the range (2,5), since there were no echoes with amplitude A lower than 100 since this is well below the noise floor for CMOR. For all four priors, we use a uniform distribution within their ranges.
From our tests, we also found the optimal internal settings required to ensure MultiNest would converge to good solutions. The maximum number of live points is set to 1600. We find this number is the best trade-off between accuracy of the solution and the speed of the code. The evidence tolerance factor is set to 0.01. We do not limit the maximum number of iterations that the code is allowed to perform. In some more complicated cases, or for very bad datasets, the code might be very slow in finding the solution; however, we did not encounter any infinite loops or runs longer than a few hours.
The final result of the search is a set of equally weighted posterior samples that enables us to determine parameters for the best fit, the standard deviations of the parameters, and also the local logarithmic evidence of the fit. Figure 3 shows results of the Multinest fitting procedure applied to the Quadrantid meteor shower in 2012. Here all echoes recorded on 29.85 MHz between λ = 282° and λ = 284° that have echo directions within 5 degrees of specular to the Quadrantid radiant were selected. This procedure includes some sporadic meteors, but given the strength of the Quadrantids at maximum, the majority of echoes selected using this specular condition should be from the shower as shown by Blaauw et al. (2011).
Figure 4 shows the distribution of weighted posterior samples for all parameters, together with correlations among all parameters for the data in Fig. 3. The resulting fit in this case is well determined with a very low slope uncertainty, a fact visually apparent from Fig. 4, since the curve exhibits a very long linear portion without significant rounding. Additionally, all parameters are tightly correlated, an indication of a very good fit.
 |
Fig. 3 Logarithm of the cumulative number of observed meteors N versus the logarithm of the amplitude A for all Quadrantid radar meteor echoes in 2012 detected during the three solar longitudes 282°−284° by CMOR. Black dots represent individual echoes and the green line is the best linear fit to the data found by MultiNest. |
 |
Fig. 4 Posterior distribution of four parameters used in our fitting procedure as applied to the Quadrantids meteors shower. Histograms in the outer plots show a distribution of statistically equivalent solutions. The plots inside the triangular structure show projections of these solutions onto two-dimensional planes of two selected parameters, where the color coding represents the density of solutions (increasing in density from blue to red). The graphs (left to right columns) show the distribution and correlation of the following parameters: (1) slope a; (2) offset b; (3) lower bound x1; and (4) upper bound x2. |
5. Results and discussion
5.1. One year of data from 29.85 MHz and 38.15 MHz
We apply our method to investigate the annual variation of the mass index s of the sporadic meteoroid background during 2014, as measured independently by the 29.85 MHz and 38.15 MHz CMOR radars. In our analysis we use all meteors recorded by the main station without any constraints for the radiant position or incident velocity, an approach which provides very high statistics (of order 104 or more total echoes each day, but only 20% of these fall into our 110–130 km range bin) but is not suitable for isolating activity from meteor showers or specific sporadic meteor sources. Rather, these measurements represent the overall mass index of the entire meteoroid population on average to the limiting sensitivity of CMOR.
In Fig. 5 we show the measured mass index s (black solid line in Fig. 5) for every degree of the solar longitude λ in 2014 with its associated uncertainty (blue error bars in Fig. 5) based on our analysis, which is applied to data collected by the 29.85 MHz radar. We also show the number of observed meteors (in range bins between 110–130 km) for every degree of λ (green bars with the corresponding y-axis on the right side in Fig. 5) during 2014. Several days showed local interference, which dramatically increased the number of raw observed meteors (green spikes in Fig. 5); we excluded such days from our analysis (gaps in the black solid line in Fig. 5).
We find that s remains almost constant during the whole year, except for a noticeable dip at λ = 250°. Averaging these individual values for the whole year produces s = −2.024 ± 0.064, where the error is the standard deviation of measured values. If we exclude the region around the observed dip (λ = 230°−270°), we obtain a slightly different average value s = −2.036 ± 0.056. Typical individual solar longitude uncertainties of s throughout the year are between 0.07–0.15.
As an independent check of these results, we performed the same analysis for 2014 on data gathered by the 38.15 MHz radar (Fig. 6). The overall behavior of the mass index during the year is very similar to the 29.85 MHz system with most values agreeing within uncertainty (blue error bars in Fig. 6). One difference, however, is that the dip observed or the 29.85 MHz radar is less noticeable and shifted by approximately 20° to λ = 270°. The average value for the whole year is s = −2.063 ± 0.063; while excluding values of the region around the observed dip (λ = 250°−290°) produces s = −2.071 ± 0.060. Individual uncertainties in the value of s throughout the year range between 0.8–0.15. These values agree within uncertainty with the values found for 29.85 MHz.
As a final check on these average annual values that were computed as a mean of individual daily mass indices, we stacked all data measured during 2014 by the 29.85 MHz radar, which produced a single distribution with more than 750 000 measured echoes. The resulting mass index s for the stack data is s = −2.033 ± 0.08 identical within uncertainties of our daily average for 2014.
 |
Fig. 5 Mass index distribution throughout the whole year 2014 for the sporadic meteoroid complex observed by the 29.85 MHz CMOR radar. Blue points represent the mass index s for a given one degree bin in the solar longitude, where error bars are obtained from the Bayesian posterior equal weight distribution. Green boxes represent the number of meteors in each of one degree bins in the solar longitude. The intervals with large green spikes represent interference and are removed from the analysis. |
 |
Fig. 6 Same as Fig. 5, but now for 38.15 MHz single station observations. From the general behavior we see that 29.85 MHz and 38.15 MHz single station results are comparable and agree well within determined uncertainty ranges. We note that the mass index for both frequencies has almost identical temporal variations, which agrees with variations of the sporadic meteoroid background previously reported by Blaauw (2010). |
5.2. Multi-year data comparison
We expect the mass index to show similar values and variations year-to-year. This expectation is based on the stationarity of the overall sporadic background which, on dynamical grounds, we do not expect to show changes in timescales as short as a few years. However, other effects may have influence our measured mass index values, including instrumental effects and long-term changes in the upper atmosphere (particularly its mass density). This can affect the ablation behavior of meteoroids (notably their trail length) and hence their radar detectability, an effect long recognized as a bias in meteor radar data (Ellyett 1977). Indeed, such long-term atmospheric density changes have been inferred from CMOR measurements (Stober et al. 2014).
However, Stober et al. (2014) and a similar study from the southern hemisphere by Lima et al. (2015) suggest that, during the whole solar cycle, the neutral air density varies by only a few percent, resulting in an annual mean meteor peak height as measured by radar changing by no more than one kilometer. Between 2011–2015, solar activity as measured by the 10.7 cm flux increased by only 20% with the most pronounced increase towards the end of 2015 (Stober et al. 2014). It is clear that changes in the mass density of the upper atmosphere affect meteor echo counts (Lindblad 1968; Hughes 1976; Ellyett & Kennewell 1980; Elford 1980; Lindblad 2003) and likely also affect the begin and end heights of meteor ablation (Pellinen-Wannberg et al. 2010), but the solar cycle impact on mass index measurements by radar is yet to be determined.
The current CMOR detection and radar-processing pipeline for the 29.85 MHz has been stable since 2011, hence we expand our analysis to 2011–2015 data to confirm if the same general intrannual trends repeat as expected, if the signal is mainly reflecting intrinsic changes in the mass index.
Figure 7 shows the mass index s variation with the solar longitude (dots color-coded by years) for years 2011–2015, as measured by the 29.85 MHz radar. To increase the readability of the plot, we omitted error bars for each recorded s, noting that uncertainties remain very similar to the year 2014. We introduce a moving average with a 10° sliding window (solid lines color-coded by years) to better follow the data trend. Examination of Fig. 7 leads us to conclude: (a) the mass index s retains its global features during 2011–2015, though experiencing some fluctuations in absolute value; (b) the dips observed in 2014 (see Fig. 5) are not artifacts and appear during previous years as well. We suggest the intrannual fluctuations are due to strong showers in the data, while the absolute interannual changes in the apparent mass index are likely caused by solar activity affecting the mass density of the atmosphere at meteor ablation heights.
 |
Fig. 7 Variations of the mass index measured over five consecutive years 2011–2015 by the 29.85 MHz CMOR radar. Color-coded dots represent the mass index for each 1° solar longitude bin and color-coded lines show the moving average with 10° window averages. Arrows with labels denote maxima of Arietids (ARI), Southern Delta Aquariids (SDA), and Geminids (GEM) meteor showers. |
From Fig. 7, we see that some dips reappear each year at exactly the same time; these dips originate from the strongest annual meteor showers, which produce a large number of all detected echoes at the time of their maximum. Using the results of Brown et al. (2010), we readily associate the dip at λ = 45° with the Eta Aquariids, λ = 81° with the Daytime Arietids (ARI), the dip at λ = 126° with the South Delta Aquariids (SDA), and the final dip at λ = 261° with the Geminids (GEM). Indeed, these four showers were found by Brown et al. (2010) to be among the top five strongest detected by CMOR. Table 1 summarizes the overall average mass index for each year, as well as the cumulative index for all data. Our overall best fit for all 29.85 MHz data is s = −2.015 ± 0.072 (Fig. 8).
Data measured at 38.15 MHz are shown in Fig. 9 for the years 2014–2015. The raw data-processing pipeline for 38.15 MHz included many non-specular trails prior to Nov. 2013 so we exclude earlier data for comparison with 29.85 MHz. The Daytime Arietids at λ = 81° are less noticeable than on 29.85 MHz, while the South Delta Aquariids at λ = 126° result in a significant drop in s. The 2014 and 2015 average values from Table 1 for 38.15 MHz are similar to the overall average of s = −2.080 ± 0.075.
We find 29.85 and 38.15 MHz produce similar mass indices, both as averages and as yearly distribution aggregates. This provides confidence that we are not heavily affected by frequency dependent biases in detection. Taken together, the raw radar best estimate for the global meteoroid background from CMOR multi-frequency data is s = −2.05 ± 0.08, which encompasses the spread in the means and the temporal variability.
The measured mass index for each year as a single aggregate distribution for 29 and 38 MHz.
5.3. Bias owing to initial trail radius effect on mass index measurement
Our previous result is the apparent mass index of the observed echo population. However, it is well known that the height distribution and flux measurements of underdense meteor echoes are biased owing to the initial trail radius (or echo height ceiling) effect (Jones & Campbell-Brown 2005). This effect results in severe attenuation of the reflected radio signal when the meteor trail dimension is comparable to the radar wavelength. In most cases, echoes with large radii relative to the radar wavelength go entirely undetected. One aspect of this effect is that even echoes that are detected will have their amplitudes damped relative to trails of the same electron line density with no initial radius and this may affect the apparent mass index (Jones 1968). The finite-velocity effect (Ceplecha et al. 1998) has a similar attenuation on forming trails, but is generally smaller in magnitude than the initial radius effect for CMOR and is ignored here (Campbell-Brown & Jones 2003).
Previous work has suggested theoretical corrections for apparent mass indices based on initial radius attenuation (Jones 1968; McIntosh & Simek 1969) but were based on single-body (non-fragmenting) assumptions about ablation. The results of these studies suggested that the apparent mass index would be an underestimate of the true mass index (possibly by as much as 0.5), primarily due to initial radius effects. However, actual meteoroid ablation is affected by fragmentation (Ceplecha et al. 1998) and the resulting influence on the mass index is less clear.
As a means for checking our mass determination technique and accuracy of our results without recourse to any model assumptions, we choose an empirical approach. We make use of optical meteor observations obtained by the Canadian Automated Meteor Observatory (CAMO) wide-field influx camera system (Weryk et al. 2013), an automated two-station video meteor system located in southern Ontario that has been operating since 2009. The limiting meteor magnitude of the CAMO influx system is +7M (Campbell-Brown 2015), which is similar to CMOR, based on simultaneous optical-radar meteor measurements (Weryk & Brown 2013).
 |
Fig. 8 Logarithm of the cumulative number of observed meteors N versus the logarithm of the amplitude A for all radar meteor echoes measured over five consecutive years 2011–2015 by the 29.85 MHz CMOR radar. Black dots represent individual echoes and the green line is the best linear fit to the data found by MultiNest. |
Our intention is to compare the mass and height distribution of all meteors measured by CAMO to obtain the population of meteors that CMOR should be able to observe if it were not affected by the initial trail radius effect, i.e. we take the CAMO influx height distribution to represent the true distribution that CMOR samples. Using the CAMO-observed height distribution, we apply the initial trail radius attenuation based on Jones & Campbell-Brown (2005) to the observed population of CAMO optical meteors and compare the results with radar meteors recorded by CMOR. Here we begin with the de-biased data set from the influx cameras as described in Campbell-Brown (2015) of 3437 manually measured meteors with masses in range 10-3 kg to 10-7 kg based on a constant luminous efficiency value of 0.7% (Campbell-Brown & Koschny 2004). In addition, we removed all shower meteors that match any of the established IAU (International Astronomical Union) Meteor showers. This left 3 106 meteors in our optical “sporadic” sample.
Figure 10 shows the logarithm of the cumulative number of these 3106 observed CAMO meteors versus the logarithm of meteoroid mass (black points). Applying our MultiNest fitting procedure to this distribution, we obtain s = −2.090 ± 0.045 (black solid line in Fig. 10). This value agrees within uncertainty with our results obtained from CMOR. This outcome suggests that the CMOR distribution is minimally affected by the height-ceiling effect. To check this assertion, we applied the attenuation to the echo amplitude caused by the initial trail radius to all the CAMO meteors following the procedure outlined in Jones & Campbell-Brown (2005), using the optically measured speed and height of peak luminosity of the meteor (blue points in Fig. 10). Here we use the photometric mass of the CAMO meteoroids as a proxy for the peak radar echo amplitude each meteor would produce in the absence of any attenuation effects. Taking the original CAMO distribution and applying the initial radius attenuation produces a small offset in the slope of the mass distribution, which modifies the apparent mass index to the slightly smaller value of s = −2.043 ± 0.025 (blue solid line in Fig. 10). This agrees within the respective uncertainties of the previously obtained values from radar measurements. Finally, we used the measured CAMO peak brightness alone to simulate the initial radius correction, excluding the effect of the measured velocity (green points in Fig. 10). The resulting change is again negligibly different from the measured radar values, with a resulting index s = −2.053 ± 0.026.
 |
Fig. 9 Same as Fig. 7, but now for the years 2014–2015 for 38.15 MHz. Years 2011–2013 are unavailable owing to a change in the software detection, which resulted in many non-specular overdense echoes being selected, biasing the mass index value to lower values. |
Based on our empirical checks, the attenuation owing to the initial trail radius effect only has a minor influence on our measured mass index, since it tends to translate the entire curve rather than changing its slope significantly. This change should cause a systematic shift of no more than 0.05 to the larger values. Applying this shift in s to our best fit of observed radar-determined mass index gives us a so-called corrected value s = −2.10 ± 0.08.
However, the initial radius effect is important when considering the observed radar height distribution. We can use the CAMO height distribution as ground truth and then apply the attenuation based on peak brightness height and velocity measurements, and then compare the resulting height distribution with CMOR measurements. Figure 11 shows the height distribution of 3106 CAMO meteors (gray histogram), the equivalent effect of attenuation on this population if it were observed by CMOR (red histogram), and finally the observed height distribution of 1.5 million meteors measured at 29.85 MHz by CMOR in 2014 (blue histogram). The height distribution of CMOR meteors was normalized to match the maximum value of the attenuated population. While the observed CAMO height distribution is very different from observed CMOR echo height distribution, the fact that the corrected population is a reasonable match to the CMOR height distribution validates our earlier approach of simulating the effects of initial radius on the mass index. We note that the largest difference between the predicted CAMO-attenuated height distribution and the CMOR observed heights between 100–110 km may reflect larger initial radii at these heights than originally found by Jones & Campbell-Brown (2005). This would be consistent with recent optical measurements from Stokan & Campbell-Brown (2014), who measured much larger apparent initial radii at such heights.
5.4. Mass index comparison with earlier studies
The most recent study of the meteoroid environment mass index based on CMOR data comes from Blaauw et al. (2011). This study uses the same radar with 29.85 MHz frequency before it underwent a major upgrade that doubled its power. In principle, their findings should be similar to ours, since this upgrade decreased the limiting mass limit by only 40%. For the whole meteoroid complex during 2007–2010, Blaauw et al. (2011) find s = 2.17 ± 0.07, slightly higher than our value, but using a manual method for curve-fitting and a different meteor-echo detection code.
Many earlier measurements of the mass index from radar and optical measurements (Simek & McIntosh 1968) found values for s in the range 2.2−2.5 in our mass-magnitude range. The widely used interplanetary meteoroid model flux given by Grün et al. (1985) adopts the mass index s = 2.34 for the mass range from 10-5 to 102 g. This is based on the photographic meteor studies by Hawkins & Upton (1958) who found s = 2.34 ± 0.06, which was obtained by reducing and fitting a data set consisting of 300 brighter Super-Schmidt meteors. This is appropriate to meteors of −2 <MPh< + 3.5, corresponding to observed limiting masses of order 0.01–0.1g using the mass-magnitude-velocity relation of Jacchia et al. (1967) and a mass weighted mean speed of 17 km s-1 (Erickson 1968). This value was later used in a comprehensive study of Whipple (1967) and subsequently widely reproduced.
The direct comparison of our findings with the Grün curve is shown in Fig. 12. Here the top panel shows the original flux curve of Grün et al. (1985) appropriate to 1 AU from the Sun as a function of the meteoroid mass. The bottom panel of Fig. 12 shows the equivalent mass index s of the Grün curve (blue solid line) compared with our findings for CMOR s = −2.05 (green solid line) in the range 10-4.5 to 10-3.5 g, and with CAMO s = −2.08 (red solid line) in the range 10-3.6 to 10-0.6 g. Our data show a systematically shallower mass index compared to Hawkins & Upton (1958), as well as the Grun curve at our masses.
 |
Fig. 10 Logarithm of the cumulative number of observed meteors N relative to the logarithm of their mass for meteors observed with CAMO between 2009 and 2012. We show CAMO data not affected by the initial trail radius (black dots) correction with the best fit (black line). This is the true mass index. The distribution once the initial trail radius bias (blue dots) is applied retains an almost identical slope (blue line). We also show the effect of applying the initial radius bias with a velocity term to the distribution and find it produces a negligible difference (green dots and green for the best fit). |
 |
Fig. 11 Distribution of heights for uncorrected CAMO data (gray histogram), CAMO data corrected for the initial radius (red histogram), and the 29.85 MHz CMOR heights in 2014 (blue histogram) rescaled to match CAMO corrected distribution. The effect of the correction is evident, minimizing the contribution of meteors with higher heights while keeping meteors with lower heights untouched. |
 |
Fig. 12 Logarithm of cumulative particle flux at 1 AU distance from the Sun with respect to the logarithm of meteoroid mass adapted from Grün et al. (1985) (top panel). Mass index s for meteoroids at 1 AU distance from the Sun derived as the first derivative from the curve in the top panel (solid blue line) compared to the mass index s = 2.03 ± 0.01 for meteoroid environment measured by AMOR in 1995–1999 (Galligan & Baggaley 2004), mass index s = 2.05 ± 0.08 for background meteoroid environment from CMOR multi-frequency data, and with mass index s = 2.09 ± 0.05 derived from CAMO observations. |
Galligan & Baggaley (2004) examined more than half a million high-quality meteor echoes from the Advanced Meteor Orbit Radar (AMOR) and found s = −2.027 ± 0.006. AMOR had a limiting radio magnitude of +14, corresponding to a limiting mass of roughly 3 × 10-7 g, approximately two orders of magnitude lower than CMOR. Surprisingly, their value is very close to our results. We suggest that this implies the turnover to shallower values of the mass index, which only begins near m ~ 10-5 g in Grün et al. (1985), should actually occur at roughly an order of magnitude larger mass or that the asymptotic mass index at larger masses should be smaller than the canonical s = 2.34 value. Alternatively the absolute mass scales may be offset.
6. Conclusions
We have applied a new fully automated Bayesian-approach based on the MultiNest software package to the measurement of meteoroid mass indices. Application of this technique to CMOR echo amplitude distributions yields a mean overall value for the mass index of s = −2.05 ± 0.08, with a yearly variation showing an amplitude of ±0.1. We note that major apparent “dips” in the mass index throughout the year are correlated with a handful of the strongest showers, consistent with the fact that most meteor showers have much lower mass indices than the sporadic background (Jenniskens 2006).
We successfully applied our code on data from two single-station radars performing measurements at 29.85 and 38.15 MHz during 2011–2015. After applying several filters for the range and height of the meteor and removing other known biases, we obtained diurnal variations of the mass index s for the meteoroid complex seen by CMOR. The mass index undergoes noticeable variations that are beyond uncertainty ranges obtained by our algorithm, where several dips in the mass index value were associated with known major meteors showers (Fig. 7). The average value for the whole meteoroid complex for the 29.85 MHz radar is s = −2.015 ± 0.072, and for the 38.15 MHz radar s = −2.080 ± 0.075. Our adopted best fit observed that the radar-determined mass index is s = −2.05 ± 0.08.
Optical measurements from the influx system of CAMO produced a sporadic-only mass index of s = −2.08 ± 0.06. Applying initial radius biases to the CAMO “true” distribution suggests our radar mass index is minimally affected by ITR corrections, with a systematic shift to larger values of s of no more than 0.05, so that a final “corrected” mass index is best estimated as being s = −2.10 ± 0.08.
These numbers are within uncertainty ranges comparable with works of Blaauw et al. (2011) and Galligan & Baggaley (2004). Our mass index is shallower than that used in Grün et al. (1985) and we suggest that the turnover to shallower values of the mass index, which only begins near m ~ 10-5 g in Grün et al. (1985), should actually occur at roughly an order of magnitude larger mass or that the value for s at large mass should be smaller than the 2.34 value commonly quoted.
The MultiNest package can be downloaded at https://ccpforge.cse.rl.ac.uk/gf/project/multinest/
Acknowledgments
P.G.B. thanks the Canada Research Chair program. This work is supported in part by the Natural Sciences and Engineering Research Council of Canada and by the NASA Meteoroid Environment Office through NASA co-operative agreement NN15AC94A. We would like to thank Althea Moorhead and Laura Lenkić for helpful comments.
References
- Baggaley, W. 1999, Meteoroids 1998, 311 [Google Scholar]
- Baggaley, W. 2002, in Meteors in the Earth’s Atmosphere, eds. I. Murad, & E. Williams (Cambridge, UK: Cambridge Univ Press), 123 [Google Scholar]
- Blaauw, R. C. 2010, Masters Thesis, University of Western Ontario [Google Scholar]
- Blaauw, R. C., Campbell-Brown, M. D., & Weryk, R. 2011, MNRAS, 412, 2033 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. G., Weryk, R., Wong, D., & Jones, J. 2008, Icarus, 195, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. G., Wong, D., Weryk, R., & Wiegert, P. 2010, Icarus, 207, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-Brown, M. D. 2015, Planetary and Space Science, 1 [Google Scholar]
- Campbell-Brown, M. D., & Jones, J. 2003, MNRAS, 343, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 422, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W., et al. 1998, Adv. Space Res., 84, 327 [Google Scholar]
- Close, S., Oppenheim, M., Durand, D., & Dyrud, L. 2005, J. Geophys. Res., 110, 1 [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1967, ApJ, 149, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Dohnanyi, J. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Elford, W. 1968, Phys. Dyn. Meteors, 33, 352 [NASA ADS] [Google Scholar]
- Elford, W. 1980, in Solid particles in the solar system: symp. 90 organized by the IAU, in cooperation with COSPAR, held at Ottawa, Canada, August 27–30, 1979 (Springer), 101 [Google Scholar]
- Ellyett, C. 1977, J. Geophys. Res., 82, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Ellyett, C., & Kennewell, J. 1980, Nature, 287, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Erickson, J. E. 1968, J. Geophys. Res., 73, 3721 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., Cameron, E., & Pettitt, A. N. 2013, ArXiv e-prints [arXiv:1306.2144] [Google Scholar]
- Galligan, D. P., & Baggaley, W. 2004, MNRAS, 353, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Grün, E., Zook, H., Fechtig, H., & Giese, R. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Grün, E., Baguhl, M., Svedhem, H., & Zook, H. A. 2001, in In situ Measurements of Cosmic Dust, eds. E. Grün, B. A. S. Gustafson, S. Dermott, & H. Fechtig (Springer), 295 [Google Scholar]
- Harris, A., & D’Abramo, G. 2015, Icarus, 257, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkins, G., & Upton, E. 1958, ApJ, 128, 727 [Google Scholar]
- Hughes, D. 1976, in Cosmic Dust, ed. J. McDonnell, 123 [Google Scholar]
- Hughes, D. W. 1978, Meteors (John Wiley & Sons Ltd), 123 [Google Scholar]
- Jacchia, L., Verniani, F., & Briggs, R. E. 1967, in Smithson. Contrib. to Astrophysics, 139 [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge University Press) [Google Scholar]
- Jones, J. 1968, Can. J. Phys., 46, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J., & Campbell-Brown, M. D. 2005, MNRAS, 359, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J., Webster, A., & Hocking, W. 1998, Radio Science, 33, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J., Brown, P. G., Ellis, K. J., et al. 2005, Planet. Space Sci., 53, 413 [Google Scholar]
- Kaiser, T. 1960, MNRAS, 121, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Koschack, R., & Rendtel, J. 1990, WGN, 18, 119 [Google Scholar]
- Lima, L., Araújo, L., Alves, E., Batista, P., & Clemesha, B. 2015, J. Atmospheric and Solar-Terrestrial Physics, 133, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, B. 2003, in Solar Variability as an Input to the Earth’s Environment, 535, 755 [Google Scholar]
- Lindblad, B.-A. 1968, Meddelanden fran Lunds Astronomiska Observatorium Serie I, 237, 835 [NASA ADS] [Google Scholar]
- McBeath, A. 2014, 2015 Meteor Shower Calendar (IMO Publ.) [Google Scholar]
- McDonnell, T., McBride, N., Green, S. F., et al. 2001, in Interplanetary Dust (Springer), 163 [Google Scholar]
- McIntosh, B., & Simek, M. 1969, Can. J. Phys., 47, 7 [NASA ADS] [CrossRef] [Google Scholar]
- McKinley, D. W. R. 1951, ApJ, 113, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, D. A., & Zinner, E. 1977, in Lun. Planet. Sci. Conf. Proc. 8, ed. R. B. Merril, 841 [Google Scholar]
- Nesvorný, D., Jenniskens, P., Levison, H., et al. 2010, ApJ, 713, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Janches, D., Vokrouhlický, D., et al. 2011, ApJ, 743, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Pellinen-Wannberg, A., Murad, E., Brosch, N., Häggström, I., & Khayrov, T. 2010, in Icy Bodies of the Solar System, eds. J. A. Fernandez, D. Lazzaro, D. Prialnik, & R. Schulz, IAU Symp., 263, 249 [Google Scholar]
- Plane, J. 2012, Chem. Soc. Rev., 41, 6507 [NASA ADS] [CrossRef] [Google Scholar]
- Simek, M., & McIntosh, B. A. 1968, in Physics and Dynamics of Meteors, eds. L. Kresak, & P. M. Millman, IAU Symp., 33, 362 [Google Scholar]
- Stober, G., Matthias, V., Brown, P. G., & Chau, J. L. 2014, Geophys. Res. Lett., 41, 6919 [NASA ADS] [CrossRef] [Google Scholar]
- Stokan, E., & Campbell-Brown, M. D. 2014, Icarus, 232, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, R., Whitham, P., & Elford, W. 1988, J. Atmospheric and Terrestrial Physics, 50, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Weryk, R., & Brown, P. G. 2012, Planet. Space Sci., 62, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Weryk, R., & Brown, P. G. 2013, Planet. Space Sci., 81, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Weryk, R., Campbell-Brown, M. D., Wiegert, P., et al. 2013, Icarus, 225, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. 1967, in The Zodiacal Light and the Interplanetary Medium (NASA SP-150), 409 [Google Scholar]
All Tables
The measured mass index for each year as a single aggregate distribution for 29 and 38 MHz.
All Figures
 |
Fig. 1 Logarithm of the cumulative number of echoes log N vs. log A for one solar longitude bin (λ = 283° in 2012) as measured at 29.85 MHz for probable Quadrantid echoes. |
| In the text | |
 |
Fig. 2 Same echoes as Figure 1, but now with a 110–130 km range filter imposed. |
| In the text | |
 |
Fig. 3 Logarithm of the cumulative number of observed meteors N versus the logarithm of the amplitude A for all Quadrantid radar meteor echoes in 2012 detected during the three solar longitudes 282°−284° by CMOR. Black dots represent individual echoes and the green line is the best linear fit to the data found by MultiNest. |
| In the text | |
 |
Fig. 4 Posterior distribution of four parameters used in our fitting procedure as applied to the Quadrantids meteors shower. Histograms in the outer plots show a distribution of statistically equivalent solutions. The plots inside the triangular structure show projections of these solutions onto two-dimensional planes of two selected parameters, where the color coding represents the density of solutions (increasing in density from blue to red). The graphs (left to right columns) show the distribution and correlation of the following parameters: (1) slope a; (2) offset b; (3) lower bound x1; and (4) upper bound x2. |
| In the text | |
 |
Fig. 5 Mass index distribution throughout the whole year 2014 for the sporadic meteoroid complex observed by the 29.85 MHz CMOR radar. Blue points represent the mass index s for a given one degree bin in the solar longitude, where error bars are obtained from the Bayesian posterior equal weight distribution. Green boxes represent the number of meteors in each of one degree bins in the solar longitude. The intervals with large green spikes represent interference and are removed from the analysis. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but now for 38.15 MHz single station observations. From the general behavior we see that 29.85 MHz and 38.15 MHz single station results are comparable and agree well within determined uncertainty ranges. We note that the mass index for both frequencies has almost identical temporal variations, which agrees with variations of the sporadic meteoroid background previously reported by Blaauw (2010). |
| In the text | |
 |
Fig. 7 Variations of the mass index measured over five consecutive years 2011–2015 by the 29.85 MHz CMOR radar. Color-coded dots represent the mass index for each 1° solar longitude bin and color-coded lines show the moving average with 10° window averages. Arrows with labels denote maxima of Arietids (ARI), Southern Delta Aquariids (SDA), and Geminids (GEM) meteor showers. |
| In the text | |
 |
Fig. 8 Logarithm of the cumulative number of observed meteors N versus the logarithm of the amplitude A for all radar meteor echoes measured over five consecutive years 2011–2015 by the 29.85 MHz CMOR radar. Black dots represent individual echoes and the green line is the best linear fit to the data found by MultiNest. |
| In the text | |
 |
Fig. 9 Same as Fig. 7, but now for the years 2014–2015 for 38.15 MHz. Years 2011–2013 are unavailable owing to a change in the software detection, which resulted in many non-specular overdense echoes being selected, biasing the mass index value to lower values. |
| In the text | |
 |
Fig. 10 Logarithm of the cumulative number of observed meteors N relative to the logarithm of their mass for meteors observed with CAMO between 2009 and 2012. We show CAMO data not affected by the initial trail radius (black dots) correction with the best fit (black line). This is the true mass index. The distribution once the initial trail radius bias (blue dots) is applied retains an almost identical slope (blue line). We also show the effect of applying the initial radius bias with a velocity term to the distribution and find it produces a negligible difference (green dots and green for the best fit). |
| In the text | |
 |
Fig. 11 Distribution of heights for uncorrected CAMO data (gray histogram), CAMO data corrected for the initial radius (red histogram), and the 29.85 MHz CMOR heights in 2014 (blue histogram) rescaled to match CAMO corrected distribution. The effect of the correction is evident, minimizing the contribution of meteors with higher heights while keeping meteors with lower heights untouched. |
| In the text | |
 |
Fig. 12 Logarithm of cumulative particle flux at 1 AU distance from the Sun with respect to the logarithm of meteoroid mass adapted from Grün et al. (1985) (top panel). Mass index s for meteoroids at 1 AU distance from the Sun derived as the first derivative from the curve in the top panel (solid blue line) compared to the mass index s = 2.03 ± 0.01 for meteoroid environment measured by AMOR in 1995–1999 (Galligan & Baggaley 2004), mass index s = 2.05 ± 0.08 for background meteoroid environment from CMOR multi-frequency data, and with mass index s = 2.09 ± 0.05 derived from CAMO observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


