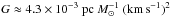| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527977 | |
| Published online | 09 August 2016 | |
7.1 keV sterile neutrino constraints from X-ray observations of 33 clusters of galaxies with Chandra ACIS
1 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
e-mail: fhofmann@mpe.mpg.de
2 Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA
3 Einstein and Spitzer Fellow
Received: 16 December 2015
Accepted: 13 June 2016
Context. Recently an unidentified emission line at 3.55 keV has been detected in X-ray spectra of clusters of galaxies. The line has been discussed as a possible decay signature of 7.1 keV sterile neutrinos, which have been proposed as a dark matter (DM) candidate.
Aims. We aim to put constraints on the proposed line emission in a large sample of Chandra-observed clusters and obtain limits on the mixing angle in a 7.1 keV sterile neutrino DM scenario.
Methods. For a sample of 33 high-mass clusters of galaxies, we merge all observations from the Chandra data archive. Each cluster has more than 100 ks of combined exposure. The resulting high signal-to-noise spectra are used to constrain the flux of an unidentified line emission at 3.55 keV in the individual spectra and a merged spectrum of all clusters.
Results. We obtained very detailed spectra around the 3.55 keV range and limits on an unidentified emission line. Assuming all DM were made of 7.1 keV sterile neutrinos, the upper limits on the mixing angle are sin2(2Θ) < 10.1×10-11 from ACIS-I and < 40.3×10-11 from ACIS-S data at 99.7 per cent confidence level.
Conclusions. We do not find evidence for an unidentified emission line at 3.55 keV. The sample extends the list of objects searched for an emission line at 3.55 keV and will help to identify the best targets for future studies of the potential DM decay line with upcoming X-ray observatories like Hitomi (Astro-H), eROSITA, and Athena.
Key words: galaxies: clusters: general / X-rays: galaxies: clusters / dark matter
© ESO, 2016
1. Introduction
Bulbul et al. (2014) and Boyarsky et al. (2014) recently found indications for a weak unidentified emission line (E ~ 3.55 keV) in X-ray CCD spectra of the Andromeda galaxy and in deep cluster observations using Chandra and XMM-Newton data. There is an ongoing discussion on the existence and possible nature of the line with studies using other instruments, such as the Suzaku observatory (Urban et al. 2015), and looking at other objects, such as individual galaxies (e.g. Anderson et al. 2015). The line has been proposed as a candidate for a dark matter (DM) decay line and could be explained by decay of sterile neutrinos with a mass of ms = 7.1 keV. In this model they decay into an X-ray photon with Eγ = ms/ 2 and an active neutrino ν. Sterile neutrinos with masses in the keV range have long been discussed as a possible component of DM (e.g. Dodelson & Widrow 1994; Abazajian et al. 2001; Boyarsky et al. 2009), but up until recently only upper limits could be derived (e.g. from observations of the Andromeda galaxy or the Bullet Cluster by Boyarsky et al. 2008a,b).
In the case of sterile neutrino decay the measured additional flux at ~ 3.55 keV would be related to two defining properties of the particles: The particle mass ms and the mixing-angle sin2(2Θ), which describes the interaction of the sterile neutrinos with its active neutrino counter-parts and thus the likelihood of decay in the γ/ν channel. These properties are related through (as used by Bulbul et al. 2014) 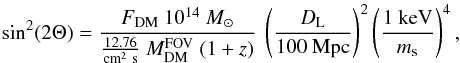 (1)where FDM is the observed flux of the DM decay line,
(1)where FDM is the observed flux of the DM decay line, 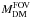 is the expected DM mass within the field of view (FOV) of the observation, DL is the luminosity distance of the cluster, and z its redshift.
is the expected DM mass within the field of view (FOV) of the observation, DL is the luminosity distance of the cluster, and z its redshift.
The paper is structured as follows: Sect. 2 describes the sample of clusters and the data reduction, Sect. 3 describes the fitting of individual cluster spectra, in Sect. 4 the procedure for fitting merged spectra is introduced, Sect. 5 explains how DM masses in the FOV were estimated, in Sect. 6 the upper limits for an additional 3.55 keV line emission are presented, in Sect. 7 the results are discussed comparing to other studies, and in Sect. 8 our findings are summarised.
For all our analysis, we used a standard ΛCDM cosmology with H0 = 71 km s-1 Mpc-1, ΩM = 0.27 and ΩΛ = 0.73 and relative solar abundances as given by Anders & Grevesse (1989).
2. Observations and data reduction
We studied X-ray spectra of a sample of 33 clusters of galaxies. For a detailed description of the sample selection and data reduction see Hofmann et al. (2016). They were selected as the most X-ray luminous clusters with more than 100 ks raw exposure with the Chandra Advanced CCD Imaging Spectrometer (ACIS; energy range about 0.1 to 10 keV, Garmire et al. 2003). The combined exposures of the sample are ~ 5.7 Ms for ACIS-I and ~ 2.3 Ms for the ACIS-S detectors. The redshift range of the sample is 0.025 <z< 0.45 with a mass range of 1 × 1014M⊙ to 2 × 1015M⊙.
The instruments spectral resolution is ~ 110−150 eV, which is broader than the energy difference to some neighbouring emission lines in the 3.55 keV region so their influence has to be carefully modelled (see discussion in Sect. 7). We obtained the observational data from the Chandra data archive and reprocessed them using standard data processing. We added all available observations for each cluster to obtain the deepest images of the systems. On the reduced images a spatial-spectral extraction was performed using the contour binning technique contbin (see Sanders 2006), which divides the cluster emission into smaller regions of equal signal-to-noise (here S/N = 50 or 25 depending on data quality). Based on the obtained maps of the cluster, we added all spectra above a fixed surface brightness where the cluster emission is homogeneously covered by all observations and obtained deep X-ray spectra for each cluster (separately for ACIS-I/-S). For a detailed description of the data reduction, see Hofmann et al. (2016).
3. Fitting individual spectra
For every cluster we added the source and background spectra of every spatial bin from the maps (see Sect. 2, only inner regions with high surface brightness and homogeneous coverage for both ACIS-I/-S). The background was renormalised to match the count rate in the 10.0−12.5 keV energy range. The response files were averaged and weighted by the number of counts in the spectrum (both auxiliary response files, ARF, and redistribution matrix files, RMF). We used XSPEC version 12.9.0 (Arnaud 1996) and ATOMDB version 2.0.2 to analyse the spectra (Foster et al. 2012).
To estimate the upper limit of the flux allowed for an additional emission line, we searched for the best-fitting apec model (with two temperature components) for collisionally ionised plasma with absorption (nH) and an additional zero-width Gaussian line redshifted corresponding to the cluster distance (see Fig. E.1 for spectra of individual clusters). The normalisation of the Gaussian was allowed to be negative to avoid bias. All spectra were grouped to contain a minimum of 22 raw counts in each bin (using grppha) and we used the range from 2−5 keV for fitting the spectral model to the data (using χ2 statistics). Free parameters of the fit were the normalisation of the spectral components, temperatures, and relative abundances of the apec models. The fit was carried out using a fixed foreground column density (nH [cm-2]), which was determined from the Leiden/Argentine/Bonn (LAB) survey of Galactic HI (based on Kalberla et al. 2005). Where we found the absorption to vary significantly across the FOV of an observation, nH was set as additional free parameter of the fit (only for pks0745, see Hofmann et al. 2016). Additional absorption of about 5 per cent can be caused by molecular hydrogen in the foreground (H2 X-ray absorption; see Willingale et al. 2013). We did not include the additional absorption by H2 because the influence on the spectral form in the 3 keV range is negligible. If the two temperatures were separated by less than 30 per cent or if the normalisation of one component was less than one per cent of the second, we discarded the second component and fit only a one-temperature apec model (see Table D.1).
Once the best fit was identified, we calculated the confidence intervals (99.7 per cent) for the additional flux added by the Gaussian using a Monte Carlo Markov chain (MCMC) method with length of 10 000 and burn-in length of 1000. As a robustness test we used a Bayesian fitting code (BXA; Buchner et al. 2014) with flat priors for the same parameter ranges as our standard fitting method and obtained consistent results. A non-negative prior for the additional Gaussian flux did not improve the constraints.
4. Fitting merged spectra
We added all cluster spectra in our sample to obtain deeper limits on the line. We de-redshifted all spectra by re-binning the counts to the channel-grid of the new spectra after randomising each count position within the channel width. The ARFs were de-redshifted by calculating the new energy values of the spectral channels and then mapping back to the original channel-grid by interpolating the shifted response. For the RMF, we treated the integer value of the response matrix in each pixel (two-dimensional detector response matrix for channel to energy mapping) as a number of counts and applied the same de-redshifting procedure with randomisation as to the spectra. We repeated the process 100 times and calculated the average to approximate the new response files better. Residual noise from the re-mapping (caused by the discrete energy grid) was reduced by smoothing the responses with a Gaussian filter (σ = 1 pixel). The width of the energy bins is ~ 0.01 keV for both detectors (see response in Fig. B.1). The de-redshifting was based on optical redshifts known from previous catalogues (see Table D.2). We added all de-redshifted, unabsorbed spectra and averaged the response files with weights according to the fraction of the total counts of the merged spectrum (in the 2−5 keV range). In the fitted range 2−5 keV, the merged spectra contain 3.2×106 counts (ACIS-I) and 2.7×106 counts (ACIS-S). The average exposure times of each observation were added to obtain an average count rate in the final spectra. The background spectrum was renormalised to match the 10.0−12.5 keV energy range count rate. We used the XSPEC models apec+apec+zgauss without absorption and z = 0 to fit the spectra and estimate the additional flux allowed for a line at 3.55 keV. The fit of the merged spectra was performed between 3−5 keV because there is no strong variation in the detector response in that region and thus possible systematics in the calculated average response are minimal. Figure 1 shows some residual structures due to the modelling of a complex stack of cluster spectra with a two-temperature apec model.
 |
Fig. 1 Merged X-ray spectra (ACIS-I top and ACIS-S bottom) of the cluster sample with residuals of different fitted models. Fitted XSPEC models: apec+apec+zgauss with best fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. For the effective-area curve see Fig. B.1. |
We tested fitting the emission features in the spectrum with separate Gaussian lines on top of an apec model without lines (compare e.g. Bulbul et al. 2014). This procedure provided a goodness of fit comparable to the fitting process used in this study. We concluded that the modelling with two temperature collisionally ionised plasma emission (XSPEC apec model) is appropriate for the spectra in this study.
There are some remaining residuals between the model and data in the merged spectra. A high percentage of these residuals are caused by the systematic effects of averaging and de-redshifting the responses and spectra (see simulated spectra in Fig. B.1). As these features are narrower than the response, they cannot and should not be fitted by Gaussian lines. Modelling the emission lines separately (e.g. as Bulbul et al. 2014) does not significantly improve the fit, except for the two strongest features at 3.85 and 4.7 keV (perhaps due to incomplete modelling of the temperature structure, as discussed in Appendix C). If these two features are included in our model, there is no significant change to our limits. We conclude that the two temperature plasma model is appropriate for this study. There are no strong emission lines expected over the range in temperature in the region of the 3.55 keV line, which could explain the strength of previous detections.
Figure 1 shows additional residuals at ~ 3.85 keV and ~ 4.7 keV. The shape of spectral features in the CCD spectra can change with temperature because they are blends of several neighbouring emission lines and the ratio between those is temperature dependent.
 |
Fig. 2 Top: limits on an additional Gaussian flux component at 3.55 keV for all clusters in the sample. Bottom: limits on the mixing angle in case of a 7.1 keV sterile neutrino. The limits are calculated separately for ACIS-S and ACIS-I, which are indicated by -s or -i following the cluster identification on the x-axis. Most lower limits and some best-fit values lie outside the plotted range. The dashed line shows the Bulbul et al. (2014) detection in their full XMM-Newton MOS sample. Limits show the 1σ (small symbols) and 3σ (big symbols) confidence range. |
Limits from merged spectra.
We used simulations to verify the line-detection efficiency of our stacking and modelling method (see Appendix B) and show that small additional residuals from modelling the many averaged temperatures of the ICM with a two temperature model does not affect the limits derived for the 3.55 keV line (see Appendix C).
5. Estimating cluster masses
We need to estimate the DM mass in the FOV to constrain the expected strength of the DM emission line in the cluster spectra. With the measured average temperatures of the clusters, we used temperature-mass scaling relations from Vikhlinin et al. (2009) to estimate the overall cluster mass M500 and the related over-density radius r500 (see Hofmann et al. 2016, for details).
We assumed the cluster density follows a NFW profile (Navarro et al. 1997) and used a fixed concentration (C = 4), as the expected average value of the sample (compare e.g. Vikhlinin et al. 2006). By integrating ρ(r) along the line of sight we obtained the DM mass surface density profiles (see e.g. Wright & Brainerd 2000; Urban et al. 2015). We estimated the DM mass in the FOV of an observation by adding up the surface densities within the footprint of the extraction region for the spectra. The footprints of each observation and the maximum covered radius have been published by Hofmann et al. (2016).
For A 1795 we obtained an 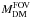 of 1.6×1014M⊙ (2.75×1014M⊙ for M2500 given by Vikhlinin et al. 2006). We estimate the systematic uncertainties of
of 1.6×1014M⊙ (2.75×1014M⊙ for M2500 given by Vikhlinin et al. 2006). We estimate the systematic uncertainties of 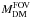 to be 35 per cent on average owing to scatter in the scaling relations for the total mass and scatter around the average concentration. The scatter averages out when adding together properties of the whole sample, which means that we expect much smaller systematic uncertainties in the average
to be 35 per cent on average owing to scatter in the scaling relations for the total mass and scatter around the average concentration. The scatter averages out when adding together properties of the whole sample, which means that we expect much smaller systematic uncertainties in the average 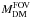 used for limits on the merged cluster spectra (see Table D.2).
used for limits on the merged cluster spectra (see Table D.2).
6. Upper limits on 3.55 keV line
We investigated the possible existence of an unidentified X-ray emission line at ~ 3.55 keV in the cluster spectra. We put limits on the existence of such a line in all the clusters individually and in a merged spectrum of the whole sample. A possible interpretation for this line has been the emission from decaying sterile neutrinos with a mass of ~ 7.1 keV, which could be a candidate for DM.
6.1. Limits in individual spectra
Figure 2 shows the upper limits on the flux derived from observations of A 1795 (deepest observation in the sample), where we obtained a 3σ upper limit of 3.22×10-6 cm-2 s-1 from merged ACIS-I observations (~ 613 ks) and 4.73×10-6 cm-2 s-1 from ACIS-S (~ 241 ks).
Using Eq. (1) this translates to one of the deepest upper limits on the mixing angle for individual clusters sin2(2Θ) ≤ 4.4×10-10 (ACIS-I data). The limits on the additional flux that we could derive in the individual systems depend on the exposure time and on how well the cluster emission is modelled by a two-component collisionally ionised plasma model. For a detailed list of constraints see Table D.3.
6.2. Limits in merged spectra
The fits to the merged data provide deeper upper limits on the flux by about a factor of three for ACIS-I compared to the individual spectra (see Fig. 1 and Table 1). To turn this flux into a limit on the expected mixing angle in the 7.1 keV sterile neutrino scenario, we estimated the average mass and luminosity distance of the cluster sample. We weighted the contributions to the average with their expected contribution ωi,DM to the DM line flux with the formula used by Bulbul et al. (2014), 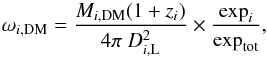 (2)where i denotes the properties of the ith cluster and expi/ exptot is the fraction of the total exposure for the ith cluster. This is carried out for ACIS-I and ACIS-S separately (see weights in Table D.2).
(2)where i denotes the properties of the ith cluster and expi/ exptot is the fraction of the total exposure for the ith cluster. This is carried out for ACIS-I and ACIS-S separately (see weights in Table D.2).
The most stringent limit on the mixing angle from this analysis is sin2(2Θ) ≲ 10×10-11 (99.7 per cent confidence) for the merged ACIS-I spectra of the sample. All 3σ (99.7 per cent) upper limits are compatible with the value of sin2(2Θ) ~ 7×10-11 found for the full sample of Bulbul et al. (2014). A simultaneous fit of the merged ACIS-I and ACIS-S spectrum did not improve the limits.
7. Discussion
We did not find evidence for an unidentified emission line at 3.55 keV (see Fig. 2). The average value of the Gaussian flux measured in the cluster sample is consistent with zero with some scatter (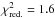 ), suggesting mild additional systematic uncertainties (~ 25 per cent). This is a conservative estimate because the high
), suggesting mild additional systematic uncertainties (~ 25 per cent). This is a conservative estimate because the high 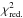 value is mainly driven by outliers like Hydra A. The average of the calculated mixing angle is much lower than the value of Bulbul et al. (2014), but is consistent within the 3σ upper limit (see Fig. 2).
value is mainly driven by outliers like Hydra A. The average of the calculated mixing angle is much lower than the value of Bulbul et al. (2014), but is consistent within the 3σ upper limit (see Fig. 2).
The highest 3σ upper limit and best fit is obtained for the spectrum of a ~ 20 ks ACIS-I observation of Hydra A. The width of the fit line in this case is unusually broad (due to inaccuracies in the calibration files of the observation, ID 575 from 1999) and the line is not detected in a ~ 200 ks observation of the same cluster with ACIS-S (see Fig. 2 for derived limits on mixing angle).
A difference from the Bulbul et al. (2014) analysis is that we used only core regions of the clusters where the gas emission causes a higher background for detection of any DM line emission and we might thus be less sensitive. Using Chandra ACIS we could not extend the analysis to larger radii as a result of the limited FOV. Another difference in the analysis is that we did not use a separately weighted response for the Gaussian DM line for modelling the merged data.
Urban et al. (2015) used deep data taken with the Suzaku observatory and found some evidence for the predicted emission line in spectra of the Perseus cluster, however their study of the Coma, Virgo, and Ophiuchus clusters disfavour the DM nature of the line. Anderson et al. (2015) excluded the existence of the DM decay line in the merged spectra of nearby galaxy halos, where the ratio of DM to baryonic, X-ray emitting matter is expected to be higher (see also Malyshev et al. 2014).
The Draco dwarf spheroidal galaxy was targeted by very deep observations with the XMM-Newton satellite. Depending on the modelling these observations are in tension with the DM interpretation of the line width ~ 2σ (see Jeltema & Profumo 2016). In the same dataset Ruchayskiy et al. (2016) found an upper limit on the sterile neutrino lifetime, which is consistent (within 1−2σ uncertainties) with previous detections in the scenario that the sterile neutrinos with 7.1 keV make up all DM in the halo. Jeltema & Profumo (2015) found evidence of a line around 3.5 keV in XMM-Newton data of the Galactic centre. Other detections of the additional line include measurements of the Galactic centre X-ray emission (Boyarsky et al. 2015). The recent XMM-Newton flux measurements for an additional line in the 3.5 keV regime in a sample of clusters of galaxies by Iakubovskyi et al. (2015) is in weak tension with our limits (e.g. ~ 2σ for Abell 2199). Riemer-Sørensen et al. (2015) used deep observations of the Bullet cluster with the NuSTAR satellite to constrain possible decay lines up to higher energies but owing to lower sensitivity at 3.5 keV do not exclude previous detections.
 |
Fig. 3 Comparison of this works constraints to selected literature values. The best-fit line energy varies between ~ 3.4−3.6 keV. This work: 95% confidence interval (CI) for Chandra ACIS-I (bottom) and ACIS-S (middle) stacked spectra and for the error-weighted average of all individual limits (top). Bulbul et al. (2014): 68% CI for the full cluster sample using the XMM-Newton MOS detectors. Boyarsky et al. (2014): 68% CI (statistical only) for the M 31 XMM-Newton data. Anderson et al. (2015): 68% CI for negative residual in stacked XMM-Newton data of galaxy halos. Jeltema+2015a (see Jeltema & Profumo 2015): range of values obtained for different mass models of the Galactic centre with XMM-Newton observations. Jeltema+2015b (see Jeltema & Profumo 2016): 95% CI upper limit from a deep observation of the Draco dwarf galaxy with XMM-Newton. Ruchayskiy et al. (2016): range of values obtained for different mass models of the Draco dwarf galaxy with the XMM-Newton PN instrument. Boyarsky et al. (2015): best-fit range for observations of the Galactic centre with the XMM-Newton MOS instrument. Iakubovskyi et al. (2015): range of best-fit values for a sample of galaxy clusters observed with XMM-Newton. Negative mixing angles are unphysical but result from Eq. (1) when allowing negative flux. The plot only shows selected constraints from the listed publications. |
The main caveat of our mixing-angle calculations is the uncertainty of the DM masses in the FOV, which are derived from scaling relations with the temperature of the hot ICM. The main caveats of the flux constraints are possible uncertainties in the calibration of the effective area and detector response and in the assumed background spectrum (derived from Chandra blank sky observations). Alternative explanations for the potential line could be unexpectedly strong plasma emission lines or charge exchange processes around 3.55 keV (see discussion by Bulbul et al. 2014; Gu et al. 2015). Candidate plasma lines are K XVIII (3.476, 3.496, and 3.515 keV), Cl XVII (3.510 and 3.509 keV) as well as Ar XVII (3.617 and 3.618 keV)1.
The merged spectra in Fig. 1 show an additional weak (≳ 1σ) residual around 4.7 keV (mainly in ACIS-S), which is not visible in the simulations (see Fig. B.1). This could be explained by an unexpectedly high abundance (higher than assumed in apec metallicity model) of titanium (Ti XXI, multiple lines between 4.70−4.76 keV). The residual at 4.7 keV disappears for 1−3 times solar abundance but in this case the line of Ti XXII at about 4.9 keV is not observed at the expected strength.
Figure 3 shows a comparison of this work to previous measurements (see also discussion above). The results show conservative limits from the Chandra ACIS-S and ACIS-I analysis and the offset shows possible systematics between instruments. The average value of all individual limits is closer to the ACIS-I measurement since the sample has higher exposure in ACIS-I and more clusters have ACIS-I observations. Most detections are consistent with our 95 per cent confidence regions. Reasons for the more conservative limits can be the smaller FOV of Chandra, with the lower combined exposure compared to some sample studies, the smaller effective area of Chandra compared to XMM-Newton, and a more conservative modelling approach.
8. Conclusions
This study presents a large sample of deep cluster spectra with limits on the previously detected emission at 3.55 keV assuming the line originated from the decay of sterile neutrino DM (ms = 7.1 keV). We extend the number of objects previously searched for the line and provide further insight to whether the line only occurs in special observations or objects. This is the first study using a large sample of Chandra-observed clusters to constrain the 3.55 keV line. The driving cluster property behind the depth of the upper limit on the mixing angle in the sterile neutrino scenario is the DM mass in the FOV where the spectra have been extracted divided by the luminosity distance squared. To maximise this property, homogeneous, deep coverage out to large radii of a massive nearby system is needed (higher [1010M⊙ Mpc-2] value in Table D.2). In this sample the best candidate for such a study with Chandra was Abell 1795 because of its very deep exposure (see Table D.2).
As demonstrated by Bulbul et al. (2014) a 1 Ms observation of the Perseus cluster with the Hitomi (Astro-H) SXS instrument (Kitayama et al. 2014) will allow us to distinguish between a plasma emission line of the ICM, broadened by the turbulence in the cluster (~ 300 km s-1) and a DM decay line, broadened by the virial velocity (~ 1300 km s-1) of the DM halo. The large FOV of the eROSITA observatory (Merloni et al. 2012) will allow for tight constraints on the line (see also Zandanel et al. 2015), homogeneously covering nearby X-ray bright clusters to large radii, even with lower effective area at 3.55 keV compared to XMM-Newton and Chandra. Only deeper observations with current or future instruments will allow us to finally decide the nature of the detection, as summarised in a recent white paper on keV sterile neutrinos (Adhikari et al. 2016).
Acknowledgments
We thank the anonymous referee for constructive comments that helped to improve the clarity of the paper. We thank J. Buchner, A. Del Moro, C. Pulsoni, and J. Ridl for helpful discussions. This research has made use of data obtained from the Chandra Data Archive, software provided by the Chandra X-ray Center (CXC) in the application package CIAO, NASA’s Astrophysics Data System, data and software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory, the tools Veusz, the matplotlib library for Python, and TOPCAT. M.G. is supported by the National Aeronautics and Space Administration through Einstein Postdoctoral Fellowship Award Number PF-160137 issued by the Chandra X-ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of the National Aeronautics Space Administration under contract NAS8-03060.
References
- Abazajian, K., Fuller, G. M., & Tucker, W. H. 2001, ApJ, 562, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, R., Agostini, M., Ky, N. A., et al. 2016, ArXiv e-prints [arXiv:1602.04816] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anderson, M. E., Churazov, E., & Bregman, J. N. 2015, MNRAS, 452, 3905 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Cosmic Abundances, eds. S. S. Holt, & G. Sonneborn, ASP Conf. Ser., 99, 409 [Google Scholar]
- Boyarsky, A., Iakubovskyi, D., Ruchayskiy, O., & Savchenko, V. 2008a, MNRAS, 387, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., & Markevitch, M. 2008b, ApJ, 673, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., & Shaposhnikov, M. 2009, Ann. Rev. Nucl. Part. Sci., 59, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., & Franse, J. 2014, Phys. Rev. Lett., 113, 251301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyarsky, A., Franse, J., Iakubovskyi, D., & Ruchayskiy, O. 2015, Phys. Rev. Lett., 115, 161301 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bulbul, E., Markevitch, M., Foster, A., et al. 2014, ApJ, 789, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S., & Widrow, L. M. 1994, Phys. Rev. Lett., 72, 17 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Garmire, G. P., Bautz, M. W., Ford, P. G., Nousek, J. A., & Ricker, Jr., G. R. 2003, in X-Ray and Gamma-Ray Telescopes and Instruments for Astronomy, eds. J. E. Truemper, & H. D. Tananbaum, Proc. SPIE, 4851, 28 [Google Scholar]
- Gu, L., Kaastra, J., Raassen, A. J. J., et al. 2015, A&A, 584, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hofmann, F., Sanders, J. S., Nandra, K., Clerc, N., & Gaspari, M. 2016, A&A, 585, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iakubovskyi, D., Bulbul, E., Foster, A. R., Savchen ko, D., & Sadova, V. 2015, ArXiv e-prints [arXiv:1508.05186] [Google Scholar]
- Jeltema, T., & Profumo, S. 2015, MNRAS, 450, 2143 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T., & Profumo, S. 2016, MNRAS, 458, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitayama, T., Bautz, M., Markevitch, M., et al. 2014, ArXiv e-prints [arXiv:1412.1176] [Google Scholar]
- Malyshev, D., Neronov, A., & Eckert, D. 2014, Phys. Rev. D, 90, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Riemer-Sørensen, S., Wik, D., Madejski, G., et al. 2015, ApJ, 810, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Ruchayskiy, O., Boyarsky, A., Iakubovskyi, D., et al. 2016, MNRAS, 460, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S. 2006, MNRAS, 371, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Urban, O., Werner, N., Allen, S. W., et al. 2015, MNRAS, 451, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. O., & Brainerd, T. G. 2000, ApJ, 534, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Zandanel, F., Weniger, C., & Ando, S. 2015, J. Cosmology Astropart. Phys., 9, 060 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Dark matter mass profiles
We assumed the cluster density follows an NFW profile (Navarro et al. 1997) depending on the radius r from the centre,
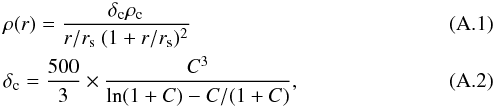 where concentration C and radius rs are empirical cluster specific values. Value C describes how strongly peaked the density profile is in the centre, rs is a specific radius depending on the extent of the cluster (here we define rs = r500/C), and ρc is the critical density of the universe at the cluster redshift. In the standard ΛCDM cosmology assumed in this study (see Sect. 1) the critical density is given as
where concentration C and radius rs are empirical cluster specific values. Value C describes how strongly peaked the density profile is in the centre, rs is a specific radius depending on the extent of the cluster (here we define rs = r500/C), and ρc is the critical density of the universe at the cluster redshift. In the standard ΛCDM cosmology assumed in this study (see Sect. 1) the critical density is given as
Appendix B: Simulated spectra
 |
Fig. B.1 Merged simulations with 10 times the exposure of original X-ray spectra and an additional Gaussian line at 3.55 keV (ACIS-I top and ACIS-S bottom) with residuals of different fitted models and the effective area (ARF and RMF combined). Fitted XSPEC models: apec+apec+zgauss with best-fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. |
We used simulated data to test our spectral stacking technique for detecting an additional line at 3.55 keV. For the simulation we created fake spectra using XSPEC. Simulated spectra were obtained for the best-fit model of every individual cluster with ten times the original exposure to get better statistics. We added a Gaussian line with the expected flux for each cluster assuming a mixing angle of ~ 7×10-11 and that all DM is made of the 7.1 keV sterile neutrinos as in previous detections (see Bulbul et al. 2014; Boyarsky et al. 2014). Exactly the same merging and modelling procedure was performed on the simulations and the real data. Figure B.1 shows the resulting stacked spectra of the simulation (compare to Fig. 1 for the real data). The additional line is recovered between 95 and 99.7 per cent confidence for both ACIS-I and ACIS-S detectors after the stacking. The measured flux can be converted into a mixing angle using the average sample properties of Table 1. The resulting mixing angles in the simulations are 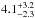 (ACIS-I, CI:68) and
(ACIS-I, CI:68) and 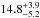 (ACIS-S, CI:68). These simulations show the detection efficiency of our stacking method. There is some hint that the limits of ACIS-S are biased high, which is in agreement with the limits obtained from real data (see Fig. 3 the best constraints). There are small fluctuations in the residuals of less than 2 per cent. To assess the uncertainties introduced by our de-redshifting technique of the RMF response files, we tested many different combinations of smoothing and number of iterations. The best results were obtained by calculating the average of 100 iterations and smoothing them using a Gaussian filter (σ = 1 pixel). This procedure proved most effective in recovering the simulated flux (see Fig. B.1). The residual structures seen in the merged spectra are partially caused by the averaging over many cluster spectra of different temperatures, which are not perfectly modelled by the two temperature component apec model. More complex models however made the fit less stable and did not improve the capability of detecting the additional line. Another source of residuals can be fluctuations in the average response (see bottom panels Fig. B.1 for combined ARF and RMF). These minor fluctuations did not affect our detection efficiency since they averaged out over the width of a spectral line. We extensively tested the detection efficiency using different stacking methods. Additional smoothing of the response files resulted in lower sensitivity for detecting the simulated line (e.g. using mean, median, and Gaussian filters) because it introduced residuals around spectral features due to broadening of the response. Using linear interpolation to remap the response resulted in smoother response but the simulated line was not recovered. The method we used for the final analysis was the most efficient at recovering the simulated line.
(ACIS-S, CI:68). These simulations show the detection efficiency of our stacking method. There is some hint that the limits of ACIS-S are biased high, which is in agreement with the limits obtained from real data (see Fig. 3 the best constraints). There are small fluctuations in the residuals of less than 2 per cent. To assess the uncertainties introduced by our de-redshifting technique of the RMF response files, we tested many different combinations of smoothing and number of iterations. The best results were obtained by calculating the average of 100 iterations and smoothing them using a Gaussian filter (σ = 1 pixel). This procedure proved most effective in recovering the simulated flux (see Fig. B.1). The residual structures seen in the merged spectra are partially caused by the averaging over many cluster spectra of different temperatures, which are not perfectly modelled by the two temperature component apec model. More complex models however made the fit less stable and did not improve the capability of detecting the additional line. Another source of residuals can be fluctuations in the average response (see bottom panels Fig. B.1 for combined ARF and RMF). These minor fluctuations did not affect our detection efficiency since they averaged out over the width of a spectral line. We extensively tested the detection efficiency using different stacking methods. Additional smoothing of the response files resulted in lower sensitivity for detecting the simulated line (e.g. using mean, median, and Gaussian filters) because it introduced residuals around spectral features due to broadening of the response. Using linear interpolation to remap the response resulted in smoother response but the simulated line was not recovered. The method we used for the final analysis was the most efficient at recovering the simulated line.
Appendix C: Multi-temperature residuals in ACIS-S
When we fit the merged spectrum of the cluster sample for the ACIS-S detectors (Fig. 1) there were two significant residuals (> 1σ). Such strong residuals are not found in the simulated merged spectra (Fig. B.1). We simulated each cluster with a two-temperature plasma X-ray emission model (XSPEC apec) and then modelled the merged spectrum with two temperatures (actually the average of 2 × 33 temperatures). The reasons for stronger residuals in the real observations of ACIS-S could be that multi-temperature effects are stronger or that there are additional components not modelled by the current plasma emission model. As discussed in the paper, there are two significant line-like residuals in ACIS-S at ~ 3.85 keV and ~ 4.7 keV. The ~ 3.85 keV residual could be explained by stronger than expected Ca XIX emission lines (several lines known between ~ 3.86−3.90 keV). The ~ 4.7 keV line could be due to Ti XXI (see Sect. 7).
To test whether the two temperature fit is sufficient to obtain reliable 3.55 keV line limits from the merged observations, we modelled the two lines with additional Gaussian lines. The line width was set to zero and the energy set to the two values estimated above. The goodness of fit improved from 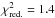 to 1.3 and the residual features seen in the original fit disappear (see Fig. C.1). Both lines are detected at > 1σ.
to 1.3 and the residual features seen in the original fit disappear (see Fig. C.1). Both lines are detected at > 1σ.
The obtained limits on the 3.55 keV flux however are very well consistent with the original fit showing that the additional residuals are negligible for our estimates.
 |
Fig. C.1 Merged X-ray spectrum (ACIS-S) of the cluster sample with residuals of different fitted models. Fitted XSPEC models: apec+apec+zgauss (3.55 keV) +zgauss (3.85 keV) +zgauss (4.7 keV) with best-fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux at 3.55 keV in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the 3.55 keV Gaussian flux. For the effective area curve, see Fig. B.1. |
Appendix D: Detailed parameters of fitting procedure
Best fit XSPEC models.
Fixed cluster parameters and weights.
Flux and mixing angle constraints.
Appendix E: 3.55 keV spectra
 |
Fig. E.1 X-ray spectra (ACIS-I and ACIS-S) with residuals of different fitted models. Fitted models: XSPEC phabs*(apec+apec+zgauss) with best-fit, upper and lower confidence values (99.7 per cent) of the Gaussian flux in cm-2 s-1. The annotations show the best-fit (Bf) value and the confidence interval obtained using Monte Carlo Markov chains (MCMC). Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. The plot title indicates the abbreviated cluster name and the exposure time of the observation. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
All Tables
All Figures
 |
Fig. 1 Merged X-ray spectra (ACIS-I top and ACIS-S bottom) of the cluster sample with residuals of different fitted models. Fitted XSPEC models: apec+apec+zgauss with best fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. For the effective-area curve see Fig. B.1. |
| In the text | |
 |
Fig. 2 Top: limits on an additional Gaussian flux component at 3.55 keV for all clusters in the sample. Bottom: limits on the mixing angle in case of a 7.1 keV sterile neutrino. The limits are calculated separately for ACIS-S and ACIS-I, which are indicated by -s or -i following the cluster identification on the x-axis. Most lower limits and some best-fit values lie outside the plotted range. The dashed line shows the Bulbul et al. (2014) detection in their full XMM-Newton MOS sample. Limits show the 1σ (small symbols) and 3σ (big symbols) confidence range. |
| In the text | |
 |
Fig. 3 Comparison of this works constraints to selected literature values. The best-fit line energy varies between ~ 3.4−3.6 keV. This work: 95% confidence interval (CI) for Chandra ACIS-I (bottom) and ACIS-S (middle) stacked spectra and for the error-weighted average of all individual limits (top). Bulbul et al. (2014): 68% CI for the full cluster sample using the XMM-Newton MOS detectors. Boyarsky et al. (2014): 68% CI (statistical only) for the M 31 XMM-Newton data. Anderson et al. (2015): 68% CI for negative residual in stacked XMM-Newton data of galaxy halos. Jeltema+2015a (see Jeltema & Profumo 2015): range of values obtained for different mass models of the Galactic centre with XMM-Newton observations. Jeltema+2015b (see Jeltema & Profumo 2016): 95% CI upper limit from a deep observation of the Draco dwarf galaxy with XMM-Newton. Ruchayskiy et al. (2016): range of values obtained for different mass models of the Draco dwarf galaxy with the XMM-Newton PN instrument. Boyarsky et al. (2015): best-fit range for observations of the Galactic centre with the XMM-Newton MOS instrument. Iakubovskyi et al. (2015): range of best-fit values for a sample of galaxy clusters observed with XMM-Newton. Negative mixing angles are unphysical but result from Eq. (1) when allowing negative flux. The plot only shows selected constraints from the listed publications. |
| In the text | |
 |
Fig. B.1 Merged simulations with 10 times the exposure of original X-ray spectra and an additional Gaussian line at 3.55 keV (ACIS-I top and ACIS-S bottom) with residuals of different fitted models and the effective area (ARF and RMF combined). Fitted XSPEC models: apec+apec+zgauss with best-fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. |
| In the text | |
 |
Fig. C.1 Merged X-ray spectrum (ACIS-S) of the cluster sample with residuals of different fitted models. Fitted XSPEC models: apec+apec+zgauss (3.55 keV) +zgauss (3.85 keV) +zgauss (4.7 keV) with best-fit (Bf), upper and lower confidence values (99.7 per cent) of the Gaussian flux at 3.55 keV in counts cm-2 s-1. The annotations show the best-fit value and the confidence interval obtained using MCMC. Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the 3.55 keV Gaussian flux. For the effective area curve, see Fig. B.1. |
| In the text | |
 |
Fig. E.1 X-ray spectra (ACIS-I and ACIS-S) with residuals of different fitted models. Fitted models: XSPEC phabs*(apec+apec+zgauss) with best-fit, upper and lower confidence values (99.7 per cent) of the Gaussian flux in cm-2 s-1. The annotations show the best-fit (Bf) value and the confidence interval obtained using Monte Carlo Markov chains (MCMC). Residuals are shown for the fit with upper (blue) and lower (red) confidence limit of the Gaussian flux. The plot title indicates the abbreviated cluster name and the exposure time of the observation. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.