| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935561 | |
| Published online | 17 May 2019 | |
Letter to the Editor
7.1 keV sterile neutrino dark matter constraints from a deep Chandra X-ray observation of the Galactic bulge Limiting Window
1
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
e-mail: fhofmann@mpe.mpg.de
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, France
Received:
27
March
2019
Accepted:
30
April
2019
Context. An unidentified emission line at 3.55 keV was recently detected in X-ray spectra of clusters of galaxies. The line has been discussed as a possible decay signature of 7.1 keV sterile neutrinos, which have been proposed as a dark matter (DM) candidate.
Aims. We aim to further constrain the line strength and its implied mixing angle under the assumption that all DM is made of sterile neutrinos.
Methods. The X-ray observations of the Limiting Window (LW) towards the Galactic bulge (GB) offer a unique dataset for exploring DM lines. We characterise the systematic uncertainties of the observation and the fitted models with simulated X-ray spectra. In addition, we discuss uncertainties of indirect DM column density constraints towards the GB to understand systematic uncertainties in the assumed DM mass in the field of view of the observation.
Results. We find tight constraints on the allowed flux for an additional line at 3.55 keV with a positive (∼1.5σ) best fit value FX3.55 keV ≈ (4.5 ± 3.5) × 10−7 cts cm−2 s−1. This would translate into a mixing angle of sin2(2Θ) ≈ (2.3 ± 1.8) × 10−11 which, while consistent with some recent results, is in tension with earlier detections.
Conclusions. We used a very deep dataset with well understood systematic uncertainties to derive tight constraints on the mixing angle of a 7.1 keV sterile neutrino DM candidate. The results highlight that the inner Milky Way will be a good target for DM searches with upcoming missions like eROSITA, XRISM, and ATHENA.
Key words: Galaxy: bulge / dark matter
© F. Hofmann and C. Wegg 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The Limiting Window (LW) is located 1.5 deg south of Sgr A* (in Galactic coordinates). With its comparatively low foreground absorption (nH ≲ 1022 cm−2) it was used to resolve about 80 per cent of the hard X-ray emission of the Galactic centre into point sources and study the source population (Revnivtsev et al. 2009).
Bulbul et al. (2014) and Boyarsky et al. (2014) recently found indications for a weak unidentified emission line (E ∼ 3.55 keV) in X-ray CCD spectra of the Andromeda galaxy and in deep observations of clusters of galaxies using Chandra and XMM-Newton data. The line has been proposed as a candidate dark matter (DM) decay line and could be explained by the decay of sterile neutrinos with a mass of ms ≈ 7.1 keV. In the model these neutrinos can decay into an X-ray photon with Eγ = ms/2 and an active neutrino ν. Sterile neutrinos with masses in the kiloelectronvolt range have long been discussed as a possible component of DM (e.g. Dodelson & Widrow 1994; Abazajian et al. 2001; Boyarsky et al. 2009), but until recently only upper limits could be derived (e.g. from observations of the Andromeda galaxy or the Bullet Cluster by Boyarsky et al. 2008a,b). A detection of the sterile neutrino decay would help to discriminate between different production mechanisms (see e.g. Merle & Schneider 2015; Kang & Patra 2016; Herms et al. 2018). For a review on the current state of constraints, see Boyarsky et al. (2019).
In the case of sterile neutrino decay the measured additional flux at ∼3.55 keV would be related to two defining properties of the particles: the particle mass ms and the mixing-angle sin2(2Θ), which describes interaction of the sterile neutrinos with their active neutrino counterparts and thus the likelihood of decay in the γ/ν channel. These properties are related through the following equation (adapted from Bulbul et al. 2014).
where FDM is the observed flux of the DM decay line and SDM = ∫ ρDM dr is the DM column density.
We used deep archival X-ray observations of the LW with the Chandra telescope to constrain the allowed additional flux in the 3.55 keV range and the strength of the proposed decay line in the direction of the Galactic bulge (GB).
The paper is structured as follows: Sect. 2 describes the data used and how it was analysed from reduction to spectral fitting. Section 3 describes how the DM mass in the field of view (FOV) was derived. Section 4 describes the obtained constraints on flux and mixing angle in the sterile neutrino DM case. In Sect. 5 we discuss the results in the context of previous work, and Sect. 6 summarises the conclusions of the analysis and gives an outlook for future missions like eROSITA. Uncertainties are quoted at the 1σ level unless stated otherwise. Abundances are according to solar abundances, as in Anders & Grevesse (1989).
2. X-ray data reduction and analysis
We used all available archival observations of the LW with the Chandra Advanced CCD Imaging Spectrometer (ACIS; Garmire et al. 2003) using the imaging (ACIS-I) CCD array (about 0.1–10 keV energy range). This instrument provides high spatial- (∼1″) and spectral resolution (∼100 eV full width half maximum, FWHM). We used the observations with ObsIDs: 5934, 6362, 6365, 9500, 9501, 9502, 9503, 9504, 9505, 9854, 9855, 9892, and 9893. The observations were reprocessed using the Chandra Interactive Analysis of Observations software package (CIAO; Fruscione et al. 2006) version 4.5 and the Chandra Calibration Database (CalDB; Graessle et al. 2007) version 4.5.9.
The data analysis is based on Hofmann et al. (2016a,b) but we describe the most important steps again in the following. We merged all ACIS-I observations of the LW, removed detected point sources, and extracted a spectrum from the remaining 66 arcmin2 (see also technique by Sanders 2006). The background was extracted from a matched “blank-sky” observation (using acis_bkgrnd_lookup) and renormalised to match the count rate of the source spectrum in the 10.0–12.5 keV energy range. The Chandra “blank-sky” background is created from observations at least 20 deg from the Galactic plane. This could potentially bias our results low by about ten per cent (see profile Fig. 3), because we might be subtracting some of the line strength with the background. The response files were averaged and weighted by the number of counts in the spectrum (both auxiliary response files, ARF, and redistribution matrix files, RMF). We used XSPEC version 12.9.1u (Arnaud 1996) and ATOMDB version 3.0.7 (Foster et al. 2012) to analyse the spectra.
To estimate the upper limit of the flux allowed for an additional emission line, we searched for the best fitting apec model (with two temperature components) for collisionally ionized plasma with absorption (nH) and an additional zero-width Gaussian line. The normalisation of the Gaussian was allowed to be negative to avoid bias. The spectrum was grouped to contain a minimum of 22 raw counts in each bin (using grppha) and we used the range from 2 to 5 keV for fitting the spectral model to the data (using χ2 statistics). Free parameters of the fit were the normalisation of the spectral components, the temperatures, and the relative abundances of the apec models.
Once the best fit was identified, we calculated the confidence intervals (99.7 per cent) for the additional flux added by the Gaussian using a Monte Carlo Markov chain (MCMC) with a length of 104 and a burn-in length of 103. The average best fit parameters of the apec models are (left free for each individual fit): foreground absorption by neutral hydrogen nH ≈ 0.5 × 1022 cm−2 (same for both components), temperature of the first model: kT1 ≈ 0.9 keV, second temperature: kT2 ≈ 0.7 keV, metallicity: Z ≈ 0.7 Z⊙ (same for both models), and goodness of fit: 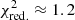 (consistent with Suzaku measurements in the region by Nakashima et al. 2013).
(consistent with Suzaku measurements in the region by Nakashima et al. 2013).
3. Dark matter mass model
Driven by data from the Gaia satellite, over the coming years the distribution of dark matter within the Milky Way will be clarified. Presently however, the dark matter profile of the Milky Way remains uncertain, particularly in the Baryon-dominated inner regions which the LW probes (for a review see Bland-Hawthorn & Gerhard 2016). The most direct estimates of the stellar surface density in the direction of the LW come from measurements of the microlensing optical depth towards the Bulge (Wegg et al. 2016). Our dark matter profile leaves sufficient baryonic mass remaining from the mass budget allowed by the Galactic rotation curve to satisfy these microlensing constraints.
Our fiducial dark matter profile is that found in Portail et al. (2017, hereafter P17) by fitting triaxial dynamical models of the barred bulge to a range of photometric and spectroscopic data on the stars in the inner Galaxy. These models constrained the amount of dark matter in the central 2 kpc of the Galaxy, and P17 found that to also simultaneously match the Galactic rotation curve and local constraints, a cored Einasto profile was preferred. The best fitting model from P17 has a dark matter profile which is flattened with axis ratio q = 0.8 and can be parameterized using the ellipsoidal radius 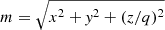 as
as
with ρ0 = 0.018 M⊙ pc−3, m0 = 7.1 kpc, α = 0.77. This corresponds to a dark matter density at the Sun of ρdm,⊙ = 0.013 M⊙ pc−3 = 0.50 GeV c−2 cm−3, consistent with recent estimates (e.g. Read 2014).
In the LW this model corresponds to a column density of SDM = 1.1 × 109 M⊙ kpc−2. However, because of the uncertainty in the DM profile of the Milky Way, in Sects. 4 and 5 we discuss the freedom there remains to alter these column densities.
4. Flux and mixing angle constraints
We obtained a 3σ upper flux limit of ∼1.5 × 10−6 cts cm−2 s−1 (see Fig. 1) which translates to a sterile neutrino mixing angle upper-limit of sin2(2Θ) ≲ 7.7 × 10−11, assuming all DM is made up of 7.1 keV sterile neutrinos. The best fit values and 1σ uncertainties are 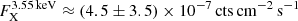 and sin2(2Θ) ≈ (2.3 ± 1.8) × 10−11.
and sin2(2Θ) ≈ (2.3 ± 1.8) × 10−11.
 |
Fig. 1. Limiting Window ∼1 Ms Chandra spectrum with constraints on an additional 3.55 keV Gaussian line on top of a standard two-temperature apec model. Uncertainties are given at 99.7 percent confidence range (∼3σ). Residuals are given as a percentage deviation from the model. Red residuals are for the model with the minimum allowed flux and blue for the model with maximum flux in the additional Gaussian line. |
Figure 1 shows the best fit and limits for the additional Gaussian line at 3.55 keV. Figure 2 and Table 1 show the best-fit and limits in flux for a range of energies between the two stronger line complexes of Sulfur (S) and Argon (Ar) at about 3.0–3.2 keV and Calcium (Ca) at about 3.8–4.0 keV. In addition we show best-fit and limits derived from a simulated spectrum with the same properties, but no line at 3.55 keV, analysed in the same way. Fluctuations of 1−2σ also appear in the simulation, but have a different form and are overall zero in the range analysed. In contrast the real data show a continuous increase towards the energy of 3.55 keV. Figure 2 shows the expected flux, scaling the detections of Boyarsky et al. (2014) in M 31, those of Bulbul et al. (2014) in clusters of galaxies, and those of Boyarsky et al. (2018) in Galactic halo observations with XMM-Newton.
 |
Fig. 2. Best-fit and 1σ limits (solid line and shaded region, respectively) on additional Gaussian flux in the LW X-ray spectrum at different energies. The dashed line and shaded region show the results for a simulated spectrum without any additional line. The 3σ uncertainties are plotted as dotted lines. The black crosses show the expected flux from selected previous detections of the line with 1σ uncertainties in flux and the typical energy resolution of the instruments (∼100 eV). The second y axis shows the corresponding mixing angle. |
Additional Gaussian flux allowed (fit in 2.5–5.0 keV range) at different line energies.
Systematic uncertainties in the DM mass models but also underestimated plasma emission lines in the 3.55 keV range could cause the observed tension. Figure 2 shows that there is good agreement of the XMM-Newton measurement of Boyarsky et al. (2018). The offset to the values from Bulbul et al. (2014) and Boyarsky et al. (2014) could be explained if the normalization of the Galactic DM profile was a factor of about two lower than the estimate from P17. This lies at the boundary of conceivable column densities in the Milky Way: even using a relatively low dark matter contribution to the circular velocity near the Sun of Vc,dm ≈ 100 km s−1 (Bovy & Rix 2013) and making the extreme assumption that this mass is a constant density sphere only reduces the dark matter column density towards the LW by a factor of approximately two to ∼0.6 × 109 M⊙ kpc−2. This is because our fiducial dark matter profile already has an approximately kiloparsec-size core, meaning there is relatively little freedom to increase the mixing angle by reducing the dark matter column density. The tension with Boyarsky et al. (2014) in M 31 may be reduced by different dark matter mass modelling in which considerable uncertainty remains (e.g. using the new models of M 31 produced by Blaña Díaz et al. 2018).
5. Discussion
Debate over the ∼7 keV sterile neutrino decay line continues, with no definite answer in favour of or against it. There have been several recent studies reaching almost 3σ exclusions (e.g. Anderson et al. 2015; Jeltema & Profumo 2016; Aharonian et al. 2017) and studies with detections of about the same significance (e.g. Neronov et al. 2016; Cappelluti et al. 2018; Franse et al. 2016; Bulbul et al. 2016). The recent debate suggests that unaccounted-for systematic uncertainties in the analysis from instruments, spectral- (Hitomi Collaboration 2018), and DM mass-modelling cause these differences. Future high-spectral resolution instruments like XRISM (Tashiro et al. 2018) will help to reduce systematic uncertainties in the spectral modelling and instrument calibration.
We were looking for the best archival datasets to constrain the line emission and identified a ∼1 Ms Chandra ACIS-I observation of the LW towards the GB among the best. This observation maximizes the expected DM decay flux, because the GB is the closest and highest DM column density object in the sky (Lovell et al. 2019).
In addition, the low foreground absorption of ∼5 × 1021 cm−2 allows us to resolve a large fraction of point sources which could contaminate the spectrum. The remaining ∼1 keV plasma emission leads to a lower continuum contribution at 3.5 keV compared to hotter objects like clusters of galaxies. The Chandra observations are mostly (∼90 percent of time) very long single exposures taken within the year 2008, limiting possible systematic uncertainties when adding many observations taken over a long period (e.g. better average response approximation).
The presented analysis focuses on minimizing systematics by using the latest available spectral models (Sect. 2), a very well understood, deep dataset, and the latest models of the expected DM mass in the FOV.
There have been many attempts to explain the line emission with alternative DM scenarios (e.g. Conlon et al. 2017) or with other unknown processes without the necessity for a DM interpretation (Gu et al. 2015; Shah et al. 2016). We focused on the DM interpretation, because the HITOMI results (Aharonian et al. 2017) excluded many other proposed explanations. Charge exchange between materials with different temperatures however remains a viable explanation for at least part of the line strength and would be expected in the LW. The HITOMI high-resolution X-ray spectroscopy data of the Perseus cluster were not quite deep enough to constrain the possible DM line if it is broadened by the expected DM velocity ∼1300 km s−1 (Aharonian et al. 2017).
Recent constraints further encouraged soft X-ray observations of the GB area as one of the best targets for DM annihilation line searches. Lovell et al. (2019) discussed an overview identifying the highest flux targets for DM decay line searches and Abazajian (2017) and Adhikari et al. (2017) summarise the current state of the 3.55 keV line discussion. At higher energies the existence of unknown lines has been further constrained by Ng et al. (2019).
Boyarsky et al. (2018) analysed the surface brightness profile of the line in the halo of the Galaxy. Their findings are consistent with ours within uncertainties. Our 3.55 keV surface brightness value of 0.09 ± 0.05 ph cm−2 s−1 sr−1 agrees very well with the Galactic DM profile and measurements of these latter authors (assuming a quantum efficiency of about 90 percent for Chandra ACIS-I at 3.55 keV; see Fig. 3). The constraints in the LW are consistent with the upper limit from Dessert et al. (2018) in the Galactic halo within uncertainties.
 |
Fig. 3. Upper panel: Boyarsky et al. (2018): B18 surface brightness expectations for an NFW DM profile of the Galaxy. Portail et al. (2017): P17 DM profile using B18 decay time of sterile neutrinos. The red data point shows the best-fit value with uncertainties from this work. The shaded area indicates where the DM mass models and X-ray measurements become more uncertain. Lower panel: as in upper plot, but with data points showing expectations for eROSITA extrapolating from the B18 measurements assuming the errors scale with the root of the relative observation time i.e. that the grasp and background of XMM and eROSITA at 3.5 keV are the same. As an all-sky survey, eROSITA will either accurately measure or rule out the 3.5 keV line from the wealth of observations far from the Galactic centre where the astrophysical backgrounds are low. |
6. Conclusions and outlook
-
We used an X-ray dataset in a region with high dark matter column density, but low astrophysical backgrounds due to the high fraction of resolved sources and low gas temperature.
-
We present a DM mass model for the analysed FOV which was derived from state-of-the-art dynamical models of the inner Galaxy.
-
We find some tension with previous measurements of the 3.55 keV line. The allowed upper limit for the mixing angle in the 7.1 keV sterile neutrino scenario would be sin2(2Θ) ≲ 7.7 × 10−11 (3σ confidence level). The 1.5σ positive best-fit flux would translate to sin2(2Θ) ≈ (2.3 ± 1.8) × 10−11 (1σ uncertainty).
-
An alternative explanation for the marginal detections and the tension between them remains to be underestimated systematic uncertainties in calibration of the instruments and modelling of the X-ray emission lines.
The 7.1 keV sterile neutrino remains one of the most easily tested DM candidates for the coming decade especially with new instruments, but there are still possibilities to improve constraints from currently available data. There is the possibility to expand the study to a recently completed XMM-Newton GB survey with approximately 500 times the FOV area (Ponti et al. 2019), but about 40 times less average exposure and a more complicated mix of plasma emission as well as much higher contribution from unresolved point sources (more difficult to remove due to lower spatial resolution and shallower exposure). A followup analysis to this work using the additional data might provide improved constraints.
The eROSITA telescope will perform the first all-sky X-ray survey in the 3.5 keV range (Merloni et al. 2012). With its all-sky coverage and comparable grasp at 3.5 keV with respect to XMM-Newton we expect to improve the current constraints from Galactic DM halo observations considerably. The largest uncertainty in the ability of eROSITA to constrain the 3.5 keV line is the level of background. In Fig. 3 we have assumed the same background as XMM-Newton, but envisage that from its observation point at L2 (second Lagragian point of the Sun-Earth system) the background might be lower, and therefore the performance better than this conservative assumption.
The lower panel of Fig. 3 shows the expected 3.5 keV surface brightness profile extrapolating from Boyarsky et al. (2018) after the four-year survey (scan number eRASS8). The XRISM telescope with its high spectral resolution in combination with the eROSITA all-sky coverage will allow for the nature of the line to be determined and the ATHENA observatory (Nandra et al. 2013) will improve constraints even further.
Acknowledgments
We thank the anonymous referee for comments which helped to improve the clarity of the paper, E. Bulbul and K. Abazajian for helpful discussions, and C. Pulsoni for comments on the manuscript. We acknowledge the use of data obtained from the Chandra Data Archive and software provided by the Chandra X-ray Center (CXC) in the application package CIAO; NASA’s Astrophysics Data System; SAOImage DS9, developed by Smithsonian Astrophysical Observatory; data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory; use of the python packages matplotlib, scipy, numpy, and pyXSPEC. F. Hofmann acknowledges financial support from the BMWi/DLR grant FKZ 50 OR 1715. C. Wegg acknowledges funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 798384.
References
- Abazajian, K. N. 2017, Phys. Rep., 711, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K., Fuller, G. M., & Tucker, W. H. 2001, ApJ, 562, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, R., Agostini, M., Ky, N. A., et al. 2017, J. Cosmol. Astropart. Phys., 2017, 025 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Akamatsu, H., Akimoto, F., et al. 2017, ApJ, 837, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anderson, M. E., Churazov, E., & Bregman, J. N. 2015, MNRAS, 452, 3905 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, S. S. Holt& G. Sonneborn, 99, 409 [Google Scholar]
- Blaña Díaz, M., Gerhard, O., Wegg, C., et al. 2018, MNRAS, 481, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Iakubovskyi, D., Ruchayskiy, O., & Savchenko, V. 2008a, MNRAS, 387, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., & Markevitch, M. 2008b, ApJ, 673, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., & Shaposhnikov, M. 2009, Annu. Rev. Nucl. Part. Sci., 59, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., & Franse, J. 2014, Phys. Rev. Lett., 113, 251301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyarsky, A., Iakubovskyi, D., Ruchayskiy, O., & Savchenko, D. 2018, ArXiv e-prints [arXiv:1812.10488] [Google Scholar]
- Boyarsky, A., Drewes, M., Lasserre, T., Mertens, S., & Ruchayskiy, O. 2019, Prog. Part. Nucl. Phys., 104, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Markevitch, M., Foster, A., et al. 2014, ApJ, 789, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Markevitch, M., Foster, A., et al. 2016, ApJ, 831, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Bulbul, E., Foster, A., et al. 2018, ApJ, 854, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Conlon, J. P., Day, F., Jennings, N., Krippendorf, S., & Rummel, M. 2017, Phys. Rev. D, 96, 123009 [NASA ADS] [CrossRef] [Google Scholar]
- Dessert, C., Rodd, N. L., & Safdi, B. R. 2018, ArXiv e-prints [arXiv:1812.06976] [Google Scholar]
- Dodelson, S., & Widrow, L. M. 1994, Phys. Rev. Lett, 72, 17 [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Franse, J., Bulbul, E., Foster, A., et al. 2016, ApJ, 829, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, Proc. SPIE Conf. Ser., 6270, 62701V [CrossRef] [Google Scholar]
- Garmire, G. P., Bautz, M. W., Ford, P. G., Nousek, J. A., & Ricker, G. R. 2003, in X-Ray and Gamma-Ray Telescopes and Instruments for Astronomy, eds. J. E. Truemper, & H. D. Tananbaum, SPIE Conf. Ser., 4851, 28 [Google Scholar]
- Graessle, D. E., Evans, I. N., Glotfelty, K., et al. 2007, Chandra News, 14, 33 [NASA ADS] [Google Scholar]
- Gu, L., Kaastra, J., Raassen, A. J. J., et al. 2015, A&A, 584, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herms, J., Ibarra, A., & Toma, T. 2018, J. Cosmol. Astropart. Phys., 2018, 036 [CrossRef] [Google Scholar]
- Hitomi Collaboration, (Aharonian, F., et al.) 2018, Publ. Astron. Soc. Jpn, 70, 12 [Google Scholar]
- Hofmann, F., Sanders, J. S., Nandra, K., Clerc, N., & Gaspari, M. 2016a, A&A, 585, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hofmann, F., Sanders, J. S., Nandra, K., Clerc, N., & Gaspari, M. 2016b, A&A, 592, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeltema, T., & Profumo, S. 2016, MNRAS, 458, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, S. K., & Patra, A. 2016, J. Korean Phys. Soc., 69, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Lovell, M. R., Barnes, D., Bahé, Y., et al. 2019, MNRAS, 485, 4071 [NASA ADS] [CrossRef] [Google Scholar]
- Merle, A., & Schneider, A. 2015, Phys. Lett. B, 749, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Nakashima, S., Nobukawa, M., Uchida, H., et al. 2013, ApJ, 773, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Neronov, A., Malyshev, D., & Eckert, D. 2016, Phys. Rev. D, 94, 123504 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, K. C. Y., Roach, B. M., Perez, K., et al. 2019, Phys. Rev. D, 99, 083005 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Hofmann, F., Churazov, E., et al. 2019, Nature, 567, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Portail, M., Gerhard, O., Wegg, C., & Ness, M. 2017, MNRAS, 465, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I. 2014, J. Phys. G Nucl. Phys., 41, 063101 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Sazonov, S., Churazov, E., et al. 2009, Nature, 458, 1142 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sanders, J. S. 2006, MNRAS, 371, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Shah, C., Dobrodey, S., Bernitt, S., et al. 2016, ApJ, 833, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Tashiro, M., Maejima, H., Toda, K., et al. 2018, SPIE Conf. Ser., 10699, 1069922 [Google Scholar]
- Wegg, C., Gerhard, O., & Portail, M. 2016, MNRAS, 463, 557 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Additional Gaussian flux allowed (fit in 2.5–5.0 keV range) at different line energies.
All Figures
 |
Fig. 1. Limiting Window ∼1 Ms Chandra spectrum with constraints on an additional 3.55 keV Gaussian line on top of a standard two-temperature apec model. Uncertainties are given at 99.7 percent confidence range (∼3σ). Residuals are given as a percentage deviation from the model. Red residuals are for the model with the minimum allowed flux and blue for the model with maximum flux in the additional Gaussian line. |
| In the text | |
 |
Fig. 2. Best-fit and 1σ limits (solid line and shaded region, respectively) on additional Gaussian flux in the LW X-ray spectrum at different energies. The dashed line and shaded region show the results for a simulated spectrum without any additional line. The 3σ uncertainties are plotted as dotted lines. The black crosses show the expected flux from selected previous detections of the line with 1σ uncertainties in flux and the typical energy resolution of the instruments (∼100 eV). The second y axis shows the corresponding mixing angle. |
| In the text | |
 |
Fig. 3. Upper panel: Boyarsky et al. (2018): B18 surface brightness expectations for an NFW DM profile of the Galaxy. Portail et al. (2017): P17 DM profile using B18 decay time of sterile neutrinos. The red data point shows the best-fit value with uncertainties from this work. The shaded area indicates where the DM mass models and X-ray measurements become more uncertain. Lower panel: as in upper plot, but with data points showing expectations for eROSITA extrapolating from the B18 measurements assuming the errors scale with the root of the relative observation time i.e. that the grasp and background of XMM and eROSITA at 3.5 keV are the same. As an all-sky survey, eROSITA will either accurately measure or rule out the 3.5 keV line from the wealth of observations far from the Galactic centre where the astrophysical backgrounds are low. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



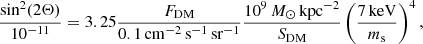
![$$ \begin{aligned} \rho _{\rm dm} = \rho _{\rm 0} \exp \left\{ -\frac{2}{\alpha }\left[ \left(\frac{m}{m_0}\right)^\alpha - 1\right]\right\} , \end{aligned} $$](/articles/aa/full_html/2019/05/aa35561-19/aa35561-19-eq5.gif)