| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527706 | |
| Published online | 29 June 2016 | |
The far-infrared emitting region in local galaxies and QSOs: Size and scaling relations
1 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
e-mail: lutz@mpe.mpg.de
2 School of Physics and Astronomy, Tel Aviv University, 69978 Tel Aviv, Israel
3 Department of Astronomy, University of Maryland, College Park, MD 20742, USA
Received: 6 November 2015
Accepted: 13 May 2016
We use Herschel 70 to 160 μm images to study the size of the far-infrared emitting region in about 400 local galaxies and quasar (QSO) hosts. The sample includes normal “main-sequence” star-forming galaxies, as well as infrared luminous galaxies and Palomar-Green QSOs, with different levels and structures of star formation. Assuming Gaussian spatial distribution of the far-infrared (FIR) emission, the excellent stability of the Herschel point spread function (PSF) enables us to measure sizes well below the PSF width, by subtracting widths in quadrature. We derive scalings of FIR size and surface brightness of local galaxies with FIR luminosity, with distance from the star-forming main-sequence, and with FIR color. Luminosities LFIR~ 1011 L⊙ can be reached with a variety of structures spanning 2 dex in size. Ultraluminous LFIR≳ 1012 L⊙ galaxies far above the main-sequence inevitably have small Re,70~ 0.5 kpc FIR emitting regions with large surface brightness, and can be close to optically thick in the FIR on average over these regions. Compared to these local relations, first ALMA sizes for the dust emission regions in high redshift galaxies, measured at somewhat longer rest wavelengths, suggest larger sizes at the same IR luminosity. We report a remarkably tight relation with 0.15 dex scatter between FIR surface brightness and the ratio of [Cii] 158 μm emission and FIR emission – the so-called [Cii]-deficit is more tightly linked to surface brightness than to FIR luminosity or FIR color. Among 33 z ≤ 0.1 PG QSOs with typical LFIR/LBol,AGN ≈ 0.1, 19 have a measured 70 μm half light radius, with median Re,70 = 1.1 kpc. This is consistent with the FIR size for galaxies with similar LFIR but lacking a QSO, in accordance with a scenario where the rest FIR emission of these types of QSOs is, in most cases, due to host star formation.
Key words: Galaxy: structure / galaxies: starburst / galaxies: active
© ESO, 2016
1. Introduction
The rate of star formation (SFR) is a primary characterizing quantity of any galaxy, and its spatial distribution holds important clues about its driving mechanisms. Over recent years, it has been established that most stars form in galaxies on a star-forming main-sequence (MS) in the M∗-SFR plane (see, e.g., Brinchmann et al. 2004 and Schiminovich et al. 2007 for the local universe and many works for redshifts up to 2 and more). These main-sequence galaxies are typically disk dominated objects (e.g., Wuyts et al. 2011; Wisnioski et al. 2015), and existence and tightness of the star-forming main-sequence imply a rather steady star formation history in these objects. On the other hand, the most intense star formation in the local universe occurs in (ultra)luminous infrared galaxies ((U)LIRGs) that are closely related to galaxy interaction or mergers (Sanders & Mirabel 1996, and references therein). These objects are well above the main-sequence, and their extreme star formation is certainly episodic. Understanding the role of steady processes, dramatic mergers, and the impact of active galactic nuclei on the level and distribution of star formation, and on its ultimate quenching, is a centerpiece of galaxy evolution studies.
Star formation in most local galaxy disks can be traced well by a variety of UV to near-IR indicators. This gets difficult if not impossible in the heavily dust-obscured IR luminous systems, where the short wavelength tracers reach only a surface layer. Longer wavelength tracers have been used instead to map star formation at sufficient spatial resolution. Resolution should be a few arcsec, or better reach down to sub-arcsec levels for optimal study of local IR-luminous systems. These tracers include mostly radio continuum (e.g., Condon et al. 1990), mid-infrared continuum and emission features (e.g., Soifer et al. 2000, 2001; Díaz-Santos et al. 2010, 2011), but also mm interferometry to the extent one can constrain the distribution of star formation from the distribution of dust or gas mass (e.g., Sakamoto et al. 1999). Each of these approaches has its particular strengths and weaknesses, related to the tightness of the link between the particular tracer and SFR, to the possible contamination by other sources such as AGN or dust heated by old stars, as well as to technicalities of available beam sizes, coverage of all relevant spatial frequencies in interferometry, and size of samples that can be realistically observed. But a clear finding is that some IR-luminous systems are characterized by very compact star formation (e.g., Condon et al. 1991).
A powerful approach uses high spatial resolution measurements of the far-infrared emission near the ~100 μm SED peak where the energy of obscured star formation is re-radiated by the dust “calorimeter”. Because of the favourable contrast of this peak to the emission that may be heated by an AGN proper, this also is arguably the best chance to map star formation in the presence of fairly powerful AGN. But sensitive far-infrared interferometry will not be available soon, and the first cryogenic space telescopes such as IRAS, ISO, Spitzer, and Akari lacked the necessary spatial resolution in the far-infrared. The best tool for the foreseeable future is the Herschel1 (Pilbratt et al. 2010) database. While the full width at half maximum (FWHM) of the point spread function (PSF) at the shorter of the 70, 100 and 160 μm wavelengths covered by Herschel-PACS (Poglitsch et al. 2010) is of order 5′′, characteristic source sizes below that scale are still derivable from their broadening effect, given the intrinsic stability of the PSF. The present paper attempts this for a sample of ~400 galaxies, including normal near main-sequence as well as IR-luminous galaxies, and QSO hosts. This approach uses a tracer that is closely linked to SFR and can be applied homogeneously to hundreds of sources, but only delivers a characteristic size rather than detailed structure that would typically need sub-arcsecond interferometry. We adopt an Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1 cosmology, redshift-independent distances for some very local galaxies, a Chabrier (2003) IMF, a conversion SFR = 1.9 × 10-10LFIR = 40−120 μm as appropriate for the Kennicutt (1998) conversion corrected to Chabrier IMF, and a ratio 1.9 of 8–1000 μm and 40–120 μm luminosity that is typical for the non-QSO galaxies in our sample.
2. Data and analysis methods
We use 70, 100, and 160 μm images from scan maps obtained with PACS (Poglitsch et al. 2010) on board Herschel (Pilbratt et al. 2010), collecting archival data from various projects. In order to cover a wide range of galaxy properties, we first obtain an IR-selected local sample ranging from normal galaxies up to (ultra)luminous infrared galaxies. For that purpose, we searched the Herschel archive for all cz ≥ 2000 km s-1 objects from the IRAS Revised Bright Galaxy Sample (RBGS, Sanders et al. 2003). Various proposals included some RBGS galaxies, overall covering a wide range of IR luminosities from normal to ULIRG. Coverage of the RBGS sample by Herschel is excellent at LIRG and ULIRG luminosities, because project OT1_dsanders_1 systematically addressed these. Objects below the LIRG threshold enter our sample via the lower luminosity ones among the RBGS galaxies observed by other proposals, and because some IRAS-defined RBGS (U)LIRGs at the better Herschel resolution are found to be sub-LIRG pairs or have companions. Also, other galaxies are serendipitously found within the mapped area. For a better sampling of normal near-main-sequence galaxies, we also include KINGFISH (Kennicutt et al. 2011) galaxies. Since this work focusses on normal star-forming galaxies and starbursts, we excluded the few dwarfs and low mass systems below log (M∗) = 8.5 as well as the elliptical NGC 1404 that are part of the KINGFISH sample. Below, we refer to the combination of RBGS galaxies, KINGFISH galaxies, and the serendipitous galaxies included in our analysis as “galaxies”, with a total of 306 galaxies. Our study in addition includes Palomar-Green (PG, Boroson & Green 1992) QSOs from Herschel proposals OT1_lho_1, OT1_rmushotz_1, and OT1_hnetzer_1, (see Petric et al. 2015) to which we refer as “QSOs”. We have 93 sources labelled QSO in our sample, because 2 of the 87 Boroson & Green (1992) objects (PG1226+023 and PG1444+407) were not observed by PACS, but 8 QSOs of equivalent properties were additionally observed in OT1_lho_1 or OT1_hnetzer_1. To assess the stability of the point spread function, we use observations of reference stars that were obtained as part of the PACS calibration program.
Several mappers have been successfully used to derive images from the PACS data, which are characterized by significant 1/f noise in the individual detector timelines. Since our goal is to derive intrinsic FIR sizes by comparing the (slightly broadened) observed source FWHM to that of a PSF reference, we use the simplemost “masked highpass filtering” strategy which can produce a very stable PSF (see below). In that specific respect it is still superior to mappers such as, e.g., UNIMAP (Piazzo et al. 2015) or Scanamorphos (Roussel 2013). While having clear advantages in other respects, these mappers may sometimes produce residuals near very bright sources and/or slightly less stable PSF wings2.
The reduction follows the standard masked high pass filtering script provided with the Herschel HIPE software. To obtain the most stable PSF, we always use a 20′′ radius circular patch mask to exclude the source from the running median high pass filter. We always centered this patch mask on the actual source position. We start from the Herschel science archive pipeline version 13.0 “Level 1” data. This is important since version 13.0 for the first time implemented an improved reconstruction of the actual Herschel pointing, reducing effects on the PSF by uncorrected pointing jitter. From the maps we measure circularized Gaussian FWHMs, and aperture photometry centered on the source that is corrected to total fluxes using standard PACS encircled energy fraction curves. By default, we use apertures of diameter 14′′ at 70 and 100 μm and 24′′ at 160 μm. Larger apertures are used where required by a clearly extended morphology. We derive rest frame 40–120 μm luminosities LFIR by fitting SED templates from Berta et al. (2013) to the PACS fluxes and integrating the best fit template over that range. We use 40–120 μm LFIR rather than 8–1000 μm LIR because it is less AGN contaminated, better sampled by PACS, and one of the common conventions in the FIR literature going back to IRAS. Most sources have been observed with two different scan angles each in the 70 μm “blue” and 100 μm “green” band, each time simultaneously with the 160 μm “red” band. The two angles for one of the blue or green bands are almost always observed in immediate succession, while the other band may be obtained at a much later date. To mitigate any slight pointing shifts that can arise due to a different star tracker orientation or different Herschel thermal state between these two dates, we average images from the two scan angles before fitting and deriving fluxes, but average the “red” results from the two epochs only at the level of the derived FWHM and fluxes. With the exception of the source position that is used to center the map and the mask, all other reduction parameters are applied identically to all sources.
2.1. PSF stability
 |
Fig. 1 Measured FWHM at 70 μm (blue) and 100 μm (green) from 185 pairs of observations of 17 different reference stars. The resulting mean FWHM in arcsec and dispersion is indicated, as derived from bright sources in the flux range indicated by the horizontal line. |
To assess the stability of the PSF in our maps, we used the primary and secondary flux calibrators β And, α Ari, α Boo, ω Cap, α Cet, α CMa, γ Dra, δ Dra, β Gem, ϵ Lep, β Peg, α Tau, HD 41047, HD 138265, HD 139669, HD 159330, HD 170693. These were observed repeatedly (total 185 pairs of observations) as part of the PACS calibration program and cover a wide range of fluxes. Data were processed and Gaussian fitted exactly as for the science targets. Figure 1 shows the resulting PSF FWHM for the blue and green bands. Results are remarkably stable for bright ≳0.2 Jy stars, and do not show a trend with flux. The resulting mean FWHM and dispersion are 5.299′′ (dispersion 0.018′′) and 6.546′′ (dispersion 0.029′′) for the blue and green bands after clipping 2 (4) outliers, respectively. These few outliers do not represent problematic non-point sources, such as dust shell stars or multiple stars, since FWHM values consistent with the mean were obtained for the same objects at different epochs. They rather indicate that in a small ~3% of observations even the improved pipeline v13.0 pointing reconstruction has imperfections leading to slightly enhanced FWHM. A basic limit to the PSF stability in PACS scan observations is set by a random 0−25 ms synchronization jitter between instrument and pointing data, set at the start of an onboard control procedure. The effect of this jitter for the observing mode that we used is below the observed dispersion. An equivalent analysis of reference star observations for the red band provides circularized FWHM 10.632′′ (dispersion 0.118′′). We adopt these values as the FWHM and uncertainty of the PSF for a point source with Rayleigh-Jeans spectral slope, as reduced with our specific procedure.
2.2. Effects of source color
The considerable spectral width of the PACS filters leads to a dependence of PSF width on spectral shape. This is confirmed on sky3, but not accurately characterized empirically, due to the lack of bright celestial point sources with a variety of non-Rayleigh-Jeans slopes. We rather use “as built” Herschel modelled PSFs4 for a range of spectral slopes Sν ∝ λα, α = −2...4. To account for optical imperfections of PACS which are not included in the model PSFs, calibration uncertainties, and residual uncorrected pointing jitter these model PSFs were Gaussian convolved to match the observed stellar PSF FWHM for the case of a Rayleigh-Jeans spectral slope. Results imply that between α = −2 and α = 2, the PSF FWHM increases by about 2.0%, 3.4%, 5.5% for the blue, green, red band, respectively.
2.3. Determination of size of the far-infrared source
We attempt to measure sizes only for sources with integrated S/N ≥ 10 in the given photometric band. To the PACS maps we fit elongated 2d Gaussians using IDL mpfit2dpeak.pro and a consistent fit area for all sources, and derive the circularized 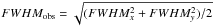 . We derive the intrinsic source FWHM by subtraction in quadrature
. We derive the intrinsic source FWHM by subtraction in quadrature 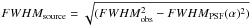 based on the PSF FWHM derived above and corrected to the spectral slope α that is matching the source’s PACS photometry. The subtraction in quadrature is strictly correct only for Gaussian structure of both source and PSF. We have verified that the non-gaussianity of the PSF leads to a systematic overestimate of the intrinsic FWHM of a Gaussian source by ≲10%. We do not attempt to correct for any specific value given it would only apply to a strictly Gaussian source structure. The error estimate for FWHMsource includes the uncertainty of FWHMobs due to the source’s S/N, the dispersion of bright reference stars around FWHMPSF, and the effect of the uncertainty in spectral slope. We consider a source as resolved if the difference of FWHMsource and FWHMPSF is larger than three times this error estimate. For brevity, we denote below with Re,70 the intrinsic half light radius at 70 μm (= 0.5 × FWHM for a Gaussian source), after conversion to a physical scale in kpc based on distances from redshift and our adopted cosmology, with the exception of redshift-independent distances for the KINGFISH sources which were taken from Kennicutt et al. (2011). Re,100 and Re,160 analogously denote the physical half light radii at the longer PACS wavelengths.
based on the PSF FWHM derived above and corrected to the spectral slope α that is matching the source’s PACS photometry. The subtraction in quadrature is strictly correct only for Gaussian structure of both source and PSF. We have verified that the non-gaussianity of the PSF leads to a systematic overestimate of the intrinsic FWHM of a Gaussian source by ≲10%. We do not attempt to correct for any specific value given it would only apply to a strictly Gaussian source structure. The error estimate for FWHMsource includes the uncertainty of FWHMobs due to the source’s S/N, the dispersion of bright reference stars around FWHMPSF, and the effect of the uncertainty in spectral slope. We consider a source as resolved if the difference of FWHMsource and FWHMPSF is larger than three times this error estimate. For brevity, we denote below with Re,70 the intrinsic half light radius at 70 μm (= 0.5 × FWHM for a Gaussian source), after conversion to a physical scale in kpc based on distances from redshift and our adopted cosmology, with the exception of redshift-independent distances for the KINGFISH sources which were taken from Kennicutt et al. (2011). Re,100 and Re,160 analogously denote the physical half light radii at the longer PACS wavelengths.
2.4. Resolved sources
The reduction described previously is optimized for sources with intrinsic width similar to or below the width of the PSF. This includes all the QSO hosts. For galaxies that are resolved over several beam widths, as frequently found among the nearby galaxies and less luminous IR selected objects, the specific masking/filtering strategy reduces the outermost emission. For objects that were found to be clearly extended on inspection of PACS maps and/or with an initial measured 70 μm FWHM above 12′′, we hence reverted to the V13.0 pipeline reduced “Level 2.5” JScanam (Graciá-Carpio et al. 2015) maps, or to the publicly released KINGFISH DR3 Scanamorphos maps. Intrinsic sizes were again derived by Gaussian fits and subtraction in quadrature of the circularized width. Both reductions give consistent results at intermediate source sizes.
2.5. Double or complex sources
Discussing physics of galaxies on the basis of sizes derived in this way is only meaningful if the size refers to a single galaxy, and not galaxy pairs or interacting systems. This is of course acknowledging that even in this case the size represents an overall scale of the galaxy’s FIR emission, that may encompass significant substructure. The measured size is not meaningful for interacting systems that have a separation of the components of order the PSF width, and down to the scales accessible to the method. The measurement then mostly reflects distance and relative strength of FIR emission of the two galaxies rather than the structure of a galaxy. We address this issue the following way:
-
Wide ≳1′ double systems with well separated galaxies and redshifts available for both were processed separately for both components, and both galaxies are used in the analysis.
-
Wide and ~0.5′ intermediate doubles where galaxies overlap and/or high pass filtering affects the structure of the respective other component were discarded. These would need mapping and fitting strategies beyond the scope of this work, in order to measure high accuracy FIR sizes. A few intermediate scale doubles were kept if the secondary component was clearly below 1/10 of the primary component’s flux and not affecting the width measurement.
-
Sizes were measured for single and close ≲10′′ double sources. However, where inspection of multiwavelength data accessible via NED and the literature (e.g., Bahcall et al. 1997; Scoville et al. 2000; Guyon et al. 2006; Haan et al. 2011; Kim et al. 2013; Petty et al. 2014; Surace et al. 2001; Veilleux et al. 2006, 2009a) indicated that the source is in fact a close double/interacting system, the source was flagged even if a double nature is not evident in the Herschel images. These flagged sources are not used in the analysis below, unless explicitly mentioned.
In summary, size measurements are obtained for single galaxies (including advanced mergers) and for widely separated interacting systems, but disfavour close interacting systems with separation of order the galaxy size, and where both components emit in the FIR. Our size measurements are summarized in Table A.1.
3. Results
 |
Fig. 2 Intrinsic half light radii of galaxies and QSOs in the 70 μm blue band as a function of redshift. Symbols or limit for QSOs are encircled in green. The blue line indicates the physical size corresponding to the half width at half maximum of the PACS point spread function at that wavelength. Pink symbols mark results for close doubles/pairs. These are not used below unless explicitly mentioned. The most local galaxies have been placed at z = 0.002 to limit plot size. A number of galaxies with very compact FIR regions are identified. For many bright and large targets, error bars are smaller than the symbol size. Lower redshift galaxies with typically higher S/N can be resolved to smaller fractions of the PSF than the fainter QSOs. |
Figure 2 shows the derived intrinsic half light radii Re,70 (effective radii) in the 70 μm blue band as a function of redshift. The 355 of 399 sources that have a photometric S/N> 10 in that band are plotted. The blue line indicates the physical size corresponding to the half width at half maximum of the PSF. In comparison to the data, this suggests that in cases with favourably high S/N the broadening by a source with intrinsic Gaussian FWHM about one fifth of the PSF FWHM is still detectable and leads to a size measurement, i.e. the difference of source and PSF size is at least three times the error. For this sample, almost all z< 0.1 results are actual measurements and upper limits only become common for the sources at z> 0.1, all from the QSO sample. Limits in the plot are placed at twice the error plus the larger of the nominal measurement and zero. There is a two order of magnitude spread in the measured intrinsic FIR sizes of the non-QSO targets. Section 4.1 discusses scalings with basic quantities that are contributing to this spread.
Signal-to-noise and PSF width lead to the largest fraction of significant size measurements being obtained in the 70 μm blue band. It is 81% compared to 80% at 100 μm and 71% at 160 μm, where the remaining objects include systems with both upper limits and photometric S/N< 10 in a band, which were not probed for size. We focus our analysis on 70 μm because of that, and because in star-forming galaxies 70 μm emission is more tightly linked to SFR than longer far-infrared wavelengths. (e.g., Calzetti et al. 2010).
Still, a comparison between sizes for different wavelengths in the same sources is in place. Figure 3 shows size ratios for the green/blue and red/blue bands, for sources with a significant size measurement in both bands. Many sources show slightly larger sizes at the longer wavelength, but still close to the 70 μm size. This is plausible given the typically negative outward dust temperature gradients in galaxies (e.g., Hunt et al. 2015). Sources with a 70 μm size measurement but unresolved at the longer wavelengths with their larger PSF will also be consistent with such size ratios near 1. There is however a significant tail to the distribution, up to size ratio Re,100/Re,70~ 5 in green vs. blue and Re,160/Re,70~ 10 in red vs. blue. Since many of these objects with large size ratios are well resolved nearby targets, visual inspection of the maps helps to identify the cause. They typically show a warm central source, e.g., a circumnuclear starburst, superposed on a larger disk with star-forming regions and with diffuse emission that is more prominent at 160 μm. A single component Gaussian fit may then emphasize the central component at 70 μm, and the disk at 160 μm. A similar argument as for a circumnuclear starburst applies if there is AGN-heated near-nuclear dust. A clear example for the effect of a central starburst is NGC 1097, where the 70 μm fit gives FWHM~ 20′′, driven by the well-known prominent r ~ 900 pc circumnuclear starburst ring (e.g., Sandstrom et al. 2010), while the 160 μm fit returns FWHM~ 2′ because of the relatively stronger emission from the diffuse disk (see also inset to Fig. 3). This is obviously a consequence of fitting a one component Gaussian in a situation where a two component fit with a wavelength dependent weight would be more appropriate. For consistency with the analysis of the majority of targets that are somewhat broadened compared to the PSF, but not well resolved, and to typical high-z observations, we adopt single component fits in the following discussion. We use 70 μm because of the smallest PSF and the closer link of emission at this wavelength to SFR for star-forming galaxies.
 |
Fig. 3 Histograms of the ratio of the intrinsic half light radius in the 100 μm (160 μm) band to the half light radius in the 70 μm band, for sources with significant measurements in either band. The numbers of sources with a measurement at 70 μm but only a limit at the longer wavelength are listed in the top left, these will typically have size ratios ~1–2. The case of NGC 1097 (insets) visualizes how a warm central starburst superposed on a cold large disk can cause large ratios Re,160/Re,70 from fitting single Gaussians. Overplotted to the inset for each band are the ellipses at half maximum of the elongated Gaussian fit (black) and the beam (red, bottom right). |
 |
Fig. 4 Scalings of half light radius at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with far-infrared luminosity. 251 galaxies with LFIR>109 L⊙ are included to avoid dwarfs and faint companions. The red line is a power law fit. In the left panel, sizes derived in the literature for high redshift submm galaxies at longer rest wavelengths ~150−400 μm are included for comparison (pink symbols). These were not used for the fit. |
Size differences in the PACS bands up to a factor of few warrant a word of caution towards the interpretation of interferometric (sub)mm continuum images of high redshift galaxies. With few exceptions, they are taken at rest wavelengths clearly longer than 160 μm, and may often not have the quality for well resolved maps or complex models. The measured sizes may hence overestimate the size of the star-forming region that is of interest for, e.g., studies of the Kennicutt-Schmidt relation. Continuum fluxes on the Rayleigh-Jeans tail of the SED are proportional to dust mass and (linearly) to dust temperature. Such long wavelength interferometric maps hence more directly trace the dust surface density rather than the SFR surface density. If the dust properties and dust-to-gas ratio are well constrained, these long wavelength continuum fluxes are a better probe of the gas surface density than of the SF surface density in the Kennicutt-Schmidt relation. Of course, gas-rich high-z systems may have different structure and quantitative size ratios between different rest wavelengths than local galaxies of similar SFR. For example, high-z galaxies with intense star formation throughout the disks (e.g., Förster Schreiber et al. 2009; Nelson et al. 2016) will almost certainly show lower ratios between size at longer wavelengths and size at rest 70 μm than the extreme values in a few local LIRGs with a quite passive disk and a bright circumnuclear starburst – these may in fact be a poor analog to high redshift galaxies of similar SFR. But even if sizes likely differ by smaller factors, the caveat is relevant at high redshift as it is locally.
4. Discussion
4.1. Scalings of FIR source size and surface brightness with FIR luminosity, main-sequence offset, and FIR color
 |
Fig. 5 Scalings of FWHM size at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with distance from the Renzini & Peng (2015) star-forming main-sequence. The figure includes 86 galaxies with published stellar masses. The red line is a power law fit. Vertical dotted lines indicate a range of ±0.6 dex around the main-sequence, as often used to separate main-sequence galaxies from bursting or passive objects. |
The very large ~2 dex spread in size of the FIR emitting regions motivates an investigation of possible links with basic galaxy parameters. We start with the 40−120 μm luminosity LFIR. Figure 4 left indicates a decrease of size with increasing FIR luminosity. Using mpfitexy.pro (Williams et al. 2010) to fit a log-linear relation (power law) we obtain: 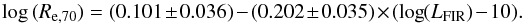 (1)We may also investigate the far-infrared surface brightness
(1)We may also investigate the far-infrared surface brightness 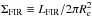 , noting that for a Gaussian source the half light radius Re equals to FWHM/2. Figure 4 right shows the strong increase of surface brightness with LFIR, which is fit by
, noting that for a Gaussian source the half light radius Re equals to FWHM/2. Figure 4 right shows the strong increase of surface brightness with LFIR, which is fit by 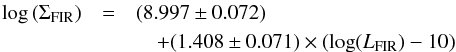 (2)and
(2)and 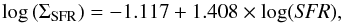 (3)where the second equation for the surface density of SFR (M⊙ yr-1 kpc-2) uses our adopted linear conversion SFR = 1.9 × 10-10LFIR. Uncertainties are hence the same as for ΣFIR. Both ΣFIR and ΣSFR refer to the plane of the sky. We did not attempt to correct for inclination, given that interacting systems can have complex morphologies and/or the inclination is not constrained for the FIR emitting regions. The increase of far-infrared surface brightness and SFR surface density with LFIR is clearly super-linear, due to a combination of the trivial increase with luminosity and the decreasing size.
(3)where the second equation for the surface density of SFR (M⊙ yr-1 kpc-2) uses our adopted linear conversion SFR = 1.9 × 10-10LFIR. Uncertainties are hence the same as for ΣFIR. Both ΣFIR and ΣSFR refer to the plane of the sky. We did not attempt to correct for inclination, given that interacting systems can have complex morphologies and/or the inclination is not constrained for the FIR emitting regions. The increase of far-infrared surface brightness and SFR surface density with LFIR is clearly super-linear, due to a combination of the trivial increase with luminosity and the decreasing size.
We also investigate the relation of size Re,70 and surface brightness ΣFIR to the distance of a galaxy from the star-forming main-sequence. Here we adopt as location of the main-sequence in the local universe log (SFR) = 0.76 × log (M∗)−7.64 (Renzini & Peng 2015) and its equivalent main-sequence specific star formation rate sSFRMS. Stellar masses for part of our sample are available from Kennicutt et al. (2011) and from U et al. (2012). Concerning the U et al. stellar masses we adopt log (Mfit)Cha from their Table 10 and exclude objects where their stellar mass combines two galaxies that we separate with Herschel. For our sample selected to contain many (U)LIRGs, 50% of the sources with a stellar mass assigned have log (sSFR/sSFRMS) > 0.6, a commonly adopted division between main-sequence galaxies and starbursting outliers above the main-sequence (Rodighiero et al. 2011). Figure 5 shows the trends for Re,70 and ΣFIR with distance from the main-sequence. Excluding a few semi-passive KINGFISH objects at log (sSFR/sSFRMS) < −0.5 we obtain:  Correlations also exist between Re,70 or ΣFIR and sSFR. This is expected from the trends shown with sSFR/sSFRMS, given that the adopted main-sequence slope is not too far from one in SFR vs. M∗, i.e. quite flat in sSFR. The IR selected (U)LIRGs reach up to sSFR ≳ 10-9 yr-1 and ΣSFR ~ 100M⊙ yr-1 kpc-2, well above the range of the local universe normal and passive galaxies for which Wuyts et al. (2011) used optical diagnostics to study the relation of sSFR and surface density of star formation. A trend between (total) infrared surface brightness and sSFR for local galaxies was also noted by Elbaz et al. (2011; their Fig. 16), with some outliers possibly due to the use of mid-IR based sizes. When relating Re,70 and ΣFIR to stellar mass, the scatter is large and no strong trends are discernible.
Correlations also exist between Re,70 or ΣFIR and sSFR. This is expected from the trends shown with sSFR/sSFRMS, given that the adopted main-sequence slope is not too far from one in SFR vs. M∗, i.e. quite flat in sSFR. The IR selected (U)LIRGs reach up to sSFR ≳ 10-9 yr-1 and ΣSFR ~ 100M⊙ yr-1 kpc-2, well above the range of the local universe normal and passive galaxies for which Wuyts et al. (2011) used optical diagnostics to study the relation of sSFR and surface density of star formation. A trend between (total) infrared surface brightness and sSFR for local galaxies was also noted by Elbaz et al. (2011; their Fig. 16), with some outliers possibly due to the use of mid-IR based sizes. When relating Re,70 and ΣFIR to stellar mass, the scatter is large and no strong trends are discernible.
 |
Fig. 6 Scalings of FWHM size at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with PACS 70 to 160 μm color, for 260 galaxies. The inset to the right panel shows the relation as a function of dust temperature. |
Finally, relations exist between far-infrared color and size or surface brightness of the FIR emission. Figure 6 shows very clear trends of both quantities with the PACS color S70/S160. In particular the relation with ΣFIR is remarkable, and takes the form: 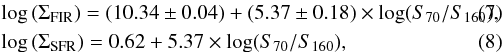 while the relation of size and color is
while the relation of size and color is 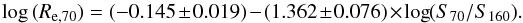 (9)A relation between ΣFIR and FIR color, which traces dust temperature, is certainly plausible and expected, but it is quite tight with a scatter of 0.6 dex in ΣFIR around a relation that covers more than five orders of magnitude in that quantity. This is notable because the relation compares a local quantity (the local radiation field intensity determining the dust temperature) with a surface brightness that is determined solely from global quantities of the galaxy (LFIR and FIR size). In contrast, the radiation field intensity to which the FIR emitting grains are exposed is influenced by the small scale distribution of stars and dust in star forming complexes as well as to the density with which sources of radiation are distributed over the total volume of the galaxy. In an extreme toy model, where one simply places more and more independent star-forming regions with identical FIR properties in the same area to drive up ΣSFR and ΣFIR, no such relation would exist.
(9)A relation between ΣFIR and FIR color, which traces dust temperature, is certainly plausible and expected, but it is quite tight with a scatter of 0.6 dex in ΣFIR around a relation that covers more than five orders of magnitude in that quantity. This is notable because the relation compares a local quantity (the local radiation field intensity determining the dust temperature) with a surface brightness that is determined solely from global quantities of the galaxy (LFIR and FIR size). In contrast, the radiation field intensity to which the FIR emitting grains are exposed is influenced by the small scale distribution of stars and dust in star forming complexes as well as to the density with which sources of radiation are distributed over the total volume of the galaxy. In an extreme toy model, where one simply places more and more independent star-forming regions with identical FIR properties in the same area to drive up ΣSFR and ΣFIR, no such relation would exist.
It is also instructive to express the ΣFIR as function of dust temperature, where we have converted color to temperature by fitting Dale & Helou (2002) SED templates at the source redshift to the color, and using the conversion of Magnelli et al. (2014) to assign dust temperatures to these templates. A similar result is obtained for a simple β = 1.5 modified blackbody. The result is shown in the inset to Fig. 6 right and can be fit as 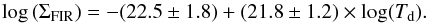 (10)This scaling can be compared to expectations from scalings of other quantities, as found above and as used in the current literature. If we assume (1) a relation of far-infrared surface brightness and main-sequence offset log (ΣFIR) = α × log (sSFR/sSFRMS) + c1 with α = 2.59 and c1 = 8.19 (Eq. (5) above); (2) that gas depletion time in yr-1 scales with main-sequence offset as log (Mgas/SFR) = ξ × log (sSFR/sSFRMS) + c2 with ξ = −0.49 and c2 = 9.1 (Genzel et al. 2015, for z = 0 and log(M∗) = 10.5), (3) assume a dust-to-gas ratio 100 (Leroy et al. 2011, for solar metallicity), and (4) that the dust is an optically thin calorimeter with log (SFR/Md) = (4 + β) × log (Td) + c3 with a dust emissivity index β = 1.5 and c3 = −15.08 (e.g., Magnelli et al. 2014; Genzel et al. 2015), then we expect
(10)This scaling can be compared to expectations from scalings of other quantities, as found above and as used in the current literature. If we assume (1) a relation of far-infrared surface brightness and main-sequence offset log (ΣFIR) = α × log (sSFR/sSFRMS) + c1 with α = 2.59 and c1 = 8.19 (Eq. (5) above); (2) that gas depletion time in yr-1 scales with main-sequence offset as log (Mgas/SFR) = ξ × log (sSFR/sSFRMS) + c2 with ξ = −0.49 and c2 = 9.1 (Genzel et al. 2015, for z = 0 and log(M∗) = 10.5), (3) assume a dust-to-gas ratio 100 (Leroy et al. 2011, for solar metallicity), and (4) that the dust is an optically thin calorimeter with log (SFR/Md) = (4 + β) × log (Td) + c3 with a dust emissivity index β = 1.5 and c3 = −15.08 (e.g., Magnelli et al. 2014; Genzel et al. 2015), then we expect 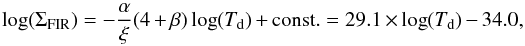 (11)which for the relevant temperature range is in reasonable agreement with what was found in Eq. (10), given the uncertainties of the various parameters, and the simplifications in the assumptions made. That means, the above set of scalings and assumptions remains consistent when bringing in size information.
(11)which for the relevant temperature range is in reasonable agreement with what was found in Eq. (10), given the uncertainties of the various parameters, and the simplifications in the assumptions made. That means, the above set of scalings and assumptions remains consistent when bringing in size information.
Given the data and scatter, we did not attempt to fit more complex functional forms than the simple power law (log-linear) relations quoted above and summarized in Table 2. One result from comparing Re,70 and LFIR (Fig. 4 left) is however worth mentioning. All ULIRGs are found at similar and relatively small ~0.5 kpc half light radii, but for less luminous log (LFIR) = 10...11 objects the variation is a substantial ≳2 dex, ranging from the typical ~1 kpc up to ~10 kpc and down to a few extremely compact ≲100 pc circumnuclear sources. Very small sizes for a ULIRG far-infrared emitting region are excluded by optical depth arguments (Sect. 4.2), but the absence of large ≳5 kpc FIR sources in ULIRGs reflects a true absence of such extended ULIRGs. Similar findings are made in the mid-IR continuum (Soifer et al. 2000; Díaz-Santos et al. 2011) and radio (Condon et al. 1991). The far-infrared data reinforce this with a closer link to the SFR and much reduced risk of a result that is biased by a compact AGN-heated source. A LFIR~ 1 × 1011 L⊙ LIRG can correspond to a 10 kpc scale large disk, a smaller few kpc region in a (perhaps interacting) galaxy, or even a compact ~100 pc circumnuclear burst. In contrast, the ~0.5 kpc radii consistently found for ULIRGs are in line with the notion that for the modest gas content of galaxies in the local universe, the corresponding huge SFRs can only be reached by compressing gas and triggering a burst of star formation, in an interaction or merging event.
The structural properties of local galaxies are an important comparison to the structure of evolving galaxies at high redshift. ALMA starts observing samples of high-z galaxies at longer submm wavelengths, for which the Herschel data are the key comparison despite their somewhat shorter rest wavelengths. Figure 4 left includes some first ALMA sizes of submm galaxies, as measured by Ikarashi et al. (2015) and Simpson et al. (2015) at rest wavelengths about 150 to 400 μm. This comparison is preliminary since their sources lack individual spectroscopic redshifts and determinations of the SED peak, which makes the adopted individual LFIR values uncertain for the quite diverse SMG population (Magnelli et al. 2012). We adopted the infrared luminosities of Ikarashi et al. (2015) and estimated them for the Simpson et al. (2015) sources using the average S850/LIR scaling of Magnelli et al. (2012) at the typical Simpson et al. submm flux. Specifically, we adopt LFIR = 5.6 × 1011S850 which also includes LIR = 1.5 × LFIR as recommended by Magnelli et al. (2012) for such SMG luminosities. We also include a number of individual SMG continuum size measurements from the literature (Younger et al. 2008, 2010; Riechers et al. 2013, 2014; Neri et al. 2014), in some cases updating the original luminosity estimates with Herschel results (Magnelli et al. 2012; Smolčić et al. 2015). We have also included the sample of Harrison et al. (2016) which consists of five modest luminosity X-ray AGN and another galaxy. We group them with galaxies since at LFIR/LBol,AGN ~10, their AGN are energetically much less prominent than in the local QSOs studied in Sect. 4.4. This first comparison suggests that on average these SMGs, likely at z ≳ 2 and in some cases reaching up to z ~ 6, have roughly twice the size of local galaxies of similar infrared luminosity. This is consistent with the notion that massive gas rich high redshift galaxies can reach SFRs in excess of 100 M⊙ yr-1 in large disks (e.g., Förster Schreiber et al. 2009; Nelson et al. 2016). Because of their increased gas fractions (e.g., Daddi et al. 2010; Tacconi et al. 2010, 2013; Saintonge et al. 2013; Carilli & Walter 2013), they can reach high SFRs without the strong gas compression that is needed to create a local ULIRG. To fully understand the role of true structural differences, and the possible dependence of size on wavelength, it will be necessary to compare the local results to (sub)mm studies of high-z samples with individual redshifts and reliable derivations of LIR and/or SFR, and to rest frame optical structure (e.g., van der Wel et al. 2014). Submm selection with its biases on, e.g., dust temperature will have to be supplemented by SFR selected and stellar mass selected samples covering a wider range of properties than the high-z systems in Fig. 4.
4.2. Optical depth of FIR emission
 |
Fig. 7 Ratio between the solid angle of a blackbody emitting half of the PACS fluxes at the blackbody temperature fitting those fluxes, and the measured half light solid angle, for 260 galaxies. Values approaching one indicate emission that is on average optically thick in the far infrared over the measured source size. Low values indicate optically thin emission and/or a scattered distribution of small sources which might still have considerable far-infrared optical depth. The inset shows the relation between this ratio of solid angles and the far-infrared surface brightness. The tightness is somewhat trivial, because both axes involve the measured solid angle and galaxies span a limited range of dust temperatures. |
Compact far-infrared sources, selected by largest ΣFIR and/or ΩBB/ Ωmeasured.
Total gas columns derived from interferometric CO or dust continuum observations (e.g., Sakamoto et al. 1999), fits to the IR to submm SED (e.g., Klaas et al. 2001), and modelling of OH absorptions (e.g., González-Alfonso et al. 2015) have been used to argue that the dust emission in ULIRGs may be optically thick out to far-infrared wavelengths. Sizes and fluxes from Herschel-PACS can provide an independent approach to this question. Figure 7 shows the ratio of the solid angle ΩBB of a blackbody emitting half of the PACS flux at the temperature determined by the PACS photometry, and the measured half light solid angle at 70 μm Ωmeasured. ΩBB is derived from the Planck function for an optically thick blackbody reproducing both the 70 and 160 μm (half) flux, and the measured solid angle is given by Ωmeasured = π(Re,70/DA)2. This ratio will be low for optically thin emission or if small regions of higher optical depth are scattered over a larger area, but will approach unity for optically thick emission. In a strict sense this is a lower limit, since emitting regions distributed in a way that is significantly different from the adopted Gaussian enlarge the measured solid angle for the same physical optical depth to the emission. It also compares the measured size to a case that is optically thick over the full PACS wavelength range, and is hence a lower limit if the emission transits from optically thick to thin between 70 and 160 μm.
Several well known ULIRGs (Arp 220 which shows the largest value in Fig. 7, Mrk 231, Mrk 273, IRAS F17207-0014, IRAS 13120-5453, see also Table 1) show lower limits or measurements of ΩBB/ Ωmeasured ≳ 0.1, consistent with being optically thick in their central regions. The same applies to some of the extremely compact circumnuclear regions in galaxies with more modest LFIR (e.g., NGC 4418, IC 860, NGC 1266, among others). In contrast, the majority of LIRGs and galaxies with lower LFIR is optically thin on average.
The case of Arp 220 may however also illustrate the complexities of declaring a galaxy “optically thick in the far-infrared”. At ΩBB/ Ωmeasured = 0.35, Arp 220 is the most optically thick system with a size measurement (rather than limit) in our sample, with a measured circularized Re,70 of 246 pc (physical) or 0.67′′ (on sky). This is larger than the best evidence for the size of the central star formation around the two nuclei: flickering supernovae have been mapped in a series of VLBI papers (Parra et al. 2007, and references therein), and a similar area is suggested from free-free radio continuum by Barcos-Muñoz et al. (2015), who give half light radii of 51 and 35 pc around the two nuclei. A putative AGN would inject energy again at very small scale. Both Ωmeasured, which may still be inflated by the presence of two semi-separated nuclei but a single Gaussian fit, and ΩBB are larger than what is suggested from the free-free continuum, indicating the need for radiative transfer in the FIR from the energy sources to the emitting surface. On the other hand, even shorter near-infrared wavelengths that would be absorbed already by much lower dust columns provide a view of part of the stars around the two nuclei (e.g., Scoville et al. 2000), indicating a complex and patchy dust distribution. A yet more extreme example is Mrk 231 with optical visibility towards its central type-1 AGN despite ΩBB/ Ωmeasured> 0.11. These indicate a much more complex geometry with some rather transparent lines of sight, that are not expected in a spherically symmetric dust distribution around a heating source.
4.2.1. A sample of compact far-infrared sources
Our data provide an opportunity to pick from a large sample of galaxies an objective selection of the most compact far-infrared sources. We do so by requiring either a large FIR surface brightness ΣFIR> 1011.75 L⊙ kpc-2 or a large value of the optical depth indicator ΩBB/ Ωmeasured> 0.08. The two criteria are linked (inset to Fig. 7) and create overlapping samples, because dust temperatures only span a limited range. Table 1 summarizes the resulting sample. Unlike most of our analysis, we include here close galaxy pairs (marked “D” in the second column of Table 1). If any, the emission from the offset second component in such a double would lower the measured ΣSFR and optical depth. Presence of such a double in our sample of compact sources hence implies that in the FIR they are dominated by one compact component.
While selected homogeneously and solely on the basis of FIR images, this sample includes objects known to be peculiar and interesting in several ways. Arp 220, IC 860, NGC 4418, for example have long been known to be “[Cii]-deficient” in comparison to their far-infrared luminosity (e.g., Malhotra et al. 2001; Luhman et al. 2003). Massive outflows of molecular gas have been detected in Mrk 231, Mrk 273, NGC 1266, IRAS F05189-2524, IRAS 13120-5453, IRAS F14378-3651, IRAS F17207-0014 (Fischer et al. 2010; Sturm et al. 2011; Veilleux et al. 2013; González-Alfonso et al. 2014; Cicone et al. 2014, and references therein). ΣFIR of the sources in Table 1 corresponds to ΣSFR≳ 100 M⊙ yr-1 kpc-2 if due to star formation. This is well above suggestions for the ΣSFR threshold for launching powerful winds from local or high-z galaxy disks (Heckman 2002; Newman et al. 2012). On the other hand, AGN may play an important role in launching the most massive winds (Sturm et al. 2011; Veilleux et al. 2013) and are present in several sources in Table 1. To which extent the conditions in and the phenomena related to these compact regions relate to extreme density star-forming regions or embedded AGN is difficult to discern at many wavelengths, given the large average optical depth even in the FIR. Unless there are favourable unobscured lines of sight, the optical and near infrared emission will be limited to a surface layer.
Another well known galaxy with a compact FIR source is NGC 1377, which has been argued to host a nascent starburst (Roussel et al. 2006). We find a very small Re,70< 60 pc far-infrared emitting region (Fig. 2), but its modest log(LFIR) = 9.7 and warm dust keep the lower limits to ΣFIR and optical depth below the thresholds used to select Table 1, despite the small size.
4.3. The [CII] deficit is closely linked to FIR surface brightness
 |
Fig. 8 Ratio of [Cii] and FIR luminosity as a function of FIR luminosity (left), FIR color (middle) and FIR surface brightness (right panel). Red lines indicate the fits to our sample (Eqs. (12) and (13)), and black lines results of Díaz-Santos et al. (2013). The two slightly outlying points marked with an overlayed asterisk in the right panel were not used for the fit that is shown in red. Suitable [Cii] data are available for the 182 galaxies that are plotted here. |
The [Cii]158 μm line typically is the major coolant of neutral interstellar gas. It is detectable with current instrumentation to redshifts above 6 and has been proposed as an SFR tracer (e.g., Stacey et al. 1991; De Looze et al. 2011; Herrera-Camus et al. 2015). Several known effects add uncertainty to the use of [Cii] for that purpose. First, low metallicity galaxies can show enhanced [Cii] from regions where [Cii] coexists with self-shielded H2 while the smaller amount of dust implies that carbon is in the form of CO only in a smaller region (e.g., Madden et al. 1997). We do not address this effect further in this work. [Cii] can also be bright in the atomic and ionized interstellar media of the outer parts of galaxies (Madden et al. 1993), with a less tight link to ongoing star formation than for PDRs around regions of active star formation. Finally, progressing from normal galaxies to LIRGs and ULIRGs a reduced ratio [Cii]/FIR for luminous objects has been reported – the “[Cii] deficit” (e.g., Malhotra et al. 1997, 2001; Luhman et al. 1998, 2003; Fischer et al. 2014). The deficit can also be linked to offset from the main-sequence (Graciá-Carpio et al. 2011; Díaz-Santos et al. 2013), a view that reconciles the [Cii] properties of high and low redshift galaxies that differ if compared at same IR luminosities. Physical explanations for the deficit discussed in these references include (i) a reduced photoelectric heating efficiency at high ratios of UV radiation field and gas density, (ii) related to this, dust competing for photons in high ionization parameter “dust-bounded” Hii regions, (iii) AGN contributions to the FIR continuum; and (iv) self-absorbed [Cii] emission.
We have supplemented our galaxy sample with [Cii] fluxes from the literature. Most are based on the measurements of Díaz-Santos et al. (2013). We have scaled their [Cii] fluxes which are based on the central spaxel of the PACS integral field spectrometer by the ratio of our total 160 μm flux density and their 157 μm continuum flux density, dropping objects with correction factor above 10 or 160 μm size above 40′′, where this correction is too uncertain. We also use [Cii] fluxes from Brauher et al. (2008), excluding galaxies that were flagged as extended in that paper, and those with a measured 160 μm size above the ISO-LWS beam size of 80′′. Finally, a few objects are added from Sargsyan et al. (2012) and Farrah et al. (2013).
Figure 8 shows the ratio of [Cii] and FIR emission as a function of three different quantities. The left panel shows for our sample the classical “deficit” at high FIR luminosities. The scatter is large, however, and some of the most extreme deficits arise at intermediate FIR luminosities, as found previously (e.g., Malhotra et al. 1997, 2001). The middle panel shows a somewhat improved trend as a function of far-infrared color, again confirming the earlier work referenced above. Our data can be fitted by ![\begin{eqnarray} \log(L_{\rm [CII]}/L_{\rm FIR}) & =& -2.583 - 1.551\times \log(S_{70}/S_{160}) \nonumber\\[2mm] &&\quad - 1.220\times (\log(S_{70}/S_{160}))^2, \label{eq:ciifitcol} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27706-15/aa27706-15-eq111.png) (12)with the fit applicable to the range log (S70/S160) ~ −0.4...0.5. The dispersion around this fit is 0.27 dex, virtually identical to the 0.275 dex that we obtain for our sample around the relation (for a color S63/S157) in Eq. (1) of Díaz-Santos et al. (2013), or the 0.28 dex that these authors quote for their sample which has significant overlap with ours, but studies lines and continuum from the central spaxel of the PACS integral field spectrometer.
(12)with the fit applicable to the range log (S70/S160) ~ −0.4...0.5. The dispersion around this fit is 0.27 dex, virtually identical to the 0.275 dex that we obtain for our sample around the relation (for a color S63/S157) in Eq. (1) of Díaz-Santos et al. (2013), or the 0.28 dex that these authors quote for their sample which has significant overlap with ours, but studies lines and continuum from the central spaxel of the PACS integral field spectrometer.
 |
Fig. 9 Comparison of observed scalings to two component toy models. Red lines show the fits to the data as previously shown in Fig. 6 (here: left and center panel) and Fig. 8 (right panel). Both toy models include a mix of a “disk” component with cold dust and a high ratio [Cii]/FIR, and a “dense star formation” component with warm dust and low [Cii]/FIR, with varying surface brightness of the warm component. Spreading the dense SF component with low filling factor over a large disk is a very poor fit, while scaling down its size with surface brightness gives a first approximation to the data. |
An extremely tight relation is observed between the ratio of [Cii] and FIR emission and FIR surface brightness (right panel). The red line shows a simple quadratic fit to the measurements and limits, where we have not used for the fit the two slightly outlying sources NGC 5866 and MCG-03-34-064 (marked with asterisk extensions to the symbols in the right panel of Fig. 8). We cannot determine with the data used here whether these are true outliers, or whether they are affected by technical issues, e.g., an unusually extended [Cii] flux distribution. The relation shown in the right panel of Fig. 8 is ![\begin{eqnarray} \log(L_{\rm [CII]}/L_{\rm FIR}) & = & -11.7044 + 2.1676\times \log(\Sigma_{\rm FIR})\nonumber\\ && \quad - 0.1235\times (\log(\Sigma_{\rm FIR}))^2. \label{eq:ciifit} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27706-15/aa27706-15-eq114.png) (13)The dispersion around this relation, covering 3.5 dex in surface brightness and 2 dex in the ratio of [Cii] and FIR, is 0.16 dex for the full sample and 0.15 dex if excluding the two outliers. Díaz-Santos et al. (2013, 2014) used sizes measured in the mid-infrared to derive a log-linear relation of deficit and IR surface brightness (Eq. (4) of Díaz-Santos et al. 2013) which we also overplot to Fig. 8 right, corrected for an adopted LIR= 1.9 ×LFIR. This relation was derived for a clearly star formation dominated (U)LIRG subsample, thus minimizing a potential distortion of mid-IR based sizes by AGN emission. Because of the more uncertain size measures and more size limits, this relation covers a smaller range ΣFIR≈ 5 × 108...3 × 1011 L⊙ kpc-2. Over this restricted range, the two relations agree well, and have small dispersions: 0.15 dex quoted by Díaz-Santos et al. (2013), 0.14 dex for our data (minus the two outliers) around their relation, and 0.12 dex for our data and our relation. Over the wider range in surface brightness that is accessible via the Herschel size measurements, Fig. 8 shows the 2nd order fit to be more appropriate than the log-linear relation. This is also reflected in the dispersions which are 0.19 dex around the log-linear relation vs. 0.15 dex around the fit of Eq. (13).
(13)The dispersion around this relation, covering 3.5 dex in surface brightness and 2 dex in the ratio of [Cii] and FIR, is 0.16 dex for the full sample and 0.15 dex if excluding the two outliers. Díaz-Santos et al. (2013, 2014) used sizes measured in the mid-infrared to derive a log-linear relation of deficit and IR surface brightness (Eq. (4) of Díaz-Santos et al. 2013) which we also overplot to Fig. 8 right, corrected for an adopted LIR= 1.9 ×LFIR. This relation was derived for a clearly star formation dominated (U)LIRG subsample, thus minimizing a potential distortion of mid-IR based sizes by AGN emission. Because of the more uncertain size measures and more size limits, this relation covers a smaller range ΣFIR≈ 5 × 108...3 × 1011 L⊙ kpc-2. Over this restricted range, the two relations agree well, and have small dispersions: 0.15 dex quoted by Díaz-Santos et al. (2013), 0.14 dex for our data (minus the two outliers) around their relation, and 0.12 dex for our data and our relation. Over the wider range in surface brightness that is accessible via the Herschel size measurements, Fig. 8 shows the 2nd order fit to be more appropriate than the log-linear relation. This is also reflected in the dispersions which are 0.19 dex around the log-linear relation vs. 0.15 dex around the fit of Eq. (13).
Existence of such a relation is clearly expected from earlier work on the [Cii] deficit in combination with the scalings presented in this paper. From resolved observations of nearby galaxies, Herrera-Camus et al. (2015) report a scaling ![\hbox{$\Sigma_{\rm SFR}\propto \Sigma_{\rm [CII]}^{1.13}$}](/articles/aa/full_html/2016/07/aa27706-15/aa27706-15-eq118.png) for a regime of low star formation surface density ΣSFR ≲ 0.1M⊙ yr-1. This suggests a relatively flat continuation towards lower surface FIR brightness of the relation shown in the right panel of Fig. 8, for a range that is not covered by the combination of our sample with the specific [Cii] literature data.
for a regime of low star formation surface density ΣSFR ≲ 0.1M⊙ yr-1. This suggests a relatively flat continuation towards lower surface FIR brightness of the relation shown in the right panel of Fig. 8, for a range that is not covered by the combination of our sample with the specific [Cii] literature data.
The noteworthy aspect of this relation is its remarkable tightness. Given that our far-infrared surface brightness is a galaxy average, one might have expected a tighter correlation of the deficit with FIR color, which is representing the local physical conditions in and around star-forming complexes, but this is not the case (Fig. 8). A large number of studies have argued that even in the ULIRGs of our sample, the total infrared (and even more the far-infrared) luminosity is typically not dominated by an AGN, even where present (e.g., Genzel et al. 1998; Lutz et al. 1998; Veilleux et al. 2009b). ΣFIR can then be directly linked to ΣSFR, and is not strongly affected by the AGN. The tightness of the link between [Cii] deficit and ΣFIR then makes a dominant role of scenario (iii) above – simple dilution by AGN-heated FIR emission – unlikely. This is in line with the conclusion from comparisons to various AGN indicators (Díaz-Santos et al. 2013).
We are thus directed at explanations that are related to the physical conditions in star-forming regions as well as the diffuse ISM. A simple test that could represent the varying conditions is to construct a two component mixed model with (1) strong [Cii] and cold dust; representative of a more diffuse galaxy disk; and (2) dense star formation with weak [Cii] and warm dust; to fit the observed trends. Such simple scenarios have often been invoked, starting from the “cirrus plus star formation” interpretation of IRAS color-color diagrams. For a toy model, we assign to the cold component S70/S160 = 0.25, [Cii]/FIR = 0.015, ΣFIR = 108 L⊙ kpc-2 and a Gaussian with size Re,70 = 5 kpc. For the dense SF component, we adopt S70/S160 = 2 and [Cii]/FIR = 0.0001. These values are picked on the basis of Fig. 6 and Fig. 8 as well as the [Cii] literature. We then vary the surface brightness of the dense SF component from zero to a maximum of ΣFIR = 1012 L⊙ kpc-2. A first toy model is to simply add the dense SF component over the entire disk, as if more and more additional small but intense star-forming regions were spread over the disk. This is a very poor representation of the data (black dotted lines in Fig. 9). Not only are size trends not captured by definition, but the fits to the trend of color and [Cii]/FIR with surface brightness are very poor, because the dense SF component quickly dominates as its surface brightness increases. In a second model we assume that the “few dense SF regions scattered over the entire disk” scenario only applies for low surface brightness of that component, but that high surface brightness of the dense SF can only be reached if the limited gas content of local galaxies is compressed into a small region. We implement this by keeping the disk component fixed as a Gaussian with Re,70 = 5 kpc, and add to it a second Gaussian for the dense SF component with size scaling as Re,70 = 5 × (1 + ΣFIR/ 108)-0.3 with Re,70 in kpc and ΣFIR in L⊙ kpc-2. This parametrization gives the dense SF the same size as the cold disk as long as its surface brightness is low, but shrinks it at high surface brightness, as motivated above. The value −0.3 for the power law slope is based on a manual adjustment, aiming at a reasonable fit to the Fig. 9 trends. Size and surface brightness are then derived by single Gaussian fitting this mix, as for the real data. This second toy model gives a more reasonable approximation of the observed trends (blue lines in Fig. 9). Given its simplicity, we refrain from further modifying the assumptions towards a better fit.
The relative success of the toy model that scales the size of the dense SF component should not be overinterpreted. It uses simplified observational facts and no ISM physics. But it provides some confidence that a coherent interpretation of the trends discussed in this paper should be possible via models implementing more realistic distributions of ISM and star formation, as well as the physics of the dusty and gaseous phases of the Hii regions, PDRs, and diffuse ISM. Likely, such models will invoke more smooth trends of properties than derived from coadding two extremes in the toy model, and a [Cii]/FIR that only decreases at somewhat higher surface brightness. The goal would be to use physical models to quantitatively relate the trends of color and [Cii]/FIR to the increase in typical radiation field intensity at higher FIR surface brightness and smaller size, while using plausible assumptions on ISM structure.
 |
Fig. 10 Left: Half light radius at 70 μm as a function of redshift for PG QSOs and their hosts. Pink symbols mark systems with literature evidence for being double/interacting, which may inflate the measured size. Right: Half light radius at 70 μm vs. FIR luminosity for the z< 0.1 subsample of QSOs with favourable ratio of size measurments to limits. The relation derived above for galaxies is overplotted. |
Summary of scalings.
4.4. A similar size of the FIR emission in QSO hosts and galaxies
Because of the favourable contrast between the SED of an AGN and the SED of a star-forming galaxy (e.g., Netzer et al. 2007), rest frame far-infrared emission has been widely used as a star formation tracer in AGN hosts, in particular in the context of Herschel surveys (Lutz 2014) up to z ~ 2 (e.g., Rosario et al. 2012). While it is often safe to simply ascribe this FIR emission to star formation, this is no longer the case for powerful AGN in hosts with low SFR. Both Herschel color arguments (Hatziminaoglou et al. 2010; Rosario et al. 2012) and attempts to construct local “intrinsic” AGN SEDs reaching out to the FIR (Netzer et al. 2007; Mullaney et al. 2011; Mor & Netzer 2012) have been used to delineate the border between these two regimes. Comparing the size of the FIR emission in QSO hosts with that in other galaxies can provide another constraint to this problem, in addition to information on the host and/or AGN proper.
Figure 10 left shows results for 59 QSOs (32 size measurements and 27 size limits). The QSOs are on average much more distant than the galaxies discussed before, leading to a less favourable ratio of Re,70 detections to limits. Also, our approach of attempting size measurements only for photometric S/N > 10 has already shrunk the sample from 93 QSOs observed by Herschel to these 59, which will miss some of the FIR-weak and distant objects. Most Re,70 measurements span a range ~ 0.5...5 kpc with a median of 1.7 kpc (1.1 kpc for the z < 0.1 subset discussed below). Limits are consistent with this range. Exceptionally, we plot here also (marked in pink) five QSOs where NED and literature give a warning of a close double nature that could inflate the size if both components emit in the FIR. Only in PG1543+489 does the Herschel image provide direct evidence for that, but we discard all five from further analysis.
In Figure 10 left, there appears to be a lack of distant but small QSOs and of local but large QSOs. The first category, to the extent it may be present in the sample, would simply be assigned upper size limits that increase with redshift. The absence of large Re,70≲ 10 kpc local hosts is more noteworthy and related to the known heterogeneity of the QSO host population, on which optical/near-infrared studies provide some insights. The hosts of z < 0.06 low luminosity QSOs show a mix of disks, ellipticals, and merger remnants, with typical near-infrared Re ~ 2 kpc and none with Re > 5 kpc (Busch et al. 2014). In contrast, the hosts of the luminous z ~ 0.2 QSOs studied by Dunlop et al. (2003) are typically Re ~ 10 kpc giant ellipticals. The PG sample, approximately UV/optical flux limited and covering a range of redshifts, bridges these two regimes – it includes a few large hosts, but only in the large volume accessible at z> 0.1 (Veilleux et al. 2009a; Dunlop et al. 2003). On the other hand, many PG QSOs may be on an evolutionary path from IR luminous mergers to moderate size “disky” ellipticals (e.g., Dasyra et al. 2007). Already in the optical/NIR tracers of the stellar population, the z< 0.1 region lacks the rare Re ~ 10 kpc QSOs, in plausible agreement with the lack of large FIR sizes in our sample, and the ratios of FIR to NIR size ≲1 that we report below.
To better compare with other galaxies, we restrict the QSO sample to the 33 z< 0.1 objects. Of those, only 4 were not fit because of S/N < 10, and the number of size measurements among the remaining 29 is high: 19 vs. 10 upper limits. Compared to the full PG sample, this redshift limit and the photometric S/N cut prefer moderate AGN luminosities and exclude the IR faintest objects, specifically the median log (LBol,AGN) is 44.8 and the median log (LFIR) is 10.2. Figure 10 right shows their Re,70 vs. LFIR, and overplotted the fit relation derived above for galaxies (Eq. (1)). Clearly, the Re,70 sizes for the QSOs are fully consistent with those of other local galaxies of the same infrared luminosity. This is consistent with their FIR emission being due to star formation in the host, giving support to the use of FIR emission as a SFR indicator in this regime of LFIR/LBol,AGN ≈ 0.1. For QSOs with a lower ratio of far-infrared and bolometric luminosity that are not sampled by our size measurements, AGN heated and/or “cirrus” dust may be relatively more important, and a similar size consistency should not be taken for granted.
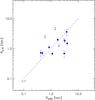 |
Fig. 11 Comparison of half light radii measured in the far-infrared (this work) with near-infrared half light radii for the same sources (Table 5 of Veilleux et al. 2009a). The dashed line visualizes a 1:1 relation, it is not a fit. |
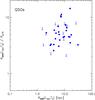 |
Fig. 12 Comparison of the radius at which an AGN of the given QSO’s luminosity heats directly exposed optically thin dust to the measured dust temperature, and the measured far-infrared half light radius. |
We may also compare the size of the far-infrared emission with the size of the stellar host as seen in the near-infrared. Veilleux et al. (2009a) present half light radii of the near-infrared emission for a sample of PG QSOs, as observed with HST-NICMOS, and after subtracting the AGN point source. Figure 11 compares NIR and FIR half light radii for 13 QSOs in that sample with Herschel size measurement (9/4 measurements/limits). The comparison suggests FIR size similar to or in some cases smaller than the stellar component, again consistent with FIR emission originating in the host, and star formation taking place on a spatial scale similar to the pre-existing stellar population.
Finally, we can compare the measured Re,70 to the radius at which the AGN can heat dust to the measured temperature. At the smaller ≪kpc scales of the circumnuclear obscuring structure discussed in the context of AGN unification, dust will be warm and the emission mostly in the mid-infrared. This is what is empirically found to dominate AGN-heated dust SEDs (e.g., Netzer et al. 2007). But strong far-infrared emission could emerge if a substantial amount of dust is exposed to the AGN radiation only at large distances, without the dominant UV component being intercepted by a modest amount of dust further in. This could occur for example in a strongly warped disk (Sanders et al. 1989). Figure 12 compares the measured Re,70 sizes to the radius at which the AGN heats optically thin dust to the measured dust temperature. Here we have adopted AGN bolometric luminosities based on the 5100 Å continuum of the PG QSOs and the bolometric correction of Eq. (7.3) in Netzer (2013). For the dust properties in Eq. (5.85) of Netzer (2013) the expected radius in kpc is 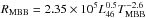 . Here, L46 is the bolometric luminosity of the AGN in units of 1046erg s-1 and TMBB is derived by fitting a modified blackbody to the PACS photometry, adopting an emissivity index β = 1.2 for consistency with the dust properties adopted by Netzer (2013). Figure 12 shows that the radii estimated this way are typically a factor ~5 larger than the measured Re,70, and also uncomfortably large compared to typical NIR host sizes as seen in Fig. 11. Dust at large radii that is directly heated by AGN light that has not been absorbed further in seems hence an unsatisfactory explanation for the measured FIR sizes. It is beyond the scope of this work to study to which extent detailed radiative transfer of the incident direct AGN UV and/or infrared reemission can avoid this problem with FIR sizes, without violating SED constraints. At this point, the analogy of QSO hosts to galaxies (Fig. 10) seems the more natural explanation. The FIR emitting dust will here be heated mostly by host star formation on scales similar to other galaxies, and in regions where the radiation field is not dominated by the AGN, for example outside the ionisation cone. In this scenario, the direct AGN radiation would be intercepted already at smaller radii by the obscuring material invoked by unified AGN models, and re-emitted mostly in the mid-IR.
. Here, L46 is the bolometric luminosity of the AGN in units of 1046erg s-1 and TMBB is derived by fitting a modified blackbody to the PACS photometry, adopting an emissivity index β = 1.2 for consistency with the dust properties adopted by Netzer (2013). Figure 12 shows that the radii estimated this way are typically a factor ~5 larger than the measured Re,70, and also uncomfortably large compared to typical NIR host sizes as seen in Fig. 11. Dust at large radii that is directly heated by AGN light that has not been absorbed further in seems hence an unsatisfactory explanation for the measured FIR sizes. It is beyond the scope of this work to study to which extent detailed radiative transfer of the incident direct AGN UV and/or infrared reemission can avoid this problem with FIR sizes, without violating SED constraints. At this point, the analogy of QSO hosts to galaxies (Fig. 10) seems the more natural explanation. The FIR emitting dust will here be heated mostly by host star formation on scales similar to other galaxies, and in regions where the radiation field is not dominated by the AGN, for example outside the ionisation cone. In this scenario, the direct AGN radiation would be intercepted already at smaller radii by the obscuring material invoked by unified AGN models, and re-emitted mostly in the mid-IR.
Among the PG QSOs with largest Re,70 in Fig. 10 left, several are marked as double. This implies that the size measurement might be inflated by a companion. For PG1543+489 we see direct evidence in the form of a weak southern extension in the 70 μm image, consistent with a companion that is present in archival NICMOS images. No literature evidence for a strong companion exists for the largest QSO source, PG2251+1113 with Re,70~9.4 kpc, similar to the largest non-QSO galaxies in our sample. This is a quite powerful QSO (LBol,AGN ~ 1046.5 erg s-1) which has made studies of the stellar component in the near-infrared difficult. The fits of Guyon et al. (2006) and Veilleux et al. (2009a) suggest Re,NIR ≳ 10 kpc. Due to the difficulty of subtracting the point source they are considered unreliable, but provide some support to the very large FIR size.
Mushotzky et al. (2014) present initial results from a Herschel study, including PACS far-infrared size information, for the BAT AGN sample that is selected in ultra-hard X-rays. The BAT sample covers AGN luminosities and redshifts typically lower than the PG QSOs, but reaches up to the level of the PG QSOs. Measured far-infrared sizes span a wide range, with about a third of size limits Re,70≲ 1 kpc but also some fairly extended objects with IR surface brightness lower than KINGFISH galaxies. For resolved sources, 160 μm sizes tend to exceed the 70 μm sizes. This is in broad agreement with our findings for galaxies and QSOs. A systematic comparison of this sample covering a wide range of AGN luminosities to LFIR-matched non-AGN galaxies will be worthwhile to extend the limited range covered by PG QSOs (Fig. 10).
In summary, the FIR size of the PG QSOs for which we could attempt measurements seems to resemble that of galaxies of same FIR luminosity, consistent with being dominated by star formation in the host. It is important to recall that this statement refers to a subset of modest luminosity PG QSOs: log (LBol,AGN) ≈ 44.8 and LFIR/LBol,AGN ≈ 0.1. It should not be blindly transferred to systems with smaller LFIR/LBol,AGN.
5. Conclusions
We have used Herschel 70, 100, and 160 μm images to study the size of the far-infrared emission in a sample of 399 local galaxies and QSOs. We rely on the stable point spread function and subtraction in quadrature to infer half light radii of the sources, reaching well below the PSF half width for sources with good S/N. We find that:
-
Galaxies with LFIR~ 1011 L⊙ can be found with very different distributions of infrared emission (hence star formation). These range from large Re ~ 10 kpc disks down to compact <100 pc circumnuclear bursts. In contrast, LFIR≳ 1012 L⊙ ULIRGs are only found with compact Re ~ 0.5 kpc morphologies, likely due to the need to compress the limited gas content to temporarily achieve the large IR luminosities. On average, but with large scatter, far infrared half light radius scales with LFIR-0.2 and far-infrared surface brightness (SF surface density) with LFIR1.4. First ALMA measurements suggest a larger size of high-z sources at equivalent LFIR, albeit at slightly longer rest wavelengths.
-
Half light radius and FIR surface density also show clear trends when moving from the main-sequence of star formation to higher sSFR, with logarithmic slopes of −0.4 and 2.6, respectively.
-
There is a fairly tight relation of both half light radius and FIR surface brightness with FIR color (dust temperature). There is consistency when comparing the scalings of FIR surface brightness with dust temperature with expectations from the scaling of ΣFIR with main-sequence offset, combined with the Genzel et al. (2015) scaling of gas depletion time with main-sequence offset and the assumption that dust is an optically thin calorimeter.
-
The average optical depth over the size of the far-infrared emitting region is large in some LIRGs and ULIRGs.
-
The ratio of [Cii] 158 μm and FIR emission and the “[Cii] deficit” is more tightly linked to FIR surface brightness than to FIR luminosity or FIR color. For our sample, the dispersion is about 0.15 dex for a relation covering 3.5 dex in surface brightness.
-
The size of the far-infrared emission in z< 0.1 PG QSOs with LFIR/LBol,AGN ≈ 0.1 is consistent with that of galaxies with same FIR luminosity. This is consistent with host star formation creating their far-infrared emission.
See “PACS map-making tools: analysis and benchmarking, 30 March 2014” http://herschel.esac.esa.int/twiki/pub/Public/PacsCalibrationWeb/pacs_mapmaking_report14_v2.pdf
Acknowledgments
We thank the anonymous referee for a careful review and helpful comments. This work would not have been possible without the efforts at the PACS ICC and Herschel science center that pushed the accuracy of Herschel pointing reconstruction beyond its limits. In particular, we would like to thank Hervé Aussel, Helmut Feuchtgruber, Craig Stephenson, and Bart Vandenbussche. H.N. acknowledges support by ISF grant no. 284/13. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/OAT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICYT/MCYT (Spain).
References
- Bahcall, J. N., Kirhakos, S., Saxe, D. H., & Schneider, D. P. 1997, ApJ, 479, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Barcos-Muñoz, L., Leroy, A. K., Evans, A. S., et al. 2015, ApJ, 799, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Lutz, D., Santini, P., et al. 2013, A&A, 551, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Brauher, J. R., Dale, D. A., & Helou, G. 2008, ApJS, 178, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Busch, G., Zuther, J., Valencia-S., M., et al. 2014, A&A, 561, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J., Helou, G., Sanders, D. B., & Soifer, B. T. 1990, ApJS, 73, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Huang, Z.-P., Yin, Q. F., & Thuan, T. X. 1991, ApJ, 378, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., Tacconi, L. J., Davies, R. I., et al. 2007, ApJ, 657, 102 [NASA ADS] [CrossRef] [Google Scholar]
- De Looze, I., Baes, M., Bendo, G. J., Cortese, L., & Fritz, J. 2011, MNRAS, 416, 2712 [Google Scholar]
- Díaz-Santos, T., Charmandaris, V., Armus, L., et al. 2010, ApJ, 723, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Charmandaris, V., Armus, L., et al. 2011, ApJ, 741, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2013, ApJ, 774, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2014, ApJ, 788, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Kukula, M. J., et al. 2003, MNRAS, 340, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farrah, D., Lebouteiller, V., Spoon, H. W. W., et al. 2013, ApJ, 776, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Abel, N. P., González-Alfonso, E., et al. 2014, ApJ, 795, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Lutz, D., Sturm, E., et al. 1998, ApJ, 498, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [NASA ADS] [CrossRef] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2014, A&A, 561, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Sturm, E., et al. 2015, ApJ, 800, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., Sturm, E., Hailey-Dunsheath, S., et al. 2011, ApJ, 728, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., Wetzstein, M., & Roussel, H. 2015, ArXiv e-prints [arXiv:1512.03252] [Google Scholar]
- Guyon, O., Sanders, D. B., & Stockton, A. 2006, ApJS, 166, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Haan, S., Surace, J. A., Armus, L., et al. 2011, AJ, 141, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Simpson, J. M., Stanley, F., et al. 2016, MNRAS, 457, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Omont, A., Stevens, J. A., et al. 2010, A&A, 518, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heckman, T. M. 2002, in Extragalactic Gas at Low Redshift, eds. J. S. Mulchaey, & J. T. Stocke, ASP Conf. Ser., 254, 292 [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Draine, B. T., Bianchi, S., et al. 2015, A&A, 576, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ikarashi, S., Ivison, R. J., Caputi, K. I., et al. 2015, ApJ, 810, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-C., Evans, A. S., Vavilkin, T., et al. 2013, ApJ, 768, 102 [Google Scholar]
- Klaas, U., Haas, M., Müller, S. A. H., et al. 2001, A&A, 379, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, M. L., Satyapal, S., Fischer, J., et al. 1998, ApJ, 504, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, M. L., Satyapal, S., Fischer, J., et al. 2003, ApJ, 594, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D. 2014, ARA&A, 52, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Spoon, H. W. W., Rigopoulou, D., Moorwood, A. F. M., & Genzel, R. 1998, ApJ, 505, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Geis, N., Genzel, R., et al. 1993, ApJ, 407, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Poglitsch, A., Geis, N., Stacey, G. J., & Townes, C. H. 1997, ApJ, 483, 200 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malhotra, S., Helou, G., Stacey, G., et al. 1997, ApJ, 491, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., Kaufman, M. J., Hollenbach, D., et al. 2001, ApJ, 561, 766 [Google Scholar]
- Mor, R., & Netzer, H. 2012, MNRAS, 420, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Mushotzky, R. F., Shimizu, T. T., Meléndez, M., & Koss, M. 2014, ApJ, 781, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, E. J., van Dokkum, P. G., Förster Schreiber, N. M., et al. 2016, ApJ, submitted [arXiv:1507.03999] [Google Scholar]
- Neri, R., Downes, D., Cox, P., & Walter, F. 2014, A&A, 562, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H. 2013, The Physics and Evolution of Active Galactic Nuclei (Cambridge: Cambridge University Press) [Google Scholar]
- Netzer, H., Lutz, D., Schweitzer, M., et al. 2007, ApJ, 666, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, S. F., Genzel, R., Förster-Schreiber, N. M., et al. 2012, ApJ, 761, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Parra, R., Conway, J. E., Diamond, P. J., et al. 2007, ApJ, 659, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Petric, A. O., Ho, L. C., Flagey, N. J. M., & Scoville, N. Z. 2015, ApJS, 219, 22 [Google Scholar]
- Petty, S. M., Armus, L., Charmandaris, V., et al. 2014, AJ, 148, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Piazzo, L., Calzoletti, L., Faustini, F., et al. 2015, MNRAS, 447, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Riechers, D. A., Carilli, C. L., Capak, P. L., et al. 2014, ApJ, 796, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Rosario, D. J., Santini, P., Lutz, D., et al. 2012, A&A, 545, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roussel, H., Helou, G., Smith, J. D., et al. 2006, ApJ, 646, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Lutz, D., Genzel, R., et al. 2013, ApJ, 778, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Scoville, N. Z., Yun, M. S., et al. 1999, ApJ, 514, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Sandstrom, K., Krause, O., Linz, H., et al. 2010, A&A, 518, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargsyan, L., Lebouteiller, V., Weedman, D., et al. 2012, ApJ, 755, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Wyder, T. K., Martin, D. C., et al. 2007, ApJS, 173, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Evans, A. S., Thompson, R., et al. 2000, AJ, 119, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015, ApJ, 807, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Karim, A., Miettinen, O., et al. 2015, A&A, 576, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soifer, B. T., Neugebauer, G., Matthews, K., et al. 2000, AJ, 119, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Soifer, B. T., Neugebauer, G., Matthews, K., et al. 2001, AJ, 122, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Geis, N., Genzel, R., et al. 1991, ApJ, 373, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Surace, J. A., Sanders, D. B., & Evans, A. S. 2001, AJ, 122, 2791 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- U, V., Sanders, D. B., Mazzarella, J. M., et al. 2012, ApJS, 203, 9 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., Peng, C. Y., et al. 2006, ApJ, 643, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Kim, D.-C., Rupke, D. S. N., et al. 2009a, ApJ, 701, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Rupke, D. S. N., Kim, D.-C., et al. 2009b, ApJS, 182, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Meléndez, M., Sturm, E., et al. 2013, ApJ, 776, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, M. J., Bureau, M., & Cappellari, M. 2010, MNRAS, 409, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Wisnioski, E., Förster Schreiber, N. M., Wuyts, S., et al. 2015, ApJ, 799, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Fazio, G. G., Wilner, D. J., et al. 2008, ApJ, 688, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Fazio, G. G., Ashby, M. L. N., et al. 2010, MNRAS, 407, 1268 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Far-infrared size and surface brightness of galaxies and QSOs.
All Tables
All Figures
 |
Fig. 1 Measured FWHM at 70 μm (blue) and 100 μm (green) from 185 pairs of observations of 17 different reference stars. The resulting mean FWHM in arcsec and dispersion is indicated, as derived from bright sources in the flux range indicated by the horizontal line. |
| In the text | |
 |
Fig. 2 Intrinsic half light radii of galaxies and QSOs in the 70 μm blue band as a function of redshift. Symbols or limit for QSOs are encircled in green. The blue line indicates the physical size corresponding to the half width at half maximum of the PACS point spread function at that wavelength. Pink symbols mark results for close doubles/pairs. These are not used below unless explicitly mentioned. The most local galaxies have been placed at z = 0.002 to limit plot size. A number of galaxies with very compact FIR regions are identified. For many bright and large targets, error bars are smaller than the symbol size. Lower redshift galaxies with typically higher S/N can be resolved to smaller fractions of the PSF than the fainter QSOs. |
| In the text | |
 |
Fig. 3 Histograms of the ratio of the intrinsic half light radius in the 100 μm (160 μm) band to the half light radius in the 70 μm band, for sources with significant measurements in either band. The numbers of sources with a measurement at 70 μm but only a limit at the longer wavelength are listed in the top left, these will typically have size ratios ~1–2. The case of NGC 1097 (insets) visualizes how a warm central starburst superposed on a cold large disk can cause large ratios Re,160/Re,70 from fitting single Gaussians. Overplotted to the inset for each band are the ellipses at half maximum of the elongated Gaussian fit (black) and the beam (red, bottom right). |
| In the text | |
 |
Fig. 4 Scalings of half light radius at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with far-infrared luminosity. 251 galaxies with LFIR>109 L⊙ are included to avoid dwarfs and faint companions. The red line is a power law fit. In the left panel, sizes derived in the literature for high redshift submm galaxies at longer rest wavelengths ~150−400 μm are included for comparison (pink symbols). These were not used for the fit. |
| In the text | |
 |
Fig. 5 Scalings of FWHM size at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with distance from the Renzini & Peng (2015) star-forming main-sequence. The figure includes 86 galaxies with published stellar masses. The red line is a power law fit. Vertical dotted lines indicate a range of ±0.6 dex around the main-sequence, as often used to separate main-sequence galaxies from bursting or passive objects. |
| In the text | |
 |
Fig. 6 Scalings of FWHM size at 70 μm (left) and of corresponding rest frame FIR surface brightness (right) with PACS 70 to 160 μm color, for 260 galaxies. The inset to the right panel shows the relation as a function of dust temperature. |
| In the text | |
 |
Fig. 7 Ratio between the solid angle of a blackbody emitting half of the PACS fluxes at the blackbody temperature fitting those fluxes, and the measured half light solid angle, for 260 galaxies. Values approaching one indicate emission that is on average optically thick in the far infrared over the measured source size. Low values indicate optically thin emission and/or a scattered distribution of small sources which might still have considerable far-infrared optical depth. The inset shows the relation between this ratio of solid angles and the far-infrared surface brightness. The tightness is somewhat trivial, because both axes involve the measured solid angle and galaxies span a limited range of dust temperatures. |
| In the text | |
 |
Fig. 8 Ratio of [Cii] and FIR luminosity as a function of FIR luminosity (left), FIR color (middle) and FIR surface brightness (right panel). Red lines indicate the fits to our sample (Eqs. (12) and (13)), and black lines results of Díaz-Santos et al. (2013). The two slightly outlying points marked with an overlayed asterisk in the right panel were not used for the fit that is shown in red. Suitable [Cii] data are available for the 182 galaxies that are plotted here. |
| In the text | |
 |
Fig. 9 Comparison of observed scalings to two component toy models. Red lines show the fits to the data as previously shown in Fig. 6 (here: left and center panel) and Fig. 8 (right panel). Both toy models include a mix of a “disk” component with cold dust and a high ratio [Cii]/FIR, and a “dense star formation” component with warm dust and low [Cii]/FIR, with varying surface brightness of the warm component. Spreading the dense SF component with low filling factor over a large disk is a very poor fit, while scaling down its size with surface brightness gives a first approximation to the data. |
| In the text | |
 |
Fig. 10 Left: Half light radius at 70 μm as a function of redshift for PG QSOs and their hosts. Pink symbols mark systems with literature evidence for being double/interacting, which may inflate the measured size. Right: Half light radius at 70 μm vs. FIR luminosity for the z< 0.1 subsample of QSOs with favourable ratio of size measurments to limits. The relation derived above for galaxies is overplotted. |
| In the text | |
 |
Fig. 11 Comparison of half light radii measured in the far-infrared (this work) with near-infrared half light radii for the same sources (Table 5 of Veilleux et al. 2009a). The dashed line visualizes a 1:1 relation, it is not a fit. |
| In the text | |
 |
Fig. 12 Comparison of the radius at which an AGN of the given QSO’s luminosity heats directly exposed optically thin dust to the measured dust temperature, and the measured far-infrared half light radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


