| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527660 | |
| Published online | 03 June 2016 | |
Differences between the Pallas collisional family and similarly sized B-type asteroids⋆
1 Laboratoire Lagrange, UMR 7293, Université de la Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, 06304 Nice Cedex 4, France
e-mail: valilagoa@oca.eu
2 Instituto de Astrofísica de Canarias (IAC), c/ vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
3 Departamento de Astrofísica, Universidad de La Laguna, 38071 La Laguna, Tenerife, Spain
4 Complejo Astronómico El Leoncito (CONICET), Av. España 1512 sur, J5402DSP San Juan, Argentina
5 Universidad Nacional de San Juan, J. I. de la Roza 590 oeste, 5400 Rivadavia, San Juan, Argentina
6 Physics Department, University of Central Florida, PO Box 162385, Orlando, FL 32816.2385, USA
7 Department of Earth and Planetary Sciences, University of Tennessee, 1412 Circle Dr, Knoxville, TN 37996-1410, USA
8 Florida Space Institute/University of Central Florida, Orlando, FL 32826-0650, USA
9 Department of Astronomy, University of Maryland, College Park, MD 20472-2421, USA
Received: 29 October 2015
Accepted: 14 March 2016
Context. B-type asteroids constitute a peculiar spectral class within the C-complex. Previous work has pointed out the difference between the visible geometric albedos of B-types and those of the Pallas collisional family (PCF), whose few members with observed spectra are B-types (one exception out of eight objects). This has been interpreted as being due to compositional differences. However, the PCF members are typically smaller than the spectroscopically classified B-types, and the following possibilities have not been ruled out: the albedo differences might be related to a size-albedo dependence and/or to the generally larger errors of the WISE data and best-fitting values of the derived parameters expected for smaller objects.
Aims. We compare albedos and beaming parameters of PCF members and B-types of similar sizes and re-examine our conclusion on the different composition of the PCF.
Methods. By modelling their WISE/NEOWISE data, we derived sizes and albedos of all objects whose Sloan Digital Sky Survey reflectances are similar to the typical B-type reflectance spectra. In particular, we derived the so-called infrared beaming parameters (η), effective diameters (D), and corresponding visible geometric albedos (pV), and studied their value distributions.
Results. We obtained the effective diameter and geometric visible albedo for ~600 B-type asteroids whose sizes range between 2 and 100 km, approximately half of which have fitted η-values that are inversely correlated to size. We found that the albedo distributions of the PCF is significantly different from that of other B-types in the same size range (2−20 km), and we rule out any size-albedo dependency or biases related to the lower quality of the pV-values of smaller objects. In addition, we also found differences between the η-value distribution of the PCF and the other similarly-sized B-types.
Conclusions. The differences in the visible albedos of PCF members and the other B-types of similar sizes is a strong indication that their compositions are different. The trend between beaming parameter and size of the B-types (excluding the PCF) is consistent with the expectation that the surfaces of smaller asteroids have coarser rocks than do those of larger objects (D> 40 km), which are thought to be covered by a finer, more insulating layer of dust.
Key words: minor planets, asteroids: general / surveys / infrared: planetary systems
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/591/A14
© ESO, 2016
1. Introduction
Asteroids can be classified into different taxonomic classes according to their reflectance spectra. Defined in different classification schemes (Tholen 1989; Bus & Binzel 2002a,b; DeMeo et al. 2009), the B-type asteroids constitute a relatively small fraction of the spectroscopic C-complex. This major group includes the primitive asteroids, so called because they are spectroscopically associated with the undifferentiated carbonaceous chondrite meteorites. In the classification of DeMeo et al. (2009), the B class includes only by the four objects whose spectra show negative slopes up to near-infrared wavelengths (2.5 microns). Thus, following the criteria of Clark et al. (2010) and de León et al. (2012), we consider as B-types all objects that have a negative spectral slope in the visible wavelength range (around 0.55 μm). This includes the asteroids classified as B-types in any of the three main schemes, as well as F-types in the Tholen taxonomy and objects with ambiguous classifications. Hereafter, these will be referred to as spectroscopic B-types.
Primitive asteroids are scientifically interesting because they are thought to contain materials that have suffered a small degree of modification since their formation 4.567 Ga ago and may provide clues about the solar system’s past and evolution. This has motivated many of the asteroid spacecraft missions currently operating or under development to select primitive asteroids as targets; in particular, (101955) Bennu, the target of NASA OSIRIS-Rex mission, is a B-type asteroid (Clark et al. 2011; Hergenrother et al. 2013; Binzel et al. 2015).
B-types are scientifically interesting for several reasons. For example, most of the activated asteroids are B-types (see e.g. Licandro et al. 2012, and references therein). A 3 μm absorption band attributed to water ice was detected in the spectrum of B-type asteroid (24) Themis (Campins et al. 2010; Rivkin & Emery 2010) and, based on 3-micron reflectances derived from WISE IR data, Alí-Lagoa et al. (2013) predicted that a significant fraction of B-types will present 3 μm bands related to water (either in the form of ice or bound in silicates). This has been confirmed observationally by Yang & Ji (2014), who report features in about half of their 16 spectra. In addition, (2) Pallas, one of the largest asteroids in the main belt, is a B-type with an associated collisional family (Lemaitre & Morbidelli 1994) that resulted from a cratering event. Because the near-Earth asteroid (3200) Phaethon, the parent body of the Geminids, has been dynamically and spectroscopically associated with Pallas (de León et al. 2010), pieces of Pallas’ surface may have reached or will reach the Earth (Madiedo et al. 2013).
In our study of the physical properties of spectroscopic B-type asteroids from WISE/NEOWISE data (Alí-Lagoa et al. 2013), we pointed out that the visible geometric albedos of the Pallas collisional family (PCF) members differ significantly from those of the other spectroscopic B-types. However, we did not consider the possibility that said differences might be the result of a relationship between size and albedo – PCF members are all smaller than 20 km, but the catalog of spectroscopically observed objects is biased in favour of larger targets – or the expectedly larger errors in the WISE data and the thermal model fits of smaller objects – Grav et al. (2012b) showed that some of the visible albedos of the smaller Jupiter Trojan asteroids reach relatively high values as a consequence of this effect. Our aim here is to study the physical properties of a large sample of small B-types and explore these possibilities. To that end, we selected objects based on their Sloan Digital Sky Survey (SDSS) reflectances. Mainzer et al. (2012) studied the physical properties derived from NEOWISE data of objects classified from SDSS data by Carvano et al. (2010), but this classification does not distinguish between C-types and B-types. Thus, we created a list of B-types following the method summarised in Sect. 2 and described in Assandri & Gil-Hutton (2008) in more detail. This allowed us to compare B-types with PCF members at similar sizes. In addition, we updated our modelling procedure of WISE data based on that of Grav et al. (2012b), and we increased the data quality requirements (Sect. 3 and Appendix A.1) to ensure the reliability of our best-fitting parameter values and the robustness of our conclusions.
2. Selection from the Sloan Digital Sky Survey reflectances: SDSS B-types
In this section we describe the process we employed to identify B-type asteroids from their Sloan Digital Sky Survey (SDSS) relative reflectances.
SDSS photometry is based on the almost-simultaneous observations in the u, g, r, i, z system of filters with band centers at λu ~ 3540 Å, λg ~ 4770 Å, λr ~ 6230 Å, λi ~ 7630 Å, and λz ~ 9130 Å, and bandwidths of Δλu ~ 570 Å, Δλg ~ 1380 Å, Δλr ~ 1380 Å, Δλu ~ 1530 Å, and Δλu ~ 1350 Å (Fukugita et al. 1996; Stoughton et al. 2002). More specifically, we use a sub-product of the SDSS catalogue called the Moving Objects Catalog (MOC). Each entry in the MOC corresponds to a single observation of a moving object, and it provides its apparent magnitudes u, g, r, i, z, and corresponding errorbars. The more than 450 000 entries contained in the fourth release of the MOC are linked with about 100 000 known asteroids (Ivezić et al. 2001; Jurić et al. 2002). In order to extract our targets’ observations we used the procedure described in Assandri & Gil-Hutton (2008).
Our list was generated by finding those objects whose SDSS reflectances were sufficiently similar to the mean B-type spectrum. The mean B-type spectrum was obtained by resampling the corresponding values found in Table 3 of Bus & Binzel (2002b) and summing the spectrum weighted by the SDSS filter set transmission profiles. To quantify the “dissimilarity” between each spectrum and the mean spectrum the following Euclidean distance was defined, 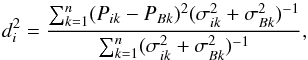 (1)where Pik and PBk are the values of reflectances in the different bands k of the ith and the mean B-type spectrum, σ refers to the corresponding errorbars, and n is the number of bands used. Since the central wavelength of filter u is much shorter than those covered in the Bus & Binzel taxonomy, this filter is not used to compute the spectral dissimilarity. Thus, our sample of Sloan B-types contains asteroids that verify di ≤ 0.05. From now on, we will refer to this sample as the SDSS B-types. Since one of the aims of this work is to study in more detail the differences between the Pallas collisional family members and the other B-types (see Alí-Lagoa et al. 2013), the former were removed from the SDSS and the spectrosocopic B-type lists to be examined separately.
(1)where Pik and PBk are the values of reflectances in the different bands k of the ith and the mean B-type spectrum, σ refers to the corresponding errorbars, and n is the number of bands used. Since the central wavelength of filter u is much shorter than those covered in the Bus & Binzel taxonomy, this filter is not used to compute the spectral dissimilarity. Thus, our sample of Sloan B-types contains asteroids that verify di ≤ 0.05. From now on, we will refer to this sample as the SDSS B-types. Since one of the aims of this work is to study in more detail the differences between the Pallas collisional family members and the other B-types (see Alí-Lagoa et al. 2013), the former were removed from the SDSS and the spectrosocopic B-type lists to be examined separately.
To evaluate the performance of this B-type selection procedure, we took the definition of B- and C-types of Bus & Binzel (2002a,b) and generated synthetic values of reflectances and corresponding standard deviations in each SDSS filter for two populations: 10 000 B-types and 10 000 C-types. While our algorithm frequently misclassifies B-types as Ch and Cb (36% and 25%), it only misclassifies 3 C-types as B-types. In other words, it is possible that we do not include many true B-types in our SDSS sample, but we definitely do include an insignificant fraction of objects with other classification among our B-types, especially P- or D-types, which have more positive spectral slopes than do C-types.
3. WISE data
This work makes use of WISE thermal infrared W3 and W4 data downloaded from the WISE All-Sky Single Exposure L1b Working Database as explained in Alí-Lagoa et al. (2013). Including the corrections to bands W3 and W4 related to the red and blue calibrator discrepancy (Wright et al. 2010), the corresponding isophotal wavelengths are W1 = 3.35 μm, W3 = 11.1 μm, and W4 = 22.64 μm (Masiero et al. 2011). To search for observations of the asteroids in the SDSS B-types list (see Sect. 2), we queried the IRSA/IPAC archive for detections within a cone search radius of 1′′ centred on the objects’ ephemerides reported to the Minor Planet Center (MPC).
The criteria used to identify and reject spurious data used by Alí-Lagoa et al. were based on a combination of different criteria taken from Mainzer et al. (2011a,b), Masiero et al. (2011), and Grav et al. (2012a). Here, we also require that the modified Julian date be within four seconds of the time specified by the MPC and split groups of epochs separated by more than three days. We do not use partially saturated data1 or data with artefact flags other than p,P, and 0 (see Masiero et al. 2011). To ensure that the data has not been contaminated by inertial sources we removed those points that returned a positive match from the WISE Source Catalog within 6′′ with fluxes higher than 5% of the asteroid fluxes. Finally, all remaining observations in a given band are rejected if they make up fewer than 40% of the data in the band with the maximum number of detections.
However, for this work, we decided to reject data with quality flags B and C, which means that we are only using data with signal-to-noise ratios (S/N) greater than or equal to 10. This effectively prevents us from significantly biasing the beaming parameter values of the smaller asteroids in the sample (a detailed analysis and a justification for this statement are presented in Appendix A).
4. Thermal modelling
The size of an asteroid can be determined from its thermal infrared data by fitting an asteroid thermal model. Here, we follow the implementation of the near-Earth asteroid thermal model (NEATM; see Harris 1998) introduced by Mainzer et al. (2011b) with some differences (see below). To represent the asteroid, we employ a spherical surface divided into ≈2000 triangular facets. The surface is assumed to be perfectly diffusing and in instantaneous thermal equilibrium so that the temperature of each facet at any given time will depend on their inclination with respect to the sunward direction and the heliocentric distance of the asteroid. Non-illuminated facets are assumed to be at 0 K. Because surfaces of asteroids are not Lambertian and thermal equilibrium is a very idealised hypothesis that neglects heat conduction to subsurface layers, the NEATM leaves the infrared beaming parameter, η, free in order to better fit the observed colour temperature of the asteroid (Harris 1998). This results in best-fitting values of asteroid size2 that are more accurate than those provided by the standard thermal model or the fast rotating model, both of which assume fixed values of η (see e.g. Lebofsky & Spencer 1989, for a review). More specifically, the temperature of a given facet is related to Bond albedo (A), heliocentric distance (r), and beaming parameter through the equation ![\begin{equation} T = \left[\frac{\mu(1-A)}{\eta\epsilon\sigma}\frac{S_\odot}{r^2}\right]^\frac{1}{4}, \label{eq:t} \end{equation}](/articles/aa/full_html/2016/07/aa27660-15/aa27660-15-eq35.png) (2)where σ is the Stefan-Boltzmann constant, ϵ the emissivity of the surface (assumed to be 0.9; see e.g. Delbo’ et al. 2007, and references therein), S⊙ is the solar power at 1 au, and μ is the cosine of the angle subtended between the facet normal and the sunward direction.
(2)where σ is the Stefan-Boltzmann constant, ϵ the emissivity of the surface (assumed to be 0.9; see e.g. Delbo’ et al. 2007, and references therein), S⊙ is the solar power at 1 au, and μ is the cosine of the angle subtended between the facet normal and the sunward direction.
Once the temperatures for each illuminated facet are determined and colour-corrected in filters W3 and W4 (see Alí-Lagoa et al. 2013, for more details), the corresponding fluxes are scaled by the cosine of the angle subtended between each facet normal and the direction towards the observer, and by the inverse of the square of the distance to the asteroid approximated by the geocentric distance. Finally, the model flux at each epoch of observation is then calculated as the sum of the fluxes from those illuminated facets that were visible to WISE at that time. This depends on the phase angle, i.e. the angle subtended by the Earth and the Sun as seen from the asteroid.
The number of parameters we can fit for a given object depends on the number of available WISE bands. Bands W3 and W4 are dominated by thermal emission, W1 is usually reflected sunlight, and W2 is a mixture of both components. In previous works, W1 and W2 have been used to fit the ratio of infrared to visible albedo, and at least two of the W2, W3, and W4 datasets have been used to fit the infrared beaming parameter. The fits were made under the assumption that the geometric albedos in bands W1 and W2 are equal, but this will bias the best-fitting values of beaming parameter in those cases when the assumption is not applicable because the relative contribution of the thermal flux in W2 will not be correct. While the resulting error in η is usually relatively small (~3% Masiero et al. 2014), it will propagate as a change of the order of 5% on the value of the size and a corresponding 10% on the visible geometric albedo, pV. We note that pV is derived from the asteroid size and absolute magnitude by means of the equation 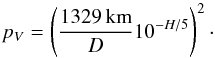 (3)Therefore, even though the constant infrared albedo approximation may be applicable in the case of B-types given their relatively flat spectra up to mid-infrared wavelengths (de León et al. 2012), we decided to adopt the approach of Grav et al. (2012a) and Masiero et al. (2014) and we did not use W2 in our modelling. This means that we can only fit the beaming parameter when both W3 and W4 data are available and that we must use a preset value otherwise. Masiero et al. (2011) find a peak value of η = 1.0 for the whole main belt population, so this has been taken as the default value. However, in the preliminary analysis presented in Appendix A we show that the small and large B-types have different average values of η, which led us to take the following approach (see also Sect. 5.1.2): we first use a default value of η = 1.0 and if the resulting size is D> 40 km (D< 40 km), we run the model again with η = 0.9 (η = 1.1). Using a default value of η allows us to fit the size and to calculate the corresponding visible geometric albedo from Eq. (3) for all the asteroids in our list.
(3)Therefore, even though the constant infrared albedo approximation may be applicable in the case of B-types given their relatively flat spectra up to mid-infrared wavelengths (de León et al. 2012), we decided to adopt the approach of Grav et al. (2012a) and Masiero et al. (2014) and we did not use W2 in our modelling. This means that we can only fit the beaming parameter when both W3 and W4 data are available and that we must use a preset value otherwise. Masiero et al. (2011) find a peak value of η = 1.0 for the whole main belt population, so this has been taken as the default value. However, in the preliminary analysis presented in Appendix A we show that the small and large B-types have different average values of η, which led us to take the following approach (see also Sect. 5.1.2): we first use a default value of η = 1.0 and if the resulting size is D> 40 km (D< 40 km), we run the model again with η = 0.9 (η = 1.1). Using a default value of η allows us to fit the size and to calculate the corresponding visible geometric albedo from Eq. (3) for all the asteroids in our list.
Best-fitting values of size (D) and beaming parameter (η) and corresponding visible geometric albedos (pV) for all our objects.
5. Results
In this section we first present our comparison between the visible geometric albedos and beaming parameters computed for the SDSS and the spectroscopic B-types. Next, we compare the properties of the Pallas collisional family (the list was taken from Nesvorny 2012) against those of all the other B-types. The statistics of our different populations are summarised in Table 2. For example, we computed sizes and corresponding visible geometric albedos of 600 objects of the SDSS B-types list (for details on how this list was generated, see Sect. 2). Fifty-five objects were observed at two stages of the WISE survey and thus have two entries in the table. For our statistical purposes, these have been considered as different objects. About half of the SDSS B-types, namely 313, had at least two data points in bands W3 and W4, which is sufficient to fit the infrared beaming parameter as well. Among these, 215 objects had ten or more such measurements. We consider this restricted sample to have high-quality fits, which is especially important for studying their beaming parameter distribution (see Appendix A). Likewise, the number of high-quality η-value fits is approximately half of the sample of Pallas collisional family members.
All best-fitting values of parameters and other relevant information such as the absolute magnitudes, slope parameters, number of observations used from each band, or the observing geometry, are compiled in Table 1. Default values of η are given in negative numbers.
5.1. SDSS versus spectroscopic B-types
5.1.1. Beaming parameter (η) distributions
The average beaming parameter of the spectroscopic and the Sloan B-types are different (see Table 2). Although their average η-values are compatible within the errorbars, the distributions are shifted relative to each other and the Kolmogorov-Smirnov (KS) test rules out the null hypothesis that both samples are drawn from the same distribution with a p-value of <0.3%. Because we assume that these asteroids are compositionally similar given their albedo (see Sect. 5.1.3) and spectral resemblances in the visible (de León et al. 2012), we take these differences as clues about the distinct physical nature of their surfaces. In this section we give a plausible physical interpretation for these differences; in Appendix A we show that they are not related to the lower quality of the fits for the smaller objects (Sect. A.1) or to the fact that the smallest objects were observed by WISE only at high phase angles (Sect. A.2).
The beaming parameter of the whole B-type population – excluding the Pallas collisional family – is inversely correlated with size. Figure 1 shows a plot of η versus equivalent diameter for all spectroscopic and SDSS B-types with ten or more observations in bands W3 and W4, which ensures the high-quality of the η values. The straight line is the best-fitting function of the form η(D) = klog 10D + η0 (D in km; the coefficients are given in Sect. 5.1.2). It is apparent how the smaller objects tend to have η> 1 and the larger ones have η< 1.
Statistics of the best-fitting values of beaming parameter (η) and visible geometric albedos (pV) computed for our populations.
Our interpretation of this trend is based on the work of Delbo’ et al. (2007) and Delbo’ & Tanga (2009). Using a more sophisticated thermophysical model, those authors derived the thermal inertias of near-Earth objects and main belt asteroids from IRAS and ground-based infrared data and found that thermal inertia3 is inversely correlated with the size of the objects (see their Figs. 6 and 1, respectively). These findings supported the intuitive view that the surfaces of the larger bodies is covered by an insulating mantle of regolith developed over their pressumed long lifetimes whereas the smaller ones, with expectedly shorter collisional lifetimes and lower gravities, have rockier surfaces.
 |
Fig. 1 Beaming parameter versus size (equivalent diameter) of the B-type population. Sloan B-types are shown in grey, spectroscopic B-types are shown in green. Members of the Pallas collisional family are not included. See the text for more information. |
In our case, we base our interpretation of the higher values of η on the same grounds. We note that the beaming parameter depends in a complicated way on several quantities in addition to thermal inertia, e.g. the orientation of the spin axis and the rotation period, the phase angle of the observation, or the global shape of the body, but the general trend is that higher values of η correspond to higher thermal inertias (for a discussion see Sect. 6). For instance, Fig. 3 of Delbo’ et al. (2007) showed this trend for the NEAs they studied: the values of η tend to be higher for those synthetic models with higher thermal inertias (which grow from green through red to blue in the figure). Also, Alí-Lagoa et al. (2014) report η = 2 for near-Earth asteroid (341843) 2008 EV5, a C-complex asteroid (Reddy et al. 2012) that was the baseline target of the Marco Polo-R mission (see e.g. Barucci et al. 2012). This is significantly larger than the average η of our sample and indeed larger than the average for NEAs (Mainzer et al. 2011a), which is expected under the present interpretation since it is much smaller than our smallest B-types (~400 m versus ~3 km) and among the smallest NEAs with η-value determined from WISE data.
Finally, we caution that we have not addressed survey incompleteness (WISE and SDSS) and other potential biases that may have an impact on our beaming parameter statistics. For example, the lower sensitivity of band W4 versus W3 coupled with our requirement to have data available in both bands in order to fit η will, in general, penalise high-pV, higher-η objects for a given size and heliocentric distance. As stated above, the beaming parameter is also difficult to interpret physically, (see Sect. 6 for further discussion), so evaluating all these biases quantitatively is outside the scope of this work, and we emphasise that this interpretation is a plausible one that requires more work to confirm it. Qualitatively, we can argue that incompleteness effects cannot solely be responsible for the trend observed in Fig. 1. First, while higher beaming parameter are penalised, we still find higher η-values among the smallest objects. Second, WISE has still detected many objects with higher pV- and η-values (the average η of the main belt is 1.5 Masiero et al. 2011) so, albeit incomplete, we should see hints of a higher-pV and/or higher-η population among our objects if it existed.
5.1.2. Default value of beaming parameter
Figure 1 suggests that the default ηd = 1.0 based on the mean value of the whole main belt population found by Masiero et al. (2011) is not in general adequate for our sample, especially at the small- and large-size ends of the distribution. Using an inadequate ηd will have a noticeable effect on the computed values of albedo; in particular, increasing ηd by 0.1 for a given object increases the size by ~5 to 10% and the corresponding albedo decreases by 10−20% (see Eq. (3)). Thus, we changed the default values of η as a function of size in order to avoid biasing the albedos when W3 or W4 data are not available (~50% of the quality-A sample). The cases where ηd has been used appear as negative values in Table 1.
We found that a function of the form η(D) = klog 10D + η0 (the straight line in the plot) fits the observed trend with coefficients k = −0.15 ± 3 and η0 = 1.24 ± 0.03, and D expressed in km. This function provides the qualitative idea that the instantaneous equilibrium assumption within the NEATM, i.e. η = 1, is not verified by many objects both significantly larger and smaller than ~40 km (dashed vertical line in Fig. 1). Taking the mean beaming parameters of all B-type objects with D< 40 km and D> 40 km separately, we find 1.1 ± 0.2 and 0.9 ± 0.1. These are our preferred default values, but because size is not known a priori, we first computed size (Dd) with the original default value ηd = 1 and ran the model again setting ηd = 1.1 if Dd< 40 km, and ηd = 0.9 otherwise.
We note that this approach is not applicable in general to the whole set of asteroids observed by WISE. It is also limited by the fact that the sample of objects for which we could compute the beaming parameter is not complete. In this sense, diameters (and particularly the corresponding albedos) obtained from NEATM with fixed η should be still taken with a grain of salt.
5.1.3. Visible geometric albedo distributions
Contrary to their differences in beaming parameter, the large and the small, i.e. the spectroscopic and the SDSS B-types, have consistent albedo distributions. In the prelimiary analysis of Appendix A, we show albedo histograms that include all objects with fitted η regardless of data quality (Fig. A.1, left panel) and only those in the restricted sample (Fig. A.4, left panel). In all cases, the average values of albedo of both sets are very similar (see Table 2) and the KS test cannot distinguish between their corresponding distributions. Unlike the beaming parameter, the geometric albedo of the SDSS B-types does not show a clear correlation with size either, although the dispersion of the values is somewhat higher for smaller objects (see Fig. 2). The latter was shown by Grav et al. (2012a) to be the result of the higher statistical fluctuations expected for the smaller objects in the Jovian Trojan population, but it is applicable to all asteroids modelled from the WISE data. This is also shown in our figure, since most of the high-pV values are not present in our restricted sample.
 |
Fig. 2 Visible geometric albedo versus size of all B-types excluding the PCF. The different sets correspond to different requirements to the fits: η was either fitted or a default value was used (grey), η was fitted (red), and η was fitted to at least 10 data points in both bands. The pV values obtained for those cases with fitted η do not spread as much as those coming from sizes fitted using default η-values. |
5.2. The Pallas collisional family versus the other B-types
Alí-Lagoa et al. (2013) pointed out that the geometric visible albedos of the PCF are significantly different from those of the spectroscopic B-types. With the advantage of the SDSS B-types, we can now confirm that these differences are not related to any albedo-size relationship or to the higher dispersion of the albedo computations due to the lower quality of the fits for smaller objects. The upper panel of Fig. 3 shows the albedo distributions of the PCF (blue boxes) and of all B-types smaller than 20 km (the largest PCF member after Pallas is <20 km). The middle panel is a plot of albedo versus size.
 |
Fig. 3 Top panel: normalised histogram of the visible geometric albedo distributions of the Pallas collisional family and all B-types smaller than 20 km for which the beaming parameter could be fitted. Middle panel: Albedo versus size of all B-types and PCF members with fitted η. Lower panel: beaming parameter versus size (equivalent diameter) of the B-type population (grey) and the Pallas collisional family (PCF). |
Again, we note that our populations are biased observationally and this analysis is limited to the completeness limits of the NEOWISE and SDSS catalogues, including the portion of the main belt that was not observed by NEOWISE (see Fig. 1 in Mainzer et al. 2012). On the other hand, we cannot think of any group of biases that can, at the same time, operate against high-pV objects in our SDSS list and against low-pV objects in the PCF list, so the conclusions drawn from Fig. 3 are robust.
Concerning the beaming parameter statistics, Alí-Lagoa et al. (2013) did not find significant differences between the η-value distributions of the PCF and the spectroscopic B-types. The situation is intriguingly different when we compare objects with similar sizes: the lower panel of Fig. 3 is a plot of beaming parameter versus size of all B-types (grey) and the PCF. The PCF members have generally lower η, and their values overlap only with the lowest values in the B-type distribution. Harris & Drube (2014) found that the average η-value of M-type asteroids from WISE data is higher than usual, which they interpret as the consequence of their higher metal content. Based on this, the lower η-values of the PCF could be a tantalising hint that the material has a lower metal content. However, as noted in Sect. 5.1.1, our samples are not complete owing to observational biases, and the beaming parameter depends complicatedly on several parameters (see e.g. Delbo’ et al. 2007), which makes it difficult to determine the causes responsible for the lower η-values of the PCF without more sophisticated modelling, e.g. thermophysical modelling (see also the end of Sect. 6). Such analysis is out of the scope of this article and will be tackled in future work since it is also relevant for other asteroid populations.
6. Discussion
The clues obtained by several recent works –including the present one– on the Pallas collisional family and B-types in general can be summarised as follows:
-
B-types are related to carbonaceous chondrites (primitivemeteorites) but have gradually varying spectral slopes in thenear-infrared (de Leónet al. 2012).
-
Pallas collisional family members appear to be end-members among the B-type population, since they have:
-
the bluest spectral slopes in the near-infrared(de Leónet al. 2012);
-
the lowest 3-micron albedos and the highest visible albedos (Fig. 11 of Alí-Lagoa et al. 2013);
-
the lowest η values.
-
These differences are not physically related to size, as shown by our comparison between the PCF members against B-types of the same sizes.
In this section, we hypothesise about the possible implications of these facts. First, given how difficult it is to determine the composition of spectrally featureless objects, it could be that Pallas and its collisional family are less compositionally related to other B-types than suggested by the spectral dataset and that they have different origins and compositions. On the other hand, the negative visible spectral slopes are relatively uncommon, so it is also plausible to assume that all B-type parent bodies were initially similar. If this is the case, the picture emerging from the growing body of information available is that Pallas may be the only such parent body that has survived collisional disruption in the main belt. In this context, and following the discussion of Campins et al. (2012) focused on (24) Themis, differences between PCF and the rest of the B-types point to a different composition between the surfaces and the interiors of these parent bodies. This would explain why only the properties of the PCF are homogeneous: the cratering event that gave origin to the family (Clark et al. 2010, and references therein) removed fragments from the parent body’s upper surface layers.
A compositional gradient towards the interior of the B-type parent bodies has already been proposed based on visible to near-infrared spectra (de León et al. 2012; Campins et al. 2012). In this work we also found that the B-types have a higher average beaming parameter than the PCF members do. Considering the arguments given in Sect. 5 and Harris & Drube (2014), this may be the result of the PCF having a lower thermal inertia and hence a lower metal content than other B-types. Within the compositional gradient interpretation, a higher metal content for the latter would also be consistent with the finding that the densities of the B-types are higher than other C-complex asteroids (Carry 2012). Indeed, one would expect the largest objects, which also happen to be the ones that have estimated densities, to be the collisional fragments that are more representative of the interior of the population of B-type parent bodies.
The visible to near-infrared spectral characteristics of the PCF versus those of other B-types, as well as the visible and 3-micron albedos computed here, might also be consistent with a surface with lower metal content if one assumes that lunar-type space weathering has operated on the surface of Pallas and the other B-type asteroids. The space weathering on the Moon is attributed to the presence of nanophase reduced iron (npFe0) on the rims of lunar soil grains as a consequence of deposition after sputtering from nearby grains or the condensation of vapours generated by micro-meteorite impacts (Pieters et al. 2000). The relevant aspect here is that the cumulative amount of npFe0 and its effect on the optical properties of the material is a function of the availability of Fe. Thus, if the Fe-rich minerals were absent in the surface of B-type parent bodies but not in their interiors, perhaps due to partial differentiation, it would explain why the albedos of Pallas and its collisional fragments have remained higher and their near-infrared spectral slopes lower.
Another possibility is that the effects of space weathering are different on the surfaces of Pallas and the Moon. Hiroi & Sasaki (2012) showed that the spectra of two carbonaceous chondrites pressed into pellets became bluer (the spectral slope decreased) under one exposure to pulse-laser irradiation. Also, Hiroi et al. (1996) showed that the near-infrared reflectance spectra of the meteorite Murchison (CM2) changed from moderately red to flat when gradually heated from ~700 to ~1300 K, which makes a heating episode another plausible cause of the rare spectral properties of Pallas down to 2.5 microns. A complication with these considerations is that, while a 3-micron absorption band has been detected on Pallas, the irradiation and the heating reduce and completely remove the 3-micron band, respectively (see e.g. Bennett et al. 2013).
Finally, we point out an important caveat: further work is required to confirm our interpretation that the lower η-values of the PCF are related to a lower metal content. First, it would be necessary to obtain shapes and rotational states from optical lightcurve inversion (see e.g. Kaasalainen et al. 2002, and references therein) of tens of members of the PCF. These would enable us to use thermophysical modelling to derive their thermal inertias, which provide more detailed information about the thermal properties of the surface material than the beaming parameter. Knowledge of the rotational estates of a sufficient number of PCF would also allow us to quantify how the η-values of the PCF are related to their rotation rates, spin axis orientations, and even their shapes (NEATM assumes a spherical body). Indeed, the η-values may be less reliable for smaller objects since they are more irregular, but this effect has not been quantified yet. The fact that the spin-axis distribution of small asteroids (D< 40 km) is non-isotropic (Hanuš et al. 2011) and that these asteroids have a larger fraction of fast/slow rotators (Warner et al. 2009) could also have an effect on the η-value distribution. Thus, all this information would not only provide a detailed characterisation of the collisional family itself, but it would help us obtain more detailed information from the study of the η-value distribution of many other asteroid populations from the huge WISE data catalogue.
7. Conclusions
In this work we used WISE W3 and W4 data to derive infrared beaming parameters, diameters and visible geometric albedos of a large set of B-type asteroids based on their Sloan Digital Sky Survey reflectances. This allowed us to study the physical properties of B-types down to smaller sizes than was possible with the spectrally classified objects (see Alí-Lagoa et al. 2013). Our aim was to compare the value distributions of albedos and beaming parameters of the Pallas collisional family members (all smaller than ~20 km) and other B-types of similar sizes. Our conclusions can be summarised as follows:
-
1.
The albedos of the B-type asteroids (exclud-ing the PCF) are consistently low (averagepV = 0.07 ± 0.02) down to small sizes (as small as D ~ 2 km).
-
2.
The albedo distribution of PCF asteroids is different from the other B-types even at similar sizes (D< 20 km), confirming that the higher albedos of the PCF are not a consequence of any physical relationship between size and albedo.
-
3.
The beaming parameters of B-types (excluding the PCF) increases as size decreases. Based on the association of higher η-values with higher thermal inertias and the correlation between thermal inertia and size (Delbo’ et al. 2007; Delbo’ & Tanga 2009), the most likely explanation is that it is caused by the lack of fine insulating dust on the surfaces of the smaller objects. The average infrared beaming parameter of the PCF is lower than that of the rest of B-types. Following the interpretation of Harris & Drube (2014) for M-types, this could be indicative of a lower thermal inertia (and hence lower conductivity) of the surfaces of the PCF. However, these interpretations require more work to be confirmed. For example, quantifying survey biases and deriving more detailed physical properties (spin axis orientation, shapes, thermal inertias) is needed.
-
4.
The significant differences in their albedo (and possibly their beaming parameter) value distributions is a clear indication that the surface composition of the Pallas collisional family are different from that of the other B-types.
The onset of saturation is reported to correspond to magnitudes mW3 = 3.6, mW4 = −0.6 (Cutri et al. 2012).
Thermal inertia is defined as the square root of the conductivity, the density, and the specific heat capacity of a material and hence plays a major role on the surface temperature distribution of the asteroids. The surfaces of several bodies without atmospheres such as the Moon, (951) Gaspra, or (433) Eros, are covered by a thick layer of insulating fine-grained dust called regolith. If the conductivity and the particle density of the regolith are small, the surface will be well-insulated. In these conditions, the surface temperature must respond rapidly to the change in illumination by solar radiation because the incident energy cannot be transmitted to lower layers and must be re-emitted. In other words, the thermal inertia is low. On the other hand, if the surface is not covered by dust, i.e. it is more rocky, the conductivity and the thermal inertia will be higher, the energy can be conducted to or from subsurface layers, and the temperatures respond less rapidly to changes in illumination. Hence, the thermal inertia is high.
Quadrature refers to the particular observation geometry in which the elongation (the angle between the sun and the asteroid as seen from WISE) is ~90 Because WISE always observes in this configuration, the phase angles and geocentric and heliocentric distances of all observations are related. In particular, observations at smaller heliocentric distances were taken at higher phase angles.
Because WISE always observes in this configuration, the phase angles and geocentric and heliocentric distances of all observations are related. In particular, observations at smaller heliocentric distances were taken at higher phase angles.
Acknowledgments
V.A.L. and J.L. acknowledge support from the project ESP2013-47816-C4-2-P. J.d.L. is grateful for financial support via a “Juan de la Cierva” contract from the Spanish Secretaría de Estado de Investigación, Desarrollo e Innovación. V.A.L., M.D.B., and J.H. acknowledge support from the French ANR project SHOCKS. R.G.H. gratefully acknowledges financial support from CONICET through PIP 114-201101-00358. This publication makes use of data products from NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology, funded by the Planetary Science Division of the National Aeronautics and Space Administration. This research also made use of the NASA/ IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Alí-Lagoa, V., de León, J., Licandro, J., et al. 2013, A&A, 554, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alí-Lagoa, V., Lionni, L., Delbo, M., et al. 2014, A&A, 561, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Assandri, M. C., & Gil-Hutton, R. 2008, A&A, 488, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barucci, M. A., Cheng, A. F., Michel, P., et al. 2012, Exp. Astron., 33, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. J., Pirim, C., & Orlando, T. M. 2013, Chem. Rev., 113, 9086 [CrossRef] [Google Scholar]
- Binzel, R. P., DeMeo, F. E., Burt, B. J., et al. 2015, Icarus, 256, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002a, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002b, Icarus, 158, 106 [CrossRef] [Google Scholar]
- Campins, H., Hargrove, K., Pinilla-Alonso, N., et al. 2010, Nature, 464, 1320 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Campins, H., de León, J., Licandro, J., et al. 2012, Planet. Space Sci., 73, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Carvano, J. M., Hasselmann, P. H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, B. E., Ziffer, J., Nesvorny, D., et al. 2010, J. Geophys. Res. (Planets), 115, 6005 [Google Scholar]
- Clark, B. E., Binzel, R. P., Howell, E. S., et al. 2011, Icarus, 216, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M. et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
- de León, J., Campins, H., Tsiganis, K., Morbidelli, A., & Licandro, J. 2010, A&A, 513, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de León, J., Pinilla-Alonso, N., Campins, H., Licandro, J., & Marzo, G. A. 2012, Icarus, 218, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo’, M., & Tanga, P. 2009, Planet. Space Sci., 57, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo’, M., Dell’Oro, A., Harris, A. W., Mottola, S., & Mueller, M. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E., Binzel, R. P., Slivan, S. M., & Bus, S. J. 2009, Icarus, 202, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J., et al. 2012a, ApJ, 744, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J. M., Masiero, J. R., & Nugent, C. R. 2012b, ApJ, 759, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., & Drube, L. 2014, ApJ, 785, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Hergenrother, C. W., Nolan, M. C., Binzel, R. P., et al. 2013, Icarus, 226, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Hiroi, T., & Sasaki, S. 2012, LPI Contributions, 1667, 6109 [NASA ADS] [Google Scholar]
- Hiroi, T., Zolensky, M. E., Pieters, C. M., & Lipschutz, M. E. 1996, Meteor. Planet. Sci., 31, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Tabachnik, S., Rafikov, R., et al. 2001, AJ, 122, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., Ivezić, Ž., Lupton, R. H., et al. 2002, AJ, 124, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Mottola, S., & Fulchignoni, M. 2002, in Asteroids III (University of Arizona Press), 139 [Google Scholar]
- Lebofsky, L. A., & Spencer, J. R. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews, 128 [Google Scholar]
- Lemaitre, A., & Morbidelli, A. 1994, Celest. Mech. Dyn. Astron., 60, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Licandro, J., Hargrove, K., Kelley, M., et al. 2012, A&A, 537, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madiedo, J. M., Trigo-Rodríguez, J. M., Castro-Tirado, A. J., Ortiz, J. L., & Cabrera-Caño, J. 2013, MNRAS, 436, 2818 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Bauer, J., et al. 2011a, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al. 2011b, ApJ, 736, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Masiero, J., Grav, T., et al. 2012, ApJ, 745, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2012, ApJ, 759, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Grav, T., Mainzer, A. K., et al. 2014, ApJ, 791, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorny, D. 2012, NASA Planetary Data System, 189 [Google Scholar]
- Pieters, C. M., Taylor, L. A., Noble, S. K., et al. 2000, Meteor. Planet. Sci., 35, 1101 [Google Scholar]
- Reddy, V., Corre, L. L., Hicks, M., et al. 2012, Icarus, 221, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Rivkin, A. S., & Emery, J. P. 2010, Nature, 464, 1322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews, 1139 [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Wolters, S. D., & Green, S. F. 2009, MNRAS, 400, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., & Ji, J. 2014, in Asteroids, Comets, Meteors 2014, eds. K. Muinonen, A. Penttilä, M. Granvik, et al., 594 [Google Scholar]
Appendix A: Preliminary parameter value distributions
In this section we provide a comparison of the visible albedo and beaming parameter value distributions of the SDSS and spectroscopic B-types that resulted from fitting their data obtained as described in Sect. 2 of Alí-Lagoa et al. (2013). We refer to these as the preliminary sample and preliminary value distributions. In particular, the difference with the criteria adopted in Sect. 3 is that the preliminary sample includes results from modelling W3 and W4 data with quality flags A, B, or C, i.e., signal-to-noise ratios S/N> 10, 3 <S/N< 10, and 2 <S/N< 3. This analysis is relevant because it helped us identify a bias affecting the η values of many of the smaller objects in the preliminary SDSS sample as a consequence of their expected lower data quality.
Figure A.1 shows the normalised beaming parameter and visible albedo distributions of the preliminary samples – the spectroscopic B-types are shown in green, the SDSS B-types in empty boxes – and Table A.1 presents the number of values in each sample and their corresponding mean, standard deviation, and median. The pV-value distributions (left panel) are very similar; they have compatible mean and identical median values, and the two-sample Kolmogorov-Smirnoff (K-S) test does not reject the null hypothesis that both sets are drawn from the same distribution. On the other hand, the η-value distributions are significantly different. The SDSS sample shows a high-η tail and even though the mean and median beaming parameters are compatible within their standard deviations, in this case the K-S test rules out the possibility that both distributions are compatible. What does this tell us? Our proposed physical interpretation for these differences is provided in Sect. 5, and the remaining sections are devoted to a detailed discussion of two potential sources of biases that must be considered before any physical interpretation is exercised.
 |
Fig. A.1 Normalised histograms of the preliminary parameter value distributions obtained for all SDSS and spectroscopic B-types observed by WISE for which the beaming parameter could be fitted. See the text for the definition of this preliminary sample. |
Appendix A.1: Data quality
The data available for smaller objects will generally have lower S/Ns, which may be relevant because ninety percent of the objects in the SDSS sample have D< 10 km, whereas most of the spectroscopic B-types are larger than 10 km. As a result of these lower S/Ns, the η-value distribution of the more numerous SDSS B-types will be wider and therefore the high-η tail could be partly due to this artefact.
 |
Fig. A.2 Average values of beaming parameter for different subsamples of the SDSS B-types. Left: mean values. Right: median values. The number ν represents the minimum number of points both in W3 and W4 bands required for an object to be part of the sample (see text). Averages corresponding to parameters computed from data with quality flags A, B, or C are plotted in red; the more restrictive case that only allows quality flag A are in blue. |
To quantify this difference, we created several new sets of SDSS B-types η-values derived from higher-quality data, namely data with quality flag A (S/N ≥ 10). To ensure even higher fit quality, we required a minimum number of data points ν in each thermal band, W3 and W4, and we compared the statistics obtained for different values of ν. For example, if ν = 10, it means that all the beaming parameters derived in that sample correspond to objects with at least ten measurements in each band. In Fig. A.2 we plot the average η-values versus ν, which runs from ν = 2 through ν = 5, 6,... 15. The red points correspond to results from data with quality flags A, B, or C, and the blue points to those with quality flag A only. This illustrates clearly how raising the requirements for the S/N and the detection repeatability in both bands increases the quality of the best-fitting η-values of the sample. In particular, notice the marked decrease of the mean η from ~1.25 at ν = 2 to ~1.15 at ν = 9 for the A, B, C sample (left panel). On the other hand, if we fit our model to data with quality flag A alone, we see that this decrease is very much reduced, and that increasing ν from 10 to 15 does not sensibly change the resulting mean. The same applies to the median values, although it is slightly less sensitive to the use of lower quality data (right panel). The higher the value of ν, the more objects are removed from the sample. Thus, given that the median value of the A-quality samples is almost unchanged for ν> 9, we decided to take ν = 10 as a guarantee of a high-quality beaming parameter computation that still leaves a sufficient number of values in the sample for meaningful statistics. More specifically, the number of derived η-values is reduced from 647 using ν = 2 and quality flags A, B, and C, to 215 using ν = 10 and quality flag A only. We refer to the latter as the restricted sample. Only 11 objects are removed from the spectroscopic B-type preliminary sample after applying the more stringent requirements, which is expected since they are larger. Figure A.3 shows η versus diameter for all SDSS and spectroscopic B-types regardless of their data quality. It illustrates the bias we avoid by applying these quality criteria when compared to Fig. 1, which features the restricted sample only.
Statistics of the best-fitting values of beaming parameter (η) and visible geometric albedos (pV) computed for all the SDSS and spectroscopic B-types observed by WISE for which η could be fitted (preliminary sample).
Next, we compare the value distribution of beaming parameters and visible geometric albedos between the restricted set of SDSS and spectroscopic B-types. The statistics of these restricted are summarised in Table A.2 and the corresponding histograms are plotted in Fig. A.4 (cf. Table A.1 and Fig. A.1). The visible albedo distributions are still very similar for the restricted sets. Their mean and median values are now almost identical and the KS distance between the two is reduced with respect to that of the preliminary samples. On the other hand, in agreement with what we already concluded from Fig. A.2, the mean and median beaming parameter of the Sloan sample decreased significantly as a result of removing the fits to lower-quality data, which proves that including these objects was partly causing the high-η tail seen in Fig. A.1. Nevertheless, the η-value distributions of SDSS and spectroscopic B-types still differ significantly since the KS test rejects the null hypothesis with a p-value lower than 0.003, i.e. the probability of obtaining such different samples from the same distribution by chance is less than 0.3%.
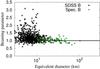 |
Fig. A.3 Beaming parameter versus size (equivalent diameter) of our B-type populations. Sloan B-types are shown in black, spectroscopic B-types are shown in green. Members of the Pallas collisional family are not included. (cf. Fig. 1). |
Appendix A.2: Effect of phase angle
The beaming parameter is not a purely thermal property of the asteroids because it also depends on the phase angle at which the observation is carried out: η increases with α (see e.g. Delbo’ et al. 2007; Wolters & Green 2009). This is important for the smallest main-belt objects in the WISE database (those with sizes in the range ~1 to ~10 km) because only those that were observed at sufficiently small geocentric distances tend to have good-quality data. However, WISE was designed to observe in quadrature4, which implies that the smallest objects were only observed at sufficiently high phase angles as well. Thus, the η distribution of the smaller asteroids in the database will be observationally biased toward higher values, which in fact may be aggravated by the broadening of the distribution related to their lower data quality (see the previous section). So can the higher mean η-value of the restricted SDSS B-types found in the previous section be explained by this phase-angle effect?
 |
Fig. A.4 Normalised histograms of parameter value distributions obtained for the restricted, higher quality SDSS and spectroscopic B-types observed by WISE. In this sample, all η-values were obtained from fitting a minimum of ten quality-A data in each of the thermal bands. Left: visible geometric albedo. Right: infrared beaming parameter. For the sake of comparison, the ranges of the axes have been kept the same as in Fig. A.1. |
From the relative shift of the phase angle histograms shown in Fig. A.5, we see how the spectroscopic B-types do tend to have smaller α than the SDSS B-types, and that the vast majority of the spectroscopic B-types were observed at α< 25°. Nonetheless, there is actually a large degree of overlap between the two distributions and, in fact, if we split the SDSS B-types into two lists, one with α> 25° and the other with α ≤ 25° (~25% of the objects versus ~75%), we find that the average η in both cases is still the same, 1.1 ± 0.2. Then, the higher mean η-value found for the restricted sample of SDSS in comparison to the spectroscopic B-types cannot be solely caused by the fact that the former were observed at somewhat higher phase angles. Furthermore, this was expected also because the η-value dependency is not strong at these relatively low phase angles, as illustrated by Fig. A.6 where we plotted η versus phase angle. The linear regression lines and corresponding coefficients shown in the plot also illustrate how the weak effect is not appreciable when we use lower quality data.
 |
Fig. A.5 Normalised histograms of phase angles at which the objects in the restricted SDSS and spectroscopic B-types samples were observed by WISE. |
 |
Fig. A.6 Beaming parameter (η) versus phase angle (α) for the restricted spectroscopic and SDSS B-type samples. The corresponding linear regression coefficients are given. |
All Tables
Best-fitting values of size (D) and beaming parameter (η) and corresponding visible geometric albedos (pV) for all our objects.
Statistics of the best-fitting values of beaming parameter (η) and visible geometric albedos (pV) computed for our populations.
Statistics of the best-fitting values of beaming parameter (η) and visible geometric albedos (pV) computed for all the SDSS and spectroscopic B-types observed by WISE for which η could be fitted (preliminary sample).
All Figures
 |
Fig. 1 Beaming parameter versus size (equivalent diameter) of the B-type population. Sloan B-types are shown in grey, spectroscopic B-types are shown in green. Members of the Pallas collisional family are not included. See the text for more information. |
| In the text | |
 |
Fig. 2 Visible geometric albedo versus size of all B-types excluding the PCF. The different sets correspond to different requirements to the fits: η was either fitted or a default value was used (grey), η was fitted (red), and η was fitted to at least 10 data points in both bands. The pV values obtained for those cases with fitted η do not spread as much as those coming from sizes fitted using default η-values. |
| In the text | |
 |
Fig. 3 Top panel: normalised histogram of the visible geometric albedo distributions of the Pallas collisional family and all B-types smaller than 20 km for which the beaming parameter could be fitted. Middle panel: Albedo versus size of all B-types and PCF members with fitted η. Lower panel: beaming parameter versus size (equivalent diameter) of the B-type population (grey) and the Pallas collisional family (PCF). |
| In the text | |
 |
Fig. A.1 Normalised histograms of the preliminary parameter value distributions obtained for all SDSS and spectroscopic B-types observed by WISE for which the beaming parameter could be fitted. See the text for the definition of this preliminary sample. |
| In the text | |
 |
Fig. A.2 Average values of beaming parameter for different subsamples of the SDSS B-types. Left: mean values. Right: median values. The number ν represents the minimum number of points both in W3 and W4 bands required for an object to be part of the sample (see text). Averages corresponding to parameters computed from data with quality flags A, B, or C are plotted in red; the more restrictive case that only allows quality flag A are in blue. |
| In the text | |
 |
Fig. A.3 Beaming parameter versus size (equivalent diameter) of our B-type populations. Sloan B-types are shown in black, spectroscopic B-types are shown in green. Members of the Pallas collisional family are not included. (cf. Fig. 1). |
| In the text | |
 |
Fig. A.4 Normalised histograms of parameter value distributions obtained for the restricted, higher quality SDSS and spectroscopic B-types observed by WISE. In this sample, all η-values were obtained from fitting a minimum of ten quality-A data in each of the thermal bands. Left: visible geometric albedo. Right: infrared beaming parameter. For the sake of comparison, the ranges of the axes have been kept the same as in Fig. A.1. |
| In the text | |
 |
Fig. A.5 Normalised histograms of phase angles at which the objects in the restricted SDSS and spectroscopic B-types samples were observed by WISE. |
| In the text | |
 |
Fig. A.6 Beaming parameter (η) versus phase angle (α) for the restricted spectroscopic and SDSS B-type samples. The corresponding linear regression coefficients are given. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


