| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 25 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201527551 | |
| Published online | 06 June 2016 | |
Measuring the stellar wind parameters in IGR J17544-2619 and Vela X-1 constrains the accretion physics in supergiant fast X-ray transient and classical supergiant X-ray binaries
1
Departamento de Física, Ingeniería de Sistemas y Teoría de la
SeñalUniversity of Alicante, PO
Box 99, 03080
Alicante, Spain
e-mail: angelgimenez@ua.es
2
Institut für Physik und Astronomie, Universität
Potsdam, Karl-Liebknecht-Str.
24/25, 14476
Potsdam,
Germany
3
Instituto Universitario de Física Aplicada a las Ciencias y las
Tecnologías, University of Alicante, PO Box 99, 03080
Alicante,
Spain
4
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
5
MAXI team, Institute of Physical and Chemical Research
(RIKEN), 2-1 Hirosawa,
Wako, 351-0198
Saitama,
Japan
Received: 13 October 2015
Accepted: 2 March 2016
Context. Classical supergiant X-ray binaries (SGXBs) and supergiant fast X-ray transients (SFXTs) are two types of high-mass X-ray binaries (HMXBs) that present similar donors but, at the same time, show very different behavior in the X-rays. The reason for this dichotomy of wind-fed HMXBs is still a matter of debate. Among the several explanations that have been proposed, some of them invoke specific stellar wind properties of the donor stars. Only dedicated empiric analysis of the donors’ stellar wind can provide the required information to accomplish an adequate test of these theories. However, such analyses are scarce.
Aims. To close this gap, we perform a comparative analysis of the optical companion in two important systems: IGR J17544-2619 (SFXT) and Vela X-1 (SGXB). We analyze the spectra of each star in detail and derive their stellar and wind properties. As a next step, we compare the wind parameters, giving us an excellent chance of recognizing key differences between donor winds in SFXTs and SGXBs.
Methods. We use archival infrared, optical and ultraviolet observations, and analyze them with the non-local thermodynamic equilibrium (NLTE) Potsdam Wolf-Rayet model atmosphere code. We derive the physical properties of the stars and their stellar winds, accounting for the influence of X-rays on the stellar winds.
Results. We find that the stellar parameters derived from the analysis generally agree well with the spectral types of the two donors: O9I (IGR J17544-2619) and B0.5Iae (Vela X-1). The distance to the sources have been revised and also agree well with the estimations already available in the literature. In IGR J17544-2619 we are able to narrow the uncertainty to d = 3.0 ± 0.2 kpc. From the stellar radius of the donor and its X-ray behavior, the eccentricity of IGR J17544-2619 is constrained to e< 0.25. The derived chemical abundances point to certain mixing during the lifetime of the donors. An important difference between the stellar winds of the two stars is their terminal velocities (ν∞ = 1500 km s-1 in IGR J17544-2619 and ν∞ = 700 km s-1 in Vela X-1), which have important consequences on the X-ray luminosity of these sources.
Conclusions. The donors of IGR J17544-2619 and Vela X-1 have similar spectral types as well as similar parameters that physically characterize them and their spectra. In addition, the orbital parameters of the systems are similar too, with a nearly circular orbit and short orbital period. However, they show moderate differences in their stellar wind velocity and the spin period of their neutron star which has a strong impact on the X-ray luminosity of the sources. This specific combination of wind speed and pulsar spin favors an accretion regime with a persistently high luminosity in Vela X-1, while it favors an inhibiting accretion mechanism in IGR J17544-2619. Our study demonstrates that the relative wind velocity is critical in class determination for the HMXBs hosting a supergiant donor, given that it may shift the accretion mechanism from direct accretion to propeller regimes when combined with other parameters.
Key words: accretion, accretion disks / methods: observational / techniques: spectroscopic / stars: atmospheres / X-rays: binaries / stars: winds, outflows
© ESO, 2016
1. Introduction
Within the wide zoo of high-mass X-ray binaries (HMXBs), we find two classes of sources where a compact object, usually a neutron star, accretes matter from the stellar wind of a supergiant OB donor. These are the classical supergiant X-ray binaries (SGXBs) and the supergiant fast X-ray transients (SFXTs). These two groups of systems, despite hosting similar stars, have distinctive properties when observed in the X-rays.
Supergiant X-ray binaries are persistent sources, with an X-ray luminosity in the range LX ~ 1033−39 erg/s. They are often variable, showing flares and off-states that indicate abrupt changes in the accretion rate (Kreykenbohm et al. 2008; Martínez-Núñez et al. 2014). However, their variability is not as extreme as of SFXTs (Walter & Zurita Heras 2007). In SGXBs, the dynamic range (ratio between luminosity in outburst and in quiescence) is approximately lower than two orders of magnitude. In contrast, the dynamic range in SFXTs can reach up to six orders of magnitude in the most extreme cases such as IGR J17544-2619 (Romano et al. 2015; in’t Zand 2005), analyzed in this work. During quiescence, SFXTs exhibit a low X-ray luminosity of LX ~ 1032 erg/s (in’t Zand 2005), but they spend most of their time emitting at an intermediate level of ~1033−34 erg/s (Sidoli et al. 2008). They display short outbursts (approximately a few hours), reaching luminosities of up to 1036−37 erg/s (Sidoli 2011; Sidoli et al. 2009).
There are other sources in between SGXBs and SFXTs, the so called intermediate SFXTs, which have a dynamic range approximately greater than two orders of magnitude. Hence, there is no sharp border clearly separating SGXBs and SFXTs. Categorization of SFXTs as a new class of HMXBs (Negueruela et al. 2006) was possible thanks to INTEGRAL observations (Sguera et al. 2005). Since then, several explanations have been proposed in order to explain their transient behavior.
Negueruela et al. (2008) suggested that intrinsic clumpiness of the wind of hot supergiant donors, together with different orbital configurations, may explain the differences in dynamic range between SGXBs and SFXTs. If the eccentricity of SFXTs is high enough, the compact object swings between dense regions with a high probability of accreting a wind clump and flare up, and diffuse regions where this probability is low and the source is consequently faint in the X-rays. In SGXBs, the compact object would orbit in a closer and more circular trajectory, accreting matter incessantly. However, the short orbital period of some SFXTs contradicts this scheme (Walter et al. 2015).
Other parameters, such as the magnetic field of the neutron star and/or the spin period, might be important. This is supported by data gathered from the monitoring of SFXTs. Tracing SFXTs for a long period, Lutovinov et al. (2013) conclude that, in SFXTs, the accretion is notably inhibited most of the time. One can invoke the different possible configurations of accretion, co-rotation, and magnetospheric radius to relax the extremely sharp density contrast required in the above mentioned interpretation (Grebenev & Sunyaev 2007; Bozzo et al. 2008; Grebenev 2010). The size of these radii depend on the wind, orbital, and neutron star parameters. For instance, if the magnetospheric radius is larger than the accretion radius (Bondi 1952), the inflow of matter is significantly inhibited by a magnetic barrier, resulting in relatively low X-ray emission from the source. Under this interpretation, SFXTs’ physical conditions make them prone to regime transitions, as a response to relatively modest variations in the wind properties of the donor, which cause abrupt changes in X-ray luminosity.
These changes might also be explained within the theory of quasi-spherical accretion onto slowly rotating magnetized neutron stars developed by Shakura et al. (2012). This theory describes the so-called subsonic settling accretion regime in detail. In slowly-rotating neutron stars, the penetration of matter into the magnetosphere is driven predominantly by Rayleigh-Taylor instabilities (Elsner & Lamb 1976). When the cooling of the plasma in the magnetosphere boundary is not sufficiently efficient, the accretion of matter is highly inhibited, and consequently the X-ray luminosity is low. On the other hand, when the cooling time is much smaller than the characteristic free-fall time (tcool ≪ tff), instability conditions are fulfilled and plasma easily enters the magnetosphere, triggering high X-ray luminosity. This last scenario is achieved when the X-ray luminosity is LX ≳ 4 × 1036 erg/s, and the rapid Compton cooling dominates over radiative cooling. For the brightest flares (LX> 1036), Shakura et al. (2014) proposed that a magnetized wind from the donor might induce magnetic reconnection, enhancing accretion up to the critical X-ray luminosity, and triggering the suction of the whole shell by the neutron star.
To understand the different behavior of SGXBs and SFXTs, we need as much information as possible about the stellar wind conditions. However, very few analyses of SGXBs and SFXTs have been performed so far in the ultraviolet-optical-infrared spectral range using modern atmosphere codes which include non-local thermodynamic equilibrium (NLTE) and line blanketing effects. Moreover, although the X-rays are mainly produced in the surroundings of the compact object, analysis of X-ray observations is directly affected by the physical properties of the donor and its wind. For instance, the assumed abundances strongly affect the derived value of one of the most important parameters in the X-rays studies: the equivalent hydrogen column density (NH). More reliable abundances make the NH estimations more reliable. Analyzing spectra by means of line-blanketed, NLTE model atmosphere codes is currently the best way to extract the stellar parameters of hot stars with winds.
In this work we analyze the optical companion of two X-ray sources: IGR J17544-2619 (SFXT) and Vela X-1 (SGXB). These sources are usually considered to be prototypical for their respective classes (Martínez-Núñez et al. 2014; Sidoli et al. 2009; Mauche et al. 2007). Hence, in addition to the important scientific value of studying these sources by themselves, this is an excellent opportunity to compare the donor parameters in these two prototypical systems, and to test how well the aforementioned resolutions for the SFXT puzzle fit with our results.
The structure of the paper is as follows. In Sect. 2, we describe the set of observations used in this work. In Sect. 3, we explain the main features of Potsdam Wolf-Rayet (PoWR) code employed in the fits. In Sect. 4, we detail the fit process and give the obtained results. In Sect. 5, we discuss several consequences arising from our results. Finally, in Sect. 6, we discuss our conclusions.
2. The observations
We used data from the International Ultraviolet Explorer (IUE)1, the fiber-fed extended range optical spectrograph (FEROS)2 operated at the European Southern Observatory (ESO) in La Silla, Chile; and the infrared (IR) spectrograph SpeX in the NASA Infrared Telescope Facility (IRTF) in Mauna Kea, Hawaii.
The IUE has two spectrographs (long-wavelength in the range 1850–3300 Å, and short-wavelength in 1150–2000 Å) and four cameras (prime and redundant camera, for each spectrograph). Each spectrograph can be used with either large aperture (a slot 10 × 20 arcsec), or small aperture (a circle 3 arcsec diameter). In addition, each spectrograph has two dispersion modes: high-resolution and low-resolution. High-resolution mode (~0.2 Å) uses an echelle grating plus a cross-disperser. Low-resolution mode (~6 Å) uses only the cross-disperser. IUE provides flux calibrated data. This is an important advantage fo two main reasons: first, we used these observations to fit the spectral energy distribution from the models, as explained below in Sect. 4.2; and second, we did not have to normalize the UV spectrum. As we can see in Figs. B.3 and 10, it is not straightforward to see the actual flux level of the UV continuum, since this spectral range is almost completely covered by spectral lines. Therefore, any normalization by visual inspection would lead to significant errors. Instead, we rectified the IUE spectra using the PoWR model continuum.
FEROS is a spectrograph that yields high resolution echelle spectroscopy (R ~ 48 000) and high efficiency (~20%) in the optical wavelength range (3600–9200 Å) (Kaufer et al. 1999). SpeX is an infrared spectrograph in the 0.8–5.5 μm range. Among the different modes available for this instrument, we used the 0.8–2.4 μm cross-dispersed mode (SXD), which yields moderate spectral resolution (R ~ 2000) (Rayner et al. 2003).
In Table C.1, we present the set of observations of IGR J17544-2619. We used an observation from SpeX taken on August 8, 2004. In the ESO archive there are 14 FEROS observations of IGR J17544-2619 taken on four different dates during September 2005. There are no publicly available IUE observations of IGR J17544-2619.
In Table C.2, we present the set of observations of Vela X-1. In the ESO archive there are six consecutive FEROS observations of 700 s taken on April 22, 2006. We used the high dispersion and large aperture IUE observations using the short-wavelength spectrograph (1150–2000 Å) and the prime camera (SWP). There are 49 observations in the public database of the IUE with these criteria.
For each instrument, we averaged over all the available observations, taking into account exposure time in order to improve the signal-to-noise ratio. We did not take into account the variability of UV spectral lines depending on the orbital phase, which has been reported for Vela X-1 (Sadakane et al. 1985). The variability consists of the presence of an extra absorption component in several spectral lines, especially those belonging to Al iii and Fe iii, mainly at phases φ> 0.5. This variability must be taken into account to interpret the full picture of the stellar wind of Vela X-1. However, in this work, we prioritized a signal-to-noise ratio as high as possible overfitting a number of phase-dependent spectra with significantly lower signal-to-noise. This permits us to estimate the stellar parameters of Vela X-1 more accurately, while not affecting any of our conclusions, as we have carefully examined.
3. The PoWR code
PoWR computes models of hot stellar atmospheres , assuming spherical symmetry and stationary outflow. Non-LTE population numbers are calculated using equations of statistical equilibrium and radiative transfer in the co-moving frame. Since these equations are coupled, the solution is iteratively found. Once convergence is reached, the synthetic spectrum is calculated by integrating along the emergent radiation rays. The main features of the code have been described by Gräfener et al. (2002) and Hamann & Gräfener (2003).
The basic input parameters in PoWR are as follows: stellar temperature (T⋆), luminosity
(L⋆), mass-loss rate
(Ṁ), surface
gravity (g⋆), and chemical
abundances. The chemical elements taken into account are detailed in Table 2. The stellar radius (R⋆) follows from
T⋆ and L⋆, using the
Stefan-Boltzmann law: 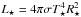 , where σ is the Stefan-Boltzmann
constant. We note that, in PoWR, R⋆ refers to the layer
where the Rosseland continuum optical depth τmax = 20, and not to the definition of
stellar radius (or photospheric radius), where τRoss = 2 / 3. Nevertheless, we will give
the stellar parameters in the next sections referring to both τmax = 20 and the
τmax = 2 /
3, in order to avoid any confusion (e.g., we will use R⋆ for the radius at
τmax =
20 and R2 / 3 for the radius at τmax = 2 / 3). The
surface gravity g⋆ and R⋆ imply the stellar mass
(M⋆) via
, where σ is the Stefan-Boltzmann
constant. We note that, in PoWR, R⋆ refers to the layer
where the Rosseland continuum optical depth τmax = 20, and not to the definition of
stellar radius (or photospheric radius), where τRoss = 2 / 3. Nevertheless, we will give
the stellar parameters in the next sections referring to both τmax = 20 and the
τmax = 2 /
3, in order to avoid any confusion (e.g., we will use R⋆ for the radius at
τmax =
20 and R2 / 3 for the radius at τmax = 2 / 3). The
surface gravity g⋆ and R⋆ imply the stellar mass
(M⋆) via
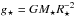 . Instead of g⋆, one may specify the
effective surface gravity geff, which accurately accounts for the
outward force exerted by the radiation field, as described thoroughly by Sander et al. (2015).
. Instead of g⋆, one may specify the
effective surface gravity geff, which accurately accounts for the
outward force exerted by the radiation field, as described thoroughly by Sander et al. (2015).
Stellar atmosphere density stratification, ρ(r), is calculated from the
continuity equation Ṁ =
4πr2ν(r)ρ(r),
given Ṁ and the
radial velocity stratification ν(r). For ν(r), PoWR distinguishes between two different
regimes: the quasi-hydrostatic domain and the wind domain. A detailed description of the
quasi-hydrostatic domain can be found in Sander et al.
(2015). In the wind domain, the β-law is adopted (Castor et al. 1975): 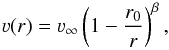 (1)where ν∞ is the terminal velocity of the
wind, r0 ≈
R⋆ (depending on the
precise location of the connection point), and β is an input parameter, typically ranging between
β = 0.6−2.0
(Puls et al. 2008). The connection point is chosen
to ensure a smooth transition between the two domains. Temperature stratification is
calculated from the condition of radiative equilibrium (Hamann & Gräfener 2003).
(1)where ν∞ is the terminal velocity of the
wind, r0 ≈
R⋆ (depending on the
precise location of the connection point), and β is an input parameter, typically ranging between
β = 0.6−2.0
(Puls et al. 2008). The connection point is chosen
to ensure a smooth transition between the two domains. Temperature stratification is
calculated from the condition of radiative equilibrium (Hamann & Gräfener 2003).
The code also allows us to account for density heterogeneities and additional X-rays from a
spherically-symmetric, shock-heated plasma. Density inhomogeneities are described in PoWR
through an optional radial-dependent input parameter: the density contrast
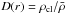 ,
where ρcl is the density of the clumped medium and
,
where ρcl is the density of the clumped medium and
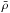 is the average density. The inter-clump medium is assumed to be empty. During analysis,
D(r) is assumed to grow from
D(rsonic) = 1 (smooth
plasma) to a maximum value D, which is reached at the layer where the stellar wind
velocity is fmax ×
ν∞. The free parameter, D, is derived in the
analysis. The spectra are modestly influenced by fmax. We assumed
fmax ~
0.6 on the basis of this moderate effect. The X-rays are described using
three parameters: the X-ray temperature TX, the filling factor XF (i.e., the
shocked to unshocked plasma ratio), and the onset radius RX, as described
in Baum et al. (1992). In this work, we assumed
TX =
107 K, RX = 1.2
R⋆ and XF = 0.05. The
main influence of X-rays on the model is via Auger ionization, which is responsible for the
appearance of resonance lines belonging to high ions such as Nv and Ovi in
O-star spectra (Cassinelli & Olson 1979; Oskinova et al. 2011). Any changes in these parameters
barely affect the spectrum, so long as they they produce a similar X-ray luminosity.
is the average density. The inter-clump medium is assumed to be empty. During analysis,
D(r) is assumed to grow from
D(rsonic) = 1 (smooth
plasma) to a maximum value D, which is reached at the layer where the stellar wind
velocity is fmax ×
ν∞. The free parameter, D, is derived in the
analysis. The spectra are modestly influenced by fmax. We assumed
fmax ~
0.6 on the basis of this moderate effect. The X-rays are described using
three parameters: the X-ray temperature TX, the filling factor XF (i.e., the
shocked to unshocked plasma ratio), and the onset radius RX, as described
in Baum et al. (1992). In this work, we assumed
TX =
107 K, RX = 1.2
R⋆ and XF = 0.05. The
main influence of X-rays on the model is via Auger ionization, which is responsible for the
appearance of resonance lines belonging to high ions such as Nv and Ovi in
O-star spectra (Cassinelli & Olson 1979; Oskinova et al. 2011). Any changes in these parameters
barely affect the spectrum, so long as they they produce a similar X-ray luminosity.
During the iterative calculation of population numbers, spectral lines are taken to be Gaussian, with a constant Doppler width of νDop = 40 km s-1; the effect of νDop on the spectrum is negligible for most lines (see discussion by Shenar et al. 2015). During the formal integration, line profiles include natural broadening, pressure broadening, and Doppler broadening. The Doppler width is decomposed for each element to a depth-dependent thermal motion and a microturbulent velocity ξ(r). The photospheric microturbulence, ξph, is derived in the analysis. Beyond the photosphere, we assumed that it grows from ξ = ξph to ξ = 100 km s-1 at the layer where the stellar wind velocity is 500 km s-1. Rotational broadening is simulated through convolution with rotational profiles, whose width corresponds to the projected rotational velocity νrot sini (denoted by νrot hereafter for simplicity), except for important wind lines, for which the convolution is no longer valid (see e.g., Hillier et al. 2012), and where an explicit angle-integration would be required (as described by Shenar et al. 2014). The macroturbulence νmac is accounted for by convolving the spectra with radial-tangential profiles (Gray 1975; Simón-Díaz & Herrero 2007).
4. The fitting procedure
We used the PoWR code to calculate synthetic spectra and a spectral energy distribution (SED) which best match the observations. The large number of free parameters, together with the long computation time for each model, do not permit the construction of a grid of models that covers the full parameter space. Instead, we attempted to identify the best-fitting model by visual inspection and systematic variation of the parameters. As an initial step, we calculate models using typical parameters of late O-/ early-B stars. We then use specific spectral lines for each parameter as a guideline for the fit. Generally, the effective gravity geff is derived from the pressure-broadened wings of the Balmer lines and He ii lines. The temperature T⋆ is derived based on line ratios belonging to different ions of the same element. The mass-loss rate Ṁ, ν∞, and D are derived from “wind-lines”, with D adjusted so that a simultaneous fit is obtained for both resonance lines (which scale as ρ) and recombination lines such as Hα (which scale as ρ2). The luminosity L⋆ and the reddening EB − V are derived by fitting the SED to photometry and flux-calibrated spectra. We apply the reddening law by Fitzpatrick (1999). Abundances are estimated from the overall strengths of the spectral lines. The photospheric microturbulence ξph is found from the strength and shape of helium lines. Finally, the parameters β, νrot and νmac are adopted on the basis of spectral line shape and depth, together with previous estimations found in the literature, when available. Upon adjusting the model, the whole spectral domain was examined to iteratively improve the fit. Overall, we managed to find models which satisfactorily reproduce the observed spectra and SEDs of the donors of the two systems analyzed here.
We show the complete fits in Appendix B. The details about the fitting procedure for the two objects are given in the following subsections. The obtained parameters are summarized in Table 1 and the chemical abundances in Table 2. Parameters that do not include an error estimation in the tables are adopted following the above mentioned criteria.
Even though the optical companion in Vela X-1 is usually known as HD 77 581, for the sake of simplicity we will refer to the donors with the name as used for the X-ray sources, namely, IGR J17544-2619 and Vela X-1. Depending on the context, the reader should easily recognize whether we are referring to the donor or X-ray source.
Stellar parameters obtained from the best fit.
Chemical abundances derived from the best fit, in mass fraction and relative to solar abundances from Asplund et al. (2009).
4.1. IGR J17544-2619
In September 2003, IGR J17544-2619 was first detected, with the IBIS/ISGRI detector on board INTEGRAL (Sunyaev et al. 2003). It is located in the direction of the galactic center, at galactic coordinates l = 3.24°, b = −0.34°. The orbital period is ~4.9d (Clark et al. 2009). According to Chandra observations, the compact object is a neutron star (in’t Zand 2005). Pellizza et al. (2006) used optical and NIR observations in order to classify the optical companion as a O9Ib. Chandra and Swift observations showed that the system exhibits a high dynamic range in its X-ray variability, changing the X-ray flux by 5 orders of magnitude (in’t Zand 2005; Romano et al. 2015).
Nowadays, the spin period Pspin of the hypothetical neutron star in IGR J17544-2619 is a matter of debate, given the results arising from observations taken at different times, different luminosities and different instruments. Drave et al. (2012) analyzed RXTE data of the source at intermediate X-ray luminosity (~1033−34 erg/s), and reported the detection of an X-ray pulsation with Pspin = 71.49 s at a statistical significance of 4.37σ. Romano et al. (2015) inspected Swift observations of the source experiencing an extraordinarily bright outburst (peak luminosity ~1038 erg/s), and reported the detection of X-ray pulsations with Pspin = 11.60 s, also at a statistical significance of about 4σ. However, these results contrast with the analyses of XMM-Newton and NuSTAR observations performed by Drave et al. (2014) and Bhalerao et al. (2015) respectively. These authors do not find any evidence of pulsations for time scales of 1–2000 s.
We have adjusted T⋆ of IGR J17544-2619 using different ions, mainly He i-He ii and Si iii-Si iv. In Fig. 1 we show an example of four helium lines for which the best-fit model provides a good description. Higher (or lower) temperatures yield more (or less) absorption than observed in the He ii lines. We have used other lines of helium, silicon, nitrogen and oxygen. The vast majority are well described by the best-fit model, within the errors. The obtained effective temperature is compatible with the donor’s spectral class O9 Ib (Martins et al. 2005).
 |
Fig. 1 Example of four helium lines in IGR J17544-2619, used to estimate T⋆. We show the observation (solid blue line), the best-fit model (red dashed line), a model with lower temperature of T⋆ = 28 kK (green dashed line), and a model with higher temperature of T⋆ = 30 kK (pink dashed line). |
The effective gravity geff was found using the hydrogen Balmer lines Hγ and Hδ. We did not use Hβ and Hα because these lines are notably affected by the stellar wind. Figure 2 shows a comparison of the observations with the best-fitting model for these two Balmer lines. We show that the observations are compatible with a relatively wide range of values, as also reflected in the errors given in Table 1.
 |
Fig. 2 Hγ and Hδ in IGR J17544-2619, used for surface gravity estimation. We show the observation (solid blue line), best-fit model (red dashed line), a model with larger effective gravity of log (geff) = 3.0 in cgs units (green dashed line). |
The distance to IGR J17544-2619 is not well known, with an estimate of 2–4 kpc Pellizza et al. (2006), based on the extinction and calibration of the absolute magnitude for O9Ib stars. Here, we improve this estimation. As a first step, we fitted the SED to photometry from the 2MASS catalogue (Cutri et al. 2003), Zacharias et al. (2012), and Rahoui & Chaty (2008), assuming the distance to be 3 kpc. We then derived initial values for donor luminosity and the reddening of the system.
As a second step, in order to provide more constraints on the distance, we employed a method based on the well-constrained luminosity of red clump giant stars (RCG). These stars can be isolated in a NIR color–magnitude diagram, and permit the estimation of the interstellar extinction along the line of sight (López-Corredoira et al. 2002). Due to their narrow luminosity function, the apparent magnitude of RCGs provides an estimation of the distance. Then, given a specific line of sight, a diagram of the extinction versus the distance can be derived (for more details see González-Fernández et al. 2014). For IGR J17544-2619 we employed the derived EJ − K from the SED fit to obtain an estimate of the distance. We note that this method is only applicable to stars in the direction of the galactic center like IGR J17544-2619, where the medium is more homogeneous, and the density of RCGs is higher. Using this method, we obtain a distance of 3.0 ± 0.2 kpc (Fig. 3). Revised luminosity and reddening values are then derived. The final results of the SED fit are shown in Fig. 4.
 |
Fig. 3 Extinction curve in the galactic direction of IGR J17544-2619. The shaded area reflects the error in the distance estimation from the errors of extinction estimation and the errors in the calculation of the extinction curve. |
 |
Fig. 4 Fit of the SED of IGR J17544-2619. The best-fit model is plotted in red. Photometry values for each band are indicated in blue. References are cited. Values of extinction, distance and luminosity are shown in Table 1. |
From the luminosity and temperature, we derive R⋆, which provides an upper limit to the eccentricity of the system. For the lower limit R⋆ = 17 R⊙, we find e< 0.25. For higher eccentricities, periodic Roche-lobe overflow is expected from the orbital solution of the system (Clark et al. 2009), at odds with the X-ray behavior of the source. Given the radius of the source and the derived surface gravity, we find M⋆ = 25.9 M⊙. This value matches very well with the estimation of M⋆ = 25−28 M⊙ (Pellizza et al. 2006) based on the mass calibration with its spectral type.
The terminal velocity of the stellar wind ν∞ was derived using the P-Cygni profile of He iλ10833 Å (see Fig. 5). The blue wing in He iλ10833 Å is a very good indicator due to its strong sensitivity to ν∞. It is reasonably well fitted when assuming ν∞ ≃ 1500 km s-1. Unfortunately, the emission exhibited by this line is not well reproduced by the best-fit model, as explained below.
 |
Fig. 5 He i at λ 10833 Å, used for the estimation of ν∞ in IGR J17544-2619 fitting the blue wing of the P-Cygni profile. We show the observation (solid blue line), best-fit model (red dashed line), a model with ν∞ = 1300 km s-1 (green dashed line), and a model with ν∞ = 1700 km s-1 (pink dashed line). |
The Ṁ and
D were
simultaneously adjusted by means of Hα and the P-Cygni profile of
He iλ10833 Å. Provided that the strength of emission in
these recombination spectral lines varies with 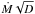 (Gräfener
et al. 2002), we cannot estimate Ṁ and D independently using these lines. As it is shown
in Fig. 6, we were not able to fit all the lines at
the same time. The best-fit model provides an acceptable description of Hα, but yields insufficient
emission for He iλ10833 Å. We choose the best description of
Hα as the
best-fit because it provides a better fit to the overall spectrum. We note that the
optical and infrared spectra were not taken at the same time, and therefore any kind of
variability in the lines might produce a disagreement. However, Hα does not show such a
large variability within the observations we have analyzed (see Fig. 7).
(Gräfener
et al. 2002), we cannot estimate Ṁ and D independently using these lines. As it is shown
in Fig. 6, we were not able to fit all the lines at
the same time. The best-fit model provides an acceptable description of Hα, but yields insufficient
emission for He iλ10833 Å. We choose the best description of
Hα as the
best-fit because it provides a better fit to the overall spectrum. We note that the
optical and infrared spectra were not taken at the same time, and therefore any kind of
variability in the lines might produce a disagreement. However, Hα does not show such a
large variability within the observations we have analyzed (see Fig. 7).
 |
Fig. 6 Hα and
He iλ10833Å lines for the estimation of
|
 |
Fig. 7 Hα in IGR J17544-2619 at different orbital phases: φ ≃ 0.01,0.61,0.75,0.97 (blue, green, pink and turquoise solid lines respectively). |
Without available resonance scattering lines in the observations at hand, we cannot
compare P-Cygni lines with recombination lines to deduce the clumping factor
D. However,
our calculations show that changing Ṁ dramatically affects the absorption spectrum in a
fashion which is not related to the product 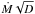 . An example is shown in Fig. 8, where we show three models calculated with different
values of Ṁ
and D, but
with a fixed product
. An example is shown in Fig. 8, where we show three models calculated with different
values of Ṁ
and D, but
with a fixed product 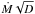 . Evidently, while the emission exhibited
by the wings of H-α (shown in Fig. 8) is similar in all models, the absorption lines are strongly affected in a
non-trivial manner. The reason for this unexpected behavior is that many of the strong
lines in the spectrum (e.g. the Balmer series) are formed significantly beyond the
photosphere (τRoss
≈ 2 / 3), where the mass-loss rate already strongly affects the density
stratification via the continuity equation. Exploiting this effect, we find that
D ≈ 4
provides the best results for the overall spectrum. However, further observations are
needed to better constrain the clumping factor in this star. Nevertheless, our final
conclusions do not strongly depend on this factor, and the implied mass-loss rate, as will
be discussed in Sect. 5.
. Evidently, while the emission exhibited
by the wings of H-α (shown in Fig. 8) is similar in all models, the absorption lines are strongly affected in a
non-trivial manner. The reason for this unexpected behavior is that many of the strong
lines in the spectrum (e.g. the Balmer series) are formed significantly beyond the
photosphere (τRoss
≈ 2 / 3), where the mass-loss rate already strongly affects the density
stratification via the continuity equation. Exploiting this effect, we find that
D ≈ 4
provides the best results for the overall spectrum. However, further observations are
needed to better constrain the clumping factor in this star. Nevertheless, our final
conclusions do not strongly depend on this factor, and the implied mass-loss rate, as will
be discussed in Sect. 5.
 |
Fig. 8 Hα and
Hδ
for the estimation of Ṁ in IGR J17544-2619. We show the observation
(solid blue line), best-fit model (Ṁ =
10-5.8M⊙/yr,
D =
4, red dashed line), a model with higher Ṁ (Ṁ =
10-5.5M⊙/yr,
D =
1, green dashed line), and a model with lower Ṁ (Ṁ =
10-5.9M⊙/yr,
D =
8, pink dashed line). Different Ṁ values do not yield
different Hα wings as long as the product
|
The chemical composition was estimated from unblended spectral lines for He, C, N, O and Si. The rest of the considered element abundances (see Table 2) were assumed solar following Asplund et al. (2009). The fit yielded moderate overabundance of He and N, together with underabundance of C and O. In all, there are indications of chemical evolution in the outer layers of the stellar atmosphere.
The photospheric microturbulent velocity (ξph) was adjusted using He i and Si iv lines. A higher ξph induced stronger absorption in several spectral lines, as shown in Fig. 9.
 |
Fig. 9 Example of two He i lines in IGR J17544-2619, used in the ξph estimation. As usual, the observation is plotted as a solid blue line, and the best-fit model as a red dashed line. Models with ξph = 15,35 km s-1 are also presented (green and pink dashed lines respectively). |
The νrot and
νmac were roughly
estimated using the width of the He lines. The derived projected rotational velocity is
around 0.3 times the critical rotation velocity (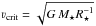 ). This high rotational velocity may favor
the chemical mixing, in line with the abundances derived in the fit.
). This high rotational velocity may favor
the chemical mixing, in line with the abundances derived in the fit.
 |
Fig. 10 Fit of the SED of Vela X-1. We plot the best fit model with the spectral lines in the domain where we have done the spectral analysis (marked in red), and the continuum where we have available photometry (marked in blue). References used for photometry are cited. True continuum in the UV range does not correspond to the apparent continuum from the observation, due to the number of spectral lines in this domain. Employed extinction, distance and luminosity values are shown in Table 1. |
To summarize, our NLTE analysis of optical and near IR spectra of IGR J17544-2619 showed that the optical O9I-type companion in this source is not peculiar and has stellar and wind parameters similar to other stars of the same spectral type, e.g. δ Ori (Shenar et al. 2015).
4.2. Vela X-1
Vela X-1 is one of the most-studied HMXBs, since it is a bright source discovered early in the X-ray astronomy age (Chodil et al. 1967). It is located at galactic coordinates l = 263.06°, b = 3.93°. The distance to the source was estimated to be 1.9 ± 0.2 kpc by (Sadakane et al. 1985). The system has a moderate eccentricity of e = 0.09 (Bildsten et al. 1997), and orbital period Porb = 8.96 days (Kreykenbohm et al. 2008). The compact object is a neutron star which pulsates with Pspin = 283 s (McClintock et al. 1976). The optical companion HD 77581 (B0.5Iae) was identified by Vidal et al. (1973).
It is very likely that the wind of Vela X-1 is disturbed by the X-ray source. The photoionization produced close to the photosphere due to the intense X-ray luminosity might hinder the wind acceleration and generate a structure known as photoionization wake (Blondin et al. 1990; Krtička et al. 2015). This structure appears in the UV spectra as an additional absorption component at phases larger than φ ~ 0.5 (Kaper et al. 1994). In addition, the hard X-rays light curves of the source in near-to-eclipse phases show asymmetries between ingress and egress, that have been interpreted as being caused by the existence of this type of structure trailing the neutron star (Feldmeier et al. 1996). Moreover, a density enhancement in the line of sight during the second half of the orbit is also observed in the X-ray absorption, although the amount of absorbing material is highly variable from one orbit to another.
 |
Fig. 11 Si iv lines used for the estimation of ν∞ in Vela X-1. We show the observation (blue solid line), best-fit model (red dashed line), and a model with ν∞ = 900 km s-1 (green dashed line). |
We derived T⋆, following the same procedure used for IGR J17544-2619. The obtained T2 / 3 is similar to previous estimations: Sadakane et al. (1985) used the equivalent width (EW) of photospheric lines to estimate the effective temperature T2 / 3 = 25 000 K; Fraser et al. (2010) used the TLUSTY code to estimate T2 / 3 = 26 500 K.
For the SED fit, we used photometry from the 2MASS catalogue (Cutri et al. 2003) and the Stellar Photometry in Johnson’s 11-color system (Ducati 2002), together with the IUE observations. We made an estimation of the reddening, distance and RV ≡ A(V) /EB − V using the SED fit. Then, we used the estimation of the stellar radius R2 / 3 = 31 R⊙ from Joss & Rappaport (1984), and T2 / 3 from the successive fits, in order to derive the luminosity (and the distance estimation) from the Stefan-Boltzmann law. Given that the obtained T2 / 3 is very similar to previous estimations, the derived distance of 2.0 ± 0.2 is almost equal to the value d = 1.9 kpc given by Sadakane et al. (1985). We show the results of the SED analysis in Fig. 10.
 |
Fig. 12 Si iv and C iv resonance lines. We plot the total averaged spectrum (blue solid line), and averaged spectrum over orbital phases φ = 0.9−0.1 (pink solid line). We also plot the best-fit model (ν∞ = 700, red dashed line), and a model with ν∞ = 1400 km s-1 (green dashed line). |
The estimation of geff was especially delicate in Vela X-1 because of its very low geff. A higher value beyond the error given in Table 1 has a strong effect in the overall spectrum and hinders a satisfying fit. The derived value enables a good fit, and is in agreement with previous estimations (Fraser et al. 2010).
We used UV resonance lines to find ν∞. In Fig. 11 we show the Si iv resonance lines λ 1394,1403 Å, where the effect of ν∞ is very clear. Models with higher terminal velocities induce a shift towards the blue part of these spectral lines. The best description of the observations is achieved for ν∞ = 700 km s-1. This value is in agreement with the estimation by van Loon et al. (2001): ν∞ = 600 km s-1; and not too far from that by Watanabe et al. (2006), who estimated ν∞ = 1100 km s-1 using Chandra X-rays observations.
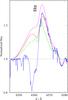 |
Fig. 13 Hα
line for the estimation of |
In contrast, it is in disagreement with the estimation of Dupree et al. (1980), namely ν∞ = 1700 km s-1. These authors used a subset of the IUE observations used in this work, and considered the UV resonance lines Si iv and C iv in the X-ray eclipse phases to make their estimation. We have revisited our ν∞ estimation using only observations taken at orbital phases φ = 0.9–0.1, in order to be able to directly compare to Dupree et al. (1980). In Fig. 12, we show the Si iv and C iv lines, as observed in the total averaged spectrum and the spectrum averaging over φ = 0.9−0.1. C iv is almost the same in both cases. The disagreement in the estimates of ν∞ does not come from orbital phase variations but from the omission of the impact of the X-rays in the stellar wind by Dupree et al. (1980). As we can see in Fig. 12, when we introduce X-rays to the models, we are able to reproduce C iv without the need for a high velocity, because of the significant enhancement of the population of C iv in the wind. The X-ray radiation we introduce into the models is an intrinsic radiation of the donor wind that is presumably produced in the shocks within the stellar wind itself (e.g. Krtička et al. 2009). This radiation does not come from the neutron star, since the effects are also noticeable at eclipsing phases. The impact of the X-rays coming from the neutron star is a different and complex issue, which has been already studied by other authors (Watanabe et al. 2006). Regarding the Si iv resonance lines, in Fig. 12 we show that high stellar wind velocities as derived by Dupree et al. (1980) do not fit, neither using the total averaged spectrum, nor using the eclipsing phases spectrum.
 |
Fig. 14 Al iii resonance lines λ1855 and λ1863Å, employed for the Ṁ estimation in Vela X-1. We show the observation (solid blue line), best-fit model (Ṁ = 10-6.2M⊙/yr, D = 11, red dashed line), a model with higher Ṁ (Ṁ = 10-5.8M⊙/yr, D = 2, green dashed line), and a model with lower Ṁ (Ṁ = 10-6.3M⊙/yr, D = 20, pink dashed line). |
The value 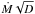 was estimated using Hα (see Fig. 13). We did not find a good fit of the blue wing of the
line, observed in absorption, but our model properly fits the emission in the red wing of
the spectral line. Unfortunately, we have no more optical observations covering further
orbital phases to check whether Hα is variable. Nevertheless, previous studies of
similar sources demonstrate that this might be the case: González-Galán (2015) reported the variability of Hα in the very similar
B0Iaep optical companion in the SGXB system XTE J1855-026. Moreover, the shape of
Hα in XTE
J1855-026 at φ =
0 (see Fig. 5.12 in González-Galán
2015), when the neutron star is hidden behind the optical counterpart, is
strongly reminiscent of the shape that our model reproduces in Fig. 13. Hence, the relative disagreement between our best-fit model and our
observation of Vela X-1 (taken at φ = 0.68), might be produced by some kind of
interaction between the neutron star and the donor and/or the stellar wind, which is
impossible to model using the assumption of spherical symmetry that PoWR employs. This
disagreement might be related to similar features observed in other strong lines, as
further discussed in Sect. 5.3.
was estimated using Hα (see Fig. 13). We did not find a good fit of the blue wing of the
line, observed in absorption, but our model properly fits the emission in the red wing of
the spectral line. Unfortunately, we have no more optical observations covering further
orbital phases to check whether Hα is variable. Nevertheless, previous studies of
similar sources demonstrate that this might be the case: González-Galán (2015) reported the variability of Hα in the very similar
B0Iaep optical companion in the SGXB system XTE J1855-026. Moreover, the shape of
Hα in XTE
J1855-026 at φ =
0 (see Fig. 5.12 in González-Galán
2015), when the neutron star is hidden behind the optical counterpart, is
strongly reminiscent of the shape that our model reproduces in Fig. 13. Hence, the relative disagreement between our best-fit model and our
observation of Vela X-1 (taken at φ = 0.68), might be produced by some kind of
interaction between the neutron star and the donor and/or the stellar wind, which is
impossible to model using the assumption of spherical symmetry that PoWR employs. This
disagreement might be related to similar features observed in other strong lines, as
further discussed in Sect. 5.3.
We derived Ṁ and D from the Al iii resonance lines λ1855 and λ1863 Å. As we can see in Fig. 14, the variation of Ṁ (and consequently D) directly affects these lines. Higher (lower) Ṁ enhances (reduces) the density of the stellar wind, producing too strong (weak) absorption.
Unfortunately, other resonance lines available in the spectrum (N v, C iv and Si iv) are saturated in the models within a reasonable range of parameters around the best-fit, and consequently are not suitable for the Ṁ diagnosis. Interestingly, in contrast to the models, the N v and Si iv resonance lines are slightly desaturated in the observations (see Fig. 15). The origin of this phenomenon might be related to the presence of optically thick clumps (macroclumping), which directly affects the mass-loss rate estimations (Oskinova et al. 2007; Šurlan et al. 2012). Undoubtedly, its study deserves further investigation, which is beyond the scope of this work.
 |
Fig. 15 Si iv and N v resonance lines in Vela X-1. While the observations show slight desaturation, all the models within a reasonable parameter space around the best-fit model produce saturated lines. |
Based on the X-ray data analysis, Manousakis & Walter
(2015) have suggested that the velocity law with the parameter β = 0.5 fits better with
the X-ray light curve of the system in near-to-eclipse phases. However, a satisfying fit
is not possible when we assume β = 0.5. We have tried models using β = 0.5 and adapting
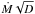 in order to fit Hα. However, as shown in
Fig. 16, Hα in our observation is not compatible with
β = 0.5. As
we mentioned above, Hα might suffer from significant variability along the
orbit. Moreover, the X-ray irradiation from the neutron star might produce variations in
the stellar wind. In our opinion, this might be the cause of apparent disagreement between
conclusions extracted from the X-rays and the optical wavebands.
in order to fit Hα. However, as shown in
Fig. 16, Hα in our observation is not compatible with
β = 0.5. As
we mentioned above, Hα might suffer from significant variability along the
orbit. Moreover, the X-ray irradiation from the neutron star might produce variations in
the stellar wind. In our opinion, this might be the cause of apparent disagreement between
conclusions extracted from the X-rays and the optical wavebands.
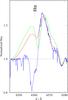 |
Fig. 16 Hα used the estimation of the parameter β in Vela X-1. We present the observation (solid blue line), best-fit model (β = 1.0, red dashed line), and a model with β = 0.5 (green dashed line), as proposed by Manousakis & Walter (2015). |
The chemical composition was estimated following the same approach as for IGR J17544-2619. Interestingly, again we found indications of chemical evolution in the star, given the moderate overabundance of He and N, together with the underabundance of C and O (see Table 2).
We adopted the value of νrot
sini = 56 km s-1 derived by Fraser et al. (2010). Previous estimations pointed to
much higher values around 115 km s-1 (Zuiderwijk
1995; Howarth et al. 1997), but such a high
rotational velocity is not compatible with some of the lines that we see unblended in the
optical observation (see Fig. 17). The rotational
velocity directly affects the estimation of the neutron star mass
(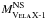 ) from radial velocity curves, as shown by
Koenigsberger et al. (2012). If νrot sini = 56
km s-1, it is
feasible that
) from radial velocity curves, as shown by
Koenigsberger et al. (2012). If νrot sini = 56
km s-1, it is
feasible that 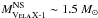 , close to the canonical value
(1.4
M⊙), instead of a high mass neutron star
, close to the canonical value
(1.4
M⊙), instead of a high mass neutron star
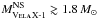 , as suggested by other authors (e.g. Quaintrell et al. 2003; Barziv et al. 2001).
, as suggested by other authors (e.g. Quaintrell et al. 2003; Barziv et al. 2001).
 |
Fig. 17 Example of unblended lines in the spectrum of Vela X-1. In red we plot a model with νrot sini = 56 km s-1. In green we plot a model with νrot sini = 116 km s-1. |
To summarize, our new analysis of Vela X-1 is in broad agreement with previous studies of this system. We find a rather low stellar wind velocity, while Ṁ is typical for the stars of its spectral type. Like other studies, we note spectral line variability in dependence on orbital phase, and attribute it to the influence of the X-rays and the compact object on the stellar wind.
The final physical parameters of the two sources obtained in this work are shown in Table 1.
5. Discussion
5.1. Wind-fed accretion
In SFXTs and SGXBs, X-ray emission is powered by the accretion of matter from the donor’s wind onto the compact object. Potential energy conversion efficiency into X-ray luminosity depends on many factors including stellar wind properties, compact object properties and the orbital separation.
The most efficient way of producing X-rays is the so called direct accretion: the stellar
wind that is gravitationally captured by the neutron star free-falls onto the compact
object. The expected luminosity is close to the accretion luminosity Lacc. The
following equations contain the most relevant parameters in this regime:  where Ra is the
accretion radius (also called Bondi radius), that is to say, the maximum distance to the
neutron star where the stellar wind is able to avoid falling onto the compact object;
G is the
gravitational constant; MNS is the mass of the neutron star,
which, in this work, is hereafter assumed to be the canonical value 1.4 M⊙;
RNS is the radius of the neutron star,
which in this work is henceforward assumed to be 12 km (Lattimer & Steiner 2014); νrel is the velocity of the wind relative to the neutron
star; fa is the fraction of stellar wind that is
gravitationally captured by the neutron star; a is the orbital distance and Lacc is the
accretion luminosity, namely, the luminosity that would arise if the whole potential
energy of the accreted matter was eventually transformed in X-ray luminosity.
where Ra is the
accretion radius (also called Bondi radius), that is to say, the maximum distance to the
neutron star where the stellar wind is able to avoid falling onto the compact object;
G is the
gravitational constant; MNS is the mass of the neutron star,
which, in this work, is hereafter assumed to be the canonical value 1.4 M⊙;
RNS is the radius of the neutron star,
which in this work is henceforward assumed to be 12 km (Lattimer & Steiner 2014); νrel is the velocity of the wind relative to the neutron
star; fa is the fraction of stellar wind that is
gravitationally captured by the neutron star; a is the orbital distance and Lacc is the
accretion luminosity, namely, the luminosity that would arise if the whole potential
energy of the accreted matter was eventually transformed in X-ray luminosity.
For IGR J17544-2619, using the results of our spectral fitting, the data shown in Table 3 and assuming a circular orbit, we obtain from Eq. (2b):
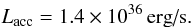 The value of Lacc is 1–2
orders of magnitude higher than the luminosity exhibited by the source most of the time:
LX< 5 ×
1034 erg/s (Bozzo et al.
2015). Most likely, some inhibition mechanism is acting in IGR J17544-2619 (Drave et al. 2014; Bozzo
et al. 2008).
The value of Lacc is 1–2
orders of magnitude higher than the luminosity exhibited by the source most of the time:
LX< 5 ×
1034 erg/s (Bozzo et al.
2015). Most likely, some inhibition mechanism is acting in IGR J17544-2619 (Drave et al. 2014; Bozzo
et al. 2008).
As a possible explanation for the variability of IGR J17544-2619, and its lower-than-expected luminosity at quiescence, Bozzo et al. (2008) discussed the application of their model to the light curve of an outburst observed by Chandra. This theoretical framework describes the mechanisms for the accretion inhibition according to the relative size of spheres defined by Ra, RM and Rco; where Ra is the already defined accretion radius, RM is the magnetospheric radius (location where the pressure exerted by the gas equals the local magnetic pressure), and Rco is the co-rotation radius (location where the angular velocity of the neutron star equals the Keplerian velocity). These radii, in turn, depend on: Ṁ, νrel, magnetic moment of the neutron star (μ), orbital separation (a) and Pspin.
For simplicity, the orbital velocity of the neutron star and the eccentricity are not considered in the model by Bozzo et al. (2008). That is to say, it is assumed that e = 0 and νwind ≃ νrel, where νwind is the stellar wind velocity in the position of the neutron star. We note that when the stellar wind velocity is not very high, this assumption might not be accurate. Indeed, the orbital velocity (νorb) in Vela X-1 is very similar to νwind (see Table 3). In IGR J17544-2619, the orbital velocity is around half the stellar wind velocity. Despite these simplifications, the model provides significant insight into the explanation of the qualitative behavior of the sources with regard to their persistence or variability, as shown below in this section. A more accurate approach, considering eccentric orbits and the orbital velocity of the compact object would be an important advancement in the model, but is beyond the scope of this paper.
Nowadays, tentative estimations of the spin period in IGR J17544-2619 (Pspin = 71.49 s by Drave et al. 2012 and alternatively Pspin = 11.58 s by Romano et al. 2015), along with the stellar wind parameters derived in this work, permit discussion of the application of the model by Bozzo et al. (2008) from a new perspective. The rest of parameters required for this section are shown in Table 3. Using those values, we can elaborate diagrams νwind-Ṁ and νwind-Pspin, where the different accretion regimes occupy different domains of the space of parameters. These domains directly arise from the Eqs. (25)–(28) by Bozzo et al. (2008).
In Fig. 18 we show the position of IGR J17544-2619 in the diagram νwind-Pspin, for the two currently available tentative estimations of the Pspin. The source lies in the direct accretion regime for Pspin = 71.49 s, and in the supersonic propeller regime for Pspin = 11.58 s. Hence, the shortest Pspin = 11.58 s matches better with the X-ray behavior of the source and its likelihood of staying in an inhibited accretion regime.
 |
Fig. 18 Position of IGR J17544-2619 in the νwind-Pspin for the two tentative estimations of Pspin. Equations (25)–(28) by Bozzo et al. (2008) represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
In Fig. 19 we show the location of IGR J17544-2619 in the diagram νwind-Ṁ. It is important to note that the position of the system in this diagram is not a fixed point, because of the intrinsic velocity variability and local density of the stellar wind in hot massive stars. Thus, we have plotted a red region in Fig. 19 showing a variability of one order of magnitude in νwind and Ṁ. That is to say, the maximum Ṁ and νwind in the encircled region is ten times higher than the minimum Ṁ and νwind. Such a variability is fully plausible, as demonstrated by hydrodynamical simulations of radiatively driven stellar winds (e.g. Feldmeier et al. 1997). These clumps of higher density, intrinsic to stellar winds of hot stars, are sometimes invoked to explain the X-ray variability of HMXBs (Oskinova et al. 2012). As we can see in Fig. 19, the encircled region intersects regimes of direct accretion and inhibited accretion. Hence, it is possible that in objects such as IGR J17544-2619, the abrupt changes in wind density may lead to the switching from one accretion regime to the other. Moreover, besides the clumping of the stellar wind, the orbit’s eccentricity (e< 0.25) would lead to additional variations in the orbital separation (and consequently in νwind and the density of the medium), which reinforce the intrinsic variability of the stellar wind and its capability to lead to transitions across regimes.
 |
Fig. 19 Position of IGR J17544-2619 in the νwind-Ṁ diagram. Upper panel: diagram calculated using Pspin = 11.58 s. Lower panel: diagram calculated using Pspin = 71.49 s. The dashed line encircles the space within one order of magnitude of νwind and Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
Considering an alternative explanation for the X-ray variability of IGR J17544-2619, Drave et al. (2014) invoked the quasi-spherical accretion model by Shakura et al. (2012). However, if the spin period is actually as short as 71.49 s or 11.58 s, the condition of a slowly rotating pulsar, i.e. RM ≪ Rco (where RM is the magnetospheric radius and Rco the co-rotation radius), assumed by this approach, would be debatable. Even though it raises doubts about the feasibility of applying this model, it cannot be ruled out until the spin period and the magnetic field of the neutron star are firmly constrained.
In the case of Vela X-1, we see in Figs. 20 and 21, that the source is well in the middle of the zone where direct accretion is expected. Hence, more extreme density or velocity jumps would be required to trigger any change of accretion regime. These extreme jumps are also plausible, but much more unlikely. However, they might sporadically occur, leading to a sudden decrease of the luminosity in Vela X-1.
Using the parameters shown in Table 3 and Eq. (2b), we obtain Lacc = 8.7 × 1036 erg/s for Vela X-1. The average source X-ray luminosity is ⟨ LX ⟩ ≃ 4.5 × 1036 (Sako et al. 1999). More specifically, Lacc ≃ 0.5 × ⟨ LX ⟩. This means that there is good agreement between Lacc and LX, which implies that the direct accretion scenario can describe the way that matter is accreted in Vela X-1.
 |
Fig. 20 Position of Vela X-1 in the νwind-Pspin. The dashed line encircles the space within one order of magnitude of νwind and Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
 |
Fig. 21 Position of Vela X-1 in the νwind-Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
The framework of different accretion regimes described by Bozzo et al. (2008) is able to explain why IGR J17544-2619 is prone to show a high X-ray variability and inhibited accretion (assuming the shortest Pspin = 11.58 s), and Vela X-1 is persistently very luminous in the X-rays. As exposed in Figs. 19 and 21, the required variability in the stellar wind for a transition in the accretion regime is far lower in IGR J17544-2619 than in Vela X-1. The main factors that make the sources so different are the Pspin (shorter in IGR J17544-2619), and the νwind (larger in IGR J17544-2619).
We may speculate whether this theoretical framework can be applied to other SGXBs and SFXTs. Unfortunately there are few sources for which complementary studies, including dedicated analysis of the stellar wind, orbital parameters and neutron star parameters have been performed. The studies of the stellar wind are especially scarce. Besides the two sources analyzed in this work, there are at least four where a comparable amount of information is available in the literature. They are IGR J11215-5952, GX 301-2, X1908+075 and OAO 1657-415. We show νwind-Pspin and νwind-Ṁ diagrams for these sources in Appendix A. Again, the diagrams seem to qualitatively explain the behavior of the systems. GX 301-2, X1908+075 and OAO 1657-415 are persistent SGXBs, and occupy regions of high likelihood of persistent emission in the diagrams. In contrast, the likelihood of regime transitions in IGR J11215-5952 is much higher.
IGR J11215-5952 is a system with very large eccentricity and long orbital period (Romano et al. 2009). It shows recurrent flares with a period of ~330d (Sidoli et al. 2006). Its high variability leads to its classification as an SFXT, even though flare predictability is not a common feature in the other SFXTs. Sidoli et al. (2007) proposed that the recurrent flares might be explained by an additional equatorial component of the stellar wind, combined with the highly eccentric orbit. In Fig. A.1 we see that a moderate clumpiness would lead to frequent transition regimes, and hence we would expect very high X-ray variability. However, the diagram shown in Fig. A.1 is calculated assuming a circular orbit, which is not accurate for IGR J11215-5952. In this source, the high eccentricity of the system might be a more important factor than the clumpiness of the wind, and the transition into the direct accretion regime might be likely only during near-periastron passages, producing periodic outbursts.
Regarding other systems, the framework used here might encounter problems in explaining the behavior of other SFXTs with larger Pspin such as IGR J16418-4532 (Pspin = 1212 s, Sidoli et al. 2012) and IGR J16465-4507 (Pspin = 228 s, Lutovinov et al. 2005). Estimation of stellar wind parameters in these systems will be very useful to measure the extent of the applicability of the model by Bozzo et al. (2008), explaining the dichotomy between SGXBs and SFXTs. Moreover, studies of X-ray absorption might provide an additional perspective on the issue. Giménez-García et al. (2015) studied a sample of SGXBs and SFXTs using XMM-Newton, and it was observed that the SGXBs included in the sample were, in general, more absorbed than the SFXTs. This may suggest a more intense interaction between the X-ray radiation and stellar wind, or, alternatively, that the neutron star orbits a more dense medium in SGXBs due to a closer orbit, or a slower donor stellar wind.
 |
Fig. 22 Evolutionary tracks from the Geneva stellar models with solar abundances and rotation. Positions of IGR J17544-2619 (square) and Vela X-1 (diamond) are overplotted. |
 |
Fig. 23 Example of four spectral lines showing notable asymmetries: He iλ3820,4026,4471 Å, and Si iiiλ4553 Å. |
Finally, we can compare the ν∞ and the νesc that we obtain from the fits. Lamers et al. (1995) collected a large dataset from hot stars with radiatively driven winds, and concluded that the ratio ν∞/ νesc decreases steeply from ~2.6 to ~1.3 when going from high to low Teff at a point near Teff ≃ 21 000 K, corresponding to a spectral type around B1. According to Vink et al. (1999), this drop is caused by a decrease in the line acceleration of Fe iii in the subsonic part of the wind. In our case, we have (see Table 1):
-
IGR J17544-2619 (O9.5I):
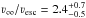 .
. -
Vela X-1 (B0.5I):
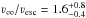 .
.
These values follow the trend observed and described by Lamers et al. (1995). We suggest that it might be the reason why IGR J17544-2619 shows higher ν∞ than Vela X-1. X-ray action can also have an important impact on stellar wind velocity, as shown by Karino (2014). However, this effect is probably local, since we do not observe sizeable differences in the terminal velocity between eclipsing and non-eclipsing orbital phases in Vela X-1. Secondary features such as asymmetries or additional absorption components in the spectral lines, which might be related to the effect of the X-rays on the stellar wind, are described and discussed below in Sect. 5.3.
5.2. Evolutionary tracks
In Fig. 22 we show the position of Vela X-1 and IGR J17544-2619 in the Hertzprung-Russell Diagram (HRD), and evolutionary tracks from the Geneva stellar models (Ekström et al. 2012). The two stars lie on the theoretical track of a star with initial mass ~25–30 M⊙. In IGR J17544-2619 the spectroscopic mass obtained from the fits is compatible with the evolutionary mass. Vela X-1 shows certain overluminosity, since its spectroscopic mass is lower than the evolutionary mass. Nevertheless, the mass of the star obviously decreases along its lifetime due to the stellar wind, and possible mass transfer episodes. These phenomena might have been stronger or longer in Vela X-1 compared to IGR J17544-2619.
The overabundance of helium and nitrogen arising from the fits in the two stars might trigger an increase in luminosity following the scaling relation L ∝ μα, where μ is the average mean molecular weight and α> 1 (Langer 1992). As a result, we expect certain overluminosity in both sources. However, as already mentioned, the overluminosity is more noticeable in Vela X-1. Overall, the sources seem to be in different evolutionary stages, or to have experienced a different evolutionary history.
The donors’ chemical evolution might have been driven by episodes of important mass transfer in the past, given the close orbits of the systems, enhancing the helium and nitrogen abundances due to the accretion of chemically enriched material (Langer 2012). Moreover, Roche-lobe overflow stages induce important spin-up in the mass gainer (Packet 1981), inducing further chemical enrichment because of rotational mixing. This scenario is supported by the observation of other HMXBs, where indications of nitrogen enhancement are also observed (González-Galán et al. 2014).
5.3. Asymmetries in Vela X-1 spectral lines
Some of the lines in the Vela X-1 spectrum show clear asymmetries that are not possible to reproduce with spherically symmetric models like PoWR (see Fig. 23). This striking feature is specially noticeable for He i lines, but it is also observed in C, N, O or Si, whenever the lines are strong enough.
Asymmetries in spectral lines were also reported by Martínez-Núñez et al. (2015) in hydrogen lines of the infrared spectrum of X1908+75, a SGXB. A natural explanation for the discrepancy between models and observations is the departure of the donor and/or the surrounding medium from the spherical symmetry. This departure may be triggered by tidally induced effects, and the persistent X-ray irradiation of the stellar wind and the stellar surface. With regard to this, Koenigsberger et al. (2012) showed that tidal effects would produce asymmetries in the line profiles.
The observed asymmetries might be related to the additional absorption that we observe in the blue part of other important lines, with special attention to Hα, Hβ, Hγ and Si ivλ 1394,1403 Å (see Fig. 24). Assuming that the absorption is produced by an independent component of matter moving at certain velocity, it is striking that the involved velocities required for explaining such a blueshift are different depending on the lines: ~200–300 km s-1 in Hα, Hβ and Hγ, ~1000 km s-1 in the Si iv resonance lines.
 |
Fig. 24 Hα, Hβ, Hγ and Si ivλ1394,1403 Å. The observations (blue solid line) show an additional blueshifted component that we are unable to reproduce with the models (red dashed line). |
In any case, we note that these asymmetries and additional absorption features have not
been observed in IGR J17544-2619. Hence, the physical cause at work is playing a
significantly more important role in Vela X-1 than in IGR J17544-2619. This fact suggests
that X-ray source interaction with the stellar wind might be fundamental for understanding
these asymmetries, given that X-rays are, on average, more intense in Vela X-1. Indeed, if
we compare the wind mechanic luminosity 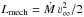 to the X-ray luminosity LX we
obtain:
to the X-ray luminosity LX we
obtain:
-
IGR J17544-2619:Lmech ≃ 1036 erg/s. That is to say, at least two orders of magnitude higher than the usual X-ray luminosity of the source.
-
Vela X-1: Lmech ≃ 1035 erg/s. In other words, about one order of magnitude lower than the X-ray luminosity of the source in quiescence.
Hence, there is a fundamental difference in the ratio Lmech/LX. The X-rays are much more powerful with respect to the stellar wind in Vela X-1 than in IGR J17544-2619. We suggest that this fact might be related to the asymmetries we observe in the spectral lines of Vela X-1, but not in IGR J17544-2619.
6. Summary and conclusions
We have performed a detailed analysis of the donors of the HMXBs IGR J17544-2619 and Vela X-1, using the code PoWR which computes models of hot stellar atmospheres. We found the luminosity, extinction, stellar mass, stellar radius, effective temperature, effective surface gravity, terminal velocity of the stellar wind, mass-loss rate, clumping factor, micro and macro-turbulent velocity, rotational velocity, and chemical abundances.
Estimation of the above mentioned parameters has implications for other physical parameters
of the system. The derived stellar radius of IGR J17544-2619 implies an upper limit in the
eccentricity of the source: e< 0.25. The rotational velocity derived for Vela
X-1 implies that the neutron star mass might be 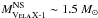 , close to the canonical value
(1.4
M⊙).
, close to the canonical value
(1.4
M⊙).
The donors of IGR J17544-2619 and Vela X-1 are similar in many of the parameters that physically characterize them and their spectra. They are also comparable in their eccentricity and orbital separation. However, in the context of accretion regimes described by Bozzo et al. (2008), their moderate differences in the stellar wind velocity and the Pspin of the neutron star lead to a very different source accretion regimes, which qualitatively explains their completely different X-ray behavior. After analyzing other sources with sufficient information available in the literature, we have observed that the same theoretical framework is valid to qualitatively explain their X-ray behavior. Further explorations addressing estimation of the stellar wind donor properties in SGXBs and SFXTs, complemented by Pspin measurements in SFXTs, will be necessary to confirm whether the conclusions exposed here can be extrapolated to additional members of these groups of HMXBs.
In summary, this study shows that wind terminal velocity plays a decisive role in determining the class of HMXB hosting a supergiant donor. While low stellar wind velocity facilitates direct steady accretion in SGXBs, the high wind velocity and velocity jumps can easily shift the accretion mechanism from direct accretion to propeller regimes in SFXTs. These effects might be enhanced by other factors, such as source eccentricity. We conclude that this is one of the mechanisms responsible for these two major sub-classes of HMXBs with supergiant donors.
Available at https://archive.stsci.edu/iue/
Available at http://archive.eso.org/
Acknowledgments
The work of AG-G was supported by the Spanish MICINN under FPI Fellowship BES-2011-050874 associated to the project AYA2010-15431. T.S. is grateful for financial support from the Leibniz Graduate School for Quantitative Spectroscopy in Astrophysics, a joint project of the Leibniz Institute for Astrophysics Potsdam (AIP) and the Institute of Physics and Astronomy of the University of Potsdam. This work has been partially supported by the Spanish Ministry of Economy and Competitiveness project numbers ESP2013-48637-C2-2P and ESP2014-53672-C3-3-P, the Generalitat Valenciana project number GV2014/088 and the Vicerectorat d’Investigació, Desenvolupament i Innovació de la Universitat d’Alacant under grant GRE12-35. We wish to thank Thomas E. Harrison for his important contribution to the paper, reducing the SpeX data. We also thank S. Popov for a very useful discussion. The authors gratefully acknowledge the constructive comments on the paper given by the anonymous referee. S.M.N. thanks the support of the Spanish unemployment agency, allowing her to continue her scientific collaborations during the critical situation of the Spanish research system. The authors acknowledge the help of the International Space Science Institute at Bern, Switzerland, and the faculty of the European Space Astronomy Centre. A.S. is supported by the Deutsche Forschungsgemeinschaft (DFG) under grant HA 1455/26. Some of the data presented in this paper were obtained from the Multimission Archive at the Space Telescope Science Institute (MAST). STScI is operated by the Association of Universities for Research in Astronomy, inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA office of space science via grant NAG5-7584 and by other grants and contracts. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the university of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barnstedt, J., Staubert, R., Santangelo, A., et al. 2008, A&A, 486, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barziv, O., Kaper, L., Van Kerkwijk, M. H., Telting, J. H., & Van Paradijs, J. 2001, A&A, 377, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baum, E., Hamann, W.-R., Koesterke, L., & Wessolowski, U. 1992, A&A, 266, 402 [NASA ADS] [Google Scholar]
- Bhalerao, V., Romano, P., Tomsick, J., et al. 2015, MNRAS, 447, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Kallman, T. R., Fryxell, B. A., & Taam, R. E. 1990, ApJ, 356, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bozzo, E., Falanga, M., & Stella, L. 2008, ApJ, 683, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Romano, P., Ducci, L., Bernardini, F., & Falanga, M. 2015, Adv. Space Res., 55, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Cassinelli, J. P., & Olson, G. L. 1979, ApJ, 229, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chodil, G., Mark, H., Rodrigues, R., Seward, F. D., & Swift, C. D. 1967, ApJ, 150, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, D. J., Hill, A. B., Bird, A. J., et al. 2009, MNRAS, 399, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Drave, S. P., Bird, A. J., Townsend, L. J., et al. 2012, A&A, 539, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drave, S. P., Bird, A. J., Sidoli, L., et al. 2014, MNRAS, 439, 2175 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog: II/246 [Google Scholar]
- Dupree, A. K., Gursky, H., Black, J. H., et al. 1980, ApJ, 238, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsner, R. F., & Lamb, F. K. 1976, Nature, 262, 356 [Google Scholar]
- Feldmeier, A., Anzer, U., Boerner, G., & Nagase, F. 1996, A&A, 311, 793 [NASA ADS] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., & Ryans, R. S. I. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Giménez-García, A., Torrejón, J. M., Eikmann, W., et al. 2015, A&A, 576, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Fernández, C., Asensio Ramos, A., Garzón, F., Cabrera-Lavers, A., & Hammersley, P. L. 2014, ApJ, 782, 86 [Google Scholar]
- González-Galán, A. 2015, Ph.D. Thesis, ArXiv e-prints [arXiv:1503.01087] [Google Scholar]
- González-Galán, A., Negueruela, I., Castro, N., et al. 2014, A&A, 566, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Koesterke, L., & Hamann, W.-R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 1975, ApJ, 202, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Grebenev, S. A. 2010, ArXiv e-prints [arXiv:1004.0293] [Google Scholar]
- Grebenev, S. A., & Sunyaev, R. A. 2007, Astron. Lett., 33, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, W.-R., & Gräfener, G. 2003, A&A, 410, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, D. J., Bouret, J.-C., Lanz, T., & Busche, J. R. 2012, MNRAS, 426, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- in’t Zand, J. J. M. 2005, A&A, 441, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joss, P. C., & Rappaport, S. A. 1984, ARA&A, 22, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Kaper, L., Hammerschlag-Hensberge, G., & Zuiderwijk, E. J. 1994, A&A, 289, 846 [NASA ADS] [Google Scholar]
- Kaper, L., van der Meer, A., & Najarro, F. 2006, A&A, 457, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karino, S. 2014, PASJ, 66, 34 [NASA ADS] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Koenigsberger, G., Moreno, E., & Harrington, D. M. 2012, A&A, 539, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Coburn, W., Wilms, J., et al. 2002, A&A, 395, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Coburn, W., et al. 2004, A&A, 427, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., Feldmeier, A., Oskinova, L. M., Kubát, J., & Hamann, W.-R. 2009, A&A, 508, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., Kubát, J., & Krtičková, I. 2015, A&A, 579, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1992, A&A, 265, L17 [NASA ADS] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Steiner, A. W. 2014, ApJ, 784, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, A. M., Rappaport, S., Remillard, R., & Savcheva, A. 2004, ApJ, 617, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., Garzón, F., & Hammersley, P. L. 2002, A&A, 394, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenzo, J., Negueruela, I., Castro, N., et al. 2014, A&A, 562, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutovinov, A., Revnivtsev, M., Gilfanov, M., et al. 2005, A&A, 444, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutovinov, A. A., Revnivtsev, M. G., Tsygankov, S. S., & Krivonos, R. A. 2013, MNRAS, 431, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., & Walter, R. 2015, A&A, 584, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Núñez, S., Torrejón, J. M., Kühnel, M., et al. 2014, A&A, 563, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Núñez, S., Sander, A., Gímenez-García, A., et al. 2015, A&A, 578, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, A. B., Clark, J. S., Norton, A. J., et al. 2012, MNRAS, 422, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W., Liedahl, D. A., Akiyama, S., & Plewa, T. 2007, Progr. Theor. Phys. Suppl., 169, 196 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Rappaport, S., Joss, P. C., et al. 1976, ApJ, 206, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Negueruela, I., Smith, D. M., Reig, P., Chaty, S., & Torrejón, J. M. 2006, in The X-ray Universe 2005, ed. A. Wilson, ESA SP, 604, 165 [NASA ADS] [Google Scholar]
- Negueruela, I., Torrejón, J. M., Reig, P., Ribó, M., & Smith, D. M. 2008, in A Population Explosion: The Nature & Evolution of X-ray Binaries in Diverse Environments, eds. R. M. Bandyopadhyay, S. Wachter, D. Gelino, & C. R. Gelino, AIP Conf. Ser., 1010, 252 [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., Cassinelli, J. P., Brown, J. C., & Todt, H. 2011, Astron. Nachr., 332, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Kretschmar, P. 2012, MNRAS, 421, 2820 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Pellizza, L. J., Chaty, S., & Negueruela, I. 2006, A&ARv, 455, 653 [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quaintrell, H., Norton, A. J., Ash, T. D. C., et al. 2003, A&A, 401, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahoui, F., & Chaty, S. 2008, A&A, 492, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Sidoli, L., Cusumano, G., et al. 2009, ApJ, 696, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Bozzo, E., Mangano, V., et al. 2015, A&A, 576, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadakane, K., Hirata, R., Jugaku, J., et al. 1985, ApJ, 288, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Liedahl, D. A., Kahn, S. M., & Paerels, F. 1999, ApJ, 525, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A., Shenar, T., Hainich, R., et al. 2015, A&A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, N., Nagase, F., Kawai, N., et al. 1986, ApJ, 304, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Sguera, V., Barlow, E. J., Bird, A. J., et al. 2005, A&A, 444, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N., Postnov, K., Kochetkova, A., & Hjalmarsdotter, L. 2012, MNRAS, 420, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N., Postnov, K., Sidoli, L., & Paizis, A. 2014, MNRAS, 442, 2325 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Hamann, W.-R., & Todt, H. 2014, A&A, 562, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shenar, T., Oskinova, L., Hamann, W.-R., et al. 2015, ApJ, 809, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sidoli, L. 2011, ArXiv e-prints [arXiv:1111.5747] [Google Scholar]
- Sidoli, L., Paizis, A., & Mereghetti, S. 2006, A&A, 450, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sidoli, L., Romano, P., Mereghetti, S., et al. 2007, A&A, 476, 1307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sidoli, L., Romano, P., Mangano, V., et al. 2008, ApJ, 687, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Sidoli, L., Romano, P., Mangano, V., et al. 2009, ApJ, 690, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Sidoli, L., Mereghetti, S., Sguera, V., & Pizzolato, F. 2012, MNRAS, 420, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., Grebenev, S. A., Lutovinov, A. A., et al. 2003, ATel, 190, 1 [Google Scholar]
- Swank, J. H., Smith, D. M., & Markwardt, C. B. 2007, ATel, 999 [Google Scholar]
- Šurlan, B., Hamann, W.-R., Kubát, J., Oskinova, L. M., & Feldmeier, A. 2012, A&A, 541, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kerkwijk, M. H., van Paradijs, J., Zuiderwijk, E. J., et al. 1995, A&A, 303, 483 [NASA ADS] [Google Scholar]
- van Loon, J. T., Kaper, L., & Hammerschlag-Hensberge, G. 2001, A&A, 375, 498 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal, N. V., Wickramasinghe, D. T., & Peterson, B. A. 1973, ApJ, 182, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 1999, A&A, 350, 181 [NASA ADS] [Google Scholar]
- Walter, R., & Zurita Heras, J. 2007, A&A, 476, 335 [Google Scholar]
- Walter, R., Lutovinov, A. A., Bozzo, E., & Tsygankov, S. S. 2015, A&ARv, 23, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S., Sako, M., Ishida, M., et al. 2006, ApJ, 651, 421 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., & Pravdo, S. H. 1979, ApJ, 233, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322 [Google Scholar]
- Zuiderwijk, E. J. 1995, A&A, 299, 79 [NASA ADS] [Google Scholar]
Appendix A: Other sources
In this appendix we show diagrams that are further discussed in Sect. 5, calculated from the available data in the literature, collected in Table A.1.
 |
Fig. A.1 Left panel: position of IGR J11215-5952 (SFXT) in the νwind-Ṁ diagram. Right panel: position of IGR J11215-5952 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
 |
Fig. A.2 Left panel: position of GX 301-2 (SGXB) in the νwind-Ṁ diagram. Right panel: position of GX 301-2 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
 |
Fig. A.3 Left panel: position of X1908+075 (SGXB) in the νwind-Ṁ diagram. Right panel: position of X1908+075 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
 |
Fig. A.4 Left panel: position of OAO 1657-415 (SGXB) in the νwind-Ṁ diagram. Right panel: position of OAO 1657-415 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
Appendix B: Spectra
Appendix B.1: IGR J17544-2619
 |
Fig. B.1 Optical spectrum of IGR J17544-2619 (blue), and the best fit model (red). |
 |
Fig. B.1 continued. |
Appendix B.2: Vela X-1
 |
Fig. B.2 Infrared spectrum of IGR J17544-2619 (blue), and the best fit model (red). |
 |
Fig. B.3 Ultraviolet spectrum of Vela X-1 (blue), and the best fit model (red). |
 |
Fig. B.4 Optical spectrum of Vela X-1 (blue), and the best fit model (red). |
 |
Fig. B.4 continued. |
Appendix C: Additional tables
IGR J17544-2619 observations.
Vela X-1 observations.
All Tables
Chemical abundances derived from the best fit, in mass fraction and relative to solar abundances from Asplund et al. (2009).
All Figures
 |
Fig. 1 Example of four helium lines in IGR J17544-2619, used to estimate T⋆. We show the observation (solid blue line), the best-fit model (red dashed line), a model with lower temperature of T⋆ = 28 kK (green dashed line), and a model with higher temperature of T⋆ = 30 kK (pink dashed line). |
| In the text | |
 |
Fig. 2 Hγ and Hδ in IGR J17544-2619, used for surface gravity estimation. We show the observation (solid blue line), best-fit model (red dashed line), a model with larger effective gravity of log (geff) = 3.0 in cgs units (green dashed line). |
| In the text | |
 |
Fig. 3 Extinction curve in the galactic direction of IGR J17544-2619. The shaded area reflects the error in the distance estimation from the errors of extinction estimation and the errors in the calculation of the extinction curve. |
| In the text | |
 |
Fig. 4 Fit of the SED of IGR J17544-2619. The best-fit model is plotted in red. Photometry values for each band are indicated in blue. References are cited. Values of extinction, distance and luminosity are shown in Table 1. |
| In the text | |
 |
Fig. 5 He i at λ 10833 Å, used for the estimation of ν∞ in IGR J17544-2619 fitting the blue wing of the P-Cygni profile. We show the observation (solid blue line), best-fit model (red dashed line), a model with ν∞ = 1300 km s-1 (green dashed line), and a model with ν∞ = 1700 km s-1 (pink dashed line). |
| In the text | |
 |
Fig. 6 Hα and
He iλ10833Å lines for the estimation of
|
| In the text | |
 |
Fig. 7 Hα in IGR J17544-2619 at different orbital phases: φ ≃ 0.01,0.61,0.75,0.97 (blue, green, pink and turquoise solid lines respectively). |
| In the text | |
 |
Fig. 8 Hα and
Hδ
for the estimation of Ṁ in IGR J17544-2619. We show the observation
(solid blue line), best-fit model (Ṁ =
10-5.8M⊙/yr,
D =
4, red dashed line), a model with higher Ṁ (Ṁ =
10-5.5M⊙/yr,
D =
1, green dashed line), and a model with lower Ṁ (Ṁ =
10-5.9M⊙/yr,
D =
8, pink dashed line). Different Ṁ values do not yield
different Hα wings as long as the product
|
| In the text | |
 |
Fig. 9 Example of two He i lines in IGR J17544-2619, used in the ξph estimation. As usual, the observation is plotted as a solid blue line, and the best-fit model as a red dashed line. Models with ξph = 15,35 km s-1 are also presented (green and pink dashed lines respectively). |
| In the text | |
 |
Fig. 10 Fit of the SED of Vela X-1. We plot the best fit model with the spectral lines in the domain where we have done the spectral analysis (marked in red), and the continuum where we have available photometry (marked in blue). References used for photometry are cited. True continuum in the UV range does not correspond to the apparent continuum from the observation, due to the number of spectral lines in this domain. Employed extinction, distance and luminosity values are shown in Table 1. |
| In the text | |
 |
Fig. 11 Si iv lines used for the estimation of ν∞ in Vela X-1. We show the observation (blue solid line), best-fit model (red dashed line), and a model with ν∞ = 900 km s-1 (green dashed line). |
| In the text | |
 |
Fig. 12 Si iv and C iv resonance lines. We plot the total averaged spectrum (blue solid line), and averaged spectrum over orbital phases φ = 0.9−0.1 (pink solid line). We also plot the best-fit model (ν∞ = 700, red dashed line), and a model with ν∞ = 1400 km s-1 (green dashed line). |
| In the text | |
 |
Fig. 13 Hα
line for the estimation of |
| In the text | |
 |
Fig. 14 Al iii resonance lines λ1855 and λ1863Å, employed for the Ṁ estimation in Vela X-1. We show the observation (solid blue line), best-fit model (Ṁ = 10-6.2M⊙/yr, D = 11, red dashed line), a model with higher Ṁ (Ṁ = 10-5.8M⊙/yr, D = 2, green dashed line), and a model with lower Ṁ (Ṁ = 10-6.3M⊙/yr, D = 20, pink dashed line). |
| In the text | |
 |
Fig. 15 Si iv and N v resonance lines in Vela X-1. While the observations show slight desaturation, all the models within a reasonable parameter space around the best-fit model produce saturated lines. |
| In the text | |
 |
Fig. 16 Hα used the estimation of the parameter β in Vela X-1. We present the observation (solid blue line), best-fit model (β = 1.0, red dashed line), and a model with β = 0.5 (green dashed line), as proposed by Manousakis & Walter (2015). |
| In the text | |
 |
Fig. 17 Example of unblended lines in the spectrum of Vela X-1. In red we plot a model with νrot sini = 56 km s-1. In green we plot a model with νrot sini = 116 km s-1. |
| In the text | |
 |
Fig. 18 Position of IGR J17544-2619 in the νwind-Pspin for the two tentative estimations of Pspin. Equations (25)–(28) by Bozzo et al. (2008) represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. 19 Position of IGR J17544-2619 in the νwind-Ṁ diagram. Upper panel: diagram calculated using Pspin = 11.58 s. Lower panel: diagram calculated using Pspin = 71.49 s. The dashed line encircles the space within one order of magnitude of νwind and Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. 20 Position of Vela X-1 in the νwind-Pspin. The dashed line encircles the space within one order of magnitude of νwind and Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. 21 Position of Vela X-1 in the νwind-Ṁ. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. 22 Evolutionary tracks from the Geneva stellar models with solar abundances and rotation. Positions of IGR J17544-2619 (square) and Vela X-1 (diamond) are overplotted. |
| In the text | |
 |
Fig. 23 Example of four spectral lines showing notable asymmetries: He iλ3820,4026,4471 Å, and Si iiiλ4553 Å. |
| In the text | |
 |
Fig. 24 Hα, Hβ, Hγ and Si ivλ1394,1403 Å. The observations (blue solid line) show an additional blueshifted component that we are unable to reproduce with the models (red dashed line). |
| In the text | |
 |
Fig. A.1 Left panel: position of IGR J11215-5952 (SFXT) in the νwind-Ṁ diagram. Right panel: position of IGR J11215-5952 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. A.2 Left panel: position of GX 301-2 (SGXB) in the νwind-Ṁ diagram. Right panel: position of GX 301-2 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. A.3 Left panel: position of X1908+075 (SGXB) in the νwind-Ṁ diagram. Right panel: position of X1908+075 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. A.4 Left panel: position of OAO 1657-415 (SGXB) in the νwind-Ṁ diagram. Right panel: position of OAO 1657-415 in the νwind-Pspin diagram. Equations (25)–(28) by Bozzo et al. (2008) are represented by a solid, dotted, triple-dot-dashed and dot-dashed lines respectively. |
| In the text | |
 |
Fig. B.1 Optical spectrum of IGR J17544-2619 (blue), and the best fit model (red). |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.2 Infrared spectrum of IGR J17544-2619 (blue), and the best fit model (red). |
| In the text | |
 |
Fig. B.3 Ultraviolet spectrum of Vela X-1 (blue), and the best fit model (red). |
| In the text | |
 |
Fig. B.4 Optical spectrum of Vela X-1 (blue), and the best fit model (red). |
| In the text | |
 |
Fig. B.4 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


