| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201527471 | |
| Published online | 24 June 2016 | |
Distance and luminosity probability distributions derived from parallax and flux with their measurement errors
With application to the millisecond pulsar PSR J0218+4232
Institute for Mathematics, Astrophysics and Particle Physics, Radboud
University Nijmegen,
PO Box 9010,
6500 GL
Nijmegen,
The Netherlands
e-mail: A.Igoshev@science.ru.nl; F.Verbunt@science.ru.nl; E.Cator@science.ru.nl
Received: 29 September 2015
Accepted: 27 April 2016
We use a Bayesian approach to derive the distance probability distribution for one object from its parallax with measurement uncertainty for two spatial distribution priors, a homogeneous spherical distribution and a galactocentric distribution – applicable for radio pulsars – observed from Earth. We investigate the dependence on measurement uncertainty, and show that a parallax measurement can underestimate or overestimate the actual distance, depending on the spatial distribution prior. We derive the probability distributions for distance and luminosity combined – and for each separately when a flux with measurement error for the object is also available – and demonstrate the necessity of and dependence on the luminosity function prior. We apply this to estimate the distance and the radio and gamma-ray luminosities of PSR J0218+4232. The use of realistic priors improves the quality of the estimates for distance and luminosity compared to those based on measurement only. Use of the wrong prior, for example a homogeneous spatial distribution without upper bound, may lead to very incorrect results.
Key words: methods: statistical / stars: luminosity function, mass function / pulsars: general / pulsars: individual: PSR J0218+4232
© ESO, 2016
1. Introduction
Distance determinations are fundamental in astronomy. The study of spatial distributions and source number densities is the most direct application. Together with proper motion measurements, distances form the basis of velocity measurements and kinematic studies. Combined with flux measurements they provide luminosities.
A standard method of distance determination is the measurement of the trigonometric parallax. The conversion of the measured parallax into the most probable actual parallax is not straightforward, as is evident from the excellent historical survey given by Sandage & Saha (2002). Most of the papers discussed in that survey use parallax and apparent magnitude measurements to derive absolute magnitude distributions, or statistical corrections between apparent and absolute magnitudes. In a much cited paper, Lutz & Kelker (1973) derive the probability distribution of the real parallax as a function of the measured parallax and its measurement error. Since that paper, there has been some debate as to whether their equation is applicable when only one object is observed (as reviewed by Sandage & Saha 2002).
In a study of radio pulsars, Faucher-Giguère & Kaspi (2006) have given a probability distribution of actual distances as a function of the measured parallax, reproduced as Eq. (21) below. In an important paper Verbiest et al. (2012) have developed a Bayesian method to combine various distance-related measurements and their uncertainties to find the probability distribution of distances, and show the importance of the choice of priors. Verbiest & Lorimer (2014) apply this method in a study of the gamma-ray luminosity of the millisecond pulsar PSR J0218+4232. Alas, they make the same error as Faucher-Giguère & Kaspi (2006) in deriving the probability distribution of actual distances as a function of the measured parallax, and make a similar error in the equation for the probability distribution of luminosity as a function of measured flux and parallax.
Much of the confusion in the existing literature arises because of the failure to discriminate between what technically are called the frequentist approach and the Bayesian approach, leading to the incorrect conclusion that a measurement by itself provides a probability density distribution centred on the measured value. We briefly explain this error in Sect. 2, where we also discuss the related confusion as to whether population priors must be taken into account in the study of single objects. In contrast to statements in several previous papers (e.g. Feast 2002; Francis 2012, and references therein), the answer is yes if a probability density is required. A more detailed explanation is given in Sect. 3. In that section we repeat some results by Bailer-Jones (2015) that appeared as we were finalizing our paper; however, we use a spatial distribution appropriate for pulsars.
The structure of our paper is as follows. In Sect. 3 we describe the spatial distributions and the luminosity distributions that we use, and explain our notation. In Sect. 4 we describe in some detail the derivation of the correct conversion of measured parallax to probability distribution of actual distances for the case of a known (or assumed) distribution in space. We consider a homogeneous distribution and a galactocentric distribution observed from Earth. The latter is applied to the case of PSR J0218+4232. In Sect. 5, we consider objects for which both parallax and flux are measured to determine the probability distributions for distance and luminosity, and illustrate our results for PSR J0218+4232. The gamma-ray luminosity of PSR J0218+4232 is discussed in Sect. 6. Finally, in Sect. 7 we briefly discuss the assumptions that we have made, and the expected consequences of relaxing these assumptions.
2. Confidence intervals and probability densities
We consider an object whose parallax is measured with accuracy σ, i.e. the measured value ϖ′ is a draw from a Gaussian centred on its real parallax ϖ1 with standard deviation σ. The probability that a draw leads to a measured value ϖ′ such that | ϖ′ − ϖ1 | <σ is then 68% (roughly), which corresponds to a 68% probability that the real value ϖ1 is in the range given by ϖ′ − σ<ϖ1<ϖ′ + σ. Similarly, if the real parallax is ϖ2 there is a 68% probability that the real value ϖ2 is in the range given by ϖ′ − σ<ϖ2<ϖ′ + σ, and so for every real distance ϖi. Thus, no matter what the real distance is, we can state that there is a 68% probability that it is in the range bounded by ϖ′ − σ and ϖ′ + σ. Analogously, for each frequency of occurrence, e.g. expressed in percentage x%, it is possible to derive the corresponding range: between ϖ′ − nxσ and ϖ′ + nxσ, where nx = 1.645 for 90%, nx = 2 for 95.5%, etc. Hence the name frequentist approach. The measured value ϖ′ does not, however, provide the probability distribution within these ranges.
To obtain such a probability distribution it is necessary to compute the relative contribution that each possible real parallax ϖi makes to the probability of measuring ϖ′, i.e. it is necessary to follow the Bayesian approach. As an illustration, we consider a population of ten sources, nine of which have ϖ = 5 mas, and one that has ϖ = 3 mas. We select one source from this population for a parallax measurement with accuracy 1 mas, and measure ϖ′ = 4 mas. The real parallax answers to the 68% probability of lying within 1 mas of the measured value. A real parallax of 5 mas has a probability of 90%, a real parallax of 3 mas of 10%, and other parallaxes have probability zero. The probability distribution of the real distance ϖ is not given by a Gaussian centred on the measured value ϖ′. Also for the case of a more realistic, continuous intrinsic distribution, the probability distribution of ϖ in general cannot be stated to be given by a Gaussian centred on the measured value ϖ′. Therefore, the use of realistic priors improves the quality of the estimate for the distance, compared to that based on one measurement only. The same is true for the estimate of the luminosity.
Finally, we consider a series of measurements ϖ′i made from a single object, each with its own accuracy σi. Each measurement is a draw from a distribution centred on the actual distance of the object. The best estimate of ϖ′ and its accuracy σ can be determined by averaging these measurements with appropriate weighting of the individual measurements, without reference to the population priors. The resulting values ϖ′ and σ are the best estimate of the parallax measurement and its error. They can be used in a frequentist approach to determine a confidence interval. To determine a probability density, they must be combined with a population prior.
3. Ingredients and notation
The analysis in this paper is based on measurements of parallax and flux, combined with an intrinsic spatial distribution, which is assumed to be known, and an intrinsic luminosity distribution, also assumed known. The measurement errors lead to probability distributions for measured values that we denote with gD and gS for parallax and flux, respectively. The intrinsic spatial and luminosity distributions are denoted with fD and fL, respectively. To illustrate the general methods, we discuss two spatial distributions and two luminosity distributions.
3.1. Measurements
A parallax measurement is subject to measurement error σ. The measurement error distribution gD(ϖ′ | D) gives the probability of measuring a parallax ϖ′ when the actual distance is D. The equation gD(ϖ′ | D) can follow a Gaussian distribution (Eq. (2)), but in general, it can also have a different, non-Gaussian form.
We assume that the distance D is given in kiloparsec, and the parallax ϖ and measurement error σ in milliarcsec, hence ϖ = 1 /D, and we assume that the parallax measurement errors follow a Gaussian distribution, centred on zero and with width σ, i.e. that the probability of measuring a parallax ϖ′ for an actual parallax ϖ is given by a Gaussian: ![\begin{equation} g_D(\varpi'|\varpi)\Delta\varpi' = {1\over\sqrt{2\pi}\sigma} \exp\left[-\,{(\varpi-\varpi')^2\over2\sigma^2}\right] \Delta\varpi' . \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq29.png) (1)In this equation ϖ is fixed, so with ϖ = 1 /D we rewrite it as
(1)In this equation ϖ is fixed, so with ϖ = 1 /D we rewrite it as ![\begin{equation} g_D(\varpi'|D)\Delta\varpi' = {1\over\sqrt{2\pi}\sigma} \exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right] \Delta\varpi' \label{e:gauss}, \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq31.png) (2)where gD(ϖ′ | D) is normalized over the range −∞ <ϖ′< ∞. (Whereas the real parallax is by definition positive, we note that the measured value may be negative.) Our results for spatially homogeneous distributions will be identical for D in parsec with ϖ and σ in arcsec.
(2)where gD(ϖ′ | D) is normalized over the range −∞ <ϖ′< ∞. (Whereas the real parallax is by definition positive, we note that the measured value may be negative.) Our results for spatially homogeneous distributions will be identical for D in parsec with ϖ and σ in arcsec.
We furthermore assume that the probability of a measured flux S′ for an actual flux S is given by ![\begin{equation} g_S(S'|S)\Delta S' = {1\over\sqrt{2\pi}\sigma_S} \exp\left[-{(S-S')^2\over2{\sigma_S}^2}\right]\,\Delta S' \label{e:gauss-s}. \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq35.png) (3)A flux S for a source at distance D corresponds to a luminosity L = LoD2S. We introduce the factor Lo to discriminate isotropically emitting sources, for which Lo = 4π, and pulsars, for which traditionally the luminosity is defined by Lo = 1. It can also be used to indicate the effect of interstellar absorption, in which case Lo itself depends on D.
(3)A flux S for a source at distance D corresponds to a luminosity L = LoD2S. We introduce the factor Lo to discriminate isotropically emitting sources, for which Lo = 4π, and pulsars, for which traditionally the luminosity is defined by Lo = 1. It can also be used to indicate the effect of interstellar absorption, in which case Lo itself depends on D.
3.2. Spatial distribution
To avoid unnecessary duplication, we subsume the two spatial distributions that we discuss in one equation: 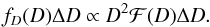 (4)For a homogeneous distribution in space, fD(D) ∝ D2, and fD(D) cannot be normalized. In realistic applications, however, the spatial distribution is always bounded: for stars by the finite extent of the galaxy. For illustrative purposes, we consider the case (in general non-realistic) where the distribution is homogeneous up to a maximum distance Dmax, and zero beyond it, and write
(4)For a homogeneous distribution in space, fD(D) ∝ D2, and fD(D) cannot be normalized. In realistic applications, however, the spatial distribution is always bounded: for stars by the finite extent of the galaxy. For illustrative purposes, we consider the case (in general non-realistic) where the distribution is homogeneous up to a maximum distance Dmax, and zero beyond it, and write 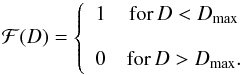 (5)Verbiest et al. (2012) consider the observations made from Earth on a galactocentric distribution, which results in a heliocentric distribution given in our notation by (cf. Eq. (21) of Verbiest et al. 2012)
(5)Verbiest et al. (2012) consider the observations made from Earth on a galactocentric distribution, which results in a heliocentric distribution given in our notation by (cf. Eq. (21) of Verbiest et al. 2012) ![\begin{equation} \mathcal{F}(D)= R^{1.9}\exp\left[ -{|z(D,b)|\over h}-{R(D,l,b)\over H}\right]\cdot \label{e:galacent} \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq45.png) (6)Here a cylindrical galactocentric coordinate system is adopted with R and Ro the distance of the pulsar and of the Earth to the galactic centre, projected onto the galactic plane, and z the distance of the pulsar to that plane. The values of h and H are the vertical and radial scaling parameters. With D the distance of the object to Earth, and l,b its galactic coordinates, we have
(6)Here a cylindrical galactocentric coordinate system is adopted with R and Ro the distance of the pulsar and of the Earth to the galactic centre, projected onto the galactic plane, and z the distance of the pulsar to that plane. The values of h and H are the vertical and radial scaling parameters. With D the distance of the object to Earth, and l,b its galactic coordinates, we have 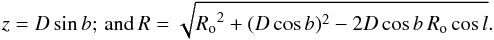 (7)The last equation shows that z and R are functions of D, l, and b, and thus ℱ(D), and through it fD(D) are functions of l and b.
(7)The last equation shows that z and R are functions of D, l, and b, and thus ℱ(D), and through it fD(D) are functions of l and b.
3.3. Luminosity functions
The luminosity function fL(L) gives the relative numbers of sources as a function of luminosity L in the range between minimum luminosity Lmin and maximum luminosity Lmax. The luminosity function fL(L), and also Lmax and Lmin, may depend on D. For example, pulsars at large distances from the galactic plane tend to be older and probably have a luminosity function different from that of young pulsars near the galactic plane. However, for the purpose of this paper, we assume a universal luminosity function, i.e. fL(L), Lmin, and Lmax do not depend on D.
As a first example we discuss a power-law distribution for the luminosity function: 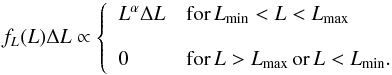 (8)We consider three values for α: α = (0,−1,−2).
(8)We consider three values for α: α = (0,−1,−2).
We also consider a luminosity function in the form derived for normal pulsars by Faucher-Giguère & Kaspi (2006), ![\begin{equation} f(x)\Delta x \propto \exp\left[-\,{(x-\mu_x)^2\over2{\sigma_x}^2}\right]\Delta x \quad\mathrm{where}\quad x\equiv\log L , \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq63.png) (9)which we rewrite as
(9)which we rewrite as ![\begin{equation} f_L(L)\Delta L = f(x){{\rm d}x\over {\rm d}L}{\rm d}L \propto \exp\left[-\,{(\log L-\mu_x)^2\over2{\sigma_x}^2}\right]{1\over L}{\rm d}L \label{e:lognormal}, \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq64.png) (10)where μx = −1.1 and σL = 0.9 (both numbers refer to the log of the luminosity in mJy kpc2). We follow Verbiest & Lorimer (2014) in applying this same distribution to millisecond pulsars.
(10)where μx = −1.1 and σL = 0.9 (both numbers refer to the log of the luminosity in mJy kpc2). We follow Verbiest & Lorimer (2014) in applying this same distribution to millisecond pulsars.
3.4. Notation for probabilities
We denote joint probabilities with capital P, in particular the joint probability of measured parallax ϖ′ and actual distance D is written P(ϖ′,D), and the joint probability for these quantities plus measured flux S′ and luminosity L as P(ϖ′,D,S′,L). These joint probabilities can be turned into conditional probabilities via Bayes’ theorem. This leads to normalization constants which we denote as follows. If the joint probability is 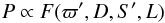 (11)with F a function of the variables indicated, then the conditional probability
(11)with F a function of the variables indicated, then the conditional probability 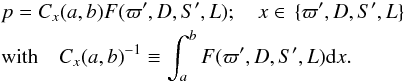 (12)Our notation for conditional probabilities is such that
(12)Our notation for conditional probabilities is such that 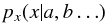 (13)gives the (normalized) probability of x for given (e.g. measured) values for a,b,....
(13)gives the (normalized) probability of x for given (e.g. measured) values for a,b,....
We use 95% credibility intervals on the posterior probability density. This credibility interval is computed from the one-dimensional posterior probability density px(x), where x is the distance or the luminosity, as the shortest interval containing 95% of the total probability: 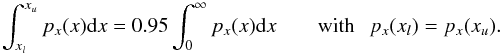 (14)This equation holds when xu<xmax; when xu = xmax, the condition px(xl) = px(xu) is dropped.
(14)This equation holds when xu<xmax; when xu = xmax, the condition px(xl) = px(xu) is dropped.
Parameters of PSR J0218+4232 used in this paper.
3.5. Sample millisecond pulsar
In the figures which illustrate probabilities involving the galactocentric distribution in Eq. (6), we use the parameters for PSR J0218+4232 listed in Table 1.
4. Distance derived from measured parallax and assumed distance distribution
Owing to the measurement error, different distances D may lead to the same measured parallax ϖ′. With the number of objects at distance D given by fD(D), and the probability of measuring parallax ϖ′ at actual distance D by gD(ϖ′ | D), the joint probability of an object having a distance D and a measured parallax ϖ′ is distributed according to 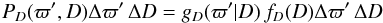 (15)and the conditional probability that the actual distance is in a range ΔD around D when the measured parallax is ϖ′ follows with Eq. (12):
(15)and the conditional probability that the actual distance is in a range ΔD around D when the measured parallax is ϖ′ follows with Eq. (12): 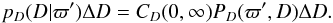 (16)In principle, only the product PD = gDfD must be normalizable with respect to D; in practice it is often useful to normalize the functions gD and fD separately as well, with respect to D and ϖ′, respectively. Eqs. (15) and (16) show that a probability distribution for the distance can be derived for a measured parallax of a single object only if a spatial distribution fD(D) of the class of objects is known or assumed.
(16)In principle, only the product PD = gDfD must be normalizable with respect to D; in practice it is often useful to normalize the functions gD and fD separately as well, with respect to D and ϖ′, respectively. Eqs. (15) and (16) show that a probability distribution for the distance can be derived for a measured parallax of a single object only if a spatial distribution fD(D) of the class of objects is known or assumed.
For a uniform prior, i.e. fD(D) = constant in the range Dmin<D<Dmax, Eqs. (14) and (15) lead to the result 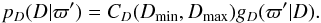 (17)Thus, for a uniform prior, the probability of measuring ϖ′ when the real distance is D is the same as the probability that the real distance is D when the measured parallax is ϖ′, apart from a normalization constant. To prevent the normalization constant from going to infinity, the prior may have to be limited to a maximum distance.
(17)Thus, for a uniform prior, the probability of measuring ϖ′ when the real distance is D is the same as the probability that the real distance is D when the measured parallax is ϖ′, apart from a normalization constant. To prevent the normalization constant from going to infinity, the prior may have to be limited to a maximum distance.
 |
Fig. 1 Probability distribution of actual distances for a measured parallax for objects distributed homogeneously in a finite sphere for values of ϖ′, σ, and Dmax as indicated. The blue line represents Eq. (18). The histogram gives the results of a Monte Carlo simulation which retains objects with 0.198 <ϖ′< 0.202. The black and red lines represent modified versions of Eq. (18) according to Faucher-Giguère & Kaspi (2006) and Verbiest et al. (2012), respectively. The intrinsic distribution given by Eqs. (4) and (5) is shown as a dashed line. All curves are normalized to the same area under the curve. |
 |
Fig. 2 Probability distribution of actual distances for a measured parallax ϖ′ = 0.2 mas for various measurement errors σ for objects distributed homogeneously in a sphere with radius Dmax = 10 kpc. The intrinsic distribution given by Eqs. (4) and (5) is shown as a dashed line. The curves are normalized to the same maximum value. |
4.1. Finite homogeneous distribution in space
Entering Eqs. (2), (4), and (5) into Eq. (16), we obtain with Eq. (12): ![\begin{equation} p_D(D|\varpi') = \left\{ \begin{array}{ll} C_D(0,D_\mathrm{max}) D^2\exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right]; &D<D_\mathrm{max} \\ \\ 0;& D>D_\mathrm{max} . \end{array}\right. \label{e:normhomogen} \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq106.png) (18)In Fig. 1 we plot pD(D | ϖ′) according to Eq. (18), computing CD(0,Dmax) numerically for a measured parallax ϖ′ = 0.2 mas, maximum distance Dmax = 10 kpc, and σ = 0.03 mas. Figure 2 illustrates the effect of varying measurement accuracies. As the error decreases, the most probable distance approaches in to the nominal measured value 1 /ϖ′, but the probability distribution of the actual distances remains asymmetric, i.e. non-Gaussian, even for small measurement errors.
(18)In Fig. 1 we plot pD(D | ϖ′) according to Eq. (18), computing CD(0,Dmax) numerically for a measured parallax ϖ′ = 0.2 mas, maximum distance Dmax = 10 kpc, and σ = 0.03 mas. Figure 2 illustrates the effect of varying measurement accuracies. As the error decreases, the most probable distance approaches in to the nominal measured value 1 /ϖ′, but the probability distribution of the actual distances remains asymmetric, i.e. non-Gaussian, even for small measurement errors.
To show that our approach is in agreement with that of Lutz & Kelker (1973), we note that for a homogeneous distribution in space fϖ(ϖ)Δϖ = fD(D)ΔD ∝ D2ΔD, hence fϖ(ϖ) ∝ ϖ-2d(1 /ϖ) /dϖ ∝ ϖ-4. This allows us to write the joint probability of a pulsar having measured parallax ϖ′ and actual parallax ϖ analogous to Eq. (15) as 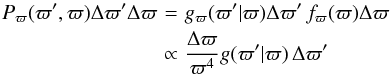 (19)thus confirming the ϖ-4 dependence found by Lutz & Kelker.
(19)thus confirming the ϖ-4 dependence found by Lutz & Kelker.
4.2. Galactocentric distribution
Entering Eqs. (2), (4), and (6) into Eq. (16), we obtain with Eq. (12) ![\begin{eqnarray} p_D(D|\varpi') \!\!&=&\!\! C_D(0,\infty) D^2\,R^{1.9}\exp\left[ -{|z(D,b)|\over h}-{R(D,l,b)\over H}\right]\nonumber \\ & & \times \exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right] \cdot \label{e:jointgal} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq115.png) (20)Figure 3 illustrates this distribution for the parameters of PSR J0218+4232.
(20)Figure 3 illustrates this distribution for the parameters of PSR J0218+4232.
 |
Fig. 3 For an assumed galactocentric distribution of objects, the distribution as a function of distance to the Earth is given by Eqs. (4) and (6), illustrated for the direction towards PSR J0218+4232 with the dotted line. The black smooth line gives the probability distribution of actual distances in this direction for the measured parallax of this pulsar, according to Eq. (20) in the approximation CD(0,∞) ≃ CD(0,Dmax), Dmax = 10 kpc. The histogram gives the results of a Monte Carlo simulation which retains objects with 0.14 <ϖ′< 0.18. The blue and red lines give the analytic distributions for hypothetically smaller measurement errors but the same value for ϖ′. The curves are normalized to the same maximum value. |
4.3. Earlier studies
Previous authors have given different expressions for pD(D | ϖ′). To understand the difference between our Eqs. (18) and (20) and these expressions, we consider the measurement process expressed in Eq. (15). Consider a class of objects distributed in space according to fD(D) (Eq. (4)). The measurement process starts with the selection of one object whose parallax we wish to measure. This corresponds to taking a draw from the fD(D) distribution. Then the parallax is measured. The measurement refers to the unique distance D of the selected object, i.e. the selection from gD(ϖ′ | D) is taken for a unique and fixed value of D.
We illustrate this separation between object selection and parallax measurement with a Monte Carlo experiment as follows. We choose a distance D randomly from a D2 distribution (corresponding to a homogeneous distribution in a sphere) with maximum distance 10 kpc; for the distance D a measured parallax ϖ′ is drawn randomly from a Gaussian distribution according to Eq. (2) with σ = 0.03 mas. We retain the distance if 0.198 <ϖ′(mas) < 0.202, and repeat the procedure until 50 000 distances are retained. The binned distribution of the distances D of the retained objects is normalized and also plotted in Fig. 1. It agrees with Eq. (18). In an analogous fashion we perform a Monte Carlo experiment for the galactocentric distribution for parameters of the millisecond pulsar PSR J0218+4232, and show in Fig. 3 that the result agrees with the analytic solution given by Eq. (20).
Faucher-Giguère & Kaspi (2006) write the probability of distance D for a measured parallax ϖ′ as (see their Eq. (2)) ![\begin{equation} p(D|\varpi') ={C\over D^2}\, {1\over\sqrt{2\pi}\sigma} \exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right] \label{e:wrong}, \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq121.png) (21)where C (in our notation) is the normalization constant. In doing so they make two related errors. First, they interpret the right-hand side of Eq. (1) as giving the probability that the real parallax is ϖ when the measured value is ϖ′, when in fact it gives the probability of measuring ϖ′ when the real parallax is ϖ. As we explain in Sect.1, this is incorrect and arises from confusing the frequentist and Bayesian methods. Second, by interpreting the right-hand side of Eq. (1) as a probability density for ϖ, they add the factor | dϖ/ dD | = 1 /D2 in converting this to a probability density for D and ignore the spatial density f(D). As can be seen from Eqs. (2), (14), and (15) this effectively corresponds to assuming f(D) ∝ 1 /D2. The effect of this double error on the homogeneous spatial distribution is to replace the D2 factor in our Eqs. (18) with D-2, and is illustrated in Fig. 1.
(21)where C (in our notation) is the normalization constant. In doing so they make two related errors. First, they interpret the right-hand side of Eq. (1) as giving the probability that the real parallax is ϖ when the measured value is ϖ′, when in fact it gives the probability of measuring ϖ′ when the real parallax is ϖ. As we explain in Sect.1, this is incorrect and arises from confusing the frequentist and Bayesian methods. Second, by interpreting the right-hand side of Eq. (1) as a probability density for ϖ, they add the factor | dϖ/ dD | = 1 /D2 in converting this to a probability density for D and ignore the spatial density f(D). As can be seen from Eqs. (2), (14), and (15) this effectively corresponds to assuming f(D) ∝ 1 /D2. The effect of this double error on the homogeneous spatial distribution is to replace the D2 factor in our Eqs. (18) with D-2, and is illustrated in Fig. 1.
Verbiest et al. (2012) and Verbiest & Lorimer (2014) make the same errors as Faucher-Giguère & Kaspi (2006), but correctly include f(D) in the probability density PD(D | ϖ′). The net effect of this is to remove the D2 factor in our Eqs. (18) and (20), which corresponds to the assumption of a uniform distance distribution fD = 1. The result is illustrated in Fig. 1 for a homogeneous spatial distribution.
Francis (2014) argues that the distance probability distribution is a Gaussian centred on the real value, because it collapses to the real value when the measurement error goes to zero. The effect of the spatial distribution prior D2ℱ diminishes when the parallax measurement error becomes smaller because a smaller range of D leads to a smaller variation of the prior D2ℱ. Thus, for smaller errors the distance probability distribution narrows towards the correct distance. However, even for small errors, the distance probability function remains asymmetric (Figs. 2 and 3). Indeed, Eq. (3.2) from Francis (2014) is wrong, and confuses the frequentist and Bayesian approach, as does his conclusion that the distance distribution is irrelevant for the derivation of the probability density for the distance.
5. Distance and luminosity from parallax and flux with assumed distance and luminosity distributions
We now consider sources for which parallax and flux have been measured, and the spatial distribution and luminosity function are known or assumed. The joint probability for D,ϖ′,L,S′ can be written with Eqs. (2), (4), and (3) as ![\begin{eqnarray} P(D,\varpi',L,S') \!\! \!\!&\propto&\!\! \!\! g_D(\varpi'|D)f_D(D)g_S(S'|S[L,D])f_L(L) = \notag \\ && \!\! \!\! {1\over\sqrt{2\pi}\,\sigma} \exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right] D^2\mathcal{F}(D) \notag \\ \!\! \!\!& \times& \!\! \!\! {1\over\sqrt{2\pi}\,\sigma_S} \exp\left[-{(L/[L_{\rm o}D^2]-S')^2\over2{\sigma_S}^2}\right] \, f_L(L). \label{e:jointall} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq131.png) (22)For fixed values of ϖ′, σ, S′, and σS, and for a chosen luminosity function fL(L), this joint probability can be computed for each combination of D and L. We show contours of equal probability in the D,L-plane in Fig. 4, as applicable to PSR J0218+4232. The maximum probabilities lie at distances well below the nominal distance D′ = 1 /ϖ′ and at luminosities well below the nominal luminosity L′ = LoS′/ϖ′2. This is due to the luminosity functions that peak at values well below L′, and thus favour low luminosities, hence small distances as far as the measurement uncertainties allow.
(22)For fixed values of ϖ′, σ, S′, and σS, and for a chosen luminosity function fL(L), this joint probability can be computed for each combination of D and L. We show contours of equal probability in the D,L-plane in Fig. 4, as applicable to PSR J0218+4232. The maximum probabilities lie at distances well below the nominal distance D′ = 1 /ϖ′ and at luminosities well below the nominal luminosity L′ = LoS′/ϖ′2. This is due to the luminosity functions that peak at values well below L′, and thus favour low luminosities, hence small distances as far as the measurement uncertainties allow.
 |
Fig. 4 Contours of equal joint probability P(D,ϖ′,L,S′) for the direction, parallax, flux, and measurement errors of PSR J0218+4232 for two power-law functions and for the lognormal luminosity function. For each luminosity function we show the maximum and also the contours containing 68% and 95% of the integrated probability. The contours for the power-law luminosity function with index −2 have two branches, one at very low luminosities and one at higher luminosities; part of the latter is indistinguishable from the contours for the lognormal luminosity function. The vertical and horizontal dashed lines show the nominal values for distance D = 1 /ϖ′ and luminosity L′ = S′/ϖ′2, respectively |
In Fig. 4 we did not apply cut-offs to the power-law luminosity functions at low or high luminosity. As can be seen from Eq. (22) such cut-offs do not change the form of the contours of P(D,ϖ′,L,S′), but only the normalization, in the range Lmin<L<Lmax. Outside this range P(D,ϖ′,L,S′) = 0.
5.1. Distances
We suppose that we are interested in the probability distribution for distances only. We note that, for a finite measurement error, a range of luminosities contributes to the probability of measuring S′. By integrating over the luminosity, we find the joint probability of D,ϖ′,S′![\begin{eqnarray} && P(D,\varpi',S') \propto g_D(\varpi'|D)f_D(D)\int g_S(S'|S[L,D])f_L(L){\rm d}L=\notag\\ && \hspace{4mm}g_D(\varpi'|D)f_D(D)\int g_S(S'|S[L,D])f_L(L_{\rm o}D^2S))\,L_{\rm o}D^2{\rm d}S \label{e:parflux}, \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq144.png) (23)where we use the fact that gD(D) and fD(D) do not depend on L.
(23)where we use the fact that gD(D) and fD(D) do not depend on L.
In many applications, the flux is measured much more accurately than the parallax, in the sense that σS/S ≪ 1. In that case, for a measurement error distribution gS according to Eq. (3), only values of S close to S′ contribute to the integral over S in Eq. (23), and fL is close to constant in that small interval. Thus the factor fL(LoD2S)LoD2 = fL(LoD2S′)LoD2 can be written outside of the integral, and the remaining integral ∫ gS(S′ | S)dS = 1. With Bayes’ theorem we then obtain (cf. Eqs. (12), (13)) ![\begin{eqnarray} p_D(D|\varpi',S')&=& C_D(0,D_\mathrm{max})D^2\mathcal{F}(D)\nonumber\\ && \quad\times\,\exp\left[-{(1/D-\varpi')^2\over2\sigma^2}\right] L_{\rm o}D^2f_L(L_{\rm o}D^2S'). \label{e:dparfluxb} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq149.png) (24)Apart from normalization, the only difference with Eqs. (18) and (20) is the extra term D2fL(LoD2S′). For fL ∝ L-1, the extra term D2fL is constant, and thus pD(D | ϖ′,S′) (Eq. (24)) is identical to pD(D | ϖ′), except for a normalization constant, provided Lmin<L<Lmax.
(24)Apart from normalization, the only difference with Eqs. (18) and (20) is the extra term D2fL(LoD2S′). For fL ∝ L-1, the extra term D2fL is constant, and thus pD(D | ϖ′,S′) (Eq. (24)) is identical to pD(D | ϖ′), except for a normalization constant, provided Lmin<L<Lmax.
 |
Fig. 5 Distance probability function determined from parallax and accurate flux with known spatial and luminosity distributions. The black line gives the values based on parallax alone (reproducing the black line in Fig. 3). For a lognormal luminosity function, the dashed blue line shows the extra term D2fL(LoD2S′) and the solid blue line the overall distribution according to Eq. (24) for values appropriate for PSR J0218+4232. The dashed and solid red lines and the brown lines idem for power-law luminosity functions both with Lmin = 0.1 mjy kpc2 and Lmax = 10 mJy kpc2 for α = −1, and Lmax = 100 mJy kpc2 for α = −2, respectively. All curves are normalized to their maximum value. |
In Fig. 5 we apply Eq. (24) to PSR J0218+4232, for three luminosity functions, where we set the uncertainty of the measured flux to zero, for illustrative purposes.
For the power-law luminosity function Eq. (8) with α = −1 we fix minimum and maximum luminosities at 0.1 mJy kpc2 and 10 mJy kpc2, respectively. The accurate flux then leads to minimum and maximum distances at 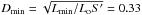 kpc and
kpc and 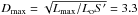 kpc. For this luminosity function pD(D | ϖ′,S′) ∝ pD(D | ϖ′) in the range Lmin<L<Lmax.
kpc. For this luminosity function pD(D | ϖ′,S′) ∝ pD(D | ϖ′) in the range Lmin<L<Lmax.
For a steeper power law with α = −2, the extra term D2fL ∝ D-2 increases the probability of smaller distances and lowers the probability of large distances. We show this for Lmax = 100 mJy kpc2.
In Fig. 5 we also show Eq. (24) for the lognormal distribution, applied to PSR J0218+4232; apart from the normalization, this is similar to the result for a power-law luminosity distribution with α = −2.
For all three luminosity functions, the lower range of allowed distances is determined mainly by the parallax and its error.
5.2. Distances: earlier derivations
Verbiest et al. (2012) use the lognormal luminosity function Eq. (10). Entering this in Eq. (24) we obtain ![\begin{eqnarray} p_D(D|\varpi',S') &=& C_D(0,D_\mathrm{max}) D^2\mathcal{F}(D) \exp\left[-\,{(1/D-\varpi')^2\over2\sigma^2}\right]\nonumber \\ && \times \exp\left[-\,{(\log\left[L_{\rm o}D^2S'\right]-\mu_x)^2\over2{\sigma_x}^2}\right]{1\over S'}\cdot \label{e:dlognormal} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq165.png) (25)In Eq. (26) of Verbiest et al. (2012), we note that the term 1 /D is used instead of the 1 /S′ term in our Eq. (25). This variant arises because their Eq. (25) has dλ/ dD instead of the correct dλ/ dS′, analogous to the error leading to Eq. (21). As a result, the probability of actual distance for measured parallax and flux given by Verbiest et al. (2012, their Eq. (27)), has a weighting factor 1 /D3, absent in the correct version of our Eq. (25) (and omits the weighting factor 1 /S′, which drops out in the normalization).
(25)In Eq. (26) of Verbiest et al. (2012), we note that the term 1 /D is used instead of the 1 /S′ term in our Eq. (25). This variant arises because their Eq. (25) has dλ/ dD instead of the correct dλ/ dS′, analogous to the error leading to Eq. (21). As a result, the probability of actual distance for measured parallax and flux given by Verbiest et al. (2012, their Eq. (27)), has a weighting factor 1 /D3, absent in the correct version of our Eq. (25) (and omits the weighting factor 1 /S′, which drops out in the normalization).
5.3. Luminosities
In the case where we are interested in luminosities alone, we write the joint probability of L, ϖ′, and S′, averaged over distances D, by integrating Eq. (22) over D. Substituting D = ϖ-1, and Dmax = 1 /ϖmin this leads to ![\begin{eqnarray} P(L,\varpi',S') &\propto& f_L(L) \int_{\varpi_\mathrm{min}}^\infty {\varpi^{-2}\mathcal{F}({1\over\varpi})\over\sqrt{2\pi}\,\sigma} \exp\left[-{(\varpi-\varpi')^2\over2\sigma^2}\right] \nonumber \\ & & \times{1\over\sqrt{2\pi}\sigma_S} \exp\left[-{(L\varpi^2/L_{\rm o}-S')^2\over2{\sigma_S}^2}\right]\,\varpi^{-2}{\rm d}\varpi. \label{e:lfromds} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq173.png) (26)
(26)
5.3.1. Luminosities with accurate distance
We first consider the case where the distance is well known, in the sense that σ/ϖ ≪ 1. Only terms with ϖ ≃ ϖ′ contribute to the integral over ϖ in Eq. (26), which can be rewritten as ![\begin{eqnarray} P(L,\varpi',S')\! &\propto& \!f_L(L) {\varpi'}^{-4}\mathcal{F}\left({1\over\varpi'}\right) \exp\left[-{(L{\varpi'}^2/L_{\rm o}-S')^2\over2{\sigma_S}^2}\right] \nonumber \\ & & \!\!\times \int_{\varpi_\mathrm{min}}^\infty {1\over\sqrt{2\pi}\,\sigma}\exp\left[-{(\varpi-\varpi')^2\over2\sigma^2}\right] \times {\rm d}\varpi . \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq176.png) (27)The integral is a constant for a given ϖmin ≡ 1 /Dmax, and approaches unity when σ/ϖ′ approaches zero, provided ϖ′>ϖmin, i.e. provided that the nominal distance D′ ≡ 1 /ϖ′ satisfies D′<Dmax. We then have
(27)The integral is a constant for a given ϖmin ≡ 1 /Dmax, and approaches unity when σ/ϖ′ approaches zero, provided ϖ′>ϖmin, i.e. provided that the nominal distance D′ ≡ 1 /ϖ′ satisfies D′<Dmax. We then have ![\begin{eqnarray} &&p_L(L|\varpi',S') = C_L(L_\mathrm{min},L_\mathrm{max}) {\varpi'}^{-4}\mathcal{F}({1\over\varpi'}) f_L(L) \nonumber \\ &&\qquad \qquad\qquad \times \exp\left[-{[L-L'(\varpi',S')]^2\over2{\sigma_S(\varpi')}^2}\right], \nonumber \\ &&\mathrm{where} \ \ L'(\varpi',S')={L_{\rm o}S'\over{\varpi'}^2};\quad \sigma_S'(\varpi') = {L_{\rm o}\sigma_s\over{\varpi'}^2}\cdot \label{e:lfromads} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq182.png) (28)Because the integral over L implicit in CL(Lmin,Lmax) does not depend on D, the factor D4ℱ = ϖ′-4ℱ(1 /ϖ′) can be dropped from this equation. Specifically, this implies that pL(L | ϖ′,S′) does not depend on the spatial distribution. Equation (28) can be interpreted directly as follows. For an accurate distance D = 1 /ϖ′, the number of sources scales with D2ℱ. An extra factor D2 is due to the conversion of a flux interval ΔS to a luminosity interval ΔL. The probability of luminosity L is given by the probability of the corresponding flux S = L/ (LoD2), weighted with the luminosity function fL. The weighting factor fL in general can cause the most probable luminosity to differ from the nominal luminosity L′ = LoD2S′, analogous to the way in which the weighting factor fD causes the most probable distance to differ from the nominal distance D′ = 1 /ϖ′ in Eqs. (18) and (20).
(28)Because the integral over L implicit in CL(Lmin,Lmax) does not depend on D, the factor D4ℱ = ϖ′-4ℱ(1 /ϖ′) can be dropped from this equation. Specifically, this implies that pL(L | ϖ′,S′) does not depend on the spatial distribution. Equation (28) can be interpreted directly as follows. For an accurate distance D = 1 /ϖ′, the number of sources scales with D2ℱ. An extra factor D2 is due to the conversion of a flux interval ΔS to a luminosity interval ΔL. The probability of luminosity L is given by the probability of the corresponding flux S = L/ (LoD2), weighted with the luminosity function fL. The weighting factor fL in general can cause the most probable luminosity to differ from the nominal luminosity L′ = LoD2S′, analogous to the way in which the weighting factor fD causes the most probable distance to differ from the nominal distance D′ = 1 /ϖ′ in Eqs. (18) and (20).
The effect of the competition between the luminosity function fL and the exponential term in Eq. (28) can be quite dramatic, as illustrated in Fig. 6. As an example we consider PSR J0218+4232, assuming for illustrative purposes that its parallax is exact. With Lo = 1, its nominal luminosity is L′ = LoS′/ϖ′2 ≃ 35 mJy kpc2, and 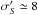 mJy kpc2. In the luminosity range considered, 0.1 <L(mJykpc2) < 10, the exponential factor in Eq. (28) increases by a factor of 130 between the low and the high luminosity limit. The relatively flat luminosity function fL ∝ L-1 decreases by a factor of 100 in the same range. As a result, the overall luminosity probability peaks both at 0.1 mJy kpc2, and – less steeply – at 10 mJy kpc2.
mJy kpc2. In the luminosity range considered, 0.1 <L(mJykpc2) < 10, the exponential factor in Eq. (28) increases by a factor of 130 between the low and the high luminosity limit. The relatively flat luminosity function fL ∝ L-1 decreases by a factor of 100 in the same range. As a result, the overall luminosity probability peaks both at 0.1 mJy kpc2, and – less steeply – at 10 mJy kpc2.
The peak at the high luminosity limit is lowered for a luminosity function that drops faster towards high luminosities, as illustrated in Fig. 6 for the lognormal distribution Eq. (10). For a power law fL ∝ L-2 the peak at 10 mJy kpc2 disappears. On the other hand, if the flux measurement error is halved from its actual value to σS = 0.1 mJy, both power-law distributions and the lognormal distribution all combine with the exponential function to give a peak only at 10 mJy kpc2 in the relative probability.
 |
Fig. 6 Luminosity probability function determined from accurate parallax and uncertain flux (values for PSR J0218+4232) with two assumed luminosity distributions. The black line gives the exponential factor in Eq. (28). The dashed red line shows a power-law luminosity function and the solid red line the product of this function and the exponential. The blue lines idem for a lognormal luminosity function. Because of the accurate distance, this luminosity probability function is valid for any spatial distribution. |
5.3.2. Luminosities with accurate flux
To compute the integral in Eq. (26) in the limit σs/S′ ≪ 1, we first make the substitution ϖ2 = uLo/L, hence 2ϖdϖ = duLo/L. Only terms with u ≃ S′ contribute to the integral, hence ![\begin{eqnarray} &&P(L,\varpi',S')\propto f_L(L) x^{-5}\mathcal{F}\left({1\over x}\right)\exp\left[-{(x-\varpi')^2\over2\sigma^2}\right] \nonumber\\ &&\qquad\ \ \quad\qquad\times \int_{u_\mathrm{min}}^\infty\exp\left[ - {(u-S')^2\over2{\sigma_S}^2}\right] {\rm d}u \,{L_{\rm o}\over L} \nonumber\\ &&\mathrm{where}\ \ x = \sqrt{L_{\rm o}S'\over L}; \quad \mathrm{and} \quad u_\mathrm{min}={\varpi_\mathrm{min}}^2{L\over L_{\rm o}} \cdot \end{eqnarray}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq199.png) (29)The integral depends on L, via umin. However, provided that S′>umin, i.e. L<LoDmax2S′, the integral approaches unity when σs/S′ approaches zero. For L>LoDmax2S′ the integral approaches zero in the same limit. Thus
(29)The integral depends on L, via umin. However, provided that S′>umin, i.e. L<LoDmax2S′, the integral approaches unity when σs/S′ approaches zero. For L>LoDmax2S′ the integral approaches zero in the same limit. Thus ![\begin{equation} p_L(L|\varpi',S') = \left\{ \begin{array}{l} C_L(L_\mathrm{min},L_\mathrm{max})f_L(L) \left({L\over L_{\rm o}S'}\right)^{5/2}{L_{\rm o}\over L}\mathcal{F}\left(\sqrt{L\over L_{\rm o}S'}\,\right) \\ \phantom{m}\times \exp\left[-{(\sqrt{L_{\rm o}S'/L}-\varpi')^2\over2\sigma^2}\right]\, \mathrm{for} \, L<L_{\rm o}{D_\mathrm{max}}^2S' \\ \\ 0 \quad \mathrm{for} \quad L>L_{\rm o}{D_\mathrm{max}}^2S'. \end{array}\right. \label{e:lumacs} \end{equation}](/articles/aa/full_html/2016/07/aa27471-15/aa27471-15-eq205.png) (30)Because the integral over L implicit in CL(Lmin,Lmax) does not depend on Lo or S′, the factor Lo(LoS′)−5/2 can be omitted from Eq. (30).
(30)Because the integral over L implicit in CL(Lmin,Lmax) does not depend on Lo or S′, the factor Lo(LoS′)−5/2 can be omitted from Eq. (30).
For the flux and parallax of PSR J0218+4232, the exponential factor in Eq. (30) increases with L up to 10 mJy kpc2 (and beyond), and this increase is amplified by the factor L1.5. In contrast, the luminosity functions increase towards the minimum luminosity of 0.1 mJy kpc2. The combined effect of these two factors is shown in Fig. 7. The luminosity probability for the galactocentric distribution observed in the direction of PSR J0218+4232 has a stronger contribution at luminosities below 10 mJy kpc2 than the homogeneous distribution. This is due to the rise of ℱ towards lower distances, hence lower luminosities.
 |
Fig. 7 Luminosity probability function determined from uncertain parallax and accurate flux (values for PSR J0218+4232). The black solid line shows the exponential factor in Eq. (30) multiplied by L1.5, the black dashed line shows ℱ. In blue, the dotted curve shows the lognormal luminosity distribution, the dashed and solid curves the corresponding luminosity probability functions for homogeneous and galactocentric spatial distributions, respectively. In red, idem for the power-law luminosity function. All curves are normalized to a value 1 at 10 kpc, except those for the luminosity functions and for ℱ, normalized to a value of 0.1 at 10 kpc. |
5.3.3. Can we do without the luminosity function?
Since the luminosity is given by L = LoD2S′, the question arises whether, in the case of accurate flux, the probability of luminosity follows the probability of distance squared, 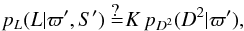 (31)where K is a proportionality constant. The answer is no. This is most easily seen if we consider a standard candle, where the luminosity function is unity for L = LS and zero for all other luminosities L ≠ LS. An accurate flux then implies that only one distance is possible, i.e. the one for which LoS′D2 = LS, whereas the right-hand side of Eq. (31) gives a non-zero value for a range of distances.
(31)where K is a proportionality constant. The answer is no. This is most easily seen if we consider a standard candle, where the luminosity function is unity for L = LS and zero for all other luminosities L ≠ LS. An accurate flux then implies that only one distance is possible, i.e. the one for which LoS′D2 = LS, whereas the right-hand side of Eq. (31) gives a non-zero value for a range of distances.
More generally, at fixed flux S′ a different part of the luminosity function fL is sampled at different distances, and thus the luminosity function is indispensable in the determination of probabilities.
The invalidity of Eq. (31) implies that the probability density function of the luminosity can be given only when the luminosity function is known or assumed, or alternatively when also the parallax is very accurate.
 |
Fig. 8 Gamma-ray luminosity probability function determined from the parallax with error and accurate gamma-ray flux of PSR J0218+4232for three different assumed power-law functions and one lognormal gamma-ray luminosity function. The realistic distance prior (Eqs. (4) and (6)) is assumed. Lsd (Eq. (32)) and 0.1Lsd are indicated with vertical dotted lines; Lmd (Eq. (34)) is indicated with a vertical dashed line. |
6. Distance and gamma-ray luminosity of PSR J0218+4232
An upper limit to the rotation-powered gamma-ray luminosity Lγ is given by the spindown luminosity Lsd, 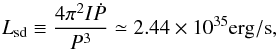 (32)where the numerical value is for PSR J0218+4232 (see Table 1), with an assumed moment of inertia I = 1045 g cm2 for the neutron star. It should be noted that the moment of inertia I of the neutron star PSR J0218+4232 is uncertain as its mass and radius are uncertain.
(32)where the numerical value is for PSR J0218+4232 (see Table 1), with an assumed moment of inertia I = 1045 g cm2 for the neutron star. It should be noted that the moment of inertia I of the neutron star PSR J0218+4232 is uncertain as its mass and radius are uncertain.
As reference values we use the nominal gamma-ray luminosity at the nominal distance Dn ≡ 1 /ϖ′ = 6.25 kpc 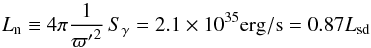 (33)and the luminosity at the most probable distance according to Eq. (19), Dmd = 4.28 kpc
(33)and the luminosity at the most probable distance according to Eq. (19), Dmd = 4.28 kpc 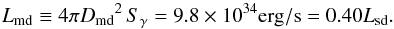 (34)We note that the gamma-ray luminosity is defined for isotropic emission (i.e. So = 4π), which the gamma pulsations show to be false.
(34)We note that the gamma-ray luminosity is defined for isotropic emission (i.e. So = 4π), which the gamma pulsations show to be false.
As noted in the previous section, the probability distribution of luminosity for measured parallax with error and accurate flux can be given only when a luminosity function is known or assumed.
The effect of using different priors is illustrated in Figs. 8 and 9 and in Tables 2 and 3.
Table 2 shows that use of a realistic distance prior, fD ∝ D2ℱ with ℱ given by Eq. (6), reduces the most probable distance to a value smaller than for fD when uniform or spatially homogeneous, also when fL is implemented. The application of realistic luminosity priors narrows the 95% distance credibility interval, in particular when an upper bound to Lγ is set equal to Lsd. In this case the upper limit of the credibility interval is close to the nominal distance of 6.25 kpc.
Figure 8 shows the probability density functions of Lγ for the realistic distance prior fD ∝ D2ℱ with ℱ given by Eq. (6). For each luminosity prior the probability that Lγ<Lsd is very small, <0.001, and the most probable luminosity Lmp is well above 0.1Lsd and well below Lsd. For steeper luminosiy functions the probability density function is pushed to lower luminosities, as expected (see Table 3).
The influence of the distance prior is much more significant. The unrealistic distance priors, combined with the large uncertainty in the parallax, lead to unrealistically high Lγ>Lsd, especially for the uniform luminosity prior.
 |
Fig. 9 Gamma-ray luminosity probability function determined from the parallax with error and accurate gamma-ray flux of PSR J0218+4232 for three different distance priors and two different luminosity priors. Lsd (Eq. (32)) and 0.1Lsd are indicated with vertical dotted lines; Lmd (Eq. (34)) is indicated with a vertical dashed line. |
Most probable distance Dmp and 95% credibility interval for different distance and luminosity priors for PSR J0218+4232.
Most probable gamma-ray luminosity Lmp and 95% credibility interval for different distance and luminosity priors for PSR J0218+4232.
7. Conclusions and discussion
A homogeneous spatial distribution is useful for pedagogical purposes to explain the importance of a prior in deriving a distance probability distribution from a measured parallax. For realistic investigations, however, a homogeneous spatial distribution is misleading. In particular, for a homogeneous spatial distribution, the number of sources increases with distance, and a measured parallax will more often correspond to an underestimated large distance than to an overestimated small distance. In this case, a parallax more often underestimates the actual distance, especially for large measurement uncertainties (see Fig. 2). In a realistic galactic distribution, as observed from Earth, a parallax tends to overestimate the distance, however, at distances where the intrinsic source distribution decreases with distance (Fig. 3). This is often the case, for example in directions away from the galactic centre and/or away from the galactic plane.
Both analytically and via a Monte Carlo simulation, we show that a prior for the spatial distribution must be used, also in the study of a single object, for the determination of the distance probability density. Similarly, when parallax and flux measurements with their errors are combined to derive probability density distributions for distances and luminosities, priors are necessary for both spatial and luminosity distributions. The nominal distance D′ = 1 /ϖ′ and luminosity L′ = LoS/ϖ′2 may be very different from the most probable values (see Fig. 4), unless both measurement errors are small. This is the consequence of the predominance of low luminosities in the luminosity functions that we use: for each flux the higher probability of a low luminosity translates into a higher probability of a lower distance – in as far as the parallax measurement allows this. In the case of PSR J0218+4232, for example, the most probable distance as derived from the parallax alone is at 4.28 kpc (Fig. 5). When parallax and radio flux are both used, the most probable distance drops to 3.74 kpc and 3.42 kpc for power-law luminosity functions with index α = −1 and α = −2, respectively; and to 3.25 kpc for the lognormal luminosity distribution (Fig. 4). Clearly, the quality of the estimates of distance and luminosity is enhanced by the use of realistic prior distributions with respect to the nominal estimates based on measurement only. On the other hand, it is important to keep in mind that using the wrong priors may deteriorate the estimate.
In particular the use of the spatial homogeneous prior is harmful in the case of an uncertain parallax: it shifts the value for most probable distance or luminosity to the upper boundary on the prior (see second line in Tables 2 and 3). In contrast, the realistic distance prior gives an estimate for the gamma-ray luminosity inside the physically motivated region (Lmp<Lsd) even when no additional restrictions on the luminosity function are imposed. An application of the lognormal luminosity prior gives an estimate for distance and gamma-ray luminosity which is in between the two values obtained if we apply a power law with α = −1 and α = −2.
We note, in particular for the power-law luminosity function, that the luminosity function can have a different form at different luminosities (for an example, see Eq. (17) of Faucher-Giguère & Kaspi 2006). This is easily implemented in the formalism described in the previous sections. More complicated is the case (probably realistic) where the luminosity function depends on the position in the Galaxy. For millisecond pulsars this is unlikely. Ordinary pulsars at large z, however, are on average older than pulsars close to the galactic plane, and may well have lower luminosities, if the pulsar luminosity depends on its period and/or period derivative. For the study of such pulsars an evolutionary model is indispensable in the determination of their distances and luminosities.
In the study of a single object, the priors of spatial and luminosity distributions must be known. In the study of a larger number of objects, however, these distributions can and indeed should be derived from prior observations. In general, one might still want to describe these distributions with a number of parameters, e.g. H and h in Eq. (6), α in Eq. (8), or μx and σx in Eq. (10). For a sufficiently large number of pulsars, the evolutionary model can also be tested. At the moment, such studies are hampered by the lack of reliable large (>1 kpc) distances.
Acknowledgments
We thank Gijs Nelemans for discussions and suggestions. The research of A.I. is supported by a NOVA grant.
References
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Du, Y., Yang, J., Campbell, R. M., et al. 2014, ApJ, 782, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Kaspi, V. M. 2006, ApJ, 643, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lyne, A. G., Kramer, M., Martin, C. E., & Jordan, C. 2004, MNRAS, 353, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., & Mohlabeng, G. 2016, J. Cosmol. Astropart. Phys., 3, 049 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, T. E., & Kelker, D. H. 1973, PASP, 85, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Saha, A. 2002, AJ, 123, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiest, J. P. W., & Lorimer, D. R. 2014, MNRAS, 444, 1859 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiest, J. P. W., Weisberg, J. M., Chael, A. A., Lee, K. J., & Lorimer, D. R. 2012, ApJ, 755, 39 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Most probable distance Dmp and 95% credibility interval for different distance and luminosity priors for PSR J0218+4232.
Most probable gamma-ray luminosity Lmp and 95% credibility interval for different distance and luminosity priors for PSR J0218+4232.
All Figures
 |
Fig. 1 Probability distribution of actual distances for a measured parallax for objects distributed homogeneously in a finite sphere for values of ϖ′, σ, and Dmax as indicated. The blue line represents Eq. (18). The histogram gives the results of a Monte Carlo simulation which retains objects with 0.198 <ϖ′< 0.202. The black and red lines represent modified versions of Eq. (18) according to Faucher-Giguère & Kaspi (2006) and Verbiest et al. (2012), respectively. The intrinsic distribution given by Eqs. (4) and (5) is shown as a dashed line. All curves are normalized to the same area under the curve. |
| In the text | |
 |
Fig. 2 Probability distribution of actual distances for a measured parallax ϖ′ = 0.2 mas for various measurement errors σ for objects distributed homogeneously in a sphere with radius Dmax = 10 kpc. The intrinsic distribution given by Eqs. (4) and (5) is shown as a dashed line. The curves are normalized to the same maximum value. |
| In the text | |
 |
Fig. 3 For an assumed galactocentric distribution of objects, the distribution as a function of distance to the Earth is given by Eqs. (4) and (6), illustrated for the direction towards PSR J0218+4232 with the dotted line. The black smooth line gives the probability distribution of actual distances in this direction for the measured parallax of this pulsar, according to Eq. (20) in the approximation CD(0,∞) ≃ CD(0,Dmax), Dmax = 10 kpc. The histogram gives the results of a Monte Carlo simulation which retains objects with 0.14 <ϖ′< 0.18. The blue and red lines give the analytic distributions for hypothetically smaller measurement errors but the same value for ϖ′. The curves are normalized to the same maximum value. |
| In the text | |
 |
Fig. 4 Contours of equal joint probability P(D,ϖ′,L,S′) for the direction, parallax, flux, and measurement errors of PSR J0218+4232 for two power-law functions and for the lognormal luminosity function. For each luminosity function we show the maximum and also the contours containing 68% and 95% of the integrated probability. The contours for the power-law luminosity function with index −2 have two branches, one at very low luminosities and one at higher luminosities; part of the latter is indistinguishable from the contours for the lognormal luminosity function. The vertical and horizontal dashed lines show the nominal values for distance D = 1 /ϖ′ and luminosity L′ = S′/ϖ′2, respectively |
| In the text | |
 |
Fig. 5 Distance probability function determined from parallax and accurate flux with known spatial and luminosity distributions. The black line gives the values based on parallax alone (reproducing the black line in Fig. 3). For a lognormal luminosity function, the dashed blue line shows the extra term D2fL(LoD2S′) and the solid blue line the overall distribution according to Eq. (24) for values appropriate for PSR J0218+4232. The dashed and solid red lines and the brown lines idem for power-law luminosity functions both with Lmin = 0.1 mjy kpc2 and Lmax = 10 mJy kpc2 for α = −1, and Lmax = 100 mJy kpc2 for α = −2, respectively. All curves are normalized to their maximum value. |
| In the text | |
 |
Fig. 6 Luminosity probability function determined from accurate parallax and uncertain flux (values for PSR J0218+4232) with two assumed luminosity distributions. The black line gives the exponential factor in Eq. (28). The dashed red line shows a power-law luminosity function and the solid red line the product of this function and the exponential. The blue lines idem for a lognormal luminosity function. Because of the accurate distance, this luminosity probability function is valid for any spatial distribution. |
| In the text | |
 |
Fig. 7 Luminosity probability function determined from uncertain parallax and accurate flux (values for PSR J0218+4232). The black solid line shows the exponential factor in Eq. (30) multiplied by L1.5, the black dashed line shows ℱ. In blue, the dotted curve shows the lognormal luminosity distribution, the dashed and solid curves the corresponding luminosity probability functions for homogeneous and galactocentric spatial distributions, respectively. In red, idem for the power-law luminosity function. All curves are normalized to a value 1 at 10 kpc, except those for the luminosity functions and for ℱ, normalized to a value of 0.1 at 10 kpc. |
| In the text | |
 |
Fig. 8 Gamma-ray luminosity probability function determined from the parallax with error and accurate gamma-ray flux of PSR J0218+4232for three different assumed power-law functions and one lognormal gamma-ray luminosity function. The realistic distance prior (Eqs. (4) and (6)) is assumed. Lsd (Eq. (32)) and 0.1Lsd are indicated with vertical dotted lines; Lmd (Eq. (34)) is indicated with a vertical dashed line. |
| In the text | |
 |
Fig. 9 Gamma-ray luminosity probability function determined from the parallax with error and accurate gamma-ray flux of PSR J0218+4232 for three different distance priors and two different luminosity priors. Lsd (Eq. (32)) and 0.1Lsd are indicated with vertical dotted lines; Lmd (Eq. (34)) is indicated with a vertical dashed line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


