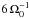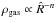| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526172 | |
| Published online | 23 June 2016 | |
Retrograde binaries of massive black holes in circumbinary accretion discs
1
Max Planck Institut für Gravitationsphysik
(Albert-Einstein-Institut),
14476
Potsdam,
Germany
e-mail:
Pau.Amaro.Seoane@gmail.com
2
Università di Milano Bicocca, Dipartimento di
Fisica, G. Occhialini, Piazza della
Scienza 3, 20126
Milano,
Italy
3
INFN, Sezione di Milano-Bicocca, Piazza della Scienza
3, 20126
Milano,
Italy
Received: 24 March 2015
Accepted: 5 April 2016
Context. We explore the hardening of a massive black hole binary embedded in a circumbinary gas disc under a specific circumstance: when the binary and the gas are coplanar and the gas is counter-rotating. The binary has unequal mass and the interaction of the gas with the lighter secondary black hole is the main cause of the braking torque on the binary that shrinks with time. The secondary black hole, revolving in the direction opposite to the gas, experiences a drag from gas-dynamical friction and from direct accretion of part of it.
Aims. In this paper, using two-dimensional (2D) hydrodynamical grid simulations we investigate the effect of changing the accretion prescriptions on the dynamics of the secondary black hole, which in turn affect the binary hardening and eccentricity evolution.
Methods. We find that realistic accretion prescriptions lead to results that differ from those inferred assuming accretion of all the gas within the Roche Lobe of the secondary black hole.
Results. When considering gas accretion within the gravitational influence radius of the secondary black hole (which is smaller than the Roche Lobe radius) to better describe gas inflows, the shrinking of the binary is slower. In addition, in this case, a smaller amount of accreted mass is required to reduce the binary separation by the same amount. Different accretion prescriptions result in different discs’ surface densities, which alter the black hole’s dynamics back. Full 3D Smoothed-particle hydrodynamics realizations of a number of representative cases, run over a shorter interval of time, validate the general trends observed in the less computationally demanding 2D simulations.
Conclusions. Initially circular black hole binaries increase their eccentricity only slightly, which then oscillates around small values (<0.1) while they harden. By contrast, initially eccentric binaries become more and more eccentric. A semi-analytical model describing the black hole’s dynamics under accretion only explores the late evolution stages of the binary in an otherwise unperturbed retrograde disc to illustrate how eccentricity evolves with time in relation to the shape of the underlying surface density distribution.
Key words: accretion, accretion disks / hydrodynamics / methods: analytical / methods: numerical
© ESO, 2016
1. Introduction
Massive black hole pairs are thought to be the natural outcome of galaxy mergers along the cosmic history (Begelman et al. 1980). When two galaxies collide, the gravitational interaction of their galactic cores with the underlying dark matter, stellar, and gaseous background guides the sinking of the two massive black holes (MBH) at the center of the galaxy remnant, which leads to the formation of a Keplerian binary. This occurs when the mass in gas and stars enclosed within the MBH orbit is smaller than the masses of the two MBHs, typically of ~parsec for MBH masses of million suns (Colpi 2014). If the binary further hardens to attain separations as small as  0.001 pc1, the emission of gravitational waves forces the two MBHs to coalesce in less than an Hubble time. Their final pairing and coalescence is measurable with a LISA-like observatory, e.g., eLISA, if the total mass is
0.001 pc1, the emission of gravitational waves forces the two MBHs to coalesce in less than an Hubble time. Their final pairing and coalescence is measurable with a LISA-like observatory, e.g., eLISA, if the total mass is  107M⊙ (Amaro-Seoane et al. 2012a,b).
107M⊙ (Amaro-Seoane et al. 2012a,b).
The evolution of the massive MBH binary (MBHB) on sub-pc scales depends on the properties of the cores of their hosts. In gas-poor remnants, MBHBs lose energy and angular momentum via scattering individual stars. The final fate of the binary depends on the effective reservoir of stars the MBHs can interact with. It has been shown that the presence of some degree of tri-axiality (naturally present in galaxy merger remnants, Preto et al. 2011; Khan et al. 2011, 2012) can excite centrophilic orbits in a high number of the stars of the galaxy remnant, bringing the two MBHs to the scales of gravitational wave-driven inspiral and coalescence (see also Berczik et al. 2006; Berentzen et al. 2009; Gualandris & Merritt 2012; Khan & Holley-Bockelmann 2013).
The presence of dense gas structures could accelerate the evolution of the binary, resulting in a faster coalescence (Begelman et al. 1980). A fundamental difference between gas-poor and gas-rich environments is that, in the presence of a consistent amount of gas, accretion onto the MBHs is expected to be significant. This would enable us to detect dual AGN as spatially resolved nuclear sources and MBHBs at shorter separations from peculiar signatures in their optical/X-ray spectra (e.g., Begelman et al. 1980; Shen & Loeb 2010; Tsalmantza et al. 2011; Eracleous et al. 2012; Montuori et al. 2011, 2012; Sesana et al. 2012; Tanaka et al. 2012; D’Orazio et al. 2013, 2015; Bogdanović 2015), enabling us to map the orbital decay of MBHs in the electromagnetic spectrum. In gas-poor environments, the most robust way of identifying MBHBs is through the detection of gravitational radiation during the inspiral phase. For large MBH 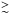 108M⊙, the Pulsar Timing Array experiment, operating at nano-Hz frequencies, might reveal their signal (Hobbs et al. 2010). Furthermore, MBHBs can be detected during the inspiral, merger and ring-down in experiments such as eLISA, at shorter wavelengths (around 0.1 mHz–1 Hz), and for lighter MBHB coalescences (~107M⊙) (Amaro-Seoane et al. 2012a).
108M⊙, the Pulsar Timing Array experiment, operating at nano-Hz frequencies, might reveal their signal (Hobbs et al. 2010). Furthermore, MBHBs can be detected during the inspiral, merger and ring-down in experiments such as eLISA, at shorter wavelengths (around 0.1 mHz–1 Hz), and for lighter MBHB coalescences (~107M⊙) (Amaro-Seoane et al. 2012a).
The presence of massive gas structures close to MBHBs is not unexpected. If the two merging galaxies initially had a significant amount of gas, their reciprocal perturbation drives gas inflows toward the center of the two structures. These inflows result in massive gas discs in the center of the galaxy remnant (e.g., Escala et al. 2005; Mayer et al. 2007; Dotti et al. 2007, 2012; Hopkins & Quataert 2010). However, the details of the interaction between the binary and a gas disc are still debated (Fiacconi et al. 2013; Roškar et al. 2015; Lupi et al. 2015b; del Valle et al. 2015). The gas disc can either be corotating or counter-rotating with respect to the MBHB (Nixon et al. 2011b; Roedig & Sesana 2014). The corotating case seems to be the more natural outcome of a gas rich galaxy merger (see, e.g., Mayer et al. 2007), since the MBHs bind in a binary during the natal process that forms the nuclear gas disc. For this reason, MBHBs embedded in co-rotating circumbinary discs have been extensively studied (Goldreich & Tremaine 1980; Lin & Papaloizou 1986; Artymowicz & Lubow 1994; Ivanov et al. 1999; Escala et al. 2005; Hayasaki et al. 2007; Dotti et al. 2007, 2009; MacFadyen & Milosavljević 2008; Cuadra et al. 2009; Lodato et al. 2009; Farris et al. 2011; Roedig et al. 2011, 2012; Noble et al. 2012; D’Orazio et al. 2013). However, the degree of misalignment between the gas in the remnant nucleus and the binary could depend on the parameters of the merger (Blecha et al. 2011; Hopkins et al. 2012) so that counter-rotating accretion is not ruled out. Furthermore, if the binary does not coalesce on a short timescale (comparable with the timescale over which star formation depletes the central co-rotating gas), subsequent inflows of gas could be uncorrelated to the angular momentum of the binary, possibly resulting in counter-rotating circumbinary discs (Goicovic, et al. 2016).
Regarding the evolution of an MBH binary, retrograde and prograde discs differ in a few important aspects: (i) in the prograde scenario, the disc-binary interaction leads to the opening of a gap, i.e., a hollow region surrounding the MBHs of a size comparable to twice the binary separation, and binary hardening is somewhat reminiscent of a planet type II migration. In the retrograde scenario resonances are either absent (for circular binaries) or weak (Nixon & Lubow 2015). In many cases the binary does not manage to excavate a gap (Bankert et al. 2015), and the MBHB-disc interaction actually enhances the inflow of matter toward the center (Nixon et al. 2011a); (ii) retrograde gas interacting with the MBHs can remove more angular momentum per unit of mass than in the prograde case, since its initial angular momentum has sign opposite to that of the binary and this leads to an increase in the eccentricity (Nixon et al. 2011a; Roedig & Sesana 2014; Schnittman & Krolik 2015); (iii) in the retrograde case, the relative velocities between the MBHs (in particular between the secondary MBH, in an unequal mass binary) and the disc are significantly larger, so that the interaction between the gas and the MBHs is confined to smaller regions.
In this work we present a suite of 2D hydro-dynamic simulations to study in detail the evolution of a MBHB embedded in a counter-rotating disc with focus on how different prescriptions on the accretion onto the secondary MBH can influence the evolution of the orbital elements. In Sects. 2 and 3 we describe the numerical tools, the initial configurations and the accretion prescriptions. In Sect. 4, we evaluate the effect of the different accretion recipes on the dynamics of the binary. Furthermore, we present results obtained from a set of 3D Smoothed-particle hydrodynamics simulations of MBHBs in a retrograde non-self gravitating disc to highlight commonalities and differences with the results from 2D simulations. In Sect. 5 we present a semi-analytical model in order to explore the long term evolution of the binary. We discuss the implications of our findings in Sect. 6.
2. Numerical tool and description of the initial models
We consider the case of MBH binaries orbiting in the orbital plane of an accretion disc. This enable us to limit the dimensions in our simulations to two. Thus, we can use Fargo2, a two-dimensional hydrodynamical grid program that integrates the isothermal Navier-Stokes equations using a staggered polar grid (Masset 2000).
The code is particularly suited for quasi-Keplerian scenarios, since it separates the azimuthal averaged motions from azimuthal and radial perturbations, resulting in longer time steps (the FARGO algorithm was originally presented in Masset 2000). This algorithm speeds up significantly the calculations and hence enable us to study the parameter space more efficiently than with other schemes. Fargo is parallelized by splitting radially the grid in rings, which are calculated in different CPUs.
We run a set of 14 simulations of unequal mass MBHBs in gaseous discs. In every run the primary MBH (M1) is treated as an external potential, and is not evolved during the simulations; it is considered a point-like source. In internal units, the mass of M1 is 1, and is placed at rest at the center of the disc. The disc is confined within an outer radius defined by the radial limits of the grid. In internal units, the outer radius is 25, and the inner radius is 0.1. The disc follows a Mestel profile, as we depict in Fig. 1, with a surface density 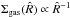 , and a total mass of 0.078, i.e., ≈1/12 of the mass of the primary.
, and a total mass of 0.078, i.e., ≈1/12 of the mass of the primary.
 |
Fig. 1 Face-on, color coded map of the disc’s surface density at the onset of each simulation. The position of the secondary is marked with a solid green circle. For all quantities, we use the internal units of the code, except for the time, which is in units of |
The disc follows an isothermal equation of state, with a thermal profile resulting in an aspect ratio 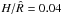 constant throughout the disc. The dynamics of the disc is initially quasi-Keplerian, since, globally, the potential is dominated by M1. The initial angular speed is however not strictly Keplerian, since the code accounts for the pressure support to the rotational equilibrium. The computational domain is divided in a grid of 128 radial and 384 azimuthal sectors.
constant throughout the disc. The dynamics of the disc is initially quasi-Keplerian, since, globally, the potential is dominated by M1. The initial angular speed is however not strictly Keplerian, since the code accounts for the pressure support to the rotational equilibrium. The computational domain is divided in a grid of 128 radial and 384 azimuthal sectors.
In every simulation a second MBH, M2, of initial mass M2,0 = 0.1 M1 is placed in the disc, at a distance d = 10 from M1. The secondary is initially moving on a bound orbit, and counter-rotates with respect to the disc. M2 can either be on a circular or on an eccentric orbit. In this last case we choose the initial eccentricity to be e0 = 0.6, corresponding to an initial apocenter 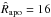 . At the beginning of each simulation, the secondary MBH is implanted in the disc as a particle with mass increasing from 0 to M2,0 over one orbital timescale. This choice prevents the growth of unphysical disc perturbations close to the secondary.
. At the beginning of each simulation, the secondary MBH is implanted in the disc as a particle with mass increasing from 0 to M2,0 over one orbital timescale. This choice prevents the growth of unphysical disc perturbations close to the secondary.
We pay particular attention on how the gas is added and removed from the disc. The amount of gas present can change only if it crosses the radial edges of the computational domain, or if it is accreted by the secondary. At the outer and inner edge of the computational domain we set outflowing boundary conditions, i.e., matter crossing the boundaries disappears from the computational domain, but no gas can inflow into the computational domain.
So as to check the stability of the initial conditions, we first corroborate that the disc is stable by setting the mass of the secondary to a very small value (a 100th of the primary). We confirm the stability for what indeed is the range of mass ratios characteristic to the code -written to study the migration of a planet of mass much smaller than that of the central star- for some tens of initial periods of the binary.
Every set of initial conditions has been run five times, using different prescriptions for the accretion onto M2. The secondary is modelled either as a sink particle that can accrete gas from the disc, or as a point mass whose mass is fixed in time. Since the accretion of mass has strong consequences on the dynamical evolution of M2 we use different prescriptions for the mass accretion, as it is discussed in the next section.
3. Accretion prescriptions
Accretion onto the secondary MBH is a key process affecting the dynamical evolution of the MBHB as (i) the accreting gas changes the mass and velocity of M2, according to conservation of the total momentum of the system; and (ii) the process of accretion itself decreases the gas density close to the secondary. In addition, the perturbation induced by the motion of M2 further changes the underlying disc density pattern, back reacting on the dynamics of the MBHs in the binary. It is therefore important to implement an accretion prescription that does not bias the evolution of the binary. The safest approach would be to follow the hydrodynamics of the gas down to the innermost stable circular orbit around each MBH, or at least around the secondary MBH. Our simulations however do not model all the physics needed to evolve gas down to such extremely small radii. Further out from this physical limit, the numerical nature of our investigation prevents us to set a too small value of the sink radius, that in a number of cases is a free parameter of the simulation. When gas reaches the sink radius, the gas itself is removed from the computational domain and its mass and momentum is added to the MBH. As a consequence, we decided to use different prescriptions for the gas accretion onto the secondary, to test if any accretion prescription results in an artificial orbital evolution of the secondary.
The first prescription we use is the standard FARGO implementation that we will refer as RL model, hereon: gas is accreted onto the secondary if its distance from M2, denoted as 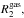 is less than a given fraction (0.75) of the Roche Lobe (RL) radius RRL around M2. The mass accretion is modelled by reducing the gas density within the RL by a factor (1 − fred), at every timestep Δt. To prevent spurious high density and pressure jumps, fred = 1/3 if
is less than a given fraction (0.75) of the Roche Lobe (RL) radius RRL around M2. The mass accretion is modelled by reducing the gas density within the RL by a factor (1 − fred), at every timestep Δt. To prevent spurious high density and pressure jumps, fred = 1/3 if 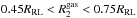 , while fred = 2/3 if R2< 0.45RRL (see for more details Kley 1999).
, while fred = 2/3 if R2< 0.45RRL (see for more details Kley 1999).
However, we note that for a binary counter-rotating with respect to the accretion disc in which it is embedded, the Roche Lobe of the secondary MBH is far from being comparable to its gravitational sphere of influence radius Rbound. The counter-rotating gas crossing the Roche Lobe in the region 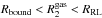 is moving too fast with respect to the secondary MBH to bind to it. For M2 ≪ M1, the Roche Lobe radius is
is moving too fast with respect to the secondary MBH to bind to it. For M2 ≪ M1, the Roche Lobe radius is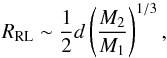 (1)where d is the separation between the two MBHs, while
(1)where d is the separation between the two MBHs, while 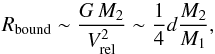 (2)where G is the gravitational constant, and Vrel is the modulus of the relative velocity between the gas and the secondary. The ratio between the two radii is then
(2)where G is the gravitational constant, and Vrel is the modulus of the relative velocity between the gas and the secondary. The ratio between the two radii is then 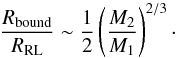 (3)As a consequence, the Roche Lobe based standard implementation of accretion could result in an overestimated accretion rate, hence in an unphysical dynamical evolution of the secondary.
(3)As a consequence, the Roche Lobe based standard implementation of accretion could result in an overestimated accretion rate, hence in an unphysical dynamical evolution of the secondary.
A second prescription we implement is based on the choice of a fixed sink radius Rfix. To prevent spurious pressure jumps we use the same two zones implementation discussed above, accreting 1/3 of the material present in the 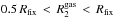 shell and 2/3 of the material with
shell and 2/3 of the material with 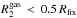 at each timestep. The size of the fixed sink radius around M2 could affect the dynamics of M2 in an unphysical manner if Rfix>Rbound. To check for this spurious effect we run the same set-up with different values of Rfix = 0.5, 0.25, and 0.05, in code units. For a circular binary at the onset of the simulation Rfix/Rbound is approximatively 2, 1, and 0.2 for Rfix = 0.5, 0.25, and 0.05, respectively; similarly Rfix = 0.5 corresponds to Rfix/RRL ≈ 0.2.
at each timestep. The size of the fixed sink radius around M2 could affect the dynamics of M2 in an unphysical manner if Rfix>Rbound. To check for this spurious effect we run the same set-up with different values of Rfix = 0.5, 0.25, and 0.05, in code units. For a circular binary at the onset of the simulation Rfix/Rbound is approximatively 2, 1, and 0.2 for Rfix = 0.5, 0.25, and 0.05, respectively; similarly Rfix = 0.5 corresponds to Rfix/RRL ≈ 0.2.
A third prescription we test requires gas to be gravitationally bound to M2 in order to get accreted. This automatically solves the problem of unbound gas spuriously binding (and accreting) to the secondary. In this case, the gas density reduction factor is either fred = 1/3 if the total gas energy per unit mass (with respect to the secondary) is (3/4)W<E< (1/2)W, or fred = 2/3 if E< (3/4)W, where W = −GM2/R2.
Finally, we test the dynamical evolution of an accreting secondary against a non-accreting one. In this case, the secondary MBH is allowed to bind gas according to the above prescription, but the bound gas is not removed from the simulation, and can either remain bound to M2, co-moving with it on retrograde orbits, or can be stripped by either the tidal field of the primary or by the ram pressure of the gas disc. In the following, for the standard FARGO implementation we will refer to as the “RL model”, as “Fix” 0.5, 0.25, and 0.05 for the models with fixed sink radii, and as “Bound” and “No-accretion” for the remaining last two.
4. Results
4.1. Effect of the accretion prescription on the dynamics
Figure 2 shows the evolution of the binary separation as a function of time, for different accretion prescriptions over a short timescale (i.e., an interval of 2 orbital times). Initially the MBHs move on a circular orbit.
 |
Fig. 2 Relative MBH orbital separation (in units of the initial separation) as a function of time in units of |
The timescale of MBH evolution strongly depends on the accretion prescription assumed. Over a timescale of a few orbital times, the binary hardening in the RL model is faster that in the Bound model, as illustrated in Fig. 2. The reason for this is simple. Gas at a distance from M2 in between the influence radius of the secondary and its Roche Lobe (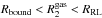 ) is, by definition, not bound. When the sink radius is forced to be equal to RRL, the full momentum of the gas (i.e., also the momentum of unbound gas) is added to the MBH, resulting in an artificially fast dynamical evolution of the binary, because of the unrealistically high accretion rate.
) is, by definition, not bound. When the sink radius is forced to be equal to RRL, the full momentum of the gas (i.e., also the momentum of unbound gas) is added to the MBH, resulting in an artificially fast dynamical evolution of the binary, because of the unrealistically high accretion rate.
We can test the above interpretation exploring additional cases varying Rfix. Whenever a fixed sink radius is assumed, the dynamics depends on the size of the sink radius itself. As expected, larger sink radii correspond to faster migration. In Fig. 2 we show how the evolution of the MBH separation, which is sensitive to Rfix, converges with continuity to the Bound model when decreasing the values of the sink radius. We further find that the No-accretion model in which the MBH does not accrete results in a binary decay very similar to the Bound model. The reason is straightforward: In both cases gas is allowed to bind to the secondary MBH. In the No-accretion run, the gas transfers its (negative) linear momentum to the secondary when it starts co-moving with it, i.e., during the binding process. The same happens in the Bound model in which the gas either binds to the MBH (transferring its linear momentum) or gets immediately accreted during the binding process. In this last case the linear momentum conservation is forced by the accretion prescription. Furthermore, material that would not bind to the secondary is not accreted by default. We further notice that in the Fix models, when the sink radius of M2 is larger than its gravitational influence radius, the MBH absorbs the linear momentum of gas that, in reality, would not be fated to interact with it. Under these conditions the MBHB separation again has a fast artificial decay.
 |
Fig. 3 Mass of the secondary MBH, in units of the initial mass M2,0, as a function of time in units of |
The amount of mass that is accreted by the secondary MBH can be used as a tracer of the linear (and angular) momentum that the disc transfers to the MBH, and in turn to the MBHB. Figure 3 shows the evolution of the secondary mass as a function of time, for the different accretion prescriptions. The MBH in the RL run displays the fastest mass growth and higher amount of accreted mass. In particular in the RL model, the MBH accretes 30% of its mass in order to reduce the separation by 25%. By contrast a reduction of 25% in the relative MBH distance is attained with a fractional mass increase ~0.3% in the Bound model. This indicates that in the process of binary hardening, the fractional decay per unit accreted mass is less effective in the RL model. In this case, the significant mass accreted by the MBH creates an empty region resulting in a much weaker frictional drag on the MBH from the torque of surrounding gas particles that contribute to the deceleration without being accreted. An interpretation of the results will also be discussed in Sect. 5.
 |
Fig. 4 MBHB orbital separation (left) and eccentricity (right) as a function of time, for e0 = 0. We follow the same notation as in Fig. 2. The RL model is not considered, here. |
4.2. Evolution of circular binaries
The evolution of a circular binary is studied further in this section. Figure 4 illustrates the run of the BH separation versus time over ~6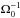 , for the different accretion prescriptions. The RL case is not included in the figure because of the too large, unrealistic accretion prescription. On such a long timespan, all the other runs but for the Fix 0.5 show similar evolutions. The discrepancy between Fix 0.5 and the other runs can be ascribed to the large sink radius of Fix 0.5 resulting in an overestimate of the accretion rate and of the orbital brake. As shown in Fig. 4 the binary eccentricity, increasing slightly at start, fluctuates around a mean of 0.08 and never exceeds 0.16 during the whole evolution.
, for the different accretion prescriptions. The RL case is not included in the figure because of the too large, unrealistic accretion prescription. On such a long timespan, all the other runs but for the Fix 0.5 show similar evolutions. The discrepancy between Fix 0.5 and the other runs can be ascribed to the large sink radius of Fix 0.5 resulting in an overestimate of the accretion rate and of the orbital brake. As shown in Fig. 4 the binary eccentricity, increasing slightly at start, fluctuates around a mean of 0.08 and never exceeds 0.16 during the whole evolution.
 |
Fig. 5 Binary separation as a function of the secondary mass, for different accretion prescriptions. The binary separation and M2 are normalized to their initial values. The evolution is followed for a time equal to |
Figure 5 shows the MBHB separation as a function of M2, the mass the secondary MBH, to illustrate again that the RL model represents the less efficient mechanism of binary hardening in terms of normalized accreted mass. In our case, the high efficiency is caused by the drastically reduced amount of matter accreted onto M2 (see Fig. 3). The not-accreted gas still exerts a non negligible gravitational torque onto the secondary, breaking its orbit and driving its pairing. Such a torque is incorrectly computed (and overestimated) in the simulations with unphysically high accretion rates, where the gas responsible for most of the torque is removed from the simulations and its mass artificially added to the secondary.
 |
Fig. 6 Upper panel: binary separation versus time, for an eccentric binary with e0 = 0.6. Units and color codes are as in the previous figures. Lower panel: evolution of the binary eccentricity versus time for an eccentric binary with e0 = 0.6. |
4.3. Evolution of eccentric binaries
In this section we study the hardening of an initially eccentric binary, in the retrograde disc. Because of the results about the accuracy of the dynamical evolution of the binary presented for the circular case, we confine the analysis of the eccentric cases to the Bound, No-accretion and Rfix = 0.05 runs. The evolution of MBHB separation (upper panel) and eccentricity (lower panel) for a binary with initial eccentricity e0 = 0.6 is shown in Fig. 6.
The initial (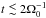 ) evolution of the MBHB is quite similar in the three cases. The binary hardens and contemporarily the eccentricity grows considerably, up to e~>0.7, in qualitative agreement with the analytical predictions of Nixon et al. (2011a). The slight differences between the different cases are due to the different amount of mass accreted. As shown in Fig. 7 the secondary accretes more gas when assuming the bound prescription with respect to, e.g., the Rfix = 0.05 run.
) evolution of the MBHB is quite similar in the three cases. The binary hardens and contemporarily the eccentricity grows considerably, up to e~>0.7, in qualitative agreement with the analytical predictions of Nixon et al. (2011a). The slight differences between the different cases are due to the different amount of mass accreted. As shown in Fig. 7 the secondary accretes more gas when assuming the bound prescription with respect to, e.g., the Rfix = 0.05 run.
 |
Fig. 7 Evolution of the mass of the secondary (M2/M2,0) as a function of time (in units of |
Such differences depend on the accretion prescriptions used. The Bound and No-accretion prescriptions avoid implicitly the inconsistency of maintaining a sink radius Rfix constant throughout the orbital phase, over the time span explored. In the eccentric case the secondary MBH experiences, along a single orbit, different regions of the disc. The disc density is the highest at pericenter where the relative velocity between the gas and the MBH is also the highest. The notion of Rbound becomes thus time (phase) dependent. The outcome of the Bound, No-accretion and Fix models can thus be different. The run with Rfix can give a consistent description of the MBH dynamics only if, along the orbital phase, Rfix remains smaller than the gravitational influence radius. On the other hand on an eccentric orbit, the bound prescription over-predicts the amount of matter accreted. Gas that is bound at apocenter is accreted promptly when using the bound prescription. However, gas bound at apocenter would unbind at pericenter due to the closer action of tidal forces from the primary MBH. The instantaneous capture prescription in the Bound model thus over-predicts the mass accreted, affecting the uderlying dynamics of the disc. In other terms, a small Rfix, smaller than the bound radius Rbound (at any time over orbital evolution), or the No-accretion model that allows gas to remain dynamically active inside the grid, can account for dynamical processes that can not be captured by the Bound prescription.
4.4. Three-dimensional Smoothed-particle hydrodynamics experiments
A clear advantage of using a 2D modelling is that we are able to run many different cases with a relatively low computational cost. However, the approach upon which the 2D models rely must be tested3. In particular, it is important to asses the role of disc thickness in affecting the results.
We hence run a few representative cases using full 3D Smoothed-particle hydrodynamics simulations with GADGET-24 (Springel 2005). The gaseous disc is modelled with 2 × 105 Smoothed-particle hydrodynamics particles, following an isothermal equation of state but for the possible heating term associated with the Smoothed-particle hydrodynamics artificial viscosity. Such viscosity is needed in order to properly recover the occurrence of shocks in the gas, as it acts when converging flows are in place. The viscosity term follows a modified Monaghan-Balsara prescription (Monaghan & Gingold 1983; Balsara 1995), with the viscosity parameter α = 0.5 and β = 2 × α. Gravity is computed on a oct-tree, with close encounters among particles being softened through a (Monaghan & Lattanzio 1985) spline kernel with the same softening parameter of 0.1 for the BHs and gas particles (in internal units).
We implemented a fixed sink radius Rfix and a bound radius Rbound to mimic the second and third prescriptions presented in Sect. 3. The same Rfix used in the 2D simulations is introduced here, i.e., 0.05, 0.25 and 0.5. For the “third” prescription, we select gas particles within a fix radius of 1 from each MBH, and among these we check which particles are gravitationally bound to the black hole. In order to do so, we include a parameter α = 0.3, similarly to the implementation discussed in (Dotti et al. 2009). This α parameter enable us to require that a gas particle is more bound to the secondary MBH using the Bondi-Hoyle-Lyttleton radius, 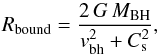 (4)where vbh is the relative velocity between the secondary MBH and the gas particle, and Cs is the sound speed of the gas. We accrete particles whenever their separations from the MBHs are less or equal to α times Rbound. We initialize the disc using GD_BASIC5 (Lupi et al. 2015a) following the same prescription for the 2D case, presented in Sect. 2, preserving the same aspect ratio
(4)where vbh is the relative velocity between the secondary MBH and the gas particle, and Cs is the sound speed of the gas. We accrete particles whenever their separations from the MBHs are less or equal to α times Rbound. We initialize the disc using GD_BASIC5 (Lupi et al. 2015a) following the same prescription for the 2D case, presented in Sect. 2, preserving the same aspect ratio 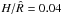 .
.
 |
Fig. 8 Same as Fig. 2, MBHB orbital separation as a function of time (in units of |
 |
Fig. 9 Same as Fig. 6, orbital separation of the binary as a function of time (in units of |
We depict the orbital separation between the two MBHs for the three-dimensional simulations in Figs. 8 and 9 for the circular and eccentric case, respectively. So as to facilitate the comparison with the 2D case, we have added a panel in which we display the bound cases for both the 2D and 3D simulations. After 5 orbital periods, which require about one week of computation on 12 CPUs, the 3D experiment reaches a value of ≈0.7 instead of the ≈0.8 value of the 2D simulation. Two important results can be inferred from the comparison of the different runs:
-
All the discussion about the importance of the accretion prescription already presented for the 2D runs is equally valid in their 3D counterparts. The very similar evolution of the MBH separation as a function of time for the Rfix = 0.05 and Rbound case strengthen the claim that resolving the MBH sphere of influence is a necessary requirement for a proper dynamical evolution.
-
We can readily see that the agreement between the 2D and 3D runs in Fig. 8 is satisfactory: in spite of the very different numerical approaches and the simplifications introduced in the 2D case, the evolution of the distance of the binary is very similar, although not identical. The small differences present in the MBH evolution are due to the fact that, in the 2D case the gas and the MBHs are confined to the plane of the disc and, hence, the MBHs are forced to interact with more gas than in the 3D case. In the 3D case, however, the non-negligible disc thickness allows some of the gas not to interact with the MBH.
The effect of the disc vertical profile on the secondary dynamics is way more significant in the eccentric case. In Fig. 9 we see a much more pronounced difference between the 2D and 3D bound cases (lower panel).
 |
Fig. 10 Same as Fig. 4, evolution of the MBHB eccentricity as a function of time (in units of |
 |
Fig. 11 Same as Fig. 6, evolution of the MBHB eccentricity as a function of time (in units of |
As a note of caution we remark that neither the 2D nor the 3D simulations are realistic and accurate representations of circumbinary discs. The idealized thermodynamics of the gas does not catch all the cooling processes taking place in such high density regions. If the disc were allowed to radiate a significant amount of the energy acquired from the interaction with the MBH, it would settle in a geometrically thinner configuration, more similar to the 2D case. In this study we aimed at isolating the effect of the accretion prescriptions on the MBH dynamics, and a detailed study of the effect of the gas thermodynamics is beyond the scope of the paper.
The comparison of the evolution of the secondary eccentricity in the different runs gives similar results. Figure 10 shows the eccentricity as a function of time for the circular cases. The trends are similar, although not identical in the 2D and 3D bound cases, reaching the same maximum value (≈0.12). The differences between these two cases are due to the reduced amount of gas mass the secondary interacts with in the 3D case, in which the disc thickens as the time goes by. The comparison among the 3D runs demonstrates again the need of resolving the secondary sphere of influence, with the bound and Rfix = 0.05 resulting in the same dynamical evolution of the binary. The same comments apply to the eccentric cases shown in Fig. 11.
5. A semi-analytical model for the evolution of a binary in an unperturbed retrograde disc
In a retrograde disc, the secondary MBH experiences a drag force resulting from gas-dynamical friction on scales larger than Rbound and from accretion on scales smaller than Rbound. Here we propose an analytical scheme that helps interpreting the run of the eccentricity and semi-major axis of the MBHB versus time (or equivalently the accreted mass), varying the slope of the underlying gas density profile.
In the simplifying assumption that the gaseous background is stationary and that the MBH motion is supersonic, the deceleration force can be approximated as 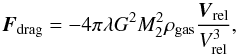 (5)where ρgas is the density of the gas at distances near Rbound, and
(5)where ρgas is the density of the gas at distances near Rbound, and 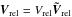 is the velocity of the accreting MBH relative to the gas velocity. The factor λ identifies with the eigenvalue of the Bondi-Hoyle-Lyttleton model for accretion (equal to 1.12 for a isothermal gas) but here λ, suitably rescaled, can also account for the gas dynamical drag according to Ostriker (1999). In Eq. (5), Vrel = V2 − Vgas, where V2 is the velocity of M2 relative to the center of mass of the binary (we here consider the limit M2 ≪ M1 for simplicity, so that the total mass M = M1 + M2 of the binary is approximated to M1, and the reduced mass μ as M2) and Vgas the Keplerian velocity of the gas, relative to M1, at the current position
is the velocity of the accreting MBH relative to the gas velocity. The factor λ identifies with the eigenvalue of the Bondi-Hoyle-Lyttleton model for accretion (equal to 1.12 for a isothermal gas) but here λ, suitably rescaled, can also account for the gas dynamical drag according to Ostriker (1999). In Eq. (5), Vrel = V2 − Vgas, where V2 is the velocity of M2 relative to the center of mass of the binary (we here consider the limit M2 ≪ M1 for simplicity, so that the total mass M = M1 + M2 of the binary is approximated to M1, and the reduced mass μ as M2) and Vgas the Keplerian velocity of the gas, relative to M1, at the current position 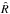 of M2, i.e.,
of M2, i.e., 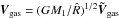 , with
, with 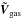 a unit vector in the direction of Vgas.
a unit vector in the direction of Vgas.
To explore the MBHB dynamics and describe the sinking of the secondary MBH in the retrograde disc, we consider the drag force as a perturbation on the Keplerian motion of M2 in the gravitational potential of the primary MBH, M1 (Vecchio et al. 1994). We then trace the dynamics of M2 computing the change of the orbital elements, i.e., the energy and angular momentum, or equivalently the semi-major axis a and eccentricity e under the action of the mean drag force, 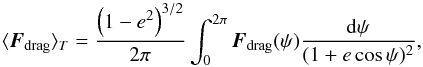 (6)where ψ the orbital phase, and the mean is over the orbital period. In this way we separate the instantaneous motion of M2 from the motion averaged over an orbital period: here on we will refer to as secular motion, and secular evolution.
(6)where ψ the orbital phase, and the mean is over the orbital period. In this way we separate the instantaneous motion of M2 from the motion averaged over an orbital period: here on we will refer to as secular motion, and secular evolution.
The drag force can be cast in the following form in order to separate the modulus from the direction, both time (phase) dependent: 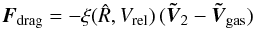 (7)with
(7)with 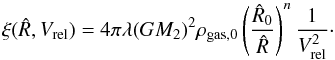 (8)In Eqs. (7) and (8), the distance
(8)In Eqs. (7) and (8), the distance 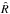 and the velocity vectors are function of phase ψ, along the Keplerian motion, while the constants
and the velocity vectors are function of phase ψ, along the Keplerian motion, while the constants 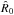 and ρgas,0 denote a reference radius and density in the retrograde, inhomogeneous disc.
and ρgas,0 denote a reference radius and density in the retrograde, inhomogeneous disc.
In Eq. (8), the power-law exponent n describes the distribution of the gas density as a function of the distance 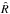 :
: 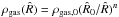 . The value n = 1 corresponds to the disc’s density profile at the onset of the hydrodynamical simulations.
. The value n = 1 corresponds to the disc’s density profile at the onset of the hydrodynamical simulations.
After some calculation (sketched in Appendix) the equations for the secular evolution of the MBH mass m2, in units of M2,0, of the semi-major axis 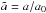 , in units of the initial semi-major axis a0, and of the eccentricity e can be cast in a simple form:
, in units of the initial semi-major axis a0, and of the eccentricity e can be cast in a simple form: 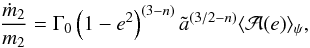 (9)where dot denotes the “secular” time derivative, m2 = M2/M2,0, and
(9)where dot denotes the “secular” time derivative, m2 = M2/M2,0, and 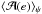 a dimensionless function of the running value of e (see Appendix). Γ0 is a constant equal to
a dimensionless function of the running value of e (see Appendix). Γ0 is a constant equal to 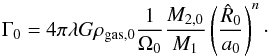 (10)In this last expression Ω0 is the Keplerian frequency of the MBHB at a0:
(10)In this last expression Ω0 is the Keplerian frequency of the MBHB at a0: 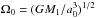 . The equation for the dimensionless semi-major axis reads
. The equation for the dimensionless semi-major axis reads ![\begin{equation} {{\dot {\tilde a}}\over {\tilde a}}=-2\,\, \Gamma_0\,m_2\,{\tilde a}^{(3/2-n)}\,\left[1-e^2\right]^{(2-n)}\langle {{\cal B}(e)}\rangle_\psi, \label{dota} \end{equation}](/articles/aa/full_html/2016/07/aa26172-15/aa26172-15-eq107.png) (11)where ⟨ ℬ(e) ⟩ ψ is given in Appendix.
(11)where ⟨ ℬ(e) ⟩ ψ is given in Appendix.
Similarly, one can calculate the rate of change of the angular momentum and in turn of the eccentricity e. As the orbit of M2 is coplanar, the direction of the binary orbital angular momentum does not vary with time as the drag is causing only a decrease in the modulus of J. According to Eq. (7), the eccentricity evolves as 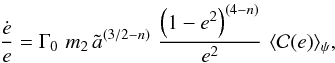 (12)where
(12)where 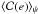 is a dimensionless function of the running value of the eccentricity e (see Appendix).
is a dimensionless function of the running value of the eccentricity e (see Appendix).
Equations (9), (11) and (12) are coupled and can be solved numerically for m2,0 = 1, 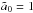 and initial eccentricity e0 at time t = 0. The results can then be rescaled for any arbitrary value of M2,0 and a0. In Eqs. (9), (11) and (12), the timescale that enters the equations is
and initial eccentricity e0 at time t = 0. The results can then be rescaled for any arbitrary value of M2,0 and a0. In Eqs. (9), (11) and (12), the timescale that enters the equations is 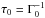 that can be displayed in the form
that can be displayed in the form 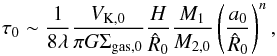 (13)where VK,0 is the Keplerian velocity at
(13)where VK,0 is the Keplerian velocity at 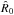 , and Σgas,0 ~ 2Hρgas,0. Recalling that
, and Σgas,0 ~ 2Hρgas,0. Recalling that 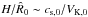 in a thin isothermal disc (with isothermal sound speed cs,0), τ0 scales as
in a thin isothermal disc (with isothermal sound speed cs,0), τ0 scales as 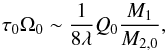 (14)where we have introduced the Toomre parameter Q0 = cs,0Ω0/ (πGΣgas,0) for disc stability. In the following we will describe the solutions of this simple model in the e versus M2/M2,0 and
(14)where we have introduced the Toomre parameter Q0 = cs,0Ω0/ (πGΣgas,0) for disc stability. In the following we will describe the solutions of this simple model in the e versus M2/M2,0 and 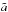 versus M2/M2,0 planes.
versus M2/M2,0 planes.
 |
Fig. 12 Orbital eccentricity e versus M2/M2,0 for e0 = 0.6, as computed within the semi-analytical model. Solid (black) line refers to a background gas density scaling with distance |
5.1. Binary evolution trends
In a fixed and non steep gaseous background (n< 3), eccentric binaries evolves into more eccentric binaries6.
Figure 12 shows the run of the eccentricity e versus M2/M2,0 for e0 = 0.6, and n = 1,1.3,2,2.2 and 3. The eccentricity grows monotonically up to unity, and this occurs before 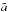 has decayed significantly (i.e., by more than two orders of magnitude). The limit e → 1 is reached after the secondary has accreted a mass comparable to 30%−60% of the initial mass M2,0.
has decayed significantly (i.e., by more than two orders of magnitude). The limit e → 1 is reached after the secondary has accreted a mass comparable to 30%−60% of the initial mass M2,0.
In the case of a steep density background, i.e., n = 3, the eccentricity shows an opposite trend and decreases with time, since the gas disc density at pericenter is so high that the secondary MBH experiences the largest drag there. A higher braking force at pericenter reduces the eccentricity and the MBH spirals inwards along orbits progressively less eccentric. The semi-major axis drops dramatically by more then three orders of magnitude, on a time τ0.
Nearly circular orbits (with e0 = 0.01) show interesting behaviors in their long-term evolution. We first notice that n = 3/2 is a critical value, separating two trends. Solutions with n< 3/2 evolve toward e → 1 before the semi-major axis has decreased significantly. By contrast, when n> 3/2, the decay of the semi-major axis is faster than the increase of e. The value of n = 3/2 is critical since the logarithmic derivatives of our variables all scale as 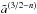 , as indicated in Eqs. (9), (11), and (12). For n> 3/2 the decay of the semi-major axis accelerates with decreasing
, as indicated in Eqs. (9), (11), and (12). For n> 3/2 the decay of the semi-major axis accelerates with decreasing 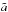 .
.
Figure 13 shows the run of e and 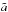 versus M2/M2,0. As a rule of thumb and for circular binaries, the secondary needs to accrete a mass of the order of (2–4) M2,0 to slide on the path leading to coalescence by gravitational waves. For n = 3, the eccentricity remains small for the entire evolution, and never rises.
versus M2/M2,0. As a rule of thumb and for circular binaries, the secondary needs to accrete a mass of the order of (2–4) M2,0 to slide on the path leading to coalescence by gravitational waves. For n = 3, the eccentricity remains small for the entire evolution, and never rises.
 |
Fig. 13 Eccentricity e (left panel) and semi-major axis |
In the early phase of the binary evolution (corresponding to M2< 0.2M2,0), nearly circular binaries remains almost circular, as their eccentricity growth occurs after a sizable increase of the MBH mass (see Fig. 13). This explains why the initially circular binary models studied with FARGO with different accretion prescription do not display a sizable increase of e, on the time span of the simulation. This is in line with the findings by Roedig & Sesana (2014).
Our semi-analytical model has applicability in the limit of M2/M1 ≪ 1. Only if M2/M1 ≪ 1 the secondary, lighter MBH causes minor perturbations in the underlying disc so that the background density can be treated as a constant over the binary evolution timescale. For high MBH ratios (as the one considered in this paper) changes in the density background occur in response to the mutual perturbation excited by the secondary MBH in the retrograde disc, and the evolution needs to be traced only via direct numerical simulations.
6. Discussion
In this paper we explored the evolution of a MBHB embedded in a counter-rotating circumbinary disc. As mentioned in the introduction, the retrograde case differs from the prograde one in three main points: (i) the gravitational torque responsible for the binary shrinking does not halt inflows of gas around the MBHs embedded in the disc; (ii) retrograde gas interacting with the MBHs can remove more angular momentum per unit of mass, since its initial angular momentum has sign opposite to that of the binary; (iii) in the retrograde case, the relative velocities between the MBHs and the disc are significantly larger, so that the interaction between the gas and the MBHs is limited to smaller regions. Since points (i) and (ii) facilitate the binary shrinking while point (iii) limits its strength, it is not obvious a priori if the interaction between a MBHB and a counter-rotating circumbinary disc results in rapid hardening of the binary.
In particular, we pointed out that, as a consequence of the high relative speed between the secondary and the gas, simulations of counter-rotating MBHB-disc systems are strongly affected by the prescription assumed for the accretion of gas onto the MBHs. We argued that in order to model the disc-MBH hydro-dynamics in an appropriate way, a necessary condition is that gas bound accretes onto the lighter, secondary MBH. We confirmed our claim running a suite of 2D hydrodynamical simulations, showing that assuming a too large accretion (sink) radius, such as e.g., the Roche Lobe radius of the secondary (Nixon et al. 2011a), results in a too fast spurious evolution of the binary (see Figs. 2, 3, 5). We further noticed that, while for secondaries moving on quasi-circular orbits the “Bound” prescription results in the correct dynamical evolution of the secondary, for MBHs moving on very eccentric orbits this prescription is not sufficient. This is due to the fact that gas bound to the secondary at the apocenter can unbind during the close pericenter passages, avoiding to be accreted. The non-accreted gas changes the effective mass of the secondary (i.e., the mass of the secondary plus the mass of the gas co-moving to it), and can rejoin the background gas distribution, possibly further interacting with the secondary at later times. For this reason, a sink radius smaller than the influence radius of the MBH, varying over the orbital phase, has to be set properly in order to predict the binary dynamical evolution (see Figs. 6, 7).
The 3D Smoothed-particle hydrodynamics simulations run in parallel for selected cases have shown a close match with the results of the 2D simulations validating the findings in 2D, despite the intrinsic physical difference related to the different dimensionality and the difference in the numerical method.
We focused on the evolution of the binary orbit giving particular emphasis to the effects of the accretion prescriptions. The present analysis still lacks of some possibly important physical effects. We limited the mass of the disc to its initial value, and we do not study the effect of a continuous (or episodic) re-fueling of the disc from the outer regions of the nucleus. Such a fueling is necessary for the coalescence of a binary in a prograde disc (as discussed in Dotti et al. 2012), and can boost the brake of the binary in the retrograde case as well. Finally, we did not model any disc fragmentation and star-formation in the disc, that (together with the fueling of the binary from large scales) is the main unknown in the evolution of binaries in prograde discs as well (see e.g., Lodato et al. 2009; Amaro-Seoane et al. 2013). The effects of these processes, together with a detailed discussion of the peculiar observational properties of counter-rotating systems, is postponed to future investigations.
The exact separation at which an MBH binary coalesces in less than a Hubble time depends on the binary eccentricity, mass, and mass ratio (see e.g., Peters 1964,for an approximation based on Keplerian ellipses).
We note that a recent release of the code includes the possibility of 3D models, as described in http://fargo.in2p3.fr/
We notice that a rapid increase in the eccentricity is also found in an analytical study by Schnittman & Krolik (2015) who expressed the negative torque of a retrograde disc on a MBHB as function of the mass accretion rate, motivated by magneto-hydrodynamical simulations by Bankert et al. (2014).
Acknowledgments
It is a pleasure to thank Frédéric Masset for his answering questions regarding Fargo, as well as Pablo Benítez Llambay, Jules Casoli and Aurélien Crida.
References
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012a, GW Notes, 6, 4 [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012b, Class. Quant. Grav., 29, 124016 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Brem, P., & Cuadra, J. 2013, ApJ, 764, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S. 1995, J. Comput. Phys., 121, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Bankert, J., Krolik, J. H., & Shi, J. 2015, ApJ, 801, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P., Merritt, D., Spurzem, R., & Bischof, H.-P. 2006, ApJ, 642, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Berentzen, I., Preto, M., Berczik, P., Merritt, D., & Spurzem, R. 2009, ApJ, 695, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, L., Cox, T. J., Loeb, A., & Hernquist, L. 2011, MNRAS, 412, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanović, T. 2015, Astrophys. Space Sci. Proc., 40, 103 [Google Scholar]
- Colpi, M. 2014, Space Sci. Rev., 183, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Cuadra, J., Armitage, P. J., Alexander, R. D., & Begelman, M. C. 2009, MNRAS, 393, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- del Valle, L., Escala, A., Maureira-Fredes, C., et al. 2015, ApJ, 811, 59 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazio, D. J., Haiman, Z., & MacFadyen, A. 2013, MNRAS, 436, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazio, D. J., Haiman, Z., & Schiminovich, D. 2015, Nature, 525, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dotti, M., Colpi, M., Haardt, F., & Mayer, L. 2007, MNRAS, 379, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Dotti, M., Ruszkowski, M., Paredi, L., et al. 2009, MNRAS, 396, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Dotti, M., Sesana, A., & Decarli, R. 2012, Adv. Astron., 2012, 940568 [CrossRef] [Google Scholar]
- Eracleous, M., Boroson, T. A., Halpern, J. P., & Liu, J. 2012, ApJS, 201, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Escala, A., Larson, R. B., Coppi, P. S., & Mardones, D. 2005, ApJ, 630, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Farris, B. D., Liu, Y. T., & Shapiro, S. L. 2011, Ph. Rv. D, 84, 024024 [Google Scholar]
- Fiacconi, D., Mayer, L., Roškar, R., & Colpi, M. 2013, ApJ, 777, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Goicovic, F. G., Cuadra, J., Sesana, A., et al. 2016, MNRAS, 455, 1989 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gualandris, A., & Merritt, D. 2012, ApJ, 744, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Hayasaki, K., Mineshige, S., & Sudou, H. 2007, PASJ, 59, 427 [NASA ADS] [Google Scholar]
- Hobbs, G., Archibald, A., Arzoumanian, Z., et al. 2010, Class. Quant. Grav., 27, 084013 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Hayward, C. C., & Narayanan, D. 2012, MNRAS, 425, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, P. B., Papaloizou, J. C. B., & Polnarev, A. G. 1999, MNRAS, 307, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, F., & Holley-Bockelmann, K. 2013, ApJ, 773, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, F. M., Just, A., & Merritt, D. 2011, ApJ, 732, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, F. M., Berentzen, I., Berczik, P., et al. 2012, ApJ, 756, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 307, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., Nayakshin, S., King, A. R., & Pringle, J. E. 2009, MNRAS, 398, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Lupi, A., Haardt, F., & Dotti, M. 2015a, MNRAS, 446, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Lupi, A., Haardt, F., Dotti, M., & Colpi, M. 2015b, MNRAS, 453, 3437 [NASA ADS] [CrossRef] [Google Scholar]
- MacFadyen, A. I., & Milosavljević, M. 2008, ApJ, 672, 83 [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayer, L., Kazantzidis, S., Madau, P., et al. 2007, Science, 316, 1874 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Monaghan, J. J., & Gingold, R. A. 1983, J. Comput. Phys., 52, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J., & Lattanzio, J. C. 1985, A&A, 149, 135 [NASA ADS] [Google Scholar]
- Montuori, C., Dotti, M., Colpi, M., Decarli, R., & Haardt, F. 2011, MNRAS, 412, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Montuori, C., Dotti, M., Haardt, F., Colpi, M., & Decarli, R. 2012, MNRAS, 425, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, C., & Lubow, S. H. 2015, MNRAS, 448, 3472 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, C. J., Cossins, P. J., King, A. R., & Pringle, J. E. 2011a, MNRAS, 412, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, C. J., King, A. R., & Pringle, J. E. 2011b, MNRAS, 417, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Mundim, B. C., Nakano, H., et al. 2012, ApJ, 755, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C. 1999, ApJ, 513, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Preto, M., Berentzen, I., Berczik, P., & Spurzem, R. 2011, ApJ, 732, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Roedig, C., & Sesana, A. 2014, MNRAS, 439, 3476 [NASA ADS] [CrossRef] [Google Scholar]
- Roedig, C., Dotti, M., Sesana, A., Cuadra, J., & Colpi, M. 2011, MNRAS, 415, 3033 [NASA ADS] [CrossRef] [Google Scholar]
- Roedig, C., Sesana, A., Dotti, M., et al. 2012, A&A, 545, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roškar, R., Fiacconi, D., Mayer, L., et al. 2015, MNRAS, 449, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2015, ApJ, 806, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Sesana, A., Roedig, C., Reynolds, M. T., & Dotti, M. 2012, MNRAS, 420, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Loeb, A. 2010, ApJ, 725, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., Menou, K., & Haiman, Z. 2012, MNRAS, 420, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Tsalmantza, P., Decarli, R., Dotti, M., & Hogg, D. W. 2011, ApJ, 738, 20 [Google Scholar]
- Vecchio, A., Colpi, M., & Polnarev, A. G. 1994, ApJ, 433, 733 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
In this Appendix we shortly outline the key steps for deriving the evolution Eqs. (9), (11) and (12) of Sect. 5. We follow closely the derivation by Vecchio et al. (1994).
First we specify the instantaneous motion of the secondary MBH, described by the velocity vector V2 and the separation vector 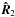 , relative to the center of mass of the binary. Since the accretion drag is a weak perturbing force, the motion is determined by the driving force by the MBH primary. The instantaneous values of
, relative to the center of mass of the binary. Since the accretion drag is a weak perturbing force, the motion is determined by the driving force by the MBH primary. The instantaneous values of 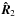 and V2 are expressed in term of the orbital phase ψ, along the Keplerian motion. They are defined uniquely by the instantaneous values of the energy and angular momentum per unit mass that we here denote as E and J, or alternatively a and e. For the distance modulus we have
and V2 are expressed in term of the orbital phase ψ, along the Keplerian motion. They are defined uniquely by the instantaneous values of the energy and angular momentum per unit mass that we here denote as E and J, or alternatively a and e. For the distance modulus we have 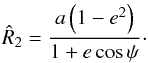 (A.1)The velocity is decomposed along the radial and tangential directions
(A.1)The velocity is decomposed along the radial and tangential directions ![\appendix \setcounter{section}{1} \begin{eqnarray} &&V_{2,{\hat R}_2} =\left[\frac{GM}{a\left(1-e^2\right)}\right]^{1/2} e\sin\psi, \label{vr} \\[4mm] &&V_{2,t}=\left[\frac{GM}{a\left(1-e^2\right)}\right]^{1/2} (1+e\cos\psi), \label{vt} \end{eqnarray}](/articles/aa/full_html/2016/07/aa26172-15/aa26172-15-eq150.png) where M = M1 + M2 ~ M1 in the limit of a massive primary. Furthermore,
where M = M1 + M2 ~ M1 in the limit of a massive primary. Furthermore, 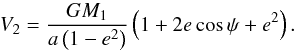 (A.4)The instantaneous deceleration on the secondary MBH due to accretion can be written as
(A.4)The instantaneous deceleration on the secondary MBH due to accretion can be written as 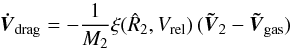 (A.5)with
(A.5)with 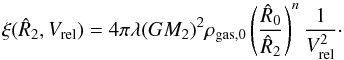 (A.6)The Keplerian velocity of the fluid elements at distance
(A.6)The Keplerian velocity of the fluid elements at distance 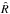 is
is 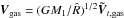 which is vector tangential to
which is vector tangential to 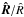 , as the gas in the retrograde disc is moving on circular orbits. According to Eqs. (A.1), (A.2), (A.3) and (A.5),
, as the gas in the retrograde disc is moving on circular orbits. According to Eqs. (A.1), (A.2), (A.3) and (A.5), 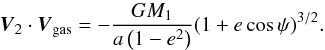 (A.7)
(A.7)
The instantaneous rate of change of the energy per unit mass and angular momentum per unit mass (in the direction of J, as the orbit is coplanar with the disc’s plane ) read:  The rate of change of the energy per unit mass correlates with the rate of change of the semi-major axis through the relation Ė/E = −ȧ/a, where E = −GM1/ 2a. Similarly, the rate of change of the eccentricity e scales as
The rate of change of the energy per unit mass correlates with the rate of change of the semi-major axis through the relation Ė/E = −ȧ/a, where E = −GM1/ 2a. Similarly, the rate of change of the eccentricity e scales as ![\hbox{$e {\dot e}=-\left(1-e^2\right)[{\dot J}/J+(1/2){\dot E}/E]$}](/articles/aa/full_html/2016/07/aa26172-15/aa26172-15-eq161.png) , where J2 = GM1a(1 − e2) (Vecchio et al. 1994). As the secondary MBH accretes gas, the instantaneous rate of change of the mass M2 is set equal to the Bondi-Holye-Littleton accretion rate:
, where J2 = GM1a(1 − e2) (Vecchio et al. 1994). As the secondary MBH accretes gas, the instantaneous rate of change of the mass M2 is set equal to the Bondi-Holye-Littleton accretion rate: 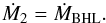 (A.10)The drag force due to accretion induces secular changes in the orbital elements of the binary. We thus calculate the secular rate of change of a,e and M2 averaging all physical quantities over the Keplerian period P. As along a Keplerian orbit, the phase ψ is related to the time coordinate by
(A.10)The drag force due to accretion induces secular changes in the orbital elements of the binary. We thus calculate the secular rate of change of a,e and M2 averaging all physical quantities over the Keplerian period P. As along a Keplerian orbit, the phase ψ is related to the time coordinate by 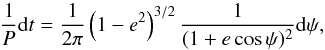 (A.11)we convert the means in the time domain to the phase domain, defining ⟨ ·⟩ T = (1 − e2)3/2 ⟨ ·(1 + ecosψ)-2 ⟩ ψ, hereon.
(A.11)we convert the means in the time domain to the phase domain, defining ⟨ ·⟩ T = (1 − e2)3/2 ⟨ ·(1 + ecosψ)-2 ⟩ ψ, hereon.
Using the above relations, we derive Eqs. (9), (11) and (12). If we define f = 1 + e2 + 2ecosψ and g = 1 + ecosψ, the expressions for the means in the phase domain introduced in Eqs. (9), (11) and (12) read: 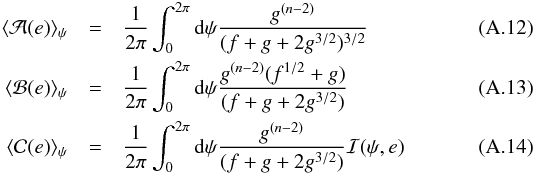 where
where 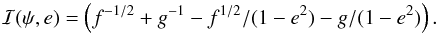 (A.15)Notice that in the limit of e → 0, ė is order
(A.15)Notice that in the limit of e → 0, ė is order  . The expansion analysis around e → 0 shows that ė/e is proportional to (11/4 − n). Thus, for small initial eccentricities and n> 11/4, the orbit circularizes while in the opposite case (n< 11/4), e grows in time. In the same limit ȧ is finite, and the MBH continues to spiral in.
. The expansion analysis around e → 0 shows that ė/e is proportional to (11/4 − n). Thus, for small initial eccentricities and n> 11/4, the orbit circularizes while in the opposite case (n< 11/4), e grows in time. In the same limit ȧ is finite, and the MBH continues to spiral in.
All Figures
 |
Fig. 1 Face-on, color coded map of the disc’s surface density at the onset of each simulation. The position of the secondary is marked with a solid green circle. For all quantities, we use the internal units of the code, except for the time, which is in units of |
| In the text | |
 |
Fig. 2 Relative MBH orbital separation (in units of the initial separation) as a function of time in units of |
| In the text | |
 |
Fig. 3 Mass of the secondary MBH, in units of the initial mass M2,0, as a function of time in units of |
| In the text | |
 |
Fig. 4 MBHB orbital separation (left) and eccentricity (right) as a function of time, for e0 = 0. We follow the same notation as in Fig. 2. The RL model is not considered, here. |
| In the text | |
 |
Fig. 5 Binary separation as a function of the secondary mass, for different accretion prescriptions. The binary separation and M2 are normalized to their initial values. The evolution is followed for a time equal to |
| In the text | |
 |
Fig. 6 Upper panel: binary separation versus time, for an eccentric binary with e0 = 0.6. Units and color codes are as in the previous figures. Lower panel: evolution of the binary eccentricity versus time for an eccentric binary with e0 = 0.6. |
| In the text | |
 |
Fig. 7 Evolution of the mass of the secondary (M2/M2,0) as a function of time (in units of |
| In the text | |
 |
Fig. 8 Same as Fig. 2, MBHB orbital separation as a function of time (in units of |
| In the text | |
 |
Fig. 9 Same as Fig. 6, orbital separation of the binary as a function of time (in units of |
| In the text | |
 |
Fig. 10 Same as Fig. 4, evolution of the MBHB eccentricity as a function of time (in units of |
| In the text | |
 |
Fig. 11 Same as Fig. 6, evolution of the MBHB eccentricity as a function of time (in units of |
| In the text | |
 |
Fig. 12 Orbital eccentricity e versus M2/M2,0 for e0 = 0.6, as computed within the semi-analytical model. Solid (black) line refers to a background gas density scaling with distance |
| In the text | |
 |
Fig. 13 Eccentricity e (left panel) and semi-major axis |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.