EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 688 (August 2024) A&A, 688 (2024) A174 Full HTML
Open Access
Issue
A&A
Volume 688, August 2024
Article Number A174
Number of page(s) 8
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202449402
Published online 20 August 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Observational evidence suggests that massive black holes (MBHs) inhabit the nuclei of (virtually all) massive galaxies (Kormendy & Ho 2013, and references therein). When two galaxies merge, the MBHs hosted in their nuclei migrate to the centre of the merger remnant, primarily due to dynamical friction against the background of stars and gas (Chandrasekhar 1943). At parsec separations, the two black holes bind into a massive-black-hole binary (MBHB). At this point, dynamical friction becomes inefficient, and further evolution of the binary requires a physical mechanism able to extract its energy and angular momentum. The main mechanisms proposed in the literature are the three-body scattering of stars intersecting the binary orbit (Quinlan 1996; Sesana et al. 2007; Bortolas et al. 2021) or the interaction with a circumbinary gaseous disc (Dotti et al. 2007, 2012; Mayer et al. 2007; Lodato et al. 2009). Since both galaxies might contain large amounts of gas, it is expected that this will sink to the centre of the newly formed galaxy and form a circumbinary accretion disc (Begelman et al. 1980; Escala et al. 2005; Cuadra et al. 2009).

The understanding of the disc binary’s coupled dynamics is crucial since at sub-pc scales the binary is too wide for GW emission to take over in driving the binary to merge. The presence of such a disc around an MBHB might facilitate its merger and potentially give rise to observational signatures in the form of electromagnetic (EM) signals (Milosavljević & Merritt 2001; Armitage & Natarajan 2002; Lodato et al. 2009).

Very early numerical simulations (Artymowicz & Lubow 1994, 1996) investigated the interaction of a binary with its gaseous circumbinary disc finding that only a small amount of material is able to enter the cavity carved by the binary and to accrete onto the binary components. The main finding of these works is that the binary’s semi-major axis decreases with time owing to the interaction with the disc. This picture was recently challenged by a few works (Muñoz et al. 2019, 2020; Duffell et al. 2020) employing 2D (and one 3D; see Moody et al. 2019) static or moving-mesh-grid numerical simulations with fixed binary orbits. In particular, these studies found that the secular angular momentum transfer onto the binary is strongly positive within the range of binary and disc parameters explored. More recently, Tiede et al. (2020) found, using the same numerical techniques, that the sign of the torque exerted by the disc onto the binary depends on the disc temperature, i.e. on its aspect ratio H/R, for locally isothermal discs. In particular, they found discs with H/R ≲ 0.04 to shrink the binary. Using 3D smoothed particle hydrodynamics (SPH) simulations of locally isothermal discs, Heath & Nixon (2020) found the threshold value for binary expansion to be H/R ≃ 0.2 instead. However, Franchini et al. (2022) found this process not to be simply regulated by the disc temperature, but also by the disc viscosity.

All these previous works did not include the disc’s self-gravity, which is negligible for compact (a < 1 Mpc) binaries, even for relatively low total mass (M < 107 M⊙) (see discussion in Franchini et al. 2021). In the regime where the disc self-gravity cannot be neglected, and the disc temperature changes with time, all previous works found binary shrinking as a result of the interaction with massive discs regardless of the disc temperature (Cuadra et al. 2009; Roedig et al. 2012; Franchini et al. 2021).

The eccentricity evolution of binaries embedded in massive self-gravitating discs was first investigated by Roedig et al. (2011), finding that binaries with mass ratios of q = M2/M1 = 0.3 evolve towards a critical eccentricity in the range 0.6 − 0.8. The important consequence of the existence of some ecrit is the detectability of a significant residual eccentricity by the Laser Interferometer Space Antenna (LISA; Amaro-Seoane et al. 2023). The excitation of MBHB eccentricity in gaseous discs also has a significant impact on pulsar timing array (PTA) sources. Many of these are at the evolutionary stage in which the environment still plays a role in their dynamical evolution and they are therefore expected to be significantly eccentric. This must be appropriately taken into account when developing dedicated data analysis algorithms. The investigation of these systems is timely to aid the interpretation of the GW signal recently detected by PTA collaborations around the globe; namely the European PTA (EPTA, EPTA Collaboration 2023; EPTA Collaboration & InPTA Collaboration 2023b,a, 2024a,b; Smarra et al. 2023), NANOGrav (Agazie et al. 2023a,b,c; Afzal et al. 2023), the Parkes PTA (PPTA, Reardon et al. 2023), and the Chinese PTA (CPTA, Xu et al. 2023).

A few recent works studied the evolution of the binary eccentricity driven by the presence of the circumbinary disc (Zrake et al. 2021; Siwek et al. 2023a). They find that binaries with large, close-to-equal mass ratios all evolve towards e ∼ 0.5, regardless of their initial conditions. These studies, however, employ 2D fixed binary orbit numerical simulations and neglect the disc’s self-gravity, therefore focusing on a specific region of the parameter space where the disc self-gravity can be neglected (Franchini et al. 2021).

In this work, we considered the dynamics of MBHBs in massive discs governed by self gravity, expanding on the work of Roedig et al. (2011). In particular, we further explore the parameter space investigating the effect that the binary mass ratio has in determining the critical eccentricity value. The paper is organised as follows. In Sect. 2 we outline the numerical setup. We present our results in Sect. 3 and draw our conclusions in Sect. 4.

2. Numerical setup

The live binary (Franchini et al. 2022, 2023, 2024) is composed of two sink particles (Bate et al. 1995) with an initial separation of a = 1 and total mass equal to M = M1 + M2 = 1 in code units. The initial binary orbital period is therefore Pb = 2π. We consider the two sinks to have the same accretion radius rsink = 0.03a. Particles inside this radius are accreted onto the respective sink particle without any further check on their angular momentum or energy. We ran several numerical simulations varying the initial binary and disc parameters. The initial value of binary eccentricity ranges in the 0.05 − 0.8 interval; i.e. from almost circular to very eccentric binaries, while the binary mass ratio was assumed to be q = 0.1, 0.3, 0.9.

The disc initially extends from R = 2a to R = 5a, where a is the binary separation, the mass is Md = 0.2 M, and the mass is composed of N = 106 equal-mass gas particles distributed according to a power-law profile Σ ∝ R−1. The resolution employed here is the same as the one used by Roedig et al. (2011) and Franchini et al. (2021).

We take the disc to be corotating and aligned with the binary orbital plane. The disc equation of state is adiabatic with γ = 5/3, and we take the Gammie (2001) cooling function, with a cooling factor β = tcool/tdyn = 10 in order for the disc to be sufficiently unstable to form large spirals but not enough to fragment, since we are not interested in the latter. We assume the disc initial aspect ratio to be H/R = 0.2, which gives an initial value of the Toomre parameter Q = 1.50 at the disc’s outer edge. The transport of angular momentum throughout the disc is regulated by gravitational instabilities (GIs; Lodato 2007; Meru & Bate 2012).

We only applied artificial viscosity to approaching particles to be able to resolve shocks; for this, we used the Cullen & Dehnen (2010) switch. The shock capturing dissipation terms are included in the code according to the approach outlined in Monaghan (1997) and consist of a linear term, αAV, which controlled by the switch, and a quadratic term, βAV, which essentially prevents particle interpenetration. Since we want the transport of angular momentum induced by gravitational instabilities to dominate, we minimised the numerical dissipation introduced by the numerical viscosity by setting α AV min = 0 , α AV max = 1 $ \alpha^{\mathrm{min}}_{\mathrm{AV}}=0,\,\alpha^{\mathrm{max}}_{\mathrm{AV}}=1 $ and βAV = 2.0 (Meru & Bate 2012).

We ran all the simulations for ∼1000 orbits, taking a snapshot every 0.1 Pb. We note that 1000 orbits corresponds to ∼9 cooling times at the disc’s outer edge. We can therefore assume the disc to have reached a stable gravitoturbulent configuration.

3. Results

We explored the parameter space by running a set of simulations varying the initial binary eccentricity and mass ratio. The values are reported in Table 1. We note that we did not vary the disc mass nor the aspect ratio as these control the stability of the disc to GIs and their effect was already investigated in Franchini et al. (2021).

Table 1.

Simulation parameters.

3.1. Critical eccentricity

The increase of the eccentricity caused by the interaction of the binary with an external disc is a known fact for very unequal binaries where the non-axisymmetric potential perturbations are small Goldreich & Tremaine (1980). In the high-mass-ratio limit, the transfer of angular momentum from the binary to the disc occurs secularly, through torques excited in the disc by the binary at discrete Lindblad and co-rotation resonances. Damping or growth of eccentricity thus depends on the relative importance of these opposing torques (and how fluid elements are distributed in the disc). Lindblad resonances are known to be responsible for opening a gap in the disc. As a consequence of disc clearance, co-rotation and inner Lindblad resonances are reduced in power. Goldreich & Sari (2003) showed that only the outer Lindblad resonances, which remain after the gap opening, cause the increase of the eccentricity for initially low eccentric binaries.

The existence of a critical eccentricity of equilibrium, ecrit, in comparable mass binaries was extensively discussed in Roedig et al. (2011). Their main argument is essentially linked to the gravitational pull of the disc onto the binary. A binary with small initial eccentricity can become more eccentric because of the larger deceleration experienced by the secondary MBH near apocentre with respect to pericentre. The longer time spent near the apocentre and the larger over-density excited in the disc by the MBH gravitational pull due to its immediate proximity lead to a significant deceleration of the MBH that causes the eccentricity to increase. This process continues as long as the secondary MBH has a larger angular velocity at its apocentre than the fluid elements in the disc. When this reverses, the density wake excited by the MBH moves ahead, imparting a net tangential acceleration to the MBH that tends to increase the angular momentum content of the binary, decreasing its eccentricity. The efficiency of this mechanism has not been, however, extensively investigated. In particular, Roedig et al. (2011) only considered systems with q = 1/3, and they extrapolated their results to other mass ratios based on analytical arguments. Furthermore, it is unclear whether, for a given q, the final eccentricity depends on the initial eccentricity of the system. We investigate these points in the following discussion.

The evolution of the binary orbital parameters is shown in Fig. 1. The first column shows the semi-major axis and the second shows the eccentricity as a function of time. The last column shows the evolution of the eccentricity as a function of the semi-major axis, both normalised to their value at orbit 100. We note that we do not show the initial transient phase that the binaries in our simulation experience due to the initial out of equilibrium disc configuration.

thumbnail Fig. 1.

Evolution of binary semi-major axis and eccentricity for initial mass ratio q = 0.1 (upper panels), q = 0.3 (middle panels), and q = 0.9 (bottom panels). The blue, red, and purple lines show the simulations with e0 = 0.05, 0.5, and 0.8 respectively. We note that we do not show the transient phase occurring within the first 100 orbits here. Therefore, e0 and a0 in the last column are the values of eccentricity and semi-major axis after 100 orbits.

As a general trend, we find that the binary separation always decreases over time, at a rate that is only mildly affected by the binary eccentricity. Conversely, for any given mass ratio, the eccentricity evolution slows down significantly with time and depends on e0, with more eccentric systems showing slower evolution; this is indicative of saturation.

We can take a closer look at the comparable mass binary q = 0.9, shown in the bottom panels of Fig. 1. The semi-major axis evolution rate (left panel) is essentially equivalent for all values of e0, and roughly constant in time. Conversely, the eccentricity evolution (central panel) is very different in the three cases. The binary with e0 = 0.05 shows a significant eccentricity growth, reaching e ≈ 0.35 after 1000 orbits. The growth then seems to continue, although at a slower rate. At the opposite end, the initially eccentric binary, e0 = 0.8, experiences a slow eccentricity dumping down to ≈0.7. We note that after few hundred orbits, e essentially saturates and stays constant. Finally, the medium-eccentricity system, e0 = 0.5, only displays a marginal evolution, which is again indicative of saturation.

The outward transport of angular momentum that the disc extracts from the binary, ultimately causes a radial expansion of the disc and therefore weakens the interaction with the binary. This is more evident in very eccentric systems, where the cavity carved by the binary is larger. Figure 2 shows the morphology of the discs around an almost equal-mass binary (q = 0.9) but with different initial eccentricities. It is important to notice, however, that this is unlikely to be the main driver of eccentricity saturation. This is evident by looking at the e/e0 versus a/a0 evolution, shown in the right panel of Fig. 1. The slope of this curve is much steeper from the e0 = 0.05 systems than for the higher eccentricity ones. This means that for these latter systems, the interaction with the disc is still efficient enough to affect the binary, causing a significant orbital shrinking. Despite this, the eccentricity hardly changes, indicating that saturation is being achieved. It is still possible that the eccentricity will evolve over tens of thousands of orbits, but it is clear that both systems with e0 = 0.5, 0.8 have reached a quasi-equilibrium eccentricity, which is different for the two systems.

thumbnail Fig. 2.

Column density plots of self-gravitating circumbinary disc around the binary (shown by the green circles) at t = 320 Pb. The view is of the x − y plane (i.e. the binary orbital plane), and the density has been integrated through z. The logarithmic colour scale spans about two orders of magnitude in density and is the same for all the plots.

These results point towards the existence of a range of critical eccentricities rather than a single value. For an almost equal-mass binary with q = 0.9, this range seems to be ecrit ∈ [0.4, 0.7], with initially highly eccentric binaries reaching higher values of ecrit.

The case of q = 0.3 (middle panels of Fig. 1) essentially displays the very same features. The e0 = 0.8 binary saturates at ecrit ≈ 0.7; the e0 = 0.5 binary only shows a mild eccentricity growth possibly saturating around ecrit ≈ 0.5; the e0 = 0.05 system is still evolving, although the eccentricity growth rate is slowing down, which indicates a possible saturation around ecrit ≈ 0.4.

The case of q = 0.1 is a bit different, mostly because the initially very eccentric binary experiences a violent transient that brings its eccentricity down to ≈0.5 after 100 orbits. In this case, it appears that the range of ecrit is narrower, i.e. ecrit ∈ [0.4, 0.5]. It is, however, hard to estimate how much this depends on the spurious transient in the first 100 orbits of the simulation. It is also possible that for such small q, a well defined ecrit exists. In fact, the upper right panel of Fig. 1 shows that the e versus a evolution is progressively faster for less eccentric binaries. This indicates that, while the e0 = 0.8 system has reached a steady configuration, the other two systems are still evolving towards higher eccentricities.

We note here that in order to ensure that our results on the critical eccentricity do not depend on resolution, we ran the simulation with q = 0.1 and e0 = 0.05 using 2 × 106 particles. We find no significant difference compared to the reference case with 106 particles. In particular, the binary eccentricity increases to roughly the same value, while the binary semi-major axis decreases at higher resolutions as well.

3.2. Cooling

The development of GIs that transport angular momentum inside the disc depends on the cooling timescale. In order to investigate how different cooling timescales affect our results in terms of binary eccentricity evolution, we also ran the simulation with q = 0.3 and initial eccentricity e0 = 0.5 with β = 50, i.e. assuming the cooling to occur on a much longer timescale. We note that ∼1000 binary orbits in this case corresponds to ∼2 cooling times at the disc’s outer edge. The evolution of the binary eccentricity is shown in Fig. 3, where the orange line shows the β = 10 case, while the red line shows the β = 50 case.

thumbnail Fig. 3.

Evolution of eccentricity with initial e0 = 0.5, q = 0.3 for β = 10 (orange line) and β = 50 (red line).

The cooling timescale is much longer than the dynamical time, and therefore the disc does not develop GIs that transport the angular momentum outwards within the 900 orbits we simulated. Figure 4 shows the column-density plots of the two circumbinary discs. The left panel shows the GIs in the disc, while the right panel does not show any spiral since the disc is warmer and more stable against cooling.

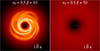thumbnail Fig. 4.

Column density plots of self-gravitating circumbinary disc around the binary (shown by the green circles). The view is of the x − y plane (i.e. the binary orbital plane), and the density has been integrated through z. The logarithmic colour scale spans about two orders of magnitude in density and is the same for all the plots.

A longer cooling timescale ultimately results in a lower final binary eccentricity. After the initial spurious transient, the eccentricity in the β = 50 case (red line in Fig. 3) remains essentially constant at around e = 0.38.

The disc stability parameter reaches a value of Q ≈ 20 in the β = 50 case, while it remains between 1 and 2 in the fiducial case with a faster cooling timescale. Similarly, the disc aspect ratio reaches H/R ∼ 0.3 in the slow-cooling case, while it stabilises around H/R ∼ 0.05 in the fiducial case, which is consistent with the results of Franchini et al. (2021).

3.3. Measuring viscosity induced by GIs

It is interesting to measure the level of viscosity in our discs with self-gravity, which essentially indicates how effective GIs are in transporting angular momentum. The main reason is that the evolution of the binary’s orbital properties critically depends on the efficiency with which the angular momentum is transferred from the binary to the disc. We can use the so-called GI Wiggles (Hall et al. 2020; Longarini et al. 2021; Terry et al. 2022), which are essentially deviations from the Keplerian velocity field generated by the spiral density wave, to infer the α induced by GIs within the disc. In particular, we used the radial velocity perturbation to constrain α in the simulation. According to Longarini et al. (2021), the amplitude of the radial velocity perturbation is

A = − 3 m α 1 / 2 ( M d M ⋆ ) 2 v K ( R ) , $$ \begin{aligned} \mathcal{A} =-3m\alpha ^{1/2}\left(\frac{M_{\rm d}}{M_\star }\right)^2 v_{\rm K}(R), \end{aligned} $$(1)

where m is the number of spiral arms set by inspecting the density structure of the simulations, and vK is the Keplerian velocity. We applied this method to the simulations with a binary with mass ratio of q = 0.3, initial eccentricity of e0 = 0.5, and for the two different cooling parameters β = 10 and β = 50. The corresponding value of the viscosity parameter is α = 0.05 for the fast cooling, while it is α = 0.008 for the slow cooling rate. This is perfectly consistent with the choice of β values since discs with a higher cooling rate (i.e. smaller β) promptly form spiral structures that transport angular momentum.

The lower value of the disc viscosity in the simulation with β = 50 is possibly the reason why the binary eccentricity does not evolve significantly after the initial transient phase. While in the β = 10 case the binary semi-major axis simply decreases with time, in the β = 50 simulation the binary experiences an initial phase of expansion, lasting through the first 200 orbits, before starting to shrink. This is somewhat expected as the initial disc aspect ratio is very large (i.e. H/R = 0.2) and comparable to the disc mass normalised by the binary mass. Therefore, the disc starts with Q ∼ 1 and the inefficient cooling allows its temperature (and thus its aspect ratio) to increase, leading to binary expansion (Tiede et al. 2020; Heath & Nixon 2020; Franchini et al. 2022). However, after the first 200 orbits, the disc reached a new thermal equilibrium as its mass has significantly decreased, allowing the binary to shrink.

We also measured the viscosity parameter by comparing simulations with different mass ratios and eccentricities, but with the same β = 10. We find the initial eccentricity value does not dramatically change the value of α. Comparing binaries with e0 = 0.5 and e0 = 0.8 (same mass ratio: q = 0.3), we find α to be 14% larger for less eccentric binaries. Instead, higher binary mass ratios cause a 30% larger viscosity compared to more equal-mass binaries. We measure the viscosity of the disc surrounding the binary with q = 0.1 and q = 0.3 to be α = 0.0726 and α = 0.05, respectively.

3.4. Accretion rate periodicity

We also investigated the periodicity of the accretion rate onto the binary. This is expected to be modulated on the binary and disc dynamical timescales (Roedig et al. 2011).

We computed the Fast Fourier Transform (FFT) of the accretion rate in our simulations with different initial binary parameters. The results are shown in Fig. 5, where the frequency is in units of the initial binary orbital frequency f0 = 2π(GM/a3)1/2. We find the peaks that correspond to the binary (i.e. f = f0) and disc (i.e. f ≃ 0.2 f0) periodicities to become more narrow with increasing eccentricity for unequal-mass binaries. In very unequal-mass (almost circular) binaries, we find the binary frequency peak to be significantly broader, indicating that the binary orbit does evolve considerably throughout the simulation. Furthermore, the periodicity associated with the disc inner edge is swamped by the sampling noise of the accretion rate. This is consistent with previous works (Farris et al. 2014) that find the disc frequency to be prominent only for equal-mass binaries, which efficiently excite an m = 1 mode (also called a lump) at the disc cavity edge. We do indeed recover the lump periodicity in the almost-equal-mass case, as shown in the bottom three panels of Fig. 5. The presence of the lump is also associated with binary eccentricity. We indeed find this modulation to be prominent even in eccentric, unequal-mass binaries. We note that for both mass ratios shown in Fig. 5, the lump peak shifts slightly at lower frequencies for larger eccentricities, which is consistent with a larger cavity (see Fig. 2). Furthermore, the peak is slightly shifted to lower frequencies for almost-equal-mass binaries, which is still consistent with a larger cavity.

thumbnail Fig. 5.

FFT of accretion rate onto the binary for e0 = 0.05 (upper panel), e0 = 0.5 (middle panel), and e0 = 0.8 (lower panel). The first three panels are for binaries with initial mass ratios of q = 0.1, while the last three have q = 0.9.

The amplitude of the binary orbit modulation tends to increase with increasing mass ratio for binaries with low-to-mild eccentricities, i.e. e ∼ 0.05 − 0.5, while it remains roughly constant for very eccentric binaries (see third and sixth panels of Fig. 5).

Our results in terms of periodicities associated with MBHBs embedded in discs are broadly consistent with the literature (D’Orazio et al. 2013; Muñoz et al. 2020), except we do find that the modulation is associated with the binary orbital period in all cases, possibly because we evolve the binary orbit (Franchini et al. 2023). Although binaries with such massive discs are expected to have long periods, if we extrapolate these findings to more compact systems, our results would indicate that more eccentric and unequal-mass binaries should be more easily identified in photometric searches for MBHBs, as the amplitude of the binary orbital period modulation is generally higher.

3.5. Preferential accretion

Finally, we investigated the preferential accretion of gas onto the secondary MBH as a function of initial binary eccentricity and mass ratio. We calculated the accretion rate onto each binary component over the entirety of the 1000 orbits we simulated. Figure 6 shows the ratio between the accretion rate on the secondary over the primary as a function of the initial binary mass ratio for different values of the initial binary eccentricity. We also show the results obtained for circular binaries by Duffell et al. (2020, orange dotted line) and Dittmann & Ryan (2021, grey dots) and for highly eccentric binaries by Siwek et al. (2023b, i.e. the pink line in their Fig. 4).

thumbnail Fig. 6.

Mass-ratio growth as function of the initial binary mass ratio calculated over the simulated 1000 Pb. The blue, violet, and pink stars show our results for e0 = 0.05, e0 = 0.5, and e0 = 0.8, respectively. The orange dotted line shows the result obtained for circular binaries by Duffell et al. (2020), while the pink solid line shows the result obtained for binaries with eb = 0.8 by Siwek et al. (2023b). The grey dots show the values obtained by Dittmann & Ryan (2021) for circular binaries.

We initially find that less eccentric binaries experience a stronger preferential accretion onto the secondary, which is consistent with previous studies in the same self-gravitating regime (Roedig et al. 2011). A similar trend has been found in previous numerical works employing 2D hydrodynamics simulations (Duffell et al. 2020). However, this trend is much milder in our case and consistent with (Roedig et al. 2011). We do, however, note that the results presented in Dittmann & Ryan (2021) for circular binaries show a milder trend with the mass ratio compared to other 2D simulation works.

We note that there is still a strong preferential accretion on the secondary in terms of Eddington ratio. Indeed, Ṁ2/Ṁ1 = 1.5 for q = 0.1 implies that the secondary is accreting at a 15 times higher Eddington ratio; so, in this sense there is still strong preferential accretion on the secondary.

We find that mass ratios grow more efficiently in low-to-moderate eccentric binaries while the growth is suppressed for highly eccentric binaries. We can see from Fig. 6 that for a fixed binary mass ratio, the mass-ratio growth is suppressed as the eccentricity increases to the point where the primary is accreting more gas than the secondary, which occurs for q = 0.3 and e0 = 0.8. This is broadly consistent with the pink line in Fig. 4 in Siwek et al. (2023b), although they find preferential accretion on the primary for slightly higher mass ratios compared to q = 0.3.

We note that the relation for preferential accretion on one of the binary components as a function of mass ratio inferred in previous studies (e.g. Muñoz et al. 2020; Duffell et al. 2020; Siwek et al. 2023b) overestimates the mass-ratio growth for low-mass ratios compared with our simulations. A possible reason for this discrepancy might be the 3D geometry we used. We simulated a finite disc thickness in the vertical direction; therefore, the gas can more easily avoid the secondary and reach the primary instead. The comparison with previous studies is not straightforward, however, as our simulations include the gas self-gravity and allow the gas to heat and cool. The dynamics of the gas inside the cavity is therefore different compared with the locally isothermal case, and this ultimately leads to a different interaction between the binary and the disc. Furthermore, the accretion of matter onto the two binary components is regulated by the GIs transporting angular momentum in our simulations. This is a major difference between our work and previous similar numerical works, as the effective viscosity provided by GIs might be significantly lower than the value assumed in previous studies.

We note that if β is larger (e.g. β = 50), meaning less efficient cooling, then the mass-ratio growth is Ṁ2/Ṁ1 = 1.06 for q = 0.3, e0 = 0.8. This is due to the fact that the disc remains warmer compared to the β = 10 case, and therefore it accretes preferentially onto the primary. This result is in agreement with previous calculations of magnetised circumbinary discs (Gold et al. 2014). Preferential accretion on one of the binary components was also investigated by Young & Clarke (2015), which showed that an increase in the gas temperature allows more material to accrete onto the primary component of the binary. The relative accretion by the primary was also found to increase at least quadratically with the sound speed of the accreted gas. However, since in our case all discs settle to roughly the same temperature as a result of self-regulation (note that they all have the same initial mass and aspect ratio), we do not speculate on the dependence of our results on the disc temperature.

4. Conclusions

In this work, we explored the dynamics of sub-pc MBHBs interacting with a massive circumbinary gaseous disc whose self-gravity is not negligible compared to the binary gravitational potential. We ran a suite of numerical simulations using the SPH code PHANTOM, changing the initial binary eccentricity e0, mass ratio q and cooling factor β. We ran all the simulations for 1000 binary orbits in order to ensure that all systems reached a quasi-steady state configuration.

The main aim of this work was to study the eccentricity evolution in these binary systems in order to search for a limiting value, which was hypothesised from previous simulations (Roedig et al. 2011). The main implication of the existence of a critical eccentricity is that we could in principle understand whether this binary has significantly interacted with its gaseous environment. We do not find one value of critical eccentricity valid for all the binaries we simulated. Instead, we find the limit eccentricity to depend on the initial mass ratio, in particular more unequal-mass binaries tend to saturate around e ∼ 0.4 − 0.5, while the range for equal-mass binaries is much larger, i.e. 0.3 − 0.7. We note that the limiting eccentricity value of the binary is also sensitive to the cooling choice. We measured the value of α that GIs generate, and we indeed find slower cooling, which leads to lower viscosity values and ultimately translates to the binary stalling at a lower value of eccentricity compared to faster cooling rates.

Our findings are in some contrast with those reported in Zrake et al. (2021). We caution, however, that the direct comparison is not completely fair, as we employed 3D hydrodynamical simulations of live binaries in a region of the parameter space where the gas self-gravity cannot be neglected, while Zrake et al. (2021) inferred their results for a locally isothermal circumbinary disc neglecting the gas self-gravity. The inclusion of the gas self-gravity significantly changes the dynamics of the gas within the disc, the amount of material that is deposited at the resonance location, and therefore ultimately the evolution of the binary orbital parameters.

As we have a finite gas reservoir, the interaction between the binary and the disc is expected to weaken with time. However, after 1000 orbits there is still a significant fraction of the disc (i.e. ∼80%) that interacts with the binary. Furthermore, at least in the highly eccentric case, we can see that as the binary mass ratio tends towards unity, the cavity becomes large (see e.g. Fig. 2), which is the expected behaviour as a consequence of the binary tidal torques; it causes the interaction with the disc to become less strong.

Since we simulated live binaries, we can directly trace the accretion rate onto each BH. We therefore computed the FFT of the accretion rate in order to investigate the effect of the initial binary eccentricity and mass ratio on the amplitude and frequency of the modulation. We recovered the modulation on the binary orbital period in every simulation, regardless of the initial mass ratio and eccentricity. The amplitude of this modulation increases with increasing mass ratio and eccentricity. The modulation on the inner disc edge’s orbital period is absent in almost circular, unequal-mass binaries. In this case, the cavity does not develop significant eccentricity and is therefore not precessed, causing the modulation.

We also measured the binary’s preferential accretion rate on one of the binary components for different eccentricities and mass ratios. We showed that, in general, the secondary BH accretes more mass than the primary in low-mass-ratio binaries. The mass-ratio growth is not strictly monotonic with either the mass ratio or the binary eccentricity. This is somewhat expected since the binary naturally evolves its properties during the simulation; therefore, relating the preferential accretion on one of the binary components to the initial properties of the binary might not be straightforward. The general trend is that the mass-ratio growth is suppressed at higher eccentricities and larger mass ratios, which is broadly consistent with previous works (Muñoz et al. 2020; Siwek et al. 2023b).

We considered binaries embedded in self-gravitating discs, therefore in a regime that is relevant for PTA. The amplitude of the GWB that is expected to be observed with PTA depends on the chirp mass of the sources with ℳ5/3, which in turn depends on the mass ratio as ℳ = (q/(1 + q)2)3/5 M. The higher the mass ratio, the larger the chirp mass, and therefore the louder the GWB signal. Furthermore, the amplitude, even when normalised to the total mass, will increase for more comparable mass ratios. Determining the evolution of an MBHB mass ratio is therefore crucial for estimating the signal amplitude that the population will produce. We find a non-monotonic dependence of the mass-ratio growth on the eccentricity. In particular, in the case of mass ratios close to q = 0.3 we find an inversion of the preferential accretion for high eccentricities (i.e. e > 0.7), meaning that the primary accretes more material, and, therefore, the mass ratio decreases.

We note that there are no evident circumBH discs in our simulations. This is simply due to the fact that since the disc temperature regulates at a correspondent aspect ratio H/R ∼ 0.03 − 0.04, the amount of material that leaks into the cavity is very small; therefore, its contribution to the binary evolution is negligible in this regime. The detailed investigation of the dynamics within the cavity in this particular regime is deferred to a future work.

Acknowledgments

We thank Daniel Price for providing the PHANTOM code for numerical simulations and acknowledge the use of SPLASH (Price 2007) for the rendering of the figures. A.F. and A.S. acknowledge financial support provided under the European Union’s H2020 ERC Consolidator Grant “Binary Massive Black Hole Astrophysics” (B Massive, Grant Agreement: 818691). C.L. acknowledges financial support by UK Science and Technology research Council (STFC) via the consolidated grant ST/W000997/1. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support.

References

  1. Afzal, A., Agazie, G., Anumarlapudi, A., et al. 2023, ApJ, 951, L11 [NASA ADS] [CrossRef] [Google Scholar]
  2. Agazie, G., Anumarlapudi, A., Archibald, A. M., et al. 2023a, ApJ, 951, L8 [NASA ADS] [CrossRef] [Google Scholar]
  3. Agazie, G., Alam, M. F., Anumarlapudi, A., et al. 2023b, ApJ, 951, L9 [CrossRef] [Google Scholar]
  4. Agazie, G., Anumarlapudi, A., Archibald, A. M., et al. 2023c, ApJ, 951, L10 [CrossRef] [Google Scholar]
  5. Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Liv. Rev. Relat., 26, 2 [NASA ADS] [CrossRef] [Google Scholar]
  6. Armitage, P. J., & Natarajan, P. 2002, ApJ, 567, L9 [NASA ADS] [CrossRef] [Google Scholar]
  7. Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
  8. Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [Google Scholar]
  10. Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [Google Scholar]
  11. Bortolas, E., Franchini, A., Bonetti, M., & Sesana, A. 2021, ApJ, 918, L15 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chandrasekhar, S. 1943, ApJ, 97, 255 [Google Scholar]
  13. Cuadra, J., Armitage, P. J., Alexander, R. D., & Begelman, M. C. 2009, MNRAS, 393, 1423 [Google Scholar]
  14. Cullen, L., & Dehnen, W. 2010, MNRAS, 408, 669 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dittmann, A. J., & Ryan, G. 2021, ApJ, 921, 71 [NASA ADS] [CrossRef] [Google Scholar]
  16. D’Orazio, D. J., Haiman, Z., & MacFadyen, A. 2013, MNRAS, 436, 2997 [Google Scholar]
  17. Dotti, M., Colpi, M., Haardt, F., & Mayer, L. 2007, MNRAS, 379, 956 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dotti, M., Sesana, A., & Decarli, R. 2012, Adv. Astron., 2012, 940568 [CrossRef] [Google Scholar]
  19. Duffell, P. C., D’Orazio, D., Derdzinski, A., et al. 2020, ApJ, 901, 25 [NASA ADS] [CrossRef] [Google Scholar]
  20. EPTA Collaboration (Antoniadis, J., et al.) 2023, A&A, 678, A48 [Google Scholar]
  21. EPTA Collaboration& InPTA Collaboration (Antoniadis, J., et al.) 2023a, A&A, 678, A50 [CrossRef] [EDP Sciences] [Google Scholar]
  22. EPTA Collaboration& InPTA Collaboration (Antoniadis, J., et al.) 2023b, A&A, 678, A49 [Google Scholar]
  23. EPTA Collaboration& InPTA Collaboration (Antoniadis, J., et al.) 2024a, A&A, in press https://doi.org/10.1051/0004-6361/202348568 [Google Scholar]
  24. EPTA Collaboration& InPTA Collaboration (Antoniadis, J., et al.) 2024b, A&A, 685, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Escala, A., Larson, R. B., Coppi, P. S., & Mardones, D. 2005, ApJ, 630, 152 [Google Scholar]
  26. Farris, B. D., Duffell, P., MacFadyen, A. I., & Haiman, Z. 2014, ApJ, 783, 134 [NASA ADS] [CrossRef] [Google Scholar]
  27. Franchini, A., Sesana, A., & Dotti, M. 2021, MNRAS, 507, 1458 [NASA ADS] [Google Scholar]
  28. Franchini, A., Lupi, A., & Sesana, A. 2022, ApJ, 929, L13 [NASA ADS] [CrossRef] [Google Scholar]
  29. Franchini, A., Lupi, A., Sesana, A., & Haiman, Z. 2023, MNRAS, 522, 1569 [NASA ADS] [CrossRef] [Google Scholar]
  30. Franchini, A., Bonetti, M., Lupi, A., & Sesana, A. 2024, A&A, 686, A288 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Gammie, C. F. 2001, ApJ, 553, 174 [Google Scholar]
  32. Gold, R., Paschalidis, V., Etienne, Z. B., Shapiro, S. L., & Pfeiffer, H. P. 2014, Phys. Rev. D, 89, 064060 [NASA ADS] [CrossRef] [Google Scholar]
  33. Goldreich, P., & Sari, R. 2003, ApJ, 585, 1024 [Google Scholar]
  34. Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
  35. Hall, C., Dong, R., Teague, R., et al. 2020, ApJ, 904, 148 [NASA ADS] [CrossRef] [Google Scholar]
  36. Heath, R. M., & Nixon, C. J. 2020, A&A, 641, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  38. Lodato, G. 2007, Nuovo Cimento Rivista Serie, 30, 293 [NASA ADS] [Google Scholar]
  39. Lodato, G., Nayakshin, S., King, A. R., & Pringle, J. E. 2009, MNRAS, 398, 1392 [NASA ADS] [CrossRef] [Google Scholar]
  40. Longarini, C., Lodato, G., Toci, C., et al. 2021, ApJ, 920, L41 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mayer, L., Kazantzidis, S., Madau, P., et al. 2007, Science, 316, 1874 [NASA ADS] [CrossRef] [Google Scholar]
  42. Meru, F., & Bate, M. R. 2012, MNRAS, 427, 2022 [NASA ADS] [CrossRef] [Google Scholar]
  43. Milosavljević, M., & Merritt, D. 2001, ApJ, 563, 34 [Google Scholar]
  44. Monaghan, J. J. 1997, J. Comput. Phys., 136, 298 [NASA ADS] [CrossRef] [Google Scholar]
  45. Moody, M. S. L., Shi, J.-M., & Stone, J. M. 2019, ApJ, 875, 66 [NASA ADS] [CrossRef] [Google Scholar]
  46. Muñoz, D. J., Miranda, R., & Lai, D. 2019, ApJ, 871, 84 [CrossRef] [Google Scholar]
  47. Muñoz, D. J., Lai, D., Kratter, K., & Miranda, R. 2020, ApJ, 889, 114 [Google Scholar]
  48. Price, D. J. 2007, PASA, 24, 159 [Google Scholar]
  49. Quinlan, G. D. 1996, New Astron., 1, 35 [Google Scholar]
  50. Reardon, D. J., Zic, A., Shannon, R. M., et al. 2023, ApJ, 951, L6 [NASA ADS] [CrossRef] [Google Scholar]
  51. Roedig, C., Dotti, M., Sesana, A., Cuadra, J., & Colpi, M. 2011, MNRAS, 415, 3033 [NASA ADS] [CrossRef] [Google Scholar]
  52. Roedig, C., Sesana, A., Dotti, M., et al. 2012, A&A, 545, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Sesana, A., Haardt, F., & Madau, P. 2007, ApJ, 660, 546 [NASA ADS] [CrossRef] [Google Scholar]
  54. Siwek, M., Weinberger, R., & Hernquist, L. 2023a, MNRAS, 522, 2707 [NASA ADS] [CrossRef] [Google Scholar]
  55. Siwek, M., Weinberger, R., Muñoz, D. J., & Hernquist, L. 2023b, MNRAS, 518, 5059 [Google Scholar]
  56. Smarra, C., Goncharov, B., Barausse, E., et al. 2023, Phys. Rev. Lett., 131, 171001 [NASA ADS] [CrossRef] [Google Scholar]
  57. Terry, J. P., Hall, C., Longarini, C., et al. 2022, MNRAS, 510, 1671 [Google Scholar]
  58. Tiede, C., Zrake, J., MacFadyen, A., & Haiman, Z. 2020, ApJ, 900, 43 [NASA ADS] [CrossRef] [Google Scholar]
  59. Xu, H., Chen, S., Guo, Y., et al. 2023, Res. Astron. Astrophys., 23, 075024 [CrossRef] [Google Scholar]
  60. Young, M. D., & Clarke, C. J. 2015, MNRAS, 452, 3085 [NASA ADS] [CrossRef] [Google Scholar]
  61. Zrake, J., Tiede, C., MacFadyen, A., & Haiman, Z. 2021, ApJ, 909, L13 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Simulation parameters.

In the text

All Figures

thumbnail Fig. 1.

Evolution of binary semi-major axis and eccentricity for initial mass ratio q = 0.1 (upper panels), q = 0.3 (middle panels), and q = 0.9 (bottom panels). The blue, red, and purple lines show the simulations with e0 = 0.05, 0.5, and 0.8 respectively. We note that we do not show the transient phase occurring within the first 100 orbits here. Therefore, e0 and a0 in the last column are the values of eccentricity and semi-major axis after 100 orbits.
In the text
thumbnail Fig. 2.

Column density plots of self-gravitating circumbinary disc around the binary (shown by the green circles) at t = 320 Pb. The view is of the x − y plane (i.e. the binary orbital plane), and the density has been integrated through z. The logarithmic colour scale spans about two orders of magnitude in density and is the same for all the plots.
In the text
thumbnail Fig. 3.

Evolution of eccentricity with initial e0 = 0.5, q = 0.3 for β = 10 (orange line) and β = 50 (red line).
In the text
thumbnail Fig. 4.

Column density plots of self-gravitating circumbinary disc around the binary (shown by the green circles). The view is of the x − y plane (i.e. the binary orbital plane), and the density has been integrated through z. The logarithmic colour scale spans about two orders of magnitude in density and is the same for all the plots.
In the text
thumbnail Fig. 5.

FFT of accretion rate onto the binary for e0 = 0.05 (upper panel), e0 = 0.5 (middle panel), and e0 = 0.8 (lower panel). The first three panels are for binaries with initial mass ratios of q = 0.1, while the last three have q = 0.9.
In the text
thumbnail Fig. 6.

Mass-ratio growth as function of the initial binary mass ratio calculated over the simulated 1000 Pb. The blue, violet, and pink stars show our results for e0 = 0.05, e0 = 0.5, and e0 = 0.8, respectively. The orange dotted line shows the result obtained for circular binaries by Duffell et al. (2020), while the pink solid line shows the result obtained for binaries with eb = 0.8 by Siwek et al. (2023b). The grey dots show the values obtained by Dittmann & Ryan (2021) for circular binaries.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.