EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 590 (June 2016) A&A, 590 (2016) A102 Full HTML
Free Access
Issue
A&A
Volume 590, June 2016
Article Number A102
Number of page(s) 14
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/201527945
Published online 23 May 2016

© ESO, 2016

1. Introduction

The gain in sensitivity and resolution of modern instruments has given access to the whole electromagnetic spectrum, allowing observations of the stellar light (thermal emission from the far-ultraviolet to the mid-infrared) and of the re-processed (dust in far-infrared/radio) and non-thermal (supernovae [SN], active galactic nuclei [AGN] in radio, mid-infrared and X-ray) emissions of distant galaxies. In the past decade a wealth of multi-wavelength data has been collected in the so-called deep fields to measure galaxy physical properties such as stellar mass, star formation activity, dust content, and AGN fraction: GOODS (Giavalisco et al. 2004), VVDS (Le Fèvre et al. 2005), COSMOS (Scoville et al. 2007), DEEP2 (Newman et al. 2013) or SXDS (Furusawa et al. 2008) among others. A clear picture has emerged for the global evolution of the star formation rate (SFR) and stellar mass densities over cosmic time (e.g., Madau & Dickinson 2014). We observe a general decline of the star formation rate density since z ~ 2, a rapid build-up of the massive end of the mass function (z ~ 1), accompanied by the emergence of quiescent galaxies. However, the physical processes responsible for these evolutions are still to be understood. The gradual decline of star formation (SF) activity could be due to the dwindling gas supply in galaxies, suppressing the fuel for star formation activity (in line with the slowing growth rate of massive dark matter halos, e.g., Bouché et al. 2010). At high redshift, hydrodynamical simulations suggest that cold streams (Katz et al. 2003) can penetrate deep into the dark matter halos and feed galaxies with fresh gas, allowing intense star formation activities and rapid formation of massive galaxies. Internal feedback processes (SN, AGN, virial shock heating; Cattaneo et al. 2006; Kereš et al. 2005) can then expel the gas and/or halt the SF activity and produce the early formation of massive quiescent galaxies. Alternatively, galaxies may also become quiescent as a result of environmental effects such as galaxy harassment (e.g., Farouki & Shapiro 1981), ram-pressure stripping (Gunn & Gott 1972), galaxy strangulation (Larson et al. 1980), or major merging. All these processes must be addressed in the global framework of large-scale structure formation and the complex filamentary network of the cosmic web, containing 90% of the baryons, in order to evaluate the relative contribution of environmental effects (nurture) versus internal effects (nature) in shaping the galaxy properties observed today.

To analyse the relationship between galaxy properties and their environment, the latter has been defined in different ways: i) galaxy clustering analyses provide a statistical link between the galaxies and their host dark matter haloes (Kauffmann et al. 2004), which, combined with their abundances, can constrain the dark matter halo occupation distribution (Zehavi et al. 2005); ii) the reconstruction of the local density field as measured with spectroscopic (Cucciati et al. 2006; Cooper et al. 2008; Kovač et al. 2010) or photometric (Scoville et al. 2013) redshifts allows high- and low-density contrast regions to be separated; iii) the direct measurement of pair, group, and cluster membership can be compared to isolated field galaxies (Haines et al. 2008; Wong et al. 2011; Peng et al. 2010; Kovač et al. 2014); and iv) the reconstruction of the large-scale structure network composed of filaments, nodes, walls, and voids (Aragón-Calvo et al. 2010; Sousbie 2011). It offers a new way to describe the anisotropic environment of the cosmic web. As mentioned before, the cosmic streams can feed galaxies in fresh gas, they also advect angular momentum into the disk of galaxies, which can lead to the alignment of the spine of spiral galaxies with the large-scale filaments, as predicted by tidal torques theory (Codis et al. 2015) and recently observed in the SDSS survey (Tempel et al. 2013).

All these investigations are performed extensively in the local Universe with the help of the large spectroscopic redshift surveys, SDSS, 2dF, and GAMA. At higher redshift, current surveys do not allow reconstructing the cosmic web because of either the small field of view or the low spectroscopic sampling rate. This situation has changed with the large VIMOS Public Extragalactic Redshift Survey (VIPERS; Guzzo et al. 2014) carried at ESO Very Large Telescope (VLT). With ~100 000 spectroscopic redshifts over 24 deg2 down to 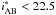in the redshift range 0.5 <z< 1.2 (Garilli et al. 2014), VIPERS probes a volume equivalent to the local 2dF survey, providing a unique high-z sample to beat the cosmic variance (~ 10%) that affects current surveys (80% for GOODS down to 25% for COSMOS at z ~ 0.8). Its spectroscopic sampling rate (~ 40%) ensures a sufficient sampling to measure the redshift-space distortions (de la Torre et al. 2013) and to reveal the cosmic web on a large scale.

The VIPERS spectroscopic survey benefits from the optical coverage of the CFHT Legacy Survey Wide (ugriz) in the W1 and W4 fields. To derive reliable stellar masses and SFR for VIPERS galaxies, we have undertaken a complete near-infrared (NIR) follow-up in the two fields and partial follow-up in near-ultraviolet (only W1), which are described in this paper. In the past ten years, stellar population synthesis (SPS) models have been extensively used to convert luminosity into physical properties using a template-fitting procedure (e.g., see recent reviews by Walcher et al. 2011; Conroy 2013). The wavelength coverage is critical to reduce the uncertainties on those parameters, however. The NIR domain samples the rest-frame optical part of the spectral energy distribution (SED) of distant galaxies. Without NIR, stellar mass measurements are uncertain (σM ~ 0.4 dex), with strong systematics at z> 0.8 that are caused by the degeneracy between age, metallicity, and extinction (Ilbert, private communication). The vast majority of VIPERS galaxies are below z< 1.0, and the CFHTLS imaging does not fully probe the rest-frame ultraviolet (UV) light emitted by massive stars, which is crucial for an SFR estimate. The VIPERS area has been partially observed with the GALEX survey (Martin et al. 2005) in the far-UV (135−175 nm) and near-UV (170−275 nm). However, measuring the GALEX photometry is a complex problem because of the large point-spread function of the telescope (FWHM ~ 5″). The standard SExtractor photometry (Bertin & Arnouts 1996) delivered by the GALEX pipeline is not optimal for faint sources because of blending problems. It requires a dedicated software (Conseil et al. 2011), as discussed in this paper.

With the physical properties of the VIPERS spectroscopic sources derived from the multi-wavelength dataset described in this paper, Davidzon et al. (2013) measured the high-mass tail of the galaxy stellar mass function (GSMF) with unprecedented accuracy for both quiescent and star-forming galaxies from z = 1.3 to z = 0.5 using the first 53608 spectroscopic redshifts from VIPERS (over 7.5 deg2). Davidzon et al. (2016) extended their GSMF analysis as a function of environment by splitting galaxies into high- and low-density regions (using a local 3D galaxy density measurement) and detected an evolution of the GSMF in high-density regions. In contrast, the GSMF remains nearly constant in low-density regions.

In addition to the VIPERS spectroscopic sample, the photometric multi-wavelength survey (F/ NUV ~ 25, ugriz ~ 24.5, Ks ~ 22) combines depth and area (~24 deg2) and provides accurate photometric redshifts and stellar masses for almost one million galaxies below z ≤ 1.5 as well as an efficient separation between active and passive galaxies based on a NUVrK colour diagram (Arnouts et al. 2013). Moutard et al. (2016) exploited this large volume to follow the evolution of the GSMF over the past 10 Gyr for massive galaxies, M ≥ 1010M⊙. It extended the precursor work by Matsuoka & Kawara (2010) performed in a 55 deg2 region of the Stripe 82 overlapping the UKIDSS-LAS K-band (Lawrence et al. 2007), where they constrained the growth history of the most massive galaxies (log (M/Mo) > 11 since z ~ 0.9. Coupon et al. (2015) used the superb image quality of the CFHT images to perform a combined analysis of galaxy clustering, galaxy-galaxy lensing1, and the GSMF to produce a new constraint on the relationship between galaxies and their host dark matter halos.

This paper is organised as follows: we present the WIRCam-Ks and GALEX-UV observations, the data reduction and the creation of the multi-colour catalogue based on the CFHTLS optical catalogue from the final TERAPIX release (T0007). We perform various tests on our photometry and completeness by comparing them with deeper overlapping datasets and simulations. We use the large spectroscopic sample to quantify the quality of our photometric redshifts. As direct applications, we present the selection of a bright BzK sample, and we illustrate the morphology of low-z (z ≤ 0.25) large galaxies in the (NUV−r) vs. (r−K) rest-frame colour diagram. Throughout the paper we adopt the following cosmology: H0 = 70 km s-1 Mpc-1 and ΩM = 0.3, ΩΛ = 0.7. We adopt the initial mass function of Chabrier (2003), truncated at 0.1 and 100 M⊙. All magnitudes are given in the AB system (Oke 1974).

2. Data

2.1. Optical CFHTLS photometry

The Canada-France-Hawaii Telescope Legacy Survey2 (CFHTLS) is an imaging survey performed with MegaCam (Boulade et al. 2000) in five optical bands u⋆,g,r,i,z. The CFHTLS-Wide covers four independent patches in the sky over a total area of 154 deg2 with sub-arcsecond seeing (median ~ 0.7″) and a typical depth of i ~ 24.8 (5σ detection in 2″ apertures). In this study we use the images and photometric catalogues of the W1 and W4 fields from the worldwide T00073 release produced by TERAPIX4. This final release includes an improved absolute and internal photometric calibration based on the photometric calibration scheme adopted by the Supernova Legacy Survey (SNLS) and described in Regnault et al. (2009). The main ingredients are i) the use of the spectrophotometric standard star BD +17 4708 instead of the Landolt standard stars; ii) a new photometric flat-fields used in the reduction pipeline by Elixir at CFHT on the raw images, which guarantees a flat photometry across the MegaCam field of view; and iii) the use of shallow photometric calibration observations covering the whole CFHTLS wide in each filter and bracketed by SNLS tertiary standards. These steps bring the absolute and relative photometric calibrations over the entire survey to an accuracy level of between 1 to 2%.

The final images were stacked with the software SWARP (Bertin 2006). The photometry was performed with SExtractor (Bertin & Arnouts 1996) in dual mode with the source detection based on the gri−χ2 image (Szalay et al. 1999). Following Erben et al. (2013), we used the isophotal apertures, extracted from the detection images, to measure the galaxy colours. The apertures are smaller than the Kron-like apertures (Kron 1980), which provides less noisy estimates of the colours and leads to an improved photometric redshift accuracy (Hildebrandt et al. 2012).

To derive the total magnitudes, we rescaled the isophotal magnitudes (MAG_ISO) to the quasi-total magnitudes (MAG_AUTO) for each source. The scaling factor, δm, combines the individual scalings in g′, r′, i′, and Ks band, when available (the Ks-band images share the same pixel grid as the optical images, see Sect. 2.2), to account for the intrinsic colours of galaxies and their respective uncertainties. It is defined as 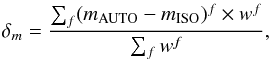(1)where f corresponds to the g′, r′, i′, and Ks filters, and the weight, wf, is defined as 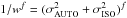. The final magnitudes for each source are then simply defined by a unique shift applied to all passbands: .

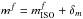thumbnail Fig. 1

Footprints of the GALEX NUV/FUV (cyan/blue) and WIRCam K band (red background) observations in the CFHTLS W1 (top) and W4 (bottom) fields. The spectroscopic sources are shown as golden points. The total area (W1 and W4) is ~7.8 and ~22 deg2 in FUV and NUV bands observed with GALEX and ~27 deg2 with WIRCam. The black layouts represent the VIDEO (W1) and UKIDSS (W4) surveys.

Finally, we also investigated the best masking procedures of the bad regions by comparing the masks produced by TERAPIX and the CFHTLenS team5. After visual inspections, we found that CFHTLenS masks provide a better cleaning of spurious objects around bright stars by adopting a large central disk region on top of the elongated spikes (Erben et al. 2013). We therefore decided to adopt their more conservative masking approach.

In conclusion, our CFHTLS optical catalogue is similar to the original T0007 in terms of source detections, but differs in the masking regions and the choice of magnitudes, where we adopted a scheme that allows optimizing the colour estimates for the photometric redshifts and the total flux for the measurements of the physical parameters. In Fig. 1 UV (GALEX) and NIR (WIRCam Ks-band) observations overlap the CFHTLS.

2.2. NIR observations

2.2.1. Observations

Since 2010, we have conducted a Ks-band follow-up of the VIPERS fields with the WIRCam instrument (Puget et al. 2004) at CFHT. The original motivation was to guarantee an almost complete detection in Ks band of the VIPERS spectroscopic galaxies (iAB ≤ 22.5). To do so, we estimate that we need to detect sources down to Ks ~ 22 (at ~2−3σ), which can be reached with a minimum integration time per pixel of ~1050 s. The observations have been executed with two separated observing groups with 21 exposures of 25 s each. The WIRCam observations are shown in red in Fig. 1. They cover a total area of 27 deg2 and correspond to a total amount of allocated time of ~120 h spread during the period 2010 and 2012. As a result of high sky background or bad seeing (IQ> 0.8″), a few observing groups have been repeated. The average seeing for each WIRCam tile is shown in Fig. 2 for the two fields. The mean image quality is very homogeneous and corresponds to ⟨ IQ ⟩ = 0.6″ ± 0.09. We note that the missing region in the W1 field corresponds to the location of the VIDEO survey. The southern extension of W4 outside the VIPERS regions was planned to cover the GALEX field that was initially not covered by the earliest release of the UKIDSS DXS survey.

2.2.2. Data reduction

All the data were reduced at CFHT and TERAPIX. The initial processing with the i’wii pipeline6 at CFHT removes the instrumental imprints on the individual images (flagging of saturated, bad, and hot pixels, correcting for non-linearity, bias removal, dome and sky flat-fielding, and guide window masking). CFHT delivers detrended images with a first astrometric solution, photometric zeropoint, and a sky subtraction for each exposure.

TERAPIX first uses QualityFITS on detrended images to produce weight-maps (with the WeightWatcher software; Marmo & Bertin 2008), source catalogues and checks the individual image qualities (e.g., seeing and depth). The validated exposures are then median-combined to produce an initial stack by using the Scamp and Swarp softwares7 (Bertin 2006). To improve the sky subtraction and the photometry of faint sources, a two-step strategy is adopted similar to the CFHT-WIRDS (Bielby et al. 2012) and the ESO-UltraVISTA (McCracken et al. 2012) surveys. The initial stack is used to produce a mask with all the faint sources. In a second pass, the mask is applied to the individual exposures and a new sky background is estimated by medianing images inside a sliding window and for images within a time window Δt< 15 min and angular separation Δθ< 10′. A last quality assessment of the individual sky-subtracted images is performed before producing the final stacks. The final WIRCam products are composed of stack images and weight images resampled on the footprint of the CFHTLS-MegaCam tiles and with the same pixel scale (0.18″/pix) using the SWARP software with a Lanczos3 resampling kernel. Like for the T0007 release, the photometry is performed in dual-image mode with the gri−χ2 image and the same SExtractor setting (Hudelot et al. 2012). A last correction is applied to the SExtractor error measurements, which are underestimated as a result of the noise correlation introduced by the stacking or resampling process. To estimate this factor, we also performed stacks on the native WIRCam grid (and original pixel-scale) with a nearest-neighbour technique to preserve the white-noise nature in the final images. When we compared the Ks uncertainties of the same sources, we found that a factor 1.5 needed to be applied to the error estimates with the megaCam grid. No masking other than the CFHTLenS masks needed to be applied to the WIRCam sample. The effective WIRCam Ks area, after applying the masks, drops from 27 deg2 to 22.4 deg2 (including W1 and W4 fields). The WIRCam number counts in the two fields are shown in Fig. 3 separately for stars and galaxies (see Sect. 3) and are compared with literature.

thumbnail Fig. 2

Colour-coded mean image quality (IQ) per WIRCam tile over the whole WIRCam survey (W1: top and W4: bottom). The layouts indicate the VIPERS regions (red layouts), the three VIDEO pointings (orange in W1), the UKIDSS-UDS (yellow in W1), and UKIDSS-DXS (orange in W4).

thumbnail Fig. 3

WIRCam Ks number counts for the galaxies (filled circles) and stars (open stars) in the W1 (red) and W4 (blue) regions. The dashed lines show the total number counts. The open dark symbols are a compilation from the literature (triangles: McCracken et al. 2012; pentagons: Jarvis et al. 2013; circles: UDS (DR8); squares: Quadri et al. 2007; stars: Bielby et al. 2012).

thumbnail Fig. 4

Comparison of the VIPERS K-band photometry with the Ultra-Deep UKIDSS field (top left), the VIDEO XMM2 field (bottom left), and the scatter distributions in three magnitude bins (right panels). The observed scatters are reported in the left panels as red circles, while the green solid lines show the mean magnitude vs. error behaviour of our VIPERS K band data after rescaling the original errors by 1.5 (see text). Larger dispersions are observed with VIDEO than with UDS because of the different depths between the two fields.

2.2.3. Comparison with deeper datasets

As shown in Fig. 2, we can use the existing deep NIR surveys, UKIDSS-Ultra Deep Survey (Lawrence et al. 2007, UDS) and VIDEO (Jarvis et al. 2013), to estimate the photometric accuracy, depth, and completeness of our Ks sample. UDS and VIDEO are significantly deeper than our dataset (K ~ 24.5 and 23.8 respectively). For both fields the relative astrometric accuracy with our sample is σ ≤ 0.09″ with systematic shifts of the same order. We adopted a maximal matching distance of 0.5″. To compare the fluxes, we used the SExtractor MAG_AUTO magnitudes for the VIDEO survey and the petrosian magnitudes for the UDS survey (which should be close to our own magnitudes). Figure 4 shows the magnitude differences as a function of magnitude (on the left) and the dispersions in three magnitude intervals (on the right) after correcting for the systematic shifts (KDEEP−KWIRCam ~ 0.06 and 0.10 mag for UDS and VIDEO, respectively). For both surveys the mean difference is stable and close to zero down to Ks ~ 22, confirming that no bias due to sky-background subtraction is present in our data. At all magnitudes, the dispersions are reasonably well fitted by a Gaussian distribution. We expect to reach σ ~ 0.3 mag (S/N ~ 3) near Ks ~ 22. The dispersions predicted with these external dataset are consistent with those estimated by SExtractor (after the 1.5 rescaling factor mentioned above).

thumbnail Fig. 5

Top panel: completeness (in %) of the WIRCam sources as a function of magnitude, based on the deep surveys UDS (blue) and VIDEO (red). The completeness is shown for WIRCam sources with various signal-to-noise ratio cuts (no cut: filled symbols; S/N> 3: dotted lines; S/N> 5: dashed lines). Bottom panel: completeness as a function of magnitude and colour (z−K), colour-coded from red (100%) to blue (0%) based on the VIDEO survey. The yellow region delineates the 50% completeness level. The dashed line contours show the source density spaced with logarithmic scale of 0.3 dex. At KAB ≤ 20.6, the WIRCam sample is close to 100% completeness and the colour variations are due to small numbers.

Because we used the gri−χ2 images for the detection, our completeness is not directly related to the background noise of the WIRCam images. To estimate the completeness, we used all the sources detected in the UDS and VIDEO images and measured the fraction of them detected in our optical-based catalogue. In Fig. 5 (top panel) we show the completeness for the UDS (circles) and the VIDEO (squares) surveys as a function of magnitude. The solid lines and filled points refer to all the WIRCam sources irrespective of their signal-to-noise ratio (S/N). Identical results are obtained in both fields, which shows that our catalogue detects more than 85% of the pure Ks-band selected surveys down to Ks ~ 22. If we restrict the detection to WIRCam sources with S/N> 3 and 5, the completeness drops slightly to 81% and 66% (based on the UDS survey), respectively, at KAB ~ 22. This confirms that our gri-based catalogue is almost complete down to the KAB ~ 22 mag.

We can investigate the nature of this incompleteness in more detail, which should preferentially reflect a bias against the reddest sources. To do so, we measured the completeness as a function of K magnitude and (z−K) colour for the VIDEO survey alone (which includes its own z-band photometry that reaches a depth z ~ 25.7 at 5σ). The bidimensional completeness is shown in Fig. 5 (bottom panel). The colour-coding reflects the completeness level, with yellow corresponding to a 50% completeness. Below KAB ~ 20.6, the catalogue is complete regardless of (z−K) colour. At fainter K sources, the completeness of the reddest sources decreases gradually. For this reason, any statistical analysis such as luminosity functions or stellar mass functions, based on a K selection, should apply a weight reflecting this bidimensional completeness map.

2.3. UV photometry

2.3.1. Observations

Launched in 2005, the GALEX satellite (Martin et al. 2005) has explored the ultraviolet sky in FUV (135−175 nm) and NUV (170−275 nm) passbands (Morrissey et al. 2005) and performed all-sky medium- and deep-imaging surveys. The UV continuum is a direct indicator (except for the dust) of the instantaneous SFR. To assess the continuum of high redshift galaxies, we here only considered the observations from the Deep Imaging Survey (DIS, with Texp ≥ 30 ks). All the GALEX pointings are shown in Fig. 1 as blue (FUV) and cyan (NUV) circles. To complete the coverage of the VIPERS-W1 field in the NUV channel (after the shut-off of the FUV channel), we observed new pointings in the western and eastern parts of the field with ~100 h of discretionary time. Only the GALEX PanStarr fields, centred on the VVDS-22hr region, are available in the W4 field, with a small overlap with the VIPERS-W4 area. All the GALEX pointings and their respective integration times are given in Table 1. The total area observed with GALEX (W1 and W4) is ~7.8 and ~22 deg2 in the FUV and NUV bands.

Table 1

GALEX fields with integration times and central positions.

2.3.2. UV photometric extraction

The data were reduced with the standard GALEX pipeline. In the specific case of the DIS observations, the large PSF (FWHM ~ 5″) affects the extraction and photometry of faint UV sources because sources are confused (Xu et al. 2005). As an alternative to the source extraction of the GALEX pipeline (based on SExtractor software), we developed a dedicated code to perform the UV photometry, EMphot (Guillaume et al. 2005; Conseil et al. 2011). EMphot uses a Bayesian approach with optical priors based on the CFHTLS (T0007) u∗-selected sources. A full description of the code and extensive simulations will be given in a forthcoming paper; we outline the main steps below.

We generate a simulated GALEX image combining all the optical priors with a relative flux contribution that must be estimated. The priors can either be considered as a simple Dirac function or as an extended 2D profile extracted from the u∗-band image (i.e., stamps), which is what we adopted here. The formalism is the following: each observed value of the GALEX pixel (xi) is considered as a sample of a random variable Xi with the expected value being μi = E { Xi }. The value μi at pixel xi is the contribution of all the input optical priors around it and the sky background. It can be defined as 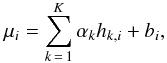(2)where bi is the background level value, hk,i = ∑ jok,jfi−j is the sum of all the objects, ok, convolved by the GALEX PSF, f. The function hk,i is normalised to unity and a set of scaling factor, αk, is applied to each prior k.

Here, we considered that the variable Xi follows a Poisson statistic: .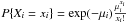

To estimate the αk values, Guillaume et al. (2005) introduced the expectation maximisation scheme (EM, see Horiuchi et al. 2001), which leads to the iterative process 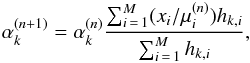(3)where 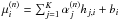. The E step compares the data image xi to the projection 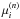of the 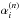estimates. The result is introduced in the M step as the corrective ratio needed for the new set of 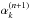estimates. Although the global system may take very many iterations to converge, we found that 100 iterations is sufficient to obtain stable αk values for the main contributors, while priors with negligible values may oscillate. To estimate the error of object k, we empirically quantify the variance σk, by the rms under the object’s area of the residual (best-fit model subtracted from the observed image) as 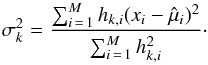(4)We find that this estimate is consistent with the errors obtained from simulations.

We tested the EM photometric technique by adding multiple sets of simulated sources inside the observed GALEX images. In Fig. 6 we show the flux ratio between the EM fluxes and the simulated fluxes as a function of magnitude. The EM algorithm allows us to derive accurate UV fluxes down to NUV ~ 25 with a S/N ≥ 5. This is consistent with the theoretical estimate of the S/N inside the PSF aperture and the measured background level. We observe a negligible mean bias (red dashed line) down to NUV ~ 26, and its behaviour can be reproduced by a small residual background offset (magenta dot-dashed line).

thumbnail Fig. 6

Comparison of the EM vs. simulated fluxes as a function of simulated magnitudes. The dotted lines show the 1σ error, the red dashed line the mean bias. The magenta dot-dashed line reflects the effect of a small background bias on the flux ratio.

In Fig. 7 we show the NUV number counts from the EM software (black line) and the GALEX pipeline (green line) in one GALEX field. First, the GALEX pipeline shows an excess of bright sources (22 ≤ NUV ≤ 25). This is explained by the deblending of the neighbouring objects in the EM technique, which leads to systematically lower fluxes for EM. This is illustrated by comparing the number counts for the same objects as a function of GALEX (red line) and EM (blue line) magnitudes. Second, the GALEX number count drops shortly after NUV ~ 24 (red line), while EM counts continue to increase down to NUV ~ 25. This is indeed expected because we used optical priors and because the sources were deblended.

thumbnail Fig. 7

NUV number counts vs. magnitude in one GALEX field. The full EM photometric catalogue is shown as a solid black line and the EM sources matched to the GALEX pipeline sources as a solid blue line. The GALEX pipeline counts in the same area (and matched to EM sources) are shown as red and green dot-dashed lines.

To conclude, the EMphot algorithm allows us to address the problem that is related to the GALEX confusion. It provides a significative improvement with respect to the GALEX pipeline photometry for the deep fields and allows us to make full use of the GALEX photometry down to the nominal S/N of the observations. The GALEX number counts with EM photometry in the FUV and NUV channels are shown in Fig. 8 separately for stars and galaxies (see Sect. 3), and they are compared with the literature.

thumbnail Fig. 8

GALEX number counts in W1 (red symbols) and W4 (blue symbols) regions for the galaxies (filled circles) and the stellar population (open stars). The FUV magnitudes are shifted by +4 mag. Open black symbols are from the literature (triangles: Hoversten et al. 2009; circles and pentagons: Gardner et al. 2000; squares: Xu et al. 2005).

3. Classification of stars, QSOs, and galaxies

To minimise the misclassification of stars and galaxies in the final samples, special care must be applied to the star-galaxy separation. For instance in the W4 field, near the Galactic plane, the VVDS survey (based on a pure i< 22.5 target selection) found more than 32% of the spectroscopic sources to be stars (Garilli et al. 2008). To distinguish between stars and galaxies without damaging the completeness of our sample, we performed a classification based on three different diagnostics:

  • We used the maximum surface bright-ness versus magnitude (hereafterμmax−mobs) plane where bright point-like sources are clearly separated from galaxies (see Bardeau et al. 2005; Leauthaud et al. 2007), as shown in Fig. 9. The method relies on the fact that the light distribution of a point-like source and its magnitude are proportional. Moreover, it allows us to detect objects with light distributions that are more peaked than the point-spread function (PSF), which are generally fake detections (gray dots) and then removed. In the inset panel of Fig. 9, one can see that the μmax selection (yellow dots), noted Sμ, is only relevant up to a certain surface brightness limit, 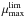. The limit depends on the seeing, thus varies from tile to tile and with the considered passband. We performed the μmax selection on the g,r,i passbands and imposed that a source is classified as compact if it belongs to Sμ in at least two bands.

  • We used the SED fitting technique to compare the reduced χ2 obtained with the galaxy templates described in Sect. 4 and a representative stellar library from Pickles (1998). An object belongs to Sχ if 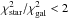, where the factor 2 has been set to catch 90% of the point-like objects.

  • To minimise the loss of galaxies in the above steps, we finally used the (g−z) vs. (z−K) colour diagram (equivalent to the BzK plane of Daddi et al. 2004) when available to isolate the stellar sequence, noted SBzK.

We adopted the latter as a sinequanon condition to be a star, which leads to these final combinations for a source to be classified as star: (5)In the bright point-like source domain (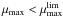), we define as QSO the objects lying on the galaxy side of the BzK diagram (corresponding to Sμ ∩ ! SBzK). Dominated by their nucleus, the emission of those AGNs is currently poorly linked to their stellar mass. They represent less than 0.5% of the global sample. By using 1119 spectroscopically confirmed AGNs from the SDSS and VIPERS surveys, we confirmed that our photometric selection of QSOs is able to catch 65% of them, without losing a single galaxy.

All the objects that were not defined as stars or QSO were then considered as galaxies. We verified on a sample of 1241 spectroscopically confirmed stars that we thereby catch 97% of them, while we keep more than 99% of our spectroscopic galaxy sample. With this selection we finally found and removed ~8% and ~19% of stars at Ks< 22 for W1 and W4, respectively (in the unmasked area). The star number counts in the WIRCam and GALEX (FUV, NUV) passbands are shown separately for the W1 and W4 fields in Figs. 3 and 8, respectively. The density of stars in W4 is higher than in W1 at all wavelengths and reaches almost a factor 3 in Ks band.

Finally, in Fig. 10 we show the star and galaxy distributions in the BzK colour diagram for the two fields separately. The low-density contours of the galaxy distributions can overlap the stellar locus. Our photometric sample of QSOs (red and blue stars) is also compared with spectroscopically confirmed AGNs (orange dots) from the SDSS and VIPERS surveys.

thumbnail Fig. 9

Photometric classification between point-like and extended sources in the μmax−mobs vs. mobs plane (for one tile of the CFHTLS in the i-band). The dashed line represents our selection of point-like sources (Sμ, yellow dots). All objects lying below the solid line (gray dots) are considered as false detections.

thumbnail Fig. 10

Distribution of galaxies, stars, and QSOs in the (z−K) vs. (g−z) colour diagram. Density levels are in logarithmic scale (Δ = 0.3 dex) for galaxies (solid lines in W1 and W4 fields shown blue and red, respectively) and stars (dashed lines in green and orange). Objects from our QSO samples are shown as open stars (blue: W1; red: W4), while the SDSS/VIPERS AGN sample is shown as orange dots. The solid black lines delineate the high-redshift BzK populations (star-forming and passive galaxies).

4. Photometric redshifts

4.1. Photometric redshift measurement

Thanks to the enlarged wavelength coverage, we can estimate new photometric redshifts for the T0007 CFHTLS sources in the VIPERS regions, which also benefit from the large spectroscopic coverage for calibration purposes. The photometric redshifts were computed with the SED-fitting code Le Phare (Arnouts et al. 2002; Ilbert et al. 2006). We adopted the galaxy SED templates used by Ilbert et al. (2009) (31 empirical templates from Polletta et al. 2007 and 12 star-forming templates from Bruzual and Charlot models, Bruzual & Charlot 2003). They were modified to better fit the photometry discussed here. We used the large VIPERS spectroscopic redshift sample (see Coupon et al. 2015, for details). The extinction was added as a free parameter with a reddening excess E(B−V) < 0.3 following different laws: Prevot et al. (1984), Calzetti et al. (2000), plus a dusty Calzetti curve including a bump at 2175 Å. No extinction was allowed for SEDs redder than Sc. The Prevot et al. (1984) extinction law was allowed for templates redder than SB3 templates (see Ilbert et al. 2009) and Calzetti et al. (2000) for bluer ones. Finally, the systematic disagreement between the photometry and the template library was corrected by Le Phare according to the method described by Ilbert et al. (2006). In brief, the code tracks a systematic shift between the predicted and the observed magnitudes in each band at known redshifts. Since our observation area is divided into 54 CFHTLS tiles of ≲ 1 deg2 with photometry varying from tile to tile, we performed a tile-by-tile colour optimisation. We used the median offset over all the tiles when there were not enough available galaxies with spectroscopic redshift in the tile (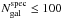), which was the case in 12 tiles.

4.2. Comparison with the spectroscopic sample

Our WIRCam survey has been designed to cover the VIMOS Public Extragalactic Survey (VIPERS; Guzzo et al. 2014) carried out with the VIMOS8 spectrograph. We used the first public data release (PDR1) described in Garilli et al. (2014), which provides a i< 22.5-limited sample of ~ 57 000 spectroscopic redshifts at 0.5 <z< 1.29 with high precision (σv = 140 km s-1, which corresponds to 0.0005(1 + z)).

The spectroscopic sample was complemented with other surveys listed in Table 2. We outline their characteristics in this table. We used the VIMOS Very Deep Survey (VVDS, Le Fèvre et al. 2013) “Wide” (i < 22.5) in W4 and “Deep” (i< 24) in W1, spanning the redshift ranges 0.05 <z< 2 and 0.05 <z< 5 respectively. Only a fraction of the VVDS survey intersects our WIRCam coverage. The deep part of the VVDS survey allowed us to test the photometric redshifts in a fainter regime and at higher redshift. For the same purpose, we also included the K< 23 limited UKIDSS spectroscopic Ultra Deep Survey (UDSz, Bradshaw et al. 2013; McLure et al. 2013), which has redshifts in 0 <z< 4.8 obtained with the VIMOS and FORS2 VLT spectrographs. We used redshifts from the Baryon Oscillation Spectroscopic Survey (BOSS, Dawson et al. 2013) when available. BOSS is a bright-limited (i < 19.9) spectroscopic survey from the Sloan Digital Sky Survey (SDSS), providing redshifts up to z = 0.7 in the entire region of our Ks-coverage. Finally, we included the most secure redshifts from the PRIsm MUlti-object Survey (PRIMUS; Coil et al. 2011). This sample is based on low-resolution spectra (λ/ Δλ ~ 40) and is limited to i ~ 23 (see Cool et al. 2013, for more details).

Table 2

Characteristics of the spectroscopic redshift sample.

We selected only the most secure spectroscopic redshifts, which means confidence levels above 95% for high-resolution surveys:

  • flags 3 and 4 with VIMOS (VIPERS, VVDS, UDSz);

  • flags A and B with FORS2 (UDSz);

  • z-warning 0 in BOSS;

and σ < 0.005 (8% of outliers with δz/ (1 + z) > 5σ) for PRIMUS flag-4 redshifts. When they were available, the redshift measurements from VIPERS were used. Otherwise, the measurements from the deepest high-resolution spectra were favoured.

In total, we collected a sample of ~ 51 396 high-quality spectroscopic redshifts to calibrate and measure the accuracy of our photometric redshifts over the entire area of the survey.

thumbnail Fig. 11

Comparison of our photometric redshifts with the VVDS, VIPERS, PRIMUS, and BOSS most secure spectroscopic redshifts, for galaxies with K ≤ 22 (top panels) and NUV ≤ 25 (bottom panels). We report the dispersion (σNMAD) by combining all the surveys, while the catastrophic fractions (fcat defined as | Δz | /(1 + zs) > 0.15) are given for all surveys but PRIMUS (black value), which is shown separately (gray value). The observed distributions of photometric errors are compared to a Gaussian distribution with the same σ (right panels).

Figure 11 shows the comparisons between our photometric redshifts and the spectroscopic redshifts for the K ≤ 22 (top panels) and NUV ≤ 25 (bottom panels) selected samples. By using the NMAD to define the scatter10, we find σΔz/ (1 + z) ≲ 0.03 for both samples with an outlier rate11η ~ 1%. The photometric redshift errors are well described by a Gaussian distribution with the same σ for the two samples, as illustrated in the right panels of Fig. 11. As reported in Table 2, we recall that this comparison is dominated by spectroscopic galaxies with i ≤ 22.5. In Fig. 12 we show the σ (left axis, open symbols and solid lines) and the catastrophic fraction rate (right axis, solid symbols and dashed lines) as a function of magnitude (i : top panel; Ks: middle panel; NUV: bottom panel) for the W1 and W4 fields. As expected, a slight deterioration of the accuracy at i > 22 is visible.

It is interesting to note that when the PRIMUS redshifts are included in our statistics, we observe a strong increase in the average number of catastrophic failures (by a factor 2, 3) in the NUV − and Ks -selected samples (as reported in Fig. 11, gray values). We show separately the catastrophic fraction for PRIMUS spectra in Fig. 12 (gray filled triangles). A strong increase is observed toward the faint magnitudes, while we do not observe this behaviour for the high-resolution spectroscopic surveys (SDSS, VVDS, VIPERS, and UDSz). This could suggest that the PRIMUS redshift flags are too optimistic regarding the quality of the spectra and redshift measurements at fainter magnitudes12.

Nevertheless, the large amount of high-resolution spectroscopic redshifts available in our area allows us to reliably quantify the quality of our photometric redshifts. As shown in Fig. 12, the dispersion is always below σ ~ 0.04 and the catastrophic fraction (excluding PRIMUS) always below 2% over the entire magnitude range at i ≤ 23 (both down to Ks ~ 22 and NUV ~ 25). However, we recall that values quoted in Figs. 11 and 12 do not account for the selection bias introduced by the spectroscopic sample against blue or red galaxies when moving toward fainter NUV or K magnitudes, respectively.

thumbnail Fig. 12

Comparison of the dispersion (σNMAD) as a function of magnitude (top panel: i; middle panel: Ks; bottom panel: NUV). The σNMAD for the W1 (black circles) and W4 (red squares) fields correspond to the open symbols and solid lines and refer to the left y-axis. The fraction of catastrophic redshifts are reported as field symbols and dashed lines and refer to the right y-axis (%). The PRIMUS spectroscopic sample in W1 field is shown separately (gray triangles).

4.3. Comparison with the VIDEO photometric redshifts

Half of the three VISTA pointings from the VIDEO survey (Jarvis et al. 2013) overlaps with our WIRCam observations (see Fig. 2). We can compare the photometric redshifts derived from the deep VIDEO Y,J,H,K data (reaching K ~ 23.5) with our WIRCam photometric redshifts to partially remove the spectroscopic bias discussed above.

We first matched the full CFHTLS-T0007 optical catalogue with the NIR VIDEO photometry (within a search radius of 0.5″), to which we added the GALEX photometry. We derived the photometric redshifts for this combined catalogue (GALEX-CFHTLS-VIDEO) using the same recipe as described above.

In Figs. 13 and 14 we compare our original photometric redshifts (referred to as zwircam) with VIDEO photometric redshifts (referred to as zvista) for a K- (KVISTA ≤ 23.5) and NUV- (NUV ≤ 25.5) selected sample. In both figures we split the data into a K-bright (KVISTA ≤ 22) and a K-faint (22 ≤ KVISTA ≤ 23.5) sample. In the left panels, we show the one-to-one comparison of the photometric redshifts for the K-bright samples (red dots), while the K-faint samples are shown with density contours spaced in logarithmic scale of 1 dex (black lines). In the right panels we show the cumulative distributions of the errors (Δz/ (1 + z)), and we report the number of sources in each selection, the dispersions, and the catastrophic fractions.

For the K-selected sample in Fig. 13, our photometric redshifts are consistent with zvista (σ ~ 0.025, η ~ 4%) up to z ~ 3 at bright magnitudes. The zwircam tend to overestimate the redshifts in between 1 <zvista < 2. In the two fainter magnitude bins, the photo-z remains unbiased up to z ~ 3, but the dispersions and the catastrophic fractions quickly increase. This is expected since our photometric redshifts are only constrained by the optical magnitudes of the CFHTLS.

For the NUV selected sample in Fig. 14, the photometric redshifts are in excellent agreement up to redshift z ~ 1.5. For the bright subsample, KVISTA ≤ 22 (red dots), we observe a very small dispersion (σ ~ 0.015) and a negligible fraction of outliers. This accuracy holds down to the magnitude range 22 ≤ KVISTA ≤ 23. At fainter magnitudes, KVISTA ≥ 23, our photometric redshifts starts to become slightly worse and has a small bias Δz/ (1 + z) ≤ 0.02. This shows that for our NUV-selected samples, we have a good confidence level in the photometric redshifts derived with WIRCam.

thumbnail Fig. 13

Comparison of the photometric redshifts measured using either WIRCam K band (zwircam) or YJHK photometry from VISTA (zvista) for galaxies with KVISTA ≤ 23.5. The left panel shows the comparison zwircam vs. zvista for KVISTA < 22 (red dots), while the density contours spaced in logarithmic scale of 1 dex are for the faint sample, 22 < KVISTA < 23.5. The right panel shows the cumulative distributions of the difference (Δz/ (1 + zvista)) split into three K-band subsamples (KVISTA ≤ 22: red line; 22 < KVISTA < 23: green line; 23 < KVISTA < 23.5: red line). We also report the dispersions (σ), the fractions of catastrophic sources (in %), and the number of sources used.

thumbnail Fig. 14

Same as Fig. 13 for a NUV-selected sample with NUV ≤ 25.5 and also split into KVISTA subsamples.

thumbnail Fig. 15

Differential number counts of star-forming (top) and passive (bottom) BzK galaxies in the W1 and W4 fields. We compare with deeper observations in CFHTLS deep fields (open squares, Arcila-Osejo & Sawicki 2013) and COSMOS (open triangles, McCracken et al. 2010) and model predictions (dashed lines, Henriques et al. 2013) The inset panels show the photometric redshift distributions with KAB ≤ 22.

5. Discussion

5.1. BzK selection

The large area covered by our K-band survey and the optical depth of the CFHTLS Wide data makes our sample unique to select a large sample of bright and massive galaxies at high redshift, z ≥ 1.4, with the BzK colour selection (Daddi et al. 2004). We adopted the criteria from Arcila-Osejo & Sawicki (2013), who adjusted the selection for the CFHTLS and WIRCam K-band photometry. This colour selection is shown in Fig. 10 (solid lines) and provides a sample of ~100 000 star-forming and ~7800 passive BzKs. The differential number counts are shown in Fig. 15 for the star-forming (top panel) and passive (bottom panel) galaxies down to K ~ 22. The error bars are from Poisson statistics. Our results are compared with the deep NIR data in the four CFHTLS deep fields (only the average of the four fields is shown, Arcila-Osejo & Sawicki 2013) and in the COSMOS field (McCracken et al. 2010). Our results provide robust constraints at the bright end. For the star-forming BzKs, we agree well with previous works in the overlapping range and down to our limit, Ks ~ 22. For the passive BzKs our result agrees with others at the bright end, but we observe a drop at Ks ≥ 20.7. Because of the optical griχ2 image detection, our data suffer from incompleteness against the reddest population. As illustrated in Fig. 5, the 50% completeness limit corresponds to (z−Ks) ~ 3 at Ks ~ 21 and drops to (z−Ks) ~ 2.5 at Ks ~22 (corresponding to the passive BzK colour threshold). At high redshift, z ≥ 1.4, our native optical selection introduced a bias against those passive galaxies, which explains the observed drop in density of the passive BzK population at Ks ≥ 20.7.

In the insets of each panel of Fig. 15, we show the photometric redshift distributions for the two populations in the two fields. The vast majority of BzKs is observed at zphot ≥ 1.2, as expected from the original work by Daddi et al. (2004), and with a negligible fraction of outliers at low redshift. The star-forming BzKs show a large spread in redshift, 1 ≤ z ≤ 3, with a peak around z ~ 1.5. Passive BzKs also peak at z ~ 1.5, but show a narrower distribution (1.2 ≤ z ≤ 1.8).

We compared the observations with the semi-analytical model of Henriques et al. (2013), based on the Millenium simulations, which has been tuned to reproduce the stellar mass functions at all redshifts. We defined our own colour criteria in the simulations to best distinguish the galaxies with high and low specific SFR (sSFR) at z ≥ 1.4. We adopted the following criterion: (z−K)−0.9(g−z) ≥ 0.7 for active and (z−K)−0.9(g−z) ≥ 0.7 and (z−K) ≥ 2.55 for passive galaxies. The predicted number densities as a function of magnitude are shown in Fig. 15. The SAM simulation shows similar behaviours as the observed ones for both the star-forming and the passive galaxy populations. The passive population agrees well over the whole magnitude range. For the star-forming population, the simulation over-predicts the density by at least a factor two at magnitudes fainter than KAB ~ 20. This is highly significant in view of the uncertainties in the observations. The redshift distributions in the simulation are concentrated in the redshift range 1 ≤ z ≤ 2, and the redshift peaks are at slightly lower redshifts than our BzK photo-zs for both the active and the passive BzK populations. This difference can be partially due to the photo-z bias affecting this redshift range, which are spread toward higher redshift as discussed in Sect. 4.3.

thumbnail Fig. 16

Illustration of the galaxy morphology in the NUVrK diagram for galaxies with z ≤ 0.25. Galaxies are split into seven categories shown in the top left inset, and background enlarged points are colour-coded according to their categories. Only the largest galaxies (with semi-major axis A > 50 pixels) are shown. The lower right inset shows the behaviour of the sSFR (log-scale colour-coded).

5.2. Galaxy morphology in the NUVrK diagram

The star-forming and quiescent galaxies form a bimodal distribution in rest-frame colours or D4000 break. However, the separation between the two populations is not straightforward because of the presence of dust obscured star-forming galaxies when a single colour diagnostic is used. Williams et al. (2010) broke this degeneracy by using a bi-colour (U−V) vs. (V−J) diagram (UVJ), which better separates the passive red galaxies from the dusty red galaxies. Arnouts et al. (2013) adopted a similar diagram (NUV−r) vs. (r−K), (NUVrK) to optimize the role of the current SFR and the dust obscuration.

In this section we use the high image quality of the CFHTLS and the large volume to investigate the morphological appearance of well-resolved low-z galaxies according to their location in the NUVrK diagram. The full sample of galaxies with z ≤ 0.25 was split into seven broad categories shown by different colours in the top left panel of Fig. 3, while the sSFR is colour-coded in the bottom right panel. In the central part of Fig. 3, we show the a set of gri colour stamps (generated with the STIFF software; Bertin 2011) of the largest galaxies (with a major axis A ≥ 50 pixels). They are randomly placed within subregions (splitting each category into four subcategories).

We are indeed limited in the number of galaxies that we can show in this diagram, and we favoured the most attractive galaxies. However, we generated several realisations of the diagram and found that it does not change the points we address below on the morphological appearances within the NUVrK diagram:

  • Star-forming galaxies fall in the categories I to IV. The bluestgalaxies (category I−II) have spiral or irregular morphologies and often show clumps of star formation and more disturbed disks. They have high specific SFRs that can reflect a high gas fraction. For the oldest population (redder (r−K) colour, category II−III) we observe a larger portion of grand-design spiral galaxies. They are more massive and have a lower sSFR. Their morphologies suggest that these spiral galaxies are more settled and more stable than their lowest mass counterparts, which is consistent with the kinematic analysis of spiral galaxies from Kassin et al. (2012).

  • Category IV (purple) reveals a specific population of edge-on galaxies. This confirms the claim of Arnouts et al. (2013) that only highly inclined disk galaxies can produce such extreme infrared excess (IRX) and red (r−K) colour (see also Patel et al. 2011, for a similar conclusion from UVJ diagram).

  • Category V (yellow) shows a variety of morphologies. According to their decreasing sSFR, it represents massive galaxies most probably transiting from the star-forming to the quiescent populations. We observe a significant fraction of mergers and post-mergers with extended tidal debris, consistent with the scenario of Hopkins et al. (2006), where mergers trigger both the quenching through AGN feedback and the morphological transformation. Conversely, some of these interaction or merger systems can also be the result of gas accreted onto red galaxies from a minor gas-rich merger, which triggers new star formation activity. This rejuvenation process is observed in the local Universe (Salim & Rich 2010; Thomas et al. 2010) and also predicted in hydrodynamical simulations (Trayford et al. 2016). We also observe several spiral galaxies with bars and rings within the disks. This could point us toward the importance of secular evolution in the star formation regulation and the disk instability leading to a morphological change. Sheth et al. (2008) showed that most massive spiral galaxies have a higher fraction of bars, associated with a bulge and have redder colours, consistent with this result.

  • Category VI (red) is exclusively dominated by massive S0 and elliptical morphologies (e.g., Bell 2008). At z ~ 1, Ilbert et al. (2010) observed a significant fraction of quiescent galaxies with disk-dominated morphologies (see also Bundy et al. 2010), but such a population is not observed in our local sample.

  • Category VII (orange) shows a small population of galaxies with blue (r−K) colour and (NUV−r) redder than the star-forming categories. In the companion paper (Moutard et al. 2016), we interpret this region through the quenching channel that characterises young (blue (r−K) colour) low-mass galaxies. Evolutionary tracks in the NUVrK diagram showed that their quenching should be faster than 0.5 Gyr. Environmental quenching such as harassment or ram-pressure stripping can be consistent with this timescale, but we exclusively observe elliptical morphology for this population (with a more compact effective radius than elliptical in category VI). The environmental quenching mechanisms discussed above do not explain the morphological transformation into elliptical. It may in turn favour a rapid morphological transformation by merging for these low-mass galaxies (Schawinski et al. 2014).

As shown in this section, the UV-optical-NIR colours combined with the morphological information provides a good basis for studying star formation activity, evolutionary timescales, and quenching processes of local galaxies. Our description is only qualitative, and we postpone a more detailed analysis of the few hundred galaxies for which detailed morphological information can be measured to a future work (Baillard et al. 2011).

6. Conclusions

We presented the multi-wavelength observations collected in the VIPERS region within the W1 and W4 fields of the CFHTLS. The NIR observations were adjusted to provide Ks-band photometry of the VIPERS spectroscopic sources (iAB ≤ 22.5). By comparing them with external deep data, we estimated the depth of our WIRCam to be Ks ~ 22 at 3σ. We combined this dataset with GALEX observations. Because of the large GALEX PSF, we developed a specific procedure to derive GALEX photometry in crowded fields based on u-band optical priors. We estimated the reliability of the method with simulations and found that we reach robust flux measurement down to NUV ~ 25 at 5σ. With this multi-wavelength catalogue (GALEX, optical, Ks) we estimated new reliable photometric redshifts for more than one million galaxies at z ≤ 1.5, with σz ≤ 0.04 and η ≤ 2% down to i ~ 23. We also pushed our analysis at higher redshift with the BzK galaxy populations. Despite our native gri detection method, we showed that we can assemble a complete sample of BzK star-forming galaxies down to Ks ~ 22 and BzK passive galaxies down to Ks ~ 20.7,

The deep multi-wavelength dataset combined with the unprecedented large area makes this sample perfectly suited for statistical analysis and constrains the rare massive galaxies. In the companion paper (Moutard et al. 2016), we use this sample to determine the massive end of the GSMF for quiescent and star-forming galaxies based on photometric redshifts at 0.2 ≤ z ≤ 1.5 with high accuracy, while Davidzon et al. (2013) performed a similar analysis in between 0.5 ≤ z ≤ 1.3 with the VIPERS spectroscopic sample. The main feature of the VIPERS Multi-Lambda Survey is its ability to investigate the galaxy properties as a function of environment at high redshift. Davidzon et al. (2016) use the VIPERS spectroscopic redshifts to investigate the changes in the GSMFs in high and low density regions at z ~ 1 while Coupon et al. (2015) use photometric redshifts combined with galaxy clustering and galaxy-galaxy lensing to provide new constraints on the relation between galaxies and their host dark matter halos. In a forthcoming work, we will reconstruct the cosmic web from the complete VIPERS spectroscopic sample and investigate how galaxy properties change in dependance on their location within the cosmic web.

We released the photometry of the VIPERS Multi Lambda Survey over its 24 deg2. The images, catalogues, and photometric redshifts for ~ 1.5 million [(NUV ≤ 25) ∪ (K ≤ 22)] sources are available online13.

1

The galaxy shape is obtained with the CFHTLenS catalogues.

8

Please refer to Le Fèvre et al. (2003) for more details.

9

The targets were preselected in colour space to enhance the probability of observing galaxies at z> 0.5. This technique results in ~ 40% sampling rate with a single pass of VIMOS.

10

σΔz/ (1 + z) = 1.48 median(|zspec−zphot|/(1 + zspec)).

11

η is the percentage of galaxies with Δz/ (1 + z) > 0.15.

12

We recall that the average redshift success of PRIMUS declines to 45% at i ~ 22.5 (see Cool et al. 2013).

Acknowledgments

We gratefully thank C. Moreau from CeSAM/LAM for her major contribution to the building of the database. We would like to thank M. Jarvis and B. Haeussler for giving us access to the VIDEO dataset in the XMMLSS field. We also wish to thank R. Overzier for providing us semi-analytical simulations, and L. Arcila-Osejo for helping us with the BzK compilations. This research is in part supported by the Centre National d’Etudes Spatiales (CNES) and the Centre National de la Recherche Scientifique (CNRS) of France, and the ANR Spin(e) project (ANR-13-BS05-0005, http://cosmicorigin.org). L.G. acknowledges support of the European Research Council through the Darklight ERC Advanced Research Grant (# 291521). This paper is based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, and with WIRCam, a joint project of CFHT, Taiwan, Korea, Canada and France, at the Canada-France-Hawaii Telescope (CFHT).The CFHT is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX available at the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. We thank the TERAPIX team for the reduction of all the WIRCAM images and the preparation of the catalogues matching with the T0007 CFHTLS data release. This paper is based on observations made with the Galaxy Evolution Explorer (GALEX). GALEX is a NASA Small Explorer, whose mission was developed in cooperation with the Centre National d’Études Spatiales (CNES) of France and the Korean Ministry of Science and Technology. GALEX is operated for NASA by the California Institute of Technology under NASA contract NAS5-98034. This paper uses data from the VIMOS Public Extragalactic Redshift Survey (VIPERS). VIPERS has been performed using the ESO Very Large Telescope, under the “Large Programme” 182.A-0886. The participating institutions and funding agencies are listed at http://vipers.inaf.it. This paper uses data from the VIMOS VLT Deep Survey (VVDS) obtained at the ESO Very Large Telescope under programs 070.A-9007 and 177.A-0837, and made available at the CeSAM data center, Laboratoire d’Astrophysique de Marseille, France. Funding for PRIMUS is provided by NSF (AST-0607701, AST-0908246, AST-0908442, AST-0908354) and NASA (Spitzer-1356708, 08-ADP08-0019, NNX09AC95G). Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The Participating Institutions of the SDSS-III Collaboration are listed at http://www.sdss3.org/

References

  1. Aragón-Calvo, M. A., van de Weygaert, R., & Jones, B. J. T. 2010, MNRAS, 408, 2163 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arcila-Osejo, L., & Sawicki, M. 2013, MNRAS, 435, 845 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnouts, S., Moscardini, L., Vanzella, E., et al. 2002, MNRAS, 329, 355 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arnouts, S., Le Floc’h, E., Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Baillard, A., Bertin, E., de Lapparent, V., et al. 2011, A&A, 532, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bardeau, S., Kneib, J.-P., Czoske, O., et al. 2005, A&A, 434, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bell, E. F. 2008, ApJ, 682, 355 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, ASP Conf. Ser., 351, 112 [NASA ADS] [Google Scholar]
  9. Bertin, E. 2011, Astrophysics Source Code Library [record ascl:1110.006] [Google Scholar]
  10. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bouché, N., Dekel, A., Genzel, R., et al. 2010, ApJ, 718, 1001 [NASA ADS] [CrossRef] [Google Scholar]
  13. Boulade, O., Charlot, X., Abbon, P., et al. 2000, in SPIE Conf. Ser. 4008, eds. M. Iye, & A. F. Moorwood, 657 [Google Scholar]
  14. Bradshaw, E. J., Almaini, O., Hartley, W. G., et al. 2013, MNRAS, 433, 194 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bundy, K., Scarlata, C., Carollo, C. M., et al. 2010, ApJ, 719, 1969 [NASA ADS] [CrossRef] [Google Scholar]
  17. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cattaneo, A., Dekel, A., Devriendt, J., Guiderdoni, B., & Blaizot, J. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  20. Codis, S., Pichon, C., & Pogosyan, D. 2015, MNRAS, 452, 3369 [Google Scholar]
  21. Coil, A. L., Blanton, M. R., Burles, S. M., et al. 2011, ApJ, 741, 8 [NASA ADS] [CrossRef] [Google Scholar]
  22. Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
  23. Conseil, S., Vibert, D., Amouts, S., et al. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 107 [Google Scholar]
  24. Cool, R. J., Moustakas, J., Blanton, M. R., et al. 2013, ApJ, 767, 118 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cooper, M. C., Newman, J. A., Weiner, B. J., et al. 2008, MNRAS, 383, 1058 [Google Scholar]
  26. Coupon, J., Arnouts, S., van Waerbeke, L., et al. 2015, MNRAS, 449, 1352 [NASA ADS] [CrossRef] [Google Scholar]
  27. Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Daddi, E., Cimatti, A., Renzini, A., et al. 2004, ApJ, 617, 746 [NASA ADS] [CrossRef] [Google Scholar]
  29. Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, 558, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Davidzon, I., Cucciati, O., Bolzonella, M., et al. 2016, A&A, 586, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
  32. de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Erben, T., Hildebrandt, H., Miller, L., et al. 2013, MNRAS, 433, 2545 [NASA ADS] [CrossRef] [Google Scholar]
  34. Farouki, R., & Shapiro, S. L. 1981, ApJ, 243, 32 [NASA ADS] [CrossRef] [Google Scholar]
  35. Furusawa, H., Kosugi, G., Akiyama, M., et al. 2008, ApJS, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gardner, J. P., Brown, T. M., & Ferguson, H. C. 2000, ApJ, 542, L79 [NASA ADS] [CrossRef] [Google Scholar]
  37. Garilli, B., Le Fèvre, O., Guzzo, L., et al. 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
  40. Guillaume, M., Llebaria, A., Aymeric, D., Arnouts, S., & Milliard, B. 2005, in Image Processing: Algorithms and Systems, Neural Networks and Machone Learning, eds. D. Astola, Egiazarian, Nasrabadi, & Rizvi, Proc. SPIE, 6064, 11 [Google Scholar]
  41. Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
  42. Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Haines, C. P., Gargiulo, A., & Merluzzi, P. 2008, MNRAS, 385, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  44. Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2013, MNRAS, 431, 3373 [NASA ADS] [CrossRef] [Google Scholar]
  45. Hildebrandt, H., Erben, T., Kuijken, K., et al. 2012, MNRAS, 421, 2355 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hopkins, P. F., Somerville, R. S., Hernquist, L., et al. 2006, ApJ, 652, 864 [NASA ADS] [CrossRef] [Google Scholar]
  47. Horiuchi, S., Kameno, S., & Ohishi, M. 2001, in Astronomical data analysis software and systems X, ASP Conf. Ser., 238, 529 [NASA ADS] [Google Scholar]
  48. Hoversten, E. A., Gronwall, C., Van den Berk, D. E., et al. 2009, ApJ, 705, 1462 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hudelot, P., Cuillandre, J.-C., Withington, K., et al. 2012, VizieR Online Data Catalog: II/317 [Google Scholar]
  50. Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
  53. Jarvis, M. J., Bonfield, D. G., Bruce, V. A., et al. 2013, MNRAS, 428, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kassin, S. A., Weiner, B. J., Faber, S. M., et al. 2012, ApJ, 758, 106 [NASA ADS] [CrossRef] [Google Scholar]
  55. Katz, N., Keres, D., Dave, R., & Weinberg, D. H. 2003, in The IGM/Galaxy Connection. The Distribution of Baryons at z = 0, eds. J. L. Rosenberg, & M. E. Putman, Astrophys. Space Sci. Libr., 281, 185 [Google Scholar]
  56. Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kovač, K., Lilly, S. J., Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kovač, K., Lilly, S. J., Knobel, C., et al. 2014, MNRAS, 438, 717 [NASA ADS] [CrossRef] [Google Scholar]
  60. Kron, R. G. 1980, ApJS, 43, 305 [NASA ADS] [CrossRef] [Google Scholar]
  61. Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
  62. Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  63. Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1670 [Google Scholar]
  64. Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Leauthaud, A., Massey, R., Kneib, J.-P., et al. 2007, ApJS, 172, 219 [NASA ADS] [CrossRef] [Google Scholar]
  67. Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
  68. Marmo, C., & Bertin, E. 2008, Astronomical Data Analysis Software and Systems, ASP Conf. Ser., 394, 619 [Google Scholar]
  69. Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
  70. Matsuoka, Y., & Kawara, K. 2010, MNRAS, 405, 100 [NASA ADS] [Google Scholar]
  71. McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [NASA ADS] [CrossRef] [Google Scholar]
  72. McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
  74. Morrissey, P., Schiminovich, D., Barlow, T. A., et al. 2005, ApJ, 619, L7 [NASA ADS] [CrossRef] [Google Scholar]
  75. Moutard, T., Arnouts, S., Ilbert, O., et al. 2016, A&A, 590, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
  77. Oke, J. B. 1974, ApJS, 27, 21 [NASA ADS] [CrossRef] [Google Scholar]
  78. Patel, S. G., Kelson, D. D., Holden, B. P., Franx, M., & Illingworth, G. D. 2011, ApJ, 735, 53 [NASA ADS] [CrossRef] [Google Scholar]
  79. Peng, Y.-J., Lilly, S., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
  80. Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
  81. Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
  82. Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
  83. Puget, P., Stadler, E., Doyon, R., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, SPIE Conf. Ser., 5492, 978 [Google Scholar]
  84. Quadri, R., Marchesini, D., van Dokkum, P., et al. 2007, AJ, 134, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  85. Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Salim, S., & Rich, R. M. 2010, ApJ, 714, L290 [NASA ADS] [CrossRef] [Google Scholar]
  87. Schawinski, K., Urry, C. M., Simmons, B. D., et al. 2014, MNRAS, 440, 889 [NASA ADS] [CrossRef] [Google Scholar]
  88. Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
  89. Scoville, N., Arnouts, S., Aussel, H., et al. 2013, ApJS, 206, 3 [NASA ADS] [CrossRef] [Google Scholar]
  90. Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef] [Google Scholar]
  91. Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
  92. Szalay, A. S., Connolly, A. J., & Szokoly, G. P. 1999, AJ, 117, 68 [Google Scholar]
  93. Tempel, E., Stoica, R. S., & Saar, E. 2013, MNRAS, 428, 1827 [Google Scholar]
  94. Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
  95. Trayford, J. W., Theuns, T., Bower, R. G., et al. 2016, MNRAS, submitted [arXiv:1601.07907] [Google Scholar]
  96. Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
  97. Williams, R. J., Quadri, R. F., Franx, M., et al. 2010, ApJ, 713, 738 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wong, K. C., Blanton, M. R., Burles, S. M., et al. 2011, ApJ, 728, 119 [NASA ADS] [CrossRef] [Google Scholar]
  99. Xu, C. K., Donas, J., Arnouts, S., et al. 2005, ApJ, 619, L11 [NASA ADS] [CrossRef] [Google Scholar]
  100. Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2005, ApJ, 630, 1 [Google Scholar]

All Tables

Table 1

GALEX fields with integration times and central positions.

In the text
Table 2

Characteristics of the spectroscopic redshift sample.

In the text

All Figures

thumbnail Fig. 1

Footprints of the GALEX NUV/FUV (cyan/blue) and WIRCam K band (red background) observations in the CFHTLS W1 (top) and W4 (bottom) fields. The spectroscopic sources are shown as golden points. The total area (W1 and W4) is ~7.8 and ~22 deg2 in FUV and NUV bands observed with GALEX and ~27 deg2 with WIRCam. The black layouts represent the VIDEO (W1) and UKIDSS (W4) surveys.

In the text
thumbnail Fig. 2

Colour-coded mean image quality (IQ) per WIRCam tile over the whole WIRCam survey (W1: top and W4: bottom). The layouts indicate the VIPERS regions (red layouts), the three VIDEO pointings (orange in W1), the UKIDSS-UDS (yellow in W1), and UKIDSS-DXS (orange in W4).
In the text
thumbnail Fig. 3

WIRCam Ks number counts for the galaxies (filled circles) and stars (open stars) in the W1 (red) and W4 (blue) regions. The dashed lines show the total number counts. The open dark symbols are a compilation from the literature (triangles: McCracken et al. 2012; pentagons: Jarvis et al. 2013; circles: UDS (DR8); squares: Quadri et al. 2007; stars: Bielby et al. 2012).
In the text
thumbnail Fig. 4

Comparison of the VIPERS K-band photometry with the Ultra-Deep UKIDSS field (top left), the VIDEO XMM2 field (bottom left), and the scatter distributions in three magnitude bins (right panels). The observed scatters are reported in the left panels as red circles, while the green solid lines show the mean magnitude vs. error behaviour of our VIPERS K band data after rescaling the original errors by 1.5 (see text). Larger dispersions are observed with VIDEO than with UDS because of the different depths between the two fields.

In the text
thumbnail Fig. 5

Top panel: completeness (in %) of the WIRCam sources as a function of magnitude, based on the deep surveys UDS (blue) and VIDEO (red). The completeness is shown for WIRCam sources with various signal-to-noise ratio cuts (no cut: filled symbols; S/N> 3: dotted lines; S/N> 5: dashed lines). Bottom panel: completeness as a function of magnitude and colour (z−K), colour-coded from red (100%) to blue (0%) based on the VIDEO survey. The yellow region delineates the 50% completeness level. The dashed line contours show the source density spaced with logarithmic scale of 0.3 dex. At KAB ≤ 20.6, the WIRCam sample is close to 100% completeness and the colour variations are due to small numbers.

In the text
thumbnail Fig. 6

Comparison of the EM vs. simulated fluxes as a function of simulated magnitudes. The dotted lines show the 1σ error, the red dashed line the mean bias. The magenta dot-dashed line reflects the effect of a small background bias on the flux ratio.

In the text
thumbnail Fig. 7

NUV number counts vs. magnitude in one GALEX field. The full EM photometric catalogue is shown as a solid black line and the EM sources matched to the GALEX pipeline sources as a solid blue line. The GALEX pipeline counts in the same area (and matched to EM sources) are shown as red and green dot-dashed lines.
In the text
thumbnail Fig. 8

GALEX number counts in W1 (red symbols) and W4 (blue symbols) regions for the galaxies (filled circles) and the stellar population (open stars). The FUV magnitudes are shifted by +4 mag. Open black symbols are from the literature (triangles: Hoversten et al. 2009; circles and pentagons: Gardner et al. 2000; squares: Xu et al. 2005).
In the text
thumbnail Fig. 9

Photometric classification between point-like and extended sources in the μmax−mobs vs. mobs plane (for one tile of the CFHTLS in the i-band). The dashed line represents our selection of point-like sources (Sμ, yellow dots). All objects lying below the solid line (gray dots) are considered as false detections.

In the text
thumbnail Fig. 10

Distribution of galaxies, stars, and QSOs in the (z−K) vs. (g−z) colour diagram. Density levels are in logarithmic scale (Δ = 0.3 dex) for galaxies (solid lines in W1 and W4 fields shown blue and red, respectively) and stars (dashed lines in green and orange). Objects from our QSO samples are shown as open stars (blue: W1; red: W4), while the SDSS/VIPERS AGN sample is shown as orange dots. The solid black lines delineate the high-redshift BzK populations (star-forming and passive galaxies).

In the text
thumbnail Fig. 11

Comparison of our photometric redshifts with the VVDS, VIPERS, PRIMUS, and BOSS most secure spectroscopic redshifts, for galaxies with K ≤ 22 (top panels) and NUV ≤ 25 (bottom panels). We report the dispersion (σNMAD) by combining all the surveys, while the catastrophic fractions (fcat defined as | Δz | /(1 + zs) > 0.15) are given for all surveys but PRIMUS (black value), which is shown separately (gray value). The observed distributions of photometric errors are compared to a Gaussian distribution with the same σ (right panels).

In the text
thumbnail Fig. 12

Comparison of the dispersion (σNMAD) as a function of magnitude (top panel: i; middle panel: Ks; bottom panel: NUV). The σNMAD for the W1 (black circles) and W4 (red squares) fields correspond to the open symbols and solid lines and refer to the left y-axis. The fraction of catastrophic redshifts are reported as field symbols and dashed lines and refer to the right y-axis (%). The PRIMUS spectroscopic sample in W1 field is shown separately (gray triangles).

In the text
thumbnail Fig. 13

Comparison of the photometric redshifts measured using either WIRCam K band (zwircam) or YJHK photometry from VISTA (zvista) for galaxies with KVISTA ≤ 23.5. The left panel shows the comparison zwircam vs. zvista for KVISTA < 22 (red dots), while the density contours spaced in logarithmic scale of 1 dex are for the faint sample, 22 < KVISTA < 23.5. The right panel shows the cumulative distributions of the difference (Δz/ (1 + zvista)) split into three K-band subsamples (KVISTA ≤ 22: red line; 22 < KVISTA < 23: green line; 23 < KVISTA < 23.5: red line). We also report the dispersions (σ), the fractions of catastrophic sources (in %), and the number of sources used.

In the text
thumbnail Fig. 14

Same as Fig. 13 for a NUV-selected sample with NUV ≤ 25.5 and also split into KVISTA subsamples.

In the text
thumbnail Fig. 15

Differential number counts of star-forming (top) and passive (bottom) BzK galaxies in the W1 and W4 fields. We compare with deeper observations in CFHTLS deep fields (open squares, Arcila-Osejo & Sawicki 2013) and COSMOS (open triangles, McCracken et al. 2010) and model predictions (dashed lines, Henriques et al. 2013) The inset panels show the photometric redshift distributions with KAB ≤ 22.

In the text
thumbnail Fig. 16

Illustration of the galaxy morphology in the NUVrK diagram for galaxies with z ≤ 0.25. Galaxies are split into seven categories shown in the top left inset, and background enlarged points are colour-coded according to their categories. Only the largest galaxies (with semi-major axis A > 50 pixels) are shown. The lower right inset shows the behaviour of the sSFR (log-scale colour-coded).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.