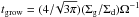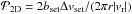| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527069 | |
| Published online | 05 April 2016 | |
On the water delivery to terrestrial embryos by ice pebble accretion
Department of Earth and Planetary Sciences, Tokyo Institute of
Technology, Meguro,
Tokyo, 152-8551, Japan
e-mail:
okuzumi@geo.titech.ac.jp
Received: 27 July 2015
Accepted: 18 December 2015
Standard accretion disk models suggest that the snow line in the solar nebula migrated interior to the Earth’s orbit in a late stage of nebula evolution. In this late stage, a significant amount of ice could have been delivered to 1 AU from outer regions in the form of mm to dm-sized pebbles. This raises the question why the present Earth is so depleted of water (with the ocean mass being as small as 0.023% of the Earth mass). Here we quantify the amount of icy pebbles accreted by terrestrial embryos after the migration of the snow line assuming that no mechanism halts the pebble flow in outer disk regions. We use a simplified version of the coagulation equation to calculate the formation and radial inward drift of icy pebbles in a protoplanetary disk. The pebble accretion cross section of an embryo is calculated using analytic expressions presented by recent studies. We find that the final mass and water content of terrestrial embryos strongly depends on the radial extent of the gas disk, the strength of disk turbulence, and the time at which the snow lines arrives at 1 AU. The disk’s radial extent sets the lifetime of the pebble flow, while turbulence determines the density of pebbles at the midplane where the embryos reside. We find that the final water content of the embryos falls below 0.023 wt% only if the disk is compact (<100 AU), turbulence is strong at 1 AU, and the snow line arrives at 1 AU later than 2–4 Myr after disk formation. If the solar nebula extended to 300 AU, initially rocky embryos would have evolved into icy planets of 1–10 Earth masses unless the snow-line migration was slow. If the proto-Earth contained water of ~1 wt% as might be suggested by the density deficit of the Earth’s outer core, the formation of the proto-Earth was possible with weaker turbulence and with earlier (>0.5–2 Myr) snow-line migration.
Key words: Earth / planets and satellites: composition / planets and satellites: formation / protoplanetary disks
© ESO, 2016
1. Introduction
Terrestrial planets in our solar system are characterized by their extremely low water content. The ocean of the Earth comprises only 0.023 wt% of the total mass of the planet. The water content of the present Earth’s interior is uncertain, but the 10% density deficit of the Earth’s outer core might suggest that that water of up to ~1 wt% existed in the proto-Earth and provided a large amount of hydrogen to the outer core (Okuchi 1997; Abe et al. 2000; see Nomura et al. 2014 for experiments supporting the large amount of hydrogen partitioning into the core). An initial water content much in excess of ~1 wt% seems unlikely because neither stellar irradiation at ~1 AU (Machida & Abe 2010) nor giant impacts (Genda & Abe 2005) are able to vaporize the majority of the water from the Earth’s gravitational potential. Mars might possess, or might have possessed, subsurface water/ice of 0.01–0.1% of the total Mars mass (Kurokawa et al. 2014). Venus has a very dry atmosphere with the low-altitude H2O mixing ratio of 10–100 ppm (Prinn & Fegley 1987; Donahue & Hodges 1992) and the high viscosity of Venus’s mantle suggests that its interior is also dry (Nimmo & McKenzie 1998). The low water content of the terrestrial planets is in stark contrast to the high ice content of outer solar system bodies; in the extreme example of comets, the ice-to-rock mass ratio is generally thought to be close to unity (e.g., A’Hearn 2011).
The fact that the Earth was born dry might not be surprising at first sight given that the Earth’s orbit is well inside the snow line of the current solar system. The snow line is defined by the orbit inside which water ice sublimates into vapor. Assuming that water ice sublimates at 170 K, the snow line of the present solar system lies at about 3 AU from the Sun. The snow line in the solar nebula, which is the protoplanetary disk that formed the solar system, would have been at the same location if the nebula was optically thin to direct stellar radiation (Hayashi 1981).
However, the solar nebula was presumably optically thick at least in its early evolutionary stage because of the presence of abundant small dust grains. In an optically thick protoplanetary disk, the snow line can be either inside or outside the Earth’s orbit (1 AU) depending on how much accretion heating is effective. The disk is hottest in its earliest evolutionary stage where the central pre-main-sequence star is most luminous (e.g., Kusaka et al. 1970; Turner et al. 2012) and where the accretion rate is the highest (e.g., Hartmann et al. 1998). Standard viscous accretion disk models show that the snow line, or the location where the gas temperature is 150–170 K, around a solar-mass star lies at about 5 AU when the accretion rate of the disk Ṁ is 10-7 M⊙ yr-1 (Davis 2005; Garaud & Lin 2007; Min et al. 2011; Oka et al. 2011; Bitsch et al. 2015; Baillié et al. 2015; Mulders et al. 2015). However, as the accretion rate decreases with time, the disk cools down and the snow line moves inward. Assuming standard viscous accretion, the snow line passes 1 AU at Ṁ ≈ a few × 10-9 M⊙ yr-1 if all dust in the disk is in the form of opacity-dominating micron-sized grains (Davis 2005; Garaud & Lin 2007; Oka et al. 2011; Bitsch et al. 2015), and at Ṁ ≈ 1 × 10-8 M⊙ yr-1 if the grains are depleted by an order of magnitude (Bitsch et al. 2015). The migration of the snow line stops at ~0.7 AU (for the stellar luminosity of 1 L⊙) when accretion heating ceases to be important around these orbits (Sasselov & Lecar 2000; Davis 2005; Garaud & Lin 2007; Oka et al. 2011). At this stage, the interior of the disk is much colder than that of an optically thin disk because the disk can only receive stellar radiation on its surface. The snow line moves out toward the final position ≈3 AU only after the interior of the disk becomes optically thin to direct stellar radiation (Ṁ ≲ 10-10 M⊙ yr-1, Oka et al. 2011).
The above picture is based on standard accretion disk models in which turbulence is assumed to be spatially uniform.For example, accretion heating would be much less significant than anticipated by the uniformly turbulent models if the disk is only turbulent on its surface. This is the case in magnetically driven accretion models where the magnetorotational instability (Balbus & Hawley 1991), which is the driver of disk turbulence, is suppressed by magnetic diffusion near the midplane (Hirose & Turner 2011; Flock et al. 2013).On the other hand, the nonsteady accretion model of Martin & Livio (2012), which incorporates the gravitational instability and suppression of magnetic turbulence by magnetic diffusion, suggests that the gas temperature at 1 AU could be maintained high enough to sublimate ice even in the late stage of disk evolution. The snow line would not have reached the terrestrial region if X-ray-driven photoevaporation had cleared the gas in that region when Ṁ ≈ 1 × 10-8 M⊙ yr-1 (Owen et al. 2010).
The inward migration of the snow line, if it really occurs in protoplanetary disks, gives two important constraints on the formation of terrestrial planets at ~1 AU like the Earth. Earth-sized terrestrial planets are generally believed to form through giant impacts of Mars-sized (~0.1 M⊕) solid bodies called planetary embryos (e.g., Wetherill & Stewart 1989; Kokubo & Ida 2002). Given the inefficiency of removing water from embryos through giant impacts (Genda & Abe 2005), water-devoid planets must form from water-devoid embryos. Such embryos can form at 1 AU only when intense accretion heating pushes the snow line to >1 AU; otherwise, like comets, they would have an ice-to-rock ratio of ≈1. In the standard viscous disk models, this constraint means that the terrestrial embryos can only form when Ṁ ≲ a few to 10 × 10-9 M⊙ yr-1 with the exact value depending on how much of the small dust grains are depleted (see above). Assuming the correlation between the stellar age and mass accretion rate suggested by observations (Hartmann et al. 1998; Bitsch et al. 2015), this also means that terrestrial planet formation needs to have been completed within ~1–3 Myr after disk formation (there is, however, a large scatter in the Ṁ-age correlation). The Hf-W dating of Martian meteorites indicates that Mars, a possible planetary embryo that survived giant impacts, formed during the first ~1–3 Myr of the solar system formation (Dauphas & Pourmand 2011). This Hf-W dating implies that the terrestrial embryo formation in the solar system barely satisfied this time constraint. One should keep in mind, however, that magnetically driven accretion models might predict very different time constraints as discussed above.
The second important constraint is that the rocky embryos must avoid accretion of a significant amount of ice that could occur after the inward migration of the snow line. It is known that solid particles in a gas disk drift toward the central star because the gas drag robs the particles of angular momentum (Adachi et al. 1976; Weidenschilling 1977). The angular momentum loss is most effective for millimeter- to meter-sized particles that are marginally decoupled from the gas disk. Models incorporating the drift and coagulation of solid particles predict that a significant amount of millimeter to decimeter-sized ice aggregates flow from outer disk regions toward the snow line (e.g., Garaud 2007; Brauer et al. 2008a; Birnstiel et al. 2010). Without any mechanisms preventing the pebble flow, the total amount of ice that is delivered to the inner orbits is comparable to the total amount of ice in the disk (~10–100 M⊕) because the majority of solids in a disk generally reside in outer regions. The problem here is that large solid bodies like planetary embryos are efficient at capturing pebble-sized particles because of the help of the disk’s gas drag (Ormel & Klahr 2010; Lambrechts & Johansen 2012). Therefore, if the snow line in the solar nebula migrated inside 1 AU, rocky embryos at 1 AU could have accreted a non-negligible amount of ice. One might expect that this water delivery mechanism is potentially relevant to the origin of the Earth’s ocean; however, the immediate problem with this interpretation is that the D/H ratio of icy pebbles from outer disk regions would presumably have been similar to those of comets, which are on average higher than the Earth ocean water value (e.g., Altwegg et al. 2015). If this is the case, the amount of water supplied by the icy pebbles must have been much smaller than that of ocean water, or at least smaller than the water capacity of the Earth’s interior, in order to avoid an enhancement of the ocean D/H ratio.
The question of how much water is delivered to terrestrial embryos by icy pebbles is closely linked to the so-called pebble accretion scenario for giant planet formation recently proposed by (Lambrechts & Johansen 2012, 2014; see also Kretke & Levison 2014; Johansen et al. 2015; Morbidelli et al. 2016, 2015; Moriarty & Fischer 2015; Levison et al. 2015a,b). They showed that efficient icy pebble accretion enables embryos of 1000 km in size outside the snow line to grow to the critical core mass for runway gas accretion (~10 M⊕) within the lifetime of protoplanetary disks. Our study focuses on another aspect of the pebble accretion scenario: while the radial pebble flux feeds giant planet cores in outer disk regions, the same pebble flux could deliver an excessive amount of water to terrestrial embryos in inner disk regions.
While this paper was under revision, a paper that discusses the issue of the snow-line migration appeared in print (Morbidelli et al. 2016). The paper proposes the scenario that proto-Jupiter halted the pebble flow from outer disk regions by carving a pebble-trapping gap in the gas nebula. Although this is one plausible scenario (see also the discussions in our Sect. 4.3), it is also important to pursue the possibility that Earth-forming embryos avoided excessive water delivery even if no mechanism stopped the icy pebble flow. This is the subject of this paper.
In this study, we calculate the amount of ice accreted by an embryo at ~1 AU based on the assumption that the snow line migrates inward across 1 AU. We employ a simple model of global dust evolution in which the collisional growth (coagulation) and radial drift of icy dust particles in a disk are treated in a self-consistent way. We compute the amount of water delivered to a terrestrial embryo for a range of model parameters including the strength of turbulence, the time at which the snow line moves interior to 1 AU, and the radial extent of the gas disk. Our model is technically similar to the analytic model of Lambrechts & Johansen (2014) in that both treat the dominant particle size at each orbital radius instead of treating the full particle size distribution. An important difference from the previous study by Lambrechts & Johansen (2014) is that we apply the concept of pebble accretion to the problem of water delivery to terrestrial planets. In addition, our numerical model includes a more detailed calculation of the relative velocity between particles and also takes the finite radial extent of a protoplanetary disk into account, both of which affect the properties of the radial pebble flow. We also calibrate our model using the result of a detailed coagulation simulation that resolves the full particle size distribution (Okuzumi et al. 2012).
The structure of the paper is as follows. In Sect. 2, we introduce the models of the solar nebula, dust evolution, and pebble accretion, emphasizing how disk turbulence affects dust coagulation and pebble accretion quantitatively. In Sect. 3, we present the results of our model calculations and highlight how the rate of pebble accretion by an embryo depends on the radial extent of the disk and on turbulence strength. We give some discussions in Sect. 4 and summarize in Sect. 5. Appendix A is devoted to the validation of the simplified dust evolution model employed in this work.
2. Model
2.1. Overview
We describe the model we use to quantify how much water is delivered to rocky embryos at 1 AU through icy pebble accretion (see Fig. 1 for a schematic of the model). We consider a solar-mass star and a protoplanetary disk of outer radius rout.We assume that the snow line is initially well beyond 1 AU and migrates in across 1 AU at time tstart after the beginning of dust evolution. We take tstart as a free parameter to avoid complications that would result from detailed modeling of the snow-line evolution. We assume that the solids in the disk are initially in the form of 0.1 μm-sized dust grains, and calculate the growth and radial inward drift of ice particles outside the snow line via a simplified dust coagulation model described in Sect. 2.3. The calculation gives us the mass flux (in the direction of the central star) and typical size of icy pebbles that arrive at 1 AU as a function of time t. The ice-to-rock mass ratio of the icy pebbles is assumed to be unity in accordance with the solar system composition compiled by Lodders (2003). Millimeter observations of protoplanetary disks suggest that rout is typically within the range 100–300 AU (e.g., Andrews & Williams 2007). We consider the two values rout = 100 AU and 300 AU.
We then place a rocky embryo of initial mass Me,0 at 1 AU and allow it to accrete ice particles at t>tstart. We consider two cases, Me,0 = 10-1 M⊕ and 10-2 M⊕. The larger Me,0 is the typical mass of terrestrial embryos predicted from planetesimal accumulation without fragmentation (e.g., Wetherill & Stewart 1989; Kokubo & Ida 2002). The final water fraction of the embryo is compared with the minimum water fraction of the present Earth given by the ocean (0.023 wt%) and with the hypothetical water fraction of the proto-Earth inferred from the density deficit of the Earth’s outer core (1 wt%).
The radial drift of ice particles considered in this study is due to their angular momentum in a sub-Keplerian rotating protoplanetary disk (Adachi et al. 1976; Weidenschilling 1977). In reality, solids in a disk have an additional inward velocity owing to the accretion of the background gas onto the central star. However, this latter velocity component is negligible compared to the former component whenever dust grows into pebble-sized particles (Brauer et al. 2008a; Birnstiel et al. 2012).
We neglect possible filtration by planetesimals, planetary embryos, or gas giants exterior to 1 AU. As already shown by previous studies (Lambrechts & Johansen 2014; Guillot et al. 2014; Morbidelli & Nesvorny 2012), a swarm of planetesimals or embryos filters only a minor fraction of the pebble flow (typically <50%) unless the size distribution of the bodies is narrowly peaked at 103–104 km in radius (see Guillot et al. 2014). By contrast, if massive planets already exist at t ~ tstart, they can efficiently halt the flow of the pebbles by opening a gap in the gas disk (e.g., Paardekooper & Mellema 2006; Rice et al. 2006; Zhu et al. 2012; Pinilla et al. 2012; Morbidelli & Nesvorny 2012; Lambrechts et al. 2014). By neglecting this effect, we effectively assume that such gap-forming planets form only after the snow line migrates inside 1 AU. We discuss this point in more detail in Sect. 4.3. We also neglect the loss of the pebble flux due to the accretion by adjacent rocky embryos. Thus, the problem we are considering reduces to the problem of calculating the pebble accretion rate of each isolated rocky embryo.
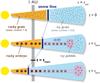 |
Fig. 1 Schematic illustration showing the radial inward drift of icy pebbles and the inward migration of the snow line in a protoplanetary disk. Rocky embryos at 1 AU accrete radially drifting icy pebbles when the snow line resides at <1 AU. Time t = tstart, at which the snow line passes 1 AU, is taken as a free parameter. |
In the following subsections, we describe our disk model in Sect. 2.2, the equations that determine the evolution of icy pebbles in Sects. 2.3 and 2.4, our pebble accretion model in Sect. 2.5, and our parameter choices in Sect. 2.6.
2.2. Disk model
The radial distribution of the gas surface density Σg is taken from the minimum mass solar nebula (MMSN) model of Hayashi (1981), 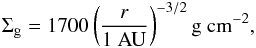 (1)where r is the distance from the central star. We cut off Σg at r>rout and take the cutoff radius rout as a free parameter (either 100 AU or 300 AU). The initial dust surface density Σd,0 is taken to be 1% of Σg. The total dust mass within the initial disk is
(1)where r is the distance from the central star. We cut off Σg at r>rout and take the cutoff radius rout as a free parameter (either 100 AU or 300 AU). The initial dust surface density Σd,0 is taken to be 1% of Σg. The total dust mass within the initial disk is 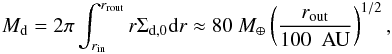 (2)where we have used rin ≪ rout. Since Md is an increasing function of rout, the dominant part of the mass resides in the outermost region of the disk. We come back to this point in Sect. 3.1.
(2)where we have used rin ≪ rout. Since Md is an increasing function of rout, the dominant part of the mass resides in the outermost region of the disk. We come back to this point in Sect. 3.1.
The gas disk is assumed to be isothermal and hydrostatic in the vertical direction. The gas density at the midplane is thus given by 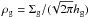 , where hg = cs/ Ω is the gas scale height,
, where hg = cs/ Ω is the gas scale height, 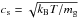 is the isothermal sound speed,
is the isothermal sound speed, 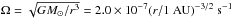 is the Keplerian frequency with kB, mg, G being the Boltzmann constant, mean molecular mass (taken to be 2.34 amu), and gravitational constant, respectively.
is the Keplerian frequency with kB, mg, G being the Boltzmann constant, mean molecular mass (taken to be 2.34 amu), and gravitational constant, respectively.
As stated earlier, we do not directly treat the evolution of the snow line and instead express the migration of the snow line with tstart. However, we do need a model of the gas temperature T when we calculate the density structure of the gas disk and the thermal and turbulent velocity of particles. For this purpose, we simply use a fixed power-law temperature profile 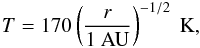 (3)where the slope has been taken from the optically thin disk model of Hayashi (1981). The value at 1 AU has been chosen so that the snow line lies at ~1 AU, which is motivated by our results that the water content of an embryo increases most rapidly just after the snow line passes the embryo (t ≈ tstart; see Sect. 3.4).This temperature profile gives cs = 7.8 × 104(r/ 1 AU)− 1 / 4 cm s-1, hg = 0.026(r/ 1 AU)5 / 4 AU, and ρg = 1.7 × 10-9(r/ 1 AU)− 11 / 4 g cm-3. In reality, in an optically thick disk, the radial temperature profile would be steeper than in Eq. (3) when accretion heating dominates (e.g., Lin & Papaloizou 1980), and would be shallower when stellar irradiation dominates (Kusaka et al. 1970; Lin & Papaloizou 1980). However, as we demonstrate in Sect. 4.1, the evolution and accretion of pebbles onto an embryo are fairly insensitive to the details of the temperature profile as long as an isolated single embryo is considered.
(3)where the slope has been taken from the optically thin disk model of Hayashi (1981). The value at 1 AU has been chosen so that the snow line lies at ~1 AU, which is motivated by our results that the water content of an embryo increases most rapidly just after the snow line passes the embryo (t ≈ tstart; see Sect. 3.4).This temperature profile gives cs = 7.8 × 104(r/ 1 AU)− 1 / 4 cm s-1, hg = 0.026(r/ 1 AU)5 / 4 AU, and ρg = 1.7 × 10-9(r/ 1 AU)− 11 / 4 g cm-3. In reality, in an optically thick disk, the radial temperature profile would be steeper than in Eq. (3) when accretion heating dominates (e.g., Lin & Papaloizou 1980), and would be shallower when stellar irradiation dominates (Kusaka et al. 1970; Lin & Papaloizou 1980). However, as we demonstrate in Sect. 4.1, the evolution and accretion of pebbles onto an embryo are fairly insensitive to the details of the temperature profile as long as an isolated single embryo is considered.
Our model takes the effects of disk turbulence on the growth and vertical diffusion of dust particles into account. Turbulent diffusion is particularly important in our model because it determines the efficiency of pebble accretion by an embryo lying at the midplane (Guillot et al. 2014; Johansen et al. 2015; Morbidelli et al. 2015; Moriarty & Fischer 2015). We parametrize the turbulent diffusion coefficient as D = αcshg, where α is a dimensionless free parameter. If D is equal to the turbulent viscosity (which is not used in this study), α corresponds to the viscosity parameter of Shakura & Sunyaev (1973). For simplicity, we take α to be constant both in time and space. The turnover time of the largest turbulent eddies, which is implicitly used in evaluating the turbulence-driven particle relative velocity, is taken to be Ω-1 in accordance with the typical correlation time of magnetorotational turbulence (e.g., Fromang & Papaloizou 2006). The role of disk turbulence as an effective viscosity is not taken into account in our model since we do not evolve Σg or T.
2.3. Dust growth and radial drift
We employ a simplified approach to calculate the mass flux of radially drifting pebbles. We assume that the mass distribution of dust particles at each orbit r is singly peaked at a mass mp(r). We then follow the evolution of the dust surface density Σd and peak mass mp due to coagulation and radial drift by assuming that particles with mass ~ mp dominate the dust surface density at each r. Such a single-size approximation, also known as the two-moment bulk approximation in cloud modeling (Ferrier 1994), has been applied to modeling dust evolution in protoplanetary disks (Kornet et al. 2001; Garaud 2007; Birnstiel et al. 2012) as well as in protoplanetary atmospheres (Ormel 2014)1. This allows us to track the global evolution of dust particles that dominate the radial mass flux at a much less computational cost than solving the exact coagulation equation that resolves the full particle size distribution. In Appendix A, we give analytic and numerical justifications of this approach as well as the formal definition of the peak mass mp.
Following Brauer et al. (2008a), the vertical distribution of the particles is approximated by a Gaussian 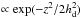 and we determine the dust scale height hd from the balance between sedimentation and diffusion (see Eq. (11) below). We neglect particle diffusion in the radial direction because its timescale (~104 yr for α = 10-2 at 1 AU) is typically longer than the drift timescale of pebble-sized particles (~103 yr at 1 AU).
and we determine the dust scale height hd from the balance between sedimentation and diffusion (see Eq. (11) below). We neglect particle diffusion in the radial direction because its timescale (~104 yr for α = 10-2 at 1 AU) is typically longer than the drift timescale of pebble-sized particles (~103 yr at 1 AU).
We assume that ice aggregates are so sticky that no fragmentation or bouncing occurs upon collision. Numerical studies of aggregate collisions (Dominik & Tielens 1997; Wada et al. 2009, 2011, 2013) have shown that aggregates made of 0.1 μm-sized icy grains undergo catastrophic disruption only at collision velocities higher than 50–80 m s-1. With this high sticking efficiency, pebble-sized aggregates do not experience disruption in protoplanetary disks (e.g., Brauer et al. 2008a). Krijt et al. (2015) have recently pointed out that erosion by small projectiles might limit the growth of icy aggregates outside the snow line. We do not consider this effect because the threshold velocity for erosion is still controversial (see the discussion in Sect. 2.3.2 of Krijt et al. 2015). We also neglect condensation growth and sintering of icy aggregates in the vicinity of the snow line. While condensation would facilitates pebble growth (Ros & Johansen 2013), sintering would induce destruction of pebble-sized aggregates (Sirono 2011a,b; Okuzumi et al. 2016). These processes could potentially change our results, but we ignore them as a first step toward a full understanding of the problem.The aggregate internal density is fixed to be ρint = 1.4 g cm-3 for simplicity, but in reality the porosity of ice aggregates may evolve as they coagulate (Suyama et al. 2008; Okuzumi et al. 2012; Kataoka et al. 2013a). Influences of the porosity evolution will be discussed in future work.
Under the assumptions mentioned above, the equations governing the evolution of Σd and mp are given by 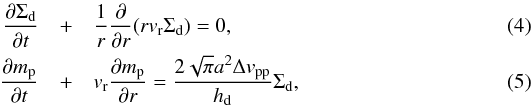 where a = (3mp/ 4πρint)1 / 3 is the particle radius corresponding to mp, and vr and Δvpp are the radial and relative velocities of the particles at the midplane, respectively. Our Eqs. (4) and (5) are essentially equivalent to Eqs. (3) and (8) of Ormel (2014), although the deposition terms are not included here. The formal derivation of Eqs. (4) and (5) from the exact coagulation equation is cumbersome (see Appendix A.1), but their physical interpretation is clear. Equation (4) is merely the equation of continuity while Eq. (5) states that the growth rate of peak-mass particles along their trajectory, dmp/ dt ≡ ∂mp/∂t + vr∂mp/∂r, is proportional to the product of the particle–particle collision cross section π(a + a)2 = 4πa2, relative velocity Δvpp, and dust density at the midplane
where a = (3mp/ 4πρint)1 / 3 is the particle radius corresponding to mp, and vr and Δvpp are the radial and relative velocities of the particles at the midplane, respectively. Our Eqs. (4) and (5) are essentially equivalent to Eqs. (3) and (8) of Ormel (2014), although the deposition terms are not included here. The formal derivation of Eqs. (4) and (5) from the exact coagulation equation is cumbersome (see Appendix A.1), but their physical interpretation is clear. Equation (4) is merely the equation of continuity while Eq. (5) states that the growth rate of peak-mass particles along their trajectory, dmp/ dt ≡ ∂mp/∂t + vr∂mp/∂r, is proportional to the product of the particle–particle collision cross section π(a + a)2 = 4πa2, relative velocity Δvpp, and dust density at the midplane 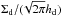 2.
2.
2.4. Particle stopping time, scale height, and velocity
The velocity and scale height of a particle depends on its stopping time ts, which is the timescale of particle’s momentum relaxation due to the gas drag. We evaluate ts with the piecewise formula 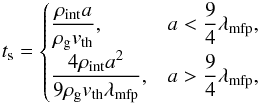 (6)where
(6)where 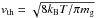 and λmfp are the thermal velocity and mean free path of gas particles, respectively. The mean free path is related to the gas density as λmfp = mg/ (σmolρg), where σmol = 2.0 × 10-15 cm2 is the molecular collision cross section. The first and second expressions of Eq. (6) are known as the Epstein and Stokes laws, respectively. In many cases, it is useful to express the stopping time in terms of the dimensionless Stokes number
and λmfp are the thermal velocity and mean free path of gas particles, respectively. The mean free path is related to the gas density as λmfp = mg/ (σmolρg), where σmol = 2.0 × 10-15 cm2 is the molecular collision cross section. The first and second expressions of Eq. (6) are known as the Epstein and Stokes laws, respectively. In many cases, it is useful to express the stopping time in terms of the dimensionless Stokes number 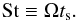 (7)Using the relations between Σg, ρg, hg, Ω, cs, and vth, one can rewrite Eq. (6) in terms of St as
(7)Using the relations between Σg, ρg, hg, Ω, cs, and vth, one can rewrite Eq. (6) in terms of St as 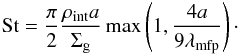 (8)The radial drift velocity of particles is given by (Adachi et al. 1976; Weidenschilling 1977)
(8)The radial drift velocity of particles is given by (Adachi et al. 1976; Weidenschilling 1977) 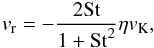 (9)where
(9)where 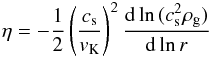 (10)is a dimensionless quantity characterizing the pressure gradient of the disk gas (which is the ultimate cause of the radial particle drift) and vK = rΩ is the Kepler velocity. Our disk model gives η = 1.1 × 10-3(r/ 1AU)1 / 2 and ηvK = 33 m s-1. The value of η is smaller than that of the optically thin MMSN model (Hayashi 1981) by the factor 0.6, which reflects the lower gas temperature in our model.
(10)is a dimensionless quantity characterizing the pressure gradient of the disk gas (which is the ultimate cause of the radial particle drift) and vK = rΩ is the Kepler velocity. Our disk model gives η = 1.1 × 10-3(r/ 1AU)1 / 2 and ηvK = 33 m s-1. The value of η is smaller than that of the optically thin MMSN model (Hayashi 1981) by the factor 0.6, which reflects the lower gas temperature in our model.
The particle scale height is given by (Dubrulle et al. 1995; Youdin & Lithwick 2007; Okuzumi et al. 2012) 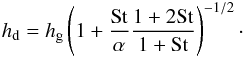 (11)Equation (11) assumes that vertical settling of the particles balances with vertical turbulent diffusion.
(11)Equation (11) assumes that vertical settling of the particles balances with vertical turbulent diffusion.
The particle collision velocity Δvpp is given by 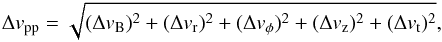 (12)where ΔvB,Δvr,Δvφ,Δvz and Δvt are the relative velocities induced by Brownian motion, radial drift, azimuthal drift, vertical settling, and turbulence, respectively. We evaluate these velocity components with the equations given in Sect 2.3.2 of Okuzumi et al. (2012), but with the assumption that the particle mass distribution is narrowly peaked at m = mp. For example, the Brownian component is given by
(12)where ΔvB,Δvr,Δvφ,Δvz and Δvt are the relative velocities induced by Brownian motion, radial drift, azimuthal drift, vertical settling, and turbulence, respectively. We evaluate these velocity components with the equations given in Sect 2.3.2 of Okuzumi et al. (2012), but with the assumption that the particle mass distribution is narrowly peaked at m = mp. For example, the Brownian component is given by 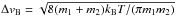 , where m1 and m2 are the masses of the colliding aggregates3, and we evaluate this by setting m1 = m2 = mp. The differential drift velocities Δvr, Δvφ, and Δvz are functions of the Stokes numbers St1 and St2 of the colliding pair. Evaluation of these components within the single-size approximation is more tricky because they vanish for St1 = St2 but have a finite value for St1 ~ St2. Since the real size distribution has a finite width, the naive choice St1 = St2 = St(mp) results in a significant underestimation of the particle velocities and, hence, of the particle growth rate s shown in Appendix A.2. We introduce a dimensionless control parameter ϵ( < 1) and set St1 = St(mp) and St2 = ϵSt(mp) whenever we evaluate the drift velocities to take the effect of the size dispersion into account. We show in Appendix A.2 that the choice ϵ = 0.5 best reproduces the results of a coagulation simulation that treats the fill size distribution. We adopt this choice throughout the paper. The turbulence-induced relative velocity Δvt is also a function of St1 and St2 (assuming that the turnover time of the largest turbulent eddies is Ω-1), and we evaluate it using Eqs. (16)–(18) of Ormel & Cuzzi (2007). For St1 ~ St2 ≪ 1, which is true for pebble-sized particles, Δvt has approximate expressions (see Eqs. (27) and (28) of Ormel & Cuzzi 2007)
, where m1 and m2 are the masses of the colliding aggregates3, and we evaluate this by setting m1 = m2 = mp. The differential drift velocities Δvr, Δvφ, and Δvz are functions of the Stokes numbers St1 and St2 of the colliding pair. Evaluation of these components within the single-size approximation is more tricky because they vanish for St1 = St2 but have a finite value for St1 ~ St2. Since the real size distribution has a finite width, the naive choice St1 = St2 = St(mp) results in a significant underestimation of the particle velocities and, hence, of the particle growth rate s shown in Appendix A.2. We introduce a dimensionless control parameter ϵ( < 1) and set St1 = St(mp) and St2 = ϵSt(mp) whenever we evaluate the drift velocities to take the effect of the size dispersion into account. We show in Appendix A.2 that the choice ϵ = 0.5 best reproduces the results of a coagulation simulation that treats the fill size distribution. We adopt this choice throughout the paper. The turbulence-induced relative velocity Δvt is also a function of St1 and St2 (assuming that the turnover time of the largest turbulent eddies is Ω-1), and we evaluate it using Eqs. (16)–(18) of Ormel & Cuzzi (2007). For St1 ~ St2 ≪ 1, which is true for pebble-sized particles, Δvt has approximate expressions (see Eqs. (27) and (28) of Ormel & Cuzzi 2007) ![\begin{eqnarray} {\Delta}v_{\rm t} \approx \begin{cases} \sqrt{\alpha}c_{\rm s}{\rm Re}_{\rm t}^{1/4}|{\rm St}_1 - {\rm St}_2|, & {\rm St}_1 \ll {\rm Re}_{\rm t}^{-1/2}, \\[2mm] \sqrt{3\alpha}c_{\rm s} {\rm St}_1^{1/2}, & {\rm St}_1 \gg {\rm Re}_{\rm t}^{-1/2}, \end{cases} \label{eq:vcolt} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq127.png) (13)where Ret = D/νmol is the turbulent Reynolds number and νmol = vthλmfp/ 2 is the molecular viscosity. We set St1 = St(mp) and St2 = ϵSt(mp) when evaluating Δvt since it vanishes for St1 = St2 in the case of
(13)where Ret = D/νmol is the turbulent Reynolds number and νmol = vthλmfp/ 2 is the molecular viscosity. We set St1 = St(mp) and St2 = ϵSt(mp) when evaluating Δvt since it vanishes for St1 = St2 in the case of 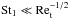 .
.
 |
Fig. 2 Components of the particle relative velocity Δvpp at 100 AU as a function of particle radius a for three values of the turbulence parameter α = 10-4 (top panel), 10-3 (middle panel), and 10-2 (bottom panel). The velocity components that depend on α are shown by the solid curves. The stopping time ratio of ϵ = 0.5 is assumed for Δvr, Δvφ, Δvz, and Δvt. |
Which component of Δvpp dominates depends not only on the particle size but also on the turbulence strength. To illustrate this, in Fig. 2 we plot all components of Δvpp at r = 100 AU as a function of a for different values of α. We assume ϵ = 0.5 when evaluating the non-Brownian components. In general, the particle relative velocity has a maximum at St ≈ 1, which corresponds to a ≈ 1 cm at this location. When α = 10-4, laminar components such as Δvz and Δvr are dominant for all a. The turbulent component Δvt becomes more important when α = 10-3, and dominates over the laminar components for all a when α = 10-2.
 |
Fig. 3 Particle growth timescale tgrow (Eq. (14)) at 100 AU as a function of particle radius a for Σd = 10-2Σg with different values of the turbulence parameter α. The dotted line shows the simple estimate |
Since Δv and hd are already given, we are able to estimate the timescale of dust growth as a function of particle size. Here we define the particle growth timescale as 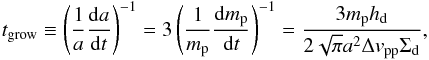 (14)where (d / dt) ≡ (∂/∂t) + vr(∂/∂r) is the Lagrangian time derivative, and we have used Eq. (5) in the final expression. Figure 3 shows tgrow at 100 AU and 1 AU as a function of a for three different values of α. Here, the dust-to-gas ratio is taken to be the initial value Σd,0/ Σg = 10-2. It can be seen that tgrow ~ 104−105 yr at 100 AU and ~1–100 yr at 1 AU, indicating that tgrow scales approximately linearly with the orbital timescale ∝Ω-1 ∝ r3 / 2. In fact, one can show that the simple relation
(14)where (d / dt) ≡ (∂/∂t) + vr(∂/∂r) is the Lagrangian time derivative, and we have used Eq. (5) in the final expression. Figure 3 shows tgrow at 100 AU and 1 AU as a function of a for three different values of α. Here, the dust-to-gas ratio is taken to be the initial value Σd,0/ Σg = 10-2. It can be seen that tgrow ~ 104−105 yr at 100 AU and ~1–100 yr at 1 AU, indicating that tgrow scales approximately linearly with the orbital timescale ∝Ω-1 ∝ r3 / 2. In fact, one can show that the simple relation 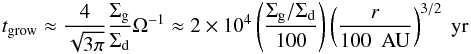 (15)holds in the special case where the conditions a ≪ λmfp, Δvpp ≈ Δvt, and
(15)holds in the special case where the conditions a ≪ λmfp, Δvpp ≈ Δvt, and 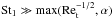 are met (see Takeuchi & Lin 2005 and Brauer et al. 2008a for the derivation). This expression, which is employed in the analytic pebble formation model of Lambrechts & Johansen (2014), is extremely useful as an order-of-magnitude estimate, since it only depends on the gas-to-dust ratio and orbital frequency. However, caution should be exercised when using Eq. (15) for more precise calculations because the expression is less accurate if one or more of the conditions mentioned above is not met. For example, we can see in Fig. 3 that Eq. (15) overestimates the actual growth timescale by a factor of several when α ≤ 10-3 and a ≲ 10-3 cm, for which Δvpp ≈ Δvz (see Fig. 2) and St ≲ α. For this reason, the time required for micron-sized dust particles to grow into pebbles is longer when α ≤ 10-3 than when α = 10-2.
are met (see Takeuchi & Lin 2005 and Brauer et al. 2008a for the derivation). This expression, which is employed in the analytic pebble formation model of Lambrechts & Johansen (2014), is extremely useful as an order-of-magnitude estimate, since it only depends on the gas-to-dust ratio and orbital frequency. However, caution should be exercised when using Eq. (15) for more precise calculations because the expression is less accurate if one or more of the conditions mentioned above is not met. For example, we can see in Fig. 3 that Eq. (15) overestimates the actual growth timescale by a factor of several when α ≤ 10-3 and a ≲ 10-3 cm, for which Δvpp ≈ Δvz (see Fig. 2) and St ≲ α. For this reason, the time required for micron-sized dust particles to grow into pebbles is longer when α ≤ 10-3 than when α = 10-2.
2.5. Pebble accretion
As mentioned at the beginning of Sect. 2, we place an rocky embryo at 1 AU in a protoplanetary disk and allow it to accrete icy pebbles at times t>tstart. Following Guillot et al. (2014), we evaluate the rate of pebble accretion by an embryo, Ṁe, as 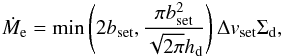 (16)where bset is the effective pebble accretion radius of the embryo and
(16)where bset is the effective pebble accretion radius of the embryo and 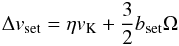 (17)is the (maximum) encounter velocity of the embryo and pebbles. In Eq. (16), the factor min(··· ) accounts for the effect of the sedimentation of the pebbles onto the midplane: the accretion is two-dimensional (Ṁe ≈ 2bsetΔvsetΣd) for bset ≫ hd and three-dimensional (
(17)is the (maximum) encounter velocity of the embryo and pebbles. In Eq. (16), the factor min(··· ) accounts for the effect of the sedimentation of the pebbles onto the midplane: the accretion is two-dimensional (Ṁe ≈ 2bsetΔvsetΣd) for bset ≫ hd and three-dimensional (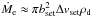 , where
, where 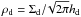 is the midplane pebble density) for the opposite limit (see Sect. 3.2 of Guillot et al. 2014). In the 3D case,
is the midplane pebble density) for the opposite limit (see Sect. 3.2 of Guillot et al. 2014). In the 3D case, 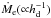 decreases with increasing α, reflecting the fact that turbulence diffuses pebbles away from the midplane where the embryo resides. The first and second terms on the right-hand side of Eq. (17) represents the encounter velocity arising from the sub-Keplerian orbital velocity of the pebbles and from the Keplerian shear, respectively (see Sect. 5.1.3 of Ormel & Klahr 2010). Equation (17) neglects the turbulence-driven encounter velocity ≈
decreases with increasing α, reflecting the fact that turbulence diffuses pebbles away from the midplane where the embryo resides. The first and second terms on the right-hand side of Eq. (17) represents the encounter velocity arising from the sub-Keplerian orbital velocity of the pebbles and from the Keplerian shear, respectively (see Sect. 5.1.3 of Ormel & Klahr 2010). Equation (17) neglects the turbulence-driven encounter velocity ≈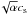 , but this does not affect our results significantly as long as α ≲ 10-3 (for which
, but this does not affect our results significantly as long as α ≲ 10-3 (for which 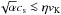 ).
).
For the accretion radius bset, we use a simple empirical relation (Ormel & Kobayashi 2012) ![\begin{eqnarray} b_{\rm set} = b_{\rm set,0} \exp\left[-({\rm St}/2)^{0.65} \right]. \label{eq:bset} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq173.png) (18)Here, bset,0 is the solution to (Ormel & Klahr 2010)
(18)Here, bset,0 is the solution to (Ormel & Klahr 2010) 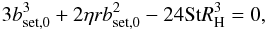 (19)where
(19)where 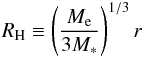 (20)is the Hill radius of the embryo. Equations (18) and (19) apply when the particles are coupled to the disk gas so strongly that they accrete onto the embryo at a terminal velocity. Ormel & Klahr (2010) called this regime the settling regime. Equation (19) originally comes from the consideration that an embryo accretes pebbles whose trajectories are greatly deflected by the embryo’s gravity (Ormel & Klahr 2010; Lambrechts & Johansen 2012). The exponential cutoff appearing in Eq. (18) assumes that RH is considerably smaller than the Bondi radius of the embryo defined with respect to the headwind ηvK,
(20)is the Hill radius of the embryo. Equations (18) and (19) apply when the particles are coupled to the disk gas so strongly that they accrete onto the embryo at a terminal velocity. Ormel & Klahr (2010) called this regime the settling regime. Equation (19) originally comes from the consideration that an embryo accretes pebbles whose trajectories are greatly deflected by the embryo’s gravity (Ormel & Klahr 2010; Lambrechts & Johansen 2012). The exponential cutoff appearing in Eq. (18) assumes that RH is considerably smaller than the Bondi radius of the embryo defined with respect to the headwind ηvK, 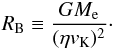 (21)Since (RH/RB)3 = (η6/ 3)(Me/M∗)-2, the assumption RH<RB holds when Me> 0.58η3M∗. At 1 AU, this condition is satisfied for Me ≳ 10-3 M⊕. The exponential cutoff accounts for the fact that efficient accretion through settling takes place only when St ≪ 1. The Bondi and Hill radii satisfy the relations RB/ (ηr) = Me/ (η3M∗) and RH/ (ηr) = 0.58(RB/RH)1 / 2. The latter relation implies that RH ≫ ηr when RH ≪ RB.
(21)Since (RH/RB)3 = (η6/ 3)(Me/M∗)-2, the assumption RH<RB holds when Me> 0.58η3M∗. At 1 AU, this condition is satisfied for Me ≳ 10-3 M⊕. The exponential cutoff accounts for the fact that efficient accretion through settling takes place only when St ≪ 1. The Bondi and Hill radii satisfy the relations RB/ (ηr) = Me/ (η3M∗) and RH/ (ηr) = 0.58(RB/RH)1 / 2. The latter relation implies that RH ≫ ηr when RH ≪ RB.
As pointed out by Lambrechts & Johansen (2012) and Guillot et al. (2014), the settling regime can be divided into two subregimes depending on which of the headwind ηvK and Keplerian shear 3bsetΩ / 2 dominates. When ηvK ≫ 3bsetΩ / 2, or equivalently bset ≪ 2ηr/ 3, the first term in Eq. (19) is negligible compared to the second term, and hence bset is approximately given by  (22)This regime was referred to as the drift accretion regime by Lambrechts & Johansen (2012, see their Eq. (27)) and the Bondi regime by Guillot et al. (2014, the third expression of their Eq. (C.3)). In the opposite limit, bset ≫ 2ηr/ 3, the second term in Eq. (19) is negligible, and we obtain
(22)This regime was referred to as the drift accretion regime by Lambrechts & Johansen (2012, see their Eq. (27)) and the Bondi regime by Guillot et al. (2014, the third expression of their Eq. (C.3)). In the opposite limit, bset ≫ 2ηr/ 3, the second term in Eq. (19) is negligible, and we obtain 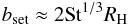 (23)(bset<RH because St ≪ 1 in the settling regime). This corresponds to the Hill accretion regime of Lambrechts & Johansen (2012, see their Eq. (40)). This regime is also essentially equivalent to the Hill regime of Guillot et al. (2014), but the factor 2St1 / 3 appearing in our Eq. (23) is neglected in their limiting expression for bset (the fourth expression of their Eq. (C.3)). A comparison between Eqs. (22) and (23) shows that the Hill accretion applies (i.e., ηvK ≫ bsetΩ) when St satisfies
(23)(bset<RH because St ≪ 1 in the settling regime). This corresponds to the Hill accretion regime of Lambrechts & Johansen (2012, see their Eq. (40)). This regime is also essentially equivalent to the Hill regime of Guillot et al. (2014), but the factor 2St1 / 3 appearing in our Eq. (23) is neglected in their limiting expression for bset (the fourth expression of their Eq. (C.3)). A comparison between Eqs. (22) and (23) shows that the Hill accretion applies (i.e., ηvK ≫ bsetΩ) when St satisfies 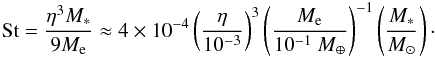 (24)At 1 AU, this condition is equivalent to a ≳ 3 mm. As we see in Sect. 3.2, the pebbles drifting to 1 AU mostly satisfy this condition.
(24)At 1 AU, this condition is equivalent to a ≳ 3 mm. As we see in Sect. 3.2, the pebbles drifting to 1 AU mostly satisfy this condition.
 |
Fig. 4 Pebble accretion radius of an embryo bset (Eq. (18); solid curve) as a function of the pebble radius a. The upper and lower solid curves show bset for embryos of masses Me = 10-1 M⊕ and 10-2 M⊕, respectively. The dashed and dotted lines indicate the Hill radii RH (Eq. (20)) and geometric radii Rgeo = (3 Me/ 4πρe)1 / 3 of the embryos, respectively, where we take ρe = 3 g cm-3. |
 |
Fig. 5 Pebble accretion probability by a single embryo, |
As an example, Fig. 4 shows bset of an embryo located at 1 AU as a function of the pebble size a and of the pebble Stokes number St. For comparison, we also plot the embryo’s geometric radius Rgeo = (3Me/ 4πρe)1 / 3 where the embryo’s internal density ρe is set to 3 g cm-3. For Me ≥ 10-3 M⊕, the accretion radius is considerably larger than Rgeo as long as a ≳ 0.1 mm (see also Fig. 10 of Guillot et al. 2014). At St ~ 1 (a ~ 1 m), the accretion radius reaches the Hill radius RH = (4πρer3/ 9M∗)1 / 3Rgeo ≈ 200 Rgeo.
Free parameters in this study.
Figure 5 shows some examples of the pebble accretion rate as a function of a. We here express the accretion rate in terms of the accretion probability 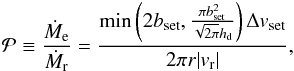 (25)where
(25)where 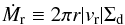 (26)is the radial inward mass flux of dust in the gas disk. By construction,
(26)is the radial inward mass flux of dust in the gas disk. By construction,  measures the fraction of radially drifting pebbles that are filtered by a single embryo. The accretion probability depends on the turbulence strength α via the pebble scale height hd. For comparison, the accretion probability in the two-dimensional limit,
measures the fraction of radially drifting pebbles that are filtered by a single embryo. The accretion probability depends on the turbulence strength α via the pebble scale height hd. For comparison, the accretion probability in the two-dimensional limit, 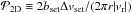 , is also plotted. Since hd decreases with increasing a, accretion of large particles (typically of sizes a ≳ 10 cm) takes place in a 2D manner. In this case, the accretion probability decreases with increasing a because larger particles have a higher drift speed | vr | (bset and Δvset also increase with a, but more slowly than | vset |). Accretion of smaller particles (a ≲ 10 cm) is limited by their large scale height hd compared to the accretion radius bset. For these reasons, the accretion probability has a maximum at the pebble size corresponding to hd ≈ bset. The maximum probability is ~10-2–10-1 for Me = 10-1 M⊕ and ~10-3–10-2 for Me = 10-2 M⊕.
, is also plotted. Since hd decreases with increasing a, accretion of large particles (typically of sizes a ≳ 10 cm) takes place in a 2D manner. In this case, the accretion probability decreases with increasing a because larger particles have a higher drift speed | vr | (bset and Δvset also increase with a, but more slowly than | vset |). Accretion of smaller particles (a ≲ 10 cm) is limited by their large scale height hd compared to the accretion radius bset. For these reasons, the accretion probability has a maximum at the pebble size corresponding to hd ≈ bset. The maximum probability is ~10-2–10-1 for Me = 10-1 M⊕ and ~10-3–10-2 for Me = 10-2 M⊕.
2.6. Parameter choice
The free parameters of our model are the disk size rout, turbulence parameter α, embryos mass before icy pebble accretion Me,0, and the initial time tstart of icy pebble accretion by an embryo at 1 AU. Table 1 lists the parameter choices adopted in this study.
 |
Fig. 6 Time evolution of the surface density Σd (top panels), radius a (middle panels), and radial mass flux Ṁr (bottom panels) of dust particles as a function of orbital radius r for models with α = 10-3 and with rout = 100 AU (left panels) and 300 AU (right panels). The black dotted lines show the initial condition, while the blue dashed, solid, dash-dotted, and dotted lines are the snapshots at times t = 0.1, 0.5, 1, and 5 Myr, respectively. The jumps in Σd and a at r ≈ 1 AU, t = 0.1 Myr are caused by rapid coagulation of particles initially located at these orbits (see text). |
3. Results
We now present the results of our calculations step by step. In Sect. 3.1, we start by presenting the global evolution of icy particles to emphasize how the parameters rout and α control the lifetime of the radial inflow of icy pebbles in a disk. Sect. 3.2 presents the properties of drifting pebbles at 1 AU in more detail. We then consider a rocky embryo forming at the Earth’s orbit and calculate its pebble accretion rate in Sect. 3.3. The resulting evolution of the embryo’s mass and water content is presented in Sect. 3.4.
3.1. Global picture of dust evolution
The top and middle panels of Fig. 6 show the global evolution of the dust surface density Σd and particle size a for α = 10-3. The left and right panels correspond to small and large disks with rout = 100 AU and 300 AU, respectively. The radial mass flux of the particles, Ṁd (Eq. (26)), is shown in the bottom panels. The results for different values of α are presented in Fig. 7. One can see that dust particles grow significantly and are piled up at r ≈ 1 AU in the very early stage of t = 0.1 Myr. This occurs because dust particles initially located at these inner orbits grow beyond the radial drift barrier owing to accelerated coagulation in the Stokes regime (Birnstiel et al. 2010; Okuzumi et al. 2012). However, this feature is immediately erased by the significant amount of pebbles flowing from outer disk regions. Furthermore, in this very early stage, the snow line would be in reality well outside 1 AU. If this is the case, dust particles near 1 AU would be made of silicates rather than water ice, and their collisional growth would be limited by fragmentation (Blum & Wurm 2008; Wada et al. 2009).Since we assume that pebble accretion starts only after t = 0.5 Myr, this early feature has no effect on the results of our pebble accretion calculations.
As demonstrated by many previous studies (e.g., Takeuchi & Lin 2005; Garaud 2007; Brauer et al. 2008a; Birnstiel et al. 2010, 2012; Okuzumi et al. 2012), global dust evolution can be understood from timescale arguments as presented in Sect. 2.4. In protoplanetary disks, dust growth commences from inside out because the growth timescale tgrow (Eq. (14)) is roughly proportional to the orbital period. At each orbital distance, dust particles initially grow without appreciable drift, conserving the dust surface density at that location. This local growth stage continues until the particles acquire a high drift velocity. Once the drift timescale becomes comparable to the growth timescale, the particles start drifting inward so that the two timescales balance each other. In this second stage, the dust surface density at each location is no longer locally conserved and is instead determined by the mass flow of particles drifting from further out. To an order of magnitude, the time required for initially micron-sized particles to grow into drifting pebbles is estimated as ~10tgrow, where the factor 10 accounts for the fact that the particles need to grow by several orders of magnitude in size to acquire a high drift velocity (Lambrechts & Johansen 2014). If we take tgrow ~ 100 / Ω (see Eq. (15)), we have 10tgrow ~ 0.1 Myr at r = 60 AU and 10tgrow ~ 1 Myr at r = 300 AU. This is consistent with the results shown in Fig. 6, where we can see that the radial dust flow originates at ≈60 AU and ≈300 AU for t = 0.1 Myr and 1 Myr, respectively. However, the growth timescale also depends on turbulence strength α as already noted in Sect. 2.4. For example, we can see in Fig. 7 that dust particles at 100 AU have already grown significantly even at 0.1 Myr in the case of α = 10-2. This is because of the short growth timescale at a ≲ 10-2 cm for this value of α (see Fig. 3).
A key parameter that controls the global dust evolution is the radial extent of the initial dust disk, rout. In a typical protoplanetary disk with a surface density gradient dlnΣg/ dlnr> −2, the dominant part of the disk mass resides in outer regions of the disk. The outer edge of a disk thus generally acts as a dust reservoir that produces inwardly drifting pebbles (Garaud 2007; Birnstiel et al. 2012; Lambrechts & Johansen 2014). For example, one can see in the top panels of Fig. 6 that the dust surface density Σd starts decreasing at all orbital distances as the outer edge of the disk gets depleted of dust. The pebble size a decreases at the same time, since the growth timescale becomes longer and longer as Σd declines (see Eq. (14)). The lifetime of this dust reservoir is essentially determined by the growth timescale of the dust at r ~ rout, and hence increases with rout. This explains why the pebble flow in the rout = 100 AU disk diminishes faster than in the rout = 300 AU disk. Our numerical simulations show that dust depletion starts at t ≈ 0.2 Myr for rout = 100 AU and at t ≈ 1 Myr for rout = 300 AU.
3.2. Size and mass flux of pebbles at 1 AU
In the context of pebble accretion, the quantities of interest are the size and radial mass flux of drifting particles at the embryo’s orbit. Figure 8 shows these quantities at the Earth’s orbit, r = 1 AU. As explained in the previous subsection, the size and surface density of the particles decrease as the outer region of the disk is depleted of dust. Before this depletion occurs, particles arriving at 1 AU have a nearly constant radius a ≈ 20–30 cm and a nearly constant Stokes number St ≈ 0.2–0.5, which is consistent with the results of previous studies (Brauer et al. 2008a; Birnstiel et al. 2012; Okuzumi et al. 2012; Lambrechts & Johansen 2014). The radial mass flux at this early time is on the order of 102 M⊕ Myr-1. This directly follows from fact that the dust in outer disk regions has a total mass of ~102 M⊕ (see Eq. (2)) and grows into drifting pebbles on a timescale of ~10 tgrow | r = rout ~ 1 Myr (see Sect. 3.1).
Once the dust depletion at the outer edge begins, the particle size and radial flux decrease with time. The decrease of the particle size can be understood from the competition between coagulation and radial drift. In general, dust particles are allowed to grow as along as the growth timescale is shorter than the drift timescale ~ r/ | vr | ∝ | vr | -1. As Σd decreases, the growth timescale increases (since 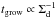 ), and consequently balances with the drift timescale at smaller particle size (since | vr | ∝ St ∝ a).
), and consequently balances with the drift timescale at smaller particle size (since | vr | ∝ St ∝ a).
3.3. Pebble accretion rate
 |
Fig. 7 Time evolution of the surface density Σd (top panel), radius a (middle panel), and radial mass flux Ṁr (bottom panel) of dust particles as a function of orbital radius r for models with rout = 100 AU and with different values of α. The dashed and dotted lines are the snapshots at times t = 0.1 and 5 Myr, respectively. |
Now we apply the results presented in Sect. 3.2 to pebble accretion by an embryo located at the Earth’s orbit. To begin with, we calculate the pebble accretion rate Ṁe (Eq. (16)) of an embryo of fixed mass Me. The evolution of Me is discussed in Sect. 3.4.
In the upper panels of Fig. 9, we plot Ṁe of an embryo with Me = 10-1 M⊕ as a function of time t for different values of rout. Again, the result significantly depends on the value of rout as it determines the lifetime of the dust reservoir at the disk outer edge. At early times when a substantial amount of dust remains at the outer edge (t ≲ 0.5 Myr for rout = 100 AU and t ≲ 1 Myr for rout = 300 AU), particles drifting to 1 AU are 20–30 cm in size (see the upper panels of Fig. 8) and, hence, are swept up by a single 10-1 M⊕ embryo at a probability of ≈1–2% (Fig. 5). Since the radial mass flux of these decimeter-sized particles is 102 M⊕ Myr-1 (the lower panels of Fig. 8), the accretion probability of about 1% results in an accretion rate of ≈1 M⊕ Myr-1 as shown in Fig. 9. This value is insensitive to the choice of α, as long as α ≤ 10-2, because the particle accretion is nearly two-dimensional (hd ≲ bset) at these particle sizes (see Fig. 5). As the dust in the outer disk is depleted, Ṁe decreases with decreasing Ṁr. In this late stage, Ṁe becomes more sensitive to α with a higher α resulting in an even smaller Ṁe. This is mainly because the smaller drifting particles in this stage accrete onto the embryo in a 3D manner (i.e., hd>bset), for which case a higher α results in a lower Ṁe. We can see that Ṁe for α = 10-2 is approximately 10–100 times smaller than that for α = 10-4 in this stage.
 |
Fig. 8 Radius a (upper panels) and radial mass flux Ṁr (lower panels) of drifting particles observed at 1 AU as a function of time t. The left and right panels are for rout = 100 AU and 300 AU, respectively. |
 |
Fig. 9 Pebble accretion rate Ṁe of a single embryo (Eq. (16)) located at 1 AU as a function of time t for Me = 10-1 M⊕ (upper panels) and 10-2 M⊕ (lower panels). The left and right panels are for rout = 100 AU and 300 AU, respectively. |
The results for Me = 10-2 M⊕ (the lower panels of Fig. 9) are qualitatively similar to those for Me = 10-1 M⊕ except that the magnitude of Ṁe is decreased by a factor of 5–10. As we show below, this directly follows from the dependence of the pebble accretion radius bset on Me. Comparison between Eq. (24) and the Stokes number plotted in Fig. 8 shows that pebble accretion occurs in the Hill accretion regime for both values of Me. Since 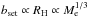 and
and 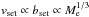 in this accretion regime (see Sect. 2.5), we obtain
in this accretion regime (see Sect. 2.5), we obtain 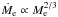 in the 2D case (bset ≲ hd) and Ṁe ∝ Me in the 3D case (bset ≳ hd). Therefore, decreasing Me by the factor of 10 results in a decrease in
in the 2D case (bset ≲ hd) and Ṁe ∝ Me in the 3D case (bset ≳ hd). Therefore, decreasing Me by the factor of 10 results in a decrease in 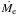 by a factor of 102 / 3–10 ≈ 5–10.
by a factor of 102 / 3–10 ≈ 5–10.
It is worth mentioning at this point that the timescale of embryo growth by pebble accretion, Me/Ṁe, is a weak function of the embryo mass: 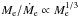 in the 2D case and
in the 2D case and 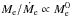 in the 3D case. This implies that the rate at which the embryo’s water mass fraction increases is insensitive to the choice of Me. We confirm this expectation in the following subsection.
in the 3D case. This implies that the rate at which the embryo’s water mass fraction increases is insensitive to the choice of Me. We confirm this expectation in the following subsection.
3.4. Evolution of embryo’s mass and water fraction
We now let an embryo grow through icy pebble accretion to study how much water is delivered to the embryo from icy pebbles. We place a rocky embryo initially devoid of water at 1 AU and allow it to start accreting icy pebbles at t = tstart. We calculate the evolution of the embryo mass Me at t>tstart by integrating Eq. (16) taking the change in the accretion radius bset with the change in Me into account. The evolution of the embryo’s water fraction, fH2O, is computed assuming that the water content of the accreted pebbles is 50 wt%, i.e., 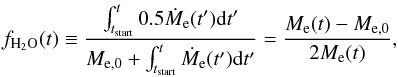 (27)where Me,0 is the initial embryo mass and Me(t) is the embryo mass at time t(>tstart). We have assumed that fH2O = 0 in the initial state.
(27)where Me,0 is the initial embryo mass and Me(t) is the embryo mass at time t(>tstart). We have assumed that fH2O = 0 in the initial state.
Table 2 lists the mass and water content in the final state (taken to be t = 6 Myr) for various sets of model parameters (see Table 1 for the parameter grid). We immediately find that the final water fraction is insensitive to Me,0, which is because the scaled pebble accretion rate Ṁe/Me is nearly independent of Me as already noted in Sect. 3.3. In the following, we focus on the results for Me = 10-1 M⊕.
Mass Me and water content fH2O of a rocky embryo at 1AU for various sets of model parameters.
 |
Fig. 10 Time evolution of the mass Me and water fraction fH2O of an embryo placed at 1 AU with initial mass Me,0 = 10-1 M⊕ for the case of rout = 100 AU. The different curves show results for different initial times of pebble accretion, tstart = 0.5, 1, 2, 3, 4, and 5 Myr (from left to right). |
Figure 10 shows the evolution of Me and fH2O in the rrout = 100 AU disk model for various values of α and tstrart. The results for the larger disk model (rrout = 300 AU) are shown in Fig. 11. In the plots of fH2O, the dashed lines indicate the minimum water content of the present Earth given by the ocean mass, 0.023 wt%. The dotted lines indicate fH2O = 1 wt%, which corresponds to the hypothetical water content of the proto-Earth assuming that the density deficit of the outer core is due to hydrogen delivered in the form of water (Okuchi 1997; Abe et al. 2000). The water content of the proto-Earth much in excess of ~1% seems unlikely (Machida & Abe 2010).
In the case of rrout = 100 AU, whether Earth-forming rocky embryos avoid excessive ice accretion depends on the values of α and tstart. For α = 10-4 (the left panels of Fig. 10), the embryo’s final water content exceeds 0.023 wt% for all tstart ≲ 5 Myr. It even exceeds 1 wt% if tstart is as short as ≲2 Myr. In the extreme case of tstart = 0.5 Myr, the final embryo mass is four times larger than the initial mass, meaning that the rocky embryo has evolved into an icy embryo mostly composed of icy pebbles. The embryo acquires a smaller amount of water if the disk is more turbulent (α is higher). For α = 10-3 and 10-2 (the middle and right panels of Fig. 10), the final fH2O does not exceed 1% if tstart> 1 Myr and 0.5 Myr, respectively. A water fraction of ≲0.023 wt% is achieved if tstart> 4 Myr for α = 10-3 and if tstart > 2 Myr for α = 10-2. This reduction is due to the combination of the accelerated coagulation and 3D pebble accretion already discussed in Sect. 3.3.
Preserving a rocky embryo from icy pebbles is much more difficult when the gas disk extends to 300 AU (Fig. 11). In this case, no parameter set is found to result in a final water content smaller than 0.023 wt%. Even a final water content of ≲1 wt% is realized only if α = 10-2 and tstart ≳ 3 Myr. Instead, we find that the initially rocky embryo evolves into a super-Earth to Neptune-mass icy planet if tstart ≲ 0.5–2 Myr (the smaller and large values correspond to α = 10-2 and 10-4, respectively). Our results for rout = 300 AU and tstart = 0.5 Myr are similar to the results of Lambrechts & Johansen (2014) for giant planet core formation in outer disk regions. This is reasonable because the pebble flow of Lambrechts & Johansen (2014) is assumed to decay on the timescale of 3 Myr, while the pebble flow in our rout = 300 AU calculations decays on a similar timescale.
In summary, we find that embryos orbiting at 1 AU can remain rocky at a level of fH2O ≲ 0.023 wt% if the disk size is 100 AU or smaller, turbulence is stronger than α = 10-3, and the snow line passes 1 AU later than 2–4 Myr after disk formation. Keeping the water fraction at a level of fH2O ≲ 1 wt% with a disk size of 100 AU is possible if the snow line migrates in after t = 0.5–2 Myr. If the disk is as large as 300 AU, a final water fraction of ≲0.024 wt% is very unlikely, and a final fraction of ≲1 wt% is possible only if turbulence is strong (α = 10-2) and if the snow line migrates later than 3 Myr.
4. Discussion
4.1. Dependence on the temperature profile
We have simplified the radial temperature profile T(r) with a single power law for an optically thin disk (Eq. (3)). In an optically thick disk, the temperature profile is steeper in inner regions where viscous heating dominates and is shallower in outer regions where stellar irradiation dominates. Detailed modeling of the temperature profile is beyond the scope of this paper, but we show below that our results are fairly insensitive to the choice of the temperature profile.
We adopt the temperature profile of an optically thick disk around a Sun-like star presented by Oka et al. (2011). We select one of their models in which Ṁ = 10-8 M⊙ yr-1 and α = 10-3 with a dust opacity mimicking that of Garaud & Lin (2007). We chose this model because the midplane temperature reaches 170 K at 1 AU as in our fiducial temperature profile. The radial profile of the midplane temperature for this model is shown in their Fig. 8 (black solid line). We find that this profile can be reasonably reproduced by a simple analytic fit ![\begin{eqnarray} T(r) = \sqrt{[160 (r/1~{\rm AU})^{-1.15}]^2 + [70 (r/1~{\rm AU})^{-0.26}])^2}~{\rm K}, \label{eq:T_ONI11} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq324.png) (28)which is shown by the dashed curve in our Fig. 12. In this model, viscous heating is effective at ≲4 AU and the temperature in that region rises toward the central star as steeply as T ∝ r-1.15. However, as far as the region 1 AU ≤ r ≤ 300 AU is concerned, the difference in the values of T between the two models is small with the maximum deviation of ≈60%. The surface density profile in this viscous disk model differs from the MMSN model (Eq. (1)). However, we keep using the MMSN density profile to isolate the effects of changing the temperature profile.
(28)which is shown by the dashed curve in our Fig. 12. In this model, viscous heating is effective at ≲4 AU and the temperature in that region rises toward the central star as steeply as T ∝ r-1.15. However, as far as the region 1 AU ≤ r ≤ 300 AU is concerned, the difference in the values of T between the two models is small with the maximum deviation of ≈60%. The surface density profile in this viscous disk model differs from the MMSN model (Eq. (1)). However, we keep using the MMSN density profile to isolate the effects of changing the temperature profile.
We fix Me,0 = 10-1 M⊕ and α = 10-3 and only vary the values of rout and tstart. The results for the two different temperature models are compared in Fig. 13. Here, the solid curves show the evolution of the embryo water fraction fH2O for our temperature profile (Eq. (3)), which is already shown in the lower center panels of Figs. 10 and 11, while the dashed curves are for the viscous disk temperature profile given by Eq. (28). One can see that the predicted water fraction of the embryo is very insensitive to the choice of the temperature profile. A closer inspection shows that in the rout = 100 AU case (the left panel of Fig. 12), the viscous temperature model leads to a slightly higher fH2O, in particular, at t ≳ 2 Myr at which the radial pebble flux has already decayed to 0.1 M⊕ Myr-1 (see the lower left panel of Fig. 8). However, the final values of fH2O in the viscous model are only larger than those in our fiducial model by a factor of less than 2. We conclude that the details of the assumed temperature profile do not affect our conclusions.
4.2. Migration timescale of the snow line
We have shown in Sect. 3 that the fate of terrestrial embryos largely depends on the timing of inward snow-line migration, tstart. Rocky embryos are able to avoid excessive icy pebble accretion only if the snow line migrates in after the radial pebble flux in the disk is sufficiently depleted. This is already obvious from the estimate of the pebble accretion rate presented in Sect. 3.3. The pebble accretion rate of a 0.1 Earth mass embryo before dust depletion is ~1 M⊕ Myr-1, which roughly amounts to 0.1 Earth ocean mass (~10-5 M⊕) in 10 years. If the Earth-forming embryos contained less water than on the ocean of the present Earth (water content ≲0.023 wt%), the snow line must have migrated to 1 AU as late as 2–4 Myr after nebula formation (assuming that the nebula had a radial extent of ~100 AU; see Fig. 10). Even if the Earth formed from wetter embryos of water content 1 wt% (Machida & Abe 2010), the migration of the snow line must have occurred no earlier than 0.5–2 Myr.
 |
Fig. 12 Temperature profiles adopted in this study (Eq. (3); solid line) and from a viscous accretion model of Oka et al. (2011; Eq. (28); dashed curve). |
The remaining question is then whether these conditions can be satisfied in a realistic protoplanetary disk. Addressing this questing with a detailed model of snow-line migration is beyond the scope of this paper. Here we attempt to estimate the timescale of snow-line migration assuming that (i) viscous heating dominates over stellar irradiation; and that (ii) the disk opacity is constant in time. In this simplest case, the timescale of snow-line evolution is essentially given by the viscous evolution timescale of the disk, 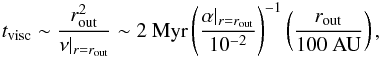 (29)where ν = αcshg is the turbulent viscosity and we have used Eq. (3) in the final expression. If we take rout = 100 AU and α | r = rout = 10-2, we obtain tvisc ~ 2 Myr, which is comparable to the time required for sufficient dust depletion. Therefore, snow-line migration after the decay of the radial pebble flow is a possible explanation for the origin of the dry Earth. However, Eq. (29) only serves as a rough estimate of tstart, and a more precise assessment taking into account viscous evolution, stellar evolution, and the evolution of the disk opacity due to dust evolution is necessary. This will be addressed in future work.
(29)where ν = αcshg is the turbulent viscosity and we have used Eq. (3) in the final expression. If we take rout = 100 AU and α | r = rout = 10-2, we obtain tvisc ~ 2 Myr, which is comparable to the time required for sufficient dust depletion. Therefore, snow-line migration after the decay of the radial pebble flow is a possible explanation for the origin of the dry Earth. However, Eq. (29) only serves as a rough estimate of tstart, and a more precise assessment taking into account viscous evolution, stellar evolution, and the evolution of the disk opacity due to dust evolution is necessary. This will be addressed in future work.
We point out that tvisc ∝ rout whereas 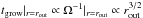 . This implies that when rout is small, the snow line tends to migrate more slowly than icy dust in the disk becomes depleted (whose timescale is ∝ tgrow at r = rout). This argument also supports the idea that preservation of rocky embryos from ice pebbles favors a compact protoplanetary disk.
. This implies that when rout is small, the snow line tends to migrate more slowly than icy dust in the disk becomes depleted (whose timescale is ∝ tgrow at r = rout). This argument also supports the idea that preservation of rocky embryos from ice pebbles favors a compact protoplanetary disk.
On the other hand, an extended disk is beneficial for forming the cores of gas giants at wider orbits through the pebble accretion mechanism (Lambrechts & Johansen 2014). As we discuss below, such fully grown cores could save the rocky embryos in the inner disk by halting the ice pebble flow.
4.3. Possible mechanisms for pebble filtration outside 1 AU
We have restricted ourselves to the simplest (and most pessimistic) case where all icy pebbles forming in outer disk regions are allowed to drift to 1 AU. In fact, there are some known mechanisms that might halt or filter the pebble flux before they reach rocky embryos. Ignoring such possibilities effectively means that we have assumed these mechanisms operate only after the snow line migrates to 1 AU. We here mention some import mechanisms and discuss whether they are likely to have operated in the solar nebula.
The most straightforward scenario would be that planetesimals or embryos outside the Earth’s orbit filter out incoming pebbles just in the same way as what we considered for Earth-forming embryos. However, it turns out an efficient filtration is not expected with this mechanism in many cases. We have shown in Sect. 3.3 that each 0.1M⊕-mass embryo captures only ≈1–2% of the pebble flux in a disk. Assuming that the total mass of terrestrial embryos in the minimum-mass solar nebula is ≈2 M⊕ (Earth + Venus), the total number of the embryos is ≈20, and therefore they filter only ≈20–40% of the pebble flux in total. The low (<50%) efficiency of dust filtration by a small number of embryos are consistent with the results by Morbidelli & Nesvorny (2012), Lambrechts & Johansen (2014), and Morbidelli et al. (2015). A more systematic study on pebble filtration by planetesimal- or embryo-sized objects has been carried out by Guillot et al. (2014) using essentially the same pebble accretion formula as ours. They found that perfect filtration beyond 1 AU is possible only if most of the dust in the planet-forming region is converted into ~1000 km-sized embryos and if disk turbulence is α = 10-4 (see their Fig. 22). Moriarty & Fischer (2015) obtained qualitatively similar results; these authors considered the accretion of cm-sized drifting pebbles by initially 100 km-sized planetesimals in an α = 10-3 gas disk and showed that the inward flux of cm-sized pebbles is nearly constant down to 1 AU (see their Fig. 2). These suggest that a swarm of outer planetesimals and embryos is only able to fully filter the icy pebble flow in a particular range of parameter space. Whether such a situation was realized in the solar nebula over the lifetime of pebble flow (~0.5–2 Myr) is unclear.
 |
Fig. 13 Same as the lower center panels of Figs. 10 and 11, but here the results for the temperature profile from an optically thick viscous disk model (Eq. (28)) are overplotted (dashed curves). |
A more promising mechanism for pebble filtration is particle trapping at pressure maxima in the gas disk. In general, the direction of particle radial drift is determined by the sign of the pressure gradient of the disk (Eq. (10)), and therefore particles tend to accumulate toward locations where the gas pressure is locally maximized (Whipple 1972). A pressure bump may be created by magnetorotational turbulence (e.g., Johansen et al. 2009; Uribe et al. 2011), by a steep gradient in the gas viscosity (e.g., Kretke & Lin 2007; Dzyurkevich et al. 2010; Flock et al. 2015), or by a massive planet or embryo that carves a gap in the gas disk (e.g., Paardekooper & Mellema 2006; Rice et al. 2006; Zhu et al. 2012; Morbidelli & Nesvorny 2012; Lambrechts et al. 2014).
Interestingly, the snow line has been regraded as a candidate that might naturally produce a pressure bump (Kretke & Lin 2007; Dzyurkevich et al. 2010; Brauer et al. 2008b; Dra¸żkowska et al. 2013). This idea is based on the assumptions that (i) the dust surface density has a jump there and that (ii) the jump in the surface density leads to a jump in the magnetic turbulent viscosity large enough to build up a pressure bump via ionization chemistry. Although the first assumption is likely to be true qualitatively, the second assumption has not yet been validated with magnetohydrodynamic simulations incorporating a realistic ionization model.
By contrast, hydrodynamical simulations have demonstrated the viability of particle trapping at the edges of planetary gaps (Paardekooper & Mellema 2006; Zhu et al. 2012). Simulations by Paardekooper & Mellema (2006) and Lambrechts et al. (2014) show that a planet larger than ~20 M⊕ in mass carves a gap that can efficiently trap incoming pebbles. This suggests that excessive water delivery to terrestrial planetary embryos may be avoided if such a massive planet forms prior to the inward migration of the snow line. This possibility has also been pointed out in a recent paper by Morbidelli et al. (2016). Assuming that the snow line moves on a timescale of ~2 Myr as estimated in Sect. 4.2, the standard planet formation from planetesimals is too slow to satisfy this requirement unless the disk is massive and the collisional fragmentation of the bodies is negligible (Kokubo & Ida 2002; Kobayashi et al. 2010). By contrast, planet growth driven by pebble accretion can take place on this timescale as demonstrated by Lambrechts & Johansen (2014).
To conclude, this study has shown that depletion of icy pebbles before the migration of the snow line is a possible explanation for the origin of water-devoid terrestrial planets, but pebble filtration by a gap-forming planet (in the solar system, Jupiter or Saturn) that forms before the snow-line migration might be an equally viable alternative. The scenario that is favored for the solar system is unclear and needs to be answered in future studies.
5. Conclusions
We have studied how icy pebbles drifting from outer regions of protoplanetary disks affect the water fraction of terrestrial embryos near the Earth’s orbit. We numerically solved a simplified version of the coagulation equation to calculate the global evolution of the characteristic size and mass flux of drifting icy pebbles. In contrast to the previous study on pebble accretion by Lambrechts & Johansen (2014), our model explicitly takes the finite radial extent of a protoplanetary disk into account, and therefore automatically includes the effect that the radial pebble flux diminishes as the outermost region of the disk is depleted of icy dust. We calculated the rate of pebble accretion by a single embryo following the analytic expressions by Ormel & Klahr (2010) and Guillot et al. (2014). Our calculation accounts for the 3D nature of pebble accretion, i.e., the reduction of the accretion rate due to vertical pebble diffusion, in the presence of strong gas turbulence. We have predicted how the mass and water content of an initially rocky embryo increase with time after icy pebble accretion sets in. The predicted water fraction was compared with the minimum water fraction of the present Earth inferred from the ocean mass (0.023 wt%) and with the hypothetical water fraction of the proto-Earth inferred from the density deficit of the Earth’s outer core (1 wt%).
Our key findings are summarized as follows:
-
1.
The evolution of the icy pebble flow largely depends on the radial extent of the gas disk rout (Sects. 3.1 and 3.2). In general, radially drifting pebbles form from inside out in protoplanetary disks because the timescale of pebble formation roughy scales with the orbital timescale. The radial extent of a disk therefore sets the lifetime of the pebble flow in the disk with smaller rout corresponding to a shorter lifetime. Turbulence somewhat accelerates pebble formation in outermost regions, but its effect is relatively minor when compared to the effect of rout. The radial pebble flux is ~102 M⊕ Myr-1 at early times, and starts decaying with time at t ≈ 0.2 Myr for rout = 100 AU and at t ≈ 1 Myr for rout = 300 AU. The pebble size observed at 1 AU is a few decimeters at early times, and decreases with the pebble flux because a lower particle density generally leads to slower particle growth.
-
2.
The rate of pebble accretion onto an embryo also decreases with time, the details of which depend on rout and on turbulence strength α (Sect. 3.3). The pebble accretion rate is initially ~1 M⊕ Myr-1, reflecting the fact that the radial mass flux is ~102 M⊕ Myr-1 and the accretion efficiency of dm-sized particles is ~1% (Fig. 5). The accretion rate roughly scales linearly with the embryo mass, and therefore the embryo’s water fraction increases with time nearly independent of the embryo mass. Turbulence suppresses the accretion rate at late times by diffusing small pebbles away from the midplane. Combining this effect with the acceleration of pebble depletion mentioned above, strong turbulence of α = 10-2 reduces the pebble flux by 1–2 orders of magnitude from the cases with weaker turbulence (α = 10-3 and 10-4).
-
3.
Preserving water-devoid embryos at 1 AU generally requires that the snow line reaches that location after the radial pebble flux through the disk has already decayed to a sufficient extent (Sect. 3.4). In a disk of rout ≲ 100 AU and α ≳ 10-3, the fractional water content of the embryos is kept below the current Earth’s water content based on the ocean mass (0.023 wt%) if the time tstart at which the snow lines passes 1 AU is longer than 2–4 Myr (smaller tstart corresponds to stronger turbulence). If rout ≥ 300 AU or α ≤ 10-4, the water content greatly exceeds 0.023 wt% for all tstart ≲ 5 Myr. Keeping the water fraction at a level of ≲1 wt% is possible in a rout = 100 AU disk if tstart ≳ 0.5–2 Myr. Keeping the water fraction at the same level is much more difficult in a rout = 300 AU disk because of a prolonged pebble flow.
Our results provide strong constraints on the formation history and environment of Earth-forming embryos in the solar nebula within the assumption that no mechanism halted the ice pebble flow upstream. Overall, our results suggest that the solar nebula must have been relatively compact (rout = 100 AU or smaller), so that the pebble flow had decayed at early times. The formation of terrestrial embryos as dry as the present Earth was possible if moderately strong turbulence (α ≳ 10-3) was present at 1 AU. However, the latest magnetohydrodynamical disk models (e.g., Bai & Stone 2013; Lesur et al. 2014) suggest that turbulence is considerably weaker than this requirement in inner regions of protoplanetary disks4 For rout = 100 AU and α = 10-4, embryos as dry as the present Earth would not have formed, but embryos containing ≲1 wt% water would have formed if the snow line migrated on a timescale of ≳2 Myr. This is one plausible scenario that can explain the origin of our dry Earth because the snow line in the nebula could indeed have migrated on a similar timescale (Sect. 4.2).
Another possible scenario, which we have not tested in this study, is that a massive planet (a gas giant or its core) formed and created a pebble gap in the nebula before the snow line reached 1 AU (Sect. 4.3; see also Morbidelli et al. 2016). The scenario favored as the explanation for the dry Earth remains to be studied in future work.
One important caveat of this study is that our pebble evolution model greatly simplifies the collisional growth of ice aggregates. Future models should include the evolution of aggregate porosity (Ormel et al. 2007; Okuzumi et al. 2009; Kataoka et al. 2013b) since porous aggregates tend to collide more frequently than compact equivalents in protoplanetary disks (Okuzumi et al. 2012; Kataoka et al. 2013a). The global simulation of dust coagulation and porosity evolution by Okuzumi et al. (2012) shows that highly fluffy ice aggregates produced in inner (≲10 AU) protoplanetary disks grow to planetesimal-mass objects with little appreciable drift. However, the simulation also shows that fluffy aggregates forming in the outer (≳10 AU) region drift in until they arrive at the snow line. The accretion rate of these fluffy aggregates onto inner embryos could be greatly different from that of compact aggregates. Bounding and fragmentation of aggregates are also potentially important, but might not be crucial given the sticky nature of ice aggregates (see Wada et al. 2009, 2011, 2013; Gundlach & Blum 2015).
Another important caveat is that it is still a matter of debate whether the snow line around a solar-mass star really migrates inward to 1 AU. The model of Martin & Livio (2012), which predicts that the snow line never reaches 1 AU in late evolutionary stages, relies on the idea that weak magnetic turbulence expected at ~1 AU (e.g., Gammie 1996; Sano et al. 2000) triggers gravitational instability that in turn heats up the disk gas at that location. On the other hand, recent magnetohydrodynamical simulations have shown that, even without magnetic turbulence, large-scale (non-turbulent) magnetic fields are still able to provide inner protoplanetary disks with high gas accretion rates (e.g., Turner & Sano 2008; Bai & Stone 2013; Lesur et al. 2014; Gressel et al. 2015). A model incorporating these important accretion mechanisms is needed to fully understand the evolution of the snow line.
The results of this study also have important implications for the water content of exoplanets lying inside the habitable zone. Mulders et al. (2015) recently predicted the water content distribution of habitable-zone terrestrial planets assuming that the planets acquire water by accreting water-bearing (water content =5%) embryos and planetesimals. However, our results suggest that a significantly higher amount of water could be delivered to habitable-zone planets in the form of icy pebbles from outer orbital radii. A significant amount of water does not necessarily make habitable-zone planets habitable because the presence of land might be required for the emergence of life (Dohm & Maruyama 2015). In any case, it would be interesting to predict the water content of habitable-zone exoplanets by taking ice pebble accretion into account.
Recently, Krijt et al. (2016) proposed a single-size scheme based on the Lagrangian description.
Precisely, the right-hand side of Eq. (5) is  times the product of 4πa2, Δvpp, and
times the product of 4πa2, Δvpp, and  .
.
There is a typographical error in the expression for ΔvB in Okuzumi et al. (2012, their Eq. (17)).
In addition, turbulence of α> 10-3 would inhibit the formation of rocky embryos via rocky pebble accretion within the lifetime of protoplanetary disks (Johansen et al. 2015; Morbidelli et al. 2015) for the same reason that it prevents excessive water delivery.
Acknowledgments
We would like to thank Takanori Sasaki for pointing out the importance of pebble accretion in the context of water delivery to the Earth. We also thank Chris Ormel for discussions on the modeling of pebble accretion; Taishi Nakamoto, Hidenori Genda, Masanobu Kunitomo, Tetsuo Taki, for helpful comments; and Sebastiaan Krijt for sharing with us an early version of his paper prior to publication. S.O. especially thanks Chris Ormel for his very insightful comments on the formulation of the single-size approach based on the moment method. Finally, we thank the referee, Michiel Lambrechts, for his prompt and constructive report which significantly improved the quality of this paper.This work is supported by Grants-in-Aid for Scientific Research (#23103005, 15H02065) from MEXT of Japan.
References
- Abe, Y., Ohtani, E., Okuchi, T., Righter, K., & Drake, M. 2000, in Water in the Early Earth, Origin of the Earth and the Moon, eds. R. M. Canup, K. Righter, et al. (Tucson: University of Arizona Press), 413 [Google Scholar]
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F. 2011, ARA&A, 49, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2015, Science, 347, 1261952 [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2007, ApJ, 659, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Baillié, K., Charnoz, S., & Pantin, E. 2015, A&A, 577, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008a, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Henning, T., & Dullemond, C. P. 2008b, A&A, 487, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauphas, N., & Pourmand, A. 2011, Nature, 473, 489 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Davis, S. S. 2005, ApJ, 620, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Dohm, J. M., & Maruyama, S. 2015, Geoscience Frontiers, 6, 95 [CrossRef] [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, T. M., & Hodges, Jr., R. R. 1992, J. Geophys. Res., 97, 6083 [Google Scholar]
- Drążkowska, J., Windmark, F., & Dullemond, C. P. 2013, A&A, 556, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Estrada, P. R., & Cuzzi, J. N. 2008, ApJ, 682, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrier, B. S. 1994, J. Atm. Sci., 51, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., González, M., & Commerçon, B. 2013, A&A, 560, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., & Papaloizou, J. 2006, A&A, 452, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P. 2007, ApJ, 671, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P., & Lin, D. N. C. 2007, ApJ, 654, 606 [Google Scholar]
- Genda, H., & Abe, Y. 2005, Nature, 433, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Turner, N. J., Nelson, R. P., & McNally, C. P. 2015, ApJ, 801, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hirose, S., & Turner, N. J. 2011, ApJ, 732, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Youdin, A., & Klahr, H. 2009, ApJ, 697, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 15109 [Google Scholar]
- Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013a, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013b, A&A, 554, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, H., Tanaka, H., Krivov, A. V., & Inaba, S. 2010, Icarus, 209, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2002, ApJ, 581, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Kornet, K., Stepinski, T. F., & Różyczka, M. 2001, A&A, 378, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretke, K. A., & Levison, H. F. 2014, AJ, 148, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2015, A&A, 574, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2016, A&A, 586, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurokawa, H., Sato, M., Ushioda, M., et al. 2014, Earth and Planetary Science Letters, 394, 179 [Google Scholar]
- Kusaka, T., Nakano, T., & Hayashi, C. 1970, Prog. Theor. Phys., 44, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015a, Nature, 524, 322 [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., Walsh, K. J., & Bottke, W. F. 2015b, Proc. National Academy of Science, 112, 14180 [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1980, MNRAS, 191, 37 [NASA ADS] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, R., & Abe, Y. 2010, ApJ, 716, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, R. G., & Livio, M. 2012, MNRAS, 425, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Dullemond, C. P., Kama, M., & Dominik, C. 2011, Icarus, 212, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bitsch, B., Crida, A., et al. 2016, Icarus, 267, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Moriarty, J., & Fischer, D. 2015, ApJ, 809, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., Ciesla, F. J., Min, M., & Pascucci, I. 2015, ApJ, 807, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Nimmo, F., & McKenzie, D. 1998, Ann. Rev. Earth Planet. Sci., 26, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, R., Hirose, K., Uesugi, K., et al. 2014, Science, 343, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, A., Nakamoto, T., & Ida, S. 2011, ApJ, 738, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Okuchi, T. 1997, Science, 278, 1781 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., & Sakagami, M.-A. 2009, ApJ, 707, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Momose, M., Sirono, S.-i., Kobayashi, H., & Tanaka, H. 2016, ApJ, in press [arXiv:1510.03556] [Google Scholar]
- Ormel, C. W. 2014, ApJ, 789, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Cuzzi, J. N. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Spaans, M. 2008, ApJ, 684, 1291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Spaans, M., & Tielens, A. G. G. M. 2007, A&A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 453, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinn, R. G., & Fegley, B. 1987, Ann. Rev. Earth Planet. Sci., 15, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sano, T., Miyama, S. M., Umebayashi, T., & Nakano, T. 2000, ApJ, 543, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lecar, M. 2000, ApJ, 528, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sirono, S.-I. 2011a, ApJ, 733, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Sirono, S.-I. 2011b, ApJ, 735, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Suyama, T., Wada, K., & Tanaka, H. 2008, ApJ, 684, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2005, ApJ, 623, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., & Sano, T. 2008, ApJ, 679, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Choukroun, M., Castillo-Rogez, J., & Bryden, G. 2012, ApJ, 748, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Uribe, A. L., Klahr, H., Flock, M., & Henning, T. 2011, ApJ, 736, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Okuzumi, S., et al. 2013, A&A, 559, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W., & Stewart, G. R. 1989, Icarus, 77, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1972, in From Plasma to Planet, Proc. of Symp., ed. A. Elvius, 211 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation and justification of the single-size approach
Appendix A.1: Derivation of Eqs. (4) and (5) from the coagulation equation
In this subsection, we derive the single-size Eqs. (4) and (5) from the coagulation (Smoluchowski) equation. We define the size distribution function n(r,z,m) as the particle number density per unit particle mass m at orbital radius r and distance from midplane z. Assuming the balance between vertical sedimentation and turbulent diffusion of the particles, the particle size distribution can be written as 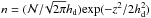 , where
, where  is the column number density of dust particles per unit m and hd(m) is the dust scale height. The evolution of
is the column number density of dust particles per unit m and hd(m) is the dust scale height. The evolution of  is given by the vertically integrated coagulation equation with the drift term (Brauer et al. 2008a)
is given by the vertically integrated coagulation equation with the drift term (Brauer et al. 2008a) ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{\partial \mathcal{N}(r,m)}{\partial t} &=& \frac{1}{2}\int_{0}^{m} K(r; m',m-m')\mathcal{N}(r,m')\mathcal{N}(r,m-m'){\rm d}m' \notag \\[-1mm] && - \mathcal{N}(r,m)\int_{0}^{\infty} K(r; m,m')\mathcal{N}(r,m'){\rm d}m' \notag \\[-1mm] && - \frac{1}{r}\frac{\partial}{\partial r}\left[ rv_{\rm r}(r,m)\mathcal{N}(r,m) \right]. \label{eq:coag_N} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq362.png) (A.1)Here, K is the vertically integrated collision rate coefficient given by
(A.1)Here, K is the vertically integrated collision rate coefficient given by ![\appendix \setcounter{section}{1} \begin{eqnarray} K(r; m_{1},m_2) &=& \frac{{\sigma}_{\rm coll}}{2{\pi}h_{\rm d,1}h_{\rm d,2}}\int_{-\infty}^{\infty} {\Delta}v_{\rm pp}\nonumber\\[-1mm] &&\times{\exp}\left[ -\frac{z^2}{2}\left(\frac{1}{h_{\rm d,1}^2} + \frac{1}{h_{\rm d,2}^2}\right)\right]{\rm d}z, \label{eq:coeffK} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq364.png) (A.2)where hd,1 and hd,2 are the scale heights of the two colliding particles. On the right-hand side of Eq. (A.1), the first term represents the gain of
(A.2)where hd,1 and hd,2 are the scale heights of the two colliding particles. On the right-hand side of Eq. (A.1), the first term represents the gain of  by coagulation of two particles of masses m′ and m − m′, the second term the loss of
by coagulation of two particles of masses m′ and m − m′, the second term the loss of 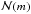 by coagulation of a particle of mass m with a particle of mass m′, and the third term the advection of
by coagulation of a particle of mass m with a particle of mass m′, and the third term the advection of 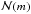 due to radial drift.Because we assume perfect sticking upon collision, the collisional cross section is simply given by σcoll = π(a1 + a2)2, where a1 and a2 are the particle radii.
due to radial drift.Because we assume perfect sticking upon collision, the collisional cross section is simply given by σcoll = π(a1 + a2)2, where a1 and a2 are the particle radii.
Since we are interested in the mass flow of radially drifting dust particles, it is useful to introduce the surface mass density of dust per unit particle mass 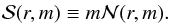 (A.3)Multiplying Eq. (A.1) by m, the equation for
(A.3)Multiplying Eq. (A.1) by m, the equation for 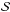 is obtained as
is obtained as ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{\partial{\cal S}(m)}{\partial t} &=& \frac{m}{2}\int_{0}^{m} K'(m',m-m') {\cal S}(m'){\cal S}(m-m'){\rm d}m' \notag \\ && - m{\cal S}(m) \int_{0}^{\infty} K'(m,m'){\cal S}(r,m'){\rm d}m' \notag \\ &&- \frac{1}{r}\frac{\partial}{\partial r} \left[ r v_{\rm r}(m){\cal S}(m) \right], \label{eq:coag_S} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq375.png) (A.4)where K′(m,m′) ≡ K(m,m′) /mm′ and we have omitted the argument r from the expression for clarity.
(A.4)where K′(m,m′) ≡ K(m,m′) /mm′ and we have omitted the argument r from the expression for clarity.
One important quantity characterizing the mass distribution 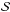 is the so-called peak mass defined by (Ormel & Spaans 2008)
is the so-called peak mass defined by (Ormel & Spaans 2008)  (A.5)When
(A.5)When  is a unimodal function of m, this quantity is approximately equal to the mass at the peak of
is a unimodal function of m, this quantity is approximately equal to the mass at the peak of 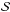 (see Ormel & Spaans 2008). Another important quantity is of course the total surface density defined by
(see Ormel & Spaans 2008). Another important quantity is of course the total surface density defined by  (A.6)We now derive the equations that determine the evolution of Σd and mp from Eq. (A.4). We begin by introducing the ith moment of the surface mass density distribution
(A.6)We now derive the equations that determine the evolution of Σd and mp from Eq. (A.4). We begin by introducing the ith moment of the surface mass density distribution  ,
,  (A.7)The quantity ℳi is equal to the (i + 1)-th moment of the surface number density distribution
(A.7)The quantity ℳi is equal to the (i + 1)-th moment of the surface number density distribution  since
since  . It follows from Eqs. (A.5) and (A.6) that the total dust surface density Σd and peak mass mp are related to ℳi as
. It follows from Eqs. (A.5) and (A.6) that the total dust surface density Σd and peak mass mp are related to ℳi as 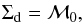 (A.8)
(A.8)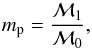 (A.9)respectively.
(A.9)respectively.
The equation that determines the evolution of ℳi can be derived by multiplying Eq. (A.4) by mi and integrating over m. After some algebra, the result can be simplified as (see, e.g., Estrada & Cuzzi 2008; Ormel & Spaans 2008, but note that they define the moment in terms of the number density) ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{\partial{\cal M}_i}{\partial t} &=& \frac{1}{2}\int_0^\infty {\rm d}m\, {\rm d}m' \, K'(m,m'){\cal S}(m){\cal S}(m') \notag \\ &&\qquad \times \left[\left(m+m'\right)^{i+1}-\left(m^{i+1}+m'^{i+1}\right)\right] \notag \\ &&\qquad - \frac{1}{r}\frac{\partial}{\partial r} \left( r \bracket{m^i{v}_{\rm r}}{{\Sigma}}_{\rm d} \right), \label{eq:evol_Mp} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27069-15/aa27069-15-eq389.png) (A.10)where
(A.10)where 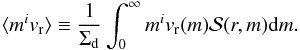 (A.11)For i = 0, Eq. (A.10) has the simple form
(A.11)For i = 0, Eq. (A.10) has the simple form 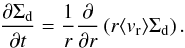 (A.12)The coagulation terms (the first and second terms) in Eq. (A.10) have canceled out, as it should be since Σd is a conserved quantity in the absence of advection and diffusion. Since ℳ1 = mpΣd, the equation for i = 1 can be written as
(A.12)The coagulation terms (the first and second terms) in Eq. (A.10) have canceled out, as it should be since Σd is a conserved quantity in the absence of advection and diffusion. Since ℳ1 = mpΣd, the equation for i = 1 can be written as  (A.13)The right-hand sides of Eqs. (A.12) and (A.13) are not closed with respect to Σd and mp because of the presence of the ⟨ mivr ⟩ terms. To derive approximate but closed equations for Σd and mp, we assume that
(A.13)The right-hand sides of Eqs. (A.12) and (A.13) are not closed with respect to Σd and mp because of the presence of the ⟨ mivr ⟩ terms. To derive approximate but closed equations for Σd and mp, we assume that 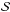 is narrowly peaked at m ≈ mp. Specifically, we assume
is narrowly peaked at m ≈ mp. Specifically, we assume 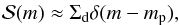 (A.14)where the normalization is determined by Eq. (A.8). If we use Eq. (A.14), the term ⟨ mivr ⟩ can now be replaced by
(A.14)where the normalization is determined by Eq. (A.8). If we use Eq. (A.14), the term ⟨ mivr ⟩ can now be replaced by 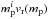 , and hence Eq. (A.12) immediately reduces to Eq. (4) in the main text. Equation (A.13) reduces to
, and hence Eq. (A.12) immediately reduces to Eq. (4) in the main text. Equation (A.13) reduces to 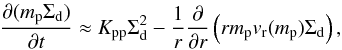 (A.15)where
(A.15)where 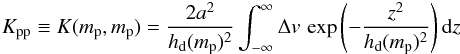 (A.16)and a is the radius of peak-mass particles. If Δv can be taken outside the vertical integration, we have
(A.16)and a is the radius of peak-mass particles. If Δv can be taken outside the vertical integration, we have 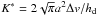 . Substituting this expression into Eq. (A.15) and combining with Eq. (4), we obtain Eq. (5) in the main text.
. Substituting this expression into Eq. (A.15) and combining with Eq. (4), we obtain Eq. (5) in the main text.
 |
Fig. A.1 Comparison between single- and full-size coagulation calculations. The solid lines show the snapshots of the peak mass mp (Eq. (A.9); upper panel) and total dust surface density Σd (Eq. (A.8); lower panel) at different times as a function of orbital radius r obtained from the full coagulation simulation for the compact aggregation model by Okuzumi et al. (2012, see also their Fig. 2). The dashed line shows our reproduction using the single-size approach (Eq. (4) for Σd and Eq. (5) for mp) with ϵ = 0.5 (see Sect. 2.4 for the definition of ϵ). |
 |
Fig. A.2 Comparison between the full-size simulation (Okuzumi et al. 2012) and single-size simulations using different values of ϵ. The solid lines show the snapshots of the peak mass mp (Eq. (A.9); upper panel) and total dust surface density Σd (Eq. (A.8); lower panel) at 105 yr, while the dotted, dashed, and dash-dotted lines show the reproductions with ϵ = 0, 0.5, and 1, respectively. The comparison shows that the single-size approach best reproduces the result of the full-size simulation when ϵ is chosen to be 0.5. |
Appendix A.2: Comparison with full-size calculations
To test the validity of the simple size approach, we attempt to reproduce the result of a full size calculation by Okuzumi et al. (2012). They calculated the evolution of the full size distribution with and without porosity evolution. We select the result of the compact aggregation model where the particle internal density is fixed to 1.4 g cm-3. In accordance with Okuzumi et al. (2012), we assume the optically thin MMSN with temperature profile T = 280(r/ 1AU)− 1 / 2 K and compute dust evolution in the region 3 AU <r< 150 AU. The particle collision velocity Δvpp is given by Eq. (12) in Sect. 2.4. As we explained there, we introduce a free parameter ϵ to Δvpp to account for the effect of a finite size dispersion. Below we consider three choices ϵ = 0, 0.5, and 1.
Figure A.1 shows the radial distribution of the particle peak mass mp and total dust surface density Σd at different times obtained from the full size calculation by Okuzumi et al. (2012, see their Fig. 2 for the corresponding snapshots of the size distribution). These are directly obtained from the data of the full size distribution together with the definitions of mp and Σd, Eqs. (A.8) and (A.9). We find that the single-size calculation with ϵ = 0.5 reproduces these results with reasonably good accuracy (see Fig. A.1). The agreement is particularly good for drifting pebbles (e.g., for t = 105 yr, particles at ≲60 AU) whose mass are determined by the balance between radial drift and local coagulation.
Figure A.2 demonstrates the importance of taking into account the effect of a finite size dispersion in evaluating Δvpp. Here we compare the snapshots of the single-size calculations with different values of ϵ at t = 105 yr. We can see that the single-size calculation significantly underestimates the rate of particle evolution if the effect of size dispersion is ignored, i.e., ϵ = 1. The reason is that equal-sized particles have vanishing non-Brownian relative velocities when they are so small (e.g., a ≲ 10-3 cm at 100 AU) that their stopping time is shorter than the turnover time of the smallest turbulent eddies (see, e.g., Ormel & Cuzzi 2007). We find that the opposite limit, ϵ = 0, gives a much better agreement and the intermediate choice, ϵ = 0.5, gives the best match to the full solution.
All Tables
Mass Me and water content fH2O of a rocky embryo at 1AU for various sets of model parameters.
All Figures
 |
Fig. 1 Schematic illustration showing the radial inward drift of icy pebbles and the inward migration of the snow line in a protoplanetary disk. Rocky embryos at 1 AU accrete radially drifting icy pebbles when the snow line resides at <1 AU. Time t = tstart, at which the snow line passes 1 AU, is taken as a free parameter. |
| In the text | |
 |
Fig. 2 Components of the particle relative velocity Δvpp at 100 AU as a function of particle radius a for three values of the turbulence parameter α = 10-4 (top panel), 10-3 (middle panel), and 10-2 (bottom panel). The velocity components that depend on α are shown by the solid curves. The stopping time ratio of ϵ = 0.5 is assumed for Δvr, Δvφ, Δvz, and Δvt. |
| In the text | |
 |
Fig. 3 Particle growth timescale tgrow (Eq. (14)) at 100 AU as a function of particle radius a for Σd = 10-2Σg with different values of the turbulence parameter α. The dotted line shows the simple estimate |
| In the text | |
 |
Fig. 4 Pebble accretion radius of an embryo bset (Eq. (18); solid curve) as a function of the pebble radius a. The upper and lower solid curves show bset for embryos of masses Me = 10-1 M⊕ and 10-2 M⊕, respectively. The dashed and dotted lines indicate the Hill radii RH (Eq. (20)) and geometric radii Rgeo = (3 Me/ 4πρe)1 / 3 of the embryos, respectively, where we take ρe = 3 g cm-3. |
| In the text | |
 |
Fig. 5 Pebble accretion probability by a single embryo, |
| In the text | |
 |
Fig. 6 Time evolution of the surface density Σd (top panels), radius a (middle panels), and radial mass flux Ṁr (bottom panels) of dust particles as a function of orbital radius r for models with α = 10-3 and with rout = 100 AU (left panels) and 300 AU (right panels). The black dotted lines show the initial condition, while the blue dashed, solid, dash-dotted, and dotted lines are the snapshots at times t = 0.1, 0.5, 1, and 5 Myr, respectively. The jumps in Σd and a at r ≈ 1 AU, t = 0.1 Myr are caused by rapid coagulation of particles initially located at these orbits (see text). |
| In the text | |
 |
Fig. 7 Time evolution of the surface density Σd (top panel), radius a (middle panel), and radial mass flux Ṁr (bottom panel) of dust particles as a function of orbital radius r for models with rout = 100 AU and with different values of α. The dashed and dotted lines are the snapshots at times t = 0.1 and 5 Myr, respectively. |
| In the text | |
 |
Fig. 8 Radius a (upper panels) and radial mass flux Ṁr (lower panels) of drifting particles observed at 1 AU as a function of time t. The left and right panels are for rout = 100 AU and 300 AU, respectively. |
| In the text | |
 |
Fig. 9 Pebble accretion rate Ṁe of a single embryo (Eq. (16)) located at 1 AU as a function of time t for Me = 10-1 M⊕ (upper panels) and 10-2 M⊕ (lower panels). The left and right panels are for rout = 100 AU and 300 AU, respectively. |
| In the text | |
 |
Fig. 10 Time evolution of the mass Me and water fraction fH2O of an embryo placed at 1 AU with initial mass Me,0 = 10-1 M⊕ for the case of rout = 100 AU. The different curves show results for different initial times of pebble accretion, tstart = 0.5, 1, 2, 3, 4, and 5 Myr (from left to right). |
| In the text | |
 |
Fig. 11 Same as Fig. 10, except for rout = 300 AU. |
| In the text | |
 |
Fig. 12 Temperature profiles adopted in this study (Eq. (3); solid line) and from a viscous accretion model of Oka et al. (2011; Eq. (28); dashed curve). |
| In the text | |
 |
Fig. 13 Same as the lower center panels of Figs. 10 and 11, but here the results for the temperature profile from an optically thick viscous disk model (Eq. (28)) are overplotted (dashed curves). |
| In the text | |
 |
Fig. A.1 Comparison between single- and full-size coagulation calculations. The solid lines show the snapshots of the peak mass mp (Eq. (A.9); upper panel) and total dust surface density Σd (Eq. (A.8); lower panel) at different times as a function of orbital radius r obtained from the full coagulation simulation for the compact aggregation model by Okuzumi et al. (2012, see also their Fig. 2). The dashed line shows our reproduction using the single-size approach (Eq. (4) for Σd and Eq. (5) for mp) with ϵ = 0.5 (see Sect. 2.4 for the definition of ϵ). |
| In the text | |
 |
Fig. A.2 Comparison between the full-size simulation (Okuzumi et al. 2012) and single-size simulations using different values of ϵ. The solid lines show the snapshots of the peak mass mp (Eq. (A.9); upper panel) and total dust surface density Σd (Eq. (A.8); lower panel) at 105 yr, while the dotted, dashed, and dash-dotted lines show the reproductions with ϵ = 0, 0.5, and 1, respectively. The comparison shows that the single-size approach best reproduces the result of the full-size simulation when ϵ is chosen to be 0.5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.