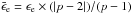| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526260 | |
| Published online | 11 April 2016 | |
Microphysics and dynamics of the gamma-ray burst 121024A
1 Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
e-mail: kvarela@mpe.mpg.de
2 Excellence Cluster Universe, Technische Universität München, Boltzmannstraße 2, 85748 Garching, Germany
3 Astrophysics Data System, Harvard-Smithonian Center for Astrophysics Garden St. 60, Cambridge, MA 02138, USA
4 European Southern Observatory, Alonso de Córdoba 3107, Vitacura, Casilla 19001 Santiago 19, Chile
5 Department of Physics, The George Washington University, 725 21st Street NW, Washington, DC 20052, USA
6 Technische Universität München, Physik Dept., James-Franck-Str., 85748 Garching, Germany
7 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
8 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
9 European Southern Observatory, Schwarzschild-Str. 2, 85748 Garching, Germany
10 Institute of Experimental and Applied Physics, Czech Technical University in Prague, Horska 3a/22, 128 00 Prague 2, Czech Republic
11 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
12 INAF–IASF Bologna, Area della Ricerca CNR, via Gobetti 101, 40129 Bologna, Italy
Received: 3 April 2015
Accepted: 1 February 2016
Aims. The aim of the study is to constrain the physics of gamma-ray bursts (GRBs) by analysing the multi-wavelength afterglow data set of GRB 121024A that covers the full range from radio to X-rays.
Methods. Using multi-epoch broad-band observations of the GRB 121024A afterglow, we measured the three characteristic break frequencies of the synchrotron spectrum. We used six epochs of combined XRT and GROND data to constrain the temporal slopes, the dust extinction, the X-ray absorption, and the spectral slope with high accuracy. Two more epochs of combined data from XRT, GROND, APEX, CARMA, and EVLA were used to set constraints on the break frequencies and therefore on the micro-physical and dynamical parameters.
Results. The XRT and GROND light curves show a simultaneous and achromatic break at around 49 ks. As a result, the crossing of the synchrotron cooling break is no suitable explanation for the break in the light curve. The multi-wavelength data allow us to test two plausible scenarios explaining the break: a jet break, and the end of energy injection. The jet-break scenario requires a hard electron spectrum, a very low cooling break frequency, and a non-spreading jet. The energy injection avoids these problems, but requires ϵe > 1 (k = 2), spherical outflow, and ϵB < 10-9.
Conclusions. In light of the extreme microphysical parameters required by the energy-injection model, we favour a jet-break scenario where νm < νsa to explain the observations. This scenario gives physically meaningful microphysical parameters, and it also naturally explains the reported detection of linear and circular polarisation.
Key words: X-rays: bursts / gamma-ray burst: general / gamma-ray burst: individual: GRB 121024A / methods: observational / radiation mechanisms: non-thermal / stars: jets
© ESO, 2016
1. Introduction
Gamma-ray bursts (GRBs) are the most luminous phenomena detected so far in the Universe (Klebesadel et al. 1973). They consist of pulses of gamma-rays emitted in a short time interval (milliseconds to hours) with an isotropic equivalent energy release of 1050−1054 erg. This is followed by fading multi-wavelength emission (from X-rays to radio), known as a GRB afterglow (Costa et al. 1997; van Paradijs et al. 1997). In the standard afterglow model, the dominant process during the afterglow phase is synchrotron emission from shock-accelerated electrons in a collimated relativistic blast wave interacting with the external medium (Mészáros & Rees 1997). This unique featureless intrinsic spectrum makes GRB afterglows perfect events to study physical processes under extreme conditions (e.g. Fermi acceleration).
The observed synchrotron spectrum is composed of four power-law segments joined at three main break frequencies. Each break frequency yields specific and correlated constraints on the acceleration processes in the shock region and the dynamics and geometry of the relativistic outflow. Assuming an initially self-similar evolution for the relativistic blast wave in the afterglow stage (Blandford & McKee 1976), the properties of the synchrotron spectrum can be expressed in terms of constraints on the model parameters (Wijers et al. 1997; Sari et al. 1998). The dynamics of the outflow are dictated by the isotropic equivalent energy in the afterglow phase Eiso, the circumburst medium density n = Ar− k (where A is a scale factor, r is the radial distance from the source, and k is the power-law slope with k = 0 or k = 2 for inter-stellar medium (ISM) or stellar wind-like medium-density profiles, respectively) and, when the jet nature of the outflow becomes apparent, the jet half-opening angle θ0 (Rhoads 1999). The micro-physics of this synchrotron emission can be captured in a simplified manner using the post-shock energy fraction in accelerated electrons ϵe, the energy fraction in the magnetic field ϵB, and the power-law index p of the non-thermal electron population.
A snapshot of the spectral energy distribution (SED) covering all break frequencies gives a number of observational constraints equal to the number of model parameters. This scenario presents an ideal case in terms of model simplicity and data availability. In practice, the sample of bursts for which all spectral breaks could be simultaneously determined is still small (aboutfive, e.g. Panaitescu & Kumar 2002; Yost et al. 2003; Resmi et al. 2005; Chandra et al. 2008; Cenko et al. 2010). This indicates the importance, in terms of sample statistics, of increasing the sample of bursts with simultaneous afterglow detections across the broadband spectrum. Common solutions when not all spectral breaks can be probed simultaneously are to extrapolate light curves in time and/or to fix one or more of the model parameters. Motivated by an apparent correlation (Frail et al. 2001; Panaitescu & Kumar 2002), Eiso has been equated to the total isotropic equivalent energy release in gamma rays Eγ,iso (e.g. Dai & Lu 1999; Pandey et al. 2003). The magnetic field energy density, ϵB has been fixed to a standard value (e.g. Frail et al. 2000; Cenko et al. 2010), or linked to the shock-accelerated electron energy, ϵe (e.g. Medvedev 2006; van Eerten & Wijers 2009). A standard value for the circumburst density has also been assumed (e.g. Chevalier et al. 2004). In these cases, the implications of the derived model parameters are conditional on the additional assumption(s).
Here, we present the analysis of the simultaneous multi-wavelength observations of GRB 121024A. It was detected with the Swift satellite and had a redshift z = 2.30 measured with the X-shooter spectrograph at the Very Large Telescope (VLT) (Tanvir et al. 2012). It was followed up by different instruments in the radio to the X-ray regimes over several days. Linear and circular optical polarisation observations of the afterglow were taken (Wiersema et al. 2014). We report on the analysis of the broad-band SED of this afterglow, including X-ray, optical/NIR, sub-mm, and radio data. From these simultaneous broad-band observations, we derive constraints on the micro-physical and dynamical parameters of the GRB afterglow.
We provide a brief summary of the observations and relevant details of the data reduction in Sect. 2. We then describe in Sect. 3 a model-independent analysis of the data, starting with the description of the X-ray and optical/NIR light curves, followed by the description of the SED including effects of dust extinction and gas absorption at these wavelengths. In Sect. 4 we include radio and sub-mm data to study the broad-band SED in the framework of jet break and energy-injection scenarios. We derive all the micro-physical and dynamical parameters based on the standard afterglow model assumptions. In Sect. 5 we discuss our results and compare the different viable scenarios. Finally, we conclude and summarise our results in Sect. 6.
2. Observations and data reduction
2.1. Swift
On 2012 October 24 at T0 = 02:56:12 UT, the Swift Burst Alert Telescope (BAT, Barthelmy et al. 2005) triggered and located GRB 121024A (Pagani et al. 2012). Swift slewed immediately to the burst, and the observations with the X-Ray Telescope (XRT, Burrows et al. 2005) started 93 s after the trigger. The observations were made in windowed timing (WT) mode during the first 242 s and then were carried out in photon counting (PC) mode (Page et al. 2012). The initial flux in the 0.2−10 keV band was 1.1 × 10-9 erg cm-2 s-1. The Swift/XRT light curve and spectral data were obtained from the XRT repository (Evans et al. 2007, 2009). The afterglow was located RA, Dec (J2000) = 04:41:53.28, –12:17:26.8 with an uncertainty of 0.̋8 (Pagani et al. 2012) by the Swift/UVOT, with a magnitude in the b band of 18.4 ± 0.2 (Holland & Pagani 2012).
 |
Fig. 1 GROND r′-band finding chart. The secondary stars used for the calibration are labelled I-VI and are reported in Table 1. North is up and east to the left. |
Secondary stars for photometric calibration.
2.2. GROND
The Gamma-Ray burst Optical Near-infrared Detector (GROND, Greiner et al. 2008) mounted at the Max-Planck-Gesellschaft (MPG) 2.2 m telescope located at ESO La Silla observatory, Chile, was designed as a GRB follow-up instrument. It provides simultaneous data in seven bands in a wavelength range from 400–2400 nm (g′r′i′z′JHKs). GROND observations started 2.96 hours after the Swift trigger (Knust et al. 2012) and continued for the next 3.8 h during the first night. The afterglow was detected in all seven bands at the position RA, Dec (J2000) = 04:41:53.30, –12:17:26.5 with an uncertainty of 0.̋4 in each coordinate (Fig. 1). After the observations during the first night, imaging of the field of GRB 121024A continued on the second, third, fourth, sixteenth, and seventeenth night after the burst. The optical/NIR data were reduced using standard IRAF tasks (Tody 1993; Krühler et al. 2008). The data were corrected for Galactic foreground reddening E(B−V) = 0.09 mag (Schlafly & Finkbeiner 2011), corresponding to an extinction of Av = 0.27 mag for Rv = 3.1. The optical magnitudes were calibrated against secondary stars in the GRB field (Table 1). On 2013 December 8 a Sloan Digital Sky Survey (SDSS) field (Aihara et al. 2011) at RA, Dec (J2000) = 04:59:42.0, -04:54:00 and the field of GRB 121024A were consecutively observed in photometric conditions. The calibration of the secondary stars was made against the corrected zeropoints of the GRB field based on the SDSS field. The NIR magnitudes were calibrated against the Two Micron All-Sky Survey (2MASS, Skrutskie et al. 2006) catalogue stars in the field of the GRB.
2.3. APEX
On 2012 October 24, we triggered an observation on the LABOCA bolometer camera (Siringo et al. 2009)1. Two observations at a frequency of 345 GHz with a bandwidth of 60 GHz were performed. The first started 19.8 ks after the GRB, the second 98.7 ks after the GRB. On both days, the observations were taken in mapping mode and in on-off mode (Schuller et al. 2010). The data were reduced using the Bolometer Array analysis software (BoA, Schuller 2012). All the subscans (ten per scan) were used. A clipping of 2σ was used to remove any background effects. The flux calibration was made using Jupiter for the focus, N2071IR as a secondary calibrator, and J0423-013 as a pointing source. There was no detection on either night, the upper limits are given in Table 2.
1σ Upper limits of the on-off measurements using the LABOCA instrument on APEX.
2.4. Millimetre and radio observations
In addition to the X-ray, GROND, and APEX data reported above, we also incorporated the following millimetre and radio observations reported in the literature in our SED analysis.
The Combined Array for Research in Millimetre-Wave Astronomy (CARMA) started observations of the field of GRB 121024A ~ 120.9 ks after the BAT trigger at a mean frequency of ~85 GHz (3 mm) (Zauderer et al. 2012). A mm counterpart was detected with a flux of 1.0 ± 0.3 mJy.
The Very Large Array (VLA) started observations of the field of GRB 121024A ~ 109.0 ks after the trigger. A radio counterpart with flux of 0.10 ± 0.03 mJy was detected at a frequency of 22 GHz (Laskar et al. 2012).
3. Phenomenological data analysis
We start with a model-independent analysis of the data. The observed flux is described by F ~ t− αν− β, with α and β the temporal and spectral slope, respectively. First, we analyse the temporal evolution of the GRB 121024A afterglow. Using the X-ray and optical/NIR light curves, we measured the temporal slope α and obtained information about particular features such as flares, breaks in the light curve, flattening, or any behaviour different from that expected for a canonical afterglow light curve (LC; Nousek et al. 2006; Zhang et al. 2006). Then, we analysed the SED from X-ray to optical/NIR wavelengths at six different epochs. We obtained the spectral slope β and checked for spectral evolution. Given that absorption and dust extinction only affect the data at X-ray and optical wavelengths, we used this SED analysis to derive the host X-ray absorbing column density (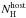 ), which is commonly quoted as an equivalent neutral hydrogen column density, and the host visual dust extinction along the GRB line of sight (
), which is commonly quoted as an equivalent neutral hydrogen column density, and the host visual dust extinction along the GRB line of sight (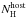 ).
).
 |
Fig. 2 Light curve of the afterglow of GRB 121024A. Top: XRT light curve from the XRT repository. Bottom: GROND light curve in g′r′i′z′JHKs. The best fit for the combined light curve (optical/NIR and X-ray data) is a smoothly broken power law with host contribution, shown with dashed lines. The epochs used for the spectral analysis are highlighted with the vertical bars. The break time tb = 49.8 ± 5.1 ks. |
3.1. Afterglow light-curve fitting
The temporal evolution of the X-ray afterglow of GRB 121024A2 shows an initial steep decay with a temporal slope α = 3.6, followed by a small flare at ~300 s. For the present work, we only used the data after 104 s, which is the start time of our GROND observations (Fig. 2). We tried to fit two models: First, a simple power law with host contribution in the optical bands (plh) and slope decay α. Second, a smoothly broken power law with constant host contribution (brplh) (Eq. (1)) (Beuermann et al. 1999), with αpre and αpost being the power-law slopes before and after the break, respectively, sm the smoothness, and tb the break time in the LC: 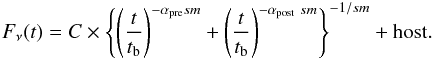 (1)The best fit to the X-ray light curve is a smoothly broken power law with a statistical significance χ2/ d.o.f. = 51/44 (simple power-law: χ2/ d.o.f. = 87/47). The best-fit parameters are an initial decay with αpre = 0.84 ± 0.09 and break time
(1)The best fit to the X-ray light curve is a smoothly broken power law with a statistical significance χ2/ d.o.f. = 51/44 (simple power-law: χ2/ d.o.f. = 87/47). The best-fit parameters are an initial decay with αpre = 0.84 ± 0.09 and break time 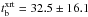 ks with sm = 5.0 ± 2.6, followed by a steeper decay with αpost = 1.67 ± 0.23.
ks with sm = 5.0 ± 2.6, followed by a steeper decay with αpost = 1.67 ± 0.23.
The optical/NIR light curves (Table 3) are well fitted by both a plh and a brplh model. A plh model gives χ2/ d.o.f. = 140/112 and a decay slope α = 1.07 ± 0.02, while a brplh model gives χ2/ d.o.f. = 107/109 and best-fitting parameters αpre = 0.71 ± 0.03, αpost = 1.46 ± 0.04, break time 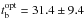 ks, and smoothness 2.7 ± 1.1. Colour evolution in the optical bands is detected in the last epoch of our observations, which we associate with the increased contribution from the host galaxy. An F-test between the two model gives a null hypothesis probability of 1.86 × 10-6. Therefore, we conclude that the brplh profile describes the data in a better way. We used this profile for the following analysis.
ks, and smoothness 2.7 ± 1.1. Colour evolution in the optical bands is detected in the last epoch of our observations, which we associate with the increased contribution from the host galaxy. An F-test between the two model gives a null hypothesis probability of 1.86 × 10-6. Therefore, we conclude that the brplh profile describes the data in a better way. We used this profile for the following analysis.
Both the X-ray and optical/NIR light curves are best fitted by a broken power law with similar break times. We therefore tried a combined fit to both the XRT and GROND light curves to test whether the same model can describe both data sets, which would thus better constrain the best-fit parameters. The best-fit model provides a good fit (χ2 = 157 and d.o.f. = 141), with a pre-break temporal slope αpre = 0.86 ± 0.05, post-break temporal slope αpost = 1.47 ± 0.03, smoothness sm = 1.7 ± 0.3, and break time tb = 49.8 ± 5.1 ks.
3.2. Afterglow SED fitting
We analysed six different spectral epochs using XRT and GROND data, spanning the time interval T0 + 10 ks to T0 + 240 ks, four before the break time in the light curve and two after it (Fig. 3). The spectral analysis includes the effect of the dust and metal attenuation along the line of sight towards the source. For the last two SEDs, given the low signal-to-noise ratio at X-ray energies, we extracted the spectrum from the same time interval (40–240 ks), during which time there was no evidence of spectral evolution within the X-ray energy range. We then renormalised the spectra so that they corresponded to the measured X-ray flux of the afterglow at the mid-time of the two corresponding SEDs (i.e. tSED V = 88 ks and tSED VI = 107 ks).
 |
Fig. 3 Spectral energy distribution for the six SEDs highlighted in Fig. 2. SEDs I – IV are from data before the observed break in the light curve. SEDs V and VI are from data taken after the break. The SEDs are scaled with an arbitrary factor for clarity in the plot. The values of β written above each line corresponds to the single power-law fit, where the slopes were left free to vary. The single power-law fit with a single tied slope has β = 0.86 ± 0.02. |
The SED analysis for all the six SEDs was performed simultaneously. The Galactic reddening was fixed to E(B−V) = 0.09 mag, corresponding to an extinction of 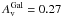 mag (Schlafly & Finkbeiner 2011) for a Milky Way (MW) reddening law. The Galactic absorbing column density
mag (Schlafly & Finkbeiner 2011) for a Milky Way (MW) reddening law. The Galactic absorbing column density 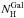 was fixed to 7.9 × 1020 cm-2 (Kalberla et al. 2005). The host magnitude was subtracted from the optical/NIR data, and the g′ band was not included in the fit because of a damped Lyα system along the line of sight towards the GRB (DLA, Friis et al. 2015). The values for the host extinction and absorption were tied between all the epochs, and the spectral slopes were left free to vary. A single power-law fit has a goodness of fit χ2/ d.o.f. = 28/46 and all the spectral slopes values (see Fig. 3) are consistent within 1σ, confirming the lack of spectral evolution. A broken power-law fit either places the break outside the optical – X-ray frequency interval or fails to improve the fit when the break is forced to lie within this interval. In the latter case, the best-fit models have a goodness of fit χ2/ d.o.f. = 32/40.
was fixed to 7.9 × 1020 cm-2 (Kalberla et al. 2005). The host magnitude was subtracted from the optical/NIR data, and the g′ band was not included in the fit because of a damped Lyα system along the line of sight towards the GRB (DLA, Friis et al. 2015). The values for the host extinction and absorption were tied between all the epochs, and the spectral slopes were left free to vary. A single power-law fit has a goodness of fit χ2/ d.o.f. = 28/46 and all the spectral slopes values (see Fig. 3) are consistent within 1σ, confirming the lack of spectral evolution. A broken power-law fit either places the break outside the optical – X-ray frequency interval or fails to improve the fit when the break is forced to lie within this interval. In the latter case, the best-fit models have a goodness of fit χ2/ d.o.f. = 32/40.
 |
Fig. 4 Broadband SEDs of the afterglow of GRB 121024A from the radio to the X-ray regime for the three models described in Sect. 4. Blue line: SED at t = 21.9 ks. Red line: SED at t = 109.0 ks. The dashed lines represent the absorbed model, the solid lines the unabsorbed model. The grey-shaded regions corresponds to the 1σ limits of the model. |
Given the lack of spectral evolution detected in our combined GROND/XRT light curve analysis out to 240 ks, we fitted all six SEDs simultaneously with the same spectral model, with only the normalisation allowed to differ between epochs. The best-fit results are given by a single power law with a spectral slope β = 0.86 ± 0.02 and goodness of fit χ2/ d.o.f. = 48/51. The best-fit host dust extinction given by a Small Magellanic Cloud (SMC) reddening law (Pei 1992) is 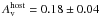 mag, and the host galaxy X-ray absorbing column is
mag, and the host galaxy X-ray absorbing column is 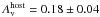 cm-2. The lack of spectral evolution together with the achromatic break observed in the light curve rule out the movement of the cooling break through the observed wavelength range.
cm-2. The lack of spectral evolution together with the achromatic break observed in the light curve rule out the movement of the cooling break through the observed wavelength range.
We extend the SED analysis in the following section with two additional epochs containing simultaneous observations with XRT, GROND, APEX, CARMA, and EVLA. The first SED at t = 21.9 ks has GROND, XRT, and APEX data. The additional APEX upper limit requires a break between the APEX and NIR energies (see Fig. 4). Then, we have a second SED at t = 109.0 ks, with two additional measurements: CARMA and EVLA data points. The CARMA data point requires a break between the millimetre and the NIR bands, and the EVLA data point implies a break between the radio and the CARMA wavelength. Therefore at least two breaks in the broad-band spectrum of GRB 121024A are needed. These breaks are analysed in more detail in Sect. 4 in the context of the afterglow synchrotron spectrum model, where we use the constraints on β, E(B−V) and 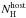 found in his section.
found in his section.
4. Physical parameters of the standard afterglow model
We now proceed with the derivation of the microphysical and dynamical parameters of the GRB afterglow, based on the standard afterglow model. In this model, the dominant emission is generally associated with synchrotron radiation from shock-accelerated electrons. These electrons are assumed to have a power-law energy distribution with slope p and minimum energy γm. The observed synchrotron spectrum is characterised by three main break frequencies (νc, νm, νsa) and a peak flux. The synchrotron injection frequency νm is defined by γm. The cooling frequency νc is defined by the critical value γc, above which electrons radiate their energy on timescales shorter than the explosion timescale. The self-absorption frequency νsa marks the frequency below which the optical depth to synchrotron-self absorption is >1. In this model, two main cooling regimes are defined by the relative position of the break frequencies: a fast cooling regime where νm>νc and most of the electron are cooling fast, and a slow cooling regime where νm<νc and most of the accelerated electrons are cooling slowly (Mészáros & Rees 1997; Granot & Sari 2002).
The number of combinations of α and β is limited when a specific dynamical model and the synchrotron spectrum are given. This gives rise to a unique set of relations between α and β known as “closure relations” (Mészáros & Rees 1997; Sari et al. 1998; Zhang & Mészáros 2004). These relations constrain the cooling regime, the circumburst environment, the jet geometry, and the electron energy distribution p. We follow two main steps to analyse the afterglow data:
-
1.
Spectral regime: the derivation of the p value and identification of the external density profile depend on the power-law segment of the synchrotron spectrum containing the observing frequency. Using the closure relations (Racusin et al. 2009) together with the measured parameters for α and β, we find that the afterglow data can be described by two different spectral regimes (see Table 4). In one case we have a spectral regime where νc<νKs (i.e. below the Ks band), and in the other case we have one where νc>νxrt (i.e. above the XRT band).
-
2.
Microphysical and dynamical parameters: We include the APEX, CARMA, and EVLA data in our analysis and fit the data using a single, a double, or a triple broken power-law model depending on each individual case (in the double and triple broken power-law fits, we only consider sharp breaks because the data at millimetre and radio frequencies are insufficient to constrain an additional free parameter i.e., smoothness). We use the standard formalism for a spherical blast wave propagating into an external cold medium during the slow cooling regime to derive all the micro-physical and dynamical parameters (Mészáros & Rees 1997; Granot & Sari 2002), and subsequently check for consistency with the slow or fast cooling transition times.
Both spectral regimes, that is, νc<νKsνc>νXRT, are explained and analysed in detail in the following subsection. The former corresponds to the jet in the light curve being associated with a jet break without energy injection, and the latter corresponds to the jet in the light curve associated with either the end of energy injection into the outflow or with a jet break with an ongoing energy injection during the whole evolution of the afterglow (i.e. the ongoing energy injection is still visible until the last observations).
Closure relations*. β = 0.86 ± 0.02 was use in the analysis.
4.1. νc <νKs: Jet break
Using the closure relations for a decelerating spherical blast wave, we find that the measured temporal slope before the break in the light curve is consistent with νc <νKs for both ISM and wind environments. This implies p = 1.73 ± 0.03, as β = p/ 2. The only plausible scenario consistent with the measured αpost and β corresponds to a non-spreading uniform jet propagating into a wind environment. We therefore associate the achromatic break observed in the light curve with a jet break (Rhoads 1999; Wiersema et al. 2014).
We proceed by including the post-break sub-mm and radio data in our analysis. The first broadband SED contains GROND, XRT, and APEX data. The best fit to this is a broken power law with both Galactic and host extinction and absorption, with χ2/ d.o.f. = 3.6/5 (see Table 5). The measured value of νc = 1.5 × 1012 Hz is a lower limit because the APEX measurement is an upper limit. The second broadband SED contains XRT, GROND, CARMA, and EVLA detections. Two possible spectral sub-regimes in the slow cooling phase give a good fit to the data: the cooling regime where νsa < νm < νc, and the one where νm < νsa<νc. Because there are only a few data points at radio wavelengths, it is difficult to distinguish between these two cooling regimes. Therefore, we analysed both cases.
When 1 < p < 2 (i.e. a hard electron spectrum), there is more energy-per-decade in high-energy electrons. This distribution has important implications for the analysis of the physics in the shock region, specifically requiring an additional high-energy cut-off in the electron population. We based our analysis on the assumption of a proportionality between γm and γ, where γ is the Lorentz factor of the shocked fluid. This implies that γm is proportional to local temperature, which is physically plausible since the non-thermal population is presumably accelerated out of a Maxwellian population. The upper cut-off in the electron distribution can be assumed to lie beyond the X-ray band and does not need to be accounted for explicitly. ϵe can no longer be interpreted as the fraction of energy in accelerated electrons. Instead, it becomes a scale factor between γ and γm, according to γm = K × γ with 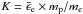 (Mészáros & Rees 1997). We followed the formalism used by Granot & Sari (2002), who derived the flux equation using a full fluid profile for the blast wave (Blandford & McKee 1976) and took the line-of-sight effect and the cooling times of the individual electrons into account.
(Mészáros & Rees 1997). We followed the formalism used by Granot & Sari (2002), who derived the flux equation using a full fluid profile for the blast wave (Blandford & McKee 1976) and took the line-of-sight effect and the cooling times of the individual electrons into account.
Based on the values for the break frequencies presented in Table 5 for both spectral regimes, νsa<νm (see Fig. 4a) and νm <νsa (see Fig. 4b), we derived the microphysical and dynamical parameters. The results are reported in Table 6 and are used to calculate the transition times between the spectral regimes. First, the transition from fast to slow cooling. This corresponds to tνc = νm ~ 2.8 × 104 s and tνc = νm ~ 2.6 × 103 s for νm > νsa and νm < νsa, respectively. In both cases, it is before the time of the analysed SED at t = 109 s, confirming the slow cooling assumption. Second, the transition from optically thin to optically thick, that is, when νm goes below νsa. This occurs at tνsa = νm ~ 1.8 × 105 s when νm > νsa and at tνsa = νm ~ 1.07 × 105 s when νm < νsa.
Results from SED fits for both a jet-break model with νsa < νm and νm < νsa, and for an energy-injection model.
4.2. νc>νxrt: energy injection
The closure relations (Table. 4) and the possible spectral break positions resulting from fitting synchrotron spectra to the SED allow for an alternative scenario, where νc>νXRT and p> 2. In this case, the break between the mm and NIR wavelength corresponds to νm and the break in the light curve is associated with the end of the ongoing energy-injection phase. Smooth energy injection into the ejecta can result from slower shells with a range of velocities that catch up with each other or from a long-term engine luminosity. In the latter case, the energy-injection parameter q is defined by L = L0(t/tb)− q. Using the flux and frequency equations for radial flow from van Eerten & Wijers (2009) and Leventis et al. (2012), we derived the closure relation for a general density profile with an arbitrary k during the deceleration stage following energy injection (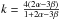 for νm<ν<νc). The best-fit results for αpost and β then imply k = 1.05 ± 0.23.
for νm<ν<νc). The best-fit results for αpost and β then imply k = 1.05 ± 0.23.
During the energy-injection phase, a forward-reverse shock system is set up in the flow. Using the flux equation describing the energy-injection phase from van Eerten (2014), we have a given relation between α, β, k and q. If the emission is dominated by that from the forward shock (FS): 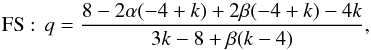 (2)and the following relation if the reverse shock (RS) emission is dominant:
(2)and the following relation if the reverse shock (RS) emission is dominant: 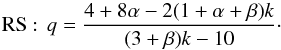 (3)The values for αpre and β derived in Sect. 3.1 imply q = 0.52 ± 0.07 for dominant FS emission and q = 0.88 ± 0.09 for dominant RS emission. These q values (as well as the pre-break temporal slopes) are consistent with those determined for Swift samples (e.g. Racusin et al. 2009; Evans et al. 2009; Margutti et al. 2013). If we fix k = 2, we obtain q ≃ 0 for both RS and FS, consistent with predictions for a magnetar model (Dai & Lu 1998; Zhang & Mészáros 2004). For an ISM density profile, q = 0.69 ± 0.04 for FS emission and q = 1.09 ± 0.03 for RS emission. RS emission can therefore not be dominant because q> 1 implies that the energy injection decays too rapidly to sustain a plateau.
(3)The values for αpre and β derived in Sect. 3.1 imply q = 0.52 ± 0.07 for dominant FS emission and q = 0.88 ± 0.09 for dominant RS emission. These q values (as well as the pre-break temporal slopes) are consistent with those determined for Swift samples (e.g. Racusin et al. 2009; Evans et al. 2009; Margutti et al. 2013). If we fix k = 2, we obtain q ≃ 0 for both RS and FS, consistent with predictions for a magnetar model (Dai & Lu 1998; Zhang & Mészáros 2004). For an ISM density profile, q = 0.69 ± 0.04 for FS emission and q = 1.09 ± 0.03 for RS emission. RS emission can therefore not be dominant because q> 1 implies that the energy injection decays too rapidly to sustain a plateau.
After the energy-injection phase, only a decelerating forward shock remains, and a standard afterglow emission model can be applied. We therefore proceeded with the analysis of the final SED at t = 109s, which contains EVLA, CARMA, GROND, and XRT data. The best-fit profile is a sharp double broken power law with χ2/ d.o.f. = 8.50/8 (Fig. 4c). The critical values reported in Table 5 were used to derive the micro-physical parameters after the energy-injection phase (see Table 6). In this scenario, νc cannot be measured and we can only place a lower limit. The k value lies just between the expected values for ISM and wind environments, and therefore we determined the values for both wind and ISM environments using Granot & Sari (2002) and for k = 1.05 using van Eerten & Wijers (2009) and Leventis et al. (2012).
4.3. νc>νxrt: energy injection and jet break
Now, we analyse the afterglow parameters assuming prolonged energy injection at all times, both before and after the break in the light curve, and the break in the light curve is associated with a jet break. As shown in Sect. 4.2, RS emission is not dominant before the break, and therefore we assumed only a dominant FS emission. To avoid too many free parameters, we restricted the study to ISM and wind density profiles. The analysis for these two medium profiles for the ongoing energy-injection phase before the break in the light curve is presented in Sect. 4.2. Here, we used αpost to derive the q values after the break and, assuming q does not evolve, we compared these post-break values with the pre-break values to check if it is possible to have ongoing energy injection together with a jet break. We analysed two cases for the post-jet-break evolution: a sideways spreading jet and a non-spreading jet. For the former case q = 0.35 ± 0.03, inconsistent with the q value before the jet break. In addition to this inconsistency, if the energy is continuously injected within θ0, while the front of the jet begins to spread, the homogeneous shell approximation leading to the closure relations used here is no longer valid. On balance, the bulk of the energy will remain confined to θ0 (see discussion in van Eerten 2014), and then the non-spreading jet approximation is favoured. The non-spreading case gives q = 0.65 ± 0.03 for an ISM density profile and q = 0.43 ± 0.03. Therefore, only the ISM density profile is consistent with the pre-break q value, and the prolonged energy injection would only be possible if the observed jet break is due to geometrical effects alone.
We analysed our last two SEDs including radio, submm, NIR, optical, and X-ray data. We used the flux and break frequency equations for energy injection presented in van Eerten (2014) together with equations for νsa (van Eerten in prep.) to obtain the model parameter values presented in Table 6. As in the previous case, where energy injection was only operating before the break in the light curve, some unphysical values for the parameters are found. The main problems are ϵe> 7.6, when it should not be greater than unity, and the value for the density ~107 cm-3, instead of being of order unity as expected.
5. Discussion
In the previous sections we have presented a detailed analysis of the afterglow observations and derived values for the microphysical and dynamical parameters. Here we compare the derived values in the different scenarios. We discuss the positive and negative aspects of each model in the framework of the standard afterglow model.
5.1. Jet break without energy injection
This scenario requires three main features: first, the cooling break must be at around a few times 1012 Hz at >T0 + 109 ks. Although a value for νc this low has been seen before (i.e. GRB 060418, Cenko et al. 2010), in more than 95% of a combined GROND-XRT sample, νc was detected above the optical frequencies (Greiner et al. 2011). Second, the closure relations require that the jet does not spread out sideways following the break time. The jet has to remain in this non-spreading state at least until aboutone day after the jet break because no spectral evolution is detected so far in the observations. This behaviour is at odds with findings from theoretical (Granot & Piran 2012) and numerical (van Eerten et al. 2010; De Colle et al. 2012; van Eerten & MacFadyen 2012) studies of afterglow jets. Third, a very hard electron spectrum (p< 2) with p = 1.73 is required, as are additional assumptions about the minimal Lorentz factor. Although this is significantly lower than the value of 2.3 expected from Fermi acceleration theory (e.g. Kirk et al. 2000; Achterberg et al. 2001), it is within the average range of values 1.5−3.0 observed in previous GRB afterglow studies (Curran et al. 2010).
Two different spectral sub-regimes were presented in Sect. 4.1, either with νsa<νm or with νm<νsa. Here the main assumption is γm ~ γ. For both spectral sub-regimes, the derived values for ϵB (Table 6) are in the same range as previous measurements reported in the literature, and the values of θ0 are consistent with a collimated outflow (0.1−0.3 rad). The values for the circumburst density therefore agree with the collapsar model and a Wolf-Rayet star as possible progenitor, with mass-loss rates of ~1.4 × 10-5M⊙ yr-1 when νsa<νm and >7.8 × 10-6M⊙ yr-1 when νm<νsa, for a wind velocity v = 1000 km s-1 (Chevalier & Li 1999, 2000). The efficiency3 requirements are extremely high. For νsa<νm the measured Eiso implies an efficiency of η ~ 98% and for νm<νsa the efficiency is η< 74%. These two efficiency values are much higher than expected in the standard fireball shock model, for which an efficiency of η< 10% is predicted (Kobayashi et al. 1997; Daigne & Mochkovitch 1998; Kumar 1999; Granot et al. 2006; Cenko et al. 2011).
As a final verification of this model, we applied a condition from Granot & Sari (2002) to the evolution of the afterglow spectrum in a wind environment for a given set of microphysical and environmental parameters. This states that if 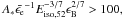 the afterglow spectrum evolves from fast to slow cooling, where in the slow cooling phase, initially νsa<νm<νc, but eventually νm<νsa<νc. If
the afterglow spectrum evolves from fast to slow cooling, where in the slow cooling phase, initially νsa<νm<νc, but eventually νm<νsa<νc. If 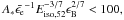 the afterglow spectrum only goes through one spectral regime in the slow cooling phase where νm<νsa<νc. In this latter scenario we are never in the regime where νsa<νm during the slow cooling phase. In our jet-break model where the spectral regime is νsa<νm, we therefore require that the derived micro-physical and dynamical parameters give
the afterglow spectrum only goes through one spectral regime in the slow cooling phase where νm<νsa<νc. In this latter scenario we are never in the regime where νsa<νm during the slow cooling phase. In our jet-break model where the spectral regime is νsa<νm, we therefore require that the derived micro-physical and dynamical parameters give 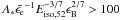 . However, we find that our best-fit values presented in Table 6 for νsa<νm give 52, inconsistent with the condition stated above, and therefore this regime can be ruled out. The favoured regime is then a slow cooling phase where νm<νsa, where our best-fit parameters give the value 257.
. However, we find that our best-fit values presented in Table 6 for νsa<νm give 52, inconsistent with the condition stated above, and therefore this regime can be ruled out. The favoured regime is then a slow cooling phase where νm<νsa, where our best-fit parameters give the value 257.
5.2. Energy injection
According to the shape of the spectrum and the closure relations, it is also possible to have νc>νXRT, implying an energy-injection model. In the energy-injection scenario, both with and without a jet break, our best-fit values for q are consistent with q ~ 0.5, corresponding to smooth energy injection, which has been observed in several other cases (e.g. Zhang et al. 2006), and the hard electron spectrum is not required anymore since we now have p = 2β + 1 = 2.73. However, further problems with the other afterglow parameters are found.
The energy-injection scenario together with a jet break in an ISM external medium and without a jet break in a wind-like (k = 2) external medium can be ruled out because ϵe> 1, therefore, this scenario is physically not meaningful. There are two other scenarios to be analysed then: the energy-injection scenario without a jet break in an ISM medium and with a general density profile with slow k = 1.05. The analysis below focuses on these two cases.
In relation to the micro-physical parameters, the derived values for ϵB differ from previous observations, but agree with theoretical predictions. In the former case ϵB is more than four orders of magnitude (<10-9) smaller than the average measured values from previous studies (e.g. Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005; Cenko et al. 2010). In the latter case, the value ϵB< 10-9 for an ISM density profile is consistent with expected values from shock compression of the seed magnetic field (B0 ~ μG) in the surrounding medium (Kumar & Barniol Duran 2009; Santana et al. 2014), and no further amplification or additional magnetic field would be required in the shock region. On the other hand, the derived value for 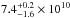 is < 0.75 consistent with theory as ϵe< 1 but higher than the average of observations where ϵe ~ 0.2 (Santana et al. 2014).
is < 0.75 consistent with theory as ϵe< 1 but higher than the average of observations where ϵe ~ 0.2 (Santana et al. 2014).
Furthermore, in the case where ϵB ≪ ϵe, as implied by our analysis, we would expect there to be a contribution to the cooling of electrons from inverse Compton (IC) scattering processes (Panaitescu & Kumar 2000; Sari & Esin 2001). The IC emission will mainly affect the cooling frequency in the slow cooling regime. The final value of νc is expected to be lower than the value with synchrotron cooling alone. The IC contribution to the total observed afterglow emission can be included using the Compton parameter defined as Y = ηcϵe/ϵB, where ηc = (γc/γm)2−p for the slow cooling regime (for more details see Sari & Esin 2001). With this parameter the cooling frequency will be lowered by a factor of (1 + Y)2. A constraint C can be derived to test whether the IC contribution is important during the evolution of the observed emission from the afterglow, or if it can be neglected (see Eq. (4.9) of Sari & Esin 2001). This constraint depends only on the observational quantities (break frequencies and peak flux) of the afterglow and is independent of the theoretical afterglow parameters. It can be expressed in terms of Y as C = Y/ (1 + Y)2 and has a consistent solution for Y only if C< 1/4. Using our measurements, we find C ~ 106 for ISM. This result indicates that the IC component is not a relevant contribution for this afterglow, contrary to the theoretical expectation when ϵB/ϵe ≪ 1 and the energy-injection scenario is not favoured.
The lower limits derived for the density are 2 (k = 1.1) and 4 (k = 0) orders of magnitude higher than previous density measurements for bursts with similar isotropic energies (Eiso ~ 1052 erg) between 10-2 and 103 for constant density circumburst profiles (n) (e.g. see Fig. 11 in Cenko et al. 2011). The values for θ0 for the case of no jet break indicate a spherical outflow, opposite to the collimated outflow usually expected and assumed in the standard afterglow theory. Finally, the energy lower limit is ~3 × 1052 erg, implying an efficiency of η< 70%.
5.3. Origin of the light-curve break
From the available data, it is difficult to make a clear case for a preferred model for this GRB afterglow. Each of the studied models has specific problems that are difficult to explain with a simple afterglow model and would probably be better understood with a more complex and detailed model of the afterglow emission, especially at early times (e.g. Waxman & Mészáros 2003; Morsony et al. 2007). However, we are able to rule out some of the possible models. For instance, the jet-break model where the spectral regime is νsa<νm is ruled out because the spectral evolution will never cross that regime in the slow cooling phase (see Sect. 4.1). In a similar way, we can rule out the energy-injection model with a wind density profile k = 2, and the energy-injection model with a jet break for k = 0 because 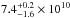 has to be larger than one, which is physically not meaningful. The energy-injection model without jet break for k = 1.1 and ISM density profiles cannot be ruled out. However, in this model the extremely high density requirements are far from theoretically expected values and previous measurements. Moreover, the resulting spherical outflow geometry, implied by the derived value for the half-opening angle, would require a very energetic explosion.
has to be larger than one, which is physically not meaningful. The energy-injection model without jet break for k = 1.1 and ISM density profiles cannot be ruled out. However, in this model the extremely high density requirements are far from theoretically expected values and previous measurements. Moreover, the resulting spherical outflow geometry, implied by the derived value for the half-opening angle, would require a very energetic explosion.
For more than 40% of the X-ray afterglows an initial plateau lasting for about 103−104 s is observed (Lazzati & Perna 2007; Margutti et al. 2013) and has been associated with a continuous energy injection during the afterglow evolution (Nousek et al. 2006; van Eerten 2014). We compared the X-ray luminosity (0.3−30 keV) (Lf) and the break time in the rest frame (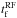 ) to the relation observed in other GRBs (Dainotti et al. 2008). Figure 5 shows the relation between Lf and
) to the relation observed in other GRBs (Dainotti et al. 2008). Figure 5 shows the relation between Lf and 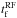 observed in a sample of 62 long GRBs studied by Margutti et al. (2013). We included GRB 121024A for both an energy-injection phase that ends at the time of the break in the light curve (red star) and for an ongoing injection phase until the end of the observations at t = 240 ks, both taking the end-time luminosity directly (green star) and correcting for the change in the slope introduced at the break (grey star). Energy injection follows the correlation very well, supporting the scenario with energy injection up to the break in the light curve. Continued energy injection is disfavoured in view of the correlation. We note that assuming energy injection to extend beyond the final data point at 240 ks will only shift the grey and green stars even farther away from the correlation.
observed in a sample of 62 long GRBs studied by Margutti et al. (2013). We included GRB 121024A for both an energy-injection phase that ends at the time of the break in the light curve (red star) and for an ongoing injection phase until the end of the observations at t = 240 ks, both taking the end-time luminosity directly (green star) and correcting for the change in the slope introduced at the break (grey star). Energy injection follows the correlation very well, supporting the scenario with energy injection up to the break in the light curve. Continued energy injection is disfavoured in view of the correlation. We note that assuming energy injection to extend beyond the final data point at 240 ks will only shift the grey and green stars even farther away from the correlation.
 |
Fig. 5 0.3−30 keV luminosity at the end of the energy-injection phase (Dainotti et al. 2008). The black dots are taken from Margutti et al. (2013). The stars correspond to the GRB 121024A afterglow: the red star to when the end of the plateau phase lies at 49.8 ks, the green star corresponds to the ongoing energy-injection phase before and after the break in the LC at t = 240 ks, and the grey star corresponds to the luminosity corrected for the jet-break effect. The dashed line in the middle corresponds to the best fit, and the shaded region is the 1σ error of the fit. |
We consider the jet-break model where νm<νsa to be the preferred scenario. In this model, all the micro-physical and dynamical parameters are within the range of previous measurements and within the expected values from the standard afterglow model. The low values for the energy are just lower limits and therefore are not a strong argument against this model. The main problem is related to the hard electron spectrum that requires additional assumptions on the acceleration process of the electrons in the shock region. However, this is certainly not the first GRB for which such a shallow electron spectrum was derived, and viable ways to handle this scenario have been put forward, two of which we investigated and found to give reasonable and physically meaningful results. The derived hard electron spectrum need not be a reason to reject a model, and more likely reflects our poor understanding of acceleration processes under extreme conditions. Finally, the linear polarisation observations reported by Wiersema et al. (2014) would agree with a jet-break model where the linear polarisation would be a direct result from the jet break. However, there are still no studies reported in the literature analysing whether it would be possible to obtain this type of polarisation from an energy-injection model.
6. Summary and conclusions
We analysed the afterglow of GRB 121024A and showed that the multi-wavelength data enable the afterglow spectra and temporal parameters to be measured to a high degree of accuracy, which sets strong constraints on the micro-physics in the shock region and on the dynamics of the jet. The combined GROND and XRT data allowed us to determine the spectral slope β in this energy regime with high accuracy, and therefore we were able to measure the electron index p. We modelled our complete set of observations using two different physical interpretations: a jet-break model and an energy-injection model. The energy-injection model requires η< 77%, 71%, and 69% for k = 2, 1.1, and 0, respectively, and does not contradict Fermi acceleration predictions for the electron index p. However, it does face some problems with the derived microphysical parameters in the case of a wind density profile, and the density values are extremely high in all three of the density profiles studied.
The jet-break model requires a hard electron spectrum. Assuming γm ∝ γ, the derived microphysical and dynamical parameters are all consistent with previous measurements and with expected values from theoretical analysis. There is a problem with the efficiency requirements, which for νsa<νm can be as high as η ~ 98%, and for νm<νsa the efficiency has an upper limit of η< 71%.
The results presented here on GRB 121024A show that broadband afterglow data from the X-ray to the radio allow for a detailed analysis of the characteristic properties of the GRB afterglow synchrotron emission spectrum. As studies of other GRBs have also shown, such datasets are invaluable for determining the range of microphysical and dynamical parameters within GRB shock-fronts with better statistics and avoiding adding additional assumptions to the analysis. Through our extensive data coverage of GRB 121024A, we have been able to constrain the position of all synchrotron breaks, which in turn has allowed us to measure, or set constraints on, all the micro-physical and dynamical parameters of a GRB afterglow. This information is crucial to further study the GRB afterglow emission process, and we are currently working on a larger sample of GRBs with sensitive and broadband afterglow data (Varela et al., in prep.). Future continual coverage of the GRB afterglows with sensitive telescopes over a wide wavelength range and at multiple epochs will enable us to place strong constraints on the micro-physical parameters for a larger sample of GRBs, and allow us for instance to investigate the evolution of these parameters.
Efficiency of the conversion of the kinetic energy in the outflow to gamma-rays during the prompt emission η = Eiso,γ/ (Eiso,γ + Eiso). Eiso,γ is the isotropic energy released in the prompt gamma-ray emission. In this case 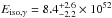 erg (Butler & Kocevski 2007; http://butler.lab.asu.edu/Swift/index.html). It is calculated using
erg (Butler & Kocevski 2007; http://butler.lab.asu.edu/Swift/index.html). It is calculated using 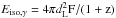 , where F is the fluence in the gamma-ray band. BAT: from 15−150 keV in the observer-frame. Eiso: energy range 1−104 keV in the rest frame.
, where F is the fluence in the gamma-ray band. BAT: from 15−150 keV in the observer-frame. Eiso: energy range 1−104 keV in the rest frame.
Acknowledgments
We express special thanks to Regís Lachaume for helping with the GROND observations. We are grateful to Rafaela Margutti for the data of Fig. 5. K.V. acknowledges support by DFG grant SA 2001/2-1. H.v.E. acknowledges support by the Alexander von Humboldt Foundation and the Carl Friedrich von Siemens Foundation. J.G. acknowledges support by the DFG cluster of excellence “Origin and Structure of the Universe” (www.universe-cluster.de). R.F. acknowledges support by Czech MEYS Grant 7AMB14DE001. P.S. acknowledges support through the Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation of Germany. J.F.G., M.T. and P.W. acknowledge support through the Sofja Kovalevskaja Award to P. Schady from the Alexander von Humboldt Foundation of Germany. S.K. and A.N.G. acknowledge support by DFG grant Kl 766/16-1. A.N.G. and D.A.K. are grateful for travel funding support through MPE. S.S. acknowledges support by the Thüringer Ministerium für Bildung, Wissenschaft und Kultur under FKZ 12010-514. A.Rossi acknowledges support by the Thüringer Landessternwarte Tautenburg. C.D. acknowledges support through EXTraS, funded from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement no 607452. APEX is operated by the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory. Part of the funding for GROND (both hardware as well as personnel) was generously granted from the Leibniz-Prize to G. Hasinger (DFG grant HA 1850/28-1). This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester.
References
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Allen de Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Reinsch, K., et al. 1999, A&A, 352, L26 [NASA ADS] [Google Scholar]
- Bhattacharya, D. 2001, BASI, 29, 107 [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1976, Physics of Fluids, 19, 1130 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, N. R., & Kocevski, D. 2007, ApJ, 663, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Frail, D. A., Harrison, F. A., et al. 2010, ApJ, 711, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Frail, D. A., Harrison, F. A., et al. 2011, ApJ, 732, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, P., Cenko, S. B., Frail, D. A., et al. 2008, ApJ, 683, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Li, Z.-Y. 1999, ApJ, 520, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Li, Z.-Y. 2000, ApJ, 536, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Li, Z.-Y., & Fransson, C. 2004, ApJ, 606, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, E., Frontera, F., Heise, J., et al. 1997, Nature, 387, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, P. A., Evans, P. A., de Pasquale, M., Page, M. J., & van der Horst, A. J. 2010, ApJ, 716, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Cheng, K. S. 2001, ApJ, 558, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1998, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., & Lu, T. 1999, ApJ, 519, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Dainotti, M. G., Cardone, V. F., & Capozziello, S. 2008, MNRAS, 391, L79 [NASA ADS] [CrossRef] [Google Scholar]
- De Colle, F., Ramirez-Ruiz, E., Granot, J., & Lopez-Camara, D. 2012, ApJ, 751, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Waxman, E., & Kulkarni, S. R. 2000, ApJ, 537, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Friis, M., De Cia, A., Krühler, T., et al. 2015, MNRAS, 451, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Lei, W.-H., Zou, Y.-C., Wu, X.-F., & Zhang, B. 2013, New Astron. Rev., 57, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., & Piran, T. 2012, MNRAS, 421, 570 [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Ramirez-Ruiz, E., & Loeb, A. 2005, ApJ, 618, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Königl, A., & Piran, T. 2006, MNRAS, 370, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holland, S. T., & Pagani, C. 2012, GRB Coordinates Network, 13901, 1 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, J. G., Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ, 542, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Klebesadel, R. W., Strong, I. B., & Olson, R. A. 1973, ApJ, 182, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Knust, F., Schady, P., & Greiner, J. 2012, GRB Coordinates Network, 13891, 1 [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Küpcü Yoldaş, A., Greiner, J., et al. 2008, ApJ, 685, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P. 1999, ApJ, 523, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Barniol Duran, R. 2009, MNRAS, 400, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, T., Zauderer, A., & Berger, E. 2012, GRB Coordinates Network, 13903, 1 [Google Scholar]
- Lazzati, D., & Perna, R. 2007, MNRAS, 375, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Leventis, K., van Eerten, H. J., Meliani, Z., & Wijers, R. A. M. J. 2012, MNRAS, 427, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Zaninoni, E., Bernardini, M. G., et al. 2013, MNRAS, 428, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. V. 2006, ApJ, 651, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1997, ApJ, 476, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Morsony, B. J., Lazzati, D., & Begelman, M. C. 2007, ApJ, 665, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Nousek, J. A., Kouveliotou, C., Grupe, D., et al. 2006, ApJ, 642, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, C., Barthelmy, S. D., Baumgartner, W. H., et al. 2012, GRB Coordinates Network, 13886, 1 [Google Scholar]
- Page, K. L., Maselli, A., Mangano, V., et al. 2012, GRB Coordinates Network, 13892, 1 [Google Scholar]
- Panaitescu, A. 2005, MNRAS, 363, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2000, ApJ, 543, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2002, ApJ, 571, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, S. B., Sahu, D. K., Resmi, L., et al. 2003, BASI, 31, 19 [NASA ADS] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Resmi, L., Ishwara-Chandra, C. H., Castro-Tirado, A. J., et al. 2005, A&A, 440, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rhoads, J. E. 1999, ApJ, 525, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Santana, R., Barniol Duran, R., & Kumar, P. 2014, ApJ, 785, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Esin, A. A. 2001, ApJ, 548, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F. 2012, in SPIE Conf. Ser., 8452, 1 [Google Scholar]
- Schuller, F., Nord, M., Vlahakis, C., et al. 2010, BoA – The Bolometer Data Analysis Software User and Reference Manual, 4th edn. (Max-Planck-Institut für Radioastronomie) [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Fynbo, J. P. U., Melandri, A., et al. 2012, GRB Coordinates Network, 13890, 1 [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
- van Eerten, H. 2014, MNRAS, 442, 3495 [NASA ADS] [CrossRef] [Google Scholar]
- van Eerten, H., Zhang, W., & MacFadyen, A. 2010, ApJ, 722, 235 [NASA ADS] [CrossRef] [Google Scholar]
- van Eerten, H. J., & MacFadyen, A. I. 2012, ApJ, 751, 155 [NASA ADS] [CrossRef] [Google Scholar]
- van Eerten, H. J., & Wijers, R. A. M. J. 2009, MNRAS, 394, 2164 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., Groot, P. J., Galama, T., et al. 1997, Nature, 386, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E., & Mészáros, P. 2003, ApJ, 584, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersema, K., Covino, S., Toma, K., et al. 2014, Nature, 509, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J., Rees, M. J., & Meszaros, P. 1997, MNRAS, 288, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Yost, S. A., Harrison, F. A., Sari, R., & Frail, D. A. 2003, ApJ, 597, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Zauderer, B., Laskar, T., & Berger, E. 2012, GRB Coordinates Network, 13900, 1 [Google Scholar]
- Zhang, B., & Mészáros., P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Alternative analysis to the jet-break model
One of the interpretations for the break in the light curve is a jet break. As mentioned in Sect. 4.1, a hard electron spectrum is required in this scenario. For completeness, we present here a second approach to analyse a hard electron spectrum (Bhattacharya 2001; Dai & Cheng 2001; Gao et al. 2013). Here, instead of assuming γm ∝ γ, the effect of an upper cut-off γM = [3e /φσTB] 1/2 in the energy range of the accelerated particle population can be included in the minimal Lorentz factor such that 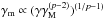 (Dai & Cheng 2001). This upper cut-off follows from equating acceleration and synchrotron cooling timescales. The advantages of this approach are that the extra cut-off is modelled explicitly and that ϵe can still be interpreted as the fraction of energy in the accelerated electrons. However, it implies that the behaviour of the electron population at low energies is dictated by the few electrons that were accelerated more efficiently, which is not supported by any clear physical mechanism.
(Dai & Cheng 2001). This upper cut-off follows from equating acceleration and synchrotron cooling timescales. The advantages of this approach are that the extra cut-off is modelled explicitly and that ϵe can still be interpreted as the fraction of energy in the accelerated electrons. However, it implies that the behaviour of the electron population at low energies is dictated by the few electrons that were accelerated more efficiently, which is not supported by any clear physical mechanism.
We calculated all the parameters for both regimes, when νsa<νm and when νm<νsa, and report them in Table A.1. The transition from the fast to slow cooling regime occurs at tνc = νm ~ 3.6 × 104 s for νsa<νm and tνc = νm ~ 6.6 × 102 s for νsa>νm, consistent with the slow cooling assumption.
The transition from optically thin to optically thick occurs at tνsa = νm ~ 9.8 × 104 s for νsa<νm and at tνsa = νm ~ 1.2 × 104 s for νsa>νm. In this case, the sub-regime where νsa<νm is ruled out because here the time that νm would cross νsa is ~12 ks, which is before the epoch of the SED (109 ks) used in the analysis. In the second sub-regime, where νm<νsa, θ0 is consistent with a collimated outflow and A∗ is in the range of expected values for a wind environment and corresponds to a mass-loss rate of >2.6 × 10-6Ṁo yr-1 for a wind velocity v = 1000 km s-1 (Chevalier & Li 1999, 2000), consistent with a Wolf-Rayet star as a possible progenitor. The efficiency η< 98%, even though it is just an upper limit, is extremely high. Our results agree with the results in Sect. 4.1 and support the jet-break scenario when νm<νsa as the preferred scenario.
γm,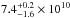 , ϵB, Eiso, n and θ0 for a jet-break model.
, ϵB, Eiso, n and θ0 for a jet-break model.
All Tables
Results from SED fits for both a jet-break model with νsa < νm and νm < νsa, and for an energy-injection model.
All Figures
 |
Fig. 1 GROND r′-band finding chart. The secondary stars used for the calibration are labelled I-VI and are reported in Table 1. North is up and east to the left. |
| In the text | |
 |
Fig. 2 Light curve of the afterglow of GRB 121024A. Top: XRT light curve from the XRT repository. Bottom: GROND light curve in g′r′i′z′JHKs. The best fit for the combined light curve (optical/NIR and X-ray data) is a smoothly broken power law with host contribution, shown with dashed lines. The epochs used for the spectral analysis are highlighted with the vertical bars. The break time tb = 49.8 ± 5.1 ks. |
| In the text | |
 |
Fig. 3 Spectral energy distribution for the six SEDs highlighted in Fig. 2. SEDs I – IV are from data before the observed break in the light curve. SEDs V and VI are from data taken after the break. The SEDs are scaled with an arbitrary factor for clarity in the plot. The values of β written above each line corresponds to the single power-law fit, where the slopes were left free to vary. The single power-law fit with a single tied slope has β = 0.86 ± 0.02. |
| In the text | |
 |
Fig. 4 Broadband SEDs of the afterglow of GRB 121024A from the radio to the X-ray regime for the three models described in Sect. 4. Blue line: SED at t = 21.9 ks. Red line: SED at t = 109.0 ks. The dashed lines represent the absorbed model, the solid lines the unabsorbed model. The grey-shaded regions corresponds to the 1σ limits of the model. |
| In the text | |
 |
Fig. 5 0.3−30 keV luminosity at the end of the energy-injection phase (Dainotti et al. 2008). The black dots are taken from Margutti et al. (2013). The stars correspond to the GRB 121024A afterglow: the red star to when the end of the plateau phase lies at 49.8 ks, the green star corresponds to the ongoing energy-injection phase before and after the break in the LC at t = 240 ks, and the grey star corresponds to the luminosity corrected for the jet-break effect. The dashed line in the middle corresponds to the best fit, and the shaded region is the 1σ error of the fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.