| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201528043 | |
| Published online | 22 March 2016 | |
Temperature condensation trend in the debris-disk binary system ζ2 Reticuli⋆
1
Instituto de Ciencias Astronómicas,
de la Tierra y del Espacio (ICATE-CONICET), CC
467,
5400
San Juan,
Argentina
e-mail: csaffe@icate-conicet.gob.ar; mflores@icate-conicet.gob.ar; mjaque@icate-conicet.gob.ar
2
Universidad Nacional de San Juan (UNSJ), Facultad de Ciencias
Exactas, Físicas y Naturales
(FCEFN), 5400
San Juan,
Argentina
3
Instituto de Astronomía y Física del Espacio
(IAFE-CONICET), 1428
Buenos Aires,
Argentina
4
Departamento de Física, Facultad de Ciencias Exactas y Naturales
(FCEN), Universidad de Buenos Aires (UBA), Buenos Aires,
Argentina
5
Observatorio Astronómico de Córdoba (OAC),
Laprida 854, X5000BGR,
Córdoba,
Argentina
6
Consejo Nacional de Investigaciones Científicas y Técnicas
(CONICET), 1428
Buenos Aires,
Argentina
Received: 24 December 2015
Accepted: 2 February 2016
Context. Detailed abundance studies have reported different trends between samples of stars with and without planets, possibly related to the planet formation process. Whether these differences are still present between samples of stars with and without debris disk is still unclear.
Aims. We explore condensation temperature Tc trends in the unique binary system ζ1 Ret −ζ2 Ret to determine whether there is a depletion of refractories that could be related to the planet formation process. The star ζ2 Ret hosts a debris disk which was detected by an IR excess and confirmed by direct imaging and numerical simulations, while ζ1 Ret does not present IR excess or planets. These characteristics convert ζ2 Ret in a remarkable system where their binary nature together with the strong similarity of both components allow us, for the first time, to achieve the highest possible abundance precision in this system.
Methods. We carried out a high-precision abundance determination in both components of the binary system via a line-by-line, strictly differential approach. First we used the Sun as a reference and then we used ζ2 Ret. The stellar parameters Teff, log g, [Fe/H], and vturb were determined by imposing differential ionization and excitation equilibrium of Fe I and Fe II lines, with an updated version of the program FUNDPAR, together with plane-parallel local thermodynamic equilibrium ATLAS9 model atmospheres and the MOOG code. We then derived detailed abundances of 24 different species with equivalent widths and spectral synthesis with the MOOG program. The chemical patterns were compared with a recently calculated solar-twins Tc trend, and then mutually between both stars of the binary system. The rocky mass of depleted refractory material was estimated according to recent data.
Results. The star ζ1 Ret is found to be slightly more metal rich than ζ2 Ret by ~0.02 dex. In the differential calculation of ζ1 Ret using ζ2 Ret as reference, the abundances of the refractory elements are higher than the volatile elements, and the trend of the refractory elements with Tc shows a positive slope. These results together show a lack of refractory elements in ζ2 Ret (a debris-disk host) relative to ζ1 Ret. The Tc trend would be in agreement with the proposed signature of planet formation rather than possible galactic chemical evolution or age effects, which are largely diminished here. Then, following the recent interpretation, we propose a scenario in which the refractory elements depleted in ζ2 Ret are possibly locked up in the rocky material that orbits this star and produce the debris disk observed around this object. We estimated a lower limit of Mrock ~ 3 M⊕ for the rocky mass of depleted material, which is compatible with rough estimations of 3−50 M⊕ of a debris disk mass around a solar-type star.
Key words: stars: abundances / planetary systems / binaries: general / stars: individual: ζ1Ret / stars: individual: ζ2Ret
Tables 1 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/588/A81
© ESO, 2016
1. Introduction
Meléndez et al. (2009,hereafter M09) showed that the Sun is deficient in refractory elements relative to volatile elements when compared to the mean abundances of 11 solar twins. They also found that the abundance differences correlate strongly with the condensation temperature Tc, which is interpreted by the authors as a possible signature of terrestrial planet formation in the solar system. They suggested that the refractory elements (Tc> 900 K) depleted in the solar photosphere are locked up in terrestrial planets and rocky material at the time of star and planet formation. In a follow-up study, Ramírez et al. (2010,hereafter R10) confirmed their findings. Gonzalez et al. (2010) and Gonzalez (2011) also found that most metal-rich exoplanet host (EH) stars have the most negative trends. These results indicate that the depletion of refractory elements in a photosphere is a consequence of both terrestrial and giant planet formation. If this hypothesis is correct, stars with planetary systems like ours may be identified through a very detailed inspection of the chemical composition.
Debris disks orbiting main-sequence stars are observationally characterized by an infrared excess over the normal photospheric fluxes of their host stars (see e.g. Aumann et al. 1984; Mannings & Barlow 1998; Habing et al. 2001; Bryden et al. 2006; Beichman et al. 2006). The excess is produced by the presence of dust in the disk which is attributed to the collisions of larger rocky bodies (see e.g. the reviews of Wyatt 2008; Moro-Martin 2013; Matthews et al. 2014, and references therein). The existence of these dusty disks is confirmed in some cases by direct imaging, starting with the first β Pictoris image by Smith & Terrile (1984) and then followed by other examples (see e.g. Krist et al. 2005; Vandenbussche et al. 2010; Soumer et al. 2014; Currie et al. 2015). Maldonado et al. (2015,hereafter MA15) compared Tc trends in a sample of stars with debris disks and stars with neither debris nor planets, and found no statistical difference between them. In other words, they do not detect a possible lack of refractory elements in debris disk stars when compared to stars without disks. The detection of a Tc trend is a challenging task that requires the highest possible precision in abundances, such as those obtained with the line-by-line differential technique (e.g. Bedell et al. 2014; Saffe et al. 2015). However, the sample of MA15 included 251 FGK stars spanning a range in Teff of ~2000 K, which prevented the authors from performing a differential analysis, as they explained. In addition, the study of binary systems with similar components greatly diminishes other Tc effects such as the galactic chemical evolution (GCE, González Hernández et al. 2013; Schuler et al. 2011a), the stellar age, and a possible inner galactic origin of the planet hosts (e.g. Adibekyan et al. 2014) thanks to the common natal environment of the pair. MA15 showed that these effects are indeed present in their sample, suggesting that an evolutionary effect is present. Then, the study of binary systems with similar components presents important advantages aiming to detect a possible Tc trend related to the planet formation process (e.g. Tucci Maia et al. 2014; Saffe et al. 2015).
To date, finding a binary system (with similar components) where only one star hosts a debris disk has been a very difficult task. Most of the IR surveys performed with the satellite Spitzer have mainly been focused on single main-sequence stars rather than multiple systems (e.g. Beichman et al. 2005; Rieke et al. 2005; Bryden et al. 2006; Su et al. 2006). Using Spitzer data, the location of the dust in a multiple system (i.e. circumstellar, circumbinary or both) could be determined only in very few cases (see e.g. Trilling et al. 2007). Rodriguez & Zuckerman (2012) showed that only ~25% of the debris disk stars in their sample of 112 main-sequence stars belong to multiple systems. The Herschel satellite overcomes some of these difficulties thanks to its greater sensivity and spatial resolution. Different Herschel surveys such as SUNS, DEBRIS (Matthews et al. 2010; Phillips et al. 2010), and DUNES (Eiroa et al. 2010, 2013; Löhne et al. 2012) include multiple systems in their samples. However, the circumstellar nature of the dust has been determined in few multiple systems (see e.g. Eiroa et al. 2013). Recently, Rodriguez et al. (2015) estimated a multiplicity of ~42% in the stars in the DEBRIS survey by using adaptive optics imaging. However, there is no physical data of many systems and most of them do not present similar components (see e.g. their Table 1). This shows how difficult it could be to find this kind of binary system.
As a part of the DUNES survey, Eiroa et al. (2010) discovered a resolved debris disk around the star ζ2 Ret (=HD 20807), which is accompanied by the star ζ1 Ret (= HD 20766). The projected distance between the stars is 3713 AU (Mason et al. 2001), while a Bayesian analysis of the proper motions indicates a very high probability (near 100%) that the pair is physically connected (Shaya & Olling 2011). This is a unique system for a number of reasons. The presence of a debris disk around ζ2 Ret was detected through a mid-IR excess (Trilling et al. 2008; Eiroa et al. 2013), it was confirmed by direct imaging (Eiroa et al. 2010), and also supported by numerical simulations (Faramaz et al. 2014). On the other hand, the companion ζ1 Ret does not present IR excess using both Spitzer and Herschel observations (Bryden et al. 2006; Trilling et al. 2008; Eiroa et al. 2013). The spectral types of the binary components are very similar (G2 V + G1 V in the Hipparcos database) allowing a chemical comparison less dependent on the fundamental parameters of the stars. The two stars are also very similar to the Sun, being both solar analogues. Also, there is no planet detected in this binary system (as we explain below), which is a condition for the sample of MA15. These characteristics show that this is a remarkable binary system, an ideal case to test a possible Tc trend in stars with and without debris disks.
Using numerical simulations, Faramaz et al. (2014) suggested that the eccentric structure of the ζ2 Ret debris disk could be caused by an eccentric (e> 0.3) planetary companion. However, both stars (ζ1 and ζ2) have been monitored by the Anglo-Australian Planet Search (AAPS) radial-velocity survey1, while ζ2 Ret was also included in the HARPS GTO planet search program (e.g. Sousa et al. 2008) giving no-planet detection. The AAPS survey rules out a Saturn-mass (0.3 MJup) or a larger planet with a period range P< 300 days and eccentricity 0.0 <e< 0.6 (Wittenmyer et al. 2010). The HARPS GTO survey suggests that there is no Jupiter-mass or a larger planet interior to ~5−10 AU (Mayor et al. 2003). Although the radial-velocity surveys cannot completely rule out the presence of planets (such as long-period perturbers or lower mass planets), these stars form, to our knowledge, the only solar-like binary system with similar components where only one component hosts a debris disk (confirmed by direct imaging) and the presence of planets has not been confirmed yet.
Surprinsingly, in this work we found a Tc trend between the components of this binary system, i.e. a lack of refractory elements in a debris disk star. We note that the MA15 statistical result does not exclude that Tc trends may be present in particular stars, such as the components of the ζ Ret system. The Tc trend would be in agreement with the proposed signature of planet formation (e.g. Meléndez et al. 2009; Ramírez et al. 2010) rather than possible GCE, age or evolutionary effects which are largely diminished here.
The abundances of the stars have been previously determined in the literature. However, there are some differences in the fundamental parameters derived for ζ2 Ret. The reported metallicities vary from −0.16 dex to −0.36 dex (Maldonado et al. 2012; Allende Prieto et al. 2004) while log g vary between 4.41 dex and 4.64 dex (Bensby et al. 2014; Maldonado et al. 2012). These differences also encouraged this work, searching for a slight difference between the components of this binary system.
This work is organized as follows. In Sect. 2 we describe the observations and data reduction, while in Sect. 3 we present the stellar parameters and chemical abundance analysis. In Sect. 4 we show the results and discussion, and finally in Sect. 5 we highlight our main conclusions.
2. Observations and data reduction
Stellar spectra of ζ1 Ret and ζ2 Ret were obtained with the High Accuracy Radial velocity Planet Searcher (HARPS) spectrograph, attached to the La Silla 3.6 m (ESO) telescope. The spectrograph was fed by a pair of fibres with an aperture of 1 arcsec on the sky, resulting in a resolving power of ~115 0002. The spectra were obtained from the ESO HARPS archive3, under the ESO program identification 072.C-0513(D).
The observations were taken on February 4, 2004, with ζ2 Ret observed immediately after ζ1 Ret, using the same spectrograph configuration. The exposure times were 3 × 150 s for both targets. We measured a signal-to-noise S/N ~ 300 for each of the binary components with a spectral coverage between 3870−6900 Å. The asteroid Ganymede was also observed with the same spectrograph set-up achieving a slightly higher S/N to acquire the solar spectrum useful for reference in our initial differential analysis. We note, however, that the final differential study with the highest abundance precision is between ζ1 Ret and ζ2 Ret because of their high degree of similarity. The data were reduced with the HARPS pipeline and combined using the software package IRAF4.
3. Stellar parameters and chemical abundance analysis
We derived the fundamental parameters (Teff, log g, [Fe/H], vturb) of ζ1 Ret and ζ2 Ret following the same procedure detailed in our previous work (Saffe et al. 2015). We started by measuring the equivalent widths (EW) of Fe I and Fe II lines in the spectra of our program stars using the IRAF task splot, and then continued with other chemical species. The lines list and relevant laboratory data (such as excitation potential and oscilator strengths) were taken from Liu et al. (2014) and Meléndez et al. (2014), and then extended with data from Bedell et al. (2014), who carefully selected lines for a high-precision abundance determination. This data, including the measured EWs, are presented in Table 1. We then imposed excitation and ionization balance of Fe I and Fe II lines, using the differential version of the program FUNDPAR (Saffe 2011) together with the 2014 version of the MOOG code (Sneden 1973) and ATLAS9 model atmospheres (Kurucz 1993).
Stellar parameters of ζ1 Ret and ζ2 Ret were differentially determined using the Sun as standard in an initial approach, and then we recalculated the parameters of ζ1 Ret using ζ2 Ret as reference. First, we determined absolute abundances for the Sun using 5777 K for Teff, 4.44 dex for log g and an initial vturb of 1.0 km s-1. Then, we estimated vturb for the Sun with the usual method of requiring zero slope in the absolute abundances of Fe I lines vs. EWr and obtained a final vturb of 0.91 km s-1. We note, however, that the exact values are not crucial for our strictly differential study (see e.g. Bedell et al. 2014; Saffe et al. 2015).
The next step was the determination of stellar parameters of ζ1 Ret and ζ2 Ret using the Sun as standard, i.e. (ζ1 Ret − Sun) and (ζ2 Ret − Sun). For ζ1 Ret the resulting stellar parameters were Teff = 5710 ± 29 K, log g = 4.53 ± 0.05 dex, [Fe/H] = −0.195 ± 0.005 dex, and vturb = 0.80 ± 0.27 km s-1. For ζ2 Ret, we obtained Teff = 5854 ± 28 K, log g = 4.54 ± 0.04 dex, [Fe/H] = −0.215 ± 0.004 dex, and vturb = 0.95 ± 0.09 km s-1. In the Table 2 we present the differential parameters ΔTeff, Δlog g, Δ(Fe/H), and Δvturb derived between the star and their corresponding reference. The errors in the stellar parameters were derived following the procedure detailed in Saffe et al. (2015), which takes into account the individual and the mutual covariance terms of the error propagation. The star ζ1 Ret resulted in a slightly higher metallicity than ζ2 Ret by ~0.02 dex. Figures 1 and 2 show abundance vs. excitation potential and abundance vs. EWr for both stars. Filled and empty points correspond to Fe I and Fe II, while the dashed lines are linear fits to the differential abundance values.
Differential parameters ΔTeff, Δlog g, Δ[Fe/H], and Δvturb derived between the star and their corresponding reference.
 |
Fig. 1 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ1 Ret relative to the Sun. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the abundance values. |
 |
Fig. 2 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ2 Ret relative to the Sun. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the abundance values. |
The parameters of ζ1 Ret were then recalculated, but using ζ2 Ret as reference instead of the Sun, i.e. (ζ1 Ret −ζ2 Ret). Figure 3 shows abundance vs. excitation potential and abundance vs. EWr, using similar symbols to those used in Figs. 1 and 2. The resulting stellar parameters for ζ1 Ret are the same as those obtained when we used the Sun as a reference, but with lower dispersions: Teff = 5710 ± 22 K, log g = 4.53 ± 0.03 dex, [Fe/H] = −0.195 ± 0.003 dex, and vturb = 0.80 ± 0.07 km s-1. The differential parameters ΔTeff, Δlog g, Δ(Fe/H), and Δvturb derived between ζ1 Ret and ζ2 Ret are also presented in Table 2. Again, we found that the metallicity of ζ1 Ret is slightly higher than ζ2 Ret by ~0.02 dex.
 |
Fig. 3 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ1 Ret relative to ζ2 Ret. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the data. |
Once the stellar parameters of the binary components were determined using iron lines, we computed abundances for all remaining chemical elements. The hyperfine structure splitting (HFS) was considered for V I, Mn I, Co I, Cu I, and Ba II using the HFS constants of Kurucz & Bell (1995) and performing spectral synthesis for these species. We derived the O I abundances by using spectral synthesis with the line 6300.304 Å5 (the O I triplet is out of the HARPS wavelength range), which is basically free of non-local thermodynamic equilibrium (NLTE) effects (Takeda 2003). Direct interpolation in the tables of Amarsi et al. (2015) also results in a null NLTE correction for this O I line. We also applied NLTE corrections to Ba II (−0.10 dex) and Cu I (+0.04 dex) in the same amount for both stars, interpolating in data of Korotin et al. (2011) and Yan et al. (2015).
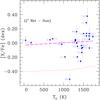 |
Fig. 4 Differential abundances (ζ1 Ret − Sun) vs. condensation temperature Tc. The dashed line is a linear fit to the differential abundance values, while the continuous line shows the solar-twins trend of Meléndez et al. (2009). |
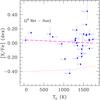 |
Fig. 5 Differential abundances (ζ2 Ret − Sun) vs. condensation temperature Tc. The dashed line is a linear fit to the differential abundance values, while the continuous line shows the solar-twins trend of Meléndez et al. (2009). |
In Table 3 we present the final differential abundances [X/Fe]6 of ζ1 Ret and ζ2 Ret relative to the Sun, and the differential abundances of ζ1 Ret using ζ2 Ret as the reference star. We present both the observational errors σobs (estimated as σ/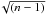 , where σ is the standard deviation of the different lines) and systematic errors due to uncertainties in the stellar parameters σpar (by adding quadratically the abundance variation when modifying the stellar parameters by their uncertainties), as well as the total error σTOT obtained by quadratically adding σobs, σpar and the error in [Fe/H].
, where σ is the standard deviation of the different lines) and systematic errors due to uncertainties in the stellar parameters σpar (by adding quadratically the abundance variation when modifying the stellar parameters by their uncertainties), as well as the total error σTOT obtained by quadratically adding σobs, σpar and the error in [Fe/H].
4. Results and discussion
The differential abundances of ζ1 Ret and ζ2 Ret relative to the Sun are presented in Figs. 4 and 5; the condensation temperatures were taken from the 50% Tc values derived by Lodders (2003). We corrected by GCE effects when comparing (star-Sun) following the same procedure of Saffe et al. (2015) by adopting the GCE fitting trends of González Hernández et al. (2013). However, this correction is discarded when comparing mutually the components of the binary system (ζ1 Ret −ζ2 Ret) owing to their common natal environment. Filled points in Figs. 4 and 5 correspond to the differential abundances for the stars ζ1 Ret and ζ2 Ret relative to the Sun. The continuous line correspond to the solar-twins trend of M09 (vertically shifted for comparison), while the dashed line in Figs. 4 and 5 is a linear fit to the abundance values. We also present in Table 4 the derived slopes with their dispersions. In order to provide another estimation of the significance of the slopes, we performed 100 000 series of simulated random abundances and errors following a similar method to MA15. Then, assuming that the distribution of the simulated slopes follows a Gaussian distribution, we compute the probability of the original slope “being by chance”. This value is also presented in the last column of Table 4.
Derived slopes (abundance vs. temperature condensation Tc), their dispersion and probability of the slope “being by chance” (see text for details).
We note that the general trend of ζ1 Ret presents a slightly higher slope than the Sun, while ζ2 Ret presents a slightly lower slope than the Sun. This would correspond, for instance, to a slight lack of refractories (Tc> 900 K) with respect to volatiles (Tc< 900 K) when comparing ζ2 Ret with the Sun. However, the general trends should be taken with caution owing to the relatively high dispersion of points (most elements spread between −0.20 dex and +0.20 dex). These dispersions are greatly diminished by comparing mutually ζ1 Ret and ζ2 Ret, which presents the advantage of the strong similarity between them, together with the independence of GCE and evolutionary effects. Also, as we see in Table 4, the slopes of the stars relative to the Sun are derived within ~1.5σ, while for the case (ζ1 Ret −ζ2 Ret) the slope values are within ~4σ, i.e. the significance of the slope increases significantly. Table 4 also includes the case of considering only the refractory elements between ζ1 Ret and ζ2 Ret, shown as (ζ1 Ret −ζ2 Ret)Refr. The probability of the slopes “being by chance” is relatively high when the Sun is used as reference (~%50); however, these values are diminished (~%28) in the mutual comparison (ζ1 Ret −ζ2 Ret), and are similar to those derived by MA15 (see e.g. their Table 9).
The abundances of Mn I and Nd II seem to deviate from the general trends for both stars (see Figs. 4 and 5). We derived the abundances of Mn I including the hyperfine structure splitting (HFS) using the constants of Kurucz & Bell (1995) in the spectral synthesis. We do not detect an HFS abundance difference between the Mn I line 4502.21 Å and other Mn I lines, as reported by MA15. For the Sun, Bergemann & Gehren (2007) estimated maximum NLTE corrections of +0.1 dex for Mn; however, even with such maximum correction the Mn abundance is still relatively low. Given the similar parameters of our stars with the Sun, we consider that the NLTE effects could also play a role in ζ1 Ret and ζ2 Ret. The abundance of Nd II was derived using the equivalent widths of two lines (4021.33 Å and 4446.38 Å). We have no evidence of an obvious blend at these lines; however, it is difficult to discard this possibility. Other Nd II lines such as 4059.95 Å or 5234.19 Å are very weak. Mashonkina et al. (2005) studied NLTE effects of Nd II, but in stars with higher temperatures (>7500 K). Then, in order to derive representative trends we excluded Mn I and Nd II from the linear fits.
The differential abundances of ζ1 Ret using ζ2 Ret as reference are presented in Fig. 6. In our calculation, this plot corresponds to the abundance values derived with the highest possible precision. The continuous line in this figure presents the solar-twins trend of M09 (vertically shifted), while the long-dashed lines are linear fits to all elements and the refractory elements. The differential abundances of the refractories (average of +0.016 dex) are higher than the volatiles (average of −0.061 dex) with a general slope of 6.27 ± 1.5510-5 dex/K, as we see in Fig. 6. Although the general trend seems to be driven by O I (which present a relatively low abundance value), when excluding O I the slope results 3.96 ± 1.05 × 10-5 dex/K, i.e. a general trend even closer to the refractory trend. The refractory elements alone also show a trend with Tc, with a slope of 3.85 ± 1.02 × 10-5 dex/K. For comparison, the slope of refractories between the components of the binary system 16 Cyg is 1.88 × 10-5 dex/K and clearly shows a higher abundance in refractory than volatile elements (Tucci Maia et al. 2014). We caution, however, that there is still no total consensus on the possible chemical differences between the components of 16 Cyg (e.g. Takeda 2005; Schuler et al. 2011b; Tucci Maia et al. 2014). Then, the higher value of the refractory elements compared to volatile elements, together with the positive slope in the trend of refractory elements with Tc, point toward a lack of refractory elements in ζ2 Ret relative to ζ1 Ret.
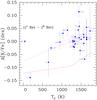 |
Fig. 6 Differential abundances (ζ1 Ret −ζ2 Ret) vs. condensation temperature Tc. The long-dashed lines are linear fits to all species and to the refractory species. The solar-twins trend of Meléndez et al. (2009) is shown with a continuous line. |
Detailed abundance studies performed on binary systems with similar components (where at least one component hosts a planet) showed different results. Some binary systems such as HAT-P-1 and HD 80606 do not seem to present significant Tc trends between their components (Liu et al. 2014; Saffe et al. 2015). On the other hand, the binary systems XO-2 and HD 20781 seem to present a relative Tc trend (Biazzo et al. 2015; Mack et al. 2014), although they are particular cases given that both components of the system host a planet. Also, possible metallicity differences of wide binary stars and multiple systems have been studied in the literature. Most of the cases present almost no metallicity differences, similar to the case of the triple system HD 132563 (Desidera et al. 2011). However, ~17% of the wide binaries do present slight metallicity differences between their components (Desidera et al. 2004, 2006). The origin of these slight differences is not totally clear, and a possible explanation lies in the planet formation process (e.g. Desidera et al. 2004, 2006).
Following the interpretation of M09 and R10, the lack of refractory elements in ζ2 Ret compared to ζ1 Ret could be identified with the signature of the planet formation process. Because no planets are detected around the stars of this binary system, the refractory elements depleted in ζ2 Ret are possibly locked up in rocky bodies (e.g. planetesimals and/or asteroids) whose collisions could produce the bright debris disk observed in this object. In fact, the slightly lower metallicity of ζ2 Ret compared to their companion (by ~0.02 dex) is also compatible with this scenario. Probably, the relatively low metallicity of the two stars prevented the formation of giant planets in this binary system. However, the presence of circumstellar material around ζ2 Ret (the debris disk) has been confirmed, as we mentioned previously. The conditions required to form a debris disk are more easily met than the conditions to form gas-giant planets and this is in agreement with the core-accretion model of planet formation (e.g. Pollack et al. 1996; Mordasini et al. 2012).
The rocky mass of depleted material in ζ2 Ret was estimated following Chambers (2010) in order to reproduce the trend of the refractory elements of Fig. 6. Using a convection zone similar to the Sun (Mcz = 0.023 M⊙) we obtain Mrock ~ 3 M⊕. However, at the time of the planet formation process Mcz could be greater than this value. For instance, adopting Mcz = 0.050 M⊙ we derive Mrock ~ 7 M⊕. Then, Mrock ~ 3 M⊕ should be considered as a lower limit. On the other hand, there is no direct estimation for the debris disk mass of ζ2 Ret (see e.g. Eiroa et al. 2010; Faramaz et al. 2014). The most precise estimates of debris disk masses comes from sub-mm observations (see e.g. Wyatt 2008). Krivov et al. (2008) modeled five solar-type debris disk stars and fitted the far-IR emission using disk masses in the range 3−50 M⊕ and radii between 100−200 AU. The mass range and radii are compatible with the mass derived from Chambers (2010) and the observed location of the disk around ζ2 Ret (R ~ 100 AU, Eiroa et al. 2010). However, Krivov et al. (2008) caution that the mass and location of the debris disk depend significantly on the collisional model and grain properties adopted.
5. Conclusions
We performed a high-precision differential abundance determination in both components of the remarkable binary system ζ1 Ret −ζ2 Ret, in order to detect a possible Tc trend. The two stars present very similar stellar parameters, which greatly diminishes the errors in the abundance determination, GCE or evolutionary effects. The star ζ2 Ret hosts a debris disk, while there is no debris disk detected (nor a planet) around ζ1 Ret. First, we derived stellar parameters and differential abundances of both stars using the Sun as the reference star and then for ζ1 Ret using ζ2 Ret as reference. Our calculation included NLTE corrections for Ba II and Cu I as well as GCE corrections for all chemical species where the Sun was used as reference. We compared the possible temperature condensation Tc trends of the stars with the solar-twins trend of Meléndez et al. (2009).
In comparing the stars to each other, ζ1 Ret resulted slightly more metal rich than ζ2 Ret by ~0.02 dex. Also, the differential abundances of the refractories were higher than the volatiles, and the general trend of the refractory elements with Tc showed a positive slope. These facts together point toward a lack of refractory elements in ζ2 Ret relative to ζ1 Ret, similar to the case of the binary system 16 Cyg (Tucci Maia et al. 2014). We caution, however, that there is still no total consensus on the possible chemical differences between the components of 16 Cyg (e.g. Takeda 2005; Schuler et al. 2011b; Tucci Maia et al. 2014). We note that the statistical result of Maldonado et al. (2015) does not exclude possible Tc trends in particular stars such as the ζ Ret system. Then, following the interpretation of M09 and R10, we propose a scenario in which the refractory elements depleted in ζ2 Ret are possibly locked up in the rocky material that orbits this star and produce the debris disk observed around this object. We estimated a lower limit of Mrock ~ 3 M⊕ for the rocky mass of depleted material according to Chambers (2010), which is compatible with a rough estimation of 3−50 M⊕ of a debris disk mass around a solar-type star (Krivov et al. 2008). We strongly encourage high-precision abundance studies in binary systems with similar components, which is a crucial tool for helping to detect the possible chemical pattern of the planet formation process.
Acknowledgments
The authors thank Drs. R. Kurucz and C. Sneden for making their codes available to us. We also thank the anonymous referee for constructive comments that improved the paper.
References
- Adibekyan, V., González Hernández, J., Delgado-Mena, E., et al. 2014, A&A, 564, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen de Prieto, C., Barklem, P., Lambert, D., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A., Asplund, M., Collet, R., & Leenaarts, J. 2015, MNRAS, 455, 3735 [Google Scholar]
- Aumann, H. H., Beichman, C. A., Gillett, F. C., et al. 1984, ApJ, 278, 23 [Google Scholar]
- Bedell, M., Meléndez, J., Bean, J., et al. 2014, AJ, 795, 23 [Google Scholar]
- Beichman, C., Bryden, G., Rieke, G., et al. 2005, AJ, 622, 1160 [Google Scholar]
- Beichman, C. A., Bryden, G., Stapelfeldt, K. R., et al. 2006, ApJ, 652, 1674 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., & Gehren, T. 2007, A&A, 473, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biazzo, K., Gratton, R., Desidera, S., et al. 2015, A&A, 583, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryden, G., Beichman, C. A., Trilling, D. E., et al. 2006, ApJ, 636, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. 2010, ApJ, 724, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Lisse, C., Kuchner, M., et al. 2015, ApJ, 807, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., Gratton, R. G., Scuderi, S., et al. 2004, A&A, 420, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desidera, S., Gratton, R. G., Lucatello, S., & Claudi, R. U. 2006, A&A, 454, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desidera, S., Carolo, E., Gratton, R., et al. 2011, A&A, 533, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eiroa, C., Fedele, D., Maldonado, J., et al. 2010, A&A, 518, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eiroa, C., Marshall, J., Mora, A., et al. 2013, A&A, 555, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faramaz, V., Beust, H., Thébault, P., et al. 2014, A&A, 563, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, G. 2011, MNRAS, 416, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., Carlson, M., & Tobin, W. 2010, MNRAS, 407, 314 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J., Delgado-Mena, E., Sousa, S., et al. 2013, A&A, 552, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J., Dominik, C., Jourdain de Muizon, M., et al. 2001, A&A, 365, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S., Mishenina, T., Gorbaneva, T., & Soubiran, C. 2011, MNRAS, 415, 2093 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J., Ardila, D., Golimowski, D., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A., Müller, S., Löhne, T., & Mutschke, H. 2008, AJ, 687, 608 [Google Scholar]
- Kurucz, R. L. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Kurucz, R., & Bell, B. 1995, Atomic Line Data, Kurucz CD-ROM No. 23 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Liu, F., Asplund, M., Ramírez, I., Yong, D., & Meléndez, J. 2014, MNRAS, 442, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, AJ, 591, 1220 [Google Scholar]
- Löhne, T., Eiroa, C., Augereau, J.-C., et al. 2012, Astron. Nachr., 333, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Mack, C., Schuler, S., Stassun, K., & Norris, J. 2014, ApJ, 787, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., et al. 2012, A&A, 541, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannings, V., & Barlow, M. J. 1998, ApJ, 497, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Ryabchikova, T., & Ryabtsev, A. 2005, A&A, 441, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B., Wycoff, G., Hartkopf, W., Douglass, G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Matthews, B., Sibthorpe, B., Kennedy, G., et al. 2010, A&A, 518, L135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, B., Krivov, A., Wyatt, M., Bryden, G., & Eiroa, C. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 521 [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, AJ, 704, L66 [Google Scholar]
- Meléndez, J., Ramírez, I., Karakas, A., et al. 2014, AJ, 791, 14 [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., et al. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moro-Martin, A. 2013, in Dusty Planetary Systems, eds. T. D. Oswalt, L. M. French, & P. Kalas (Hamburg: Springer Verlag), 431 [Google Scholar]
- Phillips, N., Graves, J., Dent, W., et al. 2010, MNRAS, 403, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Asplund, M., Baumann, P., Meléndez, J., & Bensby, T. 2010, A&A, 521, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G., Su, K., Stansberry, J., et al. 2005, AJ, 620, 1010 [Google Scholar]
- Rodriguez, D., & Zuckerman, B. 2012, AJ, 745, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, D., Duchene, G., Tom, H., et al. 2015, MNRAS, 449, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Saffe, C. 2011, Rev. Mex. Astron. Astrofis, 47, 3 [Google Scholar]
- Saffe, C., Flores, M., & Buccino, A. 2015, A&A, 582, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuler, S., Flateau, D., Cunha, K., et al. 2011a, AJ, 732, 55 [Google Scholar]
- Schuler, S., Cunha, K., Smith, V., et al. 2011b, ApJ, 737, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Shaya, E., & Olling, R. 2011, ApJS, 192, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B., & Terrile, R. 1984, Science, 226, 1421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Soumer, R., Perrin, M., Pueyo, L., et al. 2014, ApJ, 786, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S., Santos, N., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Su, K. Y., Rieke, G., Stansberry, J., et al. 2006, AJ, 653, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y. 2003, A&A, 402, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2005, PASJ, 57, 83 [NASA ADS] [Google Scholar]
- Trilling, D., Stansberry, J., Stapelfeldt, K., et al. 2007, ApJ, 658, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Trilling, D., Bryden, G., Beichman, C., et al. 2008, AJ, 674, 1086 [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, ApJ, 790, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Vandenbussche, B., Sibthorpe, B., Acke, B., et al. 2010, A&A, 518, L133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittenmyer, R., O’Toole, S., Jones, H., et al. 2010, AJ, 722, 1854 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Shi, J., & Zhao, G. 2015, AJ, 802, 36 [Google Scholar]
All Tables
Differential parameters ΔTeff, Δlog g, Δ[Fe/H], and Δvturb derived between the star and their corresponding reference.
Derived slopes (abundance vs. temperature condensation Tc), their dispersion and probability of the slope “being by chance” (see text for details).
All Figures
 |
Fig. 1 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ1 Ret relative to the Sun. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the abundance values. |
| In the text | |
 |
Fig. 2 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ2 Ret relative to the Sun. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the abundance values. |
| In the text | |
 |
Fig. 3 Differential abundance vs. excitation potential (upper panel) and differential abundance vs. reduced EW (lower panel) for ζ1 Ret relative to ζ2 Ret. Filled and empty points correspond to Fe I and Fe II, respectively. The dashed line is a linear fit to the data. |
| In the text | |
 |
Fig. 4 Differential abundances (ζ1 Ret − Sun) vs. condensation temperature Tc. The dashed line is a linear fit to the differential abundance values, while the continuous line shows the solar-twins trend of Meléndez et al. (2009). |
| In the text | |
 |
Fig. 5 Differential abundances (ζ2 Ret − Sun) vs. condensation temperature Tc. The dashed line is a linear fit to the differential abundance values, while the continuous line shows the solar-twins trend of Meléndez et al. (2009). |
| In the text | |
 |
Fig. 6 Differential abundances (ζ1 Ret −ζ2 Ret) vs. condensation temperature Tc. The long-dashed lines are linear fits to all species and to the refractory species. The solar-twins trend of Meléndez et al. (2009) is shown with a continuous line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


