| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527423 | |
| Published online | 17 March 2016 | |
Multiwavelength analysis for interferometric (sub-)mm observations of protoplanetary disks
Radial constraints on the dust properties and the disk structure
1
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
e-mail:
mtazzari@eso.org
2
Excellence Cluster Universe, Boltzmannstr. 2, 85748
Garching,
Germany
3
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi
5, 50125
Firenze,
Italy
4
Universitats-Sternwarte München, Scheinerstraße 1, 81679
München,
Germany
5
Dublin Institute for Advanced Studies, School of Cosmic
Physics, 31 Fitzwilliam
Place, Dublin 2,
Ireland
6
Department of Physics and Astronomy, Rice
University, 6100 Main
Street, Houston,
TX, 77005, USA
7
National Radio Astronomy Observatory, PO Box O, Socorro, NM
87801,
USA
8
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
9
Max Planck Institute for Astronomy, Königstuhl 17, 69117
Heidelberg,
Germany
10
Korea Astronomy and Space Science Institute,
776 Daedeok-daero, Yuseong-gu,
34055
Daejeon, Republic of
Korea
11
Joint ALMA Observatory (JAO), Av. Alonso de Cordova 3107, Vitacura,
Santiago,
Chile
12
Institute for Theoretical Astrophysics, Heidelberg
University, Albert-Ueberle-Strasse
2, 69120
Heidelberg,
Germany
13
Department of Astronomy, California Institute of
Technology, MC
249-17, Pasadena,
CA
91125,
USA
14
Department of Astronomy, University of Maryland,
College Park, MD
20742,
USA
15
Department of Astronomy, University of Michigan,
830 Dennison Building, 500 Church
Street, Ann Arbor,
MI
48109,
USA
16
School of Physics and Astronomy, University of St
Andrews, North
Haugh, St Andrews,
KY16 9SS,
UK
17
Jet Propulsion Laboratory, California Institute of Technology Pasadena,
CA
91109,
USA
18
The Netherlands Institute for Radio Astronomy
(ASTRON), 7990
Dwingeloo, The
Netherlands
Received: 22 September 2015
Accepted: 16 December 2015
Context. The growth of dust grains from sub-μm to mm and cm sizes is the first step towards the formation of planetesimals. Theoretical models of grain growth predict that dust properties change as a function of disk radius, mass, age, and other physical conditions. High angular resolution observations at several (sub-)mm wavelengths constitute the ideal tool with which to directly probe the bulk of dust grains and to investigate the radial distribution of their properties.
Aims. We lay down the methodology for a multiwavelength analysis of (sub-)mm and cm continuum interferometric observations to self-consistently constrain the disk structure and the radial variation of the dust properties. The computational architecture is massively parallel and highly modular.
Methods. The analysis is based on the simultaneous fit in the uv-plane of observations at several wavelengths with a model for the disk thermal emission and for the dust opacity. The observed flux density at the different wavelengths is fitted by posing constraints on the disk structure and on the radial variation of the grain size distribution.
Results. We apply the analysis to observations of three protoplanetary disks (AS 209, FT Tau, DR Tau) for which a combination of spatially resolved observations in the range ~0.88 mm to ~10 mm is available from SMA, CARMA, and VLA. In these disks we find evidence of a decrease in the maximum dust grain size, amax, with radius. We derive large amax values up to 1 cm in the inner disk 15 AU ≤ R ≤ 30 AU and smaller grains with amax ~ 1 mm in the outer disk (R ≳ 80 AU). Our analysis of the AS 209 protoplanetary disk confirms previous literature results showing amax decreasing with radius.
Conclusions. Theoretical studies of planetary formation through grain growth are plagued by the lack of direct information on the radial distribution of the dust grain size. In this paper we develop a multiwavelength analysis that will allow this missing quantity to be constrained for statistically relevant samples of disks and to investigate possible correlations with disk or stellar parameters.
Key words: stars: formation / planetary systems / protoplanetary disks
© ESO, 2016
1. Introduction
Planetary systems form in the dusty gaseous circumstellar disks that orbit young pre-main-sequence (PMS) stars. According to the core accretion scenario, the formation of planets proceeds with the formation of rocky cores through the growth of dust aggregates from mm/cm to km sizes and the subsequent accretion of gas onto these cores to form the planetary atmosphere (Safronov 1972; Wetherill 1980, and references therein). The initial population of sub-micron sized dust particles coming from the ancestral interstellar cloud (Mathis et al. 1977) is processed by micro-physical interactions that determine the evolution of their shape, size, and structure (Testi et al. 2014, and references therein).
Determining the size distribution of dust grains in protoplanetary disks is of paramount importance in order to understand the initial conditions of planet formation. In the recent theoretical studies by Brauer et al. (2008) and Birnstiel et al. (2010) the evolution of dust grain populations have been modeled taking into account dust growth processes (coagulation and fragmentation) and the dynamical mechanisms responsible for the transport of dust grains (radial drift, vertical settling, turbulent mixing). According to these studies, radial drift effectively depletes the large grain population in disks within 1 Myr (see also Laibe 2014) unless it is halted by the occurrence of dust traps (Whipple 1972; Weidenschilling 1977; Klahr & Henning 1997; Pinilla et al. 2012) or a different aerodynamic behavior when the grains are extremely fluffy aggregates (Okuzumi et al. 2012; Kataoka et al. 2013).
The major limitation of theoretical grain growth studies is the lack of direct information on the actual size of dust grains occurring in the different regions of the protoplanetary disks. Observing a protoplanetary disk at different wavelengths allows different parts of the disk to be investigated. Optical, near-infrared, and mid-infrared observations show evidence of micron-sized dust grains in protoplanetary disks (Bouwman et al. 2001; van Boekel et al. 2003; Juhász et al. 2010; Miotello et al. 2012); however, they effectively trace the dust content only of the inner disk and its surface layer (both directly heated by the impinging stellar radiation). In order to study the disk midplane, where the bulk of the dust mass resides and planet formation is thought to occur, millimeter and sub-millimeter continuum observations are needed. At these longer wavelengths most of the disk becomes optically thin to its own thermal radiation and therefore directly probes the entire dust emitting volume. Moreover, by approximating the (sub-)mm dust opacity with a power law κν ∝ νβ, changes in the spectral index β can be linked to changes in the dust properties (Stognienko et al. 1995; Henning & Mutschke 2010). In particular, Draine (2006) and Natta & Testi (2004) showed that β can be interpreted in terms of grain growth: large β-values are produced by small grains (μm to mm size), whereas small values β ≲ 1 are a signature of dust grains larger than 1 mm.
From multiwavelength observations we can gain insight into the dust opacity spectral index, and therefore on the level of dust processing occurring in a protoplanetary disk (Wilner et al. 2000; Testi et al. 2001, 2003; Rodmann et al. 2006). Past mm and sub-mm photometry studies allowed a disk-averaged β value to be inferred for several disks in different star forming regions, suggesting first, that grain growth processes are particularly efficient, able to produce large grains (~1 mm) within relatively short timescales of 1−3 Myr (Ricci et al. 2010a,b), and second, that local or global dust grain retention mechanisms must be occurring in disks in order to account for the observed presence of large grains in evolved disks (Testi et al. 2014).
In recent years, the improved observational capabilities offered by mm and sub-mm interferometers have allowed us for the first time to use spatially resolved observations to measure the dust grain properties as a function of the disk radius and to compare them with the theoretical predictions of grain growth models. Initial attempts using 1.3 and 3 mm observations of a sample of disks showed hints of possible radial variation of the dust properties (Isella et al. 2010; Guilloteau et al. 2011) and recent studies have successfully extended the wavelength range to cm wavelengths using the Karl G. Jansky Very Large Array (VLA; Banzatti et al. 2011; Trotta et al. 2013; Pérez et al. 2015, 2012; Menu et al. 2014; Andrews et al. 2014; Guidi et al. 2016). Azimuthal variations in the dust distribution have been recently discovered with ALMA early science observations in several disks and interpreted as dust traps, with the large grains being more concentrated than the small grains and the molecular gas (van der Marel et al. 2013, 2015; Fukagawa et al. 2013; Pérez et al. 2014; Casassus et al. 2015; Marino et al. 2015).
Pérez et al. (2012) used interferometric observations between 0.88 and 9.8 mm to constrain the radial profile of the β index in the AS 209 protoplanetary disk (and recently extended to CY Tau and DoAr 25 by Pérez et al. 2015). They fit each wavelength separately assuming a dust opacity constant with radius, and derived a disk temperature profile and an optical depth profile τν ∝ Σ κν for each wavelength, where Σ is the dust surface density and κν is the dust opacity. Then, given that the surface density must be wavelength independent, they ascribed the changes in τν to variations in κν (and therefore in the dust properties), thus deriving the β(R) profile. They found β ~ 0.5 (mm- and cm-sized grains) in the inner disk region (R ≲ 50 AU) and β ≳ βISM = 1.7 (sub-mm-sized grains) in the outer disk.
Improving on the results of Banzatti et al. (2011), Trotta et al. (2013) carried out the first attempt of a self-consistent modeling of the disk structure and the dust properties by fitting interferometric observations of the CQ Tau protoplanetary disk using a radius-dependent grain size distribution. With this model, they were able to fit observations simultaneously at 1.3, 2.6, and 7 mm, finding evidence of dust grains ranging in size from a few cm in the inner disk (<40 AU) to a few mm at 80 AU. The work by Trotta et al. (2013) laid down the basis of the study we present here, where we have developed this multiwavelength fit technique further.
In this paper we present a data analysis procedure that exploits the wealth of information carried by multiwavelength (sub-)mm observations in order to characterize the disk structure and the level of grain growth in the disk in a self-consistent way. Previous studies fit observations at different wavelengths separately, inferring for each of them a different temperature and surface density profile. We note that the discrepancy in the temperature profile inferred from fitting two different wavelengths can be as large as a factor of 2, especially in the outer disk, see Fig. B.2. Then, making assumptions on the average temperature and surface density profile that should characterize the disk, these studies reconciled the wavelength-dependent discrepancies between the models by deriving a β(R) profile. Adopting a more typical forward-modeling technique, the multiwavelength analysis we present here derives a self-consistent disk model defined by unique temperature, surface density, and grain size profile that make it capable of reproducing the observed disk emission at all the wavelengths simultaneously. The multiwavelength nature of the analysis enables us to break the degeneracy between the disk temperature, the dust opacity, and the dust surface density and thus provides us with a self-consistent physical description of the disk structure.
With ALMA reaching full science and the major upgrade of the VLA, the improving quality of the (sub-)mm observational datasets in terms of angular resolution and sensitivity make such automated multiwavelength analysis an ideal tool to investigate the disk structure and the dust properties for a large number of disks.
The paper is organized as follows. In Sect. 2 we describe in detail the method by introducing the architecture of the analysis technique, describing the details of disk and of the dust models, and clarifying the Bayesian approach adopted for the analysis. In Sect. 3 the details of the observations are given. In Sect. 4 we present the fit results and in Sect. 5 we compare and discuss the results obtained for the different disks. In Sect. 6 we draw our conclusions. In Appendix A we describe the implementation of the Bayesian analysis in detail, in Appendix B we present the results produced during the benchmarking of our analysis against previous results by Pérez et al. (2012), and in Appendix C we present the fit results for each disk.
2. Analysis technique
We developed a method for constraining the dust properties and the disk structure through the self-consistent modeling of sub-mm and mm observations. The method is based on the simultaneous uv-plane fit of several interferometric observations at different wavelengths. The strength of the method lies in the fact that it allows the derivation of a unique disk structure and dust size distribution capable of reproducing the observed flux at all the fitted wavelengths (forward-fit).
The method adopts a Bayesian approach and performs an affine-invariant Markov chain Monte Carlo (MCMC) method developed by Goodman & Weare (2010) to explore parameter space in an efficient way. The results of the fit provide probability distributions for the value of each free parameter, estimates of their correlations, and a best-fit model from which residual maps can be computed.
Furthermore, we designed the method to have a modular and flexible architecture. It is modular in the sense it allows the disk and the dust models to be changed independently of each other, making it suitable for studying disks with particular morphologies (e.g., with holes or asymmetries) or for testing different dust opacity models. It is flexible as it is designed to fit each observed (u,v)-point independently rather than binned values of deprojected visibilities (which would require an a priori knowledge of the disk center, inclination, and position angle). This makes the method ready to be applied to disks with non-axisymmetric surface brightness distributions and to be expanded in future to fit the disk inclination and position angle self-consistently with the disk structure.
It is worth noting that the major requirement of this method is the availability of a fast and efficient disk and dust model. Since the MCMC usually requires from one to two million model evaluations in order to converge, the speed and the efficiency of the model become extremely important and determine the overall computation time. For this, a huge effort was put into the optimization of the disk and the dust models and into the computation of synthetic visibilities. The average time required for one posterior evaluation1 is approximately 30 s on an IntelR◯ XeonR◯ CPU E5-2680 at 2.70 GHz, thus implying that one million evaluations would require more than 1 year to be computed. However, since half of the model evaluations required by the affine invariant MCMC can be computed independently of each other at each step, the overall computation time can be shortened to 2 days by parallelizing the code and running it on hundreds of cores. We achieved an extremely good scalability of the code performance up to 200 cores using the implementation and parameters discussed in Sect. 2.3.
2.1. Disk model
We compute the disk structure and its thermal emission adopting the two-layer disk model of Chiang & Goldreich (1997) with the refinements by Dullemond et al. (2001). According to the two-layer approximation, the disk is modeled as a surface layer directly heated by the radiation of the central star and an internal layer – hereafter called midplane – heated by the radiation reprocessed by the surface layer. Accretion, if present, is another process that would contribute to the heating of the midplane. This internal heating is most efficient in the very inner regions of the disk and only if the accretion rate is very high (see, e.g., Dullemond et al. 2007, and references therein); however, for this particular study we neglect it. Assuming that the disk is vertically isothermal (separately in each layer) and in hydrostatic equilibrium under the gas pressure and the gravitational field of the star, the two-layer approximation allows us to compute the structure of the disk by solving the vertical radiative transfer equation at each radius. The disk model is computed over a logarithmic radial grid between an inner and an outer radius, respectively Rin = 0.1 AU and Rout ≥ 300 AU; the exact value of Rout is chosen to be much larger than the continuum emission observed for the particular object that is being fitted.
Once the surface and the midplane temperature profiles, respectively Tsur(R) and Tmid(R), are computed, the radial profile of the disk thermal emission (assumed to be optically thin) at a given wavelength ν is given by 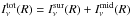 , where
, where ![\begin{eqnarray} \label{eq:Isur} I_{\nu}^{\sur}(R) &=& \frac{1}{d^{2}} \left\{1+\exp{\left[-\frac{\Sigma_{\mathrm{d}}(R)\kappa_{\nu}^{\mid}(R)}{\cos{i}}\right]}\right\}B_{\nu}[T_{\sur}(R)]\,\Delta \Sigma(R) \kappa_{\nu}^{\sur}\,,\\ \label{eq:Imid} I_{\nu}^{\mid}(R) &=& \frac{\cos{i}}{d^{2}} \left\{1-\exp{\left[-\frac{\Sigma_{\mathrm{d}}(R)\kappa_{\nu}^{\mid}(R)}{\cos{i}}\right]}\right\}B_{\nu}[T_{\mid}(R)]\,, \end{eqnarray}](/articles/aa/full_html/2016/04/aa27423-15/aa27423-15-eq30.png) and where Σd(R) is the dust surface density,
and where Σd(R) is the dust surface density, 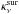 and
and 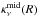 are respectively the surface and the midplane dust opacities (see the next section for details), Bν(T) is the blackbody brightness, i is the disk inclination (i = 0° for a face-on disk), ΔΣ is the surface density of the surface layer, and d is the distance to the disk. These equations are derived for a geometrically thin disk (H/R ≪ 1) and for low disk inclinations (if the disk is seen at i> 70° a proper ray tracing is needed to account for the optical depth induced by the vertical structure of the disk). We refer the reader to Dullemond et al. (2001) for a complete derivation of the above expressions.
are respectively the surface and the midplane dust opacities (see the next section for details), Bν(T) is the blackbody brightness, i is the disk inclination (i = 0° for a face-on disk), ΔΣ is the surface density of the surface layer, and d is the distance to the disk. These equations are derived for a geometrically thin disk (H/R ≪ 1) and for low disk inclinations (if the disk is seen at i> 70° a proper ray tracing is needed to account for the optical depth induced by the vertical structure of the disk). We refer the reader to Dullemond et al. (2001) for a complete derivation of the above expressions.
To complete the definition of the model, a radial profile for the gas and the dust surface density must be specified. In continuity with previous studies (Andrews et al. 2009; Isella et al. 2009), we parametrize the surface density adopting a self-similar solution for an accretion disk (derived assuming viscosity is constant in time; Lynden-Bell & Pringle 1974; Hartmann et al. 1998)![\begin{equation} \label{eq:sigma.parametrization} \Sigma_{\mathrm{g}}(R) = \Sigma_{0}\left(\frac{R}{R_{0}} \right)^{-\gamma} \exp{\left[-\left(\frac{R}{R_{\mathrm{c}}} \right)^{2-\gamma} \right]}\,, \end{equation}](/articles/aa/full_html/2016/04/aa27423-15/aa27423-15-eq41.png) (3)where Σ0 is a constant, R0 is a scale radius that we keep fixed at R0 = 40 AU, and Rc is the spatial scale of the exponential cutoff. Assuming a constant dust-to-gas mass ratio ζ = 0.01 throughout the disk, the dust surface density is Σd = ζ Σg. A fixed ζ across the disk is a commonly used simplifying assumption, which we also adopt in our models as we cannot independently constrain the gas and dust surface density profiles with our observations. It is expected (e.g., Birnstiel & Andrews 2014) that the gas and dust disk surface densities evolve differently over time. This is also confirmed by some observations that show extended, dust depleted outer gaseous disks (e.g., de Gregorio-Monsalvo et al. 2013). In addition, as discussed above, we assume that viscous evolution has been shaping the surface density profile, but that it is not important for the disk heating balance. This is a common approximation that generally describes the observations well; high spatial resolution observations reveal that these smooth surface densities are an approximation of the real dust distribution (e.g., ALMA observations of the HL Tauri disk, ALMA Partnership et al. 2015). In this paper, considering the limited angular resolution of the observations we are analyzing, there is no need to adopt a more detailed radial profile.
(3)where Σ0 is a constant, R0 is a scale radius that we keep fixed at R0 = 40 AU, and Rc is the spatial scale of the exponential cutoff. Assuming a constant dust-to-gas mass ratio ζ = 0.01 throughout the disk, the dust surface density is Σd = ζ Σg. A fixed ζ across the disk is a commonly used simplifying assumption, which we also adopt in our models as we cannot independently constrain the gas and dust surface density profiles with our observations. It is expected (e.g., Birnstiel & Andrews 2014) that the gas and dust disk surface densities evolve differently over time. This is also confirmed by some observations that show extended, dust depleted outer gaseous disks (e.g., de Gregorio-Monsalvo et al. 2013). In addition, as discussed above, we assume that viscous evolution has been shaping the surface density profile, but that it is not important for the disk heating balance. This is a common approximation that generally describes the observations well; high spatial resolution observations reveal that these smooth surface densities are an approximation of the real dust distribution (e.g., ALMA observations of the HL Tauri disk, ALMA Partnership et al. 2015). In this paper, considering the limited angular resolution of the observations we are analyzing, there is no need to adopt a more detailed radial profile.
We now discuss two fundamental modifications we implemented in the two-layer disk model for the present study. First, the two-layer model is applicable only if, at every radius, the disk absorbs all the impinging stellar radiation. However, due to the exponential tapering of the dust surface density, the outermost disk region will eventually become optically thin to the stellar radiation. In this outer region, instead of adopting the two-layer model (which becomes numerically unstable), we assume that the disk temperature decreases radially as a power law Tmid(R) ∝ R− k, where k is obtained by fitting the Tmid profile in the optically thick disk region. Hereafter we call 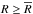 the region where we apply this power law assumption. Second, following Isella et al. (2009) we impose a lower limit on the midplane temperature, namely the equilibrium temperature with the interstellar radiation field. We model this by adding an extra radiative flux impinging on the midplane
the region where we apply this power law assumption. Second, following Isella et al. (2009) we impose a lower limit on the midplane temperature, namely the equilibrium temperature with the interstellar radiation field. We model this by adding an extra radiative flux impinging on the midplane 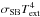 , where the temperature of the external radiation field Text = 10 K and σSB is the Stephan-Boltzmann constant. As a result, at each radius the effective midplane temperature is given by
, where the temperature of the external radiation field Text = 10 K and σSB is the Stephan-Boltzmann constant. As a result, at each radius the effective midplane temperature is given by ![\hbox{${\left[T_{\mid}^{4}(R)+10^{4}\right]^{1/4}}$}](/articles/aa/full_html/2016/04/aa27423-15/aa27423-15-eq56.png) , where Tmid(R) is the temperature computed by the two-layer model for
, where Tmid(R) is the temperature computed by the two-layer model for 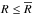 , and Tmid(R) ∝ R− k for
, and Tmid(R) ∝ R− k for 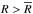 . This additional flux contribution is negligible in the inner region of the disk and starts to be relevant only in the outer parts where Tmid becomes comparable to 10 K.
. This additional flux contribution is negligible in the inner region of the disk and starts to be relevant only in the outer parts where Tmid becomes comparable to 10 K.
The geometry of the disk on the sky is defined by specifying the disk inclination i (the angle between the disk rotation axis and the line of sight, where i = 90° corresponds to an edge-on view) and position angle PA (the angle between the disk semi-major axis as it appears on the sky and the north direction, measured east of north). In the present study i and PA are fixed parameters (see Table 1 for detailed references).
Stellar and disk properties.
Furthermore, in our model we account for the possible contamination by emission from ionized gas, which is mostly relevant at longer wavelengths and is caused by thermal or non-thermal emission processes (e.g., free-free or gyro-synchrotron emission) from free electrons in the densest parts of a wind or the stellar corona (Rodmann et al. 2006; Ubach et al. 2012). We estimate and subtract this contamination by assuming that the emission is unresolved by our observations and dominates the long-wavelength emission at and beyond 3.6 cm. We estimate the maximum possible contamination extrapolating to millimeter wavelengths the flux density observed with the VLA at 6 cm (assuming that at these wavelengths there is no contribution from dust emission) and using an optically thick spherical wind approximation (Fν ~ ν0.6: Panagia & Felli 1975). This assumption is conservative in the sense that provides the maximum possible contamination at shorter wavelengths.
2.2. Dust model
In order to account for the settling of large grains toward the disk midplane, as predicted by the models and observed by the lack of large grains in the disk atmosphere (e.g., based on studies of silicate features; Natta et al. 2007 and references therein), we adopt two different dust size distributions for the surface and for the midplane, which result in two different opacities, 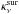 and
and 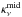 , respectively.
, respectively.
The choice of the dust grain size distribution aims at simply modeling a protoplanetary disk with a surface layer mainly composed of small grains and a midplane layer of larger pebbles (Dullemond & Dominik 2004; Tanaka et al. 2005). For both the surface and the midplane we adopt a power law distribution n(a) ∝ a− q for amin<a<amax, where a is the dust grain radius and q> 0 is the power law index, choosing 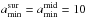 nm, kept fixed throughout the disk. The particular value chosen for amin does not affect our results as long as amin ≪ 1 μm (Miyake & Nakagawa 1993). For the surface we assume
nm, kept fixed throughout the disk. The particular value chosen for amin does not affect our results as long as amin ≪ 1 μm (Miyake & Nakagawa 1993). For the surface we assume 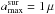 m constant throughout the disk, whereas for the midplane we allow a radial variation of
m constant throughout the disk, whereas for the midplane we allow a radial variation of 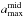 modeled as
modeled as 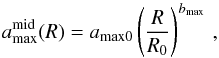 (4)where R0 = 40 AU and amax0 is a normalization constant. In the disk surface we choose q = 3.5 which describes well the size distribution of interstellar dust grains (Mathis et al. 1977; Draine & Lee 1984) out of which protoplanetary disks form, whereas for the disk midplane we assume q = 3, which accounts for an enhanced population of large grains.
(4)where R0 = 40 AU and amax0 is a normalization constant. In the disk surface we choose q = 3.5 which describes well the size distribution of interstellar dust grains (Mathis et al. 1977; Draine & Lee 1984) out of which protoplanetary disks form, whereas for the disk midplane we assume q = 3, which accounts for an enhanced population of large grains.
 |
Fig. 1 Dust opacity (per gram of dust) for amax = 0.8, 1, 3 mm, and 1 cm, computed for the midplane population of grains assuming the composition of 5.4% astronomical silicates, 20.6% carbonaceous material, 44% water ice, and 30% vacuum and a size distribution n(a) ∝ a− q for amin<a<amax with q = 3.0 and amin = 10 nm. |
In Fig. 1 we show the midplane dust opacity as a function of wavelength, computed for some amax values ranging from 0.8 mm to 1 cm (which are representative values of the grain sizes we find in the analyzed disks, see below Sect. 4). The impact of the choice of q on the resulting β value can be seen in Fig. 4 of Testi et al. (2014).
We assume the same dust composition in the surface and in the midplane. Similarly to Banzatti et al. (2011) and Trotta et al. (2013), we assume the following simplified volume fractional abundances from Pollack et al. (1994): 5.4% astronomical silicates, 20.6% carbonaceous material, 44% water ice, and 30% vacuum, thus implying an average dust grain density of 0.9 g/cm3. We choose the fractional abundances given above for continuity with previous studies on grain growth; however, we note that more recent estimates based on analysis of data from the Spitzer Space Telescope can be found in the literature (e.g., Juhász et al. 2010).
Given the dust composition and the grain size distribution, we compute the dust opacity using the Bruggeman effective medium theory (Bruggeman 1935) to calculate the dielectric function of the composite spherical grain and Mie theory to derive the dust absorption coefficients. The complex optical constants used to compute the dielectric function are taken from Weingartner & Draine (2001) for silicates, Zubko et al. (1996) for carbonaceous material, and Warren (1984) for water ice.
2.3. Modeling methodology
We adopt a Bayesian approach, which provides probability distribution functions (PDFs) for the free parameters of the model using a variant of the MCMC algorithm family. Isella et al. (2009) provide a general description of the use of this methodology for modeling protoplanetary disks.
Our disk model is defined by the following free parameters: Σ0, Rc, γ (to define the disk structure) and amax0, bmax (to define the dust distribution). In the present study the following parameters are kept fixed: the dust properties (e.g., composition, shape, porosity), the disk inclination i, the disk position angle PA, and the contaminating free-free flux density at each wavelength Fff(ν). We note, however, that in a more general approach these parameters could be added to the Bayesian analysis and derived consistently with the disk structure and the grain size distribution.
Given a set of values for these parameters, we compute the synthetic disk images (one per fitted wavelength), and then we sample their Fourier transform at the same (u,v)-plane locations of the observed visibilities. We finally compute the total χ2 as the sum of the several partial  computed for each wavelength,
computed for each wavelength, 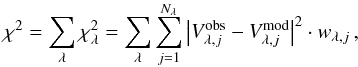 (5)where wλ,j is the visibility weight2,
(5)where wλ,j is the visibility weight2, 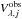 and
and 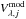 are respectively the observed and the synthetic visibilities, and Nλ is the number of visibility points at the wavelength λ.
are respectively the observed and the synthetic visibilities, and Nλ is the number of visibility points at the wavelength λ.
The posterior PDF is computed as the product of the likelihood of the observations given the model, namely exp(−χ2/ 2), by the prior PDF p(θ) (where θ is a point in the 5D space of parameters). We assume a uniform prior for all the parameters, therefore p(θ) = 1 for θ ∈ Θ and p(θ) = 0 otherwise, where Θ is a 5D domain in the space of parameters defined by the ranges given in Table 2.
Ranges defining the space of parameters explored by the Markov chain.
In principle, the domain Θ can be changed from disk to disk (e.g., the Rc interval can be changed depending on the disk size determined from observations); however, in this study we kept it fixed to the intervals given in Table 2, which are large enough to be suitable for different disks.
Details of the observations used for the fits.
In addition to the disk structure and the dust size distribution, we also derive the precise position of the disk centroid by adding two nuisance parameters for each wavelength, Δα0 and Δδ0, that measure the angular offset between the disk centroid with respect to its nominal position (α0,δ0). This method allows the derivation of the correct center position for the model even without any prior information on the star proper motion or other systematic position offsets between the different wavelength observations.
The fit is performed using a variant of the MCMC algorithm (Goodman & Weare 2010), which allows the parameter space to be explored by several Markov chains at the same time (an ensemble of hundreds to thousands of walkers3), which interact with each other in order to converge to the maximum of the posterior. There are two advantages of using several chains simultaneously. On the one hand, it allows a more complete exploration of the parameters space (each chain starts from a different initial location); on the other hand, it allows the computation to be massively parallelized. We perform the MCMC using the implementation provided in the Python package emcee (Foreman-Mackey et al. 2013), which offers the possibility of running the computation in parallel on several cores and has been used for an increasing number of astrophysical problems in recent years. In this study, we perform MCMC with 1000 chains: they are initialized with uniform random distribution in the parameter space Θ, made evolve for a burn-in phase of some hundreds steps, and finally let sample the posterior for several hundreds steps (for a detailed explanation of the criteria used to assess the convergence of the chain, see Appendix A).
The outcome of the MCMC is a collection (a chain) of posterior samples out of which we can estimate the 1D and 2D marginal distributions of the free parameters (marginalization means that all but one or two parameters of the posterior are integrated over). From the 1D marginal distributions, we do a point estimate of each parameter using the median and we estimate the uncertainty as the central interval; i.e., from the 16th to the 84th percentile. These estimators give a good representation of the marginalized distribution, and reduce to the usual central credibility interval in the Gaussian case. For each fit, we present a staircase plot with the 1D and 2D marginalized distributions of the interesting physical parameters.
For this study, the optimization of the disk model and of the imaging routines allowed us to execute the fits efficiently on hundreds of cores (hosted at the Computational Center for Particle and Astrophysics, C2PAP) and thus to reduce the time needed to perform each multiwavelength fit to 1 or 2 days. For further details on the implementation, see Appendix A.
3. Observations
In this study we apply our method to three protoplanetary disks for which multiwavelength (sub-)mm observations are available: AS 209, DR Tau, and FT Tau. The AS 209 observations have already been presented by Pérez et al. (2012) and we refer the reader to that paper for their details. DR Tau and FT Tau observations from CARMA and VLA are now described in turn. A summary can also be found in Table 3.
3.1. CARMA observations of DR Tau and FT Tau
Observations of DR Tau at 1.3 mm were obtained using CARMA between October 2007 and December 2011. Multiple array configurations (A, B, and C) provide a uv-coverage spanning 15−1290 kλ. Double-sideband single-polarization receivers were tuned to a LO frequency of 230 GHz in A configuration, 227.75 GHz in B configuration, and 228.60 GHz in C configuration. For optimal continuum sensitivity, the spectral windows in the correlator were configured to the maximum possible bandwidth per spectral window (0.47 GHz). The number of continuum spectral windows varied for different configurations: a total bandwidth of 1.9 GHz was available for the B and C configuration observations, while during the A configuration observations the total bandwidth was 8 GHz. Observations of complex gain calibrators (0530+135 and 0449+113) were interleaved with science target observations. Additionally, a strong quasar was observed to calibrate the complex bandpass. The absolute flux density scale was derived from observations of a secondary flux density calibrator (3C 84 or 3C 273), whose flux density was monitored by the CARMA observatory, resulting in a fractional uncertainty of ~15% in the absolute flux density calibration. Calibration was performed with the MIRIAD software package, with each dataset being calibrated separately. The 1 and 3 mm CARMA observations of FT Tau are presented in Kwon et al. (2015), to which we refer for the observational details. Here we give a brief description. The data were obtained over a period of about 2 years, between 2008 Oct. 15 and 2011 Jan 5. For good uv coverage, multiple array configurations were employed: 1 mm observations in B and C configurations provide a uv coverage of 17.0–620 kλ, and 3 mm observations in A and C configurations gives a uv coverage from 4.1−727.6 kλ. MIRIAD (Sault et al. 1995) was used for the data calibration. The absolute flux density was obtained through observations of a reliable flux calibrator (Uranus) and resulted in fractional uncertainties of 10% and 8% for observations at 1.3 and 2.6 mm, respectively. The complex gains were obtained through observations of a nearby bright point source (3C 111). In the case of the A configuration data at 3 mm the C-PACS (Pérez et al. 2010) was employed to remove short-period atmospheric turbulence. We note that while the images of Kwon et al. (2015) are produced with a Briggs robust parameter of 0 (which produces images with a lower signal-to-noise ratio but better beam resolution), the images in this paper use the natural weighting (which does not apply any density weighting function to the observed uv-points thus producing images with the best signal-to-noise ratio). Through the analysis procedure described in Sect. 2.3 we fit the flux measured at each uv-point, therefore we adopt the natural weighting scheme since is the most suitable to perform a direct comparison between the observed and the model data.
3.2. VLA observations of DR Tau and FT Tau
Observations of DR Tau and FT Tau using the Karl G. Jansky Very Large Array (VLA) of the National Radio Astronomy Observatory4 were made as part of the Disks@EVLA project (AC982) between 2010 November and 2012 August. DR Tau was observed using the Q-band (λ ~ 7 mm) receivers with two 1GHz basebands centered at 41.5 and 42.5 GHz in the C and B configurations, providing projected uv-spacings from 5 to 1500 kλ. FT Tau was observed using the Ka-band (λ ~ 1 cm) receivers with two 1GHz basebands centered at 30.5 and 37.5 GHz in the C and B configurations, providing projected uv-spacings from 8 to 1300 kλ. For both targets the complex gain was tracked using frequent observations of J0431+2037 (in C configuration) or J0431+1731 (in B configuration), and the complex bandpass was measured using 3C 84. The absolute flux density scale was derived from observations of 3C 147 (e.g., Perley & Butler 2013), and its overall accuracy is estimated to be 10%. The data were calibrated, flagged, and imaged using a modified version of the VLA Calibration Pipeline5. At Ka-band the calibrator source J0431+2037 turned out to have multiple components that required the source to be modeled before being used to derive calibration solutions. In addition, because of the substantial time period covering the observations, corrections for source proper motion and/or other systematic position offsets between datasets (e.g., caused by the structure of J0431+2037) also had to be applied. The astrometry reported here corresponds to that derived from the B configuration data. The VLA observations shown in this paper have been imaged using natural weighting.
Both sources were also observed with the C-band (λ ~ 6 cm) receivers in the most compact, D configuration of the VLA in 2010 July in order to evaluate any potential contamination from ionized gas at shorter wavelengths. Two 1 GHz basebands were centered at 5.3 and 6.3 GHz. Complex gain variations were tracked through observations of J0431+2037, the bandpass was measured using 3C 84, and the absolute flux density scale was obtained through observations of 3C 147. DR Tau was detected with an integrated flux density F6cm = 99 ± 31 μJy, while for FT Tau a 3σ upper limit on the 6cm flux density of 72 μJy was obtained.
4. Results
For each disk, we give a set of statistical and physical results that we describe in turn. In this section we discuss in detail the results for FT Tau and in Appendix C we provide detailed plots for the other disks.
In Fig. 2 we present a staircase plot showing the posterior PDF computed from the chain, after proper thinning; the fit needed 800 burn-in steps, and 500 further steps to sample the posterior. On the diagonal of Fig. 2 we show the marginalized 1D distributions for each parameter, which display a Gaussian-like shape; off the diagonal we show the 2D marginalized distributions, which give an overview of the correlations between the parameters. For FT Tau we obtain the following parameter values:
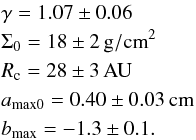 The errors are given by the central credibility interval of their marginalized distribution (i.e., the 16th and 84th percentiles). We note that the fit has some additional parameters, specifically four pairs of directional offsets (one pair (Δα0, Δδ0) for each wavelength), but for the clarity of the plot we do not show them. In Table 4 we list the derived position of the disk centroid (α,δ) determined by the fit, where α = α0 + Δα0 and δ = δ0 + Δδ0. For each disk, we also list (from the SIMBAD database) the star reference position at Epoch 2000.0 (from Hipparcos or 2MASS measurements), the proper motion estimates (from Hipparcos or US Naval Observatory Catalogs), and – for each interferometric dataset – the fitted disk center position with derived uncertainties. Within the uncertainties, the derived positions are consistent with the expected stellar positions based on the astrometric and proper motion measurements.
The errors are given by the central credibility interval of their marginalized distribution (i.e., the 16th and 84th percentiles). We note that the fit has some additional parameters, specifically four pairs of directional offsets (one pair (Δα0, Δδ0) for each wavelength), but for the clarity of the plot we do not show them. In Table 4 we list the derived position of the disk centroid (α,δ) determined by the fit, where α = α0 + Δα0 and δ = δ0 + Δδ0. For each disk, we also list (from the SIMBAD database) the star reference position at Epoch 2000.0 (from Hipparcos or 2MASS measurements), the proper motion estimates (from Hipparcos or US Naval Observatory Catalogs), and – for each interferometric dataset – the fitted disk center position with derived uncertainties. Within the uncertainties, the derived positions are consistent with the expected stellar positions based on the astrometric and proper motion measurements.
 |
Fig. 2 Representation of the MCMC results for FT Tau. On the top diagonal, the 1D histograms are the marginalized distributions of the fitted parameters; the vertical dashed lines represent (from left to right) the 16th, the 50th, and the 84th percentiles. The 2D density plots represent the bi-variate distributions for each pair of parameters, with one dot representing one sample. The plot shows the posterior sampling provided by 500 steps of the 1000-walkers chain (800 burn-in steps were performed to achieve convergence). We note that in order to obtain an independent set of samples, the chain has been thinned by a factor equal to the autocorrelation time (~80 steps in this case). |
Fitted disk centroid positions.
In Fig. 3 we compare the observed and the model images at each wavelength, showing the residuals obtained by imaging the residual visibilities (obtained by subtracting the noise-free model visibilities from the observed visibilities). The best-fit model represented in Fig. 3 corresponds to the model with median values of the marginalized distributions (γ = 1.07, Σ0 = 18 g/cm2, Rc = 28 AU, amax0 = 0.4 cm, bmax = −1.3) and we have verified that it is among the models with lowest reduced 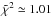 . To produce the maps we have applied the CLEAN algorithm (Clark 1980) with natural weighting. The residuals are small at all the wavelengths, with one negative 3σ residual left at 1.3 mm, a few 3σ residuals left at 3mm, and no residuals within ± 3σ left at 8.0 and 9.8 mm.
. To produce the maps we have applied the CLEAN algorithm (Clark 1980) with natural weighting. The residuals are small at all the wavelengths, with one negative 3σ residual left at 1.3 mm, a few 3σ residuals left at 3mm, and no residuals within ± 3σ left at 8.0 and 9.8 mm.
 |
Fig. 3 Comparison between the observed and the best-fit model images at different wavelengths of the FT Tau protoplanetary disk. The best-fit model is defined by the following parameters: γ = 1.07, Σ0 = 18 g/cm2, Rc = 28 AU, amax0 = 0.4 cm, bmax = −1.3. The observed images are shown in the left panels, the model images in the center panels, the residuals in the right panels. The positive and negative contour levels are spaced by 3σ (starting from −3σ) and are the same in all the panels. The synthesized beam FWHM is represented as a gray ellipse in the bottom-left corner of each map. |
Figure 4 shows the comparison between the probability distribution of the model visibilities and the observations as a function of the deprojected baseline length (uv-distance). Each panel corresponds to one wavelength, with the upper frame showing the real part Re(V) and the lower frame showing the imaginary part Im(V). The declining profile of Re(V) with increasing uv-distance shows that the disk is spatially resolved at all the wavelengths. Furthermore, we note that the visibility profile at longer wavelengths has a steeper decline with increasing baseline than the visibility profile at shorter wavelengths, thus confirming the rather general observational feature that the size of the (sub-)mm emitting region is anticorrelated with the observing wavelength (Pérez et al. 2012; Testi et al. 2014).
 |
Fig. 4 Comparison between the model and the observed visibilities as a function of deprojected baseline length (uv-distance) for FT Tau. The data are binned in 40kλ bins. Black dots represent the observed data and the colored boxes represent the probability distribution of model visibilities for each uv-distance bin. The x-axis extent of each box is the bin size, while the y-axis extent is not fixed as it depends on the probability distribution of the model at that particular uv-distance bin; in some cases they are very close to each other. The color scale represents the density of the distribution. The solid black curve is the median, the dashed black lines are the 16th and 84th percentiles, and the red dotted lines are the 2.3th and 97.7th percentiles. |
The models fit the observations with a very good agreement at the shortest wavelength (1.3 mm), and a lower degree of agreement at longer wavelengths. This should not be a surprise for two main reasons: first, the observations at the shorter wavelength also have higher signal-to-noise ratio and therefore have more weight in the fit; second, we are modeling all the wavelengths simultaneously and so the resulting best-fit models are not necessarily the models that best fit each wavelength separately. We note, however, that although the VLA observations at 8.0 and 9.83 mm have a worse signal-to-noise ratio, the models are still able to reproduce the observed total flux density (short uv-distances) and the average flux density at the longer spatial frequencies extremely well. In the case of FT Tau, the observations at 2.6 mm have a very low signal-to-noise ratio compared to those at 1.3, 8.0, and 9.8 mm.
The top-left panel of Fig. 5 shows the posterior PDF of the maximum dust grain size amax as a function of the disk radius. The maximum dust grain size is larger in the inner disk than in the outer disk, changing by one order of magnitude from 1 cm at 20 AU to 1 mm at 120 AU. We note that the smoothness of the amax(R) profile follows from the power-law parametrization in Eq. (4). The 2σ error bars (given in terms of the 2.3−97.7% credibility interval) are smaller than 10% at all radii and allow us to conclude that there is a clear signature of a radial gradient in the maximum dust grain size throughout the disk. In the top-right panel of Fig. 5 we present the posterior PDF of the dust spectral index radial profile β(R) between 1 and 10 mm, computed given the amax(R) posterior PDF according to 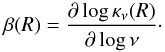 (6)The spectral index β increases with radius: the small values β< 1 for R< 50 AU signal the presence of dust grains that have reached sizes comparable to 1 mm or more (Natta & Testi 2004), whereas in the outer disk the spectral index approaches β ≳ βISM = 1.7, a signature of the presence of smaller grains. The fact that in the outer disk we obtain β ≳ βISM for grains somewhat larger (amax ≈ 1 mm) than the usual interstellar medium (ISM) dust grains (amax ≈ 1−10 μm) is consistent with the observations at different wavelengths; these observations give us information on different spatial scales in the disk and they are all fit well by a model with the amax profile shown in Fig. 5. The bottom plots in Fig. 5 present the physical structure derived for FT Tau: the gas surface density (bottom-left panel) and the midplane temperature (bottom-right) profiles. The surface density profile monotonically decreases with a power-law index γ = 1.07 ± 0.06, a normalization value Σ0 = 18 ± 2 g/cm2 at 40 AU, and a cut-off radius Rc = 28 AU. The midplane temperature profile decreases from 40 K in the inner disk to 11 K in the outer region.
(6)The spectral index β increases with radius: the small values β< 1 for R< 50 AU signal the presence of dust grains that have reached sizes comparable to 1 mm or more (Natta & Testi 2004), whereas in the outer disk the spectral index approaches β ≳ βISM = 1.7, a signature of the presence of smaller grains. The fact that in the outer disk we obtain β ≳ βISM for grains somewhat larger (amax ≈ 1 mm) than the usual interstellar medium (ISM) dust grains (amax ≈ 1−10 μm) is consistent with the observations at different wavelengths; these observations give us information on different spatial scales in the disk and they are all fit well by a model with the amax profile shown in Fig. 5. The bottom plots in Fig. 5 present the physical structure derived for FT Tau: the gas surface density (bottom-left panel) and the midplane temperature (bottom-right) profiles. The surface density profile monotonically decreases with a power-law index γ = 1.07 ± 0.06, a normalization value Σ0 = 18 ± 2 g/cm2 at 40 AU, and a cut-off radius Rc = 28 AU. The midplane temperature profile decreases from 40 K in the inner disk to 11 K in the outer region.
Parameters derived from the fits.
 |
Fig. 5 Results of the FT Tau fit. Top: in the left panel, the posterior PDF of the maximum dust grain size amax as a function of the disk radius; in the right panel, the posterior PDF of the dust spectral radial profile β(R) between 1 and 10 mm. Bottom: in the left panel, the posterior PDF of the gas surface density; in the right panel, the posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
The AS 209 and DR Tau protoplanetary disks have been fit with the same analysis presented here and the results are shown in Appendix C. For both these disks the fit performed well, as can be seen from the maps of the residuals and the comparison between the model and the observed visibilities at all the wavelengths. We note that the observations of DR Tau at 1.3 mm display an asymmetry (in the NE region) that an axisymmetric disk model like the one we are using here is not able to account for. In Table 5 we summarize the results of the fits for the FT Tau, AS 209, and DR Tau protoplanetary disks. In all disks we find sharply decreasing dust grain sizes, with amax ≈ 0.5 cm at R ≲ 40 AU, with a radial power law slope −1.8 ≤ bmax ≤ −1.17. We also note that AS 209, DR Tau, and FT Tau are fit with γ> 0 and bmax< 0. A degeneracy between γ and bmax is also apparent from the bi-variate distributions in Fig. 2 (bottom-left panel) and was already observed by Trotta et al. (2013).
Models: physical quantities.
In Table 6 we list the physical quantities derived from the models: the total mass of the disk Mdisk (computed as the sum of the dust and the gas mass), the radius R90 containing 90% of the disk mass, and the radius 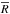 within which the temperature is computed using the two-layer approximation (see Sect. 2.1). It is reassuring that for all the disks,
within which the temperature is computed using the two-layer approximation (see Sect. 2.1). It is reassuring that for all the disks, 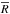 is larger than or comparable to the radius containing 90% of the mass, thus implying that the assumption of a power-law temperature profile in the region
is larger than or comparable to the radius containing 90% of the mass, thus implying that the assumption of a power-law temperature profile in the region 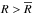 has minimal influence on the computation of the total flux density. We observe that the disk masses that we obtain with our multiwavelength analysis are comparable within a factor of 2 (or 4 in the worst case) with those derived by previous single-wavelength studies. The Andrews et al. (2009) analysis of AS 209 found Mdisk = 28 × 10-3M⊙ (γ = 0.4, Rc = 126 AU), the Isella et al. (2009) analysis of DR Tau found Mdisk = 63 × 10-3M⊙ (γ = −0.3, Rc = 41 AU), and the Guilloteau et al. (2011) analysis of FT Tau found Mdisk = 7.7 × 10-3M⊙ (γ = −0.17, Rc = 43 AU). We note that in two cases (DR Tau and FT Tau) we obtain γ> 0, whereas past analyses obtained γ< 0. Furthermore, in all the cases we obtain γ values larger than the previous single-wavelength studies. As noted by Trotta et al. (2013), this can be understood by looking at the anticorrelation between γ and bmax, clearly visible in the bottom-left frame in the staircase plot in Fig. 2: single-wavelength studies (that adopt an opacity constant with radius and therefore bmax = 0) obtain smaller γ values than a multiwavelength analysis, where bmax and γ are constrained simultaneously.
has minimal influence on the computation of the total flux density. We observe that the disk masses that we obtain with our multiwavelength analysis are comparable within a factor of 2 (or 4 in the worst case) with those derived by previous single-wavelength studies. The Andrews et al. (2009) analysis of AS 209 found Mdisk = 28 × 10-3M⊙ (γ = 0.4, Rc = 126 AU), the Isella et al. (2009) analysis of DR Tau found Mdisk = 63 × 10-3M⊙ (γ = −0.3, Rc = 41 AU), and the Guilloteau et al. (2011) analysis of FT Tau found Mdisk = 7.7 × 10-3M⊙ (γ = −0.17, Rc = 43 AU). We note that in two cases (DR Tau and FT Tau) we obtain γ> 0, whereas past analyses obtained γ< 0. Furthermore, in all the cases we obtain γ values larger than the previous single-wavelength studies. As noted by Trotta et al. (2013), this can be understood by looking at the anticorrelation between γ and bmax, clearly visible in the bottom-left frame in the staircase plot in Fig. 2: single-wavelength studies (that adopt an opacity constant with radius and therefore bmax = 0) obtain smaller γ values than a multiwavelength analysis, where bmax and γ are constrained simultaneously.
 |
Fig. 6 Left panel: radial profile of the maximum dust grain size amax constrained from the multiwavelength fits. Right panel: radial profile of the dust opacity spectral slope β(R) between 1 mm and 10 mm. The dashed black horizontal line at βISM = 1.7 represents the typical value of β for small ISM dust grains. In both panels: the thick lines represent the median (i.e., the best-fit) model, and the shaded areas represent the 1σ credibility intervals. The best-fit model lines are plotted wherever the signal-to-noise ratio is higher than 3 (computed for the observation displaying the most extended disk emission); the shaded areas are truncated at half the average beam size (inner regions) and at |
5. Discussion
In the previous section we show how our new multiwavelength fitting technique allows us to simultaneously constrain the disk structure and the radial variation of the maximum dust grain size. This is the most important difference between our method and previous attempts to use multiwavelength observations to constrain the dust properties. We derive a unique, yet simplified disk physical structure that describes the emission at all the observing wavelengths and at the same time we obtain a self-consistent distribution of particle sizes that we assume to be a continuous function. Previous analyses have either assumed a non-self-consistently derived temperature distribution across the disk (Guilloteau et al. 2011) or have used different disk physical structure fits at different wavelengths to infer from their differences a constraint on the dust properties (Banzatti et al. 2011; Pérez et al. 2012). The method we developed, extending the work of Trotta et al. (2013), improves on previous results by attempting a self-consistent modeling of the disk structure and dust radial stratification. Our models produce results that are in qualitative agreement with previous studies (larger grains in the inner disk than in the outer disk), but do show some quantitative difference even when using the same assumptions about the dust composition.
We used the AS 209 protoplanetary disk to perform a detailed comparison of the results from our multiwavelength analysis with those of Pérez et al. (2012), who constrained the disk structure and the dust radial distribution fitting each wavelength separately. The details of the comparison are given in Appendix B, while here we briefly summarize the main results. Adopting the same disk model and the same dust properties as Pérez et al. (2012) we fit the AS 209 protoplanetary disk separately at each wavelength and found an extremely good agreement with the disk structure obtained by Pérez et al. (2012). Then, we performed a multiwavelength fit again using the same disk model and dust prescriptions used by Pérez et al. (2012) and we compared the resulting amax(R) and β(R) profiles. The two techniques provide amax(R) profiles in good agreement almost throughout the disk, with some differences in the inner region where the emission is not spatially resolved. The main differences between the two approaches arise from the different derivation of the dust temperature profile. The modeling by Pérez et al. (2012) produces independent temperature profiles at different wavelengths, whereas our multiwavelength fit derives a unique temperature profile for the disk midplane that holds at all wavelengths (which is made possible by imposing a fixed parametrization of the maximum grain size with radius, in our case a power law6). Obtaining an accurate estimate of the temperature in the outer disk is difficult due to the low optical depth to the stellar radiation and the low temperature reached by the disk midplane (moreover, other external heating effects possibly start to play a role). Because we expect – within the range of wavelengths at which we observe – that the major contribution of the emission always comes from the midplane dust, modeling this emission with a unique temperature profile is more physically founded than using several different temperature profiles that apply in different disk regions. This consideration is the main motivation for the development of our joint multiwavelength analysis.
In the left panel of Fig. 6 we compare the radial profiles amax(R) obtained for the disks in the sample. The observed declining profile of amax(R) with radius is in line with the expected outcome of the viscous evolution of disks according to which the smaller dust particles (closely coupled with the gas) are brought to large stellocentric distances, whereas the larger dust grains (less coupled with the gas and more sensitive to the gas drag) drift inwards (Weidenschilling 1977; Brauer et al. 2008; Birnstiel et al. 2010; Armitage 2010). In both figures, we plot the best-fit models as lines and the 1σ credibility intervals as shaded areas. The best-fit models are truncated at the radius where the signal-to-noise ratio of the observations becomes lower than 3, computed for the observation displaying the most extended disk emission. The shaded areas are truncated in the inner region at half the synthesized beam size to give a visual representation of the average angular resolution of the observations, and in the outer regions at 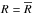 . All the objects support evidence of large grains in the inner disk (amax ≈ 1 cm) and smaller grains in the outer disk (amax ≲ 3 mm), with changes in size of at least one order of magnitude. Given the constrained amax(R) profiles, we compute the dust spectral index β(R) profiles (shown in the right panel of Fig. 6), which grow accordingly from β ≈ 0.5 in the inner disk to β ≳ 1.7 in the outer disk. These findings confirm the earlier evidence of β(R) increasing with radius obtained by Pérez et al. (2012), Banzatti et al. (2011), and Guilloteau et al. (2011) with different techniques, and by Trotta et al. (2013) with an initial implementation of this joint multiwavelength analysis.
. All the objects support evidence of large grains in the inner disk (amax ≈ 1 cm) and smaller grains in the outer disk (amax ≲ 3 mm), with changes in size of at least one order of magnitude. Given the constrained amax(R) profiles, we compute the dust spectral index β(R) profiles (shown in the right panel of Fig. 6), which grow accordingly from β ≈ 0.5 in the inner disk to β ≳ 1.7 in the outer disk. These findings confirm the earlier evidence of β(R) increasing with radius obtained by Pérez et al. (2012), Banzatti et al. (2011), and Guilloteau et al. (2011) with different techniques, and by Trotta et al. (2013) with an initial implementation of this joint multiwavelength analysis.
The amax(R) radial profiles derived for the three disks tend towards similar values amax(R) ≃ 2 cm in the innermost spatially resolved region 10 AU <R< 20 AU, but display apparent differences in the slope with AS 209, FT Tau, and DR Tau showing respectively an increasing steepness. The differences we observe in the slopes may be due to several factors: different disk ages (grain growth processes can lead to time-dependent grain size distributions), different initial grain size distributions of the primordial material out of which the disks formed, different dust compositions, and/or different disk morphologies. The limited sample of disks analyzed here clearly does not enable us to investigate in detail these effects on the dust size distribution, but the overall similarity between the profiles is remarkable. The three disks – AS 209, FT Tau, and DR Tau – appear to have progressively more concentrated large grains. Extension of our analysis to a larger sample of objects will possibly allow us to understand what drives these differences in the overall distribution of grain sizes in disks. Our work here lays down the methodology for this type of study.
6. Conclusions and outlook
This paper presents the architecture and the capabilities of a new multiwavelength analysis designed to constrain the structure and the dust properties of protoplanetary disks through a simultaneous fit of interferometric (sub-)mm observations at several wavelengths. The analysis adopts a Bayesian approach and performs a fit in the uv-plane. It requires models for the disk thermal emission and the dust opacity. The architecture of the analysis is highly modular (the disk and the dust models can be changed independently of each other) and therefore is particularly suitable for testing other models for the dust opacity or the disk structure (e.g., disks with holes or with non-axisymmetric morphology).
For this study, we modeled the disk with a two-layer disk approximation (Chiang & Goldreich 1997; Dullemond et al. 2001) and the dust opacity with Mie theory. We applied the fit technique to three protoplanetary disks (AS 209, DR Tau, and FT Tau) for which sub-mm, mm, and cm observations are available. We combined observations from the CARMA, SMA, and VLA interferometers with different angular resolution and signal-to-noise ratios. Despite the heterogeneity of the observations, the analysis technique has proven to be effective in simultaneously fitting all the datasets available for each object, as the visibility comparisons and the residual maps show. Furthermore, the convergence of the MCMC was assessed through careful statistical checks. The strength of our method lies in the fact that it allows us to derive a unique and self-consistent disk structure (Σ(r), T(r)) that is applied to all wavelengths to derive the overall variation of the maximum grain size with radius under the simplifying assumption that the radial profile amax(R) can be approximated with a smooth power law, which is a realistic assumption given the angular resolution of the observations we are analyzing here.
In the three disks analyzed here, we find a common trend of larger (cm-sized) grains in the inner disks (R< 30−40 AU) and smaller (mm-sized) grains in the outer disks, but different slopes of amax(R) for different disks. A natural question that arises is whether this is an evolutionary trend (caused by dust growth processes) or an intrinsic variability of disk properties. It is not possible to answer this question with the very limited sample we have analyzed here, but the analysis method is ready to be performed on larger samples that will have the potential of giving us some insight into possible correlations and intrinsic variability.
The highly modular architecture of the analysis makes it suitable for testing other dust opacity and disk models with relatively little coding effort. From this perspective, it will become important to develop new models that are on the one hand more computationally efficient, and on the other hand refined enough to describe the complex structures now seen in the dust and gas distribution of protoplanetary disks (e.g., ALMA Partnership et al. 2015). The versatility of the method makes this kind of multiwavelength analysis suitable for tackling many interesting questions about the dust and the gas evolution in protoplanetary disks.
A posterior evaluation consists of an execution of the disk and the dust models; the computation of the synthetic visibilities through four fast Fourier transforms (FFT) (for the test case, we fit four wavelengths and the matrix sizes were 1024 × 1024, 1024 × 1024, 4096 × 4096, and 4096 × 4096, which are defined by the range of (u,v) distances sampled by the observed visibilities); and the sampling of the synthetic visibilities at the location of the antennas (for the test case we have approximately 2.5 million uv-points).
The visibility weights wλ,j are computed theoretically as described by Wrobel & Walker (1999) and then re-scaled in order to assign the same weight to each wavelength.
This choice is justified by the outer disk maximum grain size distribution derived by other authors and by simple fits to the predictions of global dust evolution models, e.g., Birnstiel et al. (2012).
In our case, since the autocorrelation time is usually observed to be smaller than 100 steps, the thinning does not reduce the effective sample size, but allows us to save a lot of computational time during post-processing, e.g., when producing the uv-plots that show the comparison between the observed visibilities and the density of synthetic visibilities.
The code can be found at https://github.com/dfm/emcee
Acknowledgments
M.T. and L.T. acknowledge support by the DFG cluster of excellence Origin and Structure of the Universe (http://www.universe-cluster.de). A.I. acknowledges support from the NSF award AST-1109334/1535809 and from the NASA Origins of Solar Systems program through the award number NNX14AD26G. The fits have been carried out on the computing facilities of the Computational Center for Particle and Astrophysics (C2PAP) as part of the approved project “Dust evolution in protoplanetary disks”. M.T. and L.T. are grateful for the experienced support from F. Beaujean (C2PAP). M.T. thanks I. Jimenez-Serra, P. Papadopoulos, C. Manara and L. Loreta for the precious support throughout this work. Figures have been generated using the Python-based matplotlib package (Hunter 2007). Staircase plots of PDFs have been generated with a user-modified version of the Python-based triangle package (Foreman-Mackey et al. 2014). Plots of the residuals have been generated with APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work was partly supported by the Italian Ministero dell[´entity!#x2009!]Istruzione, Università e Ricerca through the grant Progetti Premiali 2012 – iALMA (CUP C52I13000140001).
References
- ALMA Partnership, A., Brogan, C. L., Pérez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Chandler, C. J., Isella, A., et al. 2014, ApJ, 787, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge University Press) [Google Scholar]
- Banzatti, A., Testi, L., Isella, A., et al. 2011, A&A, 525, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., & Andrews, S. M. 2014, ApJ, 780, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruggeman, D. A. G. 1935, Ann. Phys., 416, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Wright, C. M., Marino, S., et al. 2015, ApJ, 812, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, B. G. 1980, A&A, 89, 377 [NASA ADS] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Hollenbach, D., Kamp, I., & D’Alessio, P. 2007, Protostars and Planets V, 555 [Google Scholar]
- Eisner, J. A., Hillenbrand, L. A., & Stone, J. M. 2014, MNRAS, 443, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Price-Whelan, A., Ryan, G., et al. 2014, triangle.py v0.1.1, http://dx.doi.org/10.5281/zenodo.11020 [Google Scholar]
- Fukagawa, M., Tsukagoshi, T., Momose, M., et al. 2013, PASJ, 65, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. App. Math. Comp. Sci., 5, 65 [Google Scholar]
- Guidi, G., Tazzari, M., Testi, L., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527516 [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Mutschke, H. 2010, J. Nanophoton., 4, 041580 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Compt. Sci. Eng., 9, 90 [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2009, ApJ, 701, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2010, ApJ, 714, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Juhász, A., Bouwman, J., Henning, T., et al. 2010, ApJ, 721, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., & Welch, W. J. 2015, ApJ, 808, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Laibe, G. 2014, MNRAS, 437, 3037 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Allen, P. R., Espaillat, C., Hartmann, L., & Calvet, N. 2010a, ApJS, 189, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Allen, P. R., Espaillat, C., Hartmann, L., & Calvet, N. 2010b, ApJS, 186, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. J. C. 2003, Information Theory, Inference and Learning Algorithms (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Marino, S., Casassus, S., Perez, S., et al. 2015, ApJ, 813, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Menu, J., van Boekel, R., Henning, T., et al. 2014, A&A, 564, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miotello, A., Robberto, M., Potenza, M. A. C., & Ricci, L. 2012, ApJ, 757, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., & Testi, L. 2004, in Star Formation in the Interstellar Medium: In Honor of David Hollenbach, eds. D. Johnstone, F. C. Adams, D. N. C. Lin, D. A. Neufeeld, & E. C. Ostriker, ASP Conf. Ser., 323, 279 [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, Protostars and Planets V, 767 [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Panagia, N., & Felli, M. 1975, A&A, 39, 1 [NASA ADS] [Google Scholar]
- Pérez, L. M. 2013, Ph.D. Thesis, Caltech, USA [Google Scholar]
- Pérez, L. M., Lamb, J. W., Woody, D. P., et al. 2010, ApJ, 724, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Chandler, C. J., Isella, A., et al. 2015, ApJ, 813, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013, ApJS, 206, 16 [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes: The Art of Scientific Computing (Cambridge University Press) [Google Scholar]
- Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010a, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010b, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodmann, J., Henning, T., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the Earth and the planets, NASA TTF, 677 [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Stognienko, R., Henning, T., & Ossenkopf, V. 1995, A&A, 296, 797 [NASA ADS] [Google Scholar]
- Tanaka, H., Himeno, Y., & Ida, S. 2005, ApJ, 625, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2001, ApJ, 554, 1087 [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI, 339 [Google Scholar]
- Trotta, F., Testi, L., Natta, A., Isella, A., & Ricci, L. 2013, A&A, 558, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ubach, C., Maddison, S. T., Wright, C. M., et al. 2012, MNRAS, 425, 3137 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Waters, L. B. F. M., Dominik, C., et al. 2003, A&A, 400, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Marel, N., Pinilla, P., Tobin, J., et al. 2015, ApJ, 810, L7 [Google Scholar]
- Warren, S. G. 1984, Appl. Opt., 23, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W. 1980, ARA&A, 18, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1972, in From Plasma to Planet, ed. A. Elvius, 211 [Google Scholar]
- Wilner, D. J., Ho, P. T. P., Kastner, J. H., & Rodríguez, L. F. 2000, ApJ, 534, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wrobel, J. M., & Walker, R. C. 1999, in Synthesis Imaging in Radio Astronomy II, eds. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 171 [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Bayesian analysis: MCMC details and implementation
To efficiently compute the posterior distributions for all the free parameters (the five physical parameters that define the disk model plus two offset parameters per each fitted wavelength) we use a variant of the MCMC algorithm (Mackay 2003; Press et al. 2007), which proved to be effective in finding global maxima for a wide range of posteriors. We adopt an affine-invariant ensemble sampler for MCMC proposed by Goodman & Weare (2010), which is designed to simultaneously run several Markov chains (also called walkers) interacting with each other to converge to the maximum of the posterior. For unimodal posteriors (i.e., posteriors that exhibit only one global maximum) this algorithm is efficient at avoiding getting stuck in local maxima and allows the computation to be massively parallelized over the walkers. According to our experience, we have always observed unimodal posteriors, thus making this algorithm particularly suitable for our purpose.
In this study, we let the MCMC (usually of 1000 walkers) evolve for an initial burn-in phase, which is needed to allow the MCMC to perform a reasonable sampling of the parameter space and to find the posterior maximum (which is usually achieved after ten autocorrelation times7). After the burn-in phase, we let the MCMC run for several other autocorrelation times (3−4) to get a sufficient number of independent posterior samples. Since two consecutive steps in the MCMC are correlated (Goodman & Weare 2010), in order to extract a set of independent posterior samples out of the whole MCMC we need (1) to discard the samples of the burn-in phase and (2) to thin the remaining chain, i.e., to consider only steps separated by one autocorrelation time and to discard all the steps between them8. For completeness, we note that to estimate the chain convergence we also analyzed the acceptance ratio, i.e., the ratio of accepted over proposed moves, verifying that it is within the acceptable range between 0.2 and 0.5 in all cases. The number of steps needed to achieve convergence varies from disk to disk and depends on several factors, thus making it not predictable a priori; for the disks analyzed here, we needed at most 2000 steps including burn-in. With 1000 walkers, 2000 steps, and an acceptance fraction of ~0.2−0.5, we note that the method requires the computation of several million models and likelihoods, hence it is necessary to exploit the efficient Message Passing Interface (MPI) parallelization of the computation by advancing several hundred walkers in parallel.
As explained in Sect. 2.3, in addition to the disk structure and the dust size distribution, we also fit the position of the disk centroid by adding two nuisance parameters for each wavelength, namely Δα0 and Δδ0. To implement these offset parameters we exploit the fact that a translation in the real space corresponds to a phase shift in the conjugate (Fourier) space. Therefore, to shift the disk emission computed by the model by (Δα0, Δδ0) on the sky, we multiply the model visibilities 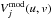 by the phase-shift exp[2πi(uΔα0/λ + vΔδ0/λ)], with Δα0 and Δδ0 given in radian units and λ in meters.
by the phase-shift exp[2πi(uΔα0/λ + vΔδ0/λ)], with Δα0 and Δδ0 given in radian units and λ in meters.
From the computational point of view, the main architecture of the analysis is written in Python and delegates the most demanding tasks, like the disk model evaluation or the visibility sampling, to C- and Fortran-compiled external libraries. Writing the main architecture of the analysis in Python allows us to use the affine-invariant MCMC algorithm implemented in the Python-based emcee package9 which enables a massive parallelization of the overall computation. By far the most costly part of the sampling is the evaluation of the posterior, which emcee allows us to do simultaneously for half the walkers (it exploits the Message Passing Interface (MPI) protocol to distribute the computation to several cores). In our case, we ran the fits on hundreds of cores hosted at the Computational Center for Particle and Astrophysics (C2PAP), decreasing the overall computational time to approximately one or two days. After a careful profiling of the analysis method, we noted that the bottleneck of the posterior evaluation (i.e., the single walker computation) is given by the several Fourier transform computations10 (one for each wavelength that is being fit) and by their sampling at the discrete locations where the antennas sampled the sky.
Appendix B: AS 209: Comparison with previous study
We present the results of the comparison between our analysis and the previous one by Pérez et al. (2012). As described below, the comparison is performed using the same observational datasets, the same disk model and the same dust opacity used by Pérez et al. (2012).
As presented in Sect. 2.3, our analysis consists of a self-consistent modeling of the disk structure and the radial distribution of the dust grains that provides us with a unique model that is capable of reproducing the multiwavelength observations simultaneously. In this framework, the radial profile of amax is constrained from observations at several wavelengths. Then, from the resulting amax(R) profile we derive the corresponding β(R) profile through the dust opacity model.
The analysis of Pérez et al. (2012) consists of two steps: first, assuming a constant amax throughout the disk, they separately fit the observations at different wavelengths and obtain radial profiles of the disk temperature and the optical depth τλ(R); then, assuming that the disk surface density Σ is unique, they interpret the wavelength dependence of τλ in terms of radial variations of β. In the end, they provide constraints on amax(R) by fitting the β(R) profile with a dust opacity model. In order to check whether we recover the results of Pérez et al. (2012) we first fit each wavelength separately. Subsequently, we perform a multiwavelength fit with the same disk and dust model and compare the results.
We perform single-wavelength fits of each observation of the AS 209 protoplanetary disk using the same setup for the disk model and the dust properties used by Pérez et al. (2012). For the disk model, we use the two-layer model described by Isella et al. (2009), which assumes the following surface density profile (Hartmann et al. 1998), ![\appendix \setcounter{section}{2} \begin{equation} \Sigma(R) = \Sigma_{\mathrm{T}}\left(\frac{R}{R_{\mathrm{T}}} \right)^{-\gamma}\exp\left\{-\frac{1}{2\left(2-\gamma \right)}\left[\left(\frac{R}{R_{\mathrm{T}}} \right)^{2-\gamma}-1 \right] \right\}\,, \end{equation}](/articles/aa/full_html/2016/04/aa27423-15/aa27423-15-eq241.png) (B.1)where RT is the radius at which the radial component of the gas velocity changes sign (gaseous material at R<RT moves inwards, at R>RT moves outwards). The dust size distribution is defined with the parametrization in Eq. (4), with
(B.1)where RT is the radius at which the radial component of the gas velocity changes sign (gaseous material at R<RT moves inwards, at R>RT moves outwards). The dust size distribution is defined with the parametrization in Eq. (4), with 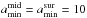 nm,
nm, 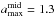 mm constant throughout the disk (
mm constant throughout the disk (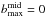 ), and qmid = qsur = 3.5. The dust grains are assumed to be compact spherical grains made of astronomical silicates (7.7%), carbonaceous material (29.5%), and water ice (62.8%) with an average dust grain density 0.9 g/cm3 (the correct value should be 1.3 g/cm3, but we adopt 0.9 g/cm3 in order to have the same setup used by Pérez et al. 2012). The dust opacity is computed through Mie theory as described in Sect. 2.2 using the same optical constants. In Fig. B.1 we show a comparison between the β(amax) profile for the dust we used in our joint multiwavelength fits (presented in Sect. 4) and the dust used by Pérez et al. (2012).
), and qmid = qsur = 3.5. The dust grains are assumed to be compact spherical grains made of astronomical silicates (7.7%), carbonaceous material (29.5%), and water ice (62.8%) with an average dust grain density 0.9 g/cm3 (the correct value should be 1.3 g/cm3, but we adopt 0.9 g/cm3 in order to have the same setup used by Pérez et al. 2012). The dust opacity is computed through Mie theory as described in Sect. 2.2 using the same optical constants. In Fig. B.1 we show a comparison between the β(amax) profile for the dust we used in our joint multiwavelength fits (presented in Sect. 4) and the dust used by Pérez et al. (2012).
 |
Fig. B.1 Dust opacity spectral index β between 0.88 and 8 mm as a function of the maximum dust grain size amax. The solid line refers to our dust composition (q = 3, 5.4% astronomical silicates, 20.6% carbonaceous material, 44% water ice, and 30% vacuum), whereas the dashed line refers to the dust composition used by Pérez et al. (2012) (q = 3.5, 7.7% astronomical silicates, 29.5% carbonaceous material, 62.8% water ice). |
In Table B.1 we list the comparison of the single wavelength fits.
Comparison of the single wavelength fits of AS 209 performed with our analysis and the results reported by Pérez et al. (2012).
The agreement between our results and those by Pérez et al. (2012) is extremely good, with all the values compatible within 1σ and only in a few cases within 2σ. Similarly to Pérez et al. (2012) we derive larger disks (RT ≳ 60 AU) at the shorter wavelengths and smaller disks (RT ≈ 25 AU) at the longer wavelengths, thus confirming the observational result that the size of emitting region is anticorrelated with the observing wavelength. As a further check, we note that the estimates of the uncertainty we obtain from our MCMC fits are similar to those obtained by Pérez et al. (2012).
In Fig. B.2 we show the midplane temperature profiles (left panel) and the optical depth profiles τν = κνΣ (right panel) obtained with the single wavelength fits. We note that both the temperature and the optical depth profiles obtained with our single wavelength modeling are found to be in complete agreement with those computed by Pérez et al. (2012). The agreement occurs at all the fitted wavelengths.
 |
Fig. B.2 Left panel: best-fit model midplane temperature obtained from fitting each wavelength separately (solid lines, one line per each wavelength) or from our multiwavelength fit (dashed line). Right panel: for the same best-fit models, the optical depth τν = κνΣ of the disk midplane to its own thermal radiation. Both panels: the single-wavelength fits have been performed assuming a constant amax = 1.3 mm (i.e., constant dust opacity) throughout the disk. The dashed lines refer to the best-fit model obtained through multiwavelength modeling. |
In Table B.2 we present the results of the multiwavelength fit that was performed with the same disk model and dust assumptions as the single wavelength fits with the only difference that in the multiwavelength fit, amax is not constant throughout the disk and its radial profile is constrained from the observations at several wavelengths.
Parameters derived from the multiwavelength fit of AS 209.
In Fig. B.2 the multiwavelength results are represented with a dashed black line.
The midplane temperature profile obtained with the multiwavelength fit is an average temperature between the four single wavelength profiles. There is close agreement between the multiwavelength temperature profile and those derived at 0.88 and 2.80 mm throughout the disk, whereas at 8.00 and 9.83 mm some discrepancies arise at R> 40 AU. The comparison of the optical depth profiles displays a similar behavior; there is good agreement at 0.88 and 2.80 mm and larger discrepancies at 8.00 and 9.83 mm in the outer disk. The discrepancies in the optical depth can be understood by considering that the Σ(R) profiles (and therefore the τλ(R) profiles) obtained with the single wavelength fits are totally independent of each other, whereas the multiwavelength fit is defined by a unique Σ(R) and produces different τλ(R) slopes at different wavelengths through radial variation of amax. In other words, the ability of the multiwavelength fit to produce different τλ(R) profiles at different wavelengths depends on the degrees of freedom of the amax parametrization11. That said, the net advantage of using the multiwavelength fit lies in the fact that it provides a unique, self-consistent disk model with a dust radial distribution, as opposed to several single wavelength fits that provide as many different disk structures.
We now compare the amax(R) and β(R) profiles obtained with our multiwavelength fit and those obtained by Pérez et al. (2012). In the left panel of Fig. B.3 we compare the amax(R) profiles, which agree to within a factor of less than 2 in the region where most of the signal comes from (between 40 and 140 AU the disk emission is spatially resolved and with signal-to-noise ratio higher than 3). It is reassuring that we both derive the same absolute dust grain size and radial slope throughout the disk. The discrepancy visible at R< 40 AU our amax(R) is not a source of concern for two reasons. First, at R< 40 AU the disk is not spatially resolved at any wavelength. Second, amax(R) is computed differently. Our amax(R) profile is by definition a power law; therefore, it cannot become arbitrarily steep since it has to accommodate both the inner and the outer disk simultaneously. Conversely, the amax(R) profile derived by Pérez et al. (2012) is independent at each radius, but goes to extremely large values amax ≳ 10 cm owing to the high degeneracy in the β(amax) curve (cf. Fig. B.1).
 |
Fig. B.3 Left panel: maximum dust grain size amax as a function of the disk radius. Right panel: dust opacity spectral index β between 0.88 and 8 mm as a function of the disk radius. Both panels: the solid black line with the shadowed blue area represent the best-fit and the 3σ region constrained by our multiwavelength analysis. The yellow shaded area represent the 3σ region obtained by Pérez et al. (2012). The vertical dashed lines represent the spatial resolution of the observations. |
In the right panel of Fig. B.3 we compare the radial profile of β between 0.88 and 8.0 mm. The two profiles agree in that they find common evidence of β(R) increasing with radius from small values β ~ 0.5 in the inner disk and β ≳ βISM = 1.7 in the outer disk. Nevertheless, they also display some important differences that can be understood by recalling the method used to derive them. In our multiwavelength analysis, the constraint is posed on the amax(R) profile, while β(R) is calculated as a post-processing result of the analysis through the Mie theory as explained in Sect. 2.2. It is then natural that a slowly decreasing amax(R) profile results in a slowly increasing β(R) profile. The analysis by Pérez et al. (2012), on the other hand, poses a direct constraint on β(R), which is computed substantially as the ratio of the optical depth profiles τλ(R) at 0.88 and 8.00 mm obtained from the single-wavelength fits, although the actual procedure they use is more refined since they employ a MCMC to compute a PDF for β(R) given the τλ(R) profiles and and average temperature 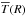 . For these reasons, the β(R) profiles obtained by these two methods are not directly comparable point by point in radius; nevertheless, they show common evidence of an increasing β with radius.
. For these reasons, the β(R) profiles obtained by these two methods are not directly comparable point by point in radius; nevertheless, they show common evidence of an increasing β with radius.
Appendix C: Fits results
As anticipated in Sect. 4, here we present the results of the multiwavelength fits for AS 209 and DR Tau. For each disk we present staircase plots with the 1D and 2D marginalized posterior PDFs, maps of the residuals at each wavelength (obtained subtracting the best-fit model from the observations), and a comparison between the observed and the model visibilities at each wavelength. We also present the physical structure derived for each disk: the gas surface density and the midplane temperature profile. In Figs. C.1−C.3 we present the results of the fit for AS 209 showing respectively the comparison of model and observed visibilities, the residual maps and the posterior PDFs, and the derived disk structure. In Figs. C.4−C.6 we present the same plots for DR Tau.
 |
Fig. C.1 AS 209 bin-averaged visibilities as a function of deprojected baseline length (uv-distance). Black dots represent the observed data, the colored area represents the density of models for each uv-distance bin, and the lines are defined as in Fig. 5. |
 |
Fig. C.2 Left panel: staircase plot showing the marginalized and bi-variate probability distributions resulting from the fit for AS 209. Right panel: AS 209 maps of the residuals at the fitted wavelengths. |
 |
Fig. C.3 Results of the AS 209 fit. Left panel: posterior PDF of the gas surface density. Right panel: posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
 |
Fig. C.4 DR Tau bin-averaged visibilities as a function of deprojected baseline length (uv-distance). Color and line conventions are defined in Fig. 5. |
 |
Fig. C.5 Left panel: staircase plot showing the marginalized and bi-variate probability distributions resulting from the fit for DR Tau. Right panel: DR Tau maps of the residuals at the fitted wavelengths. |
 |
Fig. C.6 Results of the DR Tau fit. Left panel: posterior PDF of the gas surface density. Right panel: posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
All Tables
Comparison of the single wavelength fits of AS 209 performed with our analysis and the results reported by Pérez et al. (2012).
All Figures
 |
Fig. 1 Dust opacity (per gram of dust) for amax = 0.8, 1, 3 mm, and 1 cm, computed for the midplane population of grains assuming the composition of 5.4% astronomical silicates, 20.6% carbonaceous material, 44% water ice, and 30% vacuum and a size distribution n(a) ∝ a− q for amin<a<amax with q = 3.0 and amin = 10 nm. |
| In the text | |
 |
Fig. 2 Representation of the MCMC results for FT Tau. On the top diagonal, the 1D histograms are the marginalized distributions of the fitted parameters; the vertical dashed lines represent (from left to right) the 16th, the 50th, and the 84th percentiles. The 2D density plots represent the bi-variate distributions for each pair of parameters, with one dot representing one sample. The plot shows the posterior sampling provided by 500 steps of the 1000-walkers chain (800 burn-in steps were performed to achieve convergence). We note that in order to obtain an independent set of samples, the chain has been thinned by a factor equal to the autocorrelation time (~80 steps in this case). |
| In the text | |
 |
Fig. 3 Comparison between the observed and the best-fit model images at different wavelengths of the FT Tau protoplanetary disk. The best-fit model is defined by the following parameters: γ = 1.07, Σ0 = 18 g/cm2, Rc = 28 AU, amax0 = 0.4 cm, bmax = −1.3. The observed images are shown in the left panels, the model images in the center panels, the residuals in the right panels. The positive and negative contour levels are spaced by 3σ (starting from −3σ) and are the same in all the panels. The synthesized beam FWHM is represented as a gray ellipse in the bottom-left corner of each map. |
| In the text | |
 |
Fig. 4 Comparison between the model and the observed visibilities as a function of deprojected baseline length (uv-distance) for FT Tau. The data are binned in 40kλ bins. Black dots represent the observed data and the colored boxes represent the probability distribution of model visibilities for each uv-distance bin. The x-axis extent of each box is the bin size, while the y-axis extent is not fixed as it depends on the probability distribution of the model at that particular uv-distance bin; in some cases they are very close to each other. The color scale represents the density of the distribution. The solid black curve is the median, the dashed black lines are the 16th and 84th percentiles, and the red dotted lines are the 2.3th and 97.7th percentiles. |
| In the text | |
 |
Fig. 5 Results of the FT Tau fit. Top: in the left panel, the posterior PDF of the maximum dust grain size amax as a function of the disk radius; in the right panel, the posterior PDF of the dust spectral radial profile β(R) between 1 and 10 mm. Bottom: in the left panel, the posterior PDF of the gas surface density; in the right panel, the posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
| In the text | |
 |
Fig. 6 Left panel: radial profile of the maximum dust grain size amax constrained from the multiwavelength fits. Right panel: radial profile of the dust opacity spectral slope β(R) between 1 mm and 10 mm. The dashed black horizontal line at βISM = 1.7 represents the typical value of β for small ISM dust grains. In both panels: the thick lines represent the median (i.e., the best-fit) model, and the shaded areas represent the 1σ credibility intervals. The best-fit model lines are plotted wherever the signal-to-noise ratio is higher than 3 (computed for the observation displaying the most extended disk emission); the shaded areas are truncated at half the average beam size (inner regions) and at |
| In the text | |
 |
Fig. B.1 Dust opacity spectral index β between 0.88 and 8 mm as a function of the maximum dust grain size amax. The solid line refers to our dust composition (q = 3, 5.4% astronomical silicates, 20.6% carbonaceous material, 44% water ice, and 30% vacuum), whereas the dashed line refers to the dust composition used by Pérez et al. (2012) (q = 3.5, 7.7% astronomical silicates, 29.5% carbonaceous material, 62.8% water ice). |
| In the text | |
 |
Fig. B.2 Left panel: best-fit model midplane temperature obtained from fitting each wavelength separately (solid lines, one line per each wavelength) or from our multiwavelength fit (dashed line). Right panel: for the same best-fit models, the optical depth τν = κνΣ of the disk midplane to its own thermal radiation. Both panels: the single-wavelength fits have been performed assuming a constant amax = 1.3 mm (i.e., constant dust opacity) throughout the disk. The dashed lines refer to the best-fit model obtained through multiwavelength modeling. |
| In the text | |
 |
Fig. B.3 Left panel: maximum dust grain size amax as a function of the disk radius. Right panel: dust opacity spectral index β between 0.88 and 8 mm as a function of the disk radius. Both panels: the solid black line with the shadowed blue area represent the best-fit and the 3σ region constrained by our multiwavelength analysis. The yellow shaded area represent the 3σ region obtained by Pérez et al. (2012). The vertical dashed lines represent the spatial resolution of the observations. |
| In the text | |
 |
Fig. C.1 AS 209 bin-averaged visibilities as a function of deprojected baseline length (uv-distance). Black dots represent the observed data, the colored area represents the density of models for each uv-distance bin, and the lines are defined as in Fig. 5. |
| In the text | |
 |
Fig. C.2 Left panel: staircase plot showing the marginalized and bi-variate probability distributions resulting from the fit for AS 209. Right panel: AS 209 maps of the residuals at the fitted wavelengths. |
| In the text | |
 |
Fig. C.3 Results of the AS 209 fit. Left panel: posterior PDF of the gas surface density. Right panel: posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
| In the text | |
 |
Fig. C.4 DR Tau bin-averaged visibilities as a function of deprojected baseline length (uv-distance). Color and line conventions are defined in Fig. 5. |
| In the text | |
 |
Fig. C.5 Left panel: staircase plot showing the marginalized and bi-variate probability distributions resulting from the fit for DR Tau. Right panel: DR Tau maps of the residuals at the fitted wavelengths. |
| In the text | |
 |
Fig. C.6 Results of the DR Tau fit. Left panel: posterior PDF of the gas surface density. Right panel: posterior PDF of the midplane temperature. Line conventions are the same as those in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


