EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 675 (July 2023) A&A, 675 (2023) A176 Full HTML
Open Access
Issue
A&A
Volume 675, July 2023
Article Number A176
Number of page(s) 18
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202346253
Published online 20 July 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1 Introduction

The temperature structure of inner protoplanetary disks controls the evolution of dust grains (e.g., Birnstiel et al. 2010; Okuzumi et al. 2016; Drążkowska & Alibert 2017; Ueda et al. 2021b), the subsequent formation of planets and their migration (e.g., Kley & Nelson 2012; Bitsch et al. 2014; Bitsch 2019; Savvidou & Bitsch 2021), and, eventually, the chemical composition of planets (e.g., Öberg et al. 2011; Madhusudhan et al. 2014; Ohno & Ueda 2021; Schneider & Bitsch 2021; Notsu et al. 2022). The heating resulting from disk gas accretion is thought to play a key role in determining the disk temperature, particularly at the midplane of the inner regions of disks (≲10 au). In the classical model of accretion heating, the gravitational energy of the disk gas is released near the midplane, where the energy has a hard time escaping from the disk, leading to efficient heating of the disk midplane (e.g., Hubeny 1990; Nakamoto & Nakagawa 1994). However, recent non-ideal magneto-hydrodynamical models have shown that accretion heating may be less efficient compared to the classical model when accretion is primarily driven by the magnetorotational instability (MRI) in the upper layer of the disk (Hirose & Turner 2011) or by magneto-hydrodynamical disk winds (Mori et al. 2019). This is because the gravitational energy released at the upper layer can escape from the disk more easily. Still, accretion heating in magneto-hydrodynamically accreting disks can affect the disk temperature structure depending on the disk ionization state and opacity (Béthune & Latter 2020; Kondo et al. 2023).

Even though the way in which the disk midplane is heated is crucial for the formation of planets, it is still poorly constrained by observations. The Atacama Large Millimeter/submillimeter Array (ALMA) provides an opportunity to probe the temperature structure of the inner regions of disks, where accretion heating potentially takes place. The ALMA high-resolution multi-wavelength analysis allows us to evaluate the dust properties (e.g., dust size, temperature and surface density) as a function of radial distance based on the spectral behavior of the (sub-)millimeter dust thermal emission (Carrasco-González et al. 2019; Macías et al. 2021; Sierra et al. 2021; Ueda et al. 2022; Guidi et al. 2022). However, previous studies have generally assumed that the observed dust temperatures at different ALMA wavelengths are identical (i.e., vertically isothermal). If the disk is optically thick at the observing wavelengths, the different observing wavelengths trace different heights within the disk, which may alter the interpretation of the disk properties (Sierra & Lizano 2020; Ueda et al. 2021a).

In other words, the vertical disk structure can be probed by the multi-wavelength sub-millimeter to centimeter observations by leveraging the difference in optical depth at each wavelength. For instance, recent ALMA observations of CO isotopologue line emissions have provided insights into the vertical structure of the outer regions of disks by utilizing the expected emission heights of different CO isotopologues (Law et al. 2021, 2023). For the inner regions of disks, dust continuum observations would be more suitable than the gas molecule observations as it is easier to achieve better angular resolution and sensitivity with a reasonable observing time. Okuzumi et al. (2023) demonstrated that the vertical temperature structure of the inner region (of a few au) of disks can be inferred from the multi-wavelength dust continuum observations using ALMA and the next-generation Very Large Array (ngVLA).

In this paper, we investigate the temperature structure of the disk around CW Tau using ALMA multi-wavelength dust continuum observations. The CW Tau disk has a high accretion rate (3−10 × 10−8 M⊙ yr−1; McClure 2019; Robinson et al. 2022; Gangi et al. 2022) and has been observed at ALMA Bands 4, 6, 7, and 8 (Ueda et al. 2022). This combination of a high accretion rate and rich observational data makes the CW Tau disk an excellent target for studying the vertical temperature structure of the inner region potentially heated by disk accretion. This paper is constructed as follows. In Sect. 2, we introduce our observational data and theoretical models. The models are compared with the observations in Sect. 3. Our discussion and summary are given in Sects. 4 and 5, respectively.

2 Methods

2.1 ALMA observations

We made use of the ALMA data of the CW Tau disk taken and calibrated in Ueda et al. (2022). The observations were carried out at ALMA Bands 4 (λ = 2.17 mm), 6 (1.34 mm), 7 (0.89 mm), and 8 (0.75 mm). The CW Tau disk is a Class II disk with a stellar luminosity of L* = 0.45 L⊙ (Herczeg & Hillenbrand 2014), accretion luminosity of Lacc = 0.85 L⊙ (Gangi et al. 2022), and accretion rate of Ṁ = 3−10 × 10−8 M⊙ yr−1 (McClure 2019; Robinson et al. 2022; Gangi et al. 2022), which is much higher than the typical value of the Class II disks (e.g., ~3.6 × 10−9 M⊙ yr−1; Manara et al. 2017 see also Manara et al. 2022). Its high accretion rate and relatively low stellar luminosity make the CW Tau disk suitable for studying accretion heating of the disk. In this work, we adopted Ṁ = 4 × 10−8 M⊙ yr−1, which falls within the range of observed values for CW Tau.

Figure 1 presents the observed brightness temperature at ALMA Bands 4, 6, 7, and 8. The observational data has a common angular resolution of 0″.1, corresponding to a spatial resolution of 13.2 au for the distance of CW Tau (132 pc; Gaia Collaboration 2021). The brightness temperature at ALMA Bands 4, 6, 7, and 8 shows a nearly identical value of ~35 K at ≲ 10 au. At the outer region, ≳20 au, the brightness temperature exhibits variations among the different ALMA bands. In particular, the brightness temperature at Band 4 is lower compared to the other bands.

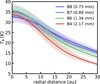thumbnail Fig. 1

Brightness temperature profile observed at ALMA Bands 4, 6, 7, and 8 obtained by Ueda et al. (2022). The transparent region denotes the uncertainty arising from both flux calibration and thermal noise.

2.2 Theoretical model

We constructed two-dimensional (2D, with radial position, r, and vertical height, z) models of the CW Tau disk to compare them with the ALMA observations. In this section, we provide a detailed description of our theoretical models of the disk structure.

2.2.1 Temperature structure

The temperature structure of the disk is determined by the combined effects of stellar irradiation and accretion heating: 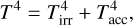(1)

where Tirr and Tacc denote the disk temperature determined by stellar irradiation and accretion heating, respectively. The temperature structure of the passively irradiated disk is calculated as 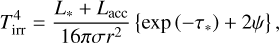(2)

where σ is the Stefan–Boltzmann constant, τ* is the radial optical depth for stellar irradiation. The angle ψ represents the angle between the ray from the central star and the disk surface. Its actual value depends on the distance from the central star and the detailed disk surface structure. We assume ψ = 0.02 which corresponds to h*/r ~ 0.07, with h* being the height of the disk photosphere above the midplane (Dullemond et al. 2001).

Equation (2) provides the black body temperature in the optically thin regime when τ* ≪ 1, whereas it yields temperature profile of the classical optically thick passive disk in the limit of τ* ≫ 1 (e.g., Dullemond et al. 2001; see also Huang et al. 2018). In the optically thick interior region (τ* ≫ 1), the temperature structure is vertically isothermal. It is worth noting that the temperature structure of the optically thin region (τ* ≪ 1) has no significant impact on our analysis as the emission observed by ALMA is dominated by the emission from the region where τ* ≫ 1. The temperature of optically thick region of the passively-heated disk can be lower than our model because of scattering of the stellar irradiation (Okuzumi et al. 2022), which is not included in our model. With our dust model, this could reduce the disk temperature by 10%. We examine the validity of Eq. (2) in Appendix A.

The temperature structure determined by accretion heating is (e.g., Nakamoto & Nakagawa 1994; Sierra & Lizano 2020) 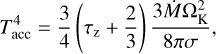(3)

where ΩK is the Keplerian frequency and τz is the vertical optical depth for the dust thermal emission integrated from each position to z = ∞ (or z = −∞ if z < 0); 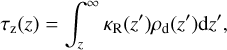(4)

with κR and ρd being the Rosseland-mean opacity and dust density, respectively. Because τz increases as z approaches the midplane, Tacc increases as z approaches the midplane. We note that the actual value of Ṁ can be lower or higher than our adopted value by a factor of ~2 (see Sect. 2.1), which then decreases or increases Tacc by ~20%. As Tacc is a function of the product of τz and Ṁ, the disk temperature structure is almost identical as long as τzṀ is identical.

In this study, we consider two scenarios: a passive disk where the temperature structure is solely determined by stellar irradiation (i.e., 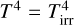) and an active disk where additional heating due to accretion is taken into account (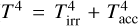). As shown in Sect. 3, accretion heating dominates over stellar irradiation (T ≈ Tacc) near the midplane within a few to a few dozen au, depending on the specific disk models.

2.2.2 Dust opacities

The dust opacity plays a crucial role in determining both the temperature structure of the disk and the (sub-)millimeter emission observed with ALMA. The dust composition is assumed to be that of the DSHARP model (Birnstiel et al. 2018), which is a mixture of water ice (Warren & Brandt 2008), astronomical silicates (Draine 2003), troilite, and refractory organics (Henning & Stognienko 1996). It is important to note that the dust composition remains highly uncertain and, therefore, we also present modeling results using an alternative dust model, the DIANA dust model (Woitke et al. 2016) in Appendix B.

The dust size distribution ranges from amin to amax with a power-law index of −pd. We assume pd = 3.5 which is similar to the so-called MRN distibution (Mathis et al. 1977) as a fiducial case, while more flat profile (pd = 2.5) is also applied to investigate its impact on the brightness temperature. The latter corresponds to more top-heavy distribution where the dust opacity is dominated by larger grains. The minimum dust size amin is set to be 0.05 µm. We confirmed that our conclusions remain unchanged even if we adopt larger amin, 0.5 µm. We consider two different dust porosity values, namely p = 0 (corresponding to compact dust) and 0.9 (corresponding to a filling factor of f = 1 and 0.1, respectively). We do not consider very porous dust (p ≫ 0.9) because extremely porous dust may not account for the high polarization degree of the dust thermal emission observed toward the CW Tau disk (Bacciotti et al. 2018; Tazaki et al. 2019; Kirchschlager et al. 2019). The opacities are computed with Optool (Dominik et al. 2021).

Figure 2 shows the effective extinction opacity, κext, effective albedo, ωeff, and Rosseland-mean opacity, κR, of our dust model. The effective extinction opacity is defined as κext = κabs + κsca(1 − g), where κabs, κsca and g are the absorption opacity, scattering opacity, and anisotropic scattering parameter, respectively. The effective albedo is given as ωeff = κsca(1 − g)/κext. The extinction opacity has a slope of κext ∝ λ−1.7 when amax ≪ λ/2π, whereas it is flatter when amax ≫ λ/2π. In the intermediate regime (amax ~ λ/2π), the opacity slope is steeper than −1.7 because of the Mie interference. The interference is significant only for compact grains, leading to a higher opacity compared to porous grains (Kataoka et al. 2014).

The effective scattering albedo at the ALMA wavelengths (~0.8−2 mm) is <0.2 for amax ≪ λ/2π ~ 300 µm. However, for amax ≳ 300 µm, the scattering albedo reaches 0.8 or even higher at the ALMA wavelengths. The high scattering albedo efficiently reduces the emergent intensity at the ALMA wavelengths, which makes the disk fainter than that without scattering (e.g., Liu 2019; Zhu et al. 2019). At the ALMA wavelengths, compact dust has slightly higher ωeff compared to porous dust. This is because porous dust scatters incident radiation more efficiently in the forward direction, resulting in a lower effective albedo. We note that the absorption and scattering opacity can be scaled by amaxf except for the behavior of the Mie interference (Kataoka et al. 2014). However, the asymmetry parameter g depends on the porosity, which makes the difference in the optical properties of compact and porous dust for a given amax f (Zhang et al. 2023).

thumbnail Fig. 2

Effective extinction opacity (top), effective albedo (middle) and Rosseland-mean opacity (bottom) of compact (p = 0; left) and porous (p = 0.9; right) dust with different amax. The power-law index of the dust size distribution is set to pd = 3.5. The vertical gray dotted lines denote the wavelength of ALMA Bands 4, 6, 7, and 8.

2.2.3 Dust disk

The dust surface density is given by 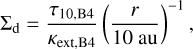(5)

where τ10,B4 is the vertical extinction optical depth at ALMA Band 4 at 10 au. Although the true dust surface density is highly uncertain, the wavelength-independent brightness temperature implies that the inner disk region is at least moderately optically thick at these wavelengths (see Ueda et al. 2022). In our model, we adopted τ10,B4 = 3 for all the models. In Appendix C, we show the effect of τ10,B4 on the brightness temperature. We confirmed that τ10,B4 needs to be larger than unity in order to match the observed brightness temperature at ALMA Band 4. We discuss the estimated dust and gas surface densities as well as the corresponding accretion efficiency parameter aacc in Sect. 4.2.

In the vertical direction, the dust density distribution is given by: 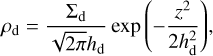(6)

where hd represents the scale height of the dust disk. In our fiducial model, we assume that the dust is well-coupled with the gas, namely, hd = hg, with hg being the gas scale height. The gas scale height is calculated by hg = cs/ΩK, with cs being the sound speed of the gas at the midplane. We also investigated the effect of dust settling. In incorporate dust settling, we define the Stokes number as 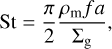(7)

where ρm = 1.675 g cm−3 is the material density, f = 1 − p is the dust filling factor, and Σg is the gas surface density and a is the dust radius. For simplicity, we assume that the gas surface density is 100 times larger than the dust surface density. The dust scale height is assumed to be in mixing-settling equilibrium (Dubrulle et al. 1995; Youdin & Lithwick 2007); 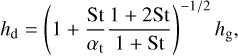(8)

where αt is the turbulence strength for vertical dust mixing. In our model with settling, we assume relatively weak vertical mixing with αt = 10−4 in order to investigate the difference from the no-settling limit.

The computational domain extends radially from r = 0.5 to 50 au that are logarithmically divided into 100 cells. For the polar direction, the calculation domain covers from θ = −π/6 to π/6 (where θ = 0 gives disk midplane) with 400 uniformly spaced cells.

To investigate the impact of different physical mechanisms on the brightness temperature, we constructed models with various setups. The details of these models are summarized in Table 1.

Table 1

Summary of our models.

2.3 Imaging simulation

Given the disk structure obtained in Sect. 2.2, we performed Monte Carlo radiative transfer calculations using RADMC-3D (Dullemond et al. 2012) to generate synthetic images. The dust opacities are the same as those described in Sect. 2.2.2. We used 107 photon packages for each simulation. To compare the synthetic images with the observations, we smoothed the images with the observing beam size of 0″.1, which corresponds to a physical distance of 13.2 au for CW Tau (d = 132 pc). The disk inclination is assumed to be 58° (Ueda et al. 2022) and the intensity is averaged over the azimuthal direction to obtain the radial intensity profile. The radial intensity profile is then converted into the brightness temperature using the full Planck function. To account for anisotropic scattering, we employed the Henyey-Greenstein approximation (Henyey & Greenstein 1941).

3 Comparison of models and observations

In this section, we compare our theoretical models with the observations.

3.1 Passive disk models

We initiated the comparison by starting with the simplest cases, namely: passive disks, where the temperature structure is determined solely by stellar irradiation.

Figure 3 shows the brightness temperature profile of the passive disk model for different amax. Here, we computed the brightness temperature with and without scattering. When scattering is considered, the emergent intensity is reduced, leading to lower brightness temperatures compared to the actual dust temperature, even in optically thick disks (Liu 2019; Zhu et al. 2019; Ueda et al. 2020).

For amax = 10 µm, the model brightness temperatures at r ≲ 10 au are identical for all wavelengths and are ~1.5 times higher than observed. Scattering has negligible effects on the brightness temperatures in this case because of the low albedo of the 10 µm-sized grains (see the center panel of Fig. 2). At ≳15 au, the brightness temperature at Band 4 is slightly lower than those at the other bands because that region is marginally optically thin at wavelengths ≳2mm.

For amax ≳ 100 µm, the brightness temperatures are comparable to or lower than those for amax = 10 µm. The observed brightness temperature in our models without scattering is affected by the optical depth of the disk. In our model, the dust surface density is adjusted such that the extinction optical depth at ALMA Band 4 reaches a value of 3 at a radial distance of 10 au (τ10,B4 = 3). In the models without scattering, the effect of scattering is taken into account in the calculation of the dust surface density. This means that the dust surface density remains the same for models with and without scattering. However, when calculating the emergent intensity, scattering is ignored. Because of this setup, the vertical optical depth is effectively smaller for the models without scattering if scattering dominates over absorption. For instance, dust with amax = 300 µm has the effective albedo of ~0.9 at ALMA Band 4, which corresponds to the absorption optical depth of τabs,10,B4 = τext,10,B4(1 − ωeff) ~ 0.3. Therefore, the no-scattering model with amax = 300 µm is optically thin at ALMA Band 4 and hence shows lower brightness temperature. For the models with scattering, the model disks are always optically thick at < 10 au at all wavelengths we considered.

We see from Fig. 3 that the brightness temperatures from the passive disk models without scattering exceed those from the observations. This implies that the scattering-induced intensity reduction takes place in the inner region of the CW Tau disk. For amax ~ 150 µm, the brightness temperatures are reduced by ~30% by scattering, which makes the passive disk with 150 µm-sized dust consistent with the observations. The model with amax = 300 µm has a high effective albedo (≳0.8) at all wavelengths considered, yielding brightness temperatures lower than observed. For amax ≳ 300 µm, the effective albedo at ALMA Bands 7-8 decreases as dust size increases, which makes the models with large grains consistent with the observations at ALMA Bands 7-8. However, at Band 4, dust with sizes in the range of 300 µm ≲ amax ≲ 1 mm still exhibit a high albedo, leading to brightness temperatures that are too low compared to the observed values. Because the scattering albedo at ALMA Band 4 decreases for amax ≳ 1 mm, very large dust with amax ≳ 10 cm may account for what is seen in the observations.

Figure 4 presents the brightness temperature at the center of the model images normalized by the observed value, providing insight into the temperature structure within the central region with diameter of ~13 au, which corresponds to the size of one beam. We see that the brightness temperature of models with amax ≲ 100 µm exceeds the observed values by ~30%. In contrast, the brightness temperatures are significantly lower than the observations if amax = 300 µm. The intermediate size, amax ~ 150 µm, explains the observations reasonably well. If the dust size is larger than millimeter, the model brightness temperatures are more similar to the observed values as dust size increases, showing that very large grains (≳few cm) are roughly consistent with the observations.

In summary, when considering a disk heated solely by stellar irradiation, two possible ranges for the maximum dust radius emerge to explain the observed brightness temperatures: ~ 150 µm or more than a few cm. Very small dust grains, amax ≪ 150 µm, are unlikely to account for the observations due to their low effective albedo at millimeter wavelengths, which results in higher brightness temperatures than observed. On the other hand, millimeter-sized dust grains are also improbable as their high effective albedo at ALMA Band 4 leads to significantly lower model brightness temperatures compared to the observed values.

thumbnail Fig. 3

Brightness temperature profile of the passive disk model (p = 0, τ10,B4 = 3 and pd = 3.5) with (top) and without (bottom) scattering with different amax. The transparent shaded region shows the observed brightness temperature. The model brightness temperature is calculated after the intensity is convolved with the beam size of 0″.1 which corresponds to the physical distance of 13.2 au. The black dotted line denotes the midplane temperature profile convolved with a Gaussian with a full width at half maximum (FWHM) of 13.2 au.
thumbnail Fig. 4

Brightness temperature at the center of model images normalized by the observed brightness temperature. The gray shaded region denotes the region where the model explains the observations with an accuracy of 10%, which is the typical ALMA calibration uncertainty.

3.2 Active disk models

The passive disk models considered in the previous subsection ignore any internal heating sources. However, the inner region of the disk can be heated by gas accretion, and hence, the disk may have a vertical temperature gradient that affects the brightness temperature. In this subsection, we show how accretion heating affects the brightness temperature of the CW Tau disk.

3.2.1 Case of amax = 10 µm

To clarify the impact of the vertical temperature structure on the ALMA brightness temperatures, we start the analysis by considering the scenario of amax = 10 µm, wherein the scattering of dust thermal emission is negligible. The most notable factor in this case is the substantial vertical optical depth τz, which establishes the accretion heating as the primary determinant of the inner disk temperature.

Figure 5 shows the 2D temperature structure of the disk with amax = 10 µm, both with and without considering the effects of accretion heating. It is evident that within a radius of approximately 20 au, the temperature structure is primarily influenced by accretion heating when amax = 10 µm. Additionally, Fig. 5 presents the dust temperatures at the surfaces where the extinction optical depths at ALMA wavelengths reach unity (hereafter, ALMA surfaces). It is worth noting that despite having identical total vertical optical depths in the passive and active disk models, the ALMA surfaces are higher in the active disk model due to the elevated gas scale height, as compared to the passive model.

The dust temperature at the ALMA surfaces remains constant regardless of the observing wavelengths in the case of a passively heated disk. However, in the presence of accretion heating, the dust temperature at the ALMA wavelengths becomes wavelength-dependent. This dependence arises because longer observing wavelengths probe regions closer to the midplane, where accretion heating is more efficient. Consequently, longer observing wavelengths result in higher dust temperatures. For instance, at 10 au, the dust temperature observed with ALMA Band 8 is ~100 K, while the dust temperature observed with ALMA Band 4 is ~180 K. In comparison, the midplane temperature is ~200 K.

Figure 5 (bottom panels) also compares the brightness temperature profile obtained from the radiative transfer simulation with the observed values. The bottom-left panel of Fig. 5 corresponds to the top-left panel in Fig. 3. The brightness temperature of the fiducial active disk is more than two times higher than that of the passive disk. Furthermore, a wavelength-dependent brightness temperature is seen within ~10 au, which is not seen in the observations. This is because of the vertical temperature gradient shown in the top and middle panels in Fig. 5. The brightness temperature is independent of the inclusion of scattering because of the negligible scattering albedo. Based on these, we conclude that the maximum dust size of 10 µm is unlikely regardless of the efficiency of accretion heating.

thumbnail Fig. 5

2D temperature structure (top), dust temperature at the ALMA surfaces (middle) and synthetic brightness temperature profiles (bottom). The maximum dust size is 10 µm. The left panels show the passive disk model where the disk is heated only by the stellar irradiation, whereas the right panels show the active disk model where the disk is heated by both stellar irradiation and disk accretion. The light green lines in the top panels denote the height where the vertical extinction optical depth reaches unity (ALMA surfaces) at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). The dust temperatures shown in the middle panels are not beam-convolded, while the brightness temperatures shown in the bottom panels are taken from the synthetic images convolved with a Gaussian with a FWHM of 13.2 au. The transparent regions denote the observed brightness temperatures.
thumbnail Fig. 6

2D temperature structure and dust temperature at ALMA surfaces for different values of amax. Top: 2D temperature structure of the fiducial active disk. The light green lines denote the height where the vertical extinction optical depth reaches unity at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). Bottom: Dust temperature at the height where the vertical extinction optical depth at the ALMA wavelengths reaches unity. The radial profile are not beam-convolved. The dust settling is not taken into account. The dust is assumed to be compact with a size distribution of pd = 3.5. The dust surface density is set so that τ10,B4 = 3.

3.2.2 Fiducial active disks

Figure 6 shows the 2D temperature structure of the fiducial active disk, considering different values of amax. We see that the temperature of the inner disk region is higher for smaller amax because of the higher vertical optical depth for dust thermal emission (τz). For amax ≲ 300 µm, the dust temperature at the ALMA surfaces is higher at longer wavelengths, as shown in Sect. 3.2.1. In contrast, For amax ≳ 1 mm, the dust temperature is not sensitive to the observing wavelengths. This is because the extinction opacity of large dust (≳1 mm) is less sensitive to the ALMA wavelength than that of small dust (see Fig. 2); hence, all ALMA observations trace similar disk heights. The difference in the dust temperature is the most significant at amax ~ 100 µm because of its steep slope in the extinction opacity. Although the dust temperature is nearly independent on the observing wavelengths when amax ≳ 1 mm, it remains lower than the midplane temperature at ≲6 au.

The temperature structure is almost identical for models with amax = 1 mm and 1 cm. This similarity arises because we ensure that the vertical extinction optical depth at ALMA Band 4 (τ10,B4) is constant across all models. In the regime of amax ≳ 1 mm, both the millimeter extinction opacity and the Rosseland-mean opacity decrease with increasing dust radius in the same manner (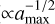). To keep τ10,B4 to be constant, the dust surface density is inversely proportional to the millimeter extinction opacity. Consequently, despite the decrease in the Rosseland-mean opacity as the dust radius increases, the infrared optical depth τz, which governs the magnitude of accretion heating, remains unchanged when τ10,B4 is held constant.

Figure 7 shows the brightness temperature profile of the fiducial active disk model. In contrast to the case of amax = 10 µm, when amax ≳ 100 µm, scattering is no longer negligible and reduces the brightness temperature, which makes the interpretation of the brightness temperature more complicated.

For amax = 155 µm, the model brightness temperatures are significantly higher than the observed values. The millimeter-wave scattering makes the brightness temperatures lower than that of no-scattering limit. The model with amax = 300 µm shows similar brightness temperatures with the observations if scattering is included. The brightness temperatures with scattering are about two times lower than that without scattering. Furthermore, the midplane temperature is about three times higher than the brightness temperatures. This clearly demonstrates that even if the disk is fully optically thick, the observed brightness temperature can be much lower than the true midplane temperature because of the combined effect of scattering and vertical temperature gradient (see also Sierra & Lizano 2020).

When amax is of the order of 1 mm, the brightness temperature at Band 4 is significantly lower than the observed value because of scattering even if the accretion heating takes place (see also Fig. 8). In contrast, when amax is greater than ~1 cm, the model brightness temperatures are similar to the observations as seen for amax = 300 µm. This is because the effective albedo at ALMA Band 4 decreases as amax increases in the regime of amax ≳ 1 mm. In this case, the midplane temperature is about two times higher than the observed brightness temperatures.

The central brightness temperature of the fiducial active disks is shown in Fig. 8. In the small dust regime (<300 µm), the model brightness temperature are too high to account for the observations because of the efficient accretion heating. While the passive disk model with amax ~ 300 µm underestimates the brightness temperature at ALMA Bands 4–7, the fiducial active disk model with amax ~ 300 µm aligns well with the observations. This is attributed to the enhancement of brightness temperature by accretion heating, particularly at longer wavelengths. Large grain models (≳few cm) are roughly consistent with the observations, although they tend to overestimate the brightness temperature at Band 8.

thumbnail Fig. 7

Same as Fig. 3, but for the fiducial active disk.
thumbnail Fig. 8

Same as Fig. 4, but for the fiducial active disk.

3.3 Effect of dust settling, size distribution and porosity

In this section, we explore the influence of dust settling, dust size distribution, and dust porosity on the brightness temperatures of the active disk. Figure 9 shows the 2D temperature structure of the fiducial active disk (same as the second right column of Fig. 6), settling model, top-heavy model, and porous dust model. The maximum dust size is set to 1 mm. We discuss the effect of each component in the following subsections.

3.3.1 Effect of dust settling

As dust grains grow larger, they are expected to settle down towards the midplane of the disk. If dust settling takes place, the effective dust size that contributes to the millimeter emission decreases because larger grains can be hidden within the optically thick midplane layer (Ueda et al. 2021a).

Figure 9 compares the dust temperature at the ALMA surfaces of the models without (left) and with (second left) dust settling with at = 10−4. We find that dust settling effectively increases the temperature of dust observed with ALMA. This behavior can be explained as follows: the efficiency of accretion heating is primarily determined by the distribution of small grains, whereas the height of the ALMA surfaces is predominantly influenced by the distribution of large grains. Due to settling, larger grains tend to selectively settle towards the mid-plane, causing the ALMA surfaces to descend more rapidly towards the midplane compared to the isotherm height of the active disk (as shown in the top rows of Fig. 9). This allows ALMA to observe a hotter layer.

Figure 10 shows the central brightness temperature of the beam-convolved images of the settling model. The radial brightness temperature profile of each model is shown in Appendix D (see Fig. D.1). For amax ≲ 3 mm, the brightness temperature is systematically higher than that of the fiducial active disk model (i.e., without settling). This is because of the effect explained above. Particularly for amax = 300 µm, the settling model overpredicts the brightness temperatures because of the higher temperature of the dust responsible for the emission. We note that the settling model with amax = 300 µm reasonably explains the observations if at = 10−3 because dust settling is less effective compared to at = 10−4. We also note that if the disk is active, the turbulence strength for dust mixing may not be significantly lower than that for accretion (aacc; Eq. (10)), implying that at = 10−3 may be more likely for the active disk model (see also Sect. 4.2).

For amax ≳ 3 mm, the brightness temperatures of the settling model are not simply higher than those of the model without settling. The temperature of dust observed with ALMA is higher for the models with settling compared to those without settling. However, the differential settling makes effective dust size smaller, which increases the scattering albedo and, hence, reduces the emergent intensity at the ALMA wavelengths. The emergent intensity and, hence, the brightness temperature, is determined by the balance between these two effects.

Overall, large grain models (amax ≳ 3 mm) predict the brightness temperatures similar to the observations. Compared to the no-settling models (Fig. 8), the settling model is more consistent with the observations if amax ≳ 3 mm. We note that if at = 10−3, dust settling has no significant impact on the brightness temperatures when amax ≲ 1 mm (see also Sect. 4.2).

thumbnail Fig. 9

2D temperature structure and dust temperature at ALMA surfaces for different disk models. Top: 2D temperature structure of the fiducial active disk model (left), Settling model (at = 10−4, second left), Top-heavy model (second right), and Porous model (right). The light green lines denote the height where the vertical extinction optical depth reaches unity at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). The maximum dust size amax is 1 mm in the all models. Bottom: Dust temperature at the height where the vertical extinction optical depth at the ALMA wavelengths reaches unity. The radial profile is not convolved.
thumbnail Fig. 10

Same as Fig. 4, but for the settling model with αt= 10−4.
thumbnail Fig. 11

Same as Fig. 4, but for the top-heavy dust model.

3.3.2 Effect of dust size distribution

The dust size distribution plays a critical role in both the millimeter thermal emission and the efficiency of accretion heating. In our fiducial case, we assume a slope of pd = 3.5 for the dust size distribution. However, it is important to note that the dust size distribution in protoplanetary disks is uncertain and is influenced by dust coagulation and fragmentation processes. In particular, if dust fragmentation is not efficient, the dust size distribution can exhibit a more top-heavy nature, meaning it is dominated by larger grains, rather than following a slope of pd = 3.5 (e.g., Birnstiel et al. 2011).

In the top-heavy model, we adopted a dust size distribution with a slope of pd = 2.5, instead of 3.5. As shown in Fig. 9, the top-heavy dust size distribution leads to a cooler disk region near the midplane compared to the fiducial active disk. This is because the dust mass is more dominated by large grains which have lower surface-to-mass ratio and hence accretion heating is less efficient.

Figure 11 shows the central brightness temperature of the beam-convolved images of the top-heavy model. The radial brightness temperature profile of each model is shown in Fig. D.2. Although the dust temperature is lower than that of fiducial active disk model, the brightness temperature does not simply follow the dust temperature. In the regime of amax ≲ 1 mm, scattering is more efficient than the case of pd = 3.5 because mm-sized grains have higher scattering albedo than micron-sized grains at ALMA wavelengths. Therefore, for amax ≲ 1 mm, the brightness temperatures of the top-heavy model are lower compared to the fiducial active disk model. In contrast, in the regime of amax ≳ 1 mm, scattering is less efficient than the case of pd = 3.5 because cm-sized or larger grains have lower scattering albedo than mm-sized grains at ALMA wavelengths. Therefore, for amax ≳ 1 mm, the brightness temperatures of the top-heavy model are higher compared to the fiducial active disk model. In the middle of these two regimes (amax ~ 1 mm), the brightness temperature is not sensitive to pd. Overall, the top-heavy models do not appear to be consistent with the observations.

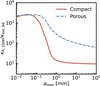thumbnail Fig. 12

Ratio between the Rosseland-mean opacity (at 100 K) and the extinction opacity at ALMA Band 4. The red solid and blue dashed lines denote the compact and porous dust, respectively.

3.3.3 Effect of porosity

In the previous sections, we focused on studying the brightness temperature of disks with compact dust grains. However, it is important to consider that dust in protoplanetary disks can be porous due to the pairwise collisional growth (e.g., Okuzumi et al. 2012).

In Fig. 9, we compare the dust temperature between the fiducial active disk model (left) and the porous dust model (right). We see that the accretion heating is more efficient in the porous dust model. This is because, for a given optical depth at ALMA wavelengths (e.g., τB4), the optical depth for the dust thermal emission (τz) is higher for porous dust. Figure 12 shows the ratio between the Rosseland-mean opacity (at 100K) and the extinction opacity at ALMA Band 4. For amax ≳ 100 µm, porous dust has higher κR,1400K/κext,B4. This means that for a given optical depth at ALMA wavelength, porous dust has larger vertical optical depth for accretion heating and hence the accretion heating is more efficient compared to compact dust.

Figure 13 shows the central brightness temperature of the convolved images of the porous dust model. The radial brightness temperature profile of each model is shown in Fig. D.3. If dust is porous, the brightness temperature is higher than that of compact dust model regardless of the dust size. We see that the porous dust models predict ≳1.5 times higher brightness temperatures than the observations. We also confirm that the brightness temperatures of porous dust model are still higher, even if pd = 2.5.

4 Discussion

4.1 Dust size in the inner region of the CW Tau disk

Our study reveals that the preferred maximum dust size in the inner region (≲ 10 au) of the CW Tau disk is ~ 150–300 µm (small grain solution) or larger than a few centimeters (large grain solution). Distinguishing between these two scenarios is essential for gaining insights into grain growth and temperature structure of the disk.

The CW Tau disk shows the strong scattering-induced polarization at ALMA Band 7 with a polarization degree of ≳l% (Bacciotti et al. 2018). This indicates that the thermal emission at ALMA Band 7 is primarily contributed by dust grains with a radius of λ/2π ~ 140 µm (Kataoka et al. 2015), although the angular resolution of the Polarimetrie observations (~0″.2) is worse than ours (0″.1). This implies that the small grain solution is more consistent with the Polarimetrie observations than the large grain solution.

The effective observed-dust size can be smaller than the true maximum dust size if differential dust settling takes place (Sierra & Lizano 2020; Ueda et al. 2021a), which potentially makes the large grain solution matches with the Polarimetrie observation. However, it is important to note that achieving the observed high polarization degree (≳1%) with amax larger than ~1 mm is unlikely, even under the assumption of extremely low turbulence strength (Ueda et al. 2021a).

The polarization degree also depends on the detailed structure of dust grains. Recent laboratory experiment suggests that non-spherical irregular shape dust can produce strong scattering-induced polarization even if the dust size is significantly larger than the observing wavelength (Lin et al. 2023). If this is the case, the polarization degree of non-spherical grains is less sensitive to the observing wavelength than the compact spherical grains. Furthermore, the inclusion of small amount of porosity (p ≲ 0.9) also makes the polarization degree less sensitive to the dust size (Tazaki et al. 2019; Zhang et al. 2023). However, we note that, if the porosity is as high as 0.9, the accretion heating is so efficient that the model brightness temperatures exceed the observed values. Therefore, if p ≳ 0.9, some sort of reduction of accretion heating due to, for instance, wind-driven accretion (Mori et al. 2019; Kondo et al. 2023) is required. Future multi-wavelength Polarimetrie observations would help us constrain the detailed dust structure.

thumbnail Fig. 13

Same as Fig. 4, but for the porous dust model.

4.2 Surface densities and effective accretion α

In this section, we discuss the expected dust and gas surface densities, as well as the effective turbulence strength for the accretion of the CW Tau disk.

Figure 14 shows the gas surface density of our fiducial active disk models (assuming a hundred times the amount of the dust).

The gas surface density of the minimum mass solar nebula (MMSN), 1700(r/au)−1.5 g cm−2 (Hayashi 1981), is also shown for comparison. We also plot the criterion for the disk to be graivationally unstable (Toomre 1964): 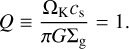(9)

In general, our model disks are expected to be gravitation-ally stable within the region of focus, approximately ≲ 10 au. If amax = 100 µm, the gas surface density reaches Q = 1 around ~10 au. If amax were 10 µm, the disk mass would be ~ 1.5 times higher; however, as already shown in Sect. 3, the model with amax = 10 µm fails to reproduce the observed brightness temperatures. On the other hand, for amax ≳ 300 µm, the gas surface density is estimated to be much lower than the Q = 1 line within 20 au. Moreover, the estimated gas surface density aligns closely with the MMSN model within 10 au for amax ≳ 300 µm. This indicates that the CW Tau disk has enough capability to form a planetary system similar to our solar system.

Figure 14 also shows the effective turbulence strength for the disk accretion; 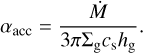(10)

For the given accretion rate of 4 × 10−8Μ⊙ yr−1, the effective turbulence strength accounting for the disk accretion needs to be ~10−4 for amax = 100 µm, while it is ~10−3−10−2 for amax ≳ 300 µm. The estimated αacc falls into a reasonable range of αacc = 10−4−10−2, although the high αacc (~10−2) found for the models of amax = 1–10 mm is higher than the typical value estimated from the observed disk lifetime in various star-forming regions (Manara et al. 2022; but see also Hartmann et al. 1998).

The model with amaĸ = 300 µm yields aacc ~ 10−3. As shown in Sects. 3.2.2 and 3.3.1, the model with amax = 300 µm can account for the observations if vertical dust settling is ignored but cannot if dust settling takes place with αt = 10−4. To further investigate this, we conducted a simulation of the settling model with αt = 10−3 and confirm that the model with amax = 300 µm reasonably matches the observations if αt = 10−3. This suggests that the effective turbulence strength for vertical dust mixing, αt, is not much lower than the effective turbulence strength for disk accretion, αacc, if amax = 300 µm.

thumbnail Fig. 14

Gas surface density (hundred times of the dust; top) and effective turbulence strength for the disk gas accretion (bottom) estimated from our fiducial active disk models. The gray dashed line denotes the gas surface density of the minimum mass solar nebula (MMSN; Hayashi 1981). The dotted lines denote the criteria for the disk to be gravitation-ally unstable (Q = 1).

4.3 Predictions for future observations

Our results show that the observed brightness temperatures at ALMA Bands 4–8 can be explained by either the passive or active disk models. It is crucial to distinguish between these models for the purposes of understanding the heating mechanisms in the inner region of disks.

Figure 15 shows the brightness temperatures at λ = 3.1 (ALMA Band 3), 4.1 (ALMA Band 2), and 7.0 mm (ALMA Band 1 or VLA Q band) computed from our models. The angular resolution is assumed to be (0″.05. The active disk with amax = 300 µm has ~ 1.5–2 times higher brightness temperatures at λ = 3.1 and 4.1 mm than the other models. The peak brightness temperature reaches ~80 Κ at λ = 3.1 and 4.1 mm. In contrast, at λ = 7.0 mm, the brightness temperature of the active disk model with amax = 300 µm is not significantly different from that with amax = 10 cm. This is because the small grain solution has higher temperature but lower optical depth, resulting in the cancellation of these effects.

The passive disk with amax = 300 µm can be distinguished from the other models by using λ = 7.0 mm because it has significantly lower brightness temperature. This is because the passive disk has lower temperature than the active disk and the optical depth is lower than the large grain model.

If amax = 10 cm, the accretion heating is not so significant that both the passive and active disk predict similar brightness temperature. However, the difference in those models is potentially distinguishable by ALMA because typical uncertainty in the ALMA flux is 5–10%, which is smaller than the difference in the brightness temperatures predicted by the models.

Even though the finest angular resolution of current facilities (ALMA and VLA) at λ ≳ 3 mm is limited to ~0″.05, it can achieve ~0″.02 at shorter wavelengths. Figure 16 shows the brightness temperature at λ = 0.75 (ALMA Band 8), 0.89 (Band 7) and 1.34 mm (Band 6) computed from our models with the angular resolution of 0″.02. We can see that the higher spatial resolution observations at shorter wavelengths can also distinguish between the active and passive disk models. The higher angular resolution allows us to detect a steeper brightness temperature profile in the active disk model. However, the difference in the brightness temperatures of the active and passive disks decreases with observing wavelength decreases because the shorter wavelength traces a more upper layer where the accretion heating is less effective. The difference in the brightness temperatures of the two passive disk models is maximized at λ ~ 1.34 mm because 300 µm-sized grain has a maximum effective albedo at that wavelength. In contrast, the active disk models with amax = 300 µm and 10 cm have similar brightness temperature profile because the 300 µm dust model has a higher dust temperature, which compensates for the efficient intensity reduction by scattering.

thumbnail Fig. 15

Brightness temperature profile at λ = 3.1, 4.1, and 7.0 mm predicted by our active disk models (solid lines) and passive disk models (dotted lines). The angular resolution is assumed to be 0″.05. The scattering-induced intensity reduction is included.
thumbnail Fig. 16

Brightness temperature profile at λ = 0.75, 0.89 and 1.34 mm predicted by our active disk models (solid lines) and passive disk models (dotted lines). The angular resolution is assumed to be 0.02. The scattering-induced intensity reduction is included.

4.4 Spectral energy distribution

Although our focus is on comparing our models with observations at ALMA wavelengths, it is worthwhile to compare them at infrared wavelengths as well. Figure 17 shows the comparison between our model spectral energy distributions (SEDs) and the observed data. The observed SED is taken from Andrews et al. (2013, see also references therein). In order to evaluate the SEDs, we extrapolate the disk model down to 0.01 au and remove the dust with temperature higher than 1400 K, which mimics the sublimation of silicate dust. This modification is necessary because the dust responsible for infrared emission could be located within 0.5 au, which is the inner boundary used for the calculations in the comparison at ALMA wavelengths.

We find that the active disk models have higher luminosity at infrared wavelengths (~1–20 µm) than the passive disk models (see also, e.g., D’Alessio et al. 1998; Dullemond et al. 2007). The passive disk models tend to underestimate the fluxes observed at infrared wavelengths. For the active disk models, the large grain models (amax = 1 mm and 1 cm) still underestimate the infrared fluxes, while the model with amax = 300 µm overestimates them. Although neither of these models fully explains the observed SED at infrared wavelengths, the active disk models are more resemble to the observations compared to the passive disk models.

However, it is important to note that the infrared SED is highly influenced by the intricate structure of the innermost region of the disk, specifically in the vicinity of the silicate sublimation radius (see Dullemond & Monnier 2010 and Kraus 2015 for review), which is beyond the scope of our study. For instance, the emission in the near-infrared range (~2 µm) is expected to be predominantly attributed to the scattering of stellar light at the inner rim of the disk (e.g., Monnier & Millan-Gabet 2002), rather than the thermal emission from the region we focus on. Additionally, the presence of a dust halo surrounding the inner disk, potentially induced by the inner disk wind, is anticipated to enhance the near-infrared flux (e.g., Vinković & Jurkić 2007). Therefore, detailed modeling of the innermost region of the disk is necessary to obtain accurate fluxes at near-infrared wavelengths. While significant uncertainties remain in the near-infrared range, the observed high fluxes at mid-infrared wavelengths may suggest a higher likelihood of active heating within the CW Tau disk.

thumbnail Fig. 17

Comparison between our model spectral energy distributions and observed SED. The observed values are from Andrews et al. (2013) and references therein.

5 Summary and conclusions

We investigate the impact of accretion heating on the brightness temperatures of the inner region of the CW Tau disk. The key findings are as follows:

  • If amax ≲ 100 µm, the model brightness temperatures are too high to explain the observations regardless of the efficiency of accretion heating;

  • If the disk is passively heated, the maximum dust size needs to be either ~150 µm or more than a few cm;

  • If the disk is actively heated, small grain models significantly overpredict the brightness temperatures and, hence, the maximum dust size needs to be either ~300 µm or more than a few cm;

  • The midplane temperature would be ~ 1.5–3 times higher than the observed brightness temperatures because of the combined effect of scattering and accretion heating;

  • If dust settling occurs in the active disk, the ALMA observations trace deeper disk layers compared to the disk with no-settling. Therefore, the dust settling effectively increases the temperature of the dust responsible for the millimeter emission from the active disk;

  • If the turbulence strength parameter for vertical dust mixing αt is 10−4, the active disk model with amax = 300 µm over-predicts the brightness temperatures, indicating that αt > 10−4;

  • The estimated effective accretion efficiency aacc falls into a reasonable range of 10−4−10−2, depending on the dust size. If amax = 300 µm, the value of αacc is expected to be ~10−3, indicating that αt is not much smaller than αacc;

  • The efficiency of accretion heating needs to be reduced if dust is porous (p = 0.9) because the accretion heating is too efficient to explain the observations regardless of the dust size.

Future observations using longer wavelengths, such as ALMA Bands 1–3 and VLA, will play a crucial role in distinguishing between the active and passive disk models. The results of our work highlight the importance of multi-wavelength observations in improving our understanding of the physical properties of the inner regions of protoplanetary disks.

Acknowledgements

We thank the anonymous referee for useful comments. We also thank Sean Andrews for providing the observed SED of CW Tau. T.U. acknowledges the support of the DFG-Grant “Inside: inner regions of protoplan-etary disks: simulations and observations” (FL 909/5-1). S.O. is supported by JSPS KAKENHI Grant Numbers JP18H05438, JP20H00182, and JP20H01948. M.F. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 757957).

Appendix A Midplane temperature of the passive disks

In this section, we examine the accuracy of our temperature of the passive disk models. In our temperature model (Equation 2), we do not consider the effect of scattering of the stellar irradiation and adopt constant value for the incident angle of the stellar irradiation ψ (0.02). To see the validity of our simplified model, we perform thermal Monte Carlo radiative transfer simulations with RADMC3D (Dullemond et al. 2012), while also taking the anisotropic scattering into account.

Figure A.1 compares the midplane temperature profiles obtained from the Monte Carlo radiative transfer simulations and analytical model (Equation 2). Although our analytical model slightly overestimates the midplane temperature, the difference from the radiative transfer model is ≲10%, which is comparable to the uncertainty of the ALMA flux. Therefore, we think that the analytical model has sufficient accuracy to estimate the brightness temperatures at the ALMA wavelengths.

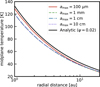thumbnail Fig. A.1

Comparison of the midplane temperature profiles of the passive disks obtained from the Monte Carlo radiative transfer simulations and analytical prescription (Equation 2).

Appendix B Effect of the dust composition

In this section, we present the modeling results using the DIANA dust, which is an alternative to the DSHARP dust used previously. The DIANA dust consists of pyroxene (Mg0.7Fe0.3SiO3; Dorschner et al. 1995) and amorphous carbon (Zubko et al. 1996), with a mass ratio of 0.87 for pyroxene and 0.13 for carbon, and has a porosity of 0.25 (Woitke et al. 2016). While the DSHARP dust contains carbonaceous material in the form of organics, the DIANA dust consists of amorphous carbon as the carbonaceous material, which efficiently absorbs incident irradiation.

Figure B.1 shows the effective albedo of the DIANA dust. The DIANA dust has lower effective albedo than the DSHARP dust because of the high absorbing efficiency of carbon. Specifically, the effective albedo of the DIANA dust remains below 0.8 at the wavelengths of interest, while that of the DSHARP dust is as high as ~ 0.9 (Figure 2).

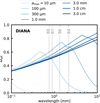thumbnail Fig. B.1

Effective albedo of the DIANA dust model.

Figure B.2 shows the normalized brightness temperature at the center of the passive disk model using the DIANA dust model. Due to its smaller effective albedo, the brightness temperatures consistently exceed those of the DSHARP model (Figure 4). Particularly at ALMA Band 8, the brightness temperature of the DIANA dust model is higher than the observed value, regardless of the calue of amax. The central brightness temperature of the active disk model using the DIANA dust is shown in Figure B.3. When taking into account the effect of accretion heating, the brightness temperature is higher compared to the passive disk model, thereby making the DIANA dust model less consistent with the observations.

thumbnail Fig. B.2

Same as Figure 4, but for the DIANA dust model.
thumbnail Fig. B.3

Same as Figure 8, but for the DIANA dust model.

In general, the DIANA dust models predict higher brightness temperature than the DSHARP dust models. Consequently, the DSHARP dust model appears to be more in line with the observed data.

Appendix C Dependence of the surface density

In this appendix, we discuss the effect of the dust surface density on the brightness temperature. Figure C.1 shows the brightness temperature at the center of the synthetic images of different values of τ10,B4. The brightness temperature at longer wavelength is more sensitive to the dust surface density (i.e., τ10,B4) because it traces the region closer to the midplane where the accretion heating dominates the irradiation heating. In addition to that, smaller grain model is more sensitive to τ10,B4 because of efficient accretion heating (see Figure 12).

If τ10,B4 = 1, the brightness temperature at ALMA Band 4 is always lower than the observed value when amax ≳ 300 µm. This suggests that τ10,B4 needs to be sufficiently larger than unity. The brightness temperature at Band 4 increases as τ10,B4 increases. If τ10,B4 = 3, the brightness temperature at Band 4 is consistent with the observation when amax = 300 µm, as shown in the main text. If τ10,B4 > 3, the brightness temperature at Band 4 can be consistent with the observation even when amax > 300 µm. However, in this regime, the brightness temperature at ALMA Band 8 is higher than the observed value.

Appendix D Radial brightness temperature profile of different models

Figure D.1 shows the brightness temperature profile of models with dust settling. The midplane temperature is independent on the presence of dust settling (see Figure 7 and D.1) as the vertical optical depth at the midplane is identical. The dust differential settling effectively increase the temperature of dust observed with ALMA as explained in Sect. 3.3.1. This can be confirmed by comparing the brightness temperature shown in Figure 7 and D.1 in the limit of no scattering; the brightness temperature in the no-scattering limit is higher for the model with settling. When scattering is taken into account, the brightness temperature of the settling model is not simply higher than the model without settling because the magnitude of scattering-induced intensity reduction is affected by the dust settling.

In Figure D.2, we show the brightness temperature of models with pd = 2.5 instead of 3.5. The smaller pd corresponds to the more top-heavy dust size distribution in which larger grains is more dominant in the opacity. Because of the top-heavy dust size distribution, the dust temperature is lower than that of the fiducial active disk. This can be confirmed by comparing the brightness temperature in Figure 7 and D.2 in the limit of no-scattering (dashed lines); the brightness temperature in the no-scattering limit is lower for the model with pd = 2.5. When scattering is taken into account, the brightness temperature of the top-heavy model is lower than that of the fiducial active disk in the regime of amax ≲ 1 mm, because large grains have higher scattering albedo at ALMA wavelengths. In contrast, in the regime of amax ≳ 1 mm, the brightness temperature of the top-heavy model is higher than the fiducial active disk model because of low scattering albedo.

Figure D.3 shows the brightness temperature profile of models with porous grains (p = 0.9; filling factor of 0.1). The dust temperature of the active disk with porous dust is higher than that of compact dust as explained in Section 3.3.3. This can be confirmed by comparing the brightness temperature in Figure 7 and D.3 in the limit of no-scattering (dashed lines); The brightness temperature in the no-scattering limit is higher for the model with porous dust. Furthermore, the effective scattering albedo of the porous dust is slightly lower than that of compact dust, which result in inefficient scattering-induced intensity reduction. Due to these reasons, the model brightness temperature is significantly higher than the observations.

thumbnail Fig. C.1

Same as Figure 8, but for different values of τ10,B4·
thumbnail Fig. D.1

Same as Figure 7, but with dust settling.
thumbnail Fig. D.2

Same as Figure 7, but with pd = 2.5.
thumbnail Fig. D.3

Same as Figure 7, but with p = 0.9.

References

  1. Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [Google Scholar]
  2. Bacciotti, F., Girart, J. M., Padovani, M., et al. 2018, ApJ, 865, L12 [Google Scholar]
  3. Béthune, W., & Latter, H. 2020, MNRAS, 494, 6103 [Google Scholar]
  4. Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A & A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2011, A & A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Birnstiel, T., Dullemond, C. P., Zhu, Z., et al. 2018, ApJ, 869, L45 [CrossRef] [Google Scholar]
  7. Bitsch, B. 2019, A & A, 630, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bitsch, B., Morbidelli, A., Lega, E., & Crida, A. 2014, A & A, 564, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Carrasco-González, C., Sierra, A., Flock, M., et al. 2019, ApJ, 883, 71 [Google Scholar]
  10. D’Alessio, P., Cantö, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [Google Scholar]
  11. Dominik, C., Min, M., & Tazaki, R. 2021, OpTool: Command-line driven tool for creating complex dust opacities, Astrophysics Source Code Library [record ascl:2184.818] [Google Scholar]
  12. Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A & A, 300, 503 [NASA ADS] [Google Scholar]
  13. Draine, B. T. 2003, ARA & A, 41, 241 [Google Scholar]
  14. Drążkowska, J., & Alibert, Y. 2017, A & A, 608, A92 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [Google Scholar]
  16. Dullemond, C. P., & Monnier, J. D. 2010, ARA & A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dullemond, C. P., Hollenbach, D., Kamp, I., & D’Alessio, P. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 555 [Google Scholar]
  19. Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
  20. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A & A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gangi, M., Antoniucci, S., Biazzo, K., et al. 2022, A & A, 667, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Guidi, G., Isella, A., Testi, L., et al. 2022, A & A, 664, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
  24. Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
  25. Henning, T., & Stognienko, R. 1996, A & A, 311, 291 [NASA ADS] [Google Scholar]
  26. Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [Google Scholar]
  27. Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [Google Scholar]
  28. Hirose, S., & Turner, N. J. 2011, ApJ, 732, L30 [NASA ADS] [CrossRef] [Google Scholar]
  29. Huang, J., Andrews, S. M., Dullemond, C. P., et al. 2018, ApJ, 869, L42 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kataoka, A., Okuzumi, S., Tanaka, H., & Nomura, H. 2014, A & A, 568, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Kataoka, A., Muto, T., Momose, M., et al. 2015, ApJ, 809, 78 [Google Scholar]
  33. Kirchschlager, F., Bertrang, G. H. M., & Flock, M. 2019, MNRAS, 488, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kley, W., & Nelson, R. P. 2012, ARA & A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kondo, K., Okuzumi, S., & Mori, S. 2023, ApJ, 949, 119 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kraus, S. 2015, Ap & SS, 357, 97 [NASA ADS] [CrossRef] [Google Scholar]
  37. Law, C. J., Teague, R., Loomis, R. A., et al. 2021, ApJS, 257, 4 [NASA ADS] [CrossRef] [Google Scholar]
  38. Law, C. J., Teague, R., Öberg, K. I., et al. 2023, ApJ, 948, 60 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lin, Z.-Y. D., Li, Z.-Y., Yang, H., et al. 2023, MNRAS, 520, 1210 [NASA ADS] [CrossRef] [Google Scholar]
  40. Liu, H. B. 2019, ApJ, 877, L22 [NASA ADS] [CrossRef] [Google Scholar]
  41. Macías, E., Guerra-Alvarado, O., Carrasco-González, C., et al. 2021, A & A, 648, A33 [CrossRef] [EDP Sciences] [Google Scholar]
  42. Madhusudhan, N., Amin, M. A., & Kennedy, G. M. 2014, ApJ, 794, L12 [Google Scholar]
  43. Manara, C. F., Testi, L., Herczeg, G. J., et al. 2017, A & A, 604, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Manara, C. F., Ansdell, M., Rosotti, G. P., et al. 2022, arXiv e-prints [arXiv:2203.09930] [Google Scholar]
  45. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [Google Scholar]
  46. McClure, M. K. 2019, A & A, 632, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Monnier, J. D., & Millan-Gabet, R. 2002, ApJ, 579, 694 [Google Scholar]
  48. Mori, S., Bai, X.-N., & Okuzumi, S. 2019, ApJ, 872, 98 [NASA ADS] [CrossRef] [Google Scholar]
  49. Nakamoto, T., & Nakagawa, Y. 1994, ApJ, 421, 640 [Google Scholar]
  50. Notsu, S., Ohno, K., Ueda, T., et al. 2022, ApJ, 936, 188 [NASA ADS] [CrossRef] [Google Scholar]
  51. Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [Google Scholar]
  52. Ohno, K., & Ueda, T. 2021, A & A, 651, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
  54. Okuzumi, S., Momose, M., Sirono, S.-i., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [Google Scholar]
  55. Okuzumi, S., Ueda, T., & Turner, N. J. 2022, PASJ, 74, 828 [NASA ADS] [CrossRef] [Google Scholar]
  56. Okuzumi, S., Momose, M., & Kataoka, A. 2023, arXiv e-prints [arXiv:2384.14192] [Google Scholar]
  57. Robinson, C. E., Espaillat, C. C., & Rodriguez, J. E. 2022, ApJ, 935, 54 [NASA ADS] [CrossRef] [Google Scholar]
  58. Savvidou, S., & Bitsch, B. 2021, A & A, 650, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Schneider, A. D., & Bitsch, B. 2021, A & A, 654, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Sierra, A., & Lizano, S. 2020, ApJ, 892, 136 [Google Scholar]
  61. Sierra, A., Pérez, L. M., Zhang, K., et al. 2021, ApJS, 257, 14 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tazaki, R., Tanaka, H., Kataoka, A., Okuzumi, S., & Muto, T. 2019, ApJ, 885, 52 [Google Scholar]
  63. Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
  64. Ueda, T., Kataoka, A., & Tsukagoshi, T. 2020, ApJ, 893, 125 [Google Scholar]
  65. Ueda, T., Kataoka, A., Zhang, S., et al. 2021a, ApJ, 913, 117 [Google Scholar]
  66. Ueda, T., Ogihara, M., Kokubo, E., & Okuzumi, S. 2021b, ApJ, 921, L5 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ueda, T., Kataoka, A., & Tsukagoshi, T. 2022, ApJ, 930, 56 [NASA ADS] [CrossRef] [Google Scholar]
  68. Vinković, D., & Jurkić, T. 2007, ApJ, 658, 462 [CrossRef] [Google Scholar]
  69. Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res. (Atmos.), 113, D14220 [Google Scholar]
  70. Woitke, P., Min, M., Pinte, C., et al. 2016, A & A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
  72. Zhang, S., Zhu, Z., Ueda, T., et al. 2023, ApJ, submitted [arXiv:2386.88158] [Google Scholar]
  73. Zhu, Z., Zhang, S., Jiang, Y.-F., et al. 2019, ApJ, 877, L18 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [Google Scholar]

All Tables

Table 1

Summary of our models.

In the text

All Figures

thumbnail Fig. 1

Brightness temperature profile observed at ALMA Bands 4, 6, 7, and 8 obtained by Ueda et al. (2022). The transparent region denotes the uncertainty arising from both flux calibration and thermal noise.
In the text
thumbnail Fig. 2

Effective extinction opacity (top), effective albedo (middle) and Rosseland-mean opacity (bottom) of compact (p = 0; left) and porous (p = 0.9; right) dust with different amax. The power-law index of the dust size distribution is set to pd = 3.5. The vertical gray dotted lines denote the wavelength of ALMA Bands 4, 6, 7, and 8.
In the text
thumbnail Fig. 3

Brightness temperature profile of the passive disk model (p = 0, τ10,B4 = 3 and pd = 3.5) with (top) and without (bottom) scattering with different amax. The transparent shaded region shows the observed brightness temperature. The model brightness temperature is calculated after the intensity is convolved with the beam size of 0″.1 which corresponds to the physical distance of 13.2 au. The black dotted line denotes the midplane temperature profile convolved with a Gaussian with a full width at half maximum (FWHM) of 13.2 au.
In the text
thumbnail Fig. 4

Brightness temperature at the center of model images normalized by the observed brightness temperature. The gray shaded region denotes the region where the model explains the observations with an accuracy of 10%, which is the typical ALMA calibration uncertainty.
In the text
thumbnail Fig. 5

2D temperature structure (top), dust temperature at the ALMA surfaces (middle) and synthetic brightness temperature profiles (bottom). The maximum dust size is 10 µm. The left panels show the passive disk model where the disk is heated only by the stellar irradiation, whereas the right panels show the active disk model where the disk is heated by both stellar irradiation and disk accretion. The light green lines in the top panels denote the height where the vertical extinction optical depth reaches unity (ALMA surfaces) at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). The dust temperatures shown in the middle panels are not beam-convolded, while the brightness temperatures shown in the bottom panels are taken from the synthetic images convolved with a Gaussian with a FWHM of 13.2 au. The transparent regions denote the observed brightness temperatures.
In the text
thumbnail Fig. 6

2D temperature structure and dust temperature at ALMA surfaces for different values of amax. Top: 2D temperature structure of the fiducial active disk. The light green lines denote the height where the vertical extinction optical depth reaches unity at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). Bottom: Dust temperature at the height where the vertical extinction optical depth at the ALMA wavelengths reaches unity. The radial profile are not beam-convolved. The dust settling is not taken into account. The dust is assumed to be compact with a size distribution of pd = 3.5. The dust surface density is set so that τ10,B4 = 3.
In the text
thumbnail Fig. 7

Same as Fig. 3, but for the fiducial active disk.
In the text
thumbnail Fig. 8

Same as Fig. 4, but for the fiducial active disk.
In the text
thumbnail Fig. 9

2D temperature structure and dust temperature at ALMA surfaces for different disk models. Top: 2D temperature structure of the fiducial active disk model (left), Settling model (at = 10−4, second left), Top-heavy model (second right), and Porous model (right). The light green lines denote the height where the vertical extinction optical depth reaches unity at ALMA Bands 4 (solid), 6 (dashed), 7 (dash-dotted), and 8 (dotted). The maximum dust size amax is 1 mm in the all models. Bottom: Dust temperature at the height where the vertical extinction optical depth at the ALMA wavelengths reaches unity. The radial profile is not convolved.
In the text
thumbnail Fig. 10

Same as Fig. 4, but for the settling model with αt= 10−4.
In the text
thumbnail Fig. 11

Same as Fig. 4, but for the top-heavy dust model.
In the text
thumbnail Fig. 12

Ratio between the Rosseland-mean opacity (at 100 K) and the extinction opacity at ALMA Band 4. The red solid and blue dashed lines denote the compact and porous dust, respectively.
In the text
thumbnail Fig. 13

Same as Fig. 4, but for the porous dust model.
In the text
thumbnail Fig. 14

Gas surface density (hundred times of the dust; top) and effective turbulence strength for the disk gas accretion (bottom) estimated from our fiducial active disk models. The gray dashed line denotes the gas surface density of the minimum mass solar nebula (MMSN; Hayashi 1981). The dotted lines denote the criteria for the disk to be gravitation-ally unstable (Q = 1).
In the text
thumbnail Fig. 15

Brightness temperature profile at λ = 3.1, 4.1, and 7.0 mm predicted by our active disk models (solid lines) and passive disk models (dotted lines). The angular resolution is assumed to be 0″.05. The scattering-induced intensity reduction is included.
In the text
thumbnail Fig. 16

Brightness temperature profile at λ = 0.75, 0.89 and 1.34 mm predicted by our active disk models (solid lines) and passive disk models (dotted lines). The angular resolution is assumed to be 0.02. The scattering-induced intensity reduction is included.
In the text
thumbnail Fig. 17

Comparison between our model spectral energy distributions and observed SED. The observed values are from Andrews et al. (2013) and references therein.
In the text
thumbnail Fig. A.1

Comparison of the midplane temperature profiles of the passive disks obtained from the Monte Carlo radiative transfer simulations and analytical prescription (Equation 2).
In the text
thumbnail Fig. B.1

Effective albedo of the DIANA dust model.
In the text
thumbnail Fig. B.2

Same as Figure 4, but for the DIANA dust model.
In the text
thumbnail Fig. B.3

Same as Figure 8, but for the DIANA dust model.
In the text
thumbnail Fig. C.1

Same as Figure 8, but for different values of τ10,B4·
In the text
thumbnail Fig. D.1

Same as Figure 7, but with dust settling.
In the text
thumbnail Fig. D.2

Same as Figure 7, but with pd = 2.5.
In the text
thumbnail Fig. D.3

Same as Figure 7, but with p = 0.9.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.