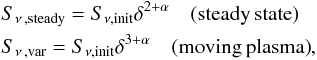| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527139 | |
| Published online | 24 March 2016 | |
Spectral evolution of flaring blazars from numerical simulations
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: cfromm@mpifr.de
2 Institut für Theoretische Physik, Goethe Universität, Max-von-Laue-Str. 1, 60438 Frankfurt, Germany
3 Departament d’Astronomia i Astrofísica, Universitat de València, Dr. Moliner 50, 46100 Burjassot, València, Spain
4 Observatori Astronòmic, Parc Científic, Universitat de València, C/ Catedràtic José Beltrán 2, 46980 Paterna, València, Spain
Received: 7 August 2015
Accepted: 18 January 2016
Context. High-resolution Very Long Baseline Interferometry (VLBI) observations of active galactic nuclei revealed traveling and stationary or quasi-stationary radio components in several blazar jets. The traveling radio components are, in general, interpreted as shock waves generated by pressure perturbations injected at the jet nozzle. The stationary features can be interpreted as recollimation shocks in nonpressure matched jets if they show a quasi-symmetric bump in the spectral index distribution. In some jets there may be interactions between the two kinds of shocks. These shock-shock interactions are observable with VLBI techniques and their signature should also be imprinted on the single-dish light curves.
Aims. In this paper, we investigate the spectral evolution produced by the interaction between a recollimation shock with traveling shock waves to address the question of whether these interactions contribute to the observed flares and what their signature in both single-dish and VLBI observations looks like.
Methods. We performed relativistic hydrodynamic simulations of overpressured and pressure-matched jets. To simulate the shock interaction we injected a perturbation at the jet nozzle once a steady state was reached. We computed the nonthermal emission, including adiabatic and synchotron losses, resulting from the simulation.
Results. We show that the injection of perturbations in a jet can produce a bump in emission at GHz frequencies previous to the main flare, which is produced when the perturbation fills the jet in the observer’s frame. The detailed analysis of our simulations and the nonthermal emission calculations show that interaction between a recollimation shock and traveling shock produce a typical and clear signature in both the single-dish light curves and in the VLBI observations: the flaring peaks are higher and delayed with respect to the evolution of a perturbation through a conical jet. This fact can allow us to detect such interactions for stationary components lying outside of the region in which the losses are dominated by inverse Compton scattering.
Key words: hydrodynamics / radiation mechanisms: non-thermal / galaxies: active / galaxies: jets
© ESO, 2016
1. Introduction
The kinematic analysis of high-resolution VLBI images of active galactic nucleus (AGN) jets within long-term monitoring programs such as the MOJAVE1 program (Lister et al. 2009) at 15 GHz, the Boston University Blazar Monitoring2 program (Jorstad et al. 2005) at 43 GHz or the TANAMI3 program at 8.4 GHz and 23 GHz (Ojha et al. 2010) reveal a number of components that are stationary, i.e., constant separation from the core and nearly constant flux density. These features are typically interpreted as recollimation shocks in an overpressured (OP) jet and cannot be explained by traveling shock waves within a pressure matched (PM) and, therefore, conical jet (see, e.g., Daly & Marscher 1988).
The signature of standing features could also be imprinted in the single-dish light curves. The spectral analysis of single-dish observations in the cm-mm and submillimetre regime for the blazar CTA 102 during a major outburst leads to double hump structure in the turnover frequency – turnover flux density plane (Fromm et al. 2011) and, at the same time, the kinematic analysis of this source from VLBI observations revealed several standing features, one of them 18 pc (deprojected) from the core (Fromm et al. 2013a). The spectral analysis applied to the VLBI observations exhibit an increase in the particle density and magnetic field strength at the location of the standing features (Fromm et al. 2013b). A conclusion derived from those works was that the double hump in the light curve was caused by the interaction between the traveling perturbation and a standing shock. The interaction between traveling shock waves and recollimation shocks could also be the onset of the γ-ray flares. Agudo et al. (2010) and Schinzel et al. (2012, see also references therein) combined multifrequency observations and 43 GHz VLBI observations and found a correlation between the crossing of a traveling component through a stationary feature and the onset of the high energy flare.
The hydrodynamics of nonpressure matched relativistic jets was studied in an analytical way by Daly & Marscher (1988). More recently, Nalewajko (2011) studied the formation of recollimation shocks for the case of an ultrarelativistic equation of state and a constant ambient medium density. Using the characteristics method, these authors provide several analytical solutions on the location of the pressure minimum and on the location of the first recollimation shock. Falle (1991) took into account a decreasing pressure in the ambient medium density and numerically calculated the evolution of the jet. A more detailed treatment on the formation of recollimation shocks with both analytical approximations and numerical simulations can be found in Komissarov & Falle (1997). The simulations of Falle (1991) and Komissarov & Falle (1997) studied the formation of recollimation shocks in the context of the propagation of relativistic jets. A different approach was followed by Gómez et al. (1997), who studied the propagation of relativistic shock waves in PM and OP steady-state jets and computed synthetic radio maps assuming adiabatic losses. Mimica et al. (2009) recomputed the emission of the simulations performed by Gómez et al. (1997) and included the influence of temporal and spatial radiative losses on the distribution of the relativistic particles. So far, most of the studies focused on the propagation of the relativistic shock waves, which could be connected to the observed superluminal components observed in several AGN jets. In this paper we concentrate on the interaction between traveling shock waves and recollimation shocks and the resulting spectral evolution. With this aim, we have performed relativistic hydrodynamical numerical simulations. The current paradigm for jet launching (Blandford & Znajek 1977) assumes that the jet is strongly magnetized close to the black hole (see e.g., Tchekhovskoy et al. 2009; Komissarov et al. 2009, and references therein). The magnetization of the flow decreases further out, but it is still possible that the flow is magnetized far away from the acceleration zone, especially in the gamma-ray burst (GRB) case (Thompson 1994; Spruit et al. 2001; Lyutikov & Blandford 2003; Giannios & Spruit 2006; Granot et al. 2011; Lyutikov 2011; Levinson 2011; Granot 2012; Komissarov 2012). However, since CTA102 is a blazar, Mimica & Aloy (2012) and Rueda-Becerril et al. (2014) show that to be compatible with the current blazar observations, the blazar jets are at most moderately magnetized at blazar distances (σ ≤ 0.01). For these values, Mimica & Aloy (2012) show that the dynamics and emission depend only very weakly on sigma (Figs. 1 and 7 in Mimica & Aloy 2012). Therefore, the assumption about the nonmagnetized jet dynamics with ϵB ~ 0.1 at those distances is justified. Further out of that zone, at distances of interest to us, the magnetization should be even smaller.
The organization of this work is the following: in Sect. 2 we introduce our numerical setup. The results of the simulations and the nonthermal emission calculations are presented in Sect. 3.1 and in Sect. 3.2. The discussion of our results is provided in Sect. 4. Throughout the paper, we use an ideal equation of state 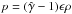 , with pressure, p, adiabatic index,
, with pressure, p, adiabatic index, 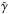 , specific internal energy, ϵ, and density, ρ.
, specific internal energy, ϵ, and density, ρ.
2. Relativistic hydrodynamic simulations
We performed several 2D axisymmetric simulations of supersonic relativistic hydrodynamical jets using the finite-difference code Ratpenat (for more details see Perucho et al. 2010, and references therein). The simulations were performed on up to 64 processors at the local cluster at the Max Planck Institute for Radio Astronomy (MPIfR) and at Tirant, the Valencian Node of the Spanish Supercomputing Network (RES).
2.1. Simulation setup
The numerical grid includes 320 cells in the radial direction and 9600 cells in the axial direction. Using a numerical resolution of 32 cells per jet radius (Rj), the grid covers 10 Rj × 300 Rj. We define the z-axis in the direction of the jet propagation and the x-axis as the radial axis in cylindrical coordinates. The boundary conditions are a reflection at the jet axis, injection at the jet nozzle and outflow conditions elsewhere. The basic setup of our simulation for an OP jet is sketched in Fig. 1. The initial parameters at the jet nozzle are the velocity of the jet, vb, the bulk Lorentz factor, Γ, the classical Mach number of the jet, M, the density of the jet, ρb, the adiabatic index, γ, and the initial pressure mismatch between the jet and the ambient medium, dk = pb/pa. The pressure, pb at the jet nozzle is computed from the Mach number using an ideal-gas equation of state. Since we are mainly interested in the first traveling shock–recollimation shock interaction we used a homogeneous ambient medium (see, e.g., Fromm 2015). We additionally simulate a PM jet, dk = 1, in a decreasing pressure ambient, which leads to the formation of a conical jet without recollimation shocks, to study shock-jet interaction from a single traveling shock. We model the decrease in the ambient medium pressure with a pressure profile presented in Gómez et al. (1997)![\begin{equation} p_{\rm a}(z)=\frac{p_b}{d_k}\left[1+\left(\frac{z}{z_c}\right)^n\right]^{\frac{m}{n}}, \label{pamb} \end{equation}](/articles/aa/full_html/2016/04/aa27139-15/aa27139-15-eq23.png) (1)where zc can be considered as the spatial scale and the exponents n and m control the steepening of the ambient pressure. The initial conditions, given in code units (speed of light c = 1, jet radius Rj, and ambient medium density, ρa = 1) for both simulations are listed in Table 1.
(1)where zc can be considered as the spatial scale and the exponents n and m control the steepening of the ambient pressure. The initial conditions, given in code units (speed of light c = 1, jet radius Rj, and ambient medium density, ρa = 1) for both simulations are listed in Table 1.
 |
Fig. 1 Sketch of an OP jet with characteristic parameters and regions (adopted from Daly & Marscher 1988). |
Initial parameters for the simulations in code units.
Once the steady state is reached (after approximately five longitudinal grid crossing times), we injected a perturbation at the jet nozzle. In order to develop a shock wave we increased the pressure and density of the perturbation by a factor of 4 (compared to the steady state pressure and density), while keeping the same velocity as the jet flow. The parameters for the perturbation, in code units, are presented in Table 3.
Perturbation parameters for the simulations in code units.
3. Results
3.1. Relativistic hydrodynamic (RHD)
Figure 2 shows the 2D distribution of rest mass density (top) and pressure (bottom) in case of the OP jet (dk = 3) for the steady state. Owing to the pressure mismatch at the jet nozzle, two shock waves form at the discontinuity between the jet and the ambient. One of them propagates outward in the radial direction and the other propagates toward the axis. Between them, a rarefaction region forms in which the flow expands radially until pressure equilibrium between the jet and the ambient medium is established. This state is first reached at the jet boundary and leads to the formation of an inward traveling sound wave. As a result of the finite speed of the waves, the inner layers of the jet continues to expand while the outer layers are already being collimated. This expansion of each inner layer stops as soon as the waves cross it. The recollimation shock, related to the shock wave that propagates toward the axis, occurs at different locations for different values of the radial coordinate of the stream line: the expansion and recollimation of the flow is clearly visible in Fig. 2. The recollimation shock reaches the axis at z = 110 Rj. At this position there is a local maximum in pressure and density and the flow emerging from this region expands again as a result of increased pressure. In other words, the recollimation shock can be considered as a new “jet nozzle” and the process begins anew. In our case the second recollimation shock is formed at z = 270 Rj. A different scenario is obtained for the PM jet (dk = 1). The distribution of the rest mass density and the pressure is smooth along the jet (see Fig. 3) as the jet expands, adapting to the ambient pressure (compare Figs. 3 to 2).
 |
Fig. 2 Steady-state results for the simulation of the OP jet. Top panel: 2D distribution of the logarithm of the rest mass density in units of ρa. Bottom panel: logarithm of the pressure in units of ρac2. |
 |
Fig. 3 Steady-state results for the simulation of a PM jet. Top panel: 2D distribution of the logarithm of the rest mass density in units of ρa. Bottom panel: logarithm of the pressure in units of ρac2. |
Once the perturbation is injected, a shock wave (forward) and a rarefaction wave (reverse) are generated (see, e.g., Martí & Müller 1999). The jet material swept up by the shock wave is compressed (pressure and density increase), while the crossing of the rarefaction wave induces a decrease in both quantities. As an example of the propagation of a perturbation, Fig. 4 (OP jet) and Fig. 5 (PM jet) show the variation in pressure at three selected times. The entire evolution of the axial density during the propagation of the shock wave is presented in Figs. 6 and 7. The variation in the pressure and the rest mass density during the propagation of the shock during the first 50 Rj is similar in the OP and PM jet until 50 Rj. The opening of the jet leads to an expansion of the shock wave and the compression of the gas produced by the shock falls with the distance. While the PM jet continues expanding (adapting to the decreasing ambient medium pressure), the OP jet starts collimating and forms a strong recollimation shock. The differences in the properties of the underlying jet change the evolution of the perturbation significantly. The compression induced by shock wave continues to decrease in the PM jet (see Fig. 7). In contrast to this, in the OP jet the increase in the compression of the pressure and density during and after the interaction between the shock wave and the recollimation shock is seen at z ≈ 120 Rj (see Fig. 6). In addition to the differences in the compression of the underlying flow, the trailing features (secondary perturbations generated in the wake of the main pertubation) are stronger and broader in the OP jet than in the PM jet (best seen at t ≈ 150 Rj/c in Figs. 6 and 7), and appear to be associated with the interaction between the perturbation and the standing shock in the case of the OP jet. This is the physical setup and in the next section we proceed to compute the nonthermal emission from the simulated jets.
 |
Fig. 4 Snapshots for the propagation of a perturbation in an OP jet. The panels show the 2D distribution of the logarithm of the pressure in units of ρac2. |
 |
Fig. 5 Snapshots for the propagation of a perturbation in a PM jet. The panels show the 2D distribution of the logarithm of the pressure in units of ρac2. |
 |
Fig. 6 Time-space plot for the variation of the axial density for the OP jet. |
 |
Fig. 7 Time-space plot for the variation of the axial density for the PM jet. |
3.2. Emission
3.2.1. SPEV setup
We used the code SPEV (Mimica et al. 2009) to compute the radio emission. Within SPEV a representative population of Lagarangian particles are injected at the jet nozzle and evolved in space and time according to the conditions of the underlying relativistic outflow. The radiative losses and adiabatic effects of the emitting nonthermal electrons (NTEs) are taken into account during the computation of their time- and frequency-dependent synchrotron emission. This code then performs the radiative transfer taking special relativistic effects and time delays into account. The radiation is collected on a virtual detector consisting of a number of pixels.
Regarding the possible effect of the implicit assumption in our simulations of a purely hydrodynamical flow, the absence of a dynamically relevant magnetic field could have an important effect in the emission calculations. In particular, it has been shown by Sironi et al. (2015) that strongly magnetized flows are not very efficient in accelerating nonthermal electrons to high energies. However, we have argued at the introduction that the jets are probably only weakly magnetized at the scales that we study, and, in addition, we also try to take this effect into account, even if the effect is small in our case by assuming a finite maximum electron energy, which is inversely proportional to the square root of the magnetic field strength (see Eq. (2)) 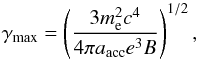 (2)where γmax is the upper cutoff of the injected nonthermal energy distribution, me and c are the electron mass and the speed of light, B is the comoving magnetic field, and aacc is the acceleration efficiency parameter (see Böttcher & Dermer 2010). We use aacc = 106 (Mimica & Aloy 2012, similar to). Furthermore, we assume that the emitting particles are accelerated in the inner parts of the jet (not simulated by us), and are injected though the nozzle at the inner boundary in our simulation.
(2)where γmax is the upper cutoff of the injected nonthermal energy distribution, me and c are the electron mass and the speed of light, B is the comoving magnetic field, and aacc is the acceleration efficiency parameter (see Böttcher & Dermer 2010). We use aacc = 106 (Mimica & Aloy 2012, similar to). Furthermore, we assume that the emitting particles are accelerated in the inner parts of the jet (not simulated by us), and are injected though the nozzle at the inner boundary in our simulation.
In this work, we use ≃3000 snapshots produced by Ratpenat as a dynamic background for the evolution of LPs. We averaged the hydrodynamical quantities in the direction transverse to the jet, but kept track of the jet radius at each point to make the calculations feasible. This allows us to reduce the amount of intermediate data we need to store; at each point along the jet it is only necessary to store one set of hydrodynamical quantities (density, pressure, and velocity). However, since the radius is recorded as well, we can reconstruct the jet geometry at any point and time (see Fig. 8).
 |
Fig. 8 Variation of the axial, ρaxial, and the cross section averaged rest mass density, ρmedian along the jet (red lines) and the variation of the jet radius along the jet (black line) for the OP jet. |
The data are used by SPEV to continuously inject 48 LP families at the jet nozzle (see Sect. 3.3 of Mimica et al. 2009, for a detailed explanation of this process). The LP families are distributed transversally along the jet nozzle and their trajectories follow the jet geometry (i.e., where the jet gets narrower the trajectories come closer together, and vice-versa). We assume that each LP represents a volume uniformly filled with NTEs, an isotropic NTE velocity distribution within each LP and only track the NTE energy distribution. With this in mind, we initially we assume a power-law distribution
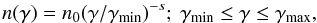 where n(γ) is the differential number of NTEs with Lorentz factor γ, n0 and s are the normalization and the power-law index, and γmin and γmax are the lower and upper cutoffs of the distribution. We assume that the total number density of injected NTEs is proportional to the fluid number density, where ζe is the ratio of nonthermal particles to thermal particles (see e.g., Böttcher & Dermer 2010; Mimica & Aloy 2012),
where n(γ) is the differential number of NTEs with Lorentz factor γ, n0 and s are the normalization and the power-law index, and γmin and γmax are the lower and upper cutoffs of the distribution. We assume that the total number density of injected NTEs is proportional to the fluid number density, where ζe is the ratio of nonthermal particles to thermal particles (see e.g., Böttcher & Dermer 2010; Mimica & Aloy 2012),
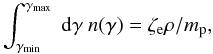 and that the total NTE energy density is proportional to the fluid internal energy density ε,
and that the total NTE energy density is proportional to the fluid internal energy density ε,
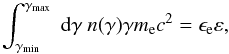 where ϵe is ratio between the energy stored the thermal particles and in the nonthermal particles. The upper cutoff of the spectral distribution is determined by the balance between synchrotron cooling and acceleration timescales (see e.g., Mimica et al. 2010; Mimica & Aloy 2012)
where ϵe is ratio between the energy stored the thermal particles and in the nonthermal particles. The upper cutoff of the spectral distribution is determined by the balance between synchrotron cooling and acceleration timescales (see e.g., Mimica et al. 2010; Mimica & Aloy 2012)
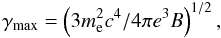 where B is the comoving magnetic field (see below). Combining the equations above and inserting for ε the equation of state (here ideal equation of state) leads to the following relation for the lower electron Lorentz factor, γmin:
where B is the comoving magnetic field (see below). Combining the equations above and inserting for ε the equation of state (here ideal equation of state) leads to the following relation for the lower electron Lorentz factor, γmin:
![$$ \gamma_\mathrm{min}=\left\{ \begin{array}{ll} \frac{p}{\rho} \frac{m_{\rm p}}{m_{\rm e}c^2}\frac{(s-2)}{(s-1)(\hat{\gamma}-1)}\frac{\epsilon_{\rm e}}{\zeta_{\rm e}} & \textrm{if }s>2\\ \left[\frac{p}{\rho} \frac{m_{\rm p}}{m_{\rm e}c^2}\frac{(2-s)}{(s-1)(\hat{\gamma}-1)}\frac{\epsilon_{\rm e}}{\zeta_{\rm e}} \gamma_\mathrm{max}^{s-2}\right]^{1/(s-1)} & \textrm{if }1<s<2\\ \frac{p}{\rho}\frac{\epsilon_{\rm e}}{\zeta_{\rm e}} \frac{m_{\rm p}}{m_{\rm e}c^2(\hat{\gamma}-1)}/\ln\left(\frac{\gamma_\mathrm{max}}{\gamma_\mathrm{min}}\right) & \textrm{if } s=2. \end{array}\right. $$](/articles/aa/full_html/2016/04/aa27139-15/aa27139-15-eq73.png) The preceding three equations, together with the assumption that s is constant, allow us to determine the four parameters needed to compute the injected NTE spectrum4. The magnetic field is assumed to be tangled, and its energy density is assumed to be proportional to the fluid internal energy density,
The preceding three equations, together with the assumption that s is constant, allow us to determine the four parameters needed to compute the injected NTE spectrum4. The magnetic field is assumed to be tangled, and its energy density is assumed to be proportional to the fluid internal energy density,
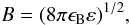 with ϵB as the equipartition ratio between the magnetic field energy density and the internal energy density of the thermal particles. The injected LPs gradually fill the jet volume so that at the end of the calculation the total number of LPs that emit is ≃4 × 108. The spatial resolution of the virtual detector is 1.5 × 1016 cm/pixel (≃0.005 pc/pixel). We computed the images for 200 temporal snapshots spanning four years of the observer time. The frequencies at which we computed the images are the standard VLBI bands and parameters used for the calculation of the emission are presented in Table 3.
with ϵB as the equipartition ratio between the magnetic field energy density and the internal energy density of the thermal particles. The injected LPs gradually fill the jet volume so that at the end of the calculation the total number of LPs that emit is ≃4 × 108. The spatial resolution of the virtual detector is 1.5 × 1016 cm/pixel (≃0.005 pc/pixel). We computed the images for 200 temporal snapshots spanning four years of the observer time. The frequencies at which we computed the images are the standard VLBI bands and parameters used for the calculation of the emission are presented in Table 3.
Parameters for the emission simulations.
3.2.2. Single-dish light curves and light curve parameters
Using the parameters and the technique presented above, we computed single-dish light curves by integrating the overall emission generated at a given frequency. For the detailed comparison with observations, we computed the single-dish emission for 12 frequencies that are commonly used in mm-cm single-dish observations. For the calculation of the emission, we used a typical blazar viewing angle of ϑ = 3° (it is also is the estimated viewing angle for the jet of CTA 102 Fromm et al. 2013a, see, e.g.). The small viewing angle leads to a Doppler boosting of the emission
with Doppler factor δ = 1/(Γ(1−βcosϑ)) and optically thin spectral index α = (1−s)/2. Besides the Doppler boosting of the emission, the small viewing angle leads to a piling up of the emission along the line of sight. The light rays encounter different fractions of absorption and emission depending on the physical properties of the crossed regions. In addition to the influence of the viewing angle, ϑ, we have to take cosmology into account for the proper calculations of the observed emission, which leads to an additional factor of 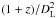 , where z is the redshift of the source and DL its luminosity distance. In Fig. 9 we present the single-dish light curves for the OP jet and in Fig. 10 we present the single-dish light curves for the PM jet model.
, where z is the redshift of the source and DL its luminosity distance. In Fig. 9 we present the single-dish light curves for the OP jet and in Fig. 10 we present the single-dish light curves for the PM jet model.
 |
Fig. 9 Single-dish light curves for several frequencies computed for the OP jet. The time is given in the observers frame. The first flux density variations are observed two years after the injection of the perturbation (second dashed vertical line from the left). The inlet shows the variation of the spectrum for six different times indicated by dash-dotted vertical lines. |
We list here our main results, which are discussed in detail in Sect. 4. The light curves corresponding to both the OP and PM jets show one major flare, located at t = 3.1 yr in the case of the OP jet and around t = 2.6 yr for the PM jet. Both flares are followed by a strong drop in the emission before a steady state is reached. This time span is around 1.5 yr for the OP jet and roughly 1 yr for the PM jet. In addition, the main flare of the OP jet is broader and shows a break in the decaying edge of the main flare (see Fig. 9).
The variation in the spectrum and the shift of the turnover point, i.e., the turnover frequency, νm, and the turnover flux density, Sm, for six different times is plotted in the inlays of Figs. 9 and 10. A more detailed evolution of the turnover over values is presented in Fig. 11.
 |
Fig. 11 Evolution of the turnover values for the OP and PM jet. Top panel: evolution of the perturbation in the turnover frequency – turnover flux density (νm−Sm)-plane. The diamond marker indicates the start position of the flare and the temporal evolution is indicated with arrows. Bottom left: temporal evolution of the turnover frequency, νm. Bottom right: temporal evolution of the turnover flux density, Sm. |
 |
Fig. 12 Single-dish light curve parameters for the PM and OP jet. The panels show the flare amplitude, ΔS, (top), the flare timescale, Δtrise, (middle) and the cross-band delays, τ, with respect to the peak of 1 THz light curve (bottom). |
Figure 12 shows single-dish light curve parameters that can help to quantify different aspects of the flare (see, e.g., Fromm et al. 2015). The parameters are the following:
-
Flare amplitude: in order to characterize the frequency-dependent strength of the synthetic flares, we compute the lightcurve standard deviations ΔS from the ground values.
-
Flare timescale: the timescale of a flare can be obtained from the rising and/or from the decaying edge of the individual light curves. The rising timescale of a given flare is obtained as Δt = tmax−tmin,r, with the time between the start of flux density increase (tmin,r) and the time at the flare maximum (tmax).
-
Cross-band delay: in general, there is a delay between the flux density peaks at different frequencies. We compute the time difference between the flux density peak at our highest frequency (1000 GHz) and the flux density peaks of the other frequencies to quantify these multifrequency delays.
3.2.3. Synthetic radio maps
The results presented in Sect. 3.2.2 have been obtained by integrating the synthetic radio maps. In this section we explain the features in the radio maps themselves.
Figure A.1 shows the PM jet radio maps. The first row of panels shows the quiescent PM jet, before a perturbation is injected through the jet nozzle (left boundary). The subsequent rows show the passage of the perturbation through the jet. The perturbation is seen as an increase in the emission traveling down the jet (second row of panels), but it also leaves intermittent brightness regions behind it because of the decrease in emission in the reverse rarefaction wave (see Sect. 3.1). As discussed in Sect. 3.2.2, the flare is not seen at 15.4 GHz, but it is clearly seen at 22.4 GHz, where it peaks at approximately 2.6 yr (between the second and third rows of panels in Fig. A.1). The flare is even more pronounced at 43.4 GHz (third column of panels in Fig. A.1). At the start of the flare (t ~ 2.4 yr, second row in the figure) the spectral index in the core increases and, as the component progresses down the jet and interacts with the previously quiescent fluid, the spectrum hardens there as well; this is better observed between 22.4 GHz and 44.4 GHz in Fig. A.1. In the reverse rarefaction (in the jet reference frame) wave behind the perturbation the opposite is observed; the spectrum softens and the spectral index eventually returns to its quiescent value.
In the quiescent OP jet (top row of panels in Fig. A.2) we observe the increase in the emission at the position of the first cross-shock (x ~ 8.5Rj). The spectrum at this position is harder than in the rest of the jet. In fact, at 43 GHz (third column in Fig. A.2), most of the emission from the quiescent jet comes from the cross-shock, while at lower frequencies (left panel in Fig. A.2) the emission at the position of the cross-shock is strongly absorbed. Once the perturbation enters the jet (second row of panels in Fig. A.2), it initially behaves very similarly as in the PM jet, i.e., it is seen as an increase in the emission and in spectral index. However, once the perturbation reaches the cross-shock (fourth row of panels), the region of high emission becomes geometrically smaller and the intensity of its radiation increases (especially at 22.4 and 43.4 GHz). After the perturbation passes through the cross-shock, it produces trailing components in its wake. However, in contrast to the PM case, the location of these components is in clear relation to the location of the cross-shock and not to the position of the main perturbation. Another clear difference between OP and PM jet is that the observed main component splits in two parts (fourth and fifth row of panels, see e.g., Aloy et al. 2003; Mimica et al. 2009, for a thorough discussion).
Figure A.3 shows the axial emission of the OP jet at 43 GHz with time. The top panel shows the emission taking opacity effects into account, whereas the bottom panel shows the optically thin emission. The optically thin emission is obviously larger than the emission given when opacity is considered. In both cases, however, we observe that the time delays have an important effect on the observed emission. The emission that travels across the jet at the viewing angle collects contributions from different regions along the jet. The net effect is that the emission from the closest edge of the jet produces an initial increase of the brightness (t ≃ 2.3−2.5 yr). This increase in brightness is followed by a composition of emission from rarefied and shocked jet regions (t ≃ 2.5−2.8 yr) until the jet cross section from the observer’s point of view, which corresponds to the full development of the flare in the observer’s frame (t ≃ 2.8−3.2 yr).
3.2.4. Turnover frequency and turnover flux maps
In this section we discuss the behavior of the turnover frequency and the turnover flux density of the synthetic images. Figure A.4 shows the distribution of νm and Sm in the PM jet (left and middle panel columns, respectively), as well as the instantaneous single-dish spectrum for each of the eight epochs discussed in Sect. 3.2.3. The figure shows that the turnover frequency and flux steadily decrease along the quiescent jet. Once the component is introduced (second row of panels), νm and Sm increase dramatically at the base of the jet; this fact is also reflected in the 15% increase in the total νm and Sm (see also red lines in Fig. 11). After the passage of the component, the quiescent jet values gradually reestablish, but the temporarily intermittent jet emission triggered by the passage of the perturbation (rows 3−6) introduces changes in the single-dish spectrum due to missing contributions from places where the rarefaction waves decrease the emission; see Sect. 3.2.3.
Figure A.5 shows the case of the OP jet. Here the situation is somewhat more complex, since the geometry of the jet changes along the path of the perturbation. The images at 43 GHz (third column in Fig. A.2) show that the biggest contribution to the emission from the OP jet comes from the cross-shock. At higher frequencies, the jet is transparent everywhere except at the very center of the cross-shock, whereas at lower frequencies it is self-absorbed (νm ≳ 30 GHz in the cross shock and ~10 GHz elsewhere; see middle column in Fig. A.5). Once the perturbation is injected, it temporarily increases the emission at the base of the jet (top three panels of Fig. A.5, for t ≤ 3 yr). A peak in Sm is reached at t = 3.1 yr, when the perturbation is crossing the widest point of the jet between the nozzle and the recollimation shock. The opacity at high frequencies is also increased by the induced increase of the flow density. Once the perturbation starts to cross the shock itself, its emitting region becomes smaller as a result of compression, though the opacity increases even more (see the images at t = 3.37 yr along the fifth row of the figures). The opacity in the perturbation increases, but it decreases behind the perturbation (in the larger, rarefied region). The overall effect is the net decrease of the opacity and flux. After the perturbation exits the narrow region (t ≥ 3.5 yr), its opacity starts to decrease, but the size of the emitting region increases, which leads to the second peak in total opacity followed by a decline in the peak frequency (the blue line in the left panel of Fig. 11) since the spectral peak of the source lies around 43 GHz. We note that Sm does not experience the second peak since the stationary, quiescent jet already establishes itself back to equilibrium at the widest point (x ≃ 4 Rj) and the subsequent decrease of emission is not compensated by the intense emission from the post-cross-shock perturbation.
4. Discussion
Our emission simulations do not include Compton losses, although they are deemed important in blazars. Taking this into account, we now discuss our results, and subsequently compare the synthetic single-dish emission we computed to the radio observations of blazars flares.
4.1. Summary of synthetic observations
Figures 9 and 10 show that the injection of a perturbation introduces an increase of the emission and opacity in the simulated jets. The flux increase is larger and the duration of the flare is longer in the OP than in the PM jet. The flare in the former shows a small decrease in the slope after the main peak, followed by a steeper decrease. The emission at high frequencies is optically thin when the flare starts due to the absence of Compton scattering.
Figure 11 shows that the flux density and peak frequency increase as the shock evolves, since the amount of shocked gas increases and fills the cross section of the jet in the observer’s frame, as shown in Fig. A.3. Therefore, the maximum flux density is observed some time after the injection of the perturbation. After this point, in the case of the PM jet, both the peak frequency and flux of the perturbed spectrum decrease as the shock expands along the jet. On the contrary, in the case of the OP jet the interaction with the standing shock changes the evolution on the νm−Sm-plane; the flux increases in the beginning of the interaction and instead of following a parallel track to that of the PM jet, an increase in the opacity and a decrease in the flux can be observed (see Sect. 3.2.4 for a detailed explanation of this feature).
From Figs. A.4 and A.5, which show the map of the distribution of peak frequency (left column) and peak flux (right column), we can easily see that the cross-shock of the OP jet completely changes the temporal and spatial properties of the spectral distribution. It introduces a delay in the peaks with respect to the PM jet (also seen observed in Fig. 11). The outcome of the interaction between the traveling perturbation and the standing shock is the production of a stronger, delayed peak, which can be clearly distinguished from that produced by a perturbation propagating through a PM jet.
4.1.1. Adiabatic and radiative losses
As in the case studied by Mimica et al. (2009), the losses in the simulated regions are dominated by adiabatic losses, which explains why we do not observe a synchrotron stage in the νm−Sm plane. Therefore, we limit our discussion to this fact, which influences the tracks followed by the spectral peaks in that plane (Fig. 11). We note that in the quiescent OP jet the particle populations undergo compressions when they encounter the cross-shock, but the energy gained there is not sufficient for the synchrotron losses to become dominant in the cross-shock. Similarly, the forward shock of the perturbation is not strong enough to cause the synchrotron loss zone to become active at this position. The passage of the perturbation causes a reverse rarefaction wave in the jet behind it. Through this wave, the particles experience strong adiabatic losses, a feature that can nicely be seen as a decrease (or even absence) of emission in the rows 4−6 of Fig. A.1. We note that the observed spectral index also decreases. Although the adiabatic losses cannot change the electron distribution spectral index, the strong adiabatic cooling in the rarefaction can cause almost all the particle distribution characteristic frequencies to fall below the observational frequency (especially at 43.4 GHz, see Fig. A.1). Once the quiescent jet reestablishes itself, both the emission and the spectral index quickly return to the original values.
4.2. Comparison with theoretical models
Comparing the evolution of the single-dish light curve parameters obtained from the simulations and those expected from purely theoretical modeling (Fig. 12, see also Fromm et al. 2015), we can see that
-
1.
The flare amplitudes in the simulations behave in the sameexpected qualitative way as predicted by the theoreticalmodeling, showing a peak at tens of GHz;
-
2.
The flare timescales show a continuous decrease in the PM simulation as predicted by the theoretical modeling, but in the case of the OP jet we observe an inversion of this timescale at 43 GHz; and
-
3.
The cross-band delays show the same qualitative behavior for the PM and theoretical modeling, i.e., a decrease in the value of this delay from lower to higher frequencies, but an inversion in the OP jet at 43 GHz.
Actually, one of the main differences between both models is the fact that the peak in the OP jet occurs at 22 GHz before it occurs at any other frequency. At frequencies ν ≥ 90 GHz, both the PM and OP models produce a similar qualitative evolution (the lines are basically parallel in the top and mid panels, and coincide in the bottom panel). The main quantitative differences between both simulations occur precisely at the frequencies within which the spectral peak oscillates (see Fig. 11).
The different quantitative jump in flux increase and the delay in the peaks between both models (bottom panels in Fig. 11) show that the presence of a recollimation shock changes the spectral evolution of a perturbation. Whereas in the case of the PM model, the flux increase is purely dominated by the injection, in the OP case, the flare is delayed and shows a stronger increase in flux. Both the delay and increase in flux can only be attached to the interaction of the perturbation with the standing shock, as discussed in the previous section. Therefore, we should expect stronger flares and a sudden increase in flux for the case of flares that interact with recollimation shocks. This signature can only be tested in those jets in which the interaction is resolved, i.e., in which the second peak can be clearly separated from that due to the injection in the Compton/synchrotron stages, and has indeed been observed by Fromm et al. (2011, 2013a); Fromm et al. (2013b, 2015), and by Agudo et al. (2012). The comparison presented here between jets with and without recollimation shocks and the implications for the expected observations supports the interpretation given in those papers.
4.3. Comparison with observations of CTA 102
In this subsection, we discuss the similarities and differences found when comparing the results shown in the single-dish light curves (Figs. 9 and 10) with the observed light curve from the 2006 flare in CTA 102 (Fig. 1 in Fromm et al. 2011) and between the radio maps at different frequencies (Figs. A.1 and A.2) and VLBI observations (Fromm et al. 2013a,b).
Regarding flux variations, we must recall that the highest frequencies start to show an increase in flux before the low frequencies in CTA 102, whereas this does not happen in the models simulated by construction. We simulate a jet that does not include the most compact regions, thus the lack of the necessary opacity to reproduce this effect. Despite this difference, we find similar behaviors that are relevant in the flare evolution; all cases show a prebump in flux at intermediate frequencies (14.5 and 37 GHz in the case of CTA 102, 43, and 86 GHz in the case of the PM jet, and 22, 43, and 86 in the OP jet); the perturbation produces little or no increase of the flux at low frequencies, which is seen both in the light curve of CTA 102 and in the simulated models, and the flux increase is maximum at tens of GHz in all cases. After the flare, we observe a dip in emission at all frequencies, which is also seen in the light curve of CTA 102 and in the simulated models.
It is difficult to separate the peak in flux produced by the injection of the perturbation and that produced by the interaction with the cross-shock in our simulations, as it all occurs within a short time and the filling factor of the perturbation is large. However, the delay in the peak observed in the OP jet would help to distinguish the increase due to a shock-shock interaction with respect to the increase due to the injection of the perturbation, in real sources, if the standing shock producing the increase in the emission is located at a given distance interval from the radio core. This second peak necessarily produces a more homogeneous increase of the observed flux at frequencies ranging from ≃10 to 100’s of GHz, as opposed to the first peak, which is mainly visible at 100’s of GHz. This global increase is observed in both the light curve of CTA 102 and the simulations.
The main difference between the observations of CTA 102 and the simulation of the OP jet is that the second peak in CTA 102 does not imply an increase in the peak frequency (between 2006.0−2006.3, the peak frequency remains basically constant; see Fig. 5 in Fromm et al. 2011), but it increases in the simulation. This might be the result of the relative contribution of the interaction region to the total emission and opacity as would be derived by a single-dish observation. This contribution can be exaggerated in the case of the simulations.
Finally, the observed spectral evolution of the simulated jets is comparable to that observed in a number of the so-classified types-1, 2, and 3 flares in Angelakis et al. (2012), which all claimed to correspond to the same physical mechanism, namely the injection of perturbations. The main difference between the different observed types is the role of the extended emission of the jet, the relative flux variations at different frequencies, and the redshift of the source. As we show here, some of the different phenomenology observed in the sources covered by the F-GAMMA sample could be explained in terms of shock-shock interaction, such as delayed and strong peaks of emission, probably distinguishable from the Compton peak if the temporal sampling is sufficient, and variable opacity along the jet as the flare evolves.
The 3° radio maps (Figs. A.1 and A.2) show that the knotty structures and flux variations obtained from the simulations are comparable to VLBI radio maps of sources undergoing an injection of radio components. This was already discussed by Gómez et al. (1997), Agudo et al. (2001), and Mimica et al. (2009). The main differences between the PM and the OP jet come from the spectral index at the cross-shock, which shows an increase in the OP jet, as opposed to the steady decrease of the spectral index in the PM case (Figs. A.1 and A.2). This kind of behavior can be observed with VLBI observations (Fromm et al. 2013b). Both models show sharp decreases of flux at the rarefied regions following the perturbations and consequent trailing features, which can also be observed in VLBI maps following superluminal radio components (Agudo et al. 2001; Mimica et al. 2009).
Comparing the simulated νm – Sm evolution (top panel in Fig. 11) with the observed values (Fig. 20 of Fromm et al. 2013b), we note that both in the simulated and observed jets the opacity increases following the peak of the emission (Sect. 3.2.4, second paragraph). From our simulations we know that this happens far downstream from the jet core, and is therefore free of any Compton and synchrotron losses. Thus, our neglect of the Compton losses does not influence the results obtained for the shock interaction, and the mechanism we propose can be used to explain the observed phenomenology of CTA 102 (Fromm et al. 2013b).
5. Conclusions
In this work we studied blazar flares in a conical (pressure-matched) and in an overpressured jet. We show that the injection of perturbations in a jet can produce a bump in emission at GHz frequencies previous to the main flare, which is produced when the perturbation fills the jet in the observer’s frame. We also show that the flare spectral evolution can be completely changed in an overpressured jet with respect to the conical case. The interaction between the injected perturbation and the standing shock produces a larger relative increase in the peak flux and introduces significant changes in the evolution of the peak frequency, as a result of the interplay between emissivity and absorption at the interaction region. Furthermore, for the overpressured jet, we observe differences in the light curve parameters; the cross-band delay is negative between 22 GHz and the fiducial frequency of 1 THz, and flaring timescales are shorter at 22 GHz. The reason for this is that 22 GHz is the closest to the peak frequency of the spectral distribution before the injection of the perturbation, and is associated with the standing shock. These features can be better observed in interactions downstream of the core (Fromm et al. 2013b), but a detailed analysis of the light curves during flares can also provide hints of such shock interactions within the core.
In summary, the detailed analysis of our simulations and the nonthermal emission calculations show that interaction between a recollimation shock and traveling shock produce a typical and clear signature in both the single-dish light curves and in the VLBI observations. The flaring peaks are higher and delayed with respect to the evolution of a perturbation through a conical jet, and the cross-band delay and the flaring timescales can show negative and shorter values, respectively, at tens of GHz as compared to higher frequencies; we recall that this is expected to be the opposite in coincal jets. These features can allow us to detect such interactions for stationary components lying outside of the region in which the losses are dominated by inverse Compton scattering.
Our results predict a number of observational signatures that could be detected in single-dish observations (with enough temporal sampling) and also with VLBI (Fromm et al. 2013a,b). Future work in this direction should include the analysis of a number of sources that are tracked within survey programs such as MOJAVE and show hints of interactions between traveling and standing components downstream of the radio core (e.g., 0202+149 -4C+15.05-, 0415+379 -3C111-, 0528+134, 0738+313, 0829+046, 0851+202 -OJ287-, 1127-145, 1156+295 -4C+29.45-, 1219+285, 1253-055 -3C279-, 1418+546, 1823+568, 2200+420 -BL Lac-, 2201+315 -4C+31.63, 2230+114 -CTA102-, 2251+158 -3C454.3-). This should provide a further step in the characterization of a scenario, which has been claimed to be important in explaining very high energy emission in a number sources (e.g., Agudo et al. 2010; Schinzel et al. 2012, and references therein) and in facilitating the search for correlations between radio and gamma-ray flares. A detailed analysis will also require full RMHD simulations learn about the exact role of the magnetic field intensity and configuration on our results.
Monitoring of Jets in Active galactic nuclei with VLBA Experiments http://www.physics.purdue.edu/MOJAVE
We note that, depending on the fluid properties at the injection point, it might occur that γmin ≤ 1. In this case we follow the prescriptions of Sec. 2.1.1 of Sironi & Giannios (2013) for the “deep Newtonian” regime: we set γmin = 1 and recompute n0.
Acknowledgments
M.P. is a member of the working team of projects AYA2013-40979-P and AYA2013-48226-C3-2-P, funded by MINECO. P. M. acknowledges the support from the European Research Council (grant CAMAP-259276), the government of Spain (MINECO grant AYA2013-40979-P), and the regional government of Valencia (grant PROMETEO-II-2014-069).
References
- Agudo, I., Gómez, J.-L., Martí, J.-M., et al. 2001, ApJ, 549, L183 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Jorstad, S. G., Marscher, A. P., et al. 2010, ApJ, 726, L13 [Google Scholar]
- Agudo, I., Gómez, J. L., Casadio, C., Cawthorne, T. V., & Roca-Sogorb, M. 2012, ApJ, 752, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Aloy, M.-Á., Martí, J.-M., Gómez, J.-L., et al. 2003, ApJ, 585, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Angelakis, E., Fuhrmann, L., Nestoras, I., et al. 2012, J. Phys. Conf. Ser., 372, 012007 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., & Dermer, C. D. 2010, ApJ, 711, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Daly, R. A., & Marscher, A. P. 1988, ApJ, 334, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Falle, S. A. E. G. 1991, MNRAS, 250, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Fromm, C. 2015, Spectral Evolution in Blazars: The Case of CTA 102 (Berlin: Springer-Verlag) [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2011, A&A, 531, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Ros, E., Perucho, M., et al. 2013a, A&A, 551, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Ros, E., Perucho, M., et al. 2013b, A&A, 557, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Fuhrmann, L., & Perucho, M. 2015, A&A, 580, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannios, D., & Spruit, H. C. 2006, A&A, 450, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, J. L., Marti, J. M., Marscher, A. P., Ibanez, J. M., & Alberdi, A. 1997, ApJ, 482, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J. 2012, MNRAS, 421, 2442 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Komissarov, S. S., & Spitkovsky, A. 2011, MNRAS, 411, 1323 [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, ApJ, 130, 1418 [Google Scholar]
- Komissarov, S. S. 2012, MNRAS, 422, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., & Falle, S. A. E. G. 1997, MNRAS, 288, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Vlahakis, N., Königl, A., & Barkov, M. V. 2009, MNRAS, 394, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Levinson, A. 2011, in IAU Symp. 275, eds. G. E. Romero, R. A. Sunyaev, & T. Belloni, 24 [Google Scholar]
- Lister, M. L., Aller, H. D., Aller, M. F., et al. 2009, AJ, 137, 3718 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2011, MNRAS, 411, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., & Blandford, R. 2003, unpublished [arXiv:astro-ph/0312347] [Google Scholar]
- Martí, J. M., & Müller, E. 1999, Liv. Rev. Relativ., 2, 3 [NASA ADS] [Google Scholar]
- Mimica, P., & Aloy, M. A. 2012, MNRAS, 421, 2635 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, P., Aloy, M. A., Agudo, I., et al. 2009, ApJ, 696, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, P., Giannios, D., & Aloy, M. A. 2010, MNRAS, 407, 2501 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2011, MNRAS, 420, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Ojha, R., Kadler, M., Böck, M., et al. 2010, A&A, 519, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Martí, J. M., Cela, J. M., et al. 2010, A&A, 519, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rueda-Becerril, J. M., Mimica, P., & Aloy, M. A. 2014, MNRAS, 438, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Schinzel, F. K., Lobanov, A. P., Taylor, G. B., et al. 2012, A&A, 537, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sironi, L., & Giannios, D. 2013, ApJ, 778, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., Petropoulou, M., & Giannios, D. 2015, MNRAS, 450, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., Daigne, F., & Drenkhahn, G. 2001, A&A, 369, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tchekhovskoy, A., McKinney, J. C., & Narayan, R. 2009, ApJ, 699, 1789 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C. 1994, MNRAS, 270, 480 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1 Synthetic observations of the PM jet at 15.4 GHz (first column), 22.4 GHz (second column), and 43.4 GHz (third column) seen at 3° observing angle for eight different epochs. The fourth and the fifth column on the right show the spectral index between the frequencies. The quiescent jet is shown in the first row, while the subsequent rows show the passage of the perturbation and the eventual reestablishment of the quiescent jet after the perturbation exists in the grid (last row). |
 |
Fig. A.3 Time-space plot for the variation of the axial emission at 43 GHz for the OP jet in the observer’s frame at a viewing angle of 3°. The top panel shows the emission taking opacity effects into account, whereas the bottom panel shows the optically thin emission. The solid black line indicates propagation at the speed of light, so any structure that propagates with a flatter slope is superluminal. The emission values are normalized to their maximum value (given by the optically thin map). |
 |
Fig. A.4 Turnover frequency (left column), turnover flux (middle column), and the instantaneous single-dish spectra for eight different epochs of the PM jet observed at 3° viewing angle. The first row shows the quiescent jet, while the remaining rows show the state of the jet after a perturbation has been introduced through the nozzle. In the last row the quiescent jet has almost been reestablished. |
All Tables
All Figures
 |
Fig. 1 Sketch of an OP jet with characteristic parameters and regions (adopted from Daly & Marscher 1988). |
| In the text | |
 |
Fig. 2 Steady-state results for the simulation of the OP jet. Top panel: 2D distribution of the logarithm of the rest mass density in units of ρa. Bottom panel: logarithm of the pressure in units of ρac2. |
| In the text | |
 |
Fig. 3 Steady-state results for the simulation of a PM jet. Top panel: 2D distribution of the logarithm of the rest mass density in units of ρa. Bottom panel: logarithm of the pressure in units of ρac2. |
| In the text | |
 |
Fig. 4 Snapshots for the propagation of a perturbation in an OP jet. The panels show the 2D distribution of the logarithm of the pressure in units of ρac2. |
| In the text | |
 |
Fig. 5 Snapshots for the propagation of a perturbation in a PM jet. The panels show the 2D distribution of the logarithm of the pressure in units of ρac2. |
| In the text | |
 |
Fig. 6 Time-space plot for the variation of the axial density for the OP jet. |
| In the text | |
 |
Fig. 7 Time-space plot for the variation of the axial density for the PM jet. |
| In the text | |
 |
Fig. 8 Variation of the axial, ρaxial, and the cross section averaged rest mass density, ρmedian along the jet (red lines) and the variation of the jet radius along the jet (black line) for the OP jet. |
| In the text | |
 |
Fig. 9 Single-dish light curves for several frequencies computed for the OP jet. The time is given in the observers frame. The first flux density variations are observed two years after the injection of the perturbation (second dashed vertical line from the left). The inlet shows the variation of the spectrum for six different times indicated by dash-dotted vertical lines. |
| In the text | |
 |
Fig. 10 Same as Fig. 9 for the PM jet. |
| In the text | |
 |
Fig. 11 Evolution of the turnover values for the OP and PM jet. Top panel: evolution of the perturbation in the turnover frequency – turnover flux density (νm−Sm)-plane. The diamond marker indicates the start position of the flare and the temporal evolution is indicated with arrows. Bottom left: temporal evolution of the turnover frequency, νm. Bottom right: temporal evolution of the turnover flux density, Sm. |
| In the text | |
 |
Fig. 12 Single-dish light curve parameters for the PM and OP jet. The panels show the flare amplitude, ΔS, (top), the flare timescale, Δtrise, (middle) and the cross-band delays, τ, with respect to the peak of 1 THz light curve (bottom). |
| In the text | |
 |
Fig. A.1 Synthetic observations of the PM jet at 15.4 GHz (first column), 22.4 GHz (second column), and 43.4 GHz (third column) seen at 3° observing angle for eight different epochs. The fourth and the fifth column on the right show the spectral index between the frequencies. The quiescent jet is shown in the first row, while the subsequent rows show the passage of the perturbation and the eventual reestablishment of the quiescent jet after the perturbation exists in the grid (last row). |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for the OP jet. |
| In the text | |
 |
Fig. A.3 Time-space plot for the variation of the axial emission at 43 GHz for the OP jet in the observer’s frame at a viewing angle of 3°. The top panel shows the emission taking opacity effects into account, whereas the bottom panel shows the optically thin emission. The solid black line indicates propagation at the speed of light, so any structure that propagates with a flatter slope is superluminal. The emission values are normalized to their maximum value (given by the optically thin map). |
| In the text | |
 |
Fig. A.4 Turnover frequency (left column), turnover flux (middle column), and the instantaneous single-dish spectra for eight different epochs of the PM jet observed at 3° viewing angle. The first row shows the quiescent jet, while the remaining rows show the state of the jet after a perturbation has been introduced through the nozzle. In the last row the quiescent jet has almost been reestablished. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.4, but for the OP jet. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.