| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 21 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526577 | |
| Published online | 15 March 2016 | |
New models for the evolution of post-asymptotic giant branch stars and central stars of planetary nebulae⋆
1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 8574 Garching, Germany
e-mail: marcelo@mpa-garching.mpg.de
2 Instituto de Astrofísica de La Plata, UNLP-CONICET, Paseo del Bosque s/n, 1900 La Plata, Argentina
Received: 21 May 2015
Accepted: 13 December 2015
Context. The post-asymptotic giant branch (AGB) phase is arguably one of the least understood phases of the evolution of low- and intermediate- mass stars. The two grids of models presently available are based on outdated micro- and macrophysics and do not agree with each other. Studies of the central stars of planetary nebulae (CSPNe) and post-AGB stars in different stellar populations point to significant discrepancies with the theoretical predictions of post-AGB models.
Aims. We study the timescales of post-AGB and CSPNe in the context of our present understanding of the micro- and macrophysics of stars. We want to assess whether new post-AGB models, based on the latter improvements in TP-AGB modeling, can help us to understand the discrepancies between observation and theory and within theory itself. In addition, we aim to understand the impact of the previous AGB evolution for post-AGB phases.
Methods. We computed a grid of post-AGB full evolutionary sequences that include all previous evolutionary stages from the zero age main sequence to the white dwarf phase. We computed models for initial masses between 0.8 and 4 M⊙ and for a wide range of initial metallicities (Z0 = 0.02, 0.01, 0.001, 0.0001). This allowed us to provide post-AGB timescales and properties for H-burning post-AGB objects with masses in the relevant range for the formation of planetary nebulae (~0.5−0.8 M⊙). We included an updated treatment of the constitutive microphysics and included an updated description of the mixing processes and winds that play a key role during the thermal pulses (TP) on the AGB phase.
Results. We present a new grid of models for post-AGB stars that take into account the improvements in the modeling of AGB stars in recent decades. These new models are particularly suited to be inputs in studies of the formation of planetary nebulae and for the determination of the properties of CSPNe from their observational parameters. We find post-AGB timescales that are at least approximately three to ten times shorter than those of old post-AGB stellar evolution models. This is true for the whole mass and metallicity range. The new models are also ~0.1−0.3 dex brighter than the previous models with similar remnant masses. Post-AGB timescales only show a mild dependence on metallicity.
Conclusions. The shorter post-AGB timescales derived in the present work are in agreement with recent semiempirical determinations of the post-AGB timescales from the CSPNe in the Galactic bulge. The lower number of post-AGB and CSPNe predicted by the new models might help to alleviate some of the discrepancies found in the literature. As a result of the very different post-AGB crossing times, initial final mass relation and luminosities of the present models, the new models will have a significant impact on the predictions for the formation of planetary nebulae and the planetary nebulae luminosity function. In particular, the new models should help to understand the formation of low-mass CSPNe as inferred from asteroseismic and spectroscopic determinations.
Key words: stars: AGB and post-AGB / stars: low-mass / stars: evolution / planetary nebulae: general
Tables containing the evolution of luminosity, temperature, surface gravity, and other relevant quantities are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/588/A25
© ESO, 2016
1. Introduction
The transition between the asymptotic giant branch (AGB) and white dwarf phases is arguably one of the least understood phases of the evolution of low- and intermediate-mass single stars (Mi ~ 0.8–8 M⊙). During this phase, stars are expected to evolve as OH/IR stars, protoplanetary nebula central stars and, under the right conditions, the central stars of planetary nebulae (van Winckel 2003; Herwig 2005; Kwitter et al. 2014). While there are many grids of stellar models covering all phases from the zero age main sequences (ZAMS) to the AGB regime (e.g., Pietrinferni et al. 2004; Karakas & Lattanzio 2007; Siess 2007; Dotter et al. 2008; Karakas 2010; Cristallo et al. 2009, 2011), this is not the case for the post-AGB and CSPNe phases of stellar evolution. Only two main grids covering the relevant range of final masses (Mf ~ 0.5–0.8 M⊙) are available. Those are the grids computed by Vassiliadis & Wood (1994) from the AGB models of Vassiliadis & Wood (1993) and the grids computed by Blöcker (1995a) from the AGB models of Blöcker (1995b), which are usually complemented at low masses by the models of Schönberner (1983).
Other the fact that they are very interesting objects in themselves, post-AGB stars are also useful for other fields of astrophysics (Kwitter et al. 2014). In particular, planetary nebulae (PNe) are bright, easy to identify, and their progenitors are expected to have ages spanning from ~0.1 Gyr to ~10 Gyr. In the most simple scenario, PNe are formed when the progenitor stars lose their external layers at the end of the AGB and cross the HR diagram on their way to the white dwarf cooling sequence. While crossing the HR diagram the central stars of the PNe (CSPNe) become sufficiently hot to ionize the previously ejected material (Shklovsky 1957; Abell & Goldreich 1966; Paczyński 1970). Planetary nebulae and CSPNe offer unique insight into the nucleosynthesis during the TP-AGB phase. Extragalactic PNe can be used to understand metallicity gradients and their temporal evolution in galaxies. In addition masses and numbers of extragalactic PNe can be used to derive stellar formation rates. Last but not least, the PN luminosity function (PNLF) has proven to be a good distance indicator as far as ~20 Mpc, although we still do not understand why (Ciardullo 2012). The formation and detectability of PNe depends strongly on the relationship between two different timescales: Evolutionary timescales of the CSPNe, which provide ionizing photons, and dynamical timescales of the circumstellar material ejected at the end of the AGB (Marigo et al. 2001). If the CSPN evolves too fast the PN is ionized for a short time, and thus has a low detection probability or might even not be ionized at all. Conversely, if the star evolves too slowly, the ionization of the nebula takes place when the ejected material has already dispersed too much to be detectable. In this work, we address the first of these timescales. Namely, we present full stellar evolution computations of the post-AGB and CSPNe phases. The evolutionary timescale of the post-AGB remnant is mainly set by the speed at which the H-rich envelope is consumed before reaching its final value on the WD stage. Models departing from the TP-AGB with less massive H-rich envelopes, higher luminosities, or more intense winds must evolve faster than those with more massive envelopes, lower luminosities, and less intense winds. In its turn, the post-AGB luminosity and the mass of the envelope at the departure from the AGB depends on the details of the TP-AGB evolution. Consequently, proper modeling of the previous evolutionary phases is needed to obtain accurate post-AGB timescales.
There are some indications that available models of the post-AGB and CSPN phases are not accurate enough. First, the two available grids of post-AGB models (Vassiliadis & Wood 1994; Blöcker 1995a) do not agree with each other on the predicted timescales (Zijlstra et al. 2008). Second, consistency between the masses of white dwarfs and those of CSPNe seems to require faster evolutionary speeds than predicted by both sets of models (Gesicki et al. 2014). Third, present models of the CSPNe phase are unable to explain why the cut-off of the PNe luminosity function is constant in most galaxies (Marigo et al. 2001, 2004). Lastly, post-AGB stellar evolution models, computed with updated physics in a reduced mass range (Kitsikis 2008; Weiss & Ferguson 2009), show a strong disagreement with the previous grids. This is not a surprise since many improvements have been carried out in the field of stellar physics in recent decades. Most importantly, available grids have been computed with opacities, which are now 45 years old (Cox & Stewart 1970b,a) before the big changes introduced by the OPAL (Iglesias & Rogers 1996), and Opacity Project (Seaton 2007) redeterminations. Similarly, nuclear reaction rates, equation of states, conductive opacities, and neutrino emission rates adopted in the models date from the early eighties and even earlier. In addition, Herwig et al. (1997) showed that the existence of carbon stars at low luminosities can be explained by the addition of mixing beyond the formal convective boundaries during the thermal pulses (TP) on the AGB. Finally, Marigo (2002) showed that C-rich molecular opacities are essential to predict the correct effective temperatures once the AGB models become carbon rich (NC/NO> 1, by number fractions). This is particularly important because of the impact of effective temperatures on the mass loss rates. While all these improvements in stellar modeling have been implemented in AGB stellar models, and very detailed and exhaustive grids and models are available (Weiss & Ferguson 2009; Cristallo et al. 2009, 2011; Ventura & Marigo 2010; Karakas 2010; Lugaro et al. 2012; Constantino et al. 2014; Doherty et al. 2015), the inclusion of these improvements in post-AGB stellar models is still missing. It is time for a recomputation of the post-AGB models in the light of all these advances.
The aim of our study is to assess the post-AGB timescales and properties with the help of post-AGB stellar evolution models, which include an updated treatment of the relevant physics, and in particular of the AGB phase. In Sect. 2, we describe the input physics and calibration of free parameters in the stellar evolution models. In Sect. 3 we show the agreement of our models with several observables and with the other state-of-the-art AGB models. This shows the reliability of the new models. In Sect. 4 we describe the results of our computations and discuss differences with previous post-AGB models. Then, in Sect. 5 we discuss possible consequences of our results and the uncertainties behind the present computations. Finally, we close the article with a summary and some conclusions.
2. Input physics, numerics, and set up
The calculations reported here have been carried out with the last version of LPCODE stellar evolutionary code. This code has been used to study different problems related to the formation and evolution of white dwarfs (Althaus et al. 2013; Miller Bertolami et al. 2013; Salaris et al. 2013; Althaus et al. 2015). The LPCODE is a well-tested stellar evolution code and has been recently tested against other stellar evolution codes during the main sequence, red giant, and white dwarf phases (Salaris et al. 2013)1. The numerical methods adopted in LPCODE are extensively described in Althaus et al. (2003, 2005). Recent improvements in the numerical scheme, as well as convergence problems and how we circumvented them, are briefly described in Appendix C. In what follows, we describe the adopted micro- and macrophysics in the present work.
2.1. Microphysics
We have adopted state-of-the-art ingredients for the microphysics relevant for the evolution and structure of low- and intermediate-mass stars to supersede previous post-AGB grids. The nuclear network accounts explicitly for the following elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne, together with 34 thermonuclear reaction rates for the pp-chains, CNO bi-cycle, and helium burning. These reaction rates are identical to those described in Althaus et al. (2005) with the exception of the reactions 12C+p → 13N + γ → 13C + e+ + νe and 13C(p, γ)14N, which are taken from Angulo et al. (1999), and the reaction rate 14N(p, γ)15O, which was taken from Imbriani et al. (2005). High temperature radiative opacities are taken from OPAL (Iglesias & Rogers 1996) and conductive opacities are taken from Cassisi et al. (2007), respectively. We use updated low-temperature molecular opacities with varying C/O ratios. For this purpose, we have adopted the low-temperature opacities of Ferguson et al. (2005) extended with the tables for varying C/O ratios presented in Kitsikis (2008) and Weiss & Ferguson (2009). In LPCODE, molecular opacities are computed by adopting the opacity tables with the correct abundances of the unenhanced metals (e.g., Fe) and C/O ratio. Interpolation is carried out by means of separate quadratic interpolations in R = ρ/T63, T and XH, but linearly in NC/NO. This approach is inferior to the on the fly computation of opacities (Marigo et al. 2013), but allows us to capture the first order effect of the formation of a C-rich envelope without the need to follow the huge number of ions and elements that participate in the opacity of AGB envelopes. The equation of state during the main-sequence evolution is the updated EOS_20052 version of the OPAL EOS (Rogers et al. 1996) for H- and He-rich composition and a given metallicity. Neutrino emission rates for pair, photo, and bremsstrahlung processes are those of Itoh et al. (1996), while plasma processes are included with the expressions presented by Haft et al. (1994). For the early white dwarf regime, we use the equation of state of Magni & Mazzitelli (1979) for the low-density regime, while for the high-density regime we consider the equation of state of Segretain et al. (1994). Outer boundary conditions are set by simple Eddington gray T(τ)-relations.
2.2. Macrophysics
While the microphysics of stellar models is relatively well established, macrophysical processes are their main uncertainty. In particular, the modeling of convective and nonconvective mixing processes and stellar winds are among the main uncertainties in the computation of stellar evolution sequences. This is even worst in the case of stellar evolution computations from the ZAMS all the way down to the white dwarf stage, such as those presented in this work. In these computations one must deal with many convective regions and with winds during many, and very different, stages of the evolution; see Weiss & Heners (2013) for a nice review on this topic. In what follows, we describe the prescriptions adopted for the stellar winds during the different stages of the evolution and how we have calibrated the different free parameters involved in the treatment of convection.
2.2.1. Stellar winds
Mass loss during the RGB is usually included in stellar evolutionary computations following the empirical formula of Reimers (1975). More recently Schröder & Cuntz (2005, 2007) argued for a reinterpretation of this formula in terms of a more physical picture of the mechanism behind mass loss. This led to the update of Reimers’ formula including two more factors. Girardi et al. (2010) and Rosenfield et al. (2014) showed that this new formula also provides a better description of predust AGB winds. In line with these recent studies, we have included winds from cold giants following the prescription of Schröder & Cuntz (2005), i.e., 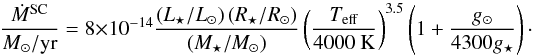 (1)Since the seminal work of Schönberner (1979), it became evident that steady stellar winds play a decisive role in the AGB. In particular, it is stellar winds that rule the length of the thermally pulsating AGB phase (TP-AGB). Stellar winds during the AGB lead to the (almost) complete removal of the H-rich envelope, forcing the remnant star to contract to the white dwarf phase. Yet, AGB stellar winds are not fully understood. While theoretical and observational evidence of the existence of pulsation-enhanced, dust-driven winds is strong for C-rich stars, the situation of O-rich (M-type) AGB stars is much less clear. In particular, numerical simulations of pulsation-enhanced, dust-driven winds are unable to find efficient mass loss rate (Woitke 2006), although there is still hope for this mechanism (Norris et al. 2012; Höfner 2012; Bladh et al. 2015).
(1)Since the seminal work of Schönberner (1979), it became evident that steady stellar winds play a decisive role in the AGB. In particular, it is stellar winds that rule the length of the thermally pulsating AGB phase (TP-AGB). Stellar winds during the AGB lead to the (almost) complete removal of the H-rich envelope, forcing the remnant star to contract to the white dwarf phase. Yet, AGB stellar winds are not fully understood. While theoretical and observational evidence of the existence of pulsation-enhanced, dust-driven winds is strong for C-rich stars, the situation of O-rich (M-type) AGB stars is much less clear. In particular, numerical simulations of pulsation-enhanced, dust-driven winds are unable to find efficient mass loss rate (Woitke 2006), although there is still hope for this mechanism (Norris et al. 2012; Höfner 2012; Bladh et al. 2015).
The inclusion of C-rich molecular opacities implies a different treatment of O- and C-rich AGB stars, as both radius (R⋆) and effective temperature (Teff) are very sensitive to the C/O ratio of the model. In its turn, pulsation-enhanced, dust-driven winds are themselves very sensitive to the values of R⋆ and Teff. Then, a consistent treatment of pulsation-enhanced dust-driven winds with the actual C/O ratio is needed. In order to have a internally consistent description of AGB winds we cannot rely on theoretical determinations, as those are unavailable for O-rich stars. Fortunately, Groenewegen et al. (1998, 2009) has determined mass loss rates for both C- and M-type AGB stars adopting the same techniques. Following the suggestions by Groenewegen et al. (1998, 2009), we adopted for pulsating O-rich AGB stars the relation 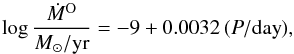 (2)while the mass loss for the winds of pulsating carbon stars was adopted as
(2)while the mass loss for the winds of pulsating carbon stars was adopted as 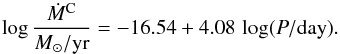 (3)To compute the mass loss from Eqs. (2) and (3), it is necessary to estimate the value of the pulsation period P. We compute P from the relation of Ostlie & Cox (1986), i.e.,
(3)To compute the mass loss from Eqs. (2) and (3), it is necessary to estimate the value of the pulsation period P. We compute P from the relation of Ostlie & Cox (1986), i.e., 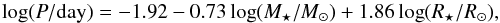 (4)which for values of log (R⋆/R⊙) ≳ 2.5 and 1 <M⋆/M⊙< 10 is always within a 10% of the P(M,R) relation of Wood (1990) (as given by Vassiliadis & Wood 1993).
(4)which for values of log (R⋆/R⊙) ≳ 2.5 and 1 <M⋆/M⊙< 10 is always within a 10% of the P(M,R) relation of Wood (1990) (as given by Vassiliadis & Wood 1993).
It is well known that there must be some kind of upper limit for the intensity of the winds. It has usually been argued that pulsation-enhanced, dust-driven winds must be constrained by the single scattering limit (e.g., Vassiliadis & Wood 1994), i.e., the situation in which all the momentum of the stellar radiation field is transferred to the wind 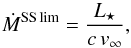 (5)where c is the speed of light and v∞ is the terminal wind velocity, for which we assume v∞ = 10 km s-1 as suggested by the results of Groenewegen et al. (2009). However, as argued by Mattsson et al. (2010), there are theoretical reasons to think that such a limit is not appropriate for pulsation-enhanced, dust-driven winds. In fact, the numerical simulations from Mattsson et al. (2010) show many models with mass loss rates beyond the single scattering limit given by Eq. (5). In addition, more recent observational evidence (Groenewegen & Sloan 2013) supports the existence of mass loss rates beyond the single scattering limit. Following the results presented in Mattsson et al. (2010) we constrained the mass loss rates of Eqs. (2) and (3) not to exceed three times the value given by Eq. (5). This is a rather arbitrary choice, but in line with the results presented in Mattsson et al. (2010) and Groenewegen & Sloan (2013).
(5)where c is the speed of light and v∞ is the terminal wind velocity, for which we assume v∞ = 10 km s-1 as suggested by the results of Groenewegen et al. (2009). However, as argued by Mattsson et al. (2010), there are theoretical reasons to think that such a limit is not appropriate for pulsation-enhanced, dust-driven winds. In fact, the numerical simulations from Mattsson et al. (2010) show many models with mass loss rates beyond the single scattering limit given by Eq. (5). In addition, more recent observational evidence (Groenewegen & Sloan 2013) supports the existence of mass loss rates beyond the single scattering limit. Following the results presented in Mattsson et al. (2010) we constrained the mass loss rates of Eqs. (2) and (3) not to exceed three times the value given by Eq. (5). This is a rather arbitrary choice, but in line with the results presented in Mattsson et al. (2010) and Groenewegen & Sloan (2013).
Finally, during the CSPN phase, radiation-driven winds must also be included. Following Blöcker (1995a), we derived a similar relation from the results of Pauldrach et al. (2004), i.e., 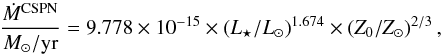 (6)which is, for the range of luminosities of interest, always within a factor of two from the mass loss rates derived by Blöcker (1995a) from the earlier results of Pauldrach et al. (1988). Given that our grid spans a factor 20 in the initial metal content of the stars, the dependence with Z0 in Eq. (6) was included after the derivation. The factor Z02/3 reproduces the known dependence of radiation-driven winds with the heavy metal content of the star, i.e., mostly of iron; see Vink et al. (2001).
(6)which is, for the range of luminosities of interest, always within a factor of two from the mass loss rates derived by Blöcker (1995a) from the earlier results of Pauldrach et al. (1988). Given that our grid spans a factor 20 in the initial metal content of the stars, the dependence with Z0 in Eq. (6) was included after the derivation. The factor Z02/3 reproduces the known dependence of radiation-driven winds with the heavy metal content of the star, i.e., mostly of iron; see Vink et al. (2001).
Finally, all these prescriptions (Eqs. (1)–(3), (5) and (6)) for stellar winds in different regimes must be combined. This is done under the assumption that the mechanism driving cool winds in RGB stars is always active until pulsation-driven winds develop. Specifically, once P> 100 days, we take the cool wind rate to be the maximum between Eqs. (1) and (2) (Eq. (3)), when NC/NO< 1 (NC/NO> 1) 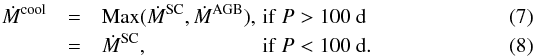 Where ṀAGB stands for ṀC or ṀO, depending on whether NC/NO is above or below unity, and constrained not to exceed three times the single scattering limit.
Where ṀAGB stands for ṀC or ṀO, depending on whether NC/NO is above or below unity, and constrained not to exceed three times the single scattering limit.
While all mass loss prescriptions are somewhat uncertain, the mass loss rates during the transition from the cold AGB to the hot CSPN phase is completely unconstrained. Schönberner & Steffen (2007) argue that cool winds must last until Teff ~ 5000–6000 K to reproduce the spectral energy distribution of post-AGB objects. We have chosen to exponentially decrease the cool wind rates to its CSPN values (Eq. (6)), as the model evolves from log Teff = 3.8 to log Teff = 4.1, by means of a simple linear interpolation in the logarithmic rates 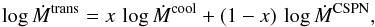 (9)where x = (log Teff−3.8)/0.3. The accuracy of this interpolation between the extrapolation of two prescriptions outside their validity range is completely questionable. However, we show in the following sections that, unless mass loss rates are much higher than these values, they are of no relevance for post-AGB evolution.
(9)where x = (log Teff−3.8)/0.3. The accuracy of this interpolation between the extrapolation of two prescriptions outside their validity range is completely questionable. However, we show in the following sections that, unless mass loss rates are much higher than these values, they are of no relevance for post-AGB evolution.
2.2.2. Convection and convective boundary mixing
We treat convection according to the Kippenhahn et al. (2012) formalism of mixing length theory (MLT; Biermann 1932; Böhm-Vitense 1958). The MLT free parameter αMLT has been fixed with solar calibration and kept constant for all masses during all evolutionary phases. For the solar calibration, one needs to find the combination of initial He (Y) and metal (Z) mass fractions and the value of the mixing-length parameter that reproduce the solar radius (R⊙ = 6.96 × 1010 cm), luminosity (L⊙ = 3.842 × 1033 erg s-1; Bahcall et al. 1995), and ratio Z/X = 0.0245 ± 0.005 (Grevesse & Noels 1993) at an age of t⊙ = 4.57 Gyr. Solar models without microscopic diffusion or with new Asplund et al. (2009) compositions cannot properly account for some seismic properties of the Sun. For this reason, we decided to account for atomic diffusion and to adopt the Grevesse & Noels (1993) initial chemical composition for the calibration of the Sun. Once the calibration of the mixing length and initial composition is carried out, the accuracy of the solar model can be tested by comparing the depth of the outer convective layers and surface Y value with the values obtained from helioseismological studies (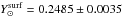 ;
; 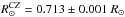 ; Serenelli et al. 2009). Our treatment of time dependent element diffusion is based on the multicomponent gas picture of Burgers (1969) taking the effects of gravitational settling, chemical diffusion, and thermal diffusion into account, but neglecting radiative levitation. In particular, we solved the diffusion equations within the numerical scheme described in Althaus et al. (2003).
; Serenelli et al. 2009). Our treatment of time dependent element diffusion is based on the multicomponent gas picture of Burgers (1969) taking the effects of gravitational settling, chemical diffusion, and thermal diffusion into account, but neglecting radiative levitation. In particular, we solved the diffusion equations within the numerical scheme described in Althaus et al. (2003).
We computed several 1 M⊙ models starting from the ZAMS and adopting different values of the initial composition and mixing length. The best solar model was obtained by assuming Xini = 0.7092, Z0 = 0.0194 and a value of the MLT parameter of αMLT = 1.825. With these values, we obtain values of L = 0.9994 L⊙, Teff = 5776.85 K, Ysurf = 0.24415, (Z/X)surf = 0.02488, and RCZ = 0.7144 R⊙ at an age of t = 4.5684 Gyr. We consider this an overall good solar model and, consequently, we adopt αMLT = 1.825 throughout this work.
Turbulent mixing beyond the formal convective boundaries described by a bare Schwarzschild criterion (Schwarzschild 1906) is one of the main uncertainties in stellar astrophysics. From now on, we call this process convective boundary mixing (CBM). In LPCODE, CBM processes are included following the suggestion of Freytag et al. (1996) of an exponentially decaying velocity field. The diffusion coefficient beyond convective boundaries is (Herwig et al. 1997) ![\begin{equation} D_{\rm OV }=D_0\times \exp\left[\frac{-2z}{f H_{\rm P}}\right], \label{eq:OV} \end{equation}](/articles/aa/full_html/2016/04/aa26577-15/aa26577-15-eq84.png) (10)where D0 is the diffusion coefficient provided by the MLT (D0 = vMLTαMLTHP) close to the convective boundary, HP is the pressure scale height at the convective boundary, z is the geometric distance to the formal convective boundary, and f is a free parameter that must be calibrated. We take D0 as the mean value of the MLT diffusion coefficient in the region within 0.1 HP from the formal convective boundary and the CBM region is extended until the diffusion coefficient falls 10 orders of magnitude, i.e., Dcut−off = 10-10D0. The value Dcut−off (which is rarely stated in the literature) is as important as the value of f in slow evolutionary stages, where mixing of the main chemical elements is always complete and only the extension of the CBM region, and not the mixing speed, becomes relevant (e.g., core H- and He-burning).
(10)where D0 is the diffusion coefficient provided by the MLT (D0 = vMLTαMLTHP) close to the convective boundary, HP is the pressure scale height at the convective boundary, z is the geometric distance to the formal convective boundary, and f is a free parameter that must be calibrated. We take D0 as the mean value of the MLT diffusion coefficient in the region within 0.1 HP from the formal convective boundary and the CBM region is extended until the diffusion coefficient falls 10 orders of magnitude, i.e., Dcut−off = 10-10D0. The value Dcut−off (which is rarely stated in the literature) is as important as the value of f in slow evolutionary stages, where mixing of the main chemical elements is always complete and only the extension of the CBM region, and not the mixing speed, becomes relevant (e.g., core H- and He-burning).
For our aims, the main convective boundaries (and related f values) are the boundaries of convective cores during core H- and He-burning (fCHB and fCHeB), the lower boundaries of the convective envelope (fCE), and the pulse-driven convective zone (fPDCZ) during the thermal pulses on the AGB.
There is a general agreement, within uncertainties, that an extension of 0.2 HP in the convective core of upper main-sequence stars offers a relatively good agreement with observation of the main sequence in open clusters and the field (Maeder & Meynet 1991; Stothers & Chin 1992; Schaller et al. 1992; Herwig et al. 1997; Pietrinferni et al. 2004; Weiss & Ferguson 2009; Ekström et al. 2012). With our choice of Dcut−off, this is reproduced by assuming a value of fCHB ~ 0.0174. This value of the extension of the convective core is in good agreement with determinations coming from eclipsing binaries; see Claret (2007), Stancliffe et al. (2015). It is well known that the inclusion of CBM processes in small convective cores of low-mass main-sequence stars must be restricted. Following previous works (Pietrinferni et al. 2004; Weiss & Ferguson 2009), we adopted a linear dependence of fCHB with the initial mass of the star, so that it attains fCHB = 0.0174 in the upper main sequence (M>M2) and decreases to zero for stars without convective cores (M<M1) (see Table 1). Following Ekström et al. (2012), we checked that this choice allows us to reproduce the width of the upper main sequence as presented by Wolff & Simon (1997).
M1 and M2 values for the boundary mixing recipe at the convective core in the main sequence, i.e., fCHB = 0.0174×(Mi−M1)/(M2−M1) for Mi between M1 and M2.
The CBM at the border of the He-burning core is significantly less understood. While there are some physical arguments (e.g., Castellani et al. 1985) and asteroseismic inferences (Charpinet et al. 2013; Constantino et al. 2015) in favor of the existence of CBM at convective boundaries, its extension is much less constrained. In the absence of a better constraint, we set fCHeB = 0.0174 (i.e., =0.2 HP) in our simulations for all stars.
Of particular interest for the present work are the CBM processes during the thermal pulses on the AGB. In LPCODE and in many other codes (e.g., Herwig et al. 1997; Weiss & Ferguson 2009, and references therein) third dredge up (3DUP) does not appear, or is not very efficient, in low-mass (luminosity) AGB models without CBM processes. This contradicts the existence of carbon stars (NC/NO> 1 by number fractions) in the lower AGB and at all metallicities. Furthermore, CBM processes at the lower boundary of the convective envelope (fCE) are also needed to create the 13C pockets needed for the creation of s-process elements. Also, CBM at the lower boundary of the pulse-driven convective zone (fPDCZ) is needed to reproduce the oxygen abundances of post-AGB PG1159 stars, which are believed to display the intershell abundances of AGB stars (Herwig et al. 1999). The values of fCE and fPDCZ are certainly not well constrained. The early exploration of Herwig (2000) suggested that 0.01 ≲ fPDCZ ≲ 0.03 would reproduce the abundances of PG1159 stars, while fCE should be significantly larger. Studying the production of s-process elements, Lugaro et al. (2003) suggested that these values should be of fPDCZ ~ 0.008 and fCE ~ 0.128. Herwig (2005) argued that the oxygen abundances in PG1159 stars can be reproduced with values of 0.005 ≲ fPDCZ ≲ 0.015 and that a value of fCE ~ 0.13 would be enough to account for the s-process production, but would lead to neutron exposures that are too large and an overabundance of second peak elements. Unfortunately, it has been shown by Salaris et al. (2009) and Weiss & Ferguson (2009) that the inclusion of CBM processes both at the convective envelope and the pulse-driven convective zone leads to an initial-final mass relation (IFMR) in disagreement with observations. This is particularly true for initial masses of ~3 M⊙, which would have final masses of ~0.6 M⊙. These masses are far from the final masses of ≳0.7 M⊙ suggested by semiempirical determinations of the IFMR from stellar clusters (Catalán et al. 2008; Salaris et al. 2009; Gesicki et al. 2014, and references therein).
We performed several exploratory computations with LPCODE that confirm the previous picture. We find that values of 0.005 ≲ fPDCZ ≲ 0.01 are needed to reproduce the high O abundances of PG1159 stars, while the simultaneous inclusion of fCE ≳ 0.002 leads to final masses not in agreement with our expectation from semiempirical IFMRs. In fact, in a preliminary study (Miller Bertolami 2015; from now on M15, see Appendix B), we adopted values of fPDCZ = 0.005 and fCE = 0.13, and the resulting IFMR of the theoretical models is far from that suggested by Galactic clusters at solar metallicity, and even stars with M ≲ 1 M⊙ become carbon stars, at variance with observations of stellar clusters in the Magellanic Clouds (Girardi & Marigo 2007). In the next section, we show that choosing fPDCZ = 0.0075 and fCE = 0 allows us to reproduce many relevant AGB and post-AGB observables. Note that we do not claim that fCE should be fCE = 0 at all times3, but only that this choice of parameters allow us to reproduce many relevant AGB and post-AGB observables. Among them are the C/O ratios of AGB and post-AGB stars in the Galactic disk, the IFMR at near solar metallicities, the C/O intershell abundances of AGB stars as observed in PG1159 stars, and the mass range of C-rich stars in the stellar clusters of the Magellanic Clouds. In addition, the resulting AGB stellar models show properties (core growth, carbon enrichment, and IFMR) well within the predictions of available AGB grids. Then, the predicted structures and timescales obtained with this choice of fPDCZ and fCE can be considered good representatives of state-of-the-art AGB stellar evolution modeling for the post-AGB phase.
Main properties of the sequences from the ZAMS to TP-AGB.
3. Evolution from the ZAMS to the end of the AGB
We computed a grid of 27 sequences with initial masses (Mi) between 0.8 M⊙ and 4 M⊙ and four different metallicities to study the evolution of stars after the AGB at different masses and metallicities. The final masses (Mf) of the model sequences are between ~0.5 M⊙ and ~0.85 M⊙, correspondingly. This is the main range of interest for the formation of PNe. The initial metal content of the star (Z0) is taken to be solar scaled with overall metal mass fractions of Z0 = 0.02, 0.01, 0.001 and 0.0001. We follow the suggestion by Weiss & Ferguson (2009) for the initial helium (Y) content and we take it to be 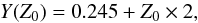 (11)in good agreement with our present understanding of Big Bang nucleosynthesis (Steigman 2007; Izotov et al. 2013; Aver et al. 2013; Coc et al. 2014) and close to our calibration of the solar model.
(11)in good agreement with our present understanding of Big Bang nucleosynthesis (Steigman 2007; Izotov et al. 2013; Aver et al. 2013; Coc et al. 2014) and close to our calibration of the solar model.
The evolution of low- and intermediate-mass stars up to the beginning of the TP-AGB is relatively well understood. An updated description of the main relevant phases and the physics involved can be found in Kippenhahn et al. (2012). Table 2 shows the main characteristics of our sequences from the ZAMS to the end of the TP-AGB phase. Lifetimes during the main sequence, the red-giant branch, and the He-core burning stage are denoted by τMS, τRGB, and τHeCB, respectively. As is well known, timescales become longer as initial mass decreases and metallicity increases. The main exception to this general trend is observed around the transition from degenerate to nondegenerate He-ignition as stellar mass increases. Column 4 in Table 2 indicates whether He-ignition happened in the form of a He-core flash (HeCF) or did not occur for each sequence. As shown in Col. 5 of Table 2, τHeCB attains a local maximum around Mi ~ 2 M⊙ for solar-like metallicities (Z0 = 0.02, 0.01), and at slightly lower Mi for lower metallicities. Below this maximum, sequences that undergo an HeCF have an almost constant He-burning lifetime of τHeCB ~ 108 yr, irrespective of initial mass and metallicity. In contrast, sequences of higher masses show the typical trend of decreasing lifetimes with increasing mass. The behavior of τHeCB is due to the different sizes of the H-free core (HFC) during He-core burning. The HFC at the beginning of He-burning is approximately constant for sequences that undergo a HeCF. The HFC decreases at the transition between degenerate and nondegenerate He-ignition and monotonically increases with increasing initial mass; see for example Montalbán et al. (2013). The mass of the HFC during He-burning not only affects τHeCB, but also the properties of the next evolutionary stages. The mass and also the composition of the HFC keeps a memory of the previous evolutionary history. For example, we see in Table 2 that the duration from the end of He-core burning to the first thermal pulse (early AGB phase; τeAGB) also reflects, to a certain extent, the different HFC sizes left by He-core burning. More importantly, for the same reason, the HFC at the first thermal pulse shows a clear minimum as a function of Mi (see Col. 7 in Table 2). This is why models with very efficient 3DUP (Weiss & Ferguson 2009; Miller Bertolami 2015) predict a very pronounced plateau in the IFMR below Mi ~ 2.5 M⊙.
In the last two decades, the TP-AGB has been the object of many detailed studies (see Herwig 2005; Karakas & Lattanzio 2007, 2014; Cristallo et al. 2009, and references therein). Grids of models and yields for TP-AGB stars are now available for a wide range of masses and metallicities; e.g., Karakas (2010), Cristallo et al. (2011). A detailed discussion of the present models in the TP-AGB phase would take us too far afield from the goal of the present work, and add almost nothing to the present knowledge in the field. Yet, as we discuss in the next sections and analyze in Appendix A, the main results of the present work are related to the accurate modeling of the TP-AGB phase. Specifically, the post-AGB sequences are sensitive to the properties of the HFC and the CNO content of the envelope. Both the properties of the core and the envelope of post-AGB stars are determined by 3DUP episodes; see Herwig (2005) for a detailed description of the process. Third dredge-up intensity not only determines the amount of carbon pollution of the envelope but also the IFMR, especially at Mi ≲ 3 M⊙ (Salaris et al. 2009). The same post-AGB mass Mf is attained by models with very different initial masses and evolutionary histories depending on the intensity of 3DUP. It is then important to know to which extent the present models offer an accurate description of the main structural properties of AGB stars. In the following paragraphs we show that with the calibration of Sect. 2 (fPDCZ = 0.0075 and fCE = 0) our sequences are able to reproduce several key observables of AGB and post-AGB stars in our Galaxy and in the Magellanic Clouds. We also compare the IFMRs, HFC growth, and carbon enrichment of our sequences during the TP-AGB with those of state-of-the-art TP-AGB models. This comparison shows that our models are good representatives of modern AGB stellar evolution models.
On the AGB most of our sequences undergo efficient 3DUP events and carbon enrichment of the envelope. Only the lower mass models avoid a carbon enrichment of the envelope. As a consequence of efficient 3DUP events, during the TP-AGB most of our models become C-rich; i.e., NC/NO> 1; see Table 2. The lower limit for the formation of carbon stars is dependent on the initial metallicity of the sequences, being at Mi ~ 1.5 M⊙, 1.25 M⊙, 1 M⊙ and 0.85 M⊙ for Z0 = 0.02, 0.01, 0.001 and 0.0001, respectively. Figure 1 shows that our sequences reproduce the range of masses for the formation of carbon stars inferred from the study of globular clusters in the Magellanic Clouds (Girardi & Marigo 2007). Almost no carbon stars are predicted at low masses (≲1.25 M⊙, the exact value depending on initial metallicity) because of the lack of 3DUP events and almost no carbon stars are predicted at higher masses (≳3 M⊙).
When AGB models become C rich, they become colder owing to the presence of C-rich molecules, as originally shown by Marigo (2002); see also Weiss & Ferguson (2009), Ventura & Marigo (2010), Lugaro et al. (2012), Constantino et al. (2014) for discussions on the impact of C-rich molecular opacities in full stellar evolution models. Because of larger radii and different mass-loss rates of carbon stars, mass loss is strongly increased. This causes our models to undergo only a few more thermal pulses as C-rich stars before most of the H-rich envelope is removed and they evolve away from the AGB. This is in agreement with observational data of the C/O ratio of PNe; see Fig. 2. If many thermal pulses were to follow the carbon-star formation, planetary nebulae C/O ratio would cover a much larger range; see Herwig (2005) for a similar discussion. This shows that our models depart from the TP-AGB at the right time in terms of carbon enrichment, which gives us confidence in the accuracy of the post-AGB models. In addition, our models also reproduce the C/O ratios observed in M- and C-type stars (Lambert et al. 1986; Smith & Lambert 1990) and post-AGB objects (Kingsburgh & Barlow 1994; Milanova & Kholtygin 2009; Mello et al. 2012; Delgado-Inglada & Rodríguez 2014) of the Galactic disk; see Fig. 2.
 |
Fig. 1 Lifetimes of our Z0 = 0.01 and Z0 = 0.001 sequences as C and M stars on the AGB as compared with the timescales derived by Girardi & Marigo (2007) from the Magellanic Clouds. In the case of M-type stars, we computed the lifetime of the star as a O-rich object with MBol< −3.6 to be consistent with the values presented by Girardi & Marigo (2007). This is why the values plotted here do not agree with the τTP−AGB(M) in Table 2. |
 |
Fig. 2 Carbon and oxygen abundances of AGB and post-AGB objects in the Galactic disk as compared with the predictions of the Z0 = 0.02 (upper set) and Z0 = 0.01 sequences (lower set). Tracks in blue lines correspond to those that experience significant 3DUP, while thick black lines indicate sequences with no significant 3DUP. The red line corresponds to the evolution of the 4 M⊙ (Z0 = 0.02) sequence that experiences both 3DUP and hot-bottom burning. Abundances are presented in the customary astronomical scale for logarithmic abundances, log ϵX = log (NX/NH) + 12, where NX and NH are the number densities of elements X and H, respectively. |
 |
Fig. 3 Initial final mass relation of the sequences computed in this work and those of (Miller Bertolami 2015, M15). The semiempirical IFMR derived from clusters for solar-like metallicities by Salaris et al. (2009), and also that of Gesicki et al. (2014), are shown for comparison. |
 |
Fig. 4 He-, C-, and O- intershell abundances in the post-AGB phase as compared with the derived abundances of PG1159 type stars of similar mass (Werner & Rauch, in prep.). Most of the high log g stars (see color bar) are probably undergoing gravitational settling, and thus the high He abundances might not reflect the original intershell composition. |
Third dredge up is a key process in the shaping of the IFMR (Salaris et al. 2009) and the core-luminosity relation (Herwig et al. 1998; Mowlavi 1999). Both the core-luminosity relation and the IFMR set the timescales of the post-AGB remnants (see Appendix A). A proper modeling of 3DUP episodes becomes of utmost importance for the accuracy of post-AGB sequences. Figure 3 shows that our sequences reproduce the semiempirical IFMR (e.g., Salaris et al. 2009; Gesicki et al. 2014). This implies that our post-AGB models of a given mass Mf descend from reliable progenitor models. Models with high CBM efficiencies at the bottom of the convective envelope (e.g., Weiss & Ferguson 2009 and M15) produce final masses that are too low at Mi ~ 3 M⊙.
Our models also reproduce to a good extent the range of He-, C-, and O-intershell abundances of AGB stars, as determined from the observations of PG1159 stars (Fig. 4; see Werner & Herwig 2006; Werner & Rauch, in prep.). This is an important result, as PG1159 stars are the only way to constrain the value of fPDCZ, which does affect the intensity of the He flashes and the consequent 3DUP episodes. Figure 4 shows that the choice of fPDCZ = 0.0075 allow our models to reproduce the O-rich abundances of PG1159 stars; see Herwig et al. (1999) and Herwig (2005) for a detailed discussion.
 |
Fig. 5 Upper panel: IFMR of the models presented here for Z0 = 0.02 compared with the results from state-of-the-art AGB model grids available in the literature (Karakas & Lattanzio 2007; Cristallo et al. 2011; Weiss & Ferguson 2009) and the IFMR of Weidemann (2000). Lower panel: third dredge up efficiencies (λ) during the TP-AGB for different models of a 3 M⊙ and Z0 = 0.02 (Herwig 2000; Stancliffe et al. 2004; Karakas & Lattanzio 2007; Cristallo et al. 2011). |
 |
Fig. 6 C/O ratios at the end of the TP-AGB of the present models as compared with results available in the literature (Weiss & Ferguson 2009; Cristallo et al. 2011). |
The reproduction of the key AGB and post-AGB observables related to the HFC growth and carbon pollution during the TP-AGB (Figs. 1–4) give us confidence that our post-AGB sequences begin with accurate post-AGB structures. Yet, it is possible to wonder to which extent our AGB models, and consequently the following post-AGB phase, are representative of our current understanding of stellar evolution. The upper panel of Fig. 5 shows the IFMR of our models compared with the IFMR of available state-of-the-art AGB models (Karakas & Lattanzio 2007; Weiss & Ferguson 2009; Cristallo et al. 2011). The final masses of our models are well within those predicted by available grids. The lower panel of Fig. 5 shows the evolution of the 3DUP efficiency4λ as a function of the mass of the HFC for the benchmark case of a Mi = 3 M⊙, Z0 = 0.02 sequence. Also in this case our model shows a behavior well within the spread of the predictions of different state-of-the-art AGB models. This spread is mostly due to the different treatments of boundary mixing processes in different stellar evolution codes and is representative of the present uncertainties. In particular, our model is in good agreement with the predictions by Karakas & Lattanzio (2007).
Figure 6 shows the predictions for the C/O ratio of our post-AGB models compared with the C/O-ratios at the end of the AGB for available grids. As shown in the upper panel of Fig. 6, our models predict very similar C/O ratios to the models of Weiss & Ferguson (2009) and Cristallo et al. (2011) at solar metallicities. The only exception is the high C/O ratio of our Mi = 1.5 M⊙ (Z0 = 0.02) model. The high C/O ratio of this model is explained by the occurrence of a final thermal pulse at the very end of the TP-AGB. In those cases, the C dredged up to the surface is diluted into a significantly smaller mass of H, leading to a higher surface carbon abundance. While the three sets of models predict rather similar values at solar metallicities, they differ at lower metallicities. In particular, the models of Cristallo et al. (2011) predict very high C/O ratios of NC/NO> 20 for Z0 = 0.001, while our models and also those of Weiss & Ferguson (2009) predict a more moderate carbon enrichment. The values of NC/NO> 10 are in significant disagreement with the observed C/O ratios of PNe (Fig. 2) and also with the recent study of Ventura et al. (2015). As in the case of the comparisons of Fig. 5, we see that the calibration and choice of physics described in Sect. 2 leads to TP-AGB properties in good agreement with independent works.
We have shown in this section that the models we present here are able to reproduce several observed AGB and post-AGB properties both of the Galactic disk and the Magellanic Clouds; see Figs. 4, 3, 2, and 1. In addition, when compared with other state-of-the-art AGB models they usually predict properties that are in between those predicted by the available state-of-the-art AGB models; see Figs. 5 and 6. Our models are good representatives of the predictions of modern AGB computations.
4. Post-AGB evolution
4.1. Description of the results
 |
Fig. 7 Upper panel: HR diagram of our Z0 = 0.001 sequences that departed from the AGB as H-burners. Lower panel: mass of the H-rich envelope as a function of log Teff for the same sequences. Red dots indicate the moment in which Menv/Mstar = 0.01, which has been used to define the beginning of the post-AGB. |
 |
Fig. 8 HR diagrams of the H-burning post-AGB sequences we computed for different masses and initial metallicities. Tracks are presented from the beginning of the post-AGB phase when the H-rich envelope drops below Menv = 0.01 M⋆ to the moment in which the star has already entered its white dwarf cooling sequence at L⋆ = L⊙. At that point gravitational settling should have already started to turn post-AGB stars into DA-WDs, a process not included in the present computations. Red lines indicate computed isochrones for different ages since the zero point defined at log Teff = 3.85. Thin gray lines in the Z0 = 0.001 and Z0 = 0.0001 panels correspond to the evolution of the Mi = 0.8 M⊙ He-burning sequences shown in Fig. 10 (Mf = 0.4971 M⊙ and 0.5183 M⊙, respectively). |
In our models, the departure from the AGB occurs as a consequence of steady winds reducing the mass of the H-rich envelope Menv (Schönberner 1979). Consequently, this transition occurs gradually and the definition of the beginning of the post-AGB phase (i.e., end of the AGB) is somewhat arbitrary. The mass of the envelope as function of effective temperature is shown in Fig. 7 for our H-burning sequences with Z0 = 0.001. As soon as the mass of the envelope becomes comparable to the mass of the core (Menv/Mstar = 0.5–0.1, depending on mass; see Fig. 7), models move to the blue with decreasing envelope mass. First, big changes in the envelope mass lead only to a modest increase in temperature. This phase lasts until the mass of the envelope becomes a few times (between three and five times in the sequences shown in Fig. 7) larger than the final mass of the white dwarf envelope. After this point, small changes in the envelope mass lead to big changes in the effective temperature of the model. Most models depart from the AGB region in the HR diagram during the first, slower stage. Consequently, there is no natural definition of the end of the AGB. We have defined the beginning of the post-AGB phase as the moment in which Menv/Mstar = 0.01. At this moment, models have already moved significantly to the blue, which is true at all masses and metallicities. This choice defines the end of the AGB in a homogeneous way independently from their mass and metallicities, and is based on the underlying physical reason behind the departure from the AGB.
Main post-AGB properties of the H-burning sequences.
Figure 8 displays the evolution of our H-burning post-AGB sequences in the theoretical HR diagram for different metallicities and masses. In works dealing with the evolution of post-AGB stars and CSPNe (Renzini 1989; Schönberner 1990; Vassiliadis & Wood 1994; Marigo et al. 2004; Weiss & Ferguson 2009), it is customary to define two different timescales, τtr and τcross, for the discussion of the post-AGB evolution. The quantity τtr corresponds to the duration of the early post-AGB evolution when AGB-like winds might still be important and Teff does not depend strongly on Menv. The value τcross, in turn, gives the timescale of the later post-AGB evolution when there is a tight Teff−Menv relation, from the end of the early phase to the point of maximum effective temperature. Our simulations show that around log Teff ~ 3.85 all our sequences have started the fast part of the post-AGB evolution. In addition, at these temperatures (and beyond) winds play only a secondary role in setting the timescales. This makes timescales in the second phase more reliable than in the early post-AGB phase. Splitting the post-AGB timescale in τcross and τtr allows τcross to be a useful and reliable quantity. The quantity τcross is then unaffected by our lack of understanding of the early post-AGB winds and the absence of a clear end of the TP-AGB. We define τtr as the time from the end of the AGB (taken at Menv = 0.01 M⋆) to the moment in which log Teff = 3.85, while τcross is the timescale from log Teff = 3.85 to the point of maximum effective temperature. The value of τcross is almost independent of the precise definition and would have been practically the same if the initial point were set at log Teff = 4 as in Vassiliadis & Wood (1994) and Weiss & Ferguson (2009) or if we had adopted the definition of Blöcker (1995a)5.
Table 3 and Fig. 8 show the main post-AGB properties of the H-burning sequences computed in this work. We emphasize the extreme mass dependence of the post-AGB timescales. While higher mass models (≳0.7 M⊙) require only a few hundreds of years to cross the HR diagram and only thousands of years to fade two orders of magnitude, lower mass models (≲0.55 M⊙) require more than 10 kyr to cross the HR diagram and more than 100 kyr to decrease their luminosity only by an order of magnitude. The predicted post-AGB timescales do not depend strongly on the initial metallicity of the population (i.e., iron content). A sudden decrease in timescales, around Mf ~ 0.58 M⊙ for most metallicities, is apparent in both Table 3 and Fig. 9. This corresponds to the transition from models that did, and did not, undergo a HeCF in the previous evolution, i.e., models with Mi = 1.5 and 2 M⊙ for Z0 = 0.02, 0.01, and to Mi = 1.25 and 1.75 M⊙ for Z0 = 0.001. These sequences end with similar Mf but they reached the AGB with different HFC masses (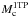 ; Table 2). Consequently, the time spent on the AGB and the chemical and thermal structure of the core at the end of the AGB are not the same. As discussed in Appendix A, the thermal structure of the core and CNO enrichment of the envelope play a key role in setting the properties of the post-AGB models. As a result of a different 3DUP history, the composition of the envelope is different, with models on the high-mass side of the transition showing more efficient 3DUP. Models on the high-mass side of the transition have higher luminosities and less massive H envelopes. As the timescale for the crossing of the HR diagram (τcross ) is given by the speed at which the envelope is depleted, both higher H-burning rates and smaller initial H envelopes lead to shorter timescales for models with Mf ≳ 0.58 M⊙.
; Table 2). Consequently, the time spent on the AGB and the chemical and thermal structure of the core at the end of the AGB are not the same. As discussed in Appendix A, the thermal structure of the core and CNO enrichment of the envelope play a key role in setting the properties of the post-AGB models. As a result of a different 3DUP history, the composition of the envelope is different, with models on the high-mass side of the transition showing more efficient 3DUP. Models on the high-mass side of the transition have higher luminosities and less massive H envelopes. As the timescale for the crossing of the HR diagram (τcross ) is given by the speed at which the envelope is depleted, both higher H-burning rates and smaller initial H envelopes lead to shorter timescales for models with Mf ≳ 0.58 M⊙.
 |
Fig. 9 Crossing timescales from the zero point, set at log Teff = 4 to allow comparisons with all previous works, to the point of maximum effective temperature in the HR diagram; i.e., the so-called knee of the evolutionary tracks shown in Fig. 8. Timescales are shown for all the sequences presented and the H-burning post-AGB sequences available in the literature, i.e., (Vassiliadis & Wood 1994, VW94); (Schönberner 1983, Blöcker 1995a, B95+S83); and (Weiss & Ferguson 2009, WF09). Crossing timescales of the new sequences (this work and also Weiss & Ferguson 2009) are much shorter than the crossing timescales of the H-burning models of Schönberner (1983), Vassiliadis & Wood (1994), Blöcker (1995a). The sudden decrease in τcross at Mf ~ 0.58 M⊙ (Z0 = 0.02, 0.01 and 0.001) can be traced back to differences in the previous evolutionary history of the models (see text). Because of slightly different definitions of the zero point, the numbers do not completely agree with the value of τcross given in Table 3. |
We can estimate the so-called transition times (τtr, Table 3) immediately after the departure form the AGB. Table 3 shows that τtr has a very steep decrease for remnant masses between ~0.53 M⊙ and ~0.58 M⊙ and a flatter decrease at higher masses. The value of τtr is both sensitive to the precise definition of the end of the AGB and to the intensity of winds during the early post-AGB phase, which are poorly known. Changing the definition of the end of the AGB from 0.01 M⋆ to 0.007 M⋆ can change τtr by more than 50%. With this in mind the value of τtr predicted by the new models goes from τtr ~ 2–7 kyr at Mf ~ 0.53 M⊙ to τtr ~ 0.5–1 kyr Mf ≳ 0.7 M⊙ with exact values depending on the precise definition of the end of the AGB and the metallicity.
In light of the fact that no effort was made to control the phase at which the models depart from the AGB, we stress that a big majority of our sequences depart from the AGB, and evolve through the post-AGB, as H-burning models. Only the very low-mass and low metallicity models (0.8 M⊙ and Z0 = 0.001, 0.0001) evolved away from the AGB as He-burning models. In addition, one sequence underwent a late thermal pulse (LTP; Blöcker 2001) in the post-AGB evolution (1.5 M⊙, Z0 = 0.001) and two other sequences underwent a very late thermal pulse (VLTP, Blöcker 2001) already on the white dwarf cooling track (1.25 and 2 M⊙ models with Z0 = 0.02).
Figure 10 shows the evolution of log Teff and log L/L⊙ of the only three He-burning sequences computed in this work. The time lapse from6log Teff = 3.85 to the point of maximum effective temperature is of ~487 kyr (~334 kyr) for the 0.4971 M⊙ (0.5183 M⊙) sequence. These values are much higher than the crossing times of the H-burning sequences of lower mass (τcross ~ 20–60 kyr for Mf ~ 0.53 M⊙; Table 3). While we refer to these low-mass sequences as He-burners, they do not spend the whole post-AGB as He-burners. Figure 10 shows that only in the first ~100 kyr the sequences are He-burners (LHe>LH) while for the rest of the post-AGB H-burning becomes dominant again, as is typical from the interpulse phase in the TP-AGB. The reignition of the H-shell in the post-AGB phase leads to a temporary decrease in Teff as the model readjusts to the new structure. Only objects with very low H abundances in the envelope can evolve through the whole post-AGB phase as He-burners. This is the case for our LTP Mi = 1.5 M⊙, Z0 = 0.001 sequence, which undergoes a LTP and finally becomes an object with surface abundances of [H/He/C/N/O/Ne] = [0.036/0.504/0.353/5.8 × 10-4/0.075/0.029] because of the dilution of the H envelope during 3DUP. Although H is reignited immediately after the LTP, it never overtakes the He-burning energy release and the sequence remains a He-burner throughout the post-AGB phase (see Fig. 10). The crossing timescale for this sequence is τcross = 12.4 kyr, which is much larger than the crossing timescales of H-burning sequences of similar mass and metallicity (3.4 and 2.1 kyr, see Table 3). The evolution of very low-mass post-AGB sequences can be very involved with even several flashes taking place in the post-AGB phase (Blöcker 1995a). This is the case of our 0.4971 M⊙ sequence (green curve in Fig. 10), which undergoes two post-AGB thermal pulses with he first at t ~ −375 kyr in Fig. 10. Very low-mass post-AGB sequences also experience some sudden enhancements in the H-burning shell just before the point of maximum temperature, as the star model contracts toward the white dwarf cooling phase; the spikes in LH are just at the point of maximum effective temperature; Fig. 10.
 |
Fig. 10 Evolution of log Teff (upper panel) and log L/L⊙ (lower panel) during the post-AGB phase and the end of the TP-AGB. The zero point of the x-axis was taken at the last time the sequence had log Teff = 3.85 before evolving toward the white dwarf cooling phase. Time is shown in years for the Mi = 0.8 M⊙ sequences, but it has been multiplied by a factor 10 for the Mi = 1.5 M⊙ sequence to allow proper visualization. |
4.2. Comparison with previous post-AGB grids
The main result of our study is the finding that new models predict post-AGB timescales (τcross) that are three to ten times shorter than the older models of Vassiliadis & Wood (1994) and Blöcker (1995a) (see Fig. 9). This result is in agreement with the previous results found by Weiss & Ferguson (2009) in the low-mass range (Fig. 9). The agreement is reassuring because the results of Weiss & Ferguson (2009) were computed with a different stellar evolution code, but also include a state-of-the-art modeling of the TP-AGB. The new models are also brighter by about ~0.1...0.3 dex for most remnant masses, as shown in Fig. 11.
The speed of the post-AGB evolution of H-burning sequences is set by the speed at which the H-rich envelope is consumed. Models departing from the TP-AGB with less massive H-rich envelopes, higher luminosities, or more intense winds must evolve faster than those with more massive envelopes, lower luminosities, and less intense winds. With the exception of the sequence with the highest metallicity and mass (Z0 = 0.02 and Mi = 4 M⊙), post-AGB winds always play a secondary role in the depletion of the H-rich envelope and even become negligible at lower metallicities (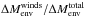 , Table 3). Yet, mass loss still plays a relevant role, on the order of
, Table 3). Yet, mass loss still plays a relevant role, on the order of 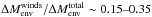 , in setting the exact timescale of the higher metallicity sequences (Z0 = 0.01, 0.02). The secondary role of mass loss for the post-AGB timescales implies that the reason for the fast evolution of the new models must be related to the other two ingredients that define post-AGB timescales, post-AGB luminosities, and H-envelope masses.
, in setting the exact timescale of the higher metallicity sequences (Z0 = 0.01, 0.02). The secondary role of mass loss for the post-AGB timescales implies that the reason for the fast evolution of the new models must be related to the other two ingredients that define post-AGB timescales, post-AGB luminosities, and H-envelope masses.
The reason why post-AGB models have different luminosities or H-rich envelope masses is involved and is related to the core mass-luminosity relation on the TP-AGB. Modern sequences have updated microphysics and a better modeling of mixing processes on the AGB. This leads to very different core-luminosity relations in the AGB and post-AGB phases, as shown in Fig. 11. These differences also produce different masses of the H envelope at the moment of the departure from the TP-AGB. As discussed in Appendix A, new models depart from the AGB with brighter luminosities and smaller H-envelope masses, producing a faster post-AGB evolution. In addition, the efficient 3DUP of most of the sequences affects the properties of post-AGB models through the carbon enrichment of the H-rich envelope and its impact on the IFMR (see also Appendix A). The fact that the new sequences are able to reproduce several AGB and post-AGB observables (Figs. 1–4) not reproduced by the older models implies that the new models should be preferred over older models. The difference in envelope masses, carbon enrichment, and IFMR explains the much faster post-AGB evolution that we obtained, as compared with the older grids (Schönberner 1983; Vassiliadis & Wood 1994; Blöcker 1995a); see Appendix A for a detailed discussion.
 |
Fig. 11 Post-AGB mass-luminosity relation of the old H-burning models as compared with that of the new models we present here and in Miller Bertolami (2015). There is a much higher luminosity for the same remnant mass of the new models. |
 |
Fig. 12 Same as Fig. 9 (although with the zero points set at log Teff = 3.85), but comparing the H-burning sequences with those originally computed by Miller Bertolami (2015) under different assumptions of the evolution on the TP-AGB with the same code and microphysics. This shows the uncertainty in the computed post-AGB crossing timescales due to uncertainties in the treatment of 3DUP episodes on the TP-AGB. Miller Bertolami (2015) models show a better agreement with the results of Weiss & Ferguson (2009), which were also computed under the assumption of very efficient CBM processes on the TP-AGB. |
Figure 9 shows that the models by Weiss & Ferguson (2009) predict even shorter timescales than our models. This is consistent with the fact that Weiss & Ferguson (2009) adopted higher CBM efficiencies, fCE = fPDCZ = 0.016, during the TP-AGB, and consequently have more efficient 3DUP. When our models are computed with higher CBM efficiencies, the predicted post-AGB timescales are shorter and very close to the results of Weiss & Ferguson (2009). This is shown in Fig. 12, where the value of τcross from the sequences presented here (computed with fCE = 0; Table 3) are compared with the results of Weiss & Ferguson (2009) and our preliminary computations from Miller Bertolami (2015; M15 models, computed with fCE = 0.13, see Appendix B). Different CBM efficiencies lead to different 3DUP histories. More efficient 3DUP, in turn, leads to a higher carbon enrichment of the envelopes and smaller remnant masses Mf for the same initial mass Mi. As shown in Appendix A a higher carbon enrichment of the envelope leads to brighter models (see Fig. 11) and smaller post-AGB envelopes, leading to shorter post-AGB timescales. In addition, post-AGB models of equal final mass (Mf), coming from larger initial masses (Mi), also seem to produce shorter post-AGB timescales (see also Appendix A). This explains why the post-AGB timescales of the models we present here are not as short as those of Weiss & Ferguson (2009) and M15 models. Weiss & Ferguson (2009) and the M15 models predict final masses that are too low for our present understanding of the IFMR, especially around Mi ~ 3 M⊙ (Weidemann 2000; Salaris et al. 2009; Gesicki et al. 2014). In contrast, the models in Table 3 give a much better fit of the IFMR around solar metallicities (Fig. 3).
Finally, due to the different definitions of τtr, it is very difficult to directly compare these values with those quoted by Schönberner (1990), Vassiliadis & Wood (1994), and Blöcker (1995a). It can be safely concluded, however, that our definition yields τtr values that decrease with increasing remnant mass, in agreement with both Schönberner (1990) and Blöcker (1995a), but at variance with the results of Vassiliadis & Wood (1994), which yield higher values and show no significant dependency on the remnant mass.
5. Discussion
The more accurate description of the AGB and post-AGB observables of the new models (Figs. 1–4) makes it reasonable to assume that the new timescales are more reliable than those of the old post-AGB grids. Post-AGB timescales play a role in several studies and shorter timescales certainly have an impact on the conclusions of previous works based on old stellar tracks. In the following section, we discuss these and speculate on the possible consequences of the new post-AGB models and their shortcomings.
Gesicki et al. (2014) determined that the post-AGB evolution predicted by Blöcker (1995a) needed to be accelerated by about a factor ~3 to reconcile the peaks of the mass distributions of WDs and CSPNe. Even more, one expects the peak of the mass distribution of CSPNe to lie somewhat below the peak of the mass distribution of WDs. The timescales of CSPNe are steeply dependent on mass, making lower mass central stars much more abundant than more massive central stars. While the higher luminosity of more massive CSPNe makes them more easily detectable, the difference in luminosities is less significant than the difference in timescales. One might then take the factor of ~3 as a lower limit for the accelerated evolution needed in Blöcker (1995a) post-AGB sequences. As shown in Fig. 9, the new post-AGB timescales are ~3.5 and ~8 times shorter than those computed by Blöcker (1995a) in the range of interest for the peak of the WDs and CSPNe mass distributions (0.57 ≲ M/M⊙ ≲ 0.63). Clearly, the new post-AGB timescales seem to be in very good agreement with the empirical determinations of Gesicki et al. (2014).
The faster evolutionary timescales and higher luminosities of our H-burning sequences should have an important impact on the study of the formation of PNe (Schönberner et al. 2014; Toalá & Arthur 2014). The low-mass models of Schönberner (1983), which are still in use to complement the sequences of Blöcker (1995a), show crossing timescales of ~340 kyr (0.546 M⊙) and ~20 kyr (0.565 M⊙). Our H-burning sequences of similar mass and metallicity (Z0 = 0.02) show crossing timescales about ~3.5 to ≳15 times faster and even faster in the case of M15 models. The discrepancy is even larger in the case of the low-mass models of Vassiliadis & Wood (1994). In order to be able to produce PNe, the central stars need to evolve in less than a few tens of thousand years. If that is not the case, the circumstellar material dissipates before the star becomes hot enough to ionize it. This fact, together with the very long timescales of τcross ≳ 100 kyr of the low-mass models of older grids, leads to the conventional wisdom that low-mass post-AGB stars (≲0.55 M⊙) cannot form PNe; see, e.g., Jacoby et al. (2013), Bond (2015). In this context, the new models might help to explain the existence of single CSPNe with masses lower than ~0.55 M⊙ (Althaus et al. 2010; Werner & Rauch, in prep.). The new models should also have an impact on the question of whether single stellar evolution can form PNe in globular clusters (Jacoby et al. 2013; Bond 2015). Our H-burning post-AGB sequences with ages similar to that of globular clusters (9 to 12 Gyr) have values of τcross ~ 25–70 kyr. Timescales drop to τcross ~ 5–10 kyr for post-AGB sequences with slightly younger progenitors (5 to 7 Gyr); see Tables 2 and 3. Timescales are even shorter in the case of the models of Weiss & Ferguson (2009) and M15 (see Appendix B). The much shorter timescales of the new H-burning post-AGB sequences call into question the idea that single stellar evolution cannot produce PNe in globular clusters.
Some studies of the number of post-AGB stars in old populations like M32 (Brown et al. 2008) and the Galactic halo (Weston et al. 2010) point to a significant lack of post-AGB stars in comparison with the prediction of older stellar evolution models. The fastest evolution of our models can help to diminish these discrepancies, but they will hardly solve them. Because of the age of the hosting population, the post-AGB stars in those systems should be of low mass. In the case of the study of Weston et al. (2010), reproducing the number of post-AGB stars just by increasing the evolutionary speed would require an evolution faster than that of the low-mass models of Weiss & Ferguson (2009). As our models evolve somewhat slower than the models of Weiss & Ferguson (2009) it is clear that our models cannot solve the discrepancy. We can reach a similar conclusion about the discrepancy reported by Brown et al. (2008) in M32. M32 has an almost solar like metallicity and is composed of two main populations: an intermediate age population (2–5 Gyr) of stars that contribute to ~40% of the mass and an old population (>5 Gyr) that contributes to ~55% of the mass (Monachesi et al. 2012). This means that the vast majority of the post-AGB stars should have progenitors between ~1 and ~1.5 M⊙. While our models are faster than the models adopted by Brown et al. (2008) for the same final mass, the difference is smaller when compared at similar progenitor masses (this is also true in the case of our M15 models). In the relevant mass range, our post-AGB timescales are only ~1.4 and ~2.6 (for Mi = 1 and 1.5 M⊙, respectively) times faster than the older models. This seems insufficient to completely solve the discrepancy with the observations.
Finally, a more quantitative comparison with the lifetimes derived by Girardi & Marigo (2007) from the clusters of the Magellanic Clouds point to some shortcomings of the present models. While our models reproduce the right qualitative behavior of the C and M star lifetimes, they quantitatively predict lower timescales by a factor of a few (Fig. 1). This is particularly significant at the higher metallicities of the LMC, where our models predict timescales that are more than four times too short for both M- and C-type stars. While the failure to quantitatively reproduce the timescales of carbon stars might point to an overestimation of the mass-loss rate, the duration of the M-type stars phase cannot be solved this way. This is because in our sequences the duration of the M-type star phase is determined by the intensity of 3DUP, which sets the number of thermal pulses after which the model becomes a carbon star. Given that the CBM at the inner boundary of the convective envelope is already set to a minimum in these sequences (fCE = 0) a decrease of their dredge-up efficiency could only be attained by a decrease in the CBM at the pulse-driven convective zone (fPDCZ). However, as mentioned in the previous section, a decrease of this value would lead to a disagreement between the O abundances at the intershell and those observed in PG1159 stars. It might be necessary to explore alternative mixing processes and the parameter space of pre-AGB stellar evolution models to reproduce all AGB and post-AGB observables simultaneously.
6. Conclusions
We present a detailed grid of post-AGB sequences computed with updated micro- and macrophysics. This is the first grid of post-AGB sequences in the whole range of masses of interest for the formation of PNe that takes the developments in stellar astrophysics in the last 20 years into account. The new models include updated opacities both for the low- and high-temperature regimes and for the C- and O-rich AGB stars. Also, conductive opacities and nuclear reaction rates have been included according to the last developments in the field. During the AGB phase, the models also include a consistent treatment of the stellar winds for the C- and O-rich regimes. In addition, they include CBM processes during the thermal pulses and previous evolutionary stages. This allows the new models to reproduce several AGB and post-AGB observables not reproduced by the older grids (Vassiliadis & Wood 1994; Blöcker 1995a). In particular, the new models reproduce the C/O ratios of several AGB and post-AGB objects of the Galactic disk (Lambert et al. 1986; Smith & Lambert 1990; Kingsburgh & Barlow 1994; Milanova & Kholtygin 2009; Mello et al. 2012; Delgado-Inglada & Rodríguez 2014) and also the mass range of carbon stars in the Magellanic Clouds (Girardi & Marigo 2007). In addition, the IFMR and intershell abundances of the new post-AGB models are consistent with semiempirical determinations from globular clusters (Salaris et al. 2009) and the determinations in post-AGB PG1159 stars (Werner & Rauch, in prep.; Werner & Herwig 2006), respectively.
The main result from our study is that new post-AGB sequences predict post-AGB evolutions, which are at least three to ten times faster than the models of similar mass in the older grids (Vassiliadis & Wood 1994; Blöcker 1995a). Also, the new post-AGB models are 0.1 to 0.3 dex more luminous than the older sequences of similar remnant masses. Qualitatively, the shorter timescales are agreement with the results obtained by Kitsikis (2008) and Weiss & Ferguson (2009), for a restricted mass range and by means of a completely independent code but also assuming updated modeling. The faster evolution of our post-AGB models is in very good quantitative agreement with the empirical determination of Gesicki et al. (2014) from the study of CSPNe in the Galactic bulge. These agreements give us confidence in the main conclusion of our work. The differences between the new models and the older grids is traced back to the update in microphysics and, in particular, to a better modeling of 3DUP events during the TP-AGB. This improved modeling changes the IMFR and final C content of the envelope of post-AGB models, leading to shorter post-AGB timescales.
The new grids should have a significant impact in studies of CSPNe. On the theoretical side, we expect the much faster evolution will have a significant impact for the formation and evolution of PNe. Radiation-hydrodynamic numerical simulations (Schönberner et al. 2014; Toalá & Arthur 2014) of the formation of PNe based on new post-AGB stellar evolution models would be very valuable. The faster post-AGB evolution of the new models calls into question the conventional wisdom that single stellar evolution cannot lead to the formation of PNe in globular clusters (Jacoby et al. 2013; Bond 2015). In particular, the fastest evolution of the new models should allow for the formation of low-mass CSPNe (M ~ 0.55M⊙) in line with spectroscopic and asteroseismic determinations (Althaus et al. 2010; Werner & Rauch, in prep.). In addition, the brighter core mass-luminosity relation of the new models (see Fig. 11) will affect estimations of the masses of post-AGB stars based on their luminosity; e.g. Jacoby et al. (2013). Finally, it would also be worthwhile to carry out another study of the implications of the new timescales for the properties of the PNLF for different populations (Marigo et al. 2004).
Our models might help to diminish the discrepancies between the predicted and observed number of post-AGB objects in M32 and the Galactic Halo. A simple estimation of the timescales indicates that they might be unable to completely solve these discrepancies, but a detailed study is necessary.
The agreement of the new models with all the previously mentioned AGB and post-AGB observational constraints along with the much updated modeling of the stellar physics, strongly suggest that these models should be preferred over the older models. However, it would be unwise to assume the current models to be perfect. Our sequences fail to quantitatively reproduce the number of M- and C-type AGB stars as derived from the Magellanic Clouds. As discussed in the previous section, it is not clear that it is possible to quantitatively reproduce all AGB and post-AGB observational constraints simultaneously within the present framework for CBM processes on the AGB. An exhaustive calibration of models on the basis of the AGB and post-AGB observables is needed to improve our knowledge of the post-AGB phase.
Finally, but not of least importance, the sequences we present here were computed under the assumption of steady winds on and after the TP-AGB. While it is possible to devise tricks to avoid the instabilities at the end of the TP-AGB, it is clear that there are some physical reasons behind these instabilities (Wagenhuber & Weiss 1994b; Lau et al. 2012) and a proper assessment of the consequences of these instabilities is needed to improve our understanding of the post-AGB phase. An almost total ejection of the envelope could produce post-AGB stars that depart from the AGB with less massive envelopes. Consequently, these instabilities could produce much faster post-AGB evolutions than predicted by our current models.
The main grid of H-burning post-AGB sequences computed in this work, as well as the M15 models (also presented in Tables B.1 and B.2), are provided in tabulated electronic form and at similar points in the HR diagram to allow for an easy interpolation. Sequences are available in electronic form at our web site7 and at the CDS.
Testing of the code at the main sequence and red giant phases was performed in a series of workshops “The Aarhus Red Giants Workshops”, which can be found at http://users-phys.au.dk/victor/rgwork/
Available at http://opalopacity.llnl.gov/EOS_2005/
The existence of the 13C pocket needed for s-process nucleosynthesis implies the need for a layer with both H and 12C after the 3DUP. While the problem with the IFMR comes from the inclusion of CBM at the bottom of the convective envelope before and during the development of the 3DUP. As the entropy barrier drops during the thermal pulse, it seems plausible that CBM or other mixing processes are not equally effective before and at the end of the thermal pulse.
Blöcker (1995a) defines the end of the transition stage at the point where the pulsation period P = 50 d, which also sets the zero age for their post-AGB tracks. This definition corresponds to a point in the HR diagram where the post-AGB object has log Teff = 3.78–3.90, depending on mass.
Acknowledgments
This work was supported by a fellowship for postdoctoral researchers from the Alexander von Humboldt Foundation. M3B. thanks A. Weiss, A. Serenelli, L. Althaus, M. Viallet for helpful discussion during the development of this work and K. Werner for the new data on PG1159 stars. A. Weiss is also warmly acknowledged for reading and commenting on the manuscript. We thank the first anonymous referee for very detailed reports and, in particular, the second referee (J. Lattanzio) for very constructive and helpful reports that strongly improved the final version of this manuscript. Finally, we are especially grateful to the editor (R. Kotak) for her patience and positive approach to the peer review process.
References
- Abell, G. O., & Goldreich, P. 1966, PASP, 78, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aver, E., Olive, K. A., Porter, R. L., & Skillman, E. D. 2013, J. Cosmol. Astropart. Phys., 11, 17 [Google Scholar]
- Bahcall, J. N., Pinsonneault, M. H., & Wasserburg, G. J. 1995, Rev. Mod. Phys., 67, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, L. 1932, Z. Astrophys., 5, 117 [NASA ADS] [Google Scholar]
- Bladh, S., Höfner, S., Aringer, B., & Eriksson, K. 2015, A&A, 575, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blöcker, T. 1995a, A&A, 299, 755 [NASA ADS] [Google Scholar]
- Blöcker, T. 1995b, A&A, 297, 727 [NASA ADS] [Google Scholar]
- Blöcker, T. 2001, Ap&SS, 275, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bond, H. E. 2015, AJ, 149, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Smith, E., Ferguson, H. C., et al. 2008, ApJ, 682, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Burgers, J. M. 1969, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán, S., Isern, J., García-Berro, E., & Ribas, I. 2008, MNRAS, 387, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Van Grootel, V., Brassard, P., et al. 2013, in EPJ Web Conf., 43, 4005 [Google Scholar]
- Ciardullo, R. 2012, Ap&SS, 341, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2007, A&A, 475, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coc, A., Uzan, J.-P., & Vangioni, E. 2014, J. Cosmol. Astropart. Phys., 10, 50 [Google Scholar]
- Constantino, T., Campbell, S., Gil-Pons, P., & Lattanzio, J. 2014, ApJ, 784, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N., & Stewart, J. N. 1970a, ApJS, 19, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N., & Stewart, J. N. 1970b, ApJS, 19, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado-Inglada, G., & Rodríguez, M. 2014, ApJ, 784, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Doherty, C. L., Gil-Pons, P., Siess, L., Lattanzio, J. C., & Lau, H. H. B. 2015, MNRAS, 446, 2599 [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Ludwig, H.-G., & Steffen, M. 1996, A&A, 313, 497 [Google Scholar]
- Gesicki, K., Zijlstra, A. A., Hajduk, M., & Szyszka, C. 2014, A&A, 566, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., & Marigo, P. 2007, A&A, 462, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Williams, B. F., Gilbert, K. M., et al. 2010, ApJ, 724, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse (Cambridge University Press), 15 [Google Scholar]
- Groenewegen, M., & Sloan, G. C. 2013, in Proceedings of The Life Cycle of Dust in the Universe: Observations, Theory, and Laboratory Experiments (LCDU2013), 18–22 November, Taipei, Taiwan., 94 [Google Scholar]
- Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum, F. 1998, MNRAS, 293, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, AR&AA, 43, 435 [Google Scholar]
- Herwig, F., Blöcker, T., Schönberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Herwig, F., Schönberner, D., & Blöcker, T. 1998, A&A, 340, L43 [NASA ADS] [Google Scholar]
- Herwig, F., Blöcker, T., Langer, N., & Driebe, T. 1999, A&A, 349, L5 [NASA ADS] [Google Scholar]
- Höfner, S. 2012, Nature, 484, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Stasińska, G., & Guseva, N. G. 2013, A&A, 558, A57 [Google Scholar]
- Jacoby, G. H., Ciardullo, R., De Marco, O., et al. 2013, ApJ, 769, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A., & Lattanzio, J. C. 2007, PASA, 24, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, 30 [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 271, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (New York: Springer) [Google Scholar]
- Kitsikis, A. 2008, Ph.D. Thesis, Ludwig-Maximilians-Universität München [Google Scholar]
- Kwitter, K. B., Méndez, R. H., Peña, M., et al. 2014, Rev. Mexicana Astron. Astrofis., 50, 203 [Google Scholar]
- Lambert, D. L., Gustafsson, B., Eriksson, K., & Hinkle, K. H. 1986, ApJS, 62, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, H. H. B., Gil-Pons, P., Doherty, C., & Lattanzio, J. 2012, A&A, 542, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lugaro, M., Herwig, F., Lattanzio, J. C., Gallino, R., & Straniero, O. 2003, ApJ, 586, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 1991, A&AS, 89, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Marigo, P. 2002, A&A, 387, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Weiss, A., & Groenewegen, M. A. T. 1999, A&A, 351, 161 [NASA ADS] [Google Scholar]
- Marigo, P., Girardi, L., Groenewegen, M. A. T., & Weiss, A. 2001, A&A, 378, 958 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Weiss, A., Groenewegen, M. A. T., & Chiosi, C. 2004, A&A, 423, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Bressan, A., Nanni, A., Girardi, L., & Pumo, M. L. 2013, MNRAS, 434, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2010, A&A, 509, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mello, D. R. C., Daflon, S., Pereira, C. B., & Hubeny, I. 2012, A&A, 543, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milanova, Y. V., & Kholtygin, A. F. 2009, Astron. Lett., 35, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2015, in 19th European Workshop on White Dwarfs, eds. P. Dufour, P. Bergeron, & G. Fontaine, ASP Conf. Ser., 493, 83 [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & García-Berro, E. 2013, ApJ, 775, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Monachesi, A., Trager, S. C., Lauer, T. R., et al. 2012, ApJ, 745, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N. 1999, A&A, 344, 617 [NASA ADS] [Google Scholar]
- Norris, B. R. M., Tuthill, P. G., Ireland, M. J., et al. 2012, Nature, 484, 220 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ostlie, D. A., & Cox, A. N. 1986, ApJ, 311, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1970, Acta Astron., 20, 47 [NASA ADS] [Google Scholar]
- Pauldrach, A., Puls, J., Kudritzki, R. P., Mendez, R. H., & Heap, S. R. 1988, A&A, 207, 123 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Méndez, R. H. 2004, A&A, 419, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [Google Scholar]
- Renzini, A. 1989, in Planetary Nebulae, ed. S. Torres-Peimbert, IAU Symp., 131, 391 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfield, P., Marigo, P., Girardi, L., et al. 2014, ApJ, 790, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schönberner, D. 1979, A&A, 79, 108 [NASA ADS] [Google Scholar]
- Schönberner, D. 1983, ApJ, 272, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D. 1990, in From Miras to Planetary Nebulae: Which Path for Stellar Evolution?, eds. M. O. Mennessier, & A. Omont (Editions Frontières), 355 [Google Scholar]
- Schönberner, D., & Steffen, M. 2007, in Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, eds. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 343 [Google Scholar]
- Schönberner, D., Jacob, R., Lehmann, H., et al. 2014, Astron. Nachr., 335, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, K. 1906, Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen. Math.-phys. Klasse, 195, 41 [Google Scholar]
- Seaton, M. J. 2007, MNRAS, 382, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A. M., Basu, S., Ferguson, J. W., & Asplund, M. 2009, ApJ, 705, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Shklovsky, I. S. 1957, in Non-stable stars, ed. G. H. Herbig, IAU Symp., 3, 83 [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., Tout, C. A., & Pols, O. R. 2004, MNRAS, 352, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., Fossati, L., Passy, J.-C., & Schneider, F. R. 2015, A&A, 575, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steigman, G. 2007, Annual Review of Nuclear and Particle Science, 57, 463 [Google Scholar]
- Stothers, R. B., & Chin, C.-W. 1992, ApJ, 390, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Toalá, J. A., & Arthur, S. J. 2014, MNRAS, 443, 3486 [NASA ADS] [CrossRef] [Google Scholar]
- Tuchman, Y., Glasner, A., & Barkat, Z. 1983, ApJ, 268, 356 [NASA ADS] [CrossRef] [Google Scholar]
- van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1994, ApJS, 92, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., & Marigo, P. 2010, MNRAS, 408, 2476 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Stanghellini, L., Dell’Agli, F., García-Hernández, D. A., & Di Criscienzo, M. 2015, MNRAS, 452, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagenhuber, J., & Weiss, A. 1994a, A&A, 286, 121 [NASA ADS] [Google Scholar]
- Wagenhuber, J., & Weiss, A. 1994b, A&A, 290, 807 [NASA ADS] [Google Scholar]
- Weidemann, V. 2000, A&A, 363, 647 [NASA ADS] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Heners, N. 2013, in EPJ Web of Conf., 43, 1002 [Google Scholar]
- Werner, K., & Herwig, F. 2006, PASP, 118, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Weston, S., Napiwotzki, R., & Catalán, S. 2010, in AIP Conf. Ser. 1273, eds. K. Werner, & T. Rauch, 197 [Google Scholar]
- Woitke, P. 2006, A&A, 460, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolff, S., & Simon, T. 1997, PASP, 109, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, P. R. 1990, in From Miras to Planetary Nebulae: Which Path for Stellar Evolution?, eds. M. O. Mennessier, & A. Omont (Editions Frontières), 67 [Google Scholar]
- Zijlstra, A. A., van Hoof, P. A. M., & Perley, R. A. 2008, ApJ, 681, 1296 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The physics behind the crossing time (τcross)
In Sects. 4 and 5 we have discussed that the timescales of the post-AGB evolution (τcross) predicted by the new models are much shorter than those of the older sequences of Vassiliadis & Wood (1994) and Blöcker (1995a) (Fig. 9); this is in agreement with the more recent results presented by Weiss & Ferguson (2009) and Miller Bertolami (2015). The value of τcross during the post-AGB phase is mainly set by the speed at which the remaining H-rich envelope (Menv) is consumed to its final value in the white dwarf phase. Models that depart from the AGB with less massive envelopes or with higher luminosities (i.e., faster H-burning) display shorter timescales. In what follows, we show that updated microphysics and pre-AGB modeling, together with carbon pollution of the envelope and lower values of Mf(Mi), lead to post-AGB models that are brighter and depart from the AGB with smaller Menv, leading to a faster post-AGB evolution.
 |
Fig. A.1 Evolution of the main quantities of the sequences with Mf = 0.5281 M⊙ and Mf = 0.5615 M⊙ (Z0 = 0.02). These sequences have higher luminosities and smaller final envelope masses than the models of similar final mass of Schönberner (1983). |
Figure A.1 shows the evolution of the main quantities of the sequences with Mf = 0.5281 M⊙ and Mf = 0.5615 M⊙ (Z0 = 0.02) we present here. These sequences do not undergo 3DUP on the TP-AGB and their envelope composition is not enriched in CNO elements. As a result of the similar masses and metallicities, these two sequences can be directly compared with the 0.546 M⊙ and 0.565 M⊙ sequences of Schönberner (1983). The 0.546 M⊙ (0.565 M⊙) of Schönberner (1983) depart from the AGB (i.e., log Teff = 3.85) with Menv ~ 0.0073 M⋆ (Menv ~ 0.0022 M⋆) and a post-AGB luminosity of ~1500 L⊙ (~3900 L⊙). As shown in Fig. A.1, our Mf = 0.5281 M⊙ (Mf = 0.5615 M⊙) sequence departs from the AGB with Menv ~ 0.0031 M⋆ (Menv ~ 0.0014 M⋆) and a post-AGB luminosity of ~3260 L⊙ (~5360 L⊙). We see that models with an updated treatment of the previous evolution, in particular, opacities and nuclear reaction rates, lead to models that depart from the AGB with smaller H-envelope masses and brighter luminosities. Consequently, the new models do evolve much faster than the older models.
There is another improvement of the new models that leads to even shorter timescales. As we discussed in Sect. 3, the new models are able to agree with the expected carbon enrichment as observed in many AGB and post-AGB observables (Figs. 1 and 2). This is a consequence of the more efficient 3DUP present in the new models. Next, we discuss two numerical experiments to show that more efficient 3DUP on the TP-AGB leads to post-AGB models that evolve faster than in the absence of 3DUP.
 |
Fig. A.2 Evolution of the main quantities of the sequences with Mf = 0.5340 M⊙ (Z0 = 0.001) with different degrees of CNO pollution in the H envelope (see text for a discussion). There are higher luminosities, smaller final envelope masses and, consequently, shorter post-AGB timescales when the envelope is polluted with C and O. |
Figure A.2 shows the main properties of a model with Mf = 0.5340 M⊙ (Z0 = 0.001) when different degrees of CNO pollution are added to the H-rich envelope. The original sequence corresponds to the Mf = 0.5340 M⊙ (Z0 = 0.001) of initially 0.9 M⊙ (see Table 3), which does not undergo 3DUP episodes and has a CNO element mass fraction of XCNO = 0.0007. For the other sequences in Fig. A.2, we artificially increased the CNO mass fraction by factors of 2, 4, 8. and 16, before the departure from the AGB, and recomputed the post-AGB evolution. The proportion of the polluting material is 82% 12C and 12% 16O so that NC/NO ~ 5 for highest adopted pollution, as observed in the detailed models; see Table 3. As shown in Fig. A.2, the higher the CNO pollution of the envelope, the higher the luminosity and the lower the mass of the H envelope at the departure from the AGB. A qualitative explanation of this behavior can be obtained from the study of toy envelope models; see (Tuchman et al. 1983; Marigo et al. 1999). The enrichment of the envelope with CNO element alters both the CNO burning rate and the molecular weight of the envelope, leading to higher luminosities for the same core mass. Models with efficient 3DUP consequently show shorter post-AGB timescales.
Our models of Mi ≳ 1.5 M⊙ undergo efficient 3DUP and CNO pollution of the envelope. Consequently, they show higher luminosities, smaller post-AGB H envelopes, and shorter post-AGB timescales than models with no efficient 3DUP (as those of the older grids). This effect is more important for sequences at low initial metallicities (Z0), as the relative increase of the CNO elements is much higher.
 |
Fig. A.3 Evolution of the main quantities of the sequences A, B and B∗ from the numerical experiment described in Sect. 5 and Table A.1. |
In addition to the CNO pollution of the envelope, 3DUP changes the IFMR of the models; see Salaris et al. (2009) for a discussion. Intense 3DUP delays the growth of the HFC during the TP-AGB evolution, leading to smaller final masses Mf than in the absence of 3DUP for the same initial mass Mi. Different HFC histories lead to different core mass-luminosity relations and also to different H envelopes at the departure from the AGB. The following simple numerical experiment shows this point. We have taken two of our H-burning post-AGB sequences with different evolutionary histories, but similar core masses, and changed the envelope on top of one of them to match the composition of the other; Z0 = 0.01 sequences with initial masses Mi = 2 and 1.5 M⊙ in Table 3, from now on sequences A and B, respectively. This was done on the TP-AGB to allow the H-shell to advance to the location of the new composition and to give time for the envelope structure to relax. As shown in Fig. A.3, when the envelope composition of sequence A is put on top of the HFC of sequence B (from now on sequence B∗), the luminosity is increased due to a higher molecular weight and the mass fraction of CNO elements. Yet, the luminosity of sequence B∗ is lower than that of sequence A, in spite of having the same envelope composition and almost the same core mass. In fact, the core mass is even slightly larger; see Fig. A.3. This experiment shows that the influence of the core goes beyond the value of its core mass. The burning shell is not influenced either by the core mass or the core radius alone, but only through the gravitational acceleration g(r) at the location of the burning shell. Table A.1 shows some relevant quantities of the sequences A, B and B∗ at a similar point in the HR diagram. As can be seen, the change in the envelope composition of ~39% in the CNO-mass fraction8 and of 1.3% in the molecular weight can help to understand the ~5.5% change in the luminosity between sequences with the same core but different envelopes (see Marigo et al. 1999 for a very similar discussion). However, in spite of the ~5.5% luminosity increase resulting from a different envelope composition, model B∗ is still ~9% less luminous than sequence A (whose core is 0.09% smaller). A closer examination of the model shows that the gravitational pull at the location of the H-burning shell is ~10% higher than that of sequence B and B∗. This experiment shows that at the moment of the departure from the AGB our models show a core still warm enough that the strict core mass-radius relation does not hold (they are yet not “converged” in the sense discussed by Paczyński 1970). Consequently, previous evolutionary histories still play a significant role in determining the post-AGB timescales and luminosities. This also helps to explain why our 2 M⊙ (Z0 = 0.02) is ~50% faster than our 1.5 M⊙ (Z0 = 0.02) in spite of having similar core masses and the second having almost twice the mass fraction of CNO elements (Table 3). The influence of the core through the gravitational pull at the H-burning shell is even more important than the chemical change due to 3DUP.
We have shown that the short post-AGB timescales of the new post-AGB models we present (Table 3) can be traced to three main causes. First, as a result of the update in the micro- and macrophysics of the evolutionary models, the new models depart with smaller H envelopes and brighter luminosities. Second, because of the CNO pollution of the envelope produced by 3DUP in most of the sequences, the post-AGB models have even smaller H envelopes with brighter luminosities. Third, also because of the existence of 3DUP, the post-AGB models of a given mass Mf originate from initial models of higher mass Mi. Post-AGB models derived from initial models of higher mass have more compact HFCs and also depart from the AGB with smaller H envelopes and with brighter luminosities.
Appendix B: M15 Post-AGB sequences (Miller Bertolami 2015)
M15 models have been computed with the same code and microphysics but a different choice of the CBM processes during the TP-AGB. In particular, M15 models were computed under the assumption of efficient CBM process at the base of all convective envelopes, setting9fCE = 0.13. Consequently, M15 models undergo more efficient 3DUP episodes than the models of our main grid; Tables 3 and 2. As discussed in Sect. 5, previous evolutionary history can play an important role in the determination of the post-AGB timescales of the models. In particular, models with more efficient 3DUP during the TP-AGB have lower final masses (Mf) for the same initial mass (Mi). Consequently, and in line with the discussion of Sects. 4 and 5, more efficient 3DUP leads to faster post-AGB evolution for the same value of Mf. While M15 models fail to reproduce the IFMR at almost solar metallicities, we consider these models valuable at assessing the uncertainty behind the results we present. In fact, these models predict lifetimes of the C-rich phase in better agreement with the determinations of Girardi & Marigo (2007) from the study of the Magellanic Clouds. For this reason, we present in this appendix the main properties of the M15 model in the previous evolutionary history (table B.1) and during the post-AGB phase (Table B.2 and Fig. B.1).
Main properties of the M15 sequences from the ZAMS to the TP-AGB.
Main post-AGB properties of the H-burning sequences computed by M15.
 |
Fig. B.1 HR diagrams of the H-burning post-AGB sequences computed by M15 for different masses and initial metallicities (Table B.2). Tracks are presented from the beginning of the post-AGB phase when the H-rich envelope drops below Menv = 0.01 M⋆ to the moment in which the star has already entered its white dwarf cooling sequence at L⋆ = L⊙. At that point gravitational settling should have already started to turn post-AGB stars into DA-WDs, a process not included in the present computations. Red lines indicate computed isochrones for different ages since the zero point defined at log Teff = 3.85. |
Appendix C: Numerical improvements and convergence issues
The computation of the very end of the TP-AGB suffers from convergence problems (Wagenhuber & Weiss 1994a; Weiss & Ferguson 2009; Lau et al. 2012). This implies that a lot of human time (babysitting) is required to compute the transition from the TP-AGB to the CSPNe phase. Even when codes converge, convergence happens at the expense of prohibitively small time steps (even down to Δt ~ 1 h). In the following, we describe the methods and tricks adopted to improve the convergence of the code during the very end of the AGB.
The main difference with previous works is that now remeshing in LPCODE can be done by checking the assumption of linearity made on the differential equations of structure, 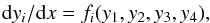 as suggested by Wagenhuber & Weiss (1994a), where yi are some function of the structure variables l, P, r, and T and x is a function of the Lagrangian coordinate m. However, we adopt a much more straightforward approach than that of Wagenhuber & Weiss (1994a). Instead, we simply check that the relative changes of dyi/dx from one shell (n) to the next (n + 1) are kept under a certain value, i.e.,
as suggested by Wagenhuber & Weiss (1994a), where yi are some function of the structure variables l, P, r, and T and x is a function of the Lagrangian coordinate m. However, we adopt a much more straightforward approach than that of Wagenhuber & Weiss (1994a). Instead, we simply check that the relative changes of dyi/dx from one shell (n) to the next (n + 1) are kept under a certain value, i.e., 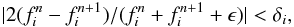 where ϵ is an arbitrary value to avoid divergence in the case of
where ϵ is an arbitrary value to avoid divergence in the case of 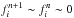 . According to this criterion, a mesh point is added when it is not fulfilled at least for one equation, and removed when all equations fulfill this mesh point by more than one order of magnitude.
. According to this criterion, a mesh point is added when it is not fulfilled at least for one equation, and removed when all equations fulfill this mesh point by more than one order of magnitude.
Despite numerical improvements and debugging, our computations of the end of the AGB still face several converge problems. In particular, two main instabilities were found during the computation of these sequences. Although we have not studied them in detail they can be traced back to the instabilities already mentioned in the literature. Both were found in late TP-AGB models in which the H-rich envelope mass has been significantly reduced and is already comparable to the mass of the HFC. The first instability might already develop in intermediate-mass models during the TP-AGB just after the thermal pulses when the envelope expands as a consequence of the energy injected by the thermal pulse and the H-burning shell is temporarily shut down. We find that as the luminosity of the star increases a behavior arises that is similar to the thermal hydrogen instability described by Wagenhuber & Weiss (1994b), and our simulations crash. While it would be worth studying whether such instability finally develops into a sudden ejection of the upper parts of the envelope, our code is unable to deal with such hydrodynamic situations. The instability develops in the upper part of the H-rich envelope and thus it is very unlikely that it would lead to the ejection of the whole H-rich envelope and the termination of the AGB phase. We assume that the mean mass ejection during the TP-AGB is well described by the steady winds (Eqs. (1)–(3), (5) and (6)). To avoid the lack of convergence, we force the integration of the outer stellar envelope (were dS/dt = 0 is assumed; see Althaus et al. 2003 for details) below the point where H recombination takes place. A second instability was found in intermediate-mass (Mi ≳ 2 M⊙) models already departing from the AGB at the base of the H-rich envelope where the iron opacity peak is found, causing convection to become slightly superadiabatic and radiation pressure to become dominant, at some points becoming even more than one order of magnitude larger than the gas pressure. This instability is thus related to the instability discussed in detail by Lau et al. (2012) and references therein. In our sequences we do not find a clear runaway instability as in the study of Lau et al. (2012), probably because of the lower luminosity and mass of our sequences. This instability does, however, force the timestep to very small values (even less than one hour). This transition time, between the end of the AGB and the beginning of the CSPNe phase, is on the order of 1000 to 10 000 yrs and, with such small timesteps, it would require several millions of timesteps to compute this short-lived phase. This has to be compared with the few thousand to tens of thousands of models required to compute the whole evolution up to the beginning of the AGB phase. Even if the models do not fail to converge, such small timesteps are unaffordable. This instability becomes worse for more massive (i.e., luminous) models. In order to overcome this difficulty we have forced the bottom of the convective envelope to the adiabatic regime. As discussed by Lau et al. (2012) forcing adiabatic convection helps to avoid this instability. In fact, when this is carried out, we find that the oscillations in the eg = −T∂s/∂t term in the energy equation are damped, which facilitates much larger timesteps. This was done only at the very bottom of the convective envelope where convection is only slightly superadiabatic to allow the outer regions of the envelope to be superadiabatic and thus obtain the correct stellar radius and effective temperature. This is important because our mass-loss prescriptions (Eqs. (1)–(3), (5) and (6)) are strongly dependent on having the right surface parameters. In addition we have checked that this procedure does not affect our results by computing a Mi = 2 M⊙ (Z0 = 0.01) sequence with and without this alteration of the temperature profile at the base of the convective envelope and obtaining the same results. Finally, a different convergence problem arose (only) in the case of our most massive and highest metallicity sequence (Mi = 4 M⊙, Z0 = 0.02). In that sequence convergence problems also arose during the integration of the outer boundary conditions of the model at high effective temperatures (log Teff ≳ 5). This is not surprising since, at those
Teff values, the opacity bump of the iron group elements is located close to the photosphere and even in the atmosphere. Then at high luminosities, the Eddington limit is very close and hydrostatic solution might not exist. We avoided this convergence issue by adopting a very rough boundary condition for the photospheric pressure as 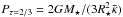 , where
, where  is a mean value of the Rosseland opacity in the atmosphere.
is a mean value of the Rosseland opacity in the atmosphere.
All Tables
M1 and M2 values for the boundary mixing recipe at the convective core in the main sequence, i.e., fCHB = 0.0174×(Mi−M1)/(M2−M1) for Mi between M1 and M2.
All Figures
 |
Fig. 1 Lifetimes of our Z0 = 0.01 and Z0 = 0.001 sequences as C and M stars on the AGB as compared with the timescales derived by Girardi & Marigo (2007) from the Magellanic Clouds. In the case of M-type stars, we computed the lifetime of the star as a O-rich object with MBol< −3.6 to be consistent with the values presented by Girardi & Marigo (2007). This is why the values plotted here do not agree with the τTP−AGB(M) in Table 2. |
| In the text | |
 |
Fig. 2 Carbon and oxygen abundances of AGB and post-AGB objects in the Galactic disk as compared with the predictions of the Z0 = 0.02 (upper set) and Z0 = 0.01 sequences (lower set). Tracks in blue lines correspond to those that experience significant 3DUP, while thick black lines indicate sequences with no significant 3DUP. The red line corresponds to the evolution of the 4 M⊙ (Z0 = 0.02) sequence that experiences both 3DUP and hot-bottom burning. Abundances are presented in the customary astronomical scale for logarithmic abundances, log ϵX = log (NX/NH) + 12, where NX and NH are the number densities of elements X and H, respectively. |
| In the text | |
 |
Fig. 3 Initial final mass relation of the sequences computed in this work and those of (Miller Bertolami 2015, M15). The semiempirical IFMR derived from clusters for solar-like metallicities by Salaris et al. (2009), and also that of Gesicki et al. (2014), are shown for comparison. |
| In the text | |
 |
Fig. 4 He-, C-, and O- intershell abundances in the post-AGB phase as compared with the derived abundances of PG1159 type stars of similar mass (Werner & Rauch, in prep.). Most of the high log g stars (see color bar) are probably undergoing gravitational settling, and thus the high He abundances might not reflect the original intershell composition. |
| In the text | |
 |
Fig. 5 Upper panel: IFMR of the models presented here for Z0 = 0.02 compared with the results from state-of-the-art AGB model grids available in the literature (Karakas & Lattanzio 2007; Cristallo et al. 2011; Weiss & Ferguson 2009) and the IFMR of Weidemann (2000). Lower panel: third dredge up efficiencies (λ) during the TP-AGB for different models of a 3 M⊙ and Z0 = 0.02 (Herwig 2000; Stancliffe et al. 2004; Karakas & Lattanzio 2007; Cristallo et al. 2011). |
| In the text | |
 |
Fig. 6 C/O ratios at the end of the TP-AGB of the present models as compared with results available in the literature (Weiss & Ferguson 2009; Cristallo et al. 2011). |
| In the text | |
 |
Fig. 7 Upper panel: HR diagram of our Z0 = 0.001 sequences that departed from the AGB as H-burners. Lower panel: mass of the H-rich envelope as a function of log Teff for the same sequences. Red dots indicate the moment in which Menv/Mstar = 0.01, which has been used to define the beginning of the post-AGB. |
| In the text | |
 |
Fig. 8 HR diagrams of the H-burning post-AGB sequences we computed for different masses and initial metallicities. Tracks are presented from the beginning of the post-AGB phase when the H-rich envelope drops below Menv = 0.01 M⋆ to the moment in which the star has already entered its white dwarf cooling sequence at L⋆ = L⊙. At that point gravitational settling should have already started to turn post-AGB stars into DA-WDs, a process not included in the present computations. Red lines indicate computed isochrones for different ages since the zero point defined at log Teff = 3.85. Thin gray lines in the Z0 = 0.001 and Z0 = 0.0001 panels correspond to the evolution of the Mi = 0.8 M⊙ He-burning sequences shown in Fig. 10 (Mf = 0.4971 M⊙ and 0.5183 M⊙, respectively). |
| In the text | |
 |
Fig. 9 Crossing timescales from the zero point, set at log Teff = 4 to allow comparisons with all previous works, to the point of maximum effective temperature in the HR diagram; i.e., the so-called knee of the evolutionary tracks shown in Fig. 8. Timescales are shown for all the sequences presented and the H-burning post-AGB sequences available in the literature, i.e., (Vassiliadis & Wood 1994, VW94); (Schönberner 1983, Blöcker 1995a, B95+S83); and (Weiss & Ferguson 2009, WF09). Crossing timescales of the new sequences (this work and also Weiss & Ferguson 2009) are much shorter than the crossing timescales of the H-burning models of Schönberner (1983), Vassiliadis & Wood (1994), Blöcker (1995a). The sudden decrease in τcross at Mf ~ 0.58 M⊙ (Z0 = 0.02, 0.01 and 0.001) can be traced back to differences in the previous evolutionary history of the models (see text). Because of slightly different definitions of the zero point, the numbers do not completely agree with the value of τcross given in Table 3. |
| In the text | |
 |
Fig. 10 Evolution of log Teff (upper panel) and log L/L⊙ (lower panel) during the post-AGB phase and the end of the TP-AGB. The zero point of the x-axis was taken at the last time the sequence had log Teff = 3.85 before evolving toward the white dwarf cooling phase. Time is shown in years for the Mi = 0.8 M⊙ sequences, but it has been multiplied by a factor 10 for the Mi = 1.5 M⊙ sequence to allow proper visualization. |
| In the text | |
 |
Fig. 11 Post-AGB mass-luminosity relation of the old H-burning models as compared with that of the new models we present here and in Miller Bertolami (2015). There is a much higher luminosity for the same remnant mass of the new models. |
| In the text | |
 |
Fig. 12 Same as Fig. 9 (although with the zero points set at log Teff = 3.85), but comparing the H-burning sequences with those originally computed by Miller Bertolami (2015) under different assumptions of the evolution on the TP-AGB with the same code and microphysics. This shows the uncertainty in the computed post-AGB crossing timescales due to uncertainties in the treatment of 3DUP episodes on the TP-AGB. Miller Bertolami (2015) models show a better agreement with the results of Weiss & Ferguson (2009), which were also computed under the assumption of very efficient CBM processes on the TP-AGB. |
| In the text | |
 |
Fig. A.1 Evolution of the main quantities of the sequences with Mf = 0.5281 M⊙ and Mf = 0.5615 M⊙ (Z0 = 0.02). These sequences have higher luminosities and smaller final envelope masses than the models of similar final mass of Schönberner (1983). |
| In the text | |
 |
Fig. A.2 Evolution of the main quantities of the sequences with Mf = 0.5340 M⊙ (Z0 = 0.001) with different degrees of CNO pollution in the H envelope (see text for a discussion). There are higher luminosities, smaller final envelope masses and, consequently, shorter post-AGB timescales when the envelope is polluted with C and O. |
| In the text | |
 |
Fig. A.3 Evolution of the main quantities of the sequences A, B and B∗ from the numerical experiment described in Sect. 5 and Table A.1. |
| In the text | |
 |
Fig. B.1 HR diagrams of the H-burning post-AGB sequences computed by M15 for different masses and initial metallicities (Table B.2). Tracks are presented from the beginning of the post-AGB phase when the H-rich envelope drops below Menv = 0.01 M⋆ to the moment in which the star has already entered its white dwarf cooling sequence at L⋆ = L⊙. At that point gravitational settling should have already started to turn post-AGB stars into DA-WDs, a process not included in the present computations. Red lines indicate computed isochrones for different ages since the zero point defined at log Teff = 3.85. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


