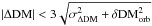| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 27 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201527178 | |
| Published online | 08 January 2016 | |
A LOFAR census of millisecond pulsars
1
ASTRON, the Netherlands Institute for Radio Astronomy,
Postbus 2,
7990 AA
Dwingeloo,
The Netherlands
e-mail:
kondratiev@astron.nl
2
Astro Space Centre, Lebedev Physical Institute, Russian Academy of
Sciences, Profsoyuznaya Str.
84/32, 117997
Moscow,
Russia
3
Fakultät für Physik, Universität Bielefeld,
Postfach 100131, 33501
Bielefeld,
Germany
4
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
5
Anton Pannekoek Institute for Astronomy, University of
Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
6
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
7
Jodrell Bank Centre for Astrophysics, School of Physics and
Astronomy, University of Manchester, Manchester
M13 9PL,
UK
8
Centre for Astrophysics and Supercomputing, Swinburne University
of Technology, Mail H30, PO Box
218, VIC
3122,
Australia
9
ARC Centre of Excellence for All-sky Astrophysics (CAASTRO), The
University of Sydney, 44 Rosehill
Street, Redfern,
NSW
2016,
Australia
10
SKA Organisation, Jodrell Bank Observatory,
Lower Withington, Macclesfield,
Cheshire, SK11 9DL, UK
11
School of Physics and Astronomy, University of
Southampton, SO17 1BJ, UK
12
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
13
LPC2E – Université d’Orléans/CNRS, 45071
Orléans Cedex 2,
France
14
Station de Radioastronomie de Nançay, Observatoire de Paris, PSL
Research University, CNRS, Univ.
Orléans, OSUC, 18330
Nançay,
France
15
Oxford Astrophysics, Denys Wilkinson Building, Keble
Road, Oxford
OX1 3RH,
UK
16
Department of Physics & Astronomy, University of the
Western Cape, Private Bag
X17, 7535
Bellville, South
Africa
17
Department of Physics and Electronics, Rhodes
University, PO Box
94, 6140
Grahamstown, South
Africa
18
NAOJ Chile Observatory, National Astronomical Observatory of
Japan, 2-21-1 Osawa, Mitaka,
181-8588
Tokyo,
Japan
19
INAF–Osservatorio Astronomico di Cagliari,
via della Scienza 5,
09047
Selargius ( Cagliari),
Italy
20
CSIRO Astronomy and Space Science, PO Box 76,
Epping, NSW
1710,
Australia
21
Laboratoire AIM (CEA/IRFU – CNRS/INSU – Université Paris Diderot),
CEA DSM/IRFU/SAp, 91191
Gif-sur-Yvette,
France
22
Thüringer Landessternwarte, Sternwarte 5,
07778
Tautenburg,
Germany
23
Department of Astrophysical Sciences, Princeton
University, Princeton, NJ
08544,
USA
24
LESIA, Observatoire de Paris, CNRS, UPMC, Université
Paris-Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
Received: 12 August 2015
Accepted: 19 October 2015
We report the detection of 48 millisecond pulsars (MSPs) out of 75 observed thus far using the LOw-Frequency ARray (LOFAR) in the frequency range 110–188 MHz. We have also detected three MSPs out of nine observed in the frequency range 38–77 MHz. This is the largest sample of MSPs ever observed at these low frequencies, and half of the detected MSPs were observed for the first time atfrequencies below 200 MHz. We present the average pulse profiles of the detected MSPs, their effective pulse widths, and flux densities and compare these with higher observing frequencies. The flux-calibrated, multifrequency LOFAR pulse profiles are publicly available via the European Pulsar Network Database of Pulsar Profiles. We also present average values of dispersion measures (DM) and discuss DM and profile variations. About 35% of the MSPs show strong narrow profiles, another 25% exhibit scattered profiles, and the rest are only weakly detected. A qualitative comparison of the LOFAR MSP profiles with those at higher radio frequencies shows constant separation between profile components. Similarly, the profile widths are consistent with those observed at higher frequencies, unless scattering dominates at the lowest frequencies. This is very different from what is observed for normal pulsars and suggests a compact emission region in the MSP magnetosphere. The amplitude ratio of the profile components, on the other hand, can dramatically change towards low frequencies, often with the trailing component becoming dominant. As previously demonstrated this can be caused by aberration and retardation. This data set enables high-precision studies of pulse profile evolution with frequency, dispersion, Faraday rotation, and scattering in the interstellar medium. Characterising and correcting these systematic effects may improve pulsar-timing precision at higher observing frequencies, where pulsar timing array projects aim to directly detect gravitational waves.
Key words: telescopes / radio continuum: stars / stars: neutron / pulsars: general
© ESO, 2016
1. Introduction
Radio millisecond pulsars (MSPs) are commonly held to have been spun up by mass transfer from a binary companion (Alpar et al. 1982; Radhakrishnan & Srinivasan 1981) and are evolutionarily linked with X-ray binary systems (Bhattacharya & van den Heuvel 1991; Archibald et al. 2009; Papitto et al. 2013; Stappers et al. 2014). Their observed properties are in many respects quite different from those of the long-period, “normal” pulsars. Both the spin periods, P, and period derivatives, Ṗ, of MSPs (P ~ 1–10 ms, Ṗ ~ 10-19 s s-1) are a few orders of magnitude lower than for normal pulsars (P ~ 1 s, Ṗ ~ 10-15 s s-1), and thus the inferred values of surface magnetic fields for MSPs are three to four orders of magnitude lower than the typical value of 1012 G for normal pulsars. Despite these differences, MSP studies at 1.4, 2.7, and 4.9 GHz by Kramer et al. (1998, 1999) and Xilouris et al. (1998) suggest that the radio emission mechanisms for normal pulsars and MSPs are essentially the same – even though their magnetospheres differ in size by two to three orders of magnitude.
This conclusion is mainly based on the similarity of their spectra and profile complexity. The same result was also obtained by Toscano et al. (1998) for a sample of MSPs in the southern hemisphere at frequencies between 0.4 and 1.6 GHz. This is also confirmed by single-pulse studies at 1.4 GHz of PSR J0437−4715 by Jenet et al. (1998), who find that its individual pulses are very similar to those of slowly rotating pulsars. Finally, Edwards & Stappers (2003) came to the same conclusion in their study of individual pulses from several pulsars with the Westerbork Synthesis Radio Telescope (WSRT) at several frequencies between 328 and 2240 MHz.
Even though the radio emission mechanism of both MSPs and normal pulsars seems to be the same, there are a number of differences in the observed emission properties. Multifrequency studies above 400 MHz generally1 show remarkably little frequency evolution in the average profiles of MSPs; in particular, the width of components and their separation typically remain almost constant (Kramer et al. 1998, 1999). This is different from what is generally observed in normal pulsars (see e.g. Thorsett 1991; Xilouris et al. 1996; Pilia et al. 2016), and may result from a small radio emission region in the very compact magnetospheres of MSPs. Kramer et al. (1998) also show that MSPs are somewhat less luminous and less efficient radio emitters than normal pulsars, with isolated MSPs being even less luminous than their binary counterparts. These findings are in accordance with results from recent works by Levin et al. (2013) and Burgay et al. (2013). All these results suggest that MSP magnetospheres might not simply represent scaled versions of the magnetospheres of normal pulsars (Xilouris et al. 1998), and the differences could be caused by the different evolutionary histories of normal pulsars and MSPs.
MSP studies at low radio frequencies, i.e. below ≲300 MHz, are valuable, as they expand our ability to compare flux-density spectra, polarisation and profile evolution to those of normal pulsars and probe the compactness of MSP emission regions (Cordes 1978a). Normal pulsars often show a spectral turnover between 100 and 250 MHz (e.g. Sieber 1973; Kuzmin et al. 1978; Izvekova et al. 1981; Malofeev 2000; Malofeev et al. 2000), raising the question of whether MSPs behave similarly. A study of 30 MSPs with narrow bandwidths at frequencies of 102 and 111 MHz by Kuzmin & Losovsky (2001) concluded that the spectra of the MSPs they studied mostly do not show any low-frequency turnover. Only in the case of PSR J1012+5307 did they find a possible turnover near 100 MHz. Kuzmin & Losovsky (1999) analysed the frequency dependence of profile widths of 12 MSPs between 102 and 1400 MHz. They found that profile widths remained nearly constant within this frequency range, and in the case of PSR J2145−0750, the component separation became even smaller at 102 MHz than at higher frequencies (Kuzmin & Losovsky 1996). Both results provide further evidence for the compactness of the emission region of MSPs.
Standard setup for the LOFAR observations of MSPs.
Although Kuzmin & Losovsky (2001, and references therein) provided a first insight into low-frequency MSP profiles and flux densities, their data suffered from poor time resolution (only 0.128–0.64 ms). This was mainly due to the necessity to form many narrow frequency channels to minimise dispersion smearing. Observations of MSPs at such low frequencies indeed present a challenge because of the large pulse broadening caused by both scattering and dispersion in the interstellar medium (ISM). Dispersion in the cold ionised plasma of the ISM scales as f-2. Though computationally intensive, it can be fully accounted for by coherent dedispersion (Hankins 1971; Hankins & Rickett 1975), unlike scattering, which also has an even stronger frequency dependence (scales as f-4.4 for a Kolmogorov spectrum of electron density inhomogeneities in the ISM). Because the pulses of the MSPs have much shorter durations than those of normal pulsars, they can be completely scattered out, preventing detection.
On average, pulsars have a steep negative spectral index of −1.4 (Bates et al. 2013), and MSP spectra are found to be consistent with the normal pulsar population (Kramer et al. 1998). However, the background sky temperature of the Galactic synchrotron radiation is also frequency dependent, and this dependence is steeper (f-2.55; Lawson et al. 1987). Thus, even if one assumes no turnover in the spectra of MSPs above 100 MHz, the majority of the MSPs, especially those located along the Galactic plane, will be more difficult to detect below 250 MHz than at higher frequencies.
In the past decade, higher-quality, low-frequency MSP observations have been enabled by a new generation of pulsar backends that provide wide-bandwidth, coherent dedispersion (sometimes in real-time). For example, Stappers et al. (2008) used WSRT and the PuMaII pulsar backend (Karuppusamy et al. 2008) in the frequency range of 115–175 MHz to coherently dedisperse the data to a final time resolution of 25.6–51.2 μs. They detected eight out of 14 MSPs observed and did not find any clear relationship between the detectability of a source and any combination of its period, DM or flux density at higher frequencies. Nevertheless, the majority of the non-detections were pulsars with lower flux densities. Stappers et al. (2008) did not detect two MSPs, PSRs J1024−0719 and J1713+0747, that were detected by Kuzmin & Losovsky (2001)2. They did not find any obvious reason for these non-detections. The authors suggested scattering to be the main reason for all of their six non-detections. For PSR J2145−0750 Stappers et al. (2008) also found the reduced separation between the peaks of the components with regard to the high frequencies and even found this separation to be smaller than in Kuzmin & Losovsky (1996), which can be attributed to residual dispersive smearing. However, Stappers et al. (2008) cast doubt on whether these components are the same as at high frequencies, because the leading component at 150 MHz more resembles the trailing component in the high-frequency profile. Recently, Dowell et al. (2013) also found the dominant component at low frequencies to be narrower than reported by Kuzmin & Losovsky (1996) in their observations with the Long Wavelength Array (LWA) at 37–81 MHz.
Since the work of Stappers et al. (2008) and until the recent study of PSR J2145−0750 by Dowell et al. (2013), there have been no other MSP studies at frequencies below 200 MHz that have provided high-quality profiles at these low frequencies. At the same time, the number of known MSPs in the Galactic field (many at distances <2 kpc, and at high Galactic latitudes) has substantially grown, owing to many detections in Fermi/LAT unassociated sources (see e.g. Keith et al. 2011; Ransom et al. 2011; Kerr et al. 2012; Barr et al. 2013b). About 75 MSPs were discovered in the Galactic field between the discovery of the first MSP (PSR B1937+21; Backer et al. 1982) and the Fermi launch in 2008. In the last five years we have experienced an MSP renaissance as this number has almost tripled to 218 (ATNF catalogue3; Manchester et al. 2005, and ongoing pulsar surveys). This is mainly a result of Fermi discoveries, but also includes a number of discoveries by ongoing pulsar surveys. These include the Green Bank Telescope (GBT) 350-MHz Drift-scan (Boyles et al. 2013; Lynch et al. 2013) and Green-Bank Northern Celestial Cap (GBNCC; Stovall et al. 2014a) surveys, the Pulsar Arecibo L-band Feed Array (PALFA) survey (Nice et al. 2013; Crawford et al. 2012; Deneva et al. 2012), and the Parkes/Effelsberg High Time Resolution Universe Survey (HTRU; e.g. Keith et al. 2010, 2012; Barr et al. 2013a). Therefore, there is also a significantly larger sample of MSPs that can be observed for the first time below 200 MHz.
The LOw-Frequency ARray (LOFAR) is a digital aperture array radio telescope operating from 10–240 MHz – i.e. the lowest four octaves of the “radio window” observable from the Earth’s surface (see van Haarlem et al. 2013 for a description of LOFAR). It is an interferometric array of dipole antenna stations distributed over Europe, with the Core of 24 stations located within an area approximately 2 km across near the Dutch village of Exloo. Compared to previous low-frequency radio telescopes, LOFAR offers many advantages in its observing capabilities (Stappers et al. 2011). Among them are the large fractional bandwidth (80 MHz of bandwidth in the 10–90 or 110–250 MHz range), sensitivity that is at least 20 times better than the low-frequency frontends at WSRT (Stappers et al. 2008), and an unrestricted ability to track sources from rise to set, thus accumulating a large number of pulses in a single observing session. The latter is very valuable as many of the old low-frequency arrays, such as the Large Phased Array in Pushchino (Russia), are transit instruments.
In this paper we present the results of the first exploratory observations of MSPs with LOFAR. In Sect. 2 we describe the LOFAR observing setup and data analysis. In Sect. 3 we present the results of our MSP observations, give lists of detected and non-detected pulsars, show folded pulse profiles and provide measurements of flux densities at 110–188 MHz. In Sect. 4 we discuss the detectability of MSPs, provide new measurements of their DMs and compare these with previously published values. We also discuss DM and profile variations of MSPs and qualitatively compare profiles for several pulsars with profiles at higher frequencies. We give a summary in Sect. 5.
2. Observations and data reduction
The observations presented in this paper were taken between 19 December 2012 and 3 November 2014 with the LOFAR Core stations using the High-Band Antennas (HBAs) in the frequency range 110–188 MHz and the Low-Band Antennas (LBAs) from 10–88 MHz (see van Haarlem et al. 2013; Stappers et al. 2011 for more information on the LOFAR observing system and set-up). A single clock system allows all Core stations to be combined into one or multiple coherent tied-array beams, and an eight-bit sampling mode allows 80 MHz of instantaneous bandwidth (limited by filters that avoid the FM frequency range from 90–110 MHz). This provides a factor ~5 increase in sensitivity compared with early LOFAR pulsar observations that were restricted to using the six stations on the “Superterp” and 48 MHz of bandwidth (e.g. Kondratiev et al. 2013).
2.1. Data acquisition
After coherent addition of the data streams from all available Core stations (typically 20–23 stations), the raw complex-voltage (CV) data were recorded at 5.12 μs. The 78-MHz bandwidth is split into 400 channels of 195.312 kHz each. The typical length of our observations was 20 min, although subsequent observations for monitoring and timing purposes were adjusted depending on the pulsar’s signal-to-noise ratio (S/N) in the LOFAR band.
The standard observing setup is summarised in Table 1. During the observations the data from the stations were streamed for further online processing (beamforming, etc.) to the Blue Gene/P (BG/P) supercomputer4 in Groningen. The output data products (in our case the raw CV data) were written in HDF55 format to the CEP2 cluster6 for further offline processing.
2.2. Pulsar pipeline
After each observation, we ran the LOFAR PULsar Pipeline (PULP), a Python-based suite of scripts that provides basic offline pulsar processing (dedispersion and folding) for standard observing modes including CV data. PULP collects information about the observation itself and location of the data on the CEP2 nodes and then executes data reduction tools from the PRESTO7 (Ransom 2001), dspsr8 (van Straten & Bailes 2011) and PSRCHIVE9 (Hotan et al. 2004) software suites, and creates a number of summary diagnostic plots and PSRFITS10 (Hotan et al. 2004) data files.
To process CV data we used dspsr to read raw LOFAR data via the LOFAR Direct Access Library (DAL) interface. Each channel was coherently dedispersed and folded with a pulsar ephemeris. Where possible, we used the most recent published timing models for folding, but in some cases we used updated ephemerides from ongoing timing campaigns that are not yet published. We set the length of the folding sub-integrations to be 5 s and the number of pulse profile bins equal to the closest and lowest power of two for P/ Δt (where P is the MSP period, and Δt = 5.12 μs is the sampling interval), but not higher than 1024 bins per period. The data were combined in frequency using psradd. In early observations, we used paz -r to perform zapping of a radio frequency interference (RFI) with a median smoothed automatic channel zapping algorithm. In later observations, we used the clean.py tool from CoastGuard11 (Lazarus et al., in prep). This RFI excision routine with the -F surgical option provided much better excision, and for this publication all pipeline products were reprocessed using this tool. The data were then dedispersed, i.e. appropriate time delays between frequency channels (note that each channel was already coherently dedispersed with dspsr) were applied, using pam. In the last step we ran the pdmp tool that enables the determination of a best DM and P by optimising the S/N of the profile. The output data files were further updated with these best DM and P values. Diagnostic plots were then produced to enable quick inspection of the data quality.
3. Results
At present we have observed 75 Galactic field MSPs with the LOFAR HBAs, and detected 48 of them. This is the largest sample of MSPs ever observed/detected at these low frequencies. Of these sources, 25 are recent MSP discoveries and have never before been detected at 110–188 MHz. We discuss the detectability of MSPs in more detail in Sect. 4.1. The lists of detected and non-detected MSPs are given in Tables 2 and 3, respectively. For the detected MSPs we list the profile significance of the best individual observation and its S/N, observing epoch/ID, and integration length, Tobs. For both detected and non-detected MSPs we also list whether they were previously observed with the WSRT (Stappers et al. 2008; Archibald et al. 2009 for PSR J1023+0038) or by the Large Phased Array (BSA) in Pushchino at 102/111 MHz (Kuzmin & Losovsky 2001). From the 27 MSPs that we did not detect, only one, PSR J0613−0200, was observed by Stappers et al. (2008) and they also did not detect it. Three out of these 27 have flux density measurements by Kuzmin & Losovsky (2001; including PSR J0613−0200). However, they did not publish the profiles of these MSPs and their flux density estimates have very large uncertainties.
3.1. Pulse profiles
We present the best individual profiles for all 48 detected MSPs in Fig. 1. They are the sum of ~3 × 105 spin periods, ranging from about 3 × 104 for the 59.8-ms PSR J2235+1506 to about 1.3 × 106 periods for the 1-h observation of PSR J0337+1715 (the pulsar triple system; Ransom et al. 2014).
Many of the MSPs are detected with high S/N. For example, the black widow pulsar J1810+1744, discovered in the 350-MHz GBT Survey of faint Fermi γ-ray sources (Hessels et al. 2011), was detected with S/N = 65 using a 20-min LOFAR observation. Furthermore, the eclipsing pulsar J1816+4510, discovered in the GBNCC pulsar survey (Stovall et al. 2014a), was detected with S/N = 159 using a sum of four 5-min LOFAR observations. LOFAR profiles for four PSRs J0214+5222, J0636+5129, J0645+5158, and J1816+4510 were also presented in Stovall et al. (2014a) together with the GBT profiles at 350, 820, and 1500 MHz. About 35% of the detected MSPs show strong narrow profiles, while only 25% of MSPs have scattered profiles with a clear exponential tail. The profiles of the remaining MSPs (~40%) are weak, which could be due to the intrinsic spectrum, and/or due to scattering, where the exponential scattering tail may approach or exceed a pulse period. Later in this Section we discuss the HBA detections of a few individual MSPs, and in Sect. 4.5 we discuss the profiles in general and make a comparison to high frequencies. Flux-calibrated, multifrequency LOFAR profiles from this paper are available via the European Pulsar Network (EPN) Database of Pulsar Profiles12 (Lorimer et al. 1998).
List of the 48 detected MSPs.
List of the 27 non-detected MSPs.
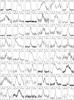 |
Fig. 1 LOFAR total-intensity pulse profiles for all detected MSPs from the best (highest S/N) individual observations. The horizontal axes show the pulse phase, and the vertical axes are the flux density in arbitrary units. |
3.1.1. Folding and vorb/c caution
For binary MSPs, the low observing frequencies and large fractional bandwidth of the LOFAR data mean that special care is needed when folding the data. This is because, in standard analyses, phase-folding is done based on a timing model evaluated at the central frequency of the band. If the dispersion delay across the band is large enough for the orbital phase to change significantly during this time, then data can be assigned an incorrect orbital phase. In such a case, the monochromatic timing model will not be able to correctly predict the pulse period across the entire bandwidth, but will have a frequency-dependent bias that changes with orbital phase (Ransom et al. 2004). Given that the error introduced in the pulse times-of-arrival (TOAs) is of the order vorb/c × ΔtDM, where ΔtDM is the dispersion delay between the central frequency and the lowest frequency in the band, it is clear that this effect can most easily be countered by splitting up the band into narrower sub-bands, and then applying the timing model separately to each of these. Alternatively, two-dimensional phase predictors can be employed.
Without using two-dimensional phase predictors the actual error in TOAs will depend on the orbital phase of the pulsar and the projection of the orbit on the plane of the sky, and is largest for edge-on orbits when the pulsar is at periastron – i.e. when the pulsar’s radial acceleration is strongest. In general, the effect is larger for higher-DM pulsars in compact (short orbital period) binary systems. In our MSP sample, the double pulsar J0737−3039A has the largest value of vorb/c ~ 10-3. For pulsars J0621+1002, J2145−0750, J0751+1807, J1023+0038, J1022+1001, J2215+5135, and J1816+4510, it is about (1−2) × 10-4, and for other binaries it is of the order of 10-5 or less. Using a single “polyco” file (a file generated by the pulsar timing program Tempo 13 which contains a polynomial description of the apparent pulse phase as a function of time) applicable to the central frequency of the total band, would result in TOA errors of 8.4 ms or 0.37 of the spin phase at the lowest observed frequency of 110 MHz for the pulsar J0737−3039A. In our observations we normally split the total bandwidth into 20 parts and then process them separately, each with their own polyco files. This helps to mitigate the effect, giving a maximum TOA error for the lowest-frequency part on the order of ~10 μs for most MSPs, with the most problematic pulsars being J0737−3039A (0.64 ms residual smearing), J2215+5135 (0.16 ms), J1816+4510 (55 μs), J0218+4232 (52 μs), J0621+1002 (46 μs), and J0751+1807 (39 μs). The largest error in terms of spin phase occurs for PSR J2215+5135, where the effect is equivalent to 0.06 rotational cycles. For most of our observed MSPs, this error is about 0.01 cycles or less.
 |
Fig. 2 Profile evolution of pulsar B1937+21 within the LOFAR HBA band in the range 105–197 MHz. Each profile has 128 bins and is folded in ~9.2-MHz wide sub-bands centred at the labelled frequency in MHz. |
3.1.2. Double pulsar J0737−3039A
Despite its low declination and maximum elevation of 6.4° (as seen from the LOFAR Core), we detected the 22-ms A-pulsar in the double pulsar system J0737−3039 in a single 1-h observation (see Fig. 1). To exclude any broadening due to the effect described in Sect. 3.1.1 we have also reprocessed the data, folding each channel separately. It did not make any noticeable difference to the profile, because at the epoch of observation the pulsar had a relatively low orbital velocity (orbital phase ~0–0.4, longitude of periastron ~300.5°). From high-frequency observations it is known that the B-pulsar is not visible anymore due to large orbital (17 °/yr; Kramer et al. 2006a) and geodetic (5 °/yr; Breton et al. 2008) precession, but is expected to reappear again in ~2035 (Perera et al. 2010). However, we might be able to catch its emission at our low frequencies with LOFAR, if a wider low-frequency beam (Cordes 1978b) is still grazing our line-of-sight. Thus, we folded our data with the B-pulsar ephemeris as well, but we did not detect it after also searching in period and DM. Radio emission from the B-pulsar was only ever visible at two narrow orbital phase windows (~0.58 and ~0.78) when emission from the A-pulsar affected the magnetosphere of the B-pulsar (Lyne et al. 2004), and we missed these windows in our observation. Therefore, more observations are needed to rule out emission from the B-pulsar at low frequencies.
3.1.3. PSR J1023+0038
We detected the 1.69-ms pulsar J1023+0038, which is in a 4.7-h orbit with a bloated stellar companion and has been called the “missing link” between low-mass X-ray binaries (LMXBs) and radio MSPs (Archibald et al. 2009). We observed it five times, with 20-min integration times per observation, before February 2013 and detected it twice in the orbital phase ranges 0.64–0.71 and 0.84–0.91. The pulsar was very likely eclipsed in the other three observations (at the observed frequencies, it is expected to be eclipsed for at least orbital phases 0.0–0.5, see Archibald et al. 2013). The profile from the best observation on January 23, 2013 is shown in Fig. 1. The profile has a two-component shape, as seen in WSRT observations at 155–157 MHz by Archibald et al. (2009). Two observations on August 31, 2013 and October 5, 2013 at non-eclipse orbital phases did not show any emission from PSR J1023+0038. This was confirmed earlier with high-frequency observations using other radio telescopes. This is evidence that it switched again into its accreting LMXB phase (Patruno et al. 2014; Stappers et al. 2014).
3.1.4. PSR B1937+21
We successfully detected the first millisecond pulsar, B1937+21, in the LOFAR HBA band. This is the first ever published detection of the pulse profile of this pulsar at these low frequencies (see Fig. 2). The main pulse (MP) and interpulse (IP) components are clearly distinguished at the highest frequencies. Figure 2 shows the profile evolution in the HBA band from 105 to 197 MHz. The rapid change in the profile shape due to scattering is evident. Below 150 MHz the IP is no longer visible and below 120 MHz the whole profile is completely washed out by scattering. As mentioned before, scattering time, τscat, scales as f-4.4 with frequency, f. Following the empirical relationship between τscat, DM and f from Bhat et al. (2004), the τscat should increase from ~2 to ~19 ms when going from 197 to 105 MHz, i.e. from ~1 to almost ~12 spin periods (P = 1.56 ms). Joshi & Kramer (2009) reported on the IP giant-pulse component in the average profile from their observations at a frequency of 238 MHz with the Giant Metrewave Radio Telescope (GMRT). We do not see this giant-pulse-related hump in the average profile of either the MP or the IP components, most likely because of much larger profile broadening. Kuzmin & Losovsky (2002) reported the detection of four individual giant pulses at 112 MHz, though the pulse trains they present are very noisy. We have also performed a search for strong giant pulses in the full band, but did not find anything significant. Only searching the high-frequency half of the band or using the cyclic spectroscopy technique (Demorest 2011; Walker et al. 2013; Archibald et al. 2014) may be needed. We defer more detailed single-pulse study of PSR B1937+21 for a subsequent paper.
3.2. Flux densities
3.2.1. Contributing factors
For a number of reasons, flux calibration of beamformed LOFAR data is non-trivial. The main uncertainty comes from the fact that the characteristic beam shape and sensitivity strongly depend on the elevation and azimuth of the source. LOFAR also has a very large fractional bandwidth, thus the frequency dependence of the beam size and differences in the sky temperature across the bandpass should be considered. Overall, the following aspects have to be taken into account:
-
Effective area. The total effective collecting area of the LOFAR array, Aeff, or gain, G, is frequency dependent. For a 48-tile HBA station the upper limit on the effective area,
 (λ), is given by van Haarlem et al. (2013)14:
(λ), is given by van Haarlem et al. (2013)14: 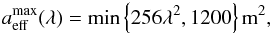 (1)where λ is the observing wavelength in m.
(1)where λ is the observing wavelength in m. -
Beam model. An accurate beam model of the LOFAR HBAs at 110–190 MHz provides the dependence of the antenna gain, G, on the zenith angle and azimuth for a single tile or station, and preferably takes into account the shadowing of individual tiles within a station at low elevations.
-
System temperature. The system temperature, Tsys = Tsky + TA, is also frequency dependent. The main contribution to Tsys comes from the sky temperature, Tsky, which strongly changes with frequency as f-2.55 (Lawson et al. 1987). We should note, that, although the spectral index is remarkably uniform for most of the Galactic emission, it does vary across the sky in the range from −2.40 to −2.55 (Roger et al. 1999). The antenna temperature, TA, is not constant either. At the centre of the band its average value is about 400 K (Arts et al. 2013), although it increases slightly towards higher frequencies (van Haarlem et al. 2013). Below 120 MHz and above 180 MHz TA increases rapidly. We used a sixth-order polynomial function of frequency based on Tsys measurements from Wijnholds & van Cappellen (2011) to fit for TA and calculate its value for each frequency channel.
-
Broken tiles. In practice, not all the HBA tiles are operational at all times, and on average about 5–10% of them are unused while observing, making the effective area smaller. For some of the earlier observations this fraction was as high as 30%.
-
Coherent station summation. Coherent summation of the stations should increase the sensitivity linearly with the number of stations added. In practise, however, we found the dependence of the S/N to scale as
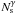 , where Ns is the number of 48-tile stations, and γ = 0.85 is the coherence factor. The possible reasons for this non-linear dependence are correlated noise between stations and uncalibrated non-zero phase offsets in the phase-frequency dependence for each of the polarisations/stations, which can be caused by the station’s electronics themselves or the influence of the ionosphere. This measurement was based on the BG/P data, and we used BG/P for most of our observations. Similar tests are currently being done for the Cobalt correlator, where these non-zero phase offsets will be taken into account.
, where Ns is the number of 48-tile stations, and γ = 0.85 is the coherence factor. The possible reasons for this non-linear dependence are correlated noise between stations and uncalibrated non-zero phase offsets in the phase-frequency dependence for each of the polarisations/stations, which can be caused by the station’s electronics themselves or the influence of the ionosphere. This measurement was based on the BG/P data, and we used BG/P for most of our observations. Similar tests are currently being done for the Cobalt correlator, where these non-zero phase offsets will be taken into account. -
Radio frequency interference. RFI clipping reduces the total on-source time and bandwidth. On average, 25–30% of our data were clipped, the smallest and largest fractions being 10% and 46%, respectively. This large zapping fraction is an unfortunate consequence of keeping a frequency resolution of only 195 kHz (this is needed in order to achieve the desired time resolution). The typical spectral width of the RFI seen by LOFAR is ~1 kHz, and thus higher-frequency-resolution data can be excised of RFI without sacrificing such a large fraction of the data.
3.2.2. Calibration
The Stokes vector, S0 = (I0,Q0,U0,V0), of the incident radiation is related to the measured Stokes vector, S = (I,Q,U,V), via a 4 × 4 Mueller matrix, M, as S = M·S0. The measured Stokes I component will depend on the initial Stokes S0 as I = mIII0 + mIQQ0 + mIUU0 + mIVV0, where mij are corresponding elements of M. In our observations mII is the dominant factor and we can assume that all observed power comes in Stokes I. Pulsars are predominantly very weakly circularly polarised, thus mIV is small compared to mII (≲1%). For linear polarisation, mIQ and mIU are of the order 5–10% and strongly depend on the hour angle (Noutsos et al. 2015). Noutsos et al. (2015) also report significant leakage to circular polarisation at large hour angles, however all our observations were carried out near transit where the leakage is minimal. Moreover, Faraday rotation from the ISM removes most of the contribution from linear polarisation in our large observing band. Therefore, we can simply consider I ≈ mIII0.
In our flux density measurements we used the Hamaker beam model (Hamaker 2006, and references therein), which is also used in the LOFAR software for initial phase calibration of interferometric imaging data (van Haarlem et al. 2013). Based on this model we calculated the Jones matrices of antenna response for a given HBA station, frequency and sky direction using the mscorpol package15. Then, Jones matrices (e.g. Jones 1941; Fymat 1971) can be transformed to a corresponding Mueller matrix, and in particular for the mII: 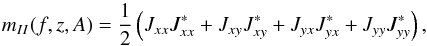 (2)where Jij are components of the Jones matrices, f is the frequency, z is the zenith angle, and A is the azimuth (e.g. Hamaker et al. 1996). Finally, to link with the absolute flux scale we normalised our mII(f,z,A) by the corresponding values for a reference observation of Cassiopeia A by Wijnholds & van Cappellen (2011). In calculations of Jones matrices we always used the station CS001 as our template. The difference in flux densities when other stations are used to derive Jones matrices is much smaller than the nominal flux uncertainty. Using mII, the aeff for a given frequency and direction can be simply calculated as:
(2)where Jij are components of the Jones matrices, f is the frequency, z is the zenith angle, and A is the azimuth (e.g. Hamaker et al. 1996). Finally, to link with the absolute flux scale we normalised our mII(f,z,A) by the corresponding values for a reference observation of Cassiopeia A by Wijnholds & van Cappellen (2011). In calculations of Jones matrices we always used the station CS001 as our template. The difference in flux densities when other stations are used to derive Jones matrices is much smaller than the nominal flux uncertainty. Using mII, the aeff for a given frequency and direction can be simply calculated as: 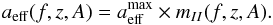 (3)To determine the pulse-phase-averaged flux density of the pulsar (hereafter referred to as “mean flux density”), we adapt Eq. (7.10) of Lorimer & Kramer (2005) to obtain the flux density, Si, of the ith profile bin:
(3)To determine the pulse-phase-averaged flux density of the pulsar (hereafter referred to as “mean flux density”), we adapt Eq. (7.10) of Lorimer & Kramer (2005) to obtain the flux density, Si, of the ith profile bin:
 (4)where β is a digitisation correction factor, (S/N)i is the signal-to-noise ratio of the ith profile bin, np = 2 is the number of polarisations summed, Tobs is the observation length, B is the observation bandwidth, Nb is the number of profile bins, G = Aeff/ 2k is the telescope gain, Aeff is the total effective area, k is the Boltzmann constant, and Tsys is the system temperature. For systems with a large number of bits per sample (8 in our case) β ≈ 1.
(4)where β is a digitisation correction factor, (S/N)i is the signal-to-noise ratio of the ith profile bin, np = 2 is the number of polarisations summed, Tobs is the observation length, B is the observation bandwidth, Nb is the number of profile bins, G = Aeff/ 2k is the telescope gain, Aeff is the total effective area, k is the Boltzmann constant, and Tsys is the system temperature. For systems with a large number of bits per sample (8 in our case) β ≈ 1.
Expanding this expression to apply to LOFAR, for the flux density Si(f,z,A) in Jy of the ith profile bin of a given frequency channel and sub-integration, we derive: ![\begin{eqnarray} S_i(f,z,A)&=&\,\frac{2\beta k({S/N})_i^{f,z,A}[T_{\rm A}(f) + T_{\rm sky}(f,l,b)]}{N_{\rm s}^{\gamma} a_{\rm eff}(f,z,A)m_{II}(f,z,A)[1-\xi]} \notag \\ &&\times\frac{1}{\sqrt{n_{\rm p}[1-\zeta(f)](\frac{T_{\rm int}}{N_{\rm b}})\Delta f}}~, \end{eqnarray}](/articles/aa/full_html/2016/01/aa27178-15/aa27178-15-eq111.png) (5)where l and b are Galactic longitude and latitude, ξ is the overall fraction of bad tiles, ζ(f) is the RFI fraction, Tint is the length of a sub-integration, Δf is the width of the frequency channel, and
(5)where l and b are Galactic longitude and latitude, ξ is the overall fraction of bad tiles, ζ(f) is the RFI fraction, Tint is the length of a sub-integration, Δf is the width of the frequency channel, and  is the S/N of the ith profile bin of the individual frequency channel and sub-integration, with
is the S/N of the ith profile bin of the individual frequency channel and sub-integration, with 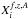 the value of the ith profile bin, ⟨ X ⟩ the mean and σX the rms value (and both ⟨ X ⟩ and σX are calculated in the off-pulse window). To calculate Tsky we use the reference sky temperature at 408 MHz from the skymap determined by Haslam et al. (1982) and scale it to the frequency of the channel using f-2.55 (Lawson et al. 1987). At present there are few sophisticated sky models available (de Oliveira-Costa et al. 2008; Polisensky 2007), which are based on published reference sky maps, and that we can use in the future especially for the calibration in the LBA frequency range 10–90 MHz (see also Nelles & et al. 2015).
the value of the ith profile bin, ⟨ X ⟩ the mean and σX the rms value (and both ⟨ X ⟩ and σX are calculated in the off-pulse window). To calculate Tsky we use the reference sky temperature at 408 MHz from the skymap determined by Haslam et al. (1982) and scale it to the frequency of the channel using f-2.55 (Lawson et al. 1987). At present there are few sophisticated sky models available (de Oliveira-Costa et al. 2008; Polisensky 2007), which are based on published reference sky maps, and that we can use in the future especially for the calibration in the LBA frequency range 10–90 MHz (see also Nelles & et al. 2015).
Finally, to measure the mean flux density Smean we find the average value of Si(f,z,A) as: 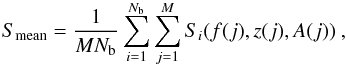 (6)where M = NchNint − Nzap with Nch the total number of frequency channels, Nint the total number of sub-integrations, and Nzap the number of completely zapped frequency channels and sub-integrations.
(6)where M = NchNint − Nzap with Nch the total number of frequency channels, Nint the total number of sub-integrations, and Nzap the number of completely zapped frequency channels and sub-integrations.
We estimated the nominal uncertainty, σi(f,z,A), on Si(f,z,A) by taking 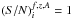 for every individual channel and sub-integration, i.e.
for every individual channel and sub-integration, i.e. 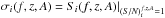 . Then, we find the nominal uncertainty, σmean, on the mean flux density, Smean, as:
. Then, we find the nominal uncertainty, σmean, on the mean flux density, Smean, as: 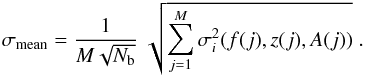 (7)However, there are also other factors that can affect our flux measurements, but which are very difficult (or not possible) to take account of, and were not addressed here. For completeness we note that these are:
(7)However, there are also other factors that can affect our flux measurements, but which are very difficult (or not possible) to take account of, and were not addressed here. For completeness we note that these are:
-
Scattering. Our flux density measurements can be seriously affected if τscat is close to or exceeds a pulse period. In these cases, the measured S/N is reduced and we underestimate Tsys due to the contribution from the scattered pulse signal.
-
Refractive scintillation. Diffractive scintillation should not affect our measurements because the decorrelation bandwidths are lower than the width of a channel (195 kHz) for all of our sources, so many scintles are averaged out. On the other hand, refractive interstellar scintillation (RISS) can change the pulsar flux density by a factor of ~1.5 at low observing frequencies. Gupta et al. (1993) found the characteristic RISS time scale to vary from a few days to several weeks at a frequency of 74 MHz for a sample of nearby pulsars. The measured modulation indices (ratio of the standard deviation of the observed flux densities to their mean) ranged from 0.15–0.45. The RISS time scale and modulation index scale with the observing frequency as ∝f-2.2 and ∝f0.57, respectively (Rickett et al. 1984; Coles et al. 1987). Observations spanning dozens of months are required to measure the average flux densities more accurately. Here we provide only the flux density measurements for the best individual observation for each pulsar.
-
Beam jitter. The jitter of the tied-array beam is caused by the ionosphere and can be as large as ~2–3′, equal to the half-width at half-maximum of the HBA full-core tied-array beam16, but is usually much smaller than this. However, when the ionosphere is excited, e.g. around sunset/sunrise, it could move the source to the edge of the beam leading to inferred flux densities lower by a factor of ~2. In future analyses forming a ring of tied-array beams around the pointing position could eliminate this problem by choosing the beam with highest S/N in the post-processing. This, however, is expensive with respect to both data volume and processing time.
-
Galactic plane. Variation of the system temperature with time due to rise/set of the Galactic plane can increase Tsys by 30–40% if it is in the field-of-view (FoV) of the primary station beam or grating lobes. This is also possible for other strong background sources in the FoV. Also, Tsys can vary with pointing direction due to noise coupling effects.
To get realistic values for the systematic uncertainty on our flux density measurements, we also estimated the flux density using images from the Multifrequency Snapshot Sky Survey (MSSS, Heald et al. 2015) for a sample of bright MSPs and slow pulsars that we could unambiguously identify. On average our mean flux density measurements agree with those from MSSS data within ~40%. The same calibration technique was used to get several monthly flux density measurements for ten bright non-millisecond pulsars in the LOFAR HBA range (Bilous et al. 2015). Comparing measured fluxes to spectra fit through the literature values, the authors estimate the uncertainty of a single LOFAR flux measurement as 50%. Thus, MSP fluxes reported here should also be used with this uncertainty.
Mean flux densities for the detected MSPs in the frequency range 110–188 MHz.
3.2.3. Flux measurements
Table 4 lists the measured 110–188 MHz flux densities of our MSP sample. In the Table we give the catalogued value of DM for reference, followed by our measurements of effective pulse width, Weff (Col. 3), duty cycle, δ = Weff/P (Col. 4), and mean flux density measurements, Smean (Col. 5). Given Smean errors in parentheses are nominal uncertainties only from the Eq. (7). For each MSP the 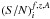 was calculated based on ⟨ X ⟩ and σX in the pre-selected off-pulse window. For MSPs with broad profiles (due to scattering) we tried to place the off-pulse window just before the leading edge of the profile, but most likely this still resulted in underestimated S/N and flux density. The Weff was calculated as the integrated flux density in the pulse profile over its peak flux density. In Col. 6 we list the flux density measurements at 102/111 MHz reported by Kuzmin & Losovsky (2001). In Col. 7 we provide the predicted mean flux density using the reference flux density value, Sref (Col. 8) at the reference observing frequency, νref (Col. 9), and spectral index (Col. 10) from published data. We give references in Col. 11 to all the published data we used in our calculations of the predicted flux density. The values of the predicted mean flux densities listed are the average between the values at the edges of our frequency range of 110–188 MHz. If the spectral index was not known, we used the mean value of −1.4 ± 1 for the pulsar population (Bates et al. 2013). We used this recently published value instead of the generally accepted value of −1.8 ± 0.2 by Maron et al. (2000) as it takes into account the sample bias in the spectral index measurements available. Although the work of Bates et al. (2013) focused on the normal pulsar population, MSP spectra seem to be similar to those of normal pulsars (Kramer et al. 1998), and thus we follow that assumption here. For the non-detected MSPs, we provide upper limits Slim (Table 3). We calculated Slim as three times the nominal error on the mean flux density measurement.
was calculated based on ⟨ X ⟩ and σX in the pre-selected off-pulse window. For MSPs with broad profiles (due to scattering) we tried to place the off-pulse window just before the leading edge of the profile, but most likely this still resulted in underestimated S/N and flux density. The Weff was calculated as the integrated flux density in the pulse profile over its peak flux density. In Col. 6 we list the flux density measurements at 102/111 MHz reported by Kuzmin & Losovsky (2001). In Col. 7 we provide the predicted mean flux density using the reference flux density value, Sref (Col. 8) at the reference observing frequency, νref (Col. 9), and spectral index (Col. 10) from published data. We give references in Col. 11 to all the published data we used in our calculations of the predicted flux density. The values of the predicted mean flux densities listed are the average between the values at the edges of our frequency range of 110–188 MHz. If the spectral index was not known, we used the mean value of −1.4 ± 1 for the pulsar population (Bates et al. 2013). We used this recently published value instead of the generally accepted value of −1.8 ± 0.2 by Maron et al. (2000) as it takes into account the sample bias in the spectral index measurements available. Although the work of Bates et al. (2013) focused on the normal pulsar population, MSP spectra seem to be similar to those of normal pulsars (Kramer et al. 1998), and thus we follow that assumption here. For the non-detected MSPs, we provide upper limits Slim (Table 3). We calculated Slim as three times the nominal error on the mean flux density measurement.
 |
Fig. 3 Measured mean flux densities at 110–188 MHz versus predicted flux densities using high-frequency data for 48 MSPs. The dotted line shows the loci of measured mean fluxes equal to predicted fluxes, and dashed lines mark the region where measured mean flux density deviates from predicted flux density by a factor of two. Open symbols show the MSPs for which spectral indices are not known, and the average index from Bates et al. (2013) was used, while solid symbols are for those with known spectral indices (see Table 4). Blue squares and green circles indicate MSPs with measured duty cycles >20% and <20%, respectively. Pulsars are labelled by their right ascension. |
 |
Fig. 4 Same as the Fig. 3, but predicted mean flux densities are those from Kuzmin & Losovsky (2001) scaled to the frequency range of 110–188 MHz using the spectral indices from Table 4. |
Figure 3 shows the comparison between the measured and predicted flux densities for our 48 detected MSPs. Predicted flux densities were calculated from the available high-frequency data and known spectral indices as given in Table 4. For at least a third of the MSPs the main uncertainty on the predicted flux density comes from our poor knowledge of the spectral indices. However, for about another third of the MSPs, the measured flux densities are still lower than the predicted ones even including the uncertainty on their spectral indices. This can be explained by contributions from other factors given in Sect. 3.2.1. For instance, the profiles of PSRs B1937+21, B1957+20, J0218+4232, B1953+29 are dominated by scattering, so our flux density measurements are underestimated for them. PSR J1023+0038 has a very large predicted flux of up to ~1.7 Jy. This could be due to significant intrinsic variability (Archibald et al. 2009). For others, we note that their profiles are quite narrow and show only a small scattering tail or none at all. It is thus possible that the spectra of these pulsars turnover within or above our observing band. For example, Kuzmin & Losovsky (2001) report a turnover for PSR J1012+5307 near 100 MHz. We can not rule out this possibility, but more accurate measurements are needed at both HBA and LBA bands. Also, Kuniyoshi et al. (2015) recently reported that PSRs J1640+2224 and J1911−1114 likely have a spectral break near 100 MHz.
Refractive scintillation could also affect our measurements, although not by more than a factor of ~1.5 (see Sect. 3.2.1). Another possible explanation for the discrepancy between measured and predicted flux density values, is that published flux densities at high frequencies were over- or underestimated, most likely due to scintillation as was recently noted by Levin et al. (2013). To exclude the influence of overestimated flux densities at higher frequencies, we used the flux density measurements at frequencies 102/111 MHz from Kuzmin & Losovsky (2001) to predict flux densities at 150 MHz. The corresponding plot is shown in Fig. 4. If there is a real turnover in the spectra we would expect our flux density measurements to be higher than the predicted flux density and, hence, located in the top-left part of the plot. Our flux density value for PSR J1012+5307 is indeed large which speaks in favour of spectral turnover for this MSP. The same could also apply for PSR J0034−0534, although its flux density is consistent with what is expected from high-frequency measurements, and the flux density value reported by Kuzmin & Losovsky (2001) could be underestimated. For PSR J1640+2224Kuniyoshi et al. (2015) report a possible turnover below 100 MHz, however our flux measurement is still lower than that predicted from the Kuzmin & Losovsky (2001) measurements at 102/111 MHz. Assuming all flux measurements are not affected by other factors (see Sect. 3.2.2), turnover must occur sharply below 100 MHz. Similarly to the predictions from high-frequency data, our measured flux densities lie below the predicted ones for about ten out of 21 pulsars with available flux densities from Kuzmin & Losovsky (2001). Not ruling out other explanations including our own flux densities being somewhat underestimated due to scattering, RISS, beam jitter or contribution to the system temperature from the Galactic plane in the FoV, the 100-MHz flux density measurements from Kuzmin & Losovsky (2001) could be subject to a significant bias due to diffractive scintillation. The decorrelation bandwidth, Δνd, at 100 MHz is of the order of ≲80 kHz (Cordes et al. 1985), and the receiver bandwidth, B, of Kuzmin & Losovsky (2001) was only 160 kHz, comparable to the frequency scale of diffractive scintillation. This would modulate the pulsar flux density by a factor of 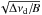 (Popov & Soglasnov 1984). If a pulsar is weak enough to be only detected during the favourable ISM conditions, then the measured flux density will be overestimated.
(Popov & Soglasnov 1984). If a pulsar is weak enough to be only detected during the favourable ISM conditions, then the measured flux density will be overestimated.
LOFAR’s observing bandwidth is much larger than the characteristic decorrelation bandwidth at 150 MHz (Δνd ≲ 0.2 MHz), so diffractive scintillation cannot affect our measurements. However, to make firm flux density estimates one needs to perform a long-term monitoring campaign to account for RISS.
3.3. LBA detections
We also observed nine bright MSPs with the LOFAR LBAs in the frequency range 15–93 MHz. We detected three MSPs, namely PSRs J0030+0451, J0034−0534, and J2145−0750. All detected and non-detected MSPs in LBA observations are listed in the last column of Table 2. Only PSR J2317+1439 was observed for 20 min, for the others the integration time was 1 h.
It is currently unclear which effect plays the dominant role in the non-detections of MSPs below 100 MHz: scattering, increased sky temperature, or smaller flux densities due to a possible turnover in their spectra. However, using the empirical relationship from Bhat et al. (2004) for DM = 10 pc cm-3 one would expect the scattering time to be about 0.37 ms at 57 MHz, or about ~0.07 cycles or less for PSRs J1012+5307, J1022+1001, J1024−0719, and B1257+12. Hence, scattering is most likely not the primary reason for the non-detections of these four MSPs. From HBA profiles of these pulsars we determined rough upper limits on the τscat at 57 MHz to be 9, 6.4, 28, and 9 ms, respectively. The limits do not contradict the prediction of τscat from the Bhat et al. (2004) relationship. However, although rough, our limits still give the possibility for scattering to play a role in the non-detections of PSRs J1012+5307, J1024−0719, and B1257+12, as the uncertainty in the Bhat et al. (2004) relationship can be up to two orders of magnitude. For PSR J1022+1001 the spin period is about three times longer than our rough limit on τscat, thus most likely other factors contribute to the non-detection of this MSP – more so than scattering.
These four non-detected MSPs are located at high Galactic latitudes similar to the three MSPs detected with the LBAs, and the sky temperatures in these directions are very similar. However, the spectral indices for two of the detected MSPs, PSRs J0030+0451 and J0034−0534 (−2.2 ± 0.2 and −2.6 ± 1, respectively, see Table 4; approximately equivalent to the spectral index of Galactic synchrotron radiation), are steeper than for these four non-detected MSPs. Hence, the influence of the increased background temperature at low radio frequencies for PSRs J0030+0451 and J0034−0534 is much smaller than for the non-detected MSPs with shallower spectral indices. Alternatively, these four non-detected MSPs might have a turnover in their radio spectra at frequencies ≲120 MHz (for PSR J1012+5307 Kuzmin & Losovsky (2001) reported a possible turnover in its spectrum near 100 MHz).
For PSR J2317+1439 the predicted scattering time at 57 MHz is about 3 ms, comparable to the pulse period. The rough upper limit on τscat from the HBA profile is somewhat lower, about 2.5 ms. Thus, similarly to the other four non-detected MSPs, scattering is not the dominant factor in its non-detection.
For the black widow PSR J1810+1744, with a DM of 39.7 pc cm-3, the scattering time is already four times longer than the spin period, and the profile is scattered out (Archibald et al. 2014). One can already see profile evolution within the HBA band for this MSP in Fig. 9 (left), where the profile at the low-frequency edge is notably more scattered than at the high-frequency end of the HBA band.
For completeness, we should also consider the influence of vorb/c smearing on LBA profiles of binary MSPs as was discussed in Sect. 3.1.1, as this effect becomes even more significant at lower observing frequencies. PSRs J0030+0451 and J1024−0719 are isolated, so this effect is not relevant for them. For the remaining seven MSPs we calculated the extra smearing of the profile due to this effect in a 3.9-MHz frequency band near a frequency of 58 MHz, where we have our highest sensitivity. For four out of seven MSPs (PSRs J1012+5307, J1022+1001, B1257+12, and J2145-0750) this effect is minor with less than 0.01 cycles of extra broadening of the profiles. For PSR J2317+1439, which we did not detect, the broadening is 0.04 cycles, still quite small, so we should have been able to detect it regardless of this effect. In contrast, for PSR J1810+1744 the effect is quite significant producing additional profile scattering of about 0.1 cycles. However, as we already showed, the expected broadening due to the scattering itself is 100 times larger.
 |
Fig. 5 Profile evolution of the three MSPs detected in the LBA frequency range of 38.2–77.2 MHz. The grey profile on top of each panel is the average profile within the 39-MHz wide band. All profiles are from 1-h LBA observations. There are 64 bins in the profiles of PSRs J0030+0451 and J0034−0534 and 128 bins in the profiles of PSR J2145−0750. The numbers on the left in each panel show the central frequency in MHz of the corresponding 7.8-MHz sub-band. |
Figure 5 shows the profile evolution for the three detected MSPs. The profile on top of each panel is the average profile from 38–77 MHz. Among these three, PSR J0034−0534 has the largest DM of 13.8 pc cm-3 and shows significant profile evolution with its profile clearly being scattered towards lower frequencies. The profile shape in the total LBA band is largely determined by scattering at the lower part of the band, although the profile in the higher-frequency sub-band at 73.3 MHz resembles the profile in the HBA band (see Fig. 1). At this observing frequency we measured the scattering time to be about 440 μs by fitting the trailing part of the profile with an exponential function. The extra profile broadening due to the vorb/c effect is about 0.05 cycles for a 7.8-MHz sub-band around 57.7 MHz. It does scatter the profile but not at a large enough level to scatter it out completely for the lowest sub-band shown in Fig. 5 (middle). Therefore, the profile broadening must be dominated by scattering in the ISM.
The profiles of the other two MSPs, PSRs J0030+0451 and J2145−0750, do not show significant evolution in comparison to PSR J0034−0534. They have smaller DMs (4.3, 9.0, 13.8 pc cm-3 for PSRs J0030+0451, J2145−0750, and J0034−0534, respectively), and the scattering conditions must be temperate towards them. We measured the scattering time to be about 300 μs for PSR J0030+0451 at 42.1 MHz and less than 700 μs for PSR J2145−0750 at 57.7 MHz. Although there is no significant broadening of the profile for PSR J2145−0750 its profile almost vanishes at 42 MHz. For PSR J2145−0750 the sky temperature is four times higher at 42 MHz than at 73 MHz. The LOFAR LBA bandpass response is not uniform and peaks at approximately 58 MHz (see van Haarlem et al. 2013, Fig. 19). However, we do not think that lower sensitivity is the reason for the much weaker profile at 42 MHz. For PSR J0030+0451 the change in the sky temperature and bandpass response is the same, but it has a clearly detected profile at 42 MHz, only slightly weaker than the profile at 58 MHz. Hence, we believe that this weakening is due to a turnover in the spectrum of PSR J2145−0750. Our assumption qualitatively agrees with the recent conclusion by Dowell et al. (2013), who found that the radio spectrum of PSR J2145−0750 is best fit with a model with spectral curvature and a roll-over frequency of 730 MHz using data from the LWA. Recently, Kuniyoshi et al. (2015) also reported on a spectral turnover between 100 and 400 MHz based on archival and LWA data.
Stovall et al. (2014b) also report on the detection of the same three MSPs with the LWA between 30–88 MHz from their 6-h observations of PSR J0030+0451 and 8-h observations of PSRs J0034−0534 and J2145−0750.
 |
Fig. 6 MSP detectability, or dependence of the ratio of predicted scattering time at 150 MHz over the pulsar period, τscat/P, on dispersion measure, DM. The green colour map corresponds to the measured mean flux density, Smean, at 110–188 MHz. Non-detected MSPs are shown with brown squares and their green intensity level corresponds to the measured upper limit of the mean flux density at 110–188 MHz. Scattering times at 150 MHz were calculated from the NE2001 Galactic free electron density model (Cordes & Lazio 2002) assuming a Kolmogorov spectrum of electron density inhomogeneities. The dashed line shows the empirical dependence between τscat and DM at 150 MHz from Bhat et al. (2004), where τscat is arbitrarily normalised by P = 4.075 ms, which is the median value of MSP periods in our sample of detected and non-detected MSPs. The top subplot shows the histograms of DMs for detected and non-detected MSPs. The inset plot is the same as the main plot but only for the non-detected PSR J1903+0327, which did not fit into the range of the main plot. PSR J1400−1438 was recently detected with LOFAR using the updated coordinates (J. Swiggum, priv. comm.) derived from over three years of timing with the GBT. The previously used catalogued position was off by about 6′, which is about two times larger than the full-width at half-maximum of LOFAR’s full-core tied-array beam at 150 MHz. |
4. Discussion
4.1. Detectability of MSPs
In order to explore the degree to which propagation in the ISM affects the detectability of the MSPs presented here, we plotted the ratio of the predicted τscat at 150 MHz, over the pulsar period, P, on DM and Smean at 110–188 MHz. This dependence is shown in Fig. 6 for both detected and non-detected MSPs, with the green colour indicating the Smean. For non-detected MSPs, the green intensity shows the upper limit on Smean as given in Table 3 (Col. 10). For τscat we used the NE2001 Galactic free electron density model (Cordes & Lazio 2002) and assumed a Kolmogorov spectrum of electron density inhomogeneities (see Table 5, last column).
The histogram on top of Fig. 6 presents the number of detected and non-detected MSPs as a function of DM. We detected 25 out of 28 observed MSPs with DMs≲20 pc cm-3. On the high-DM side, we did not detect two MSPs with DM >110 pc cm-3 that we tried, namely PSR J1949+3106 with DM = 164 pc cm-3 and PSR J1903+0327 with DM = 297 pc cm-3. On the other hand, one of the detected MSPs, PSR B1953+29, has a DM of 104.5 pc cm-3. For the DM range of 20–100 pc cm-3 we have almost parity between detected (22) and non-detected MSPs (23).
There is no clear dependence of the MSP detectability on the predicted scattering measure. If it were the case, we would see the majority of non-detected MSPs clustering close to or above the line τscat/P = 1, where a pulse profile would be completely washed out by the scattering. However, most of our non-detected MSPs lie below τscat/P = 1 line populating the DM range of ~20–50 pc cm-3. The dependence of τscat/P on DM follows the empirical relationship between DM and τscat provided by Bhat et al. (2004). However, there is more than two orders of magnitude of scatter in this relationship, hence its predictive power for individual pulsars is very limited. Therefore, it is certainly possible that for some of the non-detected MSPs the scattering conditions are much worse than we can infer from their DM (and/or their detectability depends on other factors).
Another factor that can play an equal or even larger role than scattering in the MSP detectability is our lack of sensitivity resulting from the increased sky temperature background at 150 MHz. In Fig. 6, all five detected MSPs with DM > 40 pc cm-3 have Smean above 27 mJy, larger than the average value for the rest of the detected MSPs. Also, except for the double pulsar, PSR J0737−3039A, four others pulsars – PSRs J0218+4232, B1937+21, B1953+29, and J2215+5135 – have significantly scattered profiles, and their Smean most likely is underestimated. For PSRs J0218+4232, B1937+21, and B1953+29 spectral indices derived from high-frequency data are −2.8, −2.3, and −2.2, respectively, significantly larger than the average for the pulsar population and comparable with the spectral index of the synchrotron background radiation. In fact, PSRs B1937+21 and J0218+4232 were first recognised as steep-spectrum, highly linearly polarised, compact radio sources in interferometric imaging data (Erickson 1980; Navarro et al. 1995), which is what led to their discovery. Most of the other detected MSPs have shallower spectral indices. Together with the possible turnover in their spectra and scattering, this could hinder MSP detection at 150 MHz. For instance, PSR J1713+0747 is very bright (S/N ~ 4000) at 1.4 GHz (see e.g. Dolch et al. 2014). However, the LOFAR detection was very weak, with Smean of only about 11 mJy (S/N ~ 8), and the profile is not very scattered (τscat ~ 120 μs). Thus, in this case the main reason for a weak detection is not due to the scattering, but rather the spectral index of roughly −1.5 being smaller than for the synchrotron background radiation, or the possible turnover in its radio spectrum between 200 and 1400 MHz, or both.
 |
Fig. 7 Dispersion measure versus the MSP duty cycle, δ. Green circles show MSPs with profiles which do not show an evident scattering tail – see δ values marked by an asterisk (⋆) in Table 4. Light yellow squares show all other MSPs. Errors in DMs including δDMorb (see Sect. 4.3) are smaller than the size of the marker for all MSPs. For MSPs without error bars, the uncertainty on δ is also less than the size of the marker. The top subplot shows the histogram of duty cycles for all detected MSPs. |
Three of our non-detected MSPs, PSRs J0613−0200, B1620−26, and J2229+2643, were previously reported to be detected at 102/111 MHz by Kuzmin & Losovsky (2001). As we discussed in Sect. 3.2.3, their detection and flux measurements could be significantly biased due to diffractive scintillation. PSR J0613−0200 was observed by Stappers et al. (2008) with the WSRT at 150 MHz and they did not detect it. Also, for these and other non-detected MSPs additional factors discussed in Sect. 3.2.1 could affect their detection, most notably the ionospheric beam jitter and RISS.
4.2. Profile widths
Table 4 lists measured values of Weff and δ in Cols. 3 and 4 for the total observing bandwidth of 110–188 MHz. At low observing frequencies scattering broadens the intrinsic pulse profiles, and our measured Weff is essentially affected by scattering for many of the observed MSP profiles. For MSPs with narrow, visibly unscattered profiles, Weff and δ in Table 4 are marked with an asterisk (⋆). Figure 7 shows δ vs. DM for detected MSPs. Almost all MSPs with δ ≳ 20% show profiles widened by scattering (yellow squares). Also, between them there is a trend of δ being larger with an increasing DM. The only exception here is PSR J0034−0534 which has a very broad profile (δ ≈ 29%), which mostly likely is genuinely broad by comparing with the WSRT profile at 376 MHz (see Fig. 10).
For the majority of the detected MSPs, δ< 20%. Among them, MSPs with low DMs ≲20 pc cm-3 have sharp narrow profiles and are weakly (if at all) affected by scattering (green circles). Others, at moderately high DMs, have profiles that are strongly affected by scattering and/or intrinsically weak at 110–188 MHz.
Table 4 gives nominal 1σ errors on Weff and δ values. The actual error for Weff can be up to two times larger for the majority of binary MSPs depending on the ratio vorb/c (see Sect. 3.1.1). The actual error on δ could be larger by 0.1%, and does not affect our conclusions on MSP widths.
4.3. DM variations
It is known that, on time scales of months to years, DM and τscat towards some pulsars change due to the varying line-of-sight through the ISM (e.g. Hobbs et al. 2004b). For instance, Hemberger & Stinebring (2008) showed that detectable variations of the scattering measure towards PSR B1737+13 occurred roughly on a time scale of a fortnight for observations in the 1.1–1.5-GHz range. Keith et al. (2013) reported on long-term DM variations for MSPs on time scales of a few months. Correction for such DM variations is crucial for high-precision timing.
To measure DM at the epochs of the individual observations we split the observing band into four–five sub-bands and for each of them generated a single TOA for the whole observation by cross-correlation with a profile template. The template was based on the average pulse profile of all available observations in the total HBA band. We then used the pulsar timing package Tempo217 (Hobbs et al. 2006) to fit the generated TOAs only for DM. In Table 5 we present the weighted average, DMHBA, of our DM measurements (Col. 5) for each of the individual observing epochs during the given time span (Col. 7). The reference epoch that corresponds to the middle of the observing time span is given in Col. 6. The number of observations, Nobs, performed within a given span is listed in Col. 8. For 11 out of 48 detected MSPs we carried out only one exploratory observation, therefore the presented DMs are individual DM measurements for the epoch of the observation. We calculated the DM offset, ΔDM = DMref − DMHBA, between the catalogue DM value, DMref, and LOFAR’s DM measurement, DMHBA (Col. 9), with the uncertainty, σΔDM, being the quadrature sum of uncertainties of both DMref and DMHBA.
Column 11 of Table 5 lists measured DMs for the best individual observations. The uncertainties for most of the MSPs are lower than the errors on DMref, owing to the low observing frequency and large fractional bandwidth of LOFAR. The uncertainty on the weighted average DM value, DMHBA, on the other hand is larger than the uncertainty of the individual measurements for the majority of the MSPs. This is most likely evidence for short-term DM variations. However, care should be taken to account for artificial orbital DM variations for binary MSPs as was discussed in Sect. 3.1.1. These DM variations, δDMorb = vorb/c × DM, are larger for higher-DM pulsars in compact binary orbits. We list δDMorb for all binary MSPs in Col. 10 of Table 5. For vorb we used the maximum orbital velocity of the pulsar at periastron, vp/c = (2πx/Pb) [ (1 + e)/(1 − e) ] 1/2, where x is the projected semi-major axis, e is the eccentricity, and Pb is the orbital period of the pulsar. In our binary MSP sample | δDMorb | is highest for the double pulsar J0737−3039A (0.054 pc cm-3), and lowest for PSR B1257+12 (<10-7 pc cm-3). The influence of δDMorb on the weighted average DMHBA and ΔDM should be even smaller, as the actual δDMorb depends on vorb at the epoch of observation.
Armstrong et al. (1995) have shown that the structure of the ISM has a steep red power spectrum of electron density that results in DM variations becoming more prominent at longer time scales. Hence, one would expect to see larger DM offsets for larger epoch offsets. In Fig. 8 we plotted DM offset, ΔDM, against the epoch offset between the reference catalogue epoch and LOFAR epoch of DM measurements. To account for different uncertainties of DM measurements for different MSPs and, more importantly, to exclude the influence from δDMorb for binary MSPs, we normalised ΔDM by the quadrature sum of its uncertainty, σΔDM, and δDMorb. Note, that for the average DM value over a given time span δDMorb should be also taken as the average contribution from all (Nobs) observations. We will, however, use the most conservative estimate on δDMorb to avoid any influence on our conclusions.
For about 25% of the MSPs, ΔDM is more than three times its DM uncertainty including δDMorb as well. The rest of the DM offsets lie within ± 3σΔDM area including all MSPs for which the δDMorb is larger than σΔDM (brown error bars). We do not see any obvious trends for ΔDM between binary and isolated MSPs. Finally, we also do not see any trends for ΔDM to become larger for larger epoch offsets. There are five MSPs with large ΔDM within five years from the reference DM epoch. This discrepancy in DM may be due to large secular DM drift in the corresponding line of sights. Another possibility for large DM differences at such short-term scales may reflect the fact that at low frequencies the radio emission probes somewhat different regions of interstellar space, thus providing a slightly different DM (Cordes et al. 2015). Multifrequency simultaneous observations and DM measurements are needed to confirm this point conclusively or rule it out.
Keith et al. (2013) presented DM variations for 20 MSPs from the Parkes Pulsar Timing Array (PPTA); eight sources overlap with our sample. Unfortunately, observing time spans do not overlap, with the last measurement in their paper being for MJD 55800. Hence, we cannot make a direct comparison of DM offsets. However, a few of the overlapping MSPs show large regular DM drifts, in particular PSRs J1730−2304 and B1937+21, so we can try to extrapolate the DM offsets at our observing epochs for at least these two MSPs. For PSR J1730−2304 the extrapolation to the reference epoch of MJD 56474 gives ΔDM of about 4.5 × 10-3 pc cm-3, comparable with our measured offset of 0.006 pc cm-3. We see similar agreement for PSR B1937+21, where DM shows a secular decrease with an expected value at the reference epoch of MJD 56385 of ~5 × 10-3 pc cm-3 smaller than the DMref. This is somewhat smaller than our offset of 0.016 pc cm-3, but the amount of DM drift in Keith et al. (2013) for this MSP does show significant variations (see also Kaspi et al. 1994). One of the three LOFAR observations of PSR B1937+21 at MJD 56258.75 also overlaps with the intense multifrequency observing campaign of this pulsar presented in Yi et al. (2014). Our DM measurement for this observing epoch is about 5 × 10-4 pc cm-3 larger than theirs. In their timing analysis they accounted for the broadening of the profile due to scattering in each frequency channel across the 310–390 MHz band, which likely explains the observed DM offset between our measurements.
Precise LOFAR DM measurements on time scales of two–four weeks could provide valuable data for DM corrections of higher-frequency pulsar timing data, especially for the MSPs that do not show variations within the uncertainties of their measurements at higher frequencies, e.g. PSRs J1022+1001, J1713+0747, and J2145−0750. We have already started regular monthly observations of MSPs with LOFAR and we also perform observations with shorter cadence using international LOFAR stations. With these regular timing observations we will measure DM values and provide them to the broader pulsar community for use in ISM studies and high-precision timing. A detailed analysis of DM variations will be presented elsewhere.
Dispersion measures of detected MSPs in the frequency range 110–188 MHz.
 |
Fig. 8 Top: histogram of normalised DM offsets, ΔDM = DMref − DMHBA. Values of ΔDM are normalised by the quadrature sum of DM offset uncertainty, σΔDM, and δDMorb (see text). Bottom: dependence of normalised ΔDM on the epoch offset between reference catalogue epoch and LOFAR epoch of DM measurements. Isolated MSPs are shown with open circles, and binary MSPs with filled circles. Brown bold error bars with caps are for MSPs, where δDMorb is larger than σΔDM. The grey area shows the region where |
 |
Fig. 9 Profile evolution for three MSPs within the LOFAR HBA band. The number on the left in each panel gives the central frequency of the corresponding sub-band in MHz. The profile in grey on top of each panel is the average profile within the 78-MHz wide band. The profiles for each sub-band are normalised by its noise rms deviation. Each sub-band profile is overlaid with the average profile of the total band, in grey. To keep the integrated flux densities the same, the overlaid total-band average profile (in grey) is normalised by the ratio of areas under the total-band profile and the sub-band profile. |
4.4. Profile variations
In the previous Section we assumed there is no profile variation within the observing band. However, at LOFAR frequencies this is usually not the case as there are several factors that can affect the observed profile shape within the band, such as the intrinsic profile evolution and profile smearing due to scattering. For pulsar timing, normally a single profile template is used for cross-correlation with the observed profile to get a TOA. If the profile at the low-frequency edge of the band is significantly scattered, it will artificially increase the uncertainty at the lower end of the band and produce a later TOA, which can be wrongly accounted for by fitting for DM, resulting in an inaccurate DM with larger DM uncertainty than without profile variation. The importance of taking pulse profile evolution into account was already demonstrated in Hassall et al. (2012), where they tested the accuracy of the dispersion law through wide-band simultaneous observations with LOFAR at 40–190 MHz and the Lovell and Effelsberg radio telescopes at 1.4 and 8 GHz, respectively.
To see if this was indeed the case for our MSPs, we calculated DM values using both the Tempo2 and pdmp (van Straten et al. 2012) programs. For pdmp, DM optimisation is based on the S/N of the entire profile, while for Tempo2 it is based on cross-correlation between template and observed profile. In the ideal case of a simple, unscattered Gaussian profile, identical across the whole observing band, both Tempo2 and pdmp should provide the same DM measurements. For scattered profiles, one would expect pdmp to give larger DM values due to overcompensation for scatter-broadening, although a DM measurement by Tempo2 would be biased as well. If there is a variation of the profile in amplitude due to changes in the bandpass gain or intrinsic to the pulsar itself, then this should not matter for pdmp, but for Tempo2 it will depend on how well the match is between the template and profiles across the band. Therefore, generally in the case of any profile variation one would expect to see a discrepancy between DM measurements provided by Tempo2 and pdmp.
Columns 11 and 12 of Table 5 list the Tempo2 and pdmp DM measurements for the best individual observations. To characterise the difference between these values we also calculated the parameter ϵDM as: 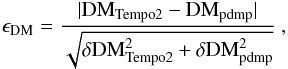 where δDMTempo2 and δDMpdmp are DM uncertainties from Tempo2 and pdmp. For 30 MSPs in our sample the value of ϵDM is less than one, and for all of them we do not see any profile variation. For the other 15 pulsars ϵDM> 1, and all of them manifest a visible change of profile shape and/or amplitude across the band. Among these 15 pulsars, six MSPs have ϵDM> 2, namely PSRs J1640+2224 (ϵDM = 2.1), J1853+1303 (2.2), B1937+21 (2.65), J2051−0827 (2.65), J1810+1744 (3.1), and J1816+4510 (3.4) in ascending value of ϵDM. Figure 2 already shows the profile evolution of PSR B1937+21, and that profile becomes completely scattered out below 150 MHz. Profile evolution for the other three MSPs with the largest ϵDM values is shown on Fig. 9. One can see how the profiles of PSRs J1810+1744 and J1816+4510 are scattered towards lower frequencies. For PSR J2051−0827 scattering does not seem to be relevant, but the pulse amplitude differs significantly at the centre and edges of the band. Therefore, the ϵDM parameter could be used as indirect indication for noticeable profile variation within the observing band, and whether it is needed to be taken into account for accurate DM measurements.
where δDMTempo2 and δDMpdmp are DM uncertainties from Tempo2 and pdmp. For 30 MSPs in our sample the value of ϵDM is less than one, and for all of them we do not see any profile variation. For the other 15 pulsars ϵDM> 1, and all of them manifest a visible change of profile shape and/or amplitude across the band. Among these 15 pulsars, six MSPs have ϵDM> 2, namely PSRs J1640+2224 (ϵDM = 2.1), J1853+1303 (2.2), B1937+21 (2.65), J2051−0827 (2.65), J1810+1744 (3.1), and J1816+4510 (3.4) in ascending value of ϵDM. Figure 2 already shows the profile evolution of PSR B1937+21, and that profile becomes completely scattered out below 150 MHz. Profile evolution for the other three MSPs with the largest ϵDM values is shown on Fig. 9. One can see how the profiles of PSRs J1810+1744 and J1816+4510 are scattered towards lower frequencies. For PSR J2051−0827 scattering does not seem to be relevant, but the pulse amplitude differs significantly at the centre and edges of the band. Therefore, the ϵDM parameter could be used as indirect indication for noticeable profile variation within the observing band, and whether it is needed to be taken into account for accurate DM measurements.
It is clear that for accurate measurements of DM, especially at low frequencies, profile evolution must be taken into account. Even very small profile variations at higher frequencies can also systematically bias the derived arrival times and must be taken into account for high-precision pulsar timing. Frequency-dependent profile templates that take profile broadening due to scattering into account must be used for this purpose, as implemented in the software package PulsePortraiture18 (Pennucci et al. 2014), or using a Generative pulsar timing analysis framework (Lentati et al. 2015). Recently, Liu et al. (2015) considered the double-lens model that reproduces the parameters of the observed diffractive scintillation with high accuracy, and discussed its prospects for removing scattering to improve pulsar timing.
 |
Fig. 10 LOFAR MSP average profiles (blue) in comparison with profiles at other frequencies (black) mostly from the EPN Database of Pulsar Profiles (Lorimer et al. 1998), where available. Each profile is normalised to peak amplitude. These profiles are taken from: Pushchino – Kuzmin & Losovsky (1999) and Kuzmin & Losovsky (1996), WSRT – Stappers (priv. comm.), Effelsberg – Kramer et al. (1998), GB140 – Camilo et al. (1996a) and Sayer et al. (1997), Parkes – Bailes et al. (1997) and Lorimer (1994), Arecibo – Camilo et al. (1996a), Foster et al. (1993) and Camilo et al. (1993), and Lovell – Stairs et al. (1999), Bailes et al. (1997), Gould & Lyne (1998), and Lorimer et al. (1996). |
4.5. Multifrequency MSP profiles
Here we discuss qualitatively the wide-band (100–1510 MHz) profile evolution and compare our findings to other available low-frequency data. Quantitative comparison including high-energy light curves will be presented in subsequent work.
For qualitative comparison we used radio profiles from the EPN Database of Pulsar Profiles19 (Lorimer et al. 1998). For these EPN profiles timing information is not available, therefore we visually aligned them by the phase of the profile peaks. In case of two or more components in a profile we followed alignment from previously published data (Kramer et al. 1999) or our own reasoning. These profiles are presented in Fig. 10, where we also plot (where available) the previous low-frequency Pushchino profiles at 102/111 MHz from Kuzmin & Losovsky (1999). LOFAR profiles (blue) are generally of better quality, with higher S/N ratio and time resolution. More importantly, they do not suffer from intra-channel dispersion smearing, as the Pushchino profiles do. Hence, they provide a clearer view of profile evolution at low frequencies. Stappers et al. (2008) detected eight MSPs at 115–175 MHz with the WSRT. Profiles of two pulsars, PSRs J0034−0534 and J2145−0750, are presented in their paper (Stappers et al. 2008), and their shapes fully resemble the shape of the LOFAR profiles. Contrary to our LOFAR observations in 2013 and BSA observations by Kuzmin & Losovsky (1999) in 1999, Stappers et al. (2008) did not detect PSR J0218+4232 in 2008. This could simply be due to a lack of sensitivity of WSRT, but it might also hint in favour of regular variations in the scattering conditions in the ISM on time scales of several years towards this pulsar. Regular monitoring with LOFAR will answer this question for this and other pulsars in our MSP timing campaign.
Based on how the MSP profiles in Fig. 10 evolved in the LOFAR HBA band, we can clearly divide the presented MSPs into two distinct groups: (a) with LOFAR profiles strongly affected by scattering; and (b) LOFAR profiles that do not show profile broadening due to scattering, or do so very weakly. Only two MSPs from Fig. 10, PSRs J0621+1002 and J1911−1114, fall into the first group. From Fig. 1 we can certainly conclude that there are more MSPs with significantly scattered profiles in the LOFAR HBA band, e.g. PSRs J0218+4232, B1937+21, B1953+29, but we will leave the discussion of their profile evolution for a future paper. Both MSPs with scattered profiles in Fig. 10 have relatively large DMs, 37 and 31 pc cm-3 for PSRs J0621+1002 and J1911−1114, respectively. They do not seem to show the development of other profile components. In the case of PSR J0621+1002 the visual alignment was arbitrary as the scattering moves the peak of the profile to later pulse phases (see e.g. the LBA profile of PSR J0034−0534 in Fig. 5).
The other 11 MSPs from Fig. 10 form the second group, all with unscattered or weakly scattered LOFAR profiles. In fact, for PSR J2145−0750 Kuzmin & Losovsky (1999) claimed that the separation between components decreased at 102 MHz, which they interpreted as an effect caused by the quadrupole magnetic field. Kramer et al. (1999) did not see this abnormal frequency dependence at higher frequencies neither for this nor the other MSPs they studied. This conclusion by Kuzmin & Losovsky (1999) might be due to the fact that they did not use coherently dedispersed profiles and they were affected by intrachannel dispersion that made it more difficult to measure the separation. Kramer et al. (1999) also argued against this conjecture by Kuzmin & Losovsky (1999) because the trailing component itself consists of two overlapping components (see also Sallmen 1998). Similarly to Kuzmin & Losovsky (1999) we do not see a decrease in the component separation for PSR J2145−0750 at LOFAR frequencies in comparison with higher radio frequencies. Also, there is no broadening of the profile due to scattering in the HBA band, and we could only measure the scattering time to be less than 0.7 ms in the LBA band at 57.7 MHz.
It is quite interesting that for those MSPs with overlapping profile components (except maybe for PSR J0034−0534), which constitute half of the second group, the leading component weakens while the trailing component becomes dominan. In particular, this is clearly evident for PSRs J1022+1001, B1257+12, J1640+2224, J2145−0750, and J2317+1439. This might explain the apparent narrowing of MSP profiles at low frequencies. Dyks et al. (2010) demonstrated that such an enhancement of the trailing component in MSP profiles is caused by aberration and retardation. There is also an opposing co-rotation effect, namely the weakening of the trailing side of the profile due to asymmetry of curvature radiation about the dipole axis. Therefore, whether an MSP profile shows such a rotation asymmetry is determined by the dominant effect. Dyks et al. (2010) showed that a sharp edge of the trailing component should be accompanied by a maximum in the gradient of the polarisation angle curve at the same spin phase. We indeed confirm this for PSR J1022+1001 (see Noutsos et al. 2015).
The profile evolution of PSR J1024−0719 is a very interesting case. At present we aligned the LOFAR profile with the peak of the trailing component of the 436-MHz Parkes profile, because i) the tail is reminiscent of the tail in the high-frequency profiles, and ii) the apparent tendency for a weakening leading component from 1.4 GHz to 436 MHz. However, the Pushchino profile at 102 MHz is inconclusive and looks somewhat similar to the two-component profile at 436 MHz. Proper profile alignment is needed to make a firm conclusion.
In general, without considering the broadening of profiles due to scattering, the MSP profiles continue to show constant separation between profile components and their widths at frequencies below 200 MHz. The same lack of profile evolution of MSPs was reported by Kramer et al. (1999) between frequencies of several GHz down to about 400 MHz. This is different from what is observed for normal pulsars and indicates that the emission must originate from a very compact region in the magnetosphere.
5. Summary
We have carried out a LOFAR census of 75 Galactic MSPs in the frequency range 110–188 MHz, and detected 48 of them (25 of which were detected at these frequencies for the first time). We have also detected three MSPs out of nine observed with the LOFAR LBAs in the frequency range 38–77 MHz, namely PSRs J0030+0451, J0034−0534, and J2145−0750. For the detected MSPs:
-
We provide average profiles for all detected MSPs, with about half of them being the best high-quality profiles so far at these frequencies. For 25 MSPs the presented profiles are the first at 110–188 MHz. About 35% of the MSPs show strong narrow profiles, another 25% exhibit undoubtedly scattered profiles, and the rest have low signal-to-noise profiles.
-
We measure the mean flux density at 110–188 MHz and compare it with the predicted values derived from high-frequency observations. For at least a third of the MSPs, the main uncertainty on the predicted flux density originates from poor knowledge of the spectral index. For about another third, the measured flux densities are still lower than the predicted ones even within the uncertainty on their spectral indices. In Sects. 3.2.1 and 3.2.3 we consider different factors that could affect our flux measurements.
-
We also measure the effective pulse width at 150 MHz. For the majority of the detected MSPs, their pulse duty cycle, δ, is less than 20%. Almost all MSPs with δ ≳ 20% show profiles widened by scattering.
-
There is no clear dependence of the MSP detectability on the predicted scattering. We discuss this and other possible factors that affect the MSP detectability in Sect. 4.1.
-
We present average values of DM and their offsets from the catalogue values. For 14 MSPs in our sample the absolute value of their DM offsets is more than three times larger than their errors, and we do not see any trend of DM offsets becoming larger for larger epoch offsets.
-
Finally, we qualitatively compare LOFAR profiles for a subset of MSPs with their profiles at higher radio frequencies. If not broadened by scattering, they show apparent consistency in the width of their profile components and their separation within the frequency range from 150 MHz to a few GHz. This is very different from what is observed for normal pulsars and suggests a compact emission region in the MSP magnetosphere.
There are notable exceptions, such as PSRs J2145−0750 and J0751+1807, that show large frequency evolution in the amplitude ratio of their profile components (Kramer et al. 1999; Kuzmin & Losovsky 1996), and a few other MSPs have new profile components appearing at higher/lower frequencies.
Pulsar J0218+4232 was also not detected by Stappers et al. (2008), though Kuzmin & Losovsky (2001) reported it to be detected and provided its flux density estimates, but did not present its profile.
Hierarchical Data Format 5, http://www.hdfgroup.org/HDF5/
For a demonstration, see: http://www.astron.nl/dailyimage/ index.html?main.php?date=20140123
Acknowledgments
The LOFAR facilities in the Netherlands and other countries, under different ownership, are operated through the International LOFAR Telescope foundation (ILT) as an international observatory open to the global astronomical community under a joint scientific policy. In the Netherlands, LOFAR is funded through the BSIK program for interdisciplinary research and improvement of the knowledge infrastructure. Additional funding is provided through the European Regional Development Fund (EFRO) and the innovation program EZ/KOMPAS of the Collaboration of the Northern Provinces (SNN). ASTRON is part of the Netherlands Organisation for Scientific Research (NWO). V.K. thanks Michiel Brentjens, Stefan Wijnholds, Ger de Bruyn and George Heald for very helpful discussions regarding the LOFAR beam model and flux calibration, and ASTRON’s Radio Observatory Science Support for the help with the observations. We are endlessly thankful to Willem van Straten for implementing code for the dspsr program suite to read raw LOFAR pulsar data. V.K. is grateful to Anne Archibald who provided the best available ephemerides for PSR J0337+1715, to Patrick Lazarus for providing the RFI zapping package CoastGuard, and Tobia Carozzi for development of the mscorpol package. We acknowledge the use of pulsar profiles at high radio frequencies from the European Pulsar Network (EPN) database at the Max-Planck-Institut für Radioastronomie, and its successor, the new EPN Database of Pulsar Profiles, developed by Michael Keith and maintained by the University of Manchester. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement nr. 337062 (DRAGNET; PI JWTH). SO is supported by the Alexander von Humboldt Foundation. SC acknowledges financial support from the UnivEarthS Labex program of Sorbonne Paris Cité (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02), and J.v.L. acknowledges funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement No. 617199.
References
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009, ApJ, 699, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 712, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Archibald, A. M., Kaspi, V. M., Hessels, J. W. T., et al. 2013, ApJ, submitted [arXiv:1311.5161] [Google Scholar]
- Archibald, A. M., Kondratiev, V. I., Hessels, J. W. T., & Stinebring, D. R. 2014, ApJ, 790, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, J. W., Rickett, B. J., & Spangler, S. R. 1995, ApJ, 443, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Arts, M. J., Kant, G. W., & Wijnhols, S. J. 2013, Sensitivity Approximations for Regular Aperture Arrays, Internal Memo SKA-ASTRON-RP-473, ASTRON, The Netherlands [Google Scholar]
- Arzoumanian, Z., Fruchter, A. S., & Taylor, J. H. 1994, ApJ, 426, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Backer, D. C., Kulkarni, S. R., Heiles, C., Davis, M. M., & Goss, W. M. 1982, Nature, 300, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Bailes, M., Johnston, S., Bell, J. F., et al. 1997, ApJ, 481, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Bailes, M., Bates, S. D., Bhalerao, V., et al. 2011, Science, 333, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, E. D., Champion, D. J., Kramer, M., et al. 2013a, MNRAS, 435, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, E. D., Guillemot, L., Champion, D. J., et al. 2013b, MNRAS, 429, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, S. D., Lorimer, D. R., & Verbiest, J. P. W. 2013, MNRAS, 431, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Bhat, N. D. R., Cordes, J. M., Camilo, F., Nice, D. J., & Lorimer, D. R. 2004, ApJ, 605, 759 [CrossRef] [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, B., Roy, J., Ray, P. S., et al. 2013, ApJ, 773, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Bilous, A. V., Kondratiev, V. I., Kramer, M., et al. 2015, A&A, submitted [arXiv:1511.01767] [Google Scholar]
- Boriakoff, V., Buccheri, R., Fauci, F., Turner, K., & Davis, M. 1984, in Birth and Evolution of Neutron Stars: Issues Raised by Millisecond Pulsars, eds. S. P. Reynolds, & D. R. Stinebring, 24 [Google Scholar]
- Boyles, J., Lynch, R. S., Ransom, S. M., et al. 2013, ApJ, 763, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Breton, R. P., Kaspi, V. M., Kramer, M., et al. 2008, Science, 321, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Burgay, M., Joshi, B. C., D’Amico, N., et al. 2006, MNRAS, 368, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Burgay, M., Bailes, M., Bates, S. D., et al. 2013, MNRAS, 433, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F. 1995, Ph.D. Thesis, Princeton University [Google Scholar]
- Camilo, F., Nice, D. J., & Taylor, J. H. 1993, ApJ, 412, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Nice, D. J., Shrauner, J. A., & Taylor, J. H. 1996a, ApJ, 469, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Nice, D. J., & Taylor, J. H. 1996b, ApJ, 461, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Champion, D. J., Lorimer, D. R., McLaughlin, M. A., et al. 2005, MNRAS, 363, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Cognard, I., Bourgois, G., Lestrade, J.-F., et al. 1995, A&A, 296, 169 [NASA ADS] [Google Scholar]
- Cognard, I., Guillemot, L., Johnson, T. J., et al. 2011, ApJ, 732, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, W. A., Rickett, B. J., Codona, J. L., & Frehlich, R. G. 1987, ApJ, 315, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 1978a, ApJ, 222, 1006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cordes, J. M. 1978b, ApJ, 222, 1006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-print [arXiv:astro-ph/0207156] [Google Scholar]
- Cordes, J. M., Weisberg, J. M., & Boriakoff, V. 1985, ApJ, 288, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., Shannon, R. M., & Stinebring, D. R. 2015, ArXiv e-print [arXiv:1503.08491] [Google Scholar]
- Crawford, F., Stovall, K., Lyne, A. G., et al. 2012, ApJ, 757, 90 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira-Costa, A., Tegmark, M., Gaensler, B. M., et al. 2008, MNRAS, 388, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Camilo, F., Reynolds, J. E., & Halpern, J. P. 2012, ApJ, 748, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B. 2011, MNRAS, 416, 2821 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deneva, J. S., Freire, P. C. C., Cordes, J. M., et al. 2012, ApJ, 757, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Desvignes, G., et al. 2015, MNRAS, submitted [Google Scholar]
- Dolch, T., Lam, M. T., Cordes, J., et al. 2014, ApJ, 794, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshenko, O., Löhmer, O., Kramer, M., et al. 2001, A&A, 379, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dowell, J., Ray, P. S., Taylor, G. B., et al. 2013, ApJ, 775, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., Wright, G. A. E., & Demorest, P. 2010, MNRAS, 405, 509 [NASA ADS] [Google Scholar]
- Edwards, R. T., & Bailes, M. 2001, ApJ, 553, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, R. T., & Stappers, B. W. 2003, A&A, 407, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erickson, W. 1980, in BAAS, 12, 799 [Google Scholar]
- Foster, R. S., Fairhead, L., & Backer, D. C. 1991, ApJ, 378, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, R. S., Wolszczan, A., & Camilo, F. 1993, ApJ, 410, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Berman, G., Bower, G., et al. 1990, ApJ, 351, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Fymat, A. L. 1971, Appl. Opt, 10, 2499 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, M. E., Stairs, I. H., Ferdman, R. D., et al. 2011, ApJ, 743, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, D. M., & Lyne, A. G. 1998, MNRAS, 301, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Guillemot, L., Freire, P. C. C., Cognard, I., et al. 2012, MNRAS, 422, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, Y., Rickett, B. J., & Coles, W. A. 1993, ApJ, 403, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaker, J. P. 2006, A&A, 456, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hankins, T. H. 1971, ApJ, 169, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hankins, T. H., & Rickett, B. J. 1975, in Radio astronomy, eds. B. Alder, S. Fernbach, & M. Rotenberg, Methods in Computational Physics, 1414, 55 [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hassall, T. E., Stappers, B. W., Hessels, J. W. T., et al. 2012, A&A, 543, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G. H., Pizzo, R. F., Orrú, E., et al. 2015, A&A, 582, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hemberger, D. A., & Stinebring, D. R. 2008, ApJ, 674, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Roberts, M. S. E., McLaughlin, M. A., et al. 2011, in AIP Conf. Ser., 1357, eds. M. Burgay, N. D’Amico, P. Esposito, A. Pellizzoni, & A. Possenti, 40 [Google Scholar]
- Hobbs, G., Faulkner, A., Stairs, I. H., et al. 2004a, MNRAS, 352, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lyne, A. G., Kramer, M., Martin, C. E., & Jordan, C. 2004b, MNRAS, 353, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., Bailes, M., & Ord, S. M. 2006, MNRAS, 369, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Izvekova, V. A., Kuzmin, A. D., Malofeev, V. M., & Shitov, I. P. 1981, Ap&SS, 78, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A. 2005, Ph.D. Thesis, California Institute of Technology [Google Scholar]
- Jacoby, B. A., Bailes, M., Ord, S. M., Knight, H. S., & Hotan, A. W. 2007, ApJ, 656, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Janssen, G. H., Stappers, B. W., Bassa, C. G., et al. 2010, A&A, 514, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenet, F. A., Anderson, S. B., Kaspi, V. M., Prince, T. A., & Unwin, S. C. 1998, ApJ, 498, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, R. C. 1941, JOSA, 31, 500 [Google Scholar]
- Joshi, B. C., & Kramer, M. 2009, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 345 [Google Scholar]
- Kaplan, D. L., Bhalerao, V. B., van Kerkwijk, M. H., et al. 2013, ApJ, 765, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Karuppusamy, R., Stappers, B., & van Straten, W. 2008, PASP, 120, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., Taylor, J. H., & Ryba, M. F. 1994, ApJ, 428, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Jameson, A., van Straten, W., et al. 2010, MNRAS, 409, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Johnston, S., Ray, P. S., et al. 2011, MNRAS, 414, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Johnston, S., Bailes, M., et al. 2012, MNRAS, 419, 1752 [NASA ADS] [CrossRef] [Google Scholar]
- Keith, M. J., Coles, W., Shannon, R. M., et al. 2013, MNRAS, 429, 2161 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, M., Camilo, F., Johnson, T. J., et al. 2012, ApJ, 748, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Konacki, M., & Wolszczan, A. 2003, ApJ, 591, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratiev, V., Stappers, B., & LOFAR Pulsar Working Group. 2013, in IAU Symp. 291, ed. J. van Leeuwen, 47 [Google Scholar]
- Kramer, M., Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Lange, C., Lorimer, D. R., et al. 1999, ApJ, 526, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Stairs, I. H., Manchester, R. N., et al. 2006a, Science, 314, 97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kramer, M., Stairs, I. H., Manchester, R. N., et al. 2006b, Science, 314, 97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuniyoshi, M., Verbiest, J. P. W., Lee, K. J., et al. 2015, MNRAS, accepted [arXiv:1507.03732] [Google Scholar]
- Kuzmin, A. D., & Losovsky, B. Y. 1996, A&A, 308, 91 [NASA ADS] [Google Scholar]
- Kuzmin, A. D., & Losovsky, B. Y. 1999, A&A, 352, 489 [NASA ADS] [Google Scholar]
- Kuzmin, A. D., & Losovsky, B. Y. 2001, A&A, 368, 230 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuzmin, A. D., & Losovsky, B. Y. 2002, Astr. Lett., 28, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzmin, A. D., Malofeev, V. M., Shitov, Y. P., et al. 1978, MNRAS, 185, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, C., Camilo, F., Wex, N., et al. 2001, MNRAS, 326, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Lawson, K. D., Mayer, C. J., Osborne, J. L., & Parkinson, M. L. 1987, MNRAS, 225, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Lentati, L., Alexander, P., & Hobson, M. P. 2015, MNRAS, 447, 2159 [NASA ADS] [CrossRef] [Google Scholar]
- Levin, L., Bailes, M., Barsdell, B. R., et al. 2013, MNRAS, 434, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Lewandowski, W., Wolszczan, A., Feiler, G., Konacki, M., & Sołtysiński, T. 2004, ApJ, 600, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., Pen, U.-L., Macquart, J., Brisken, W., & Deller, A. 2015, ApJ, submitted [arXiv:1507.00884] [Google Scholar]
- Löhmer, O., Lewandowski, W., Wolszczan, A., & Wielebinski, R. 2005, ApJ, 621, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Lommen, A. N., Zepka, A., Backer, D. C., et al. 2000, ApJ, 545, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. 1994, Ph.D. Thesis, University of Manchester [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge University Press) [Google Scholar]
- Lorimer, D. R., Nicastro, L., Lyne, A. G., et al. 1995, ApJ, 439, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Lyne, A. G., Bailes, M., et al. 1996, MNRAS, 283, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Jessner, A., Seiradakis, J. H., et al. 1998, A&AS, 128, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorimer, D. R., Xilouris, K. M., Fruchter, A. S., et al. 2005, MNRAS, 359, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., McLaughlin, M. A., Champion, D. J., & Stairs, I. H. 2007, MNRAS, 379, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Lundgren, S. C., Zepka, A. F., & Cordes, J. M. 1995, ApJ, 453, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, R. S., Boyles, J., Ransom, S. M., et al. 2013, ApJ, 763, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Burgay, M., Kramer, M., et al. 2004, Science, 303, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Malofeev, V. M. 2000, in Pulsar Astronomy – 2000 and Beyond, ed. M. Kramer, N. Wex, & R. Wielebinski, IAU Colloq. 177, ASP Conf. Ser., 202, 221 [Google Scholar]
- Malofeev, V. M., Malov, O. I., & Shchegoleva, N. V. 2000, Astron. Rep., 44, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Maron, O., Kijak, J., Kramer, M., & Wielebinski, R. 2000, A&AS, 147, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J., de Bruyn, A. G., Frail, D. A., Kulkarni, S. R., & Lyne, A. G. 1995, ApJ, 455, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Nelles, A., Hörandel, T., karskens, M. K., et al. 2015, JInst, submitted [arXiv:1507.08932] [Google Scholar]
- Ng, C., Bailes, M., Bates, S. D., et al. 2014, MNRAS, 439, 1865 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, L., Lyne, A. G., Lorimer, D. R., et al. 1995, MNRAS, 273, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Nice, D. J., Taylor, J. H., & Fruchter, A. S. 1993, ApJ, 402, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Nice, D. J., Splaver, E. M., Stairs, I. H., et al. 2005, ApJ, 634, 1242 [Google Scholar]
- Nice, D. J., Altiere, E., Bogdanov, S., et al. 2013, ApJ, 772, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Noutsos, A., Sobey, C., Kondratiev, V. I., et al. 2015, A&A, 576, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., Ferrigno, C., Bozzo, E., et al. 2013, Nature, 501, 517 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Patruno, A., Archibald, A. M., Hessels, J. W. T., et al. 2014, ApJ, 781, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Pennucci, T. T., Demorest, P. B., & Ransom, S. M. 2014, ApJ, 790, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Perera, B. B. P., McLaughlin, M. A., Kramer, M., et al. 2010, ApJ, 721, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Pilia, M., Hessels, J. W. T., Stappers, B. W., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201425196 [Google Scholar]
- Polisensky, E. 2007, LFmap: A Low Frequency Sky Map Generating Program, Long Wavelength Array Memo Series 111, Naval Research Lab [Google Scholar]
- Popov, M. V., & Soglasnov, V. A. 1984, Soviet Ast., 28, 424 [NASA ADS] [Google Scholar]
- Radhakrishnan, V., & Srinivasan, G. 1981, in Proc. 2nd Asian–Pacific Regional Meeting of the IAU, eds. B. Hidayat, & M. W. Feast (Jakarta: Tira Pustaka), 423 [Google Scholar]
- Ransom, S. M. 2001, Ph.D. Thesis, Harvard University, USA [Google Scholar]
- Ransom, S. M., Backer, D. C., Demorest, P., et al. 2004 [arXiv:astro-ph/0406321] [Google Scholar]
- Ransom, S. M., Ray, P. S., Camilo, F., et al. 2011, ApJ, 727, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Stairs, I. H., Archibald, A. M., et al. 2014, Nature, 505, 520 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ray, P. S., Abdo, A. A., Parent, D., et al. 2012, in Fermi symp. proc. – eConf C110509, ArXiv e-prints [arXiv:1205.3089] [Google Scholar]
- Rickett, B. J., Coles, W. A., & Bourgois, G. 1984, A&A, 134, 390 [NASA ADS] [Google Scholar]
- Roger, R. S., Costain, C. H., Landecker, T. L., & Swerdlyk, C. M. 1999, A&AS, 137, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosen, R., Swiggum, J., McLaughlin, M. A., et al. 2013, ApJ, 768, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Sallmen, S. M. 1998, Ph.D. thesis, University of California, Berkeley, USA [Google Scholar]
- Sayer, R. W., Nice, D. J., & Taylor, J. H. 1997, ApJ, 474, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Sieber, W. 1973, A&A, 28, 237 [NASA ADS] [Google Scholar]
- Splaver, E. M., Nice, D. J., Arzoumanian, Z., et al. 2002, ApJ, 581, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Stairs, I. H., Thorsett, S. E., & Camilo, F. 1999, ApJS, 123, 627 [Google Scholar]
- Stairs, I. H., Faulkner, A. J., Lyne, A. G., et al. 2005, ApJ, 632, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Stappers, B. W., Bailes, M., Lyne, A. G., et al. 1996, ApJ, 465, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Stappers, B. W., Karappusamy, R., & Hessels, J. W. T. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 593 [Google Scholar]
- Stappers, B. W., Hessels, J. W. T., Alexov, A., et al. 2011, A&A, 530, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stappers, B. W., Archibald, A. M., Hessels, J. W. T., et al. 2014, ApJ, 790, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Stovall, K., Lynch, R. S., Ransom, S. M., et al. 2014a, ApJ, 791, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Stovall, K., Ray, P. S., Blythe, J., et al. 2014b, ApJ, submitted [arXiv:1410.7422] [Google Scholar]
- Thorsett, S. E. 1991, ApJ, 377, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Toscano, M., Bailes, M., Manchester, R. N., & Sandhu, J. S. 1998, ApJ, 506, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Toscano, M., Sandhu, J. S., Bailes, M., et al. 1999, MNRAS, 307, 925 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Straten, W., & Bailes, M. 2011, PASA, 28, 1 [NASA ADS] [CrossRef] [Google Scholar]
- van Straten, W., Demorest, P., & Oslowski, S. 2012, Astron. Res. Technol., 9, 237 [NASA ADS] [Google Scholar]
- Verbiest, J. P. W., Bailes, M., Coles, W. A., et al. 2009, MNRAS, 400, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. A., Demorest, P. B., & van Straten, W. 2013, ApJ, 779, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnholds, S. J., & van Cappellen, W. A. 2011, IEEE Transactions on Antennas and Propagation, 59, 1981 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., Doroshenko, O., Konacki, M., et al. 2000, ApJ, 528, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Xilouris, K. M., Kramer, M., Jessner, A., Wielebinski, R., & Timofeev, M. 1996, A&A, 309, 481 [NASA ADS] [Google Scholar]
- Xilouris, K. M., Kramer, M., Jessner, A., et al. 1998, ApJ, 501, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Stappers, B. W., Sanidas, S. A., et al. 2014, MNRAS, 445, 1245 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 LOFAR total-intensity pulse profiles for all detected MSPs from the best (highest S/N) individual observations. The horizontal axes show the pulse phase, and the vertical axes are the flux density in arbitrary units. |
| In the text | |
 |
Fig. 2 Profile evolution of pulsar B1937+21 within the LOFAR HBA band in the range 105–197 MHz. Each profile has 128 bins and is folded in ~9.2-MHz wide sub-bands centred at the labelled frequency in MHz. |
| In the text | |
 |
Fig. 3 Measured mean flux densities at 110–188 MHz versus predicted flux densities using high-frequency data for 48 MSPs. The dotted line shows the loci of measured mean fluxes equal to predicted fluxes, and dashed lines mark the region where measured mean flux density deviates from predicted flux density by a factor of two. Open symbols show the MSPs for which spectral indices are not known, and the average index from Bates et al. (2013) was used, while solid symbols are for those with known spectral indices (see Table 4). Blue squares and green circles indicate MSPs with measured duty cycles >20% and <20%, respectively. Pulsars are labelled by their right ascension. |
| In the text | |
 |
Fig. 4 Same as the Fig. 3, but predicted mean flux densities are those from Kuzmin & Losovsky (2001) scaled to the frequency range of 110–188 MHz using the spectral indices from Table 4. |
| In the text | |
 |
Fig. 5 Profile evolution of the three MSPs detected in the LBA frequency range of 38.2–77.2 MHz. The grey profile on top of each panel is the average profile within the 39-MHz wide band. All profiles are from 1-h LBA observations. There are 64 bins in the profiles of PSRs J0030+0451 and J0034−0534 and 128 bins in the profiles of PSR J2145−0750. The numbers on the left in each panel show the central frequency in MHz of the corresponding 7.8-MHz sub-band. |
| In the text | |
 |
Fig. 6 MSP detectability, or dependence of the ratio of predicted scattering time at 150 MHz over the pulsar period, τscat/P, on dispersion measure, DM. The green colour map corresponds to the measured mean flux density, Smean, at 110–188 MHz. Non-detected MSPs are shown with brown squares and their green intensity level corresponds to the measured upper limit of the mean flux density at 110–188 MHz. Scattering times at 150 MHz were calculated from the NE2001 Galactic free electron density model (Cordes & Lazio 2002) assuming a Kolmogorov spectrum of electron density inhomogeneities. The dashed line shows the empirical dependence between τscat and DM at 150 MHz from Bhat et al. (2004), where τscat is arbitrarily normalised by P = 4.075 ms, which is the median value of MSP periods in our sample of detected and non-detected MSPs. The top subplot shows the histograms of DMs for detected and non-detected MSPs. The inset plot is the same as the main plot but only for the non-detected PSR J1903+0327, which did not fit into the range of the main plot. PSR J1400−1438 was recently detected with LOFAR using the updated coordinates (J. Swiggum, priv. comm.) derived from over three years of timing with the GBT. The previously used catalogued position was off by about 6′, which is about two times larger than the full-width at half-maximum of LOFAR’s full-core tied-array beam at 150 MHz. |
| In the text | |
 |
Fig. 7 Dispersion measure versus the MSP duty cycle, δ. Green circles show MSPs with profiles which do not show an evident scattering tail – see δ values marked by an asterisk (⋆) in Table 4. Light yellow squares show all other MSPs. Errors in DMs including δDMorb (see Sect. 4.3) are smaller than the size of the marker for all MSPs. For MSPs without error bars, the uncertainty on δ is also less than the size of the marker. The top subplot shows the histogram of duty cycles for all detected MSPs. |
| In the text | |
 |
Fig. 8 Top: histogram of normalised DM offsets, ΔDM = DMref − DMHBA. Values of ΔDM are normalised by the quadrature sum of DM offset uncertainty, σΔDM, and δDMorb (see text). Bottom: dependence of normalised ΔDM on the epoch offset between reference catalogue epoch and LOFAR epoch of DM measurements. Isolated MSPs are shown with open circles, and binary MSPs with filled circles. Brown bold error bars with caps are for MSPs, where δDMorb is larger than σΔDM. The grey area shows the region where |
| In the text | |
 |
Fig. 9 Profile evolution for three MSPs within the LOFAR HBA band. The number on the left in each panel gives the central frequency of the corresponding sub-band in MHz. The profile in grey on top of each panel is the average profile within the 78-MHz wide band. The profiles for each sub-band are normalised by its noise rms deviation. Each sub-band profile is overlaid with the average profile of the total band, in grey. To keep the integrated flux densities the same, the overlaid total-band average profile (in grey) is normalised by the ratio of areas under the total-band profile and the sub-band profile. |
| In the text | |
 |
Fig. 10 LOFAR MSP average profiles (blue) in comparison with profiles at other frequencies (black) mostly from the EPN Database of Pulsar Profiles (Lorimer et al. 1998), where available. Each profile is normalised to peak amplitude. These profiles are taken from: Pushchino – Kuzmin & Losovsky (1999) and Kuzmin & Losovsky (1996), WSRT – Stappers (priv. comm.), Effelsberg – Kramer et al. (1998), GB140 – Camilo et al. (1996a) and Sayer et al. (1997), Parkes – Bailes et al. (1997) and Lorimer (1994), Arecibo – Camilo et al. (1996a), Foster et al. (1993) and Camilo et al. (1993), and Lovell – Stairs et al. (1999), Bailes et al. (1997), Gould & Lyne (1998), and Lorimer et al. (1996). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.