| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 19 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526783 | |
| Published online | 22 December 2015 | |
Consistent metallicity scale for cool dwarfs and giants
A benchmark test using the Hyades⋆
1
Departamento de Física Teórica e ExperimentalUniversidade Federal do Rio
Grande do Norte, Campus Universitário Lagoa Nova, 59072-970
Natal, RN, Brazil
e-mail: leticia@dfte.ufrn.br
2
Universidade do Federal do Rio de Janeiro, Observatório do
Valongo, Ladeira do Pedro Antônio
43, 20080-090
Rio de Janeiro,
Brazil
3
European Southern Observatory, 85748
Garching bei München,
Germany
4
Department for Astrophysics, Nicolaus Copernicus Astronomical Center, ul. Rabiańska
8, 87-100
Toruń,
Poland
5
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
Received:
19
June
2015
Accepted:
31
August
2015
Context. In several instances chemical abundances of main-sequence and giant stars are used simultaneously under the assumption that they share the same abundance scale. This assumption, if wrong, might have important implications in different astrophysical contexts.
Aims. It is therefore crucial to understand whether the metallicity or abundance differences among dwarfs and giants are real or are produced by systematic errors in the analysis. We aim to ascertain a methodology capable of producing a consistent metallicity scale for giants and dwarfs.
Methods. To achieve that, we analyzed giants and dwarfs in the Hyades open cluster, under the assumption that they share the same chemical composition. All the stars in this cluster have archival high-resolution spectroscopic data obtained with HARPS and UVES. In addition, the giants have interferometric measurements of the angular diameters. We analyzed the sample with two methods. The first method constrains the atmospheric parameters independently from spectroscopic method. For that we present a novel calibration of microturbulence based on 3D model atmospheres. The second method is the classical spectroscopic analysis based on Fe lines. We also tested two different line lists in an attempt to minimize possible non-LTE effects and to optimize the treatment of the giants.
Results. We show that it is possible to obtain a consistent metallicity scale between dwarfs and giants. The preferred method should constrain the three parameters Teff, log g, and ξ independent of spectroscopy. A careful selection of Fe lines is also important. In particular, the lines should not be chosen based on the Sun or other dwarfs, but specifically to be free of blends in the spectra of giants. When attention is paid to the line list, the classical spectroscopic method can also produce consistent results. In our test, the metallicities derived with the well-constrained set of stellar parameters are consistent independent of the line list used. Therefore, for this cluster we favor the metallicity of +0.18 ± 0.03 dex obtained with this method. The classical spectroscopic analysis, using the line list optimized for the giants, provides a metallicity of +0.14 ± 0.03 dex, in agreement with previous works.
Key words: stars: abundances / stars: fundamental parameters / stars: late-type / techniques: spectroscopic / Galaxy: evolution / planets and satellites: formation
© ESO, 2015
1. Introduction
The determination of chemical abundances in stars by spectral synthesis or curve of growth is a rather well-established technique, largely available to most astronomers. A more detailed view of stellar abundances has become possible since the advent of 8–10 m class telescopes coupled with high-efficiency spectrographs, which produced high quality spectra for many stars. As a consequence, uncertainties in abundance analyses are mainly dominated by systematic errors rather than by observational limitations regarding spectral resolution and/or signal-to-noise ratio (S/N). In this context, we should recall that the determination of stellar abundances requires a number of assumptions, some of which might not be valid for stars in different evolutionary stages, such as dwarfs and giants.
Although cool dwarfs and giants are often analyzed following a single methodology, the differences in their photospheric properties might introduce distinct systematic effects on the final atmospheric parameters derived during the analysis. An example is the large experiment with multiple analysis pipelines conducted within the Gaia-ESO Spectroscopic Survey. In this survey, it was clearly demonstrated that the multiple analysis methodologies perform differently in distinct regions of the parameter space (see Smiljanic et al. 2014). It is thus important to understand if differences on metallicities and abundances between giants and dwarfs are real or produced by systematic errors in the analysis. The interpretation of some open questions in astronomy depends on these kinds of comparisons.
For instance, metallicity plays a role in one of the most accepted scenarios in planet formation theories, which is the core accretion scenario. (see, e.g., Pollack et al. 1996). Concerning the gas-giant planet formation, many works have shown that main-sequence FGK-type stars hosting giant planets (>1.0 MJ) are usually metal-rich when compared with their counterparts without giant planets (Gonzalez 1997; Santos et al. 2004; Fischer & Valenti 2005). However, a giant planet versus metallicity correlation is not well established for evolved stars. Pasquini et al. (2007) showed that giant stars with planets do not tend to have high metallicities. A similar result was found by other works (Schuler et al. 2005; Takeda et al. 2008; Ghezzi et al. 2010; Mortier et al. 2013), but not by Hekker & Meléndez (2007), Reffert et al. (2015) who also argued in favor of a planet metallicity correlation in giants.
The situation for giants is more complex because of many factors as, for example, the limited sample size of giants hosting planets, inhomogeneities in the planetary properties, and the higher masses of giant stars in comparison to dwarfs. Indeed, there is a stellar mass vs. planet vs. metallicity correlation when we consider the giant planet occurrence frequency in evolved stars. Some authors have reported that there is a trend toward higher metallicities for stars with masses above 1.5 M⊙ (Johnson et al. 2010; Maldonado et al. 2013). Understanding the metallicity distribution of stars with planets would provide an important constraint for planet formation theories.
The comparison between the metallicity scale of giants and dwarfs is also important in studies of Galactic chemical evolution. For instance, the metallicity distribution (MD) of the Galactic bulge provides clues about how similar bulge stars are to thin and thick disk stars. As a consequence, it aids the determination of the bulge age. Initial studies of the bulge were focused on giant stars (e.g., McWilliam & Rich 1994; Zoccali et al. 2006) because these are intrinsically brighter objects. Later, the microlensing technique was used to observe dwarfs and subgiants in the Galactic bulge. This revealed discrepancies between the MD of bulge giants and dwarfs (Cohen et al. 2008; Bensby et al. 2010, 2011). More recent studies, however, show a better agreement between the two MDs (Bensby et al. 2013; Anders et al. 2014), although the authors recognize some evidence of a bias toward the high-metallicity tail of the giants’ distribution (Taylor & Croxall 2005; Hill et al. 2011). Indeed, it is difficult to analyze giants in the high-metallicity regime since their spectra are severely affected by blending and molecules features because of their cool atmospheres. A better picture of the MD of giants requires a full knowledge of the source of this bias in the metal-rich regime.
Methodological limitations may affect the analysis of giants and dwarfs differently, e.g., how realistic are the adopted atmospheric models, continuum normalization, and atomic and molecular constants used. The use of the same line list can be a challenge since the intensity of the spectral lines is different in these objects. Moreover, departures from the local thermodynamical equilibrium (LTE) are particularly important for low-gravity and low-metallicity stars (Asplund 2005). Spectroscopic gravities derived by the ionization equilibrium may be unreliable because of Fe i overionization. High-temperature dwarfs (Teff> 6000 K) may also suffer from non-LTE effects (Mashonkina et al. 2010). Additionally, the gf values need to be very accurate for giants since a differential analysis with respect to the Sun does not cancel out uncertainties in these constants.
Open clusters are the optimal sites to evaluate the limitations of abundance analyses when applied to giants and dwarfs. They are made of stars with basically the same distance, and in general, it is reasonable to assume that all stars share the same overall chemical composition, except for the elements affected by mixing in giants (see, e.g., Takeda et al. 2008; Smiljanic et al. 2009; Smith et al. 2013). Stars in an open cluster also share the same age, outlining a common isochrone curve in the HR diagram, making it easier to constrain stellar parameters in these environments.
Few studies so far have attempted the simultaneous analysis of giants and dwarfs in open clusters, aiming to explore possible discrepancies in the abundance patterns between these two classes of objects. Pasquini et al. (2004) investigated dwarfs and giants of the intermediate-age cluster IC 4651, and found, in general, excellent agreement between stars of different evolutionary status. Pace et al. (2010) investigated the metallicity of five dwarfs and three giants in two open clusters and found differences in the metallicity of up to 0.10 dex for one of the clusters. They also pointed out enhancements of sodium, aluminium, and silicon for the giants. A similar study was performed by Santos et al. (2009, 2012), who investigated the abundance pattern of several open clusters performing a simultaneous and homogeneous spectroscopic analysis. These authors noticed that the discrepancy on the metallicity scale of giants and dwarfs belonging to the same cluster may depend on the line list used. The explanation about the source of these differences is still a matter of investigation.
In this work, we chose the Hyades open cluster to perform a simultaneous and homogeneous study of giant and dwarf stars. Our aim is to define an analysis method that can deliver metallicities in a consistent scale for both types of stars. Once this method is tested and established, it can be applied to different astrophysical problems, such as the comparison of MDs of planet host dwarfs and giants. We choose the Hyades, as atmospheric parameters can be constrained by other methods than the classical spectroscopic analysis (see below), and because this cluster is young enough that it should be free of atomic diffusion effects. The paper is organized as follows. Section 2 reviews the main properties of the cluster, while Sect. 3 presents a description of the data. Section 4 is dedicated to the analysis and Sect. 5 to the discussion of the results. In Sect. 6 we draw our final conclusions.
Selected objects in the Hyades cluster.
2. Hyades: the benchmark test
The Hyades is a relatively young cluster, with an estimated age of ~625 ± 50Myr (Perryman et al. 1998), and is the closest open cluster to the Sun (~46.5 pc, van Leeuwen 2009). Spectroscopic studies of FGK-type dwarfs in the Hyades find a metallicity of about +0.13 dex (Cayrel et al. 1985; Boesgaard & Friel 1990; Paulson et al. 2003; Schuler et al. 2006). Regarding the giants, the metallicity values range from +0.10 up to +0.20 dex, where this scatter is usually attributed to the star HIP 20455, a spectroscopic binary (Schuler et al. 2006; Carrera & Pancino 2011).
The slightly over-solar metallicity provides a safe regime to test the classical spectroscopic analysis. At this regime, departures from LTE are not expected to be significant for Fe i. Also, close to the solar metallicity, the mean temperature stratification is close to the radiative equilibrium expectation, and therefore, the difference between 1D and 3D model atmospheres is expected to be relatively small (Asplund 2005).
A relevant advantage of the stars in the Hyades is that their atmospheric parameters can be very well constrained. From the standpoint of the giants, interferometric measurements of the angular diameters are available, which enables the direct determination of absolute effective temperatures (Boyajian et al. 2009). Furthermore, precise Hipparcos parallaxes (van Leeuwen 2007) are available. Thus, a reliable determination of the surface gravities is possible. Finally, a large amount of spectroscopic data is available for the numerous dwarfs and all four giants of this cluster. All these make the Hyades the optimal benchmark to test the limitations of the classical spectroscopic analysis method.
The Hyades is also a target of planet searches using the radial velocity technique (Cochran et al. 2002; Paulson et al. 2004). So far, one of the four giants in the Hyades was reported to host a giant planet. The clump giant HIP 20889 has a long period planet (~594 days) with ~7.6 MJ (Sato et al. 2007). More recently, Quinn et al. (2014) reported the discovery of the first hot Jupiter orbiting a K dwarf HD 285507 in this cluster.
Our sample was selected as follows. The dwarfs were selected primarily from the list of van Bueren (1952) and then cross-checked with the reliable sample of cluster members defined by Perryman et al. (1998). Three additional dwarfs were selected exclusively from Perryman et al. (1998) to complement the cooler end of our sample (these are the stars without the vB number in Table 1). Among them, one cool dwarf (HIP 13976) appears slightly away from the cluster’s main sequence. However, this object was classified as a reliable member of the cluster by Perryman et al. (1998) and has radial velocity and distance fully compatible with the cluster distribution. Moreover, this star is present in many analyses of the cluster (e.g., Paulson et al. 2003; Yong et al. 2004; Schuler et al. 2006).
Several studies investigated binaries in the Hyades (Stefanik & Latham 1985, 1992) and our stars were chosen to avoid binary systems. Among the giants, we excluded HIP 20885, as it is a spectroscopic binary (SB1) with a blue companion. Torres et al. (1997) estimated that the secondary star contributes about 3% of the flux of the primary. An accurate abundance analysis should take this contribution into account. Finally, whenever possible, we chose stars that have been studied in previous works for comparison purposes (in particular, Paulson et al. 2003; Schuler et al. 2006). Table 1 presents the basic data of the 14 dwarfs and the three giants selected for our sample. Their position in the CMD is shown in Fig. 1. In this figure, the magnitude V and the (B − V) color are from Perryman et al. (1998). We highlight that our sample encompasses stars in a large range of effective temperatures (4700 K ≤Teff≤ 6200 K). This facilitates the investigation of possible systematic effects from the analysis as a function of this parameter.
 |
Fig. 1 Color magnitude diagram (CMD) of the Hyades. The large black triangles correspond to the sample selected for our analysis. The small gray dots are the other cluster members. The magnitude V and the (B − V) color are from Perryman et al. (1998) and all stars shown fulfill the membership criterion of this work. |
3. Observations and data reduction
All spectra used in this work were downloaded from the European Southern Observatory (ESO) science archive facility1. The giants were observed during ESO program 088.C-0513 with the HARPS (High Accuracy Radial velocity Planet Searcher, Mayor et al. 2003) high-resolution spectrograph (R = 110 000), situated at the 3.6 m telescope in La Silla, Chile. The spectral range covers from 3800 to 6900 Å, with a small gap between 5300–5330 Å because of the arrangement of the CCD mosaic. The average S/N @6109 Å is about 400. All the spectra were reprocessed by the last version of the HARPS pipeline (Data Reduction Software version 3.5). We only carried out the Doppler correction and the continuum normalization with standard IRAF2 routines.
The dwarfs were observed during ESO program 70D-0356 with UVES (Ultraviolet and Visual Echelle Spectrograph, Dekker et al. 2000) at the 8.2 m Kueyen telescope of the Very Large Telescope (VLT) with and spectral resolution of R ~ 60 000. For consistency, we used spectra acquired with the same instrument configuration for all the observations: slit width of 0.8″ and central wavelength at 580 nm in the red arm. The wavelength coverage is from 4780–6800 Å with a gap between 5750–5830 Å because of thee arrangement of the CCD mosaic. The S/N varies from 150 to 400. Data reduction was carried out with the ESO Reflex environment (Freudling et al. 2013) version 2.3, with the exception of Doppler correction, which was performed with IRAF routines.
We adopt two spectra as solar proxies. For comparison with the giants, we use the reflected spectrum of the Jupiter’s moon Ganymede3, which was obtained with the same HARPS configuration as the spectra of the giants. For the comparison with the dwarfs, we use the UVES solar spectrum4, which was obtained with the moonlight illuminating the slit. Both spectra have, on average, a S/N ≥ 300.
4. Analysis
The atmospheric parameters (effective temperature, Teff, surface gravity, log g, and microturbulence, ξ) of the sample stars were determined using two different methods. In this way, we can compare the final metallicity scale obtained under different assumptions. The first method, hereafter M1 and described in Sect. 4.3, takes constraints into account that do not depend on the classical spectroscopic method, but that are still fine-tuned using Fe i and Fe ii lines. The second method, hereafter M2 and described in Sect. 4.4, is the classical spectroscopic analysis where the parameters are determined using the Fe i and Fe ii ionization and excitation equilibria. In addition, in the implementation of each method, we make use of two different line lists. We, therefore, derived four sets of atmospheric parameters for each star. Before describing the two methods, we present the two line lists and discuss the measurement of equivalent widths (EWs).
4.1. Line lists selection
The two line lists that we adopted were assembled with two goals. First, we aim to minimize non-LTE effects as it will differentially affect stars of different gravities and temperatures. Therefore, the first list contain a set of lines for which non-LTE effects would be minimized or neglected, at least in the metallicity regime of the Hyades. Mashonkina et al. (2011) evaluated the non-LTE line formation of the two ions of iron in cool reference stars, some of them, with metallicity comparable to the Hyades. In that study, the authors concluded that non-LTE effects are virtually negligible for Fe ii lines (i.e., they affect the abundances by less than 0.01 dex) and are very small for Fe i lines, for stars of metallicity slightly higher than the Sun. We selected a total of 42 Fe i and 15 Fe ii, from their line list, among weak to moderately strong transitions, which were well isolated and as free as possible from blending features. We excluded 14 lines of the original list for which the measured EW in the Sun was in the saturated regime of the curve of growth. Mashonkina et al. (2011) claimed that the accuracy of their iron abundances might be affected by the uncertainties in the gf values that were used. Their gf values were obtained from experimental measurements collected from different papers. We improved some of the gf values in this line list with more recent determinations that were kindly provided by Maria Bergemann (priv. comm.). Table A.1 lists the selected lines, their atomic data and, in addition, the equivalent widths and individual abundances obtained for the solar reflected spectrum of Ganymede using M1. This line list is hereafter referred to as MASH.
The second list was chosen to be suitable for the analysis of giants. Often, line lists assembled for the analysis of the Sun may not be optimized for giants because of the more pronounced spectral transitions present in these stars. We have used a line list with transitions carefully chosen to avoid blends in giants and with accurate gf values determination provided through the courtesy of Dr. Martin Asplund (priv. comm.). This list includes a total of 34 Fe i and 7 Fe ii transitions and hereafter is referred to as ASPL. Table A.2 lists the lines, as well their atomic data, and the equivalent widths and individual abundances for the solar reflected spectrum of Ganymede using M1. There are 15 lines in common between the MASH and ASPL lists. Nevertheless, the abundances in the Sun are sometimes distinct because of the different atomic data adopted in each list. This difference is greater than 0.05 dex for about 20% of the lines, while for the remaining it is about ~0.02 dex on average.
 |
Fig. 2 Comparison of EWs obtained with ARES and splot. Left: the solar reflected spectrum of Ganymede; middle: the star HIP 20205; and right: the star HIP 22566. The one-to-one relation is shown with the dashed line, and the red line represents the linear regression fit in each plot. The slope, the intercept, and the rms of the fits are also given in each plot. |
4.2. Equivalent width measurements
We used the code ARES (Automatic Routine for line Equivalent widths in stellar Spectra; Sousa et al. 2007) to perform automatic measurements of the EWs of the Fe i and Fe ii lines. This code applies a Gaussian fit to the profile of the absorption lines, taking a local continuum into account, which is determined on the basis of a set of input parameters provided by the user. We tested different combinations of input parameters for both UVES and HARPS spectra, and chose those which visually produced the best fits to the line profile. The best fits were determined by a visual check and by comparing the EWs computed with ARES and the EWs computed with IRAF for a given set of stars. These were the same stars selected for the EWs comparison between IRAF and ARES (see below). With this approach, the input fitting parameters for ARES were optimized. The spectral resolution we use is such that, in general, the instrumental profile dominates the observed profile, and therefore, a Gaussian fit can well reproduce the observed profile of the lines. Additionally, we removed all EWs < 5 mÅ from our analysis to avoid lines severely affected by noise or uncertainties related to the continuum fit, therefore, with larger relative errors in the EW measurement. We also removed EWs > 120 mÅ, to avoid the flat part of the curve of growth, in which a Gaussian fit may not adequately reproduce the observed line profiles.
The quality of the automatic measurements is comparable to the manual method obtained with the task splot of IRAF for the majority of the HARPS and UVES spectra as shown by Sousa et al. (2007). Notwithstanding, we repeated this comparison with the line lists used in our work to verify if the manual EWs obtained with splot are comparable with those computed using ARES for both giants and dwarfs.
IRFM Teff obtained with three different calibrations for the giants of the Hyades.
Figure 2 shows the results of such comparison. In addition to the solar spectrum, we select as examples the hot dwarf HIP 22566, where the continuum placement is more challenging because of the enhanced rotation, and the giant HIP 20205, where we have fewer good lines available for the analysis. There is in general a good agreement between the automatic and the manual measurements. The mean difference between the measurements is 0.717 ± 1.505 mÅ for Ganymede, 1.907 ± 1.933 mÅ for HIP 20205, and 1.074 ± 2.413 mÅ for HIP 22566. As seen in Fig. 2, the slope and the intercept values of the linear regressions between the two sets of EWs are close to one and zero, respectively.
Although the difference between the two sets of EWs is small, it is not negligible, but the comparison indicates the same trend for all stars tested, i.e, the EWs obtained with splot are systematically higher than those obtained with ARES. To quantify the effect of the EW measurement differences on the final metallicities, we computed the abundances for the stars shown in Fig. 2 using both the automatic and the manual measurements. The mean difference of the metallicities is ~0.03 dex for the Sun, and ~0.04 dex for both HIP 22205 and HIP 22566. Based on the small differential variation found in the derived abundances, we therefore decided to measure all the EWs using ARES. We visually inspected the fits for each line, and removed from our analysis those fits that were judged of poor quality. Bad line fits were mainly attributed to poor estimates of the local continuum regions or lines that were significantly affected by noise.
4.3. Method M1: well-constrained parameters independent of spectroscopy
The first method used to constrain the atmospheric parameters makes use of input values that have been determined independent of the classical spectroscopic method. With this new approach, we expect to be able to investigate which are the possible systematics that can arise from the classical spectroscopic analysis.
For the red giants, we adopted the direct determinations of Teff by Boyajian et al. (2009). Angular diameters were obtained with long-baseline optical interferometry and transformed into linear radii using the Hipparcos parallaxes. The direct estimations of Teff are calculated combining these radii and the bolometric flux of the star (see Boehm-Vitense 1981, for the definition of direct measurements of Teff for FGK stars). The bolometric fluxes were determined using the bolometric corrections from Allende Prieto & Lambert (1999) and assuming MBOL, ⊙ = 4.74. Effective temperatures derived by this method can reach an accuracy of 1% and are the state of the art in Teff determinations.
For the dwarfs, as interferometric angular diameters are not available, we obtained Teff from photometric calibrations derived with the InfraRed Flux Method (IRFM). Although the IRFM provides semidirect estimations of Teff, the temperature scale is almost model independent. We use the JHKs magnitudes from 2MASS (Skrutskie et al. 2006) and the (B − V) color from the Hipparcos catalog (van Leeuwen 2007). We adopt the calibrations from Casagrande et al. (2010) to derive photometric temperatures using the colors (V − J), (V − H), (V − Ks), and (B − V). The adopted photometric Teff was calculated with an average of the four different temperatures estimates weighted by the errors of the calibrations. Effective temperatures derived by this method reach and accuracy of a few percent (Casagrande et al. 2014).
Since the Teff of the giants were derived from interferometric measurements and those of the dwarfs were derived from IRFM, it is interesting to evaluate how well the two methods agree for the giants. The IRFM Teff for the giants are shown in Table 2. da Silva et al. (2006) showed that 2MASS colors are unsuitable to determine Teff of bright stars. For this reason, we used only the (B − V) color combined with the calibrations of González Hernández & Bonifacio (2009), Ramírez & Meléndez (2005) and Alonso et al. (1996), which are more appropriated for evolved stars. Interferometric effective temperatures (Teff(int)) obtained from Boyajian et al. (2009) are also shown for comparison in Table 2. The average IRFM Teff are in a excellent agreement with the interferometric values within less than 50 K, as shown in the last column of Table 2. A difference between individual IRFM and interferometric Teff as large as 100 K is found only for the star HIP 20889 when using the calibration of González Hernández & Bonifacio (2009), which gives values systematically lower than the others.
Stellar parameters and iron abundances for giants and dwarfs derived according to method M1.
Surface gravities were determined according to the following equation:
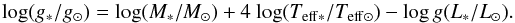 (1)For the dwarfs, the
masses were computed with the theoretical evolutionary tracks of Girardi et al. (2000) and a Bayesian estimation method, which takes the
error of each quantity for the mass determination into account (see da Silva et al. 2006, for details). Luminosities were taken from de Bruijne et al. (2001) and the Teff are those
computed as mentioned above. For the giants we adopted a value of mass of 2.48
M⊙; the mass of a clump giant in a Girardi et al. (2002) isochrone of 625 Myr and
[ Fe/H ] = +0.13 (see
Smiljanic 2012, for details).
(1)For the dwarfs, the
masses were computed with the theoretical evolutionary tracks of Girardi et al. (2000) and a Bayesian estimation method, which takes the
error of each quantity for the mass determination into account (see da Silva et al. 2006, for details). Luminosities were taken from de Bruijne et al. (2001) and the Teff are those
computed as mentioned above. For the giants we adopted a value of mass of 2.48
M⊙; the mass of a clump giant in a Girardi et al. (2002) isochrone of 625 Myr and
[ Fe/H ] = +0.13 (see
Smiljanic 2012, for details).
One free parameter that can not be constrained by our observational knowledge of the cluster is the microturbulence velocity (ξ). For M1, we fixed ξ adopting predictions obtained with 3D atmospheric models. The details on how these values were obtained are described in Sect. 4.3.1.
To calculate the metallicities, we used 1D-LTE plane-parallel atmospheric models computed using the Linux version of the ATLAS9 code (Sbordone et al. 2004; Sbordone 2005) originally developed by Kurucz (see, e.g., Kurucz 1993) and adopting the ODFNEW opacity distribution from Castelli & Kurucz (2003). The mixing length parameter adopted was 1.25 and no overshooting was considered for both giants and dwarfs. Chemical abundances of Fe i and Fe ii were derived using WIDTH package Kurucz (1993), under some minor optimizations to facilitate handling the input data.
Our main innovation in method M1 is that the spectroscopy independent parameters described above were used as input values and subjected to a further controlled fine-tuning. The best set of parameters for each star was determined as follows. First, we allowed the stellar parameters to vary within a range of conservative errors to find the best agreement between the abundances of the Fe i and Fe ii lines. The ranges were ±50 K for Teff, with steps of 10 K; ±0.10 dex for log g, with steps of 0.05 dex; and ±0.10 km s-1 for ξ, with steps of 0.05 km s-1. These ranges were chosen because they represent typical error values of the classical abundance analysis. We tested variations using smaller steps, but no major improvement on the final solution was found. Next, after reaching a solution, we applied a 2σ-clipping to remove lines classified as outliers with respect to the average abundances of the previous iteration. The final set of atmospheric parameters is given by looking for the best possible agreement between the abundances of Fe i and Fe ii in the 3D-plane Teff − log g − ξ. The stellar parameters and metallicities derived with this approach, for giants and dwarfs, with both MASH and ASPL lists, are shown in Table 3.
The main aspect of M1 is that the final parameters shown in Table 3 can vary within a very narrow range, constrained by independent methods. Thus, the errors for the stellar parameters in M1 are the uncertainties in the input parameters. An error of about ~50 K corresponds to the error of the IRFM calibrations and is comparable with the interferometric errors presented in the work of Boyajian et al. (2009, see their Table 4). For log g, we adopted an error of 0.10 dex because we have very small errors in the parallaxes, thus the main source of error in the gravities comes from our mass determination. An error of 20% in the masses changes the surface gravities by ~0.10 dex. Since the evolutionary status of the Hyades is well known, we consider the gravity error of 0.1 dex as conservative and most likely the highest source of uncertainty is in the mass-loss estimate for the giants. For ξ we adopted an error of 0.10 km s-1, which corresponds to the uncertainty estimated with the 3D microturbulence calibration (see Sect. 4.3.1). The dispersion for the Fe i and Fe ii abundances shown in Table 3 correspond to the standard deviation of each abundance distribution.
We also evaluate how the uncertainty in the physical parameters of the stars affect the retrieved abundances when using M1. To this end, we assumed the parameters presented in Table 3 for the giant HIP 20205 and the dwarf HIP 19148, and then vary Teff, log g and ξ separately for both ASPL and MASH lists. The results are given in Table 4. We emphasize that the variations in Fe i and Fe ii follow the same direction for both, the giant and main-sequence star.
Abundance changes (Δ[X/H]) in a giant (HIP 20205) and in a main-sequence (HIP 19148) star in response to variations of Teff, log g and ξ.
We obtain a good agreement between the metallicity of giants and dwarfs with this method. Moreover, since we are able to retrieve stellar parameters with a good agreement between Fe i and Fe ii abundances, we do not see evidence for significant LTE departures either among the giants or the dwarfs according to this method. In Table 3, we find the metallicities obtained using MASH list are slightly higher than those using the ASPL list. The systematic offset of about ~0.04–0.06 dex is likely related to the different selection of lines, but can also be considered part of the internal errors of the analysis, as an accuracy better than 0.05 dex can hardly ever be achieved without a line-by-line differential analysis. We further discuss this behavior in Sect. 5.
4.3.1. Probing microturbulence velocities with 3D models
Aside from the different techniques one can adopt to determine the microturbulence velocity, it is important to recall that this parameter arises from a limitation of the classical 1D model atmospheres into fully describing all the velocity fields present in the stellar photosphere. As a consequence, the inclusion of an extra velocity field is required to describe the broadening observed in the lines placed in the partly saturated regime of the curve of growth (Struve & Elvey 1934; van Paradijs 1972). In practice, it is essential to use this parameter to obtain the same abundance for lines with small and large EWs. Thus, the optimal value of ξ is obtained by imposing the absence of a correlation between the abundances and the EWs of a set of lines. This analysis, of course, depends on a good statistics of weak and moderately strong lines. This is usually a challenge in the simultaneous analysis of giant and dwarf stars.
One alternative to overcome the limitations cited above is to use 3D atmospheric models to predict ξ. Three-dimensional models treat convection in a physically consistent way, without the need of defining free parameters like ξ. This approach has been adopted by Steffen et al. (2009, 2013), and it is based on the comparison between lines computed with spectral synthesis using 3D and 1D models. Given a sample of spectral lines, the EWs computed from the 3D model with a fixed abundance are taken to represent the observation. For each line, the 1D abundance is obtained by matching the “observed” 3D EW with the synthetic line profiles derived from the 1D models (using exactly the same atomic line parameters as in the 3D synthesis). The best value of ξ for use with 1D models is taken to be that which eliminates the correlation between line strength and derived 1D abundance. In fact, the best ξ depends somewhat on the choice of the line list. Ideally, the lines should be insensitive to temperature fluctuations and have similar properties as the lines to be used for the abundance determinations. High-excitation Fe i lines and Fe ii lines are an obvious choice.
Microturbulence values computed from 3D models in correspondence with 1D models.
 |
Fig. 3 Microturbulence determination for the model of the dwarf with Teff = 5000 K and log g = 4.5 dex. Left: Δlogϵi versus the 3D equivalent width for ξ = 0.90km s-1 (symbols). The dashed line represents the linear regression to the data points. Right: slope of the linear regression as a function of microturbulence. The optimal microturbulence is derived by the condition that the slope is zero. |
We used 3D hydrodynamic models taken from the CIFIST grid (Ludwig et al. 2009)5 computed with the CO5BOLD code6 (Freytag et al. 2012). The metallicity of all selected models is solar since this grid does not have models available for stars more metal-rich than the Sun yet. Indeed, the differences between temperature stratification of 3D and 1D models are expected to be small at slightly super solar metallicity. At this regime, the line opacities act toward heating the optically thin layers and, as a result, the mean temperature of the layer is close to radiative equilibrium. We do not expect the small metallicity differences to have any noticeable effect on the derived microturbulence velocities.
The required 1D hydrostatic reference models were computed with LHD code (Caffau & Ludwig 2007) using the same stellar parameters and opacity scheme as the 3D models. Table 5 shows the stellar parameters of the computed models used for two giants, four subgiants, and six dwarfs, which were selected to be representative of the Hyades HR diagram. For giants and dwarfs, the models were selected to cover as well as possible the range of temperatures and gravities of our sample (e.g. Table 3). For the subgiants, the models cover the cool part of the temperature range expected for subgiants in the Hyades, but have slightly higher log g (~3.50) with respect to what is expected from the cluster theoretical isochrone (log g ~ 3.0). Models for subgiants with log g smaller than 3.50 were not available in the grid.
For computing the ξ values, we used 30 Fe i plus 7 Fe ii lines from the ASPL list and applied a method similar to method 3a of Steffen et al. (2013). The selected lines are identified in Table A.2. Here again, lines with EW> 120 mÅ were rejected to make this analysis compatible with the clipping criteria that were adopted in both M1 and M2. Briefly, for each line, we computed the equivalent width using the 3D model, W3D. Then, we computed for the very same lines a 2D curve of growth from the adopted 1D reference model, W1D(Δlogϵ, ξ), where Δlogϵ is the abundance difference with respect to the original abundance used in the 3D spectrum synthesis. This grid allows us to find, by interpolation for given ξ value, Δlogϵi for each line i from the condition W3Di = W1Di. In other words, this abundance correction, Δlogϵi, is the difference of the abundance computed in the 1D model by fitting the equivalent width of the 3D line, and the true abundance used in the 3D spectrum synthesis. We computed Δlogϵi for a grid of microturbulence values ranging from 0 to 2 km s-1 with intervals of 0.1 km s-1. The only exception was the giant with Teff = 5000 K, where the grid was ranging from 0 to 3 km s-1 in steps of 0.15 km s-1.
For each ξ value, we plot Δlogϵi as a function of W3D (see Fig. 3, left side, for an example). This graph illustrates the classical concept of defining the microturbulence. We then determine the slope of the linear regression from each of the plots described above. These slopes are plotted against the corresponding microturbulence values, as shown in Fig. 3 (right side). The best value of ξ for each star is taken to be that where the slope is zero in this curve. By following the procedure described here, we estimated the microturbulence values for each of the model stars with parameters as listed in Table 5.
We used the data listed in Table 5 to establish
an empirical relation of the microturbulence as a function of effective temperature and
surface gravity. We tested different functional forms for the calibration and adopted
that which gave the best statistical response. We searched for a calibration that shows
no significant trend in the residuals distribution, but we have also assessed the
quality of the fit by inspecting its correlation coefficient (R), the standard
deviation σ
of the fit, and the p-values for each term of the calibration. The best
fit was found for the following equation: 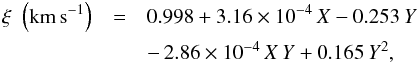 (2)where
X ≡
Teff − 5500 [K] and Y ≡ log g −
4.0. The rms scatter of the residuals of this relation is 0.05
km s-1.
However, we assume as the total uncertainty of the calibration a more conservative value
of 0.10 km s-1
because of the small number of stars used in the fit. Although other calibrations in the
literature (e.g., Edvardsson et al. 1993; Feltzing & Gustafsson 1998; Bruntt et al. 2012) have considered a larger number
of stars, their estimates of microturbulence are based on spectroscopic analyses with
different line lists, while Eq. (2)
presents a relation that reflects predictions from 3D models with a single line list,
albeit for a limited set of stellar parameters.
(2)where
X ≡
Teff − 5500 [K] and Y ≡ log g −
4.0. The rms scatter of the residuals of this relation is 0.05
km s-1.
However, we assume as the total uncertainty of the calibration a more conservative value
of 0.10 km s-1
because of the small number of stars used in the fit. Although other calibrations in the
literature (e.g., Edvardsson et al. 1993; Feltzing & Gustafsson 1998; Bruntt et al. 2012) have considered a larger number
of stars, their estimates of microturbulence are based on spectroscopic analyses with
different line lists, while Eq. (2)
presents a relation that reflects predictions from 3D models with a single line list,
albeit for a limited set of stellar parameters.
The results for the microturbulence values on Table 5 are consistent with those presented in Table 3 of Steffen et al. (2013), although these authors adopted a different selection of lines (Fe i lines with a lower excitation potential greater than 2 eV only) and a slightly different method (their method 3b). In this case, the microturbulence is given by the value that minimizes the scatter of the abundance corrections Δlogϵi. Steffen et al. (2013) prefer method 3b over 3a, arguing that 3a is more susceptible to details of the spectral line sample. Nevertheless, we decided to follow 3a because it is closer to the usual analysis applied to determine ξ in the literature, and thus facilitates the comparison with values derived in a classical spectroscopic analysis.
We remark that our values display a trend for increasing ξ toward higher temperatures and (perhaps) lower gravities. However, the limited number of stars tested here is not sufficient to provide more than a rough idea of the microturbulence behavior across larger areas of the HR diagram. More details about these trends can be found in Steffen et al. (2013).
4.4. Method M2: the classical spectroscopic analysis
The second method used to constrain the atmospheric parameters is the classical spectroscopic analysis based on the ionization and excitation equilibria of the Fe i and Fe ii lines. We want to investigate whether a consistent metallicity scale between giants and dwarfs can be recovered through this method. Effective temperatures are calculated, forcing the Fe i line abundances to be independent of the excitation potential, i.e., forcing the excitation equilibrium. The microturbulence velocity is determined, forcing the Fe i abundances to be independent of the EWs. Surface gravities are calculated, forcing the lines of Fe i and Fe ii to produce the same abundance, fulfilling the ionization equilibrium. As a consequence, the metallicity ([Fe/H]) is obtained as a spin-off of this procedure. All these criteria must converge in a fully consistent way and the final solution should be independent of the initial input parameters and iteration path.
For this method, we use the same models as in Sect. 4.3, i.e, 1D-LTE plane-parallel models (ATLAS9+ODFNEW). We also used the package WIDTH9 for the abundances computation, under some modifications to facilitate the handling of the input/output files. Extra IDL7 routines were written to optimize the calculation through the spectroscopic requirements mentioned before. First, the program computes the atmospheric model correspondent to the values of Teff, log g, [Fe/H], and ξ given as initial guess. The code optimizes one parameter at a time, always checking if the optimization of the previous parameter is still valid. If the previous optimization is still satisfied the code moves forward to the next parameter. If not, the code returns to the previous parameter and recalculates the optimization. The final set of spectroscopic parameters is obtained once all parameters are optimized consistently. An example of the convergence of M2 is shown in Fig. 4 for the star HIP 20205, and for both ASPL and MASH lists.
 |
Fig. 4 Fe i and Fe ii abundances as a function of the excitation potential (χ), the logarithm of the reduced EW and the wavelength. The continuous red line is the regression between the quantities shown in each plot. The dashed line corresponds to the Fe ii final abundance derived according to M2. In all plots, the black asterisks correspond to the Fe i lines and the red filled triangles correspond to the Fe ii lines. Left: spectroscopic analysis for HIP 20205 using ASPL list. Right: spectroscopic analysis for HIP 20205 using MASH list. |
The internal errors of the M2 set of spectroscopic stellar parameters were obtained as follows: for the Teff, we changed the slope of the linear regression in the [Fe/H] versus χ diagram by its own 1σ error. The error in temperature is the difference between this new temperature and the previous best value. Similarly, for ξ, we applied the same idea, changing the slope of the linear regression in the [Fe/H] versus log (EW/λ) diagram. The log g error is estimated by changing this parameter until we obtain a difference between the Fe i or Fe ii abundances that is equal to the larger of their dispersions. For the metallicity, we adopted the standard deviation of the Fe i abundance distribution. Table 6 shows the stellar parameters derived using M2 for ASPL and MASH lists.
The metallicities derived by this method agree between giants and dwarfs, within the presented uncertainties. However, the internal metallicity uncertainties of M2 are relatively larger than for M1, when compared within the same line list. On average, the internal uncertainties of M2 are about ~0.10 dex when using the MASH list and ~0.06 with the ASPL list. The difference in the metallicity scale obtained for both lists are also larger when using M2. These differences are more significant for the giants and for the hottest dwarf of the sample. This result reflects how the line lists were assembled. The MASH line list was selected using the Sun as a proxy and has a larger number of transitions. This reduces the number of well-isolated lines, free from neighboring features, in the spectra of the giants. On the other hand, the ASPL list was chosen to have only isolated and uncontaminated transitions in the spectra of giants, which consequently reduced the number of lines used in the analysis. We discuss the quality of the line lists again in Sect. 5. On average, the difference between the atmospheric parameters obtained with the MASH and ASPL lists for M2 is +68 ± 92 K for Teff, +0.12 ± 0.24 for log g, −0.13 ± 0.21 for ξ and +0.09 ± 0.08 for [Fe/H]. These values are not significantly different from typical errors of spectroscopic analyses and from typical comparisons between multiple analyses methods (see, e.g., Hinkel et al. 2014; Smiljanic et al. 2014).
4.5. Solar abundances and differential analysis
We also computed the solar metallicity using our solar proxy spectra. This is useful to understand the behavior of the metallicity scale derived with methods M1 and M2. As mentioned in Sect. 3, for the comparison with the giant stars we used the solar reflected spectrum of Ganymede, hereafter Sun HARPS. For the comparison with the dwarf stars, we used the solar spectrum observed with UVES, hereafter Sun UVES. We decided to have two solar proxies to avoid any inconsistencies that may arise from the use of two different spectrographs and, therefore, different spectral resolution, instrumental profiles, or possible scattered light influence that affects a particular spectrograph.
Solar abundances were derived applying the same two methods presented before and for both MASH and ASPL lists. For M1, in particular, we fixed the solar atmospheric parameters to 5777/4.44/0.90 instead of ranging them within its expected errors. For the Sun, we prefer to keep fixed these parameters since its errors are too small to produce a noticeable difference in the metallicity determination. A 2σ clipping of the lines was also applied. For M2, the solar parameters were computed exactly as describe in Sect. 4.4.
Table 7 shows the abundances of Fe i and Fe ii for our solar proxies, according to M1 and M2, using the ASPL and MASH lists. The solar atmospheric parameters found through M2 are very similar to the canonical values adopted as fixed in M1. The mean differences between M1 and M2 for the solar parameters are 41 K for Teff, with minimum and maximum values of 16 K and 52 K; 0.01 dex for log g, with minimum and maximum values of 0.01 dex and 0.02 dex; and 0.09 km s-1 for ξ, with minimum and maximum values of 0.01 km s-1 and 0.18 km s-1.
Stellar parameters and iron abundances for giants and dwarfs derived according to method M2.
Finally, we used the solar values of Table 7 as a reference and derived the abundances of Fe i and Fe ii with respect to the Sun for the Hyades stars. The results of this differential analysis are shown in Table 8, for M1 and M2 and for both ASPL and MASH lists. Also given are the average metallicities obtained for giants and dwarfs according to each methodology. The internal dispersions presented in the table were obtained by the squared sum of the internal uncertainty relative to the Fe abundance of the star and the Sun.
Solar abundances of Fe i and Fe ii obtained with M1 and M2 for both MASH and ASPL lists.
5. Results and discussion
5.1. The quality of the EWs
One step in the spectral analysis that has a substantial influence on the final parameters and abundance is the measurement of the EWs. In this work, EWs were measured with the automatic code ARES. This code been used on many abundance analyses in the literature (e.g., Adibekyan et al. 2012; Tabernero et al. 2012). Such kind of automatic codes are a fast and systematic way to compute EWs that minimize the subjectivity of manual measurements using, for example, IRAF. Nevertheless, it has been shown in the analysis of the Gaia-ESO Survey spectra that different groups measuring EWs in the same spectra, using the same code, can still find considerably different values (see the discussion in Sect. 6 of Smiljanic et al. 2014). This is the case mainly for two reasons: i) there are still some crucial free parameters that need to be adjusted for the optimal measurement of EWs by automatic codes, in particular, for continuum fitting; and ii) quality control of the measured EWs is still important, as the codes just measure all possible EWs without recognizing potential local problems (e.g., unrecognized blends). Regarding the continuum placement, in general, there is no consensus on the best way to define the continuum, which can be done adopting either a local or a global solution.
It is not our aim in this paper to advocate in favor of choosing a global or local continuum normalization. We just stress that regardless of the type of normalization that was chosen, care is needed to evaluate whether the continuum solution was of good quality or whether it is affecting the measured EWs in a negative way. As ARES adopts a local continuum normalization, lines in crowded regions of the spectrum can have their EWs underestimated because of a low local continuum solution. This effect can become important in the spectra of giants, where many lines are stronger than in the spectra of dwarfs. Of course, if the line list is composed solely of well-isolated spectral features, the local and the global continuum solution should give similar results. However, this is not always the case, especially when analyzing stars in a wide range of Teff. For this reason, as stated before, we were careful to visually inspect and exclude measurements that could be underestimated because of continuum misplacement. This was particularly important in the MASH list, where the lines were basically chosen in the solar spectrum and, consequently, this list has spectral features that can be blended in the spectra of giants.
Metallicity, with respect to the Sun, derived using M1 and M2.
We find that the EWs obtained with IRAF are systematically higher than the EWs obtained with ARES. We attribute this behavior mainly to the different continuum normalization. The larger discrepancies were found for hot dwarfs and for the giants. If we compare the EWs of all transitions, without excluding those with suspicious normalization, the differences between IRAF and ARES reach up to 13.6 mÅ for the hot star HIP 22566 and up to 7.4 mÅ for the giant HIP 20205. The use of all these measurements would certainly lead to an extra source of uncertainties. After the visual inspection and exclusion, the difference in EWs causes an effect on the abundances that is smaller than 0.05 dex (see Sect. 4.2). This is similar to typical errors found in abundance analyses that are not line-by-line differential.
We also noticed some difficulties of measuring EWs with ARES in hot stars where rotational broadening becomes to be important. After several tests with different ARES input options, we decided to limit our sample to those stars where we were confident that the EWs were well measured with this automatic tool. Therefore, we do not include stars hotter than ~6300 K.
Finally, we also tested the influence of using spectra obtained with two different instruments on the EWs scale. To this end, we used a spectrum of the giant HIP 20455 observed with UVES, under the same configuration set as the dwarfs. We computed metallicities using M1 for the two sets of EWs of this star. The mean differences were 0.03 dex for the ASPL list and 0.05 dex for the MASH list. Although the difference is slightly higher for the MASH list, it is still within the internal uncertainties of this method. Consequently, if there is any systematic error in the metallicity introduced by the use of different spectrographs, this is comparable to the internal errors of our analysis. Therefore, we concluded that the use of spectra from both UVES and HARPS instruments should not compromise the metallicity scale between giants and dwarfs.
5.2. Comparison between the line lists
The use of different line lists has already been reported as one of the possible sources of the discrepancies between the metallicity scale of giants and dwarfs in open clusters (Santos et al. 2009, 2012). However, in those works only the classical spectroscopic analysis was tested. Here, we are able to compared the spectroscopic method (M2) with a set of parameters that is independent (method M1). Thus, we can test the performance of the different line lists in these different approaches.
When considering the analysis performed with the MASH list, the metallicity scale of giants and dwarfs agree better under M1. The difference between the average metallicity of giants and dwarfs is −0.02 dex with M1 and increases to 0.11 dex with M2. This increased difference seems to be driven by the giants. The uncertainties of the atmospheric parameters are larger for the giants than for the dwarfs (Table 6). Moreover, the metallicity and the surface gravity are substantially higher for two of the giants when M2 is applied with this list. On the other hand, with the ASPL list there is a better agreement between giants and dwarfs in both methods. The difference between the average metallicity of giants and dwarfs is −0.03 dex for M1 and −0.02 dex for M2.
We attribute the increased scatter in the metallicity of the giants seen when using the MASH list under M2 to the fact the lines were chosen from the solar spectrum. For this reason, they are likely more affected by blending features that were weak in the Sun, but are significant in the spectrum of a giant star. This result indicates that the use of fewer transitions, but that are carefully chosen to avoid contaminating blends, is fundamental for an accurate determination of atmospheric parameters and of the metallicity scale through the spectroscopic method.
We also remark that the improved gf values that we adopted for the MASH list did not reduce significantly the scatter of the metallicities. Indeed, our values of metallicity dispersion are around 0.08–0.10 dex. These are similar to the ones reported in Mashonkina et al. (2011), which are about ~0.09–0.11 dex. Perhaps the reduced number of lines in our analysis is not enough to reduce the internal statistical errors even improving the gf values sources. For the list ASPL, we found an average dispersion on the metallicity of around 0.07 dex, which is smaller but still closer to the above mentioned values.
We found a systematic difference of 0.04–0.06 dex between the abundances derived using MASH and ASPL lists, and higher for the giants when M2+MASH is applied. The metallicities derived with the MASH list are higher than the ones derived with ASPL list but also the total average temperature scale is hotter for the MASH list by about 20 K when using M1 and by about 70 K when using M2 (see Fig. 5). These variations in Teff correspond to an increase in Fe abundances of approx. 0.02–0.06 dex. In addition, the MASH list contains lines which are likely more affected by blending, thus we would expect that the cool giants show much larger abundances for the MASH list than for the ASPL list, which is the case. Thus, we attribute these systematic differences to the higher retrieved Teff and to the presence of blended lines in the MASH list. More details about the comparison between M1 and M2 are presented in the next section.
 |
Fig. 5 Comparison of the metallicity scale derived with lists MASH and ASPL as a function of the Teff obtained with ASPL list for M1 (upper panel) and M2 (lower panel). In each plot, the null, ±0.1 and ±0.2 abundance differences are represented by the continuous, the dotted and the dashed lines respectively. Red dots refer to the giants while black squares refer to the dwarfs. |
As mentioned at the beginning of this subsection, many works have demonstrated how abundances (and abundance differences or trends) depend on the adopted line list. From our analysis clearly emerges that a proper line list maximises the robustness of the results. A similar conclusion has been reached by other authors who recently proposed to improve existing line list by customising it to the stars observed, using an empirical approach. This method has been applied to cool dwarfs (Tsantaki et al. 2013) and to evolved stars (Adibekyan et al. 2015), reaching substantial improvements with respect to what obtained with a not optimised line list.
In terms of metallicity dispersion and compatibility of the metallicity scale between giants and dwarfs, the ASPL list shows a good performance for both methods tested in this work. This is likely related to the selection of well isolated line transitions which are equally appropriate for the analysis of giants and dwarfs. We, therefore, recommend the use of such list for this kind of analysis.
5.3. Comparison between the methods
In this section, we compare the performance of methods M1 and M2 to investigate possible systematic effects between them. Figure 6 shows the difference between the atmospheric parameters obtained with M1 and M2 as a function of the M1 parameters. For each parameter, we performed a linear regression to check for significant trends. These trends would appear in case of considerable differences between the atmospheric parameters derived with each method. In case of a significant trend, the ratio between the slope and its own uncertainty should be less than 0.5, i.e., x> 2σx.
 |
Fig. 6 Comparison of the atmospheric parameters obtained with methods M1 and M2, as a function of the M1 parameters. The red lines are the linear regressions between the values. The dashed lines are the mean of the difference between the values presented in the y-axis. Left: parameters obtained with the ASPL line list. Right: parameters obtained with the MASH line list. |
According to Fig. 6, only log g appears significantly different between M1 and M2, and only when using the MASH list (see the middle plot on the left panel of Fig. 6). On average, the spectroscopy surface gravities are larger when using M2 for both line lists, about 0.10 dex, but in the case of MASH the log g values are significantly overestimated. This is probably caused by overestimated EWs, due to blending contaminants, which result in larger effective temperatures and surface gravities. The ξ, on the other hand, is higher on average for M1 than for M2.
For the ASPL list, the plots shown in Fig. 6 do not indicate any significant difference between the parameters derived with M1 and M2. However, the M1 Teff values are, on average, ~47 K higher than the M2 ones. Although this is a small difference, it is probably responsible for the larger metallicities found with M1 in comparison with M2 (in absolute values, 0.05 dex for the giants and 0.06 dex for the dwarfs).
The metallicities derived with both line lists show a better agreement when M1 is applied. This behavior can be more easily noticed by inspecting Fig. 5. The differences between the [Fe/H] scale derived with the two line lists with M1 are, on average, about ~0.05 dex, and constrained within the range of ±0.1 dex (dotted lines) of this figure. For M2, these differences are on average higher about ~0.10 dex, and present a larger scatter especially for the giants and for the hottest dwarf HIP 22566. Figure 5 shows that a good constraint in the atmospheric parameters of a given set of star can produce a consistent metallicity scale for giants and dwarfs even when using line lists selected with different approaches, not optimized for the analysis of giants.
While the agreement between M1 and M2 is, on average, good, there are a few individual stars for which the differences are significant. The Teff differences are about 100–150 K for the cooler stars (Teff< 5300 K), with both line lists. Such discrepancies for the cooler stars do not compromise the overall agreement between the two Teff scales, but this results are in agreement with Ramírez et al. (2007) who argue that differences between the spectroscopic and the photometric temperature scales are more significant for stars with Teff< 5000 K. HIP 18946 and HIP 22566 are the stars that present the highest discrepancies between the effective temperatures of M1 and M2, reaching up to ~150 K for the MASH list.
Finally, we tested the compatibility of the giants temperature scale obtained with the interferometric angular diameters and the IRFM. This last test was done in order too see if, in the absence of angular diameters for the giants, the IRFM Teff scale would give similar results. As mentioned in Sect. 4.3, the agreement between the IRFM and the interferometric Teffs is excellent. The average absolute difference between them is − 6 ± 33 K. This results indicates that, for similar giants, the IRFM Teff could also be used as input values of temperature in M1.
In general, the metallicities derived using M1 are more consistent between giants and dwarfs for the two line lists tested here. This results seems to be a consequence of the well constrained set of atmospheric parameters. The metallicities of giants and dwarfs are only consistent when derived using M2 with the ASPL list. When using M2 associated with the MASH list we found systematic differences especially in the giants. Our results confirm that, for the Hyades, the line list is a primary source of systematic differences on the metallicity scale of giants and dwarfs.
5.4. The Hyades metallicity scale
In this section we discuss the metallicity scale that we obtained for the Hyades. In general, the two methods tested favor the ASPL over the MASH list, as this last one seems to introduce systematic effects on the results, in particular for M2. Thus, we consider the results obtained with the ASPL list to be of higher quality. There is a good agreement between the metallicity of giants and dwarfs when using this list for both methods. According to M1 the difference between the average values of the iron abundances of giants and dwarfs is 0.03 dex. When M2 is considered, the difference between the metallicity of the giants and the dwarfs is 0.02 dex. These values are smaller than the internal uncertainties of our methods and the typical errors found in classical abundance analysis (~0.05–0.10 dex). Therefore, we consider all the stars together, giants and dwarfs, analyzed with ASPL list to revisit the metallicity scale of the Hyades.
We combined the average abundances of Fe ii for giants and dwarfs of each list to obtain the metallicity of the cluster. We choose Fe ii abundances because they are safer abundance indicators than Fe i lines, since Fe i lines may suffer more of non-LTE effects. We found that the average metallicity of the Hyades is 0.18 ± 0.03 dex or 0.14 ± 0.03 dex, according to M1 and M2, respectively, using the ASPL list. These values are compatible with each other within 2σ. For the MASH list, under the M1 analysis, we found a metallicity for the Hyades of 0.21 ± 0.04 dex. At this point, we reinforce two main aspects of our work. When investigating giants and dwarfs simultaneously using the classical spectroscopic analysis, it is recommended to use a line list especially suitable for the spectra of giants. In case the line list was selected based on the spectrum of a dwarf star, as the Sun, we recommend that it is more appropriate to use a method in the lines of M1. This minimizes the systematic effects on the metallicity scale retrieved by the analysis.
5.5. Comparison with other works
We present here a comparison of our results with selected previous analyses of Hyades stars: Paulson et al. (2003), Schuler et al. (2006) and Carrera & Pancino (2011). These works were chosen because they have a larger number of stars in common with our analysis. As our final recommendation we select the results obtained with M1 using the ASPL list.
Paulson et al. (2003) analyzed a sample of 90 stars of the Hyades, of which 13 are present in our study. Those authors performed a differential spectroscopic analysis to derive the atmospheric parameters of the stars. For the sample in common, the average difference in Teff between Paulson et al. (2003) and this work is 58 ± 59 K. The metallicity reported by Paulson et al. (2003) is 0.13 ± 0.01 dex, which is within a 2σ range of the values found with M1 (0.18 ± 0.03 dex), but it is in excellent agreement with our metallicity derived according the same spectroscopic method (M2) of 0.14 ± 0.03 dex.
Schuler et al. (2006) analyzed the giants and dwarfs of the Hyades using a method similar to M1. The Teff was obtained with the IRFM by Blackwell & Lynas-Gray (1994, 1998). Surface gravities and ξ were determined fitting synthetic spectra (1D+LTE) to the observed spectra. For the giants, the agreement between this work and our results is remarkably good for log g, ξ and [Fe/H], and reasonable for Teff. The mean differences are 76 ± 12 K for Teff, 0.03 ± 0.06 dex for log g, 0.06 ± 0.05km s-1 for ξ and 0.02 ± 0.01 dex for [Fe/H]. Among the eight dwarfs analyzed by this work, two were also included in our analysis. For these objects the agreement between the stellar parameters is good for Teff and log g, but the differences increase up to 0.40 km s-1 for ξ. The overall metallicity for the Hyades recommended by these authors is 0.13 dex, which is also compatible within a 2σ range of our value retrieved with M1 and ASPL list (0.18 ± 0.03 dex).
Another analysis of the giants of the Hyades was performed by Carrera & Pancino (2011). These authors determined the atmospheric parameters via spectroscopy and photometry. The agreement between the set of parameters presented in Carrera & Pancino (2011) and our work is reasonably good for Teff and good for [Fe/H], with average values of about −79 ± 53 K and −0.03 ± 0.03 dex, respectively. However, the surface gravities reported by these authors are compatible with those that we derived using M2, the classical spectroscopic analysis. The differences between the surface gravities is likely responsible for the marginal agreement between the metallicity scales: 0.11 ± 0.01 dex derived by Carrera & Pancino (2011) and our value of 0.18 ± 0.03 dex. Although the value of metallicity reported by these authors is in excellent agreement with our value of 0.12 ± 0.04 dex, which is the determination of the metallicity for the giants also derived using the spectroscopy method (M2 and ASPL list).
6. Conclusions
We investigated the metallicity scale obtained in a simultaneous analysis of dwarfs and giants. Inconsistencies between the metallicities of these types of stars have been reported before in the literature. Understanding whether these inconsistencies are a real or systematic effect of the analysis methods is important for advancing in a number of different areas of astrophysics. Of particular interest is the comparison of metallicities between stars of different evolutionary phases hosting planets.
As a test case, we chose a sample of giants and dwarfs in the Hyades open cluster. All stars in an open cluster are expected to share the same initial chemical composition. They are therefore optimal to test the consistency of analysis methods.
We computed metallicities using two different methods and, for each method, using two different line lists. One line list was assembled based on the solar spectrum and with the aim of minimizing non-LTE effects in the determination of the atmospheric parameters (MASH line list). The other was assembled with the specific purpose of analyzing giant stars, and therefore only includes lines that are relatively free of blends in the spectra of these objects (ASPL line list).
Analysis method M1 was based on atmospheric parameters, which are independent of spectroscopy. Effective temperatures were computed using interferometric angular diameters for the giants, and the IRFM for the dwarfs. Surface gravities were computed with the help of theoretical evolutionary tracks. For use with M1, we presented a new calibration of microturbulence based on 3D hydrodynamical models. In this way, one can also use an estimate of ξ that is independent of spectroscopic measurements. Method M2 was the classical spectroscopic method using Fe i and Fe ii lines to constrain the stellar parameters.
We investigate the main steps in the analysis that may affect the metallicity scale of dwarfs and giants of the Hyades. Our careful evaluation of EWs has shown that differences in the continuum placement can have an effect of about ~0.03 dex in the precision of the final metallicities. An effect of similar magnitude (0.05 dex) can be introduced using spectra obtained with different instruments. From the stand point of the line lists, we found larger systematic differences between the metallicity scale for giants and dwarfs using MASH list, where the line selection criteria are not optimized for evolved stars. Additionally, we found a systematic difference of 0.04–0.06 dex between the two lists used in this work. Lastly, the difference on the metallicity scale for the giants and dwarfs using the two different methods (M1 and M2) is of about 0.04–0.06 dex, disregarding the results of the giants obtained with M2+MASH list. One interesting aspect is that perhaps the use of the solar spectrum as a differential reference does not cancel out all these effects. Considering all these points, we conclude that the limit of precision of an abundance analysis that is not line-by-line strictly differential cannot be better than 0.03 dex.
We show that with a careful determination of atmospheric parameters and a well -selected line list, it is possible to simultaneously analyze giants and dwarfs and obtain consistency between their metallicities. When attention to the line list is considered, M1 and M2 produce results with a good agreement. The metallicity scale of the Hyades obtained with our preferred line list (ASPL) is 0.18 ± 0.03 dex for M1 and 0.14 ± 0.03 dex for M2, and these values are consistent among each other. At the very least, it is clear that assembling a line list well suited for the analysis of giants is mandatory to obtain consistency between the metallicity scales. When using the spectroscopy technique, the metallicity scale of giant and dwarfs using ASPL list agree with previous spectroscopic analyses of the Hyades. However, M1 does show a more efficient capability to recover the metallicity scale of giants and dwarfs regardless of the line list used. The results obtained with M1 for both MASH and ASPL lists are consistent among each other, indicating that a set of very well-constrained atmospheric parameters might compensate possible systematics from the features of the line list. Therefore, we believe that M1 results are more robust.
In the view of our results, we favor as our final metallicity for the stars in Hyades open cluster the value of 0.18 ± 0.03 dex (based on M1 and the ASPL line list). For similar studies of giants and dwarfs, in a more general approach, we suggest the use of M1 whenever possible. A simultaneous spectroscopic analysis of giants an dwarfs, as done in M2, is only recommended under the use of a line list optimized for giant stars.
COnservative COde for the COmputation of COmpressible COnvection in a BOx of L Dimensions, L = 2,3. http://www.astro.uu.se/~bf/co5bold_main.html
Acknowledgments
L.D.F. acknowledges support through the ESO Studentship Programme, CAPES Programme and CNPq fellowship Programme (166880/2014-0). L.P. acknowledges the Visiting Researcher program of CNPq Brazilian Agency, at the Fed. Univ. of Rio Grande do Norte, Brazil. Support for C.C. is provided by the Ministry for the Economy, Development and Tourism’s Programa Iniciativa Científica do Milênio through grant IC20009, awarded to the Millennium Institute of Astrophysics (MAS). G.F.P.M. acknowledges financial support by CNPq grant 476909/2006-6, FAPERJ grant APQ1/26/170.687/2004 and ESO, for financial support for a trip to Garching, which enabled participation in this work. We thank Dr. Martin Asplund and Dr. Maria Bergemann for their contribution with the line lists used in this work. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, of NASA’s Astrophysics Data System, of the WEBDA database, operated at the Department of Theoretical Physics and Astrophysics of the Masaryk University, and of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Benamati, L., Santos, N. C., et al. 2015, MNRAS, 450, 1900 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., & Lambert, D. L. 1999, A&A, 352, 555 [NASA ADS] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2014, A&A, 564, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., Johnson, J. A., et al. 2010, A&A, 512, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackwell, D. E., & Lynas-Gray, A. E. 1994, A&A, 282, 899 [NASA ADS] [Google Scholar]
- Blackwell, D. E., & Lynas-Gray, A. E. 1998, A&AS, 129, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehm-Vitense, E. 1981, ARA&A, 19, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., & Friel, E. D. 1990, ApJ, 351, 467 [Google Scholar]
- Boyajian, T. S., McAlister, H. A., Cantrell, J. R., et al. 2009, ApJ, 691, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., & Ludwig, H.-G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, R., & Pancino, E. 2011, A&A, 535, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, 20 [Google Scholar]
- Cayrel, R., Cayrel de Strobel, G., & Campbell, B. 1985, A&A, 146, 249 [NASA ADS] [Google Scholar]
- Cochran, W. D., Hatzes, A. P., & Paulson, D. B. 2002, AJ, 124, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Huang, W., Udalski, A., Gould, A., & Johnson, J. A. 2008, ApJ, 682, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Bruijne, J. H. J., Hoogerwerf, R., & de Zeeuw, P. T. 2001, A&A, 367, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in SPIE Conf. Ser. 4008, eds. M. Iye, & A. F. Moorwood, 534 [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Feltzing, S., & Gustafsson, B. 1998, A&AS, 129, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Ghezzi, L., Cunha, K., Schuler, S. C., & Smith, V. V. 2010, ApJ, 725, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkel, N. R., Timmes, F. X., Young, P. A., Pagano, M. D., & Turnbull, M. C. 2014, AJ, 148, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., & Knuckles, C. F. 1955, ApJ, 122, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Mitchell, R. I., & Iriarte, B. 1962, ApJ, 136, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. Italiana, 80, 711 [Google Scholar]
- Maldonado, J., Villaver, E., & Eiroa, C. 2013, A&A, 554, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J., Korn, A., & Grupp, F. 2010, in IAU Symp. 265, eds. K. Cunha, M. Spite, & B. Barbuy, 197 [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 557, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pace, G., Danziger, J., Carraro, G., et al. 2010, A&A, 515, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Randich, S., Zoccali, M., et al. 2004, A&A, 424, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Döllinger, M. P., Weiss, A., et al. 2007, A&A, 473, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paulson, D. B., Sneden, C., & Cochran, W. D. 2003, AJ, 125, 3185 [NASA ADS] [CrossRef] [Google Scholar]
- Paulson, D. B., Saar, S. H., Cochran, W. D., & Henry, G. W. 2004, AJ, 127, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, S. N., White, R. J., Latham, D. W., et al. 2014, ApJ, 787, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2007, A&A, 465, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reffert, S., Bergmann, C., Quirrenbach, A., Trifonov, T., & Künstler, A. 2015, A&A, 574, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Lovis, C., Melendez, J., et al. 2012, A&A, 538, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, B., Izumiura, H., Toyota, E., et al. 2007, ApJ, 661, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It. Suppl., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93 [Google Scholar]
- Schuler, S. C., Kim, J. H., Tinker, Jr., M. C., et al. 2005, ApJ, 632, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., King, J. R., Terndrup, D. M., et al. 2006, ApJ, 636, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R. 2012, MNRAS, 422, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Gauderon, R., North, P., et al. 2009, A&A, 502, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, V. V., Cunha, K., Shetrone, M. D., et al. 2013, ApJ, 765, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stefanik, H. P., & Latham, D. W. 1992, in Complementary Approaches to Double and Multiple Star Research, eds. H. A. McAlister, & W. I. Hartkopf, IAU Colloq. 135, ASP Conf. Ser., 32, 173 [Google Scholar]
- Stefanik, R. P., & Latham, D. W. 1985, in Stellar Radial Velocities, eds. A. G. D. Philip, & D. W. Latham, 213 [Google Scholar]
- Steffen, M., Ludwig, H.-G., & Caffau, E. 2009, Mem. Soc. Astron. Italiana, 80, 731 [NASA ADS] [Google Scholar]
- Steffen, M., Caffau, E., & Ludwig, H.-G. 2013, Mem. Soc. Astron. It. Suppl., 24, 37 [Google Scholar]
- Struve, O., & Elvey, C. T. 1934, ApJ, 79, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Tabernero, H. M., Montes, D., & González Hernández, J. I. 2012, A&A, 547, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J., & Croxall, K. 2005, MNRAS, 357, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Stefanik, R. P., Andersen, J., et al. 1997, AJ, 114, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Bueren, H. G. 1952, Bull. Astron. Inst. Netherlands, 11, 385 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Paradijs, J. 1972, Nature Phys. Sci., 238, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Lambert, D. L., Allen de Prieto, C., & Paulson, D. B. 2004, ApJ, 603, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional tables
Atomic line data for the list MASH and iron abundances according to M1.
Atomic line data for the list ASPL and iron abundances according to M1.
All Tables
IRFM Teff obtained with three different calibrations for the giants of the Hyades.
Stellar parameters and iron abundances for giants and dwarfs derived according to method M1.
Abundance changes (Δ[X/H]) in a giant (HIP 20205) and in a main-sequence (HIP 19148) star in response to variations of Teff, log g and ξ.
Stellar parameters and iron abundances for giants and dwarfs derived according to method M2.
Solar abundances of Fe i and Fe ii obtained with M1 and M2 for both MASH and ASPL lists.
All Figures
 |
Fig. 1 Color magnitude diagram (CMD) of the Hyades. The large black triangles correspond to the sample selected for our analysis. The small gray dots are the other cluster members. The magnitude V and the (B − V) color are from Perryman et al. (1998) and all stars shown fulfill the membership criterion of this work. |
| In the text | |
 |
Fig. 2 Comparison of EWs obtained with ARES and splot. Left: the solar reflected spectrum of Ganymede; middle: the star HIP 20205; and right: the star HIP 22566. The one-to-one relation is shown with the dashed line, and the red line represents the linear regression fit in each plot. The slope, the intercept, and the rms of the fits are also given in each plot. |
| In the text | |
 |
Fig. 3 Microturbulence determination for the model of the dwarf with Teff = 5000 K and log g = 4.5 dex. Left: Δlogϵi versus the 3D equivalent width for ξ = 0.90km s-1 (symbols). The dashed line represents the linear regression to the data points. Right: slope of the linear regression as a function of microturbulence. The optimal microturbulence is derived by the condition that the slope is zero. |
| In the text | |
 |
Fig. 4 Fe i and Fe ii abundances as a function of the excitation potential (χ), the logarithm of the reduced EW and the wavelength. The continuous red line is the regression between the quantities shown in each plot. The dashed line corresponds to the Fe ii final abundance derived according to M2. In all plots, the black asterisks correspond to the Fe i lines and the red filled triangles correspond to the Fe ii lines. Left: spectroscopic analysis for HIP 20205 using ASPL list. Right: spectroscopic analysis for HIP 20205 using MASH list. |
| In the text | |
 |
Fig. 5 Comparison of the metallicity scale derived with lists MASH and ASPL as a function of the Teff obtained with ASPL list for M1 (upper panel) and M2 (lower panel). In each plot, the null, ±0.1 and ±0.2 abundance differences are represented by the continuous, the dotted and the dashed lines respectively. Red dots refer to the giants while black squares refer to the dwarfs. |
| In the text | |
 |
Fig. 6 Comparison of the atmospheric parameters obtained with methods M1 and M2, as a function of the M1 parameters. The red lines are the linear regressions between the values. The dashed lines are the mean of the difference between the values presented in the y-axis. Left: parameters obtained with the ASPL line list. Right: parameters obtained with the MASH line list. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


