| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526639 | |
| Published online | 23 December 2015 | |
The ATLASGAL survey: distribution of cold dust in the Galactic plane
Combination with Planck data
1 Max-Planck Institute for Radioastronomy, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: ctimea@mpifr-bonn.mpg.de
2 European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
3 Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
4 OASU/LAB-UMR 5804, CNRS, Université Bordeaux 1, 33270 Floirac, France
5 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
6 I. Physikalisches Institut, Universität zu Köln, Zülpicher Strasse 77, 50937 Köln, Germany
Received: 30 May 2015
Accepted: 20 October 2015
Context. Sensitive ground-based submillimeter surveys, such as ATLASGAL, provide a global view on the distribution of cold dense gas in the Galactic plane at up to two-times better angular-resolution compared to recent space-based surveys with Herschel. However, a drawback of ground-based continuum observations is that they intrinsically filter emission, at angular scales larger than a fraction of the field-of-view of the array, when subtracting the sky noise in the data processing. The lost information on the distribution of diffuse emission can be, however, recovered from space-based, all-sky surveys with Planck.
Aims. Here we aim to demonstrate how this information can be used to complement ground-based bolometer data and present reprocessed maps of the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL) survey.
Methods. We use the maps at 353 GHz from the Planck/HFI instrument, which performed a high sensitivity all-sky survey at a frequency close to that of the APEX/LABOCA array, which is centred on 345 GHz. Complementing the ground-based observations with information on larger angular scales, the resulting maps reveal the distribution of cold dust in the inner Galaxy with a larger spatial dynamic range. We visually describe the observed features and assess the global properties of dust distribution.
Results. Adding information from large angular scales helps to better identify the global properties of the cold Galactic interstellar medium. To illustrate this, we provide mass estimates from the dust towards the W43 star-forming region and estimate a column density contrast of at least a factor of five between a low intensity halo and the star-forming ridge. We also show examples of elongated structures extending over angular scales of 0.5°, which we refer to as thin giant filaments. Corresponding to > 30 pc structures in projection at a distance of 3 kpc, these dust lanes are very extended and show large aspect ratios. We assess the fraction of dense gas by determining the contribution of the APEX/LABOCA maps to the combined maps, and estimate 2−5% for the dense gas fraction (corresponding to Av> 7 mag) on average in the Galactic plane. We also show probability distribution functions of the column density (N-PDF), which reveal the typically observed log-normal distribution for low column density and exhibit an excess at high column densities. As a reference for extragalactic studies, we show the line-of-sight integrated N-PDF of the inner Galaxy, and derive a contribution of this excess to the total column density of ~ 2.2%, corresponding to NH2 = 2.92 × 1022 cm-2. Taking the total flux density observed in the maps, we provide an independent estimate of the mass of molecular gas in the inner Galaxy of ~ 1 × 109 M⊙, which is consistent with previous estimates using CO emission. From the mass and dense gas fraction (fDG), we estimate a Galactic SFR of Ṁ = 1.3 M⊙ yr-1.
Conclusions. Retrieving the extended emission helps to better identify massive giant filaments which are elongated and confined structures. We show that the log-normal distribution of low column density gas is ubiquitous in the inner Galaxy. While the distribution of diffuse gas is relatively homogenous in the inner Galaxy, the central molecular zone (CMZ) stands out with a higher dense gas fraction despite its low star formation efficiency.Altogether our findings explain well the observed low star formation efficiency of the Milky Way by the low fDG in the Galactic ISM. In contrast, the high fDG observed towards the CMZ, despite its low star formation activity, suggests that, in that particular region of our Galaxy, high density gas is not the bottleneck for star formation.
Key words: surveys / submillimeter: ISM / stars: formation / ISM: structure / Galaxy: structure
© ESO, 2015
1. Introduction
Large area surveys of the Galaxy in the (sub)millimeter regime are essential to study the distribution of dust and star-forming gas. While space-based missions, such as Herschel (André et al. 2010; Molinari et al. 2010; Motte et al. 2010) provide high sensitivity images at submillimeter wavelengths with unprecedented dynamic range, ground-based facilities have the advantage of providing up to 3 × better angular resolution at a similar frequency. In this context, the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL survey; Schuller et al. 2009) provides one of the most extensive ground-based mapping of the inner Galaxy at submillimeter wavelengths.
Ground-based bolometer arrays are, however, not well suited to measure emission from angular scales larger than a fraction of the field-of-view of the array. This is because variations of the atmosphere mimic emission from extended astronomical objects, and therefore this signal is removed when subtracting the correlated noise from the maps in the data reduction process. As a consequence, depending on the data acquisition method and the reduction, the final emission maps have limited sensitivity above certain angular scales. With the advent of sensitive space-based missions, such as the all-sky survey of Planck (Tauber et al. 2010), this missing information can now be retrieved.
In particular, the Planck/High Frequency Instrument (HFI; Lamarre et al. 2010) surveyed the sky at 353 GHz, i.e. at a similar frequency range as the APEX/Large APEX Bolometer Camera (LABOCA) at 345 GHz used for the ATLASGAL survey. Here we present newly processed maps of the ATLASGAL survey that have been corrected for the loss of the filtered emission based on the Planck data. We describe the method in Sect. 2, then present and briefly describe the new data products in Sect. 3. With this dataset, we investigate the large-scale properties of the Galactic cold dust in Sect. 4.
2. Observations and data processing
2.1. APEX/LABOCA
The ATLASGAL survey imaged in total ~ 420 sq. deg of the inner Galactic plane at 870 μm (centred on 345 GHz) with the LABOCA camera (Siringo et al. 2009) on the APEX Telescope (Güsten et al. 2006) at a 19.′′2 spatial resolution. The highest sensitivity part of the ATLASGAL survey (Schuller et al. 2009) covers the Galactic plane between Galactic longitude, −60° ≤ ℓ ≤ + 60°, and Galactic latitude, −1.5° ≤ b ≤ + 1.5°, with an rms noise of ~ 70−90 mJy/beam. The survey was then extended towards Galactic longitude −80° ≤ ℓ ≤ −60° and Galactic latitude −2° ≤ b ≤ + 1.0° with an rms noise of ~ 110 mJy/beam (see also Csengeri et al. 2014).
The observing strategy and the main steps of the data reduction procedure are described in detail by Schuller et al. (2009). The data were reduced with the BoA software (Schuller 2012)1. As a result of removing the correlated noise in the time series of bolometer signals, the information of emission from extended astronomical objects is lost. This can be partially recovered through an iterative data reduction process (see also Belloche et al. 2011). The data reduction of the ATLASGAL survey has been optimized for compact sources, and convergence was reached after 15 iterations. The maps are sensitive to emission with angular scales up to 2.′5. The absolute flux uncertainty is estimated to be less than ~ 15% (Schuller et al. 2009). The catalogue optimized to extract the properties of the embedded compact sources is provided in Csengeri et al. (2014), while a catalogue of the more extended sources is presented in Contreras et al. (2013; see also Urquhart et al. 2014).
2.2. Planck/HFI
Planck performed an all-sky survey between 30 and 857 GHz (Planck Collaboration I 2014), mainly focusing on measuring the structure of the cosmic microwave background radiation (CMBR). For this purpose, it is mandatory that all foreground emission is carefully measured, modelled, and subtracted. To this end, the differing wavelength dependences of the foreground emission’s components (mainly, synchrotron, thermal free-free, and dust emission) are fully characterised by all sky maps made in a total of nine frequencies between 30 and 857 GHz. Of relevance here is that the HFI instrument (Lamarre et al. 2010; Planck Collaboration IX 2014) provides high sensitivity maps of the dust at 353 GHz with an angular resolution of 4.′8.
In the bright region of the Galactic plane, it is reasonable to assume that the 353 GHz emission is dominated by the interstellar dust, and CMBR,free-free emission, cosmic infrared background (CIB), and zodiacal dust emission have minor (< 5%) contamination (see e.g. Planck Collaboration Int. VIII 2013; Planck Collaboration XIV 2014; Planck Collaboration Int. XIV 2014; Planck Collaboration Int. XIII 2015, and references therein). As a result of similar centre frequencies, overlapping bandpasses and sensitivity at nearly matching angular scales, this dataset therefore well complements the ATLASGAL survey to recover emission from larger spatial scales. For this purpose, we used the publicly available Release 1 maps of the Planck mission (Planck Collaboration I 2014).
2.3. Colour corrections for LABOCA and the HFI
Since the calibration and spectral shape of the passbands of LABOCA and Planck’s HFI-353 GHz channel are different (see Fig. 1 upper panel), colour corrections need to be applied to combine both datasets. Two corrections have to be taken into account: a) the difference of the nominal centre frequency for both intstruments; and b) colour corrections to the intensity calibration. Both depend on the intrinsic source spectrum and we here assume that the spectrum across the passbands, S(ν), can be approximated by a power law with 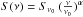 , where ν0 is the nominal centre frequency and α is the spectral index of the source spectrum. The nominal centre frequencies for the HFI-353 and LABOCA are 353 and 345 GHz, respectively. The centre frequency correction from the HFI-353 to LABOCA is therefore given by F(α) = (345/353)α. The intensity calibration for the HFI-353 is based on the IRAS convention (Iν ·ν = const.), while the LABOCA calibration is based on planet spectra (Iν ∝ ν2). Colour corrections to other source spectral indices can be computed by
, where ν0 is the nominal centre frequency and α is the spectral index of the source spectrum. The nominal centre frequencies for the HFI-353 and LABOCA are 353 and 345 GHz, respectively. The centre frequency correction from the HFI-353 to LABOCA is therefore given by F(α) = (345/353)α. The intensity calibration for the HFI-353 is based on the IRAS convention (Iν ·ν = const.), while the LABOCA calibration is based on planet spectra (Iν ∝ ν2). Colour corrections to other source spectral indices can be computed by 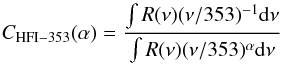 (1)and
(1)and 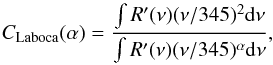 (2)where R(ν) and R′(ν) are the HFI-353 and LABOCA passbands, respectively. These corrections are shown as a function of the source spectral index in the bottom panel of Fig. 1.
(2)where R(ν) and R′(ν) are the HFI-353 and LABOCA passbands, respectively. These corrections are shown as a function of the source spectral index in the bottom panel of Fig. 1.
The average spectrum of the disk of the Milky Way is well described by a modified black-body spectrum with β = 1.8 (Planck Collaboration XXV 2011; Planck Collaboration XIX 2011; Planck Collaboration XI 2014). We therefore compute the corrections using a spectral index of α = 3.8, which yields F = 0.917, CHFI−353 = 0.868, and CLaboca = 0.988. The HFI-353 GHz data is provided in KCMB brightness temperature units. Conversion to MJy sr-1 (IRAS convention) is provided by a factor of U = 287.450 MJy sr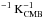 (Planck Collaboration IX 2014). Flux conversions to a common reference frequency at 345 GHz and source spectral index of α = 3.8 thus include
(Planck Collaboration IX 2014). Flux conversions to a common reference frequency at 345 GHz and source spectral index of α = 3.8 thus include ![\begin{equation} S_{{\rm HFI},345,3.8} = F\,\cdot\,C_{\rm HFI-353}\,\cdot\,U\,\cdot\,T_{\rm CMB}\,\,\left[\rm {MJy\,sr}^{-1}\right] \end{equation}](/articles/aa/full_html/2016/01/aa26639-15/aa26639-15-eq48.png) (3)and
(3)and ![\begin{eqnarray} S_{{\rm Laboca},345,3.8} = C_{\rm Laboca}\,\cdot\,S_{\rm Laboca}\,\,\left[{\rm Jy\,beam}^{-1}\right]. \end{eqnarray}](/articles/aa/full_html/2016/01/aa26639-15/aa26639-15-eq49.png) (4)
(4)
 |
Fig. 1 Top: relative spectral response (passband) for Planck’s HFI-353 GHz channel (solid line, Planck Collaboration 2013) and LABOCA (dashed line, Siringo et al. 2009). Bottom: colour corrections for the HFI-353 (solid line) and LABOCA (dashed line) as a function of the spectral index of the assumed source spectrum. The dotted line shows the conversion factor to scale the HFI-353 intensities to the nominal centre frequency of LABOCA. |
 |
Fig. 2 Amplitude versus spatial scales for the APEX/LABOCA (red), original Planck/HFI (blue), corrected Planck/HFI (green) and the combined dataset (black). The vertical lines indicate the centre and the effective width of the Butterworth filter used to combine both visibility sets. The dashed grey lines indicate the visibility amplitudes of the normalised LABOCA and Planck/HFI beams (scaled to a peak amplitude of 1000 for better visualisation). |
2.4. Combination of LABOCA and HFI
The procedure to correct for the filtered emission maps of ground-based bolometers is very similar to that used to account for the missing short-spacing information in interferometric observations. With the aim of recovering the larger scale emission, we therefore combined the APEX/LABOCA with the Planck/HFI data, where the latter provides the so-called short-spacing information.
We combined the two datasets in the Fourier domain (uv plane thereafter) with the method described in detail in Weiß et al. (2001). In brief, the combination replaces the central part of the uv plane of the APEX/LABOCA data (which is affected by the filtering) with the appropriate values calculated from the Planck/HFI data. The method relies on the accuracy of the absolute calibration of the two maps and only requires knowledge of the shape of the telescope beam for both datasets. The LABOCA beam is approximated by a circular Gaussian with a FWHM of 19.′′2 (Siringo et al. 2009). The effective Planck/HFI beam shape is a function of the position on sky (Planck Collaboration Int. VIII 2013). To determine the beam variation across the ATLASGAL survey area, we fit a 2D Gaussian to the effective beams retrieved from the Planck data archive at different Galactic longitudes. This test shows that the beam’s major and minor FWHM do not change significantly across the region of interest and we used the mean effective beam parameters for the Planck/HFI with FWHM of 5.′19 × 4.′52 (Planck Collaboration Int. VIII 2013). The position angle, however, rotates from PA = −12° at ℓ = 280° to PA = 60° at ℓ = 330° and stays roughly constant out to ℓ = 60°. In the combination we therefore used a variable position angle with values determined from a linear interpolation of the effective beams fits derived at sampling points spaced by 10° in Galactic longitude between ℓ = 280−330° and PA = 60° for larger Galactic longitudes.
 |
Fig. 3 An example field showing the original APEX/LABOCA maps from the ATLASGAL survey (left), the corresponding tile from Planck/HFI (middle) converted to 870 μm, and the combined map (right). The intensity scale is identical on the left and right panels going from 0.35 Jy/beam to 4 Jy/beam on logarithmic scale. Four arc-shaped, equidistant features bended to the Galactic plane are indicated in grey dotted lines and with arrows. Red crosses indicate the position of the velocity measurements from Wienen et al. (2012). |
First, we scale the Planck/HFI and the LABOCA intensities to a common reference frequency at 345 GHz and source spectral index of α = 3.8 as described in Sect. 2.3. Then we re-grid the Planck/HFI map to the same spatial grid as the LABOCA map and convert both maps to a Jy pixel-1 intensity scale. Next, both maps and beams are Fourier transformed to the uv domain, the Planck/HFI visibility2 amplitudes are divided by the amplitudes of the Planck/HFI beam (deconvolution of the Planck/HFI data) and the result is finally multiplied by the amplitudes of the LABOCA beam (convolution of the Planck/HFI data with the LABOCA beam). In these steps, the amplitudes of both beams are normalised to 1 in the uv domain.
After these operations the amplitudes of the Planck/HFI and APEX/LABOCA can be compared to each other to determine which part of the uv plane of the APEX/LABOCA is affected by filtering and needs to be replaced by the Planck/HFI data (the only free parameter in the combination). An example of the generated amplitudes versus the spatial frequencies based on a 3 × 3 deg field is shown in Fig. 2. The figure demonstrates that for spatial scales larger than ~ 5′ the APEX/LABOCA amplitudes fall systematically below the corrected Planck/HFI values due to the spatial filtering. Likewise, for scales smaller than ~ 2.′5 the corrected Planck/HFI visibility amplitudes deviate from the LABOCA values because of our simplistic Gaussian approximation of the Planck/HFI beam shape. We use a Butterworth weighting function centred at a scale of 3.′8 to combine the corrected Planck/HFI and the LABOCA visibility amplitudes. The width of the weighting function was set such that for scales > 4.′3 visibilities are purely based on Planck/HFI, and for scales < 3.′5 visibilities are purely based on LABOCA. The weighting function is indicated by the vertical lines in Fig. 2. Finally, the combined data is transformed back to the image domain and converted to the Jy/beam flux density scale.
To test the relative calibration between the datasets and the critical Planck/HFI beam model, we computed the relative difference between the amplitudes of the LABOCA and corrected Planck/HFI visibilities for spatial scales between 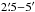 . We find a good agreement between both datasets with an rms of15.5% across the survey. The relative small angular scale of 3.′8 chosen for the combination implies large correction factors for the Planck/HFI visibility amplitudes (up to 8.2). Because of the much higher signal-to-noise ratio of the Planck/HFI data compared to the LABOCA data, however, this has a negligible effect on the noise properties of the combined map, which is dominated by the LABOCA noise. In the few outer regions of the survey where no significant emission is seen in the Planck/HFI data the noise level of the combined map is only ~ 5% higher than in the ATLASGAL maps.
. We find a good agreement between both datasets with an rms of15.5% across the survey. The relative small angular scale of 3.′8 chosen for the combination implies large correction factors for the Planck/HFI visibility amplitudes (up to 8.2). Because of the much higher signal-to-noise ratio of the Planck/HFI data compared to the LABOCA data, however, this has a negligible effect on the noise properties of the combined map, which is dominated by the LABOCA noise. In the few outer regions of the survey where no significant emission is seen in the Planck/HFI data the noise level of the combined map is only ~ 5% higher than in the ATLASGAL maps.
In practice, the combination is performed with the MIRIAD software package (Sault et al. 1995) on 3.0 × 3.0 deg subfields of the ATLASGAL survey. To avoid Fourier-transform artifacts from strong emission at the edge of these tiles, we multiplied the LABOCA and the re-grided Planck/HFI data prior to transformation to the uv domain with a 2D Butterworth filter. This effectively reduces the size of each zero-spacing corrected tile to 2.8 × 2.8 deg. To compensate for this edge effect along the Galactic plane, the individual tiles are spaced by 1.5 deg in Galactic longitude so that no information is lost except for the 0.1 deg broad edges in Galactic latitude. The combined data are publicly available3.
To check the consistency of the method, we compared the total flux density in the original Planck/HFI maps and the combined maps, which were found to agree to better than 5%. This is less than the calibration uncertainty of the LABOCA data.
 |
Fig. 4 Overview of the Galactic dust emission with the Planck+APEX combined maps at 870 μm. Colour scale goes from 0.15 to 5 Jy/beam on logarithmic scale. GMCs and cloud complexes are labelled based on Wienen et al. (2012). |
3. Results
3.1. Large-scale structures in cold dust
In Fig. 3, we show the maps, before and after the combination procedure, of one of the most spectacular regions of the ATLASGAL survey, 3 deg wide centred at ℓ ~ 332°. The extended emission clearly adds new information to the original LABOCA maps, and the large-scale structures become more prominent and seemingly connected in the 2D projection of the dust.
In particular, we visually identify elongated diffuse structures bending to the Galactic plane. These arm-like structures, extending over almost 0.5−1°, are visible in several regions along the inner Galaxy. Prominent examples are shown in Fig. 3 with several, equidistant dust lanes that are parallel to each other and are distributed over a spatial extent of ~ 2°. Pointed spectral line observations of high density tracers towards the embedded compact sources by Wienen et al. (2012) suggest a dispersion in vlsr between −57 to −42 km s-1, corresponding to kinematic distance estimates of 3−3.5 kpc. Located at these distances their extension is ~ 30−60 pc large. These features are qualitatively similar to the results of hydrodynamic simulations of our Galaxy (see for example Dobbs et al. 2011, 2015), which produce equidistant streams of inter-arm material produced by shears between spiral arms. A more detailed comparison to numerical models is, however, needed to interpret these features observed in the large-scale structure of the Galactic cold gas.
Figure 4 shows an overview of the APEX/LABOCA and the Planck/HFI combined maps (in the following, we simply refer to them as combined maps) over the Galactic plane in the highest sensitivity part of the survey covering | ℓ | < 60°. This complete view of the cold dust in the inner Galaxy clearly reveals the confined dust lane of our Galaxy, which is brightest between at ℓ ≲ 40° and ℓ ≳ 312°. Outside these longitude ranges the intensity of the emission along the plane gets significantly weaker.
The brightest and most prominent emission is observed towards the Galactic centre and the central molecular zone (CMZ) extending over several degrees (Fig. 5). The other most prominent large-scale structures are associated with the brightest known star-forming giant molecular clouds (GMCs). These were also found to be coherent structures in the velocity domain by Wienen et al. (2012).
As an example, in Fig. 6 we show the W43 GMC (Nguyen Luong et al. 2011; Motte et al. 2014), which seems to be surrounded by a large, extended haloover an area of ~200 × 160 pc seen in projection, and showing lower intensity diffuse emission. To estimate the total mass towards this region, including the low intensity diffuse gas, we sum up the emission in the area outlined in Fig. 6. We also use the formulae and the same assumptions as in Schuller et al. (2009) and Csengeri et al. (2014), assuming optically thin emission of dust at 870 μm ![\begin{equation} M [M_\odot]=\frac{S_\nu\,R\,d^2}{B_\nu(T_d)\,\kappa_{\nu}} \simeq 6.33 \times S_\nu \times \left( \frac{d}{[\rm kpc]} \right)^2 , \end{equation}](/articles/aa/full_html/2016/01/aa26639-15/aa26639-15-eq84.png) (5)where Sν is the integrated flux density over the selected area, and d corresponds to the heliocentric distance. To be consistent with our previous studies (e.g. Csengeri et al. 2014), we use a gas-to-dust mass ratio (R) of 100 and κν = 1.85 cm2 g-1 for ν = 345 GHz from Table 1, Col. 5 of Ossenkopf & Henning (1994). The numerical constant is obtained using a typical dust temperature dominated by the interstellar radiation field of Td = 18 K (Bernard et al. 2010). Here we adopt a distance of 5.5 kpc based on maser parallax measurements towards W43 (Zhang et al. 2014). This gives a total mass estimate from the dust of ~1.1 × 107M⊙, which is in a good agreement with the 8 × 106M⊙ estimate of Motte et al. (2014) based on molecular gas.
(5)where Sν is the integrated flux density over the selected area, and d corresponds to the heliocentric distance. To be consistent with our previous studies (e.g. Csengeri et al. 2014), we use a gas-to-dust mass ratio (R) of 100 and κν = 1.85 cm2 g-1 for ν = 345 GHz from Table 1, Col. 5 of Ossenkopf & Henning (1994). The numerical constant is obtained using a typical dust temperature dominated by the interstellar radiation field of Td = 18 K (Bernard et al. 2010). Here we adopt a distance of 5.5 kpc based on maser parallax measurements towards W43 (Zhang et al. 2014). This gives a total mass estimate from the dust of ~1.1 × 107M⊙, which is in a good agreement with the 8 × 106M⊙ estimate of Motte et al. (2014) based on molecular gas.
To calculate the H2 column density contrast between the diffuse halo around the GMC and the star-forming sites, we use the following expression: ![\begin{eqnarray} \label{eq:nh2} N({\rm H_2})&=&\frac{F_\nu\,R}{B_\nu(T_{\rm d})\,\Omega\,\kappa_{\nu}\,\mu_{\rm H_2}\,m_{\rm H}}\nonumber\\ &\simeq& 2.945\times10^{22}\times\frac{F_\nu}{[\rm Jy\,beam^{-1}]}\,\rm{\left[cm^{-2}\right] } \end{eqnarray}](/articles/aa/full_html/2016/01/aa26639-15/aa26639-15-eq95.png) (6)where Fν is the flux density, Ω is the solid angle of the beam calculated by Ω = 1.13 × Θ2, where Θ is the beam FWHM. The μH2 is the mean molecular weight of the interstellar medium with respect to hydrogen molecules, which is equal to 2.8 (Kauffmann et al. 2008), and mH is the mass of an hydrogen atom. The numerical constant is obtained for a centre frequency of 345 GHz, Td = 18 K, and beam size smoothed to 21′′.
(6)where Fν is the flux density, Ω is the solid angle of the beam calculated by Ω = 1.13 × Θ2, where Θ is the beam FWHM. The μH2 is the mean molecular weight of the interstellar medium with respect to hydrogen molecules, which is equal to 2.8 (Kauffmann et al. 2008), and mH is the mass of an hydrogen atom. The numerical constant is obtained for a centre frequency of 345 GHz, Td = 18 K, and beam size smoothed to 21′′.
We find a mean H2 column density of 1.71 ± 0.88 × 1022 cm-2 in thelarger environment of the W43 complex. This includes the halo and excludes the most active site of star formation associated with the Z-shaped region of W43 Main, also described by Bally et al. (2010) and Louvet et al. (2014), shown in a smaller polygon in Fig. 6. Here we measure a mean H2 column density of 7.45 ± 5.51 × 1022 cm-2, which implies an increase of column density contrast of > 5 between the low intensity halo and the star-forming massive ridgesgoing from ~200 pc to ~10−20 pc scales (Fig. 6).
 |
Fig. 5 CMZ shown in the combined maps. The intensity scale goes from 0.4 to 34 Jy/beam on logarithmic scale. |
 |
Fig. 6 W43 GMC shown in the combined maps. The intensity scale goes from 0.4 to 6 Jy/beam on a logarithmic scale. Dashed lines indicate the area where the emission has been summed up for mass and column density estimates (see text for details). |
3.2. Thin giant filaments
By revealing the structure of the lower density material connecting the highest density filament-fragments revealed by ATLASGAL, the combined maps allow us to visually identify thin, but spatiallyelongated filamentary structures. An example is shown in Fig. 7, revealing the large-scale environment of the IRDC G34.43+00.24 (Garay et al. 2004). Since ATLASGAL has a similar angular resolution as the Herschel/SPIRE 250 μm band, the strength of the survey lies in its sensitivity to cold dust. To illustrate this, in Fig. 7 we also show the SPIRE 250 μm band maps observed within the Hi-GAL Herschel key programme (Molinari et al. 2010), which has similar angular resolution as the combined maps. Since the highest density central regions of these filaments are colder than the diffuse surroundings, they show a higher contrast in the ATLASGAL maps, as for instance in the Herschel/SPIRE 250 μm image.
Typical examples of these kinds of confined filamentary structures are the Snake (G11.11-0.12; Pillai et al. 2006; Henning et al. 2010) and the Nessie filament (Jackson et al. 2010; Goodman et al. 2014), which have been studied in great detail. These structures have been characterised as giant molecular filaments (e.g. Li et al. 2013; Ragan et al. 2014) and massive molecular filaments (Battersby & Bally 2014), and based on their dust emission have also been identified by Wang et al. (2015). The filaments we report here typically extend over ≳ 0.5° seen in projection, and are elongated structures. Taking a typical distance of 3−6 kpc, such structures have a linear extension larger than 27−54 pc. The presented new maps of the ATLASGAL survey contain a handful of these visually identified structures, however, it is beyond the scope of this paper to discuss them in detail.
 |
Fig. 7 Top: APEX/LABOCA and Planck/HFI combined map of the IRDC G34.43+00.24. Grey contour shows an H2 column density limit of 2.1 × 1022 cm-2. A cross indicates the position of the UC-H II region of G34.26+0.15.Bottom: Herschel/250 μm map of the same region from the Hi-GAL survey (Molinari et al. 2010). We show level three data products obtained from the publicly available Herschel Science Archive. |
 |
Fig. 8 Percentage of the total flux in the APEX/LABOCA maps compared to the combined maps. Black dots correspond to the total flux estimated from all positive pixel values, while grey dots are estimated from summing up all pixel values above the 3σ. (See text for details.) Error bars indicate the 15% flux uncertainty in the APEX/LABOCA maps that dominate the noise distribution.Dotted lines show the median of the measured total flux percentage using the two methods. |
3.3. Properties of compact sources
The small-scale structures in the original ATLASGAL maps have been identified using two complementary methods in Contreras et al. (2013) and Csengeri et al. (2014). In particular, the latter method has been optimised to extract the properties of the embedded compact sources, and therefore background emission from the embedding clouds has been systematically removed. Consequently, adding the large-scale emission does not have an impact on the determined compact source properties (see also König et al. 2015).
4. Statistical properties of the Galactic cold dust
4.1. Dense gas fraction
In Fig. 8 we determine what fraction of the emission is contained in the APEX/LABOCA data compared to the combined maps in the highest sensitivity part of the ATLASGAL survey, i.e. in the inner Galaxy with | ℓ | < 60°. Since the filtered APEX/LABOCA maps are most sensitive to the highest column densities, and intrinsically filter the large-scale diffuse gas, the flux ratio between the APEX/LABOCA data and the Planck/HFI combined maps is representative of the dense gas fraction in the cold dust (fDG). In the following, we discuss two methods to estimate fDG based on column densities from the maps and their implications.
First we converted the maps to Jy/pixel units and then to avoid bias due to varying noise as a function of Galactic longitude, we applied a σ-clipping method for both the APEX/LABOCA only and the combined maps. We determine σ for each individual tile by fitting a Gaussian function to the histogram of pixel values considering only the low intensity below 3 Jy/beam values, and excluding 20′ at the edges in Galactic longitude and 15′ in Galactic latitude. In this region the flux was then summed up above 3σ. The ratio of integrated flux in the two maps gives a Galactic average of fDG ~ 5%. Because of the contribution of the lower intensity background from the Planck/HFI data, in particular, towards the inner Galaxy, this method may overestimate the noise in the combined maps, and therefore the derived total flux may be underestimated. This is seen, in particular, in confused regions in the inner Galaxy, where this method gives higher fDG. The estimated average fDG ~ 5% flux ratio is therefore a conservative upper limit on the dense gas fraction in the cold gas.
We also determine fDG using a more stringent threshold considering the fraction of dense gas that is likely to be directly involved in the star formation process. Based on Herschel studies in the Gould-belt, André et al. (2010) suggests Av ~ 7 mag (6.58 × 1020 cm-2)4 as a threshold for the formation of dense cores, i.e. the entities where star formation takes place (see also Lada et al. 2010). Using this criterion, we find fDG< 2%, which is a factor of two lower compared to our previous, upper limit estimate.
As shown in Fig. 8, the dense gas fraction is found to be constant in the inner Galaxy, despite the large variation in star formation activity. The only outstanding field is towards the Galactic centre region (the CMZ), where both methods give a systematically higher fDG of 10−13%. The higher dense gas fraction found towards the Galactic centre is intriguing given the low star formation efficiency towards this region (Immer et al. 2012; Urquhart et al. 2013; Longmore et al. 2013; Csengeri et al. 2014; Johnston et al. 2014).
Our estimates provide an independent, and consistent measure of the dense gas fraction in GMCs, relying on the same tracer for the gas. Other commonly used methods rely on comparing observations of dust and molecular tracers of gas, or different molecular tracers in external galaxies. Despite the difference in the applied method, our results are in good agreement with the upper limit estimates of 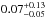 of Battisti & Heyer (2014), which are based on comparing masses of dense clumps derived from the Bolocam Galactic Plane Survey (BGPS; Aguirre et al. 2011), and GMC masses from the 13CO (1−0) molecular line data from the Galactic Ring Survey (Jackson et al. 2006). For comparison, Ragan et al. (2014) also find dense gas mass fractions between 3% to 18% for giant filaments, and based on CO measurements towards more than 90 GMCs identified in the IVth quadrant, García et al. (2014) estimate massive star formation efficiencies on average of 3% from their available molecular mass. These are in agreement with our results in the present paper. Using similar datasets, Eden et al. (2013) estimate ~ 5% for the clump formation efficiency (CFE), and find no difference for the CFE between the spiral arm and inter-arm regions. Except for the CMZ, our results support their conclusions. Our findings are also in good agreement with a dense gas fraction between 2−5% obtained for normal spiral galaxies by Gao & Solomon (2004) using HCN as a tracer for dense gas.
of Battisti & Heyer (2014), which are based on comparing masses of dense clumps derived from the Bolocam Galactic Plane Survey (BGPS; Aguirre et al. 2011), and GMC masses from the 13CO (1−0) molecular line data from the Galactic Ring Survey (Jackson et al. 2006). For comparison, Ragan et al. (2014) also find dense gas mass fractions between 3% to 18% for giant filaments, and based on CO measurements towards more than 90 GMCs identified in the IVth quadrant, García et al. (2014) estimate massive star formation efficiencies on average of 3% from their available molecular mass. These are in agreement with our results in the present paper. Using similar datasets, Eden et al. (2013) estimate ~ 5% for the clump formation efficiency (CFE), and find no difference for the CFE between the spiral arm and inter-arm regions. Except for the CMZ, our results support their conclusions. Our findings are also in good agreement with a dense gas fraction between 2−5% obtained for normal spiral galaxies by Gao & Solomon (2004) using HCN as a tracer for dense gas.
4.2. Isothermal column density PDFs of the cold Galactic dust
To analyse the statistical properties of the structures in the cold Galactic dust emission, we show the H2 column density probability distribution function (N-PDF) for all fields (Fig. 9, upper panel). We calculate the H2 column density for each pixel, assuming a single dust temperature of Td = 18 K and using Eq. (6), and we caution that assuming a single dust temperature is a crude simplification. More realistic H2 column density maps should be obtained using multi-wavelength data from Herschel surveys such as shown in e.g. Peretto et al. (2010), Schneider et al. (2015a).
 |
Fig. 9 Top: column density probability distribution function (N-PDF) for all 3 deg tiles overplotted. Only the | b | < 1° regions are considered due to the increasing noise towards the edges of the ATLASGAL fields. Red lines show the fields, which include the Galactic centre. Bottom: the N-PDF of the inner Galaxy (| ℓ | < 60°). Green dashed line shows a log-normal function with σ = 0.41 at a peak of NH2 = 1.10 × 1022 cm-2. Red dotted line shows where excess from the power-law tail sets in at NH2 = 2.92 × 1022 cm-2. |
We define η = ln(NH2/ ⟨ NH2 ⟩) as the natural logarithm of the column density divided by the mean column density of the corresponding tile.We only use pixels that are above the lowest ~3σ noise level determined from the LABOCA only maps. The probability of the NH2 column density in the range of (NH2,NH2 + dNH2) is then given by 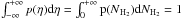 ; see also Schneider et al. (2015a) for more details. This formalism follows previous works using numerical simulations to describe the density structure of molecular clouds (Federrath et al. 2008), and pη is adopted to describe a 2D-PDF. Projection effects average out the 3D density distribution and the underlying dense gas fraction of the ISM, and therefore conversion from 2D column density PDFs to 3D density PDFs have to consider the isotropy of molecular clouds. Numerical simulations show, however, that systematic differences reflecting the gas properties can still be recovered with N-PDFs as well (e.g. Federrath & Banerjee 2015). Conversion to volume densities (ρ-PDF) has been discussed in Kainulainen et al. (2014).
; see also Schneider et al. (2015a) for more details. This formalism follows previous works using numerical simulations to describe the density structure of molecular clouds (Federrath et al. 2008), and pη is adopted to describe a 2D-PDF. Projection effects average out the 3D density distribution and the underlying dense gas fraction of the ISM, and therefore conversion from 2D column density PDFs to 3D density PDFs have to consider the isotropy of molecular clouds. Numerical simulations show, however, that systematic differences reflecting the gas properties can still be recovered with N-PDFs as well (e.g. Federrath & Banerjee 2015). Conversion to volume densities (ρ-PDF) has been discussed in Kainulainen et al. (2014).
Figure 9 (upper panel) shows the N-PDFs for all 3 by 3 deg tiles. This representation suffers from line-of-sight contamination (see Schneider et al. 2015b; Lombardi et al. 2015) and does not consider boundaries of molecular clouds. The characteristic log-normal shape at low column density is, however, ubiquitous in the inner Galaxy. Similarly, an excess at high column density regimes is observed towards all regions, consistent with what was found in star-forming regions (e.g. Kainulainen et al. 2009; André et al. 2010; Lombardi et al. 2010; Froebrich & Rowles 2010; Schneider et al. 2012).
This excess at high-column densities in the form of a power-law tail requires power-law density structures, which can be achieved by either a hydrostatic configuration where the power law arises from a balance of gravitational forces and pressure gradients (Kainulainen et al. 2009; Tremblin et al. 2014) or directly in a dynamically collapsing system (Schneider et al. 2013, 2015b). From a theoretical point of view, gravitational collapse reproduces well the observed high-density excess (e.g. Ballesteros-Paredes et al. 2011; Kritsuk et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014). Other explanations, such as non-isothermal flows (Passot & Vázquez-Semadeni 1998), have also been invoked, while magnetic fields have been shown to slow down the collapse process and reduce the excess at high densities (Heitsch et al. 2001).
These characteristics show that the APEX/LABOCA and Planck/HFI combined maps trace well a substantial fraction of the low-density diffuse material in the Galactic plane, whose line-of-sight averaged density structure resembles that of the more nearby GMCs (e.g. Schneider et al. 2012; Russeil et al. 2013; Schneider et al. 2013).
We also point out that the N-PDFs are similar for each field despite their different properties. The mean of the log-normal fit to each tile is constant across the Galactic plane and peaks at a value of NH2 = 1.06 × 1022 cm-2. The width of the log-normal (ση) shows larger variations with an average value of 0.41, and a median of 0.34. We find the regions covering the CMZ exhibit a more significant excess of high-density gas. This is again intriguing because of the low star formation efficiency in this region.
As a reference for extragalactic comparison, in Fig. 9 (lower panel) we show the overall N-PDF describing the inner | ℓ | < 60° range of the Galaxy. Again, the low column density part of the distribution is well fitted with a log-normal function with the parameters given above. A power-law tail showing an excess at high column densities is likely associated with star formation (e.g. Kainulainen et al. 2009; Schneider et al. 2012). The high-density, power-law tail starts at ~2.92 × 1022 cm-2, and has a contribution of 2.2% to the total fraction of gas, which is consistent with our results obtained in Sect. 4.1, and corresponds to a Galactic average of dense gas fraction. This suggests that the formation of high-density structures is highly inefficient, and relates to the observed low efficiency of star formation in the Milky Way. Given the high dense gas fraction towards the CMZ, the formation of high-density structures, however, cannot be the bottleneck for star formation process to settle in.
4.3. Mass estimation from dust for the inner Galactic plane
Since the ATLASGAL APEX/LABOCA and Planck/HFI combined maps contain emission at alllarge scales, we use them to assess the global properties of the dust in the inner Galaxy to provide a reference for external galaxies. Summing up the total flux along the Galactic plane, we determine a total flux density of 1.93 MJy. This total flux density is assigned to a mass estimate for the inner Galaxy in Fig. 10. Attributing the total emission to a lower and upper distance limit of 2 to 20 kpc, assuming isothermal dust emission with Td = 18 K and the same dust parameters as in Sect. 4.2, we arrive at an upper limit estimate of Mtot ≲ 5 × 109 M⊙ as a strict upper limit for the total gas mass in the inner Galaxy. To obtain a more realistic estimate, we use three models with synthetic distance distributions using a Monte-Carlo method. In Fig. 10 (top panel) we show the observed distance distribution from Wienen et al. (2012) with NH3 measurements towards ATLASGAL sources. In Model-1, we use a normal distribution of distance estimates adopting the mean distance from Wienen et al. (2012). In Model-2, we use a normal distribution peaking at the Galactic centre of 8.5 kpc distance (Reid et al. 2014), while in Model-3 we adopt the sum of three normally distributed components, one at the Galactic centre, and two symmetric distributions representing the molecular ring. We show that despite the different distribution, Model-2 and Model-3 give similar estimates of ~0.87−0.94 × 109 M⊙, while Model-1 gives a lower estimate of ~0.12 × 109 M⊙. The most recent estimate for the total gas mass in the Milky Way is 1.0 ± 0.3 × 109 M⊙ (Heyer & Dame 2015), with about 70% of the mass within the solar circle. As a comparison, the total mass of molecular gas is estimated to be ~ 2 × 109 M⊙ using CO measurements by Scoville & Solomon (1975) and Solomon et al. (1987). Our estimate based on an independent method is within an order of magnitude in agreement with these previous studies.
 |
Fig. 10 Top: distance distributions used for the mass estimates. Solid line corresponds to the NH3 observations by Wienen et al. (2012). Dashed lines show the three models discussed in Sect. 4.3. Bottom: molecular gas mass estimate for the inner Galaxy (| ℓ | < 60° and | b | < 1.4°) from the ATLASGAL APEX/LABOCA and Planck/HFI combined maps of dust emission at 870 μm. Dots show the observed total mass as a function of a single adopted distance. Dashed line shows the mass estimation estimated with a Monte Carlo simulation. Red line shows the total estimated molecular gas mass based on CO measurements (Solomon et al. 1987). |
4.4. Galactic star formation rate
From the total mass estimate and the measure of the dense gas fraction we can derive the total mass of dense gas in the inner Galaxy. Using the most realistic model for the distance distribution (Model-3, see Sect. 4.3), and considering a threshold of NH2 = 6.58 × 1021 cm-2 within the smoothed beam of the combined map of 21′′, we obtain on average ~2 × 107 M⊙. This corresponds to the Galactic average of ~2% for the fraction of dense gas and a total mass of ~ 109 M⊙.
Direct estimates of star formation rate (SFR) in nearby molecular clouds with Herschel (Andre et al. 2014) give a star formation rate per solar mass of 4.5 × 10-8 yr-1, which is very close to the empirical values derived by Lada et al. (2012) and Gao & Solomon (2004). Based on this we can directly measure a total SFR in the inner Galaxy of 0.9 M⊙/yr. Considering the distribution of gas mass, if 70% of the star formation activity occurs in the inner Galaxy, we obtain a total SFR of 1.3 M⊙ yr-1 outside the Galactic centre regions. This is in good agreement with the value of 2.44 ± 0.81 M⊙ yr-1, estimated by Csengeri et al. (2014)based on a different, clump and star counting method using the fraction of star-forming versus quiescent massive clumps in ATLASGAL. Independent estimates of the Galactic SFR arrive to 2 M⊙ yr-1 (Chomiuk & Povich 2011). Extragalactic studies by e.g. Wu et al. (2005) use a factor of ~ 4 lower conversion factor for SFR estimates, which is still consistent with the estimates of Galactic SFR.
A part of the Galactic star formation is also expected in the Galactic centre regions, however, these regions exhibit a lower efficiency of star formation (e.g. Csengeri et al. 2014). While the overall star formation efficiency is low, the fraction of dense gas is found to be very high with a fraction up 13%. This indicates that the origin of the low star formation efficiency is not due to a low efficiency of producing dense gas, but rather on small scales within the dense gas, which everywhere else in the Galaxy would collapse and form stars at a fast rate.
5. Summary
We present here reprocessed maps of the ATLASGAL survey, where the APEX/LABOCA maps have been complemented with the Planck/HFI all-sky survey data at 353 GHz to correct for the filtering by ground-based bolometer observations. These new maps cover emission at larger angular scales and, thereby, reveal the structure of cold Galactic dust in great detail. We summarise our main findings below:
-
A halo of diffuse dust emission is seen towards the direction ofGMCs. We show two examples, first theℓ ~ 332° region where large structures extending over 0.5° seem to bend to the Galactic plane. As a second example, the W43 star-forming region is shown with its surrounding dust halo. We use the full information of dust to estimate H2 column densities and determine a density contrast of > 5 between the diffuse halo emission and the massive ridge of W43 Main from ~200 to a few tens of parsec scales.
-
Adding information from large angular scales helps to better identify the large-scale properties of the cold Galactic interstellar medium. Based on visual inspection of the data we show examples of giant filaments, which show a linear extension larger than 0.5°, corresponding to > 30 pc at distances above 3 kpc. These filaments have more confined high-density regime and similarly to Nessie, they exhibit large aspect ratios.
-
The presented maps trace well a substantial fraction of the low-density diffuse material in the Galactic plane. Using N-PDFs we conclude that the diffuse dust emission shows very similar properties as a function of Galactic longitude. From this, we estimate on average an upper limit on the dense gas fraction of 5% on the inner Galaxy and find a relatively constant efficiency for the formation of dense gas. The Galactic centre region has a larger dense gas fraction, fDG ~ 13−15%, which is intriguing considering its low star formation efficiency. We conclude that the low fDG in the Milky Way is consistent with its globally low star formation efficiency. The high fDG observed towards the CMZ suggests that the formation of dense gas is not the bottleneck for star formation.
-
We show that the global N-PDF for the inner Galaxy is well described by a log-normal distribution, which is well explained by the large-scale turbulent nature of the ISM. An excess at high column densities shows a power-law tail, which contributes 2.2% to the total distribution. This is a Galactic average for column densities above 2.92 × 1022 cm-2.
-
From the total dust emission in the inner Galaxy we provide an independent estimate of the gas mass of ~ 109 M⊙, which is in good agreement with the results of CO measurements by Solomon et al. (1987).
-
Based on the mass estimate for the Galactic plane and the fDG of 2%, assuming that 70% of the star formation takes place in the inner Galaxy, we estimate a total Galactic SFR of Ṁ = 1.3 M⊙ yr-1 outside the Galactic centre regions.
-
Although the CMZ is efficient in producing a larger amount of dense gas compared to other molecular clouds in the Galaxy, the low star formation efficiency suggests that either the local or the global properties of the dense gas must be different from other star-forming regions.
With the presented dataset, a more detailed analysis of the dust content of the Milky Way is now possible. Furthermore, as also shown by Schneider et al. (2015b), the presented dataset can be well used to complement the Herschel Hi-GAL survey (Molinari et al. 2010) to derive column density maps of H2 at better angular resolution than only based on Herschel data.
We convert H2 column densities to Av using NH2/AV = 0.94 × 1021 cm-2 mag-1 (Bohlin et al. 1978).
Acknowledgments
This work was partially funded by the ERC Advanced Investigator Grant GLOSTAR (247078) and was partially carried out within the Collaborative Research Council 956, sub-project A6, funded by the Deutsche Forschungsgemeinschaft (DFG). T.Cs acknowledges support from the Deutsche Forschungsgemeinschaft, DFG via the SPP (priority programme) 1573 “Physics of the ISM”. L.B. acknowledges support by CONICYT Grant PFB-06. N.S. acknowledges supported by the DFG, through project number Os 177/2-1 and 177/2-2 and central funds of the DFG-priority programme 1573 (ISM-SPP).
References
- Aguirre, J. E., Ginsburg, A. G., Dunham, M. K., et al. 2011, ApJS, 192, 4 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Andre, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI, 24 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Anderson, L. D., Battersby, C., et al. 2010, A&A, 518, L90 [Google Scholar]
- Battersby, C., & Bally, J. 2014, Astrophys. Space Sci. Proc., 36, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Battisti, A. J., & Heyer, M. H. 2014, ApJ, 780, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, Y., Schuller, F., Urquhart, J. S., et al. 2013, A&A, 549, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., Burkert, A., & Pringle, J. E. 2011, MNRAS, 417, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Pringle, J. E., & Duarte-Cabral, A. 2015, MNRAS, 446, 3608 [NASA ADS] [CrossRef] [Google Scholar]
- Eden, D. J., Moore, T. J. T., Morgan, L. K., Thompson, M. A., & Urquhart, J. S. 2013, MNRAS, 431, 1587 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Banerjee, S. 2015, MNRAS, 448, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Garay, G., Faúndez, S., Mardones, D., et al. 2004, ApJ, 610, 313 [NASA ADS] [CrossRef] [Google Scholar]
- García, P., Bronfman, L., Nyman, L.-Å., Dame, T. M., & Luna, A. 2014, ApJS, 212, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Alves, J., Beaumont, C. N., et al. 2014, ApJ, 797, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heitsch, F., Mac Low, M.-M., & Klessen, R. S. 2001, ApJ, 547, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M., & Dame, T. 2015, ARA&A, 53, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Immer, K., Menten, K. M., Schuller, F., & Lis, D. C. 2012, A&A, 548, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Finn, S. C., Chambers, E. T., Rathborne, J. M., & Simon, R. 2010, ApJ, 719, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. G., Beuther, H., Linz, H., et al. 2014, A&A, 568, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2014, Science, 344, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- König, et al. 2015, submitted [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G.-X., Wyrowski, F., Menten, K., & Belloche, A. 2013, A&A, 559, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longmore, S. N., Bally, J., Testi, L., et al. 2013, MNRAS, 429, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Louvet, F., Motte, F., Hennebelle, P., et al. 2014, A&A, 570, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Nguyên Luong, Q., Schneider, N., et al. 2014, A&A, 571, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nguyen Luong, Q., Motte, F., Schuller, F., et al. 2011, A&A, 529, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Fuller, G. A., Plume, R., et al. 2010, A&A, 518, L98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Menten, K. M., & Krügel, E. 2006, A&A, 447, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2013, The Explanatory Supplement to the Planck 2013 results [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2014, A&A, 571, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VIII. 2013, A&A, 557, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XIV. 2014, A&A, 564, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XIII. 2015, A&A, 580, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Henning, T., Tackenberg, J., et al. 2014, A&A, 568, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Klessen, R. S., et al. 2015a, A&A, 578, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015b, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F. 2012, in SPIE Conf. Ser., 8452 [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N. Z., & Solomon, P. M. 1975, ApJ, 199, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J. S., Moore, T. J. T., Schuller, F., et al. 2013, MNRAS, 431, 1752 [Google Scholar]
- Urquhart, J. S., Csengeri, T., Wyrowski, F., et al. 2014, A&A, 568, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, K., Testi, L., Ginsburg, A., et al. 2015, MNRAS, 450, 4043 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Weiß, A., Neininger, N., Hüttemeister, S., & Klein, U. 2001, A&A, 365, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A&A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, J., Evans, II, N. J., Gao, Y., et al. 2005, ApJ, 635, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Moscadelli, L., Sato, M., et al. 2014, ApJ, 781, 89 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Top: relative spectral response (passband) for Planck’s HFI-353 GHz channel (solid line, Planck Collaboration 2013) and LABOCA (dashed line, Siringo et al. 2009). Bottom: colour corrections for the HFI-353 (solid line) and LABOCA (dashed line) as a function of the spectral index of the assumed source spectrum. The dotted line shows the conversion factor to scale the HFI-353 intensities to the nominal centre frequency of LABOCA. |
| In the text | |
 |
Fig. 2 Amplitude versus spatial scales for the APEX/LABOCA (red), original Planck/HFI (blue), corrected Planck/HFI (green) and the combined dataset (black). The vertical lines indicate the centre and the effective width of the Butterworth filter used to combine both visibility sets. The dashed grey lines indicate the visibility amplitudes of the normalised LABOCA and Planck/HFI beams (scaled to a peak amplitude of 1000 for better visualisation). |
| In the text | |
 |
Fig. 3 An example field showing the original APEX/LABOCA maps from the ATLASGAL survey (left), the corresponding tile from Planck/HFI (middle) converted to 870 μm, and the combined map (right). The intensity scale is identical on the left and right panels going from 0.35 Jy/beam to 4 Jy/beam on logarithmic scale. Four arc-shaped, equidistant features bended to the Galactic plane are indicated in grey dotted lines and with arrows. Red crosses indicate the position of the velocity measurements from Wienen et al. (2012). |
| In the text | |
 |
Fig. 4 Overview of the Galactic dust emission with the Planck+APEX combined maps at 870 μm. Colour scale goes from 0.15 to 5 Jy/beam on logarithmic scale. GMCs and cloud complexes are labelled based on Wienen et al. (2012). |
| In the text | |
 |
Fig. 5 CMZ shown in the combined maps. The intensity scale goes from 0.4 to 34 Jy/beam on logarithmic scale. |
| In the text | |
 |
Fig. 6 W43 GMC shown in the combined maps. The intensity scale goes from 0.4 to 6 Jy/beam on a logarithmic scale. Dashed lines indicate the area where the emission has been summed up for mass and column density estimates (see text for details). |
| In the text | |
 |
Fig. 7 Top: APEX/LABOCA and Planck/HFI combined map of the IRDC G34.43+00.24. Grey contour shows an H2 column density limit of 2.1 × 1022 cm-2. A cross indicates the position of the UC-H II region of G34.26+0.15.Bottom: Herschel/250 μm map of the same region from the Hi-GAL survey (Molinari et al. 2010). We show level three data products obtained from the publicly available Herschel Science Archive. |
| In the text | |
 |
Fig. 8 Percentage of the total flux in the APEX/LABOCA maps compared to the combined maps. Black dots correspond to the total flux estimated from all positive pixel values, while grey dots are estimated from summing up all pixel values above the 3σ. (See text for details.) Error bars indicate the 15% flux uncertainty in the APEX/LABOCA maps that dominate the noise distribution.Dotted lines show the median of the measured total flux percentage using the two methods. |
| In the text | |
 |
Fig. 9 Top: column density probability distribution function (N-PDF) for all 3 deg tiles overplotted. Only the | b | < 1° regions are considered due to the increasing noise towards the edges of the ATLASGAL fields. Red lines show the fields, which include the Galactic centre. Bottom: the N-PDF of the inner Galaxy (| ℓ | < 60°). Green dashed line shows a log-normal function with σ = 0.41 at a peak of NH2 = 1.10 × 1022 cm-2. Red dotted line shows where excess from the power-law tail sets in at NH2 = 2.92 × 1022 cm-2. |
| In the text | |
 |
Fig. 10 Top: distance distributions used for the mass estimates. Solid line corresponds to the NH3 observations by Wienen et al. (2012). Dashed lines show the three models discussed in Sect. 4.3. Bottom: molecular gas mass estimate for the inner Galaxy (| ℓ | < 60° and | b | < 1.4°) from the ATLASGAL APEX/LABOCA and Planck/HFI combined maps of dust emission at 870 μm. Dots show the observed total mass as a function of a single adopted distance. Dashed line shows the mass estimation estimated with a Monte Carlo simulation. Red line shows the total estimated molecular gas mass based on CO measurements (Solomon et al. 1987). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


