| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526757 | |
| Published online | 13 November 2015 | |
The interaction of core-collapse supernova ejecta with a companion star
1
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail:
zwliu@ynao.ac.cn
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
3
Heidelberger Institut für Theoretische Studien,
Schloss-Wolfsbrunnenweg 35,
69118
Heidelberg,
Germany
4
Zentrum für Astronomie der Universität Heidelberg, Institut für
Theoretische Astrophysik, Philosophenweg 12, 69120
Heidelberg,
Germany
5
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
Received: 16 June 2015
Accepted: 10 September 2015
Context. The progenitors of many core-collapse supernovae (CCSNe) are expected to be in binary systems. After the SN explosion in a binary, the companion star may suffer from mass stripping and be shock heated as a result of the impact of the SN ejecta. If the binary system is disrupted by the SN explosion, the companion star is ejected as a runaway star, and in some cases as a hypervelocity star.
Aims. By performing a series of three-dimensional (3D) hydrodynamical simulations of the collision of SN ejecta with the companion star, we investigate how CCSN explosions affect their binary companion.
Methods. We use the BEC stellar evolution code to construct the detailed companion structure at the moment of SN explosion. The impact of the SN blast wave on the companion star is followed by means of 3D smoothed particle hydrodynamics (SPH) simulations using the Stellar GADGET code.
Results. For main-sequence (MS) companion stars, we find that the amount of removed stellar mass, the resulting impact velocity, and the chemical contamination of the companion that results from the impact of the SN ejecta strongly increases with decreasing binary separation and increasing explosion energy. Their relationship can be approximately fitted by power laws, which is consistent with the results obtained from impact simulations of Type Ia SNe. However, we find that the impact velocity is sensitive to the momentum profile of the outer SN ejecta and, in fact, may decrease with increasing ejecta mass, depending on the modeling of the ejecta. Because most companion stars to Type Ib/c CCSNe are in their MS phase at the moment of the explosion, combined with the strongly decaying impact effects with increasing binary separation, we argue that the majority of these SNe lead to inefficient mass stripping and shock heating of the companion star following the impact of the ejecta.
Conclusions. Our simulations show that the impact effects of Type Ib/c SN ejecta on the structure of MS companion stars, and thus their long-term post-explosion evolution, is in general not dramatic. We find that at most 10% of their mass is lost and their resulting impact velocities are less than 100 km s-1.
Key words: supernovae: general / stars: kinematics and dynamics / binaries: close
© ESO, 2015
1. Introduction
The discovery of many low-mass X-ray binaries and millisecond pulsars in tight orbits, i.e., binary neutron stars with orbital periods of less than a few hours, provides evidence for supernova (SN) explosions in close binaries with low-mass companions. The nature of the SN explosion determines whether any given binary system remains bound or is disrupted (Hills 1983). An additional consequence of the SN explosion is that the companion star is affected by the impact of the shell debris ejected from the exploding star (Wheeler et al. 1975). Besides chemical enrichment, this kind of an impact has kinematic effects and may induce significant mass loss and heating of the companion star.
Core-collapse supernovae (CCSNe) arise from massive stars. Determining the relationship between SNe and their progenitor stars remains an important problem (see Langer 2012, for a recent review). Despite the fact that the amount of SN ejecta is decisive for the aftermath of a SN in a binary system, the mechanism of significant, or even complete, removal of the hydrogen (H) envelope in H-deficient CCSNe (Type Ib/c, IIb, and IIL) is not well understood.
Although it was originally proposed that H-deficient SNe might arise from massive, metal-rich single stars through stellar wind mass loss (Woosley et al. 1993; Maeder & Meynet 2003; Eldridge & Tout 2004), it has long been considered that mass transfer via Roche-lobe overflow (RLO) in binary systems is a likely mechanism to produce the progenitors of H-deficient CCSNe (Paczyński 1967; Podsiadlowski et al. 1992, 1993; Maund et al. 2004; Eldridge et al. 2008; Stancliffe & Eldridge 2009; Yoon et al. 2010; Dessart et al. 2011). There is growing observational evidence that the fraction of massive stars in close binary systems is large (Chini et al. 2012; Duchêne & Kraus 2013). Sana et al. (2012) found that more than 70% of massive stars are in close binary systems, which supports the idea that binary progenitors contribute significantly to the observed H-deficient SNe.
Evidence from statistical samples of Type Ib/c SNe suggests that stripped, relatively low-mass, exploding stars in binaries are likely to be progenitors of most Type Ib/c SNe (Drout et al. 2011; Bianco et al. 2014; Lyman et al. 2014; Taddia et al. 2015). In some cases, like SN 2005ek, there is even evidence of extreme stripping of the SN progenitor star, with only ~0.1 M⊙ of material being ejected (Drout et al. 2013; Tauris et al. 2013, 2015). With HST analysis of pre-SN images, Cao et al. (2013) report the detection of a possible progenitor candidate at the location of a young, H-deficient Type Ib SN, iPTF13bvn1. Further light-curve modeling, and analysis of pre-SN and late-time photometry, of iPTF13bvn suggests that an interacting binary system is likely to be the progenitor of iPTF13bvn rather than a standard single Wolf-Rayet star (Bersten et al. 2014; Fremling et al. 2014; Eldridge et al. 2015; but see Groh et al. 2013). All these findings indicate that H-deficient CCSNe and in particular Type Ib/c SNe, can naturally be produced in binary progenitor systems.
In the binary progenitor scenario of Type Ib/c CCSNe, the metal core of a massive star (originally 8–30 M⊙) undergoes gravitational collapse to form a neutron star (NS), while the outer parts of its envelope are expelled at a high velocity and impact on the binary companion star. Depending on the amount of sudden mass loss because of the SN explosion and the momentum kick imparted on the newborn NS, the outcome of the SN explosion is either a bound system (Hills 1983), which may later evolve into an X-ray binary system (Tauris & van den Heuvel 2006), or two single runaway stellar components, which are left behind if the binary is unbound (Tauris & Takens 1998). This kind of a disruption of close binaries by a SN explosion has been proposed as a possible mechanism for producing hypervelocity stars (HVSs) that will leave our Galaxy because both ejected stars can receive high runaway velocities when asymmetric SNe are considered (Tauris & Takens 1998; Tauris 2015).
After a SN explosion occurs in a binary system, the ejected debris is expected to expand freely for a few minutes to hours and eventually impact the companion star. As a result, the early supernova light curve can be brightened by the collision of the supernova ejecta with the companion star (Kasen 2010; Moriya et al. 2015; Kutsuna & Shigeyama 2015; Liu et al. 2015). Also, the companion star may be significantly heated and shocked by the SN impact, causing the envelope of the companion star to be partially removed due to the stripping and ablation mechanism (Wheeler et al. 1975; Fryxell & Arnett 1981; Taam & Fryxell 1984). Many numerical simulations of collisions of SN ejecta with the companion star in single-degenerate Type Ia SNe have been carried out by different groups (Wheeler et al. 1975; Taam & Fryxell 1984; Marietta et al. 2000; Pakmor et al. 2008; Liu et al. 2012, 2013b; Pan et al. 2010, 2012b). All these studies suggest that about 2–30% of the companion mass, or almost the whole envelope of the companion star (depending on its structure), is removed by the SN impact. Nondegenerate companion stars are expected to survive the impact of the SN explosion and show some peculiar properties, such as high runaway velocities, overluminosity, and probably enrichment in heavy elements, which may be identified by observations.
Whereas simulations of Type Ia SNe are generally performed based on a fixed (or small range of) explosion energy, Eej, and a fixed ejecta mass, Mej, CCSNe can have a large spread in Eej and Mej. Hirai et al. (2014) carried out two-dimensional impact simulations to investigate the collision of CCSN ejecta with a 10 M⊙ giant star companion. However, most companion stars to CCSNe are on the main sequence (MS) at the moment of first SN explosion in a binary system (see Kochanek 2009, and also our population synthesis calculations in Sect. 4.4).
In this work, we perform impact simulations using a three-dimensional (3D) smoothed particle hydrodynamics (SPH) method to systematically study, for the first time, the impact of CCSN ejecta on MS companion stars. In Sect. 2, we describe the methods and initial models used in this work. Our impact simulations are presented in Sect. 3, and a parameter survey and a detailed discussion follow in Sect. 4. Our conclusions are summarized in Sect. 5.
2. Numerical methods and models
In this section, we introduce the codes and methods used in this work, and we construct the initial companion star models and SN ejecta models. Also, initial conditions and setup of our hydrodynamical impact simulations are described in detail.
2.1. Numerical codes
To construct the detailed structure of the companion star at the moment of the CCSN explosion, we use the one-dimensional (1D) implicit Lagrangian stellar evolution code BEC (Langer 1991, 1998; Yoon et al. 2006, 2012), which solves the hydrodynamic stellar structure and evolution equations (Kippenhahn & Weigert 1990). A recent description of the updated code is found in Yoon et al. (2006, 2010). In our default models we assume a mixing-length parameter α = l/HP = 1.5 (Langer 1991) and a core convective overshooting parameter of δov = 0.10. We evolve stars with a given mass and solar metallicity (Z = 0.02) to construct 1D stellar models for our subsequent impact simulations.
In our hydrodynamical simulation of the collision of the SN ejecta on the binary companion star, we use the 3D smoothed particles hydrodynamics (SPH) code Stellar GADGET (Pakmor et al. 2012). An advantage of applying SPH for the problem under investigation is that no material leaves the computational domain, and also that momentum, energy, and angular momentum are strictly conserved. The GADGET code (Springel 2005) was originally intended for cosmological simulations, but it has been modified by Pakmor et al. (2008, 2012) for stellar astrophysics problems (Pakmor et al. 2008; Liu et al. 2012). As mentioned above, several studies have successfully used the Stellar GADGET code to investigate the SN impact on the companion star in single-degenerate SNe Ia (Pakmor et al. 2008; Liu et al. 2012, 2013c,b,a). In particular, Pakmor et al. (2008) have shown that the SPH-based approach reproduces previous results obtained with a grid-based 2D scheme by Marietta et al. (2000). This shows that the SPH approach with the Stellar GADGET code captures the main dynamical effects of the collision between SN ejecta and its companion star.
2.2. Binary companion star models
The maximum possible runaway velocities for MS HVSs ejected from disrupted binaries in asymmetric SN explosions have been investigated by Tauris (2015). In their systematic Monte Carlo simulations of SN-induced HVSs, they chose to focus on MS companion stars with masses M2 = 0.9 M⊙ and 3.5 M⊙. This selection is based on observations of the main class of HVSs (G/K-dwarf, Brown et al. 2005, 2009, 2012, 2014) and the recently discovered late-type B-star HVS candidates (Palladino et al. 2014). In this work, the same two companion stars used in Tauris (2015) are used in our impact hydrodynamical simulations. Using BEC, we evolved zero-age main-sequence (ZAMS) stars of these two masses to an age of about 6 Myr, roughly the lower limit of their expected age when their massive companion star explodes. The structure profiles of these two companion stars at the moment of the SN explosion are shown in Fig. 1.
2.3. The supernova model
To introduce a SN explosion, we adopt a simple analytical explosion ejecta model which is constructed based on numerical simulations of SN explosions by Matzner & McKee (1999). We assume that the SN ejecta is already in homologous expansion, whereby the radius of a fluid element is given by r = vejt, where vej is the expansion velocity, and t is the time since the explosion. The density profile of the expanding SN ejecta, ρej(vej,t), is described by a broken power law, ρej ∝ r− n for the outer part of the SN ejecta and ρej ∝ r− δ for the inner part of the SN ejecta, as follows (Kasen 2010; Moriya et al. 2013): ![\begin{equation} \label{eq:1} \small \rho_{\rm{ej}}(v_{\rm{ej}},{\it t}) = \left\{ \begin{array}{lll} \displaystyle \frac{1}{4\pi(n-\delta)} \frac{[2(5-\delta)(n-5)\,E_{\rm{ej}}]^{(n-3)/2}}{[(3-\delta)(n-3)\,M_{\rm{ej}}]^{(n-5)/2}}\,t^{-3}\,v_{\rm{ej}}^{-n} & (v_{\rm{ej}}>v_{{t}}), \\ & & \\ \displaystyle \frac{1}{4\pi(n-\delta)} \frac{[2(5-\delta)(n-5)\,E_{\rm{ej}}]^{(\delta-3)/2}}{[(3-\delta)(n-3)\,M_{\rm{ej}}]^{(\delta-5)/2}}\,t^{-3}\,v_{\rm{ej}}^{-\delta} & (v_{\rm{ej}}<v_{{t}}), \end{array} \right. \end{equation}](/articles/aa/full_html/2015/12/aa26757-15/aa26757-15-eq23.png) (1)where Eej and Mej are the SN explosion energy and SN ejecta mass, respectively, and
(1)where Eej and Mej are the SN explosion energy and SN ejecta mass, respectively, and ![\begin{equation} \label{eq:2} v_{{t}} =\left [\frac{2(5-\delta)(n-5)\,E_{\rm{ej}}}{(3-\delta)(n-3)\,M_{\rm{ej}}}\right]^{1/2}\cdot \end{equation}](/articles/aa/full_html/2015/12/aa26757-15/aa26757-15-eq26.png) (2)In SNe Ib/c, typically n ≃ 10 and δ ≃ 1 (Matzner & McKee 1999), and we adopt these to construct a homologously expanding SN ejecta model based on the above Eqs. (1) and (2). Ideally one should start from a detailed simulation of the collapse of the exploding star, however, we limit ourselves to exploring the basic processes during the SN impact. A more realistic SN explosion model from hydrodynamical simulations may slightly change our numerical results. However, detailed parameter surveys are addressed in Sect. 4 to mimic different SN ejecta models, and, therefore, we do not expect a significant change in our main conclusions.
(2)In SNe Ib/c, typically n ≃ 10 and δ ≃ 1 (Matzner & McKee 1999), and we adopt these to construct a homologously expanding SN ejecta model based on the above Eqs. (1) and (2). Ideally one should start from a detailed simulation of the collapse of the exploding star, however, we limit ourselves to exploring the basic processes during the SN impact. A more realistic SN explosion model from hydrodynamical simulations may slightly change our numerical results. However, detailed parameter surveys are addressed in Sect. 4 to mimic different SN ejecta models, and, therefore, we do not expect a significant change in our main conclusions.
The CCSN explosion energy (Eej = 1.0−8.0 × 1051erg), the amount of mass ejected (Mej = 0.7−5.0M⊙), and the pre-SN orbital separation (a = 1.0−6.0amin) are treated as free parameters (amin is defined below).
 |
Fig. 1 Profiles of mass density ρ, temperature T, and hydrogen abundance XH as a function of M(r) /M2 for a 0.9 M⊙ G/K-dwarf (red solid lines) and a 3.5 M⊙ late-type B-star (blue dashed lines) companion star model at the moment of the CCSN explosion. Here, M(r) is the mass enclosed within radius r, M2 is the total mass. |
2.4. Initial setup
Our basic setup and initial conditions for the impact simulations are similar to those of Liu et al. (2012, 2013c,a). We use the healpix method described in Pakmor et al. (2012) to map the profiles of density and internal energy of a 1D companion star model to a particle distribution suitable for the SPH code (Liu et al. 2013a). Before we start the actual impact simulations, the SPH model of each companion star is relaxed for ten dynamical timescales (tdyn = (Gρ)−1/2/2) to reduce numerical noise introduced by the mapping. If the relaxation succeeds, the velocities of the particles stay close to zero. Otherwise, we reject the SPH model and redo the relaxation after adjusting the relaxation parameters (Pakmor et al. 2012). We use 6 × 106 SPH particles to represent the B-type star or G/K-dwarf companion star.
The SN ejecta model described above is placed at a distance larger than amin from the companion star in the x − y plane. A star in a binary cannot be closer to its companion than the Roche-lobe radius because mass transfer would result. We therefore use the Roche-lobe radius of MS companion star (Eggleton 1983) to set the minimum possible separation amin in our systems (Tauris 2015), 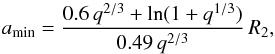 (3)where q is the mass ratio between the companion star (M2) and the exploding star (MHe), i.e. q = M2/MHe, and R2 is the radius of the companion star (Eggleton 1983). As a consequence, the minimum orbital separations between the exploding star and our companion stars are 2.74 R⊙ (G/K-dwarf companion) and 5.56 R⊙ (late-type B-star companion), corresponding to amin = 3.55R2 and amin = 2.55R2, respectively. We assume that the exploding star is an evolved helium star of a mass MHe = 3.0M⊙ which corresponds to a SN ejecta mass of ≈1.4M⊙ with the formation of a NS with a gravitational mass of ≈1.4M⊙, given that about 0.2M⊙ is released by neutrinos from lost gravitational binding energy during the explosion. The impact of the SN ejecta on the binary companion is simulated for more than 6000 s, at which point the amount of mass removed from the companion envelope and its resulting impact velocity have converged (Fig. 3).
(3)where q is the mass ratio between the companion star (M2) and the exploding star (MHe), i.e. q = M2/MHe, and R2 is the radius of the companion star (Eggleton 1983). As a consequence, the minimum orbital separations between the exploding star and our companion stars are 2.74 R⊙ (G/K-dwarf companion) and 5.56 R⊙ (late-type B-star companion), corresponding to amin = 3.55R2 and amin = 2.55R2, respectively. We assume that the exploding star is an evolved helium star of a mass MHe = 3.0M⊙ which corresponds to a SN ejecta mass of ≈1.4M⊙ with the formation of a NS with a gravitational mass of ≈1.4M⊙, given that about 0.2M⊙ is released by neutrinos from lost gravitational binding energy during the explosion. The impact of the SN ejecta on the binary companion is simulated for more than 6000 s, at which point the amount of mass removed from the companion envelope and its resulting impact velocity have converged (Fig. 3).
3. Hydrodynamical results
In this section, our impact simulations of a G/K-dwarf companion star model (M2 = 0.9 M⊙) with an initial binary separation of a = 5.48 R⊙ (≈7.1R2 ≈ 2.0 amin) are chosen as an example. The detailed evolution of the companion star during the impact of the SN ejecta is qualitatively described. Under the assumption of homologous expansion, a typical SN ejecta model in our simulation is constructed according to Eqs. (1) and (2), with Eej = 1.0 × 1051 erg and Mej = 1.4 M⊙. The maximum velocity at the ejecta front is set large enough (≈30 000 km s-1) that the assumed Eej is actually contained in the ejecta.
Resolution test for a G/K-dwarf companion model.
 |
Fig. 2 Amount of mass removed from the companion star as a function of time in the impact simulation of a G/K-dwarf companion (M2 = 0.9 M⊙, a = 5.48 R⊙ ≈ 7.1R2) with different resolutions, i.e., different total numbers of SPH particles in the simulation (Table 1). The standard resolution used in our simulation is highlighted in red. |
3.1. Resolution test
To assess the reliability of our numerical results, we have performed a convergence test to check the sensitivity of our results to different resolutions by varying the particle numbers from 5000 to 6 × 106 in the companion star (Table 1). Because all our SPH particles have the same mass, the number of SPH particles representing the SN ejecta is fixed once the SPH companion model is created.
The amount of removed companion mass as a function of time in our impact simulations on a G/K-dwarf companion star model (a = 5.48 R⊙) with different resolutions is shown in Fig. 2. To calculate the amount of mass removed (evaporated) from the companion star by the SN impact, we sum over the masses of all unbound SPH particles (stripped+ablated particles) that originally belonged to it. Whether or not a particle is bound to the star is determined by calculating its total energy, Etot = Ekin + Epot + Ein, where Ekin, Epot and Ein are the kinetic energy (positive), potential energy (negative) and internal energy (positive), respectively. If Etot> 0, the particle is unbound. The center-of-mass motion of the star is subtracted when calculating the kinetic energy of each particle. To make the difference between the results obtained with particle numbers above 2 million better visible, only the results with a resolution ranging from about 1.3 × 105 to 1.5 × 107 SPH particles are plotted in Fig. 2. The difference in removed companion mass between simulations with 5.1 × 106 (the solid line) and 1.0 × 107 (the dash-dotted line) SPH particles is smaller than 4%, the difference between 1.0 × 107 and 1.5 × 107 (the dotted line) SPH particles is less than 2% (Table 1). We find that the amount of removed companion mass (ΔM2), the impact velocity (vim) and the amount of accreted ejecta mass (ΔMacc) are sufficiently converged (Table 1) when using more than 4 × 106 SPH particles to represent the companion star and we thus settle on the number 6 × 106 (which corresponds to a total of about 107 particles in the simulation). The mass of a single particle, MSPH, is then ≈10-6−10-7M⊙.
3.2. Description of evolution during/after SN ejecta impact
Figure 4 demonstrates the typical evolution of the gas density in the orbital plane in our impact simulation of a 0.9 M⊙ G/K-dwarf companion model with an initial binary separation of 5.48 R⊙ ≈ 7.1R2. The basic impact processes are quite similar to previous hydrodynamical simulations with a MS donor model in normal SNe Ia (Liu et al. 2012; Pan et al. 2012b).
At the beginning of the simulation, the MS companion star is in equilibrium (Fig. 4a). The SN explodes on the right side of the companion star, the SN ejecta expands freely for a while and hits the MS companion star, removing H-rich material from its surface through stripping (momentum transfer) and ablation (SN shock heating). The latter is caused by a bow shock propagating through the star, leading to internal heating and additional loss of mass from the far side of the companion star (Fig. 4e).
 |
Fig. 3 Amount of mass removed from the companion star (top panel) and the impact velocity caused by the SN ejecta (bottom panel) as a function of time after the SN explosion in our impact simulations of a G/K-dwarf companion (M2 = 0.9 M⊙) with an initial binary separation of a = 5.48 R⊙ ≈ 7.1R2 ≈ 2.0amin. Here, amin is the minimum possible separation of the binary system. |
In the final snapshot (t = 5000s), all removed companion material caused by the SN impact is largely embedded in a low-velocity SN debris behind the companion star. At the end of the simulation, we calculate the amount of removed companion mass, ΔM2 ≈ 0.0055 M⊙. Mass loss caused by the SN impact reaches a steady state by the end of the simulation, we therefore do not expect any further loss (Fig. 3). In Fig. 3, a small peak of the removed mass is seen in the early phase after the SN ejecta hits the companion star. This is because a shocked particle in the center of the star can have a larger kinetic than potential energy when the shock wave passes through the star. However, it is not able to leave the star and soon loses its kinetic energy to some neighbor particles and therefore becomes bound again.
Despite the fact that the kinetic energy of the SN ejecta incident upon the companion star is much greater than the total binding energy of this star, the star survives the impact because energy is deposited in only a small fraction of the stellar mass and excess energy is redirected into kinetic energy of the expelled material (Fryxell & Arnett 1981; Taam & Fryxell 1984). However, the companion star receives linear momentum and hence a resulting impact velocity because of the collision with the SN ejecta, causing the star to move in the same direction as the SN ejecta with a speed of ≈22 km s-1. Furthermore, the surviving companion star is forced out of thermal equilibrium by internal heating from the passing shock wave. Hence it is expected that it remains bloated on a thermal timescale (up to tens of Myr) after the SN explosion (cf. Sect. 4.5). To illustrate how the supernova ejecta are mixed with the removed companion material after the SN explosion, the amount of material that originally belonged to the companion star is shown relative to the total amount of material for the simulation of a G/K-dwarf companion star model in Fig. 5. It is evident that most of the removed companion material is confined to the downstream region behind the companion star, creating a hole in the SN ejecta with an opening angle of ≈30° with respect to the x-axis in our simulation.
Qualitatively, the impact proceeds in the same way in all our simulations. The numbers given above are derived in the special case of a simulation using Eej = 1.0 × 1051erg. However, as we demonstrate systematically below, increasing the explosion energy enhances the effects of the SN ejecta impact.
3.3. Impact velocity of the companion star
The impact velocity kick (up to about 100km s-1, cf. Sect. 4), which the companion star receives as a consequence of absorption of linear momentum from the SN ejecta, is in the orbital plane and opposite to the direction to the exploding star. Although this impact velocity is small compared to the pre-SN orbital velocity of the companion star, it increases the probability of disrupting the binary system and, in that case, also contributes (although with a relatively small amount) to the escape velocity of the ejected star (Tauris & Takens 1998; Tauris 2015). In addition, this impact velocity affects the eccentricity of the binary system if it survives the SN explosion.
The symmetry-breaking effect of orbital motion is ignored in our impact simulations because the orbital and spin velocities of the companion stars are much lower than the typical ejecta expansion velocity of a few 104 km s-1. We expect that some small morphological differences, such as the post-impact density distribution of all removed companion material and SN ejecta, would be seen if the orbital motion of the companion star is included, but it should not affect the basic results presented in this work (see also Liu et al. 2013b).
 |
Fig. 4 Density distributions of all gas material as a function of the explosion time in the impact simulations for a G/K-dwarf companion model (M2 = 0.9 M⊙) with a binary separation of 5.48 R⊙ (=7.1R2). The direction of motion of the incoming SN shell front is from right to left (see arrow symbols). The impact is initiated at t ≈ 100s after the explosion. The color scale shows the logarithm of the mass density in g cm-3. |
3.4. Contamination from the SN ejecta
After the interaction with the SN ejecta, the envelope of the companion star may be enriched by heavy elements from the SN ejecta while part of its H-rich material is stripped off by the SN impact. As a consequence, a surviving companion star may show unusual chemical signatures compared to a normal MS star, in case a significant amount of SN-ejecta material is accumulated onto it. These chemical peculiarities, if detected, can potentially differentiate between SN-induced HVSs from HVSs ejected from the Galactic center (Hills 1988) or from dense stellar clusters by dynamical interactions (Leonard 1991). Possibly even the explosion mechanism (thermonuclear vs. CCSN) could be determined for these chemically enriched HVSs (Schaffenroth et al. 2015).
In our hydrodynamical simulations, we trace at every timestep all bound particles that originally belonged to the SN ejecta after the explosion. It takes some time (about 4000 s in our typical G/K-dwarf companion model) for this captured ejecta material to settle onto the surface of the companion star. At the end of the simulations, the amount of ejecta mass accreted onto the surface of the surviving companion star remains at a (roughly) constant value. In our example model (Fig. 4), we find a total ejecta mass of ~10-3M⊙ is accumulated onto the surface of the companion star at the end of the simulation compared to the removal of 5.5 × 10-3M⊙ of H-rich material. Unfortunately, we cannot provide detailed information of the chemical elements of the SN ejecta material that accumulate onto the surface of the star. This is because in our simulations only a simple ejecta model is constructed according to Eqs. (1) and (2), without any information about the chemical composition the ejecta material.
From our simulations, we find that most of the contamination is attributed to particles with low expansion velocity in the SN ejecta, i.e. the innermost region of the SN ejecta model (Liu et al. 2013a). This is explained by the lower kinetic energy of those particles which makes it easier to accrete onto the surface of the companion star after the momentum transfer. Therefore, we argue that the composition of the ejecta material that pollutes the companion star is sensitive to the nuclear burning at the center of the explosion. Based on CCSN modeling (e.g., Nomoto et al. 2006), we expect a potentially observable chemical enrichment of Fe, Si, and possibly Ca (e.g., Schaffenroth et al. 2015; Sabach & Soker 2015), if mixing processes (e.g., Stancliffe et al. 2007; Stancliffe & Glebbeek 2008) are not efficient on a long timescale. Simulations with a more detailed model of the exploding star are needed to address the issue of chemical contamination in a future study.
In addition, we point out that the SPH method suppresses hydrodynamical instabilities seen in grid-based simulations, which may affect the estimated contamination from SN ejecta. However, earlier impact simulations with the same SPH approach (Liu et al. 2013c) and 3D grid-based simulations (Pan et al. 2012b) found the same order of magnitude in the amount of nickel contamination on a He star donor from SN Ia ejecta. This indicates that the degree of instability captured in our SPH method is sufficient for our study, or these instabilities may not play an important role in determining the amount of accreted SN ejecta in the simulation. This, however, should be tested in more detailed future studies.
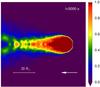 |
Fig. 5 Mass fraction of companion material in the SN ejecta in our simulation of the G/K-dwarf companion star model with a binary separation of 5.48 R⊙ (=7.1R2). The purple end of the color scale corresponds to pure SN ejecta material, while the red end of the color scale represents pure companion material. |
4. Discussion
The kinetic energy, mass of the SN ejecta, the separation between the exploding star and its companion, and the structure of the companion star at the time of the explosion are expected to be four major physical parameters of the progenitor system that influence the dynamics of the SN ejecta impact on the companion star. Different binary systems evolve to various evolutionary stages and have distinct binary parameters when the SN explodes. Consequently, some properties of the companion star and the binary system differ significantly from our example models. For instance, the binary separation (a), the mass of the exploding star (MHe, which leads to different ejecta masses), and the structure (mass, M2, and radius, R2, and thus density profile) of the companion star at the moment of the SN explosion, are all expected to be different in various binary systems.
In this section, we treat the binary separation (a) at the time of the explosion, the ejecta mass (Mej), or the SN explosion energy (Eej), as independent physical parameters, and we carry out a parameter survey to investigate the dependence of our numerical results on these parameters. Predictions from our population synthesis calculation are also discussed.
4.1. Binary separation dependency
To test the influence of the ratio of binary separation to the companion star radius, a/R2, we adjust the binary separation for a given companion star model. A fixed SN explosion model with an ejecta mass Mej = 1.4 M⊙ and an explosion energy Eej = 1.0 × 1051 erg is used to model the SN event.
 |
Fig. 6 Total removed companion mass (left panel), resulting impact velocity of the companion star (middle panel) and the amount of accreted contamination from the SN ejecta (right panel), as a function of initial binary separations for a G/K-dwarf (square symbols, M2 = 0.9 M⊙ and R2 ≈ 0.77 R⊙) and a late-type B-star (filled circle symbols, M2 = 3.5 M⊙ and R2 ≈ 2.18 R⊙) companion model. The results of our example model (Sect. 3) are shown with red filled square symbols. Power-law fits are also presented in each panel. |
Figure 6 shows the effects of varying the orbital separation parameter a/R2, by a factor of about 6, on the total amount of removed companion mass (ΔM2), the resulting impact velocity (vim), and total accumulated ejecta mass (ΔMacc), for the 0.9 M⊙ and 3.5 M⊙ companion star models. It shows that all three quantities decrease when increasing the orbital separation of the pre-SN binary. For instance, ΔM2 decreases by a factor of almost 10 as the parameter a/R2 increases by a factor of 2. The relations can be approximately fitted with power-law functions (Fig. 6), which are consistent with previous impact simulations of thermonuclear (Ia) SNe (e.g., Marietta et al. 2000; Pakmor et al. 2008; Liu et al. 2012; Pan et al. 2012b) and CCSNe with a red giant companion star (Hirai et al. 2014).
A more careful inspection of Fig. 6 shows that the decrease in ΔM2 weakens systematically as the binary separation increases to be large, so systems with a/R2 ≳ 8 deviate slightly from the power law. This indicates that the detailed interactions are possibly more complex. For example, the amount of evaporated companion star material, and the accreted (bound) SN ejecta mass, may be poorly determined at long orbital separation because numerical difficulties were encountered when the removed mass (or accreted SN ejecta mass) is very small, i.e., when only a small number of SPH particles are involved. Furthermore, it cannot be ruled out that the impact simulation process also depends on the time evolution of the density of the SN ejecta hitting the star. However, we do not expect these uncertainties to strongly affect our basic results and conclusions, and the power-law fits presented here are fairly good approximations for the full range of a/R2.
4.2. SN explosion energy dependency
The influence of the SN explosion energy on the ejecta interaction with the companion is studied on the basis of our G/K-dwarf companion star model with a ≈ 5.48 R⊙ ≈ 7.1R2. All parameters but the SN energy are kept constant. With a fixed ejecta mass of Mej = 1.4M⊙, we create four different SN ejecta models, using Eqs. (1) and (2), with ejection energies (1.0−8.0) ×1051 erg (Taddia et al. 2015).
 |
Fig. 7 Total removed companion mass (ΔM2, in a unit of M2) as a function of the SN explosion energy for our 0.9M⊙ G/K-dwarf companion model. All parameters except the SN explosion energy are kept constant, meaning that we only change the SN explosion energy according to Eqs. (1) and (2). Thus, for a fixed initial binary separation of 5.48 R⊙ (2 amin) and a total ejecta mass of 1.4 M⊙, different SN explosion energies of (1.0, 4.0, 6.0, 8.0) × 1051 erg are investigated. The fitting function and fitting parameters are also shown. |
 |
Fig. 9 As Figs. 7 and 8, but as a function of the SN ejecta mass. All parameters (binary separation of 5.48 R⊙ and a SN explosion energy of 1.0 × 1051 erg) except the SN ejecta mass (Mej) are kept constant. Different values of Mej = 0.7, 1.4, 2.5, 4.0, and 5.0 M⊙ are applied. |
 |
Fig. 10 As Fig. 9, but for the amount of mass accreted from the SN ejecta (ΔMacc) as a function of the SN ejecta mass (Mej). |
 |
Fig. 11 Top: momentum within each velocity shell of initial SN ejecta as a function of ejecta velocity. Bottom: total momentum of outer SN ejecta within regions with ejecta velocities ≳5000, 6000, 7000, and 7500 km s-1. Different ejecta masses of Mej = 0.7, 1.4, 2.5, 4.0 and 5.0 M⊙ are applied. |
Numerical results for the total removed companion mass, ΔM2, the resulting impact velocity, vim, and total accreted mass from the SN ejecta (i.e., contamination), ΔMacc, are illustrated in Figs. 7 and 8 as a function of the SN explosion energy, Eej. The correlation between ΔM2 and Eej is, to a good approximation, linear (Fig. 7). As expected, ΔM2 increases with Eej. The behavior of both vim and ΔMacc are better described by power-law functions (Fig. 8). Whereas vim increases with Eej, ΔMacc is smaller at larger Eej.
4.3. SN ejecta mass dependency
To investigate the influence of the SN ejecta mass, Mej, on the outcome of the SN impact, (i.e., ΔM2, vim and ΔMacc) we vary the SN ejecta mass by fixing all other parameters, i.e., Eej = 1.0 × 1051 erg, a = 5.48 R⊙, and apply a maximum ejecta velocity ≈30 000 km s-1. Under these assumptions, five SN ejecta models with ejecta masses 0.7, 1.4, 2.5, 4.0, and 5.0 M⊙ are created using Eqs. (1) and (2).
Figures 9 and 10 show the effect of the varying SN ejecta mass on the interaction between the SN ejecta and the companion star for our 0.9M⊙ G/K-dwarf companion model. With our method for creating different SN explosion profiles, we find that the SN ejecta does not significantly affect ΔM2 (Fig. 9a). However, it is found that the impact velocity of the companion star (Fig. 9b) decreases nonmonotonically with increasing ejecta mass. This is a somewhat surprising and perhaps counterintuitive result given that for a fixed total kinetic energy, Eej = 1.0 × 1051 erg, the incident momentum (i.e., the momentum of the SN ejecta that hits the star) is expected to increase by a factor of 2.7 as the ejecta mass increases from 0.7 to 5.0 M⊙ (using Eej = p2/ (2Mej)). Therefore, the impact velocity of the star is expected to increase by a factor of about 2.7 by the analytic analysis of Wheeler et al. (1975), which is, however, not seen in our simulations. There are several reasons for this discrepancy between expected values from the analytic work and the results of our simulations. In Fig. 3, it is shown that the impact velocity of the star almost reaches a maxium value about 600 –700 s after the SN explosion. This suggests that the impact velocity of the star is mostly determined by the momentum transfer during the collisions with high-velocity ejecta at early-time phase. Late-time interactions between the SN ejecta and the star do not significantly increase the impact velocity further because the drag on the companion star is significantly reduced at the late-time phase (Fryxell & Arnett 1981), and the momentum transfer due to ablation (which is dominant at the late-time phase) is quite inefficient. In addition, the shape of the companion star is changing while its mass is being removed by the SN impact, which may reduce its cross-sectional area and thus reduce the momentum transfer and drag efficiency (Fryxell & Arnett 1981). All these effects were not included in the analytic calculations of Wheeler et al. (1975). Therefore, the impact velocity of the companion star is very sensitive to the total momentum of the very outer SN ejecta layers with high expansion velocities. We refer to Fryxell & Arnett (1981) for further detailed descriptions of the impact velocity of the companion star after the SN impact.
In Fig. 11a, we present the momentum within each spherical velocity shell of the initial SN ejecta as a function of ejecta velocity for different ejecta mass models. In addition, the total momenta of the outer SN ejecta regions with an expansion velocity in excess of 5000,6000,7000, and 7500 km s-1 are calculated for different ejecta mass models, respectively (Fig. 11b). Our ejecta model leads to most of the momentum being distributed in the inner part, i.e., low expansion velocity region, of the SN ejecta rather than in the outer part, i.e., high expansion velocity region, as we increase the SN ejecta mass (Fig. 11a). For example, as shown in Fig. 11b, the total momentum within a region with expansion velocities larger than 7000 km s-1 increases first, then decreases with the increase of the SN ejecta mass. This high-velocity part of the SN ejecta hits the star within ≲600 s after the explosion and is expected to be the main factor that determines the final impact velocity of the companion star (Fig. 3). Therefore, it is not surprising that the dependence of the impact velocity (vim) on the SN ejecta mass (Mej) in our simulations follows a pattern as shown in Fig. 9b, keeping in mind that the impact velocity of the star strongly depends on the momentum distribution of the outer part of the SN ejecta. Adopting a SN ejecta model that is different from ours is therefore expected to yield a change in the resulting impact velocity of the star.
As expected, ΔMacc increases with larger Mej and is approximately fitted by a power-law function (Fig. 10). As already mentioned in Sect. 3.4, most of the ejected material captured by the companion star comes from the innermost low-velocity part of the SN ejecta (Liu et al. 2013c). The enclosed mass of the low-velocity ejecta increases as Mej increases, which leads to more ejecta material being captured by the companion star after the momentum transfer.
4.4. Population synthesis predictions
To estimate the fraction of CCSNe in which light-curve brightening by the collision of SN ejecta with a stellar companion can be observed, Moriya et al. (2015) perform populations synthesis calculations for SNe with the binary_c/nucsyn code (Izzard et al. 2004, 2006, 2009). Under an assumption of a Galactic star formation rate of 0.68−1.45 M⊙ yr-1 and the average stellar mass of the Kroupa initial mass function (0.83 M⊙), the total CCSN rate of the Galaxy predicted from their population synthesis is 0.93−1.99 × 10-2 yr-1 (36% SNe Ib/c, 10% SNe IIb, 54% SNe II), consistent with the estimated Galactic CCSN rate of 2.30 ± 0.48 × 10-2 yr-1 from recent surveys (Li et al. 2011). In this section, we use the data from their population synthesis calculations directly to discuss the effects of an explosion on the companion star in SNe Ib/c. The basic parameters and assumptions in their calculations are summarized as follows. The initial mass function of Kroupa (2001) is applied in combination with a flat distribution of mass ratios (q = M2/M1) and the assumption of circular binary orbits. The stars have a metallicity Z = 0.02. The orbital period distribution follows that of Sana et al. (2012) for O-type primary stars in excess of 16 M⊙, Raghavan et al. (2010) for solar-like primary stars with a mass below 1.15 M⊙ and a fitting function interpolated linearly in primary mass between these two limiting masses. The common-envelope ejection efficiency is set to αCE = 1 and the envelope binding energy parameter, λ, is adapted from (Dewi & Tauris 2000, 2001; Tauris & Dewi 2001). Systems with primary masses 3−80 M⊙ and mass ratios between 0.1 M⊙/M1 and 1.0 are evolved with orbital periods between 0.1 and 1010 days.
Figure 12 presents the distributions of the companion mass and the ratio of binary separation to companion radius (a/R2) at the moment of the explosion for SNe Ib/c. Most SNe Ib/c have an orbital separation of ≳5.0R2, which is about a fraction of ≳95% in our binary population synthesis calculations. Furthermore, with the distributions of a/R2 in Fig. 12, we can simply estimate ΔM2, vim and ΔMacc by applying our power-law relationships stated in Fig. 6. Typically, we find that less than 5% of the companion mass is removed by the Type Ib/c SN impact and the star receives an impact velocity of only a few 10 km s-1. In addition, typically a few 10-3M⊙ of SN ejecta mass is found to accumulate onto its stellar surface after the SN impact.
 |
Fig. 12 Population synthesis distribution of the companion star mass (M2) as a function of the binary separation (a) in case the SN explodes as a Type Ib/c. Nothing is plotted in the regions with number fraction smaller than 10-3.5. |
The above results are rough estimates based on the power-law relationships obtained from our simulations for a G/K-dwarf and a late-type B companion star model (Fig. 6). However, different fitting parameters are found for these two companion stars, which indicates that the detailed structures of the companion star could affect our numerical results. Based on previous simulations (Liu et al. 2012) the fitting parameters are expected to change slightly for different companion structures. Nevertheless, we do not expect significant discrepancies because, according to our population synthesis, a major fraction of the companion stars (≳85%) are found to be in their MS phase when the Type Ib/c SNe occur.
4.5. Surviving companion stars
After the SN explosion, the binary system may be disrupted. As mentioned in Sects. 3.2 and 3.4, the companion stars surviving the SN explosion probably exhibit some peculiar luminosity and chemical signatures and may thus be identified (e.g., Pan et al. 2012a) if these companion stars are strongly impacted and significantly heated by the SN ejecta.
Figure 13 shows the mass density structures of surviving companion stars from our simulations of a late-type B-star companion model with different initial orbital separations. Again, we use the default SN ejecta model described in Sect. 4.1. At small orbital separations, the companion star is strongly impacted and heated by the passing shock wave and hence it is bloated after the SN impact (top-right panel of Fig. 13). As the orbital separation increases to ≈5 R2, the SN impact and heating of the companion star are reduced. Only a small amount of companion mass is removed and the SN heating is too inefficient to make the surviving companion star inflate by much (bottom row of Fig. 13).
Our population synthesis modeling suggests that most CCSNe (≳95%) occur in systems with an orbital separation larger than about 5.0 R2 (Sect. 4.4). We caution that there are large uncertainties in population synthesis studies, which may influence the results. In this case, these mainly relate to the input physics of common-envelope evolution and the subsequent Case BB RLO from the naked helium star prior to its explosion (Tauris & van den Heuvel 2006, and references therein). In addition, Fig. 12 shows that at the moment of SN explosion most companion stars have a higher mass than our 3.5 M⊙ late-type B-star companion. More massive stars have higher surface escape velocities and hence less companion mass is removed. Also, the fractional change in the internal stellar energy created by the shock wave is smaller because of higher internal energy in more massive stars. Consequently, if our population synthesis is correct, we do not expect that SN explosions significantly affect the detailed structures of companion stars in most CCSNe. This also implies that the effect on the post-impact evolution of the companion stars is not expected to be very dramatic. Therefore, some observable signatures, e.g., swelling and overluminosity, predicted for MS companions in SNe Ia systems are, in general, not expected to be seen dramatically to the same extent in SNe Ib/c and SNe IIb systems. The difference is caused by the pre-SN orbital separations, which are, in general, smaller in SNe Ia compared to SN Ib/c systems. Simulations of SNe Ia in the literature have been calculated with small binary separations, assuming that the companion stars fill their Roche-lobe radii at the time of the explosions (Liu et al. 2012; Pan et al. 2012b). Nevertheless, one should keep in mind that the ejected stars that become HVSs originate from the closest pre-SN orbits (Tauris 2015), hence, SN-induced HVSs could suffer from SN ejecta impact effects.
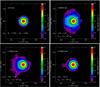 |
Fig. 13 Density distribution simulations of the companion star using a 3.5 M⊙ B-star MS model with different initial binary separations. Only the bound material that originally belonged to the companion star and final accreted ejecta are shown. The logarithm of density is color-coded. The top-left panel shows the initial configuration for all three cases. The motion of the incoming SN ejecta is from right to left. The following three panels (for initial orbital separations of a/R2 = 2.55, 5.10 and 10.20, respectively) show snapshots of the mass density at the moment that the removed companion mass, the resulting impact velocity, and the contamination from the SN ejecta, have converged to (almost) constant values. In the widest system (lower-left panel), the impacted star is not significantly inflated compared to its initial state before the SN impact. The white curves show constant density contours (log10ρ = −2.0). |
Hirai & Yamada (2015) studied SN ejecta-companion interactions for iPTF 13bvn and found that the companion star may expand extremely after the SN impact. They considered binary systems with a companion mass of M2 ≈ 7.0−8.0 M⊙ and an orbital separation ratio of a/R2 ≈ 20−30. This result is different from the predictions for these wide binary systems in our simulations. However, it is difficult to discuss the reasons that cause these differences because the descriptions of detailed hydrodynamical impact simulations in Hirai & Yamada (2015) are limited. If the companion stars in binaries evolve to be red giant stars at the moment of CCSN explosion, the effect of the explosion is much greater because of the significantly reduced binding energy of the companion envelope (Hirai et al. 2014). However, as we have argued here, the probability that companion stars are red giant stars at the moment of a SN explosion is relatively low (<15%).
Finally, for fixed values of Eej and Mej the calibrated fitting formulae for the removed mass or impact velocity in Appendix A of Tauris (2015), for a 1.0M⊙ MS star, are in good agreement with our hydrodynamical simulations for a 0.9M⊙ MS star, yielding similar values for ΔM2 and vim.
5. Summary and conclusions
We have investigated the impact of SN ejecta on the companion stars in CCSNe of Type Ib/c using the SPH code Stellar GADGET. We focused on 0.9 and 3.5M⊙ MS companion stars constructed with the BEC stellar evolution code. Our main results can be summarized as follows:
-
1.
The dependence of total removed mass (ΔM2) and resulting impact velocity (vim) on the pre-SN binary separation (a) can be fitted with power-law functions, which is consistent with previous work on SNe Ia. The amount of accreted SN ejecta mass (ΔMacc) is found to be dependent on a with a power-law relationship. All three quantities are shown to decrease significantly with increasing a, as expected.
-
2.
The relation between ΔM2 and the SN explosion energy (Eej) is linear. The quantities vim and ΔMacc can better be fitted with power-law functions and their values increase and decrease, respectively, with larger values of Eej.
-
3.
With a fixed value of Eej, the amount of SN ejecta mass (Mej) is found to not affect ΔM2 by much. However, more ejecta mass can be accumulated onto the companion star in simulations with larger value of Mej for a fixed value of Eej. The impact velocity, vim, is sensitive to the momentum profile of the outer SN ejecta. With our SN ejecta model, we find that the impact velocity, vim, decreases at larger Mej.
-
4.
Our population synthesis calculations predict that in most CCSNe less than 5% of the MS companion mass can be removed by the SN impact (i.e., ΔM2/M2< 0.05). In addition, the companion star typically receives an impact velocity, vim, of a few 10 km s-1, and the amount of SN ejecta captured by the companion star after the explosion, ΔMacc, is most often less than 10-3M⊙.
-
5.
Because a typical CCSN binary companion is relatively massive and can be located at a large pre-SN distance, we do not expect, in general, that the effects of the SN explosion on the post-impact stellar evolution will be very dramatic.
-
6.
In the closest pre-SN systems, the MS companion stars are affected more strongly by the SN ejecta impact, leading to ΔM2/M2 ≃ 0.10, vim ≃ 100km s-1 and ΔMacc ≃ 4 × 10-3M⊙, depending on the mass of the companion star. In addition, these stars are significantly bloated as a consequence of internal heating by the passing shock wave.
-
7.
It is possible that the SN-induced high velocity stars (HVSs), or more ordinary, less fast, runaway stars, may be sufficiently contaminated to be identified by their chemical peculiarity as former companion stars to an exploding star if mixing processes are not efficient on a long timescale.
Acknowledgments
We thank the anonymous referee for his/her valuable comments and suggestions that helped to improve the paper. We would like to thank Carlo Abate for helpful discussions. This work is supported by the Alexander von Humboldt Foundation. T.M.T. acknowledges the receipt of DFG Grant: TA 964/1-1. The work of F.K.R. is supported by the ARCHES prize of the German Federal Ministry of Education and Research (BMBF). T.J.M. is supported by Japan Society for the Promotion of Science Postdoctoral Fellowships for Research Abroad (26·51). R.J.S. is the recipient of a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation. R.G.I. thanks the AvH and Science and Technologies Research Council UK for his Rutherford Fellowship. Z.W.L. acknowledges the computing time granted by the Yunnan Observatories and provided on the facilities at the Yunnan Observatories Supercomputing Platform. The simulations were partially carried out using Supercomputing Platform of the Yunnan Observatories, Kunming, People’s Republic of China.
References
- Bersten, M. C., Benvenuto, O. G., Folatelli, G., et al. 2014, AJ, 148, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, F. B., Modjaz, M., Hicken, M., et al. 2014, ApJS, 213, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2005, ApJ, 622, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Geller, M. J., & Kenyon, S. J. 2009, ApJ, 690, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Geller, M. J., & Kenyon, S. J. 2012, ApJ, 751, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Geller, M. J., & Kenyon, S. J. 2014, ApJ, 787, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Y., Kasliwal, M. M., Arcavi, I., et al. 2013, ApJ, 775, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Livne, E., et al. 2011, MNRAS, 414, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2001, in Evolution of Binary and Multiple Star Systems, eds. P. Podsiadlowski, S. Rappaport, A. R. King, F. D’Antona, & L. Burderi, ASP Conf. Ser., 229, 255 [Google Scholar]
- Drout, M. R., Soderberg, A. M., Gal-Yam, A., et al. 2011, ApJ, 741, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Soderberg, A. M., Mazzali, P. A., & et al. 2013, ApJ, 774, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Tout, C. A. 2004, MNRAS, 353, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Fraser, M., Maund, J. R., & Smartt, S. J. 2015, MNRAS, 446, 2689 [NASA ADS] [CrossRef] [Google Scholar]
- Fremling, C., Sollerman, J., Taddia, F., et al. 2014, A&A, 565, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fryxell, B. A., & Arnett, W. D. 1981, ApJ, 243, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Groh, J. H., Georgy, C., & Ekström, S. 2013, A&A, 558, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
- Hirai, R., & Yamada, S. 2015, ApJ, 805, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Hirai, R., Sawai, H., & Yamada, S. 2014, ApJ, 792, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasen, D. 2010, ApJ, 708, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
- Kochanek, C. S. 2009, ApJ, 707, 1578 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kutsuna, M., & Shigeyama, T. 2015, PASJ, 67, 5414 [Google Scholar]
- Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, P. J. T. 1991, AJ, 101, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Chornock, R., Leaman, J., et al. 2011, MNRAS, 412, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z. W., Pakmor, R., Röpke, F. K., et al. 2012, A&A, 548, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Z.-W., Kromer, M., Fink, M., et al. 2013a, ApJ, 778, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z.-W., Pakmor, R., Röpke, F. K., et al. 2013b, A&A, 554, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Z.-W., Pakmor, R., Seitenzahl, I. R., et al. 2013c, ApJ, 774, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z.-W., Moriya, T. J., & Stancliffe, R. J. 2015, MNRAS, 454, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J., Bersier, D., James, P., et al. 2014, MNRAS, submitted [arXiv:1406.3667] [Google Scholar]
- Maeder, A., & Meynet, G. 2003, A&A, 411, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Maund, J. R., Smartt, S. J., Kudritzki, R. P., Podsiadlowski, P., & Gilmore, G. F. 2004, Nature, 427, 129 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Moriya, T. J., Maeda, K., Taddia, F., et al. 2013, MNRAS, 435, 1520 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Liu, Z.-W., & Izzard, R. G. 2015, MNRAS, 450, 3264 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1967, Acta Astron., 17, 355 [NASA ADS] [Google Scholar]
- Pakmor, R., Röpke, F. K., Weiss, A., & Hillebrandt, W. 2008, A&A, 489, 943 [Google Scholar]
- Pakmor, R., Edelmann, P., Röpke, F. K., & Hillebrandt, W. 2012, MNRAS, 424, 2222 [NASA ADS] [CrossRef] [Google Scholar]
- Palladino, L. E., Schlesinger, K. J., Holley-Bockelmann, K., et al. 2014, ApJ, 780, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2010, ApJ, 715, 78 [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012a, ApJ, 760, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012b, ApJ, 750, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Hsu, J. J. L., Joss, P. C., & Ross, R. R. 1993, Nature, 364, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabach, E., & Soker, N. 2015, ApJ, 806, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Schaffenroth, V., Przybilla, N., Butler, K., Irrgang, A., & Heber, U. 2015, ArXiv e-prints [arXiv:1501.07816] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Eldridge, J. J. 2009, MNRAS, 396, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Stancliffe, R. J., Glebbeek, E., Izzard, R. G., & Pols, O. R. 2007, A&A, 464, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E., & Fryxell, B. A. 1984, ApJ, 279, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Taddia, F., Sollerman, J., Leloudas, G., et al. 2015, A&A, 574, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauris, T. M. 2015, MNRAS, 448, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & Dewi, J. D. M. 2001, A&A, 369, 170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauris, T. M., & Takens, R. J. 1998, A&A, 330, 1047 [NASA ADS] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2006, Formation and evolution of compact stellar X-ray sources (Cambridge University Press), 623 [Google Scholar]
- Tauris, T. M., Langer, N., Moriya, T. J., et al. 2013, ApJ, 778, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Podsiadlowski, P. 2015, MNRAS, 451, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Lecar, M., & McKee, C. F. 1975, ApJ, 200, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Langer, N., & Weaver, T. A. 1993, ApJ, 411, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Dierks, A., & Langer, N. 2012, A&A, 542, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Profiles of mass density ρ, temperature T, and hydrogen abundance XH as a function of M(r) /M2 for a 0.9 M⊙ G/K-dwarf (red solid lines) and a 3.5 M⊙ late-type B-star (blue dashed lines) companion star model at the moment of the CCSN explosion. Here, M(r) is the mass enclosed within radius r, M2 is the total mass. |
| In the text | |
 |
Fig. 2 Amount of mass removed from the companion star as a function of time in the impact simulation of a G/K-dwarf companion (M2 = 0.9 M⊙, a = 5.48 R⊙ ≈ 7.1R2) with different resolutions, i.e., different total numbers of SPH particles in the simulation (Table 1). The standard resolution used in our simulation is highlighted in red. |
| In the text | |
 |
Fig. 3 Amount of mass removed from the companion star (top panel) and the impact velocity caused by the SN ejecta (bottom panel) as a function of time after the SN explosion in our impact simulations of a G/K-dwarf companion (M2 = 0.9 M⊙) with an initial binary separation of a = 5.48 R⊙ ≈ 7.1R2 ≈ 2.0amin. Here, amin is the minimum possible separation of the binary system. |
| In the text | |
 |
Fig. 4 Density distributions of all gas material as a function of the explosion time in the impact simulations for a G/K-dwarf companion model (M2 = 0.9 M⊙) with a binary separation of 5.48 R⊙ (=7.1R2). The direction of motion of the incoming SN shell front is from right to left (see arrow symbols). The impact is initiated at t ≈ 100s after the explosion. The color scale shows the logarithm of the mass density in g cm-3. |
| In the text | |
 |
Fig. 5 Mass fraction of companion material in the SN ejecta in our simulation of the G/K-dwarf companion star model with a binary separation of 5.48 R⊙ (=7.1R2). The purple end of the color scale corresponds to pure SN ejecta material, while the red end of the color scale represents pure companion material. |
| In the text | |
 |
Fig. 6 Total removed companion mass (left panel), resulting impact velocity of the companion star (middle panel) and the amount of accreted contamination from the SN ejecta (right panel), as a function of initial binary separations for a G/K-dwarf (square symbols, M2 = 0.9 M⊙ and R2 ≈ 0.77 R⊙) and a late-type B-star (filled circle symbols, M2 = 3.5 M⊙ and R2 ≈ 2.18 R⊙) companion model. The results of our example model (Sect. 3) are shown with red filled square symbols. Power-law fits are also presented in each panel. |
| In the text | |
 |
Fig. 7 Total removed companion mass (ΔM2, in a unit of M2) as a function of the SN explosion energy for our 0.9M⊙ G/K-dwarf companion model. All parameters except the SN explosion energy are kept constant, meaning that we only change the SN explosion energy according to Eqs. (1) and (2). Thus, for a fixed initial binary separation of 5.48 R⊙ (2 amin) and a total ejecta mass of 1.4 M⊙, different SN explosion energies of (1.0, 4.0, 6.0, 8.0) × 1051 erg are investigated. The fitting function and fitting parameters are also shown. |
| In the text | |
 |
Fig. 8 As Fig. 7, but for the resulting impact velocity (vim) and bound SN ejecta mass (ΔMacc). |
| In the text | |
 |
Fig. 9 As Figs. 7 and 8, but as a function of the SN ejecta mass. All parameters (binary separation of 5.48 R⊙ and a SN explosion energy of 1.0 × 1051 erg) except the SN ejecta mass (Mej) are kept constant. Different values of Mej = 0.7, 1.4, 2.5, 4.0, and 5.0 M⊙ are applied. |
| In the text | |
 |
Fig. 10 As Fig. 9, but for the amount of mass accreted from the SN ejecta (ΔMacc) as a function of the SN ejecta mass (Mej). |
| In the text | |
 |
Fig. 11 Top: momentum within each velocity shell of initial SN ejecta as a function of ejecta velocity. Bottom: total momentum of outer SN ejecta within regions with ejecta velocities ≳5000, 6000, 7000, and 7500 km s-1. Different ejecta masses of Mej = 0.7, 1.4, 2.5, 4.0 and 5.0 M⊙ are applied. |
| In the text | |
 |
Fig. 12 Population synthesis distribution of the companion star mass (M2) as a function of the binary separation (a) in case the SN explodes as a Type Ib/c. Nothing is plotted in the regions with number fraction smaller than 10-3.5. |
| In the text | |
 |
Fig. 13 Density distribution simulations of the companion star using a 3.5 M⊙ B-star MS model with different initial binary separations. Only the bound material that originally belonged to the companion star and final accreted ejecta are shown. The logarithm of density is color-coded. The top-left panel shows the initial configuration for all three cases. The motion of the incoming SN ejecta is from right to left. The following three panels (for initial orbital separations of a/R2 = 2.55, 5.10 and 10.20, respectively) show snapshots of the mass density at the moment that the removed companion mass, the resulting impact velocity, and the contamination from the SN ejecta, have converged to (almost) constant values. In the widest system (lower-left panel), the impacted star is not significantly inflated compared to its initial state before the SN impact. The white curves show constant density contours (log10ρ = −2.0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


